The Effect of Ca²⁺ and Mg²⁺ on the Dispersion and Flocculation Behaviors of Muscovite Particles

Abstract

The dispersion and flocculation behavior of muscovite suspensions in the presence of Ca²⁺ and Mg²⁺ are relevant for industrial processing of pre-concentrated muscovite from stone coal, a primary source of vanadium. In this study, the dispersion and flocculation behavior were investigated by means of sedimentation, zeta potential, and ion absorption experiments, as well as the force between particles and ion speciation calculations. The results indicated that the dispersion and flocculation behavior of muscovite particles without excess ions were in qualitative agreement with the classical DLVO theory. The muscovite particles aggregated mainly due to basal surface-edge interactions in acidic suspensions but were dispersed in alkaline suspension by electrostatic repulsion of the total particle surface. In acidic suspensions, the ability of muscovite to form dispersions of muscovite was increased with the decrease in the electrostatic attraction between the basal surface and the edge caused by the compression of the electric double layers withCa²⁺ and Mg²⁺. In alkaline suspension, the main adsorption form of Ca²⁺ and Mg²⁺ on muscovite surface was the ion-hydroxy complexes. The flocculation behavior of muscovite was affected by the static bridge effect of the ion-hydroxy complexes.

1. Introduction

Muscovite is the primary vanadium-bearing mineral in stone coal [1], which is an important resource of vanadium making up more than 87% of the domestic reserves of vanadium in China [2]. Hence, efficient processing methods of the vanadium-bearing stone coal has become increasingly important, and it has been confirmed that the pre-concentration of muscovite from the stone coal by roasting-flotation was an effective method [3]. Previous studies have found that the suspension produced by the roasted stone coal and water contain large quantities of metal ions and micro-fine particles. Metal ions and micro-fine particles can seriously reduce the separation efficiency of the pre-concentration of muscovite by flotation [3,4]. Hence, the removal of micro-fine particles has an important role in the pre-concentration steps of muscovite. Meanwhile, the effect of their removal depends on the dispersion and flocculation behavior of the specific minerals, so the study of the dispersion and flocculation behavior of muscovite is important.

The simplest framework to address the dispersion and flocculation behavior of minerals is the classical DLVO theory presented by Derjaguin, Landau, Verwey, and Overbeek [5]. The application of DLVO theory for fine particles and colloid has long been considered to be credible. This theory suggests that the total potential energy between charged interfaces is described as the sum of the Van der Waals attraction potential and the electrostatic potential. The strength of the Van der Waals attraction potential is related to the material itself and the distance between particles, but the roughness of the particle surface may also contribute [6,7]. The electrostatic potential is principally influenced by the surface charge density and the composition of ions in solution [8,9,10,11]. The surface charge determined the magnitude of this force, while multivalent metal ions may adsorb strongly to negatively charged interfaces, thereby reducing the magnitude of the potential [12,13,14].

Such interactions of metal ions adsorbed on the mineral surface have broad implications in mineral processing. The flotation of spodumene with fatty acid anionic collector can be implemented by adding Ca²⁺ and Fe³⁺ [15]. Ca²⁺ can render the positive charge of the surface of magnetite in the pH range from 3 to 10 and reduce the dispersion ability of silicates [16,17]. It was also evidenced that Ca²⁺ and Mg²⁺ can affect the surface properties of apatite, which can reduce the recovery of flotation [18,19]. Chlorite and lizardite, but also quartz, can be floated with xanthate in the pH range from 7 to 10 by adding Cu²⁺ and Ni²⁺ [20]. Cu²⁺ and Ca²⁺ can enhance the adsorption density of carboxymethyl cellulose (CMC) on the surface of chlorite [21]. It has been shown that Ca²⁺ and Mg²⁺ adsorbed on the surface of diaspore could cause the compression of the electric double layer, and result in the decrease of the repulsion force between diaspore particles [22,23]. Previous studies have found that the valence of cation plays a major role in the ability of dispersion of diaspore, kaolinite, illite, and pyrophyllite with sodium carbonate and sodium hexametaphosphate suspensions [24]. The mechanism of metal ion adsorption on the mineral surface has also been studied, relying mainly on a hydroxy complex hypothesis and surface precipitation theory. James and Hu et al. [25,26] suggest that the key form was the precipitate of metal hydroxide. Others studies have shown that the dominant species was the hydrolyzed metal ions. For high valence and small radius ions, like Fe³⁺, the dominant species would be in the form of hydroxide precipitate, i.e., Fe(OH)₃. While for the low valence and large radius ions, like Ca²⁺, the effective species would mainly be hydroxy complexes of the metal ions, i.e., Ca(OH)⁺ [27].

Previous studies have been based on the effect of metal ions on the flotation behavior of minerals, but very few studies have focused on the actual dispersion and flocculation properties. In this study, the dispersion and flocculation behavior of muscovite influenced by Ca²⁺ and Mg²⁺ were investigated. The objective was to improve understanding of the dispersion and flocculation behavior of muscovite and thus improve the effect of pre-concentration of vanadium-bearing muscovite.

2. Experimental Section

2.1. Materials

Natural pure muscovite was obtained from the town of Lingshou in Hebei province, China. The chemical composition of the sample is listed in Table 1, which is similar to the theoretical chemical composition of muscovite (SiO₂ 45.2%, Al₂O₃ 38.5%, K₂O 11.8%, H₂O 4.5%). The sample was hand-picked and ground to −25 µm in an agitating mill with a zirconia ball. The particle size of the sample was measured by BT-9300H laser particle size analyzer (Bettersize instruments Ltd., Dandong, China), and the result is given in Figure 1. The D90 is 21.69 μm and the average particle diameter is 10.75 μm. One fraction of the sample was further ground to about −5 µm by an agate mortar for zeta potential measurements. The Ca²⁺ and Mg²⁺ solutions were obtained from analytical reagents of CaCl₂ and MgSO₄ purchased from Sinopharm Chemical Reagent Co., Ltd. (Wuhan, China). HCl and NaOH were used for the pH adjustment of the suspension. The pH of the suspension was monitored using a digital pH meter. All experiments were carried out at room temperature of 22 ± 2 °C with deionized water.

Table 1. Chemical composition of pure minerals (wt %).

Chemical Composition	Na2O	MgO	Al2O3	SiO2	K2O	Fe2O3
Content	0.50	0.92	30.64	46.95	10.57	5.12

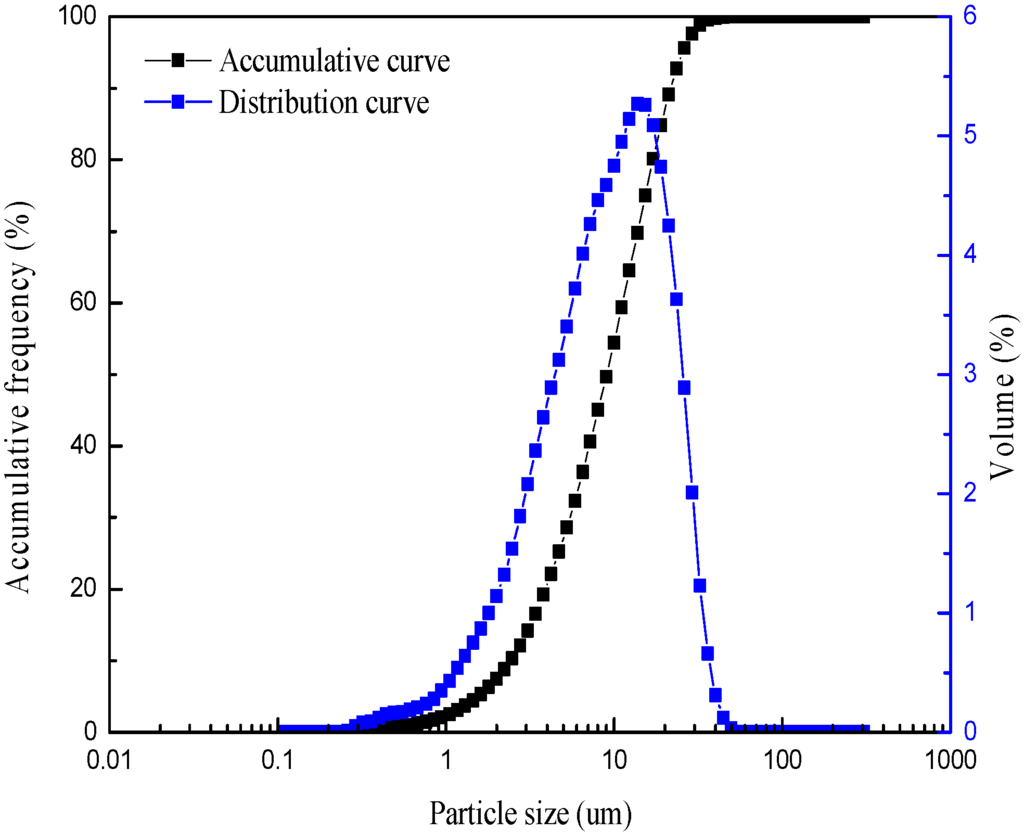
Figure 1. Particle size of the sample.

2.2. Methods

2.2.1. Sedimentation Test

To evaluate the dispersion properties, 2 g of muscovite was placed into a beaker with 50 mL of deionized water, agitated for 10 min in UP500HE ultrasonic oscillators (Leijunda Ultrasonic Electronic Equipment Ltd., Nanjing, China), and transferred into a 100-mL glass measuring cylinder. Metal ions and HCl or NaOH were added into the measuring cylinder with water up to 100 mL. The cylinder was turned upside down three times and was set aside for 10 min. The upper part, approximately 50% of the total volume, was siphoned out to a beaker for pH measurement. The sediment and the upper part were collected, dried, and weighed. The degree of dispersion (D) was calculated as

$$D=m_{sed}/(m_{susp}+m_{sed})\times 100\%,$$

(1)

where m_susp is the mass of the upper part, and m_sed is the mass of the sediment.

2.2.2. Zeta Potentials Measurement

The zeta potentials of the sample in the different suspension were measured by Zetasizer Nano ZS90 (Malvern Instrument Co., Malvern, UK). The sample (2 mg) was placed in 100 mL of deionized water, and the suspension was conditioned with Ca²⁺ or Mg²⁺ ions over the pH range from 2 to 12. An average zeta potential value of at least six individual measurements was recorded.

2.2.3. Calculation of Interfacial Energy between Particles

Based on the classical DLVO theory, the total potential energy is described as the sum of the Vander Waals attraction potential and the electrostatic potential [22].

$${{\displaystyle V}}_T={{\displaystyle V}}_W+{{\displaystyle V}}_S,$$

(2)

where V_W is the Van der Waals attraction potential and V_S is the electrostatic potential.

The DLVO theory can be used to model perfectly smooth surfaces of certain geometries (i.e., flat surfaces spheres, or cylinders). Here, the muscovite was assumed as spherical particle.

The Van der Waals attraction potential was calculated as

$${{\displaystyle V}}_W=-\frac{{{\displaystyle A}}_{131}}{6H}\times \frac{{{\displaystyle R}}_1{{\displaystyle R}}_2}{{{\displaystyle R}}_1+{{\displaystyle R}}_2},$$

(3)

where A₁₃₁ is the Hamaker constant, H is the distance between the particles, and R is the particle radius.

Meanwhile, the electrostatic potential was calculated as

$${{\displaystyle V}}_S=\frac{{\displaystyle \mathsf{\pi }\mathsf{\epsilon }}{{\displaystyle R}}_1{{\displaystyle R}}_2}{{{\displaystyle R}}_1+{{\displaystyle R}}_2}\left({{\displaystyle \mathsf{\varphi }}}_{01}^2+{{\displaystyle \mathsf{\varphi }}}_{02}^2\right)\left(\frac{2{{\displaystyle \mathsf{\varphi }}}_{01}{{\displaystyle \mathsf{\varphi }}}_{02}}{{{\displaystyle \mathsf{\varphi }}}_{01}^2+{{\displaystyle \mathsf{\varphi }}}_{02}^2}p+q\right);$$

(4)

$$p=\ln \left[\frac{1+\exp \left(-\mathsf{\kappa }H\right)}{1-\exp \left(-\mathsf{\kappa }H\right)}\right];\text{ and}$$

(5)

$$q=\ln \left[1-\exp \left(-2\mathsf{\kappa }H\right)\right],$$

(6)

where ϕ₀ is approximatively replaced the measured value of zeta potential, R is the particle radius, and the Debye length κ⁻¹ represents the thickness of the double layer. ε is the dielectric constant [28,29].

2.2.4. Adsorption Capacity Measurement

The concentration of Ca²⁺ and Mg²⁺ ions was measured by a Prodigy 7 inductively coupled plasma-optical emission spectrometer (Leeman Labs Inc., Hudson, NH, USA). Again, 2 g of muscovite was mixed with Ca²⁺ or Mg²⁺ ions (1 × 10⁻³ mol/L) in a suspension of 100 mL in a glass measuring cylinder, and HCl and NaOH were used for pH adjustment. The cylinder was turned upside down three times and set aside for 10 min. The solid particles were separated by centrifugation for 12 min with 2000 r/min, and the concentration of the Ca²⁺ or Mg²⁺ ions in the supernatant was measured. The amount adsorbed was calculated as

$$\Gamma =\frac{\left(C_0-C_{eq.}\right)}{m}V$$

(7)

where Γ is the unit mass mineral adsorption quantity, C₀ is the initial concentration of the ions, C_eq. is the ion concentration in the supernatant, V is volume (100mL), and m is the quality of muscovite.

3. Results and Discussion

3.1. Sedimentation Behavior of Muscovite

The sedimentation behavior of muscovite in deionized water, with and without the Ca²⁺ and Mg²⁺ ions, were investigated at different pH levels.

It can be seen from Figure 2 and Figure 3 that, in the absence of excess Ca²⁺ and Mg²⁺ ions, the sedimentation yield of the sample decreased with increasing pH, within a range from 1 to 6, after the yield was around 50% in a pH range from 6 to 12, indicating that the muscovite particles aggregated in an acidic solution and dispersed in alkaline suspension.

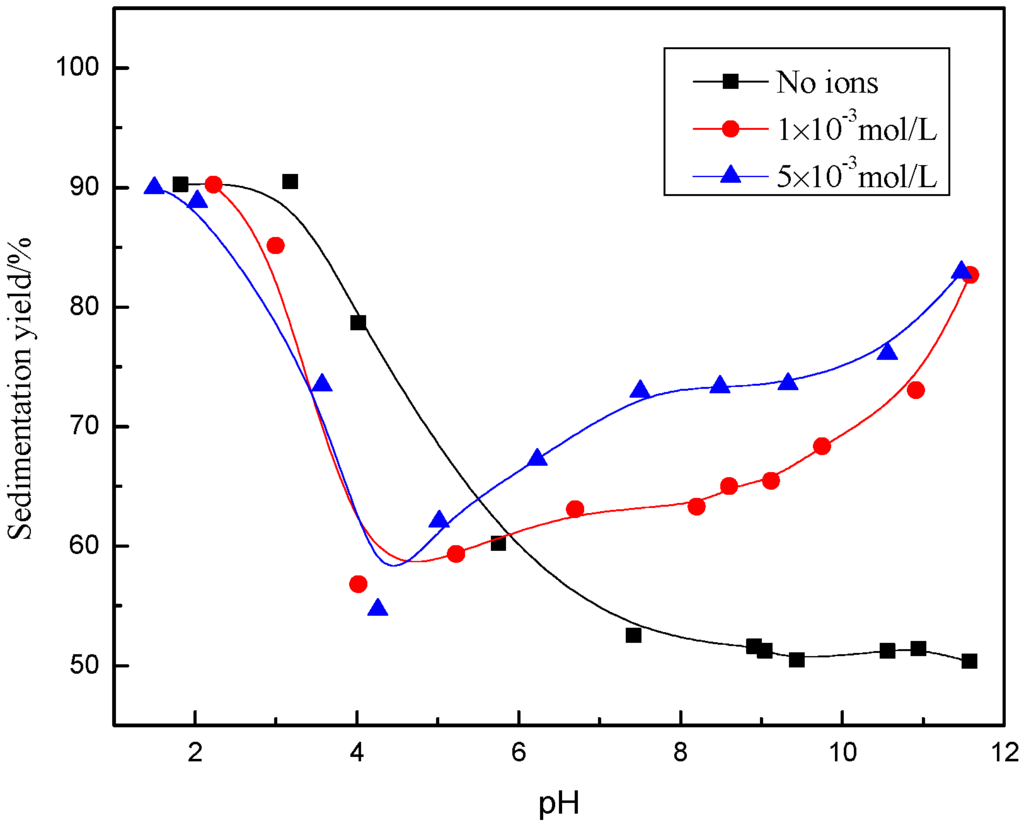
Figure 2. The effect of pH value on dispersion and flocculation of mineral with the presence of Ca²⁺.

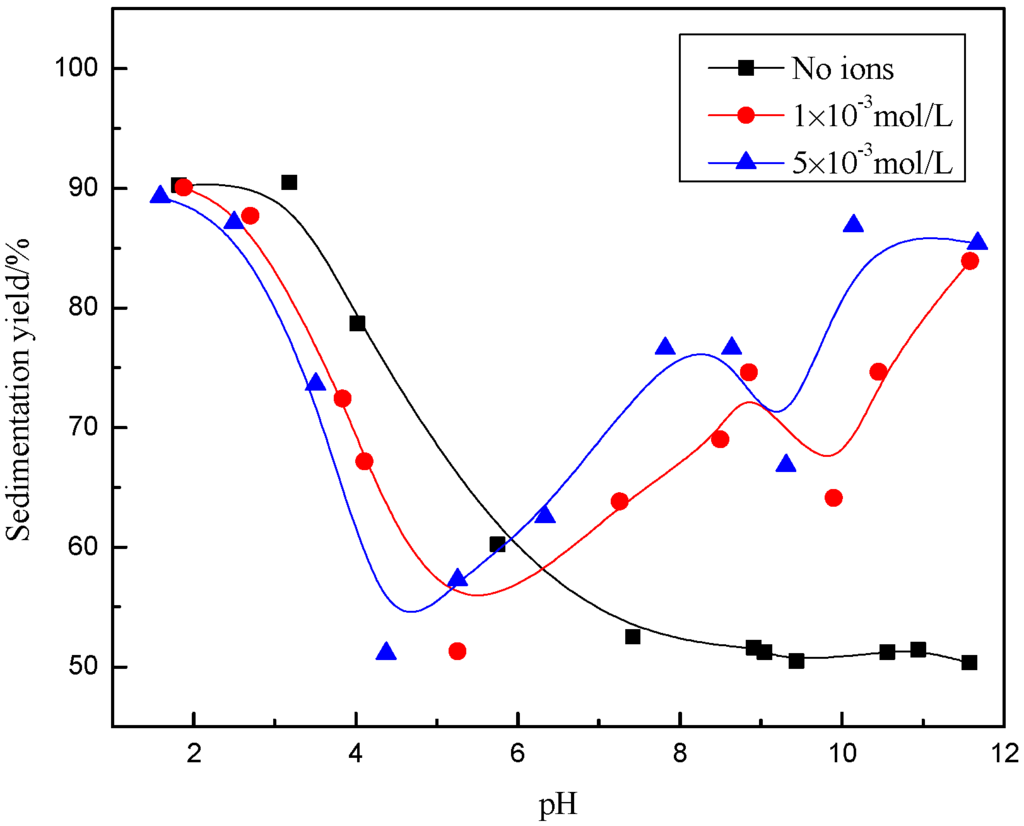
Figure 3. Effect of pH value on dispersion and flocculation of mineral with the presence of Mg²⁺.

In the presence of Ca²⁺ (Figure 2), the sedimentation yield decreased with increasing pH to a certain point and then increased again, with an inflexion point near pH = 4. The sedimentation yield decreased in pH range from 2 to 4 compared with no ions, which indicated that the flocculation behavior of muscovite was hindered by Ca²⁺. With pH being > 4, sedimentation yield increased as a function of pH, indicating that the flocculation of muscovite particles was caused by the addition of Ca²⁺. Increasing the concentration of Ca²⁺, the sedimentation yield basically remained unchanged in acidic suspension, but increased in alkaline suspension. With the presence of Mg²⁺ (Figure 3), the trend of sedimentation was basically similar to that with Ca²⁺. The difference was that the sedimentation yield increased first and decreased later at around pH = 9 with 1 × 10⁻³ mol/L Mg²⁺ and at around pH = 10 with 5 × 10⁻³ mol/L Mg²⁺.

3.2. Zeta Potential Analysis

Changes in the pH of suspensions can influence the surface properties of minerals [30]. Zeta potentials of muscovite as a function of pH in deionized water with and without Ca²⁺ and Mg²⁺ is presented in Figure 4. It can be seen that the zeta potentials of muscovite were negative over a wide range of pH from 2 to 14 and decreased with the increase in pH, which is consistent with previous studies [31,32,33]. The trend of the decreasing zeta potential with an increase in pH is similar to the presence of Ca²⁺ and Mg²⁺, but the absolute value of the potential was lower and found to decrease with increasing ion concentration. Surprisingly, in high alkaline suspension containing Mg²⁺, namely, when the pH range from 10 to 12, the negatively charged surface became positively charged.

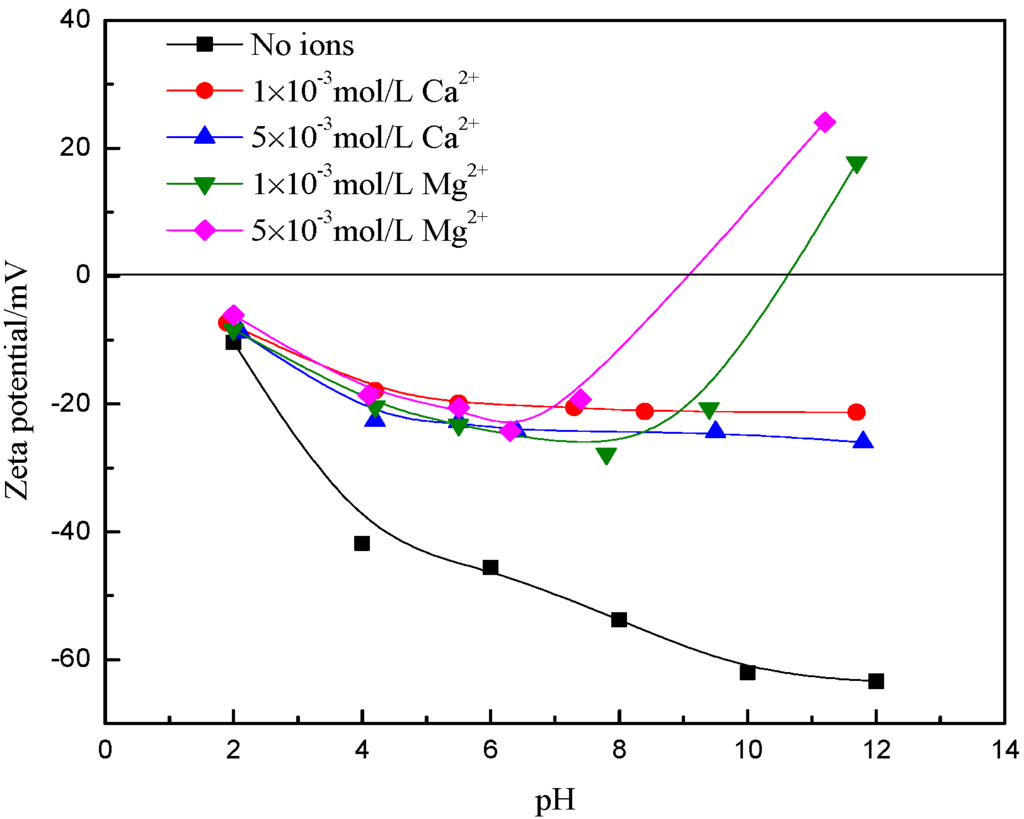
Figure 4. Zeta potentials of muscovite as a function of pH in deionized water with Ca²⁺ and Mg²⁺.

3.3. Calculation of Surface Energy of Particles Using Classic DLVO Theory

Assuming spherical particle geometry, the interaction energy values of the particles in the presence or absence of Ca²⁺ and Mg²⁺ was calculated according to the classical DLVO theory, with the results from the zeta potential measurements, and the Hamaker constant of A₁₃₁ = 2.2 × 10⁻²⁰ J, the dielectric constant of ε = 6.95 × 10⁻¹⁰ C²·J⁻¹·m⁻¹, κ = 0.104 nm⁻¹ [28,29], and R₁ = R₂ = 10.75/2 μm. As can be seen from the results in Figure 5, the energy barrier increased with increasing pH, so the ability to from a dispersion was improved with increasing pH, which was found to be consistent with the settling experiments. However, the presence of Ca²⁺ and Mg²⁺ can reduce the surface potential and thus reduce the interaction energy values of the particles. This should increase flocculation, but it is in contrast to the experimental results presented earlier.

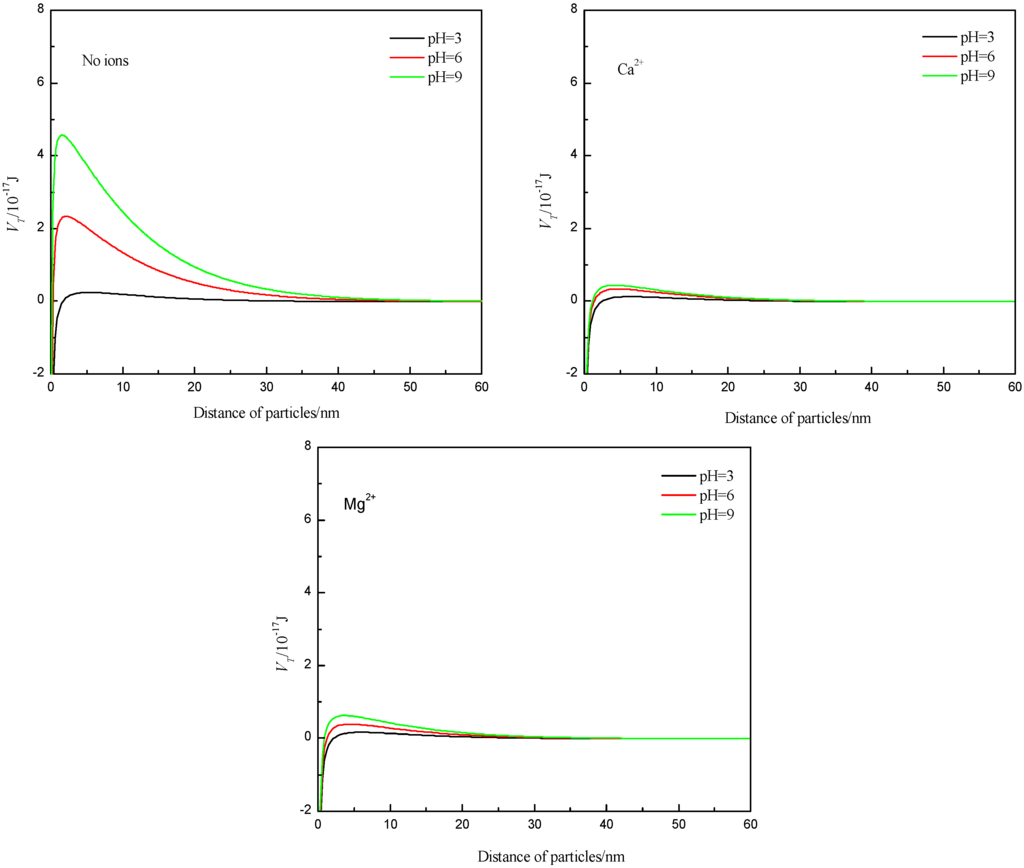
Figure 5. Total interaction energy of particles at different pH values without and with Ca²⁺, Mg²⁺.

Muscovite is a kind of layered crystal structure of mineral, which is formed from an octahedral layer sandwiched between two identical tetrahedral (SiO₄) layers. So particle–particle flocculation may occur through three types of structural interaction: basal surface (001)—basal surface, basal surface-edge, and edge-edge. In general, the measurement of zeta potential can represent the mineral surface electrical property; however, considering the crystal anisotropy of muscovite, the zeta potential of muscovite is the overall electrical properties of the basal surface and the edge. The basal surface of muscovite has a negative charge, which is not affected by pH [31]. As a result, its value can be approximated to the zeta potential when the pH value of the suspension is equal to the point of zero charge of the edge (PZC_edge). When the net charge of the surface is zero, the PZC is defined as a point on the pH-scale, and the PZC_edge of muscovite in theory is 6.84 [34]. The potential computation formula of the edge is as follows: ${\mathsf{\phi }}_{edge}=0.059\left({\mathrm{PZC}}_{edge}-\mathrm{pH}\right)$. Considering the smaller edge area compared to the basal surface area, the R_edge was assumed to be one tenth of the R_{basal·surface}(10.75/2 μm). The interaction energy values of the particles were re-calculated, and the results are shown in Figure 6. The results show that the interaction energies of the form of basal surface-edge were negative at pH values of 3 and 6, which means that the particles can undergo flocculation, consistent with the experimental phenomenon, testifying that the particles were aggregated in acidic suspension mainly by the form of the basal surface-edge. Adding the 1 × 10⁻³ mol/L Ca²⁺ and Mg²⁺, the surface potential was reduced, and the electrostatic attraction between the basal surface and the edge was then also reduced, so the dispersion increased, which was also consistent with the experimental phenomenon.

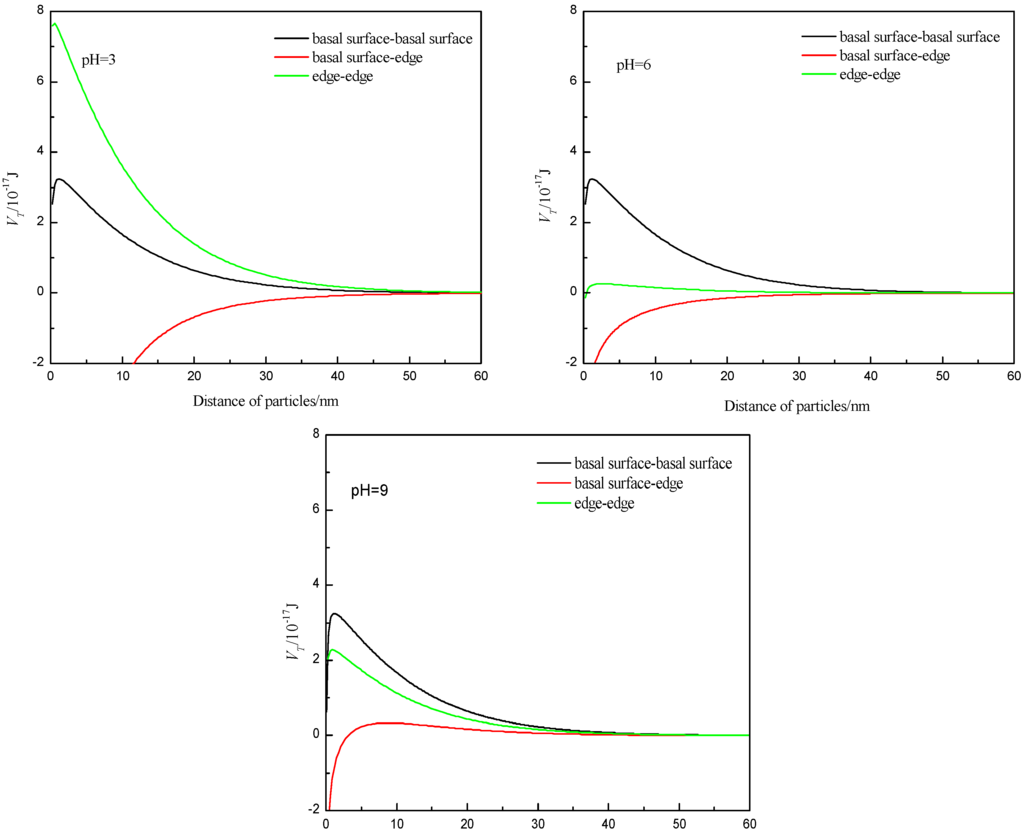
Figure 6. Total interaction energy of three kinds of form at different pH values.

3.4. Metal Species in Different Solution

In the solution with different pH values, the species and the content of the species in the presence of 1 × 10⁻³ mol/L Ca²⁺ or Mg²⁺ ions were analyzed and calculated using the stability constants for hydroxide formation, and the results are shown in Figure 7 and Figure 8, respectively. When pH < 12, the dissociative Ca²⁺ and Ca(OH)⁺ are the key species in the solution. Ca²⁺ and Ca(OH)⁺ lowered the absolute value of zeta potential of muscovite by compressing electric double layer [22,23], which was consistent with the zeta potential analysis. Mg²⁺ and Mg(OH)⁺ are the key species in the solution at pH < 9.92, and they had a similar effect to that of Ca²⁺ and Ca(OH)⁺. However, Mg(OH)₂(s) is the main species at pH > 9.92. At a pH range from 10 to 12, the zeta potential was zero, caused by Mg(OH)₂(s), and this phenomenon agrees with the results researched by Krishnan and Iwasaki [35].

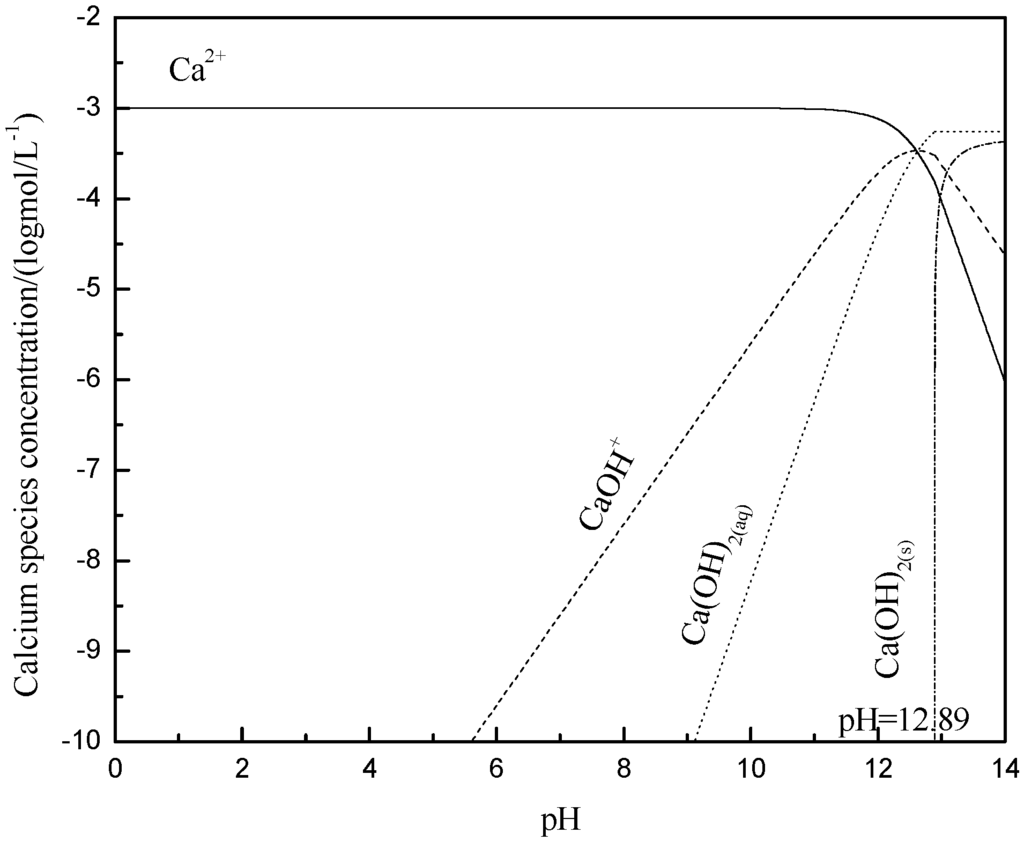
Figure 7. Calculated concentration of calcium species in solution with 1 × 10⁻³ mol/L Ca²⁺.

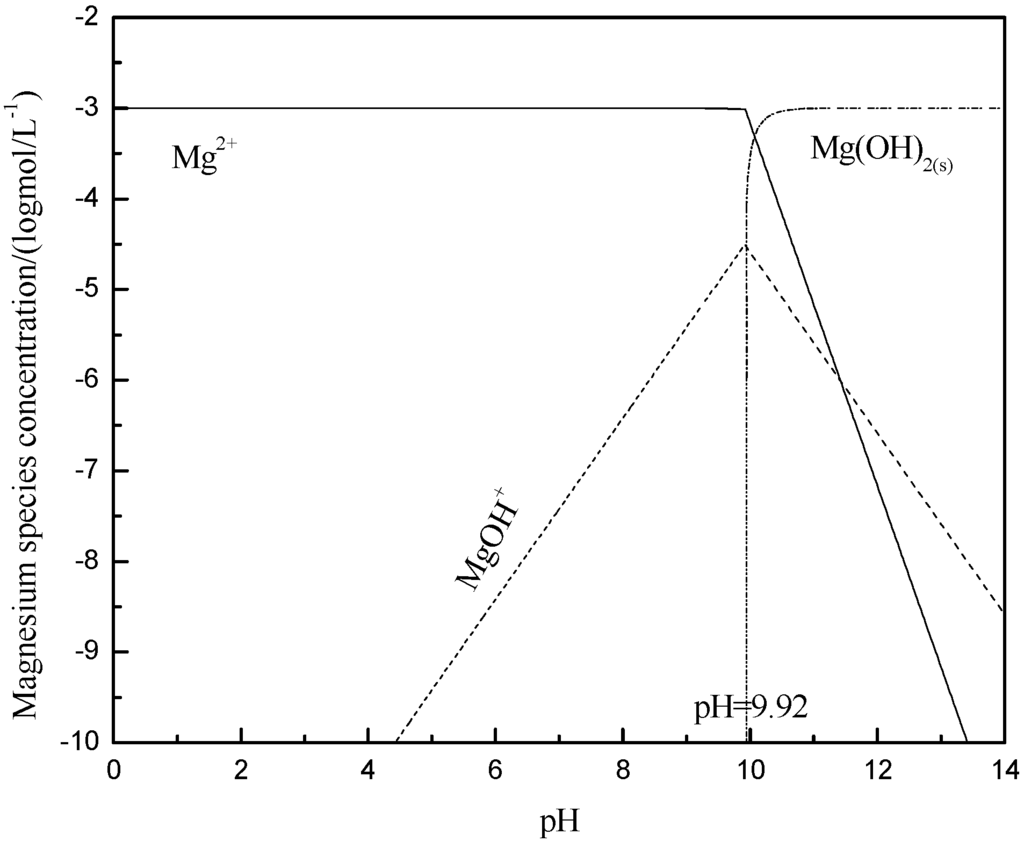
Figure 8. Calculated concentration of magnesium species in solution with 1 × 10⁻³ mol/L Mg²⁺.

The adsorption capacity of Ca²⁺ and Mg²⁺ on muscovite is shown in Figure 9. When pH < 4, there was less adsorption capacity of Ca²⁺ and Mg²⁺ ions on muscovite. When pH > 4, the adsorption capacity of calcium and magnesium ions began to increase, which was consistent with the sedimentation experiment, namely, the agglomeration increased when pH > 4. Combined with Figure 7 and Figure 8, it can be found that the ion and the hydroxyl complexes were the key species in the solution; the concentration of the hydroxyl compounds and the adsorption quantity all increased with the increase in the pH. Thus, it was confirmed that the hydroxy complex was the key form adsorbed on the muscovite, which may make the partial surface of muscovite with a positive charge. The flocculation of muscovite was caused by a bridging effect of the hydroxy complex, as shown in Figure 10. With the increase of pH and the concentration of Ca²⁺ and Mg²⁺, the hydroxy complex increased, and the bridging effect increased, so the sedimentation rate increased. Mg(OH)₂(s) was the main form when pH > 9.92, which led to the changing property of the suspension system, thus making the anomalous changes of sedimentation rate when the pH neared 9.92.

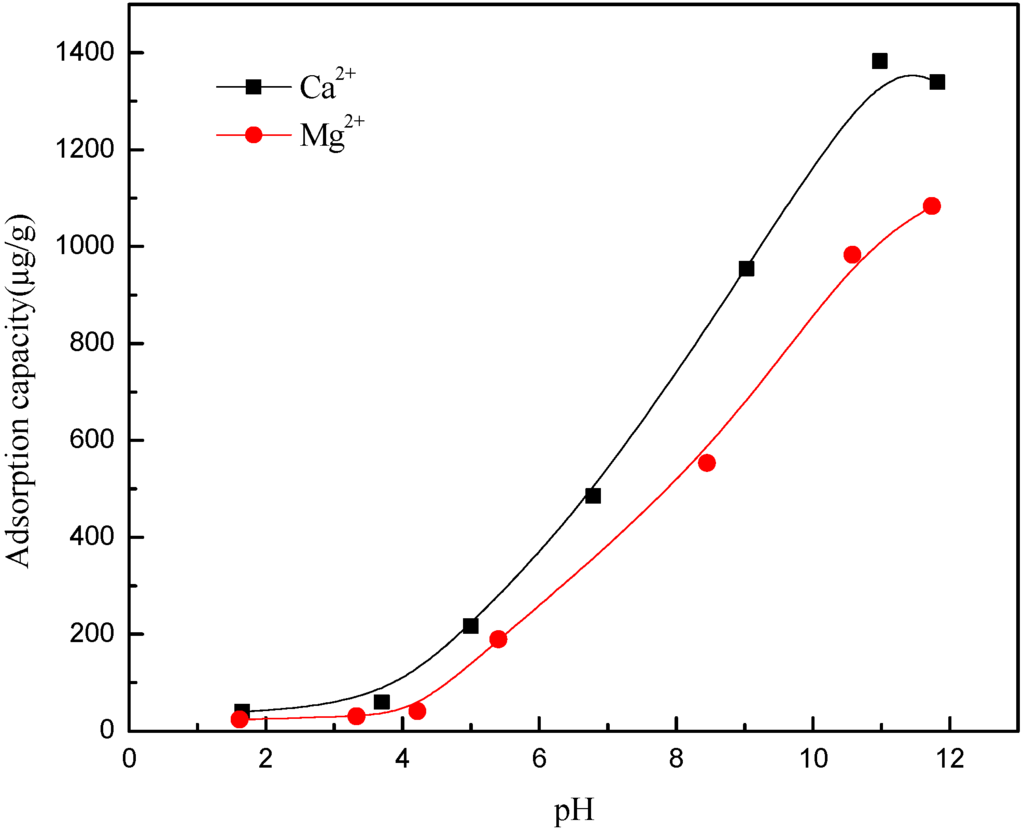
Figure 9. Adsorption capacity of Ca²⁺ and Mg²⁺ at different pH levels.

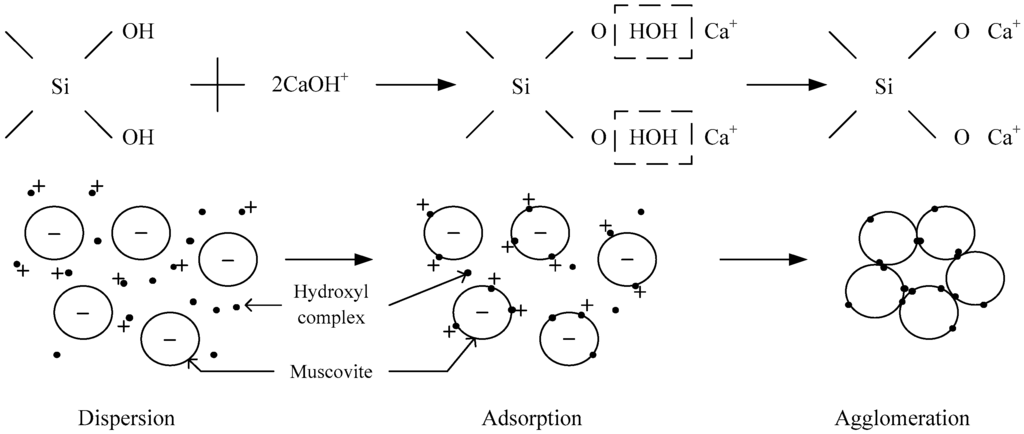
Figure 10. Bridging effect of hydroxy complex.

4. Conclusions

The conclusions from this research can be summarized as follows:

• The dispersion and flocculation behavior of muscovite in the absence of excess Ca²⁺ and Mg²⁺ agree with the classic DLVO theory based on the crystal anisotropy. The muscovite particles were aggregated in acidic suspension mainly by the form of basal surface-edge.
• The hydroxy complex of Ca²⁺ and Mg²⁺ was the main adsorption form on the mineral surface. The flocculation of muscovite was caused by a bridging effect of the hydroxy complex, which destroyed the excellent dispersion stability in alkaline suspension.