Abstract
Optimisation of three-dimensional (3D) underground stope layouts is a computationally complex process since it involves the modelling of many variables and constraints. As the number of variables and constraints increases to reflect the actual mining practice, the model complexity and solution time tend to increase exponentially, making the optimisation problem intractable. Metaheuristic approaches have therefore been used predominantly to solve the problem, but do not guarantee ‘true’ optimality. To minimise this limitation, a dual interchange algorithm (DIA) was developed by combining the strengths of two metaheuristic generic algorithms, namely the particle swarm optimisation (PSO) and genetic algorithm (GA). The DIA performance was compared to that of the Mineable Shape Optimizer (MSO) on four different design scenarios. The DIA generated stope layout economic values (SLEV) for three scenarios which were 0.3%, 3.4%, and 8.3% higher than for MSO under fixed and variable stope width conditions, while MSO produced a SLEV which was 9.7% higher than the DIA for a fixed stope width. This paper demonstrates that the DIA is a novel way of solving 3D optimisation of stope layouts under variable stope widths as encountered in actual mining practice.
1. Introduction
Mineral resources are extracted using surface and underground mining methods to generate maximum economic value for various stakeholders such as mining companies, governments, communities, and employees. The objective of maximising the value realised from extracting a mineral deposit necessitates the development and application of optimisation algorithms in mine planning to ensure that maximum value can be generated. In underground mine planning, some algorithms have been developed for optimisation in four main areas, namely development layouts, stope layouts, production scheduling, and equipment selection and deployment [1]. However, there are many algorithms that have been developed to optimise open pit geometries and these include the Lerchs-Grossman (LG) algorithm and dynamic programming (DP). Some researchers, such as Ataee-pour [2], have observed that the study of open pit geometry optimisation has probably reached saturation levels because there are many algorithms that have been developed to generate ‘optimal’ solutions. In contrast, the underground stope layout optimisation problem remains largely unsolved due to its complexity [3]. Therefore, it is necessary to develop algorithms for the optimisation of underground stope layouts, particularly in three-dimensional (3D) space, because existing algorithms can easily solve the stope layout optimisation in two-dimensional (2D) space but have shortcomings in 3D space [3]. This paper is, therefore, a contribution to optimising 3D stope layouts under conditions of variable stope widths as encountered in actual mining practice. This was done by developing an algorithm called a dual interchange algorithm (DIA).
The DIA works by combining the key strengths of two generic metaheuristic algorithms, namely the particle swarm optimisation (PSO) algorithm and the genetic algorithm (GA). The PSO algorithm has never been applied to solve the stope layout optimisation problem but is well-suited to solving the optimisation problem in 3D space due to its architecture of integrating the global best and personal best locations in 3D space for each particle in a swarm. The PSO algorithm can be used for mining projects to optimise the stope layout economic value (SLEV) in the long term (global best) and profit in the short term (personal best). This is the reason why the PSO algorithm was selected for the stope layout optimisation problem to exploit its 3D capability for optimisation. The GA was applied to optimise the stope layouts initially generated from the PSO algorithm since its evolution capabilities are well-suited to improving the solutions from one generation of solutions to the next. The DIA is a metaheuristic algorithm, so cannot guarantee ‘true’ optimality, but can generate higher value stope layouts by exploiting the strengths of the PSO algorithm and GA in 3D space. It was necessary to identify a 3D block model for testing the DIA.
2. Creation of a Synthetic Platreef Block Model
A geological block model is created from borehole data and geological information gathered from the exploration for a mineral(s) of economic interest. The geological block model is developed by dividing the mineral deposit into regular blocks in three dimensions with each block defined by characteristics or attributes such as lithology, grade, volume, and density [4]. In this paper, a synthetic block model was created for testing the DIA such that the block model mimicked the characteristics of the Platreef deposit. The Platreef mineralisation is found in the Northern Limb of the Bushveld Complex in South Africa. This area of study was selected because the mining of South Africa’s platinum group elements (PGE) is expected to gravitate to the Northern Limb in the future since several large-scale mines are being planned for that area. Furthermore, as noted in Cawthorn [5], the Northern Limb is regarded as the third largest PGE deposit in the world after the Merensky and Upper Group 2 (UG2) reefs. The ore types in the Platreef mineralisation consist of platinum (Pt), palladium (Pd), rhodium (Rh), iridium (Ir), ruthenium (Ru), osmium (Os), gold (Au), copper (Cu), and nickel (Ni). Consequently, the synthetic block model which was generated had to mirror the grade distribution and prill split of the 4E grade of the Platreef deposit. The 4E grade represents the sum of the grades of the four most valuable precious metals (or elements), i.e., platinum, palladium, rhodium, and gold, expressed in grammes per tonne. According to Chigumira and Raymond [6], the Northern Limb prill split, which must add up to 100%, has:
- Platinum at 43%.
- Palladium at 48%.
- Rhodium at 3%.
- Gold at 6%.
The synthetic block model was created using Microsoft Excel as a .csv file, and the steps followed were [3,7]:
- Step 1 involved creating x, y, and z block dimensions along X, Y, and Z directions which were 5 m, 5 m, and 5 m, respectively. The block dimensions were selected because block sizes and non-cubic shapes affect the performance of the stope layout optimisation process but may enhance computational time. Smaller block sizes that are cubic in shape are desirable to minimise dilution since block model peripheries tend to be irregular. However, as the block size becomes smaller, more blocks must be evaluated, thus slowing down the optimisation process and increasing the computational time. The block size of 25 m3 created an acceptable balance between block size and performance of the optimisation process.
- Step 2 involved applying average density values in t/m3 to the blocks.
- Step 3 involved the generation of random 4E grade values between typical low values of about 0.01 g/t and high values of about 21.9 g/t since Thormann et al. [7] noted that the Platreef orebody has a highly variable grade distribution.
Equation (1) was used to calculate the 4E grade for each block where and represent the proportion (%) and grade (g/t) for platinum, palladium, rhodium, and gold, respectively.
The synthetic block model shown in Figure 1 contains 50,000 blocks with the x, y, and z-axes extents being 640 m, 175 m, and 55 m, respectively. The synthetic block model was visualised using the Mineable Shape Optimizer (MSO) module in Datamine commercial software. The synthetic block model characteristics are depicted in Table 1, including a derived block economic value (BEV) attribute.

Figure 1.
Synthetic Platreef block model with the legend showing BEV in USD. Source: [3].

Table 1.
Synthetic Platreef block model specifications. Source [3].
3. Construction of the Economic Block Model
A 3D geological block model comprises a set of blocks with estimates of block characteristics such as grades. The grade is used to classify blocks as either ore or waste for a specified cut-off grade. The grade of each block in the model, together with other geological data, and technical and economic parameters are then used to derive the block’s economic value called a block economic value (BEV) [8]. The BEV is generally used as a block attribute because most algorithms developed for the optimisation of the mining process use this attribute [9]. Equation (2) is a typical formula for calculating the BEV [10].
The synthetic geological block model was converted to an economic block model by applying several parameters such as density, grade dilution, recovery, cost of extraction, cost of processing, cost of refining commodity, and basket price which represents the aggregated commodity price for multimineral deposits such as the Platreef deposits.
The individual blocks in the block model can be identified by their corresponding x, y, z coordinates in the X, Y, and Z directions, respectively, such that a block entry can be denoted as Bxyz [11]. Equations (3) and (4) were applied to the block model to convert it into an economic block model. For compatibility, it was necessary to convert the metal price in USD/oz and grade in g/t to their equivalent USD/t and percentage (%), respectively, assuming that 1t is equivalent to 32150.75 troy ounces [3]. Table 2 summarises the conversion factors for transforming the block model into an economic block model.

Table 2.
Conversion factors and input values for economic block model construction. Source: Adapted from [3].
A basket price is used as a proxy for commodity price when there is more than one mineral considered for extraction. The 4E basket price was calculated using Equation (3) where and , respectively, represent the basket price, and individual metal price in USD/oz and proportion (%) for each metal.
where:
- block economic value (USD) for block r
- basket metal price (USD/oz)
- refining cost of block r (USD/t)
- grade of block r (g/t)
- recovery from block r (%)
- extraction or mining cost for block r (USD/t)
- concentrating or processing cost of block r (USD/t)
- tonnage of block r (t)
- dilution and mining losses incurred in block r (%)
Each block in the economic block model has an equal opportunity of being included in the optimal stope layout if it adds value to the realisation of the objective function, i.e., maximising the economic value of the mineral deposit or to guarantee that the stope dimension constraint is not violated. Blocks with positive BEVs are classified as ore, while those with negative BEVs are classified as waste and those with zero BEVs are classified as marginal blocks. Thereafter, the objective function for the optimisation process was set as the maximisation of the stope layout economic value (SLEV), which is a proxy for measuring the ‘snapshot’ economic value. The SLEV concept resembles the concept of undiscounted profit maximisation for the ultimate pit limit (UPL) determination in open pit mining. The UPL optimisation principles were adopted because the UPL is the largest possible envelope that contains all the blocks that are candidates for mining in a single period provided that the transition to underground does not occur earlier than the UPL. This adoption ensured that all blocks were evaluated for inclusion in the final stope layout irrespective of their BEVs. In addition, the minimum and maximum stope sizes were defined based on the practicality of implementation during the ore extraction process [3]. The ore extraction process is described in the next section.
4. Extraction of the Platreef Deposit
The Platreef deposit is amenable to extraction using surface and underground mining methods depending on the viability of the method as dictated by factors such as the depth of reef below surface and environmental restrictions. For underground mining, several mining methods can used to exploit different sections of the mineral deposit. These methods include drift and fill, and drift and bench for thinner ore zones, and sublevel open stoping for thicker ore zones. A large part of the Platreef deposit is in the thicker ore zone category; thus, it will be predominantly mined using the sublevel open stoping mining method. Therefore, the algorithm presented in this paper was developed to produce stope layouts for the sublevel open stoping mining method.
Sources such as Atlas Copco [12] provide a detailed discussion and illustration of a typical sublevel open stoping mining method, where the ore is recovered in large open stopes that are normally backfilled to eliminate the need of leaving pillars between adjacent stopes following an alternating sequence. One of the main parameters considered during stope design is the stope dimension, which constitutes the height, width, and strike length. For the stope layout, the stope height and strike length were kept constant to ensure stability of the mining area and production per stope. The stope width may vary depending on the thickness of the mineral deposit and geotechnical constraints such as the hydraulic radius. The next section discusses the mining constraints considered for the stope layout design.
5. Mining Constraints
Some of the main constraints considered for the practical extraction of a mineral deposit are the stope dimension, dilution, stope location, non-overlapping stopes, and unique stopes. There are numerous combinations of stope dimensions that can be used to produce a stope layout. These combinations are constrained by various factors such as the geological conditions, geotechnical environment, and type of equipment to be employed during mining. Therefore, it is important that these factors are considered during the selection of an appropriate stope dimension. An appropriate stope dimension is one that permits for mining to follow irregular mineral deposit peripheries to minimise dilution, among other key considerations.
The DIA randomly creates several stope dimensions constrained by the input of the minimum and maximum dimensions of the stope width. Consequently, the DIA selects an appropriate stope dimension to be utilised for the optimisation process throughout the economic block model. Once the appropriate stope dimension has been determined, various stopes are generated throughout the block model.
After the stope generation process is complete, the DIA then randomly selects a starting stope. The height of the starting stope is fixed and then the stope is floated throughout the economic block model during the optimisation process using the principles of the GA. Thereafter, the search process continues upward or downward along the z-axis depending on the position of the starting stope to complete the search process in the economic block model. Subsequently, an optimum stope layout is produced subject to the constraints and optimisation process termination criterion.
There are several combinations of stopes that are evaluated to determine the optimum combination of stopes. The selection of any of the possible stope layouts is governed by the SLEV. The generation of possible stope layouts is a cumbersome activity that increases the computational time exponentially and can make the optimisation problem intractable. This challenge was overcome by adopting GA principles in generating possible stope combinations and selecting the highest value stope combinations for inclusion in the final stope layout. An overview of how the DIA executes these processes is described in the next section.
6. Dual Interchange Algorithm Anatomy
A study by Myburgh et al. [13] developed a heuristic hybrid approach for cut-off grade optimisation in open pit mining, which uses three algorithms working simultaneously but performing different functions with an evolutionary ‘master’ algorithm controlling two subservient algorithms and combining the outputs from both algorithms into a single cut-off grade optimisation strategy. A study by Phillips et al. [14] presented a dual interchange algorithm which works as a parent algorithm supervising two subservient algorithms and selects the better solution generated in each run from the two algorithms, while simultaneously penalising the algorithm that produced an inferior solution and rewarding the one that produced a better solution. The DIA presented in this paper works by exploiting the principles of the particle swarm optimisation (PSO) and GA algorithms. A detailed discussion on the PSO and GA adaptation and mapping can be found in Nhleko [3] and Nhleko and Musingwini [11]. The LG algorithm is used for optimising the long-term open pit mine planning problem, and its principles were used as analogies for the underground stope layout optimisation. The analogy between the LG algorithm and DIA is presented in Table 3.

Table 3.
Adaptation of the UPL optimisation principles to stope layout optimisation. Source: [3].
Based on the work of Nhleko and Musingwini [11] and Qi et al. [15], the generic PSO algorithm was adapted for the optimisation of the stope layout as applied in the DIA. Figure 2 illustrates a schematic mapping of the PSO parameters to the DIA parameters. The other PSO parameters, namely and , are common control parameters to both PSO and DIA to prevent convergence on local optima and non-convergence of the algorithm during the search process.
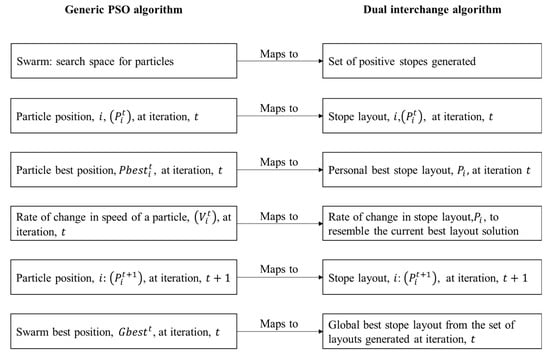
Figure 2.
Schematic mapping of the PSO algorithm to DIA.
The DIA uses a set of positive stopes to initialise the optimisation process as indicated in the pseudocode starting from Step 1 and terminates once the stopping criterion is met (see Figure 3). The optimum stope layout is produced in Step 10. Figure 4 shows the flowchart for the integration of the PSO and GA algorithms for the optimisation of stope layout for an underground mine. Furthermore, it illustrates how the PSO and GA iteratively interchange outputs as inputs until the termination criterion is satisfied.

Figure 3.
Pseudocode for the dual interchange algorithm. Source: [3].
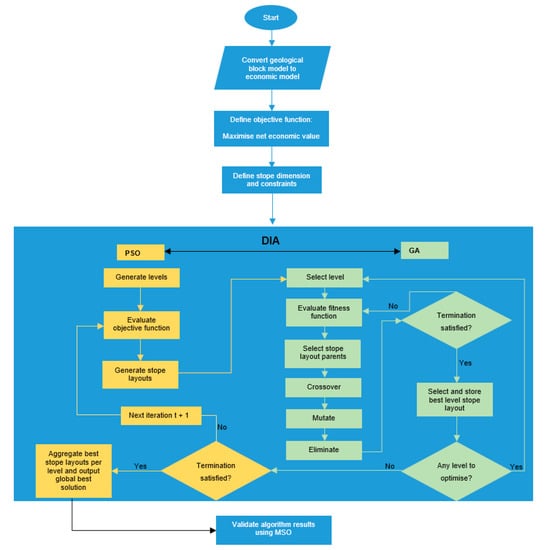
Figure 4.
Schematic illustration of the proposed dual interchange algorithm integrating the PSO and GA. Source: [3].
To decide on a suitable number of iterations for the DIA, a reference was drawn from the study by Alam [16] on the PSO algorithm, which recommended that the number of iterations generally used ranges between 500 and 10,000. In addition, the study by Sandanayake [17] used 500 iterations for the stope layout optimisation problem. However, since computational time increases exponentially as the block model size increases and number of constraints and/or iterations increase, it was decided to limit the iterations to initially limit the iterations 200 since at a higher number of iterations the DIA could fail to achieve convergence based on the number of constraints and block size used in the evaluation. The DIA creates 25 stope layouts per iteration using the PSO algorithm and these are modified through 200 iterations per each layout to generate 5000 possible stope layout solutions. The GA modifies each initial stope layout several times using evolutionary principles until there is no improvement on the SLEV.
The architecture of the DIA also ensures that variable stope widths can be evaluated since the periphery contours of mineral deposits are generally irregular. As stated earlier, variable stope widths provide the benefit of selective mining and capability for mining to follow irregular mineral deposit peripheries, consequently, reducing the effect of dilution. The preceding discussion outlined the architecture of the DIA, and the next section provides a comparison of the performance of the DIA to MSO, when applied to the Platreef synthetic block model.
7. Comparison of MSO and DIA Performance
According to Edorgan et al. [18], MSO is based on the floating stope algorithm. The DIA also uses an approach to float stopes as described earlier in this paper. Hence, it was reasonable to compare the performance of the DIA to that of MSO. The comparison was done on four scenarios, A to D, to represent different mining situations. The stope width is fixed for Scenarios A and C and is variable for Scenarios B and D. Table 4 shows the stope dimensions the different scenarios. The cut-off BEV was set to zero to ensure that all stopes with positive stope economic values (SEV) could be included in the final stope layout generated.

Table 4.
Input parameters considered for the optimisation problem Source: [3].
The synthetic block model contains 6940 blocks that are classified as waste. The inclusion of any waste block leads to a reduction in the SEV. Furthermore, if a block is created outside of the spatial dimensions of the economic block during the optimisation process to avoid violating the stope dimension constraint, it is categorised as a dummy block. A dummy block is attributed the same characteristics as a waste block. Therefore, dummy block attracts costs associated with activities from extraction to refining if they are included in the optimum stope layout. The next section summarises the results obtained for Scenario A and other scenarios were analysed in a similar manner.
7.1. Comparison of MSO and DIA for Scenario A
For Scenario A, a stope dimension of 20 m, 25 m, and 40 m for the strike length, stope height, and stope width, respectively, was used as indicated previously in Table 4. Figure 5 shows the stope layout solution generated using MSO for Scenario A. Figure 5a,b, present the section views of the block model showing that MSO creates stopes outside the spatial dimensions of the economic block model to avoid violating the stope dimension constraint. As explained earlier, the creation of stopes outside the economic block model envelope will reduce the value to be realised from mining the mineral deposit because when the associated costs are incorporated, they may deem a stope uneconomic, consequently reducing the SLEV. However, the stopes created with dummy blocks do not violate the cut-off value constraints. Figure 5c shows the 3D block model for the optimised 3D stope layout from MSO. The economic block model has several blocks with negative BEVs in the central area, hence, not many stopes were created in the middle portion of the deposit. The generated stopes pose a challenge in terms of planning the production tunnels due to the spatial overlaps that may require manual adjustment by the mine planner, possibly violating optimality. Figure 5d presents the 3D stope layout solution, showing that the stopes outside of the block model will require dedicated drilling tunnels which will increase the cost of extraction of these stopes. The MSO produced a stope layout solution that comprised 217 stopes with a combined SLEV of USD 35.87 billion.
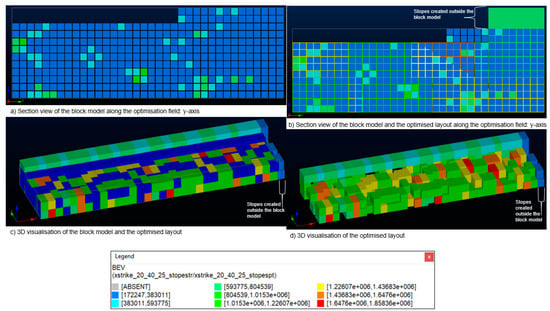
Figure 5.
Scenario A: visualisations of the optimum stope layout solution using the MSO with the legend showing SEV in USD. Source: [3].
Figure 6 shows the SLEV solutions obtained from the DIA for 200 iterations. It can be observed from Figure 6 that the optimum stope layout was generated within about 50 iterations. The visualisation of the optimum stope layout solution for Scenario A using the DIA is presented in Figure 7 showing that all stopes were created within the block model. The DIA produced a stope layout solution that comprised 213 stopes with a combined SLEV of USD 35.87 billion.
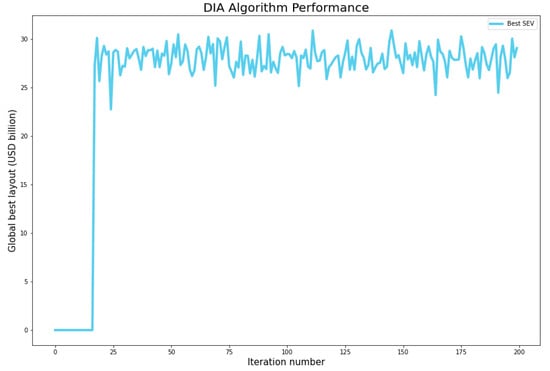
Figure 6.
Scenario A: optimum solution convergence using the DIA. Source: [3].

Figure 7.
Scenario A: visualisations of the optimum stope layout solution using the DIA with the legend showing SEV in USD. Source: [3].
7.2. Summary of Results from the Four Scenarios
Figure 8 illustrates the results obtained for the four scenarios that were described earlier in Table 4. Figure 8 shows that the DIA generated superior results compared to MSO for Scenarios A, B, and D, which are more profitable by 0.3%, 3.4%, and 8.3%, respectively, while MSO generated a superior solution for Scenario C which was 9.7% more profitable than the DIA solution. Table 5 summarises the output solutions for each scenario, indicating that the solution time of MSO is shorter compared to that of the DIA.
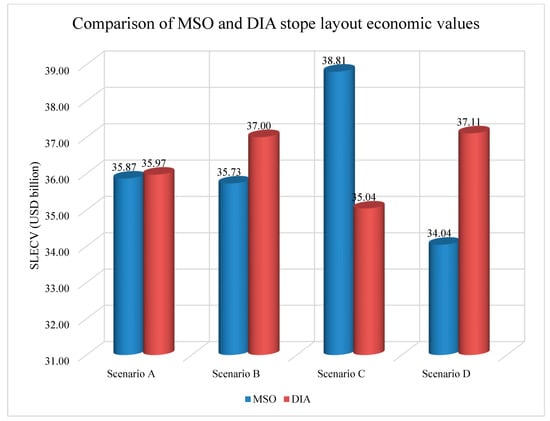
Figure 8.
Comparison of the performance of the DIA and MSO. Source: [3].

Table 5.
Comparison of the optimum solutions generated by the MSO and DIA. Source: Adapted from [3].
In Scenarios A and C, the stope width is fixed. In Scenario A, the DIA slightly outperforms MSO, while in Scenario C the DIA’s performance is well below that of MSO. Fixed stope width is not desirable for the extraction process because the mineral deposit envelope is irregular; thus, if the stope width is fixed, waste is included, and geological contacts may be violated creating a safety issue. Furthermore, the DIA remained confined within the block model, i.e., the DIA does not generate dummy blocks outside of the block model during the optimisation process, thus eliminating chances of eroding SLEVs. Since there are waste blocks within the block model, the stope width of 50 m caused the DIA to produce several possible stope combinations to reduce the effect of dilution from the internal waste. Furthermore, the GA optimisation process would be prolonged because the termination criterion is based on lack of improvement in the solution not the number of iterations. Consequently, if a new generation of solutions is poor in terms of fitness, then more generations of solutions are created to improve the fitness value represented by SLEV.
The stope width for Scenarios B and D is variable, and the DIA appeared to generate superior SLEV. Variable stope width is desirable in mine planning because the mineral deposit envelopes are generally irregular. The results for Scenarios B and D confirm that the architecture of the DIA is best suited for optimisation under conditions of variable stope width.
In the four scenarios, it is evident that the solution time for MSO is shorter compared to that of the DIA. The optimum solution convergence using the DIA for all the scenarios indicates that the highest SLEV is achieved within about 50 iterations. This observation suggested that the DIA can be modified to have shorter running times by capping the number of iterations to below 200. Therefore, the performance of the DIA in terms of solution time was further investigated by varying the number of iterations between 50 and 200 for each scenario.
8. DIA Performance Evaluation under Different Numbers of Iterations
The number of iterations per run were varied between 50 and 200 for the four scenarios to further investigate the robustness of the DIA. Table 6 presents the results concerning the global best SLEV, number of stopes and computational time for each scenario. It is observed that the highest SLEV for all the scenarios were generated when using 200 iterations. The SLEV results for the individual scenarios are discussed further investigated in the next subsections.

Table 6.
Summary of DIA performance results.
8.1. Optimisation Results for Scenario A under Different Numbers of Iterations
Figure 9a shows that when using 100 iterations for Scenario A, the generated solution is inferior compared against solutions generated using 50, 150, and 200 iterations. At 100 iterations, the SLEV is USD 32.13 billion with the lowest number of stopes at 190 stopes. This value is alluded to by the DIA ensuring that the stope dimension constraint is not violated, thus including positive stopes with a high number of waste blocks in the final layout. The highest SLEV of USD 35.97 billion was produced when using 200 iterations. This phenomenon is alluded to by the fact that the DIA is a metaheuristic algorithm; thus, the solutions vary per run given its random nature of optimisation. The highest SLEV solution had the highest number of stopes as shown in Figure 9b. For Scenario A, the arithmetic mean of the generated solutions is USD 34.96 billion and the standard deviation is USD 1.89 with a range of USD 3.84 billion and standard error of USD 0.94. Therefore, the solutions generated at these iterations are more dispersed from the mean SLEV.
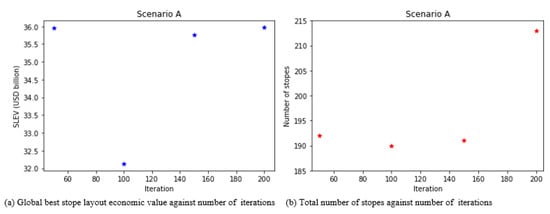
Figure 9.
Scenario A: optimisation results of SLEV and number of stopes.
8.2. Optimisation Results for Scenario B under Different Numbers of Iterations
Figure 10a shows that the SLEV for Scenario A increased with an increase in number of iterations, and the highest SLEV was generated after 200 iterations with a value of USD 37.23 billion where the number of stopes created was 667 stopes (see Figure 10b). The arithmetic mean for Scenario B solutions is USD 37.01 billion and the standard deviation and range are USD 0.28 and USD 0.63 billion, respectively. The standard error is USD 0.14, which shows that the SLEV solutions are close to the mean SLEV.
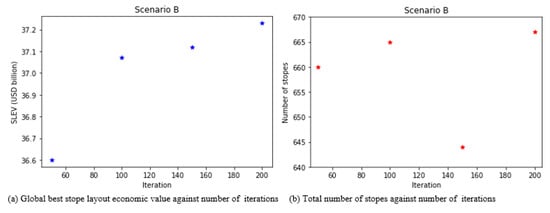
Figure 10.
Scenario B: optimisation results of SLEV and number of stopes.
8.3. Optimisation Results for Scenario C under Different Numbers of Iterations
Figure 11a shows that for Scenario C, the DIA produced a lower SLEV of USD 30.28 billion when using 100 iterations. This phenomenon is the same as that which was observed in Scenario A and can be alluded to by the DIA ensuring that the stope dimension constraint is not violated, thus including stopes containing more waste blocks in the final layout than the other solutions. The highest SLEV solution of USD 36.50 billion was produced after 200 iterations with 181 stopes being created (see Figure 11b). The arithmetic mean for Scenario C is USD 34.35 billion and the standard deviation and range are USD 2.77 and USD 6.22 billion, respectively. The standard error is USD 1.39, which shows that the SLEVs generated are more dispersed from the mean SLEV. This range is high because of a low SLEV obtained at 100 iterations, while the SLEVs at 50, 150, and 200 iterations are relatively close to each other.
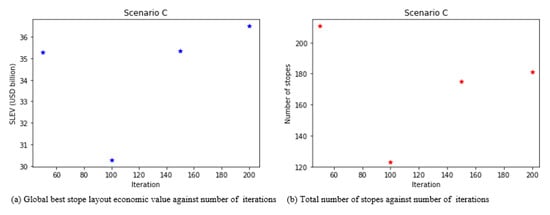
Figure 11.
Scenario C: optimisation results of SLEV and number of stopes.
8.4. Optimisation Results for Scenario D under Different Numbers of Iterations
Figure 12a shows that for Scenario D, the SLEV increased with an increase in number of iterations. The highest SLEV was generated after 200 iterations with a value of USD 37.83 billion and the number of stopes created was 669 stopes (Figure 12b). The arithmetic mean for Scenario D solutions is USD 36.98 billion and the standard deviation and range are USD 0.59 and USD 1.37 billion, respectively. The standard error is USD 0.30, which shows that the SLEV solutions are close to the mean SLEV.
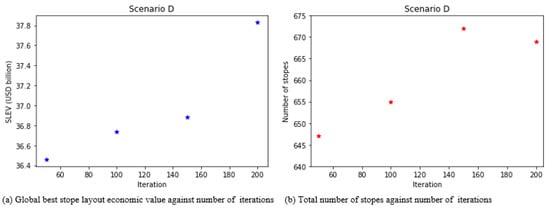
Figure 12.
Scenario D: optimisation results of SLEV and number of stopes.
9. Summary of the DIA Structure and Findings in Relation to Similar Studies
The four scenarios show that the DIA as a metaheuristic algorithm generated solutions that differed per iteration. In Scenarios A and C, the stope width was fixed, and the DIA generated inferior SLEVs compared to SLEVs generated under conditions of variable stope widths in Scenarios B and D. This observation confirms that the DIA performs better for stope layout optimisation under conditions of variable stope width, which is more suited the real mining environments.
Janiszewski et al. [19] stated that the benefits to be realised from an algorithm must be showcased by case studies, hence the approach to use four different scenarios in this paper. The four scenarios demonstrated the robustness and benefits of using the DIA compared to the MSO for the stope layout optimisation problem. It should be noted that the MSO is an industry-standard automated stope design tool [20]. Appiang and Ben-Awuah [21] mentioned that optimum stope layouts can only be generated once the economic values of the blocks are known, and this view is seen in the architecture of the DIA allowing the generation of stope layouts with the highest SLEVs. The DIA structure combines some PSO and GA functions in support of the suggestion by Nikbin et al. [22] who developed a 3D hybrid algorithm combining greedy and dynamic programming algorithms but concluded that the greedy algorithm could be substituted with PSO or GA to improve the solutions generated for the stope boundary optimisation problem.
10. Conclusions
Optimisation in underground mine planning requires that the economic value derived from the extraction of mineral resources be maximised through the application of the most appropriate or optimal mine designs and plans. However, the optimisation becomes a computationally complex process as the number of variables and constraints increases to reflect actual mining practice. This paper presented an innovative technique called the DIA to handle the complexity of optimising the stope layout problem. The DIA combines the key strengths of two metaheuristic algorithms, namely the PSO algorithm and GA, to improve the economic value created. The DIA was implemented on a block model that mimics the Platreef deposit. Four scenarios were defined to demonstrate the performance of the DIA when solving the stope layout optimisation problem under different conditions.
The solutions generated by the DIA were more profitable by 0.3%, 3.4%, and 8.3% for Scenarios A, B, and D compared to those generated by MSO, while MSO produced a superior stope layout economic value for Scenario C where it was 9.7% more profitable than the DIA solution under conditions of a fixed stope width. Therefore, the DIA generated solutions that were superior to MSO when applied to an underground stope layout optimisation problem under conditions of variable stope widths typically encountered in actual mining practice.
The DIA took more time than the MSO to solve the stope layout optimisation problem; thus, it was necessary to investigate the performance of the DIA using fewer iterations. The iterations were in increments of 50, starting from 50 iterations up to 200 iterations. For the four scenarios, the DIA generated better SLEVs when 200 iterations were applied. Superior SLEVs were generated for variable stope width compared to fixed stope width, which is ideal for actual mining practice where the mineral deposit envelope is irregular. The DIA generates better SLEVs for underground stope layout optimisation; thus, it is recommended that it can be adapted for application to other different mineral projects.
Author Contributions
Conceptualization, A.S.N. and C.M.; methodology, A.S.N. and C.M.; software, A.S.N.; validation, A.S.N.; formal analysis, A.S.N.; investigation, A.S.N.; writing—original draft preparation, A.S.N.; writing—review and editing, C.M.; visualization, A.S.N.; supervision, C.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. The APC was funded by the School of Mining Engineering, University of the Witwatersrand, Johannesburg.
Data Availability Statement
The method presented in this manuscript can be applied on any similar geological block model data. However, specific data supporting reported results can be requested Sihesenkosi.Nhleko@wits.ac.za.
Acknowledgments
The work presented in this paper forms part of the work undertaken for a PhD thesis by A.S.N. at the University of the Witwatersrand, Johannesburg, South Africa.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Musingwini, C. Presidential Address: Optimization in underground mine planning—Developments and opportunities. J. South. Afr. Inst. Min. Met. 2016, 116, 809–820. [Google Scholar] [CrossRef] [Green Version]
- Ataee-Pour, M. A Heuristic Algorithm to Optimise Stope Boundaries. Ph.D. Thesis, Faculty of Engineering, University of Wollongong, Wollongong, Australia, 2000. Available online: http://ro.uow.edu.au/cgi/viewcontent.cgi?article=3923&context=theses (accessed on 15 February 2016).
- Nhleko, A.S. A Dual Interchange Algorithm for Three-Dimensional Stope Boundary Optimisation for Underground Mines. Ph.D. Thesis, University of the Witwatersrand, Johannesburg, South Africa, 2022. [Google Scholar]
- Nhleko, A.S.; Tholana, T.; Neingo, P.N. A review of underground stope boundary optimization algorithms. Resour. Policy 2018, 56, 59–69. [Google Scholar] [CrossRef]
- Cawthorn, R.G. The Platinum Group Element Deposits of the Bushveld Complex in South Africa. Platin. Met. Rev. 2010, 54, 205–215. [Google Scholar] [CrossRef]
- Chigumira, D.; Raymond, T. Platinum Essentials. 2017. Available online: https://www.platinuminvestment.com/files/126548/WPIC_Platinum_Essentials_January_2018.pdf (accessed on 30 April 2019).
- Thormann, L.; Buchspies, B.; Mbohwa, C.; Kaltschmitt, M. PGE Production in Southern Africa, Part I: Production and Market Trends. Minerals 2017, 7, 224. Available online: https://www.mdpi.com/2075-163X/7/11/224/htm (accessed on 6 November 2020). [CrossRef] [Green Version]
- Chung, J.; Topal, E.; Ghosh, A.K. Where to make the transition from open-pit to underground? Using integer programming. J. South. Afr. Inst. Min. Metall. 2016, 116, 801–808. [Google Scholar] [CrossRef] [Green Version]
- Ataee-Pour, M. A Linear Model for Determination of Block Economic Values. In Proceedings of the 19th International Mining Congress and Fair of Turkey, IMCET 2005, Izmir, Turkey, 9–12 June 2005; pp. 289–294. [Google Scholar]
- Jamshidi, M.; Osanloo, M. Determination of block economic value in multi-element deposits. In Proceedings of the 6th International Conference on Computer Applications in the Minerals Industries (CAMI2016-06), Istanbul, Turkey, 5–7 October 2016; pp. 1–9. [Google Scholar]
- Nhleko, A.S.; Musingwini, C. Analysis of the particle swarm optimization (PSO) algorithm for application in stope layout optimisation for underground mines. In Proceedings of the Mine Planner’s Colloquium 2019, Johannesburg, South Africa, 22–23 May 2019; The Southern African Institute of Mining and Metallurgy: Johannesburg, South Africa, 2019; pp. 57–68. [Google Scholar]
- Atlas Copco. Mining Methods in Underground Mining, 2nd ed.; Ulf Linder: Stockholm, Sweden, 2007. [Google Scholar]
- Myburgh, C.; Deb, K.; Craig, S. Applying modern heuristics to maximising NPV through cut-off grade optimization. In Proceedings of the Orebody Modelling and Strategic Planning Conference, Perth, Australia, 24–26 November 2014; The Australasian Institute of Mining and Metallurgy: Perth, Australia, 2014. Available online: https://www.maptek.com/pdf/insight/AUSIMM_Applying_Modern_Heuristics.pdf (accessed on 2 January 2018).
- Phillips, R.A.; Ali, M.M.; Musingwini, C. A Metaheuristic Dual Interchange Algorithm (DIA) for Optimising Long-term Production Scheduling in Open-pit Mine Planning. In Proceedings of the Application of Computers and Operations Research in the Minerals Industries (APCOM2021), Johannesburg, South Africa, 30 August–1 September 2021; The Southern African Institute of Mining and Metallurgy: Johannesburg, South Africa, 2021; pp. 167–180. [Google Scholar]
- Qi, H.; Sun, S.C.; He, Z.Z.; Ruan, S.T.; Ruan, L.M.; Tan, H.P. Inverse Geometry Design of Radiative Enclosures Using Particle Swarm Optimization Algorithms. In Optimization Algorithms; IntechOpen: London, UK, 2016; pp. 43–69. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.N. Particle swarm optimisation: Algorithm and its codes in MATLAB. ResearchGate 2016, 8, 1–10. [Google Scholar] [CrossRef]
- Sandanayake, D.S.S. Stope Boundary Optimisation in Underground Mining Based on a Heuristic Approach. Ph.D. Thesis, Western Australian School of Mines, Curtin University, Bentley, Australia, 2014. [Google Scholar]
- Edorgan, G.; Cigla, M.; Topal, E.; Yavuz, M. Implementation and Comparison of Four Stope Boundary Optimisation Algorithms in an Existing Underground Mine. In Proceedings of the 6th International Conference on Computer Applications in the Minerals Industries, Istanbul, Turkey, 5–7 October 2016; pp. 1–10. [Google Scholar]
- Janiszewski, M.; Pontow, S.; Rinne, M. Industry Survey on the Current State of Stope Design Methods in the Underground Mining Sector. Energies 2022, 15, 240. [Google Scholar] [CrossRef]
- Faria, M.F.E.; Dimitrakopoulos, R.; Pinto, C. Stochastic stope design optimisation under grade uncertainty and dynamic development costs. Int. J. Min. Reclam. Environ. 2021, 36, 81–103. [Google Scholar] [CrossRef]
- Appianing, E.J.A.; Ben-Awuah, E. Underground Mining Stope Layout Optimization and Production Scheduling: A Review of Existing Solvers and Algorithms; Mitsui O.S.K. Lines: Tokyo, Japan, 2018; pp. 271–304. Available online: https://sites.ualberta.ca/MOL/DataFiles/2018_Papers/308%20Underground%20Mining%20Stope%20Layout%20Optimization%20and%20Production%20Scheduling%20A%20Review%20of%20Existing%20Solvers%20and%20Algorithms.pdf (accessed on 4 April 2022).
- Nikbin, V.; Ataee-pour, M.; Shahira, K.; Pourrahimian, Y. A 3D approximate hybrid algorithm for stope boundary optimization. Comput. Oper. Res. 2020, 115, 104475. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).