Abstract
This research work is aimed at optimizing the availability of a framework comprising of two units linked together in series configuration utilizing Markov Model and Monte Carlo (MC) Simulation techniques. In this article, effort has been made to develop a maintenance model that incorporates three distinct states for each unit, while taking into account their different levels of deterioration. Calculations are carried out using the proposed model for two distinct cases of corrective repair, namely perfect and imperfect repairs, with as well as without opportunistic maintenance. Initially, results are accomplished using an analytical technique i.e., Markov Model. Validation of the results achieved is later carried out with the help of MC Simulation. In addition, MC Simulation based codes also work well for the frameworks that follow non-exponential failure and repair rates, and thus overcome the limitations offered by the Markov Model.
1. Introduction and Literature Review
According to international standards, maintenance is defined as a blend of specialized and administrative activities planned to keep a unit or a framework in, or reestablish it to, a state in which it can accomplish its desired task (ISO 14224, 2006) [1]. Intricacy, and the cost of units as well as the frameworks, has amplified with the onset of state-of-the-art technology, thus making it ever more important to make the best use of these units and frameworks all through their lifetime. As the maintenance cost is a significant percentage of the total cost for overall operating expenditures of the framework, there exists a compelling requirement for developing a prudent and efficient maintenance strategy for manufacturing as well as industrial engineers.
Traditional maintenance strategies only incorporate basic preventive and corrective maintenance for the frameworks. Huang [2] gave a philosophy that perfectly matches the concept of corrective maintenance. He asked not to fix a framework, if it is still working. On the contrary, preventive maintenance comprises of planned operations which are executed when the framework is still operational. The main objective behind preventive maintenance is to lessen the quantity of unscheduled stoppages owing to the failure of a unit or framework.
The dynamic reliability concept relaxes the somewhat inflexible assumptions of traditional maintenance procedures, by taking into consideration multi-state frameworks while also taking into account different changes in their design conditions. Due to its complexity, the said issue cannot be dealt with using currently available analytical techniques, which therefore requires simulation techniques to reach to some workable solution. In this regard, Stochastic Hybrid Automaton (SHA) is considered to be a good simulation technique, capable of breaking down a framework into physical as well as stochastic models, linked together through common variables and few synchronizing operations (Chiacchio et al., [3]). Another approach combines the Dynamic Fault Tree technique with SHA to deal with the issue (Chiacchio et al., [4]).
Li et al. [5] developed reliability techniques for a multi-state framework operating under the discrete-time dynamic regime. In this technique, the regime-switching process and the framework’s functioning process are handled by separate Markov chains with different probabilities of transition. In order to illustrate the progression of the dynamic framework, a new Markov chain, combining the ones mentioned above, was constructed. Using this formalism, reliability indices and sojourn time distributions for the framework are obtained.
In order to evaluate the reliability of Phased-Mission Systems (PMS), an analytical technique was proposed by Lu et al. [6], while taking into account Combinatorial Phase Requirements (CPR) as well as repairable units. The process involved decomposition of overall mission success into corresponding behaviors of framework as well as its units, by means of continuous time Markov chains so as to analyze CPR; this resulted in the exclusion of redundant states from the model. In another related work, integrated modeling techniques were presented by Shrestha et al. [7] for the reliability analysis of repairable PMS, considering ordered as well as unordered states. In this technique, decision diagram models for the framework are integrated with Markov models so as to describe their unit-level dependencies and transitions.
Keeping in view the ever increasing demand and plethora of worldwide competition, it can be rightly concluded that such basic maintenance strategies are not enough to give an edge over the present day contenders. From the maintenance perspective, this favorable edge can be acquired by enhancing the availability of units or the framework while decreasing their downtime without undermining the reliability of framework. As a result more effective maintenance strategies are being adopted that include condition based maintenance and opportunistic maintenance. The later is envisaged as a productive merger of corrective and preventive maintenance; wherein, it utilizes much of its time, dedicated for corrective maintenance of a unit or the framework, in performing preventive maintenance of the units that may be requiring some maintenance action eventually. Nicolai and Dekker [8] describe opportunistic maintenance as a maintenance strategy that works for single as well as multiple units in a framework.
Radner and Jorgenson [9] worked in the area of opportunistic maintenance and applied this concept to un-monitored units and frameworks. Van Der Duyn Schouten and Vanneste [10] implemented this strategy on a two unit framework in series; however they did not propose any numerical treatment for measuring the availability of the framework. In this context, Wang and Pham [11,12] applied the concept of imperfect maintenance. From there onward, numerous research directions have been identified in the field of opportunistic maintenance. In this regard, many authors have adopted the concepts of Markov process and Markov chain to evaluate diverse maintenance strategies. Castanier et al. [13] demonstrated a Markov restoration process in order to develop a cost model for maintenance of a basic multi-unit framework. Ambani et al. [14] described the deterioration of a unit with the help of a continuous time Markov chain process. A cost model, incorporating the resource constraints, was presented by the authors in their work. Zhang et al. [15] analyzed an opportunistic maintenance model for a two unit degrading framework using a dynamic programming approach. Jain [16] used the renewal theory to study the transient conduct of a multi-unit framework. He calculated the instantaneous availability of the framework while keeping the time constant and developed a methodology to compute the times for opportunistic and preventive maintenance, in such a way that the cost is reduced. For ease of calculations, he fixed only two levels of deterioration, i.e., working and failed.
Aizpurua et al. [17] has given a new concept for unavailability estimation by presenting a framework based on a prognostics approach, while taking into account the assessment of dynamic dependability of a system. In another work, Aizpurua et al. [18] presented an online system maintenance procedure that can distinguish between critical and non-critical resources, presenting accurate suggestions for Condition-Based Maintenance (CBM) of critical resources and reactive repair recommendations for the non-critical ones. These research works are expected to have a positive impact in the field of CBM and the prognostics approach for more complex frameworks. In study [17], the exponential deterioration concept was used; whereas in study [18], the concept of constant deterioration was adopted for the purpose of the research.
In this article, an effort has been made to overcome the aforementioned limitations by initially proposing a model for opportunistic maintenance, incorporating the concept of multi-state deterioration, and then analyzing the availability of the framework with the help of Markov Model and Monte Carlo (MC) Simulation. In this regard, two types of corrective repairs were taken into account; namely perfect and imperfect repairs. Markov Model works well only for the units with exponential failure and repair rates. In extension to this analysis, for the frameworks with non-exponential failure and repair rates, MC Simulation technique has been incorporated in this research work that validate the results achieved from the Markov Model, while also addressing the above mentioned limitation. While evaluating the benefits of an opportunistic maintenance strategy with regards to availability of a framework, it has been noticed that this not only serves as an appropriate tool for decision making, but also considers different combinations of the units with regards to their availability for a specific maintenance strategy.
Software, for example, RAPTOR 6.0 (ARINC Engineering Services, Annapolis, MD, USA), and BlockSim (Reliasoft, Tucson, AZ, USA), etc., are generally used to perform availability, maintainability, reliability and other types of analyses for repairable frameworks. This software, however, does not have an opportunistic maintenance module so far. Therefore, the proposed model can be developed further to be incorporated as an extension to these analytical software programs to address their limitations.
This paper is organized into different sections. Section 2 describes the methodologies adopted. In Section 3, the modeling procedure for the framework has been defined that incorporates multi-level deterioration processes, as well as the three types of corrective repairs, both with and without opportunistic maintenance. The results achieved using Markov Model and MC Simulation are presented in Section 4. A case study to validate the proposed approach is illustrated in Section 5. Conclusions are drawn in Section 6 of the paper.
2. Markov Model and Monte Carlo Simulation for Deteriorating Frameworks
2.1. Markov Model
Markov Models are often utilized to deal with problems associated with availability and reliability of a framework, especially in situations where a unit can either fail or get repaired instantly. These models help in assessing switching probability from one state to the other in a logical manner. In this research work, ‘continuous time Markov chain process’ has been used. This process lasts until the final or completely failed state of the framework under consideration has arrived, or until a specific duration of the assigned operation is completed. The primary hypothesis related to the Markov Model declares that the conduct of the framework is to be memory less in every individual state (Fuqua, [19]).
A basic characteristic of the memory less framework is that its subsequent state depends on its present state only. In a stationary framework, the probabilities that are responsible for the transitions from one state to another are independent of time; thereby, the switching probability from a state to another state of a framework will remain unchanged, irrespective of the period when that transition takes place. Transition states are generally characterized by failure rates of the units in a framework. These transitional probabilities within individual states of a framework are defined as a function of failure rates of different units of the framework. Keeping in view the switching probability of a unit from one state to another, a system of differential equations (DEs) has been developed. All these DEs are of first-order. The number of DEs in the system will be exactly the same as in those of states defined for the framework. Therefore, it helps in limiting the problem solving to one of the following systems of DEs:
where and are the transitional probability and rate of change, respectively. Let be the number of states in the framework, then and will be vectors and will be a matrix. Solution to Equation (1) will, therefore, be given by the following expression:
where will be an matrix and will define the probability of the initial state of the framework.
Figure 1 shows a simple state diagram for a repairable framework comprising two basic states, i.e., State 0: Working and State 1: Failed. The arrow going from left to right shows the failure while the recovery is depicted by the arrow going from right to left. Let and denote the failure and repair rates respectively, and and present the framework’s probability for being at a state during any time and the rate of change thereafter, respectively.
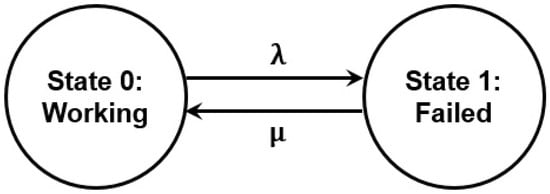
Figure 1.
State diagram for a repairable framework.
System of DEs for this basic framework can be expressed by Equations (3)–(5) below:
For initial conditions , DEs will take the following form:
For the aforementioned set of equations, the solution that we obtain in light of Equation (2) is as under (Zio, 2010) [20]. For resolution of the system of DEs, an ‘infinitesimal generator’ of continuous time Markov chain has been used [21]:
2.2. MC Simulation
MC Simulation can be graded as a dynamic and flexible tool, having significance for a wide variety of research areas. It works on the concept of random sampling i.e., with a greater sample size, there is more probability of its mean to be a precise approximation of the population mean (Amo, [22]). Similarly, it can be used to demonstrate and validate the availability of the frameworks. In this regard, it exploits the failure as well as repair rates of the units or frameworks, in order to evaluate the conduct of frameworks during a specified period of time (Alexander, [23]).
Firstly, simulation times in lieu of recorded failure and repair times of the units or frameworks are worked out. Then, pseudorandom numbers are generated utilizing a steady distribution function within an interval . After that, an appropriate conversion technique is adopted to change these pseudorandom numbers into corresponding failure and repair times for the units. The techniques utilized for the said purpose include the acceptance–rejection method, the composition method and the inverse transform method. Owing to its simplicity and ease of application, the inverse transform method has been used in this research. Nonetheless, its utilization is restricted only to the condition when the failure and repair rates can be empirically inverted. Using the inverse transform method, the interpretation of a random variable , that is either the time of failure or repair for a unit or a framework, can be expressed in terms of an exponential distribution with parameter as shown in Equation (8) below:
As distribution of is the same as that of , therefore can also be expressed as:
Likewise, applying the concept on the Weibull distribution [24], with scale parameter as and shape parameter as ‘β’, we get following expression:
After generating the failure and repair times for all units and frameworks as per some suitable distribution, simulation of a series of failure and repair times for the framework is carried out over a particular work period. A large number of iterations, encompassing the said procedure, are performed. Availability of the framework is then calculated, for the specified mission time, using the following formula:
3. Description of the Framework
A multi-unit framework has been contemplated in this research work that consists of two units, linked together in series configuration, as illustrated in Figure 2 below. The word ‘unit’ is used here to depict a sub-system, a set of units, or even a single unit that may be a part of a more resilient and complicated industrial framework.

Figure 2.
Model of the framework.
3.1. Multi-Level Deterioration Modeling
Almost every unit that belongs to some industrial framework experiences numerous levels of deterioration before it reaches a completely failed state. It can, therefore, be inferred that the deterioration rate of a unit will not be constant as it moves towards its failed state; rather, it will keep on changing through its journey to the final state. In this research work, every unit is considered to have three deterioration levels:
- State 1—Fully Operational State;
- State 2—Partially Operational State; and,
- State 3—Failed State.
3.2. Repair Procedure
Using a framework with series configuration implies that in the case of failure of a single unit, the whole framework will cease to work. Therefore, corrective repair action should be taken against the faulty unit so as to keep the framework in working condition. As already highlighted, two types of corrective repairs have been considered in this research work, i.e., perfect and imperfect repairs. Perfect repair indicates the complete repair of the unit; thereby, converting it back to its ‘fully operational state’ (State 1) from the ‘failed state’ (State 3). Imperfect repair, on the other hand, indicates that the unit is repaired to its ‘partially operational state’ (State 2) from the 'failed state' (State 3). It also indicates a less intense and swifter repair action in comparison to the perfect repair technique. It is pertinent to mention that an opportunity to carry out preventive maintenance of the unit that is still operational is also presented by the aforementioned interim period, during which the failed unit is subjected to a corrective repair procedure.
3.3. Developing the Model
The suggested model of the two unit framework with series configuration assimilating multiple levels of deterioration can be developed while taking into account the multi-level deterioration modeling and repair procedure, as highlighted in Section 3.1 and Section 3.2 above.
The framework consists of two units, each of which can be in any of the three defined states at any specific time. Series configuration of these units results in a total of nine feasible states that the framework can experience during its lifespan. These states also include the state of framework when both the units are in State 3, i.e., the failed state. As far as a series framework is considered, it is only possible when both the units fail at the same time. The possibility of this eventuality is negligible and it can therefore be discarded. Assumptions made for the framework are as follows:
- The opportunistic maintenance process will finish before the completion of repair process for the failed unit.
- The unit can perform its intended task in fully operational and partially operational states only.
4. Implementation of Analytical and Simulation Approaches for Problem Solving
4.1. Analytical Approach—Markov Model
Steps involved in reaching to the solution of the problem using the Analytical Markov approach are illustrated in Figure 3.
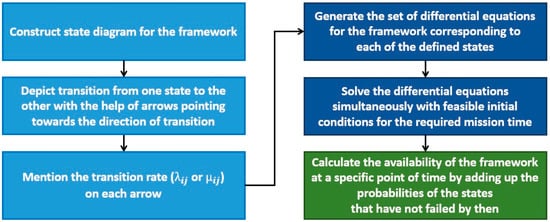
Figure 3.
Steps involved in reaching the solution using the Markov approach.
4.2. Simulation Approach—MC Simulation
In this technique, initial MC Simulation codes are developed that simulate the working of framework for the complete duration of the specified mission. Afterwards, availability of the framework is calculated for a large number of simulation runs. For the purpose of this research, MC Simulation codes were assessed for a confidence level of 0.95 and a confidence interval of 10−5. The algorithm used for developing the MC Simulation codes is depicted using a flow chart in Figure 4, as below:
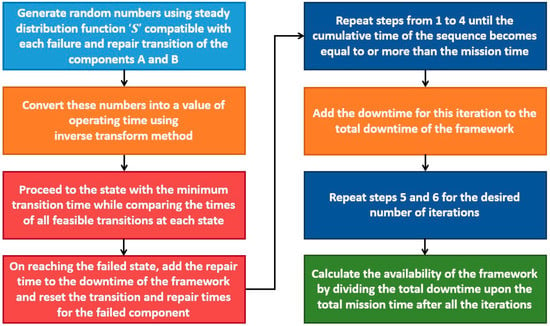
Figure 4.
Algorithm for Monte Carlo (MC) Simulation codes.
5. Case Study
5.1. Problem Formulation
Let us consider a framework comprising of two units, i.e., a transformer (Unit A) and a safety unit for the transformer (Unit B). Both the units are linked together in series configuration. The above mentioned framework will be used to exhibit the significance of the proposed technique in dealing with the availability analysis of the framework. In this case study, exponential distribution for failure and repair rates has been considered for each unit. Data in this regard is obtained from the research work by Roos and Lindah (2004) [25]. Table 1 below enumerates the failure and repair rates for both the units as highlighted in the said literature.

Table 1.
Literature values of failure rates and repair times for the units.
In order to include the concept of multi-level deterioration in the case study, it is assumed that the failure rate for each unit grows as it degrades. This assumption has been made on the basis of discussions with maintenance specialists. Basic two state data for the framework was acquired from the literature. The same was then segregated based on discussions with the professionals from the industry, so as to obtain the failure and repair rates corresponding to different deteriorating states of the framework. The indices of failure and repair rates denotes the established states of the framework. Numerical values calculated for failure and repair rates of the units are enumerated in Table 2 below:

Table 2.
Failure and repair rates of the units.
5.2. Numerical Solution to the Problem
First, state diagrams for the problem are drawn based on the identified failure and repair rates for all the state transitions. State diagrams for perfect repair, with and without opportunistic maintenance, are illustrated in Figure 5 and Figure 6 respectively. In this way, state diagrams for imperfect repair, with and without opportunistic maintenance, can also be drawn. Failure and repair rates for the framework are denoted with the terms and respectively; where index exhibits the state before transition, and state of the framework after transition is exhibited by index . It can be noticed from Figure 5 and Figure 6 below that . Let denotes the framework’s probability for being at state at any interval , then in the light of discussion in Section 2.1 above, DEs for the problem can be formulated from the state diagrams illustrated in Figure 5 and Figure 6. These systems of first-order DEs are enumerated in Appendix A and Appendix B, respectively.
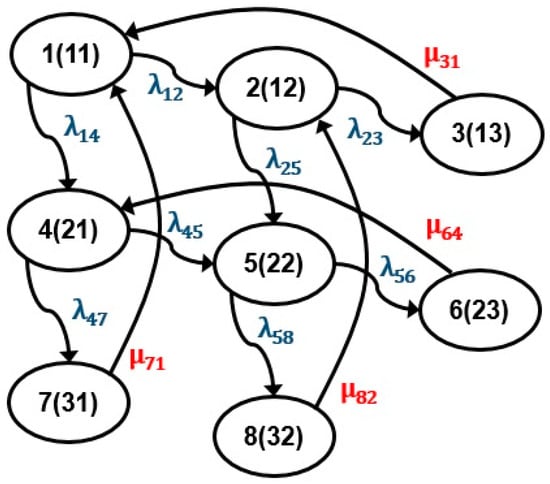
Figure 5.
Perfect repair without opportunistic maintenance.
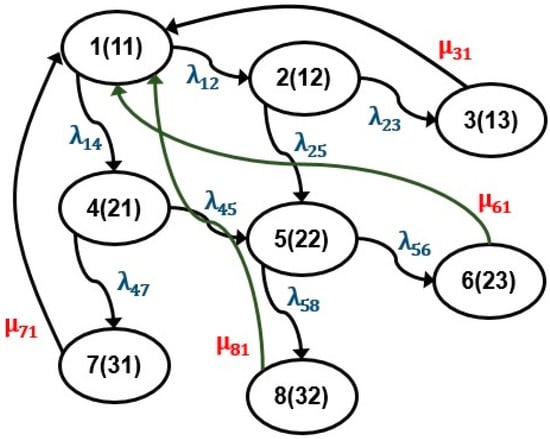
Figure 6.
Perfect repair with opportunistic maintenance.
In this way, DEs for imperfect repair can also be developed for both cases. These systems of DEs are then solved in MATLAB (MathWorks, Natick, MA, USA) using initial conditions as . Using Markov Model, availability of the framework is then acquired by adding up the probabilities of all the working states. The results of availability thus achieved are illustrated in Table 3 below.

Table 3.
Availability of the framework.
In addition, solution to the problem is also achieved using the MC Simulation technique. In this regard, the algorithm defined in Section 4.2 above has been used to develop the simulation codes. The results of availability achieved using MC Simulation are also illustrated in Table 3 above.
It can be clearly seen from the results in Table 3, that when the framework is monitored under the conditions of opportunistic maintenance, it experiences a certain increase in the availability of the framework for perfect as well as imperfect repair. Therefore, it can be inferred that the availability of the given framework will increase with the adoption of opportunistic maintenance strategy, regardless of the types of repair. Identical results for availability of the framework are achieved using both Markov Model and MC Simulation techniques. This validates the algorithm developed for the MC Simulation and, hence, it can be expanded further for the frameworks with non-exponential failure and repair distributions, for instance, Lognormal or Weibull. An appropriate maintenance strategy that results in maximizing the availability of a framework can, thus, be identified by assessing the benefits of opportunistic maintenance strategy using the yardstick of availability. The aforementioned results for the problem under discussion illustrate that the availability of the framework will be maximized when opportunistic maintenance strategy under imperfect repair is adopted. It is pertinent to mention that this strategy is effective only for the data set that has been considered for the purpose of this case study and, that, the same may vary based upon the values used for failure and repair rates of the framework. Therefore, it cannot be considered as an optimal maintenance strategy. In order to reach a cost-effective maintenance solution for a specific problem, effort should be made to look for the trade-offs in costs and its effect on life of the unit. Moreover, financial benefits acquired as a result of the increased availability of the framework should compensate for the additional cost incurred on carrying out opportunistic maintenance of the framework.
5.3. Graphical Solution to the Problem
Using the MC Simulation technique, a graphical solution to the problem has also been obtained. In this regard, different dimensions of the solution are presented. These dimensions range from combined availability to individual availability of the units. In addition, optimal values for mean times of failure and repair, and estimated probability of the operational units of the framework have also been illustrated through graphs. Figure 7 illustrates the combined percentage of availability, based on operational units of the framework over a specified period of time. Using the opportunistic maintenance strategy, both the units remained operational for of the total time, while the framework was only under maintenance for of the time. Thus, an overall high percentage of availability has been achieved using the opportunistic maintenance strategy.
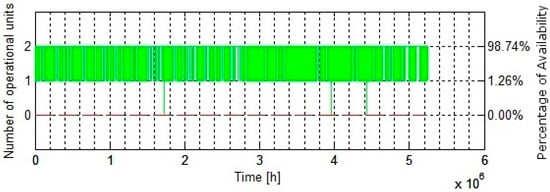
Figure 7.
Combined availability of operational units over the specified period of time.
Availability of individual units of the framework over the given time duration is shown in Figure 8 below. Percentage of availability for both the units comes out to be and the individual downtime for each unit appears to be only. It is pertinent to mention that these values are obtained for the framework being monitored under the conditions of opportunistic maintenance using the MC Simulation technique. In addition to the high percentage of combined availability of the framework, even higher values are achieved for the availability of individual units under opportunistic maintenance conditions.
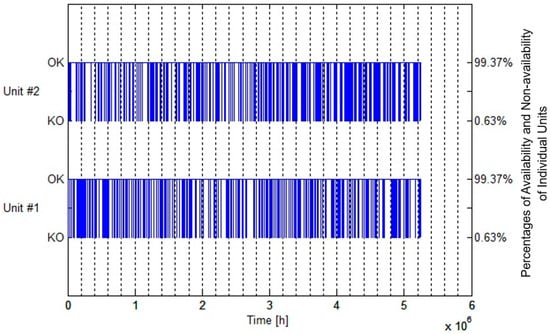
Figure 8.
Availability of individual units over specified period of time.
Mean time to failure (MTTF) and mean time to repair (MTTR) are two very important performance indicators as far as availability of a framework is concerned. If these indicators are known, they can be best utilized to calculate the availability. Figure 9 depicts the optimal values for MTTF and MTTR for the framework under an opportunistic maintenance strategy. In this case, these values appears to be and , respectively.
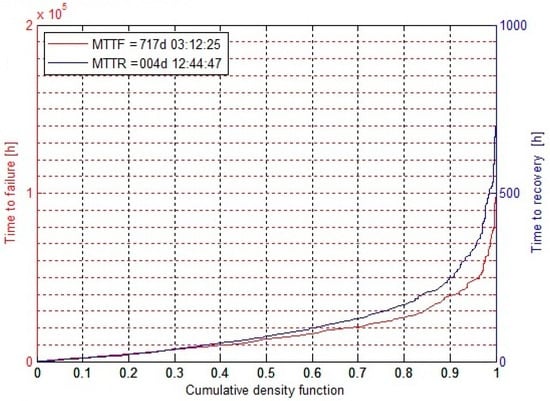
Figure 9.
Optimal values of mean time to failure (MTTF) and mean time to repair (MTTR) for the framework under an opportunistic maintenance strategy.
Estimated probability of operational units of the framework is illustrated in Figure 10 below. This horizontal bar graph is actually the inverse of the graph for combined availability, as shown in Figure 7 above. In this case, the estimated probability for both the units of the framework to be operational is .
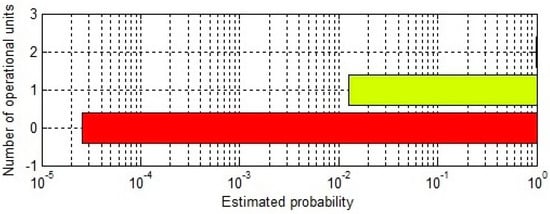
Figure 10.
Estimated probability of operational units of the framework.
6. Conclusions
In this research work, an analytical approach in the form of a Markov Model has been used to evaluate availability of the framework comprising two units in series configuration, while implementing an opportunistic maintenance strategy. In this regard, models for two types of corrective repairs, i.e., perfect and imperfect repairs, were developed, with as well as without opportunistic maintenance. Validation of the results achieved for the availability of the framework in all cases was then carried out using the MC Simulation technique. Thus, it is evident that the said technique can be expanded further for frameworks with non-exponential failure and repair distributions, for instance, Lognormal or Weibull. In addition, this model can be further developed to be incorporated as an extension to currently available analytical software that does not have an opportunistic maintenance module. As the concept of multi-state deterioration has also been incorporated in this presented framework, therefore, the recommended technique gives a more pragmatic approximation of availability for a repairable framework. Future work in this arena includes implementation of the concept on more complex frameworks having multiple units linked together in different configurations and with increased deterioration levels. Moreover, in order to analyze the financial advantages and disadvantages of opportunistic maintenance, a cost function should also be generated as part of future research. This cost function along with availability can then be used to develop a model for optimal maintenance strategy with restricted maintenance assets.
Acknowledgments
Funding is partially from the National University of Sciences & Technology and partially from the contribution of the authors.
Author Contributions
Shahid Ikramullah Butt and Omer Gilani conceived and designed the experiments along with guidance during the research phase; Mansoor Ahmed Siddiqui did the literature review, performed the simulation modelling and wrote the paper; Mohsin Jamil, Adnan Maqsood and Faping Zhang analyzed the results.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A. System of DEs Corresponding to the State Diagram Illustrated as Figure 5
Appendix B. System of DEs Corresponding to the State Diagram Illustrated as Figure 6
References
- Collection and Exchange of Reliability and Maintenance Data for Equipment (ISO 14224); International Standards Organization: Geneva, Switzerland, 2006.
- Huang, J.S.; Okogbaa, O.G. Preventive Replacement/Maintenance Program Development and Evaluation for Multi-unit Systems with Economic Dependency: Stochastic Modeling and Simulation Study. Ph.D. Thesis, University of South Florida, Tampa, FL, USA, 1993. [Google Scholar]
- Chiacchio, F.; D’Urso, D.; Manno, G.; Compagno, L. Stochastic hybrid automaton model of a multi-state system with aging: Reliability assessment and design consequences. Reliab. Eng. Syst. Saf. 2016, 149, 1–13. [Google Scholar] [CrossRef]
- Chiacchio, F.; D’Urso, D.; Compagno, L.; Pennisi, M.; Pappalardo, F.; Manno, G. SHyFTA, a Stochastic Hybrid Fault Tree Automaton for the modelling and simulation of dynamic reliability problems. Expert Syst. Appl. 2016, 47, 42–57. [Google Scholar] [CrossRef]
- Li, Y.; Cui, L.; Lin, C. Modeling and analysis for multi-state systems with discrete-time Markov regime-switching. Reliab. Eng. Syst. Saf. 2017. [Google Scholar] [CrossRef]
- Lu, J.M.; Wu, X.Y. Reliability evaluation of generalized phased-mission systems with repairable components. Reliab. Eng. Syst. Saf. 2014, 121, 136–145. [Google Scholar] [CrossRef]
- Shrestha, A.; Xing, L.; Dai, Y. Reliability analysis of multistate phased-mission systems with unordered and ordered states. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2011, 41, 625–636. [Google Scholar] [CrossRef]
- Nicolai, R.P.; Dekker, R. Optimal maintenance of multi-component systems: A review. In Complex System Maintenance Handbook; Springer: London, UK, 2008; pp. 263–286. [Google Scholar]
- Radner, R.; Jorgenson, D.W. Opportunistic replacement of a single part in the presence of several monitored parts. Manag. Sci. 1963, 10, 70–84. [Google Scholar] [CrossRef]
- Van Der Duyn Schouten, F.A.; Vanneste, S.G. Analysis and computation of (n, N)-strategies for maintenance of a two-component system. Eur. J. Op. Res. 1990, 48, 260–274. [Google Scholar] [CrossRef]
- Wang, H.; Pham, H. Optimal preparedness maintenance of multi-unit systems with imperfect maintenance and economic dependence. Reliab. Optim. Maint. 2006, 135–150. [Google Scholar] [CrossRef]
- Pham, H. System Reliability Concepts. In System Software Reliability; Springer: London, UK, 2006; pp. 9–75. [Google Scholar]
- Castanier, B.; Grall, A.; Bérenguer, C. A condition-based maintenance policy with non-periodic inspections for a two-unit series system. Reliab. Eng. Syst. Saf. 2005, 87, 109–120. [Google Scholar] [CrossRef]
- Ambani, S.; Li, L.; Ni, J. Condition-based maintenance decision-making for multiple machine systems. J. Manuf. Sci. Eng. 2009, 131, 1–9. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, S.; Li, B. A condition-based and opportunistic maintenance model for a two-unit deteriorating system. In Proceedings of the 2011 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Xi’an, China, 17–19 June 2011; pp. 590–595. [Google Scholar]
- Jain, S. Opportunistic Maintenance Policy of a Multi-Unit System under Transient State. Ph.D. Thesis, University of South Florida, Tampa, FL, USA, 2005. [Google Scholar]
- Aizpurua, J.I.; Catterson, V.M.; Papadopoulos, Y.; Chiacchio, F.; Manno, G. Improved dynamic dependability assessment through integration with prognostics. IEEE Trans. Reliab. 2017, 1–21. [Google Scholar] [CrossRef]
- Aizpurua, J.I.; Catterson, V.M.; Papadopoulos, Y.; Chiacchio, F.; D’Urso, D. Supporting group maintenance through prognostics-enhanced dynamic dependability prediction. Reliab. Eng. Syst. Saf. 2017. [Google Scholar] [CrossRef]
- Fuqua, N.B. The Applicability of Markov Analysis Methods to Reliability, Maintainability, and Safety; Selected Topic in Assurance Related Technologies (START); Reliability Analysis Center: Rome, NY, USA, 2003; Volume 2, pp. 1–8. [Google Scholar]
- Zio, E. Availability analysis: Concepts and methods. In Wiley Encyclopaedia of Operations Research and Management Science; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Padma, G.; Vijayalakshmi, C. An analysis of continuous time Markov chains using generator matrices. Int. J. Comput. Appl. 2011, 35, 20–24. [Google Scholar]
- Amo, R.G. Handbook, Electronic Reliability Design; MIL-HDBK-338B; Air Force Research Laboratory/IFTB: Rome, NY, USA, 1998. [Google Scholar]
- Alexander, D. Application of Monte Carlo simulations to system reliability analysis. In Proceedings of the 20th International Pump User Symposium, Texas A&M University, Houston, TX, USA, 17–20 March 2003; pp. 91–94. [Google Scholar]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables, and Stochastic Processes; Tata McGraw-Hill Education: New Delhi, India, 2002. [Google Scholar]
- Roos, F.; Lindah, S. Distribution system component failure rates and repair times—An overview. In Proceedings of the Nordic Distribution and Asset Management Conference, Espoo, Finland, 23–24 August 2004; pp. 1–6. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).