Abstract
A new DS (Dempster-Shafer) combination method is presented in this paper. As data detected by a single sensor are characterized by not only fuzziness, but also partial reliability, the development of multi-sensor information fusion becomes extremely indispensable. The DS evidence theory is an effective means of information fusion, which can not only deal with the uncertainty and inconsistency of multi-sensor data, but also handle the inevitably ambiguity and instability under noise or possible interference. However, the application of DS evidence theory has some limitations when multi-sensor data are conflicting. To address this issue, the DS evidence theory is modified in this paper. Adopting the idea of cluster analysis, we firstly introduce the Lance distance function and spectral angle cosine function to revise original evidence separately before the combination of evidence. Then, based on the modifications of original evidence, an improved conflict redistribution strategy is ulteriorly raised to fuse multi-sensor information. Finally, the numerical simulation analyses demonstrate that the improvement of the DS evidence theory available in this paper overcomes the limitations of conventional DS evidence theory, and realizes more reliable fusion with multi-sensor conflicting information compared to the existing methods.
1. Introduction
Sensors are the main tool to capture information in actual monitoring systems. With the rapid development of multifarious sensor technology, the research of multi-sensor information fusion has become the mainstream. Simultaneously, as single-sensor systems have certain uncertainty and potential unreliability, multi-sensor information fusion has become an inevitable trend [1]. By means of information fusion, multi-sensor systems can obtain more abundant, precise and reliable information, which successfully overcome the limitations of single-sensor systems. The Dempster–Shafer evidence theory, also called DS theory, is a widely used technique in the multi-sensor information fusion field. DS theory can operate without priori knowledge and conditional probability, which is considered an inexact derivation of probability theory and Bayesian reasoning [2]. Hence, DS theory is applied to various smart areas, like monitoring systems [3,4], decision making [5,6], fault diagnosis [7,8], target tracking [9,10], and so forth. The wide application of DS theory has attracted a lot of scholars. Through the research of DS application, it is found that the large amount of conflict among evidence is generally caused by uncertain information in multi-sensor systems, and DS theory would obtain the counterintuitive results when evidence is highly conflicting [11]. Thus, the way to solve the evidence conflict is the key to achieving a reasonable and reliable fusion for multi-sensor systems.
Since the fuse paradox was presented by Zadeh [12], the combination of conflicting evidence has become one of the most important pieces of research for the DS theory. Existing modified methods are divided into two categories—the modification of combination equations in DS theory and the revision of original evidence before combination.
The former kind of methods [13,14,15,16,17,18] optimize the DS combination rule to avoid counterintuitive results caused by the normalization procedure. Smets [13] argued that the conflict is caused by the incompleteness of the frame of discernment under a partially unknown monitoring environment. Hence, Smets gave the mass of conflict directly to ∅, which is regarded as an unknown proposition. Yager [14] followed Smets’ idea and gave the mass of conflict directly to instead. Although these two methods solve the conflict situation theoretically, the uncertainty of the system still exists. In addition, Sun [15] modified these two methods by realizing the distinction between reliable evidence and conflict evidence. Furthermore, by taking advantage of the information quantity of conflict, Li [16] reasonably used a weighted redistribution to resolve the conflict situations. These two methods successfully improve the reliability and accuracy of combination results. Additionally, from the viewpoint of local conflict, references [17,18] respectively proposed two kinds of local conflict assignment methods. However, these methods sometimes violate the theoretical properties of DS combination rule like commutativity and associativity.
The latter methods [19,20,21,22,23,24] modify original evidence before using the DS combination rule. Murphy [19] and Horiuchi [20] replaced the original evidence with average evidence and weighted evidence separately, which led to a new trend of conflict resolution. By the introduction of distance function, Deng [21] presented an improved combination rule based on evidence credibility. Adopting this idea, Guo [22] put forward a modified combination rule based absolute credibility. These two methods both use distance function to calculate the evidence credibility, which successfully produces a great description of information quantity among evidence. In addition, Wei [23] introduced the K-L (Kullback-Leibler) distance function to present a novel fusion method for conflict evidence. Considering that different distance functions have different description effects of evidence credibility, Lin [24] proposed a new combination method based on the Mahalanobis distance function. However, the Mahalanobis distance function requires the covariance computation of matrix, which is not suitable for large-scale data processing.
Through the comparison between two kinds of conflict resolutions, it is easy to see that the former methods directly cancel the normalization step in DS theory and redistribute the conflict with different measure, while the latter methods consider the essential differences of sensors in multi-sensor systems, and solve the conflict by modifying the original evidence instead. Therefore, two kinds of existing methods realize the multi-sensor fusion with conflicting information from different viewpoints, which have different advantages and disadvantages.
In this paper, we propose a novel combination method to solve the fusion of multi-sensor conflicting information by adopting both ideas’ merits. Before combining the evidence, we firstly revised the original evidence separately by the introduction of the Lance distance function and a spectral angle cosine function. The Lance distance function and spectral angle cosine function are two indexes to measure the difference or similarity in the cluster analysis theory [25,26]. Thus, the usages of the Lance distance function and spectral angle cosine function reasonably describe the evidence conflict, which can provide a powerful support for later processing. Then, an improved conflict redistribution strategy is ulteriorly raised to assign the mass of conflict. This conflict redistribution strategy is processed based on the local conflict analysis, which is used to approximate the global optimization of multi-sensor fusion. Thus, the novel conflict redistribution strategy is able to enhance the reliability and rationality of synthesis results. After the comprehensive processing of conflicting information, the multi-sensor system will obtain an accurate and effective fusion results.
The rest of this paper is organized as follows. Section 2 presents the theoretical foundations of DS theory in detail. In Section 3, the fuse paradoxes are given to show the shortcomings of conventional DS theory. In Section 4, two typical existing modified methods are introduced. Section 5 derives the improvement of DS theory in this paper, and gives the specific implementation of the proposed algorithm. Section 6 presents the numerical simulation results and analyses to show the great conflict resolution performance of the proposed algorithm. Finally, Section 7 concludes the paper.
2. Theoretical Foundations
Dempster and Shafer separately presented and perfected DS theory in 1967 and 1976 [27,28]. It is the foundation of multi-sensor information fusion that can deal with incomplete, uncertain and unclear information in multi-sensor systems.
2.1. Frame of Discernment
DS theory is built up on a finite and non-empty set, called frame of discernment (the frame). It contains M mutually exclusive and exhaustive hypotheses.
where M is the number of hypotheses in system, and represents the ith hypothesis that reflects the ith possible recognition result.
Based on the definition of the frame, the power set can be derived as
for .
2.2. Basic Probability Assignment
In order to describe the support degree for hypotheses, basic probability assignment, also called mass function, is introduced based on . Mass function is a function , which satisfies the following Equations:
where is the basic support degree of evidence m to proposition H.
Equations (3) and (4), respectively, reflect the non-negativity and normalization of mass function. Due to the lack of further knowledge, cannot be subdivided to any proper subset of H. Moreover, if , H is called the focal set, and the union of all focal sets is referred to as the core of mass function.
2.3. Uncertainty Description
According to the definition of mass function, belief function () and plausibility function () on can be defined separately as
It is easily seen in Equations (5) and (6) that describes the true possibility of proposition H, while expresses the unsuspicious possibility of proposition H. Therefore, and , respectively, present the lower and upper bounds of probability, which forms the uncertainty interval (shown in Figure 1).
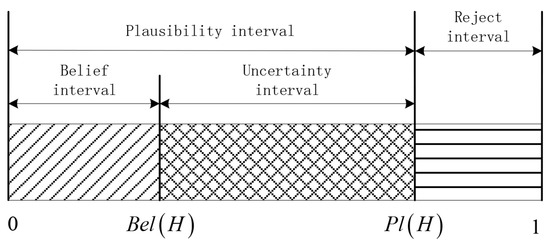
Figure 1.
Uncertainty description of proposition H.
The uncertainty description reveals that DS theory can describe the uncertainty of probability, which reflects the fact that DS theory is an uncertainty reasoning theory. Thus, DS theory can realize the information fusion in multi-sensor systems. The relationship between and can be deduced from Equations (5) and (6) as
where is the complement set of H.
2.4. DS Combination Rule
Assuming that the system’s frame is , and two independent and reliable pieces of evidence are separately obtained from two sensors, the DS combination rule can be defined as
where K is the conflict factor that reflects the conflict degree of two pieces of evidence :
The DS combination rule directly sums two pieces of evidence ; thus, Equation (9) is also called the direct sum operation, expressed as . is the normalized factor, which makes the synthetic evidence m in Equation (9) meet non-negativity and normalization in Equations (3) and (4).
According to a similar principle, the combination rule of multiple evidence can be deduced as:
where the conflict degree K of N evidence is
Obviously, the DS combination rule satisfies both commutative law and associate law, which are shown separately as follows:
3. Fuse Paradoxes of DS Theory
Due to the fuzziness and uncertainty in multi-sensor systems, the application of DS theory will obtain counterintuitive results when evidence is highly conflicting. The conflict situations are called fuse paradoxes [12]. According to the summary of references [12,13,14,15,16,17,18,19,20,21,22,23,24], the fuse paradoxes are generally caused by the normalization step of the DS combination rule. In Equation (10), K represents the conflict degree of evidence . The larger the value of K is, the greater the conflicts are between , and it is the conflict between that will lead to counterintuitive results in Equation (9). In particular, if , Equation (9) cannot be employed since the denominator of the normalized factor is 0. Moreover, some conflict cases are discussed in this section.
Case 1: Assuming that the frame of system is , and there are two pieces of evidence that are processed by the system:
According to Equation (10), the conflict degree . It is apparent that evidence conflict completely, which causes the denominator in Equation (9) to become zero. Under such circumstances, the DS combination rule is unable to synthesize.
Case 2: Assuming that the frame of system is , and the evidence set is :
From the viewpoint of intuitive judgment, the accurate synthesis results should drastically support proposition A because that evidence all assign proposition A with a large amount of support. Unfortunately, the fusion result is
The counterintuitive result is caused by conflict evidence . Evidence totally denies proposition A as , which leads to a high conflict degree of . The “one ballot veto” phenomenon reflects the typical shortcomings of DS theory when fusing highly conflicting evidence.
Case 3: Assuming that the frame of system is , and the evidence set is :
According to Equations (11) and (12), the conflict degree is , and the synthesis result is:
It is obvious that reasonable synthetic results should support proposition A most. However, the “one ballot veto” paradox described in Case 2 triggers error reasoning results of . In addition, most pieces of evidence such as give proposition B little support, while the synthetic results give proposition B the biggest support. This counterintuitive situation further reflects the possible error reasoning processing of conventional DS theory.
Based on the discussions above, we can draw a general conclusion:
- Conflict situations commonly occur in multi-sensor fusion systems. The way to fuse conflicting information is the key to realizing multi-sensor information fusion.
- All three conflict situations have one common point—the conflict degree K is high. The way to combine highly conflicting evidence is the key to solving conflict situations.
Thus, to realize reliable and accurate fusion for multi-sensor systems, a novel combination method for high conflict evidence is put forward in this paper.
4. Existing Modified Methods
In order to solve the fuse paradoxes in DS theory, several researchers have presented different ingenious solutions. According to the discussion in Section 1, existing modified methods can be classified into two categories. Among them, two typical methods are introduced in this section.
4.1. Combination Rule Based on Local Conflict Degrees
One way to solve conflict situations is the modification of the DS combination rule. Reference [15] proposes a new combination rule based on evidence credibility,
for , where represents the combination mass in Equation (9) without normalization, and represents the average support of proposition H. is the evidence credibility:
By taking consideration of local conflict degrees into account, the evidence credibility is calculated. Thus, the introduction of the local conflict concept is the innovation of this modified combination method:
where is the local conflict of evidence , and is the average conflict degree of all local conflict , which represents the global conflict of system.
Obviously, is neither equal to the conflict degree K in Equation (10) nor the local conflict degree in Equation (25). Ulteriorly, it is apparent that reflects the conflict degree of the system more accurately. Owing to the fact that is the decreasing function of , is available to express the credibility degree of the system as Equation (23) adopts the idea of local analysis.
4.2. Combination Method Based on Mahalanobis Evidence
Another way to solve conflict situations is the revision of conflict evidence before combination. Based on the introduction of Mahalanobis distance, reference [24] presents an improved fusion method based on modified evidence. The modified evidence is defined as:
where is the credibility degree of evidence.
The calculation of evidence credibility is shown below.
Step 1: Calculate the distance degree of evidence by the introduction of the Mahalanobis distance function.
Suppose X and Y are two sample sets obtained from population G, with the same mean vector and covariance matrix . The Mahalanobis distance between X and Y is defined as follows:
and the Mahalanobis distance between X and population G is defined as:
Then, the Mahalanobis distance between evidence is derived:
where is the covariance matrix of evidence vector :
Step 2: After the calculation of Mahalanobis distance, the distance matrix D can be defined:
In addition, the average distance of evidence to other evidence can be obtained:
Step 3: As represents the unreliable degree of evidence , the evidence reliability is derived:
According to the modification of original evidence in reference [24], we can see that if one piece of evidence is far away from other evidence, then the evidence has a low support from other evidence. Thus, its reliability is lower than other evidence. On the contrary, the evidence has a high degree of support, and its reliability is higher than other evidence.
5. The Improvement of DS Theory
To improve the accuracy, validity and reliability of multi-sensor fusion, the proposed algorithm firstly adopts the Lance distance function and spectral angle cosine function to revise original evidence, respectively, and then employs an improved conflict redistribution strategy to fuse multi-sensor evidence. In addition, the algorithm scheme is illustrated in this section.
5.1. Revised Evidence Based on the Lance Distance Function
The revised evidence is generally obtained by the Minkowski distance function and Mahalanobis distance function. However, the Minkowski distance function requires the same attribute dimension that loses the consistency of evidence, and the Mahalanobis distance function requires the covariance computation of matrix that is not suitable for large-scale data processing [29]. Therefore, we introduce a more ideal distance measurement as the Lance distance function.
Assuming that the system’s frame is , and there are N sensors in system, the mass functions of evidence can be defined as and , where . The Lance distance between evidence is
The Lance distance function is very sensitive to small changes close to . It is often regarded as a generalization of the dissimilarity measure for binary data [29]. According to Equation (34), is the average distance of evidence among different hypotheses in . is a dimensionless attribute, which is not sensitive to large singular values. Hence, overcomes the defects of the Minkowski distance function and the Mahalanobis distance function, which is more ideal for evidence revision.
Then, we can define the reliability degree of evidence :
where satisfies
In Equation (36), represents the total distance between evidence and other evidence. In Equation (35), the evidence reliability is the decreasing function of ; thus, reflects the reliability of evidence .
Adopting to revise conflict evidence, the modified evidence is deduced:
5.2. Revised Evidence Based on Spectral Angle Cosine Function
At present, the modification of evidence is mainly completed by the distance function [21,22,23,24]. Considering that the distance function is not the only measurement of two pieces of evidence in the cluster analysis theory, we introduce a measurement method based on similarity analysis. Accordingly, from the viewpoint of similarity measurement, we further modify the evidence by the introduction of a spectral angle cosine function.
Employing the spectral angle cosine function, the similarity degree between evidence is
Then, the support degree and credibility degree of evidence can be separately defined by :
Equations (38)–(40) reveal that if one piece of evidence is close to other evidence, then the piece of evidence has a high level of support from other evidence. Thus, its credibility is higher than other evidence. On the contrary, the evidence has a low degree of support, and its reliability is lower than other evidence. Therefore, the introduction of a spectral angle cosine function reasonably calculates the credibility of evidence .
Since meets the normalization condition , the revised evidence based on spectral angle cosine function is deduced:
5.3. Improved Conflict Redistribution Strategy
As the correction of original evidence has been finished, the DS fusion method should be applied. Referring to reference [18], we put forward an improved conflict redistribution strategy to avoid the counterintuitive results that are caused by the normalization step:
where is the conflict redistribution indicator:
where is the threshold of conflict redistribution. The value of can be set based on priori knowledge, or can be generally selected in . To ensure the unity standard of simulation in this paper, .
In Equation (43), the local conflict degree between pieces of evidence is assigned to the proposition with larger support when its numerical difference is larger than the threshold . When the different values between pieces of evidence are less than the threshold , pieces of evidence are regarded as bearing the same responsibility for the conflict. Thus, the local conflict degree is evenly distributed to two propositions .
It is clear that the local conflict analysis of the proposed conflict redistribution strategy conforms to intuitive judgment criterion. Compared with the global conflict allocation schemes in references [16,17], the local conflict redistribution strategy enhances the rationality and availability of conflict assignment. Furthermore, the improved conflict redistribution strategy solves the fuse paradoxes by abolishing the normalization step, while ensuring the normalization property of synthetic evidence by distributing the conflict degree reasonably.
5.4. Flow Chart of the Proposed Algorithm
Through the above analyses, the algorithm scheme of the proposed multi-sensor conflicting information fusion approach is summarized in Figure 2.
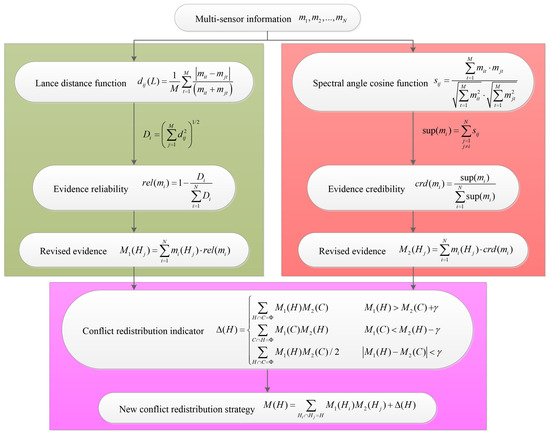
Figure 2.
Implementation chart of the multi-sensor conflicting information fusion algorithm.
The innovation points of the novel algorithm are marked by the dashed rectangles. The specific implementation of the proposed algorithm can be summarized:
- Step 1:
- Revise original evidence by the introduction of the Lance distance function.
- Step 2:
- Revise original evidence by the introduction of the spectral angle cosine function.
- Step 3:
- Redistribute the conflict degree of two pieces of revised evidence by employing a new redistribution strategy.
6. Simulation Results and Analyses
In order to verify the effectiveness and priority of the proposed algorithm, two numeric simulation examples in reference [24] are adopted. One is the consistent information, and the other is the conflicting information. In addition, some existing modified methods, especially two discussed in Section 4, are applied as comparison methods. These two simulations can respectively prove the validity and superiority of the proposed algorithm.
6.1. Multi-Sensor Fusion with Consistent Information
Assume the frame of multi-sensor system is , and the evidence set is . Suppose that A is the true target, and the consistent information is shown in Table 1.

Table 1.
Mass functions of consistent information.
It is evident in Table 1 that all evidence of multi-sensor systems are relatively consistent in identifying target A. Thus, the effective fusion method should give target A the biggest support.
Then, the fusion results of the comparison methods and proposed algorithm are obtained in Table 2.

Table 2.
Fusion results of different methods with consistent information.
Where, DS combination is the Dempster-Shafer combination method, K-L distance represents the improved combination method based on K-L distance, and Mahalanobis distance represents the new combination method based on Mahalanobis distance.
According to Table 2, we can get the following analyses about the existing modified methods:
- In the fusion results of the DS combination rule, although the support to the true target A is the biggest, the support to target B is always 0. Through the observation of Table 1, we can conclude that the “one ballot veto” paradox described in Section 3 leads to the unreasonable reasoning, and the paradox is caused by .
- References [15,16] represent the former kind of methods that are discussed in Section 1, while K-L distance [23] and Mahalanobis distance [24] represent the latter kind of methods that are discussed in Section 1. These four methods all give reasonable fusion results and recognize the true target A precisely.
The fusion results of the proposed algorithm tell us that no matter how many consistent pieces of evidence are combined, the proposed algorithm always identifies the true target A with the biggest support. In addition, compared to the existing methods, the support to true target A in the proposed algorithm is the biggest. Therefore, it is an effective and reliable combination method.
6.2. Multi-Sensor Fusion with Conflicting Information
As the effectiveness of the neoteric algorithm is verified, we adopt the conflicting information to prove its priority. Under the same assumption of Table 1, the conflicting information is shown in Table 3. Comparing Table 3 with Table 1, it can easily be checked that is the conflict evidence.

Table 3.
Mass functions of conflicting information.
According to Table 4, we can get the following analyses about the existing modified methods:

Table 4.
Fusion results of different methods with conflicting information.
- The fusion result of the DS combination rule completely believes that B is the true target, which is contrary to intuition judgement. Obviously, the DS combination rule cannot achieve reliable fusion for conflicting information.
- In the fusion results of reference [15], the support to is always the biggest, which illustrates that the uncertainty in the fusion results is still high. Thus, reference [15] cannot identify the true target under highly conflicting situations.
- With the combination of added evidence , the support degree of true target A in reference [16], K-L distance [23], and Mahalanobis distance [24] is growing. However, the growth is slow, which means that reference [16], K-L distance [23], and Mahalanobis distance [24] are not completely reliable combination methods under conflict situations.
Compared to the existing modified methods, the proposed algorithm can identify the true target A with the added 3rd sensor . Obviously, the novel algorithm has a better convergence effect that can deal with highly conflicting situations more effectively. Thus, it has priority in the multi-sensor fusion with highly conflicting information.
After that, the fusion results of the comparison methods and proposed algorithm are exhibited in Table 4.
7. Conclusions
The potential error of sensor measurement, uncertainty of unknown monitoring environment, and even possible man-made interference would lead to fuzzy and conflicting information in multi-sensor systems. Since conflicting information is common in multi-sensor systems, the way to combine conflicting information becomes the core to realizing reliable and accurate multi-sensor fusion. In this paper, a neoteric combination method for multi-sensor conflicting information is proposed. Firstly, the introductions of Lance distance function and spectral angle cosine function separately revises original evidence from different standpoints, and, then, the novel conflict redistribution strategy assigns the local conflict reasonably. By means of the comprehensive processing of conflict evidence, reasonable and effective fusion results can be obtained. Through the comparison to existing methods, simulation results and analyses demonstrate that the proposed algorithm can not only obtain accurate fusion results with consistent information, but also obtain reliable fusion results with conflicting information. Hence, the novelty and practicability of the proposed algorithm are verified. As the reliability and accuracy of information fusion are both solved, the effective application of multi-sensor systems is further guaranteed.
Acknowledgments
The paper is funded by the National Key Research and Development Program of China (Grant No. 2016YFF0102806), and the National Natural Science Foundation of China (Grant No. 51509049). In addition, the work is partially supported by the Natural Science Foundation of Heilongjiang Province China (Grant No. F201345), and the Fundamental Research Funds for the Central Universities of China (No. GK2080260140).
Author Contributions
Yibing Li conceived the research subject and background, Fang Ye contributed to the two revisions of original evidences, Jie Chen contributed on the conflict redistribution strategy and carried out the experiments. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fan, X.; Zuo, M.J. Fault diagnosis of machines based on D-S evidence theory. Part 1: D-S evidence theory and its improvement. Pattern Recognit. Lett. 2006, 27, 366–376. [Google Scholar] [CrossRef]
- Deng, Y. Deng entropy. Chaos Solitons Fractals 2016, 91, 549–553. [Google Scholar] [CrossRef]
- Deng, Y. A threat assessment model under uncertain environment. Math. Probl. Eng. 2015, 201, 1–12. [Google Scholar] [CrossRef]
- Parikh, C.R.; Pont, M.J.; Jones, N.B. Application of Dempster–Shafer theory in condition monitoring applications: A case study. Pattern Recognit. Lett. 2001, 22, 777–785. [Google Scholar] [CrossRef]
- Dymova, L.; Sevastjanov, L. An interpretation of intuitionistic fuzzy sets in terms of evidence theory: Decision making aspect. Knowl. Based Syst. 2010, 23, 772–782. [Google Scholar] [CrossRef]
- Kang, J.; Gu, Y.B.; Li, Y.B. Multi-sensor information fusion algorithm based on DS evidence theory. J. Chin. Inert. Technol. 2012, 20, 670–673. [Google Scholar]
- Fan, X.F.; Zuo, M.J. Fault diagnosis of machines based on D-S evidence theory. Part 2: Application of the improved D-S evidence theory in gearbox fault diagnosis. Pattern Recognit. Lett. 2006, 27, 377–385. [Google Scholar] [CrossRef]
- Basir, O.; Yuan, X. Engine fault diagnosis based on multi-sensor information fusion using Dempster–Shafer evidence theory. Inf. Fusion 2007, 8, 379–386. [Google Scholar] [CrossRef]
- Dong, G.; Kuang, G. Target Recognition via Information Aggregation Through Dempster–Shafer’s Evidence Theory. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1247–1251. [Google Scholar] [CrossRef]
- Dezert, J. Autonomous navigation with uncertain reference points using the PDAF. In Multitarget-Multisensor Tracking; Bar-Shalom, Y., Ed.; Artech House: Norwood, MA, USA, 1991; Volume 2, pp. 271–324. [Google Scholar]
- Smarandache, F.; Dezert, J. An introduction to DSm theory of plausible, paradoxist, uncertain, and imprecise reasoning for information fusion. Octogon Math. Mag. 2007, 15, 681–722. [Google Scholar]
- Zadeh, L.A. Book Review: A Mathematical Theory of Evidence. Bull. Am. Math. Soc. 1984, 10, 235–247. [Google Scholar] [CrossRef]
- Smets, P. The combination of evidence in the transferable belief model. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 447–458. [Google Scholar] [CrossRef]
- Yager, R.R. On the aggregation of prioritized belief structures. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 26, 708–717. [Google Scholar] [CrossRef]
- Sun, Q.; Ye, X.Q.; Gu, W.K. A new combination rules of evidence theory. Chin. J. Electron. 2000, 28, 117–119. [Google Scholar]
- Li, B.C.; Huang, J.; Yin, H.J. Two efficient combination rules for conflicting belief functions. In Proceedings of the International Conference on Artificial Intelligence and Computational Intelligence, Shanghai, China, 7–8 November 2009; Volume 61, pp. 421–426. [Google Scholar]
- Zhang, B.; Lu, H.Z. Combination method of conflict evidence in multi-sensor automatic target recognition. Syst. Eng. Electron. 2006, 28, 857–860. [Google Scholar]
- Zhang, S.; Pan, Q.; Zhang, H. A New Kind of Combination Rule of Evidence Theory. Control Decis. 2000, 15, 540–544. [Google Scholar]
- Murphy, C.K. Combining belief functions when evidence conflicts. Decis. Support Syst. 2000, 29, 1–9. [Google Scholar] [CrossRef]
- Horiuchi, T. Decision rule for pattern classification by integrating interval feature values. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 440–448. [Google Scholar] [CrossRef]
- Deng, Y.; She, W.K.; Zhu, Z.F. Efficient combination approach of conflict evidence. J. Infrared Millim. Waves 2004, 23, 27–32. [Google Scholar]
- Guo, H.W.; Shi, W.K.; Liu, Q.K.; Deng, Y. A new combination rule of evidence. J. Shanghai Jiaotong Univ. 2007, 40, 1895–1900. [Google Scholar]
- Wei, Y.C. An improved D-S evidence combination method based on K-L distance. Telecommun. Eng. 2011, 27, 255–257. [Google Scholar]
- Lin, Y.; Wang, C.; Ma, C.; Dou, Z.; Ma, X. A new combination method for multisensor conflict information. J. Supercomput., 2016, 72, 2874–2890. [Google Scholar] [CrossRef]
- Hardle, W.; Simar, L. Applied Multivariate Statistical Analysis; Springer: New York, NY, USA, 2015; pp. 41–60. [Google Scholar]
- Banks, D.; Mcmorris, F.R.; Arabie, P.; Gaul, W. Classification, Clustering, and Data Mining Applications. In Proceedings of the Meeting of the International Federation of Classification Societies (IFCS), Chicago, IL, USA, 15–18 July 2004; Illinois Institute of Technology: Chicago, IL, USA, 2004. [Google Scholar]
- Dempster, A.P. Upper and lower probabilities induced by a multi-valued mapping. Ann. Math. Stat. 1967, 38, 325–329. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Everitt, B.S.; Landau, S.; Leese, M.; Stahl, D. Cluster Analysis, 5th ed.; John Wiley and Sons, Ltd.: London, UK, 2011; pp. 43–70. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).