Abstract
This paper proposes a novel approach to cope with the multi-criteria group decision-making problems. We give the pairwise comparisons based on the best-worst-method (BWM), which can decrease comparison times. Additionally, our comparison results are determined with the positive and negative aspects. In order to deal with the decision matrices effectively, we consider the elimination and choice translation reality (ELECTRE III) method under the intuitionistic multiplicative preference relations environment. The ELECTRE III method is designed for a double-automatic system. Under a certain limitation, without bothering the decision-makers to reevaluate the alternatives, this system can adjust some special elements that have the most influence on the group’s satisfaction degree. Moreover, the proposed method is suitable for both the intuitionistic multiplicative preference relation and the interval valued fuzzy preference relations through the transformation formula. An illustrative example is followed to demonstrate the rationality and availability of the novel method.
1. Introduction
Multi-criteria group decision-making (MCGDM) is characterized as a process of ranking the alternatives. Due to its practicability, it had been studied by some scholars in recent decades. Many methods were proposed to solve MCGDM problems and their interrelated extensions. Among them, elimination and choice translation reality (ELECTRE), including its derivations, became an important branch. The ELECTRE method was proposed in 1966 [1] firstly. Its main idea is taking advantage of the outranking relations. To date, ELECTRE I, ELECTRE II, ELECTRE III, ELECTRE IV and ELECTRE TRI are widely-known derivations. In this article, we focus on utilizing ELECTRE III to deal with the ranking problem of multi-criteria decision-making (MCDM). In order to rank the alternatives, J.C. Leyva-Lopez [2] constructed a fuzzy outranking relation depending on the ELECTRE III. A. Papadopoulos and A. Karagiannidis [3] used ELECTRE III to discuss the renewable energy source problems, obtaining an optimization of decentralized systems. Furthermore, E. Radziszewska-Zielina [4] introduced a solution to choose the best construction enterprise. M.M. Marzouk [5] proposed a method with an increase of efficiency for ranking alternatives. B. Vahdani, S.M. Mousavi and R. Tavakkoli-Moghaddam [6] studied a company manufacturing tractor components and renewed the manufacturing system. ELECTRE III is outstanding both in the practicality and efficiency aspects.
For the development of society, the decision-making problems become more complex, leading to a situation that one decision-maker (DM) or one considered criterion is not sufficient. DMs may not make exact judgments always due to lacking experience or information. These scenarios need some useful methods. The appearance of multi-criteria group decision-making under the fuzzy theory environment makes the connection between theory and practice closer. DMs can judge the alternatives by fuzzy numbers [7], interval-valued numbers [8], intuitionistic fuzzy numbers [9], interval-valued intuitionistic fuzzy numbers [10] or with hesitant fuzzy sets [11,12,13], Type-2 or type-n fuzzy sets [14,15]. Besides, pairwise comparison has also been gradually acknowledged. Generally, decision-makers can express their decision results based on multiplicative preference relations (MPRs) [16] and fuzzy preference relations (FPRs) [17]. However, it happens often that DMs may not be sure about the intensities of preferences. This means that their results may be fluctuating in some interval during the decision-making process. In 1987, Satty and Vargas introduce interval-valued multiplicative preference relations (IVMPRs) [18]. In 2004, Xu introduced interval-valued fuzzy preference relations (IVFPRs) [19]. In order to highlight the preferred degree and non-preferred degree, the concepts of intuitionistic multiplicative preference relations (IMPRs) [20] and intuitionistic fuzzy preference relations (IFPRs) [21] were introduced as extensions of the traditional multiplicative preference relations. In addition, when dealing with the practical problems, the consistency degree [22,23], the transitivity and the additivity should also be considered. H.M. Zhang [24] gave a consistency model for group decision-making (GDM) problems by constructing a novel logarithmic distance formula. Z.S. Xu [25] firstly established a quadratic programming model and then constructed new approached with respect to the consistency and additivity. S. Alonso et al. [26] proposed a method to estimate missing elements from preference relation results, depending on the consistency of the preference relation. Y. Dong and E. Herrera-Viedma [27] discussed two-tuple linguistic modeling by proposing a consistency-driven automatic methodology, which is based on the consistency of preference relation. M.R. Urea et al. [28] studied the group decision-making problem with incomplete information, under the fuzzy preference relation’s environment. They developed a new method to cope with the problem that some useful information might not be considered properly. This method’s highlight was that it can calculate the unknown values only with the preference information from that particular decision-maker. More relevant theories and applications can be found in [8,29,30,31,32,33,34].
However, for the general preference relations, DMs need to compare alternatives pairwise, leading to at least or times of comparisons. J. Rezaei [35] proposed a novel method named the best-worst-method (BWM) about multi-criteria decision-making problems, which only needed comparisons without losing the accuracies of ranking results. BWM expressed the comparison results by numbers from set and ignored the reciprocals of each pair to avoid the trouble caused by unequal distance between fractional comparisons. He discussed a practical application of the college students’ cell phone selection problem to identify that without considering the reciprocals, the results were also credible. The simplicity of BWM is obvious; then, it leads us to thinking of further discussions and more applications; because ignoring the reciprocals is not sufficient for some other situations, especially for some complicated ranking problems. Unequal distance between fractional comparisons does exist. Then, we extend the BWM to the intuitionistic preference relations environment. It is known that elimination and choice expressing the reality is a popular MCDM method, which is a comprehensive approach and has been developed into different forms: ELECTRE I, II, III, IV and TRI; and all have been applied to practical problems in many areas [36,37,38]; where ELECTRE I is introduced to solve selection problems, II, III and IV are designed for ranking alternatives and TRI for sorting problems. F. Shen et al. [39] discussed this question and proposed an automatic ranking approach for MCGDM problems, which was applied to discuss a supplier evaluation problem in a high-tech company. While few researchers have studied solving MCGDM problems with intuitionistic multiplicative preference relations, based on the ELECTRE III method, in this paper, we will study the ELECTRE III method with BWM’s idea. Additionally, the evaluating results are expressed by the intuitionistic preference relation. Then, we can get two kinds of matrices with respect to the best alternative and the worst alternative, which is a main advantage compared with the other decision-making methods. Depending on the matrices, we develop a double-automatic approach to deal with a real group ranking problem. This means that we do not need to bother DMs again, when the results are not satisfied in some certain limited conditions.
The rest of the paper is organized as follows. Section 2 shows some basic information. In Section 3, we propose an approach to solve a group decision-making problem based on the BWM method automatically. An illustrative example for demonstrating the developed method is stated in Section 4. Result discussions are given in Section 5, along with the advantages and drawbacks of the proposed method. This paper concludes in Section 6 with summarizing our developments and future research directions.
2. Preliminaries
Before proposing the novel method, we firstly introduce some basic concepts and methods that will be needed to construct the new model. Note that is a set of n alternatives; is a set of m criteria; is a set of weights corresponding to the set C; is a set of DMs or experts; is a set of the DMs’ weights. Additionally, there are three thresholds: , beneath which the DM is indifferent to two alternatives under a certain criterion, , above which the DM makes a strict preference for one alternative over another under a certain criterion, , the veto threshold means that the DM should negate any possible outranking relationship indicated by the other criteria if there exists a discordant difference in favor of one alternative greater .
Definition 1.
[20] Let be a set of n alternatives. The intuitionistic multiplicative preference relation (IMPR) is defined as , where is an intuitionistic multiplicative number (IMN); means the preferred intensity of over ; means the non-preferred intensity of over , both of which satisfy that:
Let represent the hesitation degree to which is preferred to with .
Definition 2.
[26] Let be a non-empty finite set with n elements. Its associated multiplicative reciprocal preference relation with and , . The corresponding fuzzy reciprocal preference relation associated with A is given as follows:
where and , .
Depending on Definition 2, we build the following definition to measure the distance between two IMNs.
Definition 3.
Let and be two IMNs, then:
is called an intuitionistic multiplicative fuzzy distance between and .
Deriving from Definition 3, we obtain the following propositions about :
- (1)
- ;
- (2)
- ;
- (3)
- , iff , .
For each criterion , , DM , chooses the best alternative and the worst . Additionally, give the comparison results: , , where and , are IMNs, which stand for the preferred degree of over and over with respect to the criterion . Then, obtain the decision matrices and .
Definition 4.
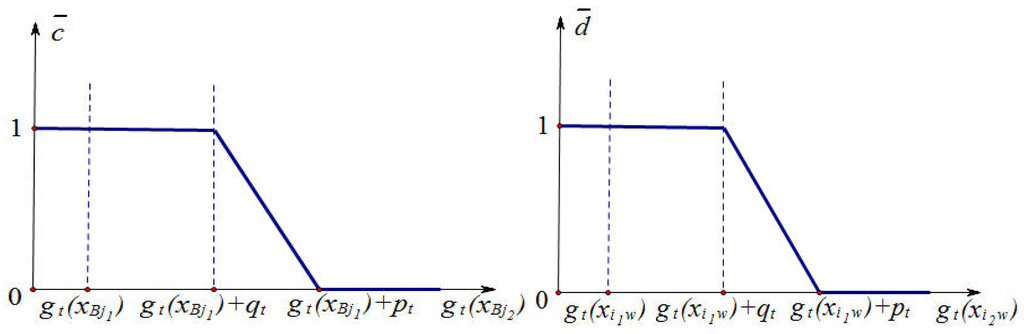
Determine the intuitionistic multiplicative positive functions about alternative outranks , which are denoted by with respect to the decision matrix and with respect to the decision matrix , stated as follows and illustrated in Figure 1:
where .
where means the positive criteria set; means the negative criteria set; , .

Figure 1.
Figure of intuitionistic multiplicative positive functions.
Therefore, obtain:
Then, the intuitionistic multiplicative positive index matrices and are written as follows:
Definition 5.
Determine the intuitionistic multiplicative hesitant functions about alternative outranks with respect to the decision matrices and under the decision criteria , denoted by and , respectively, stated as follows:
where . Then, the intuitionistic multiplicative hesitant index matrices and .
Definition 6.
Based on Definition 5, define the intuitionistic fuzzy outranking index and with respect to and , and , respectively, which aggregate the concordance and discordance indices to measure the outranking intensity about criterion .
These considerations of the intuitionistic multiplicative outranking index and combine the positive and hesitant functions together, indicating the degree to which outranks or outranks .
Definition 7.
Define the outranking flow and , which stands for the outranking character of over and is defined as follows:
which satisfy , .
Definition 8.
Define the outranking flow index , , indicating the outranking character of over all of the remaining alternatives given by DM , , and the outranking character of all of the other characters over , defined as follows:
where ;
where .
Then, the group outranking flow indexes are defined as follows:
where ;
where .
Definition 9.
Definition 10.
Theorem 1.
Let , () be a set of the DMs’ outranking flow values after s times about and , and () be a set of the DMs’ outranking flow values after s times about . The values of and , defined in Step 10, satisfy:
Proof.
Depending on Definition 10 about the automatic strategy, we can derive that the sequences and are both monotonically decreasing ones and have the lower bounds for and . Then, we know that both of the limits and exist and are denoted by ϵ and η, respectively. However, the automatic process would not stop if and , for the reason that there always exist the farthest distances from and . Continuing to run the process, we can obtain the next set after changing the farthest values for each matrices and new deviations and . As and , the values of and cannot be smaller than and , respectively. Therefore, and . ☐
2.1. The Best-Worst Multi-Criteria Decision-Making Method
In 2015, J. Rezaei [35] proposed the BWM method, in order to get the weight values of all alternatives based on the evaluationsmade by DMs. In generally, there are three steps:
Step 1. Determine the best and worst criteria from n alternatives.
Step 2. Determine the preference intensity degree of the best one compared to the others, except for the worst one, which need times. The remaining ones to the worst one need times. Add up the comparison of the best one to the worst one; there are times of comparisons in all needed.
Step 3. Calculate the weights of all alternatives and rank them (here, the details are omitted).
2.2. ELECTRE III Method
C. Giannoulis and A. Ishizaka [41] described that ELECTRE III method was a multi-criteria method extended for solving a ranking problem that was based on the outranking relations, including the constructing step and exploitation step.
3. Framework of the Proposed Novel Method
In this part, we construct a novel systematic MCGDM approach based on the ELECTRE III method and the BWM method.
Step 1. For each DM, he/she should determine three thresholds: , , , .
Step 2. DM determines the decision matrix and with respect to every criterion , , .
Step 3. Determine the weight vector for each criterion. Additionally, each DM gives his/her weight value for each criteria and calculates the average.
Step 4. Based on Definition 4, obtain the positive proposition matrix and negative proposition matrix .
Step 5. Based on Definition 5, obtain the hesitant proposition matrix and .
Step 6. Based on Definition 6, obtain outranking index and .
Step 7. Based on Definition 7, calculate the outranking flow and , which stands for the outranking character of over .
Step 8. Based on Definition 8, calculate the outranking flow index , , , and the group outranking flow indexes , .
Step 9. Based on Definition 8, calculate the consistency index of DM , and the group G with n alternatives.
Step 10. Based on Definition 10, we obtain two deviation degree matrices and . From and , picking up the maximum elements and , we would find the farthest weighted distances from and , respectively, i.e.,
Then, we replace and by and , respectively, and keep the other values unchanged, i.e.,
If , where S is the upper limit of adjusting times, then return to Step 8, otherwise, return to the first step to re-evaluate the original decision matrices or change the related parameters.
Step 11. Calculate the final group ranking results.
Step 12. End.
4. A Numerical Example
With the continuous development of the Chinese economy, people’s living standards are improving unceasingly. Meanwhile, demands for culture service and facilities are also increasing. The relevant government departments have put forward an explicit policy: enrich cultural products and services, in order to build the modern system of public cultural services. The practical cultural facilities are the foundations of the Chinese socialist cultural undertakings’ prosperity and development. Building them reasonably plays an important role. However, domestic research focuses on investment management modes. Few researchers pay attention to the decision-making problem about cultural facilities’ pre-construction. Some big cities in China, such as Tianjin, Shenzhen and Taiyuan, have built cultural centers to enrich the cultural life of the citizens. A provincial capital would also plan to construct a cultural center as a reward for complying with the policy. The first problem to solve is site selection. There are five candidates, , , , and (), to be chosen. Additionally, there are four criteria to be considered: stands for traffic conditions; stands for environment effects; stands for ancillary facilities; and stands for procurement cost (). The decision group contains three experts. In the following, we will apply the proposed method to solve these decision-making problems.
Step 1. Every DM determines the best and worst alternatives by taking consideration of each criterion, obtaining the following two kinds of decision matrices: the best-to-others comparisons about (), named as , and the others-to-worst comparisons about (), named as , entering Matrices (33)–(35).
Step 2. Enter a table about the predefined thresholds by the three DMs; details are shown in Table 1.

Table 1.
The predefined threshold values about every decision-maker (DM).
Step 3. Based on the realistic demand, determine the weight values of each criterion by DMs: , , , .
Step 4. Calculate the credibility proposition matrices by Equations (4)–(8), obtaining Matrices (36)–(38) with respect to the best aspect and the worst aspect.
Step 5. Calculate the credibility proposition of the alternative being not as good as with respect to decision matrices and under consideration of each criterion by Equations (11) and (12).
Step 6. In addition, by Equations (13) and (14), we get the intuitionistic fuzzy outranking index matrices and for every DM.
Step 8. Applying Equations (17)–(20), we summarize the next Table 2 and Table 3 and show the conditions about the original outranking flow indexes.

Table 2.
The original group outranking flow indexes of every alternative about the best aspect.

Table 3.
The original group outranking flow indexes of every alternative about the worst aspect.
What follows is the corresponding outranking flow order and , as shown in Table 4 and Table 5. We should pay attention to the elements’ meaning from the decision matrix , , ; that is, the preference degree of the best alternative to the others, meaning the smaller the values, the better.

Table 4.
The original group outranking flow orders of every alternative about the best aspect.

Table 5.
The original group outranking flow orders of every alternative about the worst aspect.
Step 9. Using Equations (21)–(24), we can calculate the satisfaction index degree of persons and the group, as shown in Table 6. In this paper, if the satisfaction index degree is higher than 0.85, we will accept it and go to Step 12; if not, we will go to Step 10. Obviously, the satisfaction index degree of others-to-worst is low. We will go to Step 10 to adjust some comparisons for a higher satisfaction degree.

Table 6.
The satisfaction index degree.
Find the max value of matrix (51) as . In addition, by Equation (30), we derive that the elements that cost these highest deviation are and from . We replace them according to Equation (32), to obtain the first around adjusted outranking flow matrix as shown in Matrix (52):
Next, we calculate the first roundadjusted outranking flow indexes about the worst-to-others aspect, shown in Table 7.

Table 7.
The first roundadjusted group outranking flow indexes of every alternative about the worst-to-others aspect.
We can calculate the adjusted group outranking flow orders, as shown in Table 8. Table 9 shows the adjusted satisfaction degree that can be accepted.

Table 8.
The first roundadjusted group outranking flow orders of every alternative about the worst aspect.

Table 9.
The first roundadjusted satisfaction index degree about the worst aspect.
Generally, we set the adjustment times as three. Although, the result is surely better by Theorem 1. Adjusted results may be too far from reality and lose the value of judging the alternatives, when we adjust too many times.
Step 11. The final ranking results are from the best-to-others aspect and from the others-to-worst aspect.
Step 12. End.
5. Discussions
For any two intuitionistic multiplicative numbers (IMNs), based on Definition 1, in order to rank them, M.M. Xia et al. [20] defined the following comparison laws:
Let be an IMN; we call the score function of and the accuracy function of . To compare any two IMNs and , the following laws can be given:
- (1)
- If , then ,
- (2)
- If and if , then ; and if , then .
Utilizing these laws, we compare the same numerical example from Section 4, and the ranking results are summarized in Table 10. Z.S. Xu [25] also studied the intuitionistic multiplicative preference relations (IMPR). He proposed a method to derive the priority weights under the IMPR environment. We apply Approach I from Xu’s method to calculate the numerical example from Section 4, and the ranking results are also summarized in Table 10.

Table 10.
The ranking results from two different methods.
Although the ranking results have some differences, the best alternative is the same. This means that our method is also reasonable. Every method has its own benefits and drawbacks, and stresses different core concerns. Next, we point out some advantages and drawbacks of the proposed methodology, comparing with the other methods for multi-criteria group decision-making problems.
Advantages:
- (a)
- The proposed method of this paper is based on BWM. It can decrease the comparison times to , compared with at least times (AHP, TOPSIS). We increase the method’s efficiency in this way. Besides, comparison results are expressed by intuitionistic multiplicative preference relations, which is different from the original BWM.
- (b)
- We study the ELECTRE III method with intuitionistic multiplicative preference relations. Additionally, we introduce a distance formula, which can measure the distance between two IMNs. This distance formula is also suitable for interval-valued fuzzy preference relations. The research scope would be expended with this formula.
- (c)
- Comparing with the general ELECTRE method [3,37,41], based on BWM, we give the outranking functions with two kinds of matrices: the best-to-others, which is about the comparison results of the best alternative over the others; the others-to-worst, which is about the comparison result of the other alternatives over the worst one. That is consistent with the practical situation and improves the rationality of the final ranking result.
- (d)
- Our method can change some improper elements from the decision matrices automatically. This means that within a limited condition, our method would readjust itself by preference relations from the given matrices, if the decision results do not meet the requirements.
Drawbacks:
- (a)
- Our decision matrices are obtained based on BWM, including two parts: the matrix about best-to-others and the matrix about others-to-worst. Each kind of matrix does not have the problems of consistency. However, there exists a consistency issue between comparisons about best-to-others and others-to-worst, which have not been discussed in this paper.
- (b)
- The proposed method is based on the intuitionistic preference relations. However, in some more complicated conditions, this tool may still be beyond expression. Therefore, this research should be discussed further with more practical tools, such as interval-valued intuitionistic preference relations.
6. Conclusions
The method proposed in this paper is a combination for solving MCGDM problems based on the BWM method and the ELECTRE III method. Specially, we express the comparison results of the BWM method with intuitionistic multiplicative preference relations, which is closer to real situations. Additionally, the BWM method decreases the comparison times from to . In addition, we discuss the decision matrices automatically, which means that we can change some improper elements in certain limitations without bothering the DMs to reappraise again. All of the highlights show that is meaningful to do this research. In the future, on the one hand, we hope that our method can be extended to solve more complex MCGDM problems with more practical tools; on the other hand, we would study the consistency degree of comparisons between best-to-others and others-to-worst.
Acknowledgments
This paper is supported by the funds: National Natural Science Foundation of China (71272148). These funds covered the costs to publish in open access.
Author Contributions
Xinshang You is responsible for the article’s theoretical demonstration, model construction, data analysis and English writing. Tong Chen takes charge of macro-direction and foundation item. Qing Yang contributes to the data collection, algorithms analysis, English editing and corresponding issues.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Benayoun, R.; Roy, B.; Sussman, N. Manual de reference du programme electre. In Note De Synthese et Formaton; Direction Scientifque SEMA: Paris, France, 1966. [Google Scholar]
- Leyva-Lopez, J.C. Multi criteria decision and application to a student selection problem. Pesqui. Oper. 2005, 25, 45–68. [Google Scholar] [CrossRef]
- Papadopoulos, A.; Karagiannidis, A. Application of the multi-criteria analysis method ELECTRE III for the optimization of decentralized energy systems. Omega 2008, 36, 766–776. [Google Scholar] [CrossRef]
- Radziszewska-Zielina, E. Methods for selecting the best partner construction enterprise in terms of partnering relations. J. Civ. Eng. Manag. 2010, 16, 510–524. [Google Scholar] [CrossRef] [Green Version]
- Marzouk, M.M. ELECTRE III model for value engineering applications. Autom. Constr. 2011, 20, 596–600. [Google Scholar] [CrossRef]
- Vahdani, B.; Mousavi, S.M.; Tavakkoli-Moghaddam, R. A new design of the elimination and choice translating reality method for multi-criteria group decision making in an intuitionistic fuzzy environment. Appl. Math. Model. 2013, 37, 1781–1799. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Baležentis, T.; Zeng, S. Group multi-criteria decision-making based upon interval-valued fuzzy numbers: An extension of the MULTIMOORA method. Expert Syst. Appl. 2013, 40, 543–550. [Google Scholar]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z.S. Consistency measures for hesitant fuzzy linguistic preference relations. IEEE Trans. Fuzzy Syst. 2014, 22, 35–45. [Google Scholar] [CrossRef]
- Liao, H.C.; Xu, Z.S.; Xia, M.M. Multiplicative consistency of hesitant fuzzy preference relation and its application in group decision-making. Int. J. Inf. Technol. Decis. Mak. 2014, 13, 47–76. [Google Scholar] [CrossRef]
- Stewart, T.; French, S.; Rios, J. Integrating multicriteria decision analysis and scenario planning-reviev and extension. Omega 2013, 41, 679–688. [Google Scholar] [CrossRef]
- Qin, J.D.; Liu, X.W. Multi-attribure group decision-making using combined ranking value under interval type-2 fuzzy environment. Inf. Sci. 2015, 297, 293–315. [Google Scholar] [CrossRef]
- Mizumoto, M.; Tanaka, K. Some properties of fuzzy sets of type 2. Inf. Control 1976, 21, 312–340. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical strutures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Orlovsky, S.A. Decision-making with a fuzzy preference relation. Fuzzy Sets Syst. 1978, 1, 155–167. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Uncertainty and rank order in the analytic hierarchy process. Eur. J. Oper. Res. 1987, 32, 107–117. [Google Scholar] [CrossRef]
- Xu, Z.S. Goal programming models for obtaining the priority vector of incomplete fuzzy preference relation. Int. J. Approx. Reason. 2004, 26, 261–270. [Google Scholar] [CrossRef]
- Xia, M.M.; Xu, Z.S.; Liao, H.C. Preference relations based on intuitionistic multiplicative information. IEEE Trans. Fuzzy Syst. 2013, 22, 113–133. [Google Scholar]
- Szmidt, E.; Kacprzyk, J. Using intuitionistic fuzzy sets in group decision-making. Control Cybern. 2002, 31, 1037–1053. [Google Scholar]
- Ergu, D.; Kou, G.; Peng, Y.; Shi, Y. A simple method to improve the consistency ratio of the pair-wise comparison matrix in ANP. Eur. J. Oper. Res. 2011, 213, 246–259. [Google Scholar] [CrossRef]
- Yager, R.; Alajlan, N. On the consistency of fuzzy measures in multi-criteria aggregation. Fuzzy Optim. Decis. Mak. 2015, 14, 121–137. [Google Scholar] [CrossRef]
- Zhang, H.M. A consistency model for group decision-making problems with interval mulitiplicative preference relations. Appl. Soft Comput. 2015, 34, 60–71. [Google Scholar] [CrossRef]
- Xu, Z.S. Consistency of interval fuzzy preference relations in group decision-making. Appl. Soft Comput. 2011, 11, 3898–3909. [Google Scholar] [CrossRef]
- Alonso, S.; Herrera, F.C.F.; Herrera-Viedma, E.; Alcalá, J.; Porcel, C. A consistency-based procedure to estimate missing pairwise preference values. Int. J. Intell. Syst. 2008, 23, 155–175. [Google Scholar] [CrossRef]
- Dong, Y.; Herrera-Viedma, E. Consistency-driven automatic methodology to set interval numerical scales of 2-tuple linguistic term sets and its use in the linguistic GDM with perference relation. IEEE Trans. Cybern. 2015, 45, 780–792. [Google Scholar] [CrossRef] [PubMed]
- Ureňa, M.R.; Chiclana, F.; Morenre-Molonera, J.A.; Herrera-Viedma, E. Managing inconplete preference relations in decision-making: A review and future trends. Inf. Sci. 2015, 302, 14–32. [Google Scholar]
- Garrido, A. Classifying Entropy Measures. Symmetry 2011, 3, 487–502. [Google Scholar] [CrossRef]
- Xu, G.L.; Liu, F. An approach to group decision-making based on interval multiplicative and fuzzy preference relations by using projection. Appl. Math. Model. 2013, 37, 3929–3943. [Google Scholar] [CrossRef]
- Yager, R.R.; Xu, Z.S. The continuous ordered weighted geometric operator and its application to decision making. Fuzzy Sets Syst. 2006, 157, 1393–1402. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, Z.S.; Yu, X.H. Compatibility measures and consensus models for group decision-making with intuitionistic multiplicative preference relation. Appl. Soft Comput. 2013, 13, 2075–2086. [Google Scholar] [CrossRef]
- Wang, Y.M.; Yang, J.B.; Xu, D.L. A two-stage logarithmic goal programming method for generating weights from interval comparison matrices. Fuzzy Sets Syst. 2005, 152, 475–498. [Google Scholar] [CrossRef]
- Xu, Z.S. Priority weight intervals derived from intuitionistic multiplicative preference. IEEE Trans. Fuzzy Syst. 2013, 21, 642–654. [Google Scholar]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Herrera, F.; Chiclana, F. A consensus model for multiperson decision-making with different preference structures. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2002, 32, 394–402. [Google Scholar] [CrossRef]
- Leyva-Lopez, J.C.; Fernandez-Gonzalez, E. A new method for group decision support based on ELECTRE III methodology. Eur. J. Oper. Res. 2003, 148, 14–27. [Google Scholar] [CrossRef]
- Dias, L.; Clmaco, J. ELECTRE TRI for groups with inprecise information on prameter valules. Group Decis. Negot. 2000, 9, 355–377. [Google Scholar] [CrossRef]
- Shen, F.; Xu, J.P.; Xu, Z.S. An automatic ranking approach for multi-criteria group decision-making under intuitionistic fuzzy environment. Fuzzy Optim. Decis. Mak. 2015, 14, 311–334. [Google Scholar] [CrossRef]
- Goletsis, Y.; Papaloukas, C.; Fotiadis, D.I.; Likas, A.; Michalis, L.K. A multicriteria decision based approach for ischaemia detection in long duration ECGs. Inf. Technol. Appl. Biomed. 2003, 160, 173–176. [Google Scholar]
- Giannoulis, C.; Ishizaka, A. A web-based decision support system with ELECTRE III for a personalised ranking of British universities. Decis. Support Syst. 2010, 48, 488–497. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).