Abstract
Frequent graph mining has been proposed to find interesting patterns (i.e., frequent sub-graphs) from databases composed of graph transaction data, which can effectively express complex and large data in the real world. In addition, various applications for graph mining have been suggested. Traditional graph pattern mining methods use a single minimum support threshold factor in order to check whether or not mined patterns are interesting. However, it is not a sufficient factor that can consider valuable characteristics of graphs such as graph sizes and features of graph elements. That is, previous methods cannot consider such important characteristics in their mining operations since they only use a fixed minimum support threshold in the mining process. For this reason, in this paper, we propose a novel graph mining algorithm that can consider various multiple, minimum support constraints according to the types of graph elements and changeable minimum support conditions, depending on lengths of graph patterns. In addition, the proposed algorithm performs in mining operations more efficiently because it can minimize duplicated operations and computational overheads by considering symmetry features of graphs. Experimental results provided in this paper demonstrate that the proposed algorithm outperforms previous mining approaches in terms of pattern generation, runtime and memory usage.
1. Introduction
Since the concept of data mining was proposed to find useful knowledge or information hidden in complicated large-scale data (also called big data), various approaches and applications for data mining have been researched [1,2,3,4,5,6]. After that, frequent pattern mining was proposed to find useful, hidden pattern information from such data and various mining techniques and applications have been developed [7,8,9,10,11,12]. Frequent graph mining approaches [13,14,15,16,17] have been proposed to satisfy the needs of users wanting to obtain mining results from large and complex graph data in the real world. It is hard to express recent data as simple structures, such as itemsets because of their complicated and multidimensional features. However, this data can easily be expressed in graph form since almost all data can be described as such. Previous traditional frequent pattern mining methods faced limitations that did not deal with such complicated databases because they were algorithms, focusing on processing item-based simple databases. For this reason, the concept of frequent graph pattern mining was suggested and studies for frequent graph mining have been increased dramatically. Since recent real world databases have become larger and more complicated, it is essential to deal with the modern data, rather than old. Due to the usefulness of graph data, a variety of relevant graph theories and applications have been studied [18,19,20]. Moreover, since graph pattern mining can draw useful data analysis results for various complicated graph databases, a variety of graph mining applications have been developed such as discovering objects based on graph mining [21], finding combinatorial splicing regulatory elements using graph mining [22], exploiting document information contents on graph mining [23], detecting intelligent malware based on graph mining [24] and analyzing market data using graph pattern mining [25].
However, previous frequent graph mining researches applied only support information for generated graph patterns (or sub-graphs) but did not consider the other valuable factors that could utilize various characteristics of graphs such as graph sizes and features of graph elements. In frequent graph mining, extracted sub-graphs have the following characteristics. Small sub-graphs with a few elements (vertices and edges) tend to be interesting if their supports are relatively high, while large sub-graphs with a large number of the elements can be interesting, although they have relatively low supports. However, previous graph mining methods cannot apply the above characteristics to mining processes since they use only one minimum support threshold, regardless of the graphs’ sizes. Moreover, if we find large sub-graphs having many elements and low supports through existing methods, we have no choice but to lower a minimum support threshold more than required, causing generations of meaningless sub-graph patterns. In addition, each element composing a graph pattern can have its own support feature. However, traditional methods always use a single threshold regardless of the element characteristics. Hence, they cannot effectively consider the rare item problem [26,27,28], which means that not only do items or patterns have large supports but also ones with small values can contain useful knowledge or information. Accordingly, traditional approaches may fail to find rare but valuable patterns depending on settings of the minimum support threshold. If we lower the threshold more than needed in order to extract such pattern results, an enormous number of useless patterns may also be mined.
In contrast to traditional pattern mining methods that deal with item-based simple databases, graph pattern mining need more complicated mining operations to discover graph patterns. Especially, in order to prevent duplicated graph patterns from being mined, graph pattern mining has to perform works for deciding graph isomorphism, which is also known as a NP-hard problem that can cause enormous computational overheads. However, we can effectively solve such problems by applying a pattern growth technique based on graph symmetry features into our mining process. The symmetry features have been used to improve mining efficiency of various approaches [29,30,31]
Motivated by the aforementioned issues, we propose an efficient algorithm for Smallest Valid Extension-based Rare Graph pattern Mining considering length-decreasing support constraints and symmetry characteristics of graphs (called SVE-RGM), where we also propose and apply techniques for improving graph mining efficiency: symmetry feature-based graph pattern growth, a smallest valid extension (SVE) method for graphs and a SVE-based pruning strategy. Through the proposed algorithm, we can obtain a set of SVE-based Rare Graph patterns, called SRGs. By using the graph symmetry features, we can prevent duplicated graph patterns from being generated and reduce computational overheads for useless operations. We can also improve mining efficiency of the proposed method by employing the SVE-based pre-pruning technique, which does not cause any pattern loss. Experimental results in this paper show that SVE-RGM outperforms state-of-the-art algorithms.
The remainder of this paper is organized as follows. In Section 2, we provide related work regarding graph mining and in Section 3 and Section 4, details of the proposed algorithm, SVE-RGM and performance analysis results are described, respectively. In Section 5, discussion for the proposed method is introduced. Finally in Section 6, we conclude this paper.
2. Related Work
2.1. Frequent Pattern Mining and Frequent Graph Pattern Mining
Since the Apriori algorithm [7] was developed, various works regarding frequent pattern mining have been suggested. The main goal of frequent pattern mining is to find all of frequent patterns from databases. If a frequency (or support) of a given pattern is higher than or equal to a minimum support threshold set by a user, it is considered as a frequent pattern. In the frequent pattern mining area, there is an important factor, called the anti-monotone property or the downward closure property. It contributes to improving mining efficiency by preventing invalid patterns from being generated. This property guarantees the following relation: if a pattern is an infrequent one, all the super patterns created from the pattern are also infrequent ones. Meanwhile, in order to overcome the drawbacks of the Apriori algorithm such as generating an enormous number of useless candidate patterns and database scanning works, a tree-based algorithm, FP-growth, was devised [32]. This algorithm mines frequent patterns without any candidate pattern generation, employing its own tree structure, called FP-tree. In addition, its mining process does not require excessive database scans, it needs only two database scans.
As in frequent pattern mining methods, frequent graph mining has also advanced through a similar process. Early studies have been researched on the basis of BFS (Breadth First Search) and subsequent researches have been conducted on the basis of DFS (Depth First Search). In addition, graph mining is also applied to extract a variety of valid patterns such as weighted frequent sub-graphs [33], closed and maximal frequent ones [13,15,33], approximate frequent ones [16,17], and so on. Similarly to frequent pattern mining, the main purpose of frequent graph pattern mining is to search for all the graph patterns satisfying a minimum support threshold from complicated databases composed of graph data. One of the major differences between them is that graph pattern mining has to consider extra conditions such as vertices, edges and graph isomorphism, in comparison to traditional pattern mining which deals only with simple items. There are several well-known fundamental graph mining algorithms such as Gaston, gSpan, FFSM, etc., where the Gaston algorithm [34,35] is most suitable for comparing the proposed algorithm, SVE-RGM, since as a state-of-the-art algorithm, Gaston, has the fastest runtime performance among these algorithms. The algorithm extracts frequent sub-graphs more efficiently by dividing mining process into three parts: path, free tree and cyclic graph steps, as well as by performing appropriate operations according to each step. In addition, an additional data structure used in the algorithm, named embedding list, makes it faster to conduct mining operations. However, such fundamental graph mining algorithms have limitations that only consider a single minimum support condition, regardless of various graph characteristics such as element types and lengths of graph patterns.
2.2. Pattern Mining On Multiple Minimum Support Constraints
In order to solve the rare item problem in the frequent pattern mining area, researchers have proposed various pattern mining algorithms based on multiple minimum support constraints [26,27,28]. Since MSApriori [28], an initial algorithm based on the framework of Apriori, was proposed, various methods have been developed. CFP-growth [26] is a tree-based algorithm that follows the basic process of FP-growth and CFP-growth++ [27] is an enhanced version of CFP-growth. Although the above approaches have found solutions of the rare item problem by applying multiple minimum support constraints, they are item-based traditional algorithms that cannot deal with various characteristics of complicated graph data.
To solve the above problem, FGM-MMS [36] and WRG-Miner [37] were proposed. They are methods that consider multiple minimum support constraints in graph pattern mining processes. In contrast to traditional graph pattern mining that uses a single minimum support threshold regardless of characteristics of elements composing graphs, they employ different minimum support threshold values for the elements in a given graph database in order to overcome the rare item problem [26,27,28] in their graph mining processes. Recall that meaningful patterns with low support values cannot be mined if a given minimum support threshold is high. Meanwhile an enormous number of invalid patterns have to be extracted, if the threshold value becomes lower to find such pattern results. However, such approaches cannot consider important length or size characteristics of mined graph patterns. On the other hand, since the proposed algorithm can set various minimum support thresholds according to the lengths or sizes of graph patterns, it can mine graph pattern results with more practically useful information.
2.3. Pattern Mining on Length-Decreasing Support Constraints
In the frequent pattern mining area, LPMiner/SLPMiner [38] is the first algorithm applying different multiple support constraints for each length of patterns. After that, advanced algorithms applying weight conditions, WLPMiner [39] and WSLPMiner [40] were suggested. LPMiner and WLPMiner find frequent and weighted frequent patterns composed of itemsets, respectively and SLPMiner and WSLPMiner discover sequential frequent and weighted sequential frequent ones. However, the above algorithms are only limited to the general frequent pattern mining area dealing with simple itemset-based databases.
FGM-LDSC [41] is an algorithm applying length-decreasing support constraints on graph mining environments. Recall that Small graph patterns having a few vertices and edges tend to be interesting if their supports are relatively high, while large ones having many vertices and edges can be interesting even though their supports are relatively low. FGM-LDSC solves the above problem by applying a different minimum support for each length factor of found graph patterns (length-decreasing minimum supports). However, such an approach cannot consider characteristics of extracted graph elements. On the other hand, the proposed algorithm can set different minimum support threshold values according to the types of elements composing graph patterns. Such an advantage also leads to mining graph patterns with more meaningful information or knowledge.
3. Smallest Valid Extension-Based Rare Graph Pattern Mining, Considering Length-Decreasing Support Constraints and Symmetry Characteristics of Graphs
In this section, we introduce the basic concept and preliminaries of graph pattern mining that can help understanding of the proposed algorithm, SVE-RGM. Thereafter, we describe details of our method including an overall architecture, a graph pattern growth technique and various pattern pruning techniques. We also propose techniques for effectively applying multiple minimum support and length-decreasing support constraints into graph mining environments without any unintended errors such as pattern losses. In addition, we show how the proposed method, SVE-RGM, operates through an overall mining procedure of the algorithm.
3.1. Preliminaries
Graph data are a structural format that can effectively express various data such as network data, chemical data and genome data. There are various definitions and theories for explaining such graph data in a mathematical manner [34,35,42,43], where we introduce essential preliminaries related to the proposed algorithm, including the definitions of graph patterns and the concept of frequent graph patterns (further information on graph theories refer to the literature cited in this paper [18,20,42,43]). We first describe a fundamental concept and several important definitions of graph pattern mining for better understanding of the proposed method. A graph pattern consists of multiple vertices and edges. In addition, graph types are classified as directed or undirected graphs depending on whether or not there are directions of edges in graphs. They can also be classified as simple or multi graphs on the basis of the number of edges between any two vertices in graphs. Moreover, other graph types can be created through numerous factors such as labels and self-edges (or loops). In this paper, we explain the proposed contents on the basis of undirected and labeled simple graph forms. However, it is trivial to consider other graph forms into our graph mining operations since we only have to consider a few additional characteristics. Figure 1 shows an example of various graph types. Figure 1a is a simple, labeled and undirected graph without any self-edges, where each vertex and edge has its own name or label. Figure 1b is a multiple graph that has two or more edges between vertices. As shown in Figure 1b, edges labels may not be expressed if they do not need to be distinguished from one another or have the same label. Figure 1c is a directed graph having a self-edge.

Figure 1.
Example of various graph pattern forms. (a) A simple, labeled and undirected graph without any self-edges; (b) A multiple graph with multiple edges between vertices; (c) A directed graph with a self-edge.
Definition 1.
(Sub-graph) Let P be a sub-graph (or a graph pattern) composed of one or more elements (vertices and edges). Then, P can be denoted as two element groups. The first one is a set of vertices, V(P) = {v1, v2, …, vi}, and a set of edges, E(P) = {e1, e2, …, ej}.
Definition 2.
(Graph isomorphism) Given a simple, labeled, and undirected graph pattern, P, its vertex and edge sets, V(P) and E(P) can also be denoted as follows:
Given two graph patterns, X and Y, we can say that X and Y are isomorphic, if their own V(P) and E(P) results are the same as each other on the basis of Equation (1) although the shapes of X and Y seem to be different from each other. Note that since all the edges in P have no directions, (v1, v2) and (v2, v1) are equal to each other.
All of the possible graph patterns have one of the following graph types: path, free tree, and cyclic graph. In addition, paths and free trees can be included in cyclic graphs and paths can be contained in free trees. In other words, the coverage of graph pattern types is denoted as path free-tree cyclic graph.
Definition 3.
(Degree of graph forms) all vertices except for both ends in a path have degree 2; meanwhile the end vertices have degree 1. Let X be a graph pattern. If X is a path with k vertices, X satisfies the following formula:
In Equation (2), D signifies a function that returns a degree number for an inputted vertex. v1, vn, |V(P)| and |E(P)| are the first and last vertices and the number of vertices and edges comprising P, respectively. A free tree should have at least one vertex of which the degree is 3 or more. In addition, there is no cyclic relation in all of its edges. If P is a free-tree with k vertices, the following conditions are satisfied:
If X has one or more cyclic edges, X becomes a cyclic graph. Then, X has the following relation between the numbers of vertices and edges.
By using Equations (2)–(4), we can easily distinguish what type every graph pattern is.
Definition 4.
(Frequent graph pattern) Let DBG = {Tr1, Tr2,…, Trn} be a given database storing n graph data records (also called graph transactions), where each graph transaction, Tr, is composed of multiple vertices and edges. Given a graph pattern, P, we can calculate the support of P, S(P), as follows:
In Equation (5), function Exist returns 1 if P is included in the corresponding Tr; otherwise, 0. Therefore, S(P) is to add all the results of Exist with respect to every Tr in DBG. In other words, the result of S(P) signifies how many times P appears in DBG. If S(P) is not smaller than a user-given minimum support threshold, we regard P as a frequent sub-graph or a frequent graph pattern. Thus, the final goal of traditional frequent graph pattern mining is to extract all the possible graph patterns of which the support values are higher than or equal to this single minimum support threshold.
3.2. Overall Architecture of the Proposed Method
Figure 2 shows an overall architecture and flows of the proposed algorithm, SVE-RGM. It first scans a give graph database and then performs a series of works for mining SRGs. SVE-RGM conducts preprocessing works by reading the information of length-decreasing support and multiple minimum support constraints. After that, it computes a Least Minimum Support (LMS) factor for pre-pruning operations. Thereafter, the algorithm performs SVE-RGM growth for finding SRGs in a recursive manner. In this process, candidate patterns are generated and the algorithm checks whether or not they are valid by using the results of the proposed inverse function and the real rarity information corresponding to the candidates. These processes are conducted until we obtain all of the possible SRGs from the given graph database. When such recursive works are finished, we can have a complete set of SRGs.
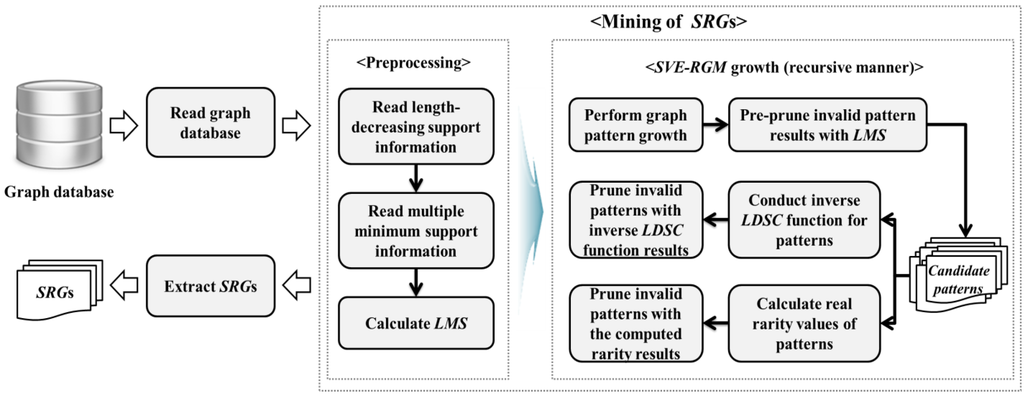
Figure 2.
Overall architecture of SVE-RGM.
3.3. Mining SRGs from Graph Databases
Figure 3 is an example of a simple graph database. Graph pattern mining approaches including the proposed method find interesting graph pattern information from such types of graph data. As shown in the procedure of Figure 2, we first scan a given graph database to calculate support values of the elements within the graph transactions, composing the database. Note that we assume that edge elements in the example database have the same edge label, for better understanding of the proposed method as shown in Figure 3. Therefore, support values for edges are not counted. Vertices that occur multiple times in a graph transaction are counted once [34,35,44]. After the database scanning work is finished, the proposed algorithm scans information of length-decreasing support constraints corresponding to the given graph database and multiple minimum support constraints for the elements composing the database.

Figure 3.
Example of a simple graph database.
3.3.1. Length-Decreasing Support Constraints and Smallest Valid Extension on Graph Mining
Recall that small sub-graphs having a few elements tend to be interesting if they have relatively high support values and large sub-graphs with many of elements can be interesting even though their support values are relatively low. It becomes important features supporting the reason why length-decreasing support constraints need to be applied into the graph mining operations. The easiest method for mining sub-graphs according to length-decreasing support constraints [41], tried to perform all of the possible pattern expansions, in order to confirm whether sub-graphs generated through the expansions satisfy each minimum support threshold, corresponding to their lengths. Therefore, this method causes fatal problems in terms of mining efficiency although correct results can be generated. To solve the problem, we define a length-decreasing support constraint function and its inverse function, and propose an SVE technique using these functions.
Definition 5.
(Length of graph) Let l be a length of a graph pattern, S. When S is a path or a free tree, l is the number of vertices in S. Meanwhile, if S is a cyclic graph, we consider l as follows. Let Sprev be a sub-graph pattern just before S becomes a cyclic graph, lprev be a length of Sprev, and k be the number of cyclic edges inserted into S. Then, l becomes an addition of lprev and k, where l can be denoted as l = L(S).
Figure 4 shows an example of length-decreasing support constraints. As shown in Figure 4a, there are various minimum support threshold values in the proposed algorithm, and one threshold value is set for each length factor. Especially, threshold settings become gradually lower according to the increase of graph pattern lengths.
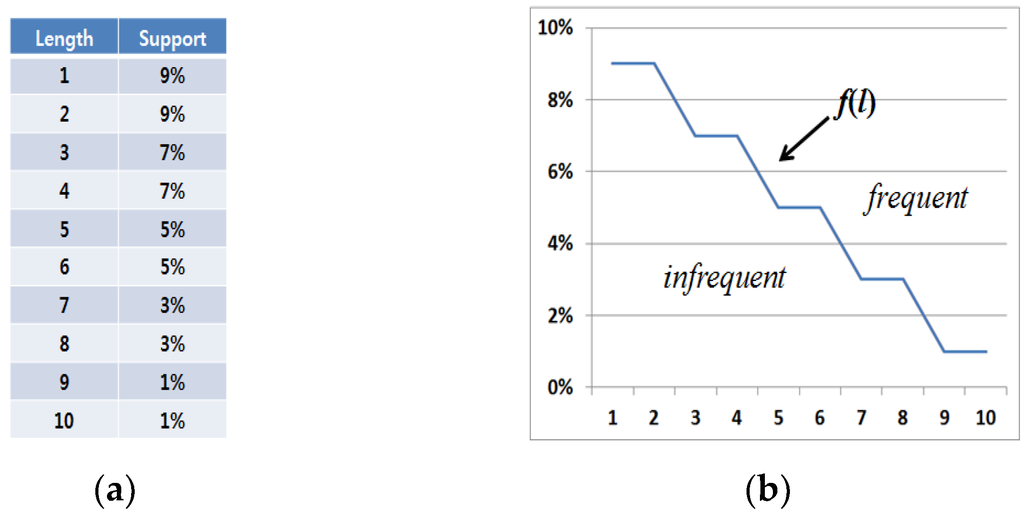
Figure 4.
Example of length-decreasing support constraints. (a) A table with length and support information; (b) A graph corresponding to the length-decreasing support constraints in Figure 4a.
Definition 6.
(Length-decreasing support constraint (LDSC) function) For the length of graph pattern S, l, length-decreasing support constraint function, denoted as f(l) returns a minimum support threshold corresponding to l’s current value. Since f(l) is constant or becomes lower as l comes to be larger, the inequality, 0 ≤ f(l + 1) ≤ f(l) ≤ 1 is satisfied.
Definition 7.
(Inverse function of LDSC) Given a support of graph pattern S, S(S), an inverse function of Definition 6 is denoted as f−1 (S(S)) and returns the minimum length that S must have in order to become a potentially frequent sub-graph pattern. Such a condition is also denoted as f−1 (S(S)) = min(l|f(l) ≤ S(S)).
Example 1.
Given length-decreasing support constraint information in Figure 4a, the corresponding LDSC function, f(l) is denoted as shown in Figure 4b. Since f(1) = 9% (=0.09), f(2) = 9% (=0.09), f(3) = 7% (=0.07)… and f(10) = 1% (=0.01), it is certain that the function satisfies the inequality, 0 ≤ f(l + 1) ≤ f(l) ≤ 1. Let us assume that a sub-graph S has a support of 4% and a length of 5 respectively. Then, f−1(S(S)) returns 7 since the minimum value is 7 among the lengths corresponding to the supports lower than or equal to 4%. Therefore, S must have more than length of 7 to be frequent. However, it is eventually infrequent since its length is 5.
We can determine that certain sub-graphs included in the “infrequent” area as shown in Figure 4b are invalid while ones contained in the “frequent” area become valid, where f(l) plays a role in distinguishing whether or not sub-graphs are frequent.
Through Definitions 5–7, we can draw the following SVE property for graph pattern mining based on length-decreasing support constraints, which helps perform the graph mining processes more efficiently by reducing the number of needless graph pattern expansions.
Definition 8.
(Smallest Valid Extension (SVE) property for graph mining) Given an infrequent graph pattern S, any super pattern of S, S’ must have a length larger than the result of f−1(S(S)) before it becomes a potentially frequent sub-graph pattern.
Unlike traditional graph pattern mining, we need to consider the following additional characteristics in length-decreasing support constraint-based graph pattern mining. If a graph pattern is not valid in traditional graph pattern mining, we can omit the pattern and all of the corresponding operations related to the pattern because it and all of its possible super patterns become useless by the anti-monotone property. This property means that, if a certain pattern is infrequent, all the super patterns generated from the pattern are also infrequent. However, because the proposed algorithm applies different minimum support thresholds according to the length characteristics of generated graph patterns, the anti-monotone property cannot be maintained. In other words, although a certain sub-graph is infrequent in the current state, any of its super patterns may become frequent again as we conduct the graph pattern growth process. The previous approach [41] solved such a problem by applying an overestimation technique into its pattern pre-pruning factor. This technique can perform LDSC-based frequent graph pattern mining operations without any pattern loss, but it is a naïve technique that wastes computing resources in generating useless candidate patterns. However, based on the SVE property, we can find permanently invalid patterns. The following lemma supports such an advantage.
Lemma 1.
Let S and S’ be a certain sub-graph pattern and a super pattern of S and L(S) and L(S’) be the lengths of S and S’ respectively. If L(S’) < f−1(S(S)) such that S(S) < f(L(S)), then S’ is always an infrequent pattern.
Proof.
Depending on the characteristics of frequent graph mining, it is always true that S(S) ≥ S(S’), and S(S) is in inverse proportion to f−1(S(S)). Therefore, we can induce the inequality, f−1(S(S)) ≤ f−1(S(S’)). In order that S’ expanded from the infrequent sub-graph S becomes frequent, these two conditions, S(S) < f(L(S)) and S(S’) ≥ f(L(S’)) must be satisfied. After we multiply the inverse function by the conditions, the result can be denoted as follows: L(S) ≤ f−1(S(S)) ≤ f−1(S(S’)) ≤ L(S’). Therefore, S’ becomes infrequent if it does not satisfy these conditions. Because the current mining step performed up to S, S’ has not yet been expanded. Therefore, we can determine the values of L(S), L(S’), and f−1(S(S)) but cannot know the value of f−1(S(S’)) (L(S’) can be inferred from L(S)). Therefore, if L(S’) ≥ f−1(S(S)) is false, i.e., L(S’) < f−1(S(S)) is true, S’ becomes an infrequent graph pattern. For this reason, we can know whether or not S’ is valid in advance even though any actual expansion process for S’ is not performed. ■
Note that the proposed overestimation technique is not an approximation method. Therefore, unlike the statistical approximation approach [45], our method does not mine any false positives. Our overestimation technique is employed to check and discard permanently meaningless graph patterns without any pattern loss during the mining process. However, since every pattern satisfying the overestimated condition is not the finally valid result (called a candidate pattern), we check the actual support of each candidate in order to mine actually meaningful graph patterns selectively. By doing this, we can obtain a complete set of frequent graph patterns considering the length-deceasing support constraints and rarity of graphs.
3.3.2. Pre-Pruning Infrequent Sub-Graphs by the SVE Property without Any Pattern Loss
Using the defined SVE property, we can determine information regarding what sub-graphs cause needless pattern expansions in advance. However, if they are directly pruned, fatal problems such as pattern losses can occur since applying the length-decreasing support constraints into graph mining generally breaks the anti-monotone property. That is, any infrequent sub-graphs can become frequent ones as their pattern expansion works are conducted. To solve the problems and maintain the anti-monotone property, we additionally consider the length information for graph transactions in graph databases as well as the SVE property.
Lemma 2.
Let S and S’ be invalid graph patterns (S’ ⊃ S) and SETS’ = {Tr1, Tr2, …, Trn} be a set of graph transactions including S’. Then, if there is any element satisfying L(Tri) < f−1(S(S)) among the elements of SETS’ (1 ≤ I ≤ n), S’ can permanently be pruned.
Proof.
In SETS’ = {Tr1, Tr2, …, Trn}, each Tr is a graph transaction with S’ in DBG, and n becomes the support of S’. If there is any Tri such that L(Tri) < f−1(S(S)) (1 ≤ i≤ n), it means that lengths of all super patterns generated from S’ are also smaller than f−1(S(S)) because the super patterns cannot have more lengths than L(Tri). Furthermore, since S’ and the super patterns of S’ do not satisfy the minimum length by the inverse function, neither of them naturally satisfies minimum support constraints. As a result, pruning S’ does not have any negative effect on maintenance of the anti-monotone property. That is, we can obtain intended mining results without any problem. ■
Example 2.
Let us consider the example in Figure 4 and assume that a certain sub-graph, S, has a length of 2 and a support of 5%, a super pattern of S, S’, has a length of 3 and a support of 4% and a set of graph transactions for S’, SETS’ includes 4 graph transactions (denoted as SETS’ = {Tr1, Tr2, Tr3, Tr4}), where the length for each Tr is set to 7, 4, 10, and 5 respectively. Then, S’ becomes an invalid pattern according to the SVE property and Lemma 1. Furthermore, since L(Tr2) is smaller than f−1(S(S)), any super patterns of S’ also become useless ones and therefore, S’ can directly be pruned.
Based on Lemma 2, we can prune all of the permanently useless patterns and omit the corresponding mining operations in advance without any pattern loss.
3.3.3. Multiple Minimum Supports of Vertex and Edge Elements on Graph Mining
In addition to the length-decreasing support constraints, we additionally consider multiple minimum supports of graph elements (vertices and edges) in this paper. Recall that meaningful graph patterns with low supports may not be extracted if a given minimum support threshold is high in traditional graph pattern mining, otherwise an enormous number of useless patterns should be mined if we lower the threshold to find such useful ones. By considering multiple, minimum support constraints of vertex and edge elements, as well as the length-decreasing support constraints, we can obtain a smaller number of more meaningful pattern results. In contrast to traditional graph pattern mining that has a single minimum support threshold, the proposed method has a different threshold for each element to consider the multiple minimum support constraints on graph pattern mining.
Definition 9.

(Minimum support constraints of vertices and edges) Given a graph database with multiple graph transactions Tr, DBG = {Tr1, Tr2, …, Trn}, a set of x vertices and y edges comprising DBG can be denoted as V(DBG) = {v1, v2, …, vx} and E(DBG) = {e1, e2, …, ey}, respectively. Then, each of minimum support threshold, δ, is set for each element as shown in Table 1, where they are assigned by a user, respectively.

Table 1.
Multiple minimum supports of graph elements (vertices and edges).
In traditional graph pattern mining, there is only one factor for deciding whether or not a found graph pattern is frequent without the characteristics of its elements. Meanwhile, we need to consider a different way to apply the multiple minimum support constraints into our method.
Definition 10.
(Minimum support constraints of graph patterns) Let P be a graph pattern extracted from DBG. Then, a set of vertices and edges can be denoted as V(P) = {v1, v2, …, vi} and E(P) = {e1, e2, …, ej}, respectively. According to Definition 9, we know that each element has its own minimum support threshold set by a user, and P is composed of multiple elements. Hence, the minimum support threshold for P, T(P), is computed as the minimum value among the threshold values of P’s elements.
If S(P) is not lower than T(P), we can say that P is a valid graph pattern satisfying the rarity of graph elements based on the multiple minimum support constraints. The reason why we compute and use the minimum support threshold for each mined graph pattern is that we can consider the different rarity of each pattern in this way.
Definition 11.
(SVE-based Rare Graph pattern (SRG)) Given a graph pattern, X, we call X an SRG if S(X) ≥ f(L(X)) and S(X) ≥ T(X). In other words, SRGs mean sub-graph patterns that satisfy both the length-decreasing support and multiple minimum support constraints.
Consequently, the main goal of the proposed algorithm, SVE-RGM, is to mine all of the possible SRGs from a given graph database without any pattern loss.
3.3.4. Pre-Pruning Invalid Graph Patterns Based on Multiple Minimum Support Constraints
Recall that fatal pattern losses can be caused if we do not apply the additional considerations mentioned in Section 3.3.2. Similarly, we can also suffer from such a pattern loss problem if we directly prune graph patterns that do not satisfy their own multiple minimum support constraints. As mentioned above, elements of a graph pattern have their own threshold values set by a user. Therefore, the anti-monotone property is not satisfied with this situation. In other words, although a certain graph pattern has a support that does not satisfy the corresponding multiple minimum support constraint in the current state, any super pattern of it may become a valid result again in the process of graph pattern expansion. Hence, if we pre-prune such patterns without any additional consideration, fatal pattern losses can occur. Moreover, an enormous number of interesting patterns can be lost by unintended pruning of a few elements or graph patterns. Satisfying the anti-monotone property during the mining process is one of the most important rules to improve mining efficiency without any negative effect such as pattern losses. For this reason, we employ an overestimation method for maintaining the anti-monotone property without any pattern loss on the proposed algorithm.
Definition 12.
(Overestimated minimum support constraint) DBG has multiple graph transactions and the corresponding elements as mentioned in Definition 9. Then, the overestimated minimum support constraint for DBG, O(DBG), is computed as the smallest value among the valid minimum support constraints of all the elements comprising DBG (it is also called Least Minimum Support (LMS)). In other words, let SETT(DBG) = {δ1, δ2, …, δx+y} (δ1 ≥δ2 ≥ … ≥ δx+y) be a sorted set of minimum support constraints for all the elements in DBG (x and y are the numbers of vertices and edges, respectively). Then, we start comparing the smallest threshold δx+y with the real support of the element corresponding to δx+y. After that, δ(x+y)−1 is compared to the corresponding element support. Such a comparison is performed until we find the first element of which the support is higher than or equal to the corresponding minimum support constraint, δk (1 ≤ k ≤ x + y). Then, we consider δk as O(DBG).
Consequently, SRGs extracted from the proposed algorithm are graph patterns that satisfy Lemmas 1 and 2 and the condition of Definition 12.
3.4. Improving Efficiency of Graph Mining Performance Based on Symmetry Features of Graphs
From the suggested definitions and constraints, we allowed the proposed method to mine a smaller number of meaningful graph pattern results, called SRGs. As mentioned above, the length-decreasing minimum support and multiple minimum support constraints also increase the mining efficiency of the proposed algorithm, SVE-RGM, by reducing the search space effectively. In addition, we can also raise the mining efficiency with the correctness of the algorithm maintained. Recall that the proposed method performs its own mining operations in a depth-first search manner. This also means that a few useless graph patterns may cause the proposed algorithm to generate an enormous number of invalid or duplicated pattern results. In contrast to the case of traditional frequent pattern mining that considers only an item-based simple format, a numerous number of duplicated graph patterns can be generated in graph pattern mining because of the complicated structures of graph data. In particular, we have to conduct graph isomorphism tests for the mined patterns in order to prevent duplicated ones from being extracted.
In order to perform the mining operations more efficiently, our algorithm applies the following order types of graph pattern growth: (1) path → cyclic graph and (2) path → free tree → cyclic graph. In other words, a certain vertex is selected as a prefix at first and a path is generated by adding another vertex and edge that can be attached to the prefix. Then, we can obtain a graph pattern in a path form. After that, there are three options for the next step. That is, it can be extracted as a longer path, a free tree, or a cyclic graph according to the attached vertex and edge types. Recall that a few useless graph patterns can cause an enormous number of invalid or duplicated pattern results. From the above features, we can determine that removing duplicated path creations has a large effect on reducing the number of useless pattern creations. In this regard, symmetry features of paths can be used as effective factors that can lead to correct choices not to cause any duplicated path result. Let P = {v1, e1, v2, e2, …, ek-1, vk} be a given path and N = {v,e’} be a pair of one vertex and edge that are supposed to be attached to P. Then, when expanding P with N, we have two choices; the first one is to add N to the front of P and the second one is to add N to the rear of P because of the characteristics of paths. If we add N to P without any consideration, an enormous number of duplicated graph patterns can be generated as the graph pattern growth works are conducted during the mining process. Meanwhile, if we set a specific constraint for limiting expansion directions of paths, we can effectively prevent such a problem.
A path has at least two vertices and one edge. Then, we can determine whether or not the path is symmetric. In other words, given a path, P = {v1, e1, v2, e2, …, ek-1, vk}, we can extract two strings from P as follows: v1-e1-v2-e2-…-ek-1-vk (original string) and vk-ek-1-vk-1-ek-2-…-e1-v1 (inverse string). Then, if they are equal to each other, we consider P as a symmetric path. In this case, we do not need to consider what direction we have to choose because any selection leads to the same result. If the first string is lower than the second one in terms of a lexicographical order, we expand P by attaching new elements to the front of P. Meanwhile, if the first string is higher than the second one, we add the new ones to the rear of P. From the above path expansion technique based on the symmetry features of paths, we can omit any path expansion causing duplicated path creation. In addition, once the symmetry result of P is calculated, we can easily determine the symmetry result of its expanded path in a few additional computations. Let Symtotal(P), Symfront(P), and Symrear(P) be symmetry functions for the entire part of P ({v1, e1, v2, e2, …, ek-1, vk}), the front part of P ({v1, e1, v2, e2, …, ek-2, vk-1}) and the rear part of P ({v2, e2, v3, e3, …, ek-1, vk}), where each function returns 0 when the corresponding string is symmetric, 1 when the corresponding original string is lower than the inverse one and −1 when the original one is higher than the inverse one. Using this method, we can easily know the symmetry result of super patterns of P. Let P’ be a longer path that adds a new vertex and edge to P. Then, if the new elements have been attached to the front of P’, we can determine that Symtotal(P) = Symrear(P’). Meanwhile, if the new ones have been added to the rear of P’, it is true that Symtotal(P) = Symfront(P’). Therefore, based on these characteristics, we can efficiently determine the symmetry results of mined patterns. By restricting directions of graph expansion based on the symmetry features of paths, we can improve the mining efficiency of the proposed method.
One of the most important considerations in frequent graph pattern mining is to enumerate all of the possible graph patterns without any redundancy. In contrast to the itemset format traditional frequent pattern mining focuses on, a graph pattern is composed of multiple vertices and edges, where the vertices can be ordered in many ways. Therefore, one graph pattern can also be denoted as a large number of topologically equivalent copies. Hence, it is essential to check graph isomorphism whenever a graph pattern is mined. Especially, checking graph isomorphism is a well-known NP-hard problem that can cause enormous computational overheads. However, as mentioned above, we do not have to check graph isomorphism for the path format because we established the symmetry-based constraint for paths in advance and allow paths to be enumerated on the constraint. When any path is expanded as a free-tree, we employ the backbone strategy of Gaston, which is different from the canonical representation used in gSpan. By using the technique, we can prevent any duplication of free-trees from being caused in the mining process without performing any works for graph isomorphism (the correctness of the backbone strategy was proved by showing that the Gaston algorithm extracted the same results as those of other approaches like gSpan [34,35]). When a path or a free-tree is expanded as a cyclic graph, we have no choice but to conduct graph isomorphism operations. However, we can reduce computational overheads by using the minimum spanning tree format when comparing cyclic graphs. A cyclic graph can be expressed as a minimum spanning tree, which is simpler than its original one. Therefore, we can compare graphs more quickly than doing in a naïve manner.
3.5. Algorithm Description: SVE-RGM
Figure 5 represents overall mining steps of the proposed algorithm, SVE-RGM. In the main procedure, SVE-RGM, the lowest value in LDSC is set as a minimum support threshold, δ and the algorithm computes LMS from the MMS data (lines 1–3). After that, it finds valid vertices and edges from DBG through the calculated minimum support and LMS value (lines 3–6). Then, for each frequent vertex, the algorithm extracts valid sub-graph patterns according to length-decreasing support constraints and multiple minimum support thresholds as it performs a series of graph pattern expansion works (lines 7–11). When function Expand_subgraphs is called, SVE-RGM determines whether G is frequent or not and then assigns a flag, true or false, into the isFrequent variable (lines 1–4), where G is entered to P if G is frequent (line 3). Thereafter, for each edge in E, appropriate pattern expansion works are selectively conducted according to the state of G such as a path, a free tree, and a cyclic graph (lines 6–8). After that, if the support of the expanded pattern, G’, is not smaller than LMS, the algorithm conducts the subsequent works (line 9). If isFrequent is false, then the algorithm decides whether to prune G’ (lines 10–13). If G’ is not pruned, SVE-RGM calls Expand_subgraphs recursively to perform the next pattern expanding operations (lines 14–16). After all of mining operations terminate, we can gain a complete set of SRGs considering the length-decreasing support constraints and the multiple minimum support constraints for rarity of graph patterns.

Figure 5.
SVE-RGM algorithm.
4. Performance Evaluation
4.1. Experimental Environment
To evaluate performance of the proposed algorithm, SVE-RGM, precisely and reasonably, the algorithm is compared with the following state-of-the-art algorithms, Gaston [34,35], FGM-LDSC [41], and WRG-Miner [37]. Gaston is a famous fundamental frequent graph pattern mining algorithm that features fast mining speed. FGM-LDSC is a Gaston-based approach that can consider length-decreasing support constraints into graph mining processes. WRG-Miner is an algorithm that extracts frequent graph patterns considering multiple minimum support constraints and different element weight factors. Note that we optimized WRG-Miner in order to compare it with ours fairly. They were written in C++ and performed in 4.0 GHz CPU, 16GB RAM, and WINDOWS 7 OS. We used real and synthetic datasets, PTE composed of chemical graph data, DTP composed of compound graph data and SYN100K composed of 100K synthetic graph data. Detailed characteristics of these two real graph datasets are available at the literature [34,35]. Figure 6 shows distributions regarding length-decreasing support constraints for the PTE, DTP, and SYN100K datasets.

Figure 6.
(a) Length-decreasing support constraints of PTE; (b) Length-decreasing support constraints of SYN100K; (c) Length-decreasing support constraints of DTP.
Each implementation of the algorithms receives a graph dataset and returns its own mining result as a file. The input format of a graph dataset is as follows. Let us express the example database shown in Figure 3 as the input format for the implementations. This graph dataset is composed of 4 graph transaction data, where they consist of 4 different vertex types and 1 edge type. Then, we denote each graph transaction as a set of relations among the links of vertices and edges. For example, the first graph transaction has 4 vertices, A, B, A and C and 1 edge (let us denote it as “a“). We first assign an index for each vertex. That is, the index of the first vertex A becomes 0 and that of the last one C becomes 3. A relation among vertices and an edge is denoted as follows. The relation corresponding to vertices A and B and edge a is denoted as 0 1 a. Table 2 is the result of changing the example dataset of Figure 3 to the input format. Note that labels of vertices and edges are expressed as integer values in real datasets. Based on the format shown in Table 2, each algorithm performs its own mining operations, where additional data for length-decreasing support constraints or multiple minimum support constraints are inputted according to the characteristics of the algorithms. Mining results are also stored like the format shown in Table 2 and the support information corresponding to each pattern is additionally stored.

Table 2.
Input format of the graph dataset transformed from Table 1.
In order to assign δ values for the elements of given graph datasets, the following methodology used in the literature [26,27,28,36,37] was employed. Let ei be an element within a given graph dataset. Then, the corresponding δ value for each ei is calculated as follows: δi = MAXIMUM(β × S(ei), LS) (LS: the smallest δ value in all the δ values). Note that the threshold of Gaston and FGM-LDSC is set to the same value as LS for fair comparisons. In the equation, β (=1/α (0 < β ≤ 1, 1 ≤ α)) is a variable showing how closely the actual support value of each element is related to the corresponding δ value. In other words, each δ is more likely to have a value more similar to the real support of the corresponding element rather than LS, if β becomes closer to 1.
4.2. Analysis of Runtime Performance
Figure 7 shows runtime results of the PTE, DTP and SYN100K datasets on changing minimum support threshold settings, where the α values of WRG-Miner and SVE-RGM are fixed as 1. In Figure 7a, all the algorithms require more runtime resources as the given minimum support threshold becomes lower. However, the proposed algorithm guarantees the fastest runtime performance in all cases, while Gaston shows the slowest performance. Especially when the threshold is 1.5%, we can observe that there are large gaps among the compared algorithms. Since the proposed algorithm employs both the length-decreasing support constraints and the multiple minimum support constraints, it extracts a smaller number of interesting patterns compared to those of the others. From the result of Figure 7a, we can determine that the length-decreasing support constraints have a better effect on improving the runtime performance compared to the multiple minimum support constraints because FGM-LDSC is faster than WRG-Miner in this case. On the other hand, the SYN100K dataset shows a different tendency. In the case of Figure 7a, the proposed method shows the best result in every case, and Gaston is the worst among the compared ones. However, in this case, we can see that WRG-Miner is better than FGM-LDSC. From these different results, we can know that the multiple minimum support constraints are more effective on this synthetic dataset. In the case of the DTP dataset, we can see that the proposed method and Gaston have similar tendencies with those of the PTE dataset. However, the other algorithms have different results. In the DTP dataset, WRG-Miner has better runtime performance than that of FGM-LDSC, which means that the multiple minimum support constraints are more effective on reducing the execution time with respect to this dataset. The proposed method also has the best runtime results in this case. Meanwhile, the Gaston algorithm is slowest in almost all cases.
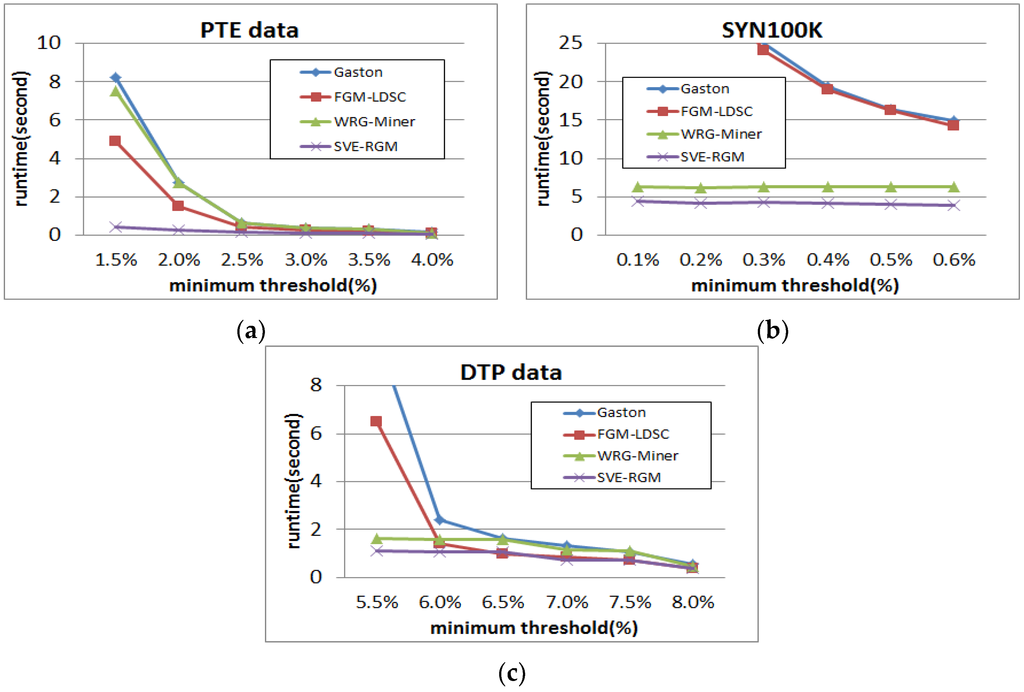
Figure 7.
(a) Runtime results of PTE on changing minimum support threshold; (b) Runtime results of SYN100K on changing minimum support threshold; (c) Runtime results of DTP on changing minimum support threshold
Figure 8 is the results of runtime performance on settings of the changing α value while the minimum support threshold is fixed. Recall that β is inversely proportional to α (β = 1/α (0 < β ≤ 1, 1 ≤ α)) and if β becomes closer to 1, δ is more likely to have a value more similar to the real support of the corresponding element rather than LS. Therefore, as α becomes lower, multiple minimum support constraint-based approaches extract a less number of pattern results. In Figure 8a,b, we can observe that all the algorithms spend stable runtime in mining their own graph patterns. However, the Gaston algorithm has the worst performance regardless of minimum support threshold or α settings. Meanwhile, the proposed method guarantees the best result in every case. The reason why the compared algorithms show such stable performance results is that PTE is not a dataset affected by the changes of the α value. For this reason, WRG-Miner does not show good performance in this case because it is a rare graph pattern mining algorithm based on multiple minimum support constraints. Meanwhile, the results of performance evaluation in SYN100K have a different tendency. In this case, FGM-LDSC outperforms WRG-Miner in almost all cases. As in the previous case, our algorithm, SVE-RGM, shows the best performance. Especially, the proposed method guarantees stable runtime performance regardless of α, while WRG-Miner becomes gradually slower as the α value becomes higher.

Figure 8.
(a) Runtime results of PTE on changing α (minsup = 1.5%); (b) Runtime results of PTE on changing α (minsup = 2%); (c) Runtime results of SYN100K on changing α (minsup = 1.5%); (d) Runtime results of SYN100K on changing α (minsup = 2%); (e) Runtime results of DTP on changing α (minsup = 5.5%); (f) Runtime results of DTP on changing α (minsup = 6%).
In contrast to the results of the above two datasets, the proposed algorithm, SVE-RGM and the compared rare graph pattern mining algorithm, WRG-Miner, show noticeable changes depending on the settings of α. They are faster than the others at lower settings of α since they can better reflect the rarity features of graph elements into their own mining processes and reduce the number of mined patterns. In addition, the proposed algorithm also guarantees better runtime efficiency than that of WRG-Miner because our approach can selectively extract a smaller number of graph patterns than those of the competitor by considering the length-decreasing support constraints additionally. As α becomes larger, the performance of WRG-Miner and ours becomes similar to the other non-rare pattern mining algorithms.
4.3. Analysis of Memory Usage Performance
The next test is memory usage performance shown in Figure 9, where the basic parameter settings are equal to the previous test. When the threshold is relatively low in Figure 9a, the algorithms have similar memory consumption. However, as the threshold becomes lower, the gaps of their memory usage results become larger. In this case, all the algorithms except for ours have similar memory usage, regardless of threshold settings. Meanwhile, our algorithm has the most efficient memory usage in all the cases. In the case of Figure 9b, the proposed method guarantees the best performance. Gaston and FGM-LDSC have similar results, while WRG-Miner has relatively good performance compared to the tendency of Figure 9a because the multiple minimum support constraints of the algorithm have a positive effect on reducing memory usage in the SYN100K dataset. Nevertheless, WRG-Miner falls behind our method in every case. That is, the proposed algorithm SVE-RGM, shows the most efficient memory usage regardless of any environmental settings. As shown in Figure 9c, all the algorithms except for WRG-Miner have similar tendencies with those of the PTE dataset. Recall that the multiple minimum support constraints are more effective on the runtime performance with respect to this dataset. This advantage also leads the algorithm to save more memory resources as shown in the figure.

Figure 9.
(a) Memory usage results of PTE on changing minimum support threshold; (b) Memory usage results of SYN100K on changing minimum support threshold; (c) Memory usage results of DTP on changing minimum support threshold.
Figure 10 shows memory usage results of the PTE and SYN100K datasets on changing α values while the threshold is fixed. As in the cases of Figure 9, the compared algorithms have similar tendencies. In the PTE dataset shown in Figure 10a,b, the first three algorithms, Gaston, FGM-LDSC, and WRG-Miner, consume similar memory in all cases, while the proposed one spends the smallest memory because of its own mining techniques and constraints. On the other hand, WRG-Miner has better performance than those of Gaston and FGM-LDSC in the SYN100K dataset because of its own constraints, multiple minimum supports for graph elements. However, its performance is still worse than our method as shown in the figure. In addition, all the algorithms show stable memory usage regardless of the α settings. This signifies that the SYN100K dataset has few effect on the α settings. Similarly to the runtime results shown in Figure 8e,f, memory usage of the rare graph pattern mining algorithms is changed according to the settings of α. However, the memory efficiency of the proposed algorithm is best among the compared ones in general. Meanwhile, since Gaston and FGM-LDSC do not consider the rarity of graph elements, they show the same results regardless of changes of α.
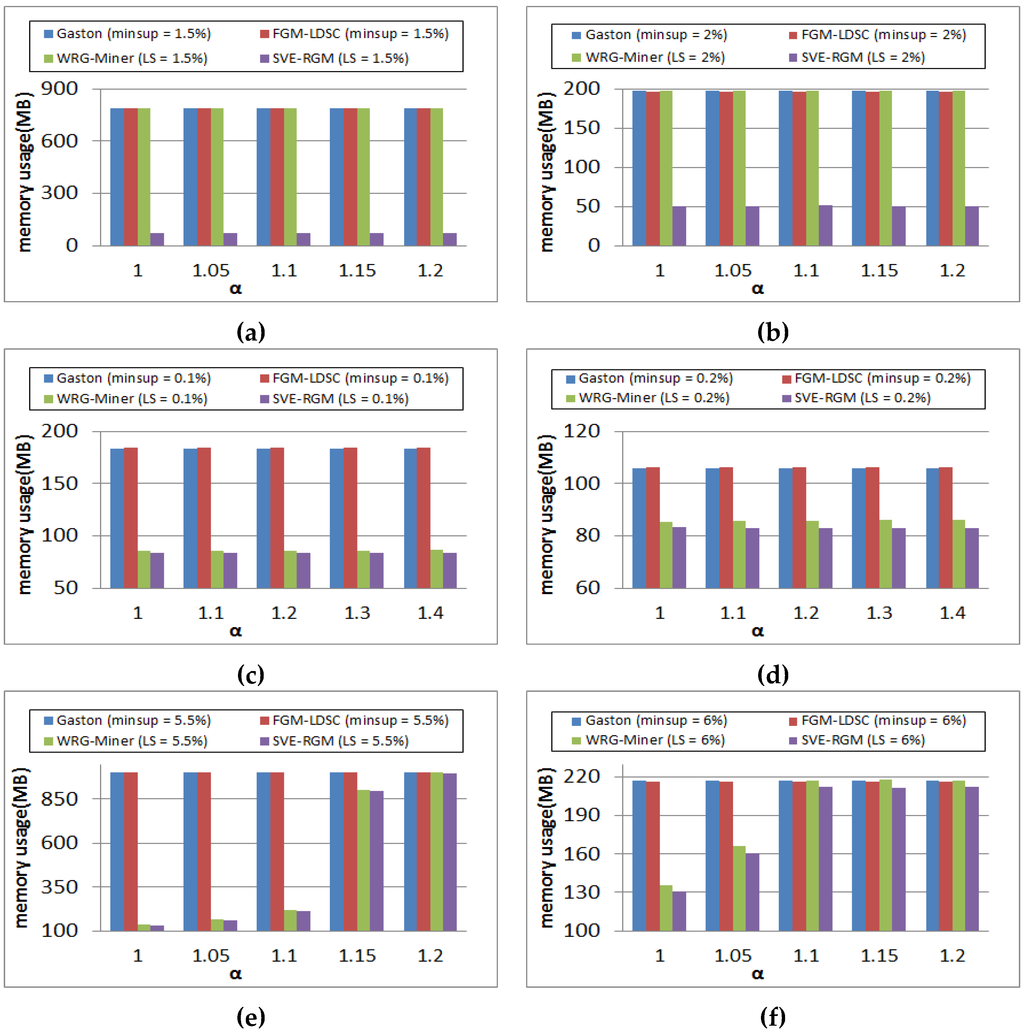
Figure 10.
(a) Memory usage results of PTE on changing α (minsup = 1.5%); (b) Memory usage results of PTE on changing α (minsup = 2%); (c) Memory usage results of SYN100K on changing α (minsup = 1.5%); (d) Memory usage results of SYN100K on changing α (minsup = 2%); (e) Memory usage results of DTP on changing α (minsup = 5.5%); (f) Memory usage results of DTP on changing α (minsup = 6%).
4.4. Analysis of Pattern Generation Performance
Figure 11 shows results of graph pattern generation for the compared algorithms in a log-scale, where the basic settings of parameters are also the same as those of the previous tests. These figures support the results of the above runtime and memory usage performance evaluation. As mentioned above, the proposed algorithm can reduce an enormous number of less meaningful graph patterns by employing both the length-decreasing support constraints and the multiple minimum support constraints. As a result, we can obtain a smaller number of interesting patterns compared to the others. In the case of Figure 11b, WRG-Miner and our SVE-RGM generate the same pattern results since the multiple minimum support constraints have a less effect on the resulting patterns. However, the mining performance of the proposed method is better than that of WRG-Miner in spite of this pattern generation result. In the case of the DTP dataset, the proposed algorithm also mines the smallest number of frequent graph patterns.
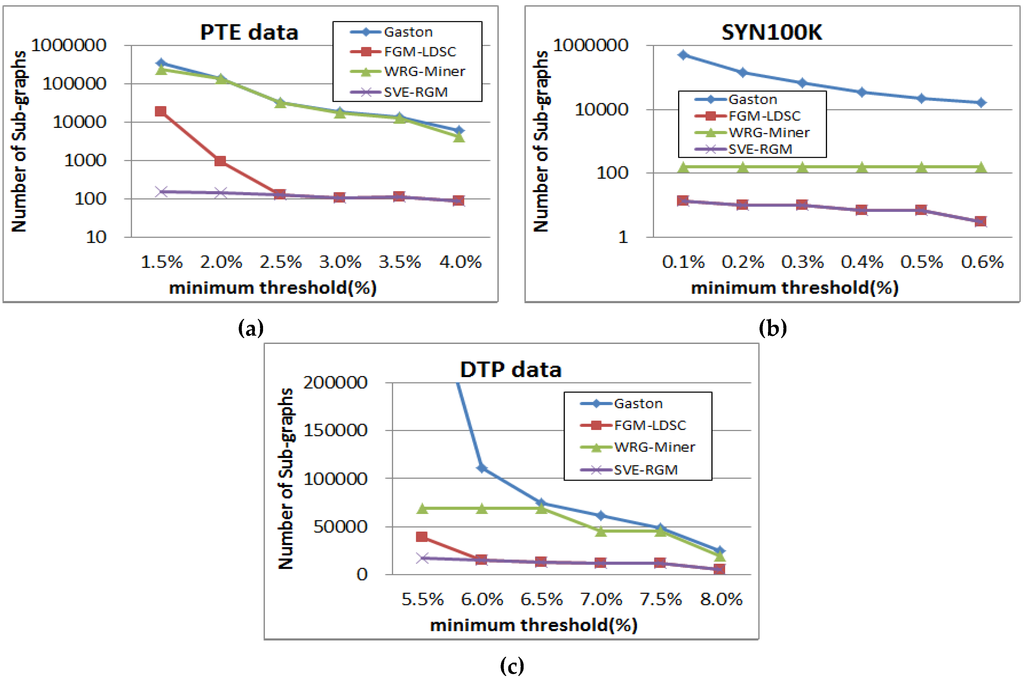
Figure 11.
(a) Pattern generation results of PTE on changing minimum support threshold; (b) Pattern generation results of SYN100K on changing minimum support threshold; (c) Pattern generation results of DTP on changing minimum support threshold.
Figure 12 shows results of graph pattern generation on changing value α settings. In Figure 12a,b, the results of Gaston and FGM-LDSC are not changeable since they do not apply the multiple minimum support constraints for considering the rare item problem. Meanwhile, the other two algorithms, WRG-Miner and SVE-RGM, also show stable pattern generation results because this dataset has a less effect on the changes of α. On the other hand, we can see that the number of graph patterns mined from WRG-Miner is increased as the α value becomes higher. Meanwhile, SVE-RGM shows stable results regardless of the α value settings. In contrast to the cases of PTE and SYN100K, the algorithms considering the rarity of graph elements, WRG-Miner and our SVE-RGM, mine a different number of mining results as shown in the figure. As α becomes lower, they extract a smaller number of patterns because they can selectively mine patterns considering the rarity of graph elements.
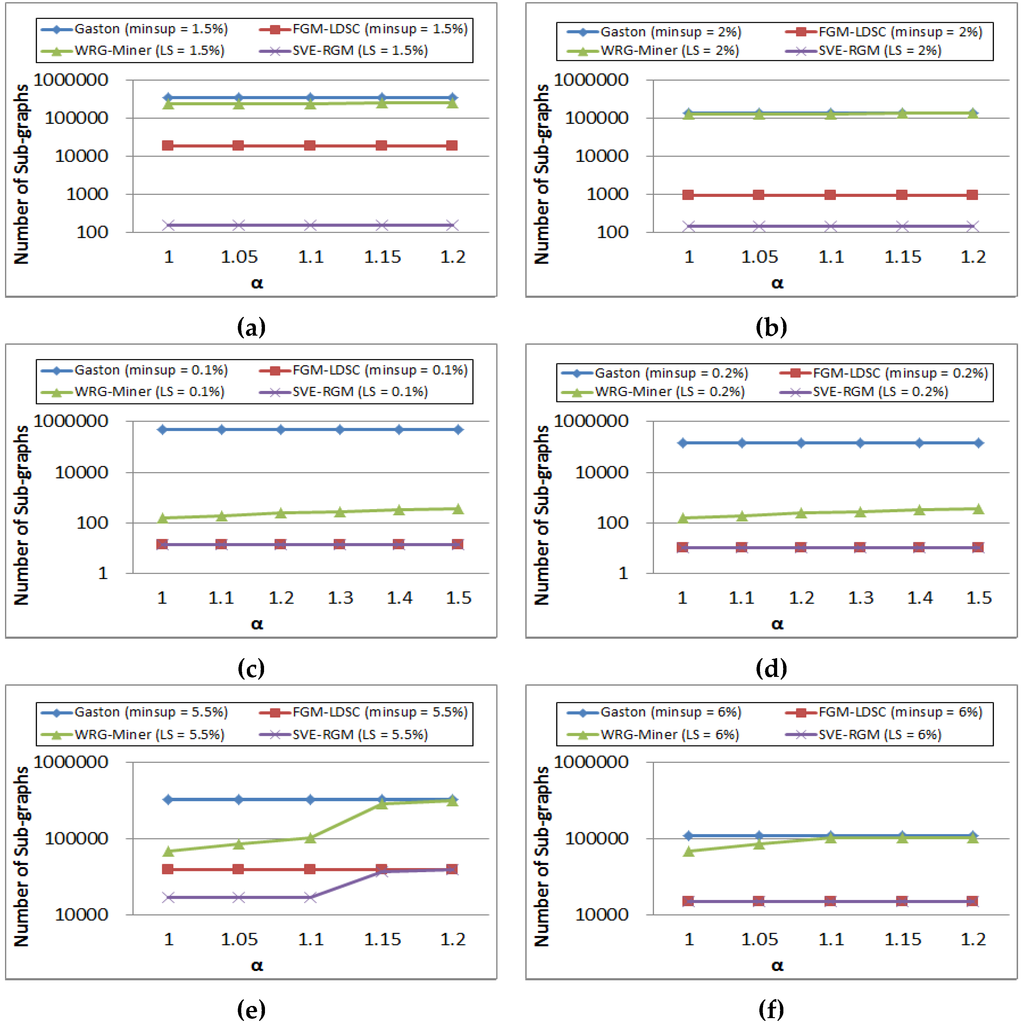
Figure 12.
(a) Pattern generation results of PTE on changing α (minsup = 1.5%); (b) Pattern generation results of PTE on changing α (minsup = 2%); (c) Pattern generation results of SYN100K on changing α (minsup = 0.1%); (d) Pattern generation results of SYN100K on changing α (minsup = 0.2%); (e) Pattern generation results of DTP on changing α (minsup = 5.5%); (f) Pattern generation results of DTP on changing α (minsup = 6%).
4.5. Analysis of Algorithm Performance on Changing Length-Decreasing Support Constraints
Next, we test the mining performance of each algorithm on changing length-decreasing support constraints. Figure 13, Figure 14 and Figure 15 show the results of the tests for each dataset, where α is fixed to 1 in order to reflect the rarity features into the mining processes of the rare graph pattern mining algorithms. Figure 13a shows the different settings of length-decreasing support constraints for the PTE dataset in this test, where the minimum support threshold is fixed to 1.5%. We show how the results of performance evaluation for the algorithms change according to these constraint settings. As shown in Figure 13b, Gaston and WRG-Miner have the same result regardless of the changing settings since they are algorithms not considering any length-decreasing support constraint. Meanwhile, the other algorithms have different runtime results depending on the constraint settings. As the condition is changed from cond. 1 to cond. 5, FGM-LDSC and SVE-RGM operate faster because they can mine a smaller number of pattern results as shown in Figure 13d. Meanwhile, memory consumption of the algorithms is different from the tendency of the runtime test. Gaston and WRG-Miner also spend the same memory regardless of the constraint settings.
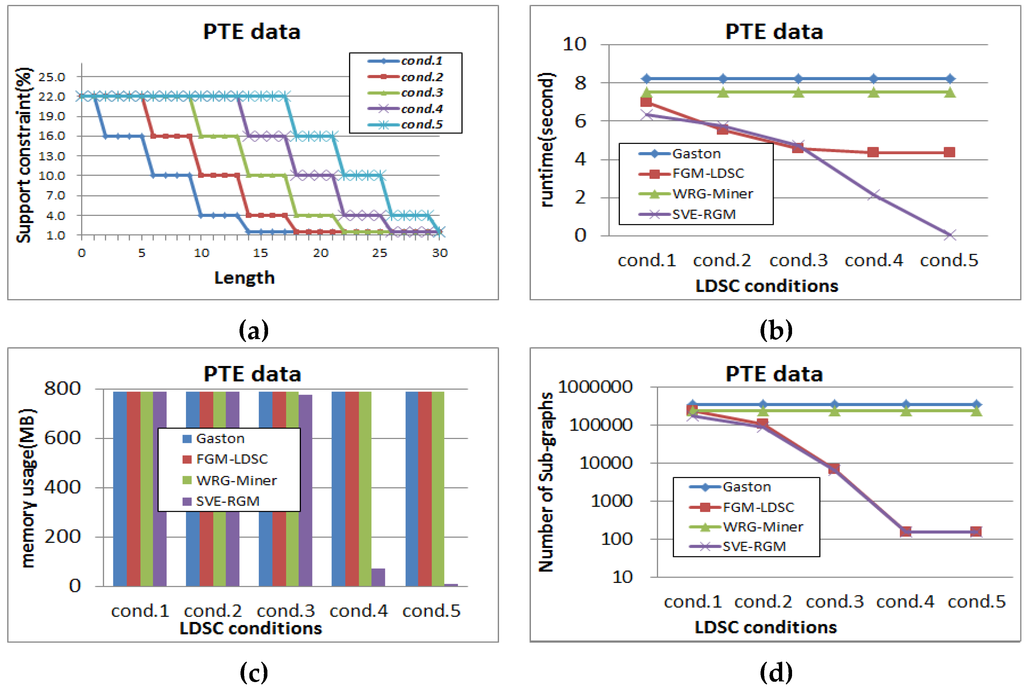
Figure 13.
(a) Different settings of length-decreasing support constraints for PTE (α = 1); (b) Runtime result for PTE (α = 1); (c) Memory usage result for PTE (α = 1); (d) Pattern generation result for PTE (α = 1).


Figure 14.
(a) Different settings of length-decreasing support constraints for DTP (α = 1); (b) Runtime result for DTP (α = 1); (c) Memory usage result for DTP (α = 1); (d) Pattern generation result for DTP (α = 1).

Figure 15.
(a) Different settings of length-decreasing support constraints for SYN100K (α = 1); (b) Runtime result for SYN100K (α = 1); (c) Memory usage result for SYN100K (α = 1); (d) Pattern generation result for SYN100K (α = 1).
While the runtime results of FGM-LDSC are differently shown in Figure 13b, its memory usage results are not changeable as shown in Figure 13c. Meanwhile, the memory consumption of the proposed algorithm becomes lower as the condition is changed from cond. 1 to cond. 5.
Figure 14 is the results of the DTP dataset, where the minimum support threshold is fixed to 5.5%. As in the case of Figure 13, the performance evaluation results of Gaston and WRG-Miner are not changeable. The runtime results of FGM-LDSC and SVE-RGM are also changeable according to the different settings of the length-decreasing support constraints. In the case of memory usage performance, they also have better results compared to Gaston and WRG-Miner. Moreover, as α becomes lower, the corresponding memory performance of the proposed algorithm also becomes better.
Figure 15 shows the experimental results for the SYN100K dataset, where the minimum support threshold is fixed to 0.1%. In this test, all the compared algorithms have stable runtime, memory usage, and pattern generation results as shown in the figure. However, the proposed algorithm guarantees the best results in all cases. As shown in Figure 13, Figure 14 and Figure 15, we can freely set the length-decreasing support constraints according to the use of given data and obtain the corresponding various results.
From the results of the above performance evaluation tests, we can determine that the proposed algorithm outperforms the state-of-the-art approaches in terms of runtime, memory usage, and pattern generation aspects.
5. Discussion
Since the concept of frequent pattern mining was considered, enormous approaches have been proposed in order to improve algorithm performance or discover more meaningful information and knowledge compared to previous methods. Since types of data are less and they have simple characteristics in the past, traditional frequent pattern mining methods were sufficiently able to analyze such data. However, as accumulated data become more complicated, the traditional ones faced technical limitations. Frequent graph pattern mining is a concept for dealing with various, complicated data that can be expressed as graph forms, and a variety of relevant works have been studied actively. We can consider a simple application example for frequent graph pattern mining. Let us assume that we are the marketing manager in a certain web-site for selling books. Then, we have to consider how to establish strategies for raising the sales more effectively. We can obtain information of web-site visits by various customers. In other words, if user A visits the main page, the book sales page and the e-book device sales page in sequence, we can regard this information as a graph pattern (each page becomes a vertex and each movement between the pages becomes an edge). Once such graph data are collected by various customers, we can construct a graph database and determine the characteristics of customer visits frequently occurring in the database by employing frequent graph pattern mining algorithms. By analyzing such mining results, we can also suggest and apply various, effective sales strategies such as exposing certain advertisements suitable for the relations of frequently occurring visits (i.e., interval between the pages) and providing customers with special offers suitable for the analyzed results.
Meanwhile, the proposed method focuses on static graph database formats. However, in recent years, it has been important to deal with dynamic data on data streams as well as static data. Moreover, there are various environments of data accumulations and different purposes of them in the pattern mining area. Traditional pattern mining approaches were designed to process normal data (also called certain or precise data). However, there is another type of data called uncertain data, which mean each element composing data cannot be expressed clearly as presence or absence; instead, they have their own existential probabilities. By considering the above issues, we can expand the proposed method in order to operate on data streams and process uncertain graph data on the length-decreasing support constraints and multiple minimum support constraints. In addition, we can also consider how to find proper threshold settings in the proposed algorithm. In practice, it is hard to find and set appropriate threshold settings because of different characteristics of given data and purposes of users. However, if we employ the concept of top-k pattern mining, we do not need to consider how to find and set reasonable thresholds. Moreover, this technique can also be integrated effectively with the length-decreasing support constraints. By considering these issues, we can mine top-k graph patterns for each graph length.
6. Conclusions
In this paper, we proposed a new graph pattern mining algorithm for mining frequent sub-graph patterns on the basis of length-decreasing support constraints for considering different characteristics of graph pattern sizes and multiple minimum support constraints for considering rarity of graph elements. In addition, the SVE property for graph mining was suggested and applied into the proposed algorithm in order to improve the mining efficiency of the proposed algorithm. The suggested graph pattern pruning strategy based on the SVE property contributed to removing meaningless sub-graph patterns in advance with the anti-monotone property maintained. Moreover, an efficient overestimation method was devised to prevent unintended pattern losses from being caused. One of the fatal problems in traditional frequent graph pattern mining was that this approach only used a single minimum support threshold without any consideration of additional meaningful factors, such as pattern lengths and characteristics of graph elements. Thus, traditional methods were unable to find meaningful frequent graph patterns, or they had to generate a huge amount of unessential graph patterns according to threshold settings. In contrast, the proposed algorithm could prevent meaningless graph patterns from being generated and it also guaranteed efficient mining performance by using the length-decreasing support constraints and the multiple minimum supports constraints for considering the characteristics of graph pattern lengths and the rarity of graph patterns, respectively. The experimental results in this paper also supported that the proposed algorithm outperformed the state-of-the-art methods in various aspects such as runtime, memory usage and pattern generation. Moreover, as future work, it is also possible to expand the proposed techniques and algorithm by considering other interesting pattern mining areas that can be effectively integrated with graph pattern mining such as real time pattern mining on data streams, uncertain pattern mining, and top-k pattern mining.
Acknowledgments
This research was supported by the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (NRF No. 20152062051, and NRF No. 20155054624), the Business for Academic-industrial Cooperative establishments funded Korea Small and Medium Business Administration in 2015 (Grants No. C0261068), and the Railway Technology Research Project of Korea Agency for Infrastructure Technology Advancement (No. 15RTRP-B082515-02).
Author Contributions
Unil Yun provided the main idea of this paper, designed the overall architecture of the proposed algorithm, and wrote the core contents of this paper. Gangin Lee implemented the proposed algorithm and wrote the main contents of this paper. Chul-Hong Kim investigated and reviewed references for graph theories and graph pattern mining applications to contribute to enhance the introduction and related work parts.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kim, J.; Yun, U.; Pyun, G.; Ryang, H.; Lee, G.; Yoon, E.; Ryu, K. A blog ranking algorithm using analysis of both blog influence and characteristics of blog posts. Cluster Comput. 2015, 18, 157–164. [Google Scholar] [CrossRef]
- Lee, G.; Yun, U.; Ryang, H. Mining weighted erasable patterns by using underestimated constraint-based pruning technique. J. Intell. Fuzzy Syst. 2015, 28, 1145–1157. [Google Scholar]
- Ryang, H.; Yun, U.; Pyun, G.; Lee, G.; Kim, J. Ranking algorithm for book reviews with user tendency and collective intelligence. Multimedia Tools Appl. 2015, 74, 6209–6227. [Google Scholar] [CrossRef]
- Ryang, H.; Yun, U.; Ryu, K. Discovering high utility itemsets with multiple minimum supports. Intell. Data Anal. 2014, 18, 1027–1047. [Google Scholar]
- Yun, U.; Lee, G. Sliding window based weighted erasable stream pattern mining for stream data applications. Future Gener. Comp. Syst. 2016, 59, 1–20. [Google Scholar] [CrossRef]
- Yun, U.; Pyun, G.; Yoon, E. Efficient Mining of Robust Closed Weighted Sequential Patterns Without Information Loss. Int. J. Artif. Intell. Tools 2015, 24, 1550007. [Google Scholar] [CrossRef]
- Agrawal, R.; Srikant, R. Fast Algorithms for Mining Association Rules. In Proceedings of the 20th International Conference on Very Large Data Bases, Santiago de Chile, Chile, 12–15 September 1994.
- Ryang, H.; Yun, U.; Ryu, K. Fast algorithm for high utility pattern mining with the sum of item quantities. Intell. Data Anal. 2016, 20, 395–415. [Google Scholar] [CrossRef]
- Ryang, H.; Yun, U. Top-k high utility pattern mining with effective threshold raising strategies. Knowl. Based Syst. 2015, 76, 109–126. [Google Scholar] [CrossRef]
- Yun, U.; Lee, G. Incremental mining of weighted maximal frequent itemsets from dynamic databases. Expert Syst. Appl. 2016, 54, 304–327. [Google Scholar] [CrossRef]
- Yun, U.; Ryang, H. Incremental high utility pattern mining with static and dynamic databases. Appl. Intell. 2015, 42, 323–352. [Google Scholar] [CrossRef]
- Yun, U.; Kim, J. A fast perturbation algorithm using tree structure for privacy preserving utility mining. Expert Syst. Appl. 2015, 42, 1149–1165. [Google Scholar] [CrossRef]
- Bifet, A.; Holmes, G.; Pfahringer, B.; Gavaldà, R. Mining frequent closed graphs on evolving data streams. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011; pp. 591–599.
- Hintsanen, P.; Toivonen, H. Finding reliable subgraphs from large probabilistic graphs. Data Min. Knowl. Discov. 2008, 17, 3–23. [Google Scholar] [CrossRef]
- Thomas, L.T.; Valluri, S.R.; Karlapalem, K. MARGIN: Maximal Frequent Subgraph Mining. In Proceedings of the 6th IEEE International Conference on Data Mining, Hong Kong, China, 18–22 December 2006.
- Zhang, S.; Yang, J.; Cheedella, V. Monkey: Approximate Graph Mining Based on Spanning Trees. In Proceedings of the 23rd International Conference on Data Engineering, Istanbul, Turkey, 11–15 April 2007.
- Zou, Z.; Li, J. Mining Frequent Subgraph Patterns from Uncertain Graph Data. IEEE Trans. Knowl. Data Eng. 2010, 22, 1203–1218. [Google Scholar]
- Dehmer, M.; Emmert-Streib, F. Quantitative Graph Theory: Mathematical Foundations and Applications; CRC Press: Boca Raton, FL, USA, 2014; pp. 1–34. [Google Scholar]
- Dehmer, M.; Sivakumar, L; Varmuza, K. Uniquely Discriminating Molecular Structures Using Novel Eigenvalue—Based Descriptors. Match-Commun. Math. Comput. Chem. 2012, 67, 147–172. [Google Scholar]
- Emmert-Streib, F.; Dehmer, M. Information Theory and Statistical Learning; Springer: New York, NY, USA, 2009; pp. 1–24. [Google Scholar]
- Zhang, Q.; Song, X.; Shao, X.; Zhao, H.; Srikant, R. Object Discovery: Soft Attributed Graph Mining. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 532–545. [Google Scholar] [CrossRef] [PubMed]
- Badr, E.; Heath, L.S. CoSREM: A graph mining algorithm for the discovery of combinatorial splicing regulatory elements. BMC Bioinform. 2015, 16, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Santosh, K.C. g-DICE: Graph mining-based document information content exploitation. Int. J. Doc. Anal. Recognit. 2015, 18, 337–355. [Google Scholar] [CrossRef]
- Eskandari, M.; Raesi, H. Frequent sub-graph mining for intelligent malware detection. Secur. Commun. Netw. 2014, 7, 1872–1886. [Google Scholar] [CrossRef]
- Videla-Cavieres, I.F.; Rios, S.A. Extending market basket analysis with graph mining techniques: A real case. Expert Syst. Appl. 2014, 41, 1928–1936. [Google Scholar] [CrossRef]
- Hu, Y.H.; Chen, Y.L. Mining association rules with multiple minimum supports: A new mining algorithm and a support tuning mechanism. Decis. Support Syst. 2006, 42, 1–24. [Google Scholar] [CrossRef]
- Kiran, R.U.; Reddy, P.K. Novel techniques to reduce search space in multiple minimum supports-based frequent pattern mining algorithms. In Proceedings of the 14th International Conference on Extending Database Technology, Uppsala, Sweden, 21–25 March 2011.
- Liu, B.; Hsu, W.; Ma, Y. Mining association rules with multiple minimum supports. In Proceedings of the 5th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 15–18 August 1999.
- Benhamou, B.; Jabbour, S.; Sais, L.; Salhi, Y. Symmetry Breaking in Itemset Mining. In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval, Rome, Italy, 21–24 October 2014.
- Desrosiers, C.; Galinier, P.; Hansen, P.; Hertz, A. Improving Frequent Subgraph Mining in the Presence of Symmetry. In Proceedings of the MLG Workshops, Firenze, Italy, 1–3 August 2007.
- Vanetik, N. Mining Graphs with Constraints on Symmetry and Diameter. In Proceedings of the WAIM Workshops, Jiuzhaigou Valley, China, 15–17 July 2010.
- Han, J.; Pei, J.; Yin, Y.; Mao, R. Mining frequent patterns without candidate generation: A frequent-pattern tree approach. Data Min. Knowl. Discov. 2004, 8, 53–87. [Google Scholar] [CrossRef]
- Ozaki, T.; Etoh, M. Closed and Maximal Subgraph Mining in Internally and Externally Weighted Graph Databases. In Proceedings of the 25th IEEE International Conference on Advanced Information Networking and Applications Workshops, Singapore, Singapore, 22–25 March 2011.
- Nijssen, S.; Kok, J.N. The Gaston Tool for Frequent Subgraph Mining. Electr. Notes Theor. Comput. Sci. 2005, 127, 77–87. [Google Scholar] [CrossRef]
- Nijssen, S.; Kok, J.N. A quickstart in frequent structure mining can make a difference. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004.
- Lee, G.; Yun, U. Frequent Graph Mining Based on Multiple Minimum Support Constraints. In Proceedings of the 4th International Conference on Mobile, Ubiquitous, and Intelligent Computing, Gwangju, Korea, 4–6 September 2013.
- Lee, G.; Yun, U.; Ryang, H.; Kim, D. Multiple Minimum Support-Based Rare Graph Pattern Mining Considering Symmetry Feature-Based Growth Technique and the Differing Importance of Graph Elements. Symmetry 2015, 7, 1151–1163. [Google Scholar] [CrossRef]
- Seno, M.; Karypis, G. Finding frequent patterns using length-decreasing support constraints. Data Min. Knowl. Discov. 2005, 10, 197–228. [Google Scholar] [CrossRef]
- Yun, U. An efficient mining of weighted frequent patterns with length decreasing support constraints. Knowl. Based Syst. 2008, 21, 741–752. [Google Scholar] [CrossRef]
- Yun, U.; Ryu, K.H. Discovering Important Sequential Patterns with Length-Decreasing Weighted Support Constraints. Int. J. Inf. Technol. Decis. Mak. 2010, 9, 575–599. [Google Scholar] [CrossRef]
- Lee, G.; Yun, U. Frequent Graph Pattern Mining with Length-Decreasing Support Constraints. In Proceedings of the Multimedia and Ubiquitous Engineering, Seoul, Korea, 9–11 May 2013.
- Dehmer, M.; Sivakumar, L. Recent Developments in Quantitative Graph Theory: Information Inequalities for Networks. PLoS ONE 2012, 7, e31395. [Google Scholar] [CrossRef] [PubMed]
- Kraus, V.; Dehmer, M.; Emmert-Sreib, F. Probabilistic Inequalities for Evaluating Structural Network Measures. Inf. Sci. 2014, 288, 220–245. [Google Scholar] [CrossRef]
- Samiullah, M.; Ahmed, C.F.; Fariha, A.; Islam, M.R.; Lachiche, N. Mining frequent correlated graphs with a new measure. Expert Syst. Appl. 2014, 41, 1847–1863. [Google Scholar] [CrossRef]
- Sugiyama, M.; Llinares-López, F.; Kasenburg, N.; Borgwardt, K.M. Significant Subgraph Mining with Multiple Testing Correction. In Proceedings of the 2015 SIAM International Conference on Data Mining, Vancouver, BC, Canada, 30 April–2 May 2015.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).