Abstract
The role of symmetry in computer vision has waxed and waned in importance during the evolution of the field from its earliest days. At first figuring prominently in support of bottom-up indexing, it fell out of favour as shape gave way to appearance and recognition gave way to detection. With a strong prior in the form of a target object, the role of the weaker priors offered by perceptual grouping was greatly diminished. However, as the field returns to the problem of recognition from a large database, the bottom-up recovery of the parts that make up the objects in a cluttered scene is critical for their recognition. The medial axis community has long exploited the ubiquitous regularity of symmetry as a basis for the decomposition of a closed contour into medial parts. However, today’s recognition systems are faced with cluttered scenes and the assumption that a closed contour exists, i.e., that figure-ground segmentation has been solved, rendering much of the medial axis community’s work inapplicable. In this article, we review a computational framework, previously reported in [1,2,3], that bridges the representation power of the medial axis and the need to recover and group an object’s parts in a cluttered scene. Our framework is rooted in the idea that a maximally-inscribed disc, the building block of a medial axis, can be modelled as a compact superpixel in the image. We evaluate the method on images of cluttered scenes.
1. Introduction
Symmetry is a long-standing, interdisciplinary form that spans across the arts and sciences, covering fields as disparate as mathematics, biology, architecture and music [4]. The roles played by symmetry are equally diverse and can involve being an abstract object of analysis, a balancing structure in nature or an attractor of visual attention. The common thread in all of the above is that symmetry is ubiquitously present in both natural objects and artificial objects. It is no accident that we constantly encounter symmetry through our eyesight, and in fact, Gestalt psychologists [5] of the previous century proposed that symmetry is a physical regularity in our world that has been exploited by the human visual system to yield a powerful perceptual grouping mechanism. Experiments show evidence that we respond to symmetry before being consciously aware of it [6].
The scope of this article lies within the domain of computer vision, a comparatively young field that has adopted symmetry since its infancy. Inspired by a computational understanding of human vision, perceptual grouping played a prominent role in support of early object recognition systems, which typically took an input image and a set of shape models and identified which of the models were visible in the image. Mid-level shape priors were crucial in grouping causally-related shape features into discriminative shape indices that were used to prune the set down to a few promising candidates that might account for a query. Of these shape priors, one of the most powerful is a configuration of parts, in which a set of related parts belonging to the same object is recovered without any prior knowledge of scene content.
The use of symmetry to recover generic parts from an image can be traced back to the earliest days of computer vision and includes the medial axis transform (MAT) of Blum (1967) [7], generalized cylinders of Binford (1971) [8], superquadrics of Pentland (1986) [9] and geons of Biederman (1985) [10], to name just a few examples. Central to a large body of approaches based on medial symmetry is the MAT, which decomposes a closed 2D shape into a set of connected medial branches corresponding to a configuration of parts, providing a powerful parts-based decomposition of the shape suitable for shape matching, e.g., Siddiqi et al. (1999) [11] and Sebastian et al. (2004) [12]. For a definitive survey on medial symmetry, see Siddiqi et al. (2008) [13].
In more recent years, the field of computer vision has shifted in focus toward the object detection problem, in which the input image is searched for a specific target object. One reason for this lies in the development of machine learning algorithms that leverage large amounts of training data to produce robust classification results. This led to rapid progress in the development of object detection systems, enabling them to handle increasing levels of background noise, occlusion and variability in input images [14]. This development established the standard practice of working with input domains of real images of cluttered scenes, significantly increasing the applicability of object recognition systems to real problems.
A parallel advance in perceptual grouping, however, did not occur for a simple reason: with the target object already known, indexing is not required to select it, and perceptual grouping is not required to construct a discriminative shape index. As a result, perceptual grouping activity at major conferences has diminished along with the supporting role of symmetry [15,16]. However, there are clear signs that the object recognition community is moving from appearance back to shape and from object detection back to multiclass object categorization. Moreover, recent work shows that shape-based perceptual grouping is playing an increasingly critical role in facilitating this transition. Namely, methods, such as CPMC [17] and selective search [18], produce hypotheses of full object regions that serve as shape-based hypotheses for object detection [14].
In attempting to bring back medial symmetry in support of perceptual grouping, we observe that the subcommunity’s efforts have not kept pace with mainstream object recognition. Specifically, medial symmetry approaches typically assume that the input image is a foreground object free from occluding and background objects and, accordingly, lack the ability to segment foreground from background, an ingredient crucial for tackling contemporary datasets. It is clear that the MAT cannot be reintroduced without combining it with an approach for figure-ground segmentation. In this article, we review current work along this trajectory as represented by Lee et al. (2013) [1] and earlier work by Levinshtein et al. (2009) [2,3].
In the context of symmetric part detection, reference [1] introduced an approach that leveraged earlier work [2] to build a MAT-based superpixel grouping method. Since the proposed representation is central to our approach, we proceed with a brief overview of [2]. A bottom-up method was introduced for recovering symmetric parts in order to non-accidentally group object parts to form a discriminative shape index. Symmetric part recovery was achieved by establishing a correspondence between superpixels and maximally inscribed discs, allowing a superpixel grouping problem to be formulated in which superpixels representing discs of the same part were grouped. A significant improvement was shown over other symmetry-based approaches.
In [1], theoretical and practical improvements were made by refining the superpixel grouping problem and incorporating more sophisticated symmetry. Specifically, the superpixel-disc correspondence was further analysed to yield a reformulation of the grouping problem as one of optimizing for good symmetry along the medial axis. This resulted in a method that was both intuitive and more effective than before. Secondly, it was recognized that the ellipse lacked sufficient complexity to capture the appearance of objects, which generally do not conform to a straight axis and constant radius. Hence, deformation parameters were used to achieve robustness to curved and tapered symmetry.
Overall, this article takes a high-level view of the work in reintroducing the MAT with figure-ground segmentation capability, enabling us to draw insights from a higher vantage point. We first develop the necessary background to trace the development from its origins in the MAT, through [2] and, finally, to [1]. In doing so, we establish a framework that makes clear the connections among previous work. For example, it follows from our exposition that [2] is an instance of our framework. More generally, our unified framework benefits from the rich structure of the MAT while directly tackling the challenge of segmenting out background noise in a cluttered scene. Our model is discriminatively trained and stands out from typical perceptual grouping methods that use predefined grouping rules. Using experimental image data, we present both qualitative results and a quantitative metric evaluation to support the development of the components of our approach.
2. Related Work
Symmetry is one of several important Gestalt cues that contribute to perceptual grouping. However, symmetry plays neither an exclusive nor an isolated role in the presence of other cues. Contour closure, for example, is another mid-level cue whose role will increase as the community relies more on bottom-up segmentation in the absence of a strong object prior, e.g., [19]. As for cue combination, symmetry has been combined with other mid-level cues, e.g., [20,21]. For brevity, we restrict our survey of related work to symmetry detection.
The MAT, along with its many descendant representations, such as the shock graph [11,12,22,23] and bone graph [24,25], provides an elegant decomposition of an object’s shape into symmetric parts; however, it made the unrealistic assumption that the shape was segmented and is, thus, not directly suitable for today’s image domains. For symmetry approaches in the cluttered image domain, we first consider the filter-based approach, which first attempts to detect local symmetries, in the form of parts and then finds non-accidental groupings of the detected parts to form indexing structures. Example approaches in this domain include the multiscale peak paths of Crowley and Parker (1984) [26], the multiscale blobs of Shokoufandeh et al. (1999) [27], the ridge detectors of Mikolajczyk and Schmid (2002) [28] and the multiscale blobs and ridges of Lindeberg and Bretzner (2003) [29] and Shokoufandeh et al. (2006) [30]. Unfortunately, these filter-based approaches yield many false positive and false negative symmetric part detections, and the lack of explicit part boundary extraction makes part attachment detection unreliable.
A more powerful filter-based approach was recently proposed by Tsogkas and Kokkinos (2012) [31], in which integral images are applied to an edge map to efficiently compute discriminating features, including a novel spectral symmetry feature, at each pixel at each of multiple scales. Multiple instance learning is used to train a detector that combines these features to yield a probability map, which after non-maximum suppression, yields a set of medial points. The method is computationally intensive yet parallelizable, and the medial points still need to be parsed and grouped into parts. However, the method shows promise in recovering an approximation to a medial axis transform of an image.
The contour-based approach to symmetry is a less holistic approach that addresses the combinatorial challenge of grouping extracted contours. Examples include Brady and Asada (1984) [32], Connell and Brady (1987) [33], Ponce (1990) [34], Cham and Cipolla (1995, 1996) [35,36], Saint-Marc et al. (1993) [37], Liu et al. (1998) [38], Ylä-Jääski and Ade (1996) [39], Stahl and Wang (2008) [40] and Fidler et al. (2014) [41]. Since these methods are contour based, they have to deal with the issue of the computational complexity of contour grouping, particularly when cluttered scenes contain many extraneous edges. Some require smooth contours or initialization, while others were designed to detect symmetric objects and cannot detect and group the symmetric parts that make up an asymmetric object. A more recent line of methods extracts interest point features, such as SIFT [42], and groups them across an unknown symmetry axis [43,44]. While these methods exploit distinctive pairwise correspondences among local features, they critically depend on reliable feature extraction.
A recent approach by Narayanan and Kimia [45] proposes an elegant framework for grouping medial fragments into meaningful groups. Rather than assuming a figure-ground segmentation, the approach computes a shock graph over the entire image of a cluttered scene and then applies a sequence of medial transforms to the medial fragments, maintaining a large space of grouping hypotheses. While the method compares favourably to figure-ground segmentation and fragment generation approaches, the high computational complexity of the approach restricts it to images with no more than 20 contours.
Our approach, represented in the literature by [1,2,3], is qualitatively different from both filter-based and contour-based approaches, offering a region-based approach, which perceptually groups together compact regions (segmented at multiple scales using superpixels) representing deformable maximal discs into symmetric parts. In doing so, we avoid the low precision that often plagues the filter-based approaches, along with the high complexity that often plagues the contour-based approaches.
3. Representing Symmetric Parts
Our approach rests on the combination of medial symmetry and superpixel grouping [1,2,3], and in this section, we formally connect the two ideas together. We proceed with the medial axis transform (MAT) [7] of an object’s shape, as illustrated by the runner in Figure 1. A central role is played by the set of maximally-inscribed discs, whose centres (called medial points) trace out the skeleton-like medial axis of the object. We can identify the object’s parts by decomposing the medial axis into its branch-like linear segments, with each object part being swept out by the sequence of maximally inscribed discs along the corresponding segment. For details on the relationship between the medial axis and the simpler reflective axis of symmetry, see Siddiqi et al. (2008) [13].
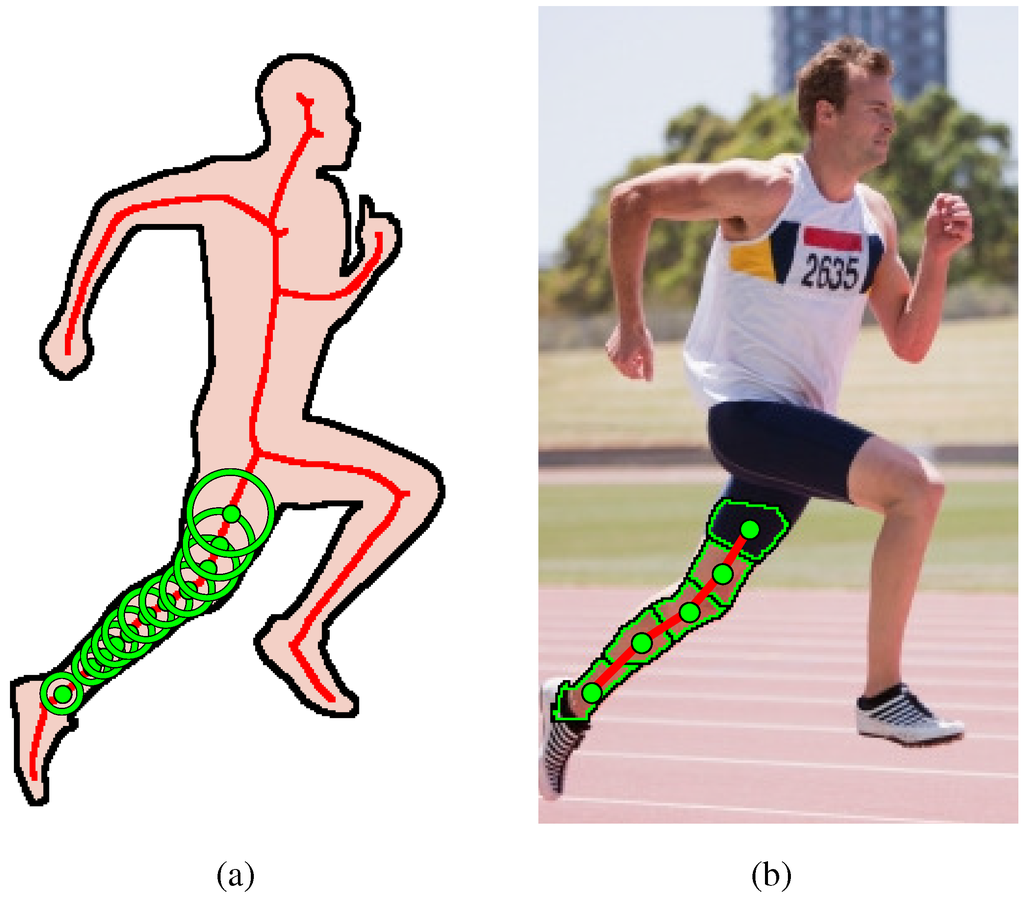
Figure 1.
Our representation of symmetric parts. (a) The shape of the runner’s body is transformed into its medial axis (red), a skeleton-like structure that decomposes the shape into branch-like segments, e.g., the leg. The leg’s shape is swept out by a sequence of discs (green) lying along the medial axis. (b) The shape of the same leg is composed from superpixels that correspond to the sequence of discs. The scope of this article’s framework is limited to detecting symmetric parts corresponding to individual branches.
The link between discs and superpixels is established by recently developed approaches that oversegment an image into superpixels of compact and uniform scale. In order to view superpixels as discs, note that just as superpixels are attracted to parts’ boundaries, imagine removing the circular constraint on discs to allow them to deform to the boundary, resulting in “deformable discs”. We will henceforth use the terms “superpixel” and “disc” interchangeably. The disc’s shape deforms to the boundary provided that it remains compact (not too long and thin), resulting in a subregion that aligns well with the part’s boundary on either side, when such a boundary exists. In contrast with the maximal disc, which is only bitangent to the boundary, as shown in Figure 1, the number of discs required to compose a part’s shape is far less than the number required using maximal discs.
In an input image domain of cluttered scenes, the vast majority of superpixels will not correspond to true discs of an object’s parts, and thus, it is suitable to treat superpixels as a set of candidate discs. Furthermore, a superpixel that is too fine or too coarse for a given symmetric part fails to relate its opposing boundaries together into a true disc, and a tapered part may be composed of discs of different sizes, as shown in Figure 2. Since we have no prior knowledge of a part’s scale and an input image may contain object parts of different scales, superpixels are computed at multiple scales. However, rather than have multiple sets of candidates corresponding to multiple scales, we merge all scales together and use a single set of candidates that contains superpixels from all scales. This avoids restricting parts to be comprised from superpixels of the same scale and allows the grouping algorithm to group superpixels from any scale into the same part, as shown in Figure 2.
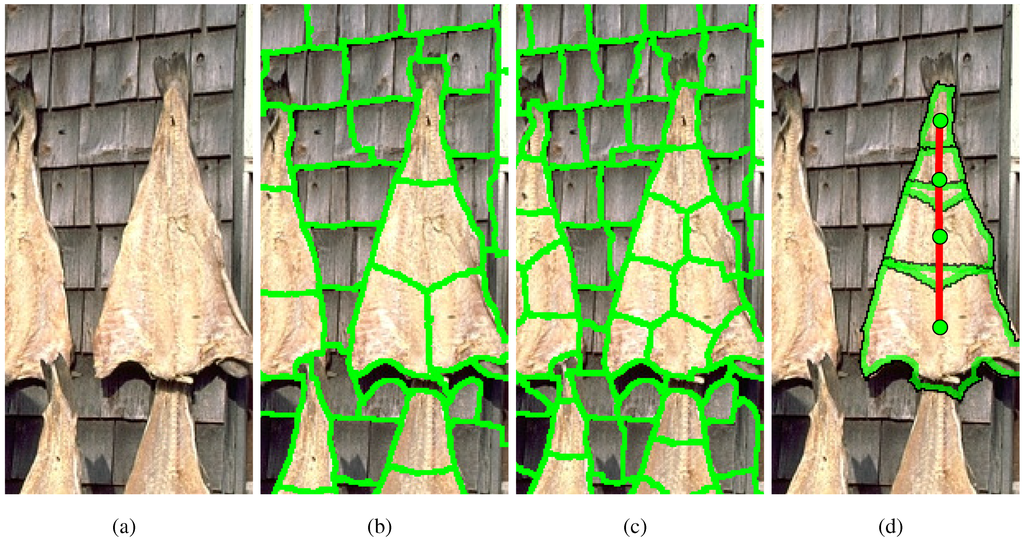
Figure 2.
To compose a part’s shape from superpixels in a given input image (a), we compute superpixels at multiple scales, for which two are shown (b,c). Superpixels from all scales are included in a single set of candidates, which allows the grouping algorithm to group superpixels from different scales into the same part. (d) The sequence-finding algorithm finds the best sequence of superpixels, comprised of different scales.
Our goal is to perceptually group discs that belong to the same part. To facilitate grouping decisions, we will define a pairwise affinity function to capture non-accidental relations between discs. Since the vast majority of superpixels will not correspond to true discs, however, we must manage the complexity of the search space. By restricting affinities to adjacent discs, we exploit one of the most basic grouping cues, namely proximity, which says that nearby discs are more likely to belong to the same medial part. We enlist the help of more sophisticated cues, however, to separate those pairs of discs that belong to the same part from those that do not. Viewing superpixels as discs allows us to directly exploit the structure of medial symmetry to define the affinity. In Section 4, we motivate and define the affinity function from perceptual grouping principles to set up a weighted graph of disc candidates. Because disc candidates come from different scales, some pairs of adjacent superpixels are overlapping; however, overlapping superpixels are excluded from adjacency when one superpixel entirely contains the other superpixel. In Section 5, we discuss alternative graph-based algorithms for grouping discs into medial parts. Section 6 presents qualitative and quantitative experiments, while Section 7 draws some conclusions about the framework.
4. Disc Affinity
Since bottom-up grouping is category agnostic, a supporting disc affinity must accommodate variations across objects of all types. More formally, the affinity between discs and must be robust against variability, not only within object categories, but also variability between object categories. Moreover, when discriminatively training the affinity, it is beneficial to use features that are not sensitive to variations of little significance. In the following sections, we define both shape and appearance features on the region scope defined by and .
4.1. Shape Features
We capture the local shape of discs with a spatial histogram of gradient pixels, as illustrated in Figure 3. By encoding the distribution of the boundary edgels of the region defined by the union of the two discs, we capture mid-level shape, while avoiding features specific to the given exemplar. This representation offers us a degree of robustness that is helpful for training the classifier; however, it remains sensitive to variations, like scale and orientation, to name a few, and can thus allow the classifier to overfit the training examples.
We turn to medial symmetry to capture these unwanted variations, as the first step in making the feature invariant to such changes. Specifically, we locally model the shape by fitting the parameters of a symmetric shape to the region. We refer to a vector w of warping parameters that subsequently defines a warping function that is used to remove the variations from the space, in effect normalizing the local coordinate system. Figure 3 visualizes the parameters w of a deformable ellipse fit to a local region, the medial axis before and after the local curvature was “warped out” from the coordinate system and the spatial histogram computed on the normalized coordinate system.
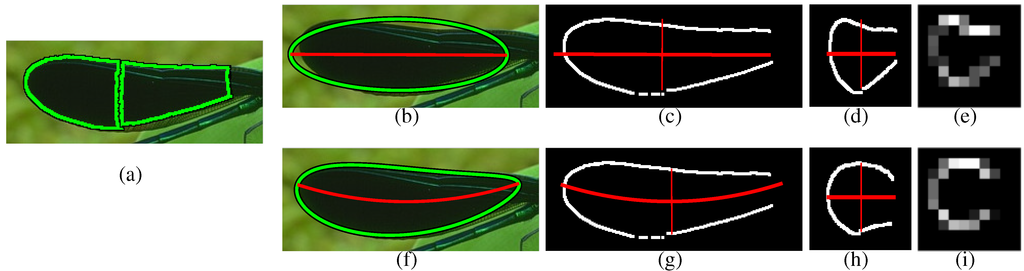
Figure 3.
Improving invariance with a deformable ellipse: given two adjacent candidate discs, the first step is to fit the ellipse parameters to the region defined by their corresponding superpixels (a). The top row shows invariance achieved with a standard ellipse. The ellipse’s fit is visualized with the major axis (b), the region’s boundary edgels before (c) and after (d) warping out the unwanted variations and the resulting spatial histogram of gradient pixels (e). See the text for details. The bottom row shows the corresponding steps (f–i) obtained by the deformable ellipse. Comparing the results, a visually more symmetric feature is obtained by the deformable ellipse, which fits tightly around the region’s boundary as compared with the standard ellipse.
Before describing the spatial histogram in detail, we discuss a class of ellipse-based models for modelling the local medial symmetry. Ellipses represent ideal shapes of an object’s parts and in particular are shapes that are symmetric about their major axes. A standard ellipse is parameterized by , where p denotes its position, θ its orientation and the lengths of its major and minor axes. The parameter vector is analytically fit to the local region and is used to define the corresponding warping function .
Historically, we first obtained the warping parameters with a standard ellipse [2]. While the advantages of using the ellipse lie in its simplicity and ease of fitting, shortcomings were identified in its tendency to provide too coarse a fit to the boundary to yield an accurate enough warping function. Therefore, in [1], we added deformation parameters to obtain a better overall fit across all examples. Despite a higher computational cost of fitting, the deformable model was shown to yield quantitative improvements.
Specifically, we obtain invariance to bending and tapering deformations by augmenting the ellipse parameters as follows: with the bending radius b along the major axis and tapering slope t along the major axis. The parameter vector is fit by initializing as a standard ellipse and iteratively fitting it to the local region’s boundary with a non-linear least-squares algorithm. The fitted parameters are then used to define the warping function corresponding to the deformable ellipse.
Only once the warping function is fit to the local region and applied to normalize the local coordinate system do we compute the spatial histogram feature. We place a grid on the warped region, and focusing on the model fit to the union of the two discs, we scale the grid to cover the area . Using the grid, we compute a 2D histogram on the normalized boundary coordinates weighted by the edge strength of each boundary pixel. Figure 3 illustrates the shape feature computed for the disc pair. We train an SVM classifier on this 100-dimensional feature using our manually-labelled superpixel pairs, labelled as belonging to the same part or not. The margin from the classifier is fed into a logistic regressor in order to obtain the shape affinity in the range [0,1].
4.2. Appearance Features
Aside from medial symmetry, we include appearance similarity as an additional grouping cue. While object parts may vary widely in colour and texture, regions of similar appearance tend to belong to the same part. We extract an appearance feature on the discs that encodes their dissimilarity in colour and texture. Specifically, we compute the absolute difference in mean RGB colour, absolute difference in mean HSV colour, RGB and HSV colour variances in both discs and histogram distance in HSV space, yielding a 27-dimensional appearance feature. To improve classification, we compute quadratic kernel features, resulting in a 406-dimensional appearance feature. We train a logistic regressor with L1-regularization to prevent overfitting on a relatively small dataset, while emphasizing the weights of more important features. This yields an appearance affinity function between two discs . Training the appearance affinity is easier than training the shape affinity. For positive examples, we choose pairs of adjacent superpixels that are contained inside a figure in the figure-ground segmentation, whereas for negative examples, we choose pairs of adjacent superpixels that span figure-ground boundaries.
We combine the shape and appearance affinities using a logistic regressor to obtain the final pairwise affinity . Both the shape and the appearance affinities, as well as the final affinity were trained with a regularization parameter of 0.5 on the L1-norm of the logistic coefficients.
5. Grouping Discs
Given a graph of discs weighted by affinities, the final step is to group discs that belong to the same symmetric part. If two adjacent discs correspond to medial points belonging to the same medial axis, they can be combined to extend the symmetry. This is the basis for defining the pairwise affinities in , and it is how we exploit our medial representation of symmetric parts for grouping. Specifically, the affinity between two adjacent discs reflects the degree to which it is believed that they not only non-accidentally relate the two opposing boundaries together, but that they are centred along the same medial axis. In this section, we adapt and discuss two alternative graph-based algorithms, namely the agglomerative clustering algorithm of Felzenszwalb and Huttenlocher (2004) [46] and the sequence-finding algorithm in the salient curve detection method of Felzenszwalb and McAllester (2006) [47].
5.1. Agglomerative Clustering
Our first grouping approach is based on agglomerative clustering [46]. The algorithm takes as input the weighted graph and merges edges in increasing order of weights. Each merge represents a grouping of discs, and the connected components that result correspond to symmetric parts. Grouping is performed efficiently in time, where e is the number of edges in . We refer the reader to [2] for details on the algorithm’s adaptation to the setting of grouping discs.
The greedy approach, while fast, is underconstrained in allowing merges to occur between branch-structured clusters, resulting in tree-like clusters, as illustrated in Figure 4. These types of clusters can occur as frequently as spuriously high affinity values (false positives) occur, thus motivating the need to restrict the growth of clusters along individual branches.
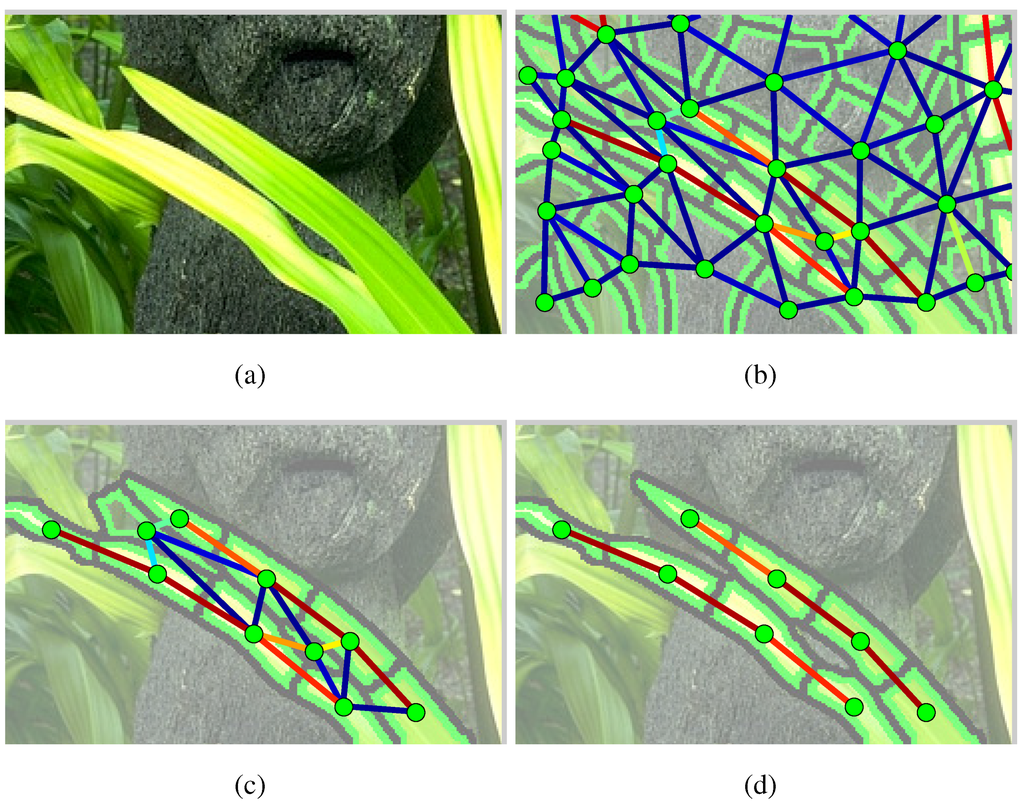
Figure 4.
In our approach, the (a) input image of foreground leaves is oversegmented into superpixels and a (b) weighted graph is built that captures the pairwise affinities that are computed among the superpixels. A graph-based grouping algorithm takes as input the graph , which may contain false positive affinities between the leaves, as shown in (b). In this figure, we illustrate the relative advantage of (d) sequence optimization over (c) agglomerative clustering. In (c), merging the vertices in results in a cluster that undersegments the leaves, combining them into a single symmetric part that violates the assumption that a part is composed of a linear sequence of discs. In (d), the branch constraint is built into the sequence-finding algorithm, which prevents symmetric parts from having tree-structured discs and correctly segments the leaves into two distinct parts.
5.2. Sequence Optimization by Dynamic Programming
Our second approach is dynamic programming used in [1], which observes that each symmetric part is swept out by an ordered sequence of discs. Discs along the same medial axis are thus not only combined in pairs, but can be traced out linearly. This allows us to reformulate the problem of superpixel grouping as finding sequences of discs in a weighted graph that belong to the same symmetric part. We thus obtain a grouping approach in which the branch constraint that is missing from agglomerative clustering is now inherent in the problem formulation. As illustrated in Figure 4, the algorithm applied to the same graph prevents the resulting clusters from violating the branching constraint.
Before describing the steps of the dynamic programming algorithm, we note that it solves a discrete optimization problem and thus represents a principled reformulation of our grouping problem. This includes defining an objective function that captures the goal of the problem and using dynamic programming that efficiently solves for a global optimum. We specifically borrow from the optimization framework used for salient curve detection in Felzenszwalb and McAllester [47] and adapt it for symmetric part detection.
The application of [47] to our setting is best explained via their method for curve detection. The method takes as input a graph with weights defined on edges and “transition weights” defined on pairs of adjacent edges. A salient curve is modelled as a valid sequence of edges, and a regularized cost function is defined on valid sequences that includes a normalized sum of the weights along the given sequence. Salient curves are found by globally optimizing the cost function using a dynamic programming algorithm.
In our setting, the graph supplies weights between adjacent discs, and we define a valid sequence of discs (of variable length) by , which represents a symmetric part. The criteria that we want to optimize—good symmetry along the medial axis and a maximally-long axis—are provided by the affinity graph . The regularized cost function, , is defined accordingly, favouring good internal affinity with a normalized sum over the affinities along the given sequence and encouraging longer sequences with a regularization term. Affinities defined over longer subsequences corresponding to the transition weights have a smoothing effect on the preferred sequences. Details on the cost function including its mathematical form can be found in [1].
We now summarize the dynamic programming steps for globally minimizing . The core step is illustrated in Figure 5, and details can be found in [47]. The algorithm initializes a priority queue Q of candidate sequences with all possible sequences of unit length, then pursues a best-first search strategy of iteratively extending the least expensive candidate sequences. Each edge is directed such that a sequence of edges terminating at can be extended with an edge starting at . At each iteration, as shown in Figure 5, the most promising sequence is removed from Q, and new candidate sequences are proposed by extending the end of with adjacent discs. If an extended sequence ending at an edge improves the cost of an existing sequence ending at the same edge, it is added back into Q. To find multiple sequences from the graph corresponding to different symmetric parts, we iteratively remove sequences that are already found and re-minimize the cost, until a maximum cost is reached.
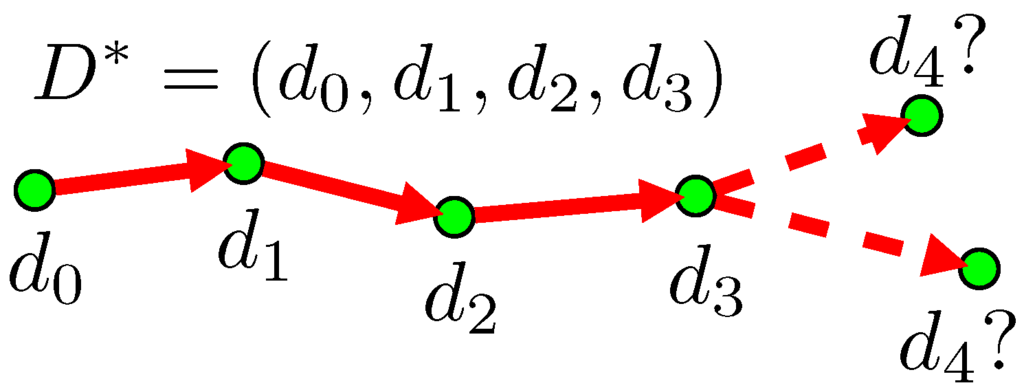
Figure 5.
Grouping by dynamic programming: the iterative step of the algorithm grows sequences by extracting a sequence from the priority queue and returning longer sequences to the queue obtained by extending the end of with adjacent discs. See the text for details.
6. Results
We present an evaluation of our approach, first qualitatively in Section 6.1, then quantitatively in Section 6.2. Our qualitative results are drawn from sample input images and illustrate the particular strengths and weaknesses of our approach. In our quantitative evaluation, we use performance metrics on two different datasets to examine the contributions of different components in our approach. Figure 6 visualizes detected masks returned by our method, specifically showing the top 15 detected parts on sample input images. Parts are ranked by the optimization objective function. On each part’s mask, we indicate the associated disc centres and the medial axis via connecting line segments. All results reported are generated with superpixels computed using normalized cuts [48], at multiple scales corresponding to 25, 50, 100 and 200 superpixels per image.

Figure 6.
Multiple symmetric parts: for each image (a,b), we show the top 15 masks detected as symmetric parts. Each mask is detected as a sequence of discs, whose centres are plotted in green and connected by a sequence of red line segments that represent the medial axis.
Our evaluation employs two image datasets of cluttered scenes. The first dataset is a subset of 81 images from the Weizmann Horse Database (WHD) [49], in which each image contains one or more horses. Aside from color variation, the dataset exhibits variations in scale, position and articulation of horse joints. The second dataset was created by Lee et al. [1] from the Berkeley Segmentation Database (BSD) [50]. This set is denoted as BSD-Parts and contains 36 BSD images, which are annotated with ground-truth masks corresponding to the symmetric parts of prominent objects (e.g., duck, horse, deer, snake, boat, dome, amphitheatre). This contains a variety of natural and artificial objects and offers a balancing counterpart to the horse dataset.
Both WHD and BSD-Parts are annotated with ground-truth masks corresponding to object parts in the image. The learning component of our approach requires ground-truth masks as input, for which we have held a subset of training images away from testing. Specifically, we trained our classifier on 20 WHD images and used for evaluation the remaining 61 WHD images and all 36 BSD-Parts images. This methodology supports a key point of our approach, which is that of mid-level transfer: by increasing feature invariance against image variability, we help prevent the classifier from overfitting to the objects on which it is trained. By training our model on horse images and applying it on other types of objects, we thus demonstrate the ability of our model to transfer symmetric part detection from one object class to another.
6.1. Qualitative Results
Figure 7 presents our results on a sample of input images. For each image, the set of ground-truth masks is shown, followed by the top several detection masks (detection masks are indicated with the associated sequence of discs). For clarity, individual detections are shown in separate images. The tiger image demonstrates the successful detection of its parts, which vary in curvature and taper. In the next example, vertical segments of the Florentine dome are detected by the same method. The next example shows recovered parts of the boat. When suitably pruned, a configuration of parts hypothesized from a cluttered image can provide an index into a bank of part-based shape models.
In the image of the fly, noise along the abdomen was captured by the affinity function at finer superpixel scales, resulting in multiple overlapping oversegmentations. The leaf was not detected, however, due to its symmetry being occluded. In the first snake image, low contrast along its tail yielded imperfect superpixels that could not support correct segmentation; however, the invariance to bending is impressive. The second snake is accompanied by a second thin detection along its shadow. We conclude with the starfish, whose complex texture was not a difficult challenge for our method. We have demonstrated that symmetry is a powerful shape regularity that is ubiquitous across different objects.
For images of sufficient complexity, our method will return spurious symmetrical regions in the background. Such examples, as found in Figure 6, are not likely to be useful for subsequent steps and result in a decrease in measured precision. While a subsequent verification step (e.g., with access to high-level information) can be developed to make a decision as to whether to keep or discard a region, we have not included one in our method.
6.2. Quantitative Results
In the quantitative part of our evaluation, we use standard dataset metrics to evaluate the components of our approach. Specifically, we demonstrate the improvement contributed by formulating grouping as sequence optimization and by using invariant features to train the classifier. Results are computed on the subset of WHD held out from training and on BSD-Parts. To evaluate the quality of our detected symmetric parts, we compare them in the form of detection masks to the ground-truth masks using the standard intersection-over-union metric (IoU). A detection mask is counted as a hit if its overlap with the ground-truth mask is greater than 0.4, where overlap is measured by IoU . We obtain a precision-recall curve by varying the threshold over the cost (weight) of detected parts.

Figure 7.
Example detections on a sample of images from Berkeley Segmentation Database (BSD)-Parts. Columns left to right: input image, ground-truth masks, top four detection masks. Note that many images have more ground-truth masks than detections that can be shown here.
Figure 8 presents the performance curves corresponding to four different settings under our framework, evaluated on both WHD and BSD-Parts: (1) ellipse + clustering combines the ellipse-warped affinity with agglomerative clustering and corresponds to [2]; we note that low precision is partly due to the lack of annotations on many background objects in both datasets; (2) ellipse + sequences combines the ellipse-warped affinity with sequence optimization; (3) deform + sequences combines deformable warping with sequence optimization and corresponds to [1]; and (4) deform + unsmooth sets the triplewise weights in uniformly to zero rather than using the affinity, as done in the previous setting. A corresponding drop in performance shows that smoothness is an important feature of symmetric parts. In summary, experimental results confirm that both the added deformations and sequence optimization are individually effective at improving the accuracy of our approach.
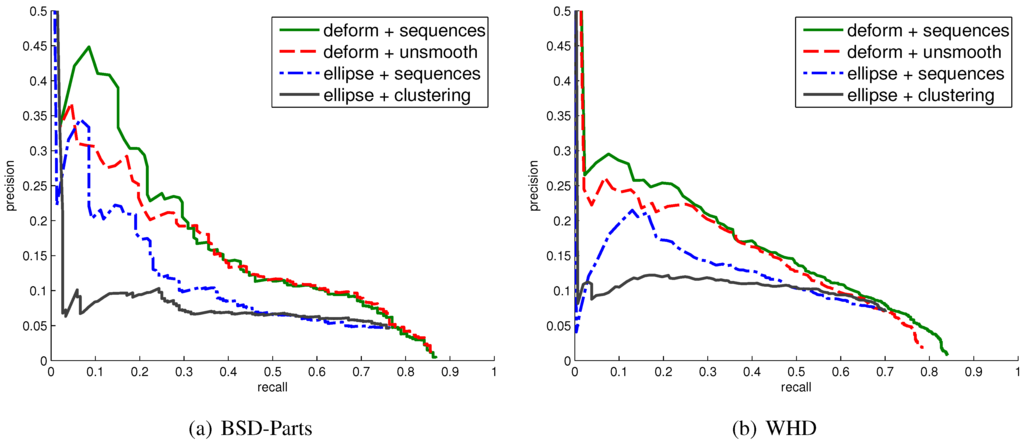
Figure 8.
Performance curves corresponding to different settings of the components of our approach on (a) BSD-Parts and (b) Weizmann Horse Database (WHD). See the text for details.
7. Conclusions
Symmetry figured prominently in early object recognition systems, but the potential of this powerful cue is largely overlooked in contemporary computer vision. In this article, we have reviewed a framework that attempts to reintroduce medial symmetry into the current research landscape. The key concept behind the framework is remodelling the discs of the MAT as compact superpixels, learning a pairwise affinity function between discs with a symmetry-invariant transform and formulating a discrete optimization problem to find the best sequences of discs. We have summarized quantitative results that encourage further exploration of using symmetry for object recognition.
We have reviewed ways in which we overcame the early limitations of our approach, such as using additional deformation parameters to improve warping accuracy and reformulating grouping as a discrete optimization problem to improve the results. There are also current limitations to be addressed in future work. Occlusion is one condition that needs to be handled before excellent performance can be reached. For symmetry, there are real-world situations in which an object’s symmetry cannot be directly recovered due to low-contrast edges or due to an occluding object. To overcome these problems, higher-level regularities would be helpful, such as axis (figural) continuity and object-level knowledge. Additionally, the success of using Gestalt grouping cues, such as symmetry, depends on effectively combining multiple cues together. To improve the robustness of our system, we are thus exploring how to incorporate additional mid-level cues, such as contour closure. Finally, our scope is bottom-up detection and, thus, is agnostic of object categories. However, in a detection or verification task, top-down cues may be available. We are thus investigating ways of integrating top-down cues into our framework.
In conclusion, we have reviewed an approach for reintroducing the MAT back into contemporary computer vision, by leveraging the formulation of maximal discs as compact superpixels to derive symmetry-based affinity function and grouping algorithms. Quantitative results encourage further development of the framework to recover medial-based parts from cluttered scenes. Finally, as initial explored in [3], detected parts must be non-accidentally grouped before they yield the distinctiveness required for object recognition.
Acknowledgements
We thank Allan Jepson for valuable discussions on dynamic programming algorithms. This work was supported in part by CNCS-UEFISCDIunder CT-ERC-2012-1 and PCE-2011-3-0438.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, T.; Fidler, S.; Dickinson, S. Detecting Curved Symmetric Parts using a Deformable Disc Model. In Proceedings of the 2013 IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013.
- Levinshtein, A.; Dickinson, S.; Sminchisescu, C. Multiscale Symmetric Part Detection and Grouping. Int. Conf. Comput. Vis. 2009. Available online: http://www.maths.lth.se/matematiklth/personal/sminchis/papers/LevSminIccv2009.pdf (accessed on 20 July 2015).
- Levinshtein, A.; Sminchisescu, C.; Dickinson, S. Multiscale Symmetric Part Detection and Grouping. Int. J. Comput. Vis. 2013, 104, 117–134. [Google Scholar] [CrossRef]
- Leyton, M. Symmetry, Causality, Mind; MIT Press: Cambridge, MI, USA, 1992. [Google Scholar]
- Wertheimer, M. Laws of organization in perceptual forms. In Source Book of Gestalt Psychology; Harcourt, Brace & World: New York, NY, USA, 1938. [Google Scholar]
- Tyler, C. Human Symmetry Perception and Its Computational Analysis; Psychology Press: London, UK, 2002. [Google Scholar]
- Blum, H. A transformation for extracting new descriptors of shape. In Models for the Perception of Speech and Visual Form; MIT Press: Cambridge, MI, USA, 1967; Volume 19, pp. 362–380. [Google Scholar]
- Binford, T. Visual Perception by Computer. In Presented at the IEEE Conference on Systems and Control, Miami, FL, USA; 1971. [Google Scholar]
- Pentland, A. Perceptual organization and the representation of natural form. Artif. Intell. 1986, 28, 293–331. [Google Scholar] [CrossRef]
- Biederman, I. Human image understanding: Recent research and a theory. Comput. Vis. Graph. Image Proc. 1985, 32, 29–73. [Google Scholar] [CrossRef]
- Siddiqi, K.; Shokoufandeh, A.; Dickinson, S.; Zucker, S. Shock graphs and shape matching. Int. J. Comput. Vis. 1999, 35, 13–32. [Google Scholar] [CrossRef]
- Sebastian, T.; Klein, P.; Kimia, B. Recognition of Shapes by Editing Their Shock Graphs. IEEE Trans. Pattern Anal. Machine Intell. 2004, 26, 550–571. [Google Scholar] [CrossRef] [PubMed]
- Siddiqi, K.; Pizer, S. Medial Epresentations: Mathematics, Algorithms and Applications; Springer Verlag: Berlin, Germany, 2008. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. CVPR 2014. Available online: http://www.cs.berkeley.edu/rbg/papers/r-cnn-cvpr.pdf (accessed on 20 July 2015).
- Dickinson, S. The Evolution of Object Categorization and the Challenge of Image Abstraction. In Object Categorization: Computer and Human Vision Perspectives; Cambridge University Press: Cambridge, UK, 2009; pp. 1–37. [Google Scholar]
- Dickinson, S.; Levinshtein, A.; Sala, P.; Sminchisescu, C. The Role of Mid-Level Shape Priors in Perceptual Grouping and Image Abstraction. In Shape Perception in Human and Computer Vision: An Interdisciplinary Perspective; Springer Verlag: Berlin, Germany, 2013; pp. 1–19. [Google Scholar]
- Carreira, J.; Sminchisescu, C. CPMC: Automatic object segmentation using constrained parametric min-cuts. IEEE Trans. Pattern Anal. Machine Intell. 2012, 34, 1312–1328. [Google Scholar] [CrossRef] [PubMed]
- Uijlings, J.; van de Sande, K.; Gevers, T.; Smeulders, A. Selective search for object recognition. Int. J. Comput. Vis. 2013, 104, 154–171. [Google Scholar] [CrossRef]
- Levinshtein, A.; Sminchisescu, C.; Dickinson, S. Optimal Image and Video Closure by Superpixel Grouping. Int. J. Comput. Vis. 2012, 100, 99–119. [Google Scholar] [CrossRef]
- Ren, X.; Fowlkes, C.; Malik, J. Cue integration for figure/ground labeling. NIPS 2005, 1121–1128. [Google Scholar]
- Lee, T.; Fidler, S.; Dickinson, S. Multi-cue mid-level grouping. In Proceedings of the 12th Asian Conference on Computer Vision, Singapore, 1–5 November 2014.
- Pelillo, M.; Siddiqi, K.; Zucker, S. Matching hierarchical structures using association graphs. IEEE Trans. Pattern Anal. Machine Intell. 1999, 21, 1105–1120. [Google Scholar] [CrossRef]
- Demirci, F.; Shokoufandeh, A.; Dickinson, S. Skeletal shape abstraction from examples. IEEE Trans. Pattern Anal. Machine Intell. 2009, 31, 944–952. [Google Scholar] [CrossRef] [PubMed]
- Macrini, D.; Dickinson, S.; Fleet, D.; Siddiqi, K. Object categorization using bone graphs. Comp. Vis. Image Underst. 2011, 115, 1187–1206. [Google Scholar] [CrossRef]
- Macrini, D.; Dickinson, S.; Fleet, D.; Siddiqi, K. Bone graphs: Medial shape parsing and abstraction. Comp. Vis. Image Underst. 2011, 115, 1044–1061. [Google Scholar] [CrossRef]
- Crowley, J.; Parker, A. A representation for shape based on peaks and ridges in the difference of low-pass transform. IEEE Trans. Pattern Anal. Machine Intell. 1984, 6, 156–170. [Google Scholar] [CrossRef]
- Shokoufandeh, A.; Marsic, I.; Dickinson, S. View-based object recognition using saliency maps. Image Vis. Comput. 1999, 17, 445–460. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. An affine invariant interest point detector. In Proceedings of the 7th European Conference on Computer Vision, Copenhagen, Denmark, 28–31 May 2002.
- Lindeberg, T.; Bretzner, L. Real-time scale selection in hybrid multi-scale representations. In Proceedings of the 4th International Conference, Scale Space 2003, Isle of Skye, UK, 10–12 June 2003.
- Shokoufandeh, A.; Bretzner, L.; Macrini, D.; Demirci, M.F.; Jönsson, C.; Dickinson, S. The representation and matching of categorical shape. Comput. Vis. Image Underst. 2006, 103, 139–154. [Google Scholar] [CrossRef]
- Tsogkas, S.; Kokkinos, I. Learning-Based Symmetry Detection in Natural Images. In Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012.
- Brady, M.; Asada, H. Smoothed local symmetries and their implementation. IJRR 1984, 3, 36–61. [Google Scholar] [CrossRef]
- Connell, J.; Brady, M. Generating and Generalizing Models of Visual Objects. Artif. Intell. 1987, 31, 159–183. [Google Scholar] [CrossRef]
- Ponce, J. On characterizing ribbons and finding skewed symmetries. CVGIP 1990, 52, 328–340. [Google Scholar]
- Cham, T.J.; Cipolla, R. Symmetry detection through local skewed symmetries. Image Vis. Comput. 1995, 13, 439–450. [Google Scholar] [CrossRef]
- Cham, T.; Cipolla, R. Geometric saliency of curve correspondences and grouping of symmetric contours. In Proceedings of the 4th European Conference on Computer Vision, Cambridge, UK, 15–18 April 1996.
- Saint-Marc, P.; Rom, H.; Medioni, G. B-spline contour representation and symmetry detection. IEEE Trans. Pattern Anal. Machine Intell. 1993, 15, 1191–1197. [Google Scholar] [CrossRef]
- Liu, T.; Geiger, D.; Yuille, A. Segmenting by seeking the symmetry axis. In Proceedings of the Fourteenth International Conference on Pattern Recognition, Brisbane, Australia, 16–20 August 1998.
- Ylä-Jääski, A.; Ade, F. Grouping symmetrical structures for object segmentation and description. Comput. Vis. Image Underst. 1996, 63, 399–417. [Google Scholar] [CrossRef]
- Stahl, J.; Wang, S. Globally optimal grouping for symmetric closed boundaries by combining boundary and region information. IEEE Trans. Pattern Anal. Machine Intell. 2008, 30, 395–411. [Google Scholar] [CrossRef] [PubMed]
- Fidler, S.; Boben, M.; Leonardis, A. Learning a Hierarchical Compositional Shape Vocabulary for Multi-class Object Representation. 2014. arXiv:1408.5516. Available online: http://arxiv.org/abs/1408.5516 (accessed on 13 July 2015).
- Lowe, D. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Loy, G.; Eklundh, J. Detecting symmetry and symmetric constellations of features. In Proceedings of the 9th European Conference on Computer Vision, Graz, Australia, 7–13 May 2006.
- Lee, S.; Liu, Y. Curved glide-reflection symmetry detection. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 266–278. [Google Scholar] [PubMed]
- Narayanan, M.; Kimia, B. Bottom-Up Perceptual Organization of Images into Object Part Hypotheses. In Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012.
- Felzenswalb, P.; Huttenlocher, D. Efficient graph-based image segmentation. Int. J. Comput. Vis. 2004, 59, 167–181. [Google Scholar] [CrossRef]
- Felzenszwalb, P.; McAllester, D. A min-cover approach for finding salient curves. In Proceedings of the Conference on Computer Vision and Pattern Recognition Workshop, 2006 (CVPRW ’06), New York, NY, USA, 17–22 June 2006. [CrossRef]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Machine Intell. 2000, 22, 888–905. [Google Scholar]
- Borenstein, E.; Ullman, S. Class-specific, top-down segmentation. In Proceedings of the 7th European Conference on Computer Vision, Copenhagen, Denmark, 28–31 May 2002.
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision (ICCV 2001), Vancouver, BC, Canada, 7–14 July 2001.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).