Abstract
The theory of Frame transformation relations between the states of Born Oppenheimer and the weak coupling approximations is developed for polyatomic molecules. The symmetry relations are a generalization of the frame transformation relations derived by Harter and Crogman for coupled rotor molecules. A key internal symmetry label (named “soul”) is defined so that it remains a constant label for frame transformation relations, and is conserved during vibronic transitions, ionization, and even dissociation provided the nuclear spin-rotation interaction is relatively small. Simplified procedures are given for obtaining selection rules, statistical weights, and matrix elements of multipole operators for common molecules having various point symmetries.
1. Introduction
It is well known that permutations or symmetric groups have an important role in the physics of many-body systems. Their importance stems from the fact that a system of identical particles has permutational symmetry and there exists an inter-relation between the permutation and the unitary groups. It is the theory of group representations that physicists use to solve and understand a variety of problems; the work of Frobenius in the 19th century and others such as Young [1], Yamanouchi [2,3], Littlewood [4], and Gel’fand [5,6,7] have established the theory of permutational group representations as a powerful tool in spite of the fact that the theory is quite difficult. With the aid of computers, the group representations theory has become a remarkably effective tool for the modern physicist.
The theory of permutation group representations is quite useful to describe many phenomenon of molecules, ions, and radicals which are made of identical points like particles (electrons, nuclei, atoms, and molecular sub-complexes such as CH3). Algorithms for representations, dimensions and characters that were developed by Shur [8], Littewood [4], Yamanouchi [2,3], Robinson [9], Coleman [10], Harter [11] and others act as a powerful tool to explore the symmetry dynamics of molecular systems. Symmetry operations involving interchange of identical particles by rotations and reflections are the reasons that finite point groups such as Dm, Cm, Oh and Td are important symmetries.
Experience has taught us that elementary quantum objects with the same quantum numbers are indistinguishable and mathematical description of multi-quantum states must not lead to a new quantum state due to a permutation of constituents. Furthermore, Fermi-Pauli and Bose-Einstein’s permutational symmetry principles strongly restrict the allowed quantum configurations, spectra, and spin states. This results ultimately in having only the particular constituents in the periodic atomic chart, the chart of the Nuclides, and finally in the allowed elementary particles of the standard quark QCD.
Harter et al. [12] have developed an approximate theory for high J spin-rotational levels and very high resolution spectra of octahedral XY6 molecules. Additionally, Harter and Patterson [13] were among the first to apply tableaus to molecular spin states and statistical weight calculations. The spin-statistics theorem says that the systems with integer spins are bosons, that is, symmetric to all permutations while the systems with half-integer spins are fermions, that is, antisymmetric to odd permutations. This theorem has a rather difficult proof based on the PCT theorem [14] and quantum field theory. This symmetry principle will influence all other symmetries defined for multi-particle states, for example, the possible values of the total angular momentum of molecules as discussed below. The effects of Spin-statistics can be rather subtle, one example is the influence of nuclear spins on the quantum numbers of molecules which is seen in the difference between ortho- and para-hydrogen. In the ortho form, the two proton spins are parallel, but in the para form they are paired to a total spin of 0. As a result of the fermion characteristic of the constituent protons, the allowed rotational degeneracies of the two forms are different, thus giving different heat capacities. The changes in the proton spin states are normally very slow, making the two forms appear as two macroscopically different gases.
Level and spectral clusters, and related tunneling dynamics are intimately related to nuclear, atomic, or molecular permutations. However, floppy molecules do operations that transcend the geometry of 3D crystal point group operations. One of the earliest attempts of permutation operations to non-rigid molecular symmetry was put forward by Longuet-Higgins [15]. He classified the spin states and states motions for molecular symmetry systems such as ethane and hydrazine. Longuet-Higgins points out that there are certain symmetry elements of non-rigid molecules; for example, the twisting of ethane which leads to configurations which cannot be brought into near-coincidence with the original one by a simple rotation of the whole molecule in space. The work of Hougen et al. [16], Harter et al. [17,18,19,20,21,22], and Bunker and Jensen [23] have allowed for an easier approach to compute spin weight, and rovibration wavefunctions, and to open new avenues to study large amplitude motions. In one approach, Groner [24] has tried to identify pinwheel rotations with crystal space groups, that is, point groups with translations. Harter and Patterson pointed out that the eigenstates of the system must be based off of the irreducible representation of Sm. This means that we can use the Young tableau labeling schemes to label the eigenstates of the systems.
In this paper, we will apply the techniques developed and used by Harter and Patterson [17,18,19,20,21,22]. The main goal is to attempt to answer the question of how molecular species come about due to some kind of coupling interactions in the strongly and weakly coupled regimes, which allows for insight into large amplitude motion of molecular systems. In this paper, Section 2 extends the frame transformation relation for couple rotor systems by Crogman and Harter [25] to include symmetry. A procedure for finding the induced symmetry that resulted from various coupled states is there developed; Section 3 shows how to Young Tableau algebra to compute spin weight for the permutation group; Section 4 provides a concrete example to illustrate our technique, and Section 5 discusses the various ways to couple two diatomics and compute the resulting tunneling matrix. It is hoped that the present work will be another step in this direction for a large number of molecular systems, which have some sort of geometrical symmetry in their structure. This work is meant to expose the simplest and most powerful symmetry analysis methods available.
2. Symmetry Relation for a Coupled System
Fano and Chang [26], and Junger et al. [27,28] have worked out a theory that describes the phenomenon that comes about for a diatomic molecule coupled to an electron. Harter et al. [12] have extended their idea to polyatomic molecules. Their work went a step further by considering the symmetry induced as a result of a polyatomic molecule interacting with an electron [12]. By using Young tableau’s mathematics, Harter et al. [12] reduced the mathematical complexity involved in the symmetry analysis. This provided a convenient way to calculate the spin weight and predict what symmetry species were excluded. Spin weights give spectral intensity ratios for different symmetry species. Here, we consider the permutation group along with Young tableau techniques [11,12,17,18,19,20,21,22,29,30] for the symmetry of two coupled diatomic molecules. Lemus [31] applied the theory of Chen [29] to generate what is known as vibrational symmetry adapted bases. This method works because of the isomorphism between the symmetric group and point group. Our exploitation of two coupled diatomic molecules allows us to utilize the power of Young tableau for the symmetry group and projector analysis as described by Harter et al. [11,12,23,29]. First, we imagine more general cases such as listed in tables of Figure 4.4 as illustrated in a previous article by Crogman and Harter [25].
2.1. Symmetry Effects for Two Coupled Rotors
The symmetry of any rotor can be written in terms of the (external) × (internal). If the rotor is free, then is R3. However, if it is confined to some crystal matrix, then is the group site symmetry of the lattice. When the rotor experiences a homogeneous electric field, the external symmetry is O2. On the other hand, is the internal symmetry of the rotor structure. The fact that a rotor is made up of nuclear points means that the real internal symmetry is finite and related to permutations groups. An external field applied to the orbitals will split into various finite symmetry species according to the molecular version of the crystal field theory.
We will start with the following expressions and develop a base transformation going from a lab weakly correlated (LWC) momentum states to a Body Oriented Angular (BOA) momentum constricted states of two strongly coupled rotors [25,32]. A bare rotor with finite symmetry (B,b) is given in [25] is defined in terms of symmetric rotor waves as follows:
where is the total angular momentum label of rotational group in three dimensions and .
The inverse relation as defined in [25] is given by the unitarity of the internal “crystal field” coefficient .
Let us now consider two rotors of finite symmetry labels (D*,d) for “little “rotor Dℓ and (B*,b) for “main” rotor DR. Consequently we can use Equations (1a) and (1b) to write the following (LWC) coupled wave function.
Using the relationship
derived in a previous work [25] to have transformation the BOA
Following the crystal field relation, Equation (1b) gives the following:
Now, an isoscalar coefficient is defined using the finite symmetry Wigner Eckart theorem and coupling coefficient .
Before moving on we will define what we mean by . As in reference [12], labels the internal symmetry of vibronic activity or excitation” (electronic , , , or vibrational symmetry). When relating the BOA states to the LWC or scattering states of angular momentum , the labels considered will be those correlates with on the other hand is the internal symmetry of bare rotor such that there must exist at least one Young Tableau associated with each of . As for the label , this labels the internal symmetry of constricted rotor by writing all IR contained in the tensor product The total angular momentum levels belonging to each triad are just those correlated with .
The preceding (LWC) state is then expressed:
(Here we consider only the real irreps (B* ≡ B, D* ≡ D) and [C] is the dimension of group irreducible representative (IR) of DC).
This amounts to a transformation between the (LWC) and the (BOA) state. The BOA basis function is defined as follows:
Here the ℓ-rotor A-wave is using the angles (ΦΘΞ) relative to the other rotor’s frame whose coordinates are lab-relative (αβχ), and whose quantum labels are (J,C) with R no longer valid. However the internal B-symmetry of the big rotor is the same as before and related to its nuclear spin state.
Suppose we begin in the LWC where both rotors have a finite symmetry, and move to the BOA basis. Then the transformation Equation (7) takes us from the BOA basis to the LWC basis and an inverse transformation Equation (8) does the reverse. According to Equation (7), the symmetry coefficient remains as part of the transformation. The ℓ-rotor locks itself as a passenger on the rotor whose frame is being observed from the lab, while B is preserved through the transformation matrix. In Equation (8), it appears that a new symmetry species A corresponding to the ℓ-passenger is defined relative to the rotor labeled by B, while the symmetry label B remains invariant. However, this may not be the whole story; it seems that there may be two ways of interpreting Equation (8).
To compare our result to that of Harter et al. [12], let us assume that the effect of the smaller rotor on the larger rotor symmetry is negligible. So the overriding symmetry then would be that of the large rotor as treated by Harter et al. [12], where the ℓ-rotor is treated as a symmetry perturbation. This then leads to one way to compute A and C symmetry labels as described previously by Harter et al. [12].
But, what if the rotors are comparable or identical? Then other choices of frames may become relevant, and each may involve another way of interpreting Equation (8). As in reference [12] the symmetry label B may label the “under all” symmetry of “bare” nuclei in the system. Then as we move from a LWC basis to the strongly coupled basis, the B label must correlate the permutation symmetry of all identical nuclei to the composite geometrical point symmetry (labeled C) for the whole of the strongly interacting system. From a mathematical perspective, there is no indication that the symmetry label B in the LWC is different in the BOA basis, but physically, the new geometry suggests that B cannot remain unchanged; it must correlate with the symmetry of the composite BOA rotor states. If the interpretation of B “under all” symmetry species B changes, then both A and C must be determined differently.
Two possible symmetries emerge; one of them specifically corresponds to the larger one of the rotors behaving like a miniature “Lab” for the other, so that the symmetry of the small rotor will correlate with the frame of the larger body. In other words, the BOA transformation has the larger body acting as a lab for the small body that is like a passenger in the frame of the larger body, and respects its symmetry. However, the coefficient of the second rotor is transferred to a transformation equation such as the equation below:
Unlike the orbiting electron of reference [12], this rotor has a finite symmetry. Moreover, identical rotor molecules present the problem of which rotor is “lab” and which is “passenger”. In fact, there can be no way to tell. But once the molecule is locked in some particular geometry, then we can begin symmetry analysis based upon whatever is the composite symmetry.
In our recent work [25,33], we have seen the effects of coupling becoming extremely strong between the molecules so that it causes them to behave as a single rigid body [25]. Where symmetry is concerned, the locking of the two rotors now appears as one body with some new symmetry. Recall that B is the symmetry label for the nuclear points in the rigid R-body but now the B symmetry label may not be the same as it was in the LWC basis. That being the case, may correlate to a new symmetry belonging to an intersection of the symmetry groups of the two rotor molecules, while the symmetry label describes the active modes of this composite geometry.
We begin with the finite symmetries of and groups, as they became correlated, the finite symmetry is lost but there is an induced symmetry that is now correlated to the symmetry group . and is the symmetry group that is correlated to that of and the total angular momentum J of the coupled rotor described by . Also, it is possible that is a higher symmetry as when two diatomic molecules  and
and  form a molecule
form a molecule  .
.
 and
and  form a molecule
form a molecule  .
.Thus, the electron-rotor correlation must be generalized further by these possibilities. An electron has no finite internal symmetry only external, therefore, the sum disappears since . Consequently Equations (7) and (8) reduce to
And
Thus, the results in Equations (10a) and (10b) are the same as first given by Harter and his colleagues [12].
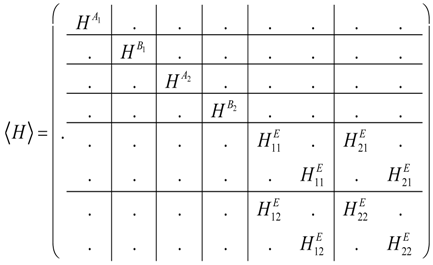
2.2. (ABC) Operators and Nuclear Exchange Symmetry
For the BOA basis there are two groups of symmetry operators that are analogous to the LWC symmetry composed of the outer product of for the ℓ-rotor, and for the R-rotor. If we consider the case where the BOA composite symmetry is the inner product of “rigid rotations” then we may apply Equations (10a) and (10b) of electron polyatomic molecule interaction based on the symmetry of the bare R-rotor. We have shown above that transformation preserves the finite symmetry of the bare rotor with labels (B,b) as seen by combining the symmetry properties to the rotor-rotor states.
is defined with respect to body coordinates as described in [12]. We consider a system in which A is weakly coupled to B, but as we turned on the coupling the symmetry is reduced from ζA × ζB to ζAB. The internal frame operator moves the whole universe except for constricted coupled systems. We must point out that only operators that move the two systems around together will commute with the coupling interaction. We discuss here the symmetry of the general symmetry properties of our general BOA states and compare that to reference [12]. Applying Equations (11a) and (11b) to the (BOA) state, Equation (7) gives the following:
Thus we conclude that the total internal molecular symmetry properties are given by the bare rotor symmetry label (B,b). This proves that the Harter–Patterson and da Paixao relation [12] for an electron coupled with a polyatomic molecule is more general than previously understood. Moreover, the very fact that multiplies the BOA state vector, implies that the operator moves both molecules rigidly together. This indicates that the symmetry label is the representation of a new symmetry or the intersection of .
2.3. Theory of ABC Symmetry Selection
The symmetry of is the overall symmetry happening when both rotor wavefunctions are strongly correlated. We must remember that the total symmetry is based on group products regardless of BOA or LWC or whatever and comes about from fundamental nuclear identity. is the permutation of all nuclei common to both and . However, the challenge come in determining the symmetry label A. This is the symmetry induced to the rotor with angular momentum ℓ by the second rotor to which it is strongly correlated.
If we consider the case where all nuclei are identical, the “under all” nuclear permutational symmetry group is where n is the number of identical nuclei. But, when the rotor molecules are uncorrelated, the relevant permutation symmetry is that of each of the individual rotors, namely and . As they become weakly coupled, the permutation symmetry is and corresponds to the number of identical nuclei with the coupled system. This symmetry is approximately since we assume that bonds between the constituent molecules are unbroken. As a result, we start with the permutation group and the outer product of the individual permutation groups of each molecule. To begin with, we write following for the two rotors:
represents the Young tableau irreducible representations whose subduction , to the group gives a B symmetry label. So by the Frobenius reciprocity, is in the induction to by , where the symbol in the parentheses describe a correlation table for each rotor constituent. Since the two constituent rotors are interacting then their geometry of the symmetry is described by the product of the external and internal symmetry of each rotor that is:
However, at first, we will only concern ourselves with the internal point symmetry. Thus, the symmetry is given by . This new group is a subgroup of the permutation where n is the number of identical nuclei common to both molecules.
The first step is to compute the character table of . Next we must perform symmetry analysis in both of our bases, namely LWC and BOA basis. As mentioned before for simplicity, we assume the simpler case where all nuclei are identical.
We will start with uncoupled bases and symmetry analysis of the individual constituent rotors. The symmetry groups are and which are subgroups of . In the weakly coupled basis it is assumed that the symmetry group is for a group of identical nuclei. For example two molecules would have a symmetric group of . We also need a correlation table between and for the rotation group of the entire rotor-rotor system.
At first, nature reduces the symmetry from to a lower symmetry since initial chemical bonds between individual rotors prevent all n! permutations from being allowed, that is, . Initially, we assume that the molecules will have some freedom to rotate individually, and subjected to the coupling between them, give rise to various geometrical structures that may become a final geometry if a very strong interaction takes effect. For example, two molecules might later find themselves locked into , or symmetry. While the system is weakly coupled, they move through all these geometries giving rise to various states that make up a generalized cluster basis, that is, an induced representation basis. In the LWC basis, we have permutation symmetry giving to two classes of operators, those that leave the two molecules together that is bi-cyclic operators like (12)(34), and those that move the individual molecules that is, monocyclic operators like (12) which is the same as transposition in group theory.
Therefore, we compute the correlation : This seems like a difficult task, in general, but by using Young tableau the procedure becomes easier. To achieve this, we must find the outer product using the Frobenius Reciprocity Theorem. If is isomorphic to a composite molecular point group, then the approach in determining the label is very easily done.
The BOA basis is approached if the coupling becomes strong enough to lock our coupled system. At this point, we assume that the coupling is so strong that molecules can only vibrate in the planes to which they are confined so the angle between them is almost constant. Then we can describe the composite system by some geometrical point group of a rigid (or semi-rigid) molecule.
We now outline a procedure to find the symmetry labels and . We find the “under all” permutational symmetry in the BOA constricted situation. Observing the intersection of which is some particular geometry point group gives us the labels. We defined to be the symmetry label of the identical nuclei within the new arrangement. The derivation of the symmetry species comes from the irreducible modes that are active. When we move to the BOA basis, certain modes become active. These active modes have an (“Activity”) symmetry label. This lets us find . Once the particular point group is determined and the modes that can be excited are found, then is just the irreducible representation of the outer product of and , that is .
This gives all the possible symmetry pieces of We will consider an example of diatomic–diatomic interaction. Since the overall external symmetry is , knowing gives a correlation induced between the irrep and that of . Similarly, the correlation between the irreducible representation of and or can be computed. The characters of is given by
We derive the character of from its outer product relation to .
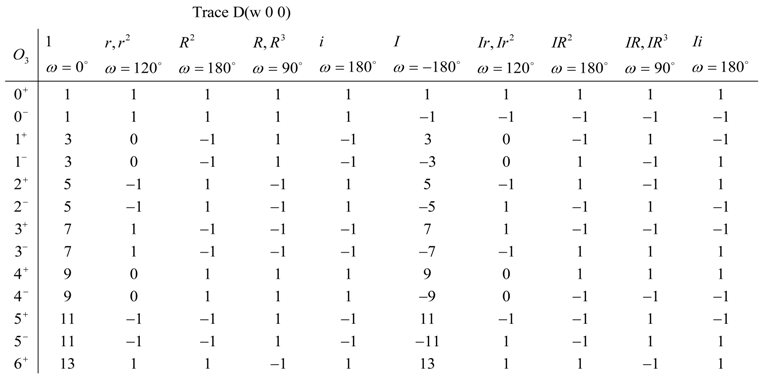
The frequency of the irreducible representation of subduced to is given by
where is the irrep label of the point group of the composite rigid body.
3. Spin Statistical Weights
One cannot speak of statistical weight without mentioning the extensive review by Bunker and Jensen [23], which outlines a procedure to calculate statistical weight for molecular symmetry. Hougen [34] has used a classical approach to classify the various labeling schemes of molecular symmetry. Alvarez-Bajo et al. [35] revisited group computed spin weight for methane using symmetry projection. As pointed out earlier, large amplitude motions may result in configurations that can be described by molecular symmetry group as shown by Bunker et al. [23]. However, we consider the treatment of such with symmetry permutation groups, which sometimes reveal details not obvious from traditional approaches. The power of such approach can be seen in a comparison study done by Harter et al. [12] with old techniques used by Hougen [34] to showcase Young tableau as a powerful tool that can be used to compute statistical weight. In their work, Harter points out that the tableau method gives the same result as long as inversion does not play a dynamical role. In comparing this method with that of Hougen [34], Harter shows that it reveals the hidden structure of the inversion doublets for various molecular symmetries.
The symmetric classification for nuclear wavefunction of a diatomic molecule is done by considering its two nuclei. However, symmetry classification may appear ambiguous because it depends on the details of the permutation of nuclei. Harter and colleagues [12] have shown how to assign Young tableau to the point symmetry species . Furthermore, n identical nuclei may have one or more orbital tableau corresponding to each labels of the spatial point group, and for each tableau, there is just one nuclear spin tableau that describes the permutational properties of the nuclear spin wavefunction. This is due to the Bose–Einstein Principle demanding the spin tableau of the nuclear state to be identical to its orbital tableau while the spin tableau of the Fermi-Dirac nuclear state is conjugated to its orbital tableau. The Bose nuclear states are those with integral spins such as a photon, or deuterium nuclei, whereas the Fermi nuclear states are those with half-integer spins such as nuclei with odd numbers of nucleons.
To compute the spin weight one must do a little algebra. The statistical weight found by using the Robinson formula along with the correlation frequencies give
where is given in Figure 28 of reference [12] as
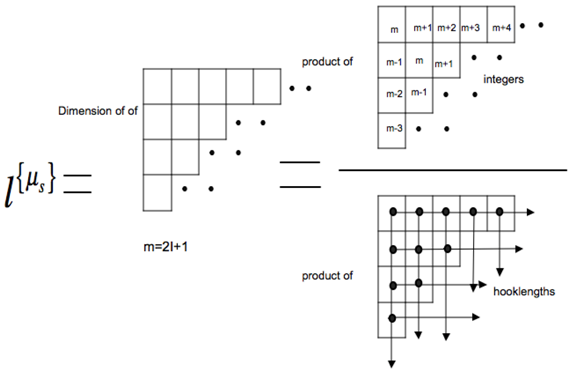

The hooklength of a box in the tableau is the number of boxes in a “hook” which includes that box and all boxes in the line to the right and in the column below it. This formula gives directly the number of nuclear spin states associated with each tableau . The sum of these numbers taken over each tableau associated with “soul” label will be the desired statistical weight.
These correlation frequencies are quite simple for point groups but not as easy for the permutation groups. We will give a few formulas for the permutation group. If for the individual molecules we have two nucleons (), the necessary is three would be since , that is:
where I is the spin angular momentum. For Bosons: use , nuclei use , and so on. For a more detailed approach and understanding of how to use tableau to compute statistical spin weight for molecular system, one should consult the work of Harter et al. [12].
4. Coupling between Two Diatomic Molecules
It is well known that diatomic molecules such as and have symmetry. However, the nuclear spins of these molecules are different. has two protons with each spins of , nuclear spin is , and nuclei each have each nuclear spins of . Thus is fermionic, whereas and are bosonic. The nuclear spins of all elements and their isotopes are very well known and can be found in tables of nuclides [36].
The spin statistical weight determines the relative intensity of spectra belonging to each label. contain two spin-1/2 protons where the state by its even parity correlates to the antisymmetric tableau of singlet (I = 0) spin tableau by Fermi-Dirac rules. The state belongs to the symmetric spin tableau that is, triplet () total spin. One should note that for a diatomic molecule with symmetry the only choices are or . Deuterated hydrogen contains two spin-1 deuterons where, by Bose-Einstein rules, the state by its parity correlates to the antisymmetric tableau and belongs to the tableau . The state has spin states of total nuclear spin angular momentum of and , while is the deuterium triplet with . However, only has ortho-states species . The para species are Pauli excluded because spin-0 states cannot be antisymmetric.
We now investigate symmetry structure and levels of two diatomic molecules. We have assumed that the interaction is between identical diatomic molecules. The energy levels for two uncoupled molecules are shown in Figure 1. As these molecules come into the vicinity of each other, we suppose they begin to interact in a weakly correlated state [25].
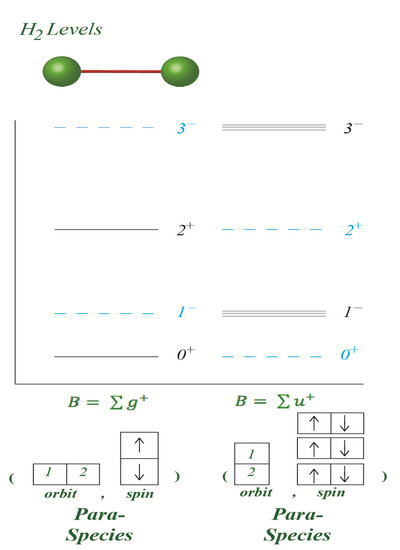
Figure 1.
Rotational Energy levels of a molecule.
In the LWC basis, the symmetry of the molecular system is nearly the permutation group, which is isomorphic to that of the tetrahedral point . The character table of is given in Equation (22) where represents the irreps of .
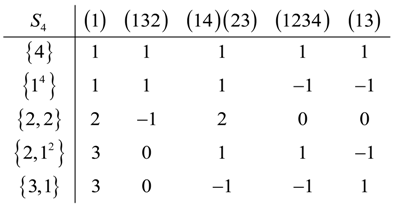
Since the overall symmetry of the group is then the correlation between and is given as follows. This uses the isomorphism of and .

Equation (23) tells us how the angular momentum energy states splits according to S4 symmetry group. As the angular momentum increases the effects of clustering begin to be manifested [11,12]. This is more noticeable in the irreps { and of . But as we go from the LWC basis to the BOA basis by increasing the coupling strength, the nuclei is locked into a particular geometry. If the energy between the molecules is not high enough to cause bond breaking in the individual diatomic molecules we may see clustering of the energy levels.
4.1. Point Group
X2 molecule has two identical nuclei, which means it has a permutation symmetry group of S2. When the molecules are weakly coupled, constituents allow full S4 permutations, but as the coupling increases the permutation symmetry may be reduced to , the outer product between the symmetry groups of the two diatomic molecules. The characters of are listed below:
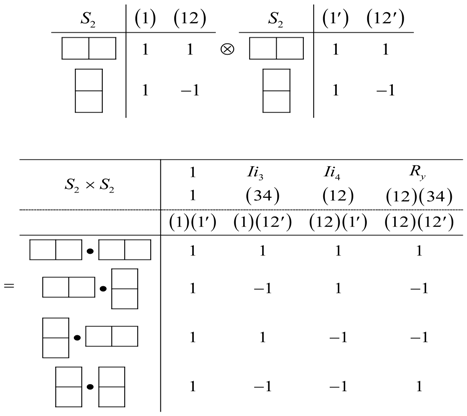

The group is isomorphic to C2. , however, it allows a 180° rotation about the center of each individual molecules, while the other stays fixed; for instance consider the configuration 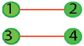 where the numbers label the position of the atoms of the molecules. Under the operation (34), the previous configuration changes to
where the numbers label the position of the atoms of the molecules. Under the operation (34), the previous configuration changes to 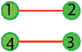 .
.
 where the numbers label the position of the atoms of the molecules. Under the operation (34), the previous configuration changes to
where the numbers label the position of the atoms of the molecules. Under the operation (34), the previous configuration changes to  .
.By using Frobenius Reciprocity theorem we obtain the reduction table. In left column of Equation (25) we give the spin tableaus for fermions and Boson nuclei:
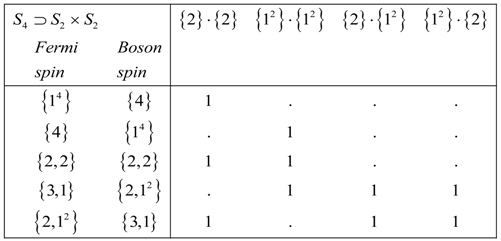

In BOA basis the interaction is so strong that their position is locked in together preventing the large amplitude motion that is allowed in LWC basis. The only symmetry operators that are allowed are those that move both molecules rigidly together. If the molecules are locked in parallel to each other then they belong to a group with or symmetry but if oriented at right angles then the group form is one with or symmetry. We investigate molecules orientation with either or symmetry.
4.2. Statistical Weight
The algebra needed is for Fermions of spin . From Equation (21) we have . This means that there are three possible choices for the numerator of by Equation (20b):  ,
, 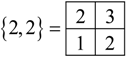 , and
, and 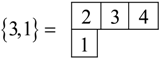 . The Frobenius Reciprocity theorem gives the correlation frequencies and using Equations (20a) and (20b) we compute the statistical weight for to be,
. The Frobenius Reciprocity theorem gives the correlation frequencies and using Equations (20a) and (20b) we compute the statistical weight for to be,
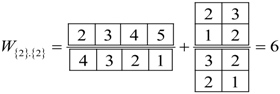
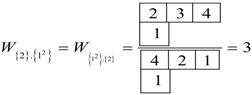
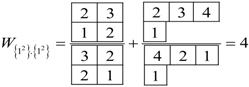
 ,
, 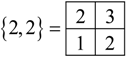 , and
, and 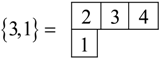 . The Frobenius Reciprocity theorem gives the correlation frequencies and using Equations (20a) and (20b) we compute the statistical weight for to be,
. The Frobenius Reciprocity theorem gives the correlation frequencies and using Equations (20a) and (20b) we compute the statistical weight for to be, 


Equations (26a–c) shows how the various symmetry levels would cluster. The state corresponding to the symmetry species {2}{2}would consist of four degenerate levels whereas the states with symmetry {2}{12} would be triply degenerated. The use of Young tableau gives information about the clustering of the level. As we continue to reduce the symmetry we will compute the statistical weight using Young tableau.
4.3. Point Group
When two X2 molecules are aligned parallel to each other, their arrangement gives a symmetry group of that is, there is a R’s rotation of 180° degrees around the x, y, and z axes. configuration contains a horizontal refection plane where is the inversion operator such that  . This operator works by inverting the spatial coordinates of all nuclei through the center of mass. The overall symmetry of configuration is the outer product of and that is contains three 180° degrees rotations about the xyz axes, an I inversion, a horizontal refection , and two vertical planes (), . The character table for symmetry group is given by Equation (27).
. This operator works by inverting the spatial coordinates of all nuclei through the center of mass. The overall symmetry of configuration is the outer product of and that is contains three 180° degrees rotations about the xyz axes, an I inversion, a horizontal refection , and two vertical planes (), . The character table for symmetry group is given by Equation (27).
 . This operator works by inverting the spatial coordinates of all nuclei through the center of mass. The overall symmetry of configuration is the outer product of and that is contains three 180° degrees rotations about the xyz axes, an I inversion, a horizontal refection , and two vertical planes (), . The character table for symmetry group is given by Equation (27).
. This operator works by inverting the spatial coordinates of all nuclei through the center of mass. The overall symmetry of configuration is the outer product of and that is contains three 180° degrees rotations about the xyz axes, an I inversion, a horizontal refection , and two vertical planes (), . The character table for symmetry group is given by Equation (27).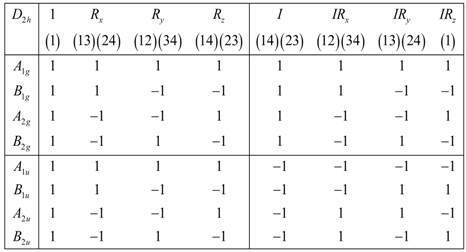
Let us consider a spring model system such as shown in the Figure 2 in order to compute the vibrational levels in the plane in which both diatomic molecules lie. Since we assume that the D2h symmetry, then the coordinates are described by following state vectors
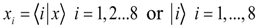
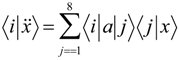 Where
Where
 And , , , , , , and .
And , , , , , , and .
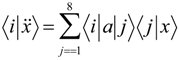

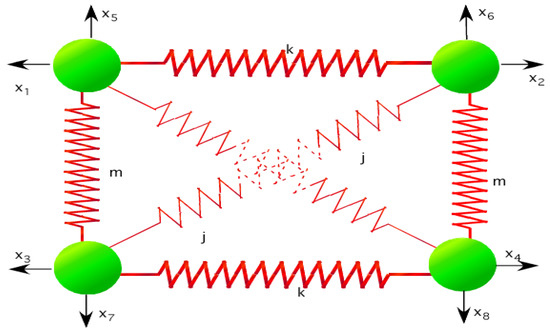
Figure 2.
Spring mass system for four nuclei.
From Equation (27) we build our D2h projectors; For example the projector . When this acts state we have The application of on gives non-zero for states parallel it and give a similar result when applied to . Only irreps give a nonzero result.
Therefore, the application of D2h projectors to the coordinates, gives the 8 × 8 transformation matrix Equation (30).
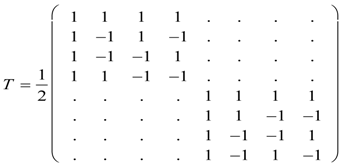
The transformation contains two 4 × 4 blocks, which block diagonalized the force matrix due to the presence of D2h symmetry. As a result, the force matrix is reduced by this transformation to two 2 × 2 matrices and four 1 × 1 matrices or eigenvalues.
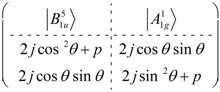
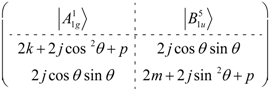
The parameter p is the spring constant if the spring system is connected to the springs along all eight coordinate axes, but we will assume that is not the situation there because p = 0. Therefore, the eigenvalues for Equation (31a) are 0 and 2j, and eigenvectors and . But for Equation (31b) we have the following eigenvalue:
where and .
The eigenvectors are listed below their eigenvalues
Where .
The other eigenvalues are (2k and 0), (0 and 2m), which corresponds eigenvectors A2g and B2u modes of the D2h respectively.
4.4. Statistical Weight for
Bunker and Jensen [23] have given a detailed development of permutation and permutation inversion groups, which one should consult for a thorough understanding. The inversion group is synonymous to their . since is absent of the inversion operation . We use the out product between the groups and such that The operator commutes with all operations; thus the group is called a complete nuclear permutation inversion (CNPI [23]) group. We are now in position to compute the correlation between and . For brevity we consider a much simpler correlation between the molecular symmetry group and since only the irreps give a non-result. The resulting correlation table is shown in Figure 3.
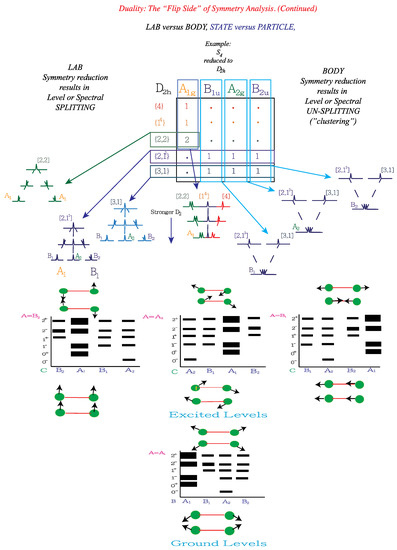
Figure 3.
Energy spectrum and correlation diagram for D2. Structure of two diatomic molecules.
From Equations (20a) and (20b) we compute the spin weight for the D2h point group by using Equation (27), along with the correlation table shown in Figure 3. As a result, the following spin state weights are found.
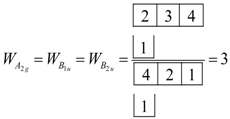
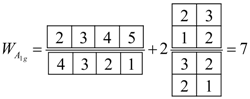
The irreps of are the only active modes and are the labels of the internal symmetry of the bare rotor. The modes of the constricted rotor come from the tensor product , as shown in the energy level diagram in Figure 3. As we move down the column of the correlation table we see clustering formation; for example the irreps and of comes together to form the cluster of as displayed in the right of Figure 3. On the other hand, moving across the row shows the splitting of the irreps of into various irreps of .
Figure 3 is an illustration of Lab-body duality. The rows represent “coerced” or forced symmetry breaking, this comes from applying some kind of external field, which would result in the energy level splitting. The columns describe what is happening in the body frame; in other words, the symmetry reduction brings about clustering. The energy level diagrams of Figure 3 were obtained from Equation (27) through Equations (34a) and (34b).
4.5. . Point Group
Diatomic rotor-rotor BOA structures of or point group symmetry may come about when the two diatomic molecules are paired at right angles to each other. Equation (35) gives the character table for the point group. It is the same character table as its isomorphic symmetry for which the operators , , , and are paired with inversion .

For a rotor-rotor locked in point symmetry, each of its tableau symmetry labeled levels must split according to a point symmetry Equation (36).
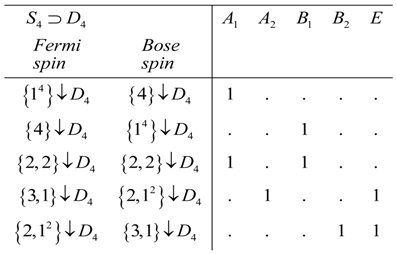
Now, reading the columns gives the induced representations such as for a Boson. From this, we construct spin–tableau correlations with symmetry states, for either Bose or Fermi nuclei.
4.6. Statistical Weight for
As with the analysis we calculate the spin weight for the irreps of . Since Fermions spin I = 1/2, the unitary algebra is U2. The B2 spin weight is zero for symmetry since in the group correlation table between and , the B2 irrep correspond only to {2,12}, and using Robinson’s hook length formula as defined in reference [11], we compute the numerator to be zero. The total sum of the spin weight is 13 and not 16. However, we need not be alarmed since the spin weight for doubly degenerated E must be double counted, hence, we still have 16 spin states in all.
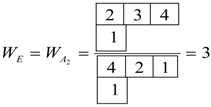
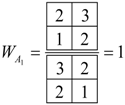
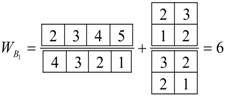
The energy level clusters shown in Figure 4 for a structure are quite different from that of . E-symmetry species indicate double degeneracy but Young Tableau assigns each of the two levels with a triple degeneracy. This is shown in the energy diagram of Figure 4.
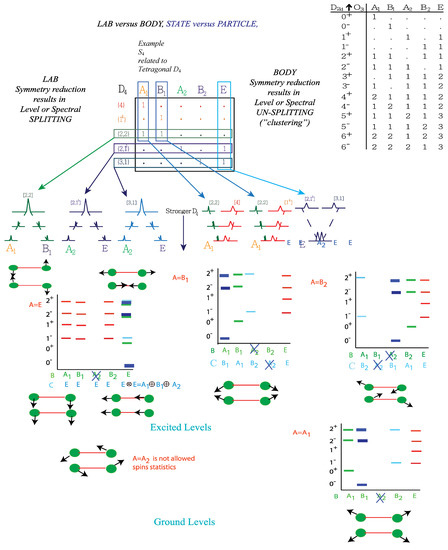
Figure 4.
Energy spectrum and correlation diagram for structure of two diatomic molecules.
Thus using (2) we can find BOA constricted wave function. Consider the angular momentum state. From the correlation table we have for labels and the bare rotor is symmetry, thus labels are irreps of point group. We now computed the labels of constricted rotor from the tenser product that is . This shows in the energy level diagram in Figure 4.
5. Tunneling Hamiltonians
We can write down various tunneling Hamiltonian matrix for each of the symmetry above as we move from symmetry to any of the others. We will start by giving the regular representation of the four particle states for each symmetry case . From we may have all the possible final point group geometry as given in Figure 5. However, and have only four possible arrangements whereas has eight. is a subset of , but although isomorphic to , is not a subset of . Figure 6 shows all the arrangements of , and .
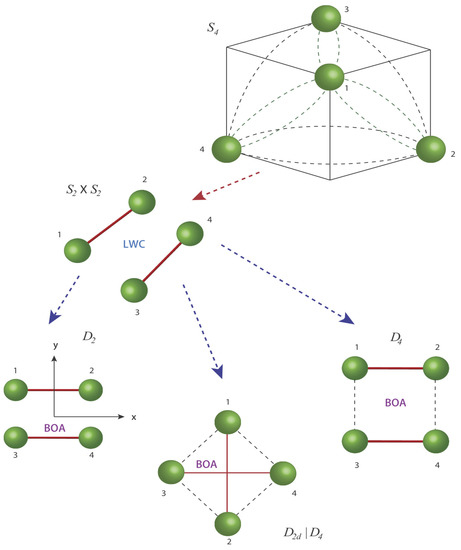
Figure 5.
All possible paths from S4 to a lower symmetry.
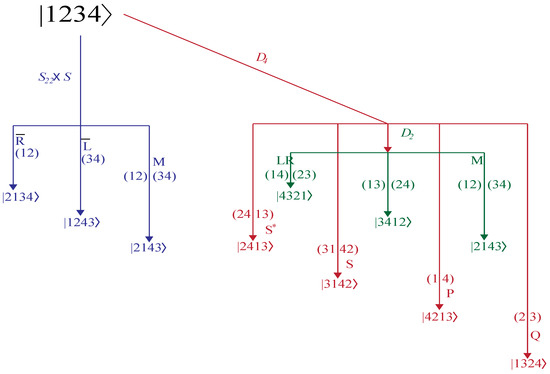
Figure 6.
All possible arrangement from to , and . The state is shown in the kets, and the possible operator is represented in parentheses. The upper case letters represent the tunneling parameter between different configurations.
The reason why we have not done all 24 arrangements is due to the existence of the bonds between the two diatomic molecules, as a result, only certain feasible operations are allowed. To take advantage of the full symmetry, it would be necessary to break the bonds between the diatomic molecules. We are ready to investigate each tunneling paths from to , and . Here is the argument (1234), and is (2143), is (2134), and is (1243) as shown in Figure 6. Each one is obtained from operations. Similarly, we can derive the states for , , or by using their operations on state .
5.1. Tunneling Hamiltonian for Point Symmetry
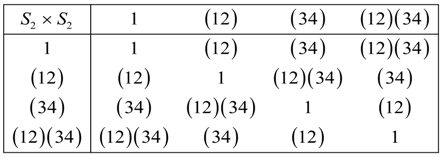
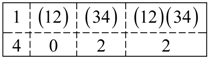
In the LWC basis the molecular system have S4 symmetry. As we increase the coupling or interaction, the symmetry is reduced. is one such symmetry reduction sub-group where the individual molecules still have some freedom to rotate in and out of the plane in which they are confined. In more recent work, Hougen et al. [37] have extended permutation-inversion group studying large amplitude motion acetylene. The earliest work in treating large amplitude motion in non-rigid molecules goes back to Longuet-Higgins [15]. has two configurations that normal symmetry operations cannot reproduce. Applying the permutation operations {1,(12),(34),(12)(34)} to each of the base states gives the following regular representation of .
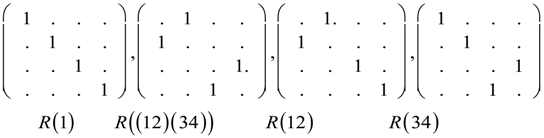
These matrixes are for a group table that is isomorphic to D2.
Consider the symmetry operators g that commutes with the Hamiltonian H, i.e., gH = Hg, but the non-commutative symmetry D3, D4, etc., we build our Hamiltonian matrix by combining the dual symmetry operators as described by Harter [38]. Equation (39) shows that forms an Abelian group, thus we can construct the Hamiltonian matrix since it naturally commutes with the operators. The resulting parameters H, , M, and can be visualized as coupling or tunneling parameters related to the symmetry path. The bar is used as an indicator that only one of is being operated on; thus the outcome does not match a point group operation. is the tunneling parameter between and , and is the tunneling parameter between and , and M is between , and . Writing the tunneling Hamiltonian in the basis of the regular representation Equation (38): which gives:
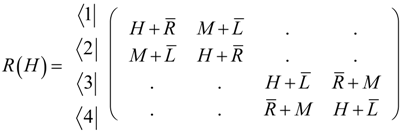
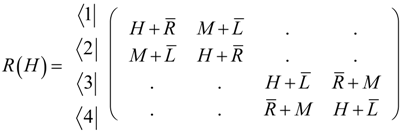
Since is isomorphic to D2, one might expect that the transformation matrix created from the projection of D2 would diagonalize Equation (40). But this is not the case. Instead, its block diagonalizes the Hamiltonian.
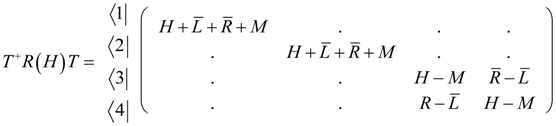
We construct a transformation Equation (42) that diagonalizes the Hamiltonian Equation (40) using the fact that diagonalizes a bilaterally symmetric matrix .
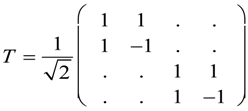
As a result, we obtained the following eigenvalues:
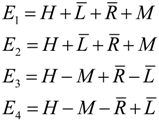
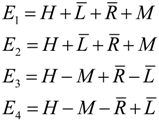
However, the eigenvectors are just the columns of the transformation matrix. There is degeneracy since two of our eigenvalues are the same. The trace of Equation (38) gives
 Therefore this splits into (2A1,B1,B2) of the D2 irreps.
Therefore this splits into (2A1,B1,B2) of the D2 irreps.

5.2. Tunneling Hamiltonian for D2 Point Symmetry
As the coupling is increased so that the two diatomic molecules become locked, we can have any of the other three cases in Figure 5. At this point, we are in BOA basis. The Bunker and Jensen work [23] is paramount for molecular symmetry groups. Although one could easily solve a rigid rotor problem with molecular symmetry, we use here symmetry projector theory [38,39], which allows for a sort of elegance when solving the coupled rotor system that is locked. Previously we saw that the D2h fundamental vibration modes are . Here, the physics of D2h and D2 are essentially the same. The group table of D2 is given by
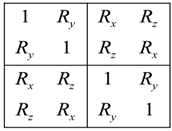 and its matrix representation as follow:
and its matrix representation as follow:
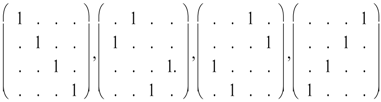


Next we have given the projectors of D2
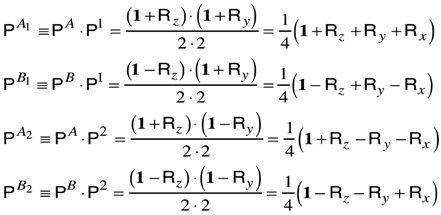
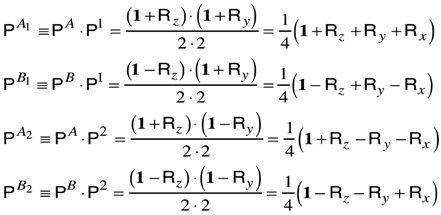
The tunneling Hamiltonian in the basis of a D2 regular presentation is given as follows:
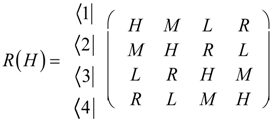
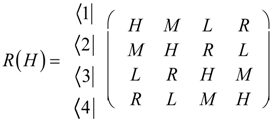
From Equation (47) we have the following diagonalizing transformation:


Applying Equation (49) to Equation (48) we obtain the eigenvalues and eigenvectors in Equation (50):
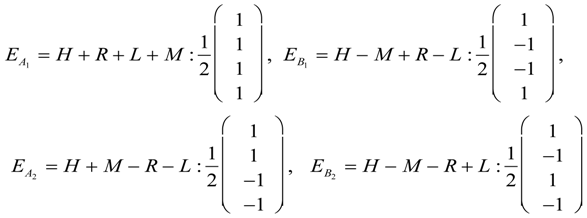
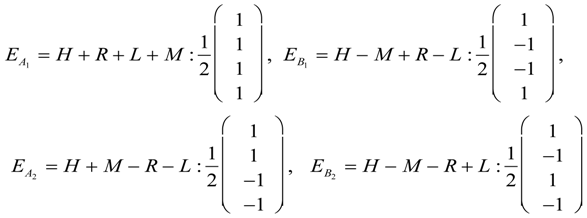
The D2 tunneling matrix produces no degeneracy in A1 mode, as it was the case with . This must be due to the fact that for structures, that an individual diatomic molecule is allowed to rotate out of the plane and it is the same symmetry configuration whether the diatomic molecule has one of its rotors out of the plane or the other one.
5.3. Tunneling Hamiltonian for Point Symmetry
Unlike , is non-Abelian since its group elements do not commute and neither will they be any faithful to the representation of . point group contains an identity operation, a 180° rotation around each of the x, y and z axis , 90° and −90° about z-axis , and finally 180° about each of the diagonals . Non-commutivity of means that we cannot write all eight of the operators as a spectral decomposition using commuting idempotents. By idempotents, we mean · and zero otherwise. We will use projector theory to give a description of its non-Abelian algebra. Since it is non-commutative it is not possible to spectral decompose all of its eight operators by using eight commutating idempotents.
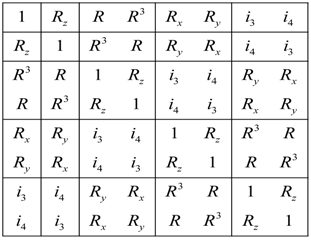
We obtain the regular representation from a group table Equation (51) rearranged so that columns are labeled by kets = , and rows are labeled by bras
(Note that the inverses of the column operators sit on the left end of the rows).
Here each matrix component is 1 (or 0) if is (or is not) at that spot in Equation (51).
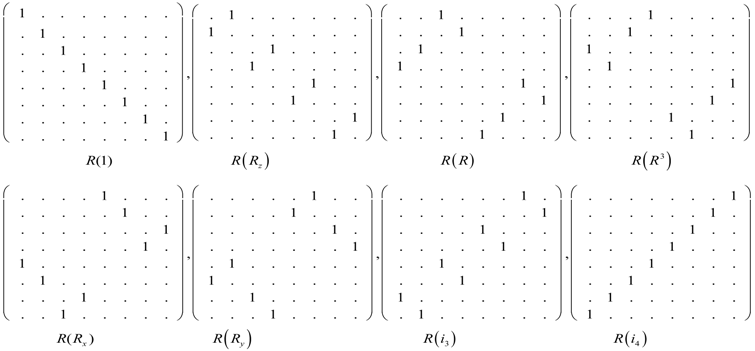
Since these representations are non-commuting, we cannot simply write the Hamiltonian in terms of them. Using the idea of mutually commuting lab based and body based operators and , we can find the dual space. Harter [38] has given a detailed description of how to do this in general. In this case, we find a body matrix representation in Equation (53a) that commutes with in Equation (53b).
The group-based D4 cannot be diagonalized but reduced or block diagonalized to a combination of irreps , and from the character Table (4.13). The character of is found by taking its trace, which gives . The trace of . All eight matrices are reducible by some transformation to a block diagonals form with , and blocks. Thus the reduction is carried out by finding all eight of the generalized projectors. This approach is described in more detail in [23,29,38,39] but will not be approached here.
The D4 Hamiltonian is made by combining body based or dual space representations in Equation (53a) since they commute with matrices Equation (53b) of the regular D4 representation as required by D4 symmetry. Thus we have,
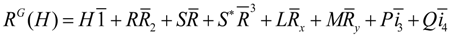

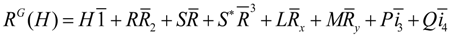

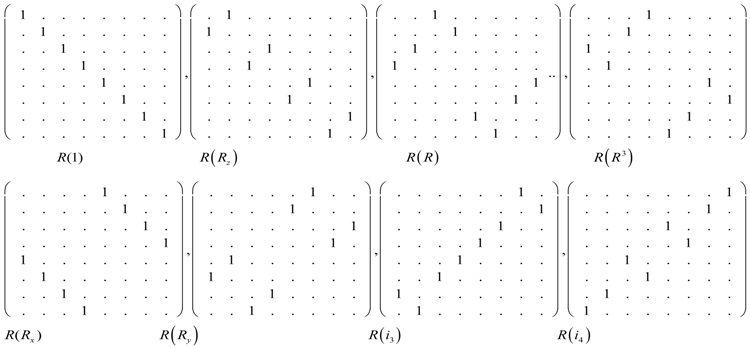
The first step in finding a transformation that would block diagonalized Equations (54a) and (54b) is to find the largest number of mutually commuting operators. This is also referred to as the Maximal Set of Commuting Operators (MSOCO). As pointed out by Harter [38], the number of operators is unique and it is the rank of the group. The rank of is six and the number of orthogonal irreducible representation (irreps) of the algebra is five, which means that there must exist another member of the set. The choice of this member is not unique. We choose an operator diagonal so we can split idempotent in a particular way in order to build a particular set of . In case of there exist three subgroups of order 4, five of order 2, and one of order 1, of which we can choose one as a temporary member to complete the maximal sets. For our computation we choose the subgroup to split idempotent. Harter [38] described a procedure that we use to split idempotent into four new projectors.
Equation (51) is divided into its five classes as seen by how the table is sectioned off in blocks that form sort of a commuting algebra. Harter [38] has gone in detailed description of non-Abelian algebra where algebra is given as an example. Since in non-Abelian algebra, not all the matrices can be diagonalized or reduced at once by a single transformation, we use a technique of class commutating algebra described by Harter [38] that simultaneously spectral decompose MSOCO. The class algebra does not form a group but allows us to derive the projectors of the group. From the projectors we are able to derive such properties as the character table Equations (34a) and (34b), eigenvectors, and the transformation matrices, etc. Since, we already know the character table we will not here follow the exact approach of reference [38] because we can derive its projectors from Equations (34a) and (34b) as was done in (Section 4). The irreps of Equations (34a) and (34b) give five projectors, however, because the rank of is 6 we need to split idempotent as discussed before. Now that we have all eight projectors, we derive a transformation Equation (55), which allows us to reduce the Hamiltonian Equation (55) to a block diagonal form as shown in Equation (56). From the projectors of D4 we found the transformation matrix Equation (55).
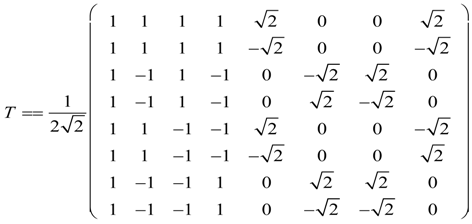
This block diagonalized Equations (53a) and (53b) to give the following:



The reduction of Equations (54a) and (54b) using the above transformation gives four singlet eigenvalues
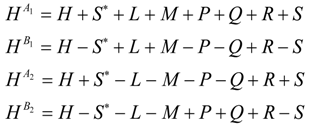
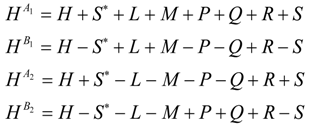
Finally, there are two pairs of identical two by two matrices each with the following matrix element:
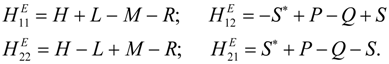
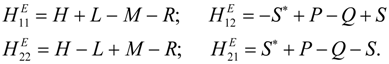
These two by two matrices will have to be further diagonalized if Q, P or are non-zero. Therefore, if we let then we can represent these two-by-two matrices as
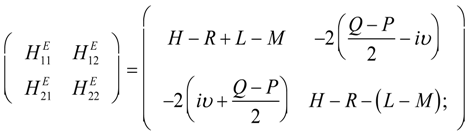
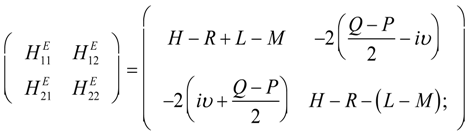
If instead we apply the transformation Equation (55) using the regular representation instead of then it would be block diagonalized like in Equation (56b).
To interpret the eigensolutions of Equation (58b), we represent our two-by-two matrix in terms of the quasi-spin vectors as defined in Figure 7.
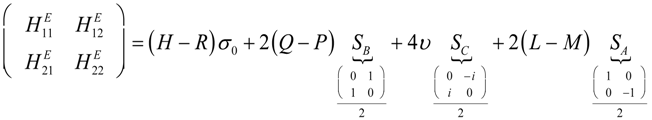
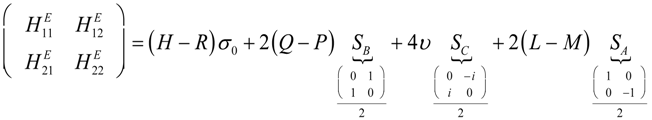
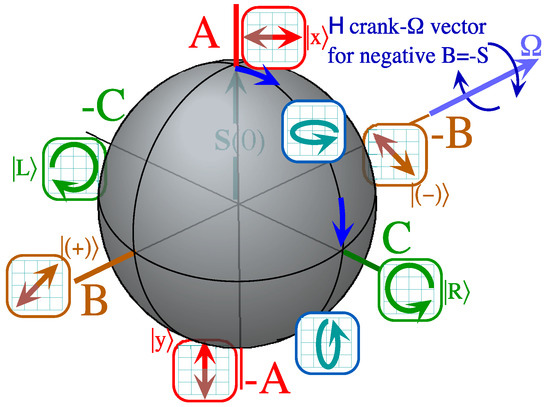
Figure 7.
(ABC) symmetry coordinates. This diagram was published by Harter [38].
Equation (59) is analogous to the description of a two state system, therefore U2 analysis may help to characterize the eigensolution. Harter [38,39] have given a general development U2 analysis for any two states system. Suppose has the form with no component on the C axis.
Also let A = D so both L and M are zero. Then there results a simple mixing between the E modes in the two by two blocks with eigenvectors ( diagonalizing bilaterally symmetric sub-Hamiltonians.
Thus the E-Hamiltonian under these conditions has a perfect bilateral symmetry. This means that if the quasi-spin vector starts out on the B axis as in Figure 7, it remains fixed. However, when , we have an asymmetric two-state system that is very much like the one in reference [39]. This is plotted in Figure 8.
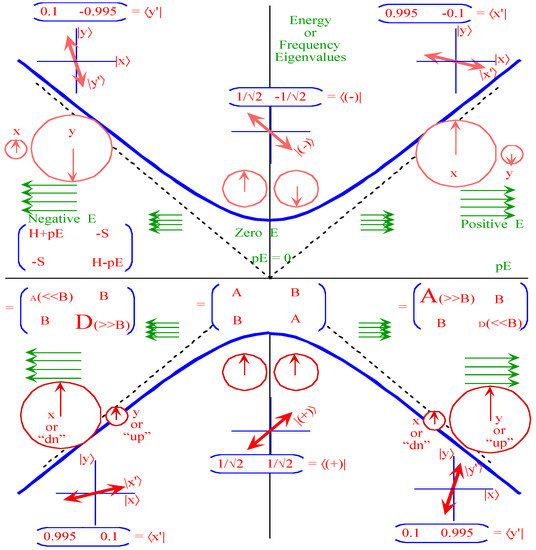
Figure 8.
Two state system eigensolutions [39].
6. Conclusions
The frame relation derived in reference [25] was developed to include the finite symmetry of a molecular geometry. The B label was shown to be the symmetry species of the nascent geometry’s point group. The transformation relation has a finite symmetry field coefficient of the small rotor included in it. It is not clear how one should choose a particular frame over. However, in a locked geometry, the choice of frame does not matter, but only the geometric point group that is formed. We investigated locked geometries for two diatomic molecules using Young tableau and unitary algebra to find the nuclear spin statistical weights. This gives approximates and preliminary insight for level structure.
Moreover, we used the frame transformation relations derived in reference [25] to calculate the transitions between angular momentum states. More general transition relations were found than those given in reference [12]. However, one could extend our relation to include symmetry for transitions in a two rotor coupled system, but this will be left for future work.
Acknowledgments
This work has been co-supported by the Research Corporation for Science Advancement.
References
- Young, A. On quantitative substitutional analysis IX. Proc. Lond. Math. Soc. 1952, 54, 219–253. [Google Scholar] [CrossRef]
- Yamanouchi, T. On the construction of unitary irreducible representation of the symmetric group. Proc. Phys. Math. Soc. Jpn. 1937, 19, 436–450. [Google Scholar]
- Yamanouchi, T. The Application of the Rotational Group and Symmetric Group; Beijing Science Press: Beijing, China, 1966. [Google Scholar]
- Littlewood, D.E. The Theory of Group Characters and Matrix Representations of Groups; Oxford Press: Oxford, UK, 1950. [Google Scholar]
- Gel’fand, M.I. The center of an infinitesimal group algebra. Mat. Sb. 1950, 26, 103–112. [Google Scholar]
- Gel’fand, M.I. Matrix elements for the unitary groups. Dokl. Akad. Nauk. 1950, 71, 825–828. [Google Scholar]
- Gel’fand, M.I. Representations of the Rotation and Lorentz and Their Applications; Pergamon Press: New York, NY, USA, 1963. [Google Scholar]
- Shur, I. Neue anwendungen der Intergralrechnung auf Probleme der Invariantentheorie; Sitzungsberichte Akademie der Wissenschaften: Berlin, Germany, 1924; pp. 189–208. [Google Scholar]
- De Beauregard Robinson, G. Representation Theory of the Symmetric Group; University of Toronto Press: Toronto, Canada, 1960. [Google Scholar]
- Coleman, A.J. Induced Representations and Applications; Queens University Press: Kingston, Ontario, Canada, 1971. [Google Scholar]
- Harter, W. Theory of hyperfine and super levels in symmetric polyatomic molecules. II Elementary cases in octahedral hexafluoride molecules. Phys. Rev. A 1981, 24, 192–263. [Google Scholar] [CrossRef]
- Harter, W.G.; Patterson, C.W.; da Paixao, F.J. Frame transformation relations and multiple transitions in symmetric polyatomic molecules. Rev. Mod. Phys. 1978, 50, 37–83. [Google Scholar] [CrossRef]
- Harter, W.; Patterson, C.W. Theory of hyperfine and super levels in symmetric polyatomic molecules. Trigonal and tetrahedral: Elementary spin ½ cases vibronic ground states. Phys. Rev. A 1979, 19, 2277–2303. [Google Scholar] [CrossRef]
- Streater, R.F.; Wightman, A.S. PCT, Spin and Statistics, and All That; Princeton University Press: Princeton, NJ, USA, 1964. [Google Scholar]
- Longuet-Higgins, H.C. The symmetry groups of non-rigid molecules. Mol. Phys. 1963, 6, 445–460. [Google Scholar] [CrossRef]
- Hougen, J.T. Classification of rotational energy levels for symmetric—Top molecules. J. Chem. Phys. 1962, 37, 1433–1441. [Google Scholar] [CrossRef]
- Harter, W.G. Alternative basis for the theory of complex spectra. Phys. Rev. A 1973, 8, 2819–2827. [Google Scholar] [CrossRef]
- Harter, W.G.; Patterson, C.W. Alternative basis for the theory of complex spectra. II. Phys. Rev. A 1976, 13, 1067–1082. [Google Scholar] [CrossRef]
- Patterson, C.W.; Harter, W.G. Canonical symmetrization for unitary bases. I. Canonical Weyl bases. J. Math. Phys. 1976, 17, 1125–1136. [Google Scholar] [CrossRef]
- Harter, W.G.; Patterson, C.W. Simple model for asymptotic level clusters in SF6 rotational spectra. Phys. Rev. Lett. 1977, 5, 224–227. [Google Scholar] [CrossRef]
- Harter, W.G.; Weeks, D.E. Rotation-vibration spectra of icosahedral molecules. I. Icosahedral symmetry analysis and fine structure. J. Chem. Phys. 1989, 90, 4727–4743. [Google Scholar] [CrossRef]
- Harter, W.G.; Patterson, C.W. Alternative basis for the theory of complex spectra. III. Phys. Rev. A 1976, 15, 2372–2379. [Google Scholar]
- Bunker, P.R.; Jensen, P. Molecular Symmetry and Spectroscopy, 2nd ed.; NRC Research Press: Ottawa, Canada, 1998. [Google Scholar]
- Groner, P. Effective rotational Hamiltonian for molecules with two periodic large-amplitude motions. J. Chem. Phys. 1997, 107, 4483–4498. [Google Scholar] [CrossRef]
- Crogman, H.T.; Harter, W.G. Frame transformation relations for fluxional symmetric rotor dimmers. J. Chem. Phys. 2004, 121, 9297–9312. [Google Scholar] [CrossRef] [PubMed]
- Chang, E.S.; Fano, U. Theory of electron-molecule collisions by frame transformations. Phys. Rev. A 1972, 6, 173–185. [Google Scholar] [CrossRef]
- Junger, C.H. Highly excited molecular states: Quantum defect and ab initio theory. Proceedings of International Symposium on Molecular and Spectroscopy, Ohio State University, Columbus, OH, USA, 16–20 June 2003. [Google Scholar]
- Junger, C.H.; Atabek, O. Rovibronic interactions in the photoabsorption spectrum of molecular hydrogen and deuterium: An application of multichannel quantum defect methods. J. Chem. Phys. 1976, 66, 5584–5609. [Google Scholar] [CrossRef]
- Chen, J.Q. Group Representation Theory for Physicist; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1989. [Google Scholar]
- Kung, P.S.J. Young Tableaux in Combinatorics Invariant Theory and Algebra; Academic Press: University of Michigan, Ann Arbor, MI, USA, 1982. [Google Scholar]
- Lemus, R. A general method to obtain vibrational symmetry adapted bases in a local scheme. Mol. Phys. 2003, 101, 2511–2528. [Google Scholar] [CrossRef]
- Crogman, H.T. A rotational energy surface study for low polyad structures of the general rovibrational Hamiltonian. Mol. Phys. 2010, 108, 705–721. [Google Scholar] [CrossRef]
- Crogman, H.T.; Harter, W.G. The emergence of a single frame and effects on quantum states and levels for rotor-rotor interactions. Proceedings of 59th Ohio State University International Symposium on Molecular Spectroscop, Ohio State University, Columbus, OH, USA, 21–24 June 2004. [Google Scholar]
- Hougen, J.T. Classification of rotational energy levels. II. J. Chem. Phys. 1971, 39, 358–365. [Google Scholar] [CrossRef]
- Alvarez-Bajo, O.; Lemus, R.; Carvajal, M.; Perez-Bernal, F. Equivalent rotations associated with the permutation inversion group revisited: Symmetry projection of the rotational functions of methane. Mol. Phys. 2011, 109, 797–812. [Google Scholar] [CrossRef]
- Lederer, C.M.; Hollander, J.M.; Perlman, I. Table of Isotopes, 6th ed.; Wiley: New York, NY, USA, 1967. [Google Scholar]
- Hougen, J.T.; Merer, A.J. Extended permutation-inversion groups for simultaneous treatment of the rovibronic states of trans-acetylene, cis-acetylene, and vinylidene. J. Mol. Spectrosc. 2011, 267, 200–221. [Google Scholar] [CrossRef]
- Harter, W.G. The Quantum Computer Age; University of Arkansas: Fayetteville, NC, USA, 2004. [Google Scholar]
- Harter, W.G. Principle of Symmetry, Dynamics & Spectroscopy; Wiley: New York, NY, USA, 1993. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).