Abstract
In the present paper we study subsolutions of the Dirac and Duffin–Kemmer–Petiau equations in the interacting case. It is shown that the Dirac equation in longitudinal external fields can be split into two covariant subequations (Dirac equations with built-in projection operators). Moreover, it is demonstrated that the Duffin–Kemmer–Petiau equations in crossed fields can be split into two 3 × 3 subequations. We show that all the subequations can be obtained via minimal coupling from the same 3 × 3 subequations which are thus a supersymmetric link between fermionic and bosonic degrees of freedom.
1. Introduction
Recently, several supersymmetric systems, concerned mainly with anyons in 2 + 1 dimensions [1,2,3,4,5] as well as with the 3 + 1 dimensional Majorana–Dirac–Staunton theory [6], uniting fermionic and bosonic fields, have been described. Furthermore, bosonic symmetries of the Dirac equation have been found in the massless [7] as well as in the massive case [8]. Our results derived lately fit into this broader picture. We have demonstrated that certain subsolutions of the free Duffin–Kemmer–Petiau (DKP) and the Dirac equations obey the same Dirac equation with some built-in projection operators [9]. We shall refer to this equation as supersymmetric since it has bosonic (spin 0 and 1) as well as fermionic 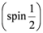 degrees of freedom. In the present paper we extend our results to the case of interacting fields.
degrees of freedom. In the present paper we extend our results to the case of interacting fields.
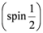 degrees of freedom. In the present paper we extend our results to the case of interacting fields.
degrees of freedom. In the present paper we extend our results to the case of interacting fields.The paper is organized as follows. In Section 2 relativistic wave equations as well as conventions and definitions used in the paper are described. In particular, several classical and not-so-classical subsolutions of the free Dirac equation are reviewed in Subsection 2.2. The notion of supersymmetry is invoked since some subequations arising in the context of the Dirac equation appear also in the Duffin–Kemmer–Petiau theory of massive bosons. In Section 3 the Dirac equation in longitudinal fields is split into two 3 × 3 subequations which can be written as two Dirac equations with built-in projection operators. In the next Section variables are separated in the subequations to yield 2D Dirac equations in 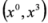 subspace and 2D Pauli equations in
subspace and 2D Pauli equations in 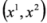 subspace. In Section 5 the Duffin–Kemmer–Petiau equation for spin 0 in crossed fields is split into two 3 × 3 subequations—these equations have the same structure as subequations arising in the Dirac theory. It follows that the free 3 × 3 equations provide a supersymmetric link between the Dirac and DKP theories—this is described in Section 6. In the last Section we discuss our results in a broader context of supersymmetry and Lorentz covariance.
subspace. In Section 5 the Duffin–Kemmer–Petiau equation for spin 0 in crossed fields is split into two 3 × 3 subequations—these equations have the same structure as subequations arising in the Dirac theory. It follows that the free 3 × 3 equations provide a supersymmetric link between the Dirac and DKP theories—this is described in Section 6. In the last Section we discuss our results in a broader context of supersymmetry and Lorentz covariance.
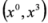 subspace and 2D Pauli equations in
subspace and 2D Pauli equations in 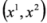 subspace. In Section 5 the Duffin–Kemmer–Petiau equation for spin 0 in crossed fields is split into two 3 × 3 subequations—these equations have the same structure as subequations arising in the Dirac theory. It follows that the free 3 × 3 equations provide a supersymmetric link between the Dirac and DKP theories—this is described in Section 6. In the last Section we discuss our results in a broader context of supersymmetry and Lorentz covariance.
subspace. In Section 5 the Duffin–Kemmer–Petiau equation for spin 0 in crossed fields is split into two 3 × 3 subequations—these equations have the same structure as subequations arising in the Dirac theory. It follows that the free 3 × 3 equations provide a supersymmetric link between the Dirac and DKP theories—this is described in Section 6. In the last Section we discuss our results in a broader context of supersymmetry and Lorentz covariance.2. Relativistic Wave Equations
In what follows tensor indices are denoted with Greek letters: μ = 0,1,2,3. We shall use the following convention for the Minkowski space-time metric tensor: gμv = diag (1,−1,−1,−1) and we shall always sum over repeated indices. For example, 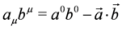 . Four-momentum operators are defined as
. Four-momentum operators are defined as 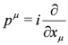 where natural units have been used: c = 1,
where natural units have been used: c = 1,  . The interaction will be introduced via minimal coupling,
. The interaction will be introduced via minimal coupling,
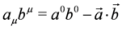 . Four-momentum operators are defined as
. Four-momentum operators are defined as 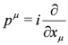 where natural units have been used: c = 1,
where natural units have been used: c = 1,  . The interaction will be introduced via minimal coupling,
. The interaction will be introduced via minimal coupling,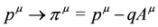
with a four-potential Aμ and a charge q. In what follows we shall work with external fields of special configuration, so-called crossed and longitudinal fields, non-standard but Lorentz covariant, see [10]. We shall also need elements of spinor calculus. Four-vectors 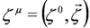 and spinors
and spinors 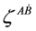 are related by the formula
are related by the formula 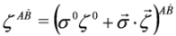 :
:
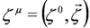 and spinors
and spinors 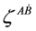 are related by the formula
are related by the formula 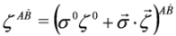 :
: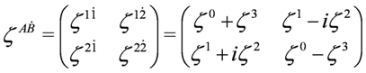
where 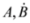 number rows and columns, respectively,
number rows and columns, respectively, 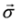 denotes vector built of the Pauli matrices and σ0 is the 2 × 2 unit matrix. Spinor with lowered indices
denotes vector built of the Pauli matrices and σ0 is the 2 × 2 unit matrix. Spinor with lowered indices 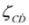 reads:
reads:
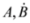 number rows and columns, respectively,
number rows and columns, respectively, 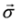 denotes vector built of the Pauli matrices and σ0 is the 2 × 2 unit matrix. Spinor with lowered indices
denotes vector built of the Pauli matrices and σ0 is the 2 × 2 unit matrix. Spinor with lowered indices 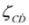 reads:
reads:
For details of the spinor calculus reader should consult [11,12,13].
2.1. The Dirac Equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by Paul Dirac in 1928 providing a description of elementary spin 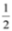 particles, such as electrons and quarks, consistent with both the principles of quantum mechanics and the theory of special relativity [14,15]. The Dirac Equation is [11,16,17]:
particles, such as electrons and quarks, consistent with both the principles of quantum mechanics and the theory of special relativity [14,15]. The Dirac Equation is [11,16,17]:
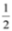 particles, such as electrons and quarks, consistent with both the principles of quantum mechanics and the theory of special relativity [14,15]. The Dirac Equation is [11,16,17]:
particles, such as electrons and quarks, consistent with both the principles of quantum mechanics and the theory of special relativity [14,15]. The Dirac Equation is [11,16,17]: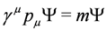
where m is the rest mass of the elementary particle. The γ’s are 4 × 4 anticommuting Dirac matrices: 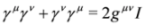 where I is the 4 × 4 unit matrix. In the spinor representation of the Dirac matrices we have:
where I is the 4 × 4 unit matrix. In the spinor representation of the Dirac matrices we have:
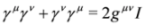 where I is the 4 × 4 unit matrix. In the spinor representation of the Dirac matrices we have:
where I is the 4 × 4 unit matrix. In the spinor representation of the Dirac matrices we have: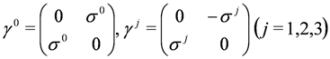
where σj are the Pauli matrices and σ0 is again the 2 × 2 unit matrix. The wave function is a bispinor, i.e., consists of 2 two-component spinors ξ, η: 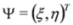 where T denotes transposition of a matrix. Sometimes it is more convenient to use the standard representation:
where T denotes transposition of a matrix. Sometimes it is more convenient to use the standard representation:
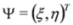 where T denotes transposition of a matrix. Sometimes it is more convenient to use the standard representation:
where T denotes transposition of a matrix. Sometimes it is more convenient to use the standard representation: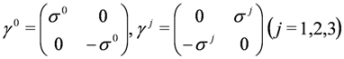
2.2. Subsolutions of the Dirac Equation and Supersymmetry
In the m = 0 case it is possible to obtain two independent equations for spinors ξ, η by application of projection operators 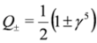 to Equation (4) since γ5 = −iγ0γ1γ2γ3 anticommutes with γμpμ:
to Equation (4) since γ5 = −iγ0γ1γ2γ3 anticommutes with γμpμ:
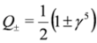 to Equation (4) since γ5 = −iγ0γ1γ2γ3 anticommutes with γμpμ:
to Equation (4) since γ5 = −iγ0γ1γ2γ3 anticommutes with γμpμ: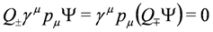
In the spinor representation of the Dirac matrices [11] we have γ5 = diag (−1,−1,1, 1) and thus 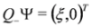 ,
, 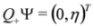 and separate equations for ξ, η follow:
and separate equations for ξ, η follow:
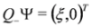 ,
, 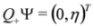 and separate equations for ξ, η follow:
and separate equations for ξ, η follow: 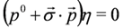
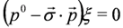
Equations (8) and (9) are known as the Weyl equations and are used to describe massless left-handed and right-handed neutrinos. However, since the experimentally established phenomenon of neutrino oscillations requires non-zero neutrino masses, theory of massive neutrinos, which can be based on the Dirac equation, is necessary [18,19,20,21]. Alternatively, a modification of the Dirac or Weyl equation, called the Majorana equation, is thought to apply to neutrinos. According to Majorana theory, neutrino and antineutrino are identical and neutral [22].
Although the Majorana equations can be introduced without any reference to the Dirac theory, they are subsolutions of the Dirac Equation [18]. Indeed, demanding in Equation (4) that 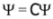 where C is the charge conjugation operator,
where C is the charge conjugation operator, 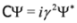 , we obtain in the spinor representation
, we obtain in the spinor representation 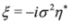 ,
, 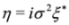 and the Dirac Equation (4) reduces to two separate Majorana equations for two-component spinors:
and the Dirac Equation (4) reduces to two separate Majorana equations for two-component spinors:
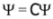 where C is the charge conjugation operator,
where C is the charge conjugation operator, 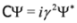 , we obtain in the spinor representation
, we obtain in the spinor representation 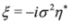 ,
, 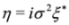 and the Dirac Equation (4) reduces to two separate Majorana equations for two-component spinors:
and the Dirac Equation (4) reduces to two separate Majorana equations for two-component spinors: 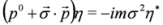
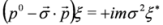
It follows from the condition 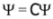 that Majorana particle has zero charge built-in condition. The problem whether neutrinos are described by the Dirac equation or the Majorana equations is still open [18,19,20,21].
that Majorana particle has zero charge built-in condition. The problem whether neutrinos are described by the Dirac equation or the Majorana equations is still open [18,19,20,21].
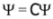 that Majorana particle has zero charge built-in condition. The problem whether neutrinos are described by the Dirac equation or the Majorana equations is still open [18,19,20,21].
that Majorana particle has zero charge built-in condition. The problem whether neutrinos are described by the Dirac equation or the Majorana equations is still open [18,19,20,21].Let us note that the Dirac Equation (4) in the spinor representation of the γμ matrices can be also separated in form of second-order Equations:
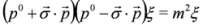
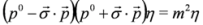
Such equations, valid also in the interacting case, were used by Feynman and Gell-Mann to describe weak decays in terms of two-component spinors [23].
More exotic subsolutions of the Dirac equation, related to supersymmetry, are also possible. In the massless case Simulik and Krivsky demonstrated that the following substitution,
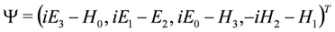
when introduced into the Dirac Equation (4), converts it for m = 0 and standard representation of the Dirac matrices Equation (6) into the set of Maxwell equations [7]. In the massive case the Dirac Equation (4) can be written as a set of two Equations:
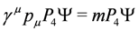
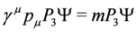
with P4 = diag (1,1,1,0), P3 = diag (1,1,0,1) and spinor representation of the γμ matrices Equation (5). Equations analogous to (15,16) appear also in the Duffin–Kemmer–Petiau theory of massive bosons [9].
Let us note finally that as shown in [24] the square of the Dirac operator is indeed supersymmetric, and this can be used for a convenient description of fluctuations around a self-dual monopole. Similar behavior has also been observed in the Taub-NUT case, see [25].
2.3. The Duffin–Kemmer–Petiau Equations
The DKP equations for spin 0 and 1 are written as:
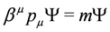
with 5 × 5 and 10 × 10 matrices βμ, respectively, which fulfill the following commutation relations [26,27,28,29]:
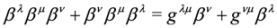
In the case of 5 × 5 (spin 0) representation of βμ matrices Equation (17) is equivalent to the following set of equations:
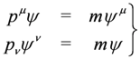
if we define Ψ in Equation (17) as:
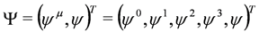
Let us note that Equation (19) can be obtained by factorizing second-order derivatives in the Klein–Gordon equation 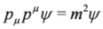 .
.
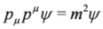 .
.In the case of 10 × 10 (spin 1) representation of matrices βμ Equation (17) reduces to:
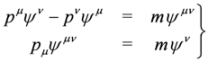
with Ψ in Equation (17) defined as  :
:
 :
: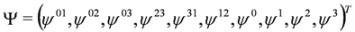
Where Ψλ are real and Ψμν are purely imaginary (in alternative formulation we have 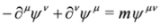 ,
, 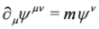 , where Ψλ, Ψμν are real). Because of antisymmetry of Ψμν we have pνΨν = 0what implies spin 1 condition. The set of Equation (21) was first written by Proca [30,31] and in a different context by Lanczos, see [32] and references therein. More on the history of the formalism of Duffin, Kemmer and Petiau can be found in [33].
, where Ψλ, Ψμν are real). Because of antisymmetry of Ψμν we have pνΨν = 0what implies spin 1 condition. The set of Equation (21) was first written by Proca [30,31] and in a different context by Lanczos, see [32] and references therein. More on the history of the formalism of Duffin, Kemmer and Petiau can be found in [33].
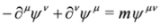 ,
, 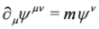 , where Ψλ, Ψμν are real). Because of antisymmetry of Ψμν we have pνΨν = 0what implies spin 1 condition. The set of Equation (21) was first written by Proca [30,31] and in a different context by Lanczos, see [32] and references therein. More on the history of the formalism of Duffin, Kemmer and Petiau can be found in [33].
, where Ψλ, Ψμν are real). Because of antisymmetry of Ψμν we have pνΨν = 0what implies spin 1 condition. The set of Equation (21) was first written by Proca [30,31] and in a different context by Lanczos, see [32] and references therein. More on the history of the formalism of Duffin, Kemmer and Petiau can be found in [33].3. Splitting the Dirac Equation in Longitudinal External Fields
The interaction is introduced into the Dirac Equation (4) via minimal coupling Equation (1). We consider a special class of four-potentials obeying the condition:
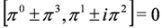
where 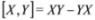 is a commutator. The condition Equation (23) is fulfilled in the Abelian case for
is a commutator. The condition Equation (23) is fulfilled in the Abelian case for
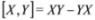 is a commutator. The condition Equation (23) is fulfilled in the Abelian case for
is a commutator. The condition Equation (23) is fulfilled in the Abelian case for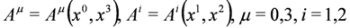
This is the case of longitudinal potentials for which several exact solutions of the Dirac equation were found [10].
The Dirac Equation (4) can be written in spinor notation as [11]:
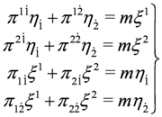
where 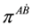 ,
, 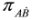 are given by Equations (2) and (3) (note that
are given by Equations (2) and (3) (note that 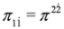 ,
,  ,
, 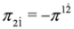 ,
,  ). Obviously, due to relations between components of
). Obviously, due to relations between components of 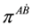 and
and 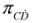 the Equation (25) can be rewritten in terms of components of
the Equation (25) can be rewritten in terms of components of 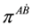 only. Equation (25) corresponds to Equation (4) in the spinor representation of γ matrices and
only. Equation (25) corresponds to Equation (4) in the spinor representation of γ matrices and 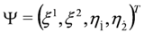 . We assume here that we deal with four-potentials fulfilling condition Equation (23).
. We assume here that we deal with four-potentials fulfilling condition Equation (23).
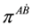 ,
, 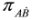 are given by Equations (2) and (3) (note that
are given by Equations (2) and (3) (note that 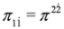 ,
,  ,
, 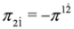 ,
,  ). Obviously, due to relations between components of
). Obviously, due to relations between components of 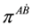 and
and 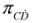 the Equation (25) can be rewritten in terms of components of
the Equation (25) can be rewritten in terms of components of 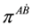 only. Equation (25) corresponds to Equation (4) in the spinor representation of γ matrices and
only. Equation (25) corresponds to Equation (4) in the spinor representation of γ matrices and 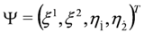 . We assume here that we deal with four-potentials fulfilling condition Equation (23).
. We assume here that we deal with four-potentials fulfilling condition Equation (23).In this Section we shall investigate a possibility of finding subsolutions of the Dirac equation in longitudinal external field, analogous to subsolutions found for the free Dirac equation in ([9]). For m ≠ 0 we can define new quantities:
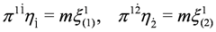
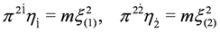
where we have:
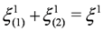
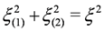
In spinor notation 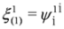 ,
, 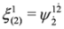 ,
, 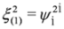 ,
, 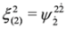 .
.
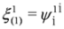 ,
, 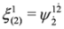 ,
, 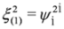 ,
, 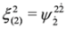 .
.The Dirac Equation (25) can be now written with help of Equations (26) and (27) as (we are now using components 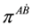 throughout):
throughout):
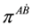 throughout):
throughout):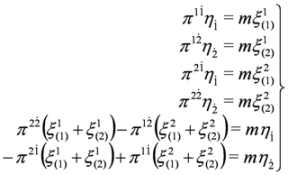
It follows from Equations (26) and (27) and Equation (23) that the following identities hold:
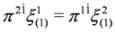
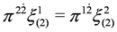
Taking into account the identities Equations (31) and (32) we can decouple Equation (30) and write it as a system of the following two Equations:
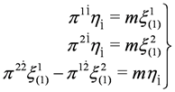
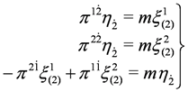
System of Equations (33) and (34) is equivalent to the Dirac Equation (25) if the definitions Equations (28) and (29) are invoked.
Due to the identities, Equations (31–34) can be cast into form:
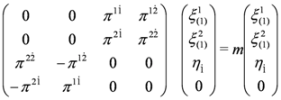
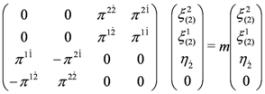
Let us consider Equation (35). It can be written as:
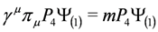
where P4 is the projection operator, P4 = diag (1,1,1,0) in the spinor representation of the Dirac matrices and 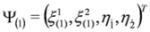 . There are also other projection operators which lead to analogous three component equations, P1= diag (0,1,1,1), P2= diag (1,0,1,1), P3= diag (1,1,0,1). Acting from the left on Equation (37) with P4 and (1−P4)we obtain two Equations:
. There are also other projection operators which lead to analogous three component equations, P1= diag (0,1,1,1), P2= diag (1,0,1,1), P3= diag (1,1,0,1). Acting from the left on Equation (37) with P4 and (1−P4)we obtain two Equations:
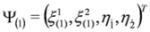 . There are also other projection operators which lead to analogous three component equations, P1= diag (0,1,1,1), P2= diag (1,0,1,1), P3= diag (1,1,0,1). Acting from the left on Equation (37) with P4 and (1−P4)we obtain two Equations:
. There are also other projection operators which lead to analogous three component equations, P1= diag (0,1,1,1), P2= diag (1,0,1,1), P3= diag (1,1,0,1). Acting from the left on Equation (37) with P4 and (1−P4)we obtain two Equations: 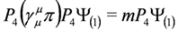
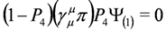
In the spinor representation of γμ matrices, Equation (38) is equivalent to Equation (33) while Equation (39) is equivalent to the identity Equation (31), respectively. The operator P4 can be written as 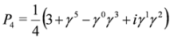 where γ5 = iγ0γ1γ2γ3 (similar formulae can be given for other projection operators P1, P2, P3, see [13] where another convention for γμ matrices was however used). It thus follows that Equation (37) is given representation independent form and is Lorentz covariant (in [9] subsolutions of form Equation (37) were obtained for the free Dirac equation).
where γ5 = iγ0γ1γ2γ3 (similar formulae can be given for other projection operators P1, P2, P3, see [13] where another convention for γμ matrices was however used). It thus follows that Equation (37) is given representation independent form and is Lorentz covariant (in [9] subsolutions of form Equation (37) were obtained for the free Dirac equation).
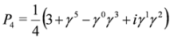 where γ5 = iγ0γ1γ2γ3 (similar formulae can be given for other projection operators P1, P2, P3, see [13] where another convention for γμ matrices was however used). It thus follows that Equation (37) is given representation independent form and is Lorentz covariant (in [9] subsolutions of form Equation (37) were obtained for the free Dirac equation).
where γ5 = iγ0γ1γ2γ3 (similar formulae can be given for other projection operators P1, P2, P3, see [13] where another convention for γμ matrices was however used). It thus follows that Equation (37) is given representation independent form and is Lorentz covariant (in [9] subsolutions of form Equation (37) were obtained for the free Dirac equation).Let us note finally that Equation (36) can be alternatively written as

where 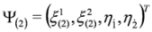 ,
, 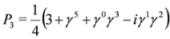 , note that
, note that 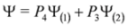 .
.
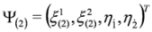 ,
, 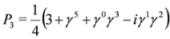 , note that
, note that 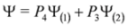 .
.4. Separation of Variables in Subequations
It is possible to separate variables in Equations (33) and (34) following procedures described in [10]. Substituting 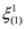 and
and 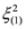 from the first two equations into the third in Equation (33) we get:
from the first two equations into the third in Equation (33) we get:
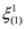 and
and 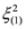 from the first two equations into the third in Equation (33) we get:
from the first two equations into the third in Equation (33) we get: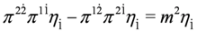
Taking into account definition of 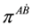 and property Equation (24) we obtain:
and property Equation (24) we obtain:
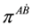 and property Equation (24) we obtain:
and property Equation (24) we obtain: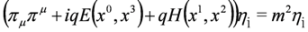
where 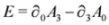 ,
, 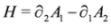 .
.
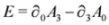 ,
, 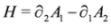 .
.To achieve separation of variables we put:
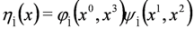
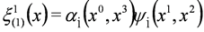
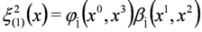
We now substitute Equation (43) into Equation (42) to get:
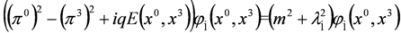
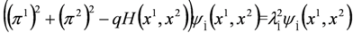
where 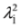 is the separation constant and we note that Equations (46a) and (46b) are analogous to Equations (12.15) and (12.19) in [10].
is the separation constant and we note that Equations (46a) and (46b) are analogous to Equations (12.15) and (12.19) in [10].
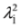 is the separation constant and we note that Equations (46a) and (46b) are analogous to Equations (12.15) and (12.19) in [10].
is the separation constant and we note that Equations (46a) and (46b) are analogous to Equations (12.15) and (12.19) in [10].Combining now Equation (46a) with the first of Equation (33) and rescaling, 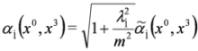 , we obtain 2D Dirac Equation:
, we obtain 2D Dirac Equation:
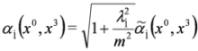 , we obtain 2D Dirac Equation:
, we obtain 2D Dirac Equation: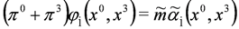

with effective mass 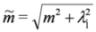 .
.
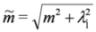 .
.On the other hand, combining Equation (46b) with the second of Equation (33) we get equations:
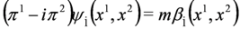
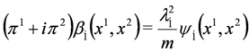
which can be written as the Pauli Equation:

The same procedure applied to Equation (34) yields the equation for 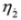 :
:
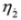 :
: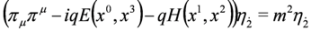
Carrying out separation of variables we get 2D Dirac Equation:
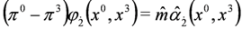
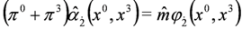
with effective mass 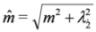 and
and 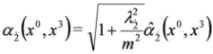 and equation:
and equation:
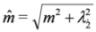 and
and 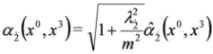 and equation:
and equation: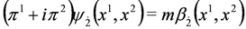
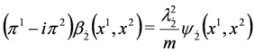
which is written as the Pauli Equation
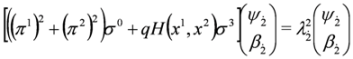
where the following definitions were used:
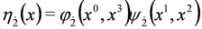
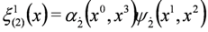
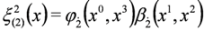
5. Splitting the Spin 0 Duffin–Kemmer–Petiau Equations in Crossed Fields
We introduce interaction into DKP Equation (19) via minimal coupling Equation (1). We consider four-potentials obeying the condition:
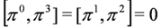
The condition Equation (57) means that 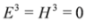 and is fulfilled by crossed fields [10]:
and is fulfilled by crossed fields [10]:
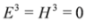 and is fulfilled by crossed fields [10]:
and is fulfilled by crossed fields [10]: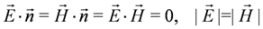
with 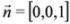 .
.
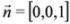 .
.Equation (19) in the interacting case can be written within spinor formalism (cf. Equations (2) and (3)) as:
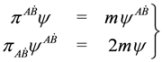
Indeed, it follows from Equation (59) that 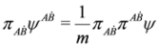 and
and 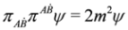 . We have
. We have 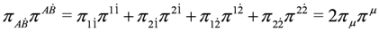 and the Klein–Gordon Equation
and the Klein–Gordon Equation 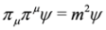 follows.
follows.
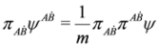 and
and 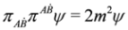 . We have
. We have 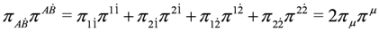 and the Klein–Gordon Equation
and the Klein–Gordon Equation 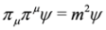 follows.
follows.Let us note now that for fields obeying Equation (57), the following spinor identities hold:
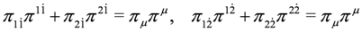
Due to identities Equation (60) we can split the last of Equation (59) and write Equation (59) as a set of two equations:
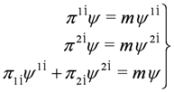
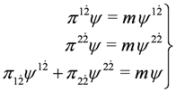
each of which describes particle with mass m (we check this by substituting e.g. 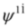 ,
, 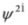 or
or 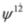 ,
, 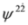 into the third equations). Equation (59) and the set of two Equations (61) and (62) are equivalent. We described Equations (61) and (62) in non-interacting case in [34,35]. Equations (61) and (62) and Equations (33) and (34) have the same structure (recall that
into the third equations). Equation (59) and the set of two Equations (61) and (62) are equivalent. We described Equations (61) and (62) in non-interacting case in [34,35]. Equations (61) and (62) and Equations (33) and (34) have the same structure (recall that 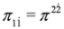 ,
,  ,
, 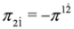 ,
,  ). However these equations cannot be written in the form of the Dirac Equations (35) and (36) because identities analogous to Equations (31) and (32) do not hold, i.e.,
). However these equations cannot be written in the form of the Dirac Equations (35) and (36) because identities analogous to Equations (31) and (32) do not hold, i.e., 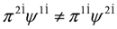 ,
, 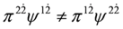 .
.
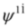 ,
, 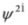 or
or 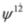 ,
, 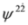 into the third equations). Equation (59) and the set of two Equations (61) and (62) are equivalent. We described Equations (61) and (62) in non-interacting case in [34,35]. Equations (61) and (62) and Equations (33) and (34) have the same structure (recall that
into the third equations). Equation (59) and the set of two Equations (61) and (62) are equivalent. We described Equations (61) and (62) in non-interacting case in [34,35]. Equations (61) and (62) and Equations (33) and (34) have the same structure (recall that 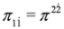 ,
,  ,
, 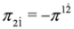 ,
,  ). However these equations cannot be written in the form of the Dirac Equations (35) and (36) because identities analogous to Equations (31) and (32) do not hold, i.e.,
). However these equations cannot be written in the form of the Dirac Equations (35) and (36) because identities analogous to Equations (31) and (32) do not hold, i.e., 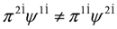 ,
, 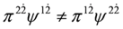 .
.Substituting first two equations into the third one in Equation (61), we get the Klein–Gordon equation 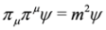 , which can be solved via separation of variables for the case of crossed fields, see Chapter 3 in [10] (the same can be done in Equation (62)).
, which can be solved via separation of variables for the case of crossed fields, see Chapter 3 in [10] (the same can be done in Equation (62)).
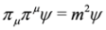 , which can be solved via separation of variables for the case of crossed fields, see Chapter 3 in [10] (the same can be done in Equation (62)).
, which can be solved via separation of variables for the case of crossed fields, see Chapter 3 in [10] (the same can be done in Equation (62)).6. A Supersymmetric Link between Dirac and DKP Theories
We have shown that subsolutions of the Dirac equation as well as of the DKP equations for spin 0 obey analogous pairs of 3 × 3 Equations (33–62), respectively.
More exactly, Equations (33) and (34) can be written as:
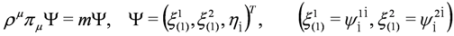
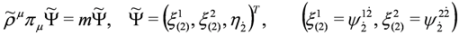
with
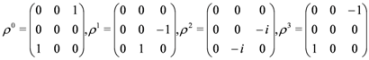
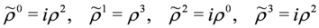
and πμ = pμ − qAμ, Aμ obeying condition of longitudinality Equation (23).
On the other hand, Equations (61) and (62) can be written in analogous form:
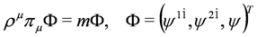
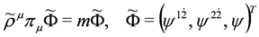
with the same matrices ρμ, 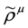 , cf. Equations (65) and (66), and πμ = pμ − qAμ, Aμ obeying condition Equation (57)—fulfilled by crossed fields.
, cf. Equations (65) and (66), and πμ = pμ − qAμ, Aμ obeying condition Equation (57)—fulfilled by crossed fields.
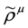 , cf. Equations (65) and (66), and πμ = pμ − qAμ, Aμ obeying condition Equation (57)—fulfilled by crossed fields.
, cf. Equations (65) and (66), and πμ = pμ − qAμ, Aμ obeying condition Equation (57)—fulfilled by crossed fields.It thus follows that the 3 × 3 free equations described in [34,35]:
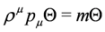
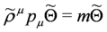
provide a link between solutions of the Dirac and DKP equations. Namely, Equations (69) and (70) in the interacting case, pμ → πμ = pμ − qAμ, lead to subsolutions of the Dirac Equations (63) and (64) in the case of longitudinal fields Equation (23), while for crossed fields Equation (57) yield DKP subsolutions Equations (67) and (68).
7. Discussion
We have shown that the Dirac equation in longitudinal external fields is equivalent to a pair of 3 × 3 subequations (33) and (34) which can be further written as Dirac equations with built-in projection operators, Equations (37) and (40). Furthermore, we have demonstrated that the Duffin–Kemmer–Petiau equations for spin 0 in crossed fields can be split into two 3 × 3 subequations (61) and (62) (subequations of the DKP equations for spin 1 were discussed in [36]). It was also shown that all the subequations can be obtained via minimal coupling from the same 3 × 3 subequations (69) and (70), which are thus a supersymmetric link between fermionic and bosonic degrees of freedom. It can be expected that for a combination of crossed and longitudinal potentials these subequations should describe interaction of fermionic and bosonic degrees of freedom. We shall investigate this problem in our future work.
Finally, we shall address problem of Lorentz covariance of the subequations. Let us have a closer look at a single subequation of spin 0 DKP equation, say Equation (67). Although both equations, Equation (67) and (68), are covariant as a whole, this subequation alone is not Lorentz covariant. Moreover, it cannot be written as manifestly covariant Dirac equation, cf. the end of Section 5. There is however another possibility of introducing full covariance. Let us consider left and right eigenvectors of the operator ρμπμ:
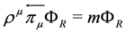
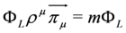
where symbols 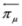 ,
, 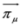 mean action of
mean action of 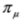 to the right or to the left, respectively (left solutions are actually used in the Dirac theory, where they are denoted as
to the right or to the left, respectively (left solutions are actually used in the Dirac theory, where they are denoted as 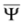 , they are however related to the right solutions by the formula
, they are however related to the right solutions by the formula 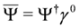 (symbol † denotes Hermitian conjugation) [11]).
(symbol † denotes Hermitian conjugation) [11]).
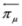 ,
, 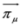 mean action of
mean action of 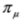 to the right or to the left, respectively (left solutions are actually used in the Dirac theory, where they are denoted as
to the right or to the left, respectively (left solutions are actually used in the Dirac theory, where they are denoted as 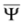 , they are however related to the right solutions by the formula
, they are however related to the right solutions by the formula 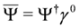 (symbol † denotes Hermitian conjugation) [11]).
(symbol † denotes Hermitian conjugation) [11]).It turns out that Equation (71), with 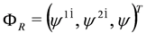 and
and  , are equivalent to Equations (61) and (62) respectively
, are equivalent to Equations (61) and (62) respectively 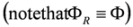 and involve components of the whole spinor
and involve components of the whole spinor 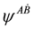 since
since 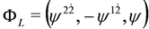 . The same analysis applies to Equation (68), i.e.,
. The same analysis applies to Equation (68), i.e., 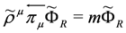 ,
, 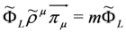 and
and 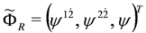 ,
, 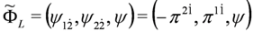 (note that
(note that 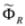 and
and 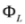 , as well as
, as well as 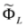 and
and 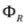 are algebraically related).
are algebraically related).
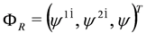 and
and  , are equivalent to Equations (61) and (62) respectively
, are equivalent to Equations (61) and (62) respectively 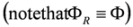 and involve components of the whole spinor
and involve components of the whole spinor 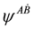 since
since 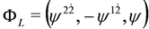 . The same analysis applies to Equation (68), i.e.,
. The same analysis applies to Equation (68), i.e., 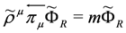 ,
, 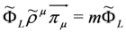 and
and 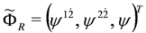 ,
, 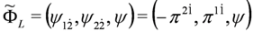 (note that
(note that 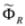 and
and 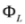 , as well as
, as well as 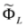 and
and 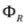 are algebraically related).
are algebraically related).We shall now discuss problem of Lorentz covariance of subequations of the Dirac equation, Equations (63) and (64). Let first note that Equations (69) and (70), as well as Equations (63) and (64), can be written in covariant form as the Dirac equation with one zero component as Equations (15,16,37,40), respectively. However, solutions of Equations (63) and (64) do not involve the whole spinor 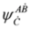 . We might consider left eigensolutions of the operator
. We might consider left eigensolutions of the operator 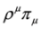 again but this does not change the picture—Equations (63) and (64) involve components
again but this does not change the picture—Equations (63) and (64) involve components 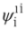 ,
, 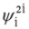 ,
, 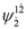 ,
,  only as well as the whole spinor
only as well as the whole spinor 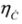 . It follows that in Equations (63) and (64) we deal with Lorentz symmetry breaking—a hypothetical phenomenon considered in some extensions of the Standard Model [37,38,39].
. It follows that in Equations (63) and (64) we deal with Lorentz symmetry breaking—a hypothetical phenomenon considered in some extensions of the Standard Model [37,38,39].
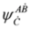 . We might consider left eigensolutions of the operator
. We might consider left eigensolutions of the operator 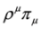 again but this does not change the picture—Equations (63) and (64) involve components
again but this does not change the picture—Equations (63) and (64) involve components 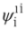 ,
, 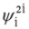 ,
, 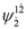 ,
,  only as well as the whole spinor
only as well as the whole spinor 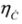 . It follows that in Equations (63) and (64) we deal with Lorentz symmetry breaking—a hypothetical phenomenon considered in some extensions of the Standard Model [37,38,39].
. It follows that in Equations (63) and (64) we deal with Lorentz symmetry breaking—a hypothetical phenomenon considered in some extensions of the Standard Model [37,38,39].References
- Jackiw, R.; Nair, V.P. Relativistic wave equation for anyons. Phys. Rev. D 1991, 43, 1933–1942. [Google Scholar] [CrossRef]
- Plyushchay, M. Fractional spin: Majorana-Dirac field. Phys. Lett. B 1991, 273, 250–254. [Google Scholar] [CrossRef]
- Horváthy, P.; Plyushchay, M.; Valenzuela, M. Bosons, fermions and anyons in the plane, and supersymmetry. Ann. Phys. 2010, 325, 1931–1975. [Google Scholar] [CrossRef]
- Horváthy, P.A.; Plyushchay, M.S.; Valenzuela, M. Supersymmetry between Jackiw–Nair and Dirac–Majorana anyons. Phys. Rev. D 2010, 81. [Google Scholar] [CrossRef]
- Horváthy, P.; Plyushchay, M.; Valenzuela, M. Supersymmetry of the planar Dirac–Deser–Jackiw–Templeton system and of its nonrelativistic limit. J. Math. Phys. 2010, 51. [Google Scholar] [CrossRef]
- Horváthy, P.; Plyushchay, M.; Valenzuela, M. Bosonized supersymmetry from the Majorana–Dirac–Staunton theory and massive higher-spin fields. Phys. Rev. D 2008, 77. [Google Scholar] [CrossRef]
- Simulik, V.; Krivsky, I. Bosonic symmetries of the massless Dirac equation. Adv. Appl. Clifford Algebr. 1998, 8, 69–82. [Google Scholar] [CrossRef]
- Simulik, V.; Krivsky, I. Bosonic symmetries of the Dirac equation. Phys. Lett. A 2011, 375, 2479–2483. [Google Scholar] [CrossRef]
- Okninski, A. Supersymmetric content of the Dirac and Duffin–Kemmer–Petiau equations. Int. J. Theor. Phys. 2011, 50, 729–736. [Google Scholar] [CrossRef]
- Bagrov, V.; Gitman, D. Exact Solutions of Relativistic Wave Equations; Springer: Berlin, Germany, 1990; Volume 39. [Google Scholar]
- Berestetskii, V.; Lifshitz, E.; Pitaevskii, V. Relativistic Quanturn Theory, Part 1; McGraw-Hill Science: New York, NY, USA, 1971. [Google Scholar]
- Misner, C.; Thorne, K.; Wheeler, J. Gravitation; WH Freeman Co.: New York, NY, USA, 1973. [Google Scholar]
- Corson, E. Theory of Tensors, Spinors, and Wave Equations; Blackie: London, UK, 1953. [Google Scholar]
- Dirac, P. The quantum theory of the electron. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1928, 117, 610–624. [Google Scholar] [CrossRef]
- Dirac, P. The quantum theory of the electron. Part II. Proc. R. Soc. Lond. Ser. A 1928, 118, 351–361. [Google Scholar] [CrossRef]
- Bjorken, J.; Drell, S. Relativistic Quantum Mechanics; McGraw-Hill: New York, NY, USA, 1964; Volume 3. [Google Scholar]
- Thaller, B. The Dirac Equation; Springer-Verlag: New York, NY, USA, 1992. [Google Scholar]
- Zralek, M. On the possibilities of distinguishing dirac from majorana neutrinos. Acta Phys. Pol. B 1997, 28, 2225–2257. [Google Scholar]
- Perkins, D. Introduction to High Energy Physics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Fukugita, M.; Yanagida, T. Physics of Neutrinos and Applications to Astrophysics; Springer Verlag: Berlin, Germany, 2003. [Google Scholar]
- Szafron, R.; Zralek, M. Can we distinguish dirac and majorana neutrinos produced in muon decay? Acta Phys. Pol. B 2009, 40, 3041–3047. [Google Scholar]
- Majorana, E. Teoria simmetrica dell’elettrone e del positrone. Il Nuovo Cimento (1924–1942) 1937, 14, 171–184. [Google Scholar] [CrossRef]
- Feynman, R.; Gell-Mann, M. Theory of the Fermi interaction. Phys. Rev. 1958, 109, 193–198. [Google Scholar] [CrossRef]
- Horvathy, P.; Feher, L.; O’Raifeartaigh, L. Applications of chiral supersymmetry for spin fields in selfdual backgrounds. Int. J. Mod. Phys. 1989, A4, 5277–5285. [Google Scholar]
- Comtet, A.; Horvathy, P. The Dirac equation in Taub-NUT space. Phys. Lett. B 1995, 349, 49–56. [Google Scholar] [CrossRef]
- Duffin, R. On the characteristic matrices of covariant systems. Phys. Rev. 1938, 54. [Google Scholar] [CrossRef]
- Kemmer, N. The particle aspect of meson theory. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1939, 173, 91–116. [Google Scholar] [CrossRef]
- Kemmer, N. The Algebra of Meson Matrices. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1943; 39, pp. 189–196. [Google Scholar]
- Petiau, G. Contribution a la théorie des équations d’ondes corpusculaires. Acad. R. Belg. Classe Sci. Mem. 1936, 16, 1–136. [Google Scholar]
- Proca, A. Wave theory of positive and negative electrons. J. Phys. Radium 1936, 7, 347–353. [Google Scholar] [CrossRef]
- Proca, A. Sur les equations fondamentales des particules elementaires. Comp. Ren. Acad. Sci. Paris 1936, 202, 1366–1368. [Google Scholar]
- Lanczos, C. Die erhaltungssätze in der feldmäßigen darstellung der diracschen theorie. Zeitschrift Phys. Hadron. Nuclei 1929, 57, 484–493. [Google Scholar]
- Bogush, A.; Kisel, V.; Tokarevskaya, N.; Red’kov, V. Duffin–Kemmer–Petiau formalism reexamined: Non-relativistic approximation for spin 0 and spin 1 particles in a Riemannian space-time. Ann. Fond. Louis Broglie 2007, 32, 355–381. [Google Scholar]
- Okninski, A. Effective quark equations. Acta Phys. Pol. B 1981, 12, 87–94. [Google Scholar]
- Okninski, A. Dynamic theory of quark and meson fields. Phys. Rev. D 1982, 25, 3402–3407. [Google Scholar] [CrossRef]
- Okninski, A. Splitting the Kemmer–Duffin–Petiau equations. Available online: http://arxiv.org/pdf/math-ph/0309013v1.pdf (accessed on 30 July 2012).
- Colladay, D.; Kostelecký, V.A. CPT violation and the standard model. Phys. Rev. D 1997, 55, 6760–6774. [Google Scholar]
- Visser, M. Lorentz symmetry breaking as a quantum field theory regulator. Phys. Rev. D 2009, 80. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Russell, N. Data tables for Lorentz and CPT violation. Rev. Mod. Phys. 2011, 83, 11–31. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).