Abstract
Using an x-y-z coordinate system, the equations of the superspheres have been extended to describe intermediate shapes between a sphere and various convex polyhedra. Near-polyhedral shapes composed of {100}, {111} and {110} surfaces with round edges are treated in the present study, where {100}, {111} and {110} are the Miller indices of crystals with cubic structures. The three parameters p, a and b are included to describe the {100}-{111}-{110} near-polyhedral shapes, where p describes the degree to which the shape is a polyhedron and a and b determine the ratios of the {100}, {111} and {110} surfaces.
1. Introduction
Small crystalline precipitates often form in alloys and have near-polyhedral shapes with round edges. Figure 1 is a transmission electron micrograph showing an example of this where the dark regions, which have shapes between a circle and a square, are Co-Cr alloy particles precipitated in a Cu matrix [1,2]. Why such precipitate shapes form has been explained by the anisotropies of physical properties of metals and alloys originating from the crystal structures [2,3]. Both the Co-Cr alloy particles and Cu matrix have cubic structures. The three-dimensional shapes of the particles shown in Figure 1 are intermediate between a sphere and a cube composed of crystallographic planes {100} as indicated by the Miller indices.
Even if the alloy system such as the Co-Cr alloy particles in the Cu matrix is fixed, the precipitate shapes change as a function of the precipitate size [1,2]. In the case of the Co-Cr alloy precipitates, the spherical to cubical shape transition occurs as the precipitate size increases [2,3]. The size dependence of the precipitate’s equilibrium shape determines the shape transitions [2,3]. When we discuss such physical phenomenon, it is convenient to use simple equations that can approximate the precipitate shapes [2,3,4,5]. In the present study, we discuss a simple equation that gives shapes intermediate between a sphere and various polyhedra.

Figure 1.
Transmission electron micrograph showing the Co-Cr alloy precipitates in a Cu matrix [1,2].
2. Cubic Superspheres
The solid figure described by
 (1)
(1)expresses a sphere with radius R when p = 2 and a cube with edges 2R as p → ∞ [2,3,4]. It is reported in [6] that the 19th century French mathematician Gabriel Lamé first presented this equation. Intermediate shapes between these two limits can be represented by choosing the appropriate value of p > 2. In [2,3,4], such shapes are called superspheres, and Figure 2 shows the shapes given by (1) for (a) p = 2, (b) p = 4 and (c) p = 20. The parameter R determines the size and p determines the polyhedrality, i.e., the degree to which the supersphere is polyhedron. If |x| > |y| and |x| > |z|, |x/R|p + |y/R|p + |z/R|p= 1 as p → ∞ means |x/R| = 1. This describes the limit for (1) as p → ∞ which gives a cube surrounded by three sets of parallel planes, x = ± R, y = ± R and z = ± R.
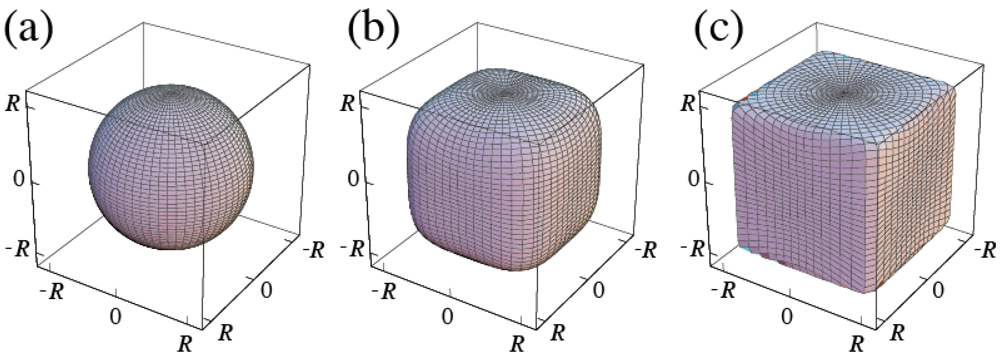
Figure 2.
Shapes of the cubic superspheres given by (1); (a) p = 2; (b) p = 4 and (c) p = 20.
3. {111} Regular-Octahedral and {110} Rhombic-Dodecahedral Superspheres
Equation (1) can be rewritten as
 (2)
(2)This expression has been extended to describe other convex polyhedra [7]. Although the original superspheres discussed in [2,3,4] are intermediate shapes between a sphere and a cube, now the superspheres can refer to shapes intermediate between various convex polyhedra and a sphere [8].
Superspheres have been used to discuss the shapes of small crystalline particles and precipitates [2,3,5,8,9]. The planes of crystal facets are indicated by their Miller indices. We use this notation in the present study. The cube given by (2) as p → ∞ is the {100} cube composed of six {100} faces. Assuming crystals with cubic structures, the regular octahedron is the {111} octahedron and the rhombic dodecahedron is the {110} dodecahedron [7].
The {111} octahedral superspheres are given by the following equation:
 (3a)
(3a)where
 (3b)
(3b)The shapes given by (3) are shown in Figure 3.
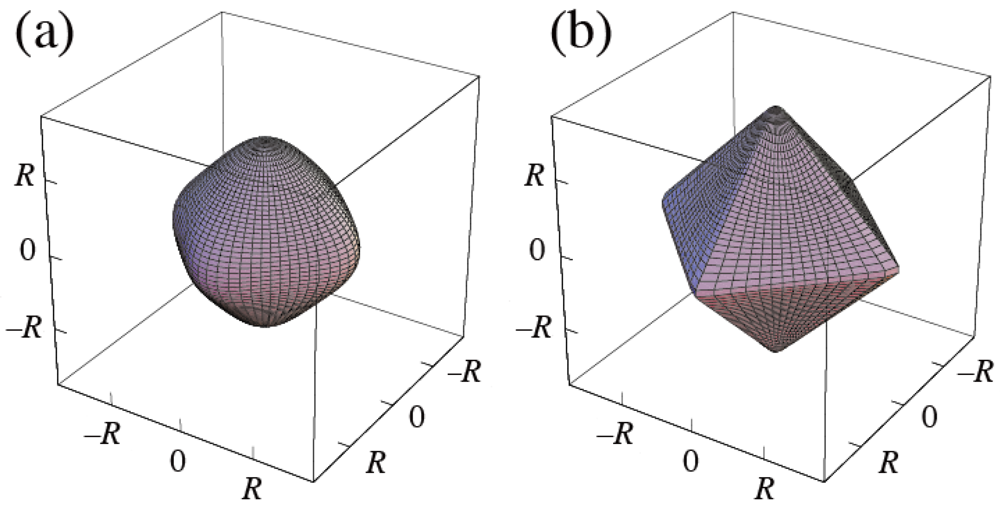
Figure 3.
Shapes of the {111} regular-octahedral superspheres given by (3); (a) p = 4 and (b) p = 40.
On the other hand, the {110} dodecahedral superspheres are given by
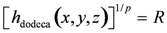 (4a)
(4a)where
 (4b)
(4b)The shapes given by (4) are shown in Figure 4. Equations (2–4) expressed by the spherical coordinate system are shown in [7].
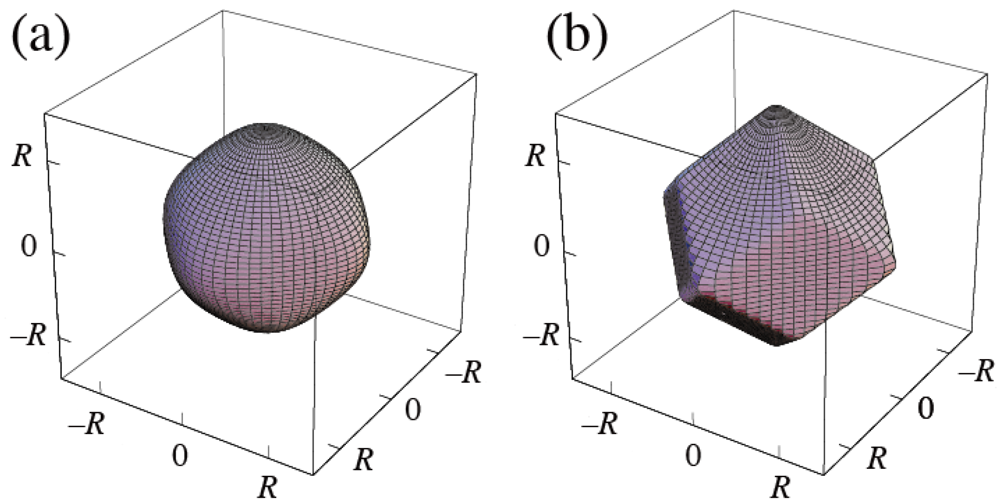
Figure 4.
Shapes of the {110} rhombic-dodecahedral superspheres given by (4); (a) p = 6 and (b) p = 40.
4. {100}-{111}-{110} Polyhedral Superspheres
Combined superspheres can be expressed by combining the equations of each supersphere. Combining (2), (3) and (4), we get
 (5)
(5)The parameters a > 0 and b > 0 are those for determining the ratios of the {100}, {110} and {111} surfaces. The shapes of the supersphere given by (5) are shown in Figure 5 when  ,
,  for two values of p.
for two values of p.
 ,
,  for two values of p.
for two values of p. 
Figure 5.
Shapes of the {100}-{111}-{110} polyhedral superspheres given by (5); (a) p = 20 and (b) p = 100.
The a and b dependences of the shapes given by (5) are understood by examining the polyhedral shapes as p → ∞. Among the three polyhedra given by [hcube (x,y,z)]1/p = R, [hocta (x,y,z)]1/p = aR and [hdodeca (x,y,z)]1/p = bR, the innermost surfaces of the polyhedra are retained to form the combined polyhedron. Figure 6 shows the effect of a and b on the shapes given by (5) as p → ∞.The shape is determined by their location in the quadrilateral surrounded by the points P (a,b) = (3,2), Q (2,2), R (1,1) and S (3/2,1). Various shapes in and around the quadrilateral are shown by the insets in Figure 6 can be summarized as follows:
- Three basic polyhedra
- (a) {100} cube at point P.
- (b) {111} octahedron at point R.
- (c) {110} dodecahedron at point S.
- Combination of two basic polyhedra
- (a) {100}-{111} polyhedra changing from the {100} cube to the {111} octahedron along the line from P to R via Q, by truncating the eight vertices of the cube (The shape at point Q is {100}-{111} cuboctahedron).
- (b) {111}-{110} polyhedra changing from the {111} octahedron to the {110} dodecahedron along the line from R to S, by chamfering the 12 edges of the octahedron.
- (c) {110}-{100} polyhedra changing from the {110} dodecahedron to the {100} cube along the line from S to P, by truncating six of the 14 vertices of the dodecahedron.
- Combinations of all three basic polyhedra
- (a) {100}-{111}-{110} polyhedra with mutually non-connected {110} surfaces in Region 1 (R-1).
- (b) {100}-{111}-{110} polyhedra with mutually connected {110} surfaces in Region 2 (R-2).
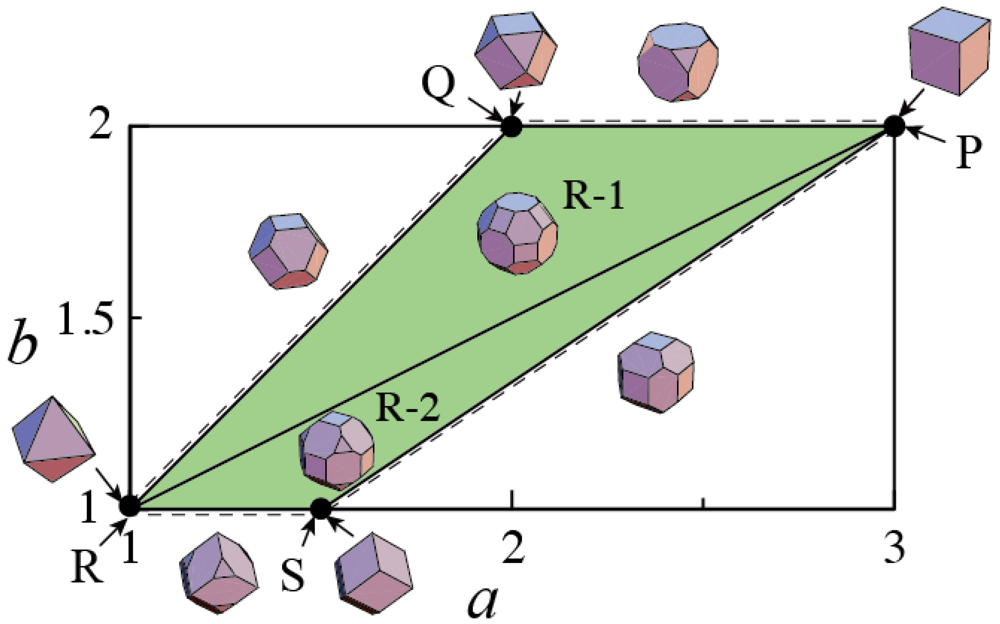
Figure 6.
Diagram showing the variation in the shapes of the {100}-{111}-{110} polyhedral superspheres given by (5) as p → ∞.
The boundary between Regions 1 and 2, expressed by the line from P to R, is written as:
 (6)
(6)Figure 6 is essentially the same as Figure 3 in [7,8] where the parameters α = 1/a and β = 1/b are used instead of a and b. In the appendix, the volume and surface area of the polyhedra shown in Figure 6 are written as a function of a and b. The use of the parameters a and b gives a more intuitive diagram (Figure 6), compared with the diagram given by α and β.
5. Discussion
5.1. Shape Transitions of Superspheres from a Sphere to Various Polyhedra
Shape transitions of superspheres from a sphere to a polyhedron are characterized by the change in the normalized surface area N = S/V2/3, where S is the surface area and V the volume of the supersphere. For a sphere, N = 62/3π1/3 ≈ 4.84. Figure 7 shows the variations in N as a function of p for the following the superspheres as indicated by the insets:
- (i) the {100} cube type given by (2),
- (ii) the {111} regular-octahedral type given by (3),
- (iii) the {110} rhombic-dodecahedral type given by (4) and
- (iv) the {100}-{111}-{110} polyhedral type given by (5) with
 and
and  .
.
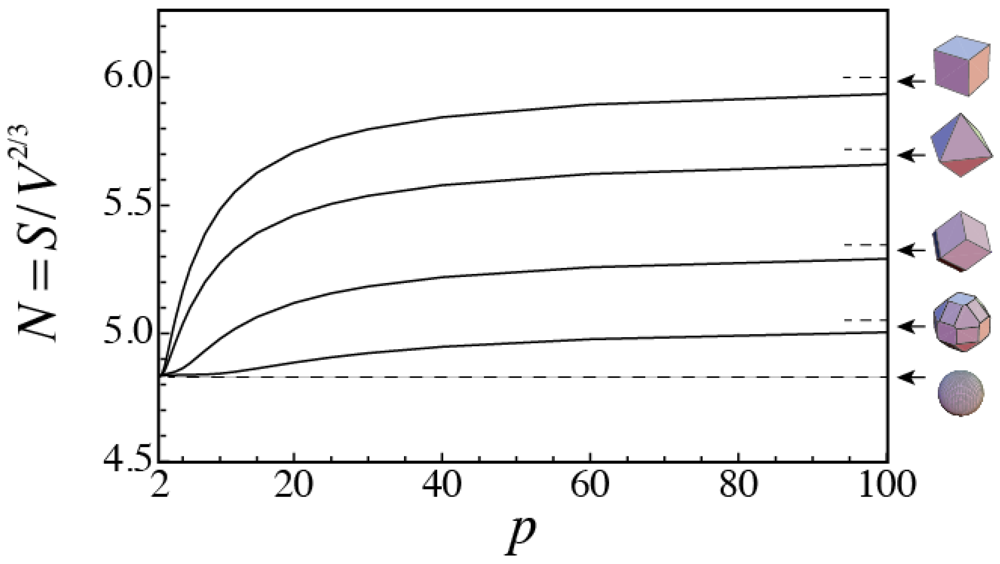
Figure 7.
Dependence of the normalized surface area N =S/V2/3 on p, where S is the surface area and V the volume for various superspheres: (i) the {100} cube type given by (2); (ii) the {111} octahedral type given by (3); (iii) the {110} dodecahedral type given by (4) and (iv) the {100}-{111}-{110} polyhedral type given by (5) with  and
and  .
.
 and
and  .
.
The broken lines at the right show the values of N for the polyhedra as p → ∞.
As shown in Figure 7, the change in N with increasing p becomes smaller as the number of faces of polyhedra increases from the {100} cube with 6 to the {100}-{111}-{110} polyhedron with 26. Among the various polyhedra shown in Figure 3, the polyhedron given by  and
and  in Region 1 with N = S/V2/3 ≈ 5.05 has the minimum total surface area
in Region 1 with N = S/V2/3 ≈ 5.05 has the minimum total surface area  for the same V [8,10]. The a and b dependence of N can be calculated easily using the results shown in the appendix.
for the same V [8,10]. The a and b dependence of N can be calculated easily using the results shown in the appendix.
 and
and  in Region 1 with N = S/V2/3 ≈ 5.05 has the minimum total surface area
in Region 1 with N = S/V2/3 ≈ 5.05 has the minimum total surface area  for the same V [8,10]. The a and b dependence of N can be calculated easily using the results shown in the appendix.
for the same V [8,10]. The a and b dependence of N can be calculated easily using the results shown in the appendix. 5.2. Shape of Small Metal Particles
The shapes of small metal particles observed in previous studies have been discussed previously using the superspherical approximation [8]. Menon and Martin reported the production of ultrafine Ni particles by vapor condensation in an inert gas plasma reactor [11]. They have also reported the crystallographic characterization of these particles by transmission electron microscopy [11]. Near-polyhedral shapes of nanoparticles have been observed to discuss their properties [12,13,14,15]. The superspherical approximation is a useful geometrical tool to describe the near-polyhedral shapes.
Acknowledgment
This research was supported by a Grand-in-Aid for Scientific Research C (22560657) by the Japan Society for the Promotion of Science.
References
- Fujii, T.; Tamura, T.; Kato, M.; Onaka, S. Size-Dependent equilibrium shape of Co-Cr particles in Cu. Microsc. Microanal. 2002, 8, 1434–1435. [Google Scholar]
- Onaka, S.; Kobayashi, N.; Fujii, T.; Kato, M. Energy analysis with a superspherical shape approximation on the spherical to cubical shape transitions of coherent precipitates in cubic materials. Mat. Sci. Eng. 2002, A347, 42–49. [Google Scholar]
- Onaka, S.; Kobayashi, N.; Fujii, T.; Kato, M. Simplified energy analysis on the equilibrium shape of coherent γ’ precipitates in gamma matrix with a superspherical shape approximation. Intermetallics 2002, 10, 343–346. [Google Scholar] [CrossRef]
- Onaka, S. Averaged Eshelby tensor and elastic strain energy of a superspherical inclusion with uniform eigenstrains. Phil. Mag. Let. 2001, 81, 265–272. [Google Scholar] [CrossRef]
- Onaka, S. Geometrical analysis of near polyhedral shapes with round edges in small crystalline particles or precipitates. J. Mat. Sci. 2008, 43, 2680–2685. [Google Scholar] [CrossRef]
- Jaklic, A.; Leonardis, A.; Solina, F. Segmentation and Recovery of Superquadrics (Computational Imaging and Vision); Kluwer Academic: Dordrecht, The Netherlands, 2000; Volume 20, pp. 13–39. [Google Scholar]
- Onaka, S. Simple equations giving shapes of various convex polyhedra: The regular polyhedra and polyhedra composed of crystallographically low-index planes. Phil. Mag. Let. 2006, 86, 175–183. [Google Scholar] [CrossRef]
- Miyazawa, T.; Aratake, M.; Onaka, S. Superspherical-shape approximation to describe the morphology of small crystalline particles having near-polyhedral shapes with round edges. J. Math. Chem. 2012, 50, 249–260. [Google Scholar] [CrossRef]
- Onaka, S.; Fujii, T.; Kato, M. Elastic strain energy due to misfit strains in a polyhedral precipitate composed of low-index planes. Acta Mater. 2007, 55, 669–673. [Google Scholar] [CrossRef]
- Suárez, J.; Gancedo, E.; Manuel Álvarez, J.; Morán, A. Optimum compactness structures derived from the regular octahedron. Eng. Struct. 2008, 30, 3396–3398. [Google Scholar] [CrossRef]
- Menon, S.K.; Martin, P.L. Determination of the anisotropy of surface free energy of fine metal particles. Ultramicroscopy 1986, 20, 93–98. [Google Scholar] [CrossRef]
- Wang, G.L. Transmission electron microscopy of shape-controlled nanocrystals and their assemblies. J. Phys. Chem. 2000, 104, 1153–1175. [Google Scholar] [CrossRef]
- Niu, W.; Zheng, S.; Wang, D.; Liu, X.; Li, H.; Han, S.; Chen, J.; Tang, Z.; Xu, G. Selective synthesis of single-crystalline rhombic dodecahedral, octahedral, and cubic gold nanocrystals. J. Am. Chem. Soc. 2009, 131, 697–703. [Google Scholar]
- Jeong, G.W.; Kim, M.; Lee, Y.W.; Choi, W.; Oh, W.T.; Park, Q.-H.; Han, S.W. Polyhedral Au Nanocrystals exclusively bound by {110} facts: The rhombic dodecahedron. J. Am. Chem. Soc. 2009, 131, 1672–1673. [Google Scholar]
- Ribis, J.; de Carlan, Y. Interfacial strained structure and orientation relationships of the nanosized oxide particles deduced from elasticity-driven morphology in oxide dispersion strengthened materials. Acta Mater. 2012, 60, 238–252. [Google Scholar] [CrossRef]
Appendix
The volume and surface area of the polyhedra shown in Figure 3.
The volume  and the
and the  ,
,  and
and  surface area, S100, S111 and S110 of the polyhedra shown in Figure 6 are written as a function of a and b. In Region 1, these are given by
surface area, S100, S111 and S110 of the polyhedra shown in Figure 6 are written as a function of a and b. In Region 1, these are given by
 and the
and the  ,
,  and
and  surface area, S100, S111 and S110 of the polyhedra shown in Figure 6 are written as a function of a and b. In Region 1, these are given by
surface area, S100, S111 and S110 of the polyhedra shown in Figure 6 are written as a function of a and b. In Region 1, these are given by
and

In Region 2, these are

and

when a = 1 and b = 1, the shape given by (5) as p → ∞ is the {111} regular-octahedron as shown by Figure 6. Since the {111} regular-octahedron belongs to both Regions 1 and 2, from both (A1) to (A4) and (A5) to (A8), we get V = (4/3)R3, S100 = 0, S111 = 4√3R2 and S110 = 0 as it should be.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).