Approximate Solutions of the Fisher–Kolmogorov Equation in an Analytic Domain of the Complex Plane

Abstract

The paper oresents the analytical construction of approximate solutions to the generalized Fisher–Kolmogorov equation in the complex domain. The existence and uniqueness of such solutions are established within an analytic domanin of the complex plane. The study employs techniques from complex function theory and introduces a modified version of the Cauchy majorant method. The principal innovation of the proposed approach, as opposed to the classical method, lies in constructing the majorant for the solution of the equation rather than for its right-hand side. A formula for calculating the analyticity radius is derived, which guarantees the absence of a movable singular point of algebraic type for the solutions under consideration. Special exact periodic solutions are found in elementary functions. Theoretical results are verified by numerical study.

1. Introduction

The extended Fisher–Kolmogorov (EFK) equation

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial u}{\partial t}}=-\gamma {\displaystyle \frac{{\partial }^{4}u}{\partial x^4}}+{\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}-u^3+u,\end{array}$$

(1)

is a generalization of the Fisher–Kolmogorov equation [1], with the addition of a fourth-order derivative term [2,3]. The EFK equation finds application in various models of hydrodynamics, bi-stable systems, population growth, plasma physics, thermonuclear reactions, reaction–diffusion processes, propagation of infectious diseases, and others [1,2,3,4,5,6,7,8,9].

For stationary cases, Equation (1) is reduced to the ordinary differential equation

$$\begin{array}{c}\hfill -\gamma u^{\prime \prime \prime \prime }+u^{″}-u^3+u=0.\end{array}$$

(2)

This equation appears when searching for wave solutions to the EFK equation, as well as in a number of other problems. In [7], it was shown that this equation can be reduced to a nonlinear Schrödinger equation.

The steady-state Equation (2) was intensively studied in [1,10,11,12,13,14,15,16,17]; the main problems addressed by the study were periodic, heteroclinic (so called kinks), and homoclinic solutions. In this context, the following methods were developed: variational methods, the topological shooting method, methods of qualitative and asymptotic theory of differential equations, the Hamiltonian method, and others [1,10,11,12,13,14,15,16,17,18,19,20]. To find solutions to Equations (1) and (2) that have certain properties in the analyticity domains, some numerical methods were used [21,22,23]; in particular, the finite element method, finite element Galerkin method, and a method based on quintic trigonometric B-spline functions.

In the present article, the Cauchy problem for Equation (2) in the complex domain is solved. Previously, the issues of existence and uniqueness of solutions for Equation (2) in the real domain were considered in [11,14,24].

This article builds upon the results obtained in [25], where existence and uniqueness of solutions in the neighborhood of a movable singular point in a complex domain were proved.

As is known, the domain of solutions in the complex plane can be divided into two parts: the neighborhood of the movable singular point and the analyticity domain. In the present article, approximate solutions in analytical form are constructed, and estimates of these solutions are performed. A formula has been derived for the radius of convergence of the approximate solution in the analyticity domain of the complex plane. Furthermore, for special values of the basic parameter q (see (3)), exact one-parametric solutions of of Equation (2) in the complex domain are found using the analytical method elaborated in [26,27,28].

The article is organized as follows: the introduction contains a brief list of relevant publications, and provides a short description of the obtained results. Section 2 presents the main results: proving the existence and uniqueness of solutions in the analyticity domain, and the error estimate for the constructed analytical approximate solutions. Section 3 presents a numerical study, where approximate solutions are constructed for two sets of initial data (complex and real), and an estimate of their errors is given. In Section 4, exact periodic complex solutions to the EFK equation are found for special values of the basic parameter. In conclusion, we summarize the obtained results.

2. The Main Result

Let us consider the EFK equation in the form [24]

$$\begin{array}{c}\hfill {\displaystyle \frac{d^{4}u}{d{z}^4}}+q{\displaystyle \frac{d^{2}u}{d{z}^2}}+u^3-u=0,\end{array}$$

(3)

with the initial conditions

$$\begin{array}{c}\hfill u\left(z_0\right)=u_0,u^{\prime }\left(z_0\right)=u_1,u^{″}\left(z_0\right)=u_2,u^{\prime \prime \prime }\left(z_0\right)=u_3,\end{array}$$

(4)

where $u\left(z\right)$ is an analytic fuction of the complex variable z, $q\in \mathbb{R}$ is a parameter, $q\ne 0$, $z_0,u_i\in \mathbb{C}$$(i=0,1,2,3)$. Let us prove a theorem on the existence and uniqueness of a solution to the Cauchy problem (3) and (4) in the analyticity domain of the complex plane.

Theorem 1.

The solution of the Cauchy problem (3) and (4), for $|q|>1$, $q\in \mathbb{R}$, is an analytic function of the form

$$\begin{array}{c}\hfill u\left(z\right)=\sum _{n=0}^{\infty }{C}_n{(z-z_0)}^n,\end{array}$$

(5)

in the domain

$$\begin{array}{c}\hfill |z-z_0| <{\displaystyle \frac{1}{\sqrt{|q|M}}},\end{array}$$

(6)

where $C_n\in \mathbb{C}$, $M=max\{|u_0|,|u_1|,|u_2|,|u_3|\}$.

Proof. 

We will use a modified majorant method, as developed in [25,29,30,31].

The main steps of the proof are as follows:

-

Derivation of recurrence relations for the coefficients of the series (5);

-

Construction of a majorant series corresponding to (5);

-

Determination of the radius of convergence of the majorant series.

We start with the recurrence relation determining the coefficients $C_n$ of the series (5). Substituting the series (5) into Equation (3), we obtain

$$\begin{array}{c}\hfill \begin{array}{c}\hfill n(n-1)(n-2)(n-3)\sum _{n=4}^{\infty }{C}_n{(z-z_0)}^{n-4}+qn(n-1)\sum _{n=2}^{\infty }{C}_n{(z-z_0)}^{n-2}\\ \hfill +\sum _{n=0}^{\infty }{C}_n^{\ast \ast }{(z-z_0)}^n-\sum _{n=0}^{\infty }{C}_n{(z-z_0)}^n=0,\end{array}\end{array}$$

(7)

where the following notations are used

$$\begin{array}{c}\hfill C_n^{\ast }=\sum _{n=0}^{\infty }{C}_i{C}_{n-i},C_n^{\ast \ast }=\sum _{n=0}^{\infty }{C}_i^{\ast }{C}_{n-i}.\end{array}$$

(8)

For $n=4$, from (7) and (8), we obtain

$$\begin{array}{c}\hfill 24C_4=-2q{C}_2-C_0^{\ast \ast }+C_0,\end{array}$$

whence it follows

$$\begin{array}{c}\hfill C_4={\displaystyle \frac{1}{24}}(-2q{C}_2-C_0^3+C_0).\end{array}$$

(9)

Similarly, at $n=5,6,7$ we obtain

$$\begin{array}{c}\hfill \begin{array}{c}\hfill C_5={\displaystyle \frac{1}{120}}(-6q{C}_3-3C_0^2{C}_1+C_1),\\ \hfill C_6={\displaystyle \frac{1}{360}}(-12q{C}_4-3C_0^2{C}_2-3C_0{C}_1^2+C_2),\\ \hfill C_7={\displaystyle \frac{1}{840}}(-20q{C}_5-3C_0^2{C}_3-6C_0{C}_1{C}_2-C_1^3+C_3).\end{array}\end{array}$$

(10)

In the general case, for $C_n$ we have a recurrence relation

$$\begin{array}{c}\hfill C_n=-{\displaystyle \frac{1}{n(n-1)(n-2)(n-3)}}(n(n-1)q{C}_{n-2}-C_{n-4}^{\ast \ast }+C_{n-4}).\end{array}$$

(11)

Using the method of mathematical induction and relation (11), we introduce the following ansatz for estimating the moduli of the coefficients $C_n(n\in \mathbb{N})$:

$$\begin{array}{c}\hfill |C_{4n}| \le {\displaystyle \frac{1}{4n}}{|q|}^{2n+1}{M}^{2n+1},\end{array}$$

(12)

$$\begin{array}{c}\hfill |C_{4n+1}| \le {\displaystyle \frac{1}{4n+1}}{|q|}^{2n+1}{M}^{2n+1},\end{array}$$

(13)

$$\begin{array}{c}\hfill |C_{4n+2}| \le {\displaystyle \frac{1}{4n+2}}{|q|}^{2n+2}{M}^{2n+1},\end{array}$$

(14)

$$\begin{array}{c}\hfill |C_{4n+3}| \le {\displaystyle \frac{1}{4n+3}}{|q|}^{2n+2}{M}^{2n+1}.\end{array}$$

(15)

Let us prove this estimate for the coefficients $C_{4n}$

$$\begin{array}{c}\hfill |C_{4n+4}| \le {\displaystyle \frac{1}{4n+4}}{|q|}^{2n+3}{M}^{2n+3}.\end{array}$$

(16)

From the recurrence relation (11), we find

$$\begin{array}{c}\hfill C_{4n+4}={\displaystyle \frac{1}{(4n+1)(4n+2)(4n+3)(4n+4)}}\left(-(4n+1)(4n+2)q{C}_{4n+2}-C_{4n}^{\ast \ast }+C_n\right);\end{array}$$

(17)

whence, taking into account the estimates (12)–(15) and notions (8),

$$\begin{array}{c}\hfill \begin{array}{c}\hfill |C_{4n+4}| \le {\displaystyle \frac{1}{(4n+1)(4n+2)(4n+3)(4n+4)}}\times |(4n+1)(4n+2)q{C}_{4n+2}\\ \hfill +(C_0^{\ast }{C}_{4n}+C_1{C}_{4n-1}+\dots +C_{4n-1}^{\ast }{C}_1+C_{4n}^{\ast }{C}_0)+C_{4n}| \le {\displaystyle \frac{1}{(4n+1)(4n+2)(4n+3)(4n+4)}}\\ \hfill \times |(4n+1)(4n+2)q{C}_{4n+2}+(C_0^2{C}_{4n}+2C_0{C}_1{C}_{4n-1}+\dots +\sum _{i=0}^{4n-1}{C}_i{C}_{4n-1-i}{C}_1+\sum _{i=0}^{4n}{C}_i{C}_{4n-i}{C}_0)+C_{4n}|\\ \hfill \le {\displaystyle \frac{1}{(4n+1)(4n+2)(4n+3)(4n+4)}}\times |{\displaystyle \frac{(4n+1)(4n+2)}{4n+2}}{q}^{2n+3}{M}^{2n+1}\\ \hfill +M^2{\displaystyle \frac{1}{4n}}{q}^{2n+1}{M}^{2n+1}+2M^2{\displaystyle \frac{1}{4n-1}}{q}^{2n}{M}^{2n-1}+\dots +(4n+1)M^2{q}^{2n}{M}^{2n-1}+{\displaystyle \frac{1}{4n}}{q}^{2n+1}{M}^{2n+1}|\\ \hfill \le {\displaystyle \frac{1}{4n+4}}{|q|}^{2n+3}{M}^{2n+3}.\end{array}\end{array}$$

In a similar way, we prove the estimates (13)–(15).

For the series

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{C}_{4n}{(z-z_0)}^{4n},\end{array}$$

(18)

and taking into consideration the estimate (12), we can construct a majorizing series

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{\displaystyle \frac{1}{4n}}{|q|}^{2n+1}{M}^{2n+1}{|z-z_0|}^{4n},\end{array}$$

(19)

which converges, in accordance with the sufficient criterion from [32], in the domain

$$\begin{array}{c}\hfill |z-z_0| \le {\displaystyle \frac{1}{\sqrt{|q|M}}}.\end{array}$$

(20)

Therefore, series (18) will converge in the domain (6).

In a similar way, we can prove the convergence of the following series in the domain (20)

$$\sum _{n=1}^{\infty }{C}_{4n+1}{(z-z_0)}^{4n+1},\sum _{n=1}^{\infty }{C}_{4n+2}{(z-z_0)}^{4n+2},\sum _{n=1}^{\infty }{C}_{4n+3}{(z-z_0)}^{4n+3}.$$

□

Remark 1.

Theorem 1 yields the convergence radius ${\displaystyle \frac{1}{\sqrt{|q|M}}}$ of solution (5) for $|q|>1$. In the case of $|q| \le 1$, the convergence region (6) has the form

$$\begin{array}{c}\hfill |z-z_0| <{\displaystyle \frac{1}{\sqrt{M}}}.\end{array}$$

(21)

Domains (20) and (21) will be free from movable singularities.

Remark 2.

Theorem 1 allows us to construct an analytic approximate solution for problem (3) and (4) in the following form

$$\begin{array}{c}\hfill u_N\left(z\right)=\sum _{n=0}^N{C}_n{(z-z_0)}^n.\end{array}$$

(22)

Theorem 2.

For the approximate analytic solution (22) to the Cauchy problem (3) and (4), in the case $|q|>1$, the following error estimate holds

$$\begin{array}{c}\hfill \mathsf{\Delta }{u}_N\left(z\right)=|\sum _{n=N+1}^{\infty }{C}_n{(z-z_0)}^n|\le \mathsf{\Delta },\end{array}$$

(23)

where $\mathsf{\Delta }\in {\mathbb{R}}^{+}$ and

$$\begin{array}{c}\hfill \mathsf{\Delta }\le {\displaystyle \frac{{|q|}^{(N+3)/2}{M}^{(N+3)/2}{|z-z_0|}^{N+4}}{1-q^2{M}^2{|z-z_0|}^4}}\left({\displaystyle \frac{1}{N+1}}+{\displaystyle \frac{|z-z_0|}{N+2}}+{\displaystyle \frac{|q||z-z_0{|}^2}{N+3}}+{\displaystyle \frac{|q||z-z_0{|}^3}{N+4}}\right)\end{array}$$

(24)

for $N+1=4n$;

$$\begin{array}{c}\hfill \mathsf{\Delta }\le {\displaystyle \frac{{|q|}^{(N+3)/2}{M}^{(N+3)/2}{|z-z_0|}^{N+2}}{1-q^2{M}^2{|z-z_0|}^4}}\left({\displaystyle \frac{1}{N+2}}+{\displaystyle \frac{|q||z-z_0|}{N+3}}+{\displaystyle \frac{|q||z-z_0{|}^2}{N+4}}+{\displaystyle \frac{{|q|}^2{M}^2{|z-z_0|}^3}{N+5}}\right)\end{array}$$

(25)

for $N+1=4n+1$;

$$\begin{array}{c}\hfill \mathsf{\Delta }\le {\displaystyle \frac{{|q|}^{(N+3)/2}{M}^{(N+1)/2}{|z-z_0|}^{N+1}}{1-q^2{M}^2{|z-z_0|}^4}}\left({\displaystyle \frac{1}{N+1}}+{\displaystyle \frac{|z-z_0|}{N+2}}+{\displaystyle \frac{|q|M^2{|z-z_0|}^2}{N+3}}+{\displaystyle \frac{|q|M^2{|z-z_0|}^3}{N+4}}\right)\end{array}$$

(26)

for $N+1=4n+2$;

$$\begin{array}{c}\hfill \mathsf{\Delta }\le {\displaystyle \frac{{|q|}^{(N+2)/2}{M}^{N/2}{|z-z_0|}^{N+1}}{1-q^2{M}^2{|z-z_0|}^4}}\left({\displaystyle \frac{1}{N+1}}+{\displaystyle \frac{|q|M^2|z-z_0|}{N+2}}+{\displaystyle \frac{|q|M^2{|z-z_0|}^2}{N+3}}+{\displaystyle \frac{q^2{M}^2{|z-z_0|}^3}{N+4}}\right)\end{array}$$

(27)

for $N+1=4n+3$, in the following domain

$$\begin{array}{c}\hfill |z-z_0| \le {\displaystyle \frac{1}{\sqrt{|q|M}}}.\end{array}$$

(28)

Proof. 

In the proof of the theorem, the modulus of the difference between the exact and approximate solutions is estimated [29,30,31,32], and four inequalities are established. The presence of these four inequalities is related to the nonlinearity of the differential equation, its order, and the powers of the unknown function and its derivatives. By definition, we have

$$\begin{array}{c}\hfill \mathsf{\Delta }{u}_N\left(z\right)=|u\left(z\right)-u_N\left(z\right)|=\left|\sum _{n=0}^{\infty }{C}_n{(z-z_0)}^n-\sum _{n=0}^N{C}_n{(z-z_0)}^n\right|=\left|\sum _{n=N+1}^{\infty }{C}_n{(z-z_0)}^n\right|;\end{array}$$

(29)

whence, taking into account the indices for coefficients $C_n$ and $N+1=4n$, we obtain

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left|\sum _{n=N+1}^{\infty }{C}_n{(z-z_0)}^n\right|=\left|\sum _{k=0}^{\infty }{C}_{4(n+k)}{(z-z_0)}^{4(n+k)}+\sum _{k=0}^{\infty }{C}_{4(n+k)+1}{(z-z_0)}^{4(n+k)+1}\right.\\ \hfill \left.+\sum _{k=0}^{\infty }{C}_{4(n+k)+2}{(z-z_0)}^{4(n+k)+2}+\sum _{k=0}^{\infty }{C}_{4(n+k)+3}{(z-z_0)}^{4(n+k)+3}\right|.\end{array}\end{array}$$

(30)

Allowing for the estimates (12)–(15), we obtain

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathsf{\Delta }{u}_N\left(z\right)\le \mathsf{\Delta }\le \left|\sum _{k=0}^{\infty }{\displaystyle \frac{{|q|}^{2(n+k)+1}{M}^{2(n+k)+1}}{4(n+k)}}{(z-z_0)}^{4(n+k)}\right.\\ \hfill \left.+\sum _{k=0}^{\infty }{\displaystyle \frac{{|q|}^{2(n+k)+1}{M}^{2(n+k)+1}}{4(n+k)+1}}{(z-z_0)}^{4(n+k)+1}+\sum _{k=0}^{\infty }{\displaystyle \frac{{|q|}^{2(n+k)+2}{M}^{2(n+k)+1}}{4(n+k)+2}}{(z-z_0)}^{4(n+k)+2}\right|\\ \hfill +\sum _{k=0}^{\infty }{\displaystyle \frac{{|q|}^{2(n+k)+2}{M}^{2(n+k)+1}}{4(n+k)+3}}{(z-z_0)}^{4(n+k)+3}\le ({\displaystyle \frac{{|q|}^{2n+1}{M}^{2n+1}{|z-z_0|}^{4n}}{4n(1-q^2{M}^2|z-z_0{|}^4)}}\\ \hfill +{\displaystyle \frac{{|q|}^{2n+1}{M}^{2n+1}{|z-z_0|}^{4n+1}}{(4n+1)(1-q^2{M}^2|z-z_0{|}^4)}}+{\displaystyle \frac{{|q|}^{2n+2}{M}^{2n+1}{|z-z_0|}^{4n+2}}{(4n+2)(1-q^2{M}^2|z-z_0{|}^4)}}\\ \hfill +{\displaystyle \frac{{|q|}^{2n+2}{M}^{2n+1}{|z-z_0|}^{4n+3}}{(4n+3)(1-q^2{M}^2|z-z_0{|}^4)}})={\displaystyle \frac{{|q|}^{2n+1}{M}^{2n+1}{|z-z_0|}^{4n}}{4n(1-q^2{M}^2|z-z_0{|}^4)}}\\ \hfill \times \left({\displaystyle \frac{1}{4n}}+{\displaystyle \frac{|z-z_0|}{4n+1}}+{\displaystyle \frac{|q||z-z_0{|}^2}{4n+2}}+{\displaystyle \frac{|q||z-z_0{|}^3}{4n+3}}\right).\end{array}\end{array}$$

Let $N+1=4n$, then we obtain

$$\begin{array}{c}\hfill \mathsf{\Delta }\le {\displaystyle \frac{{|q|}^{(N+3)/2}{M}^{(N+3)/2}{|z-z_0|}^{N+4}}{1-q^2{M}^2{|z-z_0|}^4}}\left({\displaystyle \frac{1}{N+1}}+{\displaystyle \frac{|z-z_0|}{N+2}}+{\displaystyle \frac{|q||z-z_0{|}^2}{N+3}}+{\displaystyle \frac{|q||z-z_0{|}^3}{N+4}}\right).\end{array}$$

(31)

Similarly, for the case $N+1=4n+1$, we derive

$$\begin{array}{c}\hfill \mathsf{\Delta }\le {\displaystyle \frac{{|a|}^{(N+3)/2}{M}^{(N+3)/2}{|z-z_0|}^{N+1}}{1-q^2{M}^2{|z-z_0|}^4}}\left({\displaystyle \frac{1}{N+2}}+{\displaystyle \frac{|z-z_0|}{N+3}}+{\displaystyle \frac{|q||z-z_0{|}^2}{N+4}}+{\displaystyle \frac{q^2{M}^2{|z-z_0|}^3}{N+5}}\right).\end{array}$$

(32)

For the case $N+1=4n+2$, we have

$$\begin{array}{c}\hfill \mathsf{\Delta }\le {\displaystyle \frac{{|q|}^{(N+2)/2}{M}^{N/2}{|z-z_0|}^{N+1}}{1-q^2{M}^2{|z-z_0|}^4}}\\ \hfill \times \left({\displaystyle \frac{1}{N+1}}+{\displaystyle \frac{|q|M^2|z-z_0|}{N+2}}+{\displaystyle \frac{|q|M^2{|z-z_0|}^2}{N+3}}+{\displaystyle \frac{|q|M^2{|z-z_0|}^3}{N+4}}\right).\end{array}$$

(33)

If $N+1=4n+3$, then we obtain

$$\begin{array}{c}\hfill \mathsf{\Delta }\le {\displaystyle \frac{{|q|}^{(N+2)/2}{M}^{N/2}{|z-z_0|}^{N+1}}{1-q^2{M}^2{|z-z_0|}^4}}\\ \hfill \times \left({\displaystyle \frac{1}{N+1}}+{\displaystyle \frac{|q|M^2|z-z_0|}{N+2}}+{\displaystyle \frac{|q|M^2{|z-z_0|}^2}{N+3}}+{\displaystyle \frac{|q|M^2{|z-z_0|}^3}{N+4}}\right).\end{array}$$

(34)

The obtained expressions for the estimates (31)–(34) are valid in the following domain

$$\begin{array}{c}\hfill |z-z_0| \le {\displaystyle \frac{1}{\sqrt{|q|M}}}.\end{array}$$

□

Remark 3.

If $|q| \le 1$, Theorem 2 is valid in the domain

$$\begin{array}{c}\hfill |z-z_0| \le {\displaystyle \frac{1}{\sqrt{M}}}.\end{array}$$

3. Numerical Simulation

Let us consider two examples demonstrating how the proposed method works, for complex and real initial conditions.

3.1. Example 1

Let us consider the Cauchy problem for Equation (3) with $q=1.1$ and the following initial conditions:

$$\begin{array}{c}\hfill z_0=0.5i,u\left(z_0\right)=u_0=0.5,u^{\prime }\left(z_0\right)=u_1=0.5+0.5i,u^{\prime \prime }\left(z_0\right)=u_2=1+i,u^{\prime \prime \prime }\left(z_0\right)=u_3=i.\end{array}$$

(35)

Let $z_1=0.6+0.5i;$ this point falls into the domain defined by Formula (6) $({\displaystyle \frac{1}{\sqrt{|q|M}}}=0.801763)$.

Taking into account the conditions in (35) and Formulas (9) and (10), we find the coefficients $C_4-C_7$:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill C_4=-0.0760417-0.0916667i,C_5=0.00104167-0.0539583i,\\ \hfill C_6=0.00348264+0.00197222i,C_7=0.000270337-0.00215823i.\end{array}\end{array}$$

(36)

The structure of the approximate solution (22) for $N=7$ is

$$\begin{array}{c}\hfill u_7\left(z\right)=\sum _{n=0}^7{C}_n{(z-z_0)}^n,\end{array}$$

(37)

where $C_i=u_i(i=\overline{0,3})$ and $C_k(k=\overline{4,7})$ are determined by the following relations (35) and (36).

The calculation results are presented in Table 1, where $u_7\left(z_1\right)$ is the value of the analytic approximate solution (22) in the point $z_1$, $\mathsf{\Delta }$ is the a priori error estimate for $u_7\left(z_1\right)$. The graphs of the real and imaginary parts of the surface (37), (35), and (36) are presented in Figure 1. The circle in the graphs indicates the region of convergence (6) for the series (5).

Table 1. Results of the numerical experiment.

${\mathit{z}}_1$	${\mathit{u}}_7\left({\mathit{z}}_1\right)$	$\mathsf{\Delta }$
$0.6+0.5i$	$1.15039+0.860016i$	$1.21769·{10}^{-2}$

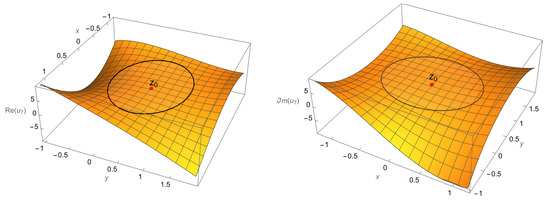
Figure 1. Plots $\Re e u_7\left(z\right)$ and $\Im m u_7\left(z\right)$ in the complex neighborhood of the point $z_0=0.5i$.

3.2. Example 2

Consider the Cauchy problem for Equation (3) with $q=1.1$ and the initial conditions in the real domain:

$$\begin{array}{c}\hfill z_0=0.5,u\left(z_0\right)=u_0=0.5,u^{\prime }\left(z_0\right)=u_1=1,u^{″}\left(z_0\right)=u_2=1.1,u^{\prime \prime \prime }\left(z_0\right)=u_3=0.4.\end{array}$$

(38)

We will perform calculations for a real point

$$z_1=0.8,$$

which falls into the region defined by Formula (6) $({\displaystyle \frac{1}{\sqrt{|q|M}}}=0.909091)$.

Taking into account the conditions (38) and Formulas (9) and (10), we find the coefficients $C_4-C_7$:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill C_4=-0.085208,C_5=-0.0199167,C_6=-0.000278472,C_7=-0.00447837.\end{array}\end{array}$$

(39)

The structure of the approximate solution (22) for $N=7$ is (37), where $C_i=u_i(i=\overline{0,3})$ and $C_k(k=\overline{4,7})$ are determined by formulas (38) and (39). The results of the calculations are presented in Table 2.

Table 2. Results of the numerical experiment.

${\mathit{z}}_1$	${\mathit{u}}_7\left({\mathit{z}}_1\right)$	$\mathsf{\Delta }$
$0.8$	$0.909061$	$7.9482·{10}^{-7}$

The plots of the real and imaginary parts on the surface (37)–(39) are shown in Figure 2.

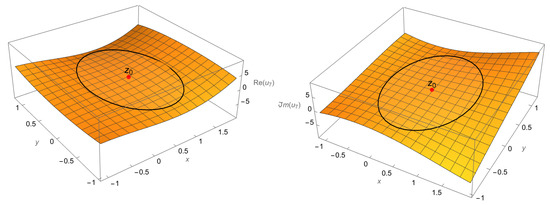
Figure 2. Plots $\Re e u_7\left(z\right)$ and $\Im m u_7\left(z\right)$ in the complex neighborhood of the point $z_0=0.5$.

3.3. Example 3

Let us consider the Cauchy problem for Equation (3) with $q=0.5$ and initial conditions (35). Let $z_1=0.7+0.5i;$ this point falls into the domain defined by the following Formula (6) $({\displaystyle \frac{1}{\sqrt{M}}}=0.840896)$.

Taking into account the conditions (35) and Formulas in (9) and (10), we find the following coefficients $C_4-C_7$:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill C_4=-0.0260417-0.0416667i,C_5=0.00104167-0.0239583i,\\ \hfill C_6=0.00112847-0.000694444i,C_7=0.000285218-0.00328621i.\end{array}\end{array}$$

(40)

The structure of the approximate solution (22) for $N=7$ is (9), where $C_i=u_i(i=\overline{0,3})$ and $C_k(k=\overline{4,7})$ are determined by the relations (35) and (40).

The calculation results are presented in Table 3, where $u_7\left(z_1\right)$ is the value of the analytic approximate solution (22) in the point $z_1$, $\mathsf{\Delta }$ is a priori error estimate for $u_7\left(z_1\right)$.

Table 3. Results of the numerical experiment.

${\mathit{z}}_1$	${\mathit{u}}_7\left({\mathit{z}}_1\right)$	$\mathsf{\Delta }$
$0.7+0.5i$	$1.33406+1.16889i$	$1.50518·{10}^{-4}$

4. Exact Complex Solutions of the EFK

Let us search for periodic complex solutions to Equation (3). Using the method [26,27,28], we construct solutions in the form

$$\begin{array}{c}\hfill u=a_{2}w{\left(z\right)}^2+a_{1}w\left(z\right)+a_0+{\displaystyle \frac{b_1{w}^{\prime }\left(z\right)}{w\left(z\right)}}+{\displaystyle \frac{b_2{w}^{\prime }{\left(z\right)}^2}{w{\left(z\right)}^2}},\end{array}$$

(41)

where function w is a solution of the Riccati equation

$$\begin{array}{c}\hfill w^{\prime }=\beta +2\alpha w-w^2,\end{array}$$

(42)

$a_2,a_1,a_0,b_2,b_1,\alpha$ and $\beta$ are constants.

Let us substitute the function (41) and (42) into Equation (3). As a result, we obtain a polynomial equation of degree 12 with respect to the function w. From the coefficient of $w^{12}$, we find

$$\begin{array}{c}\hfill \left(1\right)b_2=0,\left(2\right)b_2=-2i\sqrt{30},\left(3\right)b_2=2i\sqrt{30}.\end{array}$$

(43)

For case (43)₁, we obtain three subcases

$$\begin{array}{c}\hfill b_1=0,a_2=0,a_1=0,a_0=0,1,-1;\end{array}$$

(44)

$$\begin{array}{c}\hfill b_1=0,a_2=-2i\sqrt{30},a_1=4i\sqrt{30}\alpha ,a_0=-2i\sqrt{{\displaystyle \frac{10}{3}}}{\alpha }^2+4i\sqrt{{\displaystyle \frac{10}{3}}}\beta -{\displaystyle \frac{iq}{\sqrt{30}}};\end{array}$$

(45)

$$\begin{array}{c}\hfill b_1=0,a_2=2i\sqrt{30},a_1=-4i\sqrt{30}\alpha ,a_0=2i\sqrt{{\displaystyle \frac{10}{3}}}{\alpha }^2-4i\sqrt{{\displaystyle \frac{10}{3}}}\beta +{\displaystyle \frac{iq}{\sqrt{30}}}.\end{array}$$

(46)

The set of parameters (43)₁, (44) corresponds to a constant solution $u=a_0$. Functions $u=-1$ and $u=1$ provide equilibria solutions [21,24].

Let us introduce the notations

$$\begin{array}{c}\hfill \psi =e^{\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{i}{2}}\right)(z+c)},{\lambda }_{1,2}={\displaystyle \frac{\sqrt{-7\mp i\sqrt{15}}}{16}},{\mu }_{1,2}={\displaystyle \frac{\sqrt{-11\mp 3i\sqrt{15}}}{4}},{\nu }_{1,2}={\displaystyle \frac{\sqrt{17\mp 7i\sqrt{15}}}{64}},\end{array}$$

(47)

where c is an arbitrary constant.

For the set of parameters in (43)₁, (45) corresponds to six solutions of the following form

$$\begin{array}{c}\hfill u={\displaystyle \frac{\sqrt{30}\psi }{{\left(\psi -1\right)}^2}},q=-{\displaystyle \frac{5i}{2}};\end{array}$$

(48)

$$\begin{array}{c}\hfill u={\displaystyle \frac{\sqrt{30}\psi }{{\left(e^{z/2}+e^{-z/2}\psi \right)}^2}},q={\displaystyle \frac{5i}{2}};\end{array}$$

(49)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill u=\sqrt{2}{\lambda }_1\left(-2i\sqrt{15}{tanh}^2\left(\sqrt{{\lambda }_1}(z+c)\right)+i\sqrt{15}-1\right),q=2\left(5-i\sqrt{15}\right){\lambda }_1;\end{array}\end{array}$$

(50)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill u={\displaystyle \frac{1}{8}}i\left(\sqrt{15}+15i\right){\sec \mathrm{h}}^2\left(\sqrt{{\lambda }_2}(z+c)\right)+1,q=2\left(5+i\sqrt{15}\right){\lambda }_2;\end{array}\end{array}$$

(51)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill u={\displaystyle \frac{1}{8}}\left(15-i\sqrt{15}\right){sec}^2\left(\sqrt{{\lambda }_2}(z+c)\right)-1,q=-2i{\lambda }_2\left(\sqrt{15}-5i\right).\end{array}\end{array}$$

(52)

In order to illustrate the complex-valued solutions in (48)–(52), we chose a particular solution (52) with $c=1$. Plots of the real and imaginary parts of the solution (52) for $c=1$ are presented in Figure 3.

$$\begin{array}{c}\hfill u=\sqrt{2}{\lambda }_1\left(-2i\sqrt{15}{sec}^2\left(\sqrt{{\lambda }_1}(z+c)\right)+i\sqrt{15}+1\right),q=2i\left(\sqrt{15}+5i\right){\lambda }_1.\end{array}$$

(53)

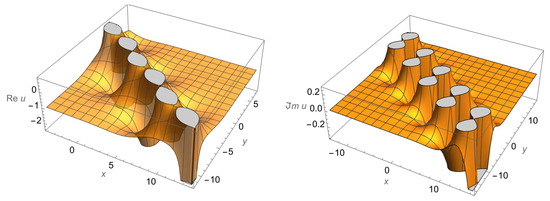
Figure 3. Plots of the real and imaginary parts of the solution (52) for $c=1$.

For the set of parameters in (43)₁, (46) correspond to the following solutions

$$\begin{array}{c}\hfill u\left(z\right)=-{\displaystyle \frac{\sqrt{30}\psi }{{\left(\psi -1\right)}^2}},q=-{\displaystyle \frac{5i}{2}};\end{array}$$

(54)

$$\begin{array}{c}\hfill u\left(z\right)=-{\displaystyle \frac{\sqrt{30}\psi }{{\left(e^{z/2}+e^{-z/2}\psi \right)}^2}},q={\displaystyle \frac{5i}{2}};\end{array}$$

(55)

$$\begin{array}{c}\hfill u=2i\sqrt{30}{\lambda }_1{tanh}^2\left(\sqrt{{\lambda }_1}(z+c)\right)+32{\lambda }_1^2,q=2\left(5-i\sqrt{15}\right){\lambda }_1;\end{array}$$

(56)

$$\begin{array}{c}\hfill u={\displaystyle \frac{1}{8}}\left(15-i\sqrt{15}\right){\sec \mathrm{h}}^2\left(\sqrt{{\lambda }_2}(z+c)\right)-1,q=2\left(5+i\sqrt{15}\right){\lambda }_2;\end{array}$$

(57)

$$\begin{array}{c}\hfill u=1+{\displaystyle \frac{1}{8}}i\left(\sqrt{15}+15i\right){sec}^2\left(\sqrt{{\lambda }_2}(z+c)\right),q=-2i\left(\sqrt{15}-5i\right){\lambda }_2;\end{array}$$

(58)

$$\begin{array}{c}\hfill u=2i\sqrt{30}{\lambda }_1{tan}^2\left(\sqrt{{\lambda }_1}(z+c)\right)-32{\lambda }_1^2,q=2i\left(\sqrt{15}+5i\right){\lambda }_1.\end{array}$$

(59)

Similarly, for the case (43)₂, we obtain

$$\begin{array}{c}\hfill b_1=4i\sqrt{30}\alpha ,a_1=-4i\sqrt{30}\alpha ,a_0=-{\displaystyle \frac{i\left(20{\alpha }^2+80\beta +q\right)}{\sqrt{30}}};\end{array}$$

(60)

and we have three subcases for $a_2$

$$\begin{array}{c}\hfill a_2=0,a_2=2i\sqrt{30},a_2=4i\sqrt{30}.\end{array}$$

(61)

For the case (43)₂, (60), (61)₁, we obtain solutions (48), (55),

$$\begin{array}{c}\hfill \begin{array}{c}\hfill u={\displaystyle \frac{i\left({\mu }_1-\sqrt{5}{\lambda }_2\left(3{coth}^2\left(\frac{1}{2}\sqrt{{\lambda }_2}(z+c)\right)+3{tanh}^2\left(\frac{1}{2}\sqrt{{\lambda }_2}(z+c)\right)-2\right)\right)}{\sqrt{6}}},\\ \hfill q=-\sqrt{5}{\mu }_1;\end{array}\end{array}$$

(62)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill u=-{\displaystyle \frac{i\left({\mu }_1+\sqrt{5}{\lambda }_2\left(3{cot}^2\left(\frac{1}{2}\sqrt{{\lambda }_2}(z+c)\right)+3{tan}^2\left(\frac{1}{2}\sqrt{{\lambda }_2}(z+c)\right)+2\right)\right)}{\sqrt{6}}},\\ \hfill q=\sqrt{5}{\mu }_1;\end{array}\end{array}$$

(63)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill u={\displaystyle \frac{i\left(\sqrt{5}{\lambda }_1\left(2-3{coth}^2\left(\frac{1}{2}\sqrt{{\lambda }_1}(z+c)\right)-3{tanh}^2\left(\frac{1}{2}\sqrt{{\lambda }_1}(z+c)\right)\right)+{\mu }_2\right)}{\sqrt{6}}},\\ \hfill q=-\sqrt{5}{\mu }_2;\end{array}\end{array}$$

(64)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill u=-{\displaystyle \frac{i}{\sqrt{6}}}\left({\mu }_2+\sqrt{5}{\lambda }_1(3{cot}^2\left({\displaystyle \frac{1}{2}}\sqrt{{\lambda }_1}(z+c)\right)+3{tan}^2\left({\displaystyle \frac{1}{2}}\sqrt{{\lambda }_1}(z+c)\right)+2)\right),\\ \hfill q=\sqrt{5}{\mu }_2.\end{array}\end{array}$$

(65)

For the case of (43)₂, (60), (61)₂, we have no new solutions.

For the case of (43)₂, (60), (61)₃, we obtain a new solution

$$\begin{array}{c}\hfill u=i\sqrt{{\displaystyle \frac{15}{22}}}{tan}^2\left({\displaystyle \frac{z+c}{2\sqrt[4]{11}}}\right)\left(1-{cot}^4\left({\displaystyle \frac{z+c}{2\sqrt[4]{11}}}\right)\right),q=-{\displaystyle \frac{10}{\sqrt{11}}}.\end{array}$$

(66)

The function (66) is a complex solution for Equation (3) with a real parameter q. The graph of this solution is shown in Figure 4. We can see that the real and imaginary parts of the solution are periodic functions; we should also note the evident symmetry among the graphs.

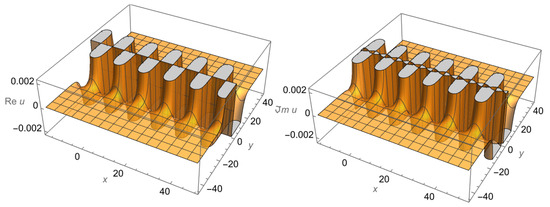
Figure 4. Plots of the real and imaginary parts of the solution (66) for $c=1$.

For the case (43)₃, we find

$$\begin{array}{c}\hfill b_1=-4i\sqrt{30}\alpha ,a_0={\displaystyle \frac{i\left(20{\alpha }^2+80\beta +q\right)}{\sqrt{30}}},a_1=4i\sqrt{30}\alpha \end{array}$$

(67)

correspondingly, we obtain three subcases for $a_2$

$$\begin{array}{c}\hfill a_2=0,a_2=-2i\sqrt{30},a_2=-4i\sqrt{30}.\end{array}$$

(68)

For the case of (43)₃, (67), (68)₁, we obtain solutions (48), (49):

$$\begin{array}{c}\hfill \begin{array}{c}\hfill u={\displaystyle \frac{{\nu }_1+i\sqrt{30}{\lambda }_2^2{tanh}^2\left(\frac{1}{2}\sqrt{{\lambda }_2}(z+c_1)\right)\left(1+{coth}^4\left(\frac{1}{2}\sqrt{{\lambda }_2}(z+c_1)\right)\right)}{2{\lambda }_2}},q=-\sqrt{5}{\mu }_1;\end{array}\end{array}$$

(69)

$$\begin{array}{c}\hfill u=i\sqrt{{\displaystyle \frac{15}{2}}}{\lambda }_2{tan}^2\left({\displaystyle \frac{\sqrt{{\lambda }_2}}{2}}(z+c_1)\right)(1+{cot}^4\left({\displaystyle \frac{\sqrt{{\lambda }_2}}{2}}(z+c_1)\right))-{\displaystyle \frac{{\nu }_1}{2{\lambda }_2}},q=\sqrt{5}{\mu }_1;\end{array}$$

(70)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill u=i\sqrt{{\displaystyle \frac{15}{2}}}{\lambda }_1{tanh}^2\left({\displaystyle \frac{1}{2}}\sqrt{{\lambda }_1}(z+c)\right)(1+{coth}^4\left({\displaystyle \frac{1}{2}}\sqrt{{\lambda }_1}(z+c)\right))-{\displaystyle \frac{{\nu }_2}{2{\lambda }_1}},q=-\sqrt{5}{\mu }_2;\end{array}\end{array}$$

(71)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill u={\displaystyle \frac{{\nu }_2+i\sqrt{30}{\lambda }_1^2{tan}^2\left(\frac{1}{2}\sqrt{{\lambda }_1}(z+c_1)\right)\left(1+{cot}^4\left(\frac{1}{2}\sqrt{{\lambda }_1}(z+c_1)\right)\right)}{2{\lambda }_1}},q=\sqrt{5}{\mu }_2.\end{array}\end{array}$$

(72)

All solutions (48)–(59), (62)–(65), (69)–(72) for Equation (3) have a similar power structure, namely sech (:), tanh (:), coth (:), tan (:), cot (:), sec (:) and exp (:) functions. One should note that some of the solutions given in hyperbolic functions can be presented in trigonometric functions.

For the case (43)₃, (67), (68)₂, we again obtain solution $u=1$.

For the case of (43)₃, (67), (68)₃, we once again obtain solution (66).

5. Conclusions

The existence and uniqueness of the solutions for EFK in the analyticity domain for a complex plane have been proved. A formula for the convergence radius of the analyticity domain has been derived, which guarantees the absence of a moveable singular point. Analytical approximate solutions are constructed for real and complex initial data. The results of numerical study are presented.

Exact one-parametric complex families of solutions are constructed for special values of one basic parameter.

The method presented in the article can be generalized to other nonlinear differential equations, both ordinary and in fractional derivatives.