Recovery-Enhanced Image Steganography Framework with Auxiliary Model Based on Invertible Neural Networks

Abstract

With the advancement of technology, the information hiding capacity has significantly increased, allowing a cover image to conceal one or more secret images. However, this high hiding capacity often leads to contour shadows and color distortions, making the high-quality recovery of secret images extremely challenging. Existing image hiding algorithms based on Invertible Neural Networks (INNs) often discard useful information during the hiding process, resulting in poor quality of the recovered secret images, especially in multi-image hiding scenarios. The theoretical symmetry of INNs ensures the lossless reversibility of the embedder and decoder, but the lost information generated in practical image steganography disrupts this symmetry. To address this issue, we propose an INN-based image steganography framework that overcomes the limitations of current INN methods in image steganography applications. Our framework can embed multiple full-size secret images into cover images of the same size and utilize the correlation between the lost information and the secret and cover images to generate the lost information by combining the auxiliary model of the Dense–Channel–Spatial Attention Module to restore the symmetry of reversible neural networks, thereby improving the quality of the recovered images. In addition, we employ a multi-stage progressive training strategy to improve the recovery of lost information, thereby achieving high-quality secret image recovery. To further enhance the security of the hiding process, we introduced a multi-scale wavelet loss function into the loss function. Our method significantly improves the quality of image recovery in single-image steganography tasks across multiple datasets (DIV2K, COCO, ImageNet), with a PSNR reaching up to 50.37 dB (an improvement of over 3 dB compared to other methods). The results show that our method outperforms other state-of-the-art (SOTA) image hiding techniques on different datasets and achieves strong performance in multi-image hiding as well.

1. Introduction

Image steganography is a technique for hiding information in digital images to transmit and receive secret data without being detected [1,2]. Initially, traditional steganography methods operate within a distortion coding framework, strategically assigning different levels of distortion to other elements of the carrier by minimizing specific distortion metrics to embed secret information [3,4,5]. Traditional image steganography techniques are mainly classified into two domains: spatial steganography [6,7,8,9,10] and transform domain steganography [11,12,13,14,15]. Spatial steganography conceals information directly within the pixel values of an image. At the same time, transform domain steganography embeds data within the transformed representation of the image, such as in the frequency or wavelet domains.

With the increasing popularity of deep learning, a lot of work has been carried out to apply neural networks to image steganography tasks. Additionally, early studies that used deep learning for image steganography typically used deep neural networks (DNNs) rather than hiding and extracting partial phase processes [16,17,18]. The current trend leans towards end-to-end training of neural networks to embed and reveal secret information, which has proven to be more efficient and offers superior performance in capacity, security, and robustness compared to traditional methods [19,20]. In recent years, invertible neural networks(INNs) have become prominent in the realm of image hiding [21,22,23,24,25,26]. Among these methods, symmetry is crucial, especially when using invertible neural networks, as it ensures a high degree of symmetry between the encoder and decoder, theoretically enabling lossless reversible recovery. However, due to the presence of information loss in practice, the symmetry of INNs is often compromised. To address this, our proposed method aims to preserve the symmetrical properties of INNs to the greatest extent possible, thereby achieving more accurate image recovery.

In this paper, we present an invertible neural network model for multi-image steganography. The experimental findings demonstrate the contribution of this paper to improving invertible neural networks. In the invertible neural networks previously used in the field of image steganography, the hiding and revealing processes share the same network parameters. However, a critical issue arises during the steganographic process: the recipient cannot obtain the lost information generated by the hidden process, making it useless as input for the revealing phase. Our proposed model effectively addresses this challenge by generating auxiliary information to replace lost information and utilizing a training strategy, as shown in Figure 1.

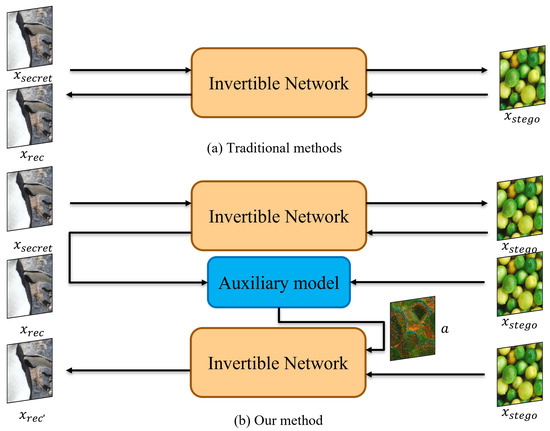
Figure 1. An illustration of the difference between traditional image hiding methods and our method.

The main contributions of this paper are summarized as follows:

• We present a novel multi-image steganography network based on an invertible neural network for high-quality recovery.
• We propose a Dense–Channel–Spatial Attention Module (DCSAM)-driven auxiliary model, employing cross-level feature fusion and dynamic weight allocation, to recover information lost during the hiding process and to provide auxiliary information for the second revealing process.
• We propose a multi-stage progressive training strategy to enhance model stability and reduce interference between the invertible neural network and the auxiliary model. This strategy prioritizes training with original secret images for rapid initial convergence, then gradually transitions to recovered images for dynamic adaptation, culminating in alternate fine-tuning for efficient fusion of the two models.
• We introduce a multi-scale wavelet loss function to restrict the multi-dimensional feature consistency of the cover image and stego image in the low-frequency approximation component and high-frequency detail component, thereby enhancing the security of the hiding process.

2. Related Works

2.1. Image Steganography

Image steganography is a key research area in steganography, where a secret image is embedded within an image and then concealed in another image. Unlike traditional low-capacity information hiding, it requires a large hiding capacity. As the amount of hidden information increases, the imperceptibility and security of the resulting image inevitably decrease, making image hiding particularly challenging.

Baluja et al. [20] first proposed using deep neural networks to hide an entire color image within another image. Rahim et al. [27] proposed a joint end-to-end training model based on the former. Weng et al. [28] further applied this technique to video steganography through temporal residual modeling. Baluja et al. [29] first tried to concatenate two secret images together and hide them in a cover image using an autoencoder-based network. Lu et al. [22] proposed a reversible network, ISN, which treats hiding and recovery as a pair of inverse problems in the image domain. All these studies demonstrate the potential of deep networks for image hiding.

In addition, in order to enhance the security of steganography, many researchers have introduced adversarial training into image steganography models. Zheng et al. [30] proposed a novel adversarial synthetic image steganography called CAIS, which combines rule-based synthesis with generative adversarial networks through a self-supervised mechanism to reduce visual artifacts and resist deep steganalysis. Yao et al. [31] proposed a novel end-to-end deep neural network for image steganography based on a generative adversarial network (GAN) and discrete wavelet transform (DWT). It can help the model find a better location for embedding information. Hu et al. [32] proposed a DIH-OAIN framework that can improve the visual quality and imperceptibility of image hiding while ensuring computational efficiency. These studies collectively demonstrate the effectiveness of adversarial training in enhancing the robustness and security of image steganography.

2.2. Invertible Neural Network

The concept of invertible neural network (INN) was first introduced by Dinh et al. [33]. Invertible neural networks are unique in that they allow forward and backward computation through the neural network. To make INN better for image-related tasks, Dinh et al. [34] introduced convolutional layers and multi-scale layers into the coupled model to reduce the computational cost and improve the regularization ability. Kingma et al. [35] introduced invertible 1 × 1 convolution to INN and proposed Glow, which is very effective for photorealistic synthesis and manipulation of images.

Due to their excellent performance, invertible neural networks have been used in many image-related tasks. For example, Ouderaa et al. [36] applied an INN to the task of image-to-image translation. Xiao et al. [37] tried image rescaling using an INN to find the mapping between a low-resolution image and a high-resolution image. Furthermore, Wang et al. [38] applied an INN to the task of digital image compression.

Benefiting from the excellent performance of invertible neural networks in image processing, researchers have introduced them into the field of image steganography. Jing et al. [21] first introduced INN into the field of image steganography and proposed the HiNet model. The model realizes invertible steganography in the wavelet domain and proposes a low-frequency wavelet loss to ensure that most information is hidden in the high-frequency sub-band, which significantly improves the security of hiding but only realizes the hiding of a single image, and the hiding capacity is not high. This algorithm improves the security to some extent, but it does not consider the robustness against attacks. Therefore, Fang et al. [23] designed an invertible noise layer (INL) based on this to simulate the distortion, which improves the robustness against attacks to some extent.

In addition, with respect to the aspects of high-capacity image steganography, Lu et al. [22] proposed a high-capacity image steganography method, which can embed multiple secret images into a cover image and obtain a high-quality stego image and recovered image at the same time. Of course, the high capacity reduces its anti-detection security. Guan et al. [24] proposed a multi-image hiding framework based on invertible neural networks and designed an Importance Map (IM) module to guide the current image hiding according to the previous image hiding results. Li et al. [25] designed a deep invertible neural network by introducing a spatial channel joint attention mechanism. This joint attention mechanism can effectively solve the problem of the visual quality and security degradation of stego images caused by high embedding capacity.

In the field of image steganography, addressing the loss of information during the hiding process has been a significant challenge. Various methods have been proposed to handle this issue, each with its strengths and limitations. Lu et al. [22] use a constant matrix as an auxiliary variable. Jing et al. [21] use random Gaussian distribution as an auxiliary variable. Although these methods achieve good results, they have little correlation with lost information in the steganography process. Therefore, only the invertible model can obtain good results by training and learning by inputting a Gaussian distribution or constant matrix as auxiliary variables in the process of disclosure. However, we have observed that these methods overlook the inherent symmetry of invertible neural networks (INNs), which is theoretically key to achieving lossless reversible recovery. In practice, due to the presence of information loss, the symmetry of INNs is disrupted, directly affecting the quality of recovery. In fact, if the lost information could be directly input, the reversibility should theoretically yield the best results, which also indirectly highlights the shortcomings of existing methods. In addition, Xu et al. [39] proposed a method to generate auxiliary variables. At the sender, the lost information r is input into an invertible neural network, and the stego image is used as the dependency to generate a Gaussian distribution. At the receiver, the Gaussian distribution is fed to the same invertible neural network, and the stego image is used as a dependency to recover the auxiliary variable z, which is close to the lost information r. However, the effect of this model is similar to that of Hinet. And Wang et al. [26] proposed a method that views image steganography as an image super-resolution task, which converts a low-resolution cover image into a high-resolution stego image while hiding the secret image. The feature dimension of the generated stego image matches the total dimension of the input secret and cover images, thus eliminating the lost information. However, due to the low resolution of the cover image, its security is not high.

3. Proposed Method

In this section, we propose a novel type of invertible neural network, designed to achieve high-quality recovery image hiding. Table 1 lists a summary of the symbols used in this paper.

Table 1. Summary of symbols in this paper.

Symbol	Meaning of Representation
$x_{cover}$	Cover image: the image used to hide secret information
$x_{secret}$	Secret image: the image to be hidden
$x_{stego}$	Stego image: the image with secret information inside
$x_{sr}$	the recovered secret image from the stego image in the first revealing process
$x_{s{r}^{\prime }}$	the recovered secret image from the stego image in the second revealing process
r	lost information: the information lost in the concealing process
z	auxiliary variable: the variable to help recover the image
a	auxiliary information: helps recover the image in the second revealing process

3.1. Framework

Figure 2 shows the model framework of the proposed method, which leverages an invertible neural network (INN), an auxiliary model module, and Discrete Wavelet Transform (DWT)/Inverse Discrete Wavelet Transform (IWT). The framework aims to achieve high-quality secret image recovery while maintaining imperceptibility in the stego image.

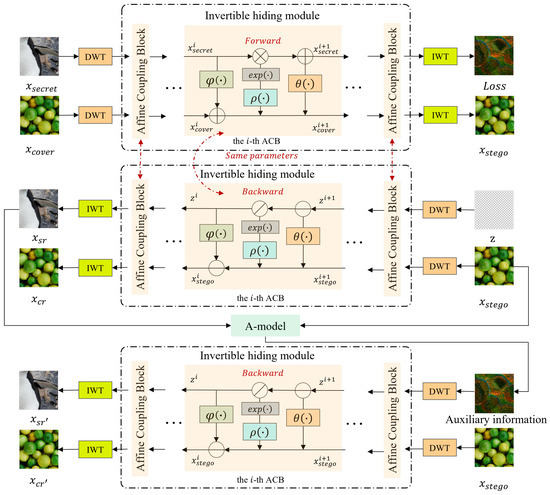
Figure 2. The framework of our model. In the forward hiding process, the secret image is hidden within the cover image through multiple hiding blocks. In the first revealing process, the stego image and the auxiliary variable z following a Gaussian distribution are sent into a series of revealing blocks to recover the secret image. Then, the recovered secret image and the stego image are sent into the A-model to obtain auxiliary information a. Finally, the stego image and the obtained auxiliary information a are sent into a series of revealing blocks to recover the final secret image.

The process begins by applying DWT to both the secret image $x_{secret}$ and the cover image $x_{cover}$. DWT decomposes the images into different frequency sub-bands, allowing for more effective hiding of the secret information. This decomposition is crucial as it allows the secret data to be placed in less perceptually important parts of the image, improving steganographic quality.

Following the DWT, the INN’s invertible blocks are used to embed the DWT-transformed secret image $x_{secret}$ into the DWT-transformed cover image $x_{cover}$. This hiding process yields the stego image $x_{stego}$ and the lost information r. The lost information r, although termed lost, actually represents the information removed from the cover image to accommodate the secret. Understanding this loss is key to improving recovery. By applying the inverse of the INN transformation to the stego image (after IWT), an initial recovered secret image $x_{sr}$ is obtained.

Then, the framework introduces the auxiliary model (A-model). The initially recovered secret image $x_{sr}$ and the hidden image $x_{stego}$ are both input into this model to output auxiliary information $L_a$. This information is used to correct the recovery results, and the auxiliary model can capture the information loss during the hiding process, thereby predicting a more accurate recovery method.

Finally, the auxiliary information $L_a$ and the DWT-transformed stego image $x_{stego}$ are passed through the reverse process of the INN. This second pass, guided by the auxiliary information, aims to refine the initial recovery. The output of this stage is the second recovered secret image $x_{s{r}^{\prime }}$. This two-stage recovery process, with the auxiliary model acting as a bridge, is a key contribution of this work.

3.2. Invertible Concealing and Revealing Process

As shown in Figure 1, the hiding and revealing blocks have the same sub-modules and share the same network parameters, but the information flows in opposite directions. There are M hiding blocks with the same architecture, which are constructed as follows. For the i-th hiding block in the forward process, the inputs are $x_{cover}^i$ and $x_{secret}^i$; the outputs $x_{cover}^{i+1}$ and $x_{secret}^{i+1}$ are as follows:

$$x_{cover}^{i+1}=x_{cover}^i+\phi \left(x_{cover}^i\right)$$

(1)

$$x_{secret}^{i+1}=x_{secret}^i·exp\left(\alpha \left(\rho \left(x_{cover}^{i+1}\right)\right)\right)+\theta \left(x_{cover}^{i+1}\right)$$

(2)

where $\alpha$ is a sigmoid function multiplied by a constant factor serving as a clamp and · indicates the dot product operation. Here, $\phi (·)$, $\rho (·)$ and $\theta (·)$ are arbitrary functions and we adopt the widely used dense block in [40] to represent them for its good representation ability. After the last concealing block, we can obtain the outputs $x_{cover}^{M+1}$ and $x_{secret}^{M+1}$, which are then fed into two IWT blocks to generate the stego image $x_{stego}$ and lost information r, respectively.

In the revealing process, the information flow direction is from the $(i+1)$-th revealing block to the i-th revealing block, which is in reverse order to the concealing process, as shown in Figure 1. Specifically, for the M-th revealing block, the inputs are $x_{stego}^{M+1}$ and $Z^{M+1}$, which are generated by the stego image $x_{stego}$ and an auxiliary variable Z through DWT. Here, Z is randomly sampled from a Gaussian distribution. The outputs of the M-th revealing block are $x_{stego}^M$ and $Z^M$. For the i-th revealing block, the inputs are $x_{stego}^{i+1}$ and $Z^{i+1}$, and the outputs are $x_{stego}^i$ and $Z^i$. Their relationship is modeled as follows:

$$Z^i=(Z^{i+1}-\theta \left(x_{stego}^{i+1}\right))·exp(-\alpha \left(\rho \left(x_{stego}^{i+1}\right)\right)))$$

(3)

$$x_{stego}^i=x_{stego}^{i+1}-\phi \left(Z^i\right)$$

(4)

After the last revealing block, i.e., the revealing block 1, the output $x_{stego}^1$ is fed into an IWT block to generate the recovery image $x_{sr}$.

3.3. A-Model (The Auxiliary Model)

In the revealing process, researchers typically use Gaussian distributions to replace lost information r, aiming to recover the secret image. Although this method produces reasonably effective recovery results, it assumes that lost information follows a specific statistical pattern, which often fails to accurately represent the complex nonlinear relationships in the image. While the Gaussian distribution provides random information to help the model’s training, enhancing its approximation of the secret image, this approach still faces limitations in recovery precision and quality.

Investigations show a strong correlation between lost information and both the cover and secret images, indicating that the lost information can be more accurately recovered by utilizing features from both images, which is shown in Figure 3. However, traditional methods based on Gaussian distribution assumptions fail to fully exploit this relationship. To address this limitation, we proposed an auxiliary model (A-model) designed to learn the underlying relationships between the cover image and the secret images for better recovery of lost information. The architecture of the A-model is shown in Figure 4 and Figure 5 below.

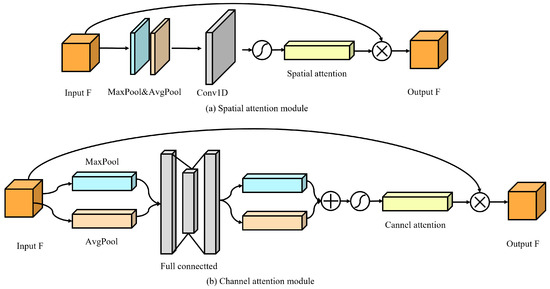
Figure 3. Visual comparison of cover image, secret image, and loss information from left to right, respectively.

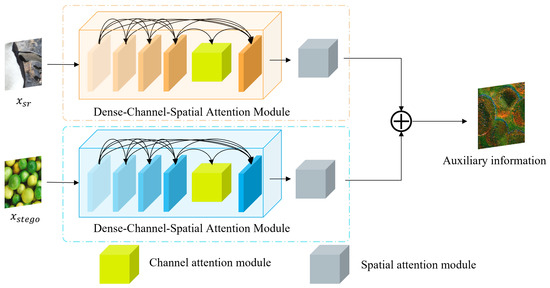
Figure 4. The architecture of the A-model. This model integrates the Dense–Channel–Spatial Attention Module to enhance image feature extraction. Specifically, the Dense Block is used to extract multi-level features, followed by the Channel Attention Layer, which performs adaptive weighting on the feature channels to highlight important channel features, while the Spatial Attention Layer further performs adaptive weighting on the feature space, focusing on key areas of the image. Finally, the outputs from the two modules are concatenated to generate auxiliary information a.

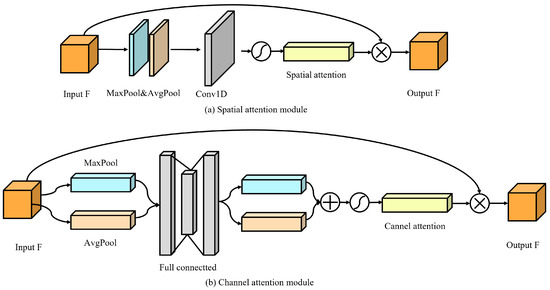
Figure 5. Architecture of spatial and channel attention module.

The structure of the A-model is as follows:

First, the model input consists of the cover image and the secret image. During recovery, the stego image replaces the cover image due to the unavailability of a high-quality cover image.

Second, the input images are processed using Dense Block Neural Networks (DenseNet) to extract features. DenseNet’s densely connected architecture effectively preserves multilevel feature representations and enhances inter-feature dependencies, which is crucial for capturing intricate details and relationships within the images. This architecture is consistent with the previous invertible neural network.

Then, to further enhance feature extraction and representation, channel attention and spatial attention modules are integrated into the DenseNet architecture, forming the Dense–Channel–Spatial Attention Module. Specifically, the channel attention layer is added before the last layer of each Dense Block, allowing the network to selectively focus on important channels and enhance the representation of key features. Because the lost information generally highlights a single color as a whole, it affects different image channels to different degrees. The channel attention module can effectively highlight these key channels by weighting the responses of important channels. This allows the model to focus more precisely on the channels containing the lost content, which is essential for improving the accuracy of secret image recovery.

In addition, after the dense block, we introduce the spatial attention module. This module can effectively identify and highlight important spatial regions in feature maps, further improving the network’s ability to capture fine-grained details and relationships in images. Since the lost information not only contains the high-frequency details of the image but also covers the texture information of the cover image and the secret image, through the guidance of the spatial attention module, the network can focus more accurately on these key areas and generate better auxiliary information to restore the image details more accurately in the recovery process.

Finally, the outputs from the two networks are concatenated to generate auxiliary information a.

3.4. Training Strategy

To enhance the model’s training stability and recovery performance, we proposed a three-stage training strategy. This method incrementally optimizes different components of the model, resolving the conflict between hiding and recovery objectives and achieving high-quality secret image hiding and recovery. The detailed steps are as follows:

Stage 1: Train only the invertible neural network (INN) to optimize its ability to embed and recover secret images independently.

Stage 2: Freeze INN parameters and train the auxiliary model (A-model) independently to generate auxiliary information from stego and secret images to ensure the convergence of the auxiliary model. Independent training avoids gradient interference. A curriculum learning strategy stabilizes training and ensures a smooth transition. The A-model is initially trained primarily with original secret images, then gradually transitioned to INN-recovered versions for robust adaptation to reconstructions.

Stage 3: Unfreeze INN parameters and conduct joint training of the entire network. This enhances overall performance by allowing gradient flow between the INN and A-model (where the input is changed to the recovered secret image), improving secret recovery quality and stego image accuracy.

3.5. Loss Function

• Concealing loss. The forward concealing process aims to hide $x_{cover}$ into $x_{secret}$ to generate a stego image $x_{stego}$. The stego image $x_{stego}$ is required to be indistinguishable from the cover image $x_{cover}$. Toward this goal, we use mean square error (MSE) to measure the difference between the cover and stego image. The concealing loss $L_{hid}$ is defined as follows:

  $$L_{hid}=MSE(x_{cover},x_{stego})$$

  (5)

  where $x_{stego}$ is equal to $M(x_{cover},x_{secret})$, with $M(·)$ indicating the invertible neural network.
• Multi-scale wavelet loss. To improve the security of steganography, we introduce a multi-scale wavelet loss function. In wavelet decomposition, low-frequency subbands (LL) usually contain the main structural information of the image, while high-frequency subbands (LH, HL, HH) contain the details of the image. Although the low-frequency subband loss calculation is effective in measuring the major structural differences between two images, it is significantly inadequate in capturing the detailed changes in the images. To achieve this, we introduce the Wasserstein distance in the high-frequency subband, which is a measure of the difference between two probability distributions and can effectively capture changes in image details. Therefore, the multi-scale wavelet loss function combines the mean square error (MSE) of the low-frequency subband with the Wasserstein distance of the high-frequency subband. Specific definitions are as follows:

  $$L_{mul}=\sum _{l=1}^L(\alpha ·L_{LL}+\beta ·(W_{LH}+W_{HL}+W_{HH}))$$

  (6)

  where L represents the number of wavelet decomposition layers and the parameters $\alpha$ and $\beta$ are weights that balance the contributions of the low-frequency and high-frequency losses, respectively. Suppose that $DWT{(·)}_{LL}$ indicates the operation of extracting low-frequency subbands after wavelet decomposition; $L_{LL}$ and $W(·)$ are calculated as follows:

  $$L_{LL}=MSE\left({DWT\left(x_{cover}\right)}_{LL},{DWT\left(x_{stego}\right)}_{LL}\right)$$

  (7)

  $$W(i,j)=\underset{\gamma \in \prod (i,j)}{inf}{\mathbb{E}}_{x,y\sim \gamma }\left[∥x-y∥\right]$$

  (8)

  where $\prod (i,j)$ represents the set of all possible joint distributions of the distributions i and j combined, and $i=DWT{\left(x_{cover}\right)}_{LH,HL,HH}$, $j=DWT{\left(x_{stego}\right)}_{LH,HL,HH}$.
• Revealing loss. The revealing loss is used to encourage the recovered secret image $x_{sr}$ to resemble the original secret image $x_{secret}$ in the backward revealing process. We also use the MSE to denote the mean square error between the recovered secret image $x_{sr}$ and the corresponding original secret image $x_{secret}$. So, we define the revealing loss $L_{rev}$ as follows:

  $$L_{rev}=MSE(x_{secret},x_{sr})$$

  (9)
• Auxiliary-model loss. The auxiliary-model loss is used to encourage the auxiliary information a to resemble the lost information r, so as to help the neural network model to better recover the secret image. Similarly, we use the MSE and Wasserstein distance to denote the mean square error between the loss information r and the auxiliary information a. So, we define the revealing loss $L_a$ as follows:

  $$L_a=MSE(r,a)+W(r,a)$$

  (10)
• Total loss function. Since our method requires three-step training, there are three total loss functions.
  The first total loss function $L_{total}$ is a weighted sum of concealing loss $L_{hid}$, revealing loss $L_{rev}$, and multi-scale wavelet loss $L_{mul}$ as follows:

  $$L_{total}={\lambda }_c{L}_{hid}+{\lambda }_r{L}_{rev}+{\lambda }_m{L}_{mul}$$

  (11)
  Here, ${\lambda }_c$, ${\lambda }_r$, and ${\lambda }_m$ are weights for balancing different loss terms. In this training process, we set ${\lambda }_r=2,{\lambda }_c=1,{\lambda }_m=1$.
  Then, the second total loss function $L_{total}^{\prime }$ is a weighted sum of the first revealing loss $L_{rev}$, auxiliary-model loss $L_a$, and second revealing loss $L_{{rev}^{\prime }}$, as follows:

  $$L_{total}^{\prime }={\lambda }_r{L}_{rev}+{\lambda }_a{L}_a+{\lambda }_r^{\prime }{L}_{re{v}^{\prime }}$$

  (12)
  Here, ${\lambda }_r$, ${\lambda }_a$, and ${\lambda }_r^{\prime }$ are weights for balancing different loss terms. In this training process, we set ${\lambda }_r=1,{\lambda }_a=1,{\lambda }_r^{\prime }=2$.
  Then, the third total loss function $L_{total}^{″}$ is a weighted sum of concealing loss $L_{hid}$, the first revealing loss $L_{rev}$, multi-scale wavelet loss $L_{mul}$, auxiliary-model loss $L_a$, and the second revealing loss $L_{re{v}^{\prime }}$, as follows:

  $$L_{total}^{″}={\lambda }_c{L}_{hid}+{\lambda }_r{L}_{rev}+{\lambda }_m{L}_{mul}+{\lambda }_a{L}_a+{\lambda }_r^{\prime }{L}_{re{v}^{\prime }}$$

  (13)
  Here, ${\lambda }_c$, ${\lambda }_r$, ${\lambda }_m$, ${\lambda }_d$, ${\lambda }_a$, and ${\lambda }_r^{\prime }$ are weights for balancing different loss terms. In this training process, ${\lambda }_r^{\prime }$ is set to 2, while others are set to 1. The overall training process of our proposed method is detailed in Algorithm 1.

Algorithm 1 The Training Process of Our proposed method for Single Image Hiding

1: Input: The cover image $x_{\mathrm{cover}}$ and the secret image $x_{\mathrm{secret}}$. 2: Output: Trained invertible neural networks $I_{\theta }(·)$ and the auxiliary model $I_{\mathrm{A}}(·)$. 3: Training Variables: $\theta$, ${\theta }_{\mathrm{A}}$ with Gaussian initialization. 4: Initialize: $\theta ,{\theta }_{\mathrm{A}}$ with Gaussian initialization. 5: while Step $<\max \_\mathrm{steps}$ do 6:     Compute $x_{\mathrm{stego}}=I_{\theta }(x_{\mathrm{cover}},x_{\sec \mathrm{ret}})$. 7:     Compute $x_{\mathrm{cr}},x_{\mathrm{sr}}=I_{\theta }^{-1}(x_{\mathrm{stego}},z)$. 8:     if TrainStep == 1 then 9:         Update $\theta \leftarrow \theta +\mathrm{lr}\times \mathrm{Adam}\left(L_{\mathrm{total}}\right)$. 10:     else 11:         if TrainStep == 2 then 12:            Compute $a=I_A(x_{\mathrm{stego}},x_{\mathrm{secret}})$. 13:            Compute $x_{c{r}^{\prime }},x_{s{r}^{\prime }}=I_{\theta }^{-1}(x_{\mathrm{stego}},a)$. 14:            Update ${\theta }_{\mathrm{A}}\leftarrow {\theta }_{\mathrm{A}}+\mathrm{lr}\times \mathrm{Adam}\left(L_{\mathrm{total}}^{\prime }\right)$. 15:         else 16:            Compute $a=I_A(x_{\mathrm{stego}},x_{\mathrm{sr}})$. 17:            Compute $x_{c{r}^{\prime }},x_{s{r}^{\prime }}=I_{\theta }^{-1}(x_{\mathrm{stego}},a)$. 18:            Update $\theta ,{\theta }_{\mathrm{A}}\leftarrow \theta ,{\theta }_{\mathrm{A}}+\mathrm{lr}\times \mathrm{Adam}\left(L_{\mathrm{total}}^{″}\right)$. 19:         end if 20:     end if 21: end while 22: Return:  $\theta ,{\theta }_{\mathrm{A}}$

4. Experiments

This section delineates the dataset, implementation specifics of the hiding and extraction processes, and the evaluation metrics utilized.

4.1. Datasets

The DIV2K [41] training dataset is used for training our model. The ratio of the training dataset to the test dataset is 8:1. To explore the influence of the secret image from different sources on the experimental results, the testing datasets include the DIV2K [41] testing dataset with 100 images at resolution 1024 × 1024, ImageNet [42] with 50,000 images at resolution 256 × 256, and the COCO [43] dataset with 5000 images at resolution 256 × 256. Note that the testing images are cropped using the center-cropping strategy to make sure the cover and secret images are with the same resolution.

4.2. Implementation Details

The number of concealing and revealing blocks M is set to 16 [21]. The Adam [44] optimizer is adopted to optimize our network. Our model adopts a three-stage training strategy to gradually optimize the invertible neural network and the A-model. In the first stage, only the INN is trained, with a total of 160K iterations (${\lambda }_c:{\lambda }_r:{\lambda }_m=1:2:1$). In the second stage, the parameters of the INN are fixed, and the A-model is trained for 80K iterations (${\lambda }_{aux}=1$). Loss weights are determined via grid search (${\lambda }_r:{\lambda }_a:{\lambda }_r^{\prime }=1:1:2$). In the third stage, jointly train the INN and the A-model for 80K iterations. Loss weights are determined via grid search (${\lambda }_c:{\lambda }_r:{\lambda }_m:{\lambda }_a:{\lambda }_r^{\prime }=1:1:1:1:2$). The entire three-stage training process took approximately 79 h in total (40 h for the first stage, 13 h for the second stage, and 26 h for the third stage).

During the training process, we used the Adam (${\beta }_1=0.9$, ${\beta }_2=0.999$) optimizer with an initial learning rate of 0.0001, halving it every 40K iterations. The training batch size was set to 4 to accommodate our experimental setup (GeForce RTX4060; 8 GB). We used the DIV2K training set for model training and split the training and test sets in an 8:1 ratio, with training image patches sized at 256 × 256. All training samples underwent the following preprocessing: random horizontal/vertical flipping ($p=0.5$), center cropping to $256\times 256$ resolution, and normalization to $[-1,1]$. The standardized preprocessing process ensured that the input data distribution was aligned, allowing other researchers to maintain model stability without needing to redesign the augmentation strategy when replacing datasets.

4.3. Evaluation Metrics

There are three metrics adopted to measure the quality of cover/stego and secret/recovery pairs, including Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) [45]. The larger values of PSNR and SSIM indicate higher image quality. PSNR and SSIM are calculated as follows:

$$MSE={\displaystyle \frac{1}{WH}}\sum _{m=1}^M\sum _{n=1}^H{(X_{m,n}-Y_{m,n})}^2$$

(14)

$$PSNR=10·lo{g}_{10}{\displaystyle \frac{{MAX}^2}{MSE}}$$

(15)

where $x_{m,n}$ and $y_{m,n}$ indicate the pixels at position $(m,n)$ of images X and Y, respectively. In addition, $MAX$ represents the maximum value of images, which is usually set as 255.

$$SSIM(c,s)={\displaystyle \frac{(2{\mu }_c{\mu }_s+C_1)(2{\sigma }_{cs}+C_2)}{({\mu }_c^2+{\mu }_s^2+C_1)({\sigma }_2^c+{\sigma }_2^x+C_2)}}$$

(16)

where ${\mu }_c$ and ${\mu }_s$ represent the average pixel values of the cover image and stego image, respectively. ${\sigma }_c$ and ${\sigma }_s$ represent standard deviation. ${\sigma }_c^2$ and ${\sigma }_s^2$ represent variance. ${\sigma }_{cs}$ is the covariance of c and s. Constants $C_1$ and $C_2$ stabilize the division with weak denominator. We set $C_1$ and $C_2$ as the default values of the original work [45]. In addition, we use the statistical steganalysis tool StegExpose [46] to evaluate the security performance of our method.

5. Results and Discussion

This section presents and discusses the experimental results evaluating the effectiveness of the proposed steganography technique. The experiments were implemented in Python (3.8.16), using a dataset of carrier images to hide one or more secret images. The evaluation focuses on the quality of the recovered secret images, the imperceptibility of the stego images, and security analysis. The recovery quality is quantitatively assessed using PSNR and SSIM, and qualitatively evaluated through visual comparison. Imperceptibility is similarly evaluated quantitatively using PSNR and SSIM, combined with visual analysis. Additionally, we conducted a security analysis, including an assessment of resistance to statistical analysis attacks. Ablation experiments were also performed to analyze the contribution of each component of the model. Subsequent subsections will detail the experimental results and their implications.

5.1. Single-Image Hiding

The field of single-image hiding encompasses a wide range of research, with existing work primarily focusing on specific application scenarios or emphasizing enhanced security and robustness. These focal points deviate from the main objective of this study. Therefore, we chose to compare our proposed model with HiNet [21], which is a pioneer in integrating reversible neural networks into the image steganography domain and has demonstrated compelling performance in single-image hiding tasks, making it a representative baseline. The following subsections detail the specific results obtained for both single-image hiding scenarios and provide a discussion of their implications.

• Quantitative results: Table 2 compares the numerical results of our model with HiDDeN [19], Baluja [20], and HiNet [21]. Table 2 presents a comprehensive comparison of our proposed model against existing state-of-the-art methods, evaluating performance across all relevant metrics for both the cover/stego image pairs and the secret/recovery image pairs. The results clearly demonstrate the superior performance of our approach.
  Table 2. Benchmark comparisons on different datasets, with the best results in red and second bests in blue. ↑ denotes higher value is better, and vice versa.

  Methods	Cover/Stego Image Pair
  	DIV2K		COCO		ImageNet
  	PSNR (dB)↑	SSIM↑	PSNR (dB)↑	SSIM↑	PSNR (dB)↑	SSIM↑
  HiDDeN [19]	35.21	0.9691	36.71	0.9876	34.79	0.9380
  Baluja [20]	36.77	0.9645	36.38	0.9563	36.59	0.9520
  HiNet [21]	46.53	0.9930	41.21	0.9852	41.60	0.9858
  Ours	47.78	0.9952	42.83	0.9871	42.20	0.9884
  Methods	Secret/Recovery Image Pair
  	DIV2K		COCO		ImageNet
  	PSNR (dB)↑	SSIM↑	PSNR (dB)↑	SSIM↑	PSNR (dB)↑	SSIM↑
  HiDDeN [19]	36.43	0.9696	37.68	0.9845	35.70	0.9601
  Baluja [20]	35.88	0.9377	35.01	0.9341	34.13	0.9247
  HiNet [21]	46.24	0.9924	40.10	0.9846	40.03	0.9807
  Ours	50.37	0.9969	43.40	0.9881	43.26	0.9901

  Specifically, our model achieves substantial improvements in PSNR for the crucial secret/recovery image pairs. We observe significant gains of 4.13 dB, 3.30 dB, and 3.23 dB on the challenging DIV2K, COCO, and ImageNet datasets, respectively. These improvements highlight the effectiveness of our model in accurately extracting the hidden secret image from the stego image.
  Furthermore, our model also yields notable PSNR improvements for the cover/stego image pairs, with gains of 1.25 dB, 1.62 dB, and 0.8 dB observed across the aforementioned datasets. These results indicate that our model is capable of hiding the secret image while maintaining high visual quality in the stego image.
  Consistent with the PSNR trends, we observe similar performance enhancements in SSIM across all datasets and image pairs. This further validates the effectiveness of our proposed approach in preserving structural information during the hiding and revealing processes. These results underscore the efficacy of our proposed multi-scale wavelet loss function, the incorporation of auxiliary models, and the design of a tailored training strategy. By jointly optimizing these components, our model effectively enhances both the hiding and revealing performance, leading to significant improvements in image quality and secret image recovery accuracy.
• Qualitative Results: Figure 6 presents a visual comparison of stego and recovered images generated by our proposed model and the HiNet method. Due to space constraints and the conceptual similarities between HiNet variants, we focus our visualization comparison on the superior performing HiNet model evaluated on the DIV2K dataset. Our method demonstrates near-perfect secret image concealment, exhibiting negligible visual discrepancies between cover and stego images. Furthermore, the accuracy of the recovery process is evident in the near-black residual map, indicating minimal information loss. In contrast, HiNet exhibits noticeable texture-copying artifacts, particularly prominent in smooth image regions. These artifacts manifest as distortions and color inconsistencies in both the stego and recovered images. Our model demonstrably outperforms HiNet in both recovery accuracy and color fidelity, effectively mitigating such artifacts and preserving image integrity throughout the hiding and extraction processes.
  

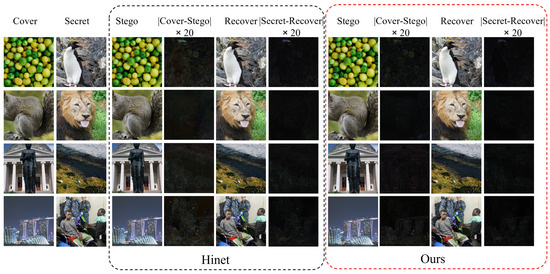  Figure 6. Visual comparisons of stego and recovery images between our model and the comparison method HiNet [21].
  Figure 7 shows the comparison between our model and the enlarged and recovered loaded images generated by the HiNet method. By zooming in, you can clearly see the difference in the processing of image details between the two methods. Here, we chose a more complex pair of carrier/secret images for comparison. It is clear that although there is some distortion in the residual image of both, our model performs better in detail retention. Specifically, our model is better able to retain the texture and edge information of the image, whereas the HiNet method is blurred on these key details. This shows that our model has stronger robustness and higher fidelity when processing complex images. For example, our model employs multi-scale wavelet loss, which allows the model to learn representations of different frequencies, thus preserving fine detail. In addition, our auxiliary model also introduces the attention mechanism, which can help the model to better focus on the important areas in the image, so as to better retain the details of these areas in the generation of auxiliary information, so as to obtain higher recovered image quality.
  

  Figure 7. Enlarged visual comparisons of stego and recovery images between our model and the comparison method HiNet [21].
• Computational efficiency analysis: On the NVIDIA GeForce RTX4060 GPU (8 GB memory), the end-to-end processing speed of a single $256\times 256$ image (including steganography generation and secret recovery) was tested and compared with HiNet. The results show that the average processing time for the HiNet method is $355\pm 3$ ms, corresponding to a real-time frame rate of FPS = 2.8. In contrast, the processing time of the proposed method is $621\pm 8$ ms, corresponding to an FPS of 1.58. Although the introduction of an auxiliary module and a secondary recovery mechanism resulted in an increase in inference time of $75\%$ and a decrease in FPS of $43.6\%$, the proposed approach achieved a better balance between performance and complexity.
  Specifically, the total number of parameters for the proposed method is 4.30 M (4.05 M for the main INN module and 0.25 M for the auxiliary model), with the auxiliary model accounting for only $5.8\%$ of the total parameters ($0.25/4.30$). Therefore, the total number of parameters is comparable to HiNet (4.05 M). In addition, the peak memory usage for a single inference is 3.1 GB, which is an increase of $10.7\%$ compared to HiNet’s 2.8 GB. However, on the same test set, the proposed method improves the PSNR of the key secret/recovered image pairs by 4.13 dB, significantly enhancing the quality of image recovery.
  In summary, although the proposed method is slightly lower in inference efficiency compared to HiNet, it successfully enhances the model’s performance by introducing auxiliary modules and a secondary recovery mechanism, while maintaining a low computational complexity.

5.2. Multi-Image Hiding

The field of multi-image hiding has involved extensive research, with diverse technologies. To evaluate the advantages of our model, we chose to compare it with DeepMIH and iSCMIS, which are recent representative models of multi-image hiding using reversible neural networks. Comparison with these advanced models can highlight the innovative contributions of our method in multi-image hiding. This comparative analysis will comprehensively assess the performance of our model in terms of hiding capacity, effectiveness, and image recovery quality.

• Quantitative results: Table 3 compares the numerical results of our model with ISN [22], DeepMIH [24], and iSCMIS [25]. Due to the presence of a second reveal phase, which increases complexity during model training, more GPU memory is required, which our experimental device (GeForce RTX4060; 8GB) cannot support. To accomplish the task of hiding multiple images on our device, we reduced the size of the input image. Thus, some of our results are naturally slightly less favorable than DeepMIH and iSCMIS.
  Table 3. Benchmark comparisons on different datasets, with the best results in red and second bests in blue. ↑ denotes higher value is better, and vice versa.

  Methods	Secret/Recovery-1 Image Pair
  	DIV2K		COCO		ImageNet
  	PSNR (dB)↑	SSIM↑	PSNR (dB)↑	SSIM↑	PSNR (dB)↑	SSIM↑
  ISN [22]	37.21	0.9627	36.09	0.9513	36.01	0.9592
  DeepMIH [24]	41.41	0.9801	36.55	0.9613	36.63	0.9604
  iSCMIS [25]	41.75	0.9832	37.06	0.9646	37.29	0.9644
  Ours	42.67	0.9880	37.62	0.9643	37.84	0.9665
  Methods	Cover/Stego-2 Image Pair
  	DIV2K		COCO		ImageNet
  	PSNR (dB)↑	SSIM↑	PSNR (dB)↑	SSIM↑	PSNR (dB)↑	SSIM↑
  ISN [22]	40.19	0.9867	36.98	0.9598	37.20	0.9594
  DeepMIH [24]	41.22	0.9838	37.21	0.9624	37.22	0.9612
  iSCMIS [25]	43.01	0.9899	39.13	0.9773	39.21	0.9772
  Ours	42.59	0.9865	38.44	0.9696	38.53	0.9723
  Methods	Secret/Recovery-2 Image Pair
  	DIV2K		COCO		ImageNet
  	PSNR (dB)↑	SSIM↑	PSNR (dB)↑	SSIM↑	PSNR (dB)↑	SSIM↑
  ISN [22]	37.81	0.9625	36.86	0.9525	35.90	0.9620
  DeepMIH [24]	42.53	0.9858	37.72	0.9696	37.83	0.9689
  iSCMIS [25]	42.53	0.9836	37.48	0.9664	37.69	0.9661
  Ours	43.90	0.9894	38.83	0.9762	38.98	0.9775

  As shown in Table 3, our model significantly outperforms the previous two methods across all four metrics for the secret/recovery-1, cover/stego-2, and secret/recovery-2 image pairs, with a slight exception in the cover/stego-2 comparison with iSCMIS. Specifically, mirroring the single-image hiding results, our method achieves substantial PSNR gains for the secret/recovery-1 image pair, improving upon the second-best performing method by 0.92 dB, 0.56 dB, and 0.55 dB on the DIV2K, COCO, and ImageNet datasets, respectively. Similarly, for the secret/recovery-2 image pair, we observe consistent PSNR improvements of approximately 1 dB across all three datasets. However, for the cover/stego-2 image pairs, our model’s PSNR is slightly lower than iSCMIS by 0.63 dB, 0.57 dB, and 0.50 dB on the DIV2K, COCO, and ImageNet datasets, respectively. This slight decrease in stego image quality for the multiple-image hiding scenario warrants further investigation. In addition, the SSIM indicator showed a similar improvement trend in secret image recovery, while the performance of hidden image quality decreased slightly in the case of multiple hiding. This comprehensive analysis of PSNR and SSIM metrics demonstrates the effectiveness of our approach in recovering hidden images, while also highlighting areas of potential improvement for maintaining steganographic image fidelity when embedding multiple secrets.
• Qualitative results: Figure 8 compares the stego and recovery images of our model and DeepMIH. Similarly, due to space constraints and model similarities, here we only compare the visualization with the better DeepMIH [24] on DIV2K (iSCMIS is not compared because its code is not publicly available). As shown in the figure, the visual difference between the cover and stego images produced by our method is nearly imperceptible, demonstrating successful concealment of the secret image. Furthermore, our method recovers the secret image more accurately compared to DeepMIH. On the DIV2K dataset, even at 20× magnification, the visual discrepancies between cover/stego and secret/recovered image pairs are negligible, validating the effectiveness of our approach. However, as observed in the quantitative analysis, the visual errors become more pronounced on the COCO and ImageNet datasets, which is consistent with the trend observed in the PSNR and SSIM results. This suggests that while our method performs exceptionally well on high-quality datasets like DIV2K, its performance may be more sensitive to the increased complexity and variability present in datasets like COCO and ImageNet.
  

  Figure 8. Visual comparisons of stego and recovery images between our model and comparison method DeepMIH [24] on DIV2K, COCO, and ImageNet datasets.

5.3. Security Analysis

Security analysis is an important part of the image hiding task, which is used to measure the security of the target image. Specifically, an analysis tool is used to measure the possibility of distinguishing between images that contain embedded secret information and those that do not. In this study, we use traditional statistical methods to verify the security of images generated by our model. The detection tool for traditional statistical methods is StegExpose [46].

As shown in Figure 9, the red color curve is the ROC curve of our model. We can see that the area under the ROC curve (AUC) value is close to 0.5, indicating that the detection accuracy is nearly equivalent to that of random guessing. This shows that the images generated by our model can effectively deceive the detection tool StegExpose, demonstrating a high level of security.

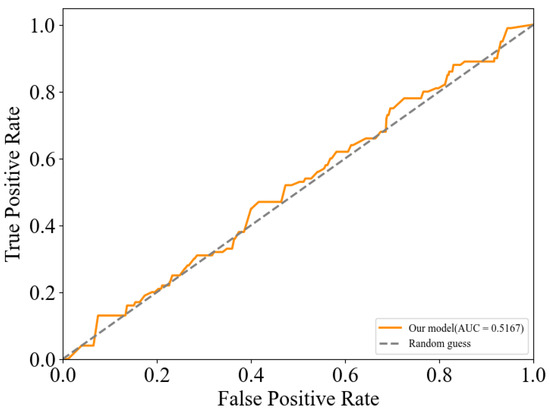
Figure 9. The ROC curve produced by StegExpose for our Model.

5.4. Ablation Study

An ablation study was conducted to evaluate the individual contributions of key components to the model’s performance. Specifically, we investigated the impact of the A-model architecture, the training strategy employed, and the inclusion of the multi-scale wavelet loss. Each of these elements was systematically removed or modified to assess its importance.

• A-model
  As shown in Table 4, the A-model plays an important role in improving the performance of our method. Specifically, as we can see from the first and second rows in Table 4, the PSNR value with the A-model increases by 1.83 dB and 1.29 dB for cover/stego and secret image/recovery pairs, respectively. The possible reason is that the A-model can successfully help the model to better recover the secret image, and the process of reducing the loss can also make it more effective for information hiding.
  Table 4. Ablation study on the A-model, training strategy, and multi-Scale wavelet loss function for single-image hiding. ✔ indicates that the policy is enabled, ✗indicates that the policy is disabled. The last row represents our model.

  A-Model	Training Strategy	Multi-Scale Wavelet Loss	Cover/Stego Image Pair		Secret/Recovery Image Pair
  			PSNR (dB)	SSIM	PSNR (dB)	SSIM
  ✗	✗	✗	41.81	0.9775	46.52	0.9917
  ✔	✗	✗	43.64	0.9889	47.83	0.9936
  ✔	✔	✗	45.54	0.9901	49.65	0.9956
  ✔	✔	✔	47.78	0.9952	50.37	0.9969

• Training strategy
  We can see from the second and third rows of Table 4 that for single-image hiding, using the training strategy improves PSRN by about 2 dB on the cover/stego and secret/recovered image pair. We have a similar effect on the hiding of multi-images. It fully demonstrates the effectiveness of the training strategy. The possible reason is that the multi-stage training strategy can successfully help the invertible neural network model and the A-model to do their respective jobs and finally perform better information concealing and revealing together.
• Multi-scale wavelet loss function
  We can see from the third and last rows of Table 4 that the application of the multi-scale wavelet loss function in single-image hiding tasks results in a significant improvement in PSNR by approximately 2 dB for the cover/stego image pair. This enhancement is also observed in the secret/recovered image pair, where the PSNR is similarly elevated by around 1 dB. The likely reason for this enhancement is that the multi-scale wavelet loss function effectively constrains the differences between the cover and stego images, ensuring that the stego image remains similar to the original cover image.

6. Conclusions

In this paper, we propose a novel invertible neural network (INN) for high-quality image hiding and recovery. The network models the image hiding and revealing processes as forward and backward operations of a reversible network, allowing parameter sharing for enhanced training efficiency. An auxiliary model performs a secondary revealing process, and a multi-stage training strategy improves secret image recovery, especially in multi-image hiding. Crucially, we integrate a Dense–Channel–Spatial Attention Module into the auxiliary model architecture, enabling it to selectively focus on important spatial and channel information for improved auxiliary information generation and recovery image quality. To further enhance steganographic performance, we introduce a multi-scale wavelet loss function. This function captures high-frequency details and multi-scale features, ensuring similarity between the hidden and cover images, thereby enhancing security. Experimental results demonstrate high-quality recovery and large-capacity image hiding, significantly outperforming state-of-the-art (SOTA) methods both quantitatively and qualitatively.

Symmetry plays a crucial role in this method. By focusing on addressing the symmetry issue of invertible neural networks (INNs) in the image steganography process, it significantly enhances the recovery performance of the secret image. Specifically, this method leverages the inherent symmetry of INNs to achieve a high degree of consistency between the embedder and decoder, thereby minimizing information loss and improving the quality of the secret image recovery. However, the practical implementation of symmetry and the relative gains it brings still require further.

The experimental results strongly support the conclusion that the proposed method exhibits excellent performance in single-image steganography, with PSNR exceeding 47 dB, and improvements in both PSNR and SSIM across multiple datasets. However, when hiding multiple images, the quality of the stego images shows a controllable yet non-negligible degradation. Specifically, when hiding two images, the PSNR decreases by 5.19 dB (from 47.78 dB to 43.59 dB), and the SSIM decreases by 0.072. This degradation phenomenon mainly stems from the fixed channel capacity of the INN layer, leading to feature competition and irreversible information loss between images during high-capacity encoding. In multi-image steganography, the feature differences between different images are significant. When they share the same channel capacity, feature competition intensifies, and some features of one image may be overshadowed or interfered with by the features of another image, leading to a decline in the quality of the stego images. At the same time, a fixed channel capacity reduces the capacity allocated to each image when encoding multiple images, making it impossible to fully express the features of all images, thereby leading to information loss.

Therefore, especially in the aspect of multi-image hiding, we observed the limitations of our model during the hiding process, which may be due to the second revelation phase generated by the auxiliary model, potentially limiting its ability to optimize the hiding phase. Even with the incorporation of wavelet techniques, the model may still struggle to fully exploit the available capacity for information hiding. This could be attributed to several factors. For instance, the auxiliary model’s revelation stage might introduce noise or biases that propagate back and hinder the refinement of the steganographic process. Alternatively, the specific wavelet transform chosen, or the way it is integrated with the loss function, might not be optimally suited for the type of data being hidden or the steganalysis methods being targeted. Further investigation is needed to explore these potential bottlenecks and identify strategies to improve the model’s hiding capabilities. This might involve exploring alternative wavelet bases, refining the architecture of the auxiliary model, or developing more sophisticated loss functions that better balance the trade-off between hiding capacity and undetectability.

In addition, since the current auxiliary model is trained only under ideal transmission conditions, it does not take into account the actual channel noise. When processing images affected by noise interference, the model-recovered secret images may exhibit significant detail loss. For example, when processing covert images that have undergone JPEG compression, the quality of the secret image recovered by the model significantly decreases. The block effect and detail loss caused by the compression of the steganographic image significantly affect the generation of auxiliary information, thereby impacting the recovery of the secret image. Therefore, introducing noise injection is expected to enhance robustness. But this will also affect the model’s recovery ability.

We identify four promising avenues for future research, focusing on both enhancements to the model’s capabilities and exploring its potential applications and broader impact:

• Enhancing Hiding Capacity via Adversarial Training: To overcome the current limitations in hiding capacity imposed by the auxiliary model’s training objective, we propose integrating adversarial training techniques. This approach aims to fortify the concealing process by training the model to generate steganographic data that are increasingly indistinguishable from cover data, thus improving its resilience against steganalysis.
• Enhancing robustness through noise injection technology: Noise injection can simulate the noise environment in actual channels during the training phase, allowing the model to learn under diverse noise conditions, thereby enhancing its adaptability to noise. Introducing this method is expected to significantly improve the model’s performance and reliability in complex real-world environments, providing a more promising solution for the development of image steganography technology.
• Extending to high-value domains: The inherent flexibility of our framework lends itself to adaptation within other sensitive domains. A particularly compelling direction is medical image steganography, where the imperative to safeguard patient data within medical images (e.g., MRI scans) while preserving their diagnostic integrity is paramount.
• Extending this framework to video steganography: This extension takes advantage of the properties of video data to hide information. Unlike methods that directly embed data in the pixel domain, video steganography converts video frames into other forms (for example, via a DCT or a wavelet transform) and then changes or emphasizes secret information in the converted data.