Symmetry-Based Enumeration of Polyominoes on C-Coloured Checkerboards

Abstract

Polyominoes are shapes formed by joining edge-connected unit squares in the square lattice. We review their symmetry classification using dihedral group actions and enumerate their distinct, coloured variants, called “chrominoes”, which arise when polyominoes are placed on a C-coloured checkerboard. This colouring method, defined via modular arithmetic, assigns colours cyclically in both directions. Our main theoretical result establishes that for $C=2$, a polyomino has either one or two chrominoes, depending on whether it has a colour-reversing symmetry. Additionally, we introduce a new classification of two-colour chrominoes into 15 symmetry-based classes. For $C\ge 3$, the number of chrominoes is a small integer multiple of C, determined by the polyomino’s symmetry class and the symmetries of the infinite C-coloured checkerboard plane. These findings have applications to integer linear programming methods for polyomino tiling problems. We validate our theoretical results through exhaustive search in MATLAB and illustrate them with examples.

1. Introduction and Background

Combinatorial geometry concerns the arrangement, combination, and enumeration of discrete geometric objects like points, lines, and polygons. It investigates how these objects interact through intersections, overlaps, and spatial organization. Modern combinatorial geometry, developed primarily in the 20th century, integrates classical geometry and combinatorial methods to study discrete structures [1,2].

This paper applies elementary group theory to analyse a combinatorial geometry problem, using symmetry and group actions to classify and enumerate distinct coloured polyomino variants. Group theory plays an important role in combinatorial geometry by providing a systematic framework for analysing symmetries, transformations, and counting arguments in discrete geometric structures. Many combinatorial problems, including those involving polyominoes, tilings, and lattice configurations, rely on group actions to classify equivalent objects under rotations and reflections [3,4]. Geometric group theory extends these ideas by treating groups as geometric objects, revealing connections between algebraic properties and spatial structures [5]. In particular, the use of group actions simplifies enumeration problems by partitioning sets into orbits, reducing computational complexity, and aiding in symmetry-based optimisation methods [6]. These techniques have been widely applied in combinatorial tiling problems [3,4], and in matroid theory (including Dowling geometries [7]), demonstrating the significant impact of group-theoretic methods in discrete mathematics.

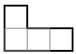
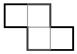
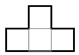
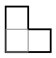
We study a class of polyforms called polyominoes, constructed from a finite number of unit squares (cells) joined edge-to-edge in the planar square lattice [8]. We assume polyominoes are simply-connected, meaning any loop within the region can contract to a point without encountering holes. The number of squares in a polyomino is called the area. Polyominoes with areas 1 through 8 are called monominoes, dominoes, trominoes, tetrominoes, pentominoes, hexominoes, heptominoes, and octominoes, respectively. We classify polyominoes broadly into two types. A free polyomino can be translated, rotated, or reflected (‘flipped’), while a fixed polyomino can only be translated (there are also one-sided polyominoes, which can be translated and rotated but not reflected; however, they are not considered in this paper). Thus, fixed polyominoes have a fixed orientation. For instance, the four tetrominoes shown in Figure 1 represent different, fixed polyominoes, but each one is the same, free tetromino.

Figure 1. The four orientations of a tetromino representing the same free polyomino.

The number of free polyominoes grows rapidly with area; for example, there are 35 free hexominoes and 369 free octominoes. Unless stated otherwise in this paper, polyominoes are considered free. Polyominoes were introduced by Solomon Golomb in his 1965 book, revised in 1994 [8,9]. For more details, see [10] or essays edited by A.J. Guttman [11]. Recreational study of polyomino tiling gained popularity through Martin Gardner’s Scientific American papers [12,13,14], which also inspired rigorous mathematical research.

This paper contributes to an ongoing study that aims to improve the scalability of an integer linear programming (ILP) method for tiling finite plane regions with polyominoes [15] (further details are provided in the conclusion (Section 7)). The existing method uses a two-colour checkerboard colouring for both the polyominoes and the target region. The improved approach generalises this to a C-coloured checkerboard colouring in such a way that the colours cycle both vertically and horizontally. For example, a six-coloured checkerboard coloured $10\times 13$ rectangle is illustrated in Figure 2.

Figure 2. A six-coloured checkerboard $10\times 13$ rectangle using the colours black, grey, red, green, yellow, and purple.

The method requires us to determine the number of distinct C-coloured variants of each polyomino, which depends on the polyomino’s symmetries and the number of colours used. A related ILP approach has been applied to combinatorial tiling problems, including the Eternity Puzzle—demonstrating the flexibility of ILP-based tiling methods [16].

The method for counting the number of coloured variants of a polyomino is illustrated here, with a rigorous description using modular arithmetic and group theory provided in later sections. Consider the tetromino in Figure 1 with four colours. To determine the number of distinct coloured variants, we examine all possible placements of the tetromino on a four-coloured checkerboard-patterned plane. It is assumed that the squares of the tetromino inherit the colours of the squares they cover. A coloured polyomino created in this way is referred to as a chromino (pl. chrominoes). Since polyominoes are assumed to be free, chrominoes are also considered to be free. A chromino can be thought of as a physical coloured puzzle piece that can be picked up, rotated, moved to different locations, and flipped. Thus, the yellow-outlined tetrominoes placed in the four-coloured, checkerboard-patterned $7\times 7$ square of Figure 3, both represent the same chromino and are different from the chromino outlined in blue. Each of the four orientations of the tetromino has at most four associated chrominoes, obtained by cycling the colours in the following order:

$$\mathrm{black}\to \mathrm{grey}\to \mathrm{red}\to \mathrm{green}(\to \mathrm{black}),\mathrm{etc}.$$

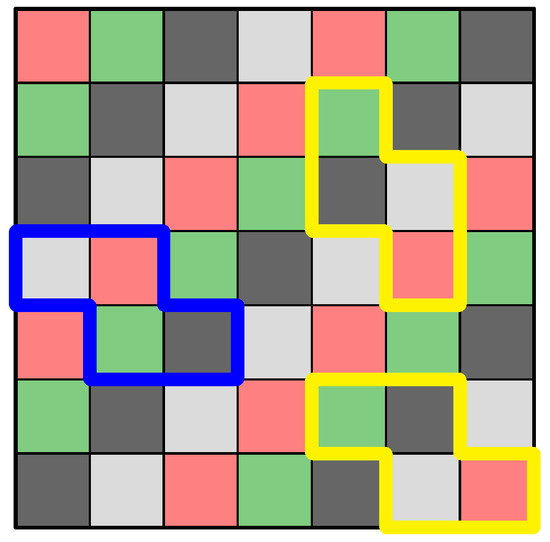
Figure 3. Three placements of a tetromino in a square checkerboard coloured square using four colours, namely, black, grey, red and green. The tetrominoes outlined in yellow represent the same chromino, which are different from the chromino outlined in blue.

After the fourth cycle, we obtain our original chromino. Thus, the number of distinct chrominoes is no more than $4\times 4=16$. However, depending on the symmetries of the polyomino and the plane some of the chrominoes will be equivalent. The enumeration problem then depends on identifying and excluding the ‘duplicate’ chrominoes. Using an appropriate computer program, such as MATLAB, we find through exhaustive search that with four colours there is a total of eight distinct chrominoes associated with the tetromino, shown in Figure 4 with a standard position.

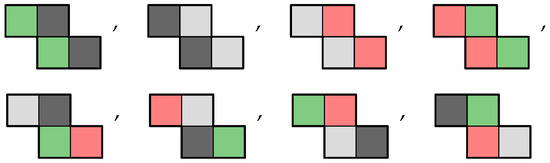
Figure 4. The eight free chrominoes using four colours associated with the tetromino illustrated in Figure 1, displayed in a standard position.

The general enumeration problem of determining the number of distinct chrominoes is a non-trivial combinatorial geometry problem and the main focus of this paper. This task involves elementary group theory and a detailed analysis of polyomino symmetries and the symmetries of the C-coloured plane.

The paper is organised as follows. Section 2 classifies polyominoes according to their symmetry using dihedral group actions. Section 3 introduces a modular arithmetic-based method for applying a C-coloured checkerboard pattern to polyominoes and defines the resulting chrominoes. Section 4 concerns the symmetry properties of the C-coloured checkerboard pattern when extended to the entire plane. Section 5 presents the main theoretical result: a formula for enumerating distinct free chrominoes based on $C\ge 2$ colours and the polyomino symmetry classes. Section 6 verifies the theoretical results numerically using MATLAB (see Appendix A) and illustrates some examples. Finally, in Section 7, we make some concluding remarks and give possible directions for future research.

2. Classification of Polyominoes by Symmetry

In this paper, we consider transformations of polyominoes that are isometries. An isometry is a transformation $\sigma :{\mathbb{R}}^2\to {\mathbb{R}}^2$ that preserves distances between pairs of points, i.e., the following condition holds for all points $p_1, p_2$ of a polyomino P:

$$d(\sigma \left(p_1\right),\sigma \left(p_2\right))=d(p_1,p_2),$$

(1)

where $d(p,q)$ represents the distance between points p and q [17]. As a result, the size and shape of a transformed polyomino remain unchanged, although its location or orientation may differ. Isometries include translations, rotations, reflections, and glide reflections. The eight isometries that we are concerned with are defined in Table 1, along with their corresponding descriptions.

Table 1. Eight isometries and their descriptions.

Isometry	Description
I	Identity transformation
${\mathrm{rot}}_{90}$	Rotation by 90° counter-clockwise
${\mathrm{rot}}_{180}$	Rotation by 180° counter-clockwise
${\mathrm{rot}}_{270}$	Rotation by 270° counter-clockwise
${\mathrm{flip}}_{\mathrm{h}}$	Reflection in the horizontal axis
${\mathrm{flip}}_{\mathrm{v}}$	Reflection in the vertical axis
${\mathrm{flip}}_{\mathrm{d}}$	Reflection in the diagonal
	(north-west corner to south-east corner)
${\mathrm{flip}}_{\mathrm{a}}$	Reflection in the anti-diagonal
	(south-west corner to the north-east corner)

The methods developed in this paper depend on our ability to classify polyominoes according to their symmetries and the number of associated fixed polyominoes. If P is a polyomino and $\sigma$ is an isometry, then we denote the image of P under the transformation $\sigma$ as $\sigma \left(P\right)$. Then, by a symmetry of P, we mean an isometry $\sigma$ that leaves the polyomino invariant, i.e., $\sigma \left(P\right)=P$ [17]. The only symmetries we are interested in are rotations and reflections.

To the best of our knowledge, polyominoes were first classified according to their symmetries over fifty years ago by W.F. Lunnon in an edited volume devoted to computing and number theory [18] (see also [19]). The same polyomino classes are also stated in a classic work by Redelmeier [20] on a polyomino enumeration method, but without justification or attributing the earlier works. The classification system used by W.F. Lunnon is based on elementary group theory, and as minimal details are provided, we give a more complete development below. The group theory we use can be found in many books, for example [21,22,23]. More recently, the enumeration of symmetry classes was extended to parallelogram polyominoes, providing explicit formulas for their generating functions [24].

Free polyominoes can be mathematically described as equivalence classes of fixed polyominoes under the group actions of the dihedral group $D_4$ of order eight. $D_4$ is the symmetry group of the square [21] (p. 75) and its group elements consist of the four rotations and four reflections that leave the square invariant, namely:

$$\{\mathrm{I},{\mathrm{rot}}_{90},{\mathrm{rot}}_{180},{\mathrm{rot}}_{270},{\mathrm{flip}}_{\mathrm{h}},{\mathrm{flip}}_{\mathrm{v}},{\mathrm{flip}}_{\mathrm{d}},{\mathrm{flip}}_{\mathrm{a}}\}.$$

The Cayley table for $D_4$ is given in Table 2, where the symbol ∘ denotes group composition [22] (p. 135).

Table 2. The Cayley table for the dihedral group $D_4$ of order 8. Group composition is denoted by ∘, and the order of a composition is right-to-left, for example, ${\mathrm{flip}}_{\mathrm{h}}\circ {\mathrm{rot}}_{90}={\mathrm{flip}}_{\mathrm{d}}$ indicates that a rotation of 90 degrees followed by a reflection in the horizontal axis is equivalent to a reflection in the diagonal.

∘	I	${\mathbf{rot}}_{90}$	${\mathbf{rot}}_{180}$	${\mathbf{rot}}_{270}$	${\mathbf{flip}}_{\mathbf{h}}$	${\mathbf{flip}}_{\mathbf{v}}$	${\mathbf{flip}}_{\mathbf{d}}$	${\mathbf{flip}}_{\mathbf{a}}$
I	I	${\mathrm{rot}}_{90}$	${\mathrm{rot}}_{180}$	${\mathrm{rot}}_{270}$	${\mathrm{flip}}_{\mathrm{h}}$	${\mathrm{flip}}_{\mathrm{v}}$	${\mathrm{flip}}_{\mathrm{d}}$	${\mathrm{flip}}_{\mathrm{a}}$
${\mathrm{rot}}_{90}$	${\mathrm{rot}}_{90}$	${\mathrm{rot}}_{180}$	${\mathrm{rot}}_{270}$	I	${\mathrm{flip}}_{\mathrm{a}}$	${\mathrm{flip}}_{\mathrm{d}}$	${\mathrm{flip}}_{\mathrm{h}}$	${\mathrm{flip}}_{\mathrm{v}}$
${\mathrm{rot}}_{180}$	${\mathrm{rot}}_{180}$	${\mathrm{rot}}_{270}$	I	${\mathrm{rot}}_{90}$	${\mathrm{flip}}_{\mathrm{v}}$	${\mathrm{flip}}_{\mathrm{h}}$	${\mathrm{flip}}_{\mathrm{a}}$	${\mathrm{flip}}_{\mathrm{d}}$
${\mathrm{rot}}_{270}$	${\mathrm{rot}}_{270}$	I	${\mathrm{rot}}_{90}$	${\mathrm{rot}}_{180}$	${\mathrm{flip}}_{\mathrm{d}}$	${\mathrm{flip}}_{\mathrm{a}}$	${\mathrm{flip}}_{\mathrm{v}}$	${\mathrm{flip}}_{\mathrm{h}}$
${\mathrm{flip}}_{\mathrm{h}}$	${\mathrm{flip}}_{\mathrm{h}}$	${\mathrm{flip}}_{\mathrm{d}}$	${\mathrm{flip}}_{\mathrm{v}}$	${\mathrm{flip}}_{\mathrm{a}}$	I	${\mathrm{rot}}_{180}$	${\mathrm{rot}}_{90}$	${\mathrm{rot}}_{270}$
${\mathrm{flip}}_{\mathrm{v}}$	${\mathrm{flip}}_{\mathrm{v}}$	${\mathrm{flip}}_{\mathrm{a}}$	${\mathrm{flip}}_{\mathrm{h}}$	${\mathrm{flip}}_{\mathrm{d}}$	${\mathrm{rot}}_{180}$	I	${\mathrm{rot}}_{270}$	${\mathrm{rot}}_{90}$
${\mathrm{flip}}_{\mathrm{d}}$	${\mathrm{flip}}_{\mathrm{d}}$	${\mathrm{flip}}_{\mathrm{v}}$	${\mathrm{flip}}_{\mathrm{a}}$	${\mathrm{flip}}_{\mathrm{h}}$	${\mathrm{rot}}_{270}$	${\mathrm{rot}}_{90}$	I	${\mathrm{rot}}_{180}$
${\mathrm{flip}}_{\mathrm{a}}$	${\mathrm{flip}}_{\mathrm{a}}$	${\mathrm{flip}}_{\mathrm{h}}$	${\mathrm{flip}}_{\mathrm{d}}$	${\mathrm{flip}}_{\mathrm{v}}$	${\mathrm{rot}}_{90}$	${\mathrm{rot}}_{270}$	${\mathrm{rot}}_{180}$	I

We observe from this table that the entire group $D_4$ is generated by just two elements, namely ${\mathrm{rot}}_{90}$ and ${\mathrm{flip}}_{\mathrm{v}}$, i.e.,

$$\begin{array}{cccccc}\hfill {\mathrm{rot}}_{90}\circ {\mathrm{rot}}_{90}& ={\mathrm{rot}}_{180},\hfill & \hfill {\mathrm{rot}}_{90}\circ {\mathrm{rot}}_{180}& ={\mathrm{rot}}_{270},\hfill & \hfill {\mathrm{rot}}_{90}\circ {\mathrm{rot}}_{270}& =\mathrm{I},\hfill \\ \hfill {\mathrm{rot}}_{90}\circ {\mathrm{flip}}_{\mathrm{v}}& ={\mathrm{flip}}_{\mathrm{d}},\hfill & \hfill {\mathrm{rot}}_{90}\circ {\mathrm{flip}}_{\mathrm{d}}& ={\mathrm{flip}}_{\mathrm{h}},\hfill & \hfill {\mathrm{rot}}_{90}\circ {\mathrm{flip}}_{\mathrm{h}}& ={\mathrm{flip}}_{\mathrm{a}}.\hfill \end{array}$$

To classify the symmetry types of polyominoes, we determine the stabiliser subgroup, $\mathrm{Stab}\left(P\right)\subseteq D_4$, which consists of all elements of $D_4$ that leave the polyomino unchanged. The stabiliser subgroup determines the number of distinct orientations of a polyomino under the group action. By the ‘Orbit-Stabilizer Theorem’ [23], the number of distinct orientations of a polyomino P is given by

$$\mathrm{Number}\mathrm{of}\mathrm{orientations}={\displaystyle \frac{|D_4|}{\left|\mathrm{Stab}\right(P\left)\right|}}.$$

Since $|D_4|=8$, the possible values for $\left|\mathrm{Stab}\right(P\left)\right|$ are 1, 2, 4, or 8, yielding 8, 4, 2, or 1 distinct orientations, respectively.

To determine these stabiliser subgroups, we identify all possible subsets of $D_4$ that are closed under composition, contain the identity, and include inverses for each element. This yields the following ten subgroups:

1. $\left\{\mathrm{I}\right\}$	6. $\{\mathrm{I},{\mathrm{flip}}_{\mathrm{a}}\}$
2. $\{\mathrm{I},{\mathrm{rot}}_{180}\}$	7. $\{\mathrm{I},{\mathrm{flip}}_{\mathrm{d}}\}$
3. $\{\mathrm{I},{\mathrm{rot}}_{90},{\mathrm{rot}}_{180},{\mathrm{rot}}_{270}\}$	8. $\{\mathrm{I},{\mathrm{flip}}_{\mathrm{v}},{\mathrm{flip}}_{\mathrm{h}},{\mathrm{rot}}_{180}\}$
4. $\{\mathrm{I},{\mathrm{flip}}_{\mathrm{h}}\}$	9. $\{\mathrm{I},{\mathrm{flip}}_{\mathrm{d}},{\mathrm{flip}}_{\mathrm{a}},{\mathrm{rot}}_{180}\}$
5. $\{\mathrm{I},{\mathrm{flip}}_{\mathrm{v}}\}$	10. $\{\mathrm{I},{\mathrm{rot}}_{90},{\mathrm{rot}}_{180},{\mathrm{rot}}_{270},{\mathrm{flip}}_{\mathrm{h}},{\mathrm{flip}}_{\mathrm{v}},{\mathrm{flip}}_{\mathrm{d}},{\mathrm{flip}}_{\mathrm{a}}\}$

Since the stabiliser subgroup determines the symmetries of a polyomino, two polyominoes with the same stabiliser subgroup belong to the same symmetry class. We observe that the pairs of subgroups 4 and 5, and 6 and 7, are isomorphic and can be combined into a single symmetry type. This is because the polyomino is free, meaning it can be rotated, which makes a vertical reflection (${\mathrm{flip}}_{\mathrm{v}}$) equivalent to a horizontal reflection (${\mathrm{flip}}_{\mathrm{h}}$) and a diagonal reflection (${\mathrm{flip}}_{\mathrm{d}}$) equivalent to an anti-diagonal reflection (${\mathrm{flip}}_{\mathrm{a}}$). As a result, there are eight distinct symmetry classes. Table 3 summarises our classification system for free polyominoes based on these eight symmetry classes.

Table 3. The table shows the eight symmetry classes of a free polyomino. The index of each symmetry class corresponds to the number of associated fixed polyominoes, or the number of distinct orientations, determined by the Orbit-Stabilizer Theorem. A representative example for each class is provided with minimal area. The table is based on [20].

Class #	Symmetries	Example	Index
1	none		8
2	${\mathrm{rot}}_{180}$		4
3	${\mathrm{flip}}_{\mathrm{h}}$ or ${\mathrm{flip}}_{\mathrm{v}}$		4
4	${\mathrm{flip}}_{\mathrm{d}}$ or ${\mathrm{flip}}_{\mathrm{a}}$		4
5	${\mathrm{rot}}_{90}$ (implies ${\mathrm{rot}}_{180}$ and ${\mathrm{rot}}_{270}$)		2
6	${\mathrm{flip}}_{\mathrm{v}}$ and ${\mathrm{flip}}_{\mathrm{h}}$ (implies ${\mathrm{rot}}_{180}$)		2
7	${\mathrm{flip}}_{\mathrm{d}}$ and ${\mathrm{flip}}_{\mathrm{a}}$ (implies ${\mathrm{rot}}_{180}$)		2
8	all of the above symmetries		1

The possible orientations of a free polyomino are represented by:

$$\begin{array}{cccccccc}\hfill & \mathrm{I}\left(P\right),\hfill & \hfill & {\mathrm{rot}}_{90}\left(P\right),\hfill & \hfill & {\mathrm{rot}}_{180}\left(P\right),\hfill & \hfill & {\mathrm{rot}}_{270}\left(P\right),\hfill \\ \hfill & {\mathrm{flip}}_{\mathrm{v}}\left(P\right),\hfill & \hfill & {\mathrm{rot}}_{90}\circ {\mathrm{flip}}_{\mathrm{v}}\left(P\right),\hfill & \hfill & {\mathrm{rot}}_{180}\circ {\mathrm{flip}}_{\mathrm{v}}\left(P\right),\hfill & \hfill & {\mathrm{rot}}_{270}\circ {\mathrm{flip}}_{\mathrm{v}}\left(P\right).\hfill \end{array}$$

(2)

The symmetries in $\mathrm{Stab}\left(P\right)$ eliminate duplicate orientations, leaving only the distinct orientations of the polyomino, illustrated in Example 1.

Example 1. 

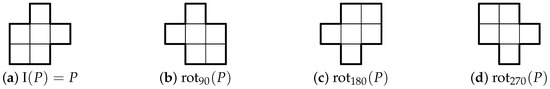
Consider the hexominowhich is invariant under the isometry ${\mathrm{flip}}_{\mathrm{a}}$, i.e., ${\mathrm{flip}}_{\mathrm{a}}\left(P\right)=\mathrm{I}\left(P\right)$. According to Table 3, the hexomino will have four distinct orientations. Using the symmetry of the hexomino we find that the last four orientations in (2) simply repeat the first four orientations:

$$\begin{array}{cc}\hfill {\mathrm{flip}}_{\mathrm{v}}\left(P\right)& ={\mathrm{flip}}_{\mathrm{v}}\circ {\mathrm{flip}}_{\mathrm{a}}\left(P\right)={\mathrm{rot}}_{90}\left(P\right),\hfill \\ \hfill \Rightarrow {\mathrm{rot}}_{90}\circ {\mathrm{flip}}_{\mathrm{v}}\left(P\right)& ={\mathrm{rot}}_{90}\circ {\mathrm{rot}}_{90}\left(P\right)={\mathrm{rot}}_{180}\left(P\right),\hfill \\ \hfill \Rightarrow {\mathrm{rot}}_{180}\circ {\mathrm{flip}}_{\mathrm{v}}\left(P\right)& ={\mathrm{rot}}_{180}\circ {\mathrm{rot}}_{90}\left(P\right)={\mathrm{rot}}_{270}\left(P\right),\hfill \\ \hfill \Rightarrow {\mathrm{rot}}_{270}\circ {\mathrm{flip}}_{\mathrm{v}}\left(P\right)& ={\mathrm{rot}}_{270}\circ {\mathrm{rot}}_{90}\left(P\right)=\mathrm{I}\left(P\right),\hfill \end{array}$$

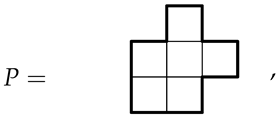leading to just four distinct orientations of the hexomino, illustrated in Figure 5:

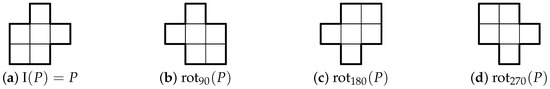
Figure 5. The four distinct orientations of a hexomino P.

3. Colouring Polyominoes Using Modular Arithmetic

To describe how a coloured checkerboard pattern is assigned to a polyomino, we first introduce some definitions. Note that we use $(\tilde{j},\tilde{i})$ as integer coordinates, where $\tilde{j}$ (the x-axis) is the horizontal index and $\tilde{i}$ (the y-axis) is the vertical index.

Definition 1. 

The square tiling of the plane, denoted Π, refers to the set of edge-to-edge connected unit squares $[\tilde{j}-1,\tilde{j}]\times [\tilde{i}-1,\tilde{i}]$ covering the Euclidean plane ${\mathbb{R}}^2$, given by

$$\mathsf{\Pi }:=\bigcup _{\tilde{i},\tilde{j}\in \mathbb{Z}}\left([\tilde{j}-1,\tilde{j}]\times [\tilde{i}-1,\tilde{i}]\right).$$

To colour the squares of any given polyomino P, we initially apply a colouring scheme to the infinite square tiling $\mathsf{\Pi }$. To this end, we define a function that associates each point $(x,y)\in \mathsf{\Pi }$ with the integer coordinates $(\tilde{j},\tilde{i})$ of the square $[\tilde{j}-1,\tilde{j}]\times [\tilde{i}-1,\tilde{i}]$ that contains it. This uniquely identifies each square within the tiling.

Definition 2. 

The ceiling map is the function $h:\mathsf{\Pi }\to {\mathbb{Z}}^2$ defined by

$$h(x,y):=(\lceil x\rceil ,\lceil y\rceil ),$$

(3)

where $\lceil z\rceil$ denotes the ceiling function, which maps z to the smallest integer greater than or equal to z.

Thus, every point in the square $[\tilde{j}-1,\tilde{j}]\times [\tilde{i}-1,\tilde{i}]$ satisfies $h(x,y)=(\tilde{j},\tilde{i})$, associating the square with its integer indices.

We assign a finite number of colours to the integer coordinates $(\tilde{j},\tilde{i})$ of the squares in $\mathsf{\Pi }$.

Definition 3. 

A colour index is an integer in $\{1,2,\dots ,C\}$ with $C\ge 2$, uniquely identifying a colour.

The illustrations in this paper use the following colour assignments: black (1), grey (2), red (3), green (4), yellow (5), and purple (6).

We assign the C colours to the squares of $\mathsf{\Pi }$ using a cyclic pattern governed by the permutation $(1,2,\dots ,C)$, an element of the symmetric group $S_C$ [23]. The formula for generating the colour indices for the squares in $\mathsf{\Pi }$ is given by

$$s_1(j,i):=(i+j)\left(\mathrm{mod}C\right)+1,$$

(4a)

$$\mathrm{where}j=\tilde{j},i=C+1-\tilde{i}\mathrm{and}(\tilde{j},\tilde{i})\in {\mathbb{Z}}^2.$$

(4b)

Here, the ‘$+1$’ in (4a) shifts the indices from a zero-based to a one-based system, ensuring they range from 1 to C, which aligns more naturally with colour counting. The change of variable in (4b) reverses the vertical order of colours, ensuring that indices cycle left-to-right while also following a top-to-bottom progression in the square tiling $\mathsf{\Pi }$. This adjustment is motivated by practical considerations, including the later matrix representation of finite regions.

Definition 4. 

A coloured square tiling of the plane, denoted ${\mathsf{\Pi }}_C$, is obtained by applying Equations (3) and (4) to assign cyclic colour indices to the squares of Π.

We now define the coloured polyominoes that are the focus of this study.

Definition 5. 

Let P be a polyomino and let ${\mathsf{\Pi }}_C$ be a C-coloured checkerboard tiling (see Definition 4). When P is placed onto ${\mathsf{\Pi }}_C$, each of its squares inherits the colour of the corresponding square in ${\mathsf{\Pi }}_C$ that it covers. The resulting coloured polyomino is called a chromino (pl. chrominoes).

If P is free, two chrominoes are equivalent if one can be transformed into the other by a translation, rotation, or reflection that preserves the colouring. If P is fixed, only translations are allowed. Thus, a chromino inherits the free or fixed property from the polyomino used to generate it.

With this setup, there are C possible coloured variants of a fixed polyomino. Once we have any given coloured variant, the other $C-1$ variants are obtained by translating the polyomino either horizontally or vertically, cycling the colours of the cells. We give a mathematical expression for these fixed chrominoes, indexed by k, by generalizing the function $s_1$ in (4). Let $S\subseteq {\mathbb{R}}^2$ be the set of integer points $(\tilde{j},\tilde{i})$ corresponding to the squares $[\tilde{j}-1,\tilde{j}]\times [\tilde{i}-1,\tilde{i}]$ of P (see (3)). Then define

$$s_k(j,i):=(i+j+k-1)\left(\mathrm{mod}C\right)+1,\mathrm{for}k=1,2,\dots ,C,$$

(5a)

$$\mathrm{where}j=\tilde{j},i=C+1-\tilde{i}\mathrm{and}(\tilde{j},\tilde{i})\in S.$$

(5b)

Note that Equation (5) reverts to (4) when $k=1$ and $S={\mathbb{Z}}^2$. The k-th checkerboard coloured fixed polyomino P is denoted $P^k$.

Definition 6. 

Let $P^k$ be the k-th fixed chromino of a polyomino P, coloured with C colours (see Definition 5). Denote by $[\tilde{j}-1,\tilde{j}]\times [\tilde{i}-1,\tilde{i}]$ each unit square in the smallest bounding rectangle of P, and define

$$j:=\tilde{j},i:=C+1-\tilde{i}.$$

The colour matrix of $P^k$, denoted $A=\left(a_{i,j}\right)$, is given by

$$a_{i,j}=\left\{\begin{array}{cc}{s}_k(j,i),\hfill & \mathit{if}[\tilde{j}-1,\tilde{j}]\times [\tilde{i}-1,\tilde{i}]\subseteq P,\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

Hence $a_{i,j}\in \{1,2,\dots ,C\}$ if the corresponding square belongs to P and $a_{i,j}=0$ if it lies outside P but inside its bounding rectangle.

The steps needed to apply a three-coloured checkerboard pattern (with $k=1$) to a P-shaped pentomino are illustrated in Figure 6.

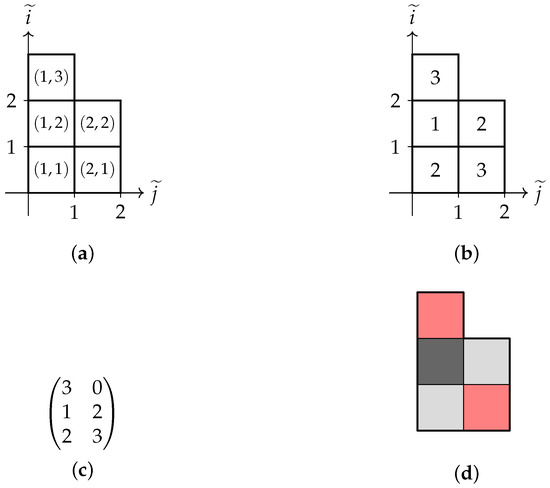
Figure 6. Steps required to apply a three-coloured checkerboard pattern to a P-shaped pentomino: (a) $(x,y)$ coordinates mapped to integer $(\tilde{j},\tilde{i})$ using (3); (b) $(\tilde{j},\tilde{i})$ mapped to colour indices using (5); (c) the colour matrix of the pentomino via Definition 6; (d) the coloured pentomino where $1, 2, 3$ represent black, grey, and red.

4. Symmetry Groups of the Plane

Since the arguments in Section 5 depend on the symmetries of the checkerboard plane ${\mathsf{\Pi }}_C$, we briefly review them here.

The 17 finite symmetry groups of the plane are known as plane crystallographic groups or wallpaper groups [17,25,26]. Simple classification systems for the wallpaper groups are given in [25] (p. 474) and [26] (p. 128), which yields that ${\mathsf{\Pi }}_2$ belongs to the symmetry group p4m, while ${\mathsf{\Pi }}_{C\ge 3}$ belongs to pm (the notation used for the wallpaper groups is the IUC (International Union of Crystallography) Notation [27]).

When $C=2$, the checkerboard ${\mathsf{\Pi }}_2$ has all the symmetries of the dihedral group $D_4$ (order 8), including ${\mathrm{rot}}_{90}\left({\mathsf{\Pi }}_2\right)={\mathsf{\Pi }}_2$ and ${\mathrm{flip}}_{\mathrm{v}}\left({\mathsf{\Pi }}_2\right)={\mathsf{\Pi }}_2$. It has rotational symmetry of 90° around the centre of each square and 180° around each vertex. Additionally, ${\mathsf{\Pi }}_2$ has reflection symmetry along the diagonals (slopes $-1$ and $+1$) and along the horizontal and vertical bisectors of the squares.

When ${\mathsf{\Pi }}_2$ is coloured with black and grey squares, its symmetries preserve colouring, meaning each black square maps to a black square and each grey square maps to a grey square. Mathematically, a colour-preserving symmetry of a polyomino P is an isometry $\sigma$ of ${\mathsf{\Pi }}_2$ that satisfies the following conditions [28]:

(i)

$\sigma \left(P\right)=P$,

(ii)

$f\left(\sigma \right(p\left)\right)=f\left(p\right)$ for all points $p\in P$,

Where $f:{\mathbb{R}}^2\to \{1,2\}$ is the colour map defined using (3) and (4) that maps every point in the Euclidean plane to its unique colour index (combining these formulas yields the explicit form $f(x,y):=(3-\lceil y\rceil +\lceil x\rceil )\left(\mathrm{mod}2\right)+1$ for all $(x,y)\in {\mathbb{R}}^2$).

Condition (i) ensures that the isometry $\sigma$ is a symmetry of P, while condition (ii) guarantees that $\sigma$ preserves the colours of its points.

In addition to colour-preserving symmetries, there are colour-reversing symmetries, which swap black and grey squares. For example, 90° rotations about a vertex and reflections across horizontal or vertical grid lines in ${\mathbb{Z}}^2$ are colour-reversing symmetries.

We define a colour-reversing symmetry of a polyomino P as an isometry $\sigma$ acting on the plane ${\mathsf{\Pi }}_2$ that satisfies the following conditions [28]:

(i)

$\sigma \left(P\right)=P$

(ii)

$f\left(\sigma \right(p\left)\right)=3-f\left(p\right)$ for all points $p\in P$

Condition (ii) ensures that $\sigma$ swaps black and grey squares, since black corresponds to $f\left(p\right)=1$ and grey to $f\left(p\right)=2$.

Distinguishing between colour-preserving and colour-reversing symmetries will be important when enumerating and classifying chrominoes with two colours (see Table 4). We note that there are no colour-reversing symmetries corresponding to reflections along a diagonal or anti-diagonal line.

Table 4. The two-colour rotation and reflection symmetries of ${\mathsf{\Pi }}_2$. The asterisked isometries are colour-reversing, while the non-asterisked versions are colour-preserving.

Isometry	Description
${\mathrm{rot}}_{90}$	Rotation by 90° counter-clockwise about the centre of a square
${\mathrm{rot}}_{90}$ *	Rotation by 90° counter-clockwise about a vertex
${\mathrm{rot}}_{180}$	Rotation by 180° counter-clockwise about either a square centre or a vertex
${\mathrm{rot}}_{180}$ *	Rotation by 180° counter-clockwise about the midpoint of an edge
${\mathrm{rot}}_{270}$	Rotation by 270° counter-clockwise about the centre of a square
${\mathrm{rot}}_{270}$ *	Rotation by 270° counter-clockwise about a vertex
${\mathrm{flip}}_{\mathrm{h}}$	Reflection in a horizontal line that bisects squares
${\mathrm{flip}}_{\mathrm{h}}$ *	Reflection in a horizontal line passing through edges of squares
${\mathrm{flip}}_{\mathrm{v}}$	Reflection in a vertical line that bisects squares
${\mathrm{flip}}_{\mathrm{v}}$ *	Reflection in a vertical line passing through edges of squares
${\mathrm{flip}}_{\mathrm{d}}$	Reflection in a diagonal line through squares
${\mathrm{flip}}_{\mathrm{a}}$	Reflection in an anti-diagonal line through squares

For $C\ge 3$, the set of symmetries is significantly reduced. The only non-trivial symmetry of the checkerboard planes ${\mathsf{\Pi }}_{C\ge 3}$, apart from translations and glide reflections, is ${\mathrm{flip}}_{\mathrm{d}}$, i.e., ${\mathrm{flip}}_{\mathrm{d}}\left({\mathsf{\Pi }}_{C\ge 3}\right)={\mathsf{\Pi }}_{C\ge 3}$. Reflections occur along diagonal lines of slope $-1$ passing through the squares. This reflection symmetry preserves colours and the concept of a colour-reversing symmetry makes no sense when there are three or more colours.

5. Enumeration of Coloured Polyominoes

The enumeration results in this section assumes an infinite checkerboard-coloured plane but also applies to sufficiently large finite regions. This holds as long as each polyomino can be placed in all necessary positions without crossing the boundary, ensuring all distinct chrominoes are generated. Under these conditions, the enumeration formulas remain valid.

Since the polyominoes are free, the corresponding chrominoes are also free (see Definition 5). For example, consider two L-shaped tetrominoes placed on a four-coloured checkerboard square, as shown in Figure 7 (outlined in black). Denote these chrominoes by $P^i$ and $P^j$. The only non-trivial symmetry of ${\mathsf{\Pi }}_4$ is ${\mathrm{flip}}_{\mathrm{d}}$, which changes a chromino’s orientation, so ${\mathrm{flip}}_{\mathrm{d}}\left(P^j\right)=P^i$. Thus, $P^i$ and $P^j$ represent the same free chromino.

Figure 7. Two placements of an L-shaped polyomino in a four-coloured checkerboard square, representing the same chromino. The chrominoes are outlined in black.

Let $N_P^C$ be the number of distinct chrominoes of a (free) polyomino P using C colours. The set of chrominoes indexed by j is

$$\{P^j\mid j=1,2,\dots ,N_P^C\}.$$

The following result provides a formula for $N_P^C$ based on the symmetry of P and the number of colours C, forming the main theoretical result of this paper.

Theorem 1. 

For $C=2$, the number of distinct chrominoes, $N_P^2$, is given by

$$N_P^2=\left\{\begin{array}{cc}1\hfill & ifandonlyif{P}^1=P^2(i.e.,acolour\text{-}reversingsymmetryexists)\hfill \\ 2\hfill & otherwise\hfill \end{array}\right..$$

Furthermore, the chrominoes can be classified into 15 two-colour symmetry classes (see Table 5).

Table 5. The table lists the 15 two-colour symmetry classes of chrominoes classified by their colour-preserving symmetries (‘non-asterisked’) and colour-reversing symmetries (‘asterisked’). Each class corresponds to a subgroup of $D_4$. Additionally, the table includes representative examples for each class and indicates whether there are one ($P^1=P^2$) or two ($P^1\ne P^2$) distinct chrominoes in each case.

Class #	Symmetries	Example	${\mathit{N}}_{\mathit{P}}^2$
1	none		2
2(a)	${\mathrm{rot}}_{180}$		2
2(b)	${\mathrm{rot}}_{180}$ *		1
3(a)	${\mathrm{flip}}_{\mathrm{h}}$ or ${\mathrm{flip}}_{\mathrm{v}}$		2
3(b)	${\mathrm{flip}}_{\mathrm{h}}$ * or ${\mathrm{flip}}_{\mathrm{v}}$ *		1
4	${\mathrm{flip}}_{\mathrm{d}}$ or ${\mathrm{flip}}_{\mathrm{a}}$		2
5(a)	${\mathrm{rot}}_{90}$ (implies ${\mathrm{rot}}_{180}$ and ${\mathrm{rot}}_{270}$)		2
5(b)	${\mathrm{rot}}_{90}$ * (implies ${\mathrm{rot}}_{180}$ and ${\mathrm{rot}}_{270}$ *)		1
6(a)	${\mathrm{flip}}_{\mathrm{v}}$ and ${\mathrm{flip}}_{\mathrm{h}}$ (implies ${\mathrm{rot}}_{180}$)		2
6(b)	${\mathrm{flip}}_{\mathrm{v}}$ and ${\mathrm{flip}}_{\mathrm{h}}$ * (implies ${\mathrm{rot}}_{180}$ *)		1
6(c)	${\mathrm{flip}}_{\mathrm{v}}$ * and ${\mathrm{flip}}_{\mathrm{h}}$ (implies ${\mathrm{rot}}_{180}$ *)		1
6(d)	${\mathrm{flip}}_{\mathrm{v}}$ * and ${\mathrm{flip}}_{\mathrm{h}}$ * (implies ${\mathrm{rot}}_{180}$)		1
7	${\mathrm{flip}}_{\mathrm{d}}$ and ${\mathrm{flip}}_{\mathrm{a}}$ (implies ${\mathrm{rot}}_{180}$)		2
8(a)	${\mathrm{rot}}_{90}$ *, (implies ${\mathrm{rot}}_{180}$ and ${\mathrm{rot}}_{270}$ *), ${\mathrm{flip}}_{\mathrm{v}}$ *, ${\mathrm{flip}}_{\mathrm{h}}$ *, ${\mathrm{flip}}_{\mathrm{a}}$, and ${\mathrm{flip}}_{\mathrm{d}}$		1
8(b)	all colour preserving symmetries		2

For $C\ge 3$, $N_P^C$ depends on the symmetry classes (see Table 3) of P and is given by

$$N_P^C=\left\{\begin{array}{cc}C\hfill & ifPisofclass\#5,6,\mathit{or}8\hfill \\ 2C\hfill & ifPisofclass\#2,3,\mathit{or}7\hfill \\ 3C\hfill & ifPisofclass\#4\hfill \\ 4C\hfill & ifPisofclass\#1\hfill \end{array}\right..$$

Proof. 

For each symmetry class in Table 3 we must determine the number of distinct chrominoes formed by placing a polyomino P on the checkerboard-coloured plane ${\mathsf{\Pi }}_C$. This count depends on the number of orientations of P and whether different orientations yield equivalent chrominoes. We also determine when different translations of P produce equivalent chrominoes. Equivalent chrominoes indicate duplicates, which must be excluded from the total count.

Consider placing a polyomino P on ${\mathsf{\Pi }}_C$. The resulting chromino has colour indices determined by the indexed modulo Formula (5). Without loss of generality, let this chromino be $P^1$, corresponding to $k=1$ in Equation (5). Keeping the orientation of P fixed, translating it one square right (or downward) shifts the colour indices forward by one step, yielding a new chromino $P^2$. Each step forward produces a new chromino until, after C steps, the original chromino $P^1$ reappears. Further translations repeat this cycle, while reversing the translation direction reverses the colour index cycle. Thus, for each orientation of P, the chrominoes cycle through at most C distinct variants: $\{P^1,P^2,\dots ,P^C\}$. With $\mathcal{O}$ orientations, this gives at most $C\mathcal{O}$ free chrominoes.

The remainder of the proof identifies duplicate chrominoes based on the symmetries of the polyomino and the embedding plane. We treat $C=2$ and $C\ge 3$ separately, as ${\mathsf{\Pi }}_2$ has colour-reversing symmetries not present in ${\mathsf{\Pi }}_{C\ge 3}$.

• Case $C=2:$

This case is simpler than $C\ge 3$ to analyse, as every isometry of a polyomino placed in ${\mathsf{\Pi }}_2$—whether a translation or a transformation in $D_4$—either preserves or reverses the colouring of its squares. As a result, each polyomino generates at most two chrominoes, $P^1$ and $P^2$, which may or may not be distinct. If a chromino possesses a colour-reversing symmetry, then $P^1=P^2$, meaning there is only one distinct chromino. If only colour-preserving symmetries exist, then $P^1\ne P^2$, i.e., there are two distinct chrominoes. The two-colour symmetries of ${\mathsf{\Pi }}_2$ are defined in Table 4, and Table 5 summarises the analysis, classifying chrominoes into 15 two-colour symmetry classes.

For example, a class $\#1$ polyomino in Table 3 is asymmetric, so $P^1$ and $P^2$ are always distinct. Chrominoes are also distinct for class $\#4$ and class $\#7$ polyominoes, since ${\mathrm{flip}}_{\mathrm{d}}$ and ${\mathrm{flip}}_{\mathrm{a}}$ are always colour-preserving. All other classes include chrominoes with both colour-preserving and colour-reversing symmetries.

If $P^1=P^2$, then the chromino is ‘balanced’ [8], meaning it contains an equal number of black and grey squares. However, the converse does not hold; there exist balanced chrominoes with $P^1\ne P^2$.

• Case $C\ge 3:$

Unlike the $C=2$ case, where colour-reversing symmetries create equivalences, the cyclic nature of three or more colour indices and the fact that the only symmetry of ${\mathsf{\Pi }}_C$ for $C\ge 3$ is ${\mathrm{flip}}_{\mathrm{d}}$ ensure that the fixed chrominoes $\{P^1,P^2,\dots ,P^C\}$ are distinct. In other words, a fixed polyomino yields exactly C distinct chrominoes.

However, two chrominoes with different orientations may still be equivalent under the diagonal reflection ${\mathrm{flip}}_{\mathrm{d}}$. An example of this was illustrated in Figure 7. To determine which orientations of a polyomino yield equivalent chrominoes, we analyse each symmetry class in Table 3. Using the dihedral group actions listed in Table 2, we first identify the distinct orientations of a polyomino P by checking whether any of its eight possible orientations in (2) are equivalent. This process is demonstrated in Example 1. Since it is straightforward, we omit the details and directly list the unique orientations for each symmetry class. We then apply ${\mathrm{flip}}_{\mathrm{d}}$ to each orientation, again using the dihedral group actions, to determine which ones yield the same chrominoes.

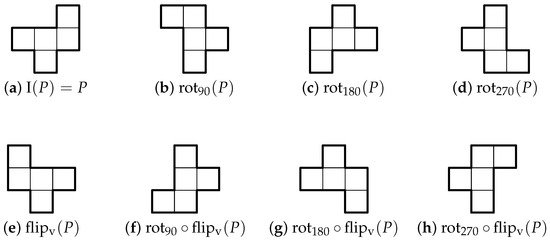
• Class #1:

For an asymmetric polyomino P of class #1 in Table 3, the eight possible orientations are shown in Figure 8, illustrated with a representative example.

Figure 8. The eight orientations of a polyomino belonging to class #1 of Table 3, illustrated with an asymmetric pentomino.

Using Table 2 and applying the symmetry ${\mathrm{flip}}_{\mathrm{d}}$ yields the following correspondences:

$$\begin{array}{cc}\hfill & {\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{rot}}_{90}\circ {\mathrm{flip}}_{\mathrm{v}}\left(P\right)={\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{flip}}_{\mathrm{d}}\left(P\right)=\mathrm{I}\left(P\right),\hfill \\ \hfill & {\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{flip}}_{\mathrm{v}}\left(P\right)={\mathrm{rot}}_{90}\left(P\right),\hfill \\ \hfill & {\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{rot}}_{270}\circ {\mathrm{flip}}_{\mathrm{v}}\left(P\right)={\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{flip}}_{\mathrm{a}}\left(P\right)={\mathrm{rot}}_{180}\left(P\right),\hfill \\ \hfill & {\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{rot}}_{180}\circ {\mathrm{flip}}_{\mathrm{v}}\left(P\right)={\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{flip}}_{\mathrm{h}}\left(P\right)={\mathrm{rot}}_{270}\left(P\right),\hfill \end{array}$$

i.e., the pairs (f) and (a), (e) and (b), (h) and (c), and (g) and (d) are equivalent for chromino generation. Therefore, class #1 polyominoes always yield $N_P^C=4C$ chrominoes.

• Class #2:

For a polyomino P of class #2 in Table 3 with symmetry ${\mathrm{rot}}_{180}$, the four possible orientations are given in Figure 9, illustrated with a representative example.

Figure 9. The four orientations of a polyomino belonging to class #2 of Table 3, illustrated with a tetromino.

Using Table 2 we apply the symmetry ${\mathrm{flip}}_{\mathrm{d}}$ and obtain the following correspondences:

$$\begin{array}{cc}\hfill & {\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{rot}}_{90}\circ {\mathrm{flip}}_{\mathrm{v}}\left(P\right)={\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{flip}}_{\mathrm{d}}\left(P\right)=\mathrm{I}\left(P\right),\hfill \\ \hfill & {\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{flip}}_{\mathrm{v}}\left(P\right)={\mathrm{rot}}_{90}\left(P\right).\hfill \end{array}$$

Thus, orientations (a) and (d), and (b) and (c), are equivalent for chromino generation. So class #2 polyominoes yield $N_P^C=2C$ chrominoes.

• Class #3:

For a polyomino P of class #3 in Table 3 with symmetry ${\mathrm{flip}}_{\mathrm{v}}$, the four possible orientations are shown in Figure 10, illustrated with a representative example.

Figure 10. The four orientations of a polyomino belonging to class #3 of Table 3, illustrated with a tetromino.

Using Table 2, we apply the symmetry ${\mathrm{flip}}_{\mathrm{d}}$ and obtain the following correspondences:

$$\begin{array}{cc}\hfill {\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{rot}}_{90}\left(P\right)& ={\mathrm{flip}}_{\mathrm{v}}\left(P\right)=I\left(P\right),\hfill \\ \hfill {\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{rot}}_{270}\left(P\right)& ={\mathrm{flip}}_{\mathrm{h}}\left(P\right)={\mathrm{rot}}_{180}\circ {\mathrm{flip}}_{\mathrm{v}}\left(P\right)={\mathrm{rot}}_{180}\left(P\right).\hfill \end{array}$$

Thus, orientations (a) and (b), and (c) and (d), are equivalent for chromino generation. Therefore, class #3 polyominoes with symmetry ${\mathrm{flip}}_{\mathrm{v}}$ yield $N_P^C=2C$ chrominoes. The argument for polyominoes of class #3 with symmetry ${\mathrm{flip}}_{\mathrm{h}}$ is similar and gives the same $N_P^C$ count.

• Class #4:

For a given polyomino P of class #4 in Table 3 with the symmetry ${\mathrm{flip}}_{\mathrm{a}}$, the four possible orientations are given in Figure 11 and illustrated for a representative example.

Figure 11. The four orientations of a polyomino belonging to class #4 of Table 3, illustrated with a tromino.

Using Table 2 and applying the symmetry ${\mathrm{flip}}_{\mathrm{d}}$ yields the following correspondences:

$$\begin{array}{cc}\hfill & {\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{rot}}_{180}\left(P\right)={\mathrm{flip}}_{\mathrm{a}}\left(P\right)=\mathrm{I}\left(P\right),\hfill \\ \hfill & {\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{rot}}_{270}\left(P\right)={\mathrm{flip}}_{\mathrm{h}}\left(P\right),\hfill \\ \hfill & {\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{rot}}_{90}\left(P\right)={\mathrm{flip}}_{\mathrm{v}}\left(P\right).\hfill \end{array}$$

Thus, the pairs (a) and (c), are equivalent orientations as far as generating chrominoes is concerned; however, orientations (b) and (d) are different. Thus, polyominoes P with the symmetry ${\mathrm{flip}}_{\mathrm{a}}$ belonging to class #4 always yield a total of $N_P^C=3C$ chrominoes when placed in the checkerboard region ${\mathsf{\Pi }}_{C\ge 3}$. The argument for a polyomino belonging to class #4 with the symmetry ${\mathrm{flip}}_{\mathrm{d}}$ is similar and yields the same total counts for $N_P^C$.

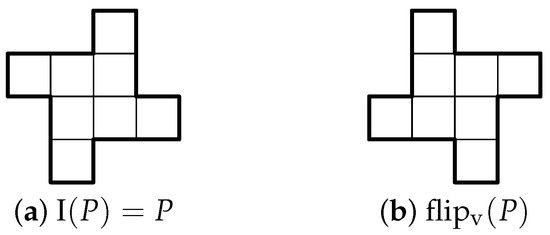
• Class #5:

For a polyomino P of class #5 in Table 3 with symmetry ${\mathrm{rot}}_{90}$, the two possible orientations are shown in Figure 12, illustrated with a representative example.

Figure 12. The two orientations of a polyomino belonging to class #5 of Table 3, illustrated with an octomino.

Using Table 2 and applying the symmetry ${\mathrm{flip}}_{\mathrm{d}}$, we obtain the following correspondence:

$${\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{flip}}_{\mathrm{v}}\left(P\right)={\mathrm{rot}}_{90}\left(P\right)=I\left(P\right).$$

Thus, the two orientations of a class #5 polyomino always yield a total of $N_P^C=C$ chrominoes.

• Class #6:

For a polyomino P of class #6 in Table 3 with symmetries ${\mathrm{flip}}_{\mathrm{v}}$ and ${\mathrm{flip}}_{\mathrm{h}}$, the two possible orientations are shown in Figure 13, illustrated with a representative example.

Figure 13. The two orientations of a polyomino belonging to class #6 of Table 3, illustrated with a domino.

Using Table 2 and applying the symmetry ${\mathrm{flip}}_{\mathrm{d}}$, we obtain the following correspondence:

$${\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{rot}}_{90}\left(P\right)={\mathrm{flip}}_{\mathrm{v}}\left(P\right)=I\left(P\right).$$

Thus, the two orientations of a class #6 polyomino always yield a total of $N_P^C=C$ chrominoes.

• Class #7:

For a polyomino P of class #7 in Table 3 with symmetries ${\mathrm{flip}}_{\mathrm{d}}$ and ${\mathrm{flip}}_{\mathrm{a}}$, the two possible orientations are shown in Figure 14, illustrated with a representative example.

Figure 14. The two orientations of a polyomino belonging to class #7 of Table 3, illustrated with an octomino.

Using Table 2 and applying the symmetry ${\mathrm{flip}}_{\mathrm{d}}$, we obtain:

$${\mathrm{flip}}_{\mathrm{d}}\circ {\mathrm{rot}}_{90}\left(P\right)={\mathrm{flip}}_{\mathrm{v}}\left(P\right)\ne I\left(P\right).$$

Thus, the two orientations of a class #7 polyomino are different and always yield a total of $N_P^C=2C$ chrominoes.

• Class #8:

For a polyomino P of class #8 in Table 3 with all the symmetries of $D_4$, the single orientation is shown in Figure 15, illustrated with a representative example.

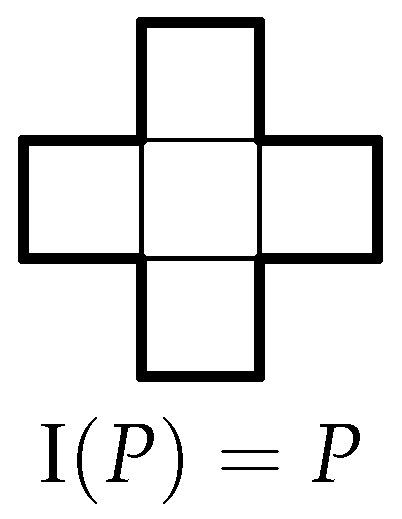
Figure 15. The single orientation of a polyomino belonging to class #8 of Table 3, illustrated with a pentomino.

Different placements of a polyomino of class #8 in the checkerboard region ${\mathsf{\Pi }}_{C\ge 3}$ yield a total of $N_P^C=C$ chrominoes.    □

6. Numerical Verification

We numerically verified the theoretical results of Theorem 1 using MATLAB R2023a on a MacBook Pro (2021) with an Apple M1 Max chip, 64 GB RAM, running macOS Sonoma 14.5.

The MATLAB code (see Appendix A) performs an exhaustive search to determine all free chrominoes for a given polyomino and a fixed number of colours. The process begins by representing the polyomino as a binary matrix, where cells of the polyomino are marked with ‘1’s and all other cells within the smallest bounding rectangle with ‘0’s, as shown in Figure 16.

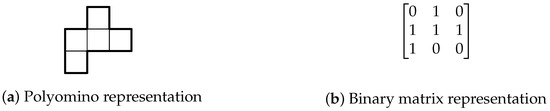
Figure 16. A pentomino and its corresponding binary matrix representation.

A polyomino generally has 8, 4, 2, or 1 distinct orientations. However, for simplicity in the MATLAB program, we generate colour matrices for all eight orientations by applying counter-clockwise 90-degree rotations and horizontal reflections to its binary matrix representation. We then apply the modular arithmetic Formula (5) for $k=1,2,\dots ,C$ and use Definition 6 to construct C colour matrices per orientation. Each coloured variant is mapped back to the polyomino’s standard position before further processing. Finally, duplicate colour matrices are removed, leaving only the unique ones corresponding to the distinct free chrominoes.

Using the MATLAB program, we validated examples from all symmetry classes in Theorem 1 for both $C=2$ and $C\ge 3$. We illustrate two examples below.

Example 2. 

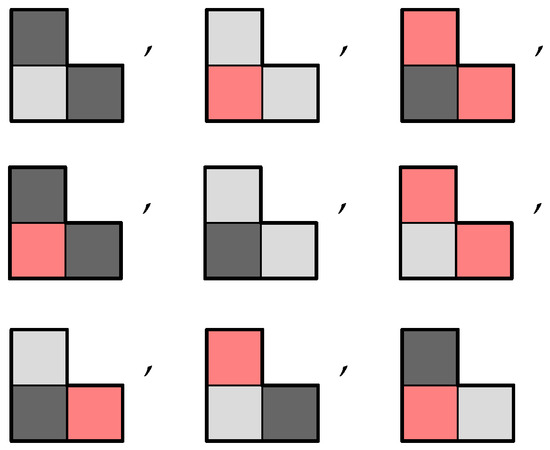
Using $C=3$ colours find all possible chrominoes for the tromino

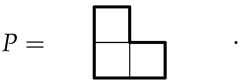From Table 3 we see that this polyomino belongs to symmetry class $\#4$ and thus from Theorem 1 there will be exactly $3C=9$ distinct chrominoes associated with this polyomino, illustrated in Figure 17.

Figure 17. The nine free chrominoes using three colours associated with a tromino, displayed in standard position.

Example 3. 

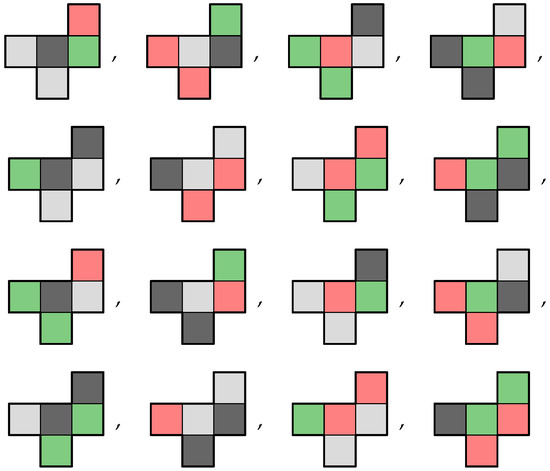
Using $C=4$ colours find all possible chrominoes for the pentomino

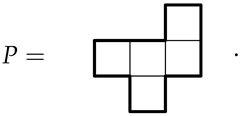From Table 3, we see that this polyomino belongs to symmetry class $\#1$ and thus from Theorem 1 there will be exactly $4C=16$ distinct chrominoes associated with this polyomino, illustrated in Figure 18.

Figure 18. The sixteen free chrominoes using four colours associated with a pentomino, displayed in standard position.

7. Conclusions and Further Research

This work introduced a group-theoretic framework for enumerating distinct checkerboard-coloured polyominoes, called chrominoes. We classified polyominoes using dihedral group actions and applied a modular arithmetic-based scheme to define the checkerboard colouring. By analysing the symmetries of both the polyominoes and the infinite checkerboard-coloured plane in which they are placed, we determined how these symmetries interact. This led to explicit formulas for the number of distinct chrominoes as a function of the polyomino’s symmetry class and the number of colours C.

We also provided a MATLAB program that validated the formulas using exhaustive search and illustrated them with examples.

Beyond its theoretical contributions, our work has practical applications in integer linear programming (ILP) methods for tiling problems, with the aim of generalizing the method in [15]. The approach begins by applying a fixed checkerboard colouring with C colours to the target region and identifying all possible chrominoes associated with each polyomino. The first ILP formulation assigns a variable to each chromino and enforces constraints ensuring that the total number of squares of each colour in the target region matches the total number of corresponding coloured squares of the selected chrominoes. It also ensures that the required counts of each polyomino are met. Solving this ILP provides a feasible set of chrominoes that may yield a tiling. The second ILP formulation assigns a variable to each valid chromino placement, ensuring that each chromino fits within the region and that its coloured squares align with the checkerboard colouring. Since this two-stage approach first determines feasible chromino combinations before enumerating their placements, it often eliminates certain tile placements, reducing the number of tile-placement variables in the second ILP. This is beneficial because the general problem of tiling finite regions with polyominoes is $\mathcal{NP}$-complete [29], making large instances intractable. Reducing the number of variables yields smaller ILP models, which can improve solver runtimes with high-performance optimisers such as CPLEX [30] and Gurobi [31]. However, the extent of these improvements depends on the problem structure and solver heuristics.

Several directions for future research remain open. One possibility is to extend these methods to three-dimensional analogues, such as polycubes, where symmetry considerations become more complex [19]. Another avenue is to explore alternative colouring schemes beyond cyclic checkerboard patterns, potentially leading to new combinatorial classifications.

An additional line of inquiry concerns digital plane rotations that provide insights into how lattice points behave under discrete transformations [32]. While our study focuses on dihedral symmetries of polyominoes, this work examines how rounding affects lattice points under rotation, proving that these transformations are generally neither injective nor surjective. Though their work does not address polyominoes or checkerboard colouring, their framework for discrete rotations may offer tools for studying how such transformations affect colour patterns on a lattice. This remains speculative but presents a potential direction for future research in combinatorial geometry.

By combining combinatorial geometry, modular arithmetic, and group theory, this work offers a structured methodology for counting and classifying chrominoes, with implications for both theoretical and applied mathematics.