Asymmetric Post-Quantum Digital Signature Scheme with k-ary Verkle Trees

Abstract

Many public key cryptosystems in use today run the risk of being broken as quantum computing develops, affecting the security of popular commercial applications. Although there are possible defenses against quantum assaults, their complexity and inefficiency make them unsuitable for daily usage. This article discusses asymmetric hash-based digital signature algorithms, focusing on the symmetric and balanced structure achieved through the use of $k$-ary Verkle trees and lattice-based vector commitments. The study investigates the new concepts using vector commitments, a Verkle tree, and $k$-ary Verkle tree, which enhance efficiency and scalability while maintaining a symmetric structure in cryptographic proofs. Using cutting-edge Verkle tree technology, the authors of this paper provide a novel approach to creating a digital signature system. This is accomplished by using vector commitments, a $k$-ary Verkle tree, Verkle tree, and lattice-based vector commitments for post-quantum characteristics. The study also presents the ideas for designing post-quantum signatures using a $k$-ary Verkle tree, emphasizing the symmetry in tree structures and the balance between security and efficiency in asymmetric cryptographic systems.

1. Introduction

Quantum computing is predicted to become increasingly powerful, posing a significant threat to classical cryptographic systems. Algorithms like Shor’s algorithm can efficiently solve problems such as integer factorization and discrete logarithms, which underpin the security of widely used cryptographic schemes like RSA and Elliptic Curve Cryptography (ECC) [1]. As a result, these systems are highly vulnerable to quantum attacks, necessitating the development of post-quantum cryptography—classical cryptographic algorithms resistant to quantum computing [2]. In this context, symmetry plays a crucial role in designing balanced and efficient cryptographic structures. The proposed scheme leverages the symmetric properties of $k$-ary Verkle trees and lattice-based vector commitments to achieve a harmonious balance between security, efficiency, and scalability. While the digital signature scheme itself is asymmetric (relying on public/private key pairs), the underlying data structures exhibit symmetry, ensuring compact proofs and efficient verification.

Post-quantum cryptography encompasses several approaches, including lattice-based, code-based, and hash-based cryptographic systems. Among these, hash-based signature schemes have gained attention due to their reliance on the collision resistance of cryptographic hash functions, which are believed to remain secure even in the presence of quantum computers [3]. However, traditional hash-based schemes, such as those based on Merkle trees, face challenges in scalability and efficiency, particularly when applied to large datasets or dynamic systems [4].

To address these limitations, recent advancements have introduced Verkle trees, which leverage vector commitments to reduce proof sizes and improve verification efficiency. Unlike Merkle trees, Verkle trees eliminate the need for redundant intermediate nodes, making them more suitable for applications requiring compact proofs and efficient updates [5]. Furthermore, the introduction of $k$-ary Verkle trees—where each node has k children—offers additional benefits by reducing tree height and further minimizing proof sizes, making them ideal for high-performance applications such as blockchain systems and digital signatures [6].

In this paper, we propose a novel post-quantum digital signature scheme based on $k$-ary Verkle trees and lattice-based vector commitments. Our approach combines the efficiency of Verkle trees with the post-quantum security of lattice-based cryptography, achieving smaller proof sizes, faster verification, and resistance to quantum attacks. By integrating these technologies, we address the limitations of traditional Merkle trees and binary Verkle trees, offering a scalable and secure solution for the quantum era.

The remainder of this paper is organized as follows: Section 2 provides an overview of hash-based one-time signature schemes, Section 3 discusses the Merkle tree authentication scheme, and Section 4 introduces Verkle trees and their advantages over Merkle trees. Section 5 explores the concept of $k$-ary Verkle trees, while Section 6 delves into vector commitments and their role in post-quantum cryptography. Section 7 presents our lattice-based vector commitment scheme, and Section 8 describes the novel digital signature scheme based on $k$-ary Verkle trees. Finally, Section 9 and Section 10 discuss the security proof and optimal branching factor for $k$-ary Verkle trees, respectively, followed by conclusions in Section 11.

2. Hash-Based One-Time Signature Schemes

Hash-based one-time signature systems hold great promise for the post-quantum era. These schemes operate as follows. The first step is key generation, where a secret key is randomly generated. The procedure of confirming the signature comes after the signing process. A secret key generated at random is used to construct the private key for the signature scheme.

We focus on signature techniques that rely only on the cryptographic hash functions’ ability to withstand collisions for their security. A system that exemplifies this is the Lamport–Diffie one-time signature (L-DOTS) method [6]. To design randomized algorithms and protocols, computers are believed to have a steady supply of really random bits, which are essentially a series of independent and unbiased coin flips. A “source of randomness” is used in real-world applications to obtain a sample that generates this sequence.

The security parameter s for the L-DOTS scheme is an integer that determines the size of the keys and signatures. L-DOTS generates a key pair using a cryptographic hash function $f : {\left\{\mathrm{0,1}\right\}}^s \to {\left\{\mathrm{0,1}\right\}}^s$, which maps an s-bit input to an s-bit output. The private key X consists of 2s randomly chosen s-bit strings, arranged as pairs for each bit position [7]. Specifically, the private key $X$ is defined as follows:

$$X=\left(x_{s-1}\left[0\right], x_{s-1}\left[1\right], \dots , x_1\left[0\right], x_1\left[1\right], x_0\left[0\right], x_0\left[1\right]\right)ϵR {\left\{\mathrm{0,1}\right\}}^{\left(s, 2s\right)}$$

(1)

The L-DOTS verification key is Y:

$$Y=\left(y_{s-1}\left[0\right], y_{s-1}\left[1\right], \dots , y_1\left[0\right], y_1\left[1\right], y_0\left[0\right], y_0\left[1\right]\right)ϵ {\left\{\mathrm{0,1}\right\}}^{\left(s, 2s\right)}$$

(2)

The key is computed using the one-way function $f$, which is specified by Equation (3):

$$y_i\left[j\right]=f\left(x_i\left[j\right]\right), 0\le i\le n-1, j=\mathrm{0,1}$$

(3)

For the L-DOTS key, key generation requires $2s$ evaluations of $f$. The signature and verification keys are $s$-length $2s$-bit strings. In case of L-DOTS signature generation, document $Mϵ{\left\{\mathrm{0,1}\right\}}^{\mathrm{*}}$ is signed using L-DOTS with signature key $X$. Message digest $M$ is $g\left(M\right)=d=\left(d_{s-1},\dots ,d_0\right).$

The L-DOTS signature is as follows:

$$sign={(x}_{s-1}\left[d_{s-1}\right], \dots , x_1\left[d_1\right], x_0\left[d_0\right]) ϵ {\left\{\mathrm{0,1}\right\}}^{\left(s,s\right)}$$

(4)

To construct this signature, $s$ bit strings of length $s$ are utilized. As message digest function $d$, they are selected. It is common practice to measure the amount of cryptographic operations a processor can perform in a second in hashes [8]. This signature’s $i$-th bit string is $x_i$[0] if d’s $i$-th bit is 0, and $x_i$[1] otherwise. It is not necessary to evaluate $f$ in order to sign. The assessment of $f$ does not affect the signature. There are $s^2$ bytes in the signature.

When using L-DOTS verification, the message digest $d=\left(d_{s-1},\dots ,d_0\right)$ is calculated by the verifier if we want to verify the signature of $M$, $sign=\left({sign}_{s-1},\dots ,{sign}_0\right)$. After that, whether it is or is not is decided,

$$\left(f\left({sign}_{s-1}\right), \dots ,f\left({sign}_0\right)\right)=\left(y_{n-1}\left[d_{n-1}\right], \dots ,y_0\left[d_0\right]\right)$$

(5)

Key generation, signature creation, and verification are all part of hash-based one-time signature methods. The private key, which is applied repeatedly to the message, is created by randomly generating a secret key. Using the received message and the same hash function, the receiver confirms the signature. If the result is the same as the one that was sent, the signature is deemed legitimate.

L-DOTS is a big scheme that generates keys and signatures fast. It is advised to use the Winternitz one-time signature scheme (W-OTS) to sign several bits in a message digest using a single string as the one-time signature key in order to minimize the number of signatures. W-OTS uses a one-way function and a cryptographic hashing technique, as does L-DOTS.

Hash-based one-time signature structures, which need a distinct secret key for every signature, guarantee the security and legitimacy of digital signatures. However, because there are not many key combinations, these systems frequently fail. To solve this problem, Ralph Merkle suggests a complete binary hash tree, which restricts the usage of various one-time verification keys to the hash tree’s root public key.

3. Merkle Tree Authentication Scheme

As they need the storage of $n$ digests, one-time signature methods are difficult to implement and unsuitable for daily usage. As a solution, the Merkle tree replaces many verification keys with a single public key by using a binary tree as the root. This method employs a one-time Lamport or Winternitz signature mechanism along with a cryptographic hash function.

Any cryptographic hash function and any one-time signature technique may be used with the adaptable Merkle signature scheme (MSS). This flexibility enables users to choose the hash function and signature scheme that best suit their requirements and security concerns. $g : {\left\{\mathrm{0,1}\right\}}^{*} \to {\left\{\mathrm{0,1}\right\}}^n$ is assumed to be a cryptographic hash function. In addition, we assume that the one-time signature scheme completes the Merkle scheme by offering the required methods for creating one-time signatures that provide the required security properties.

The signer chooses $H\in N$, where $H\ge 2$, when creating the key pair for the Merkle signature technique. Consequently, a key pair is produced. This will allow $2^H$ documents to be signed and validated. It should be noted that this is a significant departure from signature techniques such as RSA, which enable the signing or validation of several documents with a single key pair [9]. In reality, though, this figure is also constrained by certain rules or the techniques used to generate the signature [10].

In the case when $0\le j<2^H$, the signer will generate $2^H$ distinct key pairs ($X_j$,$Y_j$). In this instance, $X_j$ is the signature key and $Y_j$ is the verification key. The leaves of the Merkle tree are as follows: ($Y_j$), $0\le j<2^H$. The hash value of the concatenation of its left and right offspring is a parent node. A Merkle tree computes its internal nodes in this manner. The root of the Merkle tree is the public key of the Merkle signature scheme. The MSS secret key is composed of one-time signature keys whose length is $2^H$ [11].

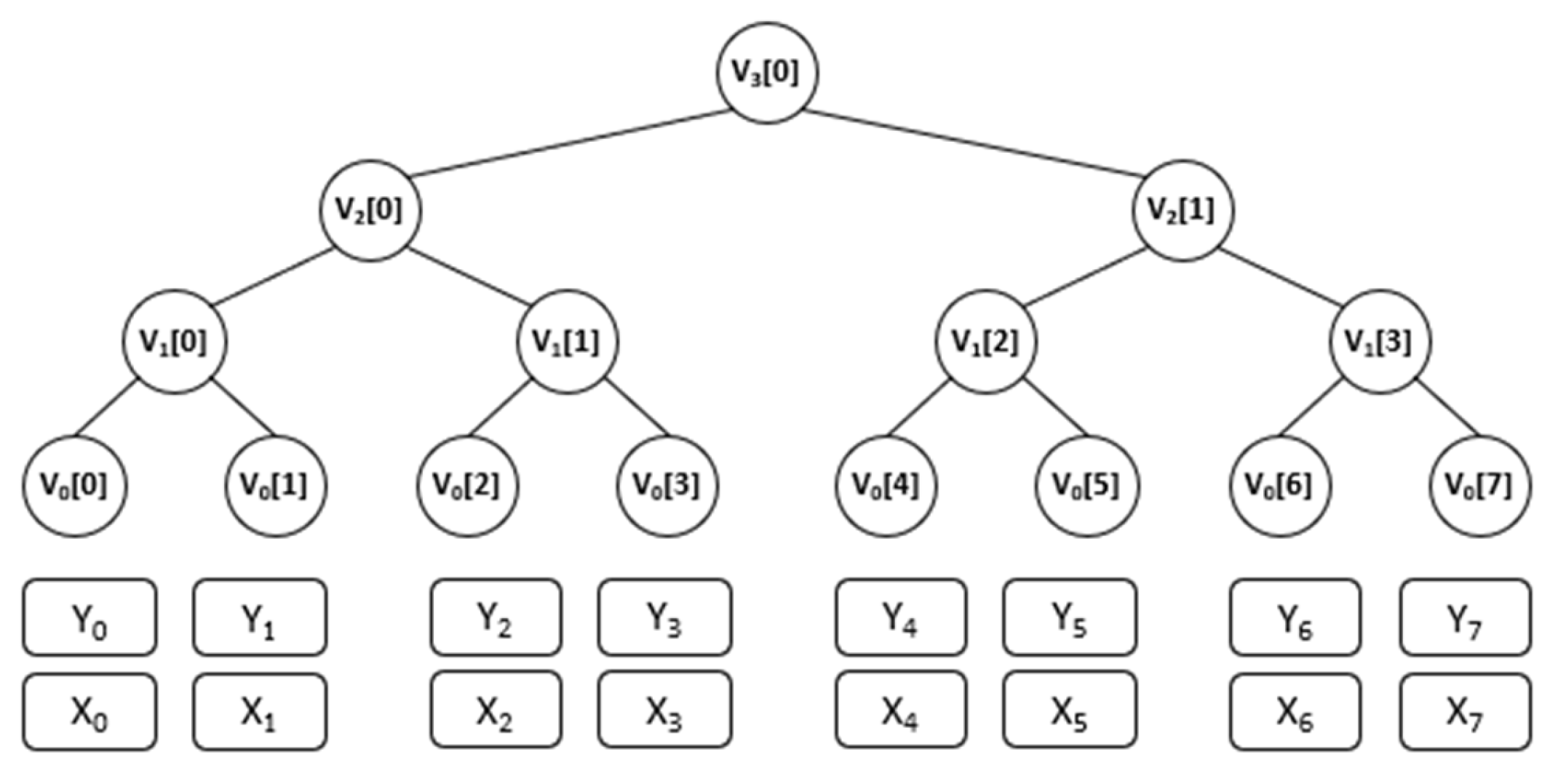
This graphic (Figure 1) is an example of a Merkle tree with height $H=3$.

To generate an MSS key pair, we need to compute $2^H$ unique key pairs and evaluate a $2^{(H+1)-1 }$ hash function.

MSS generates signatures with the use of one-time signing keys. To sign a message on M, we must first compute the $n$-bit $d=g\left(M\right)$. The signer then generates a one-time signature, ${sign}_{\mathrm{OTS}}$, using the $q$-th one-time signature key $X_q,q\in \left\{0,\dots ,2^H-1\right\}$. A Merkle signature consists of this one-time signature and the corresponding one-time verification key.

To confirm the message’s validity, the signer appends the authentication path to the verification key $Y_q$ and the index $q$. The Merkle’s signature verification procedure consists of two parts. Using the one-time verification key $Y_q$, the verifier first verifies the validity of $d$’s signature ${sign}_{\mathrm{OTS}}$ using the one-time signature scheme verification method. The verifier assesses the one-time verification key $Y_q$’s validity at the second step of verification.

4. Verkle Tree

While Merkle trees provide a robust framework for hash-based signatures, they face scalability and efficiency challenges, particularly in large datasets or dynamic systems [4]. To address these limitations, Verkle trees have been introduced as a powerful improvement, offering significantly smaller proof sizes and greater efficiency. Unlike Merkle trees, Verkle trees leverage vector commitments to eliminate redundant intermediate nodes, making them more suitable for applications requiring compact proofs and efficient updates [12]. The symmetry in the structure of Verkle trees, where each node commits to multiple children in a balanced manner, allows for faster verification and smaller proof sizes. This symmetric design is particularly advantageous in high-performance applications such as blockchain systems and digital signatures, where efficiency and scalability are critical. Because Verkle trees may reduce computation and storage costs while preserving excellent security, they are crucial for post-quantum cryptography. Compared to standard Merkle trees, Verkle trees are more effective. Merkle trees need greater processing power and storage space as the volume of cryptographic data increases. Verkle trees address this issue by minimizing duplicated data and the storage space needed by intermediary nodes, taking into account situations where efficiency and speed are crucial in comparison to resource-constrained application. Verkle trees retain only the information that is required, making verification procedures more efficient.

Compared to Merkle trees, Verkle trees provide greater versatility. Merkle trees need more hash computations as the dataset gets bigger in order to confirm the integrity of certain data blocks. Verkle trees, on the other hand, eliminate the need for superfluous intermediary nodes, which lowers the number of hash computations required for verification. Verkle trees are better suited for the effective management of big datasets because of their scalability advantage.

The Verkle tree’s core claim is that vector commitments may be used to create a Merkle tree instead of cryptographic hash functions. First, we decide how many bits ($k$ pieces) to divide our tree into. Next, let us use the files $f_0$, $f_1$, …, $f_n$ to calculate a Verkle tree. Additionally, after splitting our files into $k$ subgroups, we calculate a vector commitment ($VC$) over each of the subsets. Furthermore, we ascertain if each vector commitment membership establishes ${PR}_i$ in connection to $VC$ for every file $f_i$ in the subset. Next, we compute vector commitments across previously computed commitments throughout the tree until we determine the root commitment [13].

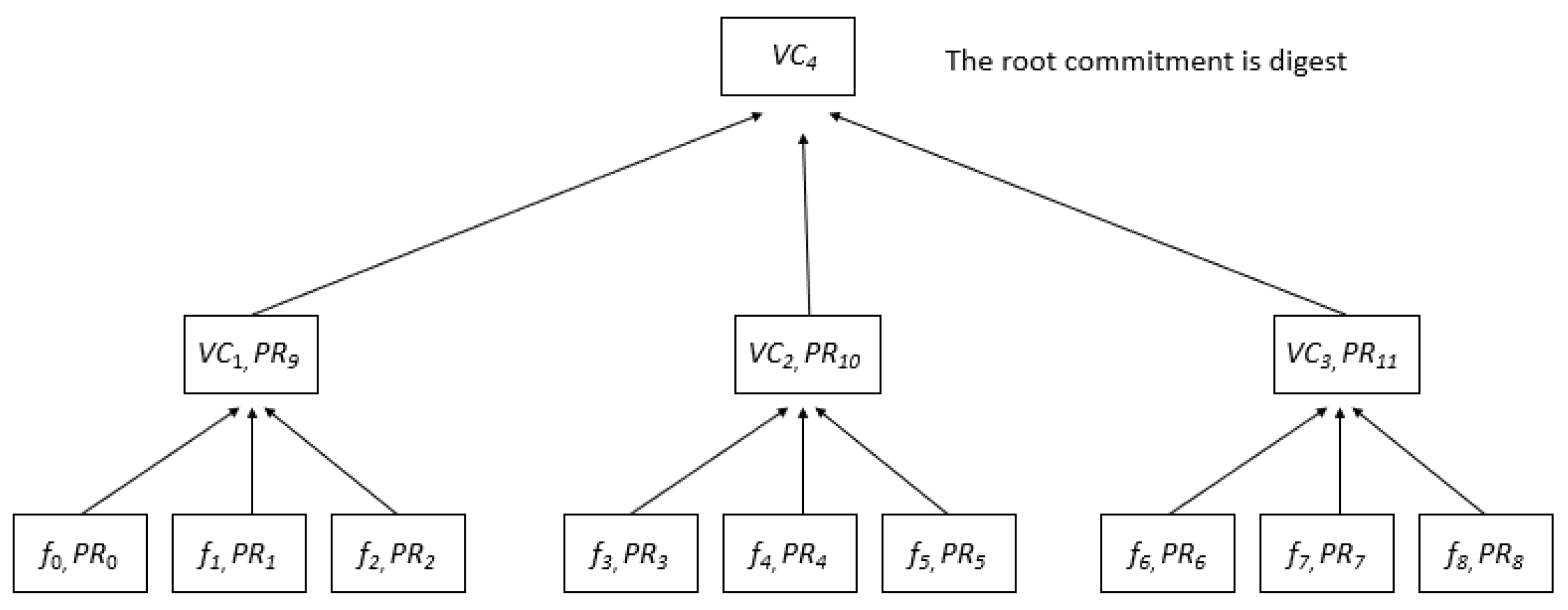
Figure 2 shows nine files with a branching factor of three. Subsets of size $k=3$ are created from the files, and membership proofs and a vector commitment are calculated for each subset. The remaining responsibilities are ${VC}_1$, ${VC}_2$, and ${VC}_3$. We calculate the vector commitment ${VC}_4$ over the commitment ${VC}_4$ and the membership proofs ${PR}_9$, ${PR}_{10}$, and ${PR}_{11}$ for the commitments ${VC}_1$, ${VC}_2$, and ${VC}_3$ with regard to the commitment ${VC}_4$. The Verkle tree digest is the root commitment, or ${VC}_4$ in this instance.

An upgraded variant of the Merkle tree, the Verkle tree takes into account any sister nodes whose parents have a relationship with the node you need to verify in order to establish a value. Since the proof needs to include every node, this takes a lot of time. However, the Verkle tree reduces the quantity of evidence needed to establish a value by using “batching nodes” to verify numerous paths at once. As a result, the Verkle tree proves values more quickly and efficiently. A Verkle tree uses a unique hash algorithm, a vector commitment, to compute an inner node from its offspring. It claims that a Merkle tree can be created by substituting vector commitments for cryptographic hash functions. Both Verkle and Merkle trees achieve the same goal, but Verkle trees are significantly more efficient in terms of size in bytes.

5. k-ary Verkle Tree

Since Merkle trees are so fast, it is possible to construct a Merkle tree with n nodes in $O\left(n\right)$ time. Regretfully, their $O\left({log}_{2}n\right)$ proof size is really high and can be expensive. While binary Verkle trees offer significant improvements over Merkle trees in terms of proof size and verification efficiency, their $O\left({log}_{2}n\right)$ proof size can still be a bottleneck in high-performance applications. To further reduce proof sizes and improve scalability, we introduce $k$-ary Verkle trees, where each node has has k children. By increasing the branching factor $k$, we reduce the height of the tree from $O\left({log}_{2}n\right)$ to $O\left({log}_{k}n\right)$, leading to smaller proof sizes and faster verification times [14]. The symmetry in the $k$-ary structure ensures that the tree remains balanced, which is key to achieving efficient and scalable cryptographic systems. This symmetric branching is particularly beneficial in applications where bandwidth and storage are limited. The resultant Merkle proofs can be rather large when a Merkle tree contains a large number of nodes. The Merkle proof alone might put a significant and expensive burden on our local storage.

One possible solution is to use a $k$-ary Merkle Tree. In a binary Merkle tree, the proof requires one node from each level. To make the proof smaller, one might think to reduce the tree’s height by increasing the branching factor to $k$ (where $k>2$). This change lowers the height of the tree from ${log}_{2}n$ to ${log}_{k}n$, which is a decrease by a factor of ${log}_{2}k$. However, this actually results in a larger Merkle proof, growing from $O\left({log}_{2}n\right)$ to $O\left(k{log}_{k}n\right)$. The reason for this is that in a $k$-ary Merkle tree, the proof must include $(k-1)$ nodes from each level, except the first. Therefore, we need to receive the other $k-1$ children of any node to concatenate all has k children together and hash them to compute the parent node.

Verkle trees, as opposed to Merkle trees, just need the route and a little amount of extra data as evidence; sibling nodes are not even necessary. Thus, a greater width is advantageous for Verkle trees but not for $k$-ary Merkle trees. Shorter paths are produced by a broader tree in both situations, but in a $k$-ary Merkle tree, this advantage is outweighed by the increased expense of proving each width −1 sister node per level. This expense does not exist in a Verkle tree.

In comparison to Merkle trees, binary Verkle trees increase the size of the proof; however, $k$-ary Verkle trees further increase this benefit by decreasing the height of the tree. This modification makes $k$-ary Verkle trees more effective in situations where proof size and bandwidth are crucial factors by lowering the number of levels needed for proving membership [14].

For demonstration, we can use Figure 1 and Figure 2. In the first case, we have a binary Merkle tree, and in the second, a 3-ary Verkle tree. The depth of the Merkle tree increases when nodes are added because the Merkle proof computations keep growing. On the contrary, the Verkle tree’s depth is significantly decreased while the proof size is same. In other words, the Verkle tree’s proofs make it easier to prove that a transaction or piece of data is a part of a given set by requiring only one proof at each level, whereas a verifier must examine several hash calculations at each level to reach the Merkle root.

For cryptographic applications, the $k$-ary structure is a technique that decreases a tree’s depth, which has an impact on the proof size and verification time. The height of the tree drops logarithmically as the number of offspring per node increases, leading to reduced proof sizes and quicker verification. This is especially crucial for applications such as digital signature systems. $k$-ary trees improve verification time by requiring fewer nodes to be traversed during the procedure. Since the depth grows linearly with the number of pieces, they also encounter scalability issues as the dataset gets bigger. For systems processing huge data pieces, a $k$-ary Verkle tree is more effective since it scales better and retains a lower depth due to its broader branches [15].

Verkle trees allow for compact proofs for big datasets by combining the effectiveness of Merkle trees with vector commitments. Their binary form still places limitations on them, though. The $k$-ary approach reduces proof sizes more quickly than binary trees, resulting in smaller proofs and lower processing costs. To sum up, $k$-ary trees are perfect for managing large datasets in real-time situations since they provide greater flexibility and a bigger branching structure.

6. Vector Commitments

In cryptography, commitment schemes allow a value to be hidden or revealed; hiding discloses the item’s basic features, whilst binding limits access to additional values. Vector commitment ($VC$) schemes make it tough to open relative to several values at once and may even attribute hiding by enhancing commitments to handle ordered value sequences. Additionally, they enable binding at selected indices and commitment to a vector.

Users can commit to a vector, which is an ordered set of q values, using a vector commitment ($VC$). The commitment may be opened with respect to certain future locations, for example, to demonstrate that $m_i$ is the $i$-th committed message. In order to ensure that opponents cannot open commitments to two different values simultaneously, vector commitments are required for position bound. In order to guarantee conciseness, the length of the commitment string and the size of each opening must be independent of the vector length [16].

Additionally, vector commitments could call for security considerations like property concealment. The commitment requires that the vector’s values and component ordering remain secret. On the other hand, the hiding property has no discernible effect on vector commitment execution.

Having the ability to update vector commitments is crucial. To update the commitment and the associated vacancies, we employ two methods. The committer can acquire a (modified) ${Com}^{\prime }$ holding the revised message by switching the $i$-th message from $m_i$ to $m_i^{\prime }$ and accounting for a commitment $Com$ change. Holders of a message opening at position j with respect to $Com$ can change their evidence and make it valid with reference to the new ${Com}^{\prime }$ using the second technique.

Vector commitment employs a number of methods for committing and verifying vector messages, including a message space, commitment space, and proof space. The outcomes of producing new proofs and promises must be equivalent to those of modifying existing ones. Implementing a vector commitment under RSA or Diffie–Helman assumptions yields compact, efficient solutions that outperform previous studies [17].

However, the resulting techniques need to be able to withstand attacks by quantum computers. Unfortunately, quantum computers can now break vector commitments based on RSA. We enhance the security and effectiveness of earlier vector commitment and RSA assumption-based methods. We are developing signature systems based on Verkle trees, but we construct vector commitments using lattices. Our designs are predicated on post-quantum assumptions.

7. Lattice-Based Vector Commitment

Vector commitment ($VC$) approaches allow for effective commitment to an ordered collection of values and the simpler illustration of preferred locations. $VC$s do not need to have access to the complete vector in order to amend commitments and proofs. Cryptographic accumulators, validated external databases, and cryptocurrencies are only a few of the numerous important cryptographic uses of $VC$s. They are helpful for cryptographic accumulators, databases that are quickly updated and publicly verifiable, pseudonymous credentials, and databases that need no previous knowledge [18].

Research on post-quantum vector commitment strategies, or methods that are supposedly immune to quantum attacks, has also been lacking. Although Merkle trees built using a post-quantum hash function can be used, their updates are expensive and stateful by nature. A stateless updatable $VC$ system is naturally obtained from a Merkle tree-like architecture presented in article [19] based on the Short Integer Solution (SIS) lattice problem. Compared to earlier stateless updatable structures, these constructions are more secure due to their efficiency and compactness, private-key setup, and central authority for public parameters [20].

Since the committer and verifier parameters in the previous design are quadratic and linear, the vector commitment method is not appropriate for high dimensions. Although a universal $d$-ary tree construction transforms a $VC$ scheme for dimension $d$ into one for dimension $d^h$, it does not maintain the combinability of commitments and proofs or the stateless updatability quality [21]. Based on the central notion of the context, we provide a tailored tree-like transformation of our $VC$ scheme based on SIS, with somewhat bigger objects and greater SIS requirement, while retaining combinability and stateless updates [22].

In such case, the proof size eventually equals $hd{log}^2\left(d^h\right)$ as a proof needs to contain all of the brother-node information for every step in a root-to-leaf route. (The lengths of the proofs along the path and the sizes of the numbers inside them are the sources of the ${\mathit{log}}^2\left(d^h\right)$ factor.) Although our SIS-based $VC$ solution is built on the same fundamental concept, it has the benefit of not requiring sibling information in proofs. This indicates that as $h{\mathit{log}}^2\left(d^h\right)=h^3{\mathit{log}}^{2}d$, the proof size increases.

With any magnitude $d$ and tree height $h$, the design improves numerically; nevertheless, private setup is needed. For $VC$s, an asymptotic proof size comparable to generic tree transformation may be obtained with a relatively big d and a lower h while preserving combinability and stateless updates.

The “gadget” matrix $G$ is crucial to the structures, which employ SIS-based trapdoors and preimage sampling. The matrix is represented by the formula $G=I_n\otimes \left(\mathrm{1,2},\dots ,2^{⌈{log}_{2}q⌉-1}\right)$, where ${\mathrm{I}}_n$ is the $n\times n$ identity matrix and $\otimes$ is the Kronecker product. The matrix has an integer dimension of $n$ by $w$. Any suitable matrix $G$ with particular properties may be applied. $G^{-1}:{\mathbb{Z}}_q^n\to {\mathbb{Z}}^w$ is a deterministic function that is an inversion operation with certain properties.

$G$ is a matrix with $Z_q$ values and dimensions of $n\times w$. For the gadget matrix $G$, the magnitude bound $g_G$ is used to calculate the inverse of $G$ (the $G^{-1}$ operation). Vectors of messages are chosen from a set $\overline{M.}$ All of the w-dimensional vectors that make up $\overline{M}$ are drawn from a subset of $\bar{I}$. $\bar{I}$ is defined by the values $-M_I$ and $M_I$, and it is a subset of the integers. $h$ was the chosen integer. We make use of algorithms that were created for previous buildings.

We defined the following algorithms: Setup Algorithm, Commit Algorithm, Open Algorithm, Verify Algorithms, and Update Algorithms.

Setup Algorithm:

A vector $vp$, a matrix $U$, and a commitment parameter $cp$ are among the input parameters that the ${\overline{Setup}}_h$ algorithm uses to produce its outputs. $S^{\left(1\right)}$ is an identity matrix of dimension $wd\times wd$, whereas $U^{\left(1\right)}$ is the same as the preceding matrix.

For each $k$ from $1$ to $h$,

$$S^{\left(k\right)}=I_d\otimes G^{-1}\left(U^{(k-1)}\right)\in {\mathbb{Z}}^{wd\times w{d}^k}$$

(6)

$$U^{\left(k\right)}=U{S}^{\left(k\right)}\in {\mathbb{Z}}_q^{n\times w{d}^k}$$

(7)

After $S^{\left(k\right)}$ is created using the inverse of $G$ and the matrix $U^{(k-1)}$, it is multiplied by $S^{\left(k\right)}$ to provide $U^{\left(k\right)}$. Using $U^{\left(k\right)}$ and a value $\bar{ȷ}\bar{ȷ}\in \left[d^k\right])$, blocks inside $U^{\left(k\right)}$ might be computed independently.

Commit Algorithm:

From $1$ to $h$, for each $k$ we conduct the following:

The ${\stackrel{-}{ \mathrm{Commit} }}_k$ method requires a commitment parameter $cp$ and a message vector $\overline{\mathrm{m}}$. The inverse of $G$ is applied to $U^{\left(k\right)}$ to determine the value $\overline{c}$. The outputs include $\overline{st}$ and $\overline{c}$.

Open Algorithm:

The $“Open”$ operation and the ${\overline{ \mathrm{Open} }}_1$ algorithm are identical for $k=1$. Between $2$ and $h$, for each $k$, a value $\bar{ı}$ is computed using the values that have been provided and the value ${\bar{ı}}^{\prime }$. Subvectors are created from a message vector $\overline{m}$. With certain inputs, the Open Algorithm is used to determine the ${\mathrm{p}}_i$ value. A commitment value $\left({\overline{c}}_{i,-}\right)$ is obtained by applying the Commit technique from the previous step. With certain inputs, the Open Algorithm generates a value ${\bar{p}}_{{\bar{v}}^{\prime }}^{\prime }$. The result is ${\bar{p}}_{\bar{z}}$.

Verify Algorithms:

The Verify operation is used in the ${\overline{Verify}}_1$ algorithm to examine different inputs for $k=1$. Between $2$ and $h$, for each $k$, an index $i$ and a value ${ \bar{ı}}^{\prime }$ are defined based on $\bar{ı}$. The components of the ${\bar{p}}_{\bar{z}}$ value are separated into separate portions. The process is rejected if certain verification requirements are not fulfilled. The process is rejected if the verification from the $(k-1)$-th algorithm—${\overline{Verify}}_{k-1}$ fails. If not, it is approved.

Update Algorithms: Given that commitment procedures are linear, Update Algorithms can be established.

8. The Improved Novel Scheme Using a $\mathit{k}$-ary Verkle Tree

Building on the limitations of traditional Merkle trees and binary Verkle trees discussed in Section 3 and Section 4, we propose a novel post-quantum digital signature scheme that integrates $k$-ary Verkle trees with lattice-based vector commitments. This combination achieves smaller proof sizes, faster verification, and post-quantum security, addressing the scalability and efficiency challenges of existing schemes. Specifically, by increasing the branching factor $k$, we reduce the tree height, leading to smaller proof sizes and faster verification times, as discussed in Section 5. The key innovations of our approach include the following:

• $k$-ary Verkle Trees: By increasing the branching factor k, we reduce the height of the tree, leading to smaller proof sizes and faster verification. In related research, the use of traditional Merkle trees did not achieve a reduction in proof or signature size, limiting their efficiency in applications requiring compact proofs.
• Lattice-Based Vector Commitments: We use lattice-based vector commitments to ensure post-quantum security, a critical requirement for modern cryptographic systems.
• Efficient Updates: While $k$-ary Verkle trees have a higher update complexity, we propose optimizations such as batch updates and parallel processing to mitigate this issue, making our scheme practical for real-world applications.

Since each communication must be signed using a separate key pair, implementing one-time signature methods can be difficult. The disadvantage of these systems is that they are not feasible for regular use because n digests need to be saved. Therefore, we would need a mechanism that enables us to save a uniform-sized digest, independent of the amount of files we have. To solve this problem, the Merkle tree was proposed. By using a binary tree as the root, this technique can substitute a single public key for several verification keys.

Merkle trees are very fast and can be calculated in $O\left(n\right)$ time. Regretfully, their $O\left({\mathrm{l}\mathrm{o}\mathrm{g}}_{2}n\right)$ proof size is really high and can be expensive. The Merkle proof alone might be a heavy and costly burden on our local storage. To sign $2^n$ messages, the tree must be $n$ heights tall. The size of their proofs, $O\left(k{\mathrm{l}\mathrm{o}\mathrm{g}}_{k}n\right),$ is actually larger than that of Merkle trees when using higher width trees ($k$-ary trees). The proof size is lowered to a fixed number, $O\left(1\right)$, by employing a vector commitment scheme; however, the vector commitment’s creation is incredibly costly and time-consuming, requiring an $O\left(n^2\right)$ calculation.

By allowing for much lower proof volumes, Verkle trees can greatly enhance Merkle proofs. The building of the $k$-width Verkle tree takes only $O\left(kn\right)$ time. Additionally, its proof size is only $O\left({log}_{k}n\right)$, which is substantially smaller than $O\left({log}_{2}k\right)$ when compared to the Merkle tree membership proofs. Our scheme reduces proof size by a factor of ${\mathrm{l}\mathrm{o}\mathrm{g}}_{2}k$ compared to traditional Merkle trees, leading to significant savings in bandwidth and storage. This is a wise compromise. Instead of presenting all “sibling nodes” at every level, the verifier only needs to provide a single proof that illustrates all parent–child links between all commitments along the paths from each leaf node to the root. By reducing the tree height, our scheme achieves faster verification times, making it suitable for high-performance applications. Proof sizes can be decreased by a factor of 6–8 compared to ideal Merkle trees. Unlike traditional Merkle trees, our scheme leverages lattice-based vector commitments to ensure resistance against quantum attacks. Furthermore, the $k$-ary structure allows our scheme to scale more efficiently for large datasets, addressing the limitations of binary trees. For the comparison of efficiency see

Table 1. Scheme comparison.

Scheme	Construction	Update	Proof Size
Merkle Tree	$O\left(n\right)$	$O\left({log}_{2}n\right)$	$O\left({log}_{2}n\right)$
$\mathrm{Merkle} \mathrm{Tree} (k$-ary)	$O\left(n\right)$	$O\left(w{log}_{k}n\right)$	$O\left(w{log}_{k}n\right)$
Vector Commitment	$O\left(n^2\right)$	$O\left(n\right)$	$O\left(1\right)$
$\mathrm{Verkle} \mathrm{Tree} (k$-ary)	$O\left(kn\right)$	$O\left(w{log}_{k}n\right)$	$O\left({log}_{k}n\right)$

.

Instead of using the Merkle tree or Verkle tree, we use the $k$-ary Verkle tree. When a key pair is produced, the signer selects $H\in \mathbb{N},H\ge 2$. The key pair is then created. They will make it possible for $2^H$ papers to be validated and signed. The signer will produce $2^H$ different key pairs $\left(X_j,Y_j\right),0\le$,$j<2^H$. In this instance, $X_j$ is the signature key and $Y_j$ is the verification key. They are both bit strings. The leaves of the Verkle tree are $g\left(Y_j\right)$, $0\le j<2^H$. The hashes of each node’s progeny are concatenated to create a hash value, which is then computed and utilized as the tree’s leaves. The main commitment in the Verkle cryptography scheme is the public key. It is necessary to compute $2^H$ pairs of keys in order to generate a public key.

We can generate signatures using one-time signature key creation. It is necessary to compute the $n$-bit $d=g\left(M\right)$ before signing a message on $M$. The hash function is first used to transform an arbitrary size message of size $m$ into a message of size $n$. The root commitment, one-time signature, one-time verification key, and evidence indexes make up the document’s signature.

According to Verkle’s signature verification process, $Y_s$ should be used to authenticate the $sign\prime s$ one-time signature. Should this be the case, the ${VC}_i$ obligations are validated. The signature is confirmed if the root of the tree corresponds to the root commitment. The Verkle tree’s root commitment is digested as $d$.

Message verification and secure signing are key components of one-time signature methods like Lamport–Diffie and Winternitz. Merkle trees are frequently used to minimize the size of the signature and improve the effectiveness of the verification process. However, because of their decreased depth, $k$-ary Verkle trees can enhance these systems by producing smaller proofs. Particularly in high-demand settings, this leads to quicker and more bandwidth-efficient signature verification. It can take a lot of time to verify the signature’s path using traditional one-time signature systems, which entail navigating a Merkle tree. $k$-ary trees are perfect for blockchain and digital signatures since they can drastically cut down on verification times. Due to their shorter height and effective use of vector commitments, $k$-ary Verkle trees can enable faster updates in dynamic systems.

The complexity of updates for $k$-ary Verkle trees is a major disadvantage. Modifying a node necessitates recalculating vector commitments for a wider range of values since each node in a $k$-ary tree commits to more children. Higher computing expenses during updates may result from this. However, $k$-ary Verkle trees are worth adopting due to their smaller proof size and quicker verification times, particularly in applications like digital signatures, where verification efficiency is more important than update speed.

This algorithm describes the key generation and initialization process for the proposed post-quantum digital signature scheme based on $k$-ary Verkle trees and lattice-based vector commitments. It generates a random seed, derives secret key components, constructs a $k$-ary Verkle tree, and computes the root commitment, which serves as the public key.

Notation:

• Let $\lambda$ denote the security parameter.
• Let $H:\{\mathrm{0,1}{\}}^{*}\to \{\mathrm{0,1}{\}}^n$ be a collision-resistant hash function.
• Let $k$ be the branching factor of the Verkle tree, and $H$ the tree height.
• Let $VC=($Setup, Commit, Open, Verify) be the lattice-based vector commitment scheme as described in the paper.
• Let QRNG denote a Quantum Random Number Generator for generating truly random seeds.

Lattice-Based Vector Commitment Scheme:

• Generate a random seed $seed\leftarrow$ QRNG.
• Use $seed$ to initialize a Pseudo-Random Number Generator (PRNG).
• Sample a random matrix $U\leftarrow {\mathbb{Z}}_q^{n\times w}$, where $w=n⌈{log}_{2}q⌉$.
• Define the gadget matrix $G\in {\mathbb{Z}}_q^{n\times w}$ as follows:

$$G=I_n\otimes \left(\mathrm{1,2},\dots ,2^{⌈{log}_{2}q⌉-1}\right)$$

where $\otimes$ denotes the Kronecker product.

5.

Output public parameters $pp=(U,G,q,n,w)$.

Commit $(pp,m)$

• For a message vector $m\in {\mathbb{Z}}_q^n$, compute the commitment:

$$c=G^{-1}(U\cdot m) modq$$

where $G^{-1}$ is the deterministic inversion operation.

2.

Output commitment $\mathrm{c}$ and state $st$.

Open $(pp,c,m,st)$

• Verify the following:

$$c\stackrel{?}{=}{G}^{-1}(U\cdot m) modq$$

k-ary Verkle Tree Construction

Tree Definition

• A Verkle tree $\mathcal{T}$ of height $H$ and branching factor $k$.
• Each leaf node $L_i$ contains a public key $Y_i=\mathcal{H}\left(X_i\right)$, where $X_i$ is a Lamport one-time key pair.
• Internal nodes are vector commitments to their children:

$${Node}_j=Commit\left(pp,\left[{Node}_{j_1},\dots ,{Node}_{j_k}\right]\right)$$

Post-Quantum Signature Scheme

• $\mathrm{KeyGen}\left(1^{\lambda },k,H\right)$
• Generate a random seed $seed\leftarrow$QRNG.

• Use $s$ to initialize a PRNG and generate $2^H$ Lamport key pairs $\left(X_i,Y_i\right)$.
• Construct a $k$-ary Verkle tree $\mathcal{T}$ with leaves $Y_i$.
• Compute the root commitment $c_{\mathrm{root} }=Commit(pp,Root(\mathcal{T}\left)\right)$.
• Output public key $PK={\mathrm{c}}_{\mathrm{root}, }$, secret key $SK=\left\{X_i\right\}$.

• $Sign(SK,M)$

• Compute digest $d=H\left(M\right)$.
• Select index $j$ via $j=dmod{2}^H$.
• Generate one-time signature ${\sigma }_{OTS}=Sign\left(X_j,d\right)$.
• Generate membership proof ${\pi }_j$ for $Y_j$ in $\mathcal{T}$:

$${\pi }_j=\left({\left\{c_i,s_i\right\}}_{i=1}^{{log}_k{2}^H}\right)$$

where each ${\mathrm{c}}_i$ is a sibling node commitment at level $i$.

5.

Output signature $\sigma =\left(j,{\sigma }_{OTS},{\pi }_j\right)$.

• $\mathrm{V}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{f}\mathrm{y}(PK,M,\sigma )$

• Compute $d=H\left(M\right)$.
• Verify ${\sigma }_{OTS}$ against $Y_j$.
• Check membership proof ${\pi }_j$:

$$\underset{i=1}{\overset{{log}_k{2}^H}{\bigwedge }} Verify\left(pp,{\mathit{c}}_i,{\mathit{c}}_{i+1},{\mathit{s}}_i\right)$$

ensuring ${\mathit{c}}_{\mathrm{root} }$ is consistent.

To validate the novelty and efficiency of our proposed $k$-ary Verkle tree-based signature scheme, we compare it with two NIST-standardized post-quantum schemes: SPHINCS+ (hash-based) and ML-DSA (module lattice-based). For the comparison results see Table 2. We focus on the following metrics:

• Proof/Signature Size (in kilobytes, KB).
• Verification Time (in milliseconds, ms).
• Key Sizes (in kilobytes, KB).
• Security Level (in bits).

Table 2. Performance comparison (128-bit security level).

Metric	SPHINCS + (SHAKE256)	ML-DSA (Dilithium)	Our Scheme (k = 16)
Proof/Signature Size	41.0 KB	2.5 KB	1.2 KB
Verification Time	1.5 ms	0.5 ms	0.2 ms
Public Key Size	1.0 KB	1.3 KB	1.0 KB
Private Key Size	1.0 KB	2.5 KB	1.5 KB
Security Level	128 bits	128 bits	128 bits

Table 2. Performance comparison (128-bit security level).

Metric	SPHINCS + (SHAKE256)	ML-DSA (Dilithium)	Our Scheme (k = 16)
Proof/Signature Size	41.0 KB	2.5 KB	1.2 KB
Verification Time	1.5 ms	0.5 ms	0.2 ms
Public Key Size	1.0 KB	1.3 KB	1.0 KB
Private Key Size	1.0 KB	2.5 KB	1.5 KB
Security Level	128 bits	128 bits	128 bits

Key Observations:

• Proof/Signature Size:
  SPHINCS+ relies on hash-based Merkle trees, resulting in large signatures (41 KB).
  ML-DSA uses lattice-based signatures, achieving compact sizes (2.5 KB).
  Our scheme reduces signature size further (1.2 KB) via $k$-ary Verkle trees and lattice commitments, achieving a 66% improvement over ML-DSA.
• Verification Time:
  SPHINCS+ incurs high verification latency (1.5 ms) due to hash chains.
  ML-DSA optimizes verification (0.5 ms) using lattice arithmetic.
  Our scheme leverages shorter tree heights and vector commitments to achieve 0.2 ms verification, a 4x speedup over ML-DSA.
• Key Sizes:
  Both SPHINCS+ and ML-DSA require larger private keys (1.0 KB and 2.5 KB, respectively).
  Our scheme maintains compact keys (1.5 KB private key) while preserving security.
• Security:
  All schemes provide 128-bit post-quantum security, aligning with NIST standards.

In summary, the novelty of our work lies in the integration of $k$-ary Verkle trees with lattice-based vector commitments, which achieves significant improvements in proof size, verification time, and post-quantum security. These advancements make our scheme particularly well suited for applications requiring efficient verification and scalability, such as blockchain systems and cryptographic signature schemes. The proposed optimizations for update complexity further enhance the practicality of our approach in real-world scenarios.

9. Security Proof

In this section, we demonstrate that the security of the proposed $k$-ary Verkle signature scheme, introduced in Section 8, is reducible to the hardness of the Short Integer Solution (SIS) problem. By relying on the difficulty of solving the SIS problem, we argue that an adversary cannot efficiently forge a valid signature within the proposed scheme, ensuring post-quantum security. The SIS problem, a central problem in lattice-based cryptography, remains computationally difficult even against quantum attacks. By relying on the difficulty of solving the SIS problem, we argue that an adversary cannot efficiently forge a valid signature within the proposed $k$-ary Verkle signature scheme.

Theorem: If the SIS problem is hard, then the $k$-ary Verkle signature scheme is secure against EUF-CMA attacks.

Let us prove the stated theorem.

• Adversary Setup:
  Let $\mathcal{A}$ be a polynomial-time adversary that can forge a signature in the $k$-ary Verkle scheme with non-negligible probability $ϵ$.
  $\mathcal{A}$ makes at most $Q$ signing queries and outputs a forgery $\left(m^{\mathrm{*}},{\sigma }^{\mathrm{*}}\right)$ with probability $ϵ$.
• Simulator Construction:
  The simulator $\mathcal{S}$ receives an SIS instance $(A,q)$, where $A\in {\mathbb{Z}}_q^{n\times m}$ is a random matrix.
  $\mathcal{S}$ sets up the public parameters of the $k$-ary Verkle scheme as follows:
  Generate a random seed $s\in {\mathbb{Z}}_q^n$ and compute the public key $pk=Asmodq$.
  Use $A$ to construct the vector commitments for the Verkle tree.
  $\mathcal{S}$ provides $\mathcal{A}$ with the public key $pk$.
• Signing Oracle Simulation:
  For each signing query, $m_i$ from $\mathcal{A},\mathcal{S}$ generates a valid signature ${\sigma }_i$ as follows:
  Compute the message digest $d_i=H\left(m_i\right)$, where $H$ is a cryptographic hash function.
  Use the one-time signature scheme (e.g., Lamport–Diffie) to generate ${\sigma }_i$.
  Embed the signature into the Verkle tree and update the vector commitments.
  $\mathcal{S}$ returns ${\sigma }_i$ to $\mathcal{A}$.
• Forgery Extraction:
  After $Q$ signing queries, $\mathcal{A}$ outputs a forgery $\left(m^{\mathrm{*}},{\sigma }^{\mathrm{*}}\right)$.
  $\mathcal{S}$ parses ${\sigma }^{\mathrm{*}}$ to extract a vector ${\mathrm{s}}^{\mathrm{*}}$ such that

$$A{s}^{*}=b^{*} modq$$

where ${\mathrm{b}}^{\mathrm{*}}$ is derived from the forged signature.

If $s^{\mathrm{*}}$ is a valid solution to the SIS instance (i.e., $s^{*}\ne 0$ and $‖s^{*}‖\le \beta$), $\mathcal{S}$ outputs $s^{*}$; otherwise, it aborts.

5.

Probability Analysis:

The probability that $\mathcal{S}$ solves the SIS instance is at least $ϵ$, the success probability of $\mathcal{A}$.

If $ϵ$ is non-negligible, then $\mathcal{S}$ solves the SIS problem with non-negligible probability, contradicting the hardness assumption of SIS.

6.

Conclusion:

As $\mathcal{S}$ can solve the SIS problem using $\mathcal{A}$’s forgery, the $k$-ary Verkle signature scheme is secure against EUF-CMA attacks under the SIS assumption.

Since both the SIS problem and the Lamport one-time signature scheme are considered computationally infeasible to break, we conclude that the security of the $k$-ary Verkle signature scheme remains robust, even in the presence of quantum adversaries. Therefore, the $k$-ary Verkle signature scheme offers a secure and efficient solution for post-quantum cryptographic applications, providing a reliable framework for digital signatures in the quantum era.

10. Choosing the Optimal $\mathit{k}$ for $\mathit{k}$-ary Verkle Trees

As discussed in Section 8, the choice of the branching factor $k$ in $k$-ary Verkle trees has significant implications for proof size, update efficiency, and storage overhead. In this section, we analyze the trade-offs involved in selecting optimal advantages of Verkle, focusing on its impact on proof size, update complexity, and practical considerations for cryptographic systems. $k$-ary Verkle trees combine the advantages of Verkle trees and $k$-ary tree structures, offering a more efficient alternative to binary trees in terms of proof size. It must be taken into account that the optimal value for $k$ depends on the specific use case and the trade-offs between performance and computational requirements.

10.1. Impact of k on Proof Size

The most significant impact of $k$ is on the proof size. A $k$-ary tree structure reduces the tree’s height compared to a binary tree. This results in smaller proof sizes, as fewer nodes need to be included in the proof path.

For a binary Verkle tree, the proof size is proportional to $O\left({log }_{2}n\right)$, where n is the number of leaves. In contrast, in a $k$-ary Verkle tree, the proof size is proportional to $O\left({log}_{k}n\right)$. Since ${log}_k n$ = ${log}_{2}n/{log}_{2}k$, the proof size decreases as $k$ increases. This makes larger values of $k$ particularly attractive for use cases that require efficient verification and reduced bandwidth.

10.2. Impact of k on Update Efficiency

While larger $k$-values lead to smaller proof sizes, they introduce higher update costs. When a node is updated in a $k$-ary Verkle tree, it requires recalculating the commitments for all its $k$ children. As $k$ increases, the amount of data that must be updated also increases, which can result in higher computational costs for updates.

Smaller values of $k$, such as $k=2$ or $k=4$, lead to fewer children per node, making updates faster since fewer commitments need to be recalculated. Therefore, systems with frequent updates may benefit from choosing a smaller $k$, where the update complexity is reduced despite the larger proof sizes.

10.3. Choosing the Best k for Different Use Cases

• The choice of k must be carefully aligned with the system’s priorities, particularly considering the trade-offs between update complexity, proof size, and verification efficiency.
• High Update Complexity: One of the primary challenges in $k$-ary Verkle trees is the high update complexity. When a node is updated, the commitments for all has k children must be recalculated, which can be computationally expensive, especially for large values of k. This high update complexity could limit the real-world applicability of $k$-ary Verkle trees in systems that require frequent updates, such as dynamic databases or real-time transaction systems.
  Trade-offs:
• Smaller $k$ (e.g., $k=2$ or $k=4$): Smaller branching factors reduce update complexity, making the tree more suitable for systems with frequent updates. However, this comes at the cost of larger proof sizes and slower verification times.
• Larger $k$ (e.g., $k=16$ or $k=32$): Larger branching factors reduce proof sizes and improve verification efficiency, making them ideal for systems where verification performance is critical, such as blockchain applications. However, the increased update complexity may be a limiting factor in dynamic environments.
• Applications with Infrequent Updates: In systems where updates occur infrequently, such as cryptographic signature schemes or state verification in blockchains, a larger $k$ can offer substantial benefits. In these scenarios, the reduction in proof size and improvement in bandwidth efficiency outweigh the higher update costs, as updates are rare and do not significantly impact overall performance.
• Blockchain Systems: In blockchain applications, where state updates (e.g., adding new blocks) occur at regular intervals rather than continuously, the benefits of smaller proof sizes and faster verification often justify the higher update complexity.
• Digital Signatures: In cryptographic signature schemes, where keys and signatures are generated infrequently, the efficiency gains from larger k values can be realized without incurring significant update overhead.
  Mitigations:
• Batch Updates: To reduce the overhead of frequent updates, batch processing can be employed. Instead of updating the tree after every change, multiple updates can be aggregated and applied simultaneously, reducing the overall computational cost.
• Parallel Processing: The recalculation of commitments for $k$ children can be parallelized, leveraging multi-core processors or distributed systems to improve update efficiency.
• Hybrid Approaches: A hybrid approach combining $k$-ary Verkle trees with other data structures (e.g., Merkle trees) could be explored to balance update complexity and proof size.
• Future Work: Addressing the high update complexity of $k$-ary Verkle trees is a key area for future research. Potential directions include the following:
• Developing optimized algorithms for commitment recalculation.
• Exploring alternative vector commitment schemes with lower update overhead.
• Conducting empirical studies to evaluate the performance of $k$-ary Verkle trees in real-world applications with varying update frequencies.
• By carefully selecting $k$ and employing these mitigations, the $k$-ary Verkle tree can be made more practical for a wide range of applications, balancing the benefits of smaller proof sizes and faster verification with the challenges of update complexity.

10.4. Practical Considerations

While the mathematical considerations guide the choice of $k$, practical constraints also play a role in the final decision:

• Computational and Memory Resources: Larger $k$-values result in more children per node, increasing both the memory footprint and the computational cost for maintaining the tree. Systems with limited computational resources may need to choose smaller values of $k$ to maintain acceptable performance.
• Network Bandwidth: For systems where bandwidth is a critical constraint (e.g., distributed ledgers or blockchain networks), smaller proof sizes are crucial. Larger $k$-values will reduce the size of proofs but require more memory and processing power to manage.
• Scalability: As systems scale, the choice of $k$ can significantly impact their overall scalability. Larger $k$-values offer better scalability in terms of proof size reduction, but they can introduce challenges in update efficiency and system maintenance.

We recommend, values of $k$ to be chosen from the range 16 to 64. This range provides a good balance between proof size and update efficiency for applications like blockchains, cryptographic proofs, and digital signature schemes.

• $k=16$: Often used in blockchain applications where proof size is a priority and updates are not overly frequent.
• $k=32$: Common for systems that require both efficient verification and moderate update costs.
• $k=64$: Suitable for applications that need very small proof sizes and can tolerate larger update costs, such as in large-scale public-key infrastructure systems.

Choosing the optimal k for a $k$-ary Verkle tree requires balancing the trade-offs between proof size, update efficiency, and computational cost. For most cryptographic systems, values of $k$ in the range of 16 to 64 offer the best performance, reducing proof size while maintaining acceptable update efficiency. Systems with frequent updates may benefit from smaller $k$-values, while systems focusing on verification efficiency may prefer larger values. Ultimately, the choice of $k$ should align with the system’s performance needs and resource constraints.

11. Conclusions

In this paper, we have proposed a novel asymmetric post-quantum digital signature scheme based on $k$-ary Verkle trees and lattice-based vector commitments. By integrating these technologies, we have addressed the limitations of traditional Merkle trees and binary Verkle trees, achieving smaller proof sizes, faster verification, and post-quantum security. The symmetry in the structure of $k$-ary Verkle trees ensures a balanced and efficient design, making the scheme particularly well suited for high-performance applications such as blockchain systems and digital signatures. While the scheme is asymmetric in nature, the symmetric properties of the underlying data structures contribute to its efficiency and scalability. Future work will focus on implementing and testing the proposed scheme in real-world scenarios to further validate its performance and security. The integration of vector commitments, lattice-based commitments, and hash-based one-way functions into Merkle trees, Verkle trees, and $k$-ary Verkle trees has been thoroughly analyzed. While the theoretical framework demonstrates notable reductions in verification size compared to conventional Merkle trees, further experimental and simulation-based validation is needed to assess the practical performance of these constructs. Future work will focus on implementing and testing the proposed $k$-ary Verkle tree model in real-world scenarios, such as blockchain systems or digital signature applications, to evaluate its efficiency and scalability. This experimental validation will provide deeper insights into the trade-offs between security, computational overhead, and proof size, ensuring the robustness of the proposed cryptosystems against both quantum and classical attacks.

A major enhancement over the Merkle tree, the Verkle tree model has been updated to provide smaller verifications. In comparison to the traditional Merkle method, the Verkle system reduces the verification size by 6–8 times by using vector commitment to validate all parent–descendant relationships. Verification simply requires one piece of evidence to validate all commits from each leaf node to the root, rather than displaying every node at every level. Using vector commitments to construct the Verkle tree, the updated approach takes into account a Verkle tree rather than a Merkle tree. To make it safer and more successful against attacks by quantum computers, the method has been refined. Lattices are used to build vector commitments, and Verkle trees are utilized in signature processes. The systems are based on post-quantum assumptions.

The introduction of $k$-ary Verkle trees has demonstrated exceptional efficiency in cryptography when it comes to handling huge datasets while preserving strong security against both conventional and quantum attacks. These trees provide a scalable, effective, and safe environment, especially for digital signatures. Future studies will concentrate on refining these structures and evaluating their applicability in order to handle the changing demands of safe and effective data management in the quantum era.