Forced Convective Heat Transfer in Tubes and Ducts: A Review of Prandtl Number, Geometry, and Orientation Effects

Abstract

This paper presents a comprehensive review of forced convective heat-transfer phenomena in fluids, emphasizing the influence of fluid properties, tube geometries, and flow orientations under varying Prandtl numbers. Key governing parameters—including velocity, viscosity, thermal conductivity, density, specific heat, surface area, and flow regime (laminar or turbulent)—are expressed through dimensionless groups such as the Nusselt (Nu), Reynolds (Re), and Prandtl (Pr) numbers. The review encompasses heat-transfer characteristics of low-, medium-, and high-Prandtl-number fluids flowing through circular, square, triangular, and elliptical tubes in both horizontal and vertical orientations, aiming to critically evaluate the effectiveness and trends reported in previous studies. Where applicable, symmetry correlations—based on equivalent thermal and hydrodynamic behaviour along geometrically symmetric boundaries—were considered to interpret flow uniformity and heat-transfer distribution across cross-sectional profiles. Analysis reveals that over 84% of the reviewed studies emphasize on horizontal configurations and 55% on circular geometries, with medium-Prandtl-number fluids dominating experimental investigations. While these studies provide valuable insights, significant research gaps remain. Limited attention has been given to vertical orientations, where buoyancy effects may alter flow behaviour due to temperature and pressure gradients arising from variations in fluid density and viscosity, to non-circular geometries that enhance boundary-layer disruption, and to extreme-Prandtl-number fluids such as liquid metals and heavy oils, which are vital in advanced industrial applications. Bridging these gaps presents opportunities to design and optimize diverse engineering systems requiring efficient convective heat transfer. Practical examples include coolant flow in nuclear reactors, heat dissipation in high-performance CPUs, and high-speed airflow over automotive radiators. This review therefore underscores the need for future research extending forced-convection studies beyond conventional configurations, with particular emphasis on vertical orientations, complex geometries, and underexplored Prandtl-number regimes.

1. Introduction

Primarily, when a temperature difference exists between two objects or regions, heat naturally transfers from the higher-temperature (warmer) body to the lower-temperature (cooler) one [1]. This phenomenon, known as thermal energy transfer, results in a change in the internal energy of both bodies. Internal energy is defined as the sum of all microscopic forms of energy associated with the intermolecular forces among the molecules within a system [2]. Heat can be transferred through the following three mechanisms: conduction, convection, and radiation and in this paper the focus will be on heat transfer by forced convection [3]. Forced convection occurs when an external force is applied to induce fluid motion, whether in gases or liquids, thereby enhancing heat transfer. Examples of such external forces include fans or pumps that circulate the fluid, promoting heat distribution by reducing the fluid’s density as it is heated, causing it to rise. In the absence of these external drivers, heat transfer occurs solely due to buoyancy effects, known as natural convection. Hence, the stronger the external driving forces, the more dominant the convective heat transfer.

These forces may originate from magnetic fields [4,5,6], electrohydrodynamic effects [7,8], acoustic excitation [9,10], or mechanical vibrations [11,12]. In situation where the convection reaches turbulent mode, an empirical formula of Dittus–Boelter correlation is applied for fully developed flow inside circular tube which relates the Nusselt number ($Nu$) to the Reynolds ($Re$) and Prandtl ($Pr$) numbers, as expressed in Equation (1).

$$Nu=0.023\hspace{0.17em}R{e}^{0.8}\hspace{0.17em}P{r}^n$$

(1)

where

• Nu = Nusselt number
• Re = Reynolds number
• Pr = Prandtl number
• n = 0.4 for heating of the fluid (wall temperature > bulk temperature)
• n = 0.3 for cooling of the fluid (wall temperature < bulk temperature)

In certain situations, both natural and forced convection mechanisms coexist, forming what is referred to as mixed convection. Classically, as natural convection correlates Nu-Ra and forced convection embodied by Dittus–Boelter correlation, both correlations did not directly validate in mixed-convection regimes due to modification of velocity and thermal boundary layers caused by the buoyancy existence [13]. This scenario was studied by Amran M.F. et al. [14], who investigated the influence of Prandtl number, geometry, and orientation in mixed convection which commonly favour horizontal circular tubes due to high heat-transfer performance with minimal pumping power, especially at low Reynolds numbers. As mixed convection typically appears in the transition regime (1000 < Re < 4000 and 0.1 < Ri < 10), forced convection predominates when Re > 4000 and Ri < 0.1. Buoyancy starts to distort forced convection velocity profile when Ri is at moderate range between 0.21 and 1 and shifts to mixed convection.

Several investigators have preferred stationary circular cylinders, including Denis et al. [15], who observed that cylinder rotation led to a complex heat-transfer phenomenon in their numerical study of forced convection. Subsequently, Denis and Badr [16] conducted further investigations on the effect of rotational speed on heat transfer from circular cylinders and found that increasing the rotational speed resulted in a reduction in the overall heat-transfer rate. Badr later extended this work to mixed convection involving laminar flow from a horizontal cylinder in a cross-stream configuration [17]. The observed decrease in heat-transfer rate was attributed to disturbances in the thermal boundary-layer structure when the cylinder was in rotational motion compared to when it was stationary, as also discussed by Baugh and Saniei [18]. Moreover, Rashid A. Ahmad [19] numerically analyzed a similar case involving uniform heat flux in an air cross-flow over a horizontal stationary circular cylinder at laminar Reynolds numbers ranging from 100 to 500. In contrast, a non-circular duct including rectangular, square, triangular, and elliptical contain corners or edges that limit the thermal performance due to flow stagnation. Vinuesa R et al. [20] and Nikitin et al. [21] both carried out investigation on the scenario known as secondary flow of the second kind (turbulence-driven vortices) induced by anisotropic Reynolds stresses in turbulent flow. The thermal boundary layer at the corner is thinning and significantly increases local and overall heat transfer.

With regard to Prandtl numbers selection, the researchers have examined fluids with both very low and very high Pr values, each exhibiting distinct heat-transfer dynamics. Ludwig Prandtl, the originator of the Prandtl number, defined it as the ratio of momentum diffusivity to thermal diffusivity, representing the relationship between the hydrodynamic and thermal boundary-layer thicknesses [22]. This boundary layer represents the region adjacent to a solid surface where flow resistance occurs due to viscous effects, and its extent is characterized by its thickness (δ) measured from the wall surface [23]. As illustrated in Figure 1, the thickness of the boundary layer can be determined from the Fourier heat-conduction equation [24], as expressed in Equation (2).

$$q={\displaystyle \frac{k · A · (T_H-T_C)}{\delta }}$$

(2)

where

• q = heat transferred per unit time (W)
• A = heat transfer area (m²)
• k = material thermal conductivity (W/m·K)
• T_H = hot temperature (K)
• T_C = cold temperature (K)
• δ = material thickness (m)

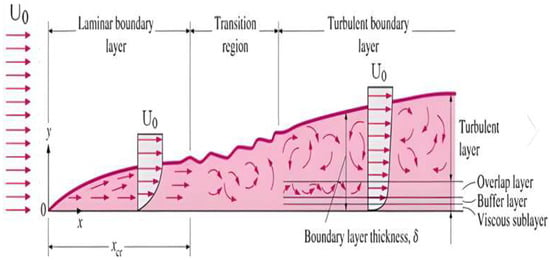
Figure 1. Thickness of laminar and turbulent boundary layers [24].

Therefore, the main objective of this paper is to consolidate previous research findings on the effectiveness of forced convection with respect to these three governing parameters (Figure 2).

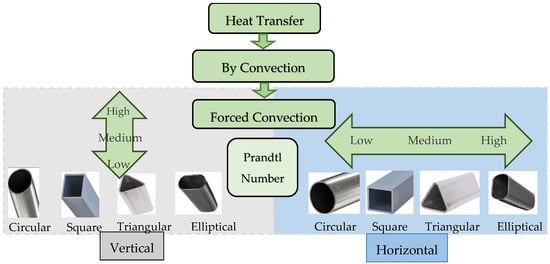
Figure 2. Summary on Pr selection with its geometry setting for forced convection.

2. Low Prandtl Number

For low-Prandtl-number fluids (Pr < 1), thermal diffusivity dominates over momentum diffusivity because of the fluid’s relatively high thermal conductivity and low kinematic viscosity and specific heat [25]. Henceforth, the thermal conductivity is higher, as expressed in Equation (3).

$$Pr={\displaystyle \frac{ {\mu }_f·C_p }{\mathrm{k}}}$$

(3)

where

• µ_f = fluid dynamic viscosity (kg/m·s)
• C_p = specific heat capacity (J/kg·K)

In simpler terms, in fluids with low Pr values, heat diffuses more rapidly than the velocity field develops, resulting in a thicker thermal boundary layer and a thinner velocity boundary layer, as illustrated in Figure 3. Most researchers have investigated heat transfer at low Prandtl numbers, typically around Pr = 0.7, which corresponds to gaseous fluids. Such fluids generally exhibit high thermal conductivity, high thermal capacity, low vapour pressure, and low melting points [26]. Furthermore, previous studies focusing on low-Prandtl-number heat transfer over circular-cylinder geometries are summarized in Table 1.

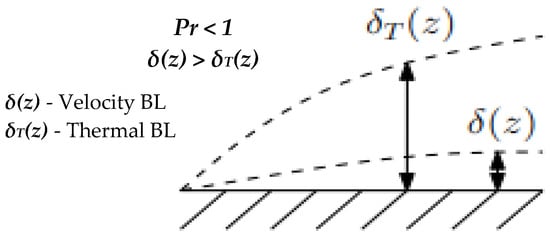
Figure 3. Boundary layer of low Pr number fluid.

Table 1. History of heat and fluid flow past a cylinder.

Authors	Re	Pr	Findings
Glauert [27]	-	0.7	Increased in rotation rate had increased lift coefficient.
Wang and Travinicek [28]	Laminar regime	-	Correlation using new concept of representative temperature.
Ahmad and Youvanovich [29]	104 to 105	0.7	Presented empirical model of forced convection.
Jeongyoung et al. [30]	02 ≤ Re ≤ 160	-	Reported flow quantities for lower Re.
Mahfouzh & Badr [31]	40	0.7	Increment of heat transfer in lock regime.
Sparrow et al. [32]	-	-	Correlations to calculate Avg Nu for circular and non-circular cylinder in cross flow.
Ahmed and Talama [33]	-	0.7	Proposed correlation for natural convection heat transfer calculation.
Khan et al. [34]	Laminar regime	0.7≤	Proposed correlation for UHF and CWT boundary condition using integral approach.
Reda I. Elghnama [35]	0 to 105	0.7	Proposed correlation for natural convection calculation.

In addition to gases, several liquid metals are also classified as low-Prandtl-number fluids. Wadim Jaeger [36] conducted a comprehensive study on twelve such metals, including sodium (Na) [37], potassium (K) [37], sodium–potassium alloy (NaK) [37], mercury (Hg) [38], lead (Pb) [39], lead–bismuth alloy (PbBi) [40], lithium (Li) [41], lithium–lead alloy (LiPb) [42], and the indium–gallium–tin alloy (InGaSn) [43]. A comparative assessment of their thermal and flow characteristics was carried out, and the results are summarized in Figure 4.

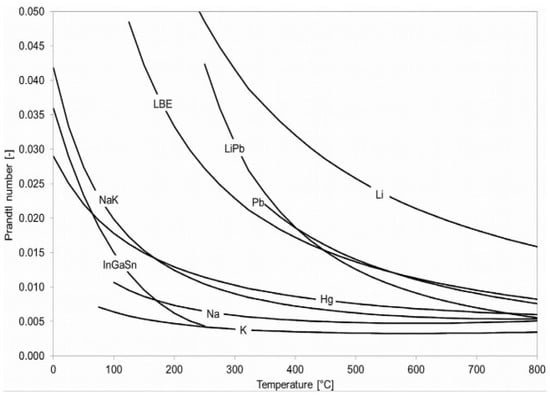
Figure 4. Comparison of Pr vs. Temperature (°C) [38].

The thermal–hydraulic behaviour of these liquid metals was studied and validated using both empirical models and experimental data under turbulent forced-convection conditions. The investigations covered various geometries, including circular pipes, annular channels, rectangular ducts, parallel plates, and rod bundles. A comparative summary of the numerical and experimental results is presented in Table 2.

Table 2. Theoretical Nu vs. Experimental Nu [38].

Numerical (Calculation/Simulation)	Experimental
Re = f (Material, Geometry, Boundary conditions)	$Nu={\displaystyle \frac{h · L}{k}}$	← Input/Geometry
Pr = f (Material, Boundary conditions)		← Material property
↑	where $h={\displaystyle \frac{{\mathrm{q}}_{\mathrm{w}\mathrm{l}}}{{\mathrm{T}}_{\mathrm{w}}-{\mathrm{T}}_{\mathrm{i}}}}$	← Input
Nu = f(Re,Pr) ← Calculation		← Measurement

Overall, low-Prandtl-number fluids exhibit lower Nusselt numbers compared to high-Pr fluids, such as oils and water, because convection is limited by their thin thermal boundary layers. Regarding geometry, both circular and non-circular ducts influence boundary layer development, with non-circular ducts providing only a slight enhancement for low-Pr fluids. Among the fluids considered, sodium–potassium alloy (NaK) typically achieves the highest Nusselt numbers, whereas mercury (Hg) exhibits the lowest.

2.1. Low Prandtl Number—Square Horizontal Tube

Researchers have long investigated forced convective heat transfer around square cylinders or tubes, as it represents a classical problem in fluid mechanics due to the complex flow patterns that arise—particularly flow separation and vortex shedding near sharp edges. These phenomena have motivated numerous experimental and computational fluid dynamics (CFD) studies aimed at analyzing the local Nusselt number distributions along the cylinder surfaces, where the heat-transfer rate varies across different faces.

A.K. Dhiman et al. [44] elucidated the significance of the Prandtl number in determining heat transfer from a solid square cylinder under steady-flow conditions (see Table 3). To capture detailed variations in the local Nusselt numbers over the obstacle surfaces, the flow domain was modelled in a rectangular coordinate system.

Table 3. Geometric configuration.

No.	Configuration
1	Incompressible, 2-Dimensional Flow
2	Steady flow: Re ¼ 1, 2, and 5 to 40 in steps of 5.
3	Unsteady flow: Re ¼ 50 to 160 in steps of 10
4	Working fluid: Air (Pr − 0.71)
5	Constant temperature
6	Constant heat flux

The findings revealed that, for square tubes, there exists a noticeable variation in the average Nusselt number on each face depending on both the Prandtl number (Pr) and Reynolds number (Re). In general, the average Nusselt number (Nu) increases progressively with increasing Re and Pr, thereby enhancing the overall heat-transfer rate.

Sharma and Eswaran [45] numerically investigated the heat-transfer characteristics of an isolated square cylinder under both steady and unsteady laminar flows for Pr = 0.7 and Re = 1–160 (two-dimensional regime). Geometrically, a square cylinder is bluffer compared to a circular one, leading to flow separation at the leading and trailing edges. Consequently, the square cylinder forms Kármán vortex streets that are significantly longer and broader, offering potential for enhanced heat and mass transfer between the cylinder surface and the surrounding fluid.

This phenomenon has drawn significant interest from other researchers seeking to further explore this fundamental fluid–thermal interaction from an engineering perspective. Zaki et al. [46] reported similar findings based on both numerical and experimental investigations of flow past a square cylinder at low and high Reynolds numbers, respectively. Sohankar et al. [47] extended these studies to Reynolds numbers in the range Re = 45–250, while in a subsequent work, Sohankar et al. [48] performed two- and three-dimensional unsteady flow simulations for Re = 150–500. Their results demonstrated the presence of stable vortex-shedding patterns at Re = 150 for 2D flow and at Re = 200 for 3D flow.

2.2. Low Prandtl Number—Circular/Sphere Horizontal Tube

For decades, numerous researchers have focused on the development of forced convective heat transfer using low-Prandtl-number working fluids in circular or spherical geometries. In as early as 1973, Dennis et al. [49] conducted a study to determine the heat transfer from an isothermal sphere subjected to a steady stream of viscous, incompressible flow. The numerically obtained Nusselt numbers were compared with experimental data at very low Reynolds and Prandtl numbers (Pr = 0.73), showing good agreement with the theoretical predictions of Rimmer [50]. However, as the Reynolds number increased, the results correlated well with the Whitaker correlation [51]. Research on low-Prandtl-number flows in circular and spherical enclosures has continued to the present day [52,53,54,55,56,57,58,59,60,61]. Overall, circular geometries are dominated by thermal conduction, resulting from thick thermal boundary layers and relatively low Nusselt numbers, with minimal dependence on Reynolds and Prandtl numbers.

2.3. Low Prandtl Number—Rectangular Horizontal Tube

V. Botton et al. [62] conducted a numerical simulation of low-Prandtl-number convection using a 2.5-dimensional (2D½) model in a rectangular cavity with dimensions 10: 6: 1 (length/height/width). The use of the 2D½ model, rather than a purely two-dimensional (2D) approach, was motivated by the presence of temperature-field inaccuracies in 2D simulations, which failed to accurately capture the underlying flow physics.

The study referenced five 2D benchmark experiments, collectively known as the AFRODITE experiments [63,64,65,66], which employed a similar cavity configuration for validation. In summary, the results demonstrated that the 2D½ simulation provided superior agreement with experimental data compared to the 2D model. It offered improved temperature-field uniformity in the transverse direction, better prediction of the Grashof number (Gr) behaviour, shorter computational time, and lower uncertainty relative to experimental results. Similarly to the square geometry, the rectangular cavity also exhibited weak sensitivity to variations in Reynolds number (Re), Prandtl number (Pr), and aspect ratio.

2.4. Low Prandtl Number—Elliptical Horizontal Tube

The impact of using horizontally oriented elliptical tubes on heat transfer was thoroughly investigated by Hussein et al. [67]. The study involved a numerical evaluation comparing three different geometries—elliptical, circular, and flat tubes—as illustrated schematically in Figure 5.

Figure 5. Schematic of investigation [65].

The findings from this study revealed that the elliptical tube achieved higher heat-transfer coefficient compared to the circular tube, when tested at the same length (500 mm) and hydraulic diameter (3 mm), as summarized in Table 4.

Table 4. Comparison by geometry and heat transfer coefficient between elliptical, circular, and flat cross-sectional area.

Shape	Tube Meshes	Cross-Sectional Area	Findings
Elliptical			The flat tube shows the highest heat transfer coefficient compared to the other tube types. The elliptical tube ranks second in heat transfer performance. The circular tube has the lowest heat transfer coefficient among the three. The superior performance of the flat tube is attributed to its larger heat transfer surface area.
Circular
Flat

In conclusion, the elongated geometry resulted in non-uniform velocity and temperature distributions, as forced convection in this configuration was largely dominated by thermal conduction. Consequently, the overall heat-transfer performance remained low, since the Nusselt number (Nu) was strongly influenced by the Reynolds number (Re), Prandtl number (Pr), and the aspect ratio.

2.5. Low Prandtl Number—Applications

Forced convection with low-Prandtl-number fluids is inherently complex because temperature and flow fields are strongly coupled. The high thermal diffusivity of such fluids leads to a thin thermal boundary layer, as heat is rapidly conducted away. One of the most significant applications of this phenomenon is in nuclear reactors, particularly in liquid-metal-cooled systems where coolants such as liquid sodium or lead–bismuth alloys are employed.

E. Cascioli et al. [68] examined the influence of low-Prandtl-number fluids in strongly forced-convection flows within a central planar cold jet, applying a series of turbulent heat-transfer models. Their results showed that at elevated temperatures, these fluids promote highly efficient heat transfer. Several other studies have similarly explored turbulent convection in jet systems using low-Prandtl-number fluids, including the works of Chua L.P. et al. [69], Di Venuta et al. [70], Errico O. et al. [71], Fregni A. et al. [72], Grotzbach G. [73], and Kyas W.M. [74].

A critical aspect of this research area lies in understanding the fluid-thermal interactions that govern reactor-cooling performance. Beyond turbulence modelling, there remain opportunities for advancement through refined computational-fluid-dynamics (CFD) simulations and the development of predictive heat-transfer correlations, which can yield more accurate predictions of flow and temperature behaviour under real reactor operating conditions. Ultimately, achieving efficient and safe thermal management depends on integrating both fundamental physical understanding and modelling enhancements.

In the automotive industry, a persistent challenge is developing radiators that deliver equal or superior thermal performance while reducing size and manufacturing cost. An improved radiator refers to a heat exchanger capable of removing excess heat from the engine more rapidly and efficiently, facilitating effective heat transfer between two or more fluids without any coolant mixing, as illustrated in Figure 6.

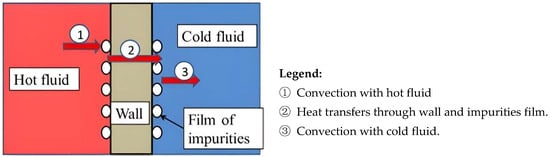
Figure 6. Transfer of heat through wall [75].

A. Faraj et al. [75] developed, simulated, and validated a new method to enhance heat exchanger performance by simultaneously measuring water and air flows under various operating conditions. The thermal performance was evaluated across sixty different combinations of air velocities and water flow rates. The procedure was deemed successful, showing very low relative errors—all below 1.6% (Figure 7a)—and minimal differences between the experimental results and the proposed innovative method for water flow rate predictions (Figure 7b).

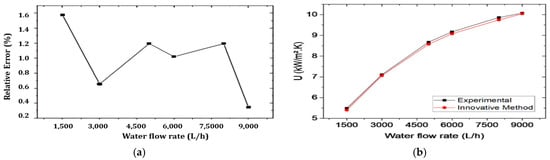
Figure 7. (a): As the water flow rate increases, the relative error between the experimental data and the predicted values decreases, indicating that the model demonstrates higher accuracy at elevated Reynolds numbers [75]. (b): The overall heat-transfer coefficient (U) steadily increases with flow rate due to enhanced turbulence and improved convection. The innovative method shows strong agreement with the experimental results (relative error <1.5%), validating the reliability of the proposed approach [75].

In the modern world, the continuous depletion of Earth’s natural resources—including fossil fuels, oil, natural gas, and coal—has shifted global attention toward renewable energy sources, particularly solar energy. Photovoltaic (PV) panels have become an essential technology for electrical power generation. Typically, water is employed as a working fluid to remove excess heat generated by solar irradiation, which accumulates on the rear surface of PV modules. This fluid-based cooling helps to maintain optimal panel temperature and improve electrical efficiency.

I. Masalha et al. [76] successfully demonstrated this concept using porous media (gravel) with varying porosities and fluid flow rates. Without cooling, the maximum surface temperature reached 49.1 °C, which was reduced to 39.4 °C after implementing the technique. Similar PV cooling approaches have been explored by other researchers. S. Yogesh et al. [77] enhanced cooling efficiency through optimized fluid design, H. Alizadeh [78] used a single-turn pulsating heat pipe, S. Jakhar et al. [79] utilized an earth–water heat exchanger, I. Masalha et al. [80] and Z. Rostami et al. [81] applied nanofluids, while H. M. Bahaidarah [82] studied jet impingement cooling.

3. Medium Prandtl Number

For medium-Prandtl-number fluids (Pr = 1), the momentum and thermal diffusivities are identical. In simpler terms, for fluids with Pr ≈ 1, heat diffuses at approximately the same rate as momentum, resulting in equal thicknesses of the thermal boundary layer δ_T(z) and the velocity boundary layer (δ(z)) as illustrated in Figure 8.

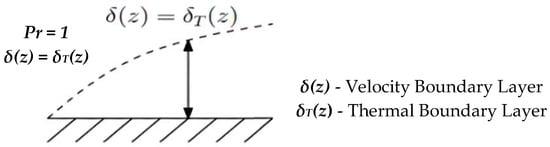
Figure 8. Boundary layer of medium-Pr-number fluid [25].

3.1. Medium Prandtl Number—Circular/Sphere Horizontal Tube

In a horizontal circular tube, there is a balance of interaction between conduction and convection, characterized by moderately thick thermal boundary layers, distinct temperature gradients near the wall, and Nusselt numbers (Nu) that vary noticeably with both Reynolds (Re) and Prandtl (Pr) numbers. Buoyancy effects remain negligible at low Richardson numbers (Ri).

Nemati et al. [83] used direct numerical simulations (DNS) to investigate how the boundary layer affects fluid flow in a circular tube. Their work examined the interaction between the wall-adjacent thermal layer and the developing turbulent flow inside the tube. The DNS employed fluid properties corresponding to the inlet Reynolds (Re) and Prandtl (Pr) numbers of a supercritical fluid. The results showed that the thermal effusivity ratio strongly influences both the Nusselt number (Nu) and the skin-friction coefficient. Another significant study on medium-Prandtl-number forced convection in circular tubes was conducted by Jian Liu et al. [84], who confirmed the effectiveness of supercritical carbon dioxide (sCO₂) as a regenerative cooling medium. Utilizing a circular tetrahedral lattice (CTL) structure, the sCO₂-cooled channel achieved a 52.5% reduction in wall temperature compared to a smooth channel, highlighting the advantages of regenerative cooling in highly heated aerospace jet engine systems.

Similarly, Tu et al. [85] compared supercritical CO₂ flow in microchannels of different cross-sectionals—circular, semicircular, rectangular, and trapezoidal. Their findings showed that the circular microchannel provided the highest heat-transfer coefficient, whereas the trapezoidal channel yielded the lowest, confirming the strong influence of geometry on thermal performance.

3.2. Medium Prandtl Number—Square Horizontal Tube

In horizontal square tube, Xingguang Zhou et al. [86] simulated turbulent heat-transfer mechanisms under constant wall temperature difference (CTD) conditions. Using OpenFOAM software, they aimed to obtain turbulent statistics and analyze the associated flow and thermal behaviours across medium Prandtl numbers ranging from 0.025 to 1.0 at a Reynolds number of 180. The simulation revealed distinct turbulent heat-transfer characteristics under both CTD and uniform heat flux (UHF) boundary conditions. The comparison of these two cases is illustrated in Figure 9a,b.

Figure 9. (a): UHF—constant heat flux from the top and bottom. (b): CTD—consistent temperature difference (Δθ) from end to end.

At the same friction Reynolds number (Re_T = 180), Kawamura et al. [87] performed direct numerical simulations (DNS) of turbulent heat transfer under uniform heat flux (UHF) conditions for a range of medium Prandtl numbers (0.025–0.71) to investigate the combined effects of Reynolds (Re) and Prandtl (Pr) numbers on flow and thermal behaviour. To date, a considerable number of DNS studies have been conducted on similar topics, including the works of Alcántara-Ávila and Hoyas [88], Abe and Antonia [89], and Priozzoli [90].

3.3. Medium Prandtl Number—Circular Vertical Tube

In circular vertical tube, one of the important applications is supercritical CO₂ (sCO₂), where flow through vertical channels is critical for the design of safe and efficient heat exchangers in sCO₂ power cycles. At Pr range between 1 and 10, sCO₂ exhibits strong coupling between turbulence and variable properties, especially near the wall regions. This incident generates positive and negative impact. On the positive note, a secondary flow of the second kind fabricating streamwise vortices enhances momentum and heat transport toward corners. In contrast, strong variations in temperature and pressure especially near the pseudocritical point cause heat transfer deterioration (HTD).

However, previous studies on convective heat transfer of sCO₂ in vertical tubes at low mass flux have reported inconsistent results, indicating that the underlying mechanisms remain insufficiently understood. To address this gap, Li et al. [91] experimentally investigated sCO₂ convective behaviour in a vertical tube, aiming to enhance heat transfer. They concluded that increasing mass flux, rather than heat flux, is the primary driver for improving convection under these conditions.

Wu et al. [92] further identified three stages characterizing vertical forced convection of sCO₂:

  i.

Deterioration stage—caused by flow laminarization,

 ii.

Recovery stage—where buoyancy effects intensify and turbulence regenerates, and

iii.

Re-deterioration stage, based on DNS of downward-flowing sCO₂.

Similar investigations have examined downward-flow sCO₂ characteristics in various configurations, including microtubes at low Reynolds numbers (E. Oztabak et al. [93]), the cooling-transfer effects of buoyancy (Y. Lei et al. [94]), and thermal–hydraulic behaviour under both heating and cooling (J. Guo et al. [95]).

3.4. Medium Prandtl Number—Applications

One of the significant modern applications of medium-Prandtl-number fluids is in pasteurization processes within the food industry. Pasteurization is primarily governed by convective heating, as conduction contributes only minimally. In such systems, temperature uniformity plays a crucial role—particularly in milk pasteurization and in solar-thermal collectors, which offer a sustainable alternative to traditional fossil-fuel-based thermal energy. At Pr of 2.605, S. K. Dabhi et al. [96] demonstrated the effectiveness of a convective pasteurizer, showing that increasing the flow rate in the cold stream significantly enhances the overall heat-transfer coefficient, as illustrated in Figure 10. Additionally, the integration of phase change materials (PCM) was shown to reduce temperature fluctuations, providing improved thermal stability, which is highly valuable for maintaining consistent pasteurization conditions.

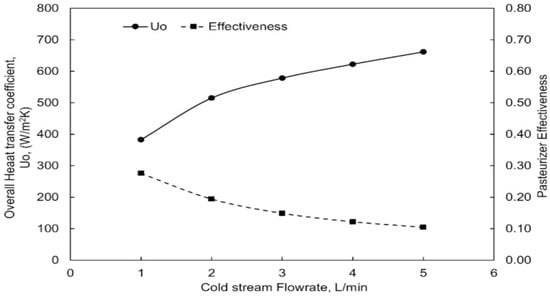
Figure 10. Effect of cold stream flow rate on overall heat transfer coefficient and effectiveness [96].

Additional research has also explored the application of medium-Prandtl-number fluids in pasteurization systems. Several studies have analyzed solar-assisted pasteurization, where solar energy serves as the primary heat source [97,98,99], while others have examined milk pasteurization using medium-Pr fluids under various thermal and flow conditions [100,101,102,103,104].

In the field of nuclear energy, the latest fourth-generation (Gen-IV) nuclear reactor systems require very high operating temperatures. These systems commonly employ medium-Prandtl-number working fluids, such as helium–xenon mixtures, lead, and sodium, which possess thermophysical properties suited to high-temperature heat transfer. Despite their relevance, conducting experiments on fast reactors involving these fluids is extremely challenging and costly, as highlighted by Schulenberg and Stieglitz [105], Wang [106], and Zhang et al. [107].

In overall, medium-Pr fluids exhibit moderate Nusselt numbers, higher than low-Pr fluids (liquid metals), because thermal transport is more efficiently coupled with momentum transport.

Unlike low-Pr fluids, geometry plays a more noticeable role as the non-circular ducts can enhance Nu more significantly and a turbulent water exhibits higher Nu compared to milk and ethylene glycol.

4. High Prandtl Number

For high-Prandtl-number fluids (Pr > 1), momentum diffusivity exceeds thermal diffusivity due to higher kinematic viscosity and specific heat. In practical terms, heat diffuses more slowly than the velocity field develops, producing a thin thermal boundary layer (δ_t) and a comparatively thick velocity boundary layer (δ) as illustrated in Figure 11.

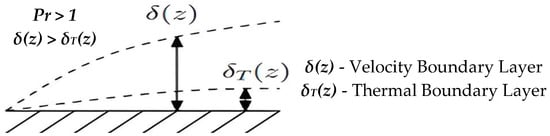
Figure 11. Boundary layer of high-Pr-number fluid [25].

M. S. Arif et al. [108] further showed that high-Prandtl-number fluids exhibit lower temperatures, a behaviour linked to their inherently low thermal diffusivity.

4.1. High Prandtl Number—Circular Horizontal Tube

Sanitjai and Goldstein [109] investigated the impact of forced convection on local heat transfer from a circular cylinder using water and water–ethylene glycol mixtures as working fluids. The Prandtl number in their experiments ranged from 7 to 176. Direct current was supplied through a thin in-line heater, providing uniform heating along the cylinder surface, as illustrated in Figure 12.

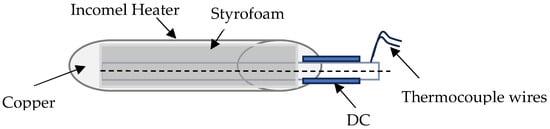
Figure 12. Test cylinder [109].

The investigation established a correlation between the local Nusselt number (Nu) and the Prandtl number (Pr). At Reynolds numbers (Re) of 4000 and 9000, the results showed that Nu increased with increasing Pr, as illustrated in Figure 13 and Figure 14.

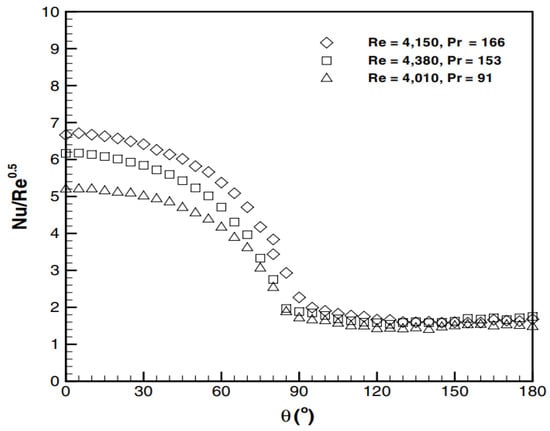
Figure 13. Distribution of local Nu at Re: 4 × 10³ [109].

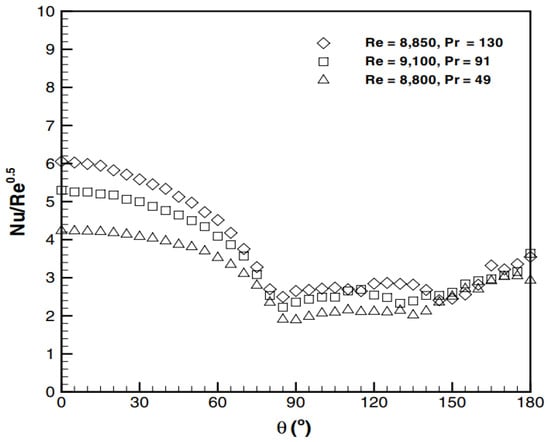
Figure 14. Distribution of local Nu at Re: 9 × 10³ [109].

Furthermore, the obtained results were compared with previous studies, as shown in Figure 15 as it revealed a similar trend among the Nusselt, Prandtl, and Reynolds numbers [110,111,112,113,114,115].

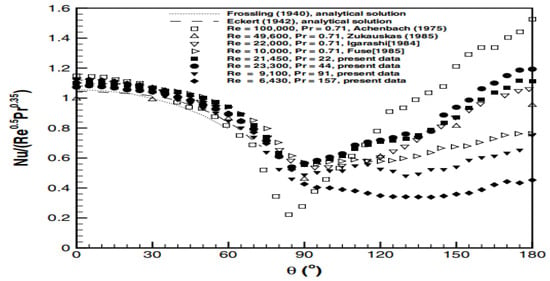
Figure 15. Comparison with other results [110,111,112,113,114,115].

Sarkar et al. [116] also investigated the correlation between Prandtl number and Richardson number. Using a circular horizontal tube, they examined forced convective flows and concluded that an increase in both Re and Pr leads to a corresponding increase in the local and average Nusselt numbers (Nu). In contrast, an increase in Ri results in a decrease in the average Nu [117].

Other studies examining the effect of high-Prandtl-number fluids in forced convection over circular horizontal tubes include those by Perkins and Leppert [118], Chang and Finlayson [119], and Sanitjai and Goldstein [120]. Collectively, these studies demonstrate that forced convection of high-Prandtl-number fluids in horizontal circular tubes is primarily governed by convective mechanisms, characterized by thin thermal boundary layers, steep wall temperature gradients, and high Nusselt numbers that are strongly dependent on both Reynolds and Prandtl numbers. Moreover, buoyancy effects become increasingly significant at higher Richardson numbers.

4.2. High Prandtl Number—Circular Vertical Tube

In addition to studies on horizontal forced convection, several investigations have also focused on vertical flow configurations. For high-Prandtl-number fluids in a vertical circular tube, heat transfer is characterized by intense convection, thin thermal boundary layers, and high Nusselt numbers (Nu). The vertical orientation introduces buoyancy effects that may either assist or oppose the flow, depending on the direction of heating.

Rasheed et al. [121] conducted a critical investigation on a vertically stretched cylinder, examining the influence of Prandtl number (Pr) along with other dimensionless parameters such as the Grashof number (Gr), Hartmann number (Ha), Schmidt number (Sc), and Eckert number (Ec) on flow velocity, temperature, concentration, skin-friction coefficient, and Nusselt number. A related study by Biswas et al. [122] analyzed the effects of a magnetic field on forced convection over a vertically stretched plate, exploring the combined influence of magnetic field, thermal radiation, heat source, and viscous dissipation within the boundary layer.

4.3. High Prandtl Number—Applications

For fluids with high Prandtl numbers, momentum diffusivity exceeds thermal diffusivity, resulting in thinner thermal boundary layers and steeper temperature gradients near the surface. In forced convection, this enhances heat-transfer performance even when the fluid’s thermal conductivity is relatively low. Introducing external driving mechanisms such as blowers, pumps, or fans further strengthens convection, often promoting turbulent flow. One notable application is the packed bed system—a column-type reactor or container filled with solid materials through which fluids (liquids or gases) flow, as defined by Almusafir et al. [123].

Packed beds are widely used in advanced nuclear reactors [124,125], thermal energy storage systems [126,127], catalytic reactors [128], and heat exchangers [129,130,131]. Within these systems, several physical and chemical phenomena occur simultaneously, including fluid flow through void spaces, heat transfer between the fluid and solid particles, dispersion effects due to mixing, chemical reactions at solid surfaces, and maldistribution caused by flow non-uniformity, as illustrated in Figure 16.

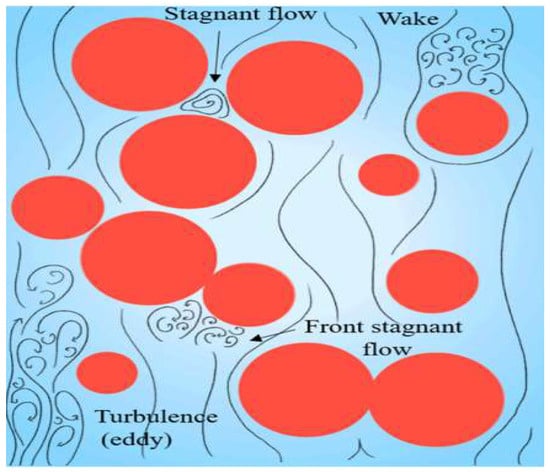
Figure 16. Flow characteristics in packed bed [132].

Park et al. [132] concluded that, to minimize adverse pressure gradients caused by stagnant flow, particular attention should be directed toward the geometric configuration of packed beds to help sustain turbulence. While traditional nuclear reactors employ fuel rods, the modern packed pebble-bed reactor (PBR) utilizes small spherical fuel elements (pebbles) to enhance coolant flow uniformity and thermal efficiency.

Another important application of high-Prandtl-number fluids is found in lubrication systems. Fluids such as oils, which exhibit Prandtl numbers ranging from 100 to 1000, can retain heat effectively due to their low thermal conductivity relative to momentum diffusivity. The resulting localized heat generation helps to stabilize the contact interfaces within the lubricant, a critical factor in maintaining lubrication performance. This thermal balance is particularly significant in automotive gearbox operations, where it directly affects fluid behaviour and efficiency. Hildebrand et al. [133] confirmed this interaction through numerical simulations of convective heat transfer between the rotating gears and lubricating fluid in a dip-lubricated gearbox, as illustrated in Figure 17.

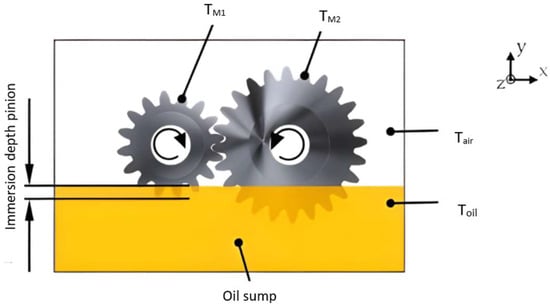
Figure 17. Illustration of interaction between gearbox and oil in oil sump through immersion depth [133].

The investigation revealed that increasing oil viscosity and circumferential gear-rotation speed both lead to a higher heat-transfer coefficient. Additional research on thermal balance in gearboxes has been conducted by Becker [134], who examined rotating machine elements to predict gearbox power loss. These studies collectively underscore the importance of balanced heat transfer in any rotating gearbox or machinery where oil serves as the working fluid [135,136,137,138,139,140,141,142]. At a Prandtl number of approximately 0.2, gas-turbine systems exhibit propulsive flow characteristics. Mixtures such as helium–xenon (He–Xe) or hydrogen–xenon (H–Xe) generate low-Prandtl-number ranges (0.16 < Pr < 0.7). M. F. Taylor et al. [143] measured these mixtures in a vertical tube, correlating their behaviour with the Colburn analogy and Dittus–Boelter relation. B. Zhou et al. [144] further emphasized the turbulent behaviour of He–Xe, a critical property for accurately simulating convective heat transfer in propulsion systems.

The food and beverage industry also benefits from advancements in heat-transfer engineering, particularly in processes such as pasteurization, decrystallization, ultra-high-temperature (UHT) treatment, and cooking, all of which ensure product safety, shelf life, and quality. Modern lifestyles, characterized by limited meal-preparation time, have driven demand for ready-to-eat and quick-cook products. Many of these, such as tomato paste and chocolate, are high-viscosity, high-Prandtl-number fluids (Pr > 100). H. Sadia and M. Mustafa [145] further explored heat transfer in food processing, covering manufactured coatings, comestibles (e.g., cheese and mayonnaise), slurries (e.g., emulsions and paper pulp), and multiphase mixtures (e.g., oil–water ointments). G. Betta et al. [146] developed a rapid method for estimating thermal diffusivity, applied to various foods including tomato purée, sauces, bacon, and eggs.

In a nutshell, the ability of high Pr fluids to maintain stable thermal gradients remain to drive innovation in material and system design. Although their thermal diffusivity is low, its high viscous losses can dominate pressure drop in lubrication channels. Design compromises are needed including shorter ducts, lower flow rates, or enhanced cooling surfaces in order to manage pressure and temperature simultaneously.

5. Findings

The primary objective of this paper—to review and synthesize past and current research on forced convection across various geometries, orientations, and Prandtl-number ranges—has been successfully achieved. A consolidated summary of the key findings is presented in Figure 18.

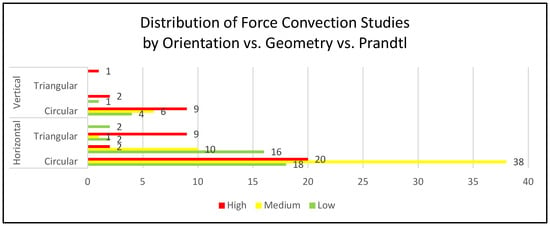
Figure 18. Studies on forced convective heat transfer.

From Figure 18, it is evident that research activities were distributed almost equally—approximately 33% each—across the three Prandtl-number categories (high, medium, and low). Most studies were conducted under horizontal flow conditions (84%), and the circular tube geometry was the most frequently used (55%). Researchers commonly preferred horizontally aligned circular tubes because it is the simplest geometry for buoyancy—dominated flow topology. Without corners or sharp edges, the flow curvature is uniform entirely especially for low Pr fluids, which deduces a predictable heating distribution. This stability and predictability had prompted most researchers to proceed with measurements or DNS in studying the boundary layer interaction, DNS solvers, new turbulence model, and engineering correlations. In contrast, a non-circular duct had created vortices and re-circulations as the boundary layer thickness is mismatched along the adjacent walls.

With respect to the influence of Prandtl number across different geometries in forced convection, the circular profile remains the dominant choice in industrial applications such as general piping systems and heat exchangers. Beyond ease of manufacture, circular tubes offer a high strength-to-weight ratio and can withstand internal pressure uniformly in all directions. However, for specific engineering requirements—particularly where enhanced turbulence and higher heat-transfer rates are desired—alternative geometries such as rectangular or non-circular ducts are also employed, albeit with the trade-off of higher pressure drops. Additional findings and comparative observations are summarized in Table 5.

Table 5. Impact of geometries towards Prandtl numbers.

Pr	Geometry	Findings	Overview
Low	Square/ Rectangular	Square corners slow down the flow. The thermal boundary layer grows even faster when Pr < 1 and becomes thick across cross-section. Nu is slightly higher than Circular duct due to surface area up.	Flow momentum modified by recirculation at corner and little thermal field. Dittus/Gnielinski/Pethukov—not valid. Require corner resolver in CFD, geometry-specific correlations, or correction factors to counter aspect ratio/shape.
	Triangular	Acute corners slower down local velocity. Thick thermal boundary layer (smoother conduction). Nu only slightly higher than circular duct (larger surface area)	Stagnation zones lead to over-/under-predicted correlations. Need CFD calibration or make use of local Nu maps during design.
	Circular	Thermal boundary layer is thicker than the velocity BL. Convection is weaker than conduction. Thermal entrance length is much longer—heat diffusion spreads over the entire cross-section before the flow becomes fully thermally developed (Nu ~3.66 at constant wall temperature along the tube).	Unreliable Dittus–Boelter/Gnielinski due to long thermal entrance. Suggested to use analytical conduction limits (i.e., Nu → 3.66). Focus on resolving thin velocity BL through CFD.
	Elliptical	Elongates the duct as velocity boundary layer varies. Thick thermal boundary layer. Relatively low Nu.	Require corrections to ellipse on aspect ratio. Apply CFD or ellipse corrections.
High	Square/ Rectangular	Square corners slow down the flow slightly. Thin thermal BL. Nu significantly higher than low Pr case. Strong convection near corners due to higher velocity gradient.	Require aspect—ratio corrections using Sieder—Tate viscosity correction for thin thermal BL. Nu = 0.027 × Re0.8 × Pr1/3(μ/μw)0.14
	Triangular	Acute corners with high Pr create thin thermal BL and the fluid cools very slowly due to zero fluid velocity at the corner. Slighter lower Nu compared to Circular. Nu significantly up over low Pr. Shorter thermal length.	Require aspect—ratio corrections to correct property gradient. Sieder—Tate correlation suggested: Nu = 0.027. Re0.8 . Pr1/3(μ/μw)0.14
	Circular	Very thin boundary layer and the layer forms rapidly. At constant wall temperature, Nu increased with Pr. The flow boosted heat transfer and temperature gradient is steep near the wall. Laminar for longer due to high viscosity and Convection dominates.	Dittus—Boelter recommended if:   i. turbulent flow.  ii. fully developed internal pipe flow. iii. smooth flow in circular. Gnielinski recommend if:   i. turbulent internal flow in circular.  ii. Re: 3000 → 500,000 iii. Pr: 0.5 → 2000.
	Elliptical	Thin thermal BL and shape-dependent. Heat transfer near minor-axis (higher velocity) better than major-axis. Nu slightly higher than low Pr.	Require viscosity correction (Sider—Tate type) to correct simple and failed Pr exponent.

In addition, variations in geometry produce distinct effects on the Nusselt number (Nu) in forced convection, as summarized in Table 6:

Table 6. Impact of geometries towards Nusselt numbers.

Geometry	Findings		Overview
	Laminar	Turbulent
Square/ Rectangular	Slightly lower than circular geometry as the corner effect reduces heat transfer.	At Low Pr, Nu is small. At Hi Pr, Nu is slightly higher due to secondary flows.	Corner vortices create low-shear zones (zero velocity) and weaker convection due to thicken thermal BL.
Triangular	Low due to stagnant zones at the corners.	At Low Pr, Nu is small. At Hi Pr, Nu is slightly lower due to recirculation (dead) zones.	Velocity almost zero at corners (three corners stagnation). Lead to overprediction of Nu when using correlations.
Circular	Highest and most uniform at laminar fully developed flow and constant wall temperature along the tube (Nu = 3.66).	At Low Pr, Nu is small. At Hi Pr, Nu is higher.	The most accurate usage of correlations (Dittus–Boelter, Petuckhov, and Gnielinski).
Elliptical	The flatter the shape, the lower Nu will be.	Nu drops with high Aspect Ratio. Nu highly affected by Aspect Ratio.	Thermal BL disproportionately thickens near major axis. Lead to overprediction of Nu when using correlations.

In terms of research methodology, two main approaches were identified: active and passive methods. In active methods, the rate of forced convection is enhanced through the application of an external force. Common active enhancement techniques include the use of magnetic fields [4,5,6], electrohydrodynamic (EHD) effects [7,8], acoustic excitation [9,10], and mechanical vibration [11,12].

In contrast, passive methods do not rely on external forces or power input. Instead, they enhance heat transfer by modifying fluid properties or surface characteristics. One passive approach involves altering the thermal conductivity of the working fluid, often through the use of nanoparticles, as demonstrated in several studies [147,148]. Another common strategy is to increase the effective heat-transfer surface area or promote flow disturbances, such as by flattening tubes [149] or inserting helical screw-tape elements [150]. Additionally, the heat-transfer surface can be specially engineered using twisted tapes [151], corrugated tube channels [152], or V-cut twisted tape inserts, with or without modifications [153].

6. Future Recommendations

Future research in forced convection is motivated by the global demand for improved thermal performance, energy efficiency, and sustainable engineering solutions. To advance the field, continuous development is required in the areas of fluid properties, geometry, and flow orientation. Area of improvement can be classified into two areas.

6.1. Fluid Properties, Geometry, and Orientation

(a)

Development of Turbulent Prandtl Number models for non-circular ducts in low-Pr flows.

(b)

Investigation of flow instability in vertical downward flows with high heat flux (opposing buoyancy).

(c)

Enhancing tube geometry and internal structures using roughened surfaces, twisted-tape and wire-coil inserts, and variable cross-sectional shapes to intensify turbulence and heat transfer.

(d)

Evaluating temperature-dependent variations in Pr, particularly under high thermal gradients encountered in combustion chambers, jet engines, and high-temperature reactors.

6.2. Advanced Physical Understanding and Experimental Needs

(a)

The potential of Machine Learning (ML) to derive universal correlations that cover the full spectrum of Pr numbers and geometries.

(b)

Exploring heat-transfer mechanisms in micro and nanoscale channels, where deviations from classical convection theory may arise due to entrance effects, wall roughness, rarefaction, and non-continuum behaviour.

(c)

Conducting experiments to validate MHD enhancements in high Pr vertical flows which are very much related to zero-carbon cooling systems. In turn, it is beneficial to these cooling technologies to reduce or eliminate CO₂ emissions and this research promotes energy efficiency and innovation in sustainable thermal management, indirectly supporting SDG 7 (Affordable and Clean Energy) and SDG 9 (Industry, Innovation, and Infrastructure).

(d)

Conducting experiments with non-conventional fluids, including nanofluids, hybrid nanoparticles, and PCM-infused fluids, in addition to molten salts and traditional water–air systems.

(e)

Conducting in-depth studies on flow physics, especially in the transition regime, to address deficiencies in existing correlations and to better understand local heat-transfer augmentation.

(f)

Giving greater attention to two-phase and multiphase flow behaviour, which plays a crucial role in overall heat transfer performance. Multiphase flow patterns—such as stratified, slug, annular, and bubbly flows—are particularly important in systems with low velocities, high viscosity, or small hydraulic diameters.

(g)

Utilizing electric or magnetic fields to manipulate flow structures and enhance heat transfer, including techniques of electrohydrodynamics (EHD) and magnetohydrodynamics (MHD).

(h)

Advancing experimental measurement techniques to obtain high-resolution, time-resolved, and spatially detailed data on local Nusselt number distributions and temperature fields, enabling more accurate model development and validation.

7. Conclusions

This review investigated forced convection across a wide range of geometries, orientations, and Prandtl numbers. Among the various configurations, the circular horizontal tube consistently demonstrated superior performance, attributable to its uniform flow distribution, lower pressure drops, and favourable heat-transfer characteristics. While these findings strengthen our understanding of forced convection mechanisms, they also reveal a noticeable imbalance in the current research landscape. Several research limitations were identified:

(i)

Limited coverage of emerging working fluids—Most studies focus on conventional fluids such as water, oil, and air, with relatively few investigations on nanofluids, supercritical fluids, or liquid metals.

(ii)

Oversimplified geometries—Many works employ basic tube or duct shapes, whereas real industrial systems often involve complex or irregular geometries.

(iii)

Restricted flow orientations and conditions—Research predominantly examines horizontal or vertical flows under steady-state conditions, with limited attention to inclined, rotating, or pulsating flows.

(iv)

Modelling and simulation constraints—Numerous CFD studies rely on simplified laminar or ideal turbulence models, despite real systems exhibiting variable thermophysical properties, multiphase interactions, and transient behaviours.

(v)

Lack of experimental standardization—Differences in measurement techniques, boundary conditions, and data reporting complicate cross-study validation and model generalization.

In summary, addressing these research limitations opens pathways for innovation in engineering systems where convective cooling is essential. Potential applications include nuclear reactor safety systems, high-performance electronics cooling, and advanced automotive and aerospace heat exchangers. Future work should prioritize vertical-orientation studies, unconventional geometries, and underrepresented Prandtl-number regimes. Such efforts will help rebalance current research trends and contribute to the development of more efficient, robust, and sustainable thermal-management technologies.