Market Game Optimization Algorithm: A Metaheuristic Inspired by Symmetric Competitive Behavior of Merchants and Consumers

Abstract

This paper introduces a market-inspired meta-heuristic named the Market Game Optimization Algorithm (MGOA), which models the symmetric competitive interactions between merchants and customers. MGOA simulates the dual dynamics of attraction and collaboration among merchants and customers, integrating a global search strategy that reflects how merchants attract customers. The optimization process includes two distinct stages, each employed with a 50% probability through a merchant cooperation mechanism designed to balance exploration and exploitation. Prior to performance evaluation, a qualitative analysis and parameter sensitivity study were conducted to clarify parameter selection and optimization characteristics. The algorithm was tested on 42 benchmark functions from the CEC2017 and CEC2022 test suites and compared against 10 well-established and 10 recently proposed meta-heuristic algorithms. Results indicate that MGOA achieves the highest overall ranking. Furthermore, its application to 11 real-world engineering design problems demonstrates high effectiveness and solution quality. All experimental findings confirm that MGOA is a robust and competitive meta-heuristic capable of solving complex real-world optimization problems.

1. Introduction

The rapid advancement of modern society necessitates the continuous adoption of intelligent methods for optimization. Whether the objective is maximization or minimization, such optimization problems are essential to societal progress [1]. Optimization algorithms—defined as stochastic or deterministic methods that optimize decision variables subject to objective functions and constraints [2,3,4]—are employed to address problems involving multiple decision variables under complex nonlinear constraints [5]. Classical optimization techniques include gradient descent [6], Newton’s method [7], the method of Lagrange multipliers [8], and simulated annealing [9]. However, real-world optimization tasks often exceed the capabilities of traditional solvers due to their large scale, high dimensionality, and inherently nonlinear nature. Such problems are frequently multimodal, causing search processes to easily become trapped in local optima and miss global solutions. Moreover, the proliferation of variables leads to an exponential expansion of the search space, resulting in the “curse of dimensionality.” The nonlinear and often non-differentiable behavior of objective functions further restricts the applicability of classical algorithms that rely on smoothness and convexity [10,11,12]. Engineering problems, especially multi-criteria optimization, are core issues in engineering design and manufacturing. Most practical optimization problems inherently involve multiple conflicting objectives [13]. Optimization algorithms can achieve material and manufacturing cost reductions while maintaining structural performance. Therefore, simple yet efficient metaheuristic algorithms are particularly suitable for solving difficult engineering optimization problems [14].

In contrast to conventional optimization approaches, genetic algorithms introduce a novel perspective on optimization [15]. As an evolution-inspired strategy and the first metaheuristic algorithm, they are capable of identifying high-quality solutions within computationally feasible time and resource constraints by evolving their own problem-solving ability, thereby enabling efficient handling of real-world optimization challenges [16]. Dokeroglu et al. argue that a new generation of metaheuristics is increasingly becoming one of the most effective avenues for tackling complex optimization problems. These methods are celebrated for their potent global search capabilities, minimal assumptions about problem structure, and exceptional scalability. They are widely applied to high-dimensional, nonlinear, and multimodal optimization landscapes that defy conventional techniques, demonstrating remarkable efficiency and practicality in real-world applications [17]. Those are also related to the challenge mentioned by Cebeci & Timur. In addition to calculating the mean ranking, the method to verify the successful development of metaheuristic algorithms also includes recording the median and the number of times the solution converges to the global optimum, since the solution is usually non-normally distributed. This successfully verifies the success of genetic algorithms in the origin of metaheuristic algorithms and the powerful engineering problem-solving capabilities they bring [18]. However, the outcomes derived from different research questions often vary. When deciding whether to use the mean or the median for comparison, researchers need to conduct analyses based on the specific context of the problem. In general, each statistical method emphasizes different aspects, thereby reflecting the diversity in how results are presented across various issues.

The new generation of metaheuristic algorithms can be primarily categorized into four types. The first category comprises variants inspired by evolutionary behavior, which are developed based on biological evolution or genetic mechanisms. The Genetic Algorithm (GA) was the first to employ evolutionary principles, simulating chromosomal crossover and mutation [19]. The Differential Evolution (DE) algorithm, proposed by Price et al., introduced vector differences between individuals in a population as a perturbation mechanism to guide the search direction, enhancing both solution accuracy and convergence efficiency in continuous optimization problems [20]. The Evolutionary Mating Algorithm (EMA), developed by Sulaiman et al., made a significant contribution by incorporating the Hardy–Weinberg equilibrium principle from population genetics into evolutionary computation. This provided a quantifiable model of genetic drift for discrete optimization, establishing a search framework based on explicit genetic mechanisms [21]. Meanwhile, Dong et al. proposed a Chaotic Enhanced Evolutionary Optimization (CEO) method, which integrates a memristive hyperchaotic system with differential evolution. This hybrid approach effectively balances global exploration and convergence speed, offering a novel dynamical optimization pathway for tackling NP-hard problems [22].

The second category consists of algorithms inspired by physical and chemical phenomena, tracing back to the Simulated Annealing (SA) algorithm by Bertsimas and Tsitsiklis. SA, inspired by the physical process of cooling, has solved numerous optimization problems and provided foundational insights into physicochemical-inspired metaheuristics [23]. Abdel-Basset et al. proposed the Kepler Optimization Algorithm (KOA), which is inspired by celestial mechanics. By simulating the orbital motion of planets under gravitational forces, KOA effectively guides the movement of candidate solutions, significantly improving global search capability and convergence efficiency [24]. Su et al. developed the Rime Optimization Algorithm (RIME), emulating the formation mechanism of frost ice in nature. Through modeling the growth behavior of soft and hard rime under varying temperature conditions, the algorithm achieves an adaptive balance between exploration and exploitation during the search process [25]. Additionally, Kashan proposed the Optics-Inspired Optimization (OIO) algorithm, which innovatively applies Fermat’s principle from optics to optimization. By mapping the path of light propagation in media to search strategies in the solution space, OIO demonstrates exceptional ability to avoid local optima in non-convex and complex function optimization [26].

The third category, and currently the most popular, is swarm intelligence metaheuristics inspired by collective behavior. Notable recent representatives are as follows: The pioneers of metaheuristic algorithms—particle swarm optimization (PSO) based on the response of particle groups and ant colony optimization (ACO) based on the communication behavior of ants—have set a precedent for the development of group behavior in metaheuristic algorithms [27,28]. The Dhole optimization algorithm (DOA) by Mohammed et al. was inspired by the vocal communication and cooperative hunting strategies of dhole. By simulating sound-guided adaptive decision-making and dynamic clustering behavior, DOA effectively balances exploration and exploitation during the search process [29]. Rüppell’s Fox Optimizer (RFO) by Braik et al., which models the diurnal and nocturnal foraging behavior of Rüppell’s fox, leverages acute sensory capabilities such as a 260° field of vision and 150° auditory perception. Its cognitive component dynamically coordinates the transition between global exploration and local exploitation [30]. The Animated Oat Optimization algorithm (AOO) by Wang et al. was based on the propagation mechanisms of animated oat seeds—including dispersal via external forces, obstacle-avoiding propulsion, and hygroscopic twisting movement. This offers a novel nature-inspired search framework for engineering optimization, such as wireless sensor network layout [31]. The Superb Fairy-Wren Optimization algorithm by Jia et al. draws inspiration from the development, brooding, and predator avoidance behaviors of superb fairy-wrens. By simulating these natural behaviors in distinct phases, the algorithm efficiently handles feature selection problems [32].

The final category represents the most recent advancement: human-inspired metaheuristics based on individual and collective human behaviors. Ahmadi pioneered the Human Behavior-Based Optimization (HBO) model, abstracting search rules from multiple cognitive stages such as knowledge acquisition, consultation, and belief evolution. This establishes an optimization framework adaptable to complex constraints with cognitive interpretability [33]. Bourechekara proposed the Most Valuable Player Algorithm (MVP), which draws on the dual mechanisms of individual excellence and collective collaboration in sports teams. It constructs a search strategy that simultaneously optimizes individual performance and group cooperation, effectively mitigating the inherent conflict between exploration and exploitation in traditional swarm intelligence algorithms [34]. Trojovský designed the Preschool Education Optimization Algorithm (PEOA) based on the phased teaching mechanisms in early childhood cognitive development. By simulating the influence gradient of teachers and a three-stage cognitive evolution process, the algorithm significantly enhances the ability to escape local optima in complex multimodal environments [35].

In summary, metaheuristic algorithms can be categorized as shown in Figure 1. The pursuit of robust and efficient optimizers is fundamental in tackling the ever-growing complexity of real-world problems. Despite the proliferation of metaheuristic algorithms, significant challenges remain, particularly in achieving a delicate balance between exploratory and exploitative behaviors—a common limitation that often leads to suboptimal performance or premature convergence. While various natural and physical phenomena have inspired numerous algorithms, the sophisticated strategic interactions inherent in human economic behavior remain a relatively untapped source of inspiration. To bridge this gap, this paper proposes the Market Game Optimization Algorithm (MGOA). Its core novelty lies in a unique two-stage mechanism that simulates, with equal probability, the competitive strategies of merchants and their coordination with customers. This design fosters a dynamic and effective search process. The efficacy of MGOA is rigorously validated through comprehensive parameter analysis, behavioral and visual inspection, extensive experiments on the CEC 2017 and 2022 benchmark suites, and applications to 11 real-world engineering design problems.

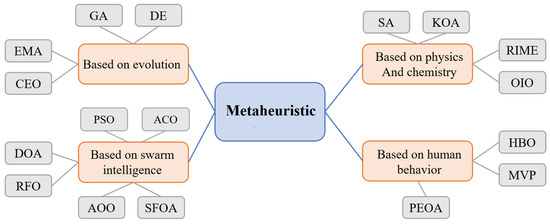
Figure 1. Summary of Metaheuristic.

The remainder of this paper is structured as follows: Section 2 delineates the interactive behaviors between merchants and customers and elucidates the underlying mechanisms that inspire the algorithm. Section 3 formalizes the merchant-customer game behavior model and introduces the proposed MGOA. Section 4 presents the experimental setup, including parameter configuration, qualitative discussions, performance evaluations, and practical applications. Section 5 concludes the study by summarizing the findings and discussing limitations and future research directions.

2. Inspiration from the Competitive Behavior of Merchants and Consumers

The essence of market activities stems from the complex strategic interplay between businesses and consumers. Companies dynamically adjust their marketing strategies to maximize profits, while consumers make choices to optimize their own utility, proving that the market has always been a game process [36]. This continual adaptation of strategies on both sides constitutes a paradigmatic game scenario. This paper conceptualizes the pivotal behavioral mechanisms inherent in commercial competition and formulates a Market Game Optimization Algorithm (MGOA).

• Gravity Phase (Exploration-oriented)
  The core characteristic of the market lies in its inherent dynamism and volatility—shifting demands, diverse consumer preferences, and an ever-evolving competitive landscape. To navigate such uncertainties, businesses must proactively sense market conditions and continuously refine their marketing strategies—such as pricing, product positioning, and promotional tactics—to attract diverse customer segments. This process is conceptualized as the Gravitational Phase: within the algorithm, “merchant agents” (candidate solutions) dynamically update their positions (strategies) based on market feedback (fitness values), emulating how businesses explore and attract distinct customer clusters (promising regions in the solution space). This phase emphasizes global exploration, preventing premature convergence to local optima, as illustrated in Figure 2.
  

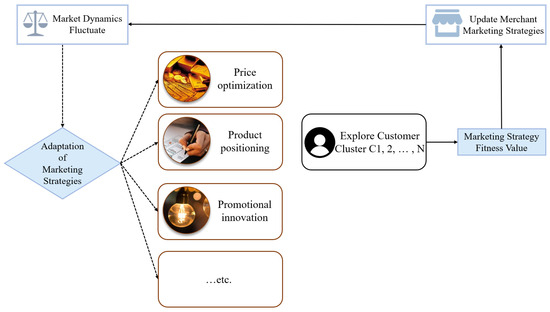  Figure 2. Merchants Adjust Marketing Strategies to Attract Customers.
• Collaboration Phase (Development-oriented)
  While attracting new customers, businesses must also prioritize retaining repeat customers to secure stable revenue streams. The interaction with this group transitions from broad outreach to deepened collaboration—achieved through personalized services, loyalty programs, and tailored solutions—enhancing mutual satisfaction and fostering long-term benefits. This behavior is mapped into the Collaborative Phase: high-performing merchant agents (solutions occupying high-value regions) engage within their neighborhoods to share strategic information and jointly refine solutions. This phase focuses on local exploitation, improving convergence accuracy through intensive search within high-potential regions, as shown in Figure 3.
  

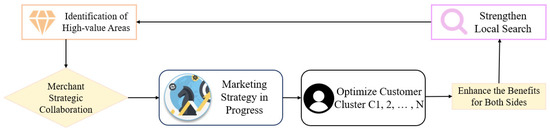  Figure 3. Merchants’ Marketing Strategies Develop in Tandem with Customers.

Ultimately, the Gravitational and Collaborative phases form a closed-loop feedback mechanism: exploration identifies promising regions, while exploitation refines and extracts value from these areas. Their dynamic balance equips the algorithm with both global search capability and local optimization efficiency, progressively converging toward the optimal market strategy.

Before starting the next section, we first clarify that all the symbols in this paper are shown in Table 1.

Table 1. Symbols and Description of Market Game Optimization Algorithm.

Term	Description
$N$	Population size
$nD$	Problem dimension
$FE{s}_{\mathit{max}}$	Maximum number of function evaluations
$FEs$	Current number of function evaluations
$lb,ub$	Lower and upper bounds of the search space
$X_{pos}^{i,:}$	Strategy vector of the i-th merchant
$fobj$	Objective function to evaluate strategy quality
$fi{t}_i$	Fitness value of the i-th merchant’s strategy
$Fi{t}_{new}$	Fitness value of the new strategy
$Po{s}_{best}$	Global best strategy position vector
$Fi{t}_{best}$	Global best fitness value
$S$	Strategy adjustment strength parameter
$A$	Base value for strategy adjustment amplitude
$n$	Market fluctuation frequency parameter
$\alpha$	Decay coefficient for strategy adjustment
$D_{new}$	Selected Dimensions
$r_1,r_2$	Random collaboration coefficients between merchants
$d{m}_1,d{m}_2$	Strategy difference vectors between merchants
$X_{i,j}$	Value of the j-th strategy dimension for the i-th merchant
$X_{i,j}^{(n)}$	Initial position of the i-th agent in the j-th dimension after n iterations
$X_L$	Leader agent with the best fitness value

3. Mathematical Model of the MGOA

This section proceeds to introduce the mathematical modeling and operational workflow of MGOA. The algorithm is designed to simulate the game-theoretic interactions between merchants and customers, wherein merchants continuously employ both attraction and collaboration strategies to maximize benefits. Through the merchant model [37], within the fluctuating cycles of the market, merchants adapt their marketing strategies to cater to a diverse customer base—a phase referred to as the Gravitational Phase. Subsequently, within the repeat-customer segment, merchants engage in cooperative behavior with these consumers to enhance mutual satisfaction and strengthen shared value, constituting the Collaborative Phase. The algorithm ultimately selects the optimal strategy emerging from this game process as the final solution.

3.1. Initialization

In the context of metaheuristic algorithms, population initialization constitutes the foundational phase of the overall optimization process. This paper employs a stochastic initialization method to generate an initial population of merchants, where each merchant represents a candidate solution. Specifically, the population consists of N individual merchants, the term “multi-dimensional marketing strategy” refers to a complete set of decisions a merchant makes across various competitive domains, mathematically, each characterized by d strategy dimensions. The values along each dimension are randomly generated within prescribed boundaries. This process can be mathematically formulated as follows:

$$X_{i,j}=l{b}_j+rand(u{b}_j-l{b}_j)$$

(1)

where $X_{i,j}\in [l{b}_j,u{b}_j]$ denotes the value of merchant i in the j-th strategy dimension, and $rand(0,1)$ represents a random number uniformly distributed within the range $[0,1]$. Following the initialization process, the fitness value $fi{t}_i$ for each merchant is evaluated.

$$fi{t}_i=fobj(X_{pos}^i)$$

(2)

where $X_{pos}^i$ denotes the marketing strategy j selected by merchant i, and $fobj$ represents the market fitness evaluation function, which assesses the attractiveness of the merchant’s strategy to the market.

The initial optimal solution $Po{s}_{best}$ and its corresponding fitness value $Fi{t}_{best}$ are subsequently identified.

$$Fi{t}_{best}=\min \{fi{t}_1,fi{t}_2,\dots ,fi{t}_N\}$$

(3)

$$Po{s}_{best}=\arg \min (X_{pos}^{i, :},fi{t}_i)$$

(4)

This stage provides a high-quality initial solution set for the subsequent optimization process.

3.2. Strategy Adjustment Strength S

Inspired by the phenomenon of cyclical market fluctuations, this paper introduces a strategy adjustment intensity mechanism into the MGOA to effectively balance the algorithm’s global exploration and local exploitation capabilities. The core formula of this mechanism is formulated as follows:

$$S=A\times \sin (2\pi \times {\displaystyle \frac{FEs}{FE{s}_{\max }}}\times n)\times \exp (-\alpha \times {\displaystyle \frac{FEs}{FE{s}_{\max }}})$$

(5)

where $A$ denotes the base amplitude of adjustment, and it is set to $\pi$. This value provides a principled and standardized initial step size for the strategy adjustment, corresponding to a half-cycle in a sinusoidal context. $FEs$ is the current number of function evaluations, $FE{s}_{\max }$ is the maximum number of evaluations, $n$ is the parameter controlling the frequency of market fluctuations, and $\alpha$ is the decay coefficient, which is a constant rigorously determined through extensive ablation experiments. $S$ represents the adjustment intensity, which starts with a higher value in the early iterations to promote global exploration and gradually decreases to enhance local exploitation as the optimization proceeds. The term $\sin (.)$ simulates the cyclical nature of market fluctuations, enabling the algorithm to maintain strong exploratory capability and high sensitivity in the early stages. Meanwhile, $\exp (.)$ ensures that the adjustment intensity decays progressively throughout the iterations, thereby improving the stability of exploitation and convergence behavior in the later phases.

3.3. Merchant and Customer Attraction Stage

The merchant attraction phase corresponds to the global exploration stage of the algorithm. Inspired by the Nash random selection, where players adjust their strategies to maximize payoff against the current strategies of others, each merchant adjusts its strategy relative to the current global best. Therefore, the algorithm is designed to model the exploratory and collaborative dynamics between merchants and customers through two distinct stages. To ensure balanced progression between these stages, each one is selected with a probability of 50% during each iteration. To prevent premature convergence that can occur from solely following the best strategy, the algorithm incorporates structured randomness by updating only a random subset of dimensions. The dimension selection mechanism is designed to balance efficiency and diversity, formulated as:

$$D_{new}=randperm(nD,k)$$

(6)

where the problem dimension $nD$ represents $nD$ strategies. $k$ represents the number of extracted dimensions. After that, in the selected dimension, the strategy update will develop in the direction of a better response in the market fluctuation environment. The displacement from the current position towards the best-known strategy is scaled by the strategy adjustment strength S, which modulates the step size. The update is given by:

$$X_{newpos}^{i,j}=X_{pos}^{i,j}-S\times (Po{s}_{best}^j-X_{pos}^{i,j})$$

(7)

Inspired by the concept of attraction in collective movement and to maintain diversity and avoid premature convergence, the mechanism performs updates only along a randomly selected subset of dimensions. This stochastic dimension selection drives merchant strategies toward more optimal directions and ensures that not all components of the strategy vector are updated simultaneously, thereby preserving population diversity and enabling a more comprehensive exploration of the solution space. The negative sign “$-$” in the equation signifies a directional movement toward the region occupied by the best merchant, facilitating convergence by reducing the discrepancy between the current and the best strategies. This form of update can be interpreted as a form of gradient-free optimization, where the search direction is biased toward the current optimum. As a result, the algorithm achieves a balance between directed convergence toward promising regions and stochastic exploration of uncharted areas, enhancing its ability to escape local optima and effectively locate the global optimum.

3.4. Merchant and Customer Collaboration Stage

The merchant-customer collaboration phase corresponds to the local exploitation stage of the algorithm. During this phase, each merchant not only draws inspiration from the optimal strategy but also synthetically incorporates strategic information from other merchants, thereby enhancing solution quality through multi-faceted strategy adjustments. The update mechanism is formulated as follows:

$$X_{newpos}^{i, :}=X_{pos}^{i, :}+r_1\times d{m}_1+r_2\times d{m}_2$$

(8)

where $r_1$ and $r_2$ represent random cooperation coefficients within range $[0,1]$ and are two adaptability capabilities of merchants to adjust their strategies during the cooperation process (computed as $\left\{\begin{array}{l}{r}_1=rand\\ r_2=rand\end{array}\right.,rand\sim U\left(0,1\right)$); $d{m}_1$ and $d{m}_2$ represents the difference between the strategies of two randomly selected merchants in the population and the customer. The utilization of only two randomly selected merchants to compute the difference vectors is a deliberate design choice, inspired by the differential mutation mechanism in evolutionary algorithms. This approach is justified by two primary considerations: computational efficiency and the preservation of population diversity. Using a small, random set of individuals introduces stochastic noise, which is crucial for preventing premature convergence and maintaining the exploratory capability of the algorithm. Business collaborations should be broadly open, so random search is used to disperse search directions, prevent premature convergence, and maintain population diversity. By combining solutions from multiple randomly selected individuals, this strategy simulates a form of recombination that allows exploration of new areas in the solution space without over-reliance on elite individuals. This is particularly effective in expanding the scope of exploration, helping to escape local optima, and promoting exploratory development in potential areas. This collaborative mechanism enriches search directions and enhances the algorithm’s ability to explore within potential optimal areas, thereby helping to obtain more accurate solutions.

After each strategy update, the new fitness value $Fi{t}_{new}$ is computed through objective function evaluation:

$$Fi{t}_{new}=fobj(X_{new}^i)$$

(9)

Subsequent strategy adoption follows greedy selection principle:

$$X_{current}^i=\left\{\begin{array}{l}{X}_{new}^i{ \mathit{if} \mathit{Fit}}_{new}^i<Fi{t}_{current}^i\hfill \\ X_{current}^i \mathit{otherwise}\hfill \end{array}\right.$$

(10)

The global optimal solution is updated through comparative assessment:

$$Fi{t}_{best}=\min (Fi{t}_{new})$$

(11)

$$Po{s}_{best}=\arg \underset{X_{new}^i}{\min } \mathit{fobj}(X_{new}^i)$$

(12)

This mechanism emulates the process through which merchants progressively seek optimal strategies by identifying the best fitness value across multiple gameplay rounds, ensuring monotonic improvement of solution quality throughout optimization.

3.5. Overall Algorithm Flow

In summary, inspired by the strategic adaptive behaviors of merchants in market competition, this paper proposes an optimization method that integrates periodic exploration and cooperative development. The algorithm begins by initializing the population and evaluating the initial fitness. In each iteration, it dynamically computes the strategy adjustment intensity S, and selects—with equal probability—either the Attraction Phase or the Collaboration Phase to execute. After each strategy update, a greedy selection mechanism is applied to update both the individual and global best solutions. The process continues until the maximum number of evaluations is reached, ultimately outputting the historical optimal solution. The overall framework of the algorithm, including its pseudocode and flowchart, is presented in Algorithm 1 and Figure 4.

Algorithm 1 Pseudocode of MGOA

Set parameters N, FEsmax, lb, ub, nD, fobj; Initialize population positions X randomly within [lb, ub]; Evaluate fitness values for all solutions; Determine the best solution Posbest and best fitness Fitbest; Initialize convergence curve cg;

For FEs = 1 : maxFEs

Calculate strategy adjustment parameter S by Equation (5);

If rand < 0.5

For i = 1 : N

Randomly select dimensions by Equation (6);

For each selected dimension j

Position update according to the exploration strategy by Equation (7);

End For

Apply boundary constraints;

End For

Else

For i = 1 : N

Randomly select two solutions from population;

Position update according to the exploitation strategy by Equation (8);

Apply boundary constraints;

End For

End If

For i = 1 : N

Evaluate new fitness value;

If new fitness is better than current fitness

Update current solution and fitness;

If new fitness is better than global best fitness

Update global best position by Equation (9);

Update global best fitness by Equation (11);

End If

End If

End For

Record current best fitness in convergence curve;

End For

Return bestfit, bestpos, cg;

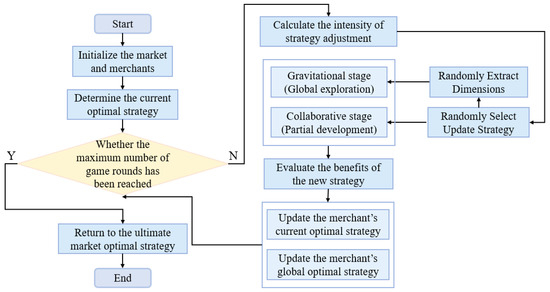
Figure 4. Overall Algorithm Flow.

4. Experiment and Analysis

To demonstrate the advantages and characteristics of MGOA, this study employs behavioral and visual analysis and parameter configuration experiments to illustrate the algorithm’s optimization capability. Subsequently, a multi-dimensional performance comparison is conducted against ten well-established metaheuristic algorithms on the CEC2017 benchmark, highlighting the superior performance of MGOA. Furthermore, comparative experiments involving ten state-of-the-art enhanced algorithms on CEC2022 and 11 real-world engineering problems are carried out, providing dual validation of MGOA’s applicability and potential in both benchmark testing and practical optimization scenarios.

4.1. Computing Environment

To ensure the fairness and repeatability of the experiments, all experiments in this paper were conducted in a unified environment. The experimental configuration is detailed in Table 2.

Table 2. Configuration Instructions.

Configuration	Description
CPU Model	Intel i7-11800H
Operating System	Windows 10 Pro
System Memory	16.0 GB
GPU Model	NVIDIA RTX-3060
GPU Memory	13.9 GB
Coding Environment	MATLAB 2023b

4.2. Behavioral and Visual Analysis

This section employs 8 classic benchmark functions to design four experiments for the behavioral and visual analysis of MGOA. First, the distribution of the optimal merchant strategies within the solution space of MGOA is analyzed to visualize the search strategy characteristics of merchants. The historical trajectories of marketing strategy searches are recorded by tracking the position of the optimal marketing strategy in each iteration. Additionally, an experiment on business strategy evolution is designed by documenting the best business strategy at every iteration. Then, to examine the overall iterative trend of the algorithm, the fitness value of the best solution after each iteration is recorded, and a convergence curve experiment is constructed. Finally, to analyze the variation trend of the fitness value over iterations, a fitness value change experiment is designed by logging the best fitness value after each update.

Figure 5 presents the results of MGOA on the four qualitative experiments described above. Specifically, Figure 5a illustrates the 3D spatial distribution of all solutions for each benchmark function, while Figure 5b depicts the two-dimensional distribution of the MGOA search history. It can be observed that a small number of historical best solutions are scattered across the solution space, while the majority cluster around the global optimum—particularly evident in functions F1, F3, F7, F11, and F13. This indicates that MGOA is capable of rapidly identifying near-optimal solutions within the solution space and transitioning earlier into the exploitation phase, thereby enhancing solution accuracy.

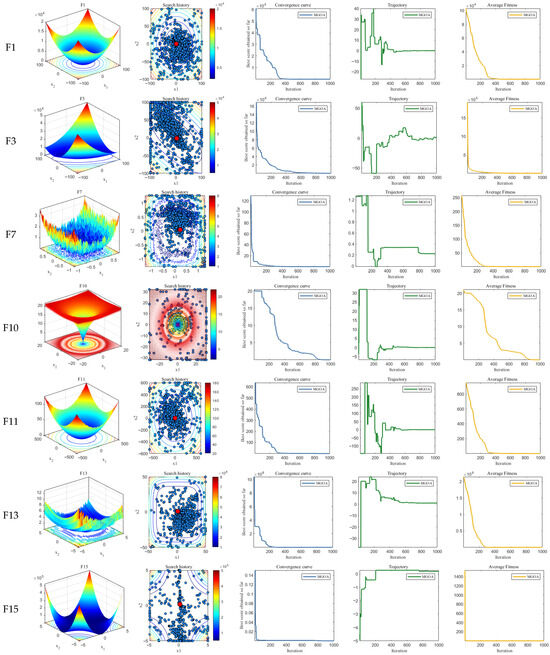
Figure 5. Behavioral and Visual Analysis of Experimental Results. (a) Function Rendering; (b) Search History; (c) Convergence Curve; (d) Trajectory; (e) Average Fitness. The red circles indicate the location of the optimal solution.

Figure 5c tracks the convergence behavior of MGOA throughout the iterative process. For most test functions, MGOA consistently improves solution quality as iterations proceed without becoming trapped in local optima. This holds true not only for unimodal functions such as F1 and F3 but also for complex multimodal and composite functions like F10 and F11. Through the synergistic effect of the attraction phase and the cooperation phase, MGOA conducts incremental search and refinement during iterations, effectively avoiding local optima.

As shown in Figure 5d, due to the influence of the attraction phase in the early search stages, MGOA exhibits relatively large search step sizes in functions such as F1, F3, F10, F11, and F13. This characteristic facilitates escaping local optima and locating the global optimum. In later iterations, the cooperation phase plays a critical role by reducing step sizes, which contributes to refining the accuracy of the best solution.

Figure 5e records the best fitness value of MGOA after each iteration. It can be seen that the fitness values fluctuate to some extent across iterations, which stems from merchants’ active strategy adjustments during updates. This behavior confirms the effectiveness of the algorithm in dynamically exploring optimal solutions and aligns with its intended design.

In summary, MGOA not only demonstrates the ability to quickly converge to near-global optima and focus on intensive exploitation for improved precision but also actively alters search positions during updates. This enhances global exploration capability and the capacity to escape local optima, all while maintaining competitive convergence speed.

4.3. Strategy Coefficient and Dimension Selection Analysis

The CEC2017 benchmark set [38] comprises a heterogeneous suite of test functions, including both unimodal and multimodal problems. These functions exhibit non-homogeneous properties—such as non-separability, robustness, and rotational invariance—enabling a comprehensive evaluation of an algorithm’s adaptability across diverse search environments. This benchmark has become a well-established standard for assessing the robustness and efficiency of optimization methods. In the performance evaluation experiments, the population size is set to 50, the maximum number of iterations is 5000, and 50 independent runs are conducted in parallel. Table 3 presents all function suites within the CEC2017 test set.

Table 3. CEC2017 Test Table.

	No.	Functions	${\mathit{F}}_{\mathit{i}}^{\ast }$
Unimodal Functions	1	Shifted and Rotated Bent Cigar Function	100
	2	Shifted and Rotated Sum of Different Power Function	200
	3	Shifted and Rotated Function	300
Simple Multimodal Functions	4	Shifted and Rotated Rosenbrock’s Function	400
	5	Shifted and Rotated Rastrigin’s Function	500
	6	Shifted and Rotated Expanded Scaffer’s $f_6$ Function	600
	7	Shifted and Rotated Lunacek Bi_Rastrigin Function	700
	8	Shifted and Rotated Non-Continuous Rastrigin’s Function	800
	9	Shifted and Rotated Levy Function	900
	10	Shifted and Rotated Schwefel’s Function	1000
Hybrid Functions	11	Hybrid Function 1 (N = 3)	1100
	12	Hybrid Function 2 (N = 3)	1200
	13	Hybrid Function 3 (N = 3)	1300
	14	Hybrid Function 4 (N = 3)	1400
	15	Hybrid Function 5 (N = 3)	1500
	16	Hybrid Function 6 (N = 3)	1600
	17	Hybrid Function 1 (N = 4)	1700
	18	Hybrid Function 2 (N = 4)	1800
	19	Hybrid Function 3 (N = 4)	1900
	20	Hybrid Function 4 (N = 4)	2000
Composition Functions	21	Hybrid Function 5 (N = 4)	2100
	22	Hybrid Function 6 (N = 4)	2200
	23	Composition Function 1 (N = 3)	2300
	24	Composition Function 2 (N = 3)	2400
	25	Composition Function 3 (N = 3)	2500
	26	Composition Function 4 (N = 3)	2600
	27	Composition Function 5 (N = 3)	2700
	28	Composition Function 6 (N = 3)	2800
	29	Composition Function 7 (N = 3)	2900
	30	Composition Function 8 (N = 3)	3000
Search range: ${\left[-100,100\right]}^D$

where $F_i^{\ast }$ represents predefined fixed optimum offset and is used to create unique target values for each function, preventing algorithms from exploiting a uniform target of zero.

In this section, we vary the value of parameter $\alpha$ in CEC 2017—introduced in Section 3.2 as the decay coefficient for strategy adjustment, which significantly influences the overall precision and stability of the algorithm. Experiments are conducted with $\alpha$ set to 1, 3, 5, 7, and 10, respectively, and compared with the original configuration, where $\alpha =1$, to illustrate the impact of parameter variation on the performance of MGOA.

As illustrated in Figure 6, the value of α directly affects the behavior of the adjustment intensity $S$. A constant value of $S$ indicates that the algorithm is conducting intensive exploitation around the current best solution, while a decreasing $S$ suggests broader exploration. Therefore, $\alpha$ plays a critical role in directly governing the balance between exploration and exploitation, making appropriate selection essential. It can be observed that as the number of iterations increases, $S$ gradually stabilizes when $\alpha =7$ or 10. For $\alpha =3$ or 5, although $S$ exhibits mild fluctuations, the amplitude remains limited. Only when $\alpha =1$ does $S$ demonstrate significant and persistent oscillations, indicating that a balance between exploration and exploitation has been achieved.

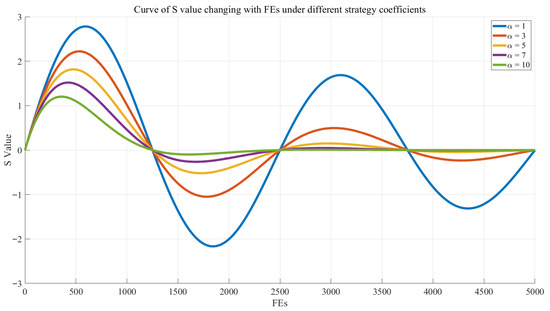
Figure 6. The Influence of $\alpha$ Value on the Adjustment Strength $S$.

Table 4 presents the comparative results and rankings of different $\alpha$ parameter configurations on the CEC2017 benchmark suite under 100-dimensional settings. Among these, bold text indicates the optimal result. MGOA (with $\alpha =1$) achieves the highest overall ranking, and its average rank is superior to those of algorithms with other parameter values. This indicates that MGOA (with $\alpha =1$) does not exhibit inferior performance in optimization tasks.

Table 4. Comparison Results and Ranking of α Parameters of MGOA.

Function	$\mathit{\alpha }=1$			$\mathit{\alpha }=3$			$\mathit{\alpha }=5$			$\mathit{\alpha }=7$			$\mathit{\alpha }=9$
	Best	Avg	Std	Best	Avg	Std	Best	Avg	Std	Best	Avg	Std	Best	Avg	Std
F1	5.50 × 106	7.81 × 109	5.50 × 106	9.50 × 107	1.17 × 1010	9.50 × 107	5.38 × 108	1.28 × 1010	5.38 × 108	9.89 × 108	1.41 × 1010	9.89 × 108	1.03 × 109	1.02 × 1010	1.03 × 109
F2	2.72 × 1080	6.96 × 10114	2.72 × 1080	6.03 × 1077	1.32 × 10104	6.03 × 1077	1.77 × 1083	1.04 × 10105	1.77 × 1083	2.87 × 1086	3.8 × 10138	2.87 × 1086	4.33 × 1079	1.61 × 10110	4.33 × 1079
F3	3.20 × 104	5.17 × 104	3.20 × 104	4.75 × 104	7.00 × 104	4.75 × 104	4.49 × 104	7.18 × 104	4.49 × 104	4.49 × 104	6.87 × 104	4.49 × 104	5.23 × 104	7.63 × 104	5.23 × 104
F4	6.24 × 102	1.70 × 103	6.24 × 102	6.42 × 102	1.95 × 103	6.42 × 102	8.37 × 102	1.58 × 103	8.37 × 102	9.13 × 102	1.75 × 103	9.13 × 102	8.53 × 102	1.90 × 103	8.53 × 102
F5	1.13 × 103	1.32 × 103	1.13 × 103	1.10 × 103	1.31 × 103	1.10 × 103	1.09 × 103	1.38 × 103	1.09 × 103	1.19 × 103	1.34 × 103	1.19 × 103	1.16 × 103	1.37 × 103	1.16 × 103
F6	6.42 × 102	6.61 × 102	6.42 × 102	6.53 × 102	6.66 × 102	6.53 × 102	6.52 × 102	6.72 × 102	6.52 × 102	6.56 × 102	6.68 × 102	6.56 × 102	6.59 × 102	6.69 × 102	6.59 × 102
F7	1.72 × 103	2.30 × 103	1.72 × 103	1.86 × 103	2.39 × 103	1.86 × 103	2.03 × 103	2.40 × 103	2.03 × 103	2.08 × 103	2.57 × 103	2.08 × 103	2.23 × 103	2.69 × 103	2.23 × 103
F8	1.36 × 103	1.70 × 103	1.36 × 103	1.43 × 103	1.70 × 103	1.43 × 103	1.53 × 103	1.70 × 103	1.53 × 103	1.41 × 103	1.69 × 103	1.41 × 103	1.46 × 103	1.72 × 103	1.46 × 103
F9	3.69 × 104	7.12 × 104	3.69 × 104	4.25 × 104	7.16 × 104	4.25 × 104	5.44 × 104	7.09 × 104	5.44 × 104	4.08 × 104	7.57 × 104	4.08 × 104	5.73 × 104	7.49 × 104	5.73 × 104
F10	1.37 × 104	2.09 × 104	1.37 × 104	1.43 × 104	2.42 × 104	1.43 × 104	1.53 × 104	2.48 × 104	1.53 × 104	1.64 × 104	2.52 × 104	1.64 × 104	1.56 × 104	2.30 × 104	1.56 × 104
F11	2.20 × 103	2.93 × 103	2.20 × 103	2.64 × 103	3.38 × 103	2.64 × 103	2.71 × 103	3.53 × 103	2.71 × 103	2.60 × 103	3.87 × 103	2.60 × 103	2.98 × 103	4.06 × 103	2.98 × 103
F12	6.28 × 106	7.55 × 109	6.28 × 106	7.12 × 106	5.53 × 109	7.12 × 106	1.09 × 107	5.37 × 109	1.09 × 107	2.90 × 107	8.92 × 109	2.90 × 107	4.13 × 107	7.49 × 109	4.13 × 107
F13	1.35 × 104	2.68 × 109	1.35 × 104	2.03 × 104	1.38 × 109	2.03 × 104	3.41 × 104	2.12 × 109	3.41 × 104	2.45 × 104	8.09 × 108	2.45 × 104	3.14 × 104	1.33 × 109	3.14 × 104
F14	2.15 × 103	5.19 × 103	2.15 × 103	2.19 × 103	6.55 × 103	2.19 × 103	2.18 × 103	5.84 × 103	2.18 × 103	2.16 × 103	7.57 × 103	2.16 × 103	2.17 × 103	1.75 × 104	2.17 × 103
F15	3.81 × 103	1.41 × 109	3.81 × 103	4.64 × 103	1.41 × 109	4.64 × 103	3.69 × 103	2.02 × 108	3.69 × 103	6.61 × 103	1.08 × 109	6.61 × 103	3.97 × 103	8.23 × 108	3.97 × 103
F16	4.10 × 103	5.63 × 103	4.10 × 103	4.39 × 103	5.52 × 103	4.39 × 103	4.50 × 103	5.57 × 103	4.50 × 103	4.51 × 103	5.72 × 103	4.51 × 103	4.01 × 103	5.77 × 103	4.01 × 103
F17	3.73 × 103	5.35 × 103	3.73 × 103	4.01 × 103	5.36 × 103	4.01 × 103	4.10 × 103	5.17 × 103	4.10 × 103	4.21 × 103	5.25 × 103	4.21 × 103	4.41 × 103	5.76 × 103	4.41 × 103
F18	1.56 × 104	1.40 × 105	1.56 × 104	3.39 × 104	1.33 × 105	3.39 × 104	4.12 × 104	1.34 × 105	4.12 × 104	3.57 × 104	1.28 × 105	3.57 × 104	2.86 × 104	1.31 × 105	2.86 × 104
F19	2.48 × 103	9.78 × 108	2.48 × 103	2.74 × 103	1.06 × 109	2.74 × 103	2.86 × 103	1.04 × 109	2.86 × 103	2.58 × 103	9.12 × 108	2.58 × 103	3.16 × 103	1.02 × 109	3.16 × 103
F20	4.28 × 103	5.69 × 103	4.28 × 103	4.44 × 103	5.70 × 103	4.44 × 103	4.02 × 103	6.02 × 103	4.02 × 103	4.36 × 103	6.03 × 103	4.36 × 103	4.33 × 103	5.88 × 103	4.33 × 103
F21	2.92 × 103	3.26 × 103	2.92 × 103	3.06 × 103	3.24 × 103	3.06 × 103	2.95 × 103	3.26 × 103	2.95 × 103	3.07 × 103	3.34 × 103	3.07 × 103	3.10 × 103	3.32 × 103	3.10 × 103
F22	2.35 × 103	2.33 × 104	2.35 × 103	2.72 × 103	2.55 × 104	2.72 × 103	2.59 × 103	2.44 × 104	2.59 × 103	3.18 × 103	2.53 × 104	3.18 × 103	1.98 × 104	2.62 × 104	1.98 × 104
F23	3.48 × 103	3.71 × 103	3.48 × 103	3.48 × 103	3.78 × 103	3.48 × 103	3.50 × 103	3.83 × 103	3.50 × 103	3.62 × 103	3.92 × 103	3.62 × 103	3.59 × 103	3.92 × 103	3.59 × 103
F24	4.04 × 103	4.39 × 103	4.04 × 103	4.06 × 103	4.48 × 103	4.06 × 103	4.13 × 103	4.54 × 103	4.13 × 103	4.04 × 103	4.51 × 103	4.04 × 103	4.17 × 103	4.62 × 103	4.17 × 103
F25	3.32 × 103	3.94 × 103	3.32 × 103	3.42 × 103	4.12 × 103	3.42 × 103	3.50 × 103	4.04 × 103	3.50 × 103	3.44 × 103	4.10 × 103	3.44 × 103	3.52 × 103	4.22 × 103	3.52 × 103
F26	5.56 × 103	1.56 × 104	5.56 × 103	5.15 × 103	1.57 × 104	5.15 × 103	6.06 × 103	1.50 × 104	6.06 × 103	7.05 × 103	1.65 × 104	7.05 × 103	8.06 × 103	1.79 × 104	8.06 × 103
F27	3.43 × 103	3.61 × 103	3.43 × 103	3.46 × 103	3.70 × 103	3.46 × 103	3.49 × 103	3.68 × 103	3.49 × 103	3.45 × 103	3.68 × 103	3.45 × 103	3.48 × 103	3.69 × 103	3.48 × 103
F28	3.42 × 103	5.30 × 103	3.42 × 103	3.46 × 103	6.81 × 103	3.46 × 103	3.65 × 103	5.48 × 103	3.65 × 103	3.66 × 103	5.56 × 103	3.66 × 103	3.77 × 103	6.70 × 103	3.77 × 103
F29	5.90 × 103	7.13 × 103	5.90 × 103	6.01 × 103	7.27 × 103	6.01 × 103	6.39 × 103	7.63 × 103	6.39 × 103	6.50 × 103	7.69 × 103	6.50 × 103	6.64 × 103	9.87 × 103	6.64 × 103
F30	2.66 × 104	5.85 × 108	2.66 × 104	6.02 × 104	8.05 × 108	6.02 × 104	1.08 × 105	6.60 × 108	1.08 × 105	9.45 × 104	8.88 × 108	9.45 × 104	1.47 × 105	6.22 × 108	1.47 × 105
Friedman Ranking	2			2.9			2.8			3.4333333			3.8666667
Final Ranking	1			3			2			4			5

Figure 7 similarly displays the ranking performance of various α values across different benchmark functions. Darker, nearly black shades indicate higher algorithm rankings under the corresponding parameter, whereas lighter, orange-like shades correspond to lower ranks. It can be observed that MGOA (with $\alpha =1$) achieves the highest number of first-place rankings—prevailing in 16 out of 30 functions—significantly outperforming all other parameter configurations.

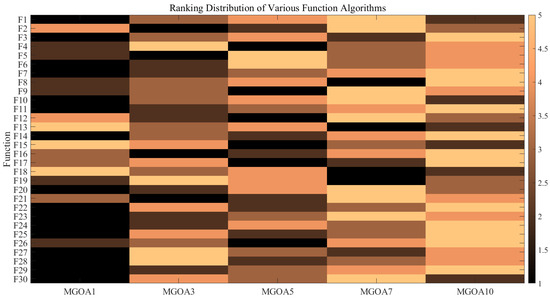
Figure 7. Heatmap of the Ranks for Different Alpha Values Across Test Functions.

Therefore, based on comprehensive consideration of algorithmic accuracy and stability, the decay coefficient $\alpha$ is set to 1 in this study.

After that, this study selects MGOA (with $\alpha =1$) for a qualitative analysis of dimension selection, setting D to 1, 3, 5, 7, and 10. As can be seen in Table 5, when the dimension selection ranges from 1 to 5, the algorithm performance improves, and when it ranges from 5 to 10, it starts to deteriorate, but it is still better than when the selection is small. In addition, MGOA (with $D=5$) has the lowest Friedman ranking, ranking first, indicating that dimension is not always better when it is larger. In addition, the methodology shows that it is related to the problem dimension. Therefore, the key to improving performance is to reasonably select a moderate number of algorithm dimensions. The number of dimensions extracted was 5 in this study.

Table 5. Comparison Results and Ranking of Dimension Selection of MGOA.

Function	$\mathit{D}=1$			$\mathit{D}=3$			$\mathit{D}=5$			$\mathit{D}=7$			$\mathit{D}=10$
	Best	Avg	Std	Best	Avg	Std	Best	Avg	Std	Best	Avg	Std	Best	Avg	Std
F1	2.61 × 108	1.02 × 1011	9.30 × 1010	3.24 × 108	4.76 × 1010	4.48 × 1010	1.33 × 106	1.16 × 109	1.63 × 109	6.58 × 106	1.17 × 108	1.98 × 108	6.42 × 106	9.79 × 109	1.36 × 1010
F2	4.81 × 1093	2.22 × 10169	1.58 × 10140	3.47 × 1085	7.08 × 10133	1.58 × 10134	2.50 × 1080	2.54 × 1092	5.53 × 1092	1.90 × 1077	1.45 × 1098	3.24 × 1098	3.18 × 1091	5.75 × 10101	1.29 × 10102
F3	9.65 × 104	1.13 × 105	1.48 × 104	4.32 × 104	6.64 × 104	1.76 × 104	4.44 × 104	5.42 × 104	9.10 × 103	3.25 × 104	4.73 × 104	2.00 × 104	3.92 × 104	6.31 × 104	2.04 × 104
F4	9.61 × 102	2.65 × 104	2.50 × 104	6.82 × 102	1.92 × 103	1.71 × 103	5.92 × 102	7.39 × 102	9.39 × 101	7.23 × 102	8.31 × 102	9.40 × 101	7.07 × 102	1.30 × 103	1.09 × 103
F5	1.23 × 103	1.47 × 103	2.03 × 102	1.35 × 103	1.39 × 103	4.27 × 101	1.08 × 103	1.25 × 103	1.42 × 102	1.18 × 103	1.26 × 103	6.86 × 101	1.16 × 103	1.27 × 103	7.09 × 101
F6	6.61 × 102	6.74 × 102	1.65 × 101	6.62 × 102	6.74 × 102	7.90	6.40 × 102	6.54 × 102	9.69	6.48 × 102	6.52 × 102	3.41	6.42 × 102	6.59 × 102	1.22 × 101
F7	2.37 × 103	2.77 × 103	2.68 × 102	1.87 × 103	2.19 × 103	2.88 × 102	2.13 × 103	2.43 × 103	3.35 × 102	1.82 × 103	2.06 × 103	2.38 × 102	1.88 × 103	2.05 × 103	1.57 × 102
F8	1.71 × 103	1.90 × 103	1.40 × 102	1.62 × 103	1.74 × 103	1.05 × 102	1.52 × 103	1.60 × 103	1.01 × 102	1.44 × 103	1.75 × 103	1.79 × 102	1.50 × 103	1.68 × 103	1.39 × 102
F9	4.88 × 104	7.09 × 104	1.40 × 104	6.59 × 104	7.69 × 104	8.18 × 103	4.10 × 104	6.54 × 104	1.71 × 104	3.81 × 104	7.05 × 104	2.45 × 104	4.62 × 104	6.26 × 104	1.30 × 104
F10	1.46 × 104	1.86 × 104	4.22 × 103	1.40 × 104	1.82 × 104	7.42 × 103	1.66 × 104	2.40 × 104	5.09 × 103	1.74 × 104	2.45 × 104	4.46 × 103	1.64 × 104	2.54 × 104	5.62 × 103
F11	3.69 × 103	5.93 × 103	3.15 × 103	2.77 × 103	3.27 × 103	4.47 × 102	2.18 × 103	2.87 × 103	5.95 × 102	2.39 × 103	2.66 × 103	2.47 × 102	2.11 × 103	2.93 × 103	6.26 × 102
F12	2.44 × 107	2.74 × 1010	6.11 × 1010	1.56 × 107	5.23 × 109	1.16 × 1010	8.24 × 106	4.52 × 107	7.39 × 107	8.17 × 106	4.69 × 109	7.09 × 109	1.76 × 107	3.78 × 109	4.96 × 109
F13	3.10 × 104	1.49 × 1010	2.08 × 1010	4.91 × 104	6.06 × 109	6.87 × 109	1.07 × 104	2.13 × 104	1.33 × 104	1.12 × 104	3.55 × 108	7.93 × 108	4.40 × 104	3.69 × 109	3.80 × 109
F14	2.34 × 103	1.56 × 107	2.24 × 107	2.46 × 103	7.68 × 103	6.46 × 103	2.25 × 103	3.06 × 103	9.73 × 102	2.29 × 103	3.67 × 103	2.47 × 103	2.27 × 103	4.43 × 103	3.56 × 103
F15	8.18 × 103	6.41 × 109	1.04 × 1010	2.85 × 103	5.10 × 109	7.74 × 109	6.19 × 103	1.13 × 104	3.87 × 103	4.35 × 103	1.71 × 107	3.82 × 107	4.74 × 103	1.35 × 104	5.32 × 103
F16	5.08 × 103	7.16 × 103	3.62 × 103	4.33 × 103	5.00 × 103	4.18 × 102	4.68 × 103	5.31 × 103	4.94 × 102	4.57 × 103	5.38 × 103	8.66 × 102	5.06 × 103	5.65 × 103	4.57 × 102
F17	4.51 × 103	5.29 × 103	6.15 × 102	4.55 × 103	9.76 × 104	1.69 × 105	4.77 × 103	5.22 × 103	3.25 × 102	4.91 × 103	5.35 × 103	3.65 × 102	4.99 × 103	5.44 × 103	3.93 × 102
F18	7.74 × 104	1.61 × 105	1.20 × 105	4.21 × 104	1.11 × 105	7.24 × 104	7.22 × 104	1.65 × 105	1.44 × 105	7.30 × 104	1.60 × 105	8.98 × 104	5.31 × 104	1.54 × 105	8.59 × 104
F19	3.00 × 103	1.07 × 1010	1.53 × 1010	6.94 × 103	3.89 × 104	2.54 × 104	2.44 × 103	2.06 × 105	4.50 × 105	1.15 × 104	4.43 × 104	5.68 × 104	4.05 × 103	2.47 × 109	5.53 × 109
F20	4.32 × 103	5.80 × 103	1.02 × 103	4.07 × 103	5.16 × 103	7.54 × 102	4.74 × 103	5.59 × 103	1.04 × 103	5.02 × 103	5.47 × 103	5.35 × 102	4.44 × 103	5.78 × 103	1.06 × 103
F21	3.21 × 103	3.33 × 103	8.10 × 101	2.99 × 103	3.22 × 103	1.93 × 102	2.94 × 103	3.09 × 103	9.98 × 101	3.07 × 103	3.22 × 103	1.07 × 102	2.95 × 103	3.07 × 103	8.83 × 101
F22	2.53 × 103	1.89 × 104	1.01 × 104	1.86 × 104	2.58 × 104	5.23 × 103	2.22 × 104	2.67 × 104	3.67 × 103	1.72 × 104	2.23 × 104	6.40 × 103	2.03 × 104	2.56 × 104	6.71 × 103
F23	3.83 × 103	3.98 × 103	1.12 × 102	3.59 × 103	3.76 × 103	1.79 × 102	3.50 × 103	3.64 × 103	1.09 × 102	3.48 × 103	3.75 × 103	1.69 × 102	3.62 × 103	3.74 × 103	1.22 × 102
F24	4.42 × 103	4.51 × 103	1.32 × 102	4.10 × 103	4.29 × 103	1.36 × 102	4.18 × 103	4.35 × 103	1.24 × 102	4.28 × 103	4.53 × 103	1.96 × 102	4.08 × 103	4.41 × 103	2.80 × 102
F25	3.58 × 103	1.44 × 104	9.93 × 103	3.40 × 103	4.01 × 103	7.97 × 102	3.37 × 103	3.84 × 103	9.44 × 102	3.26 × 103	3.60 × 103	3.02 × 102	3.39 × 103	3.63 × 103	3.44 × 102
F26	2.43 × 104	3.43 × 104	6.15 × 103	9.74 × 103	1.53 × 104	4.44 × 103	1.37 × 104	1.65 × 104	2.84 × 103	4.88 × 103	9.52 × 103	6.10 × 103	7.64 × 103	1.53 × 104	4.79 × 103
F27	3.44 × 103	3.60 × 103	1.35 × 102	3.48 × 103	3.66 × 103	1.16 × 102	3.59 × 103	3.67 × 103	6.60 × 101	3.42 × 103	3.61 × 103	1.31 × 102	3.50 × 103	3.66 × 103	1.90 × 102
F28	3.73 × 103	1.75 × 104	8.05 × 103	3.48 × 103	3.75 × 103	5.04 × 102	3.45 × 103	3.51 × 103	5.80 × 101	3.54 × 103	8.75 × 103	6.93 × 103	3.67 × 103	7.16 × 103	6.31 × 103
F29	6.77 × 103	4.52 × 105	9.93 × 105	5.79 × 103	6.37 × 103	5.46 × 102	6.24 × 103	6.70 × 103	2.58 × 102	6.09 × 103	6.84 × 103	9.49 × 102	6.58 × 103	7.02 × 103	3.15 × 102
F30	1.68 × 105	1.65 × 106	1.76 × 106	8.51 × 104	3.16 × 108	7.05 × 108	3.40 × 104	5.66 × 105	4.81 × 105	3.30 × 104	7.75 × 105	1.31 × 106	5.08 × 104	3.78 × 105	5.48 × 105
Friedman Ranking	4.366667			3.166667			2.2			2.466667			2.8
Final Ranking	5			4			1			2			3

4.4. Exploration and Development Evaluation

MGOA optimizes market strategies by balancing exploration and exploitation behaviors among merchant agents through the alternating execution of an attraction phase and a cooperation phase. To quantitatively assess the algorithm’s exploration–exploitation tendency, we track the dynamic variation in components across dimensions to quantify its search behavior. The exploration–exploitation balance is evaluated using the following formula:

$$Div\left(t\right)={\displaystyle \frac{1}{D}}{\displaystyle \sum _{d=1}^D\frac{1}{n}}{\displaystyle \sum _{i=1}^n|}median\left(X_d\left(t\right)\right)-X_{id}\left(t\right)|$$

(13)

$$ERP={\displaystyle \frac{Div(t)}{\max (Div)}}\times 100\%$$

(14)

$$ETP={\displaystyle \frac{\mid \max (Div)-Div(t)\mid }{\max (Div)}}\times 100\%$$

(15)

Figure 8 shows that as iterations proceed, the exploration curve gradually declines, while the exploitation curve rises and eventually approaches 100%. This trend indicates that the algorithm initially emphasizes exploration and progressively shifts its focus toward exploitation, refining local solutions as the search continues. Through this dynamic balance, MGOA effectively integrates global search with local refinement, thereby converging toward an optimal market strategy.

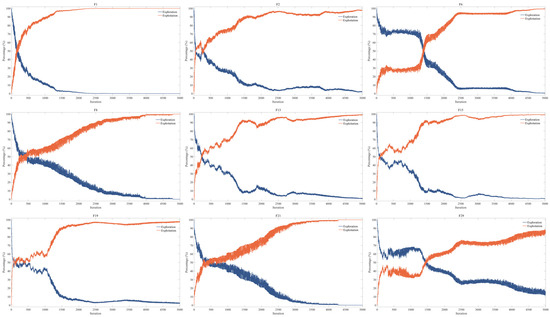
Figure 8. Exploration and Development Assessment Results.

4.5. Comparison of Mature Algorithms

Subsequently, this study compares MGOA against several established and recently proposed metaheuristic algorithms on the CEC2017 benchmark to validate its effectiveness. The compared algorithms include four highly cited classical methods: Whale Optimization Algorithm (WOA) [39], Harris Hawks Optimization (HHO) [40], Aquila Optimizer (AO) [41], and Dung Beetle Optimizer (DBO) [42]; four mature algorithms published in 2024: Black-Winged Kite Algorithm (BKA) [43], Newton-Raphson-Based Optimizer (NRBO) [44], Information Acquisition Optimizer (IAO) [45], and Bermuda Triangle Optimizer (BTO) [46]; and two latest high-performance algorithms published in 2025: Tornado Optimizer with Coriolis (TOC) [47] and Chinese Pangolin Optimizer (CPO) [48].

To ensure reproducibility, Table 6 summarizes the initial parameter configurations for all algorithms involved (excluding adaptive parameters, only fixed parameters are used).

Table 6. Initial Parameter Settings of Algorithms.

Algorithms	Parameter
MGOA	$A=\pi ,n=2,\alpha =1$
WOA	$b=1$
HHO	$\beta =1.5$
AO	$\alpha =0.1,\epsilon =0.1,u=0.265,r_0=10,\omega =0.005$
DBO	$p_{\mathit{percent}}=0.2$
BKA	$p=0.9$
NRBO	$DF=0.6,Flag=1$
BTO	$g=6.67$ × 10−11
TOC	$\mathit{nto}=4,\mathit{nt}=3,b_r=\mathrm{100,000},\mathit{chi}=4.1$
CPO	$\beta =1.5$

According to the results presented in Table 7, the classical algorithms perform well on unimodal functions but exhibit significant performance divergence on complex multimodal and hybrid functions. Some algorithms, such as BTO, even suffer a drastic decline in solution quality by several orders of magnitude in certain cases. Within this context, MGOA demonstrates comprehensive and superior performance: it achieves the theoretical optimal values on functions F1, F2, F3, F4, and F9, indicating perfect convergence capability. Moreover, it consistently yields the lowest mean values or ranks among the top performers across the majority of the remaining functions, highlighting exceptional stability and robustness. These results strongly validate the powerful global exploration and local exploitation capabilities of MGOA.

Table 7. Result of Mean Value of CEC2017 Dim 10.

Mean Value of Function	MGOA	WOA	HHO	AO	DBO	BKA	NRBO	IAO	BTO	TOC	CPO
F1	100	5959.945	171,606.80	74,507.29	8778.776	2.60 × 108	2.46 × 108	100	9.56 × 109	87,922.65	5576.248
F2	200	311.1157	200.0481	266.4285	209.7592	215.4075	189,614.30	200	1.21 × 1010	6854.658	200.3738
F3	300	343.1025	300.3728	300.2566	300	300.7931	549.7396	300	28,180.67	300.1021	300
F4	400	421.2871	406.3655	405.8008	402.9466	401.3926	424.9806	400	2449.073	415.4858	404.0064
F5	518.584	547.7375	539.9419	522.1995	530.7002	532.7523	543.5025	509.3526	591.7835	526.4319	545.0495
F6	600.0512	629.313	619.3794	604.2569	603.8028	619.4661	615.1073	601.1191	658.3785	612.9258	639.5553
F7	717.7557	768.8352	770.803	736.0459	728.5535	766.8456	760.4716	720.777	810.568	743.9799	756.9638
F8	811.7405	836.267	831.4975	819.9245	825.1861	823.8811	828.6994	807.3627	853.3433	824.9394	831.6396
F9	900	1284.815	1134.928	1004.39	902.9444	1101.124	1026.926	900.3442	1490.343	1046.668	1290.028
F10	1409.989	2221.133	1741.229	1575.553	1640.604	2071.704	2122.249	1427.196	2534.63	1918.476	2561.377
F11	1101.392	1174.811	1134.667	1151.518	1148.566	1115.653	1173.885	1101.481	3509.133	1192.002	1235.182
F12	1349.82	1,482,050	454,110.50	3,487,258	152,135.60	10,055.65	501,386.70	1385.292	1.25 × 108	24,998.51	525,846
F13	1305.048	17,006.39	16,144.89	20,522.98	4421.822	1801.741	2567.93	1305.314	37,508,801	1965.855	10,709.22
F14	1411.186	1518.654	1490.054	1524.938	1469.148	1466.904	1495.35	1406.288	4456.635	1556.229	7146.055
F15	1500.413	2414.504	1576.827	2162.609	1663.651	2724.682	1595.135	1500.494	36,684.30	1635.701	3095.249
F16	1600.839	1848.194	1829.008	1717.078	1688.169	1677.081	1669.19	1601.25	2086.604	1867.245	1924.299
F17	1725.677	1793.197	1771.239	1750.55	1748.48	1768.575	1764.753	1726.071	1891.215	1792.263	1804.924
F18	1820.162	13,404.20	6299.924	25,358.84	2778.225	2237.337	6809.099	1813.813	1.20 × 108	8591.487	12,003.14
F19	1900.113	7806.881	3504.698	5228.72	2011.212	1961.375	2106.615	1900.711	1.24 × 108	1925.848	10,243.92
F20	2033.014	2126.953	2106.8	2099.229	2066.442	2039.984	2195.645	2006.1	2233.728	2129.906	2219.382
F21	2222.853	2284.158	2297.059	2230.923	2204.595	2295.178	2329.545	2200	2297.376	2335.84	2290.698
F22	2301.93	2315.494	2314.035	2305.631	2297.903	2303.937	2326.435	2281.104	3326.938	2315.853	2304.867
F23	2616.936	2638.201	2648.954	2637.472	2634.821	2621.771	2631.82	2610.569	2745.803	2639.82	2680.62
F24	2600.444	2783.933	2732.385	2761.392	2574.903	2763.953	2714.927	2548.012	2844.693	2773.545	2879.999
F25	2897.899	2950.489	2899.349	2908.516	2911.614	2927.46	2953.11	2925.576	3278.323	2939.42	2926.557
F26	2928.343	3252.374	3670.75	2920.849	3014.771	3220.759	3034.993	2906.686	4490.742	3059.418	3716.338
F27	3088.142	3123.972	3165.687	3097.933	3098.363	3094.924	3096.434	3089.463	3231.177	3111.705	3148.404
F28	3181.678	3454.306	3338.43	3301.523	3317.062	3270.447	3395.797	3146.291	3548.959	3332.263	3341.794
F29	3135.338	3315.95	3237.585	3189.148	3172.288	3211.448	3233.776	3137.518	3677.343	3218.647	3321.711
F30	3518.073	152,590	403,515	252,996.40	256,329.90	370,760.80	62,249.21	129,534.70	34,844,544	386,731.10	1,152,416

According to Table 8, where the test dimension of CEC2017 is increased to 30, MGOA continues to demonstrate comprehensive and superior performance. It not only exhibits outstanding global optimization capability, reliably locating the global optimal region, but also maintains high convergence speed and exceptional stability.

Table 8. Result of Mean Value of CEC2017 Dim 30.

Mean Value of Function	MGOA	WOA	HHO	AO	DBO	BKA	NRBO	IAO	BTO	TOC	CPO
F1	100.0001	3,417,680	9,752,616	4,280,828	10,130.88	3.75 × 108	1.36 × 1010	2.50 × 1010	7.31 × 1010	22,682,410	3103.293
F2	6,831,728	1.68 × 1021	1.18 × 1012	2.40 × 1016	5.89 × 1022	2.34 × 1036	3.22 × 1032	5.41 × 1028	5.43 × 1048	2.09 × 1030	87,988.73
F3	300	108,693.20	2163.624	9343.254	11,012.19	2795.724	36,975.08	41,811.34	127,573.60	31,402.45	1688.015
F4	458.416	544.662	504.0959	532.1016	518.5217	543.4457	1062.162	4347.417	38,964.87	527.7219	512.6967
F5	632.7173	761.7532	704.1608	668.5544	687.8309	717.7501	779.6366	749.4105	965.1682	720.793	711.9967
F6	602.0768	668.0714	658.6609	640.818	631.2924	655.1383	669.8175	641.7763	690.4441	642.3082	668.5286
F7	866.1808	1292.528	1235.291	936.6914	912.3753	1154.527	1131.456	1134.289	2186.624	1133.204	1050.212
F8	904.0988	1026.192	947.0479	920.7804	986.4889	950.8315	1061.464	1003.439	1135.154	977.7114	980.9626
F9	1546.05	8907.899	5447.61	4986.475	5584.3	5100.316	6457.987	4993.216	11,176.28	2659.227	11,097.04
F10	4196.369	5515.25	4797.792	4678.698	4818.788	5395.967	7546.166	5646.87	9380.243	6148.924	4841.394
F11	1226.404	1598.249	1213.281	1400.864	1412.183	1265.871	1804.214	1603.895	18,350.84	1356.5	1233.982
F12	20,043.19	40,298,509	8,343,816	14,915,220	18,314,590	5.21 × 108	6.10 × 108	2.41 × 108	1.44 × 1010	21,180,687	2,118,534
F13	2195.511	192,148.30	301,740.10	133,118.50	148,388	133,854.50	88,160,130	50,763.83	1.46 × 1010	72,230.1	57,217.38
F14	1520.272	744,689.10	34,592.5	124,133.40	34,403.63	1862.46	17,987.11	1521.568	11,280,726	33,210.79	7599.143
F15	1623.701	97,411.03	51,074.55	59,650.36	69,365.23	48,389.53	30,588.12	6073.067	2.56 × 108	2624.476	14,215.75
F16	2025.822	3451.254	2948.973	2923.502	2988.552	2911.949	3776.169	2696.092	6051.157	2933.247	3315.415
F17	1868.136	2688.109	2492.014	2167.021	2315.398	2347.044	2624.869	2054.242	5180.149	2418.214	2770.918
F18	1965.333	2,354,462	755,589.50	775,493.50	455,944.30	158,689.80	429,694.60	5599.615	2.96 × 108	68,801.54	162,182
F19	1966.516	3,229,634	193,320.80	638,948.40	597,402.30	99,499.71	2,025,221	2707.319	5.50 × 109	7433.86	11,395.95
F20	2196.485	2699.072	2691.783	2381.469	2428.208	2549.944	2607.414	2268.849	3035.132	2648.78	2885.919
F21	2423.588	2549.043	2509.671	2422.862	2539.017	2533.215	2610.936	2501.92	2733.28	2494.234	2522.16
F22	4937.635	6587.544	3319.531	2315.245	3850.11	6320.732	4683.293	4987.249	8799.308	7919.721	5514.458
F23	2761.971	3047.51	3014.436	2874.375	2875.404	3012.18	2974.074	2937.667	3487.465	3152.577	3105.578
F24	2932.345	3184.064	3442.903	3062.066	3059.798	3273.667	3158.367	3155.383	3615.293	3228.04	3354.725
F25	2900.603	2968.673	2898.406	2901.589	2903.291	3501.1	3187.587	3705.305	5310.153	2961.688	2914.67
F26	4195.146	7304.984	7092.543	4475.077	6236.025	4897.184	7957.927	7062.559	11,050.82	6266.874	6067.635
F27	3218.82	3339.501	3427.121	3258.529	3302.973	3347.584	3381.214	3288.788	4136.329	3450.15	3495.562
F28	3185.115	3315.084	3245.511	3264.051	3348.326	3290.723	3941.667	4495.171	6162.723	3285.363	3203.608
F29	3631.849	4685.721	4089.977	3993.66	4159.615	4152.485	4569.92	4031.735	7315.598	4745.668	4572.707
F30	5438.628	6,277,988	1,419,482	3,780,159	3,336,061	1,084,273	14,199,346	100,589.20	1.72 × 109	214,518.20	66,632.13

As shown in Table 9, with the test dimension further raised to 50, MGOA consistently retains top-tier performance. Its powerful global exploration ability enables it to effectively escape local optima and approach the true global optimum, reflecting an excellent balance between broad search coverage and precise local exploitation.

Table 9. Result of Mean Value of CEC2017 Dim 50.

Mean Value of Function	MGOA	WOA	HHO	AO	DBO	BKA	NRBO	IAO	BTO	TOC	CPO
F1	891.0454	33,025,212	47,915,295	24,396,088	10,081,849	4.60 × 109	3.69 × 1010	7.99 × 1010	1.04 × 1011	1.03 × 109	4640.886
F2	1.83 × 1025	9.18 × 1047	4.33 × 1023	2.28 × 1037	1.37 × 1050	3.96 × 1038	5.49 × 1056	5.87 × 1057	1.24 × 1077	1.98 × 1040	8.56 × 1019
F3	427.9193	97,279.21	16,464.19	93,257.28	121,953	18,133.75	91,986.68	102,050	176,228	49,528.92	99,274.85
F4	540.2701	782.0734	679.5978	614.175	795.107	1606.173	6362.46	17,390.37	38,739.14	885.4353	593.3139
F5	785.2667	926.6469	848.6433	776.4977	944.3406	948.8585	1087.103	989.7828	1201.741	929.9467	867.2986
F6	625.0236	677.8346	668.2886	649.8734	650.3535	660.7107	685.1588	671.8417	718.5828	671.3881	668.6168
F7	1093.483	1781.965	1730.675	1299.561	1232.464	1549.834	1829.732	1711.426	2055.553	1900.465	1364.457
F8	1118.418	1262.749	1198.379	1150.903	1271.652	1277.87	1413.973	1277.284	1675.872	1231.921	1204.521
F9	16,993.01	21,921.07	19,126.02	17,751.63	11,811.21	17,627.49	24,180.34	21,272.64	38,583.86	11,845.46	28,842.79
F10	10,058.7	10,041.48	8593.914	8511.4	9309.02	7872.448	13,250.57	10,519.45	15,328.35	12,168.62	7946.584
F11	1414.579	1754.317	1365.914	1503.472	1743.87	1632.484	5078.502	7190.802	22,895.99	1705.132	1311.376
F12	412,041.80	2.89 × 108	69,560,735	49,756,039	1.80 × 108	1.42 × 108	1.18 × 1010	2.91 × 1010	8.61 × 1010	1.63 × 108	7,560,794
F13	8846.174	653,966.50	3,005,114	632,440.20	522,970.20	4,543,349	1.84 × 109	6.93 × 108	3.04 × 1010	11,909,647	74,757.13
F14	1653.905	1,927,481	419,012	1,608,011	277,536.30	457,673.10	429,466.80	2048.048	31,094,195	1,455,172	156,593.70
F15	8407.271	105,044.20	254,155.10	121,011.10	81,946.45	98,845.2	92,557,459	35,545.12	1.77 × 1010	43,356.97	13,961.56
F16	3082.016	5622.634	4200.195	3572.684	4396.629	3200.048	5757.053	3908.059	9897.313	4513.991	4486.377
F17	2829.377	3941.609	3493.958	3721.371	3967.5	3197.58	3776.476	3062.718	14,329.38	3799.897	3425.587
F18	2353.488	3,747,931	2,624,263	2,302,662	2,819,653	320,079.50	5,525,705	101,691.30	5.01 × 108	1,615,775	796,171.60
F19	2216.598	3,107,334	336,623	825,082.70	767,541	4,827,416	35,538,811	185,435.10	5.92 × 109	315,880.80	21,511.63
F20	2821.864	3873.126	3330.019	2967.67	3359.438	2913.731	3694.157	2920.733	4670.814	3849.971	3492.313
F21	2521.078	3020.805	2804.166	2600.918	2719.225	2693.26	2917.933	2792.609	3165.452	2787.892	2735.954
F22	10,670.5	12,466.62	11,084.42	7219.4	11,080.63	11,765.52	15,381.69	12,983.52	17,229.01	12,797.71	11,291.07
F23	3046.355	3839.242	3612.026	3262.6	3327.221	3662.701	3484.36	3435.792	4692.266	3760.686	3675.156
F24	3195.091	3749.265	3946.442	3376.541	3480.501	3788.563	3589.246	3513.513	4873.376	4150.808	4191.607
F25	3020.811	3170.191	3142.446	3127.702	3025.979	6937.829	6586.151	10,600.51	30,197.68	3160.965	3088.472
F26	6540.698	14,130.38	9741.908	5407.482	9804.094	8626.902	11,374.75	13,207.78	28,503.22	9823.315	6840.403
F27	3427.756	4199.16	3975.686	3619.62	3830.997	3794.466	4145.599	3888.22	6768.922	4083.629	4080.119
F28	3300.481	3609.881	3415.471	3412.316	4758.539	3617.587	6269.952	7191.606	16,590.36	3406.584	3317.045
F29	4322.089	7951.349	5031.797	5955.756	4864.555	6078.012	6740.958	6217.515	300,381.30	6163.496	5193.025
F30	1,054,302	1.22 × 108	16,259,104	37,678,711	32,015,671	15,852,424	4.55 × 108	16,928,252	4.91 × 109	14,692,597	4,764,541

Based on Table 10, where the dimension is elevated to 100, MGOA achieves optimal or near-optimal results stably across the majority of test functions. Its remarkable convergence accuracy, robustness, and reliability fully validate the significant advantages in both global exploration and local exploitation capabilities. Figure 9 displays selected convergence behaviors under the 100-dimensional CEC2017 benchmark. The dark blue curve represents MGOA, which demonstrates rapid convergence in the early stages on functions such as F11, F14, F18, F21, and F30, while significantly outperforming other comparative algorithms in later-phase exploitation, underscoring its competitiveness among state-of-the-art methods.

Table 10. Result of Mean Value of CEC2017 Dim 100.

Mean Value of Function	MGOA	WOA	HHO	AO	DBO	BKA	NRBO	IAO	BTO	TOC	CPO
F1	2.70 × 107	1.20 × 109	3.40 × 108	2.70 × 108	7.20 × 108	4.00 × 1010	1.40 × 1011	2.10 × 1011	2.60 × 1011	9.00 × 109	2.20 × 105
F2	2.50 × 1099	6.90 × 10144	7.40 × 1086	1.80 × 10112	8.70 × 10133	2.30 × 10155	1.10 × 10146	1.40 × 10150	3.70 × 10170	8.10 × 10114	1.50 × 1062
F3	5.20 × 104	8.00 × 105	1.50 × 105	2.70 × 105	3.50 × 105	1.10 × 105	2.70 × 105	2.70 × 105	1.60 × 109	4.10 × 105	3.10 × 105
F4	7.80 × 102	1.60 × 103	9.80 × 102	1.00 × 103	1.00 × 103	3.00 × 104	1.80 × 104	6.30 × 104	1.00 × 105	1.80 × 103	7.20 × 102
F5	1.30 × 103	1.50 × 103	1.50 × 103	1.30 × 103	1.70 × 103	1.60 × 103	1.90 × 103	1.80 × 103	2.10 × 103	1.80 × 103	1.30 × 103
F6	6.50 × 102	6.80 × 102	6.80 × 102	6.70 × 102	6.70 × 102	6.70 × 102	7.00 × 102	6.80 × 102	7.10 × 102	6.90 × 102	6.80 × 102
F7	2.10 × 103	3.20 × 103	3.70 × 103	2.70 × 103	2.80 × 103	3.40 × 103	3.60 × 103	3.50 × 103	4.00 × 103	3.80 × 103	2.70 × 103
F8	1.70 × 103	1.90 × 103	1.90 × 103	1.70 × 103	2.10 × 103	1.80 × 103	2.40 × 103	2.30 × 103	2.90 × 103	2.10 × 103	1.80 × 103
F9	8.00 × 104	4.20 × 104	3.60 × 104	4.10 × 104	3.30 × 104	2.70 × 104	6.90 × 104	5.80 × 104	8.00 × 104	4.50 × 104	6.10 × 104
F10	2.10 × 104	2.30 × 104	2.00 × 104	1.70 × 104	1.80 × 104	1.70 × 104	3.00 × 104	2.50 × 104	3.30 × 104	2.50 × 104	1.70 × 104
F11	2.60 × 103	4.50 × 104	3.20 × 103	5.20 × 104	1.00 × 105	1.30 × 104	6.40 × 104	8.50 × 104	6.90 × 105	3.30 × 104	8.60 × 103
F12	1.20 × 1010	1.40 × 109	4.30 × 108	6.00 × 108	9.60 × 108	2.90 × 109	5.00 × 1010	1.10 × 1011	2.60 × 1011	7.90 × 109	1.20 × 108
F13	3.00 × 104	1.10 × 106	5.50 × 106	2.40 × 106	3.90 × 107	7.90 × 106	9.80 × 109	2.70 × 1010	4.80 × 1010	7.90 × 107	4.20 × 104
F14	4.30 × 103	5.20 × 106	1.30 × 106	4.50 × 106	6.60 × 106	5.60 × 105	1.20 × 107	4.20 × 105	1.10 × 108	1.50 × 106	1.20 × 106
F15	2.10 × 104	2.00 × 105	1.50 × 106	7.40 × 105	3.00 × 106	2.70 × 106	2.30 × 109	8.00 × 109	4.40 × 1010	4.90 × 106	3.70 × 104
F16	5.00 × 103	1.10 × 104	8.10 × 103	7.80 × 103	7.90 × 103	6.10 × 103	1.30 × 104	1.10 × 104	2.30 × 104	1.00 × 104	6.30 × 103
F17	5.20 × 103	7.40 × 103	6.60 × 103	5.90 × 103	7.30 × 103	5.80 × 103	1.10 × 104	2.90 × 104	6.50 × 107	8.40 × 103	5.60 × 103
F18	9.30 × 104	5.00 × 106	2.30 × 106	3.00 × 106	5.70 × 106	7.10 × 105	1.70 × 107	2.60 × 106	1.20 × 108	9.00 × 106	2.00 × 106
F19	2.80 × 104	3.60 × 107	6.20 × 106	5.90 × 106	9.80 × 106	1.50 × 107	1.20 × 109	7.00 × 109	2.40 × 1010	2.20 × 107	1.20 × 105
F20	5.70 × 103	6.10 × 103	5.90 × 103	5.10 × 103	6.00 × 103	5.10 × 103	6.50 × 103	5.00 × 103	7.70 × 103	5.90 × 103	6.00 × 103
F21	3.20 × 103	3.90 × 103	3.80 × 103	3.80 × 103	3.80 × 103	3.80 × 103	4.00 × 103	4.00 × 103	4.70 × 103	4.00 × 103	3.80 × 103
F22	2.70 × 104	2.70 × 104	2.40 × 104	2.10 × 104	2.20 × 104	2.10 × 104	3.30 × 104	3.00 × 104	3.50 × 104	2.90 × 104	2.00 × 104
F23	3.70 × 103	5.20 × 103	4.70 × 103	4.10 × 103	4.50 × 103	4.70 × 103	4.60 × 103	4.60 × 103	6.60 × 103	5.20 × 103	5.40 × 103
F24	4.40 × 103	6.00 × 103	6.20 × 103	5.20 × 103	5.10 × 103	6.70 × 103	5.50 × 103	6.10 × 103	9.70 × 103	6.60 × 103	8.50 × 103
F25	3.40 × 103	4.10 × 103	3.60 × 103	3.70 × 103	6.70 × 103	6.10 × 103	1.40 × 104	2.40 × 104	3.00 × 104	4.70 × 103	3.30 × 103
F26	1.20 × 104	3.30 × 104	2.60 × 104	1.90 × 104	2.10 × 104	3.80 × 104	3.20 × 104	4.50 × 104	5.10 × 104	3.20 × 104	2.20 × 104
F27	3.80 × 103	4.80 × 103	4.40 × 103	4.10 × 103	4.20 × 103	5.20 × 103	5.50 × 103	5.90 × 103	1.20 × 104	4.60 × 103	4.30 × 103
F28	4.50 × 103	4.60 × 103	3.70 × 103	3.70 × 103	2.10 × 104	7.40 × 103	1.60 × 104	2.70 × 104	3.80 × 104	4.70 × 103	3.40 × 103
F29	7.00 × 103	1.40 × 104	9.60 × 103	8.90 × 103	8.30 × 103	1.80 × 104	1.60 × 104	2.00 × 104	6.50 × 105	1.60 × 104	8.50 × 103
F30	6.70 × 108	4.90 × 108	2.60 × 107	7.20 × 107	2.40 × 107	5.10 × 107	8.30 × 109	1.20 × 1010	5.70 × 1010	8.30 × 107	2.10 × 106

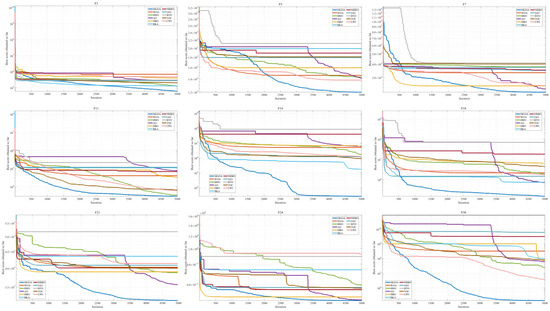
Figure 9. Convergence Curves of Various Algorithms in CEC2017 Dim 100.

As observed in Figure 10, MGOA converges to the optimal value in nearly all test functions except F30, where it exhibits relatively high fluctuation variance. Its consistently low mean values across the benchmark illustrate its powerful global optimization capability.

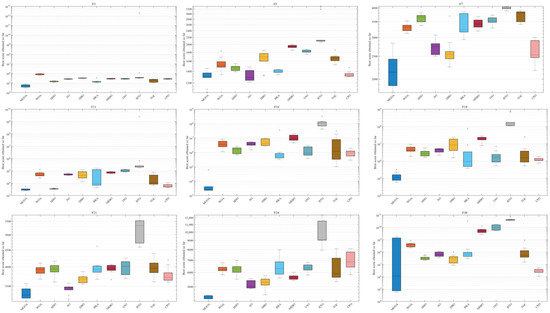
Figure 10. CEC2017 Dim 100 Box Plots of Algorithms.

Figure 11 presents the average computation time of each algorithm. The most notable trend is that IAO requires significantly more time than the others. Algorithms such as CPO, NRBO, and MGOA show noticeably lower computational costs, with MGOA achieving the shortest average time, indicating relatively high efficiency.

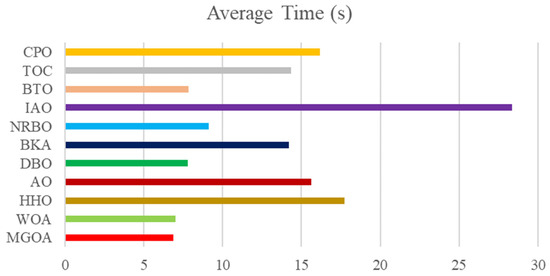
Figure 11. Mean Computing Time of Each Algorithm in CEC2017 Dim 100.

Table 11 reports the outcomes of the Wilcoxon rank-sum test on the CEC2017 benchmark suite (10 dimensions), conducted at the 95% confidence level (α = 0.05). In this table, the symbol “+” indicates that the reference algorithm MGOA performs significantly better than its counterpart, “−” denotes significantly worse performance, and “=” reflects no statistically significant difference. Inspection of the summary row reveals a striking pattern: against HHO, NRBO, and BTO, MGOA achieves superiority across all 30 test functions (30/0/0). When compared with WOA and TOC, only a single function in each case fails to reach statistical significance (29/1/0). Similarly, MGOA demonstrates a clear advantage over CPO and BKA (28/2/0 and 27/3/0, respectively). Even in comparison with AO, the results (26/4/0) remain dominated by positive outcomes. By contrast, modest instability emerges in the cases of DBO and IAO, where a handful of unfavorable instances are observed (23/6/1 and 5/24/1, respectively)—the only two columns in the table containing “−,” with IAO characterized primarily by ties. Coupled with the prevalence of exceedingly small p-values across individual functions (e.g., 1.83 × 10⁻⁴), these findings substantiate the conclusion that, on the 30 test functions of CEC2017, MGOA consistently exhibits statistically significant superiority over the majority of competing algorithms. The exceptions lie in its comparisons with IAO, where ties predominate, and with DBO, where occasional disadvantages arise. Results for other dimensional settings are provided in Appendix B. Taken together, the scarcity of “−” outcomes and the predominance of “+” and “=” outcomes underscore that MGOA’s performance is, in most cases, not inferior to—and frequently superior to—that of the other algorithms.

Table 11. Wilcoxon Test of Various Algorithms in CEC2017 Dim 10.

	MGOA	WOA	HHO	AO	DBO	BKA	NRBO	IAO	BTO	TOC	CPO
F1	-	1.10 × 10−4 (+)	1.10 × 10−4 (+)	1.10 × 10−4 (+)	1.09 × 10−4 (+)	1.10 × 10−4 (+)	1.10 × 10−4 (+)	9.57 × 10−1 (=)	1.10 × 10−4 (+)	1.10 × 10−4 (+)	1.10 × 10−4 (+)
F2	-	6.39 × 10−5 (+)	6.39 × 10−5 (+)	6.39 × 10−5 (+)	6.39 × 10−5 (+)	6.39 × 10−5 (+)	6.39 × 10−5 (+)	2.09 × 10−3 (=)	6.39 × 10−5 (+)	6.39 × 10−5 (+)	6.39 × 10−5 (+)
F3	-	1.45 × 10−4 (+)	1.45 × 10−4 (+)	1.45 × 10−4 (+)	1.00 (=)	1.45 × 10−4 (+)	1.45 × 10−4 (+)	1.00 (=)	1.45 × 10−4 (+)	1.45 × 10−4 (+)	1.45 × 10−4 (=)
F4	-	1.11 × 10−4 (+)	1.11 × 10−4 (+)	1.11 × 10−4 (+)	1.11 × 10−4 (+)	1.11 × 10−4 (+)	1.11 × 10−4 (+)	1.40 × 10−1 (=)	1.11 × 10−4 (+)	1.11 × 10−4 (+)	1.11 × 10−4 (+)
F5	-	1.82 × 10−4 (+)	5.80 × 10−4 (+)	1.21 × 10−1 (=)	3.60 × 10−3 (+)	1.82 × 10−4 (+)	1.82 × 10−4 (+)	2.12 × 10−1 (=)	1.82 × 10−4 (+)	1.82 × 10−4 (+)	1.82 × 10−4 (+)
F6	-	1.83 × 10−4 (+)	2.46 × 10−4 (+)	3.30 × 10−4 (+)	3.76 × 10−2 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.40 × 10−2 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)
F7	-	1.83 × 10−4 (+)	1.83 × 10−4 (+)	3.30 × 10−4 (+)	2.41 × 10−1 (=)	7.69 × 10−4 (+)	1.83 × 10−4 (+)	4.27 × 10−1 (=)	1.83 × 10−4 (+)	7.69 × 10−4 (+)	1.83 × 10−4 (+)
F8	-	1.83 × 10−4 (+)	1.83 × 10−4 (+)	6.40 × 10−2 (=)	3.61 × 10−3 (+)	2.57 × 10−2 (+)	2.11 × 10−2 (+)	6.92 × 10−2 (=)	1.83 × 10−4 (+)	2.11 × 10−2 (+)	1.83 × 10−4 (+)
F9	-	1.46 × 10−4 (+)	1.46 × 10−4 (+)	2.68 × 10−4 (+)	1.46 × 10−4 (+)	1.46 × 10−4 (+)	1.46 × 10−4 (+)	3.01 × 10−4 (+)	1.46 × 10−4 (+)	1.46 × 10−4 (+)	1.46 × 10−4 (+)
F10	-	5.83 × 10−4 (+)	7.69 × 10−4 (+)	2.73 × 10−1 (=)	9.11 × 10−3 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	7.34 × 10−1 (=)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)
F11	-	1.62 × 10−4 (+)	1.62 × 10−4 (+)	2.19 × 10−4 (+)	1.20 × 10−3 (+)	1.62 × 10−4 (+)	1.62 × 10−4 (+)	2.39 × 10−2 (+)	1.62 × 10−4 (+)	1.62 × 10−4 (+)	1.62 × 10−4 (+)
F12	-	1.82 × 10−4 (+)	1.82 × 10−4 (+)	1.82 × 10−4 (+)	1.82 × 10−4 (+)	1.82 × 10−4 (+)	1.82 × 10−4 (+)	9.70 × 10−1 (=)	1.82 × 10−4 (+)	4.37 × 10−4 (+)	1.82 × 10−4 (+)
F13	-	1.79 × 10−4 (+)	1.79 × 10−4 (+)	1.79 × 10−4 (+)	1.79 × 10−4 (+)	1.79 × 10−4 (+)	1.79 × 10−4 (+)	7.80 × 10−3 (+)	1.79 × 10−4 (+)	1.79 × 10−4 (+)	1.79 × 10−4 (+)
F14	-	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	5.37 × 10−2 (=)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)
F15	-	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	2.73 × 10−1 (=)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)
F16	-	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	3.30 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	9.70 × 10−1 (=)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)
F17	-	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	5.39 × 10−2 (=)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.71 × 10−3 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)
F18	-	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	3.30 × 10−4 (+)	1.83 × 10−4 (+)	2.12 × 10−1 (=)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)
F19	-	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.21 × 10−1 (=)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)
F20	-	1.83 × 10−4 (+)	1.31 × 10−3 (+)	2.46 × 10−4 (+)	1.40 × 10−2 (+)	4.40 × 10−4 (+)	1.83 × 10−4 (+)	5.78 × 10−3 (-)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)
F21	-	1.92 × 10−3 (+)	1.28 × 10−2 (+)	4.23 × 10−2 (+)	3.69 × 10−1 (=)	1.28 × 10−2 (+)	3.18 × 10−3 (+)	3.70 × 10−1 (=)	3.18 × 10−3 (+)	2.48 × 10−3 (+)	6.52 × 10−4 (+)
F22	-	2.20 × 10−3 (+)	2.20 × 10−3 (+)	5.83 × 10−4 (+)	1.13 × 10−2 (-)	9.11 × 10−3 (+)	1.71 × 10−3 (+)	9.70 × 10−1 (=)	1.83 × 10−4 (+)	2.46 × 10−4 (+)	2.83 × 10−3 (+)
F23	-	2.46 × 10−4 (+)	1.83 × 10−4 (+)	1.31 × 10−3 (+)	2.46 × 10−4 (+)	1.13 × 10−2 (+)	1.83 × 10−4 (+)	6.23 × 10−1 (=)	1.83 × 10−4 (+)	5.83 × 10−4 (+)	1.83 × 10−4 (+)
F24	-	5.80 × 10−4 (+)	1.82 × 10−4 (+)	1.00 × 10−3 (+)	9.09 × 10−1 (=)	6.39 × 10−2 (=)	1.00 × 10−3 (+)	5.68 × 10−2 (=)	1.82 × 10−4 (+)	2.45 × 10−4 (+)	1.82 × 10−4 (+)
F25	-	1.13 × 10−2 (+)	1.13 × 10−2 (+)	1.62 × 10−1 (=)	3.76 × 10−2 (+)	3.07 × 10−1 (=)	5.83 × 10−4 (+)	6.23 × 10−1 (=)	1.83 × 10−4 (+)	5.39 × 10−2 (=)	2.12 × 10−1 (=)
F26	-	1.19 × 10−1 (=)	2.68 × 10−3 (+)	2.70 × 10−1 (=)	2.49 × 10−1 (=)	1.09 × 10−2 (+)	2.28 × 10−4 (+)	8.46 × 10−1 (=)	1.69 × 10−4 (+)	1.35 × 10−2 (+)	2.09 × 10−3 (+)
F27	-	1.79 × 10−4 (+)	1.79 × 10−4 (+)	1.79 × 10−4 (+)	1.79 × 10−4 (+)	1.79 × 10−4 (+)	1.79 × 10−4 (+)	7.62 × 10−1 (=)	1.79 × 10−4 (+)	1.79 × 10−4 (+)	1.79 × 10−4 (+)
F28	-	5.16 × 10−4 (+)	1.58 × 10−4 (+)	9.01 × 10−4 (+)	2.76 × 10−3 (+)	3.03 × 10−1 (=)	1.58 × 10−4 (+)	3.18 × 10−1 (=)	1.58 × 10−4 (+)	2.88 × 10−4 (+)	9.01 × 10−4 (+)
F29	-	1.83 × 10−4 (+)	1.83 × 10−4 (+)	7.69 × 10−4 (+)	2.46 × 10−4 (+)	3.30 × 10−4 (+)	2.46 × 10−4 (+)	1.62 × 10−1 (=)	1.83 × 10−4 (+)	2.46 × 10−4 (+)	1.83 × 10−4 (+)
F30	-	1.82 × 10−4 (+)	1.82 × 10−4 (+)	1.82 × 10−4 (+)	1.82 × 10−4 (+)	1.82 × 10−4 (+)	1.81 × 10−4 (+)	1.03 × 10−1 (=)	1.78 × 10−4 (+)	1.81 × 10−4 (+)	1.82 × 10−4 (+)
Total +/=/−	-	29/1/0	30/0/0	26/4/0	23/6/1	27/3/0	30/0/0	5/24/1	30/0/0	29/1/0	28/2/0

Figure 12 displays the Friedman mean rankings of the algorithms across different dimensions (10, 30, 50, and 100), highlighting their relative performance under various settings. MGOA consistently maintains favorable rankings across all dimensions, demonstrating outstanding stability and efficiency. It achieves competitive rankings while retaining low computational time, particularly in the 100-dimensional case. In contrast, other algorithms such as IAO and BTO exhibit considerable volatility. These results distinguish MGOA as the most balanced and efficient algorithm overall, excelling in both time complexity and dimensional scalability.

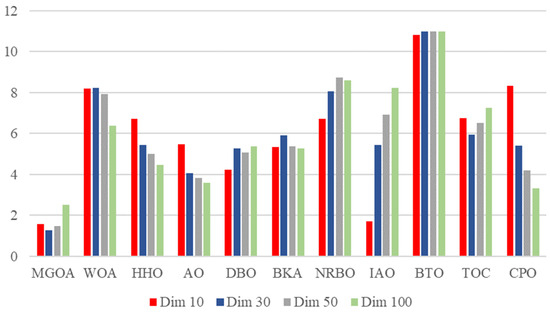
Figure 12. CEC2017 Friedman Mean Ranking of Each Algorithm in Each Dimension.

4.6. Comparison of Advanced Improved Algorithms

Subsequently, this study evaluates MGOA against ten recently published improved algorithms on the CEC2022 (shown in Table 12) benchmark to further verify its efficiency and advanced performance [49]. The compared algorithms include: Multi-population mutative moth-flame optimization algorithm (MM_MFO) [50], Dung Beetle Optimization Algorithm Based on Improved Multi-Strategy Fusion (MSFDBO) [51], Enhanced gorilla troops optimizer (EGTO) [52], Hybrid constriction coefficient-based PSO and gravitational search algorithm (CPSOGSA) [53], Black-winged kite algorithm fused with osprey (OCBKA) [54], Improved RIME (IRIME) [55], Enhanced adaptive butterfly optimization algorithm (EABOA) [56], Hybrid whale optimization algorithm (hGWOA) [57], ESHO benchmarks for hyperthermia therapy optimization (ESHO) [58], and Enhanced walrus optimization algorithm (EWO) [59].

Table 12. CEC2022 Test Table.

	No.	Functions	${\mathit{F}}_{\mathit{i}}^{\ast }$
Unimodal function	1	Shifted and full Rotated Zakharov Function	300
Basic functions	2	Shifted and full Rotated Rosenbrock’s Function	400
	3	Shifted and full Rotated Expanded Schaffer’s $f_6$ Function	600
	4	Shifted and full Rotated Non-Continuous Rastrigin’s Function	800
	5	Shifted and full Rotated Levy Function	900
Hybrid functions	6	Hybrid Function 1 (N = 3)	1800
	7	Hybrid Function 2 (N = 6)	2000
	8	Hybrid Function 3 (N = 5)	2200
Composition functions	9	Composition Function 1 (N = 5)	2300
	10	Composition Function 2 (N = 4)	2400
	11	Composition Function 3 (N = 5)	2600
	12	Composition Function 4 (N = 6)	2700
Search range: ${\left[-100,100\right]}^D$

According to the results in Table 13 and Figure 13, MGOA demonstrates comprehensive and superior performance: it achieves better mean values than other state-of-the-art improved algorithms on functions F1, F2, F3, F6, F7, F9, and F11, while matching their convergence speed. These results reflect its well-balanced global exploration and local exploitation capabilities.

Table 13. Result of Mean Value of CEC2022 Dim 20.

Mean Value of Function	MGOA	MM_MFO	MSFDBO	EGTO	CPSOGSA	OCBKA	IRIME	EABOA	hGWOA	ESHO	EWO
F1	300	27,627.49	1685.747	300	1066.558	13,100.87	306.7045	4719.505	4626.871	3,590,197	300
F2	426.1791	2214.89	464.5429	427.4689	439.5651	711.7444	458.1671	437.9337	504.1946	3321.911	437.726
F3	600.57	670.5422	616.4506	641.9724	649.1199	650.0682	601.9617	600.0329	613.1294	702.9887	608.4167
F4	851.1151	978.2873	899.1766	876.1141	916.3942	886.2337	858.6301	906.1576	882.5006	997.6244	845.6107
F5	924.458	3637.528	1452.027	2326.451	3634.493	2356.834	965.9758	900	1821.586	5104.05	1367.491
F6	1886.32	6.95 × 108	13,083.35	5395.232	9902.442	2.35 × 108	5542.187	22,971.97	8335.845	2.52 × 109	5245.455
F7	2027.908	2159.072	2081.869	2161.143	2212.616	2136.021	2047.062	2045.055	2081.71	2327.386	2053.922
F8	2227.15	2341.106	2236.041	2309.991	2311.354	2228.785	2227.555	2226.826	2251.692	3184.745	2224.861
F9	2480.781	2833.868	2480.851	2480.781	2480.782	2790.301	2481.102	2480.781	2489.669	3586.549	2480.781
F10	2617.592	2618.281	3070.151	2823.983	3995.799	2966.05	2518.351	2653.018	3046.849	6538.234	2550.243
F11	2900	9456.358	2900	2870.001	7910.758	7611.409	2964.519	2900	3287.657	10,143.18	2900
F12	2945.651	3084.061	2960.403	3040.539	3049.283	3207.837	2955.252	2938.268	3016.732	4010.215	2972.679
Friedman Ranking	2.041667	9.25	6.166667	5	7.75	8	3.916667	3.625	6.416667	11	2.833333
Final Ranking	1	10	6	5	8	9	4	3	7	11	2

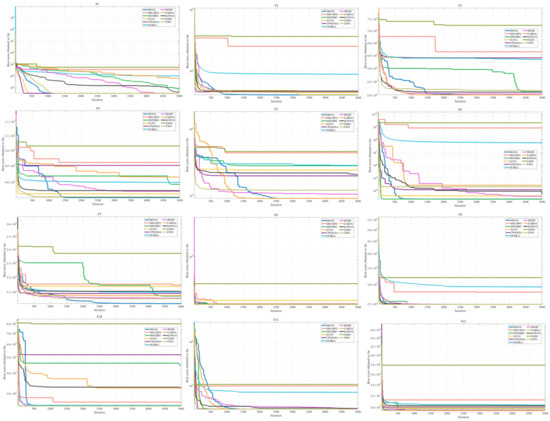
Figure 13. Convergence Curves of Various Algorithms in CEC2022 Dim 20.

As illustrated in Figure 14, MGOA attains the lowest mean values and standard deviations in almost every test function. This consistent advantage over advanced improved algorithms confirms MGOA’s strong capability in handling robustness and sensitivity challenges.

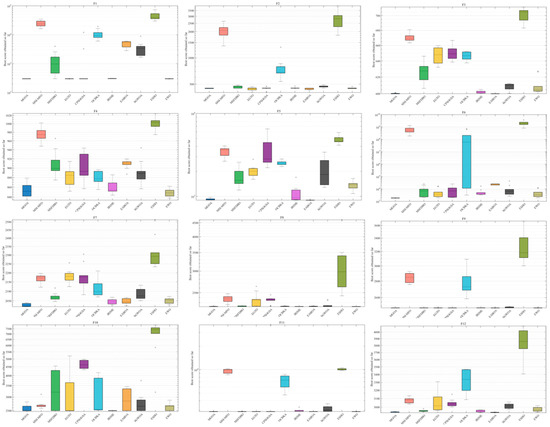
Figure 14. CEC2022 Dim 20 Box Plots of Various Algorithms.

Table 14 reports the results of the Wilcoxon rank-sum test on the CEC2022 benchmark (20 dimensions) at the 95% significance level (α = 0.05). In the table, “+” indicates that the reference algorithm, MGOA, is significantly superior to the comparator; “−” indicates it is significantly inferior; and “=” denotes no statistically significant difference. The aggregate statistics in the final row reveal that MGOA attains a 12/0/0 record against ESHO, reflecting the most consistent and pronounced overall advantage. Against hGWOA, MM_MFO, MSFDBO, OCBKA, and EWO, the tallies are 10/2/0, 11/1/0, 10/2/0, 10/2/0, and 7/4/1, respectively—outcomes dominated by “+,” with relatively few ties. Results against CPSOGSA and IRIME are 9/3/0, with no losses; versus EGTO, 7/4/1, with only a single significant loss; and against EABOA, 5/5/2, which yields the greatest number of ties and two losses, marking it as the most challenging competitor. Examination of the per-function p-values shows that most entries lie well below the 0.05 threshold (e.g., the many 1.83e−4 values in F3–F7 and F12), corroborating these significance claims; several functions (e.g., F1 and F8–F10) exhibit more “=” outcomes, indicating negligible differences. The few defeats arise primarily on F3 and F5 versus EABOA, on F11 versus EGTO, and on F10 versus EWO. Taken together, the scarcity of “−” outcomes and the preponderance of “+” and “=” indicate that, across the 12 CEC2022 test functions, MGOA is generally not inferior to—and often significantly better than—most state-of-the-art enhanced algorithms.

Table 14. Wilcoxon Test of Various Algorithms in CEC2022 Dim 20.

	MGOA	MM_MFO	MSFDBO	EGTO	CPSOGSA	OCBKA	IRIME	EABOA	hGWOA	ESHO	EWO
F1	-	1.29 × 10−4 (+)	1.41 × 10−4 (+)	1.00 (=)	3.22 × 10−1 (=)	1.41 × 10−4 (+)	1.41 × 10−4 (+)	1.41 × 10−4 (+)	1.41 × 10−4 (+)	1.41 × 10−4 (+)	1.00 (=)
F2	-	1.62 × 10−4 (+)	3.23 × 10−4 (+)	1.21 × 10−1 (=)	1.03 × 10−1 (=)	1.79 × 10−4 (+)	3.23 × 10−4 (+)	1.20 × 10−1 (=)	1.79 × 10−4 (+)	1.79 × 10−4 (+)	1.39 × 10−2 (+)
F3	-	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	2.83 × 10−3 (+)	4.21 × 10−4 (−)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)
F4	-	1.83 × 10−4 (+)	2.46 × 10−4 (+)	7.29 × 10−3 (+)	2.20 × 10−3 (+)	1.83 × 10−4 (+)	3.07 × 10−1 (=)	1.83 × 10−4 (+)	1.73 × 10−2 (+)	1.83 × 10−4 (+)	1.62 × 10−1 (=)
F5	-	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	3.12 × 10−2 (+)	1.78 × 10−4 (−)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	2.46 × 10−4 (+)
F6	-	1.83 × 10−4 (+)	1.83 × 10−4 (+)	3.30 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)
F7	-	1.83 × 10−4 (+)	2.46 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	3.30 × 10−4 (+)	2.83 × 10−3 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	4.40 × 10−4 (+)
F8	-	1.83 × 10−4 (+)	1.73 × 10−2 (+)	5.80 × 10−3 (+)	5.83 × 10−4 (+)	2.41 × 10−1 (=)	4.73 × 10−1 (=)	6.78 × 10−1 (=)	5.21 × 10−1 (=)	1.83 × 10−4 (+)	5.39 × 10−2 (=)
F9	-	1.46 × 10−4 (+)	1.31 × 10−4 (+)	2.27 × 10−3 (=)	1.79 × 10−4 (+)	1.31 × 10−4 (+)	1.31 × 10−4 (+)	7.76 × 10−2 (=)	1.31 × 10−4 (+)	1.31 × 10−4 (+)	2.24 × 10−3 (+)
F10	-	1.00 (=)	1.40 × 10−1 (=)	4.73 × 10−1 (=)	9.11 × 10−3 (+)	1.21 × 10−1 (=)	4.27 × 10−1 (=)	6.78 × 10−1 (=)	5.80 × 10−3 (+)	3.30 × 10−4 (+)	5.21 × 10−1 (−)
F11	-	1.59 × 10−4 (+)	1.31 × 10−4 (=)	2.27 × 10−3 (−)	1.31 × 10−4 (+)	1.31 × 10−4 (+)	1.31 × 10−4 (+)	1.00 (=)	1.31 × 10−4 (+)	1.31 × 10−4 (+)	1.00 (=)
F12	-	1.83 × 10−4 (+)	5.80 × 10−3 (+)	2.46 × 10−4 (+)	1.83 × 10−4 (+)	1.83 × 10−4 (+)	1.13 × 10−2 (+)	2.83 × 10−3 (−)	3.30 × 10−4 (+)	1.83 × 10−4 (+)	1.01 × 10−3 (+)
Total +/=/−	-	11/1/0	10/2/0	7/4/1	9/3/0	10/2/0	9/3/0	5/5/2	10/2/0	12/0/0	7/4/1

Figure 15 illustrates the computational time complexity of MGOA compared to state-of-the-art improved algorithms. It can be observed that MGOA achieves the lowest average computational time. Combined with its previously demonstrated superior performance, these results indicate that MGOA is not only conceptually concise but also a highly powerful metaheuristic algorithm.

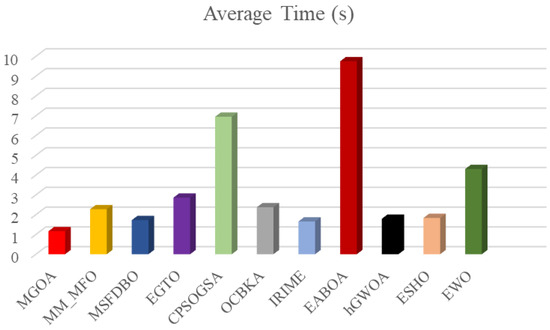
Figure 15. CEC2022 Dim 20 Mean Computing Time of Each Algorithm.

4.7. Practical Engineering Design Issues

Engineering design optimization problems aim to achieve optimal system performance through mathematical modeling and algorithmic solutions while satisfying physical constraints and performance metrics. To validate the effectiveness of the proposed method, this subsection employs 11 engineering design problems, systematically recording statistical metrics—including best value, mean value, and standard deviation—for each algorithm.

4.7.1. Tension/Compression Spring Design Problem

The tension/compression spring design problem aims to minimize the weight of a spring under constraints of minimum deflection, surge frequency, and shear stress. As illustrated in Figure 16, the problem involves three continuous decision variables: wire diameter (d), mean coil diameter (D), and number of active coils (P). The mathematical formulation is provided in Appendix A.1.

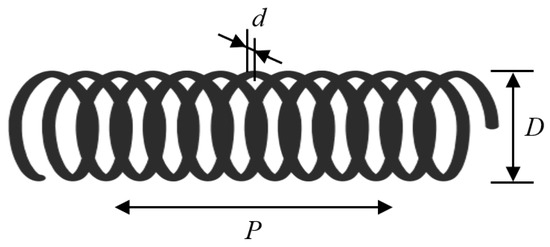
Figure 16. Tension/Compression Spring Design Problem.

As shown in Table 15, which presents the statistical results of the tension/compression spring design problem, MGOA achieves the minimum values in both the best and mean result categories, along with the smallest standard deviation. This indicates that MGOA can rapidly converge to the optimal solution for this problem, demonstrating superior performance compared to other algorithms and highlighting its effectiveness in addressing the tension/compression spring design challenge.

Table 15. Statistical Results of Tension/Compression Spring Design Problems.

	MGOA	MM_MFO	MSFDBO	EGTO	CPSOGSA	OCBKA	IRIME	EABOA	hGWOA	ESHO	EWO
Best	1.27 × 10−2	1.30 × 10−2	1.27 × 10−2	1.27 × 10−2	1.27 × 10−2	1.28 × 10−2	1.27 × 10−2	1.27 × 10−2	1.27 × 10−2	1.28 × 10−2	1.27 × 10−2
Avg	1.27 × 10−2	1.37 × 10−2	1.28 × 10−2	1.31 × 10−2	1.32 × 10−2	1.28 × 10−2	1.31 × 10−2	1.27 × 10−2	1.29 × 10−2	2.45 × 1099	1.27 × 10−2
Std	1.71 × 10−9	1.52 × 10−3	9.49 × 10−5	5.18 × 10−4	1.34 × 10−3	7.66 × 10−5	4.98 × 10−4	3.35 × 10−6	2.05 × 10−4	4.39 × 1099	7.71 × 10−6

4.7.2. Pressure Vessel Design Problem

The objective of the pressure vessel design problem is to minimize the total cost, which includes material, forming, and welding costs. As shown in Figure 17, the cylindrical pressure vessel is sealed at both ends with hemispherical heads. This optimization problem involves four decision variables: shell thickness (T_s), head thickness (T_h), inner radius (R), and the length of the cylindrical section (L). The mathematical model is provided in Appendix A.2.

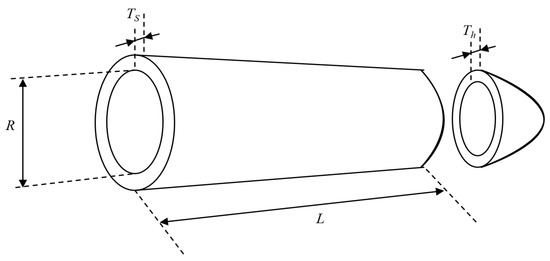
Figure 17. Pressure Vessel Design Problem.

As can be seen from Table 16, MGOA achieves the lowest values in both the best and mean results, along with the smallest standard deviation, indicating the minimal optimized cost. These results demonstrate that MGOA exhibits higher stability in locating the optimal solution, which has positive implications for this practical application.

Table 16. Statistical Results of Pressure Vessel Design Problem.

	MGOA	MM_MFO	MSFDBO	EGTO	CPSOGSA	OCBKA	IRIME	EABOA	hGWOA	ESHO	EWO
Best	5.89 × 103	6.55 × 103	5.89 × 103	5.89 × 103	5.93 × 103	5.89 × 103	5.91 × 103	5.89 × 103	5.92 × 103	3.63 × 104	5.89 × 103
Avg	5.89 × 103	9.51 × 103	5.91 × 103	6.55 × 103	6.39 × 103	5.89 × 103	6.10 × 103	5.89 × 103	6.65 × 103	1.83 × 105	5.89 × 103
Std	2.02 × 10−4	2.82 × 103	5.21 × 101	6.21 × 102	5.22 × 102	1.49	1.51 × 102	1.51 × 10−2	5.09 × 102	1.11 × 105	1.24

4.7.3. Three-Bar Truss Design Problem

The objective of the three-bar truss design problem is to minimize the volume of a truss structure by adjusting the cross-sectional areas (x₁ and x₂). The truss is subject to stress constraints (σ) on each structural member, as illustrated in Figure 18. This optimization problem involves one nonlinear fitness function, three nonlinear inequality constraints, and two continuous decision variables. The mathematical formulation is provided in Appendix A.3.

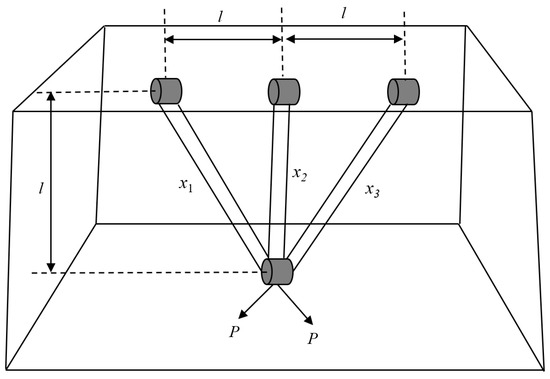
Figure 18. Three-bar Truss Design Problem.

As shown in Table 17, MGOA again ranks first with particularly notable performance—its standard deviation of zero far surpasses that of other algorithms, maintaining a significant advantage. These results confirm MGOA’s exceptional stability and superior performance, consistently enabling precise convergence to the global optimum for this problem.

Table 17. Statistical Results of Three-bar Truss Design Problem.

	MGOA	MM_MFO	MSFDBO	EGTO	CPSOGSA	OCBKA	IRIME	EABOA	hGWOA	ESHO	EWO
Best	2.64 × 102	2.64 × 102	2.64 × 102	2.64 × 102	2.71 × 102	2.64 × 102	2.64 × 102	2.64 × 102	2.64 × 102	2.64 × 102	2.64 × 102
Avg	2.64 × 102	2.64 × 102	2.64 × 102	2.64 × 102	2.76 × 102	2.64 × 102	2.64 × 102	2.64 × 102	2.64 × 102	2.69 × 102	2.64 × 102
Std	0.00	9.47 × 10−2	8.82 × 10−4	3.99 × 10−4	4.27	1.64 × 10−4	5.50 × 10−2	1.25 × 10−6	3.17 × 10−4	4.71	3.30 × 10−7

4.7.4. Welded Beam Design Problem

As depicted in Figure 19, the welded beam structure consists of a beam and welded connections. The design is constrained by multiple factors, including shear stress, bending stress in the beam, buckling load on the bar, and end deflection of the beam. Solving this problem requires identifying an optimal combination of the following structural parameters: weld thickness (h), clamped bar length (L), bar height (t), and bar thickness (b). These variables are represented as a vector x = [x₁, x₂, x₃, x₄], where x₁ to x₄ correspond to h, L, t, and b, respectively. The mathematical model is detailed in Appendix A.4.

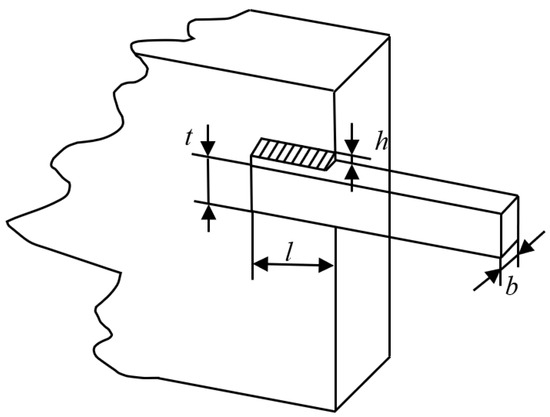
Figure 19. Welded Beam Design Problem.

Table 18 demonstrates that MGOA achieves the best results in terms of both the best and mean values, while ranking third in standard deviation, behind EABOA and EWO. However, the computational time complexity of MGOA is considerably lower than that of EABOA and EWO, particularly significantly lower than EABOA. Moreover, the standard deviation of MGOA is only marginally larger than that of EABOA and EWO, indicating that MGOA is capable of rapidly converging to high-quality solutions within a short timeframe.

Table 18. Statistical Results of Welded Beam Design Problem.

	MGOA	MM_MFO	MSFDBO	EGTO	CPSOGSA	OCBKA	IRIME	EABOA	hGWOA	ESHO	EWO
Best	1.69	1.83	1.69	1.69	1.69	1.69	1.70	1.69	1.69	1.70	1.69
Avg	1.69	2.36	1.70	1.76	1.83	1.69	1.73	1.69	1.69	3.51 × 10100	1.69
Std	5.23 × 10−9	4.68 × 10−1	1.26 × 10−2	8.26 × 10−2	1.53 × 10−1	2.84 × 10−4	3.12 × 10−2	0.00	4.53 × 10−4	1.09 × 10101	1.98 × 10−14

4.7.5. Speed Reducer Design Problem

The speed reducer design problem involves seven design variables: face width (b), gear module (m), number of gear teeth (p), length of the first shaft between bearings (l₁), length of the second shaft between bearings (l₂), diameter of the first shaft (d₁), and diameter of the second shaft (d₂). The primary objective is to minimize the total weight of the speed reducer while satisfying constraints including bending stress of the gear teeth, surface contact stress, transverse deflection of the shafts, and stress in the shafts. The mathematical model is provided in Appendix A.5.

As illustrated in Table 19, the method achieves optimal results in both the best and mean value categories, while ranking closely behind EABOA and EWO in standard deviation. Notably, the disadvantage of MGOA in standard deviation is substantially outweighed by its significant advantage in computational time complexity compared to EABOA and EWO. These outcomes indicate that MGOA maintains its lightweight characteristic while simultaneously delivering competitive stability.

Table 19. Statistical Results of Speed Reducer Design Problem.

	MGOA	MM_MFO	MSFDBO	EGTO	CPSOGSA	OCBKA	IRIME	EABOA	hGWOA	ESHO	EWO
Best	2.99 × 103	3.06 × 103	2.99 × 103	2.99 × 103	2.99 × 103	3.00 × 103	2.99 × 103	2.99 × 103	3.00 × 103	3.09 × 103	2.99 × 103
Avg	2.99 × 103	3.14 × 103	3.00 × 103	2.99 × 103	3.00 × 103	3.00 × 103	3.00 × 103	2.99 × 103	3.00 × 103	1.71 × 1097	2.99 × 103
Std	9.23 × 10−6	4.66 × 101	7.84	3.76 × 10−2	4.48	3.80	3.19 × 10−1	0.00	4.58 × 10−1	3.78 × 1097	1.52 × 10−13

4.7.6. Gear Train Design Problem

The gear train design problem represents a practical optimization challenge in mechanical engineering with no additional constraints, making it relatively straightforward. The goal is to minimize the specific transmission cost of the gear train. The variables are the number of teeth of four gears: Na (x₁), Nb (x₂), Nd (x₃), and Nf (x₄). The mathematical formulation is described in Appendix A.6.

As shown in Table 20, MGOA ranks second—behind only ESHO—in terms of both the mean and the standard deviation. This is attributable to the stringent constraints and quasi-discrete nature of the gear-train design. MGOA’s exploration-oriented updates may overshoot the narrow feasible region near the optimum, occasionally yielding near-feasible solutions and thereby increasing the mean and variance. In contrast, ESHO features a stronger late-stage exploitation or repair mechanism that better preserves feasibility and continues to refine solutions once ratios close to the optimum are identified. Nevertheless, MGOA also achieves the best-known optimum, indicating strong optimization capability and confirming its effectiveness for the gear system design problem.

Table 20. Statistical Results of Gear Train Design Problem.

	MGOA	MM_MFO	MSFDBO	EGTO	CPSOGSA	OCBKA	IRIME	EABOA	hGWOA	ESHO	EWO
Best	2.70 × 10−12	9.92 × 10−10	2.31 × 10−11	2.31 × 10−11	2.31 × 10−11	2.70 × 10−12	2.70 × 10−12	2.70 × 10−12	2.70 × 10−12	2.70 × 10−12	2.70 × 10−12
Avg	1.94 × 10−10	1.62 × 10−9	4.13 × 10−10	3.97 × 10−10	1.47 × 10−8	9.25 × 10−10	3.93 × 10−10	3.63 × 10−11	1.14 × 10−10	4.74 × 10−12	2.81 × 10−11
Std	3.66 × 10−10	1.16 × 10−9	4.18 × 10−10	4.99 × 10−10	1.28 × 10−8	8.91 × 10−10	4.87 × 10−10	3.39 × 10−11	3.09 × 10−10	6.44 × 10−12	4.56 × 10−11

4.7.7. Cantilever Beam Design Problem

The cantilever beam consists of five hollow square sections, each defined by one structural parameter while maintaining a constant thickness, resulting in a total of five decision variables. The objective of the cantilever beam optimization is to minimize its total weight under the constraint of satisfying a specified vertical displacement limit. The mathematical formulation is provided in Appendix A.7.

As shown in Table 21, MGOA achieves a standard deviation of zero and the lowest optimized weight, reflecting ideal performance. These results demonstrate that MGOA can stably and efficiently address this engineering challenge, further confirming its excellence and precision in search capability.

Table 21. Statistical Results of Cantilever Beam Design Problem.

	MGOA	MM_MFO	MSFDBO	EGTO	CPSOGSA	OCBKA	IRIME	EABOA	hGWOA	ESHO	EWO
Best	1.34	1.41	1.34	1.34	1.34	1.34	1.34	1.34	1.34	1.34	1.34
Avg	1.34	1.48	1.34	1.34	1.34	1.34	1.35	1.34	1.34	3.90	1.34
Std	0.00	5.58 × 10−2	9.00 × 10−6	1.70 × 10−6	1.18 × 10−7	4.93 × 10−6	3.45 × 10−3	1.71 × 10−7	2.29 × 10−5	2.11	5.43 × 10−8

4.7.8. Minimize I-Beam Vertical Deflection Problem

Minimizing the vertical deflection of an I-beam is a classical structural optimization problem. The main objective is to reduce the beam’s vertical deflection under load through optimal design of its cross-section and material properties. An I-beam, characterized by its I-shaped cross-section, typically consists of two flanges and a web. The beam is fixed at one end and subjected to concentrated or distributed loads at the other, leading to bending and vertical deflection. The goal is to design a beam that minimizes this deflection under applied loading. The mathematical model is described in Appendix A.8.

Table 22 shows that MGOA achieved the lowest values in terms of the best, mean, and standard deviation; however, the same results were also attained by MSFDBO and EABOA. Nevertheless, MGOA exhibited the shortest average computation time, demonstrating its lightweight nature, lower computational time complexity, and overall superior performance.

Table 22. Statistical Results of Minimizing I-Beam Vertical Deflection Problem.

	MGOA	MM_MFO	MSFDBO	EGTO	CPSOGSA	OCBKA	IRIME	EABOA	hGWOA	ESHO	EWO
Best	1.31 × 10−2	1.31 × 10−2	1.31 × 10−2	1.31 × 10−2	1.31 × 10−2	1.31 × 10−2	1.31 × 10−2	1.31 × 10−2	1.31 × 10−2	1.31 × 10−2	1.31 × 10−2
Avg	1.31 × 10−2	1.31 × 10−2	1.31 × 10−2	1.31 × 10−2	1.32 × 10−2	1.31 × 10−2	1.34 × 10−2	1.31 × 10−2	1.31 × 10−2	1.31 × 10−2	1.31 × 10−2
Std	1.83 × 10−18	4.94 × 10−5	1.83 × 10−18	1.15 × 10−8	7.22 × 10−5	1.04 × 10−8	2.63 × 10−4	1.83 × 10−18	8.23 × 10−8	1.32 × 10−6	2.08 × 10−18

4.7.9. Tubular Column Design Problem

Tubular columns are typically hollow cylindrical structures used to support other components or resist bending. Since they primarily bear axial forces, these columns are susceptible to buckling, especially under high axial compression. Thus, the main objective in tubular column design is to prevent buckling under external loads while optimizing geometric dimensions—such as outer diameter and wall thickness—so that the structure can withstand design loads with minimal material cost. The mathematical model is provided in Appendix A.9.

As shown in Table 23, while MGOA, EGTO, EABOA, and EWO all achieved the same minimum values in terms of the best, mean, and standard deviation, MGOA demonstrated a consistently shorter average computation time compared to the other three algorithms. This advantage underscores MGOA’s lightweight nature, enabling it to rapidly converge to optimal solutions and effectively address the tubular column design problem.

Table 23. Statistical Results of Tubular Column Design Problem.

	MGOA	MM_MFO	MSFDBO	EGTO	CPSOGSA	OCBKA	IRIME	EABOA	hGWOA	ESHO	EWO
Best	2.65 × 101	2.65 × 101	2.65 × 101	2.65 × 101	2.65 × 101	2.65 × 101	2.65 × 101	2.65 × 101	2.65 × 101	2.65 × 101	2.65 × 101
Avg	2.65 × 101	2.67 × 101	2.65 × 101	2.65 × 101	2.65 × 101	2.65 × 101	2.65 × 101	2.65 × 101	2.65 × 101	2.67 × 101	2.65 × 101
Std	3.74 × 10−15	1.17 × 10−1	4.27 × 10−15	3.74 × 10−15	1.40 × 10−12	4.42 × 10−4	3.11 × 10−2	3.74 × 10−15	1.52 × 10−4	7.19 × 10−1	3.74 × 10−15

4.7.10. Piston Lever Design Problem

The piston lever design problem is a mechanical optimization task aimed at developing an efficient and stable lever system to ensure desired force transmission while minimizing system size or material cost. A piston generates linear reciprocating motion via fluid pressure, and a lever is used to modify the magnitude and direction of this linear force—commonly applied in mechanical transmission, force amplification, or torque conversion. Designing such a system often involves optimizing lever dimensions within reasonable spatial and weight constraints to achieve required performance metrics such as force transmission, effectiveness, and stability. The mathematical formulation is described in Appendix A.10.

Table 24 indicates that MGOA secured the optimal best value, while it was only surpassed by MSFDBO and EABOA in the mean value, and by EABOA alone in standard deviation. Notably, the performance gaps in both the mean and standard deviation are minimal. Furthermore, MGOA exhibits slightly lower computational complexity than MSFDBO and significantly lower complexity compared to EABOA. Collectively, these findings affirm that MGOA—by virtue of its ability to identify optimal solutions with low time complexity—offers a meaningful contribution to addressing the piston lever design challenge.

Table 24. Statistical Results of Piston Lever Design Problem.

	MGOA	MM_MFO	MSFDBO	EGTO	CPSOGSA	OCBKA	IRIME	EABOA	hGWOA	ESHO	EWO
Best	8.41	9.92	8.41	8.41	1.84 × 101	1.67 × 102	8.42	8.41	8.4	9.21 × 102	8.41
Avg	7.20 × 101	1.45 × 101	8.41	1.36 × 102	2.70 × 102	1.68 × 102	8.43	8.41	8.80 × 101	1.09 × 104	2.43 × 101
Std	8.21 × 101	2.95	1.14 × 10−13	6.72 × 101	1.31 × 102	2.59 × 10−2	1.75 × 10−2	4.87 × 10−14	8.39 × 101	1.69 × 104	5.03 × 101

4.7.11. Reinforced Concrete Beam Design Problem

This problem focuses on designing a reinforced concrete beam that meets strength, stiffness, and stability requirements while minimizing material consumption and cost, without compromising structural safety. A reinforced concrete beam combines two materials: concrete, which resists compressive stresses, and steel reinforcement, which bears tensile stresses. The design must ensure the beam can support design loads without failure or excessive deformation. Key variables include beam dimensions, amount and distribution of reinforcement, and concrete strength grade. The mathematical formulation is detailed in Appendix A.11.

Table 25 demonstrates that MGOA delivers performance comparable to EGTO, EABOA, and EWO, with all four algorithms achieving identical optimal results in terms of best, mean, and standard deviation values. Moreover, MGOA required the shortest computation time among all algorithms evaluated, underscoring its inherently lightweight architecture and low computational complexity. These attributes position MGOA as a viable and efficient solution for the reinforced concrete beam design problem.

Table 25. Statistical Results of Reinforced Concrete Beam Design Problem.

	MGOA	MM_MFO	MSFDBO	EGTO	CPSOGSA	OCBKA	IRIME	EABOA	hGWOA	ESHO	EWO
Best	3.59 × 102	3.59 × 102	3.59 × 102	3.59 × 102	3.59 × 102	3.59 × 102	3.59 × 102	3.59 × 102	3.59 × 102	3.60 × 102	3.59 × 102
Avg	3.59 × 102	3.61 × 102	3.60 × 102	3.59 × 102	3.59 × 102	3.60 × 102	3.59 × 102	3.59 × 102	3.60 × 102	3.70 × 102	3.59 × 102
Std	5.99 × 10−14	1.69	9.62 × 10−1	5.99 × 10−14	7.34 × 10−14	1.61	1.41 × 10−3	5.99 × 10−14	1.60	5.30	5.99 × 10−14

5. Conclusions

The proposed high-performance algorithm, named the Market Game Optimization Algorithm (MGOA), draws inspiration from the competitive dynamics between merchants and customers and aims to solve complex real-world optimization problems. MGOA computationally models how merchants adapt their strategies in response to market changes and engage customers through attraction and collaboration. The algorithm is structured around two complementary stages, each activated with a 50% probability. In the first stage, extensive search and strategy adjustments are performed, while the second stage focuses on refining strategies based on customer feedback and coordination. This design introduces innovative behavioral inspiration and delivers highly efficient optimization performance. Qualitative analysis shows that the algorithm consistently converges toward the global optimum. Parameter analysis further identifies the optimal adjustment intensity for reacting to market volatility. In subsequent performance evaluations, MGOA was compared against 10 widely recognized algorithms and 10 recently enhanced variants, demonstrating superior effectiveness on unimodal, multimodal, hybrid, and composite functions from CEC benchmark suites. Finally, applications to 11 real-world engineering design problems confirm that MGOA achieves the most effective results in the majority of cases among all compared algorithms.

Therefore, the contributions of this work are threefold: (1) Its design inspiration stems from the intelligent behaviors of advanced biological entities, opening a novel and forward-looking heuristic design pathway in the field of optimization algorithms. (2) By incorporating the attraction and synergy mechanisms between merchants and customers, the algorithm achieves extensive exploration in the early iterations, thereby accelerating convergence, while focusing on refined exploitation in later phases to effectively avoid local optima. (3) In practical applications, MGOA exhibits superior solving efficiency and stability, contributing to the effective resolution of numerous real-world optimization problems. In addition, compared to traditional gradient-based methods, which rely heavily on gradient information and are often limited to differentiable objective functions, MGOA, as a gradient-free heuristic approach, demonstrates significant advantages in handling non-differentiable, highly nonlinear, or noisy problems. However, it should be noted that gradient-based methods may still achieve faster convergence on smooth and convex problems where explicit gradient information is available.

In summary, MGOA demonstrates exceptional global optimization capabilities. Future research directions could encompass the introduction of chaotic mechanisms to enhance its global exploration performance, the improvement of mutation strategies to strengthen its ability to escape local optima, or its integration with other intelligent behavioral models or advanced algorithms. After that, we will prioritize rigorous, head-to-head comparisons with leading CEC algorithms—such as EA4Eig, NL-SHADE-LBC, S-LSHADE-DP, and LSHADE-cnEpSin—under standardized benchmark settings and statistical testing (subject to the availability of verified implementations) to more comprehensively assess enhanced MGOA’s competitiveness. Such developments would further advance the emergence of powerful hybrid algorithms capable of efficiently handling large-scale complex optimization problems.

Appendix A.1. Extension/Compression Spring Design Issues

$$\begin{array}{l}\min f(x)=(x_3+2)x_2{x}_1^2\\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{l}{g}_1(x)=1-{\displaystyle \frac{x_3{x}_2^2}{71785x_1^4}}\le 0\\ g_2(x)={\displaystyle \frac{4x_2^2-x_1{x}_2}{12566(x_2{x}_1^3-x_1^4)}}+{\displaystyle \frac{1}{5108x_1^2}}-1\le 0\\ g_3(x)=1-{\displaystyle \frac{140.45x_1}{x_2^2{x}_3}}\le 0\\ g_4(x)={\displaystyle \frac{x_1+x_2}{1.5}}-1\le 0\\ 0.05\le x_1\le 2\\ 0.25\le x_2\le 1.3\\ 2\le x_3\le 15\end{array}\right.\end{array}$$

Appendix A.2. Pressure Vessel Design Issues

$$\begin{array}{l}minf(x)=0.6224x_1{x}_1{x}_3{x}_4+1.7781x_2{x}_3^2+3.1661x_1^2{x}_4+19.84x_1^2{x}_3\\ s.t.\left\{\begin{array}{l}{g}_1(x)=-x_1+0.0193x_3\le 0\\ g_2(x)=-x_2+0.00954x_3\le 0\\ g_3(x)=-\pi x_3^2{x}_3-{\displaystyle \frac{4\pi x_3^3}{3}}+1296000⩽0\\ g_4(x)=x_4-240\le 0\\ 0\le x_i\le 100,i=1,2\\ 10\le x_i\le 200,i=3,4\end{array}\right.\end{array}$$

Appendix A.3. Three-Bar Truss Design Problem

$$\begin{array}{l}minf(x)=(2\sqrt{2}\cdot x_1+x_2)\cdot l\\ s.t.\left\{\begin{array}{l}{g}_1(x)={\displaystyle \frac{\sqrt{2}\cdot x_1+x_2}{\sqrt{2}\cdot x_1^2+2x_1{x}_2}} P-\sigma \le 0\\ g_2(x)={\displaystyle \frac{x_2}{\sqrt{2}\cdot x_1^2+2x_1{x}_2}}P-\sigma \le 0\\ g_3(x)={\displaystyle \frac{1}{\sqrt{2}\cdot x_2+x_1}}P-\sigma \le 0\\ l=100\mathrm{cm}\\ P=2\mathrm{kN}/{\mathrm{cm}}^2\\ \sigma =2\mathrm{kN}/{\mathrm{cm}}^2\\ 0\le x_i\le 1, i=1,2\end{array}\right.\end{array}$$

Appendix A.4. Welded Beam Design Issues

$$\begin{array}{l}\min f(\overrightarrow{x})=1.10471x_2^2{x}_2+0.04811x_3{x}_4(14.0+x_2)\\ s.t.\left\{\begin{array}{l}{g}_1(\overrightarrow{x})=\tau (\overrightarrow{x})-{\tau }_{max}⩽0\\ g_2(\overrightarrow{x})=\sigma (\overrightarrow{x})-{\sigma }_{max}⩽0\\ g_3(\overrightarrow{x})=\delta (\overrightarrow{x})-{\delta }_{max}⩽0\\ g_4(\overrightarrow{x})=x_1-x_4\le 0\\ g_5(\overrightarrow{x})=P-P_e(\overrightarrow{x})\le 0\\ g_6(\overrightarrow{x})=0.125-x_1⩽0\\ g_7(\overrightarrow{x})=1.10471x_1^2{x}_2+0.04811x_2{x}_4(14.0+x_2)-5.0⩽0\\ 0.1⩽x_1⩽2\\ 0.1⩽x_3⩽10\\ 0.1⩽x_3⩽10\\ 0.1⩽x_4⩽2\\ \tau (\overrightarrow{x})=\sqrt{{({\tau }^{\prime })}^2+2{\tau }^{\prime }{\tau }^{″}{\displaystyle \frac{x_2}{2R}}+{({\tau }^{″})}^2}\\ {\tau }^{\prime }={\displaystyle \frac{p}{\sqrt{2}{x}_1{x}_2}}\\ {\tau }^{″}={\displaystyle \frac{MR}{J}}\\ M=P(L+{\displaystyle \frac{x_2}{2}})\\ R=\sqrt{{\displaystyle \frac{x_2^2}{4}}+{\left({\displaystyle \frac{x_1+x_3}{2}}\right)}^2}\\ J=2\left\{\sqrt{2} x_1{x}_2\left[{\displaystyle \frac{x_2^2}{4}}+{\left({\displaystyle \frac{x_1+x_3}{2}}\right)}^2\right]\right\}\\ \sigma (\overrightarrow{x})={\displaystyle \frac{6PL}{x_4{x}_3^2}}\\ \delta (\overrightarrow{x})={\displaystyle \frac{6P{L}^3}{E{x}_3^2{x}_4}}\\ P_c(\overrightarrow{x})={\displaystyle \frac{4.013E\sqrt{\frac{x_3^2{x}_4^6}{36}}}{L^2}}(1-{\displaystyle \frac{x_3}{2L}}\sqrt{{\displaystyle \frac{E}{4G}}})\\ P=6000 \mathrm{lb}\\ L=14 \mathrm{in}.\\ {\delta }_{max}=0.25 \mathrm{in}. \\ E=30\times 1^6 \mathrm{psi}\\ G=12\times {10}^6 \mathrm{psi}\\ {\tau }_{max}=13600 \mathrm{psi}\\ {\sigma }_{max}=30000 \mathrm{psi}\end{array}\right.\end{array}$$

Appendix A.5. Reducer Design Issues

$$\begin{array}{l}minf(\overline{z})=0.7854z_1{z}_2^2(3.333z_3^2+14.9334z_3-43.0934)-1.508z_1(z_6^2+z_7^2)\\ +7.4777(z_6^3+z_7^3)+0.7854(z_4{z}_6^2+z_5{z}_7^2)\\ s.t.\left\{\begin{array}{l}{g}_1(\overline{z})={\displaystyle \frac{27}{z_1{z}_2^2{z}_3}}-1⩽0\\ g_2(\overline{z})={\displaystyle \frac{397.5}{z_1{z}_2^2{z}_3^2}}-1⩽0\\ g_3(\overline{z})={\displaystyle \frac{1.93z_4^3}{z_2{z}_7^4{z}_3}}-1⩽0\\ g_4(\overline{z})={\displaystyle \frac{1.93z_4^3}{z_2{z}_7^4{z}_3}}-1⩽0\\ g_5(\overline{z})={\displaystyle \frac{[{(745{(z_4/z_2{z}_3)}^2+16.9\times {10}^6]}^{\frac{1}{2}}}{110z_6^3}}-1⩽0\\ g_6(\overline{z})={\displaystyle \frac{{[{(745(z_5/z_2{z}_3))}^2+157.5\times {10}^6]}^{\frac{1}{2}}}{85z_7^3}}-1⩽0\\ g_7(\overline{z})={\displaystyle \frac{z_3{z}_3}{40}}-1⩽0\\ g_8(\overline{z})={\displaystyle \frac{5z_2}{z_1}}-1⩽0\\ g_9(\overline{z})={\displaystyle \frac{z_1}{12z_2}}-1⩽0\\ g_{10}(\overline{z})={\displaystyle \frac{1.5z_6+1.9}{z_4}}-1⩽0\\ g_{11}(\overline{z})={\displaystyle \frac{1.1z_7+1.9}{z_5}}-1⩽0\\ 2.6⩽z_1⩽3.6\\ 0.7⩽z_2⩽0.8\\ 17⩽z_3⩽28\\ 7.3⩽z_4⩽8.3\\ 7.3⩽z_5\le 8.3\\ 2.9⩽z_6\le 3.9\\ 5.0⩽z_7\le 5.5\end{array}\right.\end{array}$$

Appendix A.6. Gear Train Design Issues

$$\begin{array}{l}minf(x)={({\displaystyle \frac{1}{6.931}}-{\displaystyle \frac{x_2{x}_3}{x_1{x}_4}})}^2\\ s.t.\left\{\begin{array}{l}12\le x_i\le 60\\ i=1,2,3,4\end{array}\right.\end{array}$$

Appendix A.7. Cantilever Beam Design Problems

$$\begin{array}{l}minf(x)=0.0624(x_1+x_2+x_3+x_4+x_5)\\ s.t.\left\{\begin{array}{l}g(x)={\displaystyle \frac{61}{x_1^3}}+{\displaystyle \frac{37}{x_2^3}}+{\displaystyle \frac{19}{x_3^3}}+{\displaystyle \frac{7}{x_4^3}}+{\displaystyle \frac{1}{x_5^3}}-1\\ 0.01\le x_i\le 100\\ i=1,2,3,4,5\end{array}\right.\end{array}$$

Appendix A.8. Minimizing the Vertical Deflection of I-Beams

$$\begin{array}{l}\mathit{min}\delta ={\displaystyle \frac{P{L}^3}{48EI}}\\ s.t.\left\{\begin{array}{l}\delta \le {\delta }_{\max }\\ \sigma ={\displaystyle \frac{My}{I}}\le {\sigma }_{\mathit{yield}}\end{array}\right.\end{array}$$

Appendix A.9. Tubular Column Design Issues

$$\begin{array}{l}\mathit{min}W=\rho V=\rho \pi (d_o^2-d_i^2)L\\ s.t.\left\{\begin{array}{l}{P}_{\mathit{cr}}={\displaystyle \frac{{\pi }^{2}EI}{L^2}}\\ P_{\mathit{cr}}\ge P_{\mathit{required}}\\ \sigma ={\displaystyle \frac{P}{A}}\le {\sigma }_y\\ d_o\ge d_{\min },\hspace{1em}t\ge t_{\min }\end{array}\right.\end{array}$$

Appendix A.10. Piston Lever Design Issues

$$\begin{array}{l}\mathit{minV}=A_L{L}_L\\ \mathit{minCost}=C_L{A}_L{L}_L\\ s.t.\left\{\begin{array}{l}{F}_L=F_P{\displaystyle \frac{L_P}{L_L}}\\ \sigma ={\displaystyle \frac{F_{L}y}{I}}\le {\sigma }_{\mathit{yield}}\\ L_L\ge L_{\min }\\ A_L\ge A_{\min }\end{array}\right.\end{array}$$

Appendix A.11. Design Problems of Reinforced Concrete Beams

$$\begin{array}{l}\mathit{min}V=bhL+A_s{L}_s\\ \min W={\rho }_{\mathit{concrete} }{V}_{\mathit{concrete} }+{\rho }_{\mathit{steel}}{V}_{\mathit{steel}}\\ s.t.\left\{\begin{array}{l}{M}_u=\varphi A_s{f}_y(d-{\displaystyle \frac{a}{2}})\\ \sigma ={\displaystyle \frac{My}{I}}\le {\sigma }_{\mathit{yield}}\\ V_c+V_s\ge V_{\mathit{applied}}\\ b\ge b_{\min }\\ h\ge h_{\min }\end{array}\right.\end{array}$$