Improving the Detection Ability of Binary CUSUM Risk-Adjusted Control Charts with Run Rules

Abstract

Conventional statistical process control (SPC) charting, an efficient monitoring and diagnosis scheme, is under development in several fields of healthcare monitoring. Investigation of clinical binary outcomes using risk-adjusted (RA) control charts is an important subject in this area. Different researchers have extended the monitoring of the binary outcomes of cardiac surgeries by fitting a logistic model for a patient’s death probability against the patient’s risk. As a result, different RA-based cumulative sum (CUSUM) charts have been proposed for monitoring a patient’s 30-day mortality in several studies. Here, a novel run rules method is introduced in conjunction with the RA CUSUM control chart. The suggested approach was tested and benchmarked through simulation studies based on the average run length (ARL) metric. The outcomes showed favourable results, and further analysis under beta-distributed conditions confirmed its robustness. A worked example was presented to illustrate its implementation.

1. Introduction

Monitoring healthcare processes helps to eliminate serious health problems and reduce avoidable fatalities or other negative outcomes. As a common approach, the results of a healthcare process such as an outcome of surgery, the surgical failure rate, the survival time of patients who underwent surgeries and so forth are usually monitored with statistical process control (SPC) techniques, especially control charts. For example, in monitoring surgical operations, binary response variables represent the severity of the existing patient’s health, which could be summarized as the death risk after performing an operation or a surgical process, entailing the surgeon’s virtuosity, supporting staff, hospital environment and the provided equipment, collectively defined as the ‘surgeon’. Patient covariates, including factors such as age, blood pressure, and existing health conditions such as diabetes or morbid obesity, are often combined into a single composite risk measure. The Parsonnet Scoring System (PSS) is a well-known example that has been commonly used for monitoring outcomes in cardiac surgery [1]. PSS usually ranges from 0 to 100 and is based on the patients’ gender, age, blood pressure, morbid obesity, etc. The higher the PSS of the patients, the higher the surgery’s failure probability; the patient’s survival is usually investigated after a specific time post-operation (usually 30 days).

SPC has several applications in the healthcare sector, including health management [2], hospital quality improvement [3], monitoring of surgical outcomes [4], patient’s lifetime analysis [5], and detection of virus outbreaks [6]. For additional information on healthcare applications of SPC, readers are referred to [7,8]. Among the different SPC techniques, control charts are usually employed for ensuring process stability and variability in industrial processes. For this aim, random samples are taken from an SPC process at different times, and then the sample statistics are computed and displayed on a control chart. The chart will trigger an out-of-control (OC) signal, or equivalently, the statistic will fall outside the control limits due to the occurrence of any assignable cause. To detect the occurred assignable causes and solve the problems, a systematic procedure must be carried out, and after these modifications, the process will go back to its in-control (IC) condition [9,10]. Process monitoring in SPC can be divided into Phase I and Phase II. In Phase I, a retrospective analysis is employed to obtain the historical IC state of the process and estimate the process parameters if unknown. In Phase II, the control chart is used to monitor future observations and check if the process is statistically in control. Phase II aims to use online data to quickly detect shifts from the baseline parameters established in Phase I [11].

Monitoring medical process outcomes using control charts is a well-established approach within SPC applications in healthcare. The primary goal is to enhance healthcare performance—particularly in surgical procedures—while reducing patient-specific risks. To address variations arising from individual patient characteristics, risk-adjusted (RA) control charts were introduced [12]. Among various extensions of RA charts designed to improve sensitivity to OC conditions—such as score-based approaches, graded responses, adjustments for explanatory variables, and profile-based monitoring [13,14]—the RA Bernoulli cumulative sum (CUSUM) chart proposed in [4] has received particular attention for its simplicity and effectiveness. This chart models each patient’s preoperative risk of surgical failure using logistic regression, then applies a likelihood ratio-based scoring method to construct the monitoring statistic. Building on earlier efforts to incorporate patient condition into monitoring methods, [4] made a significant contribution by developing an RA CUSUM chart that tracks the odds of patient mortality adjusted by the patient’s PSS. Their method, fitted on historical surgical data (during a 30-day period after surgery), notably a dataset of cardiac operations, became a benchmark in RA chart applications for binary surgical outcomes.

According to the RA control chart framework introduced in [4], two main categories have been developed in surgical outcome monitoring. The first focuses on binary outcomes within a defined period after surgery, usually 30 days, which corresponds to the focus of this study and is elaborated on below. The second category evaluates patient survival time following surgery. For conciseness, only the literature pertaining to the first category is discussed here, while the survival time approach, first proposed in [15], is not considered for the sake of brevity. Should any interested reader want to be more acquainted with the latter, [16,17] can be useful. References [4,18] addressed this subject by illustrating the difference between the implementation of control charts with RA and SPC in general. Ref. [13] introduced four sequential curtailed RA charts designed to maintain the total probability of false alarms across a defined series of surgical cases. Each of these methods was evaluated against the standard CUSUM chart by examining average run length (ARL) and type I error rates. Ref. [19] further adapted CUSUM charts by modelling the underlying risk with a beta distribution rather than a Bernoulli distribution. Furthermore, [20] provided recommendations and adjustments for estimating logistic regression parameters in RA CUSUM charts. Their findings highlighted that inaccurate parameter estimates can substantially impact ARL calculations, especially for high-risk patients.

Unlike previously mentioned studies, [21] continuously updated the response variables in real time rather than waiting for a fixed period, using current data in CUSUM control charts. Building on this idea, [22] evaluated the performance of a Phase II CUSUM chart for tracking binary surgical results, comparing a 30-day delay strategy to real-time updates, with ARL assessed via Monte Carlo simulations. While earlier studies assumed a fixed IC model, [23] allowed the risk model to update continuously, accommodating changes in patient characteristics or other influencing factors. For monitoring binary surgical outcomes, [24] proposed a nonparametric risk-adjusted CUSUM chart that uses a logistic regression model with coefficients that vary over time. Additionally, [25] introduced control charts with dynamic control limits to handle changing patient and surgeon characteristics, a problem also addressed in [26] when considering the effects of evolving patient populations on RA CUSUM charts. Additional uses of dynamic control limits are discussed in [25]. Like CUSUM charts, Exponentially Weighted Moving Average (EWMA) charts have also been adapted into RA formats. A reader is referred to [14,27,28,29] in which the EWMA chart was combined with variable life-adjusted display (VLAD) metrics, which are widely applied in healthcare settings [30].

Some other novel applications of RA charts have also been reported in the literature. While RA-CUSUM and RA-EWMA charts have been widely used to monitor binary surgical outcomes, recent studies extended their capabilities by incorporating survival data, nonlinear effects and machine learning. Ref. [31] demonstrated that quality control tools improve efficiency and outcomes. Subsequent works have developed adaptive approaches, such as support vector machine (SVM)-integrated EWMA charts [32], adaptive SVM-ARAEWMA charts [33], and generalized additive models (GAMs) for interpretable stroke patient profiles [34], have been proposed. Survival based monitoring has also been advanced with RA-EWMA and MA-EWMA methods ([35,36]) for continuous outcome evaluation.

In surgical monitoring, methods like CRAM and RA-SPRT [37], RA O-E CUSUM [38], slow feature analysis (SFA) [39], and state apace models with machine learning for multistage clinical process monitoring [40] have further improved real-time detection. Adaptive RA-WCUSUM charts [41] further addresses sensitivity to pre-set parameters. Collectively, these studies reflect a shift toward adaptive, data-driven methods that enhance sensitivity, interpretability, and clinical applicability. For brevity, additional related works are summarized in Table 1.

Table 1. Comparative literature review of risk-adjusted methods applied in healthcare.

Paper	Method	Outcome Type	Risk Adjustment	Key Innovation	Application
[2]	Quality Function Deployment (QFD)	Service quality metrics	Patient feedback and priority ranking	Adapts quality function deployment (QFD) to healthcare	Healthcare system
[3]	GURU-based SPC	Process indicators	None	Automate SPC chart implementation in healthcare	Hospital process control
[42]	Variable life-adjusted display (VLAD)	Binary	Parsonnet score	Graphical risk-adjusted cumulative performance monitoring	Cardiac surgery outcomes monitoring
[43]	Risk-adjusted (RA) CUSUM	Binary (30-day mortality)	Parsonnet score	First published application of control limits to risk-adjusted CUSUM for surgical mortality, enabling real-time alerts	Cardiac surgery performance monitoring
[4]	RA Bernoulli CUSUM	Binary (30-day mortality)	Logistic regression	RA-CUSUM in surgical monitoring	Cardiac surgery mortality
[18]	CUSUM/EWMA review	Binary/Counts	Logistic regression	Comparative review of methods	General healthcare
[27]	RA-EWMA	Binary	Fixed covariate effects	Simplified RA methods for non-normal outcomes	Cardiac surgery mortality
[15]	RA-CUSUM accelerated failure time (AFT)	Time to event	AFT regression (log logistic/Weibull)	Monitors survival time instead of binary outcomes	Cardiac surgery survival
[13]	Sequential score tests (1-4)	Binary (30-day mortality)	Logistic regression	Type I error control and truncation; compares sequential methods to control false alarms over time	Cardiac surgery mortality
[44]	Phase I RA-LRTCP (Likelihood-Ratio Test from Change-Point Model)	Binary	Parsonnet score	Phase I monitoring, leading to better Phase II performance	Cardiac surgery monitoring
[23]	Weighted event evaluation (WEE) chart	Binary	Logistic regression	Time weighted updates. Recent outcomes are weighed more heavily	Cardiac surgery mortality
[45]	Improved particle swarm optimization (PSO)	Continuous	Weighted thresholds	Hybrid wireless sensor network with adaptive PSO for real time risk prioritization	Remote healthcare monitoring
[25]	RA-CUSUM with dynamic performance limits	Binary	Logistic regression	Adjusts control limits dynamically for varying patient populations	General surgery
[16]	RA Bernoulli CUSUM with VLAD	Binary	Logistic regression	Combines RA-CUSUM with VLAD	Surgical quality monitoring
[46]	RA-CUSUM with multi-response	Ordinal (full recovery, partial recovery, death)	Parsonnet score	Extends RA-CUSUM to multi response outcomes	Cardiac surgery performance monitoring
[26]	RA Bernoulli CUSUM	Binary	Parsonnet score (logistic model)	Highlights the need for population-specific control limits	Cardiac surgery monitoring
[8]	SPC and interrupted time series (ITS)	Continuous	-	Combines SPC and ITS to ensure effective quality improvement	Healthcare quality improvement
[21]	Improved RA Bernoulli CUSUM	Binary	Parsonnet score	Dynamic updating of CUSUM statistics as outcomes become available	Cardiac surgery outcomes
[29]	RAEV (Risk-Adjusted EWMA VLAD)	Binary	Logistic regression	Integrates EWMA with VLAD to detect shifts	Surgical outcome monitoring
[14]	EWMA for surgical outcome	Binary	Logistic regression	Uses weights score tests for monitoring	General surgery
[24]	Nonparametric RA CUSUM	Binary	Varying-coefficient logistic regression (VCLR)	Flexible RA-CUSUM using splines to model nonlinear risk interactions	Cardiac surgery monitoring
[30]	VLAD and $V$-mask	Binary	Logistic regression	Links VLAD charts to CUSUM using $V$-mask for clear performance alerts	Cardiac surgery mortality
[47]	Risk adjusted Bernoulli chart	Binary	Logistic and state space model (SSM)	State-space framework incorporating a hidden risk factor, allowing the control limits to be dynamically updated	Thyroid cancer
[22]	RA-CUSUM (6 variants)	Binary & Survival time	Parsonnet score (logistic regression and AFT model)	Real-time updating CUSUM for faster surgical monitoring	Cardiac surgery monitoring
[20]	RA-CUSUM & Power transform	Binary	Logistic regression + Box–Cox	Improved model fit using power transformation	Cardiac surgery mortality
[6]	Optimized $np$ control chart	Binary	Baseline infection rate	Significantly improves outbreak detection speed and reduces infections by dynamically adjusting sample size and intervals	Early detection of respiratory virus outbreaks at airports
[31]	Shewhart p-control charts	Binary and continuous	Patient resource consumption score	Combined control charts with structured team feedback	Digestive surgery monitoring
[32]	SVM-EWMA control chart	Continuous (survival time)	Parsonnet score (SVM regression)	Integrate SVM with EWMA for heterogeneous data	Cardiac surgery survival time monitoring
[34]	Generalized additive model (GAM)-based D and T2 charts	Binary (ischemic vs. hemorrhagic stroke)	Demographic, clinical, and socioeconomic factors (logistic GAM)	First use of GAMs for healthcare profile monitoring, with comparative performance of $D$ and $T$2 charts	Acute stroke patient monitoring in cardiology
[36]	Risk adjusted moving average (RAMA)-EWMA chart	Survival time (AFT model)	AFT model with patient risk scores	Combines moving average with EWMA for improved sensitivity to small or moderate shifts in survival time	Cardiac surgery survival time monitoring
[39]	SPC with principal component analysis (PCA) and slow feature analysis (SFA)	Continuous	Normalization to baseline trajectories	Adapts SPC to clinical care and introduces SFA for dynamic recovery tracking	Postoperative monitoring of pediatric cardiac surgery
[40]	SSM and SVR based intraclass correlation coefficient	Continuous	Patient risk factors and decision variables	Integrate SSM with SVR, improving sensitivity to small/moderate shifts	Thyroid cancer surgery
[33]	SVM-based adaptive RA-EWMA	Continuous (survival time)	Parsonnet score (SVM regression)	Integrates SVM-based residuals into adaptive EWMA for enhanced shift detection	Cardiac surgery outcomes
[35]	RA survival EWMA based on AFT	Continuous (survival time)	Weibull AFT model with fixed and random effects	First control chart to monitor both location (mean) and scale (variability) parameters in survival time using score tests	Monitoring surgical outcomes and HIV treatment efficiency
[37]	Cumulative RA monitoring, change point model & RA-based sequential probability ratio	Binary	Euroscore	Single-surgeon analysis with risk-adjusted performance	Surgeon performance tracking
[38]	RA observed minus expected (O-E) CUSUM	Binary	Logistic model	Integrates O-E chart with CUSUM	Surgery monitoring
[41]	Adaptive RA-WCUSUM	Binary	Logistic model (Parsonnet score)	Introduces dynamic weighting for improved sensitivity	Cardiac surgery outcomes
[48]	RA Ordinal CUSUM and DPCLs	Ordinal	Ordinal logistic regression model and Latent risk	First to integrate ordinal outcomes, latent risks, and dynamic limits for multistage healthcare monitoring	Multistage surgeries (Two-stage thyroid surgery)
This paper	RA-CUSUM with run rules	Binary	Logistic model (Parsonnet score)	Combines RA-CUSUM with novel run rules	Cardiac surgery outcomes

A review of the related literature shows that while run rules have been extensively explored in conventional control charts such as Shewhart, CUSUM, and EWMA charts (e.g., Western Electric rules and $q$-of-($q+w$); see [49,50]), their integration into RA schemes for monitoring binary surgical outcomes has not yet been developed. Although modern adaptive RA procedures (e.g., [20,22]) have improved flexibility and parameter adaptation, they do not incorporate sequential run rule logic to enhance detection responsiveness. In healthcare monitoring, the rapid identification of OC conditions is crucial, as delays in detecting performance deterioration can have direct clinical consequences. In Phase II monitoring, one of the major approaches to increasing chart sensitivity is the use of run rules, typically implemented through the $q$-of-($q+w$) points concept, where a signal is triggered when a specified number of points exceed control limits within a given window. However, the approach proposed in this study is conceptually and mathematically distinct. The paper introduces a ratio-based region run rule system that evaluates the ratio between consecutive risk-adjusted likelihood scores, thereby creating dynamic detection regions rather than relying on fixed point-count rules. This novel design enhances sensitivity to emerging OC conditions while maintaining robustness to patient-specific risk variability.

The main contributions of this paper are as follows:

• Integration of run rules into an RA-CUSUM framework for binary surgical outcome monitoring;
• Development of a ratio-based region design algorithm to enhance rapid OC detection in Phase II;
• Demonstration of the method’s superior performance through simulation and real cardiac surgery data, proposed by [4].

The rest of this paper is organized as follows. A brief introduction of the RA-based CUSUM chart and run rules is provided in Section 2. The proposed method and the corresponding design procedure are presented in Section 3. In Section 4, the performance of the proposed method is evaluated on the basis of ARL measures. Section 5 discusses a practical example to demonstrate the applicability of the proposed approach. Finally, the findings of this research and concluding remarks are given in Section 6.

2. Preliminaries

In this section, the fundamental formulation of [4]’s RA-CUSUM method is described, and then, a brief introduction of the run rules theory is provided.

2.1. Risk-Adjusted Control Charts in Phase II of Binary Surgical Outcome Monitoring

To ensure comparability in monitoring binary surgical outcomes, the relations are demonstrated using cardiac surgery data characterized by Parsonnet risk scores, as described by [4]. Consider that a prior dataset is available, containing historical binary surgical outcomes, indicating whether each patient survived or died within a specified period, along with their associated Parsonnet risk score. From Phase I, the IC model is obtained as follows:

$$\mathit{log}({\displaystyle \frac{{\pi }_t}{1-{\pi }_t}})=\alpha +\beta x_t.$$

(1)

where $x_t$ indicates the Parsonnet risk associated with the $t^{th}$ patient, while ${\pi }_t$ represents the corresponding surgical failure rate. The parameters $\alpha$ and $\beta$ denote the IC intercept and slope, respectively. The RA-CUSUM chart is designed to identify changes in the odds ratio R from $R_0$ to $R_1$, where typically $R_0=1$, and $R_1$ is assigned the desired importance value from the OC possible shifts. These shifts are obtained from the information of the independent binary outcomes, denoted by $y_t$, such that if the surgical operation fails, $y_t=1$; otherwise, $y_t=0$ in the $t^{th}$ patient. To assess surgical performance in Phase II, essentially evaluating the consistency of the established IC model, the likelihood ratio statistic is derived using the odds ratio theorem as follows:

$$W_t=\left\{\begin{array}{c}\mathit{log}\left({\displaystyle \frac{\left(1-{\pi }_t+R_0{\pi }_t\right)R_A}{\left(1-{\pi }_t+R_A{\pi }_t\right)R_0}}\right) \mathrm{i}\mathrm{f} y_t=1\\ \mathit{log}\left({\displaystyle \frac{\left(1-{\pi }_t+R_0{\pi }_t\right)}{\left(1-{\pi }_t+R_A{\pi }_t\right)}}\right) \mathrm{i}\mathrm{f} y_t=0.\end{array}\right.$$

(2)

The recursive formulation of the CUSUM statistic employed to identify upward shifts in the process is expressed as follows:

$$\begin{gathered} Z_t=\mathit{max}(0,Z_{t-1}+W_t), \\ {Z}_0=0. \end{gathered}$$

(3)

when $Z_t\ge h$, the process is considered to be in a deteriorating state (OC), whereas values of $Z_t<h$indicate that the process remains IC. By slightly modifying Equation (3), the CUSUM control chart can also identify negative OC shifts. Detailed explanations are excluded for conciseness; readers are referred to [4] for more insights.

The control limit $\left(h\right)$ is determined with the desired false alarm rate specified by the steady IC ARL ($AR{L}_0$) or type I error in the literature [9]. A comparison of different control charts in Phase II with the analogous $AR{L}_0$reveals that generally, the one with the lowest $AR{L}_1$is the superior method. Because $ARL$ does not exactly conform to a geometric distribution (see Figure 1 in [14]), it is recommended to compute $h$ ($AR{L}_0$) with simulations.

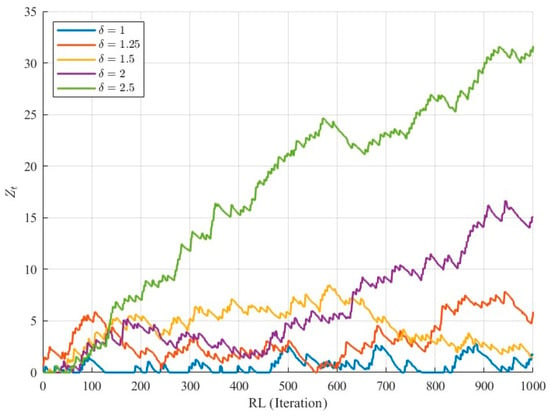
Figure 1. Evolution of 1000 simulated RA-CUSUM statistics under IC and OC conditions.

By an adjustment of $R_0$, $R_1$, and $h$ ($AR{L}_0$), the chart can be applied to real datasets; however, for comparing the performance of different control charts, the calculation of $AR{L}_1$ with simulated data is the common approach, for example, [22]. Two typical sources of OC observations are modelled in the simulations. The first arises when the surgical failure rate ${\pi }_t$ transitions from the IC value to ${\pi }_t^{*}$ as follows:

$${\pi }_t^{*}={\displaystyle \frac{\delta {\pi }_t}{1-{\pi }_t+\delta {\pi }_t}}$$

(4)

where $\delta$ indicates the extent of the positive shift. It is reasonable to assume that the larger the shift is, the quicker the detection. In the second source, the IC model from Equation (1) transforms into an OC model with a pre-specified magnitude, i.e., $\alpha +\beta x_t$ changes to $\alpha +\beta x_t+\delta$. To compute $AR{L}_1$, the Algorithm 1 describes the simulation steps using iterNum iterations under the first OC source condition when there is a deviation of size $\delta$. $AR{L}_1$can be computed for the second source of OC observations with slight modifications to the data generation. $AR{L}_0$ is obtained using the same procedure when $\delta$ is set to zero.

Algorithm 1. Steps for the CUSUM ARL1 computation corresponding to the first OC source

Define the parameters including $R_0$, $R_1$, $h$, iterNum, $\alpha$, $\beta$, $\delta$; $RL=\left[\right]$; for $i=1$: iterNum do $Z_t=0$; $Z_1=0$; $t=0$; while $Z_t<h$: do      By the historical data, a random Parsonnet risk value is generated;      Compute ${\pi }_t$ by (1);      Compute ${\pi }_t^{\mathrm{*}}$ by (4);      Generate $y_t$ by drawing a random binary value with success probability ${\pi }_t^{\mathrm{*}}$;      Compute $W_t$ by (2);      Compute $Z_t$ by (3);       $t=t+1$; end while Append $t$ to the $RL$; end for $ARL=mean$ ($RL$);

2.2. Brief Overview of the Run Rules Scheme

In contrast to conventional control chart signalling, i.e., falling the single point (charting statistic) beyond the control limits, an OC signal can be caused by the run rules using some predefined patterns. According to the definition of ‘run’ as an uninterrupted sequence of samples, run rules allow for more flexibility in the detection of OC conditions, particularly in the case of small and moderate shifts by the proposing of warning limits in place of, or in addition to the main control limits Consequently, a signal may occur not only when a single point exceeds the control limits but also when multiple consecutive pints fall within the warning regions. Despite several benefits, the main concern related to the implementation of run rules is the increase in Type I error, which occurs when an IC process is incorrectly identified as OC.

This term, i.e., run rules, has been integrated into Shewhart control charts to enhance their sensitivity, with applications dating back to the 1950s [51,52]; however, it became more applicable and well known with the proposal of the Western Electric run rules [49]. This proceeded to a systematic presentation of a set of decision rules in such a way that at least one of the following events occurred in Shewhart charts:

• A single point falls outside the three-sigma control limits;
• Two of three successive points fall beyond the two-sigma warning limits;
• Four out of five consecutive points lie at least one sigma away from the centre line;
• Eight successive points fall on one side of the centre line.

A commonly used alternative to run rules is the 1-of-1 or $q$-of-($q+w$) approach, which signals an OC state either when a single plotting statistic falls outside the lower or upper control limit (LCL or UCL), or when $q$ out of $q+w$ plotting statistics fall between the LCL (UCL) and the corresponding lower (upper) warning limit. This approach has been documented in several studies, including [53,54]. Hence, the main idea of run rules is that the IC region is divided into some regions, and then the location of some samples (statistics) with a specific sequence in this region acts as an indicator of an OC condition.

3. Results

Mathematically and conceptually, the proposed method differs from traditional run rules, Western Electric method, $q$-of-($q+w$) approaches, and truncated or curtailed sequential score methods in several important ways. Unlike conventional run rules that count a fixed number of points beyond control limits, our approach evaluates the ratio of RA-CUSUM statistics falling within predefined sub-regions of the IC range, transforming detection from a point-count rule to a proportion-based assessment of local process behaviour. Conceptually, this enables more responsive detection of subtle OC shifts, while simultaneously utilizing information from all regions rather than truncating sequences or focusing only on extremes, as in sequential score methods. Furthermore, the proposed method is designed using the $ARL$ criterion, employing a heuristic strategy that first sets the $AR{L}_0$and then adjusts the detection limits to minimize the $AR{L}_1.$ In contrast, previous approaches typically rely on Markov chain approximations to determine $ARL$ performance. By combining ratio-based detection with $ARL$-driven design, the proposed framework enhances Phase II sensitivity while maintaining robustness to patient-specific risk variation. The next subsections describe the details of our proposed method and finally, a reader is referred to consult the Supplementary Material of the paper to see the Matlab® codes that were used to derive the results herein.

3.1. Basic Idea of the Proposed Approach

This paper proposes the idea of dividing the IC region, as discussed in several papers, but considers the ratio of samples in each region instead of the exact number of samples. In this approach, the IC region of an RA-CUSUM control chart, i.e., $(0-h]$, is divided into $k$ equal regions in such a way that region 1: $\left(0,{\displaystyle \frac{h}{k}} \right]$, region 2: $\left({\displaystyle \frac{h}{k}},{\displaystyle \frac{2h}{k}}\right]$,…, region $k-1$: $\left({\displaystyle \frac{\left(k-2\right)h}{k}},{\displaystyle \frac{\left(k-1\right)h}{k}}\right]$, and region $k$:$\left({\displaystyle \frac{\left(k-1\right)h}{k}},h\right]$. The number of statistics in each region is counted and denoted as $d_1,d_2,\dots , d_{\left(k-1\right)}, d_k$in the t^th-generated sample; the ratio of samples in each region denoted as ${\displaystyle \frac{d_1}{t}},{\displaystyle \frac{d_2}{t}},\dots ,{\displaystyle \frac{d_{\left(k-1\right)}}{t}},{\displaystyle \frac{d_k}{t}}$ is compared with the $k$ predefined limits entailing $l_1,l_2,\dots ,l_{k-1},l_k$. The OC signal is triggered provided that at least one of the following conditions is satisfied: $Z_t\ge h$, ${\displaystyle \frac{d_1}{t}}>l_1$, ${\displaystyle \frac{d_2}{t}}>l_2$,…, ${\displaystyle \frac{d_{\left(k-1\right)}}{t}}>l_{k-1}$, and ${\displaystyle \frac{d_k}{t}}>l_k$. Note that the RA-CUSUM without run rules is equivalent to the $k=l_1=1$conditions, and to avoid the type I error, the first region cannot be signalled in the case of greater values of $k$.

For a better understanding of the above idea, we generated the IC and OC data with the IC model of [4]. Considering $AR{L}_0$ equal to $200$ or $h = 1.51$ (for more details, see Table 2 in [22]), three regions $(k = 3)$ were defined as $(0-0.503], (0.503-1.007]$, and $(1.007-1.51]$. Table 2 presents the results of the average number of samples and the ratio of samples in each region for the signalling sample in 10,000 iterations. Note that the $AR{L}_0$ (i.e., $\delta =$1 in Equation (4)) and ARL₁ ($\delta$ = 1.2, 1.5, …, 3, 4) values were the same as those presented in Table 2 in [22].

Table 2. The results of average of the number of samples and ratio of samples in each region in 10,000 iterations for $k = 3$ and $h = 1.51$ for [4]’s IC model.

$\mathit{\delta }$	Average of the Number of Samples in Each Region			Average of Ratio of Samples in Each Region			ARL
	(0–0.503]	(0.503–1.007]	(1.007–1.51]	(0–0.503]	(0.503–1.007]	(1.007–1.51]
1.0	143.20	43.66	12.43	0.678	0.227	0.082	200.3
1.2	89.43	32.32	10.25	0.625	0.250	0.104	129.6
1.5	49.98	23.06	8.89	0.556	0.280	0.137	82.8
2.0	28.05	15.56	7.09	0.505	0.295	0.164	50.2
2.5	18.71	11.85	5.82	0.448	0.318	0.189	35.9
3.0	13.61	8.73	4.93	0.418	0.319	0.207	28.1
4.0	8.61	6.62	4.01	0.378	0.325	0.222	20.1

For example, in the first run of the IC condition ($\delta$ = 1), the RA-CUSUM chart signalled at the $42nd$ sample in such a way that 34, 6, and 1 samples fell in the first, second, and third regions, respectively (the last one had a value greater than h, and thus, an OC signal was triggered). The ratio of samples in each region in the signalling sample became $0.81 \left({\displaystyle \frac{34}{12}}\right)$, $0.14 \left({\displaystyle \frac{6}{42}}\right)$, and $0.024 \left({\displaystyle \frac{1}{42}}\right)$. As in the first run, the following six numbers were recorded in each iteration, and their average is reported in the first row of Table 2. We observed that under the IC condition, on average, 143.2 samples were located in the first region after the RA-CUSUM triggered an OC signal.

To better understand the role of our proposed ratio-based approach, the $Z_t$ statistics are depicted for 1000 generated samples under IC and OC conditions to show the deviation from IC (Figure 1). Under IC conditions, the statistics fluctuate around the expected range without systematically approaching the control limit, while under OC conditions, they gradually increase, reflecting process deviation. The figure also illustrates that as the shift size increases, the deviation from the IC condition becomes more pronounced and tangible. These observations highlight that for small shifts, standard RA-CUSUM detection can be delayed, motivating the use of run rules. By evaluating the ratio of statistics in predefined sub-regions, the proposed method captures early deviations, enabling faster and more sensitive detection of OC conditions.

Because the ARL values decreased upon an increase in the shift magnitude, the average number of samples rationally decreased when we had greater $\delta$ values. However, the average ratio of samples in each region led us to the idea of this paper. As can be seen, the average ratio of samples increased in the above regions, and the closer the region was to h, the larger is the increase in the average ratio. For example, a comparison of $\delta =1$and 4 revealed that a larger increase in the ratios led to the greater differences (in region 2: ${\displaystyle \frac{0.222-0.08}{0.08}}=1.775$, while in region 3:${\displaystyle \frac{0.325-0.227}{0.227}}=0.432$). Similar results were obtained for different values of $k$, but for the sake of brevity, these results have not been reported here.

On the basis of the above simple example, we concluded that the RA CUSUM statistics would be likely to become adjacent to h in OC profiles in proportion to $\delta$. In these situations, more plotted statistics could be seen near h when $\delta$ becomes greater. Hence, a comparison of the ratio of samples with some predefined limits according to the definition of different regions can be a practical and effective approach to decrease the time of signalling under an OC condition. Figure 2 provides a clear illustration of the signalling process of a combination of the proposed run rules and the RA CUSUM control chart.

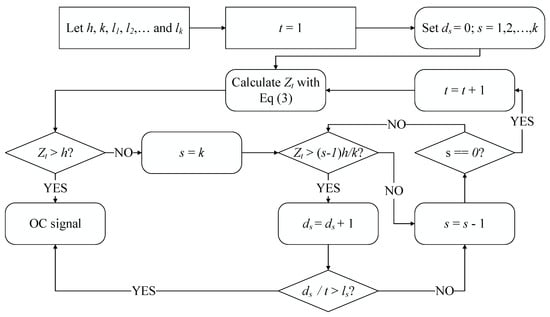
Figure 2. The signalling process of the proposed run rules in combination with RA CUSUM control chart.

3.2. Design Procedure for the Proposed Method

To obtain ARL values in control charts with run rules, two different approaches have been used in the literature. In the first approach, a closed form of ARL based on the Markov chain theorem and a transition matrix has been utilized; for example, [53,54] used this scheme to compute the ARL value. In contrast to the use of this scheme, some researchers, such as [55,56], solved the ARL computation problem with simulation studies based on a combination of run rules and control charts. Although the closed form equation needs fewer computations and less time, it may be very complicated or even insolvable for some forms of run rules; therefore, simulation studies seem to be preferred for some problems instead of the Markov chain approach.

In this study, to reach a predefined ${ARL}_0$, the parameters of the proposed control chart entailing $h,k,l_1,l_2,\dots ,l_{\left(k-1\right)}$ and $l_k$ were adjusted. Because of the complexity of the Markov chain approach, a simulation was used to achieve this aim. However, numerous combinations of the parameters could be found to set ${ARL}_0$ in this approach; therefore, the two following objectives were also necessary in the design procedure. The first one, utilized in the assignment of k, was the same as the fundamental aim of Phase II control charts, i.e., generating minimum ${ARL}_1$ values considering a fixed ${ARL}_0$. As the second guideline, the control chart limits entailing $h, l_1, l_2, \dots , l_{\left(k-1\right)}$ and $l_k$ were designed such that they had nearly similar signalling under the IC condition.

To meet these goals, a heuristic simulation-based procedure was suggested for the adjustment of the parameters of the RA-CUSUM control chart with run rules following these steps. During these steps, the number of regions (k) was augmented step by step, and in each step, h was set at an initial value; the limits varied depending on the above objectives. In this approach, ${ARL}_0^k$ and ${ARL}_1^k$ denote the IC and OC states, respectively, for the proposed method with $k$ regions. We incrementally increase the number of regions $k$ according to our proposed strategy until no tangible improvement in performance is observed. In other words, when adding complexity to the model no longer leads to meaningful gains in detection ability, the iterative process is terminated.

• Step 0: Determine ${ARL}_0$ and some OC shifts (i.e., different values of $\delta$ in Equation (4)).
• Step 1: Set $k=l_1=1$ at the beginning of the design and apply $k=k+1$ until there is no further improvement.
• Step 2: Set an initial value for h with $AR{L}_{0d}$ as follows:

  $$AR{L}_{0d}=AR{L}_0^{ k}$$

  (5)
• Step 3: Generate 10,000 IC samples. Adjust $h, l_2, l_3,\dots , l_{\left(k-1\right)}$ and $l_k$ such that the number of signals for each region becomes nearly the same and the chart has $AR{L}_0$.
• Step 4: Obtain ${ARL}_1^k$ for the OC shifts.
• Step 5: Iterate the process from Step 1 until the relative difference between the $AR{L}_1$ values (${\displaystyle \frac{{ARL}_1^k-{ARL}_1^{k-1}}{{ARL}_1^{k-1}}}$) values is greater than 2%.

Note that the auxiliary variable $AR{L}_{0d}$ in Step 2 is based on the overall false alarm rate ${\alpha }_{overall}$ [9] and offers a good opportunity to accelerate the design process. However, the initial value of h could be set with trial and error. For better illustration, the five steps described above are summarized in Algorithm 2. It is important to note that in the proposed approach, the first region threshold is fixed at l$\le 1$, and the control limit $h$ can be adjusted based on the characteristics of the IC model. This pseudocode provides a clear outline of the heuristic simulation-based procedure for tuning the RA-CUSUM control chart with run rules, including parameter initialization, iterative adjustment, and convergence checking, facilitating reproducibility and practical implementation.

Algorithm 2. Heuristic simulation-based tuning procedure for the RA-CUSUM control chart with run rules

Step 0: Define the parameters including $R_0,R_1,\alpha ,\beta ,\delta :$ Set target $AR{L}_0$ and candidate OC shifts. Step 1: Initialize $k = 1$, $l_1 = 1$. Step 2: While (${\displaystyle \frac{{ARL}_1^k-{ARL}_1^{k-1}}{{ARL}_1^{k-1}}}$) $> 0.02):$          Step 2a: Increment $k: k = k + 1$          Step 2b: Set initial $h = h\_init$ (from $AR{L}_{0d}$ or trial and error)          Step 3:            Generate $N = \mathrm{10,000}$IC samples with fixed random seed            Adjust $h,l_2,l_3,\dots , l_k$ such that:                        - Number of signals in each region is approximately equal                        - $\mathrm{Overall} AR{L}_0$$\approx \mathrm{target} AR{L}_0$          Step 4:               Generate OC samples for $\delta$ and compute $AR{L}_1$          Step 5:               Check convergence:                 If relative difference in ARL1 (${\displaystyle \frac{{ARL}_1^k-{ARL}_1^{k-1}}{{ARL}_1^{k-1}}}$) across OC shifts ≤ 2%, stop                 End While Return final $k, h, l_1, ..., l_k,$ $AR{L}_0$, and $AR{L}_1$;

4. Performance Comparison

4.1. Performance the Proposed Method

To evaluate the effectiveness of the proposed approach, the cardiac surgery dataset from [4] was used. The dataset contains details of 6994 cardiac procedures performed between 1992 and 1998, including surgery date, operating surgeon (seven different surgeons), and the Parsonnet score determined on the basis of age, gender, hypertension, diabetes, renal function, and left ventricular mass. The dataset is available upon request. Equation (6) presents the IC logistic model for the first two years (2218 records):

$$\mathit{log}({\displaystyle \frac{{\pi }_t}{1-{\pi }_t}})=-3.68+0.077x_t.$$

(6)

To establish the above IC model, the responses of the patients with a survival time of at least 30 days after the operation were considered 0; therefore, the IC dataset had 143 deaths (mortality rate equal to 6.45%). All simulation experiments were conducted using a fixed random seed to ensure reproducibility of the results. For the Parsonnet risk scores, samples were drawn directly from the original dataset of [4] using a random sampling approach. Each sample was selected independently, and therefore no temporal dependence was imposed in the simulations. Different simulation setups were applied to the above IC model, and for better illustration, the design process of the first setup is presented in Table 3. In this simulation, as in [22], the value of $AR{L}_0$ was set at 200 with the assumption of $R_1=2R_0=2$. In the design procedure, three magnitudes of shift, namely 1.2, 1.5, and 4, were selected for the $AR{L}_1$ computations. Based on the following results, the proposed design approach was selected as the red row of Table 3 with the parameters of the proposed method or equivalently $k=3, h=2.3, l_1=1, l_2=0.303,$ and $l_3=0.054$. With this tuning, the signalling times of $l_2, l_3$, and $h$ in 10,000 iterations of the IC condition were 3220, 3860, and 2920, respectively. Note that the first row of Table 3 is identical to the third column of Table 2 in [22].

Table 3. Designing of the proposed method in the first simulation setup.

k	$\mathit{A}\mathit{R}{\mathit{L}}_{0\mathit{d}}$	Initial h	Control Limits					$\mathit{\delta }$			$\mathbf{Average} \mathbf{of} \mathit{A}\mathit{R}{\mathit{L}}_0$	Relative Difference (%)
								1.2	1.5	4
1	200	1.51	h	$l_1$	-	-	-	129.6	82.8	20.1	77.5	-
			1.51	1	-	-	-
2	400	1.98	h	$l_1$	$l_2$	-	-	113.53	64.39	14.65	64.19	17.17
			1.79	1	0.195	-	-
3	600	2.32	h	$l_1$	$l_2$	$l_3$	-	109.60	64.30	14.70	62.87	2.06
			2.03	1	0.303	0.054	-
4	800	2.56	h	$l_1$	$l_2$	$l_3$	$l_4$	112.43	61.50	11.65	61.86	1.60
			2.23	1	0.440	0.142	0.021

The performance of the proposed method is evaluated through four different simulations in the following subsections. The design procedure is the same as that presented in the above table and, for the sake of brevity, has not been reported. All the results are based on 10,000 iterations. The proposed method, denoted by CUSUM-RULE, had the following two competitors in the simulations: (i) the CUSUM approach based on [4] and (ii) the EWMA method, which is the same as that implemented in [14] or [28] with the EWMA constant equal to 0.2. Furthermore, the results of the standard deviation of RL (SdRL) are reported in addition to the ARL values.

4.2. ARL and SdRL Values for the First OC Source When ARL₀ Is Equal to 200

Similarly to [22], ARL₀ is set at 200, and the parameters of the proposed method were obtained as k = 3, h = 2.3, $l_1$ = 1, $l_2$ = 0.303, and $l_3$ = 0.054 (see Table 3). We assumed that $R_1 = 2R_0 = 2$. With these setups, Table 3 summarizes the values of ARL and SdRL for different shift magnitudes. The ARL results of CUSUM were those reported in Table 2 in [22], but the EWMA results were based on our simulations.

From Table 4, we inferred that due to their similar underlying structures, the CUSUM and EWMA exhibited almost identical signalling times under OC conditions, which were greater in all of the shifts than in the case of CUSUM-RULE based on ARL. The SdRL results reveal that CUSUM-RULE improved in the cases of large shifts.

Table 4. The results of ARL and SdRL for the first OC source.

$\mathit{\delta }$	CUSUM		EWMA		CUSUM-RULE
	ARL	SdRL	ARL	SdRL	ARL	SdRL
1.0	193.3	181.0	191.8	167.6	201.8	290.0
1.1	157.7	146.5	179.1	157.8	147.0	206.3
1.2	131.0	120.1	157.8	141.7	109.1	139.5
1.3	112.9	99.9	135.8	119.9	86.8	108.4
1.4	95.5	84.4	119.6	104.2	74.0	90.0
1.5	83.3	73.0	104.0	90.7	62.0	72.3
1.6	74.2	63.7	90.6	76.8	54.6	60.5
2.0	51.0	41.1	59.7	48.6	36.4	37.8
2.1	47.4	37.9	54.2	42.4	33.7	33.5
2.2	43.7	34.5	50.4	38.2	31.4	30.7
2.5	36.1	27.3	41.5	30.5	25.8	23.9
3.0	28.7	21.3	32.1	22.3	20.5	17.7
3.2	26.2	18.5	29.3	20.1	19.0	16.2
3.5	23.7	16.5	26.5	17.4	17.3	14.4
4.0	20.4	13.6	22.6	14.7	14.8	11.8

As our proposed method is based on the concept of run rules, it is also interesting to compare its performance with other commonly used run rule schemes. Among the most well-known approaches are the “3 out of 4” and “4 out of 5” rules, which have been employed in [50,54]. In these schemes, a signal is triggered if three out of the most recent four points (3-of-4 rule) or four out of the most recent five points (4-of-5 rule) fall beyond a specified control limit—typically the warning or one-sigma limit—on the same side of the centre line. These methods are designed to enhance the sensitivity of Shewhart-type control charts to small and moderate shifts without substantially increasing the false alarm rate. While effective in conventional SPC applications, such run rule systems depend on discrete counts of consecutive points rather than a continuous evaluation of their distribution. In contrast, our proposed ratio-based approach monitors the proportion of statistics within defined subregions of the control space, providing a smoother and more adaptive sensitivity mechanism. For a fair comparison, both the RA-CUSUM with traditional run rules and our proposed CUSUM-RULE chart were calibrated to have the same $AR{L}_0=200$. The corresponding $AR{L}_1$ and $SdRL$ results are presented in Figure 3.

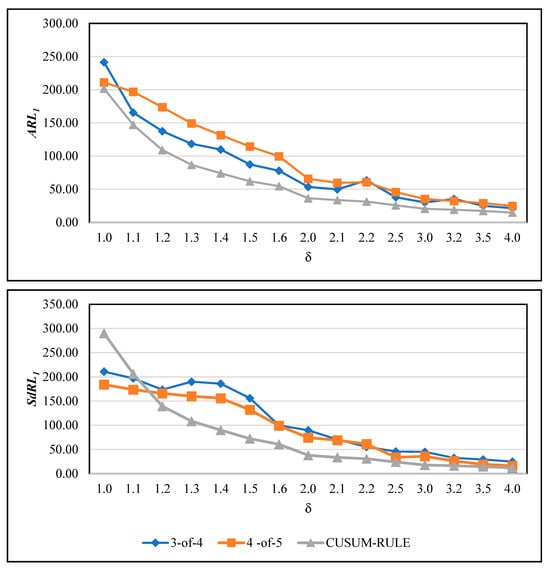
Figure 3. Comparison of the proposed CUSUM-RULE chart with traditional run rule-based RA-CUSUM charts (3-of-4 and 4-of-5 rules).

From Figure 3, the superiority of the proposed method over the two run rule-based competitors is evident in both $AR{L}_1$ and $SdR{L}_1$ values. The only exception occurs under the IC condition, where the competing charts yield slightly lower $SdR{L}_0$ values compared to the CUSUM-RULE chart. Apart from this case, the proposed approach consistently outperforms both the 3-of-4 and 4-of-5 schemes in detection performance. Moreover, the 3-of-4 rule demonstrates better detection capability than the 4-of-5 rule in terms of the $AR{L}_1$ criterion, while their $SdR{L}_1$ values do not remain nearly identical, and 4-of-5 has better performance. The reason for this phenomenon is not entirely clear and may warrant further investigation in future studies.

In memory-based control charts, the samples are not independent, so the RL does not follow a geometric distribution and exhibits heavy tails [57]. For illustration, the maximum RL values across 10,000 simulations ranged from 1919 under the IC condition to 78 for a shift of $\delta =4$. Specifically, under the IC condition, the first (Q1) and third (Q3) quartiles of the RL distribution are 34 and 263, respectively, while for $\delta =4$, they are 6 and 20. These results indicate that the RL distributions under both IC and OC conditions have large tails and are highly skewed rather than symmetric. Notably, the median RL under IC is 100.05, whereas the average ARL₀ is 200, further illustrating the right-skewed nature of the distribution. Although tables reporting the minimum, maximum, Q1, median, and Q3 are available, they are omitted for brevity and can be provided upon request for interested readers.

In the above results, we observe that $SdR{L}_0$ is greater than $AR{L}_0$, whereas in classical Shewhart-type charts, we would typically expect these values to have an approximately equal condition [9]. This difference arises because, in memory-based charts such as the proposed CUSUM-RULE, the run length distribution exhibits heavy tails and greater variability. Large $SdRL$ values imply that detection timing can be more erratic, particularly for small shifts, as signals may occur earlier or later than expected. To better illustrate this behaviour, we computed both $ARL$ and $SdRL$ under various shift magnitudes and plotted operating characteristic (OC) curves showing $AR{L}_1$ versus $\delta$. These curves highlight the trade-off between sensitivity and variability. All control limits and region thresholds were set according to our heuristic design procedure to ensure consistent calibration across experiments. In Figure 4, the $AR{L}_1$ and $SdR{L}_1$ values are shown for three different ARL₀ settings: 500, 600, and 700, to provide a clearer understanding of the chart behaviour. It can be observed that, for all adjustments, $SdR{L}_0$ values are larger than the corresponding $AR{L}_0$, reflecting the variability inherent in memory-based charts. Another notable finding is that, across all Type I error scenarios, both $AR{L}_1$ and $SdR{L}_1$ decrease as the shift magnitude increases, which aligns with the expected behaviour: larger shifts are detected more quickly, increasing the chart’s power. In practical applications, the relatively large $SdR{L}_0$ may pose challenges due to occasional false alarms, which could be addressed in future research to improve stability.

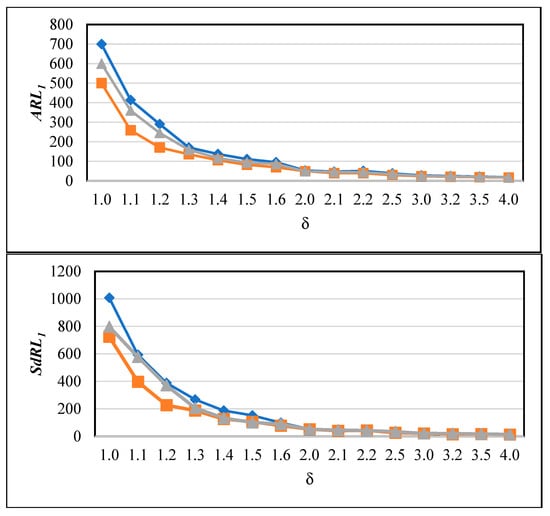
Figure 4. $AR{L}_1$ and $SdR{L}_1$ values of the proposed CUSUM-RULE chart for different ARL₀ settings (500 (orange), 600 (gray), and 700 (blue)) across varying shift magnitudes ($\delta$).

4.3. Simulation Results for the First OC Source When ARL₀ Was Approximately Equal to 7000

To investigate the performance of the CUSUM-RULE with different ARL₀, the calibration approach of [13] was adopted ($R_1$ = 1.5, $R_0$ = 1.5). To reach ARL₀ = 7000 in the CUSUM control chart, h was set at 4.5. With the proposed design approach, the parameters of CUSUM-RULE were obtained as k = 5, h = 5.275, $l_1$ = 1, $l_2$ = 0.36, $l_3$ = 0.185, $l_4$ = 0.0533, and $l_5$ = 0.011. Obtaining the exact ARL₀ for large values proved challenging due to the extended simulation time required. Table 5 reports the first (Q1), second (Q2), and third (Q3) quantiles of run length along with the average, maximum (MAX), and standard deviation values. The CUSUM results for comparison were taken from Table 2 in [13], whereas the EWMA results were based on our simulations.

Table 5. The first (Q1), second (Q2) and third (Q3) quantile of run length in addition to average, maximum (MAX) and standard deviation values when ARL₀ ≈ 7000.

$\mathit{\delta }$	Q1	Q2	ARL	Q3	MAX	SdRL	Method
1.00	2079	4871	6917	9616	77,637	6771	CUSUM
	2041	4869	6919	9600	63,442	6821	EWMA
	118	1042	7445	9278	121,784	13,132	CUSUM-RULE
1.10	1043	2327	3300	4543	22,989	3143	CUSUM
	1025	2301	3262	4473	30,106	3120	EWMA
	80	355	1991	1866	47,385	4017	CUSUM-RULE
1.20	605	1276	1814	2472	14,486	1711	CUSUM
	565	1225	1730	2368	15,772	1655	EWMA
	63	212	747	726	22,178	1475	CUSUM-RULE
1.30	402	806	1104	1497	7729	981	CUSUM
	365	766	1053	1437	9672	963	EWMA
	54	146	379	413	10,983	651	CUSUM-RULE
1.40	292	554	740	988	5958	628	CUSUM
	263	516	703	934	6709	625	EWMA
	46	122	246	292	4554	354	CUSUM-RULE
1.50	224	394	523	689	4721	426	CUSUM
	204	389	518	694	5508	442	EWMA
	40	97	176	224	2256	223	CUSUM-RULE
1.60	188	311	400	519	3045	306	CUSUM
	167	299	394	524	3394	323	EWMA
	34	81	139	179	2508	170	CUSUM-RULE
2.00	112	171	201	256	1084	125	CUSUM
	97	156	190	245	1518	131	EWMA
	24	51	76	102	679	75	CUSUM-RULE
2.10	102	153	178	224	990	107	CUSUM
	88	141	169	217	999	115	EWMA
	21	47	67	90	731	65	CUSUM-RULE
2.20	94	140	162	206	980	96	CUSUM
	80	124	149	191	825	98	EWMA
	21	44	61	83	646	59	CUSUM-RULE
2.50	76	109	123	155	637	67	CUSUM
	64	96	113	143	654	69	EWMA
	18	35	48	64	395	43	CUSUM-RULE
3.00	59	83	90	112	358	43	CUSUM
	49	72	81	103	365	44	EWMA
	13	27	36	49	250	31	CUSUM-RULE
3.20	55	76	83	103	351	39	CUSUM
	45	65	73	92	334	39	EWMA
	13	26	32	44	280	28	CUSUM-RULE
3.50	49	67	72	89	326	32	CUSUM
	41	58	64	80	316	33	EWMA
	11	22	29	39	234	24	CUSUM-RULE
4.00	42	56	61	75	230	26	CUSUM
	35	49	54	68	213	26	EWMA
	10	19	24	33	183	20	CUSUM-RULE

Table 5 shows that CUSUM-RULE exhibited excellent performance for most of the shifts with this adjustment. Furthermore, CUSUM and EWMA showed smaller values of MAX and SdRL when $\delta =$1.1; however, CUSUM-RULE had lower ARL₁ values in the case of this shift. In the case of $\delta =$1.2, CUSUM-RULE had superior performance under all conditions except MAX. Although [13] used large ARL₀ values, setting ARL₀ much larger than 500 is not common practice in SPC. The reason is that calibrating very high ARL₀ values via Monte Carlo simulation requires substantial computational effort and runtime, which is not specific to our approach—other methods face the same challenge. For example, when attempting to set ARL₀ = 7000, the required computation time on our hardware was approximately 200 min for CUSUM and EWMA, and 294 min for the proposed CUSUM-RULE. In contrast, setting ARL₀ = 200 required only about 15, 16, and 18 min for CUSUM, EWMA, and CUSUM-RULE, respectively. Based on these findings, we recommend avoiding extremely large ARL₀ values in Monte Carlo simulations for practical purposes.

4.4. Effect of Beta Distribution on ARL₁ Values for the First OC Source When ARL₀ Is Equal to 100

Note that [19] considered the failure probability in Equation (1) to follow a beta distribution rather than a logistic model. Assuming an IC model of ${\pi }_t$~beta (1,3) and ARL₀ equal to 100, the value of h was determined to be 1.607 for the CUSUM method ($R_1=2=2R_0$); for example, see Table 2 in [19], while the parameters of CUSUM-RULE were set as k = 3, h = 2.07, $l_1$ = 1, $l_2$= 0.32, and $l_3$ = 0.09. In this approach, the OC samples were produced using the same method as that used for the first OC source in Algorithm 1.

CUSUM-RULE’s superior performance over CUSUM and EWMA for different shift sizes, particularly moderate and large, in terms of ${ARL}_1$, is obvious in Table 6. This proved the superiority of the CUSUM-RULE even in the non-logistic models or equivalently, the robustness of the proposed method against the failure probability distribution. However, a weaker performance in terms of ${SdRL}_1$ was still associated with the small shifts.

Table 6. The results of ARL and SdRL for the first OC source when the failure probability was related to the beta distribution.

$\mathit{\delta }$	CUSUM		EWMA		CUSUM-RULE
	ARL	SdRL	ARL	SdRL	ARL	SdRL
1.0	99.29	91.87	103.84	88.72	99.94	138.81
1.1	79.53	70.06	95.78	82.22	71.87	95.40
1.2	66.19	58.75	85.00	70.33	54.14	67.37
1.3	54.32	45.95	73.58	61.65	42.87	51.90
1.4	47.38	40.19	63.26	49.84	37.79	42.20
1.5	41.75	34.41	55.78	43.20	31.34	33.47
1.6	37.09	29.47	48.74	36.36	27.52	28.65
2.0	25.86	19.28	32.78	21.41	19.91	17.48
2.1	24.35	17.52	30.40	19.28	18.52	15.26
2.2	22.74	15.85	28.45	18.05	17.26	14.22
2.5	19.44	13.08	24.39	14.49	15.18	11.33
3.0	16.16	10.26	19.95	10.81	11.72	8.67
3.2	15.04	9.15	18.62	9.91	10.18	8.04
3.5	13.84	8.04	16.99	8.69	9.52	7.22
4.0	12.47	6.96	15.34	7.47	8.59	6.26

4.5. Simulation Results for the Second OC Source When ARL₀ Is Approximately Equal to 400

A further source for OC detection was proposed in [14]. In this situation, the OC data generation was conducted when the IC model $\alpha +\beta x_t$ changed to $\alpha +\beta x_t+\delta$. Ref. [14] omitted the IC model in Equation (6) and assigned ARL₀ value of 400, $\alpha =$−1.386 and $\beta =$0.5. With this IC model and considering $R_1$ = 2$,R_0$ = 2, h was suggested at 2.814 for CUSUM (see Table 1 in [14]). The setup of CUSUM-RULE was as follows: $k = 4$, h = 3.49, $l_1$ = 1, $l_2$= 0.414, $l_3$ = 0.133, and $l_4$ = 0.026. On the basis of the above definition, the results of ${ARL}_0$, ${SdRL}_0$ ($\delta =$0), ${ARL}_1$, and ${SdRL}_1$ are reported in Table 7.

Table 7. The results of ARL and SdRL for the second OC source when ${ARL}_0$ is approximately set at 400.

$\mathit{\delta }$	CUSUM		EWMA		CUSUM-RULE
	ARL	SdRL	ARL	SdRL	ARL	SdRL
0.0	421.11	404.38	412.26	373.93	428.02	678.03
0.1	270.15	251.16	325.63	295.65	203.23	331.13
0.2	181.19	163.24	212.52	176.12	111.76	171.18
0.3	127.35	109.71	145.51	112.76	70.56	94.75
0.4	93.53	76.17	102.23	72.46	49.22	59.69
0.5	71.87	55.77	78.155	51.37	36.96	41.82
0.7	45.17	30.48	50.573	28.36	23.16	22.73
1.0	27.57	15.63	32.1	15.02	14.12	12.37
1.2	21.54	10.93	25.446	11.06	10.90	8.99
1.5	16.22	7.14	19.583	7.34	7.94	6.05
1.8	12.90	4.94	15.613	5.17	6.29	4.54
2.0	11.47	4.02	13.973	4.34	5.42	3.79
2.4	9.58	2.91	11.66	3.08	4.26	2.79
2.8	8.40	2.19	10.24	2.28	3.53	2.14
3.0	7.92	1.88	9.7137	2.02	3.28	1.92

As shown in Table 7, we could reach nearly the same conclusions as those from the previous tables. Except in the cases of $\delta$ = 0.1 and 0.2, where CUSUM had lower SdRL₁ values, CUSUM-RULE outperformed its competitors in terms of the ARL and SdRL.

4.6. Limitations and Future Research Directions

Although this study provides a practical monitoring approach for healthcare patients, it has some limitations. The main limitation is that our method requires complete patient data for accurate risk adjustment. In practice, there may be situations where predictions about future patient outcomes are needed, and monitoring must be performed in real time. Our current approach relies on having the full sample available, which may not always be feasible. Future research could address this limitation by exploring dynamic sampling and monitoring strategies, allowing for real-time updates as patient data become available. Previous studies, such as [58,59], have discussed sampling strategies in healthcare process monitoring, which could provide a foundation for extending the proposed method to more flexible, adaptive frameworks. Additionally, other novel ideas could be integrated into our monitoring framework. For example, combining unsupervised learning techniques [60] with the proposed run rule RA-CUSUM chart may help detect complex or previously unseen patterns. The framework could also be extended to incorporate data from other patient cohorts, such as sepsis screening datasets [61] or ischemia/reperfusion injury datasets [62], to improve its applicability and robustness across different clinical scenarios.

5. Illustrative Example

To demonstrate the practical use of the run rules, a comparison of signalling in real data was conducted using the cardiac surgery dataset from [4] along with the IC model in Equation (6). Considering previous research, we will examine two different setups here.

First, the setup in Section 4.1 (ARL₀ = 200) was utilized to detect the OC situation in the real data reported in Table 6 in [22]. For the sake of brevity, the complete data are not presented here; instead, the new surgeries were considered sequentially until an OC signal was triggered for each method. Figure 5a,b depict the CUSUM statistics (h = 1.51) and CUSUM-RULE statistics (k = 3, h = 2.03, $l_1$ = 1, $l_2$ = 0.303, and $l_3$ = 0.054), respectively. Figure 5a corresponds to Figure 3 in [22].

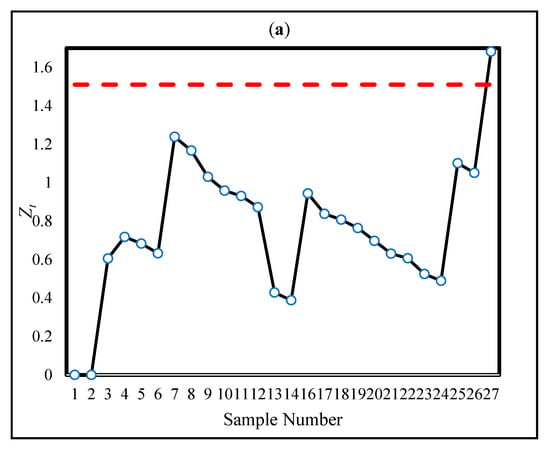
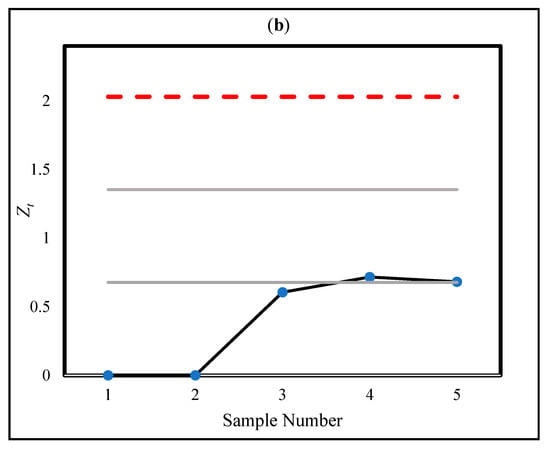
Figure 5. The statistics of CUSUM (a) and CUSUM-RULE (b) approaches in the real data in [22].

Based on our proposed design procedure, the monitoring regions are obtained as (0–0.68], (0.68–1.35], and (1.35–2.03]. The corresponding ratio limits for each region are $l_1=1$, $l_2=0.303$, and $l_3=0.054$. Accordingly, it is necessary to count the number of statistics that fall within each region and compute their ratios relative to the total number of observations. The results of this illustration are provided in Table 8, which summarizes the number of statistics in each region and their corresponding ratios. As shown in Figure 5b, the use of the proposed CUSUM-RULE approach demonstrates superior detection performance as it requires considerably fewer plotted points to detect a process shift compared to the traditional CUSUM chart. For example, in the fifth sample, an OC signal is triggered due to two statistics falling in the second region, resulting in a ratio of ${\displaystyle \frac{2}{5}}=0.4$, which exceeds the corresponding regional limit $l_2=0.303$.

Table 8. The number of statistics that fall within each region and their corresponding ratios using the real dataset from [22].

$\mathit{t}$	${\mathit{d}}_{\mathbf{1}}$	${\mathit{d}}_{\mathbf{2}}$	${\mathit{d}}_{\mathbf{3}}$	${\displaystyle \frac{{\mathit{d}}_{\mathbf{1}}}{\mathit{t}}}$	${\displaystyle \frac{{\mathit{d}}_{\mathbf{2}}}{\mathit{t}}}$	${\displaystyle \frac{{\mathit{d}}_{\mathbf{3}}}{\mathit{t}}}$
1	1	0	0	1	0	0
2	2	0	0	1	0	0
3	3	0	0	1	0	0
4	3	1	0	0.75	0.25	0
5	3	2	0	0.6	0.4	0

For the second adjustment, we followed the analysis in [28] for Surgeon 2, who conducted 330 surgical operations at the surgical centre from 1994 to 1996. Since the outcomes of Surgeon 2 were not included in the IC model in Equation (1) (obtained for 1992–1993 data), they were treated as OC. Ref. [28] applied the CUSUM approach with h = 3.65 (ARL₀ = 2336). Figure 6a illustrates the CUSUM statistics for the 330 operations, showing the OC signal was triggered at the 253rd patient ($Z_{253}$ = 3.968), corresponding to Figure 14.3 in [28].

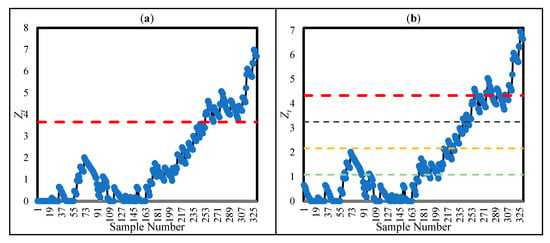
Figure 6. CUSUM (a) and CUSUM-RULE (b) statistics for the 330 surgeries conducted by Surgeon 2.

To reach ARL₀ = 2336, CUSUM-RULE was adjusted as k = 4, h = 4.33, $l_1 = 1, l_2 = 0.34, l_3 = 0.113$, and $l_4$ = 0.016. As shown by Figure 6b, CUSUM-RULE generated a signal at the 246th patient because of the location of four samples in the fourth region $\left({\displaystyle \frac{4}{46}}>0.016\right)$. Hence, CUSUM-RULE could reach the OC situation slightly earlier than CUSUM.

For a better understanding of the first signalling, the ratios of the samples in regions 2, 3, and 4 are depicted in Figure 7 in black, orange, and green, respectively. As can be seen, from the 246th sample, the ratios exceeded the control limit ($l_4$), whereas the other two regions were not able to trigger an OC signal. Moreover, note that $Z_{257}$= 4.527, so the main limit of CUSUM-RULE was able to identify an OC source; however, the first OC signal was more important than the others.

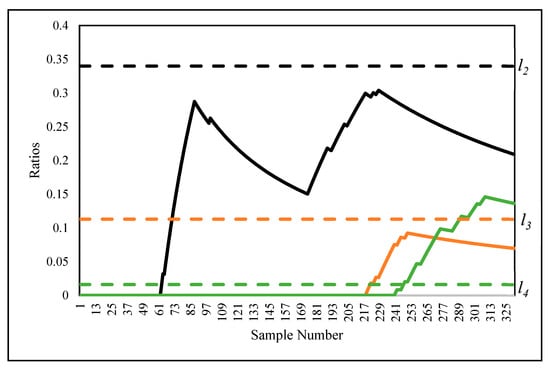
Figure 7. The ratios of the samples in Figure 6b.

6. Conclusions and Recommendations for Future Research

To monitor surgical outcomes, this paper introduces a novel RA control chart, focusing on a predefined logistic regression model where the primary goal is ensuring the relationship between patient covariates and mortality rates remains stable. The core concept of this control chart is to integrate new run rules into a CUSUM chart to detect both IC and OC process conditions. The approach employs a heuristic design algorithm and takes into account specific regions within the control chart.

Extensive simulation studies and an application to real data demonstrated that the proposed control chart outweighed other statistical methods in Phase II. The simulation results revealed smaller values of ARL₁ for the proposed method than for the other existing methods. Furthermore, applying the proposed method to a real cardiac surgery dataset confirmed that the enhanced detection performance of the proposed method extends beyond the simulation studies.

Some novel ideas suggested to extend this work in the future include (i) applying the proposed approach to Phase I, (ii) tracking patient survival durations rather than just binary outcomes, and (iii) conducting an investigation of the control charts other than CUSUM.