Symmetric Folding: An Efficient Method for Accelerating Witness-Based Random Search

Abstract

The performance of witness-based random search algorithms is highly influenced by the distribution density of witnesses. To optimize this distribution, we propose a novel method based on the symmetric folding of the objective dataset. Our approach involves establishing mathematical models for symmetrically folding points and regions in two-dimensional space and deriving a set of rigorously proven properties for folding operations on matrix-formed datasets, complete with computational formulations. Theoretical analysis and numerical experiments demonstrate that the proposed symmetric folding technique can nearly double the probability of successfully identifying a target element via random sampling. The efficacy of the method is validated by a case study on identifying a nontrivial divisor of an odd composite integer, demonstrating that the symmetric folding of the structured dataset can significantly improve the efficiency of randomized search procedures.

1. Introduction

Witness-based random search algorithms gained prominence in the early 1970s owning to their groundbreaking success in addressing problems in number theory, such as primality testing and compositeness certification. Since then, their applications have expanded significantly, spanning diverse domains including decision-making [1,2], data structures [3], network design [4], data mining [5], coding theory [6], data-flow analysis [7], IoT systems [8], cryptography [9], software verification [10], and quantum entanglement research [11].

The efficiency of a witness-based random search algorithm is largely determined by the abundance of witnesses distributed throughout the search space, as established in both classical books (e.g., [12,13,14]) and more recent literature (e.g., [15,16]). Notably, Hromkovič J. emphasized in his seminal work [17] that the concept of witness abundance is a significant gem in the design of randomized algorithms due to its deep connection with nontrivial discoveries in computer science and mathematics.

Given that witnesses are typically dispersed across a large search space that cannot be exhaustively explored [18], enhancing their distribution density constitutes a promising research direction. In light of this consideration, this paper proposes an innovative method to turn sparsely distributed witnesses closer. This method is inspired by the physical act of folding a paper sheet, as illustrated in Figure 1, which demonstrates a paper sheet $\Pi$ is folded to ${\Pi }^{\ast }$ by symmetrically folding. Suppose that several points, referred to as witnesses and marked with blue and red dots, are randomly distributed and affixed to one surface of the paper. When the paper sheet is folded along its axis of symmetry, aligning the two halves precisely, these witnesses are brought into closer proximity. Figure 1 simultaneously shows that folding can not only enhance the local density of the witnesses, but also reduce the gaps between non-witnesses. This is undoubtedly a benefit of witness-based random searches, as gaps can be traversed more quickly and there are more opportunities to encounter a witness.

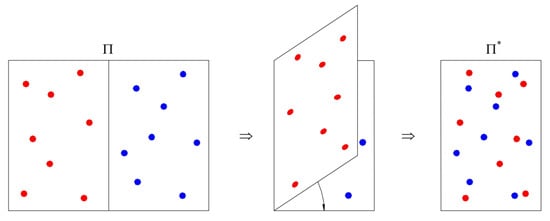
Figure 1. Symmetrical folding brings witnesses into closer proximity.

Inspired by this phenomenon, we introduced the concept of symmetric folding and conducted a preliminary investigation in [19]. However, as an initial exploration, that paper neither provided a comprehensive analysis of the properties of symmetric folding nor established a method for its calculation. This paper hence aims to present a systematic extension and formalization of the study, providing a complete method for symmetrically folding datasets to enhance the efficiency of random search. Through rigorous mathematical reasoning, we derive a set of fundamental properties of symmetric folding, formulate the laws governing the folding process, and prove that symmetric folding can significantly enhance the probability of locating a witness. Furthermore, we apply the principle of symmetric folding to datasets employed in [20,21], showing that search efficiency is considerably improved as a result.

This paper is organized as follows: Section 1 provides an overview of the research context. Section 2 establishes formal definitions and notational conventions. Section 3 synthesizes our main theoretical results, including two theorems, five corollaries, and their corresponding proofs. Section 4 presents application instances. Section 5 concludes the paper by discussing the implications of the findings and suggesting potential directions for future research.

2. Terminologies, Notations, and Definitions

This section presents the necessary symbols, notations, and definitions for subsequent mathematical reasoning.

2.1. Terminologies and Notations

The terms axis symmetry and point symmetry are consistently employed in this work, as defined in standard elementary geometry textbooks such as [22,23,24]. Symbol ${\mathbf{R}}^n$ means n-dimensional real space. Symbol $A\Rightarrow B$ means A can derive B, and $A\iff B$ means A and B can derive each other. Symbol $x\in [a,b]$ means x in interval [a, b]. Symbols $⌊x⌋$ and $⌈x⌉$ are, respectively, the floor and ceiling functions of real x such that $x - 1 < ⌊x⌋ \le x \le ⌈x⌉ < x + 1$, the details of which can be referred to in [25]. Particularly, the following identity (1), which is derived from (3.11) of [25], will be used in the subsequent reasoning.

$$⌈{\displaystyle \frac{⌈x⌉}{m}}⌉=⌈{\displaystyle \frac{x}{m}}⌉$$

(1)

Unless otherwise stated, the term "point" refers to a geometric point, which can be described with coordinates within a coordinate system. Abstract datasets are occasionally represented using specific geometric entities to provide concise descriptions. For example, a strip represents a one-dimensional set with uniformly distributed points, while a sheet denotes a two-dimensional set characterized by uniform distribution. Particularly, a segment is a part of a strip. A segment s starting at x and ending at y is denoted by an expression $s=seg[x,y]$.

For an odd composite integer N with divisors p and q satisfying $2 < p \le q$, any integer smaller than N and sharing a nontrivial common divisor with N is said to be a witness of N’s divisors, or simply a witness of N. Obviously, a divisor of N, p or q, can be obtained by computing the greatest common divisor (GCD) between N and any one of its witnesses.

It is important to note that all sets analyzed in this paper are finite, countable, and planar unless explicitly specified otherwise.

2.2. Definitions

Definition 1

(Symmetric folding of points).  Assume that X and Y are two movable points. If X is moved to the position where Y locates, or conversely, Y is moved to the position where X locates, the two points are said to be superimposed (or overlaid) and denoted by the symbol $X⊻Y$. The operation of moving X to Y is said to be a superimposition of X on (onto) Y, denoted by $X\Rsh Y$, which means that Y is the reference or base. Hence, $Y\Rsh X$ means folding Y on (onto) X. The symmetric folding of two points refers to the superimposition that moves one of the two points to the other with their bisector as the symmetric axis. If ignoring the base, the symmetric folding of X onto Y is denoted by $X\rightleftarrows Y$. Under the meaning of the symmetric folding, X and Y are called symmetric counterparts or mirror images of each other.

By Definition 1, the number of points involved in the symmetric folding must generally exceed one. Although a single point could be symmetric to itself theoretically, this scenario lacks physical and practical significance. Hence, we assume that more than one point is involved in the symmetric folding unless specific theoretical requirements dictate otherwise. Since points are always within a planar region, we have the following Definition 2.

Definition 2

(Symmetric folding of planar regions).  Let Π and ${\Pi }^{\ast }$ be two finite planar regions that have the same shape; the operation that superimposes Π onto ${\Pi }^{\ast }$ to make the two completely coincide is called a superimposition of Π to (onto) ${\Pi }^{\ast }$, denoted by $\Pi \Rsh {\Pi }^{\ast }$, meaning ${\Pi }^{\ast }$ is the base. If ${\Pi }^{\ast }$ is the symmetric counterpart of Π across a mirror axis m, the symmetric folding of Π to (onto) ${\Pi }^{\ast }$ particularly refers to the superimposition that folds each point of Π to (onto) its symmetric counterpart in ${\Pi }^{\ast }$ with respect to m. In this case, ${\Pi }^{\ast }$ is referred to as the base. If ignoring the base, the symmetric folding of Π to ${\Pi }^{\ast }$ is denoted by $\Pi \rightleftarrows {\Pi }^{\ast }$ and simply said to fold Π to ${\Pi }^{\ast }$ along m.

There are a variety of planar regions. However, our interest in this paper is in the symmetric folding of strips and rectangular sheets, as described in Definitions 3 and 4.

Definition 3

(Symmetric folding of strips).  Let $P=\{p_1,p_2,\cdots ,p_n\}$ and $Q=\{q_1,q_2,\cdots ,q_n\}$ be two strips, where n is a positive integer; the symmetric folding of P to (onto) Q, denoted by $P\Rsh Q$, meaning Q is the base, is given by

$$P\Rsh Q = \{p_i\Rsh q_{n+1-i}|1 \le i \le n\}.$$

(2)

If ignoring the base, the symmetric folding of P to Q is simply denoted by $P\rightleftarrows Q$, where P and Q are called symmetric counterparts, or mirror images of each other.

Definition 4

(Symmetric folding of a rectangular sheet). Given a rectangular sheet S with horizontal mirror axis h and vertical mirror axis v, the symmetric horizontal folding of S, denoted by h-fold, folds S along the h-axis; the symmetric vertical folding of S, denoted by v-fold, folds S along the v-axis. Folding S first with an h-fold and then the folded result with a v-fold is denoted by $vh$-fold; folding S first with a v-fold and then the folded result with an h-fold is denoted by $hv$-fold. The $vh$-fold and $hv$-fold are called mixed folds or hybrid folds.

In addition to the coordinates that describe the position (location), a point may also be associated with certain external properties. For instance, it can be marked red or assigned a numerical label. This leads to the following Definition 5.

Definition 5

(Imprint of a point).  An imprint of a point, or simply an imprint, refers to an external property, e.g., a mark or an identifier, associated with the point. A point $P(x,y)$ with an imprint i is referred to as an imprinted point, denoted by $P(x,y,i)$. The imprint of a point can be superimposed by the rule $P(x,y,i_1)⊻P(x,y,i_2)=P(x,y,i_1⊻i_2)$. A strip consisting of imprinted points is an imprinted strip, and a sheet consisting of imprinted points is an imprinted sheet.

Remark 1.

According to Definition 5, an imprinted point may possess more than one imprint. This can be analogized to a colored ball labeled with a number. The concept of the imprint coming into being, a point can either be geometric or imprinted. Regarding the purpose of this paper, the term ’point’ by default refers to the imprint point hereafter. Based on Corollary 2 in [19], when a source point is folded onto a target point, it ceases to exist geometrically while transferring its imprints to the target point. This phenomenon gives rise to the concept of "folding by imprints," formally stated in Definition 6.

Definition 6

(Folding by imprints).  Folding by imprints refers to the folding of an imprinted strip or sheet, emphasizing the transformation of points’ imprints rather than their coordinates.

Remark 2.

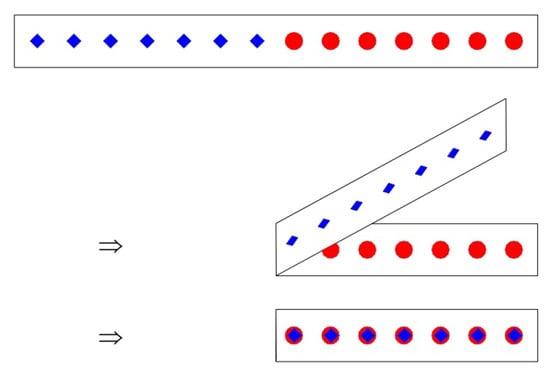
Symmetric folding of two strips, imprints of a point, and folding by imprints can be depicted with Figure 2. In the figure, two different imprints, the blue squares and red circular dots on a trip, are superimposed after performing a symmetric folding on the strip.

Figure 2. Imprints and folding of them.

Imprints can act as witnesses in identifying certain characteristics of points. This derives the following Definition 7.

Definition 7

(Witness by imprint).  If an imprint of a point can be utilized to characterize that point, that imprint is referred to as a witness to the point. In such a case, the point itself is termed a witness point.

The concept of witness by imprint permits the association of a geometric point with a specific value. For instance, we can establish a rule for generating an imprint, say an integer, for each lattice in a planar region, and then determine whether a randomly chosen lattice is associated with a multiple of a prime number. By this means, the problem of identifying a divisor of a composite integer is converted into randomly searching certain lattices in the region, as Section 4 deals with.

3. Theoretical Results

The theoretical results include two theorems and five corollaries, which are stated and proved below.

Theorem 1.

Given n points on a strip, where $n > 0$ is an integer, then for an arbitrary integer $1 \le i \le ⌈{\displaystyle \frac{n}{2}}⌉$, the symmetric folding of the strip superimposes the $i^{th}$ point onto the ${(n + 1 - i)}^{th}$ point or vice versa, resulting in a total of $⌈{\displaystyle \frac{n}{2}}⌉$ distinct overlaid points on the folded strip.

Proof. 

When n is even, let $n = 2k$ with k being an integer; it follows $⌈{\displaystyle \frac{n}{2}}⌉ = k$. Denote the n points by a set

$$S = \{\underset{k ones}{\underbrace{\begin{array}{ccc}{e}_1,& \cdots ,& e_k,\end{array}}}\underset{k ones}{\underbrace{\begin{array}{ccc}{e}_{k+1},& \cdots ,& e_{2k}\end{array}}}\}.$$

(3)

By Definition 3, $e_i$ is symmetric to $e_{n+1-i}$; hence, the symmetric folding results in $e_i⊻e_{n+1-i}$, where $1 \le i \le k$, saying that the theorem holds in the case of n being an even number.

If n is odd, letting $n = 2k + 1$ with k being an integer follows $⌈{\displaystyle \frac{n}{2}}⌉=k+1$ and

$$S = \{\underset{k ones}{\underbrace{\begin{array}{cc}{e}_1,& \cdots ,\end{array}}}{e}_{k+1},\underset{k ones}{\underbrace{\begin{array}{cc}\cdots & e_{2k+1}\end{array}}}\}.$$

(4)

This time, $e_{k+1}$ is symmetric to itself and each element $e_i$ is symmetric to $e_{n+1-i}$ with respect to $e_{k+1}$, where $1 \le i \le k$. Namely, the symmetric folding also results in $e_i⊻e_{n+1-i}$ for $1 ⩽ i ⩽ k + 1$, showing that the theorem holds when n is an odd number. Consequently, the theorem holds in all cases.   □

Corollary 1.

Given n points on a strip, where $n > 0$  is an integer, let $S_0$ be the set of these n points, namely,

$$S_0 = \{ \begin{array}{ccccc}{P}_0^1,& P_0^2,& \cdots ,& P_0^{n-1},& P_0^n\end{array} \},$$

(5)

Assume $S_1$ is the set of the symmetric folding of $S_0$; then,

$$S_1 = \{P_0^i⊻P_0^{n+1-i}|1 ⩽ i ⩽ ⌈{\displaystyle \frac{n}{2}}⌉\}.$$

(6)

Proof. 

This corollary is the alternative statement of Theorem 1.   □

Remark 3.

Let

$$S_l = \{ \begin{array}{ccccc}{P}_0^1,& P_0^2,& P_0^3,& \cdots ,& P_0^{⌈{\displaystyle \frac{n}{2}}⌉}\end{array} \}$$

and

$$S_r = \{ \begin{array}{ccccc}{P}_0^{⌈{\displaystyle \frac{n}{2}}⌉},& P_0^{⌈{\displaystyle \frac{n}{2}}⌉+1},& \cdots ,& P_0^{n-1},& P_0^n\end{array} \};$$

then, (6) says each element $P_1^i \in S_1$ is associated with one element $P_0^i \in S_l$ and one element $P_0^{n+1-i} \in S_r$. Keeping such symmetric folding by partitioning $S_l$ and $S_r$ into their respective symmetric counterparts, each partitioned subset contributes one of its elements to an element in the last folded result. Specifically, every element in the last folded result is associated with a partitioned subset exactly once.

Corollary 2.

Given $2^m$ points on a strip with $m \ge 1$ being an integer, let $S_0$ be the set of these $2^m$ points, namely,

$$S_0=\{ \begin{array}{cccccc}{e}_0^1,& \cdots ,& e_0^{2^{m-1}},& e_0^{2^{m-1}+1},& \cdots ,& e_0^{2^m}\end{array} \}.$$

(7)

Denote $S_k$ to be the set after performing k times of symmetric folding on $S_0$ and $e_k^j$ to be the $j^{th}$ element of $S_k$, where $1 \le k \le m$; then,

$$S_k = \{ \begin{array}{cccccc}{e}_k^1,& \cdots ,& e_k^{2^{m-1}},& e_k^{2^{m-1}+1},& \cdots & e_k^{2^{m-k}}\end{array} \},$$

(8)

where

$$e_k^j = e_{k-1}^j⊻e_{k-1}^{2^{m-(k-1)}+1-j} = \underset{s=0}{\overset{2^{k-1}-1}{⊻}}{e}_0^{2^{m-(k-1)}s+j}\underset{s=1}{\overset{2^{k-1}}{⊻}}{e}_0^{2^{m-(k-1)}s+1-j},$$

(9)

and $1 \le j \le 2^{m-k}$.

Proof. 

By Corollary 1, the symmetric folding of $S_0$ yields

$$S_1=\{e_1^1\begin{array}{ccccc},& e_1^2,& e_1^3,& \cdots ,& e_1^{2^{m-1}}\end{array} \},$$

(10)

where $e_1^j = e_0^j⊻e_0^{2^m+1-j}$ and the index j satisfies $1 \le j \le 2^{m-1}$.

Likewise, the symmetric folding of $S_1$ yields

$$S_2=\{e_2^1\begin{array}{ccccc},& e_2^2,& e_2^3,& \cdots ,& e_2^{2^{m-2}}\end{array} \},$$

(11)

where $e_2^s = e_1^s⊻e_1^{2^{m-1}+1-s}$ and the index s satisfies $1 \le s \le 2^{m-2}$.

Since $e_1^s = e_0^s⊻e_0^{2^m+1-s}$ and $e_1^{2^{m-1}+1-s} = e_0^{2^{m-1}+1-s}⊻e_0^{2^{m-1}+s}$, it follows

$$e_2^s = e_1^s⊻e_1^{2^{m-1}+1-s} = e_0^s⊻e_0^{2^{m-1}+1-s}⊻e_0^{2^{m-1}+s}⊻e_0^{2^m+1-s}.$$

(12)

In general, let $S_k=\left\{e_k^1\begin{array}{ccccc},& e_k^2,& e_k^3,& \cdots ,& e_k^{2^{m-k}}\end{array}\right\}$; then, the symmetric folding of $S_k$ is given by

$$S_{k+1}=\{e_{k+1}^1\begin{array}{ccccc},& e_{k+1}^2,& e_{k+1}^3,& \cdots ,& e_{k+1}^{2^{m-k-1}}\end{array} \},$$

(13)

where $e_{k+1}^t = e_k^t⊻e_k^{2^{m-k}+1-t}$ and the index t satisfies $1 \le t \le 2^{m-k-1}$.

With detail calculations it follows

$$e_{k+1}^t = e_k^t⊻e_k^{2^{m-k}+1-t} = \underset{j=0}{\overset{2^k-1}{⊻}}{e}_0^{2^{m-k}j+t}\underset{j=1}{\overset{2^k}{⊻}}{e}_0^{2^{m-k}j+1-t}.$$

(14)

Comparing (14) with (9) shows that the corollary holds.   □

Remark 4.

It is seen from (14) that $e_{k+1}^t$ is superimposed from $2^{k+1}$ points of $S_0$. Obviously $k+1=m and t=1\Rightarrow e_m^1=e_{m-1}^1⊻e_{m-1}^2$, saying all the $2^m$ points in $S_0$ are superimposed onto the first point after performing m times of symmetric folding. By Corollary 1, m times of symmetric folding also fold all the $2^m$ points onto the last point.

Corollary 3.

Given n points on a strip with n being a positive integer, it takes at least $⌊{log}_{2}n⌋$ and at most $⌊{log}_{2}n⌋+1$ times of symmetric folding to fold all these n points onto the first one or the last one.

Proof. 

If it happens to have an $m\ge 0$ such that $n=2^m$, then Corollary 2 ensures that Corollary 3 holds because $m={log}_{2}n=⌊{log}_{2}n⌋<⌊{log}_{2}n⌋+1$. Otherwise, there must exist a k such that $2^{k-1}<n<2^k$. That is ${\displaystyle \frac{1}{2}}<{\displaystyle \frac{n}{2^k}}<1$ leading to $k-1<{log}_{2}n<k\Rightarrow ⌊{log}_{2}n⌋<k⩽⌊{log}_{2}n⌋+1$. By Theorem 1 and identity (1), k times of the symmetric folding yields $⌈{\displaystyle \frac{n}{2^k}}⌉$ points. Since ${\displaystyle \frac{1}{2}}<{\displaystyle \frac{n}{2^k}}<1\Rightarrow ⌈{\displaystyle \frac{n}{2^k}}⌉=1$, the corollary holds.  □

Corollary 4.

Given $2^{m}n$ distinct points in a strip, where m and n are finite positive integers, then all these $2^{m}n$ points are folded to the first or the last n points after performing m times of symmetric folding one after another.

Proof. 

Let $S_0$ be the $2^{m}n$ points; kept in their original orders, subgroup them into $2^m$ clusters, say $s_0^1,s_0^2,\cdots$, and $s_0^{2^m}$; then, each cluster contains n elements of $S_0$. Namely, $S_0$ can be rewritten by

$$S_0=\left\{\begin{array}{cccc}{s}_0^1,& s_0^2,& \cdots ,& s_0^{2^m}\end{array}\right\}.$$

(15)

Regard each cluster as a point in ${\mathbf{R}}^n$ space; then, by Corollary 2, all the clusters are superimposed onto $s_0^1$ or $s_0^{2^m}$ after performing m times of symmetric folding. This immediately validates Corollary 4.   □

Remark 5.

Referring to (7) and (8), let $S_k=\{s_k^1,s_k^2,\cdots ,s_k^{2^{m-k}}\}$ be the set obtained by k times of symmetric folding of $S_0$ given by (15); then, it follows

$$s_k^j=s_{k-1}^j⊻s_{k-1}^{2^{m-(k-1)}+1-j}=\underset{t=0}{\overset{2^{k-1}-1}{⊻}}{s}_0^{2^{m-(k-1)}t+j}\underset{t=1}{\overset{2^{k-1}}{⊻}}{s}_0^{2^{m-(k-1)}t+1-j},$$

(16)

where $1\le k\le m$ and $1\le j\le 2^{m-k}$.

Corollary 5.

Given a rectangular sheet containing $2^m$ rows and $2^n$ columns, where m and n are finite positive integers, assume $S_{00}$ is the set of points on the sheet, namely,

$$\begin{array}{cc}\hfill S_{00}=& \begin{array}{cccccc}\{e_{0,0}^{1,1}& ,& e_{0,0}^{1,2},& e_{0,0}^{1,3},& \cdots ,& e_{0,0}^{1,2^n},\end{array}\hfill \\ \hfill & \begin{array}{cccccc}{e}_{0,0}^{2,1}& ,& e_{0,0}^{2,2},& e_{0,0}^{2,3},& \cdots ,& e_{0,0}^{2,2^n}\end{array},\hfill \\ \hfill & \cdots \cdots ,\hfill \\ & \begin{array}{cccccc}{e}_{0,0}^{2^m,1}& ,& e_{0,0}^{2^m,2},& e_{0,0}^{2^m,3},& \cdots ,& e_{0,0}^{2^m,2^n}\end{array}\}\hfill \end{array},$$

(17)

Or

$$S_{0,0}=\left\{e_{0,0}^{i,j}\right|1\le i\le 2^m,1\le j\le 2^n\}.$$

Then, the following conclusions (C1),(C2), and (C3) are true.

(C1) For a positive integer k satisfying $1\le k\le m$, let $S_{k\ast }$ be the set after performing k times of h-fold on $S_{00}$ and $e_{k,\ast }^{i,j}$ be its element at the $i^{th}$ row and $j^{th}$ column; then,

$$e_{k,\ast }^{i,j}=e_{k-1,\ast }^{i,j}⊻e_{k-1,\ast }^{2^{m-(k-1)}+1-i,j}=\underset{t=0}{\overset{2^{k-1}-1}{⊻}}{e}_{0,0}^{2^{m-(k-1)}t+i,j}\underset{t=1}{\overset{2^{k-1}}{⊻}}{e}_{0,0}^{2^{m-(k-1)}t+1-i,j},$$

(18)

where $1\le i\le 2^{m-k}$ and $1\le j\le 2^n$.

(C2) For a positive integer l satisfying $1\le l\le n$, let $S_{\ast l}$ be the set after performing l times of v-fold on $S_{00}$ and $e_{\ast ,l}^{i,j}$ be its element at the $i^{th}$ row and $j^{th}$ column; then,

$$e_{\ast ,l}^{i,j}=e_{\ast ,l-1}^{i,j}⊻e_{\ast ,l-1}^{i,2^{n-(l-1)}+1-j}=\underset{t=0}{\overset{2^{l-1}-1}{⊻}}{e}_{0,0}^{i,2^{n-(l-1)}t+j}\underset{t=1}{\overset{2^{l-1}}{⊻}}{e}_{0,0}^{i,2^{n-(l-1)}t+1-j},$$

(19)

where $1\le i\le 2^m$ and $1\le j\le 2^{n-l}$.

(C3) For positive integers k and l satisfying $1\le k\le m$ and $1\le l\le n$, let $S_{kl}$ be the set after performing a symmetric mixed fold on $S_{00}$ by k times of h-fold and l times of v-fold; denote $e_{k,l}^{i,j}$ to be the element at the $i^{th}$ row and $j^{th}$ column of $S_{kl}$; then,

$$e_{k,l}^{i,j}=\underset{t=0}{\overset{2^{k-1}-1}{⊻}}{e}_{0,0}^{2^{m-(k-1)}t+i,j}\underset{t=1}{\overset{2^{k-1}}{⊻}}{e}_{0,0}^{2^{m-(k-1)}t+1-i,j}\underset{t=0}{\overset{2^{l-1}-1}{⊻}}{e}_{0,0}^{i,2^{n-(l-1)}t+j}\underset{t=1}{\overset{2^{l-1}}{⊻}}{e}_{0,0}^{i,2^{n-(l-1)}t+1-j},$$

(20)

where $1\le i\le 2^{m-k}$, and $1\le j\le 2^{m-l}$.

Proof. 

Regarding each row as a point in ${\mathbf{R}}^{2^n}$, (C1) is true by referring to Corollary 2. Likewise, (C2) is true by regarding each column as a point in ${\mathbf{R}}^{2^m}$. With the recursive principle, (C3) is obtained.  □

Remark 6.

By (18), all the rows of $S_{00}$ are superimposed onto the first row after performing m times of h-fold; by(19), all the columns of $S_{00}$ are superimposed onto the first column after performing n times of v-fold; by (20), all the elements of $S_{00}$ are superimposed onto $e_{0,0}^{1,1}$ or $e_{0,0}^{2^m,2^n}$ after performing symmetric mixed folds of $S_{00}$ by k h-folds and l v-folds.

Theorem 2.

The symmetric folding nearly doubles the probability of randomly selecting a witness point in a strip or sheet.

Proof. 

Consider the case of symmetrically folding a strip $S_0$ to $S_1$. Partition $S_0$ into two symmetric halves, say $S_l$ and $S_r$; then, $S_1=S_l\overrightarrow{\leftarrow }{S}_r$. Suppose  S_l contains  w_l witness points, S_r contains  w_r witness points, and  S₀ totally contains  n points. Let p₁ denote the probability of randomly selecting a witness point in S₁, and  p₀ represent the probability of randomly selecting a witness point across S₀. Then, in the case  n is even, say n = 2m, it leads to $p_0={\displaystyle \frac{w_l+w_r}{2m}}$. According to Definitions 1, 3, 5, and Corollary 2 in [20], the number of points on S₁ is reduced to half that on S₀ while the total number of witness points remains unchanged. Hence, $p_1={\displaystyle \frac{w_l+w_r}{m}=2p_0}$.

If n is odd, say n = 2m + 1, the intermediate point, say M, is on the perpendicular bisector. Assume M is not a witness and it belongs to either of $S_l$ and $S_r$; then, $p_1={\displaystyle \frac{w_l+w_r}{m+1}}$ and $p_0={\displaystyle \frac{w_l+w_r}{2m+1}}$. Because ${\displaystyle \frac{w_l+w_r}{m+1}}/{\displaystyle \frac{w_l+w_r}{2m+1}}={\displaystyle \frac{2m+1}{m+1}}\approx 2$, the theorem holds for this case. Likewise, if M is a witness, then $p_0={\displaystyle \frac{w_l+w_r+1}{2m+1}}$ and $p_1={\displaystyle \frac{w_l+w_r+1}{m+1}}$, leading to the same result as the case that M is not a witness.

The case of symmetrically folding a sheet can be proven similarly, showing that the theorem holds.   □

4. Applications for Folding and Searching Rectangular Datasets

Based on the theoretical findings, this section demonstrates the folding of two distinct sheets, denoted as $\Pi$ and ${\Pi }^C$, which were employed in [20] and [21], respectively. These sheets are specifically designed to identify a divisor of an odd composite integer N through the application of the Monte Carlo algorithm. Both sheets exhibit a structural characteristic wherein witnesses are locally accumulated within a large, sparse lattice space, resulting in significant gaps between non-witnesses. Such a configuration can lead to high search efficiency in certain cases but significantly reduced performance in others. For instance, when N comprises 23 decimal digits, the maximum computational time reaches 30,481.30 s, whereas the minimum is recorded at 3054.51 s, as illustrated in the tables in Section 4. This variability stems from the fact that the search process may frequently require extensive time traversing the large gaps between non-witnesses. Since folding has the potential to increase the witness distribution density and simultaneously reduce the gaps between non-witnesses, its application to these sheets is expected to improve search effectiveness. Motivated by this consideration, we investigate the strategies and methodologies for implementing the folding.

4.1. Folding and Searching Dataset $\Pi$

This subsection elaborates on the folding characteristics of $\Pi$, outlines a folding strategy, and proposes a method to implement the folding process.

4.1.1. Structure and Folding Characteristics of $\Pi$

For an odd composite integer N and a parameter g, the dataset $\Pi$ is a lattice set described by

$$\left\{\begin{array}{c}X\in [1,N-p_u]\hfill \\ Y\in [1,g(p_u-p_b-2)+2]\hfill \end{array}\right.,$$

(21)

where $p_b=(N+3)/2$, $p_u=N-1-⌊\sqrt{N}⌋$, and the lattice point $(X,Y)$ is associated with an imprint given by

$${\omega }_{X,Y}=p_u-1-⌊{\displaystyle \frac{Y-2}{g}}⌋.$$

(22)

$\Pi$ is geometrically a rectangular sheet containing $n_{row}=N-p_u=⌊\sqrt{N}⌋+1$ rows and $n_{col}=g(p_u-p_b-2)+2=g((N-1)/2-⌊\sqrt{N}⌋-4)+2$ columns, a total of $n_{row}\times n_{col}$ elements. Expressed with imprints and by (22), each row of $\Pi$ is identical to the others. For example, taking $N=35$ and $g=2$ yields $\Pi$ as shown in Figure 3.

Figure 3. Dataset $\Pi$ generated by $N=35$ and $g=2$.

Using a solid circle • to denote a witness and an empty circle ∘ to denote a non-witness, we have the distribution pattern of witnesses and non-witnesses illustrated in Figure 4, which comes from Figure 3.

Figure 4. Witness and non-witness in $\Pi$ generated by $N=35$ and $g=2$.

Obviously, such a distribution pattern will leave a significant ‘trap’ for a random search, as the search may frequently fall into the big areas occupied by non-witnesses.

Performing one, two, and three times of v-folds on $\Pi$ results in Figure 5, among which Figure 5a has 6 rows and 9 columns, Figure 5b has 6 rows and 5 columns, and Figure 5c has 6 rows and 3 columns. It can be observed that the lattice position of the folded sheet wraps 2, 4, and 8 elements from $\Pi$ with respect to the 1 v-fold, 2 v-folds, and 3 v-folds. Particularly, seen in Figure 5c, each point is associated with at least two witnesses, greatly increasing the probability of finding a witness.

Figure 5. v-folds of $\Pi$ in Figure 4. (a) One v-fold of $\Pi$. (b) Two v-folds of $\Pi$. (c) Three v-folds of $\Pi$.

Referring to (10) in [20], the probability P of randomly selecting a witness in $\Pi$ is estimated by

$$P\approx {\displaystyle \frac{2}{\sqrt{N}-1}}>{\displaystyle \frac{2}{\sqrt{N}}}.$$

(23)

Assume $2^{2(k-1)}<N\le 2^{2k}$; then, by Theorem 2, $k-1$ times of v-fold of $\Pi$ can lead to a significantly big probability to select a witness randomly.

4.1.2. A Strategy for Folding and Searching $\Pi$

For a big N, both $n_{row}$ and $n_{col}$ are large numbers. As observed from (22), rows of $\Pi$ are identical, implying that $\Pi$ is essentially a large sheet consisting of $n_{row}$ duplicated long strips aligned up together. Hence, applying v-folding to an individual strip is computationally more efficient than folding the entire large sheet. Meanwhile, the large value of $n_{row}$ suggests that the number of points in the folded strip will remain substantially high. Therefore, partitioning the long strip into a sequence of smaller segments and utilizing parallel computing techniques to process these segments can improve the computational efficiency. Consequently, performing v-fold on an individual long strip, in conjunction with the parallel technique, constitutes the general strategy for folding and searching $\Pi$.

4.1.3. An Approach for Folding and Searching $\Pi$

There are various styles of folding a long strip. For example, a two-folded folding (symmetric folding) folds it by two halves, a three-folded folding folds it by three parts of equal length, and a multiple-folded folding folds it by more than three parts of equal length, as shown in Figure 6, where the arrows indicate the folding directions and the dashed lines mean the original configurations of the folded parts.

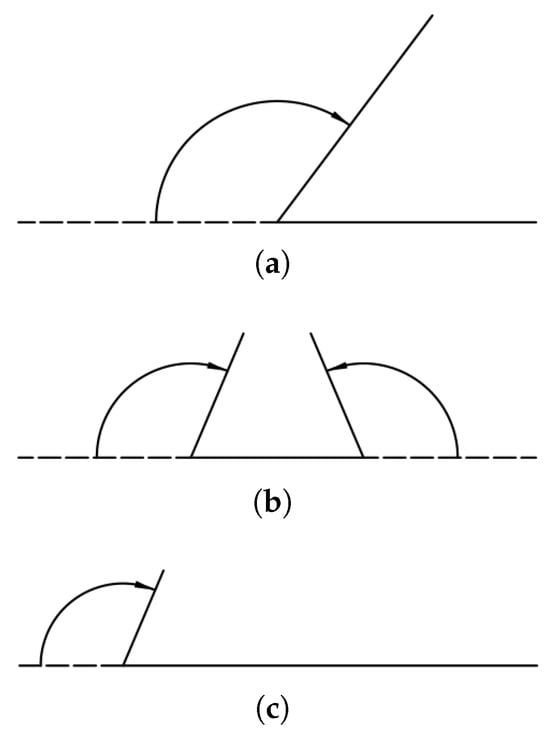
Figure 6. Various folding styles. (a) Two-folded folding. (b) Three-folded folding. (c) Multiple-folded folding.

Herein, we introduce a method that folds a long strip into a specified number of smaller segments and performs synchronized searches on these folded segments. Assume a strip S persists n points; express n in the form $2^{M}W+R$, namely,

$$n=2^{M}W+R,$$

(24)

where M, W, and R are integers such that $M\ge 1$ and $0\le R<W$.

Then S can be partitioned $2^M+1$ segments. Among these segments, the shortest one contains R points, and the remaining $2^M$ ones collectively consist of $2^{M}W$ points. Obviously, each segment can be searched independently by either a parallel or a sequential technique. However, due to the characteristic of witnesses’ local accumulation within a global sparsity, some segments might contain no witnesses. Under such circumstances, folding these segments with v-folding is a reasonable measure to reduce the occurrence of the vanity in the segments. Because the shortest segment contains the fewest points, it can be searched first. If the search does not find an expected result, according to Corollary 4 and Remark 6, for any integer k satisfying $1\le k\le M$, the $2^M$ segments can be folded onto $2^{M-k}$ segments, each containing exactly W points available for further searching.

Let $S_0=\{s_0^1,s_0^2,\cdots ,s_0^{2^M}\}$ be the strip of the $2^M$ segments; assume $S_k=\{s_k^1,s_k^2,\cdots ,s_k^{2^{M-k}}\}$ is the strip obtained after k times of the v-folds of $S_0$; then, it follows by (16)

$$s_k^i=\underset{t=0}{\overset{2^{k-1}-1}{⊻}}{s}_0^{2^{M-(k-1)}t+i}\underset{t=1}{\overset{2^{k-1}}{⊻}}{s}_0^{2^{M-(k-1)}t+1-i}=\underset{t=0}{\overset{2^{k-1}-1}{⊻}}(s_0^{2^{M-(k-1)}t+i}⊻s_0^{2^{M-(k-1)}(t+1)+1-i}),$$

(25)

where $1\le k\le M$ and $1\le i\le 2^{M-k}$.

Assume $Y_0$ is the starting Y-coordinate of $S_0$; then, for an integer j satisfying $1\le j\le 2^M$, the $j^{th}$ segment of $S_0$ is given by

$$s_0^j=seg[Y_0+(j-1)W,Y_0-1+jW].$$

(26)

Accordingly, $s_0^{2^{M-(k-1)}t+i}$ and $s_0^{2^{M-(k-1)}(t+1)+1-i}$ in (25) are, respectively, expressed by

$$s_0^{2^{M-(k-1)}t+i}=seg[s{Y}_1,e{Y}_1]$$

(27)

and

$$s_0^{2^{M-(k-1)}(t+1)+1-i}=seg[s{Y}_2,e{Y}_2],$$

(28)

where $s{Y}_1$, $e{Y}_1$, $s{Y}_2$, and $e{Y}_2$ are calculated by

$$\left\{\begin{array}{c}s{Y}_1=Y_0+(2^{M-(k-1)}t+i-1)W\hfill \\ e{Y}_1=s{Y}_1-1+W\hfill \\ s{Y}_2=Y_0+(2^{M-(k-1)}(t+1)-i)W\hfill \\ e{Y}_2=s{Y}_2-1+W\hfill \end{array}\right..$$

(29)

The three expressions, (25), (27), and (28), exhibit that each segment $s_k^i\in S_k$ is superimposed by $2^k$ segments, where $1\le k\le M$, $0\le t\le 2^{k-1}-1$. Notably, $s_0^{2^{M-(k-1)}t+i}\in S_0$ and $s_0^{2^{M-(k-1)}(t+1)+1-i}\in S_0$ superimpose each other according to the rule defined in Definition 3.

4.2. Folding and Searching Dataset ${\Pi }^C$

This subsection outlines the folding characteristic of ${\Pi }^C$, proposes a method for folding and searching it.

4.2.1. Structure and Folding Characteristics of ${\Pi }^C$

For an odd composite integer N and a parameter g, the dataset ${\Pi }^C$ defined in [21] is mathematically described by

$$\left\{\begin{array}{c}X\in [1,N-p_u]\hfill \\ Y\in [g(N-p_u),g(p_u-p_b-1)+1]\hfill \end{array}\right.,$$

(30)

where $p_b=⌊\sqrt{N}⌋$, $p_u=N-1-⌊\sqrt{N}⌋$, and the imprint of the lattice point $(X,Y)$ is given by

$${\omega }_{X,Y}=p_u+X-⌊{\displaystyle \frac{Y-1}{g}}⌋-1.$$

(31)

${\Pi }^C$ contains $n_{row}=N-p_u$ rows and $n_{col}=g(2p_u-p_b-N-1)+2=g(N-3⌊\sqrt{N}⌋-3)+2$ columns, a total of $(N-p_u)(g(2p_u-p_b-N-1)+2)$ elements. Figure 7 shows the imprints of ${\Pi }^C$ generated by $N=21$ and $g=2$.

Figure 7. Dataset ${\Pi }^C$ generated by $N=21$ and $g=2$.

Seen in [21], ${\Pi }^C$ itself is symmetric with respect to its center and the witnesses in it distribute in a right-down pattern (in the direction parallel to the line $y=gx$), also accumulating locally within global sparsity. Figure 8 depicts the witnesses and non-witnesses in Figure 7.

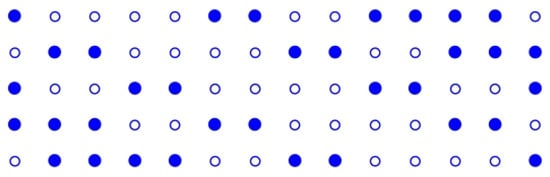
Figure 8. Witness and non-witness in ${\Pi }^C$ of $N=21$ and $g=2$.

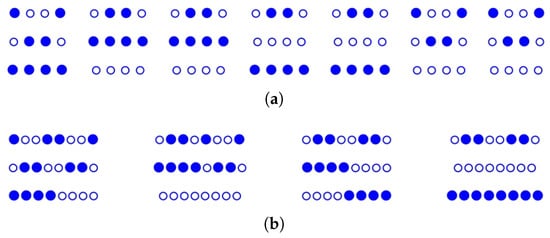
With such a distribution, both v-folds and h-folds are needed to obtain a denser distribution of the witnesses. Take the case of Figure 8 as an example; after an h-fold, it is turned into Figure 9.

Figure 9. Result of folding Figure 8 by an h-fold.

Performing 2 times of v-folds turns Figure 9 into Figure 10a and Figure 10b, respectively. It is seen that the last fold leads to quite a high probability of randomly selecting a point of witness.

Figure 10. v-folds of Figure 9. (a) One v-fold. (b) Two v-folds.

The probability of randomly selecting a witness in ${\Pi }^C$ has been estimated in [21] by

$$P_{{\Pi }^C}^{witness}⩾{\displaystyle \frac{2}{⌊\sqrt{N}⌋+1}},$$

(32)

which is approximately for a large N

$$P_{{\Pi }^C}^{witness}⩾{\displaystyle \frac{2}{\sqrt{N}}}.$$

Hence, for a given N satisfying $2^{2(k-1)}<N\le 2^{2k}$, applying $k-1$ iterations of h-folds or v-folds, or $s+t$ iterations of $hv$-folds, where positive integers s and t satisfy the condition $s+t=k-1$, can significantly increase the probability of randomly selecting a witness.

4.2.2. A Strategy for Folding and Searching ${\Pi }^C$

It has been shown in [19] that one $hv$-fold of ${\Pi }^C$ generates the same resulting sheet as one $vh$-fold, with witnesses distributed in an approximately random manner across the resultant sheet. Meanwhile, the study [26] has proven that the first and last rows contain an identical number of witnesses, and that number is the maximum count across all rows. Based on these findings, a two-step folding and searching strategy is drawn as follows:

(1)

Conduct an h-fold of the last row onto the first row to obtain a folded strip S.

(2)

Fold and search S with the same approach as folding and searching a strip of $\Pi$.

4.2.3. An Approach Folding and Searching ${\Pi }^C$

Because $n_{col}$ is a vast number for a big N, the h-fold of the last row onto the first row requires pre-partitioning the rows into smaller segments, similar to partitioning the long strip of $\Pi$. This can be achieved by still referring to Formula (24).

Consider each of the first and last rows is partitioned into $2^M+1$ segments, among which the shortest one contains R points and the other $2^M$ ones contain collectively $2^{M}W$ points, where $M\ge 1$ and $0⩽R<W$. If the shortest segment is searched without an expected result, let $S_1=\{s_1^1,s_1^2,\cdots ,s_1^{2^M}\}$, $S_L=\{s_L^1,s_L^2,\cdots ,s_L^{2^M}\}$ be the two strips formed by the consecutive segments from the first and last rows, respectively, and $S_0=\{s_0^1,s_0^2,\cdots ,s_0^{2^M}\}$ be the strip folded by the h-fold of $S_L$ onto $S_1$; then,

$$s_0^j=s_L^j\Rsh s_1^j=s_L^j⊻s_1^j,$$

(33)

where the superscript j ranges from 1 to $2^M$.

Denote $S_k=\{s_k^1,s_k^2,\cdots ,s_k^{2^{M-k}}\}$ to be the strip from $S_0$ being symmetrically folded by k times; it follows

$$\begin{array}{ccc}\hfill s_k^i& =& \underset{t=0}{\overset{2^{k-1}-1}{⊻}}(s_0^{2^{M-(k-1)}t+i}⊻s_0^{2^{M-(k-1)}(t+1)+1-i})\hfill \\ & =& \underset{t=0}{\overset{2^{k-1}-1}{⊻}}(s_L^{2^{M-(k-1)}t+i}⊻s_L^{2^{M-(k-1)}(t+1)+1-i}⊻s_1^{2^{M-(k-1)}t+i}⊻s_1^{2^{M-(k-1)}(t+1)+1-i})\hfill \end{array},$$

(34)

where the superscript k satisfies $1\le k\le M$ and i ranges from 1 to $2^{M-k}$.

Formula (34) indicates that $s_k^i$ is superimposed by $2^{k+1}$ segments, half from $S_1$ and half from $S_L$. Still use $Y_0$ to be the starting Y-coordinate of $S_0$; referring to (26) and (27) follows

$$s_1^{2^{M-(k-1)}t+i}=seg[s{Y}_{1,1},e{Y}_{1,1}],$$

(35)

$$s_L^{2^{M-(k-1)}t+i}=seg[s{Y}_{L,1},e{Y}_{L,1}],$$

(36)

$$s_1^{2^{M-(k-1)}(t+1)+1-i}=seg[s{Y}_{1,2},e{Y}_{1,2}],$$

(37)

and

$$s_L^{2^{M-(k-1)}(t+1)+1-i}=seg[s{Y}_{L,2},e{Y}_{L,2}],$$

(38)

where the superscript t ranges from 0 to $2^{k-1}-1$ and

$$\left\{\begin{array}{c}s{Y}_{1,1}=Y_0+(2^{M-(k-1)}t+i-1)W\hfill \\ e{Y}_{1,1}=s{Y}_{1,1}-1+W\hfill \\ s{Y}_{L,1}=Y_0+(2^{M-(k-1)}t+i-1)W\hfill \\ e{Y}_{L,1}=s{Y}_{L,1}-1+W\hfill \\ s{Y}_{1,2}=Y_0+(2^{M-(k-1)}(t+1)-i)W\hfill \\ e{Y}_{1,2}=s{Y}_{1,2}-1+W\hfill \\ s{Y}_{L,2}=Y_0+(2^{M-(k-1)}(t+1)-i)W\hfill \\ e{Y}_{L,2}=s{Y}_{L,2}-1+W\hfill \end{array}\right..$$

The Formulas (35)–(38) show that the search on $s_k^i$ is converted into the searches on the corresponding segments of $S_1$ and $S_L$.

4.3. Superimposing $\Pi$ on ${\Pi }^C$ and Searching It

Restrict X and Y by

$$\left\{\begin{array}{c}X\in [1,N-p_u]\hfill \\ Y\in [g(N-p_u),g(p_u-p_b-2)+2]\hfill \end{array}\right..$$

(39)

Then, $\Pi$ and ${\Pi }^C$ contain the same number of rows and columns for a given $p_b$, and thus the two can be superimposed on each other. Denote the superimposed result with the symbol $\Xi$, namely, $\Xi =\Pi ⊻{\Pi }^C$; then, the witnesses in $\Xi$ are more than in either $\Pi$ or ${\Pi }^C$. Figure 11 exhibits the witnesses and non-witnesses within $\Xi$ that are produced by taking $N=35$, $g=2$ and $p_b=⌊\sqrt{N}⌋$. This time, utilizing on $\Xi$ the SPRSA searching method introduced in [20] generally brings a higher efficiency than on ${\Pi }^C$.

Figure 11. Witnesses and non-witnesses in $\Xi$ by $N=35$ and $g=2$.

4.4. Numerical Experiments

Numerical experiments were conducted using computers equipped with an Intel(R) Core(TM) i5-10500 CPU @ 3.10 GHz, 16 GB of RAM, and the Windows 10 operating system, implemented in Python 3. The experimental data were sourced from [20,21], originally presented in [27]. The results are summarized in Table 1, Table 2, Table 3, Table 4 and Table 5. In these tables, the column labeled “Integer N” denotes the semi-prime integers to be factored; the “Digits” column indicates the number of decimal digits in N; “Time 1” represents the computational time reported in [20]; “Time 2” corresponds to the time reported in [21]; “Time 3” is the time after folding $\Pi$; “Time 4” is the time after folding ${\Pi }^C$; and “Time 5” refers to the time after superimposing $\Pi$ onto ${\Pi }^C$. All the times are measured in seconds, and the Monte Carlo search method was employed throughout, consistent with the approach used in [20,21]. The results demonstrate that folding and superimposing operations yield improved computational efficiency, thereby supporting the theoretical analysis.

Table 1. Comparison of Time Consumption in Group 1.

Integer N	Digits	Time 1	Time 2	Time 3	Time 4	Time 5
10,909,343	8	3.54	2.66	0.38	0.30	0.23
29,835,457	8	2.63	1.97	0.19	0.29	0.22
392,913,607	9	3.59	2.69	0.26	0.17	0.13
5,325,280,633	10	2.37	1.78	0..32	0.18	0.14
42,336,478,013	11	2.38	1.79	0.45	0.26	0.20
272,903,119,607	12	2.12	1.59	1.05	0.27	0.20
11,683,458,677,563	14	5.15	3.86	0.39	0.30	0.23
51,790,308,404,911	14	3.73	2.80	0.46	0.45	0.34
115,137,038,087,959	15	3.65	2.74	0.58	0.60	0.45
8,335,465,900,089,539	16	3.30	2.48	15.66	1.64	1.23
10,380,088,039,872,631	17	13.04	9.78	8.57	2.23	1.67
253,422,413,591,685,001	18	31.66	23.75	8.60	1.29	0.97
1,160,633,764,479,964,633	19	52.60	39.45	9.72	1.45	1.09
31,625,125,947,164,338,313	20	192.09	144.07	10.25	1.91	1.43
454,367,322,351,811,534,933	21	329.11	246.83	22.55	4.12	4.09
4,500,000,514,520,012,390,279	22	1875.85	1406.89	45.95	15.83	13.87
26,785,956,134,870,280,125,273	23	10,118.36	7588.77	168.75	76.05	67.04

Table 2. Comparison of Time Consumption in Group 2.

Integer N	Digits	Time 1	Time 2	Time 3	Time 4	Time 5
12,654,529	8	3.02	2.27	0.29	0.35	0.26
369,717,133	9	2.87	2.15	0.27	0.36	0.27
1,897,440,553	10	2.57	1.93	0.24	0.35	0.26
52,739,663,177	11	6.00	4.50	0.56	0.35	0.26
130,713,369,233	12	2.14	1.61	0.25	0.36	0.27
6,748,770,789,473	13	3.37	2.53	0.27	0.37	0.28
11,524,840,919,477	14	2.58	1.94	0.37	0.37	0.28
430,485,039,573,419	15	5.23	3.92	1.53	1.14	0.86
1,955,733,632,904,137	16	6.43	4.82	4.84	4.68	3.51
30,217,484,037,846,601	17	5.79	4.34	8.41	3.23	2.42
266,941,704,466,880,371	18	4.87	3.65	8.96	3.25	2.44
2,166,633,888,615,295,159	19	31.86	23.90	9.95	3.56	2.67
22,756,653,803,671,245,041	20	97.06	72.80	21.29	3.80	2.85
413,222,670,126,548,323,081	21	397.38	298.04	22.31	11.75	8.81
1,503,913,043,740,073,215,127	22	861.5	646.13	33.95	18.95	14.22
23,208,481,761,499,119,809,917	23	3054.51	2290.88	92.26	64.89	48.67

Table 3. Comparison of Time Consumption in Group 3.

Integer N	Digits	Time 1	Time 2	Time 3	Time 4	Time 5
11,157,067	8	2.21	1.66	0.29	0.35	0.29
383,910,353	9	3.37	2.53	0.24	0.35	0.24
1,438,236,853	10	2.54	1.91	0.34	0.34	0.34
59,495,473,109	11	2.37	1.78	0.35	0.36	0.35
204,338,073,419	12	1.75	1.31	0.67	0.66	0.67
4,075,254,216,277	13	3.17	2.38	0.36	0.35	0.36
16,522,992,841,517	14	2.33	1.75	0.39	0.40	0.39
415,613,171,542,577	15	3.40	2.55	1.22	1.23	1.22
2,130,887,677,054,559	16	19.12	14.34	5.07	1.05	1.07
31,043,832,317,143,097	17	7.65	5.74	8.80	1.21	1.80
209,495,243,841,913,543	18	14.38	10.79	7.99	1.25	1.99
4,082,205,679,196,499,709	19	6.14	4.61	9.34	1.68	2.34
33,019,716,065,589,397,447	20	597.08	447.81	32.28	2.77	2.28
450,574,758,051,764,161,729	21	397.38	298.04	43.81	1.71	3.81
1,878,613,353,066,239,152,189	22	2069.93	1552.45	46.03	19.71	16.03
27,913,133,719,399,938,961,837	23	7894.19	5920.64	48.06	12.60	48.06

Table 4. Comparison of Time Consumption in Group 4.

Integer N	Digits	Time 1	Time 2	Time 3	Time 4	Time 5
13,414,967	8	2.96	2.22	0.36	0.34	0.36
331,451,893	9	2.76	2.07	0.35	0.35	0.35
1,933,146,287	10	3.28	2.46	0.34	0.37	0.34
61,376,888,039	11	4.50	3.38	0.35	0.35	0.35
221,449,201,327	12	2.93	2.20	0.99	0.68	0.99
8,356,391,888,797	13	4.00	3.00	0.37	0.37	0.37
10,503,658,570,897	14	3.89	2.92	0.37	0.39	0.37
530,802,693,107,327	15	3.66	2.75	3.03	1.53	1.03
1,571,847,149,341,363	16	5.63	4.22	3.59	1.04	1.59
30,266,236,030,889,197	17	7.30	5.48	9.19	1.09	1.19
227,020,160,422,765,063	18	28.62	21.47	8.67	2.16	1.67
7,632,766,872,780,422,213	19	21.16	15.87	7.601	2.36	1.60
28,518,585,380,150,198,561	20	171.77	128.83	10.62	1.91	2.62
549,438,783,354,451,709,261	21	809.52	607.14	22.11	2.55	12.11
1,885,102,352,659,402,618,003	22	1827.62	1370.72	79.39	3.79	39.39
21,852,468,492,088,577,490,449	23	5153.08	3864.81	90.91	58.10	90.91

Table 5. Comparison of Time Consumption in Group 5.

Integer N	Digits	Time 1	Time 2	Time 3	Time 4	Time 5
11,427,677	8	1.81	1.36	0.35	0.35	0.26
405,031,259	9	1.34	1.01	0.34	0.32	0.24
1,354,177,351	10	2.03	1.52	0.36	0.33	0.25
61,111,357,501	11	2.14	1.61	0.33	0.33	0.25
190,838,622,707	12	1.88	1.41	0.39	0.39	0.29
3,856,534,651,811	13	2.98	2.24	0.46	0.35	0.26
15,286,768,369,531	14	1.41	1.06	0.38	0.34	0.26
450,109,181,452,867	15	6.94	5.21	1.20	0.21	0.16
1,317,487,523,002,697	16	2.46	1.85	3.27	0.21	0.16
31,042,285,010,899,441	17	4.01	3.01	15.25	1.04	0.78
218,532,124,445,731,211	18	3.53	2.65	8.63	1.53	1.15
8,202,929,148,558,584,683	19	111.63	83.72	8.52	2.56	1.92
24,120,674,285,926,579,159	20	218.28	163.71	20.42	1.56	1.17
464,395,777,895,275,578,169	21	715.56	536.67	38.71	3.47	2.60
1,789,550,188,834,786,401,307	22	6229.76	4672.32	46.03	29.6	30.2
29,891,632,748,859,892,878,863	23	30,481.30	22,860.98	70.19	21.53	18.15

4.5. More Application Scenarios

The method of symmetric folding can be applied to more scenarios than just identifying a divisor of a composite integer, which is an essential topic in cryptography. Since the folding operations are actually performed on the indices of the elements in a matrix-formed dataset, as expressed in the formulations (5)–(20), the method can be generally applied to any countable, structured dataset. Here are some examples.

• Blind search issue. A blind search searches for objectives within a restricted area without previously assigning information about them. A concrete example of such a search is fault diagnosis in industry, such as detecting the fault spot within a material through data analysis, identifying the faulty component in a large-scale integrated circuit, and so on. Those detections are always performed with an embedded diagnosis system. By structuring the source data, folding can improve the computational efficiency of the system.
• Database issue. A database is a structured repository for storing and frequently accessing large volumes of data. Each database can be conceptualized as a sheet composed of rows and columns. According to Remarks 4 and 6, applying k iterations of symmetric folding results in a single cell in the folded sheet corresponding to $2^k$ distinct cells in the original database. As a result, querying a single cell in the folded sheet provides simultaneous access to $2^k$ cells in the original database, thereby significantly improving search efficiency.
• Engineering optimization issue. Engineering optimization constantly searches for a solution in a large computational domain. Partitioning the domain first and then folding the partitioned result, as we do with $\Pi$ and ${\Pi }^C$, can lead to multiple subdomains being synchronically searched, thus enhancing computational efficiency.

5. Conclusions and Future Work

Based on the physical principle that symmetric folding can bring points on a paper sheet closer together, we have developed mathematical models for symmetrically folding a dataset represented in matrix form and have formulated the corresponding computational procedures. Since this folding process both increases the density of witnesses and reduces the gaps between non-witnesses, a witness-based randomized approach can either efficiently identify a witness or rapidly traverse a non-witness, thereby improving overall search efficiency. The mathematical analysis, grounded in an abstract countable dataset, ensures that our theoretical results and computational formulations can be applied to any arbitrary finite countable dataset. Although our practical examples demonstrate the method by identifying a divisor of an odd composite integer, our framework remains general.

Nevertheless, certain aspects remain for future investigation, such as the development of random search algorithms on two-dimensional regions formed through multiple hybrid folding operations and how such techniques further enhance random search efficiency. Furthermore, researches on multi-dimensional folding, finding a optimal folding sequence, and folding an irregular dataset also challenge our future work. We hope that more young researchers will engage in this area to produce even deeper and more valuable results.