Planar Graphs Without 4-Cycles Are (6, 6)-Colorable

Abstract

It has been shown that there is a planar graph without 3-cycles which is not $({\Delta }_1,{\Delta }_2)$-colorable for any given ${\Delta }_1,{\Delta }_2$. This inspires many research to obtain sufficient conditions for planar graphs without 4-cycles and other cycles to be $({\Delta }_1,{\Delta }_2)$-colorable. For example, planar graphs without k-cycles and 4-cycles are $({\Delta }_1,{\Delta }_2)$-colorable for each $k\in \{3,5\}$ and $({\Delta }_1,{\Delta }_2)=\{(2,6),(3,4)\}$. In this work, we study the values of ${\Delta }_1$ and ${\Delta }_2$ that make a planar graph without only 4-cycles $({\Delta }_1,{\Delta }_2)$-colorable. We begin with ${\Delta }_1=6$ and ${\Delta }_2=6$. Planar graphs without 4-cycles are $(6,6)$-colorable. Two colors in a $({\Delta }_1,{\Delta }_2)$-coloring, where ${\Delta }_1={\Delta }_2$ are switchable, thus reflect the symmetry of the resulting coloring. Furthermore, some proof techniques are using the symmetry of these two colors.

1. Introduction

Cowen et al. [1], Andrews and Jacobson [2], and Harary and Jones [3] independently defined an improper coloring (also known as a defective coloring or a relax coloring).

Let ${\Delta }_1,{\Delta }_2,\dots ,{\Delta }_l$ be l nonnegative integers. A $({\Delta }_1,{\Delta }_2,\dots ,{\Delta }_l)$-coloring of a graph G is an l-coloring where an induced subgraph of vertices in G that are colored with color i has maximum degree at most ${\Delta }_i$ for each $i\in \{1,2,\dots ,l\}$. If a graph G has a $({\Delta }_1,{\Delta }_2,\dots ,{\Delta }_l)$-coloring, then a graph G is a $({\Delta }_1,{\Delta }_2,\dots ,{\Delta }_l)$-colorable.

If we have ${\Delta }_1={\Delta }_2=\dots ={\Delta }_l=0$, then a $({\Delta }_1,{\Delta }_2,\dots ,{\Delta }_l)$-coloring is a proper l-coloring. This means a defective coloring generalizes a proper coloring. The Four Color Theorem, introduced by Appel and Haken [4,5], states that planar graphs are $(0,0,0,0)$-colorable. This is one approach to repeat the Four Color Theorem.

Let $k_1,k_2,\dots ,k_l$ be l distinct nonnegative integers. We obtain $\mathbb{G}$, a class of planar graphs, and ${\mathbb{G}}_{k_1,k_2,\dots ,k_l}$, a class of planar graphs, without $k_1$-cycles, $k_2$-cycles, …, and $k_l$-cycles. We will use these definitions to simplify the writing throughout the entire article.

For the use of three colors in planar graphs, it is well-known that some graphs in $\mathbb{G}$ are not $(0,0,0)$-colorable, but each graph in $\mathbb{G}$ is $(2,2,2)$-colorable and each graph in ${\mathbb{G}}_3$ is $(0,0,0)$-colorable by Grötzsch [6]. Steinberg posed the question that each graph in ${\mathbb{G}}_{4,5}$ is $(0,0,0)$-colorable. Many researchers have tried to tackle this problem; see that graph G is $(0,0,0)$-colorable when $G\in {\mathbb{G}}_{4,5,6,7}$ [7], $G\in {\mathbb{G}}_{4,6,8}$ [8] or $G\in {\mathbb{G}}_{4,6,9}$ [9]. Moreover, in the study of defective coloring, each graph in ${\mathbb{G}}_{4,5}$ is $(2,0,0)$-colorable [10] or $(1,1,0)$-colorable [11]. Afterwards, Cohen-Addad et al. [12] provided an example of a non-$(0,0,0)$-colorable graph in ${\mathbb{G}}_{4,5}$. This raises a new question: is each graph in ${\mathbb{G}}_{4,5}$$(1,0,0)$-colorable? Unfortunately, this question remains open. One of the closest known results was shown in 2022 by Kang et al., demonstrating that each graph in ${\mathbb{G}}_{4,6}$ is $(1,0,0)$-colorable [13].

For the use of two colors in planar graphs, in the case of a graph in ${\mathbb{G}}_3$, Montassier and Ochem [14] provided an example of a graph in ${\mathbb{G}}_3$ such that it is not $({\Delta }_1,{\Delta }_2)$-colorable for any ${\Delta }_1$ and ${\Delta }_2$. Additionally, Borodin et al. [15] gave an example of a graph in ${\mathbb{G}}_{3,4,5}$ such that it is not $(0,{\Delta }_2)$-colorable for any ${\Delta }_2$ and showed that a graph in ${\mathbb{G}}_{3,4}$ is $(2,6)$-colorable. Choi et al. [16] showed that a graph in ${\mathbb{G}}_{3,4}$ is $(3,4)$-colorable and Li et al. [17] showed that a graph in ${\mathbb{G}}_{3,4}$ is $(1,9)$-colorable, which improved many previous results.

For the use of two colors in planar graphs, in the case of a graph ${\mathbb{G}}_4$, a graph in ${\mathbb{G}}_{4,5}$ was first studied. In 2018, Sittitrai and Nakprasit [18] provided an example of a graph in ${\mathbb{G}}_{4,5}$ that is not $(1,{\Delta }_2)$-colorable for any ${\Delta }_2$. They showed that a graph in ${\mathbb{G}}_{4,5}$ is $({\Delta }_1,{\Delta }_2)$-colorable when $({\Delta }_1,{\Delta }_2)\in \{(2,9),(3,5),(4,4)\}$. Later, Liu and Lv [19] and Cho et al. [20] improved this result by showing that a graph in ${\mathbb{G}}_{4,5}$ is $(2,6)$-colorable and $(3,4)$-colorable, respectively. Now, we know that a graph in ${\mathbb{G}}_{4,5}$ is $(3,3)$-colorable, as demonstrated independently by Liu and Xiao [21] and Li et al. [22]. In conclusion, the strongest current results on 2-defective coloring for a graph in ${\mathbb{G}}_{4,5}$ are $(2,6)$- and $(3,3)$-coloring which complement each other. It is still unknown if the result on $(2,6)$-coloring can be extended to $(2,k)$-coloring where $k\le 5.$ Furthermore, if $k\le 2,$ then the extension would also improve the result on $(3,3)$-coloring. Note that it is not known if there exists k such that every graph in ${\mathbb{G}}_{4,5}$ is $(1,k)$-colorable.

A graph in ${\mathbb{G}}_{4,k}$, where $k\ge 6$, was studied in the same way as a graph in ${\mathbb{G}}_{4,5}$. For example, a graph in ${\mathbb{G}}_{4,6}$ is shown to be $(2,9)$-colorable and $(3,4)$-colorable by Ma et al. [23] and Nakprasit et al. [24], respectively. In addition, a graph in ${\mathbb{G}}_{3,4,6}$ is $(0,6)$-colorable and $(3,3)$-colorable by Dross and Ochem [25] and Sittitrai and Pimpasalee [26], respectively. To make it easier for readers, we have summarized the results in Table 1.

Table 1. Results for Defective 2-Coloring of Planar Graphs with Forbidden Cycles.

Forbidden Cycles on Planar Graphs	$({\mathbf{\Delta }}_1,{\mathbf{\Delta }}_2)$-Colorable	Sources
Only $C_3$	None	Montassier and Ochem [14]
$C_3,C_4$	None of $(0,{\Delta }_2)$	Borodin et al. [15]
	$(1,9)$	Li et al. [17]
	$(2,6)$	Borodin and Kostochka [27]
	$(3,4)$	Choi et al. [16]
	$(3,5)$	Choi et al. [28]
$C_4,C_5$	None of $(0,{\Delta }_2)$	Borodin et al. [15]
	$(2,9),(3,5),(4,4)$	Sittitrai and Nakprasit [18]
	$(2,6)$	Liu and Lv [19]
	$(3,4)$	Cho et al. [20]
	$(3,3)$	Liu and Xiao [21] and Li et al. [22]
$C_4,C_6$	$(2,9)$	Ma et al. [23]
	$(3,4)$	Nakprasit et al. [24]
$C_3,C_4,C_5$	None of $(0,{\Delta }_2)$	Borodin et al. [15]
$C_3,C_4,C_6$	$(0,6)$	Dross and Ochem [25]
	$(3,3)$	Sittitrai and Pimpasalee [26]
Only $C_4$	$(6,6)$	This work

It can be observed that research identifying the values of ${\Delta }_1$ and ${\Delta }_2$ to make a planar graph $({\Delta }_1,{\Delta }_2)$-colorable typically focuses on planar graphs without $k_1$-cycles, $k_2$-cycles, …, and $k_q$-cycles where $q\ge 2$ and some $i\in \{1,2,\dots ,q\}$, $k_i=4$. This leads us to study the values of ${\Delta }_1$ and ${\Delta }_2$ that make a planar graph without only 4-cycles that are $({\Delta }_1,{\Delta }_2)$-colorable.

Theorem 1.

If $G\in {\mathbb{G}}_4,$ then G is $(6,6)$-colorable.

The values of ${\Delta }_1={\Delta }_2=6$ reflect the symmetry of the coloring in Theorem 1 since two colors are switchable. To the best of our knowledge, this is the first result that forbids only a single cycle length on planar graphs providing $({\Delta }_1,{\Delta }_2)$-colorability.

Note that the converse of Theorem 1 does not hold. For instance, consider the planar graph depicted in Figure 1, which is $(6,6)$-colorable but contains a 4-cycle; hence, it does not belong to ${\mathbb{G}}_4$. In contrast, Figure 2 illustrates a planar graph without 4-cycles that satisfies the conditions of Theorem 1 with its $(6,6)$-coloring.

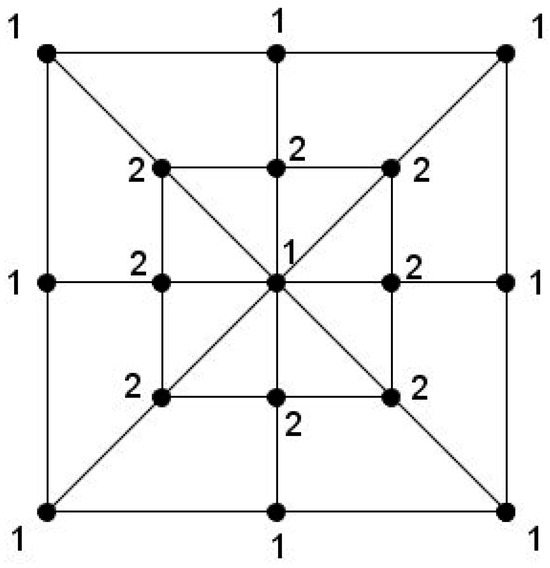
Figure 1. A $(6,6)$-colorable planar graph containing a 4-cycle, showing that the converse of Theorem 1 does not hold.

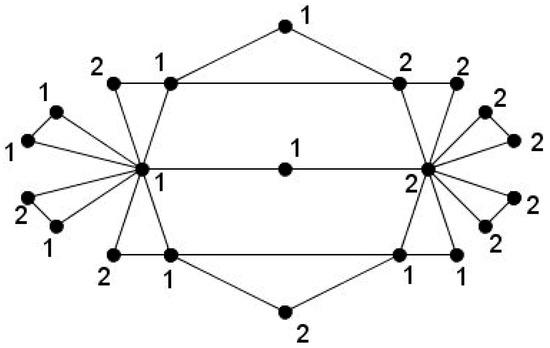
Figure 2. A planar graph without 4-cycles that satisfies Theorem 1, demonstrating the theorem guarantees a $(6,6)$-coloring.

A vertex u in a graph G is an m-vertex, an $m^{+}$-vertex, or an $m^{-}$-vertex if the degree of u is m, the degree of u is at least m, or the degree of u is at most m, respectively.

For a vertex u in a partially colored graph, we let $N_i\left(u\right)$ denote the set of neighbors of u with color $i.$

Let g be a face with $b\left(g\right)$ as its boundary. The number of edges that make up $b\left(g\right)$ is the degree of a face g. For a face g of a graph, a face g is an n-face, an $n^{+}$-face, or an $n^{-}$-face if $d\left(g\right)=n$, $d\left(g\right)\ge n$, or $d\left(g\right)\le n$, respectively.

A $(h_1,h_2,h_3)$-faceg is a face of degree 3 where all vertices on the boundary of g are an $h_1$-vertex, an $h_2$-vertex, and an $h_3$-vertex. We call a $(2,2^{+},2^{+})$-face as a poor 3-face and call a $(3^{+},3^{+},3^{+})$-face as a rich 3-face. Moreover, we call a vertex incident to some 3-faces as a poor vertex. Otherwise, we call it a rich vertex.

Let g be a 3-face where $b\left(g\right)=v{v}_1{v}_2$ and $d\left(v\right)=3$, and v has three adjacent vertices, which are $v_1,v_2,v_3$. Then, we call $v_3$ a branching neighbor of a vertex v corresponding to g.

Agreement. In each figure of this work, the solid vertices have all incident edges shown in the figure, while the hollow vertices may have additional incident edges in the figure.

2. Helpful Tools

Suppose the contrary to Theorem 1. Give G a minimal graph that is not $(6,6)$-colorable in ${\mathbb{G}}_4$. A graph G can be verified to be 2-connected. Consequently, every boundary face is a cycle. Then there are no 4-faces in G. Moreover, each vertex in a graph g has a degree of at least 2.

These are the properties of G’s faces and vertices.

Lemma 1.

Let u be a vertex of a graph G where $G-u$ has a $(6,6)$-coloring c with the color set $\{1,2\}$. Then, we have the following properties.

(a) 

For each $i\in \{1,2\}$, u has a neighbor colored by color i.

(b) 

For each $i\in \{1,2\}$, there is a neighbor w of u colored by color i such that $d\left(w\right)\ge 8$ in a graph G if u has at most six neighbors colored by color i.

Proof. 

Suppose the contrary to Lemma 1. To prove (a) and (b), it suffices to consider $i=1$.

(a) Suppose that $N_1\left(u\right)=\varnothing$. Thus, we modify a $(6,6)$-coloring c of $G-\left\{u\right\}$ to a $(6,6)$-coloring $c^{\prime }$ of G by the following steps:

1.

$c^{\prime }\left(x\right)=c\left(x\right)$ if $x\in V\left(G\right)-\left\{u\right\}$.

2.

$c^{\prime }\left(x\right)=1$ if $x=u$.

Since u does not share the color with its neighbors and each of the other vertices has the same number of neighbors sharing its colors, the coloring $c^{\prime }$ is a $(6,6)$-coloring of $G,$ a contradiction.

(b) Given that $|N_1\left(u\right)|\le 6$, suppose each vertex $w\in N_1\left(u\right)$ has a degree of at most 7 in G (and at most 6 in $G-u$). If $w\in N_1\left(u\right)$ has no neighbors colored by color 2, we reassign color 2 to w. We continue this process until each $w\in N_1\left(u\right)$ has a neighbor colored by color 2 (it is possible that $N_1\left(u\right)=\varnothing$; if so, the proof is done by (a)).

Then, each $w\in N_1\left(u\right)$ has at most five neighbors colored by color $1.$ Thus, We modify a $(6,6)$-coloring c of $G-\left\{u\right\}$ to a $(6,6)$-coloring $c^{\prime }$ of G through the following steps:

1.

$c^{\prime }\left(x\right)=c\left(x\right)$ if $x\in V\left(G\right)-\left\{u\right\}$.

2.

$c^{\prime }\left(x\right)=1$ if $x=u$.

Since $d\left(u\right)=6$ and now each $w\in N_1\left(u\right)$ has at most six neighbors colored by color $1,$ the coloring $c^{\prime }$ is a $(6,6)$-coloring of $G,$ a contradiction. □

Lemma 2.

Consider an l-vertex u of a graph G, where u is adjacent to $u_1,u_2,\dots ,u_l$. There is i where $1\le i\le l$ such that $d\left(u_i\right)\ge 8$ for $l\le 13$. Moreover, there is $i,j$ where $1\le i<j\le l$ such that $d\left(u_i\right)\ge 8$ and $d\left(u_j\right)\ge 8$ for $l\le 7$.

Proof. 

Let u be an l-vertex of a graph G, where c is a $(6,6)$-coloring of a graph $G-u$. It is clear that $|N_1\left(u\right)|+|N_2\left(u\right)|=l$. Moreover, $|N_k\left(u\right)|\ge 1$ for all $k\in \{1,2\}$ by Lemma 1(a).

If $l\le 13$, then $|N_k\left(u\right)|\le 6$ for some $k\in \{1,2\}$. It follows from Lemma 1(b) that u is adjacent to an $8^{+}$-vertex colored by a color k. Thus, there is i where $1\le i\le 13$ such that $d\left(u_i\right)\ge 8$.

If $l\le 7$, then $|N_k\left(u\right)|\le 6$ for all $k\in \{1,2\}$. It follows from Lemma 1(b) that u is adjacent to $8^{+}$-vertices colored by a color 1 and $8^{+}$-vertices colored by a color 2. Thus, there is $i,j$ where $1\le i<j\le 7$ such that $d\left(u_i\right)\ge 8$ and $d\left(u_j\right)\ge 8$. □

Lemma 3.

Consider a 3-face g of a graph G, where $b\left(f\right)=w_1{w}_2{w}_3$.

(a) 

If $w_1$ a 2-vertex, then $w_2$ or $w_3$ is a $9^{+}$-vertex.

(b) 

Given a 3-vertex $w_1$, then a branching neighbor $w_1^{*}$ of $w_1$ corresponding to g is an $8^{+}$-vertex if $w_2$ and $w_3$ are 8-vertices.

Proof. 

Consider a $(6,6)$-coloring c with the color set $\{1,2\}$ of $G-w_1$.

(a) Suppose the contrary to Lemma 3(a) that $d\left(w_1\right)=2$ and $d\left(w_i\right)\le 8$ for $i\in \{2,3\}$. By Lemma 2, $d\left(w_i\right)=8$ in a graph G (equivalently, $d\left(w_i\right)=7$ in the graph $G-w_1$) for $i\in \{2,3\}$. Without loss of generality, we give $c\left(w_2\right)=1$ and $c\left(w_3\right)=2$ by Lemma 1(a). One can see that $|N_1\left(w_2\right)|=6$ and $|N_2\left(w_3\right)|=6$; otherwise, we give color 1 or 2 to $w_1$ to make a $(6,6)$-coloring $c^{\prime }$ of G, a contradiction. This yields $N_2\left(w_2\right)=\left\{w_3\right\}$ and $N_1\left(w_3\right)=\left\{w_2\right\}$. We modify a $(6,6)$-coloring c of $G-\left\{w_1\right\}$ to a $(6,6)$-coloring $c^{\prime }$ of G by the following steps:

1.

$c^{\prime }\left(x\right)=c\left(x\right)$ if $x\in V\left(G\right)-\{w_1,w_2,w_3\}$.

2.

$c^{\prime }\left(x\right)=2$ if $x\in \{w_1,w_2\}$.

3.

$c^{\prime }\left(x\right)=1$ if $x=w_3$.

Now, $w_2$ does not share the color with its neighbors except $w_1.$ Furthermore, $w_3$ does not share the color with its neighbors. Finally, by $d\left(w_1\right)=2,$ we have a $(6,6)$-coloring on $G,$ a contradiction.

(b) Suppose the contrary to Lemma 3(b) that $d\left(w_1\right)=3$, $d\left(w_1^{*}\right)\le 7$ and $d\left(w_j\right)=8$ in a graph G (equivalently, $d\left(w_1^{*}\right)\le 6$ and $d\left(w_i\right)=7$ in the graph $G-w_1$ ) for $i\in \{2,3\}$. By Lemma 1, $c\left(w_2\right)\ne c\left(w_3\right)$. By symmetry, let $c\left(w_1^{*}\right)=1.$ If $|N_1\left(w_1^{*}\right)|=6$, then we reassign color 2 to $w_1^{*}$ and $|N_2\left(w_1^{*}\right)|=0$. In either cases, we have $|N_{c\left(w_1^{*}\right)}\left(w_1^{*}\right)|\le 5$.

Moreover, we assume $|N_1\left(w_2\right)|=6$ and $|N_2\left(w_3\right)|=6$; otherwise, we give color 1 or 2 to $w_1$ to make a $(6,6)$-coloring $c^{\prime }$ of G, a contradiction. This yields $N_2\left(w_2\right)=\left\{w_3\right\}$ and $N_1\left(w_3\right)=\left\{w_2\right\}$. Thus, we modify a $(6,6)$-coloring c of $G-\left\{w_1\right\}$ to a $(6,6)$-coloring $c^{\prime }$ of G by the following steps:

1.

$c^{\prime }\left(x\right)=c\left(x\right)$ if $x\in V\left(G\right)-\{w_1,w_2,w_3\}$.

2.

$c^{\prime }\left(x\right)=2$ if $x\in \{w_1,w_2\}$.

3.

$c^{\prime }\left(x\right)=1$ if $x=w_3$.

Now, $w_2$ does not share the color with its neighbors except $w_1.$ Furthermore, $w_3$ does not share the color with its neighbors. Also, $|N_{c^{\prime }\left(w_1^{*}\right)}\left(w_1^{*}\right)|\le 6$. Finally, by $d\left(w_1\right)=3,$ we have a $(6,6)$-coloring on $G,$ a contradiction. □

Lemma 4.

Let v be a 2-vertex incident to a face f and a face g. If f is a 3-face, then g is a $6^{+}$-face. In particular, each $5^{+}$-face g is incident to at most $d\left(g\right)-5$ poor 2-vertices.

Proof. 

Let $b\left(f\right)=u_1{u}_{2}v$. Consider a face g with a maximum degree of at most five. Then, g is a 3-face or a 5-face.

-

If g is a 3-face, then $d\left(u_1\right)=d\left(u_2\right)=2$, contrary to Lemma 2.

-

If g is a 5-face, say $g=u_1{u}_2{u}_3{u}_{4}v$, then there is an edge $u_1{u}_4$. A 4-cycle $u_1{u}_2{u}_3{u}_4$ exists, which is a contradiction.

Next, we show that an l-face g has at most $l-5$ incident poor 2-vertices for $l\ge 6$. By Lemma 2, one can obtain $b\left(g\right)$, which contains at most $\lfloor {\displaystyle \frac{l}{2}}\rfloor$ incident poor 2-vertices. It follows that a face g satisfies the condition when $l\ge 9$ because $\lfloor {\displaystyle \frac{l}{2}}\rfloor \le l-5$ when $l\ge 9$. It remains to show only the case g is an l-face when $6\le l\le 8$. Suppose that a face g has $l-4$ incident poor 2-vertices when $6\le l\le 8$. Let $b\left(g\right)=u_1{u}_2\dots u_l$. If $u_j$ is an incident poor 2-vertex of g, then there is an $(l-1)$-cycle, $u_1{u}_2\dots u_j{u}_{j-1}\dots u_l$. Proceed with this procedure until the $(l-5)$-th stage, when we have a 4-cycle, which is false. Hence, the proof is completed. □

Lemma 5.

If a k-vertex v has ${\eta }_f\left(v\right)$ incident 3-faces and ${\eta }_v\left(v\right)$ adjacent $3^{-}$-vertices not in incident 3-face of v, then ${\eta }_f\left(v\right)\le \lfloor {\displaystyle \frac{k}{2}}\rfloor$ and $2{\eta }_f\left(v\right)+{\eta }_v\left(v\right)\le k.$

Proof. 

It follows that each 3-face is not adjacent to another 3-face. □

Lemma 6.

Let v be a 9-vertex of G. If each incident 3-face of v is a $(2,8,9)$-face, then there is at least one adjacent $7^{+}$-vertex of v which is not incident to any incident 3-faces of v.

Proof. 

Let v be incident to k 3-faces, say $v{w}_1{u}_1$$v{w}_2{u}_2\dots ,v{w}_k{u}_k$, where each of them is a $(2,8,9)$-face. Then, we let $(d\left(w_i\right),d\left(u_i\right))=(2,8)$ for each $i\in \{1,\dots ,k\}$. Let $z_1,z_2,\dots ,z_{9-2k}$ be adjacent vertices of v which is not incident to any incident 3-faces of v.

Suppose, to the contrary, that $z_1,z_2,\dots ,z_{9-2k}$ are $6^{-}$-vertices. By the minimality of G, there is a $(6,6)$-coloring c of $G-v$. Since recoloring $c\left(w_i\right)$ to be different from $d\left(u_i\right)$ for each i does not increase the number of neighbors of $u_i$, sharing the color with $u_i$, and by $d\left(w_i\right)=2,$ we assume that $c\left(w_i\right)$ is different from $c\left(u_i\right)$ for each i.

Since $d\left(v\right)=9,$ we can choose $c\left(v\right)$ such that v has at most six neighbors of v sharing the color with v. Note that all neighbors of v have degrees not greater than 7 except $u_1,u_2,\dots ,u_k$. The situation that this extension of c to v is not a $(6,6)$-coloring occurs only if some $u_i$ have the same colors with seven neighbors including $v.$ By switching colors of $u_i$ and $w_i$ for such $u_i,$ we resolve this situation, and obtain a $(6,6)$-coloring of $G,$ a contradiction. □

3. The Proof of Theorem 1

After we collected all the necessary configurations in the previous section, we are in a position to give the proof of the main theorem by using the discharging method. We begin by designating initial charges to vertices and faces of a minimal counterexample of the main theorem with negative sum. By moving the charge from one element to another while maintaining the same sum, a contradiction is obtained by a final nonnegative charge.

Proof. 

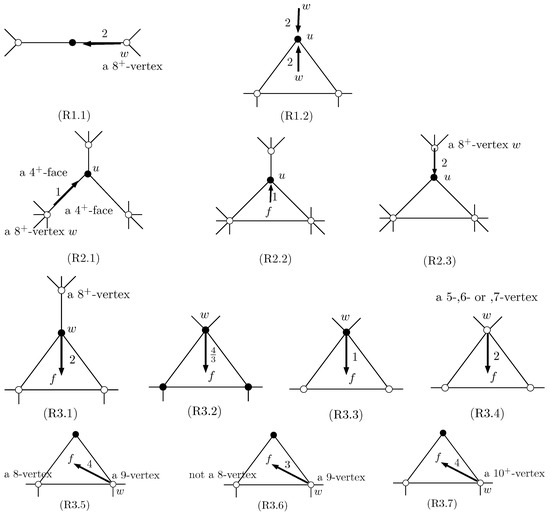
As a minimum counterexample of Theorem 1, we examine a graph $G\in {\mathbb{G}}_4$. The following describes how we begin by designating initial charges to the graph’s faces and vertices. For $x\in V\left(G\right)\cup E\left(G\right)$, $\tau \left(x\right)=3d\left(x\right)-10$ if $x\in V\left(G\right)$ and $\tau \left(x\right)=2d\left(x\right)-10$ if $x\in F\left(G\right)$.

The handshaking lemma and Euler’s formula then yield

$$\begin{array}{cc}\hfill \sum _{x\in V\left(G\right)\cup F\left(G\right)}\tau \left(x\right)& =\sum _{x\in V\left(G\right)}\tau \left(x\right)+\sum _{x\in F\left(G\right)}\tau \left(x\right)\hfill \\ \hfill & =\sum _{x\in V\left(G\right)}(3d\left(x\right)-10)+\sum _{x\in F\left(G\right)}(2d\left(x\right)-10)\hfill \\ \hfill & ={3\sum }_{x\in V\left(G\right)}d\left(x\right)-10\left|V\left(G\right)\right|+{2\sum }_{x\in F\left(G\right)}d\left(x\right)-10\left|F\left(G\right)\right|\hfill \\ \hfill & =6\left|E\right(G\left)\right|-10\left|V\right(G\left)\right|+4\left|E\right(G\left)\right|-10\left|F\right(G\left)\right|\hfill \\ \hfill & =10\left|E\right(G\left)\right|-10\left|V\right(G\left)\right|-10\left|F\right(G\left)\right|\hfill \\ \hfill & =10\left(\right|E\left(G\right)|-|V\left(G\right)|-|F\left(G\right)\left|\right)\hfill \\ \hfill & =10(-2)\hfill \\ \hfill & =-20.\hfill \end{array}$$

By moving the charge from one element to another, we produce a new charge ${\tau }^{*}\left(x\right)$ for all $x\in V\left(G\right)\cup F\left(G\right)$, and the sum of the new charge ${\tau }^{*}\left(x\right)$ continues at $-20$. The proof is complete if the final charge ${\tau }^{*}\left(x\right)\ge 0$ for all $x\in V\left(G\right)\cup F\left(G\right)$ results in a contradiction.

The following are the rules for discharge, illustrated in Figure 3.

Figure 3. Illustration of all discharging rules used in the paper.

Let v be a $3^{-}$-vertex. Then, $\psi (w\to v)$ represents the charge that a vertex v receives from an incident face, an adjacent vertex, or a branching neighbor w of v.

Let f be a 3-face. Then, $\psi (w\to f)$ represents the charge that a face f receives from an incident face or an adjacent vertex w of f.

• (R1) Let v be a 2-vertex.

(R1.1) $\psi (w\to v)=2$ when v is a rich 2-vertex, and w is an adjacent $8^{+}$-vertex of v.

(R1.2) $\psi (w\to v)=2$ when v is a poor 2-vertex, and w is an incident face of v.

• (R2) Let v be a 3-vertex.

(R2.1) $\psi (w\to v)=1$ when w is an adjacent $8^{+}$-vertex of v where v and w are not on the same boundary of a 3-face.

(R2.2) $\psi (w\to v)=1$ when w is an incident 3-face of v.

(R2.3) $\psi (w\to v)=2$ when w is a pendent $8^{+}$ neighbor of v.

• (R3) Let f be a 3-face.

(R3.1) $\psi (w\to v)=2$ when w is an incident 3-vertex where w has a pendent $8^{+}$-neighbor corresponding to f.

(R3.2) $\psi (w\to f)={\displaystyle \frac{4}{3}}$ when f is a $(4,4,4)$-face, and w is an incident 4-vertex of f.

(R3.3) $\psi (w\to f)=1$ when f is a $(4,m,n)$-face where $3\le m\le 7$ or $3\le n\le 7$, and $(m,n)\ne (4,4)$, and w is an incident 4-vertex of f.

(R3.4) $\psi (w\to f)=2$ when w is an incident k-vertex of f for $5\le k\le 8$ of f.

(R3.5) $\psi (w\to f)=4$ when f is a $(2,8,9)$-face, and w is an incident 9-vertex of f.

(R3.6) $\psi (w\to f)=3$ when f is not a $(2,8,9)$-face, and w is an incident 9-vertex of f.

(R3.7) $\psi (w\to f)=4$ when w is an incident ${10}^{+}$-vertex of f.

Next, we need to obtain that ${\tau }^{*}\left(x\right)\ge 0$ for all $x\in V\left(G\right)\cup F\left(G\right)$ by the discharging rules (R1)–(R3).

Now, let v be a k-vertex with ${\eta }_f\left(v\right)$ incident 3-faces, and ${\eta }_v\left(v\right)$ adjacent $3^{-}$-vertices which are not incident to any incident 3-faces of v.

From Case 1 to Case 7, we consider the final charge of each vertex v from the structure of v. For an l-vertex v, let $v_1,v_2,v_3,\dots ,v_l$ be adjacent vertices of v, and $f_1,f_2,f_3,\dots ,f_l$ be incident faces of v where $f_j$ is adjacent to $v_j$ and $v_{j+1}$ for each $j\in \{1,2,...,l\}$, and $j+1$ is taken modulo l.

• Case 1: A 2-vertex $v.$

(1.1) Let v be a poor 2-vertex. By (R1.2), $\psi (f_i\to v)=2$ for each $i\in \{1,2\}$. Then, ${\tau }^{*}\left(v\right)=-4+2+2=0$.

(1.2) Let v be a rich 2-vertex. By Lemma 2, $v_1$ and $v_2$ are $8^{+}$-vertices. By (R1.1), $\psi (v_i\to v)=2$ for each $i\in \{1,2\}$. Then, ${\tau }^{*}\left(v\right)=-4+2+2=0.$

• Case 2: A 3-vertex $v.$

One can observe that ${\eta }_f\left(v\right)\le 1$ by Lemma 5.

(2.1) Let ${\eta }_f\left(v\right)=1$. Then, v is a poor 3-vertex with an incident 3-face, say $f_1$, then $\psi (f_1\to v)=1$ by (R2.2). Moreover, $v_3$ is a branching neighbor corresponding to $f_1$.

-

Consider $v_3$ as a $7^{-}$-vertex,; then, ${\tau }^{*}\left(v\right)=-1+1=0$.

-

Consider $v_3$ as an $8^{+}$-vertex. Then, we have $\psi (v_3\to v)=2$ by (R2.3) and $\psi (v\to f_1)=2$ by (R3.1) since v has pendent $8^{+}$-neighbor $v_3$ corresponding to $f_1$. Thus, ${\tau }^{*}\left(v\right)=-1+1+2-2=0$.

(2.2) Let ${\eta }_f\left(v\right)=0$. Then, v is a rich 3-vertex. By Lemma 2, there exist i and j such that $v_i$ and $v_j$ are $8^{+}$-vertices for $\{i,j\}\subset \{1,2,3\}$. Then $\psi (v_i\to v)=\psi (v_j\to v)=1$ by (R1.1). Thus, ${\tau }^{*}\left(v\right)=-1+1\times 2=1.$

• Case 3: A 4-vertex $v.$

One can observe that ${\eta }_f\left(v\right)\le 2$ by Lemma 5. By Lemma 2, there exist i and j such that $v_i$ and $v_j$ are $8^{+}$-vertices for $\{i,j\}\subset \{1,2,3,4\}$.

(3.1) Let ${\eta }_f\left(v\right)\le 1$. Without loss of generality, $f_1$ is a 3-face. Then, $\psi (v\to f_1)\le {\displaystyle \frac{4}{3}}$ by (R3.2) and (R3.3). Thus, ${\tau }^{*}\left(v\right)\ge 2-{\displaystyle \frac{4}{3}}=0$.

(3.2) Let ${\eta }_f\left(v\right)=2$. Without loss of generality. $f_1$ and $f_3$ are 3-faces.

-

Consider either $f_1$ or $f_3$ as a $(4,4,4)$-face, Without loss of generality, $f_1$ is a $(4,4,4)$-face and $f_3$ is a $(4,8^{+},8^{+})$-face. Then, $\psi (v\to f_1)={\displaystyle \frac{4}{3}}$ by (R3.2). Thus, ${\tau }^{*}\left(v\right)=2-{\displaystyle \frac{4}{3}}=0$.

-

Consider both $f_1$ and $f_3$ as non-$(4,4,4)$ faces. Then, $\psi (v\to f_i)\le 1$ for $i\in \{1,3\}$ by (R3.3). Thus, ${\tau }^{*}\left(v\right)\ge 2-1\times 2=0$.

• Case 4: An l-vertex v where $5\le l\le 7$.

One can observe that ${\eta }_f\left(v\right)\le \lfloor {\displaystyle \frac{l}{2}}\rfloor$ by Lemma 5. Then, $\psi (v\to f_i)=2$ if $f_i$ is an incident 3-face of v for each $i\in \{1,2,\dots ,l\}$ by (R3.4). Thus, ${\tau }^{*}\left(v\right)\ge 3l-10-2\times \lfloor {\displaystyle \frac{l}{2}}\rfloor >0$ by $5\le l\le 7$ and (R3.2).

• Case 5: An 8-vertex $v.$

One can observe that $2{\eta }_f\left(v\right)+{\eta }_v\left(v\right)\le 9$ by Lemma 5. Then, $\psi (v\to v_i)=2$ if $v_i$ is a rich 2-vertex or v is a branching neighbor of $v_i$ for each $i\in \{1,2,\dots ,8\}$ by (R1.1) and (R2.3). Moreover, $\psi (v\to f_i)=2$ if $f_i$ is a 3-face for each $i\in \{1,2,\dots ,8\}$ by (R3.4).

(5.1) Let ${\eta }_f\left(v\right)=0$.

Since there exists i such that $v_i$ is an $8^{+}$-vertex by Lemma 5, we have ${\eta }_v\left(v\right)\le 7$. Thus, ${\tau }^{*}\left(v\right)\ge 14-2\times {\eta }_v\left(v\right)\ge 14-2\times 7=0$.

(5.2) Let ${\eta }_f\left(v\right)\ne 0$.

Since $2{\eta }_f\left(v\right)+{\eta }_v\left(v\right)\le 8$ by Lemma 5 where ${\eta }_f\left(v\right)\ne 0$, it follows that ${\eta }_f\left(v\right)+{\eta }_v\left(v\right)\le 7$. Thus, ${\tau }^{*}\left(v\right)\ge 14-2\times ({\eta }_f\left(v\right)+{\eta }_v\left(v\right))\ge 2\times 7=0$.

• Case 6: A 9-vertex $v.$

One can observe that $2{\eta }_f\left(v\right)+{\eta }_v\left(v\right)\le 9$ by Lemma 5. Then, $\psi (v\to v_i)=2$ if $v_i$ is a rich 2-vertex or v is a branching neighbor of $v_i$ for each $i\in \{1,2,\dots ,9\}$ by (R1.1) and (R2.3). Moreover, $\psi (v\to f_i)=4$ or $\psi (v\to f_i)=3$ if $f_i$ is a $(2,8,9)$-face or $f_i$ is not a $(2,8,9)$-face, respectively, for each $i\in \{1,2,\dots ,9\}$ by (R3.5) and (R3.6).

(6.1) Let ${\eta }_f\left(v\right)=0$.

Since there exists i such that $v_i$ is an $8^{+}$-vertex by Lemma 5, we have ${\eta }_v\left(v\right)\le 8$. Thus, ${\tau }^{*}\left(v\right)\ge 17-2\times 8>0$.

(6.2) Let ${\eta }_f\left(v\right)\ne 0$.

Let $g_1,g_2,\dots ,g_{{\eta }_f\left(v\right)}$ be all incident 3-faces of a vertex v.

-

If $g_j$ is a $(2,8,9)$-face for all $j\in \{1,2,\dots ,{\eta }_f\left(v\right)\}$, then there is an adjacent $7^{+}$-vertex of v which is not incident to $g_i$ for all $i\in \{1,2,\dots ,{\eta }_f\left(v\right)\}$ by Lemma 6. It follows that $2{\eta }_f\left(v\right)+{\eta }_v\left(v\right)\le 8$. Thus, ${\tau }^{*}\left(v\right)\ge 17-4\times {\eta }_f\left(v\right)-2\times {\eta }_v\left(v\right)=17-2(2{\eta }_f\left(v\right)+{\eta }_v\left(v\right))\ge 17-2\times 8>0$.

-

If there is j such that $g_j$ is not a $(2,8,9)$-face for some $j\in \{1,2,\dots ,{\eta }_f\left(v\right)\}$, then ${\tau }^{*}\left(v\right)\ge 17-3-4\times ({\eta }_f\left(v\right)-1)-2\times {\eta }_v\left(v\right)=17-3+4-2(2{\eta }_f\left(v\right)+{\eta }_v\left(v\right))\ge 18-2\times 9=0$.

• Case 7: An l-vertex v where $l\ge 10.$

One can observe that $2{\eta }_f\left(v\right)+{\eta }_v\left(v\right)\le \lfloor {\displaystyle \frac{l}{2}}\rfloor$ by Lemma 5. Then, $\psi (v\to v_i)=2$ if $v_i$ is a rich 2-vertex or v is a branching neighbor of $v_i$ for each $i\in \{1,2,\dots ,9\}$ by (R1.1) and (R2.3). Moreover, $\psi (v\to f_i)=4$ if $f_i$ is a 3-face by (R3.7). Thus, $\tau \left(v\right)=3k-10-(4\times {\eta }_f\left(v\right)+2\times {\eta }_v\left(v\right))\ge 3k-10-2d\left(v\right)=k-10\ge 0$ for $k\ge 10$.

Now, we consider an l-face f for $l\ge 3$. Note that we discuss only $k=3$ and $k\ge 6$.

• Case 8: A poor 3-face $f.$

We let $b\left(f\right)=u_1{u}_2{u}_3$ where $2=d\left(u_1\right)\le d\left(u_2\right)\le d\left(u_3\right)$. One can observe that f is a $(2,8^{+},9^{+})$-face by Lemmas 2 and 3(a). Then, $\psi (f\to u_1)=2$ for a poor 2-vertex $u_1$ by (R1.2), and $\psi (u_2\to f)=2$ if $u_2$ is an 8-vertex by (R3.4).

(8.1) Let f be a $(2,8,9)$-face or a $(2,8,{10}^{+})$-face. Then, $\psi (u_3\to f)=4$ by (R3.5) and (R3.7). Thus, ${\tau }^{*}\left(f\right)\ge -4-2+2+4=0$.

(8.2) Let f be a $(2,9^{+},9^{+})$. Then, $\psi (u_i\to f)\ge 3$ for each $i\in \{2,3\}$ by (R3.6) and (R3.7). Thus, ${\tau }^{*}\left(f\right)\ge -4-2+2\times 3=0$.

• Case 9: A rich 3-face $f.$

We let $b\left(f\right)=u_1{u}_2{u}_3$ where $3\le d\left(u_1\right)\le d\left(u_2\right)\le d\left(u_3\right)$. Moreover, we let $u_i^{*}$ be a branching neighbor of $u_i$ when $u_i$ is a 3-vertex for each $i\in \{1,2,3\}$.

It is impossible that $(d\left(u_1\right),d\left(u_2\right),d\left(u_3\right))\ne (3,3,3)$ because $u_i$ has at least two adjacent $8^{+}$-vertices for each $i\in \{1,2,3\}$ by Lemma 2. In the case that $d\left(u_1\right)=3$, we conclude that $d\left(u_1\right)\ge 8$ by Lemma 2.

(9.1) Let $d\left(u_1\right)=d\left(u_2\right)=3$ and $d\left(u_3\right)\ge 8$.

Then, $\psi (f\to u_i)=1$ for each $i\in \{1,2\}$ by (R2.2), and $\psi (u_3\to f)\ge 2$ by (R3.4), (R3.6), and (R3.7). One can obtain that $u_i^{*}$ and $u_2^{*}$ are $8^{+}$-vertices for each $i\in \{1,2\}$ by Lemma 2. This means $\psi (u_i\to f)=2$ for each $i\in \{1,2\}$ by (R2.2). Thus, ${\tau }^{*}\left(f\right)\ge -4-2\times 1+2+2\times 2=0$.

(9.2) Let $d\left(u_1\right)$, $4\le d\left(u_2\right)\le 7$, and $d\left(u_3\right)\ge 8$.

Then, $\psi (f\to u_1)=1$ by (R2.2), $\psi (u_2\to f)\ge 1$ by (R3.3), (R3.4), (R3.6), and (R3.7), and $\psi (u_3\to f)\ge 2$ by (R3.4), (R3.6), and (R3.7). One can obtain that $u_1^{*}$ is a $8^{+}$-vertex by Lemma 2. This means $\psi (u_1\to f)=2$ by (R2.2). Thus, ${\tau }^{*}\left(f\right)\ge -4-1+1+2+2=0$.

(9.3) Let $d\left(u_1\right)=3$, $d\left(u_2\right)=8$ and $d\left(u_3\right)=8$.

Then, $\psi (f\to u_1)=1$ by (R2.2), and $\psi (u_3\to f)\ge 2$ for each $i\in \{1,2\}$ by (R3.4), (R3.6), and (R3.7). One can obtain that $u_1^{*}$ is a $8^{+}$-vertex by Lemma 3(b). This means $\psi (u_1\to f)=2$ by (R2.2). Thus, ${\tau }^{*}\left(f\right)=-4-1+2\times 2+2=1$.

(9.4) Let $d\left(u_1\right)=3$, $d\left(u_2\right)\ge 8$ and $d\left(u_3\right)\ge 9$.

Then $\psi (f\to u_1)=1$ by (R2.2), $\psi (u_2\to f)\ge 2$ by (R3.4), (R3.6), and (R3.7), and $\psi (u_3\to f)\ge 3$ by (R3.6), and (R3.7). Thus ${\tau }^{*}\left(f\right)\ge -4-1+2+3=0$.

(9.5) Let $d\left(u_1\right)=d\left(u_2\right)=d\left(u_3\right)=4$.

Then, $\psi (u_i\to f)={\displaystyle \frac{4}{3}}$ for each $i\in \{1,2,3\}$ by (R3.2). Thus, ${\tau }^{*}\left(f\right)=-4+{\displaystyle \frac{4}{3}}\times 3=0$.

(9.6) Let $d\left(u_1\right)=d\left(u_2\right)=4$ and $d\left(u_3\right)\ge 5$.

Then, $\psi (u_i\to f)=1$ for each $i\in \{1,2\}$ by (R3.3), and $\psi (u_3\to f)\ge 2$ by (R3.4), (R3.6), and (R3.7). Then, ${\tau }^{*}\left(f\right)\ge -4+1\times 2+2=0$ by (R3).

(9.7) Let $d\left(u_1\right)\ge 4$, $d\left(u_2\right)\ge 5$, and $d\left(u_3\right)\ge 5$.

Then, $\psi (u_i\to f)\ge 2$ for each $i\in \{2,3\}$ by (R3.4), (R3.6), and (R3.7). Thus, ${\tau }^{*}\left(f\right)\ge -4+2\times 2=0$ by (R3).

• Case 10: An l-face f where $l\ge 6.$

We let $b\left(f\right)=u_1{u}_2{u}_3\dots u_l$. Then, $\psi (f\to u_i)=2$ if $u_i$ is an incident poor 2-vertex for each $i\in \{1,2,\dots ,l\}$. One can observe that f has at most $k-5$ incident poor 2-vertices by (R1.2). Thus, ${\tau }^{*}\left(f\right)\ge 2k-10-2\times (k-5)=0$.

Now, we can obtain that ${\tau }^{*}\left(x\right)\ge 0$ for all $x\in V\left(G\right)\cup F\left(G\right)$ from Case 1 to Case 10. Our proof is complete. □

4. Concluding Remarks and Discussion for Further Problems

It was known that for any given ${\Delta }_1,{\Delta }_2$, one can find a planar graph without 3-cycles that is not $({\Delta }_1,{\Delta }_2)$-colorable. This motivated the research on extra cycle restrictions that guarantee $({\Delta }_1,{\Delta }_2)$-colorability. Subsequently, it was found that every planar graph without 3-cycles, when adding the condition of having no 4-cycles, is $(1,9)$-, $(2,6)$-, and $(3,4)$-colorable. Since then, much attention has turned to the role of 4-cycles.

In this direction, it was found that every planar graph without 4-cycles and k-cycles, such as $k=5$ or 6, is $({\Delta }_1,{\Delta }_2)$-colorable for certain ${\Delta }_1$ and ${\Delta }_2$. One question naturally arose: does forbidding of only 4-cycles suffice for a planar graph to be $({\Delta }_1,{\Delta }_2)$-colorable for given ${\Delta }_1$ and ${\Delta }_2$? In contrast to the negative result of 3-cycles mentioned above, this work shows that every planar graph without 4-cycles is $(6,6)$-colorable.

To the best of our knowledge, this is the first result that forbids only a single cycle length yielding such a conclusion. For further investigation, one may try to find a single cycle length other than 4 that leads to an analogous result.

Another direction of the research is to investigate $({\Delta }_1,{\Delta }_2)$-coloring on a graph without 4-cycles. For example, we do not know whether the result of $(6,6)$-coloring is optimal or not. One may investigate to show that this coloring is optimal; otherwise, try to improve the result. Furthermore, one may investigate to find non-redundant $({\Delta }_1,{\Delta }_2)$ to $(6,6)$ in which every planar graph without 4-cycles is $({\Delta }_1,{\Delta }_2)$-colorable. It should be noted that the values of ${\Delta }_1={\Delta }_2=6$ in this work reflect the symmetry of the coloring in Theorem 1, since two colors are switchable.

It is informative that there are many different lines of research on defective graph coloring regarding planar graphs that readers may explore. For example, ref. [29] studies edge coloring on a graph G in a way that any given outer planar graph contained in G has all of its edges colored differently.