Low-Frequency Longitudinal Vibrations of a Fluid-Loaded Elastic Layer

Abstract

This paper concerns the low-frequency symmetric (extensional) motions of a thin elastic layer submerged in a fluid. This problem is less investigated than that for antisymmetric motion corresponding to bending vibrations, partly because the classical theory for thin-plate extension is not oriented to model the transverse compression of the plate caused by the pressure of the fluid. It is also worth noting that, in contrast to a fluid-borne bending wave, the extensional wave radiates into the fluid, resulting in complex-valued terms in the associated dispersion relation. In this paper, we derive a refined asymptotic formulation for symmetric motion starting from the 2D plane strain problem regarding fluid–structure interaction. The obtained results have the potential to be implemented for interpreting numerical and experimental data for a variety of modern engineering setups.

1. Introduction

Vibrations of a thin elastic layer under fluid loading have long been an active area of research, originating from the contributions of Lord Rayleigh [1]. Fluid–structure vibrations appear in numerous applications in the aerospace and automotive industries as well as in civil and naval engineering.

Extensional motions of a thin elastic layer loaded with fluid have received less attention across numerous publications compared to bending motions [2,3,4]. This is mainly due to the much greater extensional rigidity. At the same time, the classical theory for plate extension is not oriented to incorporate the effect of the transverse compression of the plate, in particular that associated with fluid pressure. Transverse compression is only a feature of refined plate models; see [5,6]. It is also worth noting that, in contrast to a fluid-borne bending wave—see, for example, [7,8]—the extensional one radiates into the fluid since the extensional wave speed in a plate usually exceeds the sound wave speed. The latter observation motivates special insight into the dynamic extension of a fluid-loaded elastic layer, which has not yet been paid sufficient attention in the literature.

Only very few publications consider structural vibrations under transverse compression by fluid. In particular, the papers [6,9,10] treat the pressure of the fluid as a prescribed mechanical load within the previously established formulations for thin cylindrical shells in a vacuum. An ad hoc engineering approach for tackling extensional plate vibration in the presence of fluid was studied in [11].

The aim of the paper is to derive novel high-order asymptotic models for the extensional motions of a thin elastic layer under fluid loading. For the first time, the consideration is based on the analysis of a coupled problem in which the motion of the layer is governed by the exact dynamics equations in linear elasticity. It is worth noting that, previously, fluid loading was usually treated as prescribed mechanical loads in the equations derived for elastic structures in a vacuum; see the discussion in a recent paper [8].

The paper is structured as follows. The statement of the problem and the derivation of the symmetric motion dispersion relation are outlined in Section 2. Section 3 deals with the long-wave low-frequency analysis of the aforementioned dispersion relation. Thereafter, consistent asymptotic models describing symmetric motion are derived in Section 4. Finally, concluding remarks are presented in Section 5.

2. The Dispersion Relation for Symmetric Motion

We consider small-amplitude free vibrations of an isotropic linearly elastic layer of thickness $2h$, which is surrounded by an inviscid compressible fluid. The Cartesian coordinate system is set up in such a way that axis $x_1$ goes through the mid-plane of the layer (see Figure 1), whereas axis $x_2$, perpendicular to plane $(x_1,x_3)$, is not shown in the figure. The following notations will be used throughout the paper: E is Young’s modulus, $\nu$ is Poisson’s ratio, $\lambda$ and $\mu$ are Lamé elastic constants, $\rho$ and ${\rho }_0$ are solid and fluid densities, respectively, $c_1$ and $c_2$ are the longitudinal and transverse wave speeds in solids, respectively, and $c_0$ is the wave speed in fluids.

Figure 1. Elastic layer immersed in fluid.

The equations of motion in terms of elastic potentials $\varphi$ and $\psi$ can be written as (see, for example, [12])

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^2\varphi }{\partial x_1^2}}+{\displaystyle \frac{{\partial }^2\varphi }{\partial x_3^2}}-{\displaystyle \frac{1}{c_1^2}}{\displaystyle \frac{{\partial }^2\varphi }{\partial t^2}}& =0,\hfill \\ \hfill {\displaystyle \frac{{\partial }^2\psi }{\partial x_1^2}}+{\displaystyle \frac{{\partial }^2\psi }{\partial x_3^2}}-{\displaystyle \frac{1}{c_2^2}}{\displaystyle \frac{{\partial }^2\psi }{\partial t^2}}& =0,\hfill \end{array}$$

(1)

where $c_1=\sqrt{{\displaystyle \frac{\lambda +2\mu }{\rho }}}$ and $c_2=\sqrt{{\displaystyle \frac{\mu }{\rho }}}$.

In addition, we have the fluid potential $\phi (x_1,x_3,t)$ (e.g., see [13,14,15]), satisfying the wave equation

$${\displaystyle \frac{{\partial }^2\phi }{\partial x_1^2}}+{\displaystyle \frac{{\partial }^2\phi }{\partial x_3^2}}-{\displaystyle \frac{1}{c_0^2}}{\displaystyle \frac{{\partial }^2\phi }{\partial t^2}}=0.$$

(2)

The contact conditions along the interfaces $x_3=\pm h$ are provided by

$${\sigma }_{31}=0,{\sigma }_{33}={\rho }_0{\displaystyle \frac{{\partial }^2\phi }{\partial t^2}},u_3={\displaystyle \frac{\partial \phi }{\partial x_3}},$$

(3)

where the stresses ${\sigma }_{31}$ and ${\sigma }_{33}$ and the vertical displacement $u_3$ are expressed as

$$\begin{array}{ll}{\sigma }_{31}=\hfill & \mu \left(2{\displaystyle \frac{{\partial }^2\varphi }{\partial x_1\partial x_3}}-{\displaystyle \frac{{\partial }^2\psi }{\partial x_1^2}}+{\displaystyle \frac{{\partial }^2\psi }{\partial x_3^2}}\right),\\ {\sigma }_{33}=\hfill & \lambda {\displaystyle \frac{{\partial }^2\varphi }{\partial x_1^2}}+(\lambda +2\mu ){\displaystyle \frac{{\partial }^2\varphi }{\partial x_3^2}}-2\mu {\displaystyle \frac{{\partial }^2\psi }{\partial x_1\partial x_3}},\\ u_3=\hfill & {\displaystyle \frac{\partial \varphi }{\partial x_3}}-{\displaystyle \frac{\partial \psi }{\partial x_1}}.\end{array}$$

(4)

Consider harmonic traveling wave solutions of 2D hyperbolic Equations (1) and (2). For symmetric modes, the displacement $u_3$ and the stress ${\sigma }_{31}$ are odd with respect to the vertical coordinate $x_3$, while ${\sigma }_{33}$ is even; see, for example, [12]. Hence, we obtain at $|x_3|⩽h$

$$\begin{array}{cc}\hfill \varphi & =C_1\cosh \left(k\alpha x_3\right)e^{i(k{x}_1-\omega t)},\hfill \\ \hfill \psi & =C_2\sinh \left(k\beta x_3\right)e^{i(k{x}_1-\omega t)},\hfill \end{array}$$

(5)

and at $|x_3|⩾h$

$$\phi =C_3{e}^{ik\gamma \left(\right|x_3|-h)}{e}^{i(k{x}_1-\omega t)},$$

(6)

where k is wavenumber, $\omega$ is angular frequency, and $C_j$ ($j=1,2,3$) are arbitrary constants, and

$$\alpha =\sqrt{1-{\displaystyle \frac{{\omega }^2}{k^2{c}_1^2}}},\beta =\sqrt{1-{\displaystyle \frac{{\omega }^2}{k^2{c}_2^2}}},\gamma =\sqrt{{\displaystyle \frac{{\omega }^2}{k^2{c}_0^2}}-1}.$$

(7)

As usual, the fluid potential $\phi$ in (6) satisfies the radiation condition.

Upon substituting the formulae above into contact conditions (3), we obtain the set of three linear algebraic equations

$$\begin{array}{c}2i\alpha \sinh \left(kh\alpha \right)C_1+(1+{\beta }^2)\sinh \left(kh\beta \right)C_2=0,\hfill \\ \mu (1+{\beta }^2)\cosh \left(kh\alpha \right)C_1-2i\beta \mu \cosh \left(kh\beta \right)C_2+{\rho }_0{\omega }^2{k}^{-2}{e}^{ik\gamma h}{C}_3=0,\hfill \\ \alpha \sinh \left(kh\alpha \right)C_1-i\sinh \left(kh\beta \right)C_2-i\gamma e^{ik\gamma h}{C}_3=0.\hfill \end{array}$$

This system has a non-trivial solution provided the determinant of the coefficients is zero, resulting in the dispersion relation for symmetric motion

$${(2K^2-{\Omega }^2)}^2\coth A-4K^{2}AB\coth B+i{\displaystyle \frac{{\Omega }^{4}Ar}{G}}=0,$$

(8)

where $r={\displaystyle \frac{{\rho }_0}{\rho }}$ denotes a relative density; $K=kh$ and $\Omega ={\displaystyle \frac{\omega h}{c_2}}$ stand for dimensionless wavenumber and frequency, normalized by half-thickness of the layer, whereas

$$A=\sqrt{K^2-{\Omega }^2{\kappa }^2},B=\sqrt{K^2-{\Omega }^2},G=\sqrt{{\Omega }^2{\delta }^2-K^2},$$

(9)

with $\delta ={\displaystyle \frac{c_2}{c_0}}$ and $\kappa ={\displaystyle \frac{c_2}{c_1}}=\sqrt{{\displaystyle \frac{1-2\nu }{2-2\nu }}}$ denoting wave speed ratios.

In contrast with the dispersion relation derived for a fluid-borne bending wave in [7], Equation (8) includes an imaginary term as a result of the extensional wave radiating into the fluid.

3. Asymptotic Expansion of Dispersion Relation

Consider dispersion relation (8) over the long-wave low-frequency domain

$$\Omega \ll 1,K\ll 1,$$

(10)

assuming $\Omega \sim K$, similar to the case of an extensional wave in an elastic plate in absence of fluid loading. The chosen domain covers the most important scenarios, which are related to the fundamental vibration mode of a thin elastic layer; e.g., see [5] and references therein. Also, since $c_2>c_0$ for most materials (for example, for steel $c_2=3189{\mathrm{ms}}^{-1}$ and for aluminium $c_2=3156{\mathrm{ms}}^{-1}$ compared to $c_0=1480{\mathrm{ms}}^{-1}$ for water), the expression under the square root for G, see (9), is assumed to be positive.

Now, let us substitute the polynomial expansion

$${\Omega }^2={\Omega }_0{K}^2+{\Omega }_1{K}^3+{\Omega }_2{K}^4+\dots$$

(11)

into dispersion relation (8). As a result, we obtain

$$\begin{array}{cc}\hfill {\Omega }_0& ={\displaystyle \frac{2}{1-\nu }},\hfill \\ \hfill {\Omega }_1& =-{\displaystyle \frac{2r{\nu }^2}{{(1-\nu )}^{5/2}\sqrt{2{\delta }^2+\nu -1}}}i,\hfill \\ \hfill {\Omega }_2& ={\displaystyle \frac{M}{3{(1-\nu )}^4{(2{\delta }^2+\nu -1)}^2}},\hfill \end{array}$$

(12)

where

$$\begin{array}{cc}\hfill M=& -2{\nu }^2((3r^2-1){\nu }^3+((3r^2-4){\delta }^2+3r^2+3){\nu }^2+(-4{\delta }^4+(12r^2+8){\delta }^2-9r^2-3)\nu \hfill \\ & -(3r^2-2{\delta }^2+1)(2{\delta }^2-1)).\hfill \end{array}$$

(13)

The only previous publication treating extensional vibrations of an elastic layer immersed in fluid is the paper [11] using some heuristic assumptions concerning the peculiarities of fluid–structure interaction. By scaling the dispersion relation presented in Equation (24) of Section 3.2 in [11] according to variables adapted in this paper, one obtains

$$-2K^2\left(2-i{\displaystyle \frac{r(1-\nu ){\Omega }^2}{G}}\right)+{\Omega }^2\left(2(1-\nu )-i{\displaystyle \frac{r(1-2\nu ){\Omega }^2}{G}}\right)=0.$$

(14)

A three-term expansion of this dispersion relation can be derived, with the first two coefficients, ${\tilde{\Omega }}_0$ and ${\tilde{\Omega }}_1$, being the same as provided in (12), whereas the third coefficient

$${\tilde{\Omega }}_2=-{\displaystyle \frac{2({\nu }^3+\left({\delta }^2+1\right){\nu }^2+\left(4{\delta }^2-3\right)\nu -2{\delta }^2+1){\nu }^2{r}^2}{{(2{\delta }^2+\nu -1)}^2{\left(1-\nu \right)}^4}},$$

(15)

differs from the one obtained from the exact dispersion relation; see (12). As usual, higher-order corrections cannot follow from intuitive hypothesis but require a more rigorous approach. In the next section, we derive a three-term asymptotic expansion of the dispersion relation, corresponding to the original plane strain problem in linear elasticity, which corrects the coefficient provided by (15).

Numerical results for a steel layer immersed in water are presented in Figure 2, with the following problem parameters utilized in obtaining these results: $c_0=1480{\mathrm{ms}}^{-1}$, $\nu =0.3, c_2=3189{\mathrm{ms}}^{-1}, \rho =7800{\mathrm{kgm}}^{-3}, {\rho }_0=1000{\mathrm{kgm}}^{-3}$. The dispersion curves for symmetric waves calculated from the exact dispersion relation (8), and its two-term and three-term asymptotic expansions, associated with Formula (11) with the coefficients provided by (12), are displayed in Figure 2, with Figure 2a showing the real parts of the exact dispersion relation and expansions and Figure 2b showing the imaginary parts. In this figure, the results for the real parts are similar to those for an elastic layer in vacuum, see [5], while the imaginary parts correspond to an energy loss due to radiation into the fluid.

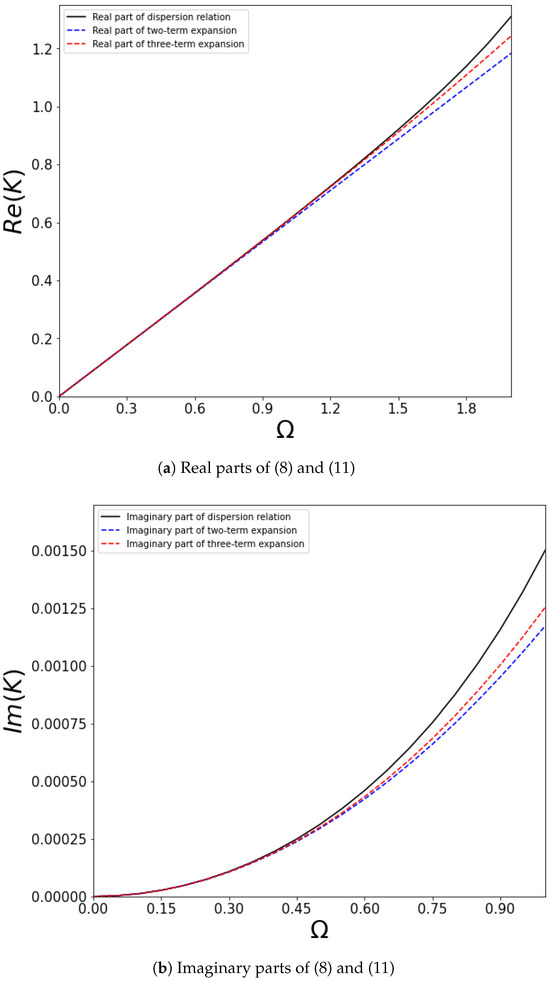
Figure 2. Dispersion relation (8) (solid black line) together with the two-term asymptotic expansion (11) (blue dashed line)—with coefficients ${\Omega }_0$ and ${\Omega }_1$ of (12) and the three-term asymptotic expansion (11) (red dashed line)—with all three coefficients of (12); real parts shown in (a) and imaginary parts shown in (b).

Figure 3 then illustrates an absolute value of a purely imaginary coefficient ${\Omega }_1$ as a function of density ratio, r, and ratio of wave speeds, $\delta$, for a fixed value of $\nu =0.3$. This provides insight into the effect of these parameters on the dissipation of energy.

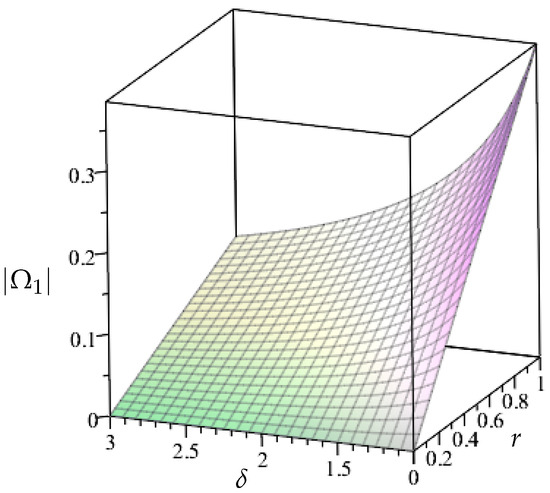
Figure 3. The absolute value of the imaginary coefficient, $|{\Omega }_1|$, versus the dimensionless problem parameters, $\delta$ and r, for $\nu =0.3$.

4. Asymptotic Models

In this section, we develop asymptotic models for an extensional motion of a fluid-loaded layer and compare associated approximate dispersion relations with the expansion of the exact one.

4.1. Plane Strain Problem

The classical equations of motion for a layer in case of a plane strain problem in linear elasticity may be written as

$$\begin{array}{c}{\displaystyle \frac{\partial {\sigma }_{11}}{\partial x_1}}+{\displaystyle \frac{\partial {\sigma }_{31}}{\partial x_3}}-\rho {\displaystyle \frac{{\partial }^2{v}_1}{\partial t^2}}=0,\hfill \\ {\displaystyle \frac{\partial {\sigma }_{31}}{\partial x_1}}+{\displaystyle \frac{\partial {\sigma }_{33}}{\partial x_3}}-\rho {\displaystyle \frac{{\partial }^2{v}_3}{\partial t^2}}=0.\hfill \end{array}$$

(16)

Here and below, ${\sigma }_{ij}(i,j=1,2,3)$ are stresses, $v_k(k=1,3)$ are displacements, and t denotes time. The stresses and displacements provided in the above equations satisfy the following relations, obtained in [5]

$$\begin{array}{cc}\hfill {\sigma }_{11}& ={\displaystyle \frac{E}{1-{\nu }^2}}{\displaystyle \frac{\partial v_1}{\partial x_1}}+{\displaystyle \frac{\nu }{1-\nu }}{\sigma }_{33},\hfill \\ \hfill {\sigma }_{22}& ={\displaystyle \frac{E\nu }{1-{\nu }^2}}{\displaystyle \frac{\partial v_1}{\partial x_1}}+{\displaystyle \frac{\nu }{1-\nu }}{\sigma }_{33},\hfill \\ \hfill {\displaystyle \frac{\partial v_3}{\partial x_3}}& ={\displaystyle \frac{1}{E}}({\sigma }_{33}-\nu ({\sigma }_{11}+{\sigma }_{22})),\hfill \\ \hfill {\displaystyle \frac{\partial v_1}{\partial x_3}}& =-{\displaystyle \frac{\partial v_3}{\partial x_1}}+{\displaystyle \frac{2(1+\nu )}{E}}{\sigma }_{31},\hfill \end{array}$$

(17)

adapted for the asymptotic analysis that will follow shortly.

In addition, we have the wave equation for the fluid potential $\phi (x_1,x_3,t)$, satisfying Equation (2), and the interfacial conditions at $x_3=\pm h$ provided by Equation (3).

4.2. Scaling

Let us begin by scaling the independent variables by

$$t=T\tau ,x_1=L\xi ,x_3=\left\{\begin{array}{cc}L\eta \zeta ,\hfill & \mathrm{if}|x_3|<h,\hfill \\ L\gamma ,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(18)

where $\eta =h/L\ll 1$ is a small geometric parameter. In addition, we assume that

$$T={\displaystyle \frac{L}{c_2}},$$

(19)

which is the same as for extensional waves on a ‘dry’, i.e., not contacting fluid, elastic plate; see, for example, [5]. Notice that (19) is independent of $\eta$, unlike for a fluid-borne bending wave, where the time scaling has dependence on $\eta$; see [8].

Now, we introduce the dimensionless stresses, displacements, and fluid potential setting

$$\begin{array}{c}{\sigma }_{11}=E{\sigma }_{11}^{*},{\sigma }_{22}=E{\sigma }_{22}^{*},{\sigma }_{31}=E{\eta }^2{\sigma }_{31}^{*},{\sigma }_{33}=E\eta {\sigma }_{33}^{*},\hfill \\ v_1=L{v}_1^{*},v_3=L\eta v_3^{*},\hfill \\ \phi =L^2\eta {\phi }^{*},\hfill \end{array}$$

(20)

where the starred quantities are assumed to be of the same asymptotic order.

Thus, Equations (16) and (17), taking into account relations (18) and (20), can be written in dimensionless form as

$$\begin{array}{c}{\displaystyle \frac{\partial {\sigma }_{11}^{*}}{\partial \xi }}-{\displaystyle \frac{1}{2(1+\nu )}}{\displaystyle \frac{{\partial }^2{v}_1^{*}}{\partial {\tau }^2}}=-\eta {\displaystyle \frac{\partial {\sigma }_{31}^{*}}{\partial \zeta }},\hfill \\ {\displaystyle \frac{\partial {\sigma }_{33}^{*}}{\partial \zeta }}=\eta \left(-\eta {\displaystyle \frac{\partial {\sigma }_{31}^{*}}{\partial \xi }}+{\displaystyle \frac{1}{2(1+\nu )}}{\displaystyle \frac{{\partial }^2{v}_3^{*}}{\partial {\tau }^2}}\right),\hfill \end{array}$$

(21)

and

$$\begin{array}{cc}\hfill {\sigma }_{11}^{*}& ={\displaystyle \frac{1}{1-{\nu }^2}}{\displaystyle \frac{\partial v_1^{*}}{\partial \xi }}+{\displaystyle \frac{\nu }{1-\nu }}\eta {\sigma }_{33}^{*},\hfill \\ \hfill {\sigma }_{22}^{*}& ={\displaystyle \frac{\nu }{1-{\nu }^2}}{\displaystyle \frac{\partial v_1^{*}}{\partial \xi }}+{\displaystyle \frac{\nu }{1-\nu }}\eta {\sigma }_{33}^{*},\hfill \\ \hfill {\displaystyle \frac{\partial v_3^{*}}{\partial \zeta }}& =\eta {\sigma }_{33}^{*}-\nu ({\sigma }_{11}^{*}+{\sigma }_{22}^{*}),\hfill \\ \hfill {\displaystyle \frac{\partial v_1^{*}}{\partial \zeta }}& ={\eta }^2\left(-{\displaystyle \frac{\partial v_3^{*}}{\partial \xi }}+2(1+\nu )\eta {\sigma }_{31}^{*}\right).\hfill \end{array}$$

(22)

Similarly, the dimensionless form of Equations (2) and (3) can be obtained, providing the following

$${\displaystyle \frac{{\partial }^2{\phi }^{*}}{\partial {\xi }^2}}+{\displaystyle \frac{{\partial }^2{\phi }^{*}}{\partial {\gamma }^2}}-{\delta }^2{\displaystyle \frac{{\partial }^2{\phi }^{*}}{\partial {\tau }^2}}=0,$$

(23)

and

$${\sigma }_{31}^{*}{|}_{\zeta =\pm 1}=0,{\sigma }_{33}^{*}{|}_{\zeta =\pm 1}={\displaystyle \frac{r}{2(1+\nu )}}{\displaystyle \frac{{\partial }^2{\phi }^{*}}{\partial {\tau }^2}}{|}_{\gamma =\pm \eta },{\displaystyle \frac{\partial {\phi }^{*}}{\partial \gamma }}{|}_{\gamma =\pm \eta }=v_3^{*}{|}_{\zeta =\pm 1},$$

(24)

where r and $\delta$ are defined in Section 2.

Next, expand the stresses, displacements, and fluid potential in an asymptotic series as

$$\begin{array}{cc}\hfill v_1^{*}& =v_1^{\left(0\right)}+\eta v_1^{\left(1\right)}+{\eta }^2{v}_1^{\left(2\right)}+\dots \hfill \\ \hfill v_3^{*}& =v_3^{\left(0\right)}+\eta v_3^{\left(1\right)}+{\eta }^2{v}_3^{\left(2\right)}+\dots \hfill \\ \hfill {\sigma }_{jj}^{*}& ={\sigma }_{jj}^{\left(0\right)}+\eta {\sigma }_{jj}^{\left(1\right)}+{\eta }^2{\sigma }_{jj}^{\left(2\right)}+\dots \hfill \\ \hfill {\sigma }_{31}^{*}& ={\sigma }_{31}^{\left(0\right)}+\eta {\sigma }_{31}^{\left(1\right)}+{\eta }^2{\sigma }_{31}^{\left(2\right)}+\dots \hfill \\ \hfill {\phi }^{*}& ={\phi }^{\left(0\right)}+\eta {\phi }^{\left(1\right)}+{\eta }^2{\phi }^{\left(2\right)}+\dots \hfill \end{array}$$

(25)

where $j=1,2,3$ and the superscripts denote the order of approximation. Using these expansions, we derive three asymptotic approximations for the exact plane strain formulation.

4.3. Leading-Order Approximation

Consider the leading-order approximation of the problem formulated in the previous subsection, keeping only the terms with the suffix “$\left(0\right)$” in the asymptotic series (25). First, integrating (21)₂ and (22)₄ along the thickness variable $\zeta$, we obtain, respectively,

$${\sigma }_{33}^{\left(0\right)}=S_{33}^{\left(0\right)}(\xi ,\tau )\mathrm{and}{v}_1^{\left(0\right)}=V_1^{\left(0\right)}(\xi ,\tau ),$$

(26)

where $S_{33}^{\left(0\right)}$ and $V_1^{\left(0\right)}$ are arbitrary functions. Substituting the stress and displacement defined here into (22)₁ and (22)₂, we obtain

$${\sigma }_{11}^{\left(0\right)}={\displaystyle \frac{1}{1-{\nu }^2}}{\displaystyle \frac{\partial V_1^{\left(0\right)}}{\partial \xi }},{\sigma }_{22}^{\left(0\right)}={\displaystyle \frac{\nu }{1-{\nu }^2}}{\displaystyle \frac{\partial V_1^{\left(0\right)}}{\partial \xi }}.$$

(27)

Next, Equation (21)₁, taking into account (26) and (27), yields

$${\displaystyle \frac{2}{1-\nu }}{\displaystyle \frac{{\partial }^2{V}_1^{\left(0\right)}}{\partial {\xi }^2}}-{\displaystyle \frac{{\partial }^2{V}_1^{\left(0\right)}}{\partial {\tau }^2}}=0,$$

(28)

corresponding to the extensional vibrations of a layer in vacuum; see [5]. Inserting Equations (26) and (27) into (22)₃ and integrating along $\zeta$ leads to

$$v_3^{\left(0\right)}=-{\displaystyle \frac{\nu }{1-\nu }}\zeta {\displaystyle \frac{\partial V_1^{\left(0\right)}}{\partial \xi }}.$$

(29)

The fluid potential at leading order can also be obtained from (23), yielding the Helmholtz equation

$${\displaystyle \frac{{\partial }^2{\phi }^{\left(0\right)}}{\partial {\xi }^2}}+{\displaystyle \frac{{\partial }^2{\phi }^{\left(0\right)}}{\partial {\gamma }^2}}-{\delta }^2{\displaystyle \frac{{\partial }^2{\phi }^{\left(0\right)}}{\partial {\tau }^2}}=0,$$

(30)

governing compressible fluid. Note that, unlike in [8] for flexural motions of a fluid-loaded layer, where the fluid compressibility comes in at third order, it now appears at leading order.

Finally, using contact conditions (24)₂ and (24)₃ at leading order, we obtain

$$S_{33}^{\left(0\right)}={\displaystyle \frac{r}{2(1+\nu )}}{\displaystyle \frac{{\partial }^2{\phi }^{\left(0\right)}}{\partial {\tau }^2}}{|}_{\gamma =\eta },$$

(31)

as well as impenetrability condition

$${\displaystyle \frac{\partial {\phi }^{\left(0\right)}}{\partial \gamma }}{|}_{\gamma =\eta }=-{\displaystyle \frac{\nu }{1-\nu }}{\displaystyle \frac{\partial V_1^{\left(0\right)}}{\partial \xi }}.$$

(32)

Note that ${\sigma }_{31}^{\left(0\right)}$ can be determined at the next step while considering first-order approximation.

4.4. First-Order Approximation

At the first order, retaining terms with the suffix “$\left(1\right)$” in (25), we have for the fluid potential

$${\displaystyle \frac{{\partial }^2{\phi }^{\left(1\right)}}{\partial {\xi }^2}}+{\displaystyle \frac{{\partial }^2{\phi }^{\left(1\right)}}{\partial {\gamma }^2}}-{\delta }^2{\displaystyle \frac{{\partial }^2{\phi }^{\left(1\right)}}{\partial {\tau }^2}}=0.$$

(33)

Displacements and stresses can be obtained as

$$\begin{array}{cc}\hfill v_1^{\left(1\right)}& =V_1^{\left(1\right)},\hfill \\ \hfill v_3^{\left(1\right)}& =\zeta \left({\displaystyle \frac{r(1-2\nu )}{2(1-\nu )}}{\displaystyle \frac{{\partial }^2{\phi }^{\left(0\right)}}{\partial {\tau }^2}}{|}_{\gamma =\eta }-{\displaystyle \frac{\nu }{1-\nu }}{\displaystyle \frac{\partial V_1^{\left(1\right)}}{\partial \xi }}\right),\hfill \\ \hfill {\sigma }_{11}^{\left(1\right)}& ={\displaystyle \frac{1}{1-{\nu }^2}}{\displaystyle \frac{\partial V_1^{\left(1\right)}}{\partial \xi }}+{\displaystyle \frac{\nu r}{2(1-{\nu }^2)}}{\displaystyle \frac{{\partial }^2{\phi }^{\left(0\right)}}{\partial {\tau }^2}}{|}_{\gamma =\eta },\hfill \\ \hfill {\sigma }_{22}^{\left(1\right)}& ={\displaystyle \frac{\nu }{1-{\nu }^2}}{\displaystyle \frac{\partial V_1^{\left(1\right)}}{\partial \xi }}+{\displaystyle \frac{\nu r}{2(1-{\nu }^2)}}{\displaystyle \frac{{\partial }^2{\phi }^{\left(0\right)}}{\partial {\tau }^2}}{|}_{\gamma =\eta },\hfill \\ \hfill {\sigma }_{33}^{\left(1\right)}& ={\displaystyle \frac{\nu }{4(1-{\nu }^2)}}(1-{\zeta }^2){\displaystyle \frac{{\partial }^3{V}_1^{\left(0\right)}}{\partial \xi \partial {\tau }^2}}+{\displaystyle \frac{r}{2(1+\nu )}}{\displaystyle \frac{{\partial }^2{\phi }^{\left(1\right)}}{\partial {\tau }^2}}{|}_{\gamma =\eta },\hfill \end{array}$$

(34)

where $V_1^{\left(1\right)}=V_1^{\left(1\right)}(\xi ,\tau )$ is an arbitrary function. Also, we can derive ${\sigma }_{31}^{\left(0\right)}$ in the form

$${\sigma }_{31}^{\left(0\right)}=\zeta \left({\displaystyle \frac{1}{2(1+\nu )}}{\displaystyle \frac{{\partial }^2{V}_1^{\left(1\right)}}{\partial {\tau }^2}}-{\displaystyle \frac{1}{1-{\nu }^2}}{\displaystyle \frac{{\partial }^2{V}_1^{\left(1\right)}}{\partial {\xi }^2}}-{\displaystyle \frac{\nu r}{2(1-{\nu }^2)}}{\displaystyle \frac{{\partial }^3{\phi }^{\left(0\right)}}{\partial \xi \partial {\tau }^2}}{|}_{\gamma =\eta }\right).$$

(35)

Above formula together with contact condition (24)₁, taken at leading order, yields an equation for determining $V_1^{\left(1\right)}$, namely

$${\displaystyle \frac{2}{1-\nu }}{\displaystyle \frac{{\partial }^2{V}_1^{\left(1\right)}}{\partial {\xi }^2}}-{\displaystyle \frac{{\partial }^2{V}_1^{\left(1\right)}}{\partial {\tau }^2}}+{\displaystyle \frac{\nu r}{1-\nu }}{\displaystyle \frac{{\partial }^3{\phi }^{\left(0\right)}}{\partial \xi \partial {\tau }^2}}{|}_{\gamma =\eta }=0.$$

(36)

The impenetrability condition takes the form

$${\displaystyle \frac{\partial {\phi }^{\left(1\right)}}{\partial \gamma }}{|}_{\gamma =\eta }=-{\displaystyle \frac{\nu }{1-\nu }}{\displaystyle \frac{\partial V_1^{\left(1\right)}}{\partial \xi }}+{\displaystyle \frac{r(1-2\nu )}{2(1-\nu )}}{\displaystyle \frac{{\partial }^2{\phi }^{\left(0\right)}}{\partial {\tau }^2}}{|}_{\gamma =\eta }.$$

(37)

4.5. Second-Order Approximation

Proceeding now towards deriving the second-order approximation, we keep the terms with the suffix “$\left(2\right)$” in the asymptotic series (25). Omitting intermediate calculations, we have an equation for fluid potential

$${\displaystyle \frac{{\partial }^2{\phi }^{\left(2\right)}}{\partial {\xi }^2}}+{\displaystyle \frac{{\partial }^2{\phi }^{\left(2\right)}}{\partial {\gamma }^2}}-{\delta }^2{\displaystyle \frac{{\partial }^2{\phi }^{\left(2\right)}}{\partial {\tau }^2}}=0,$$

(38)

together with equation of motion for a layer

$${\displaystyle \frac{2}{1-\nu }}{\displaystyle \frac{{\partial }^2{V}_1^{\left(2\right)}}{\partial {\xi }^2}}-{\displaystyle \frac{{\partial }^2{V}_1^{\left(2\right)}}{\partial {\tau }^2}}+{\displaystyle \frac{\nu r}{1-\nu }}{\displaystyle \frac{{\partial }^3{\phi }^{\left(1\right)}}{\partial \xi \partial {\tau }^2}}{|}_{\gamma =\eta }+{\displaystyle \frac{{\nu }^2}{3{(1-\nu )}^2}}{\displaystyle \frac{{\partial }^4{V}_1^{\left(0\right)}}{\partial {\xi }^2\partial {\tau }^2}}=0,$$

(39)

along with the impenetrability condition

$${\displaystyle \frac{\partial {\phi }^{\left(2\right)}}{\partial \gamma }}{|}_{\gamma =\eta }=-{\displaystyle \frac{\nu }{1-\nu }}{\displaystyle \frac{\partial V_1^{\left(2\right)}}{\partial \xi }}+{\displaystyle \frac{r(1-2\nu )}{2(1-\nu )}}{\displaystyle \frac{{\partial }^2{\phi }^{\left(1\right)}}{\partial {\tau }^2}}{|}_{\gamma =\eta }+{\displaystyle \frac{\nu ({\nu }^2-5\nu +2)}{12{(1-\nu )}^2}}{\displaystyle \frac{{\partial }^3{V}_1^{\left(0\right)}}{\partial \xi \partial {\tau }^2}}.$$

(40)

In the above, relation (28) from the leading-order problem has been used.

4.6. Approximate Equations

Below, we derive asymptotic models, comprising the approximate equations of motion for a layer immersed in fluid together with the impenetrability conditions along the interfaces. At the leading order, from (28), (30), and (32) we obtain

$${\displaystyle \frac{2}{1-\nu }}{\displaystyle \frac{{\partial }^2{v}_1^{*}}{\partial {\xi }^2}}-{\displaystyle \frac{{\partial }^2{v}_1^{*}}{\partial {\tau }^2}}=0,$$

(41)

$${\displaystyle \frac{{\partial }^2{\phi }^{*}}{\partial {\xi }^2}}+{\displaystyle \frac{{\partial }^2{\phi }^{*}}{\partial {\gamma }^2}}-{\delta }^2{\displaystyle \frac{{\partial }^2{\phi }^{*}}{\partial {\tau }^2}}=0,$$

(42)

and

$${\displaystyle \frac{\partial {\phi }^{*}}{\partial \gamma }}{|}_{\gamma =\eta }=-{\displaystyle \frac{\nu }{1-\nu }}{\displaystyle \frac{\partial v_1^{*}}{\partial \xi }},$$

(43)

where $v_1^{*}(\xi ,0,\tau )=V_1^{\left(0\right)}(\xi ,\tau )$ and ${\phi }^{*}(\xi ,\gamma ,\tau )={\phi }^{\left(0\right)}(\xi ,\gamma ,\tau )$. In terms of original variables, Equations (41) and (43) become

$${\displaystyle \frac{E}{1-{\nu }^2}}{\displaystyle \frac{{\partial }^2{v}_1}{\partial x_1^2}}-\rho {\displaystyle \frac{{\partial }^2{v}_1}{\partial t^2}}=0,$$

(44)

and

$${\displaystyle \frac{\partial \phi }{\partial x_3}}{|}_{x_3=h}=-{\displaystyle \frac{\nu h}{1-\nu }}{\displaystyle \frac{\partial v_1}{\partial x_1}},$$

(45)

with Equation (2) being the original form of Equation (42). It is important to note that, here and for the rest of this section, the displacement component $v_1$ is taken at the midplane $x_3=0$; i.e., $v_1=v_1(x_1,0,t)$.

Next, we consider the sum of Equations (28) and (36), multiplied by the small parameter $\eta$, to obtain

$${\displaystyle \frac{2}{1-\nu }}{\displaystyle \frac{{\partial }^2{v}_1^{*}}{\partial {\xi }^2}}-{\displaystyle \frac{{\partial }^2{v}_1^{*}}{\partial {\tau }^2}}+{\displaystyle \frac{\nu r}{1-\nu }}\eta {\displaystyle \frac{{\partial }^3{\phi }^{*}}{\partial \xi \partial {\tau }^2}}{|}_{\gamma =\eta }=0,$$

(46)

where $v_1^{*}=V_1^{\left(0\right)}+\eta V_1^{\left(1\right)}$, and the terms of order ${\eta }^2$ have been neglected. Likewise, we have from Equations (32) and (37)

$${\displaystyle \frac{\partial {\phi }^{*}}{\partial \gamma }}{|}_{\gamma =\eta }=-{\displaystyle \frac{\nu }{1-\nu }}{\displaystyle \frac{\partial v_1^{*}}{\partial \xi }}+{\displaystyle \frac{r(1-2\nu )}{2(1-\nu )}}\eta {\displaystyle \frac{{\partial }^2{\phi }^{*}}{\partial {\tau }^2}}{|}_{\gamma =\eta },$$

(47)

with ${\phi }^{*}={\phi }^{\left(0\right)}+\eta {\phi }^{\left(1\right)}$. Also, we obtain an equation for fluid potential in the form (42) from (30) and (33).

Returning to original variables, Equations (46) and (47) take the form

$${\displaystyle \frac{E}{1-{\nu }^2}}{\displaystyle \frac{{\partial }^2{v}_1}{\partial x_1^2}}-\rho {\displaystyle \frac{{\partial }^2{v}_1}{\partial t^2}}+{\displaystyle \frac{\nu {\rho }_0}{1-\nu }}{\displaystyle \frac{{\partial }^3\phi }{\partial x_1\partial t^2}}{|}_{x_3=h}=0,$$

(48)

and

$${\displaystyle \frac{\partial \phi }{\partial x_3}}{|}_{x_3=h}=-{\displaystyle \frac{\nu h}{1-\nu }}{\displaystyle \frac{\partial v_1}{\partial x_1}}+{\displaystyle \frac{{\rho }_{0}h(1-2\nu )(1+\nu )}{E(1-\nu )}}{\displaystyle \frac{{\partial }^2\phi }{\partial t^2}}{|}_{x_3=h},$$

(49)

together with Equation (2), governing the compressible fluid motion. Hence, Equations (2), (48), and (49) correspond to the first-order asymptotic model. We note that the second term in (49) has apparently not been observed before. In particular, it does not appear in the refined asymptotic model in [6].

Finally, similar to the derivation above, we deduce from Equations (28), (36), and (39), by neglecting $O\left({\eta }^3\right)$ terms

$${\displaystyle \frac{2}{1-\nu }}{\displaystyle \frac{{\partial }^2{v}_1^{*}}{\partial {\xi }^2}}-{\displaystyle \frac{{\partial }^2{v}_1^{*}}{\partial {\tau }^2}}+{\displaystyle \frac{\nu r}{1-\nu }}\eta {\displaystyle \frac{{\partial }^3{\phi }^{*}}{\partial \xi \partial {\tau }^2}}{|}_{\gamma =\eta }+{\displaystyle \frac{{\nu }^2}{3{(1-\nu )}^2}}{\eta }^2{\displaystyle \frac{{\partial }^4{v}_1^{*}}{\partial {\xi }^2\partial {\tau }^2}}=0,$$

(50)

where $v_1^{*}=V_1^{\left(0\right)}+\eta V_1^{\left(1\right)}+{\eta }^2{V}_1^{\left(2\right)}$ and ${\phi }^{*}={\phi }^{\left(0\right)}+\eta {\phi }^{\left(1\right)}+{\eta }^2{\phi }^{\left(2\right)}$. Likewise, the impenetrability condition, to within the same truncation error, becomes (see Equations (32), (37), and (40))

$${\displaystyle \frac{\partial {\phi }^{*}}{\partial \gamma }}{|}_{\gamma =\eta }=-{\displaystyle \frac{\nu }{1-\nu }}{\displaystyle \frac{\partial v_1^{*}}{\partial \xi }}+{\displaystyle \frac{r(1-2\nu )}{2(1-\nu )}}\eta {\displaystyle \frac{{\partial }^2{\phi }^{*}}{\partial {\tau }^2}}{|}_{\gamma =\eta }+{\displaystyle \frac{\nu ({\nu }^2-5\nu +2)}{12{(1-\nu )}^2}}{\eta }^2{\displaystyle \frac{{\partial }^3{v}_1^{*}}{\partial \xi \partial {\tau }^2}}.$$

(51)

Rewriting in original variables, Equations (50) and (51) become

$${\displaystyle \frac{E}{1-{\nu }^2}}{\displaystyle \frac{{\partial }^2{v}_1}{\partial x_1^2}}-\rho {\displaystyle \frac{{\partial }^2{v}_1}{\partial t^2}}+{\displaystyle \frac{\nu {\rho }_0}{1-\nu }}{\displaystyle \frac{{\partial }^3\phi }{\partial x_1\partial t^2}}{|}_{x_3=h}+{\displaystyle \frac{h^2{\nu }^2\rho }{3{(1-\nu )}^2}}{\displaystyle \frac{{\partial }^4{v}_1}{\partial x_1^2\partial t^2}}=0,$$

(52)

and

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \phi }{\partial x_3}}{|}_{x_3=h}=-{\displaystyle \frac{\nu h}{1-\nu }}{\displaystyle \frac{\partial v_1}{\partial x_1}}+& {\displaystyle \frac{{\rho }_{0}h(1-2\nu )(1+\nu )}{E(1-\nu )}}{\displaystyle \frac{{\partial }^2\phi }{\partial t^2}}{|}_{x_3=h}\hfill \\ & +h^3{\displaystyle \frac{\nu ({\nu }^2-5\nu +2)(1-{\nu }^2)\rho }{6E{(1-\nu )}^3}}{\displaystyle \frac{{\partial }^3{v}_1}{\partial x_1\partial t^2}},\hfill \end{array}$$

(53)

together with Equation (2), governing the motion of the fluid. Hence, the second-order asymptotic model comprises Equations (2), (52), and (53).

4.7. Testing of Shortened Dispersion Relations

Let us now compare the dispersion relations, associated with the approximate formulations established in Section 4.6, with the three-term expansion of the exact dispersion relation (8). We use the traveling wave solution in dimensionless form

$$\begin{array}{c}{v}_1=V{e}^{i{\eta }^{-1}(K\xi -\Omega \tau )},\hfill \\ \phi =\Phi e^{i{\eta }^{-1}G(\gamma -\eta )}{e}^{i{\eta }^{-1}(K\xi -\Omega \tau )},\hfill \end{array}$$

(54)

where V and $\Phi$ are constants, K and $\Omega$ are dimensionless wavenumber and frequency, defined in Section 2, and G is defined in (9). Substituting these into the leading-order Equation (44), we arrive at the dispersion relation

$${\Omega }^2={\displaystyle \frac{2}{1-\nu }}{K}^2.$$

(55)

This is in full agreement with the leading-order expansion (see coefficient ${\Omega }_0$ in (12)) of the full dispersion relation (8).

Next, using (54) in Equations (2), (48), and (49) results in the dispersion relation corresponding to the first-order model provided by

$$2i\left(2K^2-(1-\nu ){\Omega }^2\right)G+r\left(2(1-\nu )K^2-(1-2\nu ){\Omega }^2\right){\Omega }^2=0.$$

(56)

Finally, using (54) in Equations (2), (52), and (53), we arrive at the dispersion relation for the second-order model

$$\begin{array}{c}4G\left(-6(1-\nu )K^2+{\nu }^2{K}^2{\Omega }^2+3{(1-\nu )}^2{\Omega }^2\right)\hfill \\ +ir{\Omega }^2\left(12{(1-\nu )}^2{K}^2-{\nu }^3{K}^2{\Omega }^2-6(1-2\nu )(1-\nu ){\Omega }^2\right)=0.\hfill \end{array}$$

(57)

It can be easily verified that a two-term asymptotic expansion of (56) assuming the form provided by (11) has the same coefficients, ${\Omega }_0$ and ${\Omega }_1$, as provided by (12), whereas a three-term asymptotic expansion of (57) has all three same coefficients provided by (12), thus clearly highlighting the link between the three-term asymptotic expansion of the exact dispersion relation (8) and the approximate dispersion relations obtained from the asymptotic models in Section 4.

5. Concluding Remarks

This paper examined the low-frequency longitudinal vibrations of a thin elastic layer immersed in fluid. The dispersion relation (8) derived for extensional motion includes an imaginary term as a result of the extensional plate wave radiating into the fluid in contrast to the dispersion relation derived for a fluid-borne bending wave in [7]. This aspect is reflected in the long-wave low-frequency asymptotic expansion (11), together with coefficients provided by (12), in which case the first-order term is imaginary, whereas the leading- and second-order terms are real. The validity of formulae (11) and (12) is confirmed by numerical comparison with the exact dispersion relation (8); see Figure 2.

The main focus of the paper is on deriving the leading-, first-, and second-order asymptotic governing equations, including the equations of motion and the impenetrability condition. It is worth mentioning that fluid compressibility supporting radiation, which results in the imaginary term in the dispersion relation, should always be retained, while, in the case of a fluid-borne bending wave, it appears at the third order only; see [8] for more details.

The developed framework could be used as a benchmark for numerical simulations of the longitudinal wave propagation in a fluid-loaded elastic layer. It also has the potential to be implemented for interpreting delicate experimental measurements, in particular aimed at the evaluation of radiation damping; see also Figure 3.

The model problem investigated in this paper can be readily extended to more involved setups, e.g., the study of one-sided contact in which the extensional and bending waves are coupled to each other due to the presence of a fluid; e.g., see [13]. The anisotropy of an elastic material and viscosity of the fluid can also be incorporated. Finally, most of the obtained results can be naturally generalized to the 3D setup by substituting the Laplacian, divergence, and gradient instead of the spatial derivatives. The aforementioned directions form the scope for a follow-up research program inspired by the considered problem.