Trajectory Privacy-Protection Mechanism Based on Multidimensional Spatial–Temporal Prediction

Abstract

The popularity of global GPS location services and location-enabled personal terminal applications has contributed to the rapid growth of location-based social networks. Users can access social networks at anytime and anywhere to obtain services in the relevant location. While accessing services is convenient, there is a potential risk of leaking users’ private information. In data processing, the discovery of issues and the generation of optimal solutions constitute a symmetrical process. Therefore, this paper proposes a symmetry–trajectory differential privacy-protection mechanism based on multi-dimensional prediction (TPPM-MP). Firstly, the temporal attention mechanism is designed to extract spatiotemporal features of trajectories from different spatiotemporal dimensions and perform trajectory-sensitive prediction. Secondly, class-prevalence-based weights are assigned to sensitive regions. Finally, the privacy budget is assigned based on the sensitive weights, and noise conforming to localized differential privacy is added. Validated on real datasets, the proposed method in this paper enhanced usability by 22% and 37% on the same dataset compared with other methods mentioned, while providing equivalent privacy protection.

1. Introduction

The Internet industry, mobile communications, cloud computing, the Internet of Things, and other emerging technologies are rapidly developing, and smart devices with positioning functions are rapidly becoming popular. Human beings have opened a new era with intelligent interconnection and information sharing as the main symbols. These new intelligent experiences are mainly based on location-based services (LBSs), which provide specific and precise location-related services to provide users with convenient and favorable experiences. These location and trajectory data contain sensitive and complex information with essential commercial and immeasurable academic value in urban planning, disaster warning, and other public security [1,2]. Location information is a publicly available resource, but malicious attackers with ulterior motives to connect it with the relevant users can lead to serious privacy leakage problems and even crises for users’ personal and property safety.

Trajectories’ privacy protection methods are divided into the following types: trajectory generalization, trajectory suppression, trajectory encryption, dynamic pseudonyms, and trajectory protection methods based on differential privacy techniques. Trajectory generalization is a classical privacy protection method for location data, and most such protection methods are based on the k-anonymity technique [3]. The basic idea is to require each data release to make each package of released data indistinguishable from the other k − 1 entries. Trajectory suppression methods [4], on the other hand, are accomplished under the assumption that third-party anonymization servers are entirely reliable, and the most basic idea is to remove from a trajectory specific locations with sensitive identifiers that are frequently accessed by users, before the trajectory data is published. Track encryption encrypts the user’s LBNS query information. The private information retrieval (PIR) technique [5,6] is a method of location information protection based on cryptographic techniques and theories that allows the user to retrieve needed information from a database without revealing the information to be retrieved. Dynamic pseudo-anonymization replaces the user’s accurate ID information with a pseudonym when the user sends a request. The privacy-preserving model based on the differential privacy (DP) technique [7] provides strict data definition in terms of privacy preservation. It does not need to consider the background knowledge possessed by the attacker and is not affected by the change of a particular piece of data. DP was initially applied to querying databases to protect the individuals in the databases when releasing statistical information. Noise conforming to the Laplace distribution is added to the trajectory data to ensure that the query results satisfy the definition of differential privacy protection [8,9]. Since then, applying DP techniques in spatial geography has opened a new chapter in trajectory information privacy protection. The problem that all the current differential privacy-based methods for protecting user trajectory information must face is the relationship between privacy protection and data availability. How can errors caused by noisy data be reduced on the basis of protecting the user’s privacy information to improve the data’s usability? How can the degree of privacy protection of trajectory data be maximized while ensuring that the privacy protection scheme satisfies differential privacy?

Compared with previous approaches, the time-attentive sensitive area prediction mechanism we propose is highly innovative. Previous methods predicted in only the spatial dimension, whereas our work extends this prediction to the temporal dimension on the basis of spatial considerations. This not only enhances the accuracy of the prediction results but also ensures that the generated pseudo-trajectories align with the characteristics of user mobility.

The rest of this paper is organized as follows. Section 2 presents our related work on trajectory privacy-preserving methods. In Section 3, we discuss the relevant notions of trajectory privacy from the literature. In Section 4, we then describe several components and definitions of our TPPM-MP mechanism and introduce our temporal–spatial constraints areas-of-interest detection algorithm and trajectory-publishing method based on LDP. The experiment and evaluation are presented in Section 5.

2. Related Work

Differential privacy-preserving models are becoming a mainstream technique in the privacy-preserving field because of their excellent level of privacy preservation and portability. The basic idea is to randomly add noise conforming to Laplace distribution to the query result of the original data so that adding or deleting a particular record in the dataset does not affect the query result. Therefore, to realize privacy protection, no matter how much background knowledge the attacker has, it is challenging to infer through the query result whether the target data are in the queried dataset. Chen et al. [10] applied a differential privacy protection mechanism to the privacy protection of location data, adding the noise conforming to the Laplace distribution to the original trajectory dataset to make the published trajectory data satisfy the definition of differential privacy, to protect the user’s trajectory information. Previous research [11] proposed a data mining algorithm for differential privacy, using the quadtree spatial decomposition technique to preprocess the location points to realize differential privacy. Xiao et al. [12] transformed the geographic coordinate system into two coordinate systems. They assigned a privacy budget to each location, and the report mentioned that a Markov model represents the user’s location relationship in the associated moments. A spatiotemporal location protection scheme based on differential privacy was proposed in the literature. Lu et al. [13] proposed a method called a Lagrange multiplier-based differentially private algorithm to optimize the budget of the privacy mechanism to prevent the budget from being too large or too small, which would result in adding too little or too much noise. The protected trajectory privacy data can effectively defend against the problem of attackers inferring social relationships through the trajectory data. The above literature realizes trajectory protection from the perspective of noise generation methods or considering sensitive locations in the user’s trajectory location and adding noise to the whole trajectory. These approaches make overly strong assumptions about trajectory protection while ignoring the differences in the degree of privacy protection required at different locations in the trajectory. Not all location points leak the user’s private information. Not all locations need to be protected, leading to too low data availability and even less guarantee of the service quality of the user’s LBNSs. Therefore, as described in this paper, we predict sensitive areas through multidimensional spatial–temporal attention based on user movement patterns and then protect the detected sensitive areas.

In the era of big data, statistical models and machine learning methods cannot handle large-scale multivariate time series data with high dimensionality and nonlinearity. With the rapid rise of deep learning, the field of time series forecasting has been further developed. A significant advantage of deep learning models is that they can extract features from shallow information for analysis, and these features can further generate deep features [14]. As a result, deep learning models are more effective for solving complex problems than traditional models. Various improved neural networks such as RNNs, convolutional neural networks (CNNs), and graph neural networks (GNNs) have been proposed to mine temporal and spatial dependencies within time series. These are the most popular, efficient, and widely used deep learning techniques. Liu et al. [15] proposed a dual-stage two-phase model (DSTP)-based approach for extracting spatial correlations simultaneously, spatiotemporal relationships at different times, and temporal relationships between different sequences. GNNs are more widely used with multiple time-series data, e.g., traffic flow data based on road networks and air quality monitoring data in multiple areas in a city. Wang et al. [16] designed a graph convolutional network (GCN) to learn the topology of a sensor network to capture spatial correlations for traffic safety prediction. Song et al. [17] proposed a spatiotemporal synchronization mechanism to capture local spatiotemporal correlations for traffic flow prediction. However, these dynamic spatial correlations were localized due to the limitation of the neighborhood range. To solve these problems, Wang et al. [18] introduced geospatial convolution to obtain complex spatial relationships between regions for traffic accident risk prediction. Although the above GCN-based models have achieved significant performance results, some limitations remain. For multivariate time series data with actual geographic locations, not only do the data from different locations interact with each other, but they are also affected by exogenous factors relating to the current location. However, the above methods learn only one graph structure, which makes it challenging to capture the spatial–temporal correlations at different scales.

3. Related Definitions

The concept of differential privacy was first proposed as a definition by Dwork [19] in response to the problem of privacy leakage in statistical databases. This approach aims to make database query results insensitive to changes in individual records in the data set. First, the model is based on a rigorous mathematical theory, which provides a strict definition of privacy protection and scientific and rigorous proof of the level of privacy protection. Second, DP rigorously defines a privacy-preserving model entirely independent of background knowledge and theoretically assumed to be resistant to any attack originating from background knowledge. The key definitions of differential privacy are presented below.

3.1. Definition 1 (ε-Differential Privacy)

Suppose there are two neighboring datasets D and D′, that differ by only one record, and there exists an algorithm M; Range(M) is the set of all possible output values of the algorithm M. If any output S ⊆ Range(M) is satisfied for any pair of neighboring datasets D and D′, the following applies:

$$\mathrm{Pr}\left(M(D)=S\right)\le \mathrm{Pr}\left(M(D^{\prime })=S\right)\times {\mathrm{e}}^{\epsilon }$$

(1)

Then, the algorithm M is said to satisfy $\epsilon$-differential privacy [20], with $\epsilon \in \left(0,1\right)$ denoting the degree of privacy protection. In general, the smaller $\epsilon$ is, the more noise needs to be added and the higher the degree of privacy protection.

3.2. Definition 2 (Sensitivity)

There exists a function $f:D\to R^d$; the input is a dataset D, and the output is a d-dimensional vector of real numbers. Then, for any neighboring datasets $D{ \mathrm{a}\mathrm{n}\mathrm{d} D}^{\prime }$, the sensitivity of the function query $f\left(D\right)$ is as follows:

$$S_f=\underset{D,D^{\prime }}{\max }{‖f\left(D\right)-f\left(D^{\prime }\right)‖}_1$$

(2)

where ${‖f\left(D\right)-f\left(D^{\prime }\right)‖}_1$ denotes the first-order paradigm distance of the query function to the query result on the neighboring dataset [21], and $S_f$ denotes the sensitivity of the function f.

The primary implementation of differential privacy is to add noise to the query data results, and the typical noise mechanisms are categorized into the Laplace mechanism for numerical data and the exponential mechanism for non-numerical data. The exponential mechanism [22] for non-numerical data requires introducing a scoring function to obtain a score for each possible output, which is normalized to the probability value returned by the query. This paper focuses on using the Laplace mechanism to generate numeric data. The idea of the mechanism is to generate noise that meets the Laplace distribution and add the noise data to the original data; the formula is shown below:

$$f^{\prime }\left(D\right)=f\left(D\right)+N$$

(3)

The noise N obeys the Laplace distribution $Lap\left(\mu ,b\right)$, where $\mu =0,b={\displaystyle \frac{S_f}{\epsilon }}$, and satisfies Equation (1) after noise addition, which results in the probability density function of the noisy data conforming to the Laplace distribution:

$$p\left(\left.x\right|0,{\displaystyle \frac{S_f}{\epsilon }}\right)={\displaystyle \frac{\epsilon }{2\mathsf{\Delta }f}}\times {\mathrm{e}}^{{\displaystyle \frac{-\epsilon \left|x\right|}{\mathsf{\Delta }f}}}$$

(4)

In order to visualize the noisy data more, we draw its probability density image based on $Lap\left(\mu ,b\right)$, as shown in Figure 1.

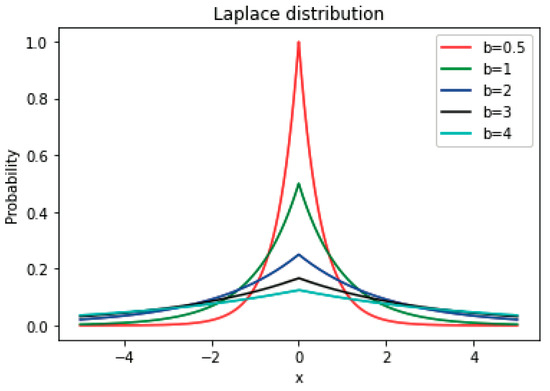
Figure 1. Laplace noise probability density.

From Figure 1, we can observe that the image exhibits central symmetry. Among these parameters, $\mu$ and $b$ determine the shape of the Laplace probability density function; the lower the value of $b$, the more noise we need to add.

The main difference between local differential privacy (LDP) and centralized differential privacy (CDP) is the different processing methods. Differential privacy scrambles the collected data and thus requires a trusted central server to aggregate and process the data. In contrast, local differential privacy pre-processes the data locally and saves it for uploading without the intervention of a central server to process the data, thus better protecting privacy.

3.3. Definition 3 (Local-Differential Privacy)

Any localized differential privacy function $f\left(l\right)$ with domain of definition $Dom\left(f\right)$ and domain of values $Ran\left(f\right)$ has for any inputs $l \mathrm{a}\mathrm{n}\mathrm{d} l^{\prime }\in Dom\left(f\right)$ and output $l^{*}\in Ran\left(f\right)$:

$$-\epsilon \le \ln \left({\displaystyle \frac{\mathrm{Pr}\left(f\left(l\right)=l^{\ast }\right)}{\mathrm{Pr}\left(f\left(l^{\prime }\right)=l^{\ast }\right)}}\right)\le \epsilon$$

(5)

According to the above formula, local differential privacy [21] ensures that the function $f$(l) satisfies ε-local differential privacy by controlling the similarity of the output results of any two records; the smaller ε is, the higher the similarity of the output results of the two records, and vice versa. The mathematical definition of local differential privacy and differential privacy is the same, but the realization of the mechanism is very different. The mainstream data perturbation technique of local differential privacy is a randomized response. Local differential privacy can be applied without considering the background knowledge of the attacker and without relying too much on a trusted third-party centralized service provider.

Randomized response techniques are the dominant perturbation mechanism to achieve local differential privacy and reduce errors caused by respondents’ wrong answers in sensitive question situations. For example, depending on the optional answer and sensitive questions, there are two cases of yes or no; in this paper, it is required to give an answer based on whether the user gives an answer based on the heads or tails of a uniform coin in n location blocks, assuming that the probability that the coin lands heads-up is p and the probability that it lands tails- up is 1 − p. The user responds to either the proper answer or an answer contrary to the truth, based on the result of the coin toss. If the actual situation is that the proportion of users in some of the n blocks is α, the position of the result answering yes against the block is k and answering otherwise is n − k. Then, the proportion of points answering yes or no according to the above is given:

$$P\left(ans=‘Yes’\right)=\alpha p+\left(1-\alpha \right)\left(1-p\right)$$

(6)

$$P\left(ans=‘No’\right)=\left(1-\alpha \right)p+\alpha \left(1-p\right)$$

(7)

The excellent likelihood estimate of the proper proportion is as follows:

$$\widehat{\alpha }={\displaystyle \frac{p-1}{2p-1}}+{\displaystyle \frac{k}{\left(2p-1\right)n}}$$

(8)

The mathematical expectation of $\widehat{\alpha }$ is as follows:

$$\begin{array}{lll}E\left(\widehat{\alpha }\right)& =& {\displaystyle \frac{1}{2\left(p-1\right)}}\left[p-1+{\displaystyle \frac{1}{n}}{\displaystyle \sum ans}\right]\\ & =& {\displaystyle \frac{1}{2(p-1)}}\left[p-1+\alpha p+\left(1-\alpha \right)\left(1-p\right)\right]\\ & =& \alpha \end{array}$$

(9)

The result guarantees that $\widehat{\alpha }$ is an unbiased estimator of the proper proportion $\alpha$ and is correctable when the estimate N of some of the n blocks is as follows:

$$N=\widehat{\alpha }\times n={\displaystyle \frac{p-1}{2p-1}}n+{\displaystyle \frac{k}{2p-1}}$$

(10)

Therefore, the estimation results satisfy the definition of local differential privacy, and the privacy preserving budget is set as follows:

$$\epsilon =\ln {\displaystyle \frac{p}{1-p}}$$

(11)

However, such a randomized response technique does not satisfy our need for accurate and pseudo-location outputs. In other words, we perturb the mechanism to control the output of any location in the location candidate set to satisfy localized differential privacy. Therefore, we use a randomized response technique that can directly randomize the response to a secure location set $L_k \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{g} k\left(k\ge 2\right)$ candidate values. Suppose RM is our randomized perturbation mechanism for any output ${loc}_i,{loc}_i^{*}\in L_m$.

For any output $l^{*}\in L$, the output of its response $\widehat{l^{*}}\in L$ is generated with the following equation:

$$\mathrm{P}\left(\left.{\widehat{l}}^{\ast }\right|l^{\ast }\right)={\displaystyle \frac{1}{k-1+{\mathrm{e}}^{\epsilon }}}\times \left\{\begin{array}{c}{\mathrm{e}}^{\epsilon }\\ 1\end{array}\right.\begin{array}{c}\hspace{1em}{\widehat{l}}^{\ast }=l^{\ast }\\ \hspace{1em}{\widehat{l}}^{\ast }\ne l^{\ast }\end{array}$$

(12)

That is, responding to any of the remaining k −1 answers with probability ${\displaystyle \frac{1}{k-1+{\mathrm{e}}^{\epsilon }}}$ and responding to the actual answer with probability ${\displaystyle \frac{{\mathrm{e}}^{\epsilon }}{k-1+{\mathrm{e}}^{\epsilon }}}$ results in satisfying the $\epsilon$-LDP.

A multivariate time series is composed of multiple exogenous and target sequences. Given n exogenous sequences, $X=\left(x^1,x^2,\dots ,x^n\right)=(x_1,x_2,\dots ,x_{\mathrm{T}})\in {\mathbb{R}}^{n\times T}$, where T denotes the time search window size, the exogenous sequence of a time window is constructed as a tree graph structure, where T is the number of nodes and the exogenous sequence $x_t=(x_t^1,x_t^2,\dots ,x_t^n)\in {\mathbb{R}}^n$ of timestamp t is used as a feature of node t.

$X=(x_{1,}{x}_2,\dots ,x_{t-1})$ denotes the node characteristics (i.e., timestamp history information) of the neighboring timestamps of node t, given the history values of the target sequence $(y_1,y_2,\dots ,y_{\mathrm{T}})$ where $y_t\in \mathbb{R}$, and the history values of the n exogenous sequences $(x_1,x_2,\dots ,x_{\mathrm{T}})\in {\mathbb{R}}^{n\times \mathrm{T}}$. The purpose of this predictive model is to learn from the graph structure to discover hidden features and predict future values ${\tilde{y}}_{T\to h}$:

$${\tilde{y}}_{T\to h}=F\left(y_1,y_2,\cdots y_{\mathrm{T}},{\mathrm{X}}_1,{\mathrm{X}}_2,\cdots {\mathrm{X}}_{\mathrm{T}}\right)$$

(13)

where ${\tilde{y}}_{T\to h}$ denotes the predicted value across h timestamps, and when h = 1, the model is used to make the next prediction for subsequent location prediction based on historical data. $F(·)$ is a nonlinear mapping function.

4. Trajectory Privacy Protection and Prediction Mechanisms

The proposed trajectory privacy protection system TPPM-MP consists of two parts, the user side, and the server side, as shown in Figure 2. The user side collects the user’s trajectory data, uses the trajectory processing mechanism based on localized differential privacy, and then publishes the processed trajectory data to the server side, which achieves the basic usability of the data published by the user without disclosing the user’s privacy information. The significance of using the localized privacy protection mechanism is that the trustworthiness of the third-party service provider can be disregarded.

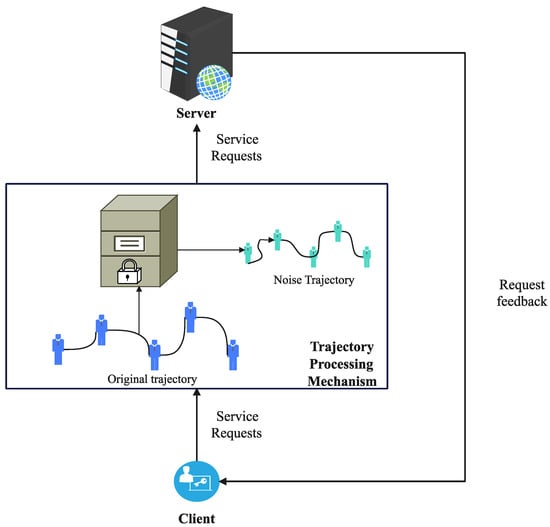
Figure 2. TPPM-MP system architecture diagram.

The user side part is divided into trajectory prediction and privacy protection mechanisms. The trajectory prediction part mainly introduces the prediction function and the objective function. Considering the multi-dimensional spatial–temporal correlation, the one-dimensional spatial–temporal feature D_t and the two − dimensional spatio − temporal feature H_t are simply aggregated as follows:

$${\mathrm{C}}_{t^{\prime }}=\left[D_{t^{\prime }}:H_{t^{\prime }}\right]$$

(14)

The final prediction of the trajectory prediction mechanism is made via a nonlinear mapping of the aggregated features:

$$\begin{array}{lll}\left({\widehat{y}}_{t^{\prime },T+1},{\widehat{y}}_{t^{\prime },T+2},\cdots ,{\widehat{y}}_{t^{\prime },T+h}\right)& =& ℱ\left({\widehat{y}}_{t^{\prime }},X_{t^{\prime }}\right)\\ & =& v_y^T\left(C_{t^{\prime }}{W}_y+b_{\omega }\right)+b_v\end{array}$$

(15)

where the parameter matrices $W_y\in {\mathbb{R}}^{p+q}$ and $b_w\in {\mathbb{R}}^T$ map the new features to dimension T. The final prediction is generated using the linear transformations $v_y\in {\mathbb{R}}^{h\times T}$ and $b_v\in {\mathbb{R}}^h$. The final prediction results use a modified hybrid strategy with the same model, which accepts multiple inputs and predicts multiple outputs. This strategy balances the drawbacks of direct, iterative, and MIMO strategies, avoids conditional independence assumptions, and allows for time dependence between the output data, while the simultaneous outputs of multiple models allow some flexibility. Figure 3 illustrates the architecture of the improved hybrid strategy proposed in this chapter, where F denotes the trajectory prediction model proposed.

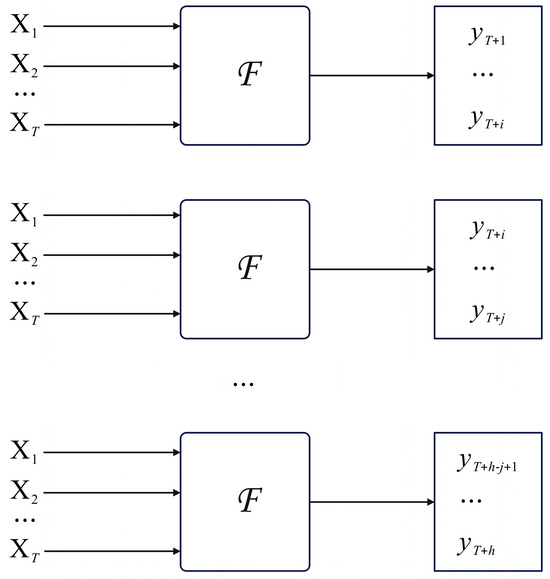
Figure 3. Structure of trajectory prediction mechanism.

All parameters of the method proposed in this paper are learned using MSE as an objective function, which can be formulated as follows:

$$ℒ\left(\theta \right)={\displaystyle \frac{1}{N\times h}}{{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{t=1}^h\left(y_t^i-{\widehat{y}}_t^i\right)}}}^2$$

(16)

where $\mathsf{\theta }$ denotes the learnable parameter, N denotes the number of training samples, h denotes the length of the predicted time step, and $y_t^i$ and ${\widehat{y}}_t^i$ denote the true and predicted values of time step t, respectively. Finally, Adam is used to optimize the objective function. Subsequently, the corresponding privacy budget is allocated based on the predicted values of the historical data. Assuming that each mobile user has $p$ locations to be protected, the importance of location $c_{u_i}^h\left(h\in \left[1,p\right]\right)$ is ${\omega }_h\left(c_{u_i}^h\right)$, and the sensitivity of the location point is $∆{\omega }_h$, from which is derived the probability that the location will be selected:

$$\mathrm{Pr}\left(c_{u_i}^h\right)={\displaystyle \frac{exp\left(\frac{\epsilon }{2∆{\omega }_h}\ast {\omega }_h\left(c_{u_i}^h\right)\right)}{{\sum }_{h=1}^{p}exp\left(\frac{\epsilon }{2∆{\omega }_h}\ast {\omega }_h\left(c_{u_i}^h\right)\right)}}$$

(17)

Given the privacy budget, our mechanism can allocate the budget according to the probability of each hotspot being selected by the utility function, $\mathrm{Pr}\left(c_{u_i}^h\right)$, and the budget ${\epsilon }_h$ allocation for each hotspot can be calculated by the following formula:

$${\epsilon }_h=\epsilon \ast \left(1-{\displaystyle \frac{\mathrm{Pr}\left(c_{u_i}^h\right)}{{\sum }_{h=1}^p\mathrm{Pr}\left(c_{u_i}^h\right)}}\right)$$

(18)

The pseudo-location candidate set of predicted location points can be generated by assigning the corresponding privacy budget value, which is denoted as ${Tr}_{sp}=\left\{({lon}_j,{lat}_j,t_j,{loc}_j),({lon}_{j+1},{lat}_{j+1},t_{j+1},{loc}_{j+1}),\cdots ,({lon}_k,{lat}_k,t_k,{loc}_k)\right\}$, where 1$\le j<k\le n$, and the generalized location residency is then generated based on the set of candidate locations in the location region. The generalized location residency given by the following equation:

$$lo{n}^{\ast }={\displaystyle \frac{lo{n}_j+lo{n}_{j+1}+\cdots +lo{n}_k}{k-j+1}}+lonNoise$$

(19)

$$la{t}^{\ast }={\displaystyle \frac{la{t}_j+la{t}_{j+1}+\cdots +la{t}_k}{k-j+1}}+latNoise$$

(20)

where $lo{n}^{\ast }$ and $la{t}^{\ast }$ represent the precision and latitude coordinates of the noise location data available for publication. The lonNoise and latNoise are noise that satisfies the Laplace distribution.

5. Experimental Evaluation

In this section, we report the evaluative testing of our experimental methodology; all algorithmic experiments were implemented on Python. Our datasets were derived from typical datasets published on the web, Geolife [23,24,25,26] and Gowalla [27]. The Geolife dataset is derived from the GPS track data of 182 users, collected by Microsoft Research Asia. The data points are in chronological order, each containing longitude, latitude, and altitude information. There are 17,621 trajectories with a total distance of more than 1.2 million km and a total duration of more than 50,000 h. The data records the location of users’ homes and workplaces and tracks a wide range of outdoor activities such as shopping, traveling, touring, biking, etc. The Gowalla dataset, collected by Stanford University, is a location-based social networking site that allows users to share information about their location by checking in. The dataset includes 6,442,890 check-in locations and 19,651 users’ check-in location information.

In order to verify the effectiveness of the proposed location prediction model in the multi-step prediction task, a statistical model and a deep learning model with excellent performance were chosen as the comparison methods in this experiment. The comparison methods are described as follows:

ARIMA: (Autoregressive Integrated Moving Average Model) [28] is a typical univariate time series forecasting statistical model. It involves a combination of difference operation and ARMA (Auto-Regressive and Moving Average Model), firstly converting the non-smooth time series into smooth data by difference operation and then using ARMA to fit the differenced series.

LSTM: (long short-term memory) [29] is a widely used RNN (recurrent neural network) variant designed to mine hidden long-term temporal dependencies in time series.

DA-RNN: Data Associated Recurrent Neural Network model uses a two-stage attention mechanism with an input attention mechanism and a temporal attention mechanism. First, the input attention mechanism adaptively selects relevant exogenous sequences. In the second stage, the temporal attention mechanism automatically selects the relevant encoder hidden states for all time steps. The DA-RNN [30] can be utilized to predict the value of the next moment efficiently.

Three different evaluation metrics were used to assess the performance of the forecasting models [31]. Two evaluation metrics, mean absolute error (MAE) and root mean squared error (RMSE), are widely used in time series forecasting to measure the error between predicted and observed values. Smaller values of MAE [32] and RMSE [33] indicate the model’s lower prediction error and more accurate prediction. In addition, the coefficient of determination (R squared, R²) was also utilized to determine the fitting effect of the model. The range of values of R² [34] was determined as [0,1], and a value of R² closer to 1 indicates that the model is fitted better. Assuming that $y_t$ is the true value of time step t, ${\widehat{y}}_t$ is the predicted value of time step t, $\overline{y}$ is the average of the true value, and N is the number of samples, the evaluation index is defined as follows:

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle {\sum }_{i=1}^N{\left(y_t^i-{\widehat{y}}_t^i\right)}^2}}$$

(21)

$$\mathrm{MAE}={\displaystyle \frac{1}{N}}{\displaystyle {\sum }_{i=1}^N\left|y_t^i-{\widehat{y}}_t^i\right|}$$

(22)

$${\mathrm{R}}^2=1-{\displaystyle \frac{{\displaystyle {\sum }_{i=1}^N\left|y_t^i-{\widehat{y}}_t^i\right|}}{{\displaystyle {\sum }_{i=1}^N\left|y_t^i-{\overline{y}}_t^i\right|}}}$$

(23)

The multi-step time series prediction results of the TPPM-MP and the comparison methods using two real datasets are given below. For a fair comparison, only the best evaluation results of each method with different parameter settings are shown. Table 1 shows the evaluation results for single-step time series prediction. To ensure clarity of results and facilitate observation, we used 1 − R² as the metric. From the table, it can be observed that the TPPM-MP model proposed in this paper achieved optimal performance on all datasets. The results of single-step prediction and multi-step prediction are analyzed below.

Table 1. Single-step time series prediction results on Geolife dataset and Gowalla dataset.

Methodologies	Geolife			Gowalla
	MAE	RMSE	1 − R2	MAE	RMSE	1 − R2
ARIMA	0.3890	0.7355	0.0812	0.3412	0.2348	0.0190
LSTM	0.3760	0.7346	0.0812	0.2780	0.2336	0.0174
DA-RNN	0.3550	0.7155	0.0735	0.1302	0.0967	0.0059
TPPM-MP	0.2806	0.6251	0.0526	0.0616	0.0454	0.0019

For single-step prediction, each method involves predicting the value of the next time step (h = 1). It can be observed from Table 1 that the MAE and RMSE values of the ARIMA model were both higher than the other compared methods or TPPM-MP. On the Geolife and Gowalla datasets, the MAE ratio of ARIMA was higher than that of TPPM-MP in both cases. This indicates that ignoring exogenous factors reduced the model’s performance. Although LSTM performed better than ARIMA, TPPM-MP had lower MAE values than LSTM on each dataset. This was because the LSTM network focused on extracting the long-term dependencies of all time series rather than selecting relevant features. The above experimental results suggest that TPPM-MP’s use of the attention mechanism to capture spatial–temporal correlations helps it achieve better prediction performance.

The following section describes the privacy performance and usability analysis of the method proposed in this paper for publishing trajectory data. We also consider different prediction scenarios and privacy-preserving budgets, and compare the algorithm in this paper with other privacy-preserving methods, DP-Srat [35] and N-gram [36]. We evaluate our privacy-preserving mechanism using four metrics, i.e., relative error, accuracy P, recall R, and F__value, as follows:

$$P={\displaystyle \frac{\left|Q\left({Traj}_{u_i}^{\prime }\right)\cap Q\left({Traj}_{u_i}\right)\right|}{\left|Q\left({Traj}_{u_i}^{\prime }\right)\right|}}$$

(24)

$$R={\displaystyle \frac{\left|Q\left({Traj}_{u_i}^{\prime }\right)\cap Q\left({Traj}_{u_i}\right)\right|}{\left|Q\left({Traj}_{u_i}\right)\right|}}$$

(25)

$${F\_}_{value}={\displaystyle \frac{\left(\mu +1\right)P\ast R}{\mu \ast P+R}}$$

(26)

where μ is the tuning parameter. In this paper, we set P and R to be equally important, so μ = 1.

In this example, the degree of privacy protection is regulated and controlled according to the privacy budget $\epsilon$ of DP, and the distance between the actual location and the pseudo location is obtained from the probability as ${\mathrm{e}}^{\epsilon }$. To facilitate the measurement of the degree of privacy protection, the result is restricted to [0,1], so the formula for the privacy protection degree (PPD) is $PPD={\mathrm{e}}^{-\epsilon }$. The results obtained using the comparative experimental real-world datasets Geolife and Gowalla are shown in Figure 4.

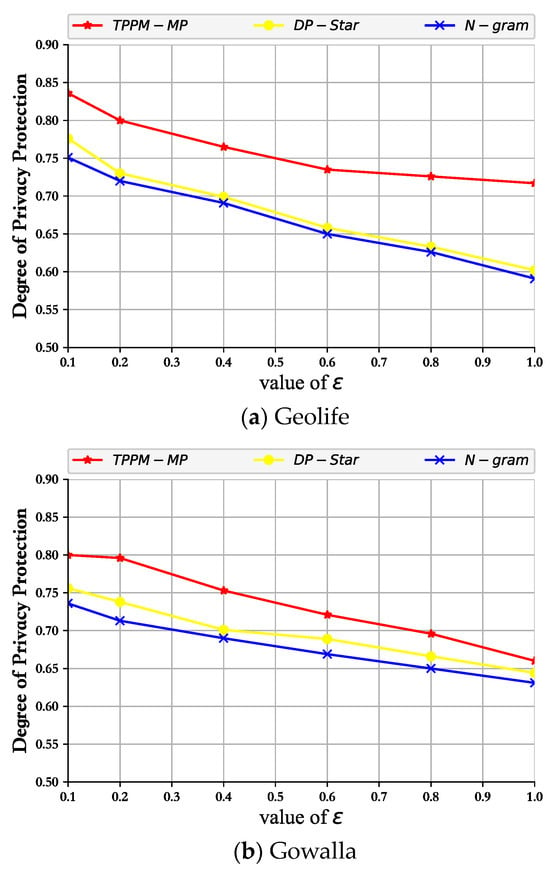
Figure 4. The effect of $\epsilon$ vs. PPD.

As shown in Figure 5, Figure 6 and Figure 7, the experimental results of TPPM-MP, N-gram, and DP-Star under different privacy budgets were assessed. Firstly, analyzing the curve shapes, that obtained via our mechanism was similar to those of the previously proposed mechanisms. Throughout the experimental results, the values of the three metric mechanisms, precision, recall, and F-value, all increased with epsilon. This is mainly because our privacy-preserving mechanism is less tolerant of noise; therefore, when epsilon increased, it added a small amount of noise. This was also the reason why the data availability could be better realized. In addition, our approach had more outstanding performance metrics than the other two schemes, mainly because our privacy budget allocation mechanism and noise control output mechanism played a good role in ensuring that the published pseudo-trajectory data was highly similar to the actual trajectory data.

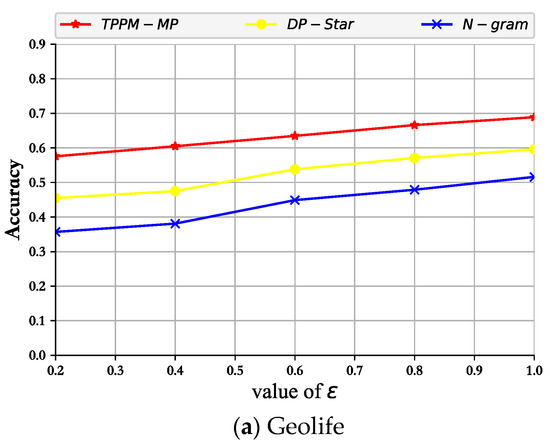
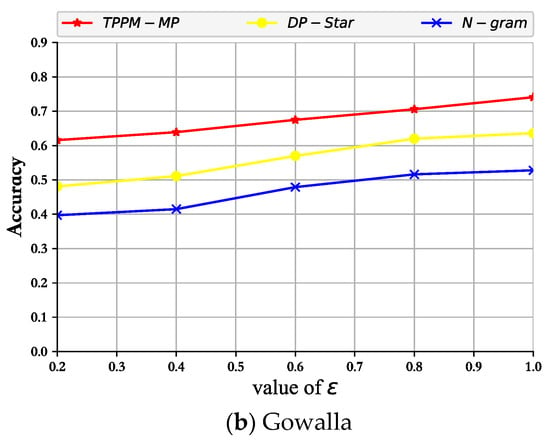
Figure 5. Variation of accuracy with privacy budget.

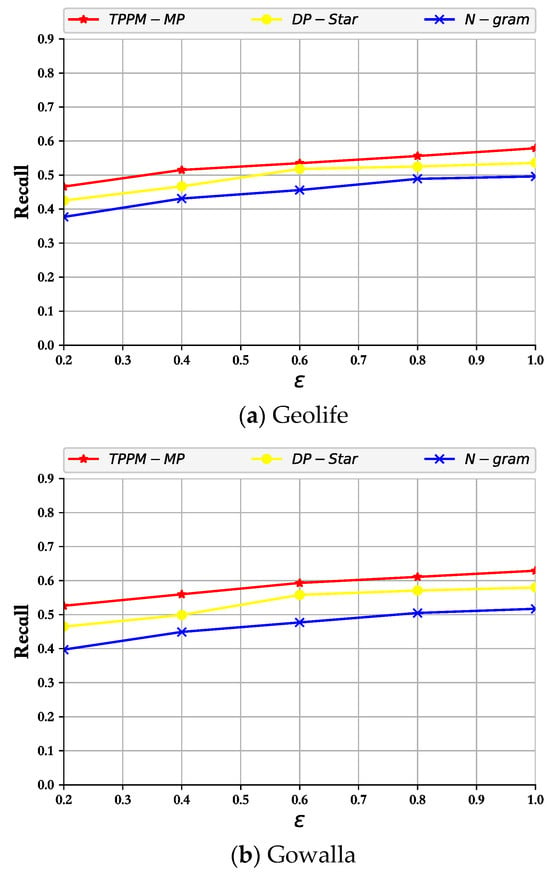
Figure 6. Recall rate variation with privacy budget.

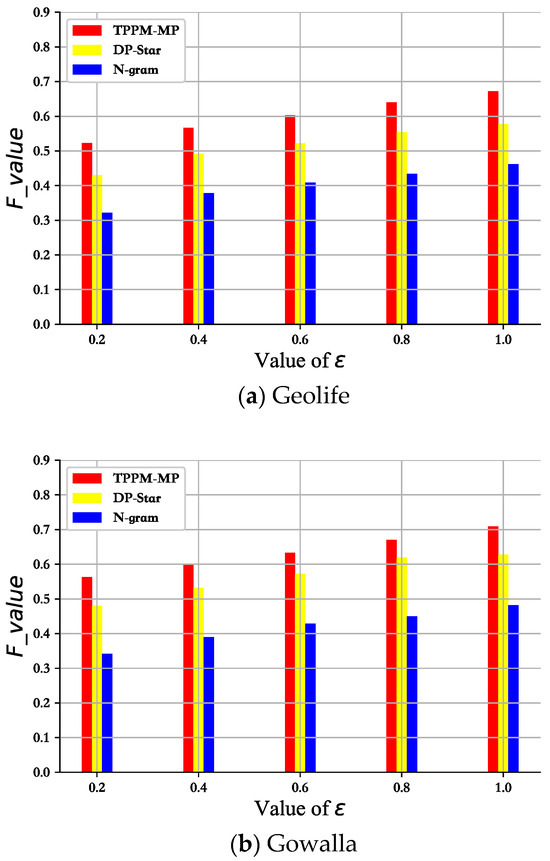
Figure 7. F-value vs. privacy budget.

The N-gram method first extracts the sensitive information in the trajectory data using a variable-length n-gram model. Then, it adds noise adaptively for each data in the trajectory sequence. This scheme adds too much noise data compared to our DPTP-LICD scheme, resulting in a significant difference between the generalized output trajectory data and the original trajectory. DP-Star also provides excellent control over the privacy budget compared with our mechanism but applies the minimal description principle to generalize the original trajectory sequence into a series of points that are representative of the trajectory. While this saves storage space and reduces budget allocation, it also guarantees the accuracy of some queries. However, this approach also makes the trajectory data more different from the original trajectory. In order to reflect the fairness and impartiality of the performance comparison experiment, we did not use the best p-value for the comparison experiment but used the average relative error to make the comparison, reconciling good p-values and bad p-values, so that the comparison experiment was closer to the fact and more objective. Especially as seen in Figure 8, we were able to achieve a relatively low average relative error with increasing privacy budget via DPTP-LICD compared with N-gram and DP-Star.

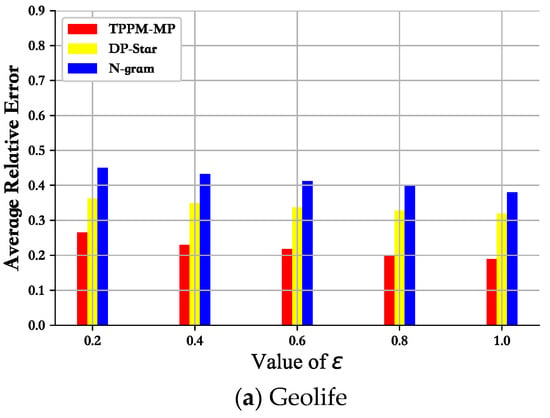
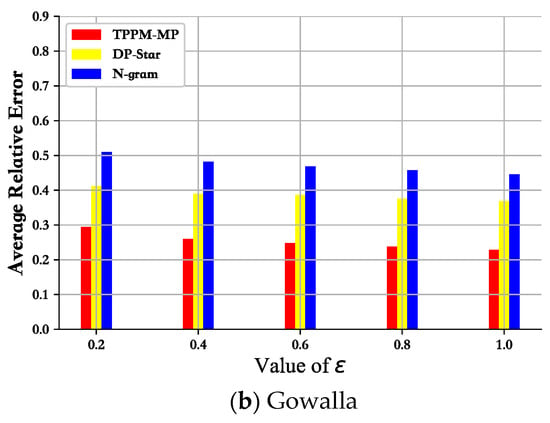
Figure 8. Mean relative error vs. privacy budget.

6. Conclusions and Outlook

In this paper, we present an RNN network based on multidimensional spatial–temporal attention, which considers local spatiotemporal correlation and global spatial–temporal correlation from different spatiotemporal dimensions, fully exploiting the dependencies in the multivariate time series and performing trajectory data prediction. The model is a specialized network architecture that integrates a LSTM network based on correlation attention with an attention mechanism, where the former is designed to extract important node features and transform them into higher-level features, thereby endowing the node features with sufficient expressive power, while the latter is employed to compute the correlation strength between nodes. The privacy budget is allocated according to the importance of the predicted location in the trajectory, and noise based on the localized differential privacy technique is added to enhance the usability of the released data under the premise of guaranteeing the privacy of the user’s trajectory. The proposed method described in this paper enhanced usability by 22% and 37% on the same dataset compared with the other methods tested, while providing equivalent privacy protection. The prediction model proposed in this paper can be applied not only in the field of trajectory prediction but also in the field of cross-domain data prediction, to visualize development trends, which is of practical significance for optimizing the future actions of decision makers. In the future, we will work on discovering more feasible and effective privacy-preserving solutions for trajectories, and our future work will shift to practical applications, as we strive to create cutting-edge technologies that are more optimized and reusable.