Spectral Properties of Dual Unit Gain Graphs

Abstract

In this paper, we study dual quaternion, dual complex unit gain graphs, and their spectral properties in a unified frame of dual unit gain graphs. Unit dual quaternions represent rigid movements in the 3D space, and have wide applications in robotics and computer graphics. Dual complex numbers have found application in brain science recently. We establish the interlacing theorem for dual unit gain graphs, and show that the spectral radius of a dual unit gain graph is always not greater than the spectral radius of the underlying graph, and these two radii are equal if, and only if, the dual gain graph is balanced. By using dual cosine functions, we establish the closed form of the eigenvalues of adjacency and Laplacian matrices of dual complex and quaternion unit gain cycles. We then show the coefficient theorem holds for dual unit gain graphs. Similar results hold for the spectral radius of the Laplacian matrix of the dual unit gain graph too.

1. Introduction

A gain graph assigns an element of a mathematical group to each of its edges, and if a group element is assigned to an edge, then the inverse of that group element is always assigned to the inverse edge of that edge [1,2,3]. If such a mathematical group consists of unit numbers of a number system, then the gain graph is called a unit gain graph. The real unit gain graph is called a signed graph. It was introduced by Harary [4] in 1953 in connection with the study of social balance and social psychology. Later, Zaslavsky [5,6] studied several combinatorial properties of signed graphs. In 2003, Hou, Li and Pan [7] studied the spectral properties of signed graphs. Also, see [8,9,10,11]. This was further extended to signed hypergraphs [12]. In 2012, Ref. [13] and Bapat et al. [14] started research on complex unit gain graphs independently. Since then, the study of complex unit gain graphs has grown explosively, including the line and subdivision graphs determined by ${\mathbb{T}}_4$-gain graphs [15], the rank of complex unit gain graphs [16], the multiplicity of an A$\alpha$-eigenvalue [17], and the determinant of the Laplacian matrix [18], etc. Then, starting in 2022, Belardo, Brunettia, Coble, Reff and Skogman [19] studied quaternion unit gain graphs and their associated spectral theories. Later, the determinant of the Laplacian matrix [20] and the row left rank [21] of a quaternion unit gain graph, etc., were studied. The study of unit gain graphs and their spectral properties forms an important part of algebraic graph theory.

Dual numbers, dual quaternions, dual complex numbers, and their applications have a long history. It was British mathematician William Kingdon Clifford who introduced dual numbers in 1873 [22]. Then, German mathematician Eduard Study introduced dual angles in 1903 [23]. These started the study and application of dual numbers in kinematics, dynamics, robotics and brain science [24,25,26,27,28]. Especially, the unit dual quaternion is an efficient mathematical tool to describe rigid body movement in the 3D space [27]. A unit dual quaternion serves as both a specification of the configuration (position and orientation) of a rigid body and a transformation, taking the coordinates of a point from one frame to another via rotation and translation. It has wide applications in robot control [24], formation control [27], hand-eye calibration [25,26], and simultaneous localization and mapping [29], etc. Recently, dual complex numbers have found application in brain science [28]. Very recently, eigenvalues of dual quaternion Hermitian matrices, as well as dual quaternion unit gain graphs, were applied to multi-agent formation control [30]. This stimulated us to study the spectral properties of dual quaternion unit gain graphs further.

In this paper, we study dual quaternion unit gain graphs as well as dual complex unit gain graphs. We combine them in a unified frame as dual unit gain graphs. Dual real unit gain graphs are nothing but signed graphs. We adopt this unified approach to avoid unnecessary repetitions.

In the next section, we review some preliminary information concerning gain graphs, dual elements and dual matrices. We study some basic properties of dual unit gain graphs in Section 3. By using dual cosine functions, we establish the closed form of the eigenvalues of adjacency and Laplacian matrices of dual complex and quaternion unit gain cycles. In Section 4, we discuss the properties of the eigenvalues of adjacency matrices of dual unit gain graphs. We establish the interlacing theorem and show that the spectral radius of a dual unit gain graph is always not greater than the spectral radius of the underlying graph, and these two radii are equal if, and only if, the dual unit gain graph is balanced. We show the coefficient theorem holds for dual unit gain graphs in Section 5. Similar results hold for the spectral radius of the Laplacian matrix of the dual unit gain graph too. We consider these in Section 6. We present several examples and numerical experiments in Section 7. Some concluding remarks are presented in Section 8.

2. Gain Graphs, Dual Elements and Dual Matrices

The field of real numbers, the field of complex numbers and the ring of quaternions are denoted by $\mathbb{R},\mathbb{C}$ and $\mathbb{H}$, respectively. Here, by $\mathbb{H}$, we mean the ring of the Hamiltonian quaternions, i.e., the skew field of quaternions. Following [30], we use $\mathbb{G}$ to represent them, i.e., $\mathbb{G}$ may be $\mathbb{R}$ or $\mathbb{C}$ or $\mathbb{H}$.

2.1. Gain Graphs

Suppose $G=(V,E)$ is a graph, where $V:=\{v_1,v_2,\dots ,v_n\}$ and $E:=\left\{e_{ij}\right\}$. Define $n:=\left|V\right|$ and $m:=\left|E\right|$. The degree of a vertex $v_j$ is denoted by $d_j=\mathrm{deg}\left(v_j\right)$ and the maximum degree is $\Delta =max{d}_j$. An oriented edge from $v_i$ to $v_j$ is denoted by $e_{ij}$. The set of oriented edges, denoted by $\overrightarrow{E}\left(G\right)$, contains two copies of each edge with opposite directions. Then, $\left|\overrightarrow{E}\right|=2m$. Even though $e_{ij}$ stands for an edge and an oriented edge simultaneously, it will always be clear in the content. G is also referred to as a bidirectional graph since both orientations of each edge are considered.

A gain graph is a triple $\Phi =(G,\Omega ,\phi )$ consisting of an underlying graph $G=(V,E)$, the gain group $\Omega$ and the gain function $\phi :\overrightarrow{E}\left(G\right)\to \Omega$ such that $\phi \left(e_{ij}\right)={\phi }^{-1}\left(e_{ji}\right)$. The gain group may be $\{1,-1\}$, or ${\mathbb{C}}^{\times }=\{p\in \mathbb{C}|p\ne 0\}$, or $\mathbb{T}=\{p\in \mathbb{C}|\left|p\right|=1\}$, etc. If the gain group $\Omega$ consists of unit elements, then such a gain graph is called a unit gain graph. If there is no potential confusion, then we simply denote the gain graph as $\Phi =(G,\phi )$.

A switching function is a function $\zeta :V\to \Omega$ that switches the $\Omega$-gain graph $\Phi =(G,\phi )$ to ${\Phi }^{\zeta }=(G,{\phi }^{\zeta })$, where

$${\phi }^{\zeta }\left(e_{ij}\right)={\zeta }^{-1}\left(v_i\right)\phi \left(e_{ij}\right)\zeta \left(v_j\right).$$

In this case, $\Phi$ and ${\Phi }^{\zeta }$ are switching equivalents, denoted by $\Phi \sim {\Phi }^{\zeta }$. Further, denote the switching class of $\Phi$ as $[\Phi ]$, which is the set of gain graphs switching equivalent to $\Phi$. The gain of a walk $W=v_1{e}_{12}{v}_2{e}_{23}{v}_3\cdots v_{k-1}{e}_{(k-1)k}{v}_k$ is

$$\phi \left(W\right)=\phi \left(e_{12}\right)\phi \left(e_{23}\right)\cdots \phi \left(e_{(k-1)k}\right).$$

(1)

A walk W is neutral if $\phi \left(W\right)=1_{\Omega }$, where $1_{\Omega }$ is the identity of $\Omega$. An edge set $S\subseteq E$ is balanced if every cycle $C\subseteq S$ is neutral. A subgraph is balanced if its edge set is balanced.

Let $\Phi =(G,\Omega ,\phi )$ be a gain graph and $A(\Phi )=\left(a_{ij}(\Phi )\right)$ and $L(\Phi )$ be the adjacency and Laplacian matrices of $\Phi$, respectively. Define $A(\Phi )$ and $L(\Phi )$ via the gain function $\phi \left(e\right)$ as follows,

$$A(\Phi )=\left(a_{ij}(\Phi )\right)\mathrm{with}{a}_{ij}(\Phi )=\left\{\begin{array}{cc}\phi \left(e_{ij}\right),& \mathrm{if}{e}_{ij}\in E(\Phi ),\hfill \\ 0,& \mathrm{otherwise},\hfill \end{array}\right.$$

(2)

and

$$L(\Phi )=D(\Phi )-A(\Phi ).$$

(3)

Here, $\phi \left(e_{ij}\right)\in \Omega$, $\phi \left(e_{ij}\right)=\phi {\left(e_{ji}\right)}^{-1}$, and $D(\Phi )\in {\mathbb{R}}^{n\times n}$ is a diagonal matrix with each diagonal element being the degree of the corresponding vertex in its underlying graph G.

Denote by $-\Phi$ the gain graph $(G,\Omega ,-\phi )$ obtained by replacing the gain of each edge with its opposite. Clearly, $A(-\Phi )=-A(\Phi )$. Furthermore, $\Phi$ is antibalanced if, and only if, $-\Phi$ is balanced.

A potential function is a function $\theta :V\to \Omega$ such that for every $e_{ij}\in E(\Phi )$,

$$\phi \left(e_{ij}\right)=\theta {\left(v_i\right)}^{-1}\theta \left(v_j\right).$$

(4)

We write $(G,1_{\Omega })$ as the $\Omega$-gain graph with all neutral edges. Note the potential function $\theta$ is not unique since for any $q\in \Omega$, $\tilde{\theta }\left(v_i\right)=q\theta \left(v_i\right)$ for all $v_i\in V$ is also a potential function of $\Phi$.

The following result can be deduced from [6]. Also, see [19].

Lemma 1.

Let $\Phi =(G,\Omega ,\phi )$ be a gain graph. Then, the following are equivalent:

(i) 

Φ is balanced.

(ii) 

$\Phi \sim (G,1_{\Omega })$.

(iii) 

φ has a potential function.

2.2. Dual Elements

Denote $ϵ$ as the infinitesimal unit, satisfying $ϵ\ne 0$ and ${ϵ}^2=0$. Here, $ϵ$ is a symbol. It is not a real number, a complex number, or a quaternion, but belongs to a different set of numbers entirely called dual numbers. The symbol $ϵ$ is commutative with numbers in $\mathbb{G}$. If $a_s,a_d\in \mathbb{R}$, then $a=a_s+a_dϵ\in \widehat{\mathbb{R}}$ is a dual number. Similarly, if $a_s,a_d\in \mathbb{C}$, then $a=a_s+a_dϵ\in \widehat{\mathbb{C}}$ is a dual complex number; if $a_s,a_d\in \mathbb{H}$, then $a=a_s+a_dϵ\in \widehat{\mathbb{H}}$ is a dual quaternion number. Here, $\widehat{\mathbb{R}},\widehat{\mathbb{C}}$ and $\widehat{\mathbb{H}}$ denote the ring of dual numbers, dual complex numbers and dual quaternion numbers, respectively. We use $\widehat{\mathbb{G}}$ to represent them in general. We call an element in $\widehat{\mathbb{G}}$ a dual element.

A dual element $a=a_s+a_dϵ\in \widehat{\mathbb{G}}$ has a standard part $a_s\in \mathbb{G}$ and a dual part $a_d\in \mathbb{G}$. The conjugate of a is defined as $a^{\ast }=a_s^{\ast }+a_d^{\ast }ϵ$, where $a_s^{\ast }$ and $a_d^{\ast }$ are the conjugates of numbers $a_s$ and $a_d$, respectively. Note that if $a\in \widehat{\mathbb{R}}$, then $a^{\ast }=a$. If $a_s\ne 0$, then we say that a is appreciable. Otherwise, we say that a is infinitesimal. The real part of a is defined by $Re\left(a\right)=Re\left(a_s\right)+Re\left(a_d\right)ϵ$, where $Re\left(a_s\right)$ and $Re\left(a_d\right)$ are the real parts of the numbers $a_s$ and $a_d$, respectively. The standard part $a_s$ and the dual part $a_d$ of a are denoted by $St\left(a\right)$ and $Du\left(a\right)$, respectively.

Suppose we have two dual elements $a=a_s+a_dϵ$ and $b=b_s+b_dϵ$. Then, their sum is $a+b=(a_s+b_s)+(a_d+b_d)ϵ$, and their product is $ab=a_s{b}_s+(a_s{b}_d+a_d{b}_s)ϵ$. In this way, $\widehat{\mathbb{G}}$ is a ring. In particular, $\widehat{\mathbb{R}}$ and $\widehat{\mathbb{C}}$ are two commutative rings, while $\widehat{\mathbb{H}}$ is a noncommutative ring.

Suppose we have two dual numbers $a=a_s+a_dϵ\in \widehat{\mathbb{R}}$ and $b=b_s+b_dϵ\in \widehat{\mathbb{R}}$. By [31], if $a_s>b_s$, or $a_s=b_s$ and $a_d>b_d$, then we say $a>b$. Then, this defines positive, nonnegative dual numbers, etc.

For a dual element $p=p_s+p_dϵ\in \widehat{\mathbb{G}}$, its squared norm is a nonnegative dual number defined by

$${\left|p\right|}^2=p^{\ast }p=p{p}^{\ast }=p_s^{\ast }{p}_s+(p_s^{\ast }{p}_d+p_d^{\ast }{p}_s)ϵ,$$

where $p_s^{\ast }{p}_s={\left|p_s\right|}^2$ and $p_s^{\ast }{p}_d+p_d^{\ast }{p}_s=p_s{p}_d^{\ast }+p_d{p}_s^{\ast }\in \mathbb{R}$. The magnitude of p is defined as a nonnegative dual number as follows:

$$|p|:=\left\{\begin{array}{cc}|p_s|+{\displaystyle \frac{(p_s^{\ast }{p}_d+p_d^{\ast }{p}_s)}{2|p_s|}}ϵ,& \mathrm{if}{p}_s\ne 0,\hfill \\ |p_d|ϵ,& \mathrm{otherwise}.\hfill \end{array}\right.$$

(5)

The dual element p is invertible if, and only if, $p_s\ne 0$. Furthermore, if p is invertible, then $p^{-1}={\displaystyle \frac{p^{\ast }}{{\left|p\right|}^2}}$.

We study unit dual complex and quaternion numbers in a unified frame as unit dual elements. We denote this group by $\widehat{\mathbb{V}}$. Then,

$$\widehat{\mathbb{V}}=\{p\in \widehat{\mathbb{G}}\left|\right|p|=1\}.$$

A unit dual number is either 1 or $-1$.

A dual complex number $p=p_s+p_dϵ$ is a unit dual complex number if, and only if, $|p_s|=1$ and $p_s^{\ast }{p}_d+p_d^{\ast }{p}_s=0$. We denote this group by $\widehat{\mathbb{T}}$. Then,

$$\widehat{\mathbb{T}}=\{p\in \widehat{\mathbb{C}}\left|\right|p|=1\}.$$

A dual quaternion number $p=p_s+p_dϵ$ is a unit dual quaternion number if, and only if, $|p_s|=1$ and $p_s^{\ast }{p}_d+p_d^{\ast }{p}_s=0$. We denote this group by $\widehat{\mathbb{U}}$. Then,

$$\widehat{\mathbb{U}}=\{p\in \widehat{\mathbb{H}}\left|\right|p|=1\}.$$

A unit dual element is always invertible and its inverse is its conjugate. The product of two unit dual elements is still a unit dual element. Hence, the set of unit dual elements forms a group by multiplication.

Given a graph G and a certain gain function $\phi :\overrightarrow{E}\left(G\right)\to \widehat{\mathbb{V}}$. We call $\Phi =(G,\widehat{\mathbb{V}},\phi )$ a dual unit gain graph. Thus, $\Phi$ may be a dual quaternion unit gain graph, a dual complex unit gain graph, or a signed graph if $\widehat{\mathbb{V}}=\widehat{\mathbb{U}},\widehat{\mathbb{T}},\{\pm 1\}$, respectively.

Lemma 2.

Let $q_1$ and $q_2\in \widehat{\mathbb{G}}$ be two dual elements. Then,

(i) 

$Re\left(q_1\right)\le \left|q_1\right|$ and the equality holds if, and only if, $q_1$ is a nonnegative dual number.

(ii) 

$Re\left(q_1\right)=Re\left(q_1^{\ast }\right)$ and $Re\left(q_1{q}_2\right)=Re\left(q_2{q}_1\right)$.

(iii) 

$|q_1{q}_2|=|q_1\left|\right|q_2|$.

(iv) 

$|q_1+q_2|\le |q_1|+|q_2|$.

(v) 

$Re\left(q_1^{\ast }{q}_2{q}_1\right)=Re\left(q_2\right){\left|q_1\right|}^2$.

Two dual elements p and q are similar if there is an appreciable dual element u such that $p=u^{-1}qu$, denoted by $p\sim q$. We also denote by $\left[q\right]$ the equivalence class containing q. In Lemma 2.1 of [32], it was shown that any quaternion number is similar to a complex number and the real part and the absolute value of the imaginary part of these two numbers are the same. In the following theorem, we generalize this result to dual quaternion numbers.

Theorem 1.

Suppose $q=q_s+q_dϵ\in \widehat{\mathbb{H}}$. Then, there exists $a\in \widehat{\mathbb{C}}$ belonging to $\left[q\right]$. In other words, for any dual quaternion number $q\in \widehat{\mathbb{H}}$, there is $u\in \widehat{\mathbb{U}}$ and $a\in \widehat{\mathbb{C}}$ such that $a=u^{\ast }qu.$ Furthermore, there is $Re\left(q\right)=Re\left(a\right)$ and $\left|Im\right(q\left)\right|=\left|Im\right(a\left)\right|$.

Proof. 

Denote $q_s=q_0+q_{11}\mathbf{i}+q_{12}\mathbf{j}+q_{13}\mathbf{k}$, ${\mathbf{q}}_1={[q_{11},q_{12},q_{13}]}^{\top }$, $q_d=q_2+q_{31}\mathbf{i}+q_{32}\mathbf{j}+q_{33}\mathbf{k}$, ${\mathbf{q}}_3={[q_{31},q_{32},q_{33}]}^{\top }$, and $a=u^{\ast }qu$. Consider the following two cases:

Suppose that $q_s\equiv q_0\in \mathbb{R}$. Let $x=q_{31}+\parallel {\mathbf{q}}_3\parallel -q_{33}\mathbf{j}+q_{32}\mathbf{k}$, $u_s={\displaystyle \frac{x}{\left|x\right|}}$, $u_d=0$. Then, it follows from Lemma 2.1 in [32] that $q_{d}x=x(q_2+\parallel {\mathbf{q}}_3\parallel \mathbf{i}).$ Thus, $u_s^{\ast }{q}_d{u}_s=x^{-1}{q}_{d}x=q_2+\parallel {\mathbf{q}}_3\parallel \mathbf{i}$ and

$$\begin{array}{ccc}\hfill a=u^{\ast }qu& =& u_s^{\ast }{q}_s{u}_s+(u_s^{\ast }{q}_s{u}_d+u_d^{\ast }{q}_s{u}_s+u_s^{\ast }{q}_d{u}_s)ϵ\hfill \\ & =& u_s^{\ast }{u}_s{q}_s+(u_s^{\ast }{u}_d+u_d^{\ast }{u}_s)q_sϵ+u_s^{\ast }{q}_d{u}_sϵ\hfill \\ & =& q_s+u_s^{\ast }{q}_d{u}_sϵ\hfill \\ & =& q_0+(q_2+\parallel {\mathbf{q}}_3\parallel \mathbf{i})ϵ\in \widehat{\mathbb{C}}.\hfill \end{array}$$

Furthermore, there is $Re\left(q\right)=Re\left(a\right)=q_0+q_2ϵ$ and $\left|Im\left(q\right)\right|=|Im\left(q_d\right)|ϵ=\parallel {\mathbf{q}}_3\parallel ϵ=|Im\left(a\right)|$.

Suppose that $q_s\in \mathbb{H}$. Let $x=q_{11}+\parallel {\mathbf{q}}_1\parallel -q_{13}\mathbf{j}+q_{12}\mathbf{k}$, $u_s={\displaystyle \frac{x}{\left|x\right|}}$, and $u_d={\displaystyle \frac{1}{2}}{u}_{s}t$, where $t=t_{11}\mathbf{i}+t_{12}\mathbf{j}+t_{13}\mathbf{k}$ is an infinitesimal quaternion. Then, $u\in \widehat{\mathbb{U}}$ for any t. We may verify that $q_{s}x=x(q_0+\parallel {\mathbf{q}}_1\parallel \mathbf{i})$. It follows from Lemma 2.1 in [32] that $a_s=u_s^{\ast }{q}_s{u}_s=x^{-1}{q}_{s}x=q_0+\parallel {\mathbf{q}}_1\parallel \mathbf{i}\in \mathbb{C}$. Thus, $Re\left(p_s\right)=Re\left(a_s\right)$ and $|Im\left(p_s\right)|=|Im\left(a_s\right)|$. Next, we focus on the dual part of $u^{\ast }qu$. By direct computation, we have

$$\begin{array}{ccc}\hfill a_d=Du\left(u^{\ast }qu\right)& =& u_d^{\ast }{q}_s{u}_s+u_s^{\ast }{q}_s{u}_d+u_s^{\ast }{q}_d{u}_s\hfill \\ & =& u_d^{\ast }{u}_s{u}_s^{\ast }{q}_s{u}_s+u_s^{\ast }{q}_s{u}_s{u}_s^{\ast }{u}_d+u_s^{\ast }{q}_d{u}_s\hfill \\ & =& u_d^{\ast }{u}_s{a}_s+a_s{u}_s^{\ast }{u}_d+u_s^{\ast }{q}_d{u}_s\hfill \\ & =& {\displaystyle \frac{1}{2}}(-t{a}_s+a_{s}t)+u_s^{\ast }{q}_d{u}_s\hfill \\ & =& \parallel {\mathbf{q}}_1\parallel (t_{12}\mathbf{k}-t_{13}\mathbf{j})+u_s^{\ast }{q}_d{u}_s,\hfill \end{array}$$

where the last inequality follows from $\mathbf{i}\mathbf{j}=-\mathbf{j}\mathbf{i}=\mathbf{k}$ and $\mathbf{k}\mathbf{i}=-\mathbf{i}\mathbf{k}=\mathbf{j}$. Let $r=u_s^{\ast }{q}_d{u}_s=r_0+r_{11}\mathbf{i}+r_{12}\mathbf{j}+r_{13}\mathbf{k}\in \mathbb{H}$, $t_{11}=0$, $t_{12}=-r_{13}{\parallel {\mathbf{q}}_1\parallel }^{-1}$ and $t_{13}=r_{12}{\parallel {\mathbf{q}}_1\parallel }^{-1}$. Then, there is $a_d=Du\left(u^{\ast }qu\right)=r_0+r_{11}\mathbf{i}\in \mathbb{C}$, where $r_0=q_2$, $r_{11}={\mathbf{q}}_1^{\top }{\mathbf{q}}_3{\parallel {\mathbf{q}}_1\parallel }^{-1}$. Furthermore, there is $\left|Im\left(a\right)\right|=|\parallel {\mathbf{q}}_1\parallel +r_{11}ϵ|=\parallel {\mathbf{q}}_1\parallel +r_{11}ϵ$ and $\left|Im\left(q\right)\right|=|Im\left(q_s\right)+Im\left(q_d\right)ϵ|=\parallel {\mathbf{q}}_1\parallel +{\mathbf{q}}_1^{\top }{\mathbf{q}}_3{\parallel {\mathbf{q}}_1\parallel }^{-1}ϵ$. Thus, $\left|Im\right(a\left)\right|=\left|Im\right(q\left)\right|$.

This completes the proof. □

Let $a=a_s+a_dϵ\in \widehat{\mathbb{R}}$. A dual function $f\left(a\right)=f_s\left(a\right)+f_d\left(a\right)ϵ$ is analytic if, and only if, ${\displaystyle \frac{\partial f_s}{\partial a_d}}=0$ and ${\displaystyle \frac{\partial f_s}{\partial a_s}}={\displaystyle \frac{\partial f_d}{\partial a_d}}$[33]. From these, it follows $f\left(a\right)=f\left(a_s\right)+a_d{f}^{\prime }\left(a_s\right)ϵ$. Similar results hold for $a\in \widehat{\mathbb{C}}$. Then, the exponential function of a is

$$e^a=e^{a_s}+a_d{e}^{a_s}ϵ.$$

If a is appreciable, its logarithm function is

$$log\left(a\right)=log\left(a_s\right)+a_s^{-1}{a}_dϵ.$$

(6)

Let $\theta ={\theta }_s+{\theta }_dϵ\in \widehat{\mathbb{R}}$ be a dual angle. Then, the cosine function of $\theta$ is

$$cos\left(\theta \right)=cos\left({\theta }_s\right)-{\theta }_{d}sin\left({\theta }_s\right)ϵ.$$

(7)

Theorem 2.

Let $a=a_s+a_dϵ\in \widehat{\mathbb{C}}$. Then, the following results hold:

(i) 

For any unit dual complex number $a\in \widehat{\mathbb{T}}$, there is a dual angle $\theta ={\theta }_s+{\theta }_dϵ\in \widehat{\mathbb{R}}$ such that $a=e^{\mathbf{i}\theta }$. Here, $\theta =-\mathbf{i}log\left(a\right)=-\mathbf{i}(log\left(a_s\right)+a_s^{\ast }{a}_dϵ)$.

(ii) 

For any positive integer n, there is $a^{{\displaystyle \frac{1}{n}}}=e^{\mathbf{i}{\displaystyle \frac{\theta +2\pi j}{n}}}$ for any $j\in \mathbb{Z}.$

(iii) 

$cos\left(\theta \right)={\displaystyle \frac{1}{2}}\left(e^{\mathbf{i}\theta }+e^{-\mathbf{i}\theta }\right).$

Proof. 

(i) Since $|a_s|=1$, there exists ${\theta }_s=-\mathbf{i}log\left(a_s\right)$ such that $a_s=e^{\mathbf{i}{\theta }_s}$. Furthermore, let ${\theta }_d=-\mathbf{i}{a}_d{a}_s^{\ast }$. We can verify that $a_d=\mathbf{i}{\theta }_d{e}^{\mathbf{i}{\theta }_s}$. It follows from $a_d{a}_s^{\ast }+a_s{a}_d^{\ast }=0$ that ${\theta }_d\in \mathbb{R}$.

(ii) Let $z_0=e^{\mathbf{i}{\displaystyle \frac{\theta }{n}}}$. We can verify that ${\left(z_0\right)}^n=a$. Suppose that $z=c{z}_0$ and $z^n=a$. Then, we can verify that $c^n=1$. Thus, there is $z=e^{\mathbf{i}{\displaystyle \frac{\theta +2\pi j}{n}}}$ for any $j\in \mathbb{Z}$.

(iii) By direct computation, there is

$$\begin{array}{ccc}\hfill e^{\mathbf{i}\theta }+e^{-\mathbf{i}\theta }& =& e^{\mathbf{i}{\theta }_s}+\mathbf{i}{\theta }_d{e}^{\mathbf{i}{\theta }_s}ϵ+e^{-\mathbf{i}{\theta }_s}-\mathbf{i}{\theta }_d{e}^{-\mathbf{i}{\theta }_s}ϵ\hfill \\ & =& 2cos\left({\theta }_s\right)+\mathbf{i}{\theta }_d(e^{\mathbf{i}{\theta }_s}-e^{-\mathbf{i}{\theta }_s})\hfill \\ & =& 2cos\left({\theta }_s\right)-{\theta }_{d}sin\left({\theta }_s\right)\hfill \\ & =& 2cos\left(\theta \right).\hfill \end{array}$$

This completes the proof. □

An n-dimensional dual vector is denoted by $\mathbf{x}={(x_1,\dots ,x_n)}^{\top }$, where $x_1,\dots ,x_n\in \widehat{\mathbb{G}}$ are dual elements. We may denote $\mathbf{x}={\mathbf{x}}_s+{\mathbf{x}}_dϵ$, where ${\mathbf{x}}_s$ and ${\mathbf{x}}_d$ are two n-dimensional vectors in ${\mathbb{G}}^n$. The 2-norm of $\mathbf{x}$ is defined as

$${\parallel \mathbf{x}\parallel }_2=\left\{\begin{array}{cc}\sqrt{{\sum }_{i=1}^n{\left|x_i\right|}^2},\hfill & \mathrm{if}{\mathbf{x}}_s\ne \mathbf{0},\hfill \\ \parallel {\mathbf{x}}_d{\parallel }_2ϵ,\hfill & \mathrm{if}{\mathbf{x}}_s=\mathbf{0}.\hfill \end{array}\right.$$

If ${\mathbf{x}}_s\ne \mathbf{0}$, then we say that $\mathbf{x}$ is appreciable. Denote ${\mathbf{x}}^{\ast }=(x_1^{\ast },\dots ,x_n^{\ast })$ as the conjugate of $\mathbf{x}$. Let $\mathbf{y}={(y_1,\dots ,y_n)}^{\top }$ be another n-dimensional dual vector. Define

$${\mathbf{x}}^{\ast }\mathbf{y}=\sum _{j=1}^n{x}_j^{\ast }{y}_j.$$

If ${\mathbf{x}}^{\ast }\mathbf{y}=0$, we say that $\mathbf{x}$ and $\mathbf{y}$ are orthogonal. Note that ${\mathbf{x}}^{\ast }\mathbf{x}={\parallel \mathbf{x}\parallel }_2^2$. Let ${\mathbf{x}}_1,\dots ,{\mathbf{x}}_n\in {\widehat{\mathbb{G}}}^n$ be n dual vectors. If ${\mathbf{x}}_i^{\ast }{\mathbf{x}}_j=0$ for $i\ne j$ and ${\mathbf{x}}_i^{\ast }{\mathbf{x}}_j=1$ for $i=j$, $i,j=1,\dots ,n$, then we say that ${\mathbf{x}}_1,\dots ,{\mathbf{x}}_n$ form an orthonormal basis of the n-dimensional dual vector space.

2.3. Dual Matrices

Assume that $A=A_s+A_dϵ$ and $B=B_s+B_dϵ$ are two dual matrices in ${\widehat{\mathbb{G}}}^{n\times n}$, where n is a positive integer, $A_s,A_d,B_s$ and $B_d$ are four matrices in ${\mathbb{G}}^{n\times n}$. If $AB=BA=I$, where I is the $n\times n$ identity matrix, then we say that B is the inverse of A and denote that $B=A^{-1}$. We have the following lemma:

Lemma 3.

Suppose that $A=A_s+A_dϵ\in {\widehat{\mathbb{G}}}^{n\times n}$ and $B=B_s+B_dϵ\in {\widehat{\mathbb{G}}}^{n\times n}$ are two dual matrices. Then, the following four statements are equivalent.

(a) $B=A^{-1}$;

(b) $AB=I$;

(c) $A_s{B}_s=I$ and $A_s{B}_d+A_d{B}_s=O$, where O is the $n\times n$ zero matrix;

(d) $B_s=A_s^{-1}$ and $B_d=-A_s^{-1}{A}_d{A}_s^{-1}$.

Given a dual matrix $A\in {\widehat{\mathbb{G}}}^{n\times n}$, denote its conjugate transpose as $A^{\ast }$. If $A^{\ast }=A^{-1}$, then A is called a dual unitary matrix. If a dual number matrix is a dual unitary matrix, then we simply call it a dual orthogonal matrix. Let $A\in {\widehat{\mathbb{G}}}^{n\times m}$. Then, the null space generated by A is

$$\mathrm{null}\left(A\right)=\{\mathbf{x}\in {\widehat{\mathbb{G}}}^n|A^{\ast }\mathbf{x}=0\},$$

and the span of A is

$$\mathrm{span}\left(A\right)=\{\mathbf{x}\in {\widehat{\mathbb{G}}}^n|\exists \mathbf{y}\in {\widehat{\mathbb{G}}}^m\mathrm{such}\mathrm{that}\mathbf{x}=A\mathbf{y}\}.$$

Theorem 3.

Let $U=[{\mathbf{u}}_1,\dots ,{\mathbf{u}}_n]\in {\widehat{\mathbb{G}}}^{n\times n}$ be such that its columns form an orthonormal basis in ${\widehat{\mathbb{G}}}^n$. Then, $U^{\ast }U=I$ and the following results hold:

(i) 

For any vector $\mathbf{x}\in {\widehat{\mathbb{G}}}^n$, there exists $\mathbf{y}\in {\widehat{\mathbb{G}}}^n$ such that $\mathbf{x}=U\mathbf{y}$.

(ii) 

Suppose that $1<k<n$ and $U=[U_1,U_2]$, where $U_1\in {\widehat{\mathbb{C}}}^{n\times k}$ and $U_2\in {\widehat{\mathbb{G}}}^{n\times (n-k)}$. Then, $\mathit{null}\left(U_1\right)=\mathit{span}\left(U_2\right)$.

Proof. 

(i) This result follows directly from $\mathbf{y}=U^{\ast }\mathbf{x}$ and $U{U}^{\ast }=I$.

(ii) By $U^{\ast }U=I$, we have $U_1^{\ast }{U}_2=O_{k\times (n-k)}$, the $k\times (n-k)$ zero matrix. Let $\mathbf{x}=U\mathbf{y}=U_1{\mathbf{y}}_1+U_2{\mathbf{y}}_2$, where ${\mathbf{y}}_1$ and ${\mathbf{y}}_2$ have the same partition as the columns of $U_1$ and $U_2$, respectively. On the one hand, if $\mathbf{x}\in \mathrm{null}\left(U_1\right)$, then ${\mathbf{y}}_1=U_1^{\ast }\mathbf{x}=\mathbf{0}$. Thus, $\mathbf{x}=U_2{\mathbf{y}}_2\in \mathrm{span}\left(U_2\right)$ and $\mathrm{null}\left(U_1\right)\subseteq \mathrm{span}\left(U_2\right)$. On the other hand, if $\mathbf{x}\in \mathrm{span}\left(U_2\right)$, then there exists ${\mathbf{y}}_2\in {\widehat{\mathbb{G}}}^{n-k}$ such that $\mathbf{x}=U_2{\mathbf{y}}_2$. Thus, $U_1^{\ast }\mathbf{x}=\mathbf{0}$ and $\mathrm{span}\left(U_2\right)\subseteq \mathrm{null}\left(U_1\right)$.

This completes the proof. □

Assume that $A\in {\widehat{\mathbb{G}}}^{n\times n}$ and $\lambda ={\lambda }_s+{\lambda }_dϵ\in \widehat{\mathbb{G}}$. If

$$A\mathbf{x}=\mathbf{x}\lambda ,$$

where $\mathbf{x}$ is appreciable, i.e., ${\mathbf{x}}_s\ne \mathbf{0}$, then $\lambda$ is called a right eigenvalue of A, with an eigenvector $\mathbf{x}$. Similarly, if

$$A\mathbf{x}=\lambda \mathbf{x},$$

(8)

where $\mathbf{x}$ is appreciable, i.e., ${\mathbf{x}}_s\ne \mathbf{0}$, then $\lambda$ is called a left eigenvalue of A, with an eigenvector $\mathbf{x}$. If $\widehat{\mathbb{G}}$ is $\widehat{\mathbb{R}}$ or $\widehat{\mathbb{C}}$, then the multiplication is commutative. In these two cases, it is not necessary to distinguish right and left eigenvalues. We just call them eigenvalues [34].

A Hermitian matrix in $\mathbb{G}$ means a symmetric matrix, or a complex Hermitian matrix, or a quaternion Hermitian matrix, depending upon $\mathbb{G}=\mathbb{R}$, or $\mathbb{C}$, or $\mathbb{H}$. Similarly, a dual Hermitian matrix in $\widehat{\mathbb{G}}$ means a dual symmetric matrix, or a dual complex Hermitian matrix, or a dual quaternion Hermitian matrix, depending upon $\widehat{\mathbb{G}}=\widehat{\mathbb{R}}$, or $\widehat{\mathbb{C}}$, or $\widehat{\mathbb{H}}$. By [34], a non-Hermitian dual number matrix may have no eigenvalue at all, or have infinitely many eigenvalues. However, a dual quaternion Hermitian matrix has exactly n dual number right eigenvalues [35]. As dual numbers are commutative with dual quaternions, they are also left eigenvalues. Thus, we may simply call them eigenvalues of A. Note that A may still have other left eigenvalues, which are not dual numbers. See an example of a quaternion matrix in [32].

Following [35], we may prove that if $A\in {\widehat{\mathbb{G}}}^{n\times n}$ is Hermitian, then it has exactly n dual number eigenvalues, with orthonormal eigenvectors. Furthermore, A is positive semidefinite (definite) if, and only if, its eigenvalues are nonnegative (positive).

If there is an $n\times n$ invertible dual matrix P such that $A=P^{-1}BP$, then we say that A and B are similar, and denote $A\sim B$. We have the following lemma:

Lemma 4.

Suppose that A and B are two $n\times n$ dual matrices, $A\sim B$, i.e., $A=P^{-1}BP$ for some $n\times n$ invertible dual matrix P, and λ is a right dual element eigenvalue of A with a dual element eigenvector $\mathbf{x}$. Then, λ is a right eigenvalue of B with an eigenvector $P\mathbf{x}$.

Suppose that $A=A_s+A_dϵ$, $\lambda ={\lambda }_s+{\lambda }_dϵ$ and $\mathbf{x}={\mathbf{x}}_s+{\mathbf{x}}_dϵ$. Then, (8) is equivalent to

$$A_s{\mathbf{x}}_s={\lambda }_s{\mathbf{x}}_s,$$

with ${\mathbf{x}}_s\ne \mathbf{0}$, i.e., ${\lambda }_s$ is an eigenvalue of $A_s$ with an eigenvector ${\mathbf{x}}_s$, and

$$(A_s-{\lambda }_{s}I){\mathbf{x}}_d-{\lambda }_d{\mathbf{x}}_s=-A_d{\mathbf{x}}_s.$$

Recently, several numerical methods for computing eigenvalues of dual quaternion Hermitian matrices arose. These include a Jacobi method [36], a power method [37], a bidiagonalization method [38], a Rayleigh quotient iteration method [39], and a supplement matrix method [30].

3. Dual Unit Gain Graphs

Let $\Phi =(G,\widehat{\mathbb{V}},\phi )$ be a dual unit gain graph. The adjacency and Laplacian matrices of $\Phi$ are defined by (2) and (3), respectively. Similar to Lemma 1, we have the following lemma for dual unit gain graphs:

Lemma 5.

Let $\Phi =(G,\widehat{\mathbb{V}},\phi )$ be a dual unit gain graph. Then, the following are equivalent:

(i) 

Φ is balanced.

(ii) 

$\Phi \sim (G,1_{\widehat{\mathbb{V}}})$.

(iii) 

φ has a potential function.

Let $\Phi =(G,\widehat{\mathbb{V}},\phi )$ be a dual unit gain graph with n vertices. Then, the adjacency matrix $A(\Phi )$ and the Laplacian matrix $L(\Phi )$ are two $n\times n$ dual Hermitian matrices. Thus, each of $A(\Phi )$ and $L(\Phi )$ has n eigenvalues. The set of the n eigenvalues of $A(\Phi )$ is called the spectrum of $\Phi$, and is denoted as ${\sigma }_A(\Phi )$, while the set of the n eigenvalues of $L(\Phi )$ is called the Laplacian spectrum of $\Phi$, and is denoted as ${\sigma }_L(\Phi )$. We also denote the eigenvalue sets of the adjacency and Laplacian matrices of the underlying graph G as ${\sigma }_A\left(G\right)$ and ${\sigma }_L\left(G\right)$, respectively. We have the following theorem:

Theorem 4.

Let $\Phi =(G,\widehat{\mathbb{V}},\phi )$ be a dual unit gain graph with n vertices. If Φ is balanced, then ${\sigma }_A(\Phi )={\sigma }_A\left(G\right)$ and ${\sigma }_L(\Phi )={\sigma }_L\left(G\right)$. Furthermore, the spectrum ${\sigma }_A(\Phi )$ consists of n real numbers, while the Laplacian spectrum ${\sigma }_L(\Phi )$ consists of one zero and $n-1$ positive numbers.

Proof. 

By Lemma 5, we have $\Phi \sim {\Phi }^1:=(G,1_{\widehat{\mathbb{V}}})$. Then, ${\Phi }^1$ is exactly the underlying graph G, and the adjacency and the Laplacian matrices of ${\Phi }^1$ are the adjacency and Laplacian matrices of G, respectively. It follows from $\Phi \sim {\Phi }^1$ that there exists a function $\zeta$ such that for all $e_{ij}\in E(\Phi )$, there is

$${\zeta }^{-1}\left(v_i\right)\phi \left(e_{ij}\right)\zeta \left(v_j\right)=1.$$

Thus, we have

$$A\left({\Phi }^1\right)=Z^{-1}A(\Phi )Z,\mathrm{where}Z=\mathrm{diag}(\zeta \left(v_1\right),\dots ,\zeta \left(v_n\right)),$$

and $L\left({\Phi }^1\right)=D\left({\Phi }^1\right)-A\left({\Phi }^1\right)=Z^{-1}(D(\Phi )-A(\Phi ))Z=Z^{-1}L(\Phi )Z$. Here, the second equality follows from $D\left({\Phi }^1\right)=D(\Phi )\in {\mathbb{R}}^{n\times n}$. In other words, $A\left({\Phi }^1\right)$ and $L\left({\Phi }^1\right)$ are similar with $A(\Phi )$ and $L(\Phi )$, respectively. Now, the conclusions of this theorem follow from Lemma 4 and the spectral properties of adjacency and Laplacian matrices of ordinary graphs. □

If G is a tree, then $\Phi$ is balanced, and the eigenvalues of the adjacency and the Laplacian matrices of $\Phi$ are the same with those of the adjacency and Laplacian matrices of G, respectively. For instance, a path is a special tree. Let $P_n$ be the path on n vertices and $\Phi =(P_n,\widehat{\mathbb{T}},\phi$). Then, the eigenvalues of $A(\Phi )$ and $L(\Phi )$ can be calculated as

$${\sigma }_A(\Phi )=\left\{2cos\left({\displaystyle \frac{\pi j}{n+1}}\right):j\in \{1,\dots ,n\}\right\},$$

(9)

and

$${\sigma }_L(\Phi )=\left\{2-2cos\left({\displaystyle \frac{\pi j}{n}}\right):j\in \{0,\dots ,n-1\}\right\},$$

respectively.

The closed form of the adjacency and Laplacian eigenvalues of a $\mathbb{T}$-gain cycle is presented in Theorem 6.1 in [13]. Let $C_n$ be the cycle on n vertices and $\Phi =(C_n,\mathbb{T},\phi$) and $\phi \left(C_n\right)=e^{i\theta }\in \mathbb{T}$. Then, the eigenvalues of $A(\Phi )$ and $L(\Phi )$ can be calculated as

$${\sigma }_A(\Phi )=\left\{2cos\left({\displaystyle \frac{\theta +2\pi j}{n}}\right):j\in \{0,\dots ,n-1\}\right\},$$

(10)

and

$${\sigma }_L(\Phi )=\left\{2-2cos\left({\displaystyle \frac{\theta +2\pi j}{n}}\right):j\in \{0,\dots ,n-1\}\right\},$$

(11)

respectively. Very recently, [19] studied the unit quaternion cycles $\Phi =(C_n,\mathbb{U},\phi$) with gain $q=\phi \left(C_n\right)\in \mathbb{U}$. They showed that $\Phi$ is similar with a unit complex cycle ${\Phi }^{\zeta }$. Furthermore, we denote $Re\left(q\right)+\left|Im\left(q\right)\right|\mathbf{i}=e^{\mathbf{i}\theta }$. Then, (10) and (11) are also eigenvalues of $A(\Phi )$ and $L(\Phi )$ of unit quaternion cycles, respectively. By using the dual element version of exponential, logarithm and cosine functions, we extend this result to dual complex and quaternion unit gain cycles.

Theorem 5.

Let $C_n:=v_1{e}_{12}{v}_2\cdots v_n{e}_{n1}{v}_1$ be the cycle on n vertices and $\Phi =(C_n,\widehat{\mathbb{V}},\phi )$. Suppose $q=\phi \left(C_n\right)\in \widehat{\mathbb{V}}$. Then, the following results hold:

(i) 

There exists a switching function $\zeta :V(\Phi )\to \widehat{\mathbb{V}}$ such that ${\phi }^{\zeta }\left(e_{i,i+1}\right)=1$ for $i=1,\dots ,n-1$ and ${\phi }^{\zeta }\left(e_{n,1}\right)=q$.

(ii) 

Suppose $\widehat{\mathbb{V}}=\widehat{\mathbb{T}}$. Then, there exists a dual angle $\theta =-\mathbf{i}log\left(q\right)\in \widehat{\mathbb{R}}$ such that the eigenvalues of $A(\Phi )$ and $L(\Phi )$ can be calculated by (10) and (11), respectively. Here, the dual logarithm and the dual cosine functions are defined by (6) and (7), respectively.

(iii) 

Suppose $\widehat{\mathbb{V}}=\widehat{\mathbb{U}}$. Then, there exists a dual complex number $a\in \widehat{\mathbb{T}}$ and another switching function ${\zeta }_1:V(\Phi )\to \widehat{\mathbb{V}}$ such that ${\phi }^{{\zeta }_1}\left(e_{i,i+1}\right)=1$ for $i=1,\dots ,n-1$ and ${\phi }^{{\zeta }_1}\left(e_{n,1}\right)=a$. Let $\theta =-\mathbf{i}log\left(a\right)\in \widehat{\mathbb{R}}$. Then, the eigenvalues of $A(\Phi )$ and $L(\Phi )$ can be calculated by (10) and (11), respectively.

Proof. 

(i)

Define the switching function $\zeta :V(\Phi )\to \widehat{\mathbb{V}}$ as follows:

$$\zeta \left(v_i\right)=\left\{\begin{array}{cc}1,\hfill & i=1,\hfill \\ {\left({\Pi }_{j=1}^{i-1}\phi \left(e_{j,j+1}\right)\right)}^{-1},\hfill & i=2,\dots ,n.\hfill \end{array}\right.$$

Then, there is

$${\phi }^{\zeta }\left(e_{12}\right)=\zeta {\left(v_1\right)}^{-1}\phi \left(e_{12}\right)\zeta \left(v_2\right)=\phi \left(e_{12}\right)\phi {\left(e_{12}\right)}^{-1}=1.$$

For $i=2,\dots ,n-1$, there is

$$\begin{array}{ccc}\hfill {\phi }^{\zeta }\left(e_{i,i+1}\right)& =& \zeta {\left(v_i\right)}^{-1}\phi \left(e_{i,i+1}\right)\zeta \left(v_{i+1}\right)\hfill \\ & =& {\Pi }_{j=1}^{i-1}\phi \left(e_{j,j+1}\right)\phi \left(e_{i,i+1}\right){\left({\Pi }_{j=1}^i\phi \left(e_{j,j+1}\right)\right)}^{-1}\hfill \\ & =& 1.\hfill \end{array}$$

For $i=n$, there is

$$\begin{array}{ccc}\hfill {\phi }^{\zeta }\left(e_{n,1}\right)& =& \zeta {\left(v_n\right)}^{-1}\phi \left(e_{n,1}\right)\zeta \left(v_1\right)={\Pi }_{j=1}^{n-1}\phi \left(e_{j,j+1}\right)\phi \left(e_{n,1}\right)=\phi \left(C_n\right).\hfill \end{array}$$

(ii)

The proof is a slight modification of Theorem 6.1 in [13]. Let

$$P=\left(\begin{array}{ccccc}0& 1& 0& \cdots & 0\\ 0& 0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & \ddots & 0\\ 0& 0& 0& \cdots & 1\\ q& 0& 0& \cdots & 0\end{array}\right),$$

and $\mathbf{x}=\left(x_i\right)\in {\widehat{\mathbb{C}}}^n$ be an eigenvector of P corresponding to the eigenvalue $\lambda$. Then, there is $x_{i+1}=\lambda x_i$ for $i=1,\dots ,n-1$ and $q{x}_1=\lambda x_n$. Thus, there is $(q-{\lambda }^n)x_1=0$. $x_1$ must be an appreciable dual number since $\mathbf{x}$ is appreciable and $x_i={\lambda }^{i-1}{x}_1$ for $i=2,\dots ,n$. Thus, $q={\lambda }^n$. It follows from Theorem 2 that $\lambda =e^{\mathbf{i}{\displaystyle \frac{\theta +2\pi j}{n}}}$ for $j=0,\dots ,n-1$.

Furthermore, we have $P{P}^{\ast }=I$ and $A=P+P^{\ast }=P+P^{-1}$. Thus, the eigenvalue of A is equal to $\lambda +{\lambda }^{-1}$. By Theorem 2, there is $\lambda +{\lambda }^{-1}=2cos\left({\displaystyle \frac{\theta +2\pi j}{n}}\right)$. This derives the closed form of ${\sigma }_A(\Phi )$. The closed form of ${\sigma }_L(\Phi )$ follows directly from $L(\Phi )=2I-A(\Phi )$.

(iii)

By Theorem 1, there exists $u\in \widehat{\mathbb{U}}$ such that $a=u^{\ast }qu\in \widehat{\mathbb{T}}$. Let ${\zeta }_1\left(v_i\right)=\zeta \left(v_i\right)u$ for $i=1,\dots ,n$. Then, there is ${\zeta }_1:V(\Phi )\to \widehat{\mathbb{V}}$ such that ${\phi }^{{\zeta }_1}\left(e_{i,i+1}\right)=1$ for $i=1,\dots ,n-1$ and ${\phi }^{{\zeta }_1}\left(e_{n,1}\right)=a$. The result of this item follows directly from that of item (ii).

This completes the proof. □

4. Eigenvalues of Adjacency Matrices

In the following theorem, we show that the switching class of dual unit gain graphs has a unique adjacency spectrum.

Theorem 6.

Let ${\Phi }_1=(G,{\phi }_1)$ and ${\Phi }_2=(G,{\phi }_2)$ be two $\widehat{\mathbb{V}}$-gain graphs. If ${\Phi }_1\sim {\Phi }_2$, then ${\Phi }_1$ and ${\Phi }_2$ have the same spectrum. That is, ${\sigma }_A\left({\Phi }_1\right)={\sigma }_A\left({\Phi }_2\right)$.

Proof. 

This theorem follows directly from Lemma 4 and $A\left({\Phi }_1\right)\sim A\left({\Phi }_2\right)$. □

Let $\Phi =(G,\phi )$ be a $\widehat{\mathbb{V}}$-gain graph, and S be a subset of V. Denote $\Phi \left[S\right]$ as the induced subgraph of $\Phi$ with vertex set S, and $\Phi -S$ as $\Phi [V\setminus S]$, respectively. Both the adjacency matrices $A(\Phi )$ and $A(\Phi [S\left]\right)$ are Hermitian matrices. As stated in Section 2, an $n\times n$ dual Hermitian matrix has exactly n eigenvalues, which are dual numbers. The following theorem shows the eigenvalues of $A(\Phi )$ interlace with those of $A(\Phi [S\left]\right)$.

Theorem 7.

(Interlacing Theorem) Let $\Phi =(G,\phi )$ be a $\widehat{\mathbb{V}}$-gain graph with n vertices and S be a subset of V with k vertices. Denote the eigenvalues of $A(\Phi )$ and $A(\Phi [S\left]\right)$ by

$${\lambda }_1\ge {\lambda }_2\cdots \ge {\lambda }_n\mathit{and}{\mu }_1\ge {\mu }_2\ge \cdots \ge {\mu }_k,$$

respectively. Then, the following inequalities hold:

$${\lambda }_i\ge {\mu }_i\ge {\lambda }_{n+i-k},\forall 1\le i\le k.$$

(12)

Proof. 

Suppose the orthonormal basis eigenvectors of $A(\Phi )$ and $A(\Phi [S\left]\right)$ are $\{{\mathbf{x}}_1,\dots ,{\mathbf{x}}_n\}$ and $\{{\mathbf{y}}_1,\dots ,{\mathbf{y}}_k\}$, respectively. Without loss of generality, assume

$$A(\Phi )=\left[\begin{array}{cc}A(\Phi [S\left]\right)& X^{\ast }\\ X& Z\end{array}\right].$$

For $1\le i\le k$, define the following vector spaces:

$$U_i=\mathrm{span}({\mathbf{x}}_i,\dots ,{\mathbf{x}}_n),V_i=\mathrm{span}({\mathbf{y}}_1,\dots ,{\mathbf{y}}_i),W_i=\left\{\left(\begin{array}{c}\mathbf{y}\\ 0\end{array}\right)\in {\widehat{\mathbb{C}}}^n,\mathbf{y}\in V_i\right\}.$$

By Theorem 4.4 in [40] and Theorem 3 (ii), we have

$${\lambda }_i=\underset{\mathbf{x}\in U_i}{max}{\parallel \mathbf{x}\parallel }^{-2}\left({\mathbf{x}}^{\ast }A(\Phi )\mathbf{x}\right)\mathrm{and}{\mu }_i=\underset{\mathbf{y}\in V_i}{min}{\parallel \mathbf{y}\parallel }^{-2}\left({\mathbf{y}}^{\ast }A(\Phi \left[S\right])\mathbf{y}\right).$$

Furthermore, the following system

$$\left[\begin{array}{cccc}{U}_{is}& O& -W_{is}& O\\ U_{id}& U_{is}& -W_{id}& -W_{is}\end{array}\right]\left[\begin{array}{c}{\mathbf{v}}_s\\ {\mathbf{v}}_d\\ {\mathbf{z}}_s\\ {\mathbf{z}}_d\end{array}\right]=\left[\begin{array}{c}O\\ O\end{array}\right]$$

always has solutions since the size of its coefficient matrix is $2n\times (2n+2)$. Let $\mathbf{v}={\mathbf{v}}_s+{\mathbf{v}}_dϵ$ and $\mathbf{z}={\mathbf{z}}_s+{\mathbf{z}}_dϵ$. Then, there exists ${\mathbf{w}}_i=U_i\mathbf{v}=W_i\mathbf{z}\in U_i\cap W_i$. Since ${\mathbf{w}}_i\in W_i$, there exists ${\mathbf{p}}_i\in {\widehat{\mathbb{G}}}^k$ such that ${\mathbf{w}}_i=\left(\begin{array}{c}{\mathbf{p}}_i\\ 0\end{array}\right)$. Then, we derive that

$${\lambda }_i\ge \parallel {\mathbf{w}}_i{\parallel }^{-2}\left({\mathbf{w}}_i^{\ast }A(\Phi ){\mathbf{w}}_i\right)={\parallel {\mathbf{p}}_i\parallel }^{-2}\left({{\mathbf{p}}_i}^{\ast }A(\Phi \left[S\right]){\mathbf{p}}_i\right)\ge {\mu }_i.$$

This proves the first part in (12).

The second inequality in (12) can be derived by choosing

$$U_i=\mathrm{span}({\mathbf{x}}_1,\dots ,{\mathbf{x}}_{n+i-k}),V_i=\mathrm{span}({\mathbf{y}}_i,\dots ,{\mathbf{y}}_k),W_i=\left\{\left(\begin{array}{c}v\\ 0\end{array}\right)\in {\widehat{\mathbb{G}}}^n,v\in V_i\right\},$$

and we do not repeat the details here. □

Corollary 1.

Let $\Phi =(G,\phi )$ be a $\widehat{\mathbb{V}}$-gain graph with n vertices. For any vertex $v\in V$, the eigenvalues of $A(\Phi )$ and of $A(\Phi -v)$ are labeled in decreasing order of interlace as follows:

$${\lambda }_1(\Phi )\ge {\lambda }_1(\Phi -v)\ge {\lambda }_2(\Phi )\ge {\lambda }_2(\Phi -v)\ge \cdots \ge {\lambda }_{n-1}(\Phi -v)\ge {\lambda }_n(\Phi ).$$

The following theorem presents some results for the eigenvalues and eigenvectors of the adjacency matrix of a dual unit gain graph.

Theorem 8.

Let $\Phi =(G,\phi )$ be a $\widehat{\mathbb{V}}$-gain graph with n vertices and $A=A(\Phi )$ be the adjacency matrix. Suppose $\lambda ={\lambda }_s+{\lambda }_dϵ$ is an eigenvalue of A and $\mathbf{x}={\mathbf{x}}_s+{\mathbf{x}}_dϵ={(x_1,\dots ,x_n)}^{\top }$ is its corresponding unit eigenvector. Then, the following results hold:

(i) 

The eigenvalue satisfies

$$\lambda ={\mathbf{x}}^{\ast }A\mathbf{x}=\sum _{e_{ij}\in E(\Phi )}2Re\left(x_i^{\ast }\phi \left(e_{ij}\right)x_j\right).$$

(ii) 

${\lambda }_s$ is an eigenvalue of the matrix $A_s$ with an eigenvector ${\mathbf{x}}_s$.

(iii) 

The dual part satisfies ${\lambda }_d={\mathbf{x}}_s^{\ast }{A}_d{\mathbf{x}}_s$. Furthermore, if $A_s$ has n simple eigenvalues ${\lambda }_{s,i}$ with associated unit eigenvectors ${\mathbf{x}}_{s,i}$’s. Then, A has exactly n eigenvalues ${\lambda }_i={\lambda }_{s,i}+{\lambda }_{d,i}ϵ$ with associated eigenvectors ${\mathbf{x}}_i={\mathbf{x}}_{s,i}+{\mathbf{x}}_{d,i}ϵ$, $i=1,\dots ,n$, where

$${\lambda }_d={\mathbf{x}}_s^{\ast }{A}_d{\mathbf{x}}_s\mathit{and}{\mathbf{x}}_{d,i}=\sum _{j\ne i}{\displaystyle \frac{{\mathbf{x}}_{s,j}{\mathbf{x}}_{s,j}^{\ast }(A_d-{\lambda }_{d,i}{I}_n){\mathbf{x}}_{s,i}}{{\lambda }_{s,i}-{\lambda }_{s,j}}}.$$

(iv) 

Two eigenvectors of A, associated with two eigenvalues with distinct standard parts, are orthogonal to each other.

These results follow directly from [35] and we omit the details of their proofs here. We should point out that when the multiplicity of ${\lambda }_s$ is greater than one, not all eigenvectors of $A_s$ corresponding to ${\lambda }_s$ are the standard part of an eigenvector of A. More discussions in this direction and a supplement matrix method for computing all eigenvalues of dual Hermitian matrices can be found in [30].

In general, the spectral radius of a dual matrix is not well defined since a dual matrix may have no eigenvalue at all or have infinitely many eigenvalues. Fortunately, the adjacency and Laplacian matrices of dual unit gain graphs are Hermitian matrices. When the dual matrix is Hermitian, all of its eigenvalues are dual numbers and we are able to define their order by [31]. Here, let ${\rho }_A\left(G\right)$ be the adjacency spectral radius of the underlying graph G and ${\rho }_A(\Phi )$ be the adjacency spectral radius of the unit gain graph $\Phi$, respectively. The following theorem generalizes that of signed graphs [1,41] and complex unit gain graphs [42].

Theorem 9.

Let $\Phi =(G,\phi )$ be a $\widehat{\mathbb{V}}$-gain graph. Then,

$${\rho }_A(\Phi )\le {\rho }_A\left(G\right).$$

(13)

Furthermore, if Φ is connected, then ${\lambda }_1(\Phi )={\rho }_A\left(G\right)$ (resp. $-{\lambda }_n(\Phi )={\rho }_A\left(G\right)$) if, and only if, Φ is balanced (resp. antibalanced). Here, ${\lambda }_1(\Phi )$ and ${\lambda }_n(\Phi )$ are the largest and the smallest eigenvalues of $A(\Phi )$, respectively.

Proof. 

Denote $A=A\left(G\right)$, and $B=\left(B_{ij}\right)=A(\Phi )=B_s+B_dϵ$ with $B_{ij}=B_{ijs}+B_{ijd}ϵ=\phi \left(e_{ij}\right)$. Suppose $\mathbf{x}\in {\widehat{\mathbb{G}}}^n$ is a unit eigenvector of B corresponding to an eigenvalue $\lambda$ of B. Let $\mathbf{y}=\left|\mathbf{x}\right|$. Then, we have

$$\begin{array}{ccc}\hfill \left|\lambda \right|& =& |{\mathbf{x}}^{\ast }B\mathbf{x}|\hfill \\ \hfill & =& 2\left|\sum _{e_{ij}\in E(\Phi )}Re\left(x_i^{\ast }\phi \left(e_{ij}\right)x_j\right)\right|\hfill \\ \hfill & \le & 2\sum _{e_{ij}\in E(\Phi )}\left|x_i^{\ast }\phi \left(e_{ij}\right)x_j\right|\hfill \\ \hfill & =& 2\sum _{e_{ij}\in E(\Phi )}|x_i^{\ast }\left|\right|\phi \left(e_{ij}\right)\left|\right|x_j|\hfill \\ \hfill & =& 2\sum _{e_{ij}\in E(\Phi )}|x_i^{\ast }\left|\right|x_j|\hfill \\ \hfill & =& {\mathbf{y}}^{\ast }A\left(G\right)\mathbf{y},\hfill \end{array}$$

(14)

where the first and the second equalities follow from Theorem 8 (i), the first inequality and the third equality follow from Lemma 2, and the fourth equality follows from $\phi \left(e_{ij}\right)\in \widehat{\mathbb{T}}$ for any $e_{ij}\in E(\Phi )$.

Therefore,

$$St\left(\right|\lambda \left|\right)\le St\left({\mathbf{y}}^{\ast }A\left(G\right)\mathbf{y}\right)\le {\rho }_A\left(G\right).$$

If $St\left(\right|\lambda \left|\right)<{\rho }_A\left(G\right)$ for any eigenvalue $\lambda$ of B, then ${\rho }_A(\Phi )<{\rho }_A\left(G\right)$. Otherwise, if there exists an eigenvalue $\lambda$ of B satisfying $St\left(\right|\lambda |)=St\left({\mathbf{y}}^{\ast }A\left(G\right)\mathbf{y}\right)={\rho }_A\left(G\right)$, we claim that ${\lambda }_d=0$.

By Theorem 8, we have

$${\lambda }_d={\mathbf{x}}_s^{\ast }{B}_d{\mathbf{x}}_s=\sum _{e_{ij}\in E(\Phi )}{x}_{is}^{\ast }{B}_{ijd}{x}_{js}=\sum _{e_{ij}\in E(\Phi )\cap {\mathcal{A}}_x}{x}_{is}^{\ast }{B}_{ijd}{x}_{js},$$

where ${\mathcal{A}}_x=\left\{e_{ij}\right|x_{is}\ne 0,x_{js}\ne 0\}$. Since $St\left(\right|\lambda \left|\right)=St\left({\mathbf{y}}^{\ast }A\left(G\right)\mathbf{y}\right)$, the equality of the standard part holds true in (14). Here, $St\left(\right|\lambda \left|\right)$ is the standard part of $\left|\lambda \right|$. Therefore, for all $e_{ij}\in E(\Phi )\cap {\mathcal{A}}_x$, we have

$$B_{ijs}={\displaystyle \frac{x_{is}}{|x_{is}|}}{\displaystyle \frac{x_{js}^{\ast }}{|x_{js}|}}.$$

(15)

Since each element in B is a unit dual complex number, there is $B_{ijs}^{\ast }{B}_{ijd}+B_{ijd}^{\ast }{B}_{ijs}=0$ for all $e_{ij}\in E(\Phi )$. Therefore,

$$\begin{array}{ccc}\hfill {\lambda }_d& =& Re\left({\mathbf{x}}_s^{\ast }{B}_d{\mathbf{x}}_s\right)\hfill \\ & =& \sum _{e_{ij}\in E(\Phi )\cap {\mathcal{A}}_x}Re\left(x_{is}^{\ast }{B}_{ijd}{x}_{js}\right)\hfill \\ & =& \sum _{e_{ij}\in E(\Phi )\cap {\mathcal{A}}_x}Re\left(B_{ijd}{B}_{ijs}^{\ast }\right)|x_{is}\left|\right|x_{js}|\hfill \\ & =& {\displaystyle \frac{1}{2}}\sum _{e_{ij}\in E(\Phi )\cap {\mathcal{A}}_x}Re\left(B_{ijd}{B}_{ijs}^{\ast }+B_{jid}{B}_{jis}^{\ast }\right)|x_{is}\left|\right|x_{js}|\hfill \\ & =& {\displaystyle \frac{1}{2}}\sum _{e_{ij}\in E(\Phi )\cap {\mathcal{A}}_x}Re\left(B_{ijd}{B}_{ijs}^{\ast }+B_{ijd}^{\ast }{B}_{ijs}\right)|x_{is}\left|\right|x_{js}|\hfill \\ & =& 0.\hfill \end{array}$$

Here, the first equality follows from the fact that ${\lambda }_d$ is a real number, the third equality follows from (15) and Lemma 2 (v), the fourth equality repeats all edges twice, the fifth equality follows from the fact that B is Hermitian, and the last equality holds because $B_{ijd}^{\ast }{B}_{ijs}=-B_{ijs}^{\ast }{B}_{ijd}$ and Lemma 2 (ii). This proves $\left|\lambda \right|\le {\rho }_A\left(G\right)$ for any eigenvalue $\lambda$ of $A(\Phi )$. Thus, ${\rho }_A(\Phi )\le {\rho }_A\left(G\right)$.

We now prove the second conclusion of this theorem. Since $\Phi$ is connected, $A\left(G\right)$ is a real irreducible nonnegative matrix. It follows from the Perron–Frobenius Theorem that ${\rho }_A\left(G\right)$ is an eigenvalue of $A\left(G\right)$, i.e., the largest eigenvalue ${\lambda }_1\left(G\right)={\rho }_A\left(G\right)$. Furthermore, the eigenvector corresponding to ${\lambda }_1\left(G\right)$ is real and positive.

On the one hand, suppose that ${\lambda }_1(\Phi )={\rho }_A\left(G\right)$, then the inequality (14) holds with equality and ${\mathbf{y}}^{\ast }A\left(G\right)\mathbf{y}={\rho }_A\left(G\right)$. Suppose $\mathbf{x}\in {\widehat{\mathbb{G}}}^n$ is a unit eigenvector of $A(\Phi )$ corresponding to the eigenvalue ${\lambda }_1(\Phi )$. This implies that $\mathbf{y}=\left|\mathbf{x}\right|$ and

$$c_{ij}:=x_i^{\ast }\phi \left(e_{ij}\right)x_j=|x_i^{\ast }\left|\right|x_j|$$

is a positive real number for all $e_{ij}\in E$ and ${\mathbf{y}}_s$ is the Perron–Frobenius eigenvector of $A\left(G\right)$. Since ${\mathbf{y}}_s$ is a positive vector, $|x_i|>0$ and $x_i$ is invertible for all $i=1,\dots ,n$. Therefore,

$$\phi \left(e_{ij}\right)={\left(x_i^{\ast }\right)}^{-1}{c}_{ij}{x}_j^{-1}=c_{ij}{\displaystyle \frac{x_i}{|x_i{|}^2}}{\displaystyle \frac{x_j^{\ast }}{|x_j{|}^2}}={\displaystyle \frac{x_i}{|x_i|}}{\displaystyle \frac{x_j^{\ast }}{|x_j|}},$$

where the last equality follows from $\left|\phi \right(e_{ij}\left)\right|=1$. In other words,

$$\theta \left(v_i\right)={\displaystyle \frac{x_i^{\ast }}{|x_i|}}$$

is a potential function of $\Phi$. This verifies that $\Phi$ is balanced.

On the other hand, suppose $\Phi$ is balanced. It follows from Theorem 6 that $A(\Phi )$ and $A\left(G\right)$ share the same set of eigenvalues. Therefore, ${\lambda }_1\left(G\right)={\lambda }_1(\Phi )$ and

$${\rho }_A(\Phi )\le {\rho }_A\left(G\right)={\lambda }_1\left(G\right)={\lambda }_1(\Phi )\le {\rho }_A(\Phi ),$$

where the first inequality follows from (13) and the second equality follows from the Perron–Frobenius Theorem. Hence, ${\lambda }_1(\Phi )={\rho }_A\left(G\right)$.

Finally, the last conclusion follows from $-{\lambda }_n(\Phi )={\lambda }_1(-\Phi )$ and $\Phi$ is antibalanced if, and only if, $-\Phi$ is balanced.

This completes the proof. □

The following result follows partially from the Gershgorian-type theorem for dual quaternion Hermitian matrices in [43].

Theorem 10.

Let $\Phi =(G,\phi )$ be a $\widehat{\mathbb{V}}$-gain graph. Then,

$${\rho }_A(\Phi )\le \Delta .$$

The equality holds if, and only if, G is Δ-regular and either Φ or $-\Phi$ is balanced. Here, Δ is the maximum vertex degree of G.

Proof. 

Suppose $\lambda \in \widehat{\mathbb{G}}$ is an eigenvalue of $A(\Phi )$ and $\mathbf{x}$ is its corresponding eigenvector; namely, $A(\Phi )\mathbf{x}=\lambda \mathbf{x}$. Let $i\in arg{max}_l\left|x_l\right|$. Then, we have

$$\left|\lambda \right||x_i|=|\lambda x_i|=\left|\sum _{j\ne i}\phi \left(e_{ij}\right)x_j\right|\le \sum _{j\ne i}|\phi \left(e_{ij}\right)\left|\right|x_j|.$$

Therefore,

$$\left|\lambda \right|\le \underset{i}{max}\sum _{j\ne i}\left|\phi \left(e_{ij}\right)\right|=\underset{i}{max}{d}_i=\Delta .$$

Furthermore, it is well known that, if G is a simple connected graph with maximum vertex degree $\Delta$, then ${\rho }_A\left(G\right)\le \Delta$, and the equality holds if, and only if, G is regular. By Theorem 9, the equality in this proposition holds if, and only if, G is $\Delta$-regular and either $\Phi$ or $-\Phi$ is balanced. This completes the proof. □

5. Coefficient Theorems of Characteristic Polynomials

Let $A=\left(a_{ij}\right)$ be a Hermitian matrix in ${\mathbb{G}}^{n\times n}$ and $\sigma$ be a permutation of $S_n=\{1,\dots ,n\}$. Write $\sigma$ as a product of the disjoint cycles, i.e.,

$$\sigma =(n_{11}\cdots n_{1l_1})(n_{21}\cdots n_{2l_2})\cdots (n_{r1}\cdots n_{r{l}_r}),$$

where $n_{i1}<n_{ij}$ for all $j>1$ and $n_{11}>n_{21}>\cdots >n_{r1}$ for each $i=1,\dots ,r$. Then, the Moore determinant for quaternion matrices, defined by Eliakim Hastings Moore [44], is written as follows,

$$\mathrm{Mdet}\left(A\right)=\sum _{\sigma \in S_n}\left|\sigma \right|a_{\sigma },$$

(16)

where $\left|\sigma \right|={(-1)}^r$ denotes the parity of $\sigma$ and

$$a_{\sigma }=(a_{n_{11},n_{12}}{a}_{n_{12},n_{13}}\cdots a_{n_{1l_1},n_{11}})(a_{n_{21},n_{22}}\cdots a_{n_{2l_2},n_{21}})\cdots (\cdots a_{n_{r{l}_r},n_{r1}}).$$

For more results on the Moore determinant, please refer to [45,46].

The adjacency and Laplacian matrices of a unit gain graph are Hermitian matrices. To study their characteristic polynomials, we need to consider the determinants of these matrices. When the Hermitian matrix is complex or real, we may use the ordinary determinant. However, if the matrix is quaternion, as the multiplication is not commutative, the ordinary determinant is not well defined. Then, the Moore determinant may be used as in [19].

Recently, [47] studied the Moore determinant of dual Hermitian matrices. Given a dual Hermitian matrix $A\in {\widehat{\mathbb{G}}}^{n\times n}$, $\mathrm{Mdet}\left(A\right)=0$ if, and only if, $A_s$ is singular and there exist at least one zero or two infinitesimal eigenvalues. The value $\mathrm{Mdet}\left(A\right)$ equals to the product of the eigenvalues of A. These pave a way for studying the characteristic polynomials of such dual Hermitian matrices.

We now study the Coefficient Theorem for dual complex and quaternion unit gain graphs. This extends the Coefficient Theorem of simple graphs [48], signed graphs [49], $\mathbb{T}$-gain graphs [42], and $\mathbb{U}$-gain graphs [19]. We begin with the following lemma:

Lemma 6.

Let $\Phi =(G,\phi )$ be a $\widehat{\mathbb{V}}$-gain graph and let $\mathcal{C}\left(G\right)$ be the set of cycles of G. Then, the following function

$$\mathcal{R}:C\in \mathcal{C}(G)\to Re(\phi ({\overrightarrow{C}}_v))\in \widehat{\mathbb{R}}$$

(17)

is well defined and independent of the choice of $v\in C$ and the direction of the directed cycle ${\overrightarrow{C}}_v$.

Proof. 

Let $v_1=v$, ${\overrightarrow{C}}_v=v_1{e}_{12}{v}_2\cdots v_l{e}_{l1}{v}_1$ and ${\overrightarrow{C}}_v^{-1}=v_1{e}_{1l}{v}_l\cdots v_2{e}_{21}{v}_1$. Then, $\phi ({\overrightarrow{C}}_v),\phi ({\overrightarrow{C}}_v^{-1})\in \widehat{\mathbb{V}}$ and $\phi ({\overrightarrow{C}}_v)\phi ({\overrightarrow{C}}_v^{-1})=1$. Therefore, the two dual unit elements $\phi ({\overrightarrow{C}}_v)$ and $\phi ({\overrightarrow{C}}_v^{-1})$ are conjugate and share the same real parts. In other words, $\mathcal{R}({\overrightarrow{C}}_v)$ is independent of the direction of the cycle.

Furthermore, let $w=v_t$ with $t\in \{2,\dots ,l\}$ and ${\overrightarrow{C}}_w=v_t{e}_{t,t+1}{v}_{t+1}\cdots v_{t-1}{e}_{t-1,t}{v}_t$. Denote $q_1=\phi (e_{12})\cdots \phi (e_{t-1,t})$ and $q_2=\phi (e_{t,t+1})\cdots \phi (e_{l,1})$. Then, there is $\phi ({\overrightarrow{C}}_v)=q_1{q}_2$, $\phi ({\overrightarrow{C}}_w)=q_2{q}_1$, and

$$Re(\phi ({\overrightarrow{C}}_v))=Re(q_1{q}_2)=Re(q_2{q}_1)=Re(\phi ({\overrightarrow{C}}_w)).$$

The proof is completed. □

Let $C_r$ denote the cycle of order r and let $K_r$ be the complete graph with r vertices. An elementary graph is any graph in the set $\{K_2,C_r(r\ge 3)\}$ and a basic graph is the disjoint union of elementary graphs. Suppose B is a basic graph. Denote $\mathcal{C}\left(B\right)$ as the class of cycles in B, $p\left(B\right)$ as the number of components of B. Let ${\mathcal{B}}_n\left(G\right)$ be the set of subgraphs of G that are basic graphs with n vertices and

$$c\left(B\right)=\left|\mathcal{C}\left(B\right)\right|,\mathcal{R}\left(B\right)={\Pi }_{C\in \mathcal{C}\left(B\right)}\mathcal{R}\left(C\right).$$

Here, $\mathcal{R}(·)$ is defined by (17).

Theorem 11

(Coefficient Theorem). Let $\Phi =(G,\phi )$ be a $\widehat{\mathbb{V}}$-gain graph with n vertices. Then,

$$\mathrm{Mdet}\left(A(\Phi )\right)=\sum _{B\in {\mathcal{B}}_n\left(G\right)}{(-1)}^{n+p\left(B\right)}{2}^{c\left(B\right)}\mathcal{R}\left(B\right).$$

Furthermore, let $p_{A(\Phi )}\left(x\right)=x^n+{\sum }_{i=1}^n{c}_i{x}^{n-i}$ be the characteristic polynomial of $A(\Phi )$. Then,

$$c_i=\sum _{B\in {\mathcal{B}}_i\left(G\right)}{(-1)}^{p\left(B\right)}{2}^{c\left(B\right)}\mathcal{R}\left(B\right).$$

Proof. 

By Lemma 6, the results can be derived following the same proof with that of [19] and we omit the details here. □

As the eigenvalues of a dual Hermitian matrix are dual numbers, the coefficients of the characteristic polynomial of a dual Hermitian matrix are also dual numbers. It is difficult to handle such a polynomial. Furthermore, the roots of such a characteristic polynomial are not necessary to be eigenvalues of the dual Hermitian matrix. For instance, the roots of ${(\lambda -1)}^2=0$ are $1+bϵ$ for all $b\in \mathbb{R}$. See [30] for more details.

We may take another approach to solve this problem. Suppose that $A(\Phi )=A_s(\Phi )+A_d(\Phi )ϵ$. Then, we may calculate the coefficients of the characteristic polynomial of $A_s(\Phi )$ by the coefficient theorem for complex or quaternion unit gain graphs. Note that this polynomial is of real coefficients as $A_s(\Phi )$ is a complex or quaternion Hermitian matrix and if ${\lambda }_s$ is a root of this characteristic polynomial, then it is the standard part of an eigenvalue $\lambda$ of $A(\Phi )$. If ${\lambda }_s$ is a single root of this characteristic polynomial, then by [30], we have $\lambda ={\lambda }_s+{\lambda }_dϵ$, where ${\lambda }_d={\mathbf{x}}_s^{\ast }{A}_d(\Phi ){\mathbf{x}}_s$ and ${\mathbf{x}}_s$ is a unit eigenvector of $A_s(\Phi )$, associated with ${\lambda }_s$. If ${\lambda }_s$ is a k-multiple root of this characteristic polynomial, then by [30], there are k eigenvalues ${\lambda }_i={\lambda }_s+{\lambda }_{di}ϵ$ of $A(\Phi )$, for $i=1,\dots ,k$, where ${\lambda }_{d1},\dots ,{\lambda }_{dk}$ are eigenvalues of the supplement matrix $W^{\ast }{A}_d(\Phi )W$, $W=({\mathbf{v}}_1,\dots ,{\mathbf{v}}_k)$ and ${\mathbf{v}}_1,\dots ,{\mathbf{v}}_k$ are k orthonormal eigenvectors of $A_s$, associated with ${\lambda }_s$. Note that the supplement matrix $W^{\ast }{A}_d(\Phi )W$ is a complex or quaternion Hermitian matrix. Its elements are not unit elements. Furthermore, $W^{\ast }{A}_d(\Phi )W$ may not keep the special structure of $A_d$. In this way, may we still use the coefficient theorem to calculate their coefficients?

6. Eigenvalues of Laplacian Matrices

Similar to Theorem 6, the switching class also has a unique Laplacian spectrum.

Theorem 12.

Let ${\Phi }_1=(G,{\phi }_1)$ and ${\Phi }_2=(G,{\phi }_2)$ be both $\widehat{\mathbb{V}}$-gain graphs. If ${\Phi }_1\sim {\Phi }_2$, then ${\Phi }_1$ and ${\Phi }_2$ have the same Laplacian spectrum. That is, ${\sigma }_L\left({\Phi }_1\right)={\sigma }_L\left({\Phi }_2\right)$.

The interlacing theorem of the adjacency matrix in Theorem 7 also holds for the Laplacian matrix.

Theorem 13.

(Interlacing Theorem of the Laplacian Matrix) Let $\Phi =(G,\phi )$ be a $\widehat{\mathbb{V}}$-gain graph with n vertices and S be a subset of V with k vertices. Denote the eigenvalues of $L(\Phi )$ and $L(\Phi [S\left]\right)$ by

$${\lambda }_1\ge {\lambda }_2\cdots \ge {\lambda }_n\mathit{and}{\mu }_1\ge {\mu }_2\ge \cdots \ge {\mu }_k,$$

respectively. Then, the following inequalities hold:

$${\lambda }_i\ge {\mu }_i\ge {\lambda }_{n+i-k},\forall 1\le i\le k.$$

The proof is similar to the proof of Theorem 7 and we omit the details of the proof here.

Let the signless Laplacian matrix be $Q\left(G\right)=D\left(G\right)+A\left(G\right)$ and ${\Phi }^1=(G,-1)$ be the $\widehat{\mathbb{T}}$-gain graph with all gains $-1$. Again, since the Laplacian matrix of a dual complex unit gain graph $\Phi$ is Hermitian, we may denote the spectral radius of that Laplacian matrix (resp. signless Laplacian matrix) of $\Phi$ as ${\rho }_L(\Phi )$ (resp. ${\rho }_Q(\Phi )$), and the spectral radius of the Laplacian matrix (resp. signless Laplacian matrix) of its underlying graph G as ${\rho }_L\left(G\right)$ (resp. ${\rho }_Q\left(G\right)$), respectively, and discuss their properties. Then, we have the following theorem:

Theorem 14.

Let $\Phi =(G,\phi )$ be a $\widehat{\mathbb{V}}$-gain graph and ${\Phi }^1=(G,-1)$. Then,

$${\rho }_L(\Phi )\le {\rho }_L\left({\Phi }^1\right)={\rho }_Q\left(G\right).$$

Furthermore, if Φ is connected, then ${\rho }_L(\Phi )={\rho }_Q\left(G\right)$ if, and only if, $\Phi \sim {\Phi }^1$.

Theorem 15.

Let $\Phi =(G,\phi )$ be a $\widehat{\mathbb{V}}$-gain graph. Then,

$${\rho }_L(\Phi )\le 2\Delta .$$

Here, Δ is the maximum vertex degree of G. Moreover, the equality holds if, and only if, G is Δ-regular and $\Phi \sim {\Phi }^1$.

Proof. 

Suppose $\lambda \in \widehat{\mathbb{G}}$ is an eigenvalue of $L(\Phi )$ and $\mathbf{x}$ is its corresponding eigenvector; namely, $L(\Phi )\mathbf{x}=\lambda \mathbf{x}$. Let $i\in arg{max}_l\left|x_l\right|$. Then, we have

$$\left|\lambda \right||x_i|=|\lambda x_i|=\left|d_i{x}_i+\sum _{j\ne i}\phi \left(e_{ij}\right)x_j\right|\le d_i|x_i|+\sum _{j\ne i}|\phi \left(e_{ij}\right)\left|\right|x_j|.$$

Therefore,

$$\left|\lambda \right|\le \underset{i}{max}{d}_i+\sum _{j\ne i}\left|\phi \left(e_{ij}\right)\right|=\underset{i}{max}2d_i=2\Delta .$$

Furthermore, it is well known that if G is a simple connected graph with maximum vertex degree $\Delta$, then ${\rho }_Q\left(G\right)\le 2\Delta$, and the equality holds if, and only if, G is regular. By Theorem 14, the equality in this theorem holds if, and only if, G is $\Delta$-regular and $\Phi \sim {\Phi }^1$.

This completes the proof. □

7. Numerical Experiments

7.1. Three-Points Cycles

If the dual unit gain graph $\Phi$ is not balanced, then the eigenvalues of $A(\Phi )$ may not be real numbers. The following example illustrates this:

Example 1.

Consider three $\widehat{\mathbb{T}}$-gain cycles in Figure 1. Their adjacency matrices are given as follows:

$$A\left({\Phi }_1\right)=\left[\begin{array}{ccc}0& 1-\mathbf{i}ϵ& -\mathbf{i}\\ 1+\mathbf{i}ϵ& 0& -\mathbf{i}+ϵ\\ \mathbf{i}& \mathbf{i}+ϵ& 0\end{array}\right],A\left({\Phi }_2\right)=\left[\begin{array}{ccc}0& 1-\mathbf{i}ϵ& {\displaystyle \frac{1-\mathbf{i}}{\sqrt{2}}}\\ 1+\mathbf{i}ϵ& 0& -\mathbf{i}+ϵ\\ {\displaystyle \frac{1+\mathbf{i}}{\sqrt{2}}}& \mathbf{i}+ϵ& 0\end{array}\right],$$

and

$$A\left({\Phi }_3\right)=\left[\begin{array}{ccc}0& 1-\mathbf{i}ϵ& {\displaystyle \frac{1-\mathbf{i}}{\sqrt{2}}}\\ 1+\mathbf{i}ϵ& 0& -\mathbf{i}+2ϵ\\ {\displaystyle \frac{1+\mathbf{i}}{\sqrt{2}}}& \mathbf{i}+2ϵ& 0\end{array}\right],$$

respectively. The $\widehat{\mathbb{T}}$-gain graph ${\Phi }_1$ is balanced. By Theorem 5, we know the eigenvalues of $A\left({\Phi }_1\right)$ are equal to that of $A\left(G\right)$, which are listed as follows:

$${\sigma }_A\left({\Phi }_1\right)=\{2,-1,-1\},$$

which are the same with the eigenvalues of the adjacency matrix of its underlying graph. Both the $\widehat{\mathbb{T}}$-gain graphs ${\Phi }_2$ and ${\Phi }_3$ are unbalanced. The gain of ${\Phi }_2$ is $q_2={\displaystyle \frac{\sqrt{2}}{2}}(1-\mathbf{i})$. By Theorem 5, we have ${\theta }_2=-\mathbf{i}log\left(q_2\right)=-{\displaystyle \frac{\pi }{4}}$ and the eigenvalues of $A\left({\Phi }_2\right)$ may be computed by (10), i.e.,

$${\sigma }_A\left({\Phi }_2\right)=\{1.9319,-0.5176,-1.4142\}.$$

The gain of ${\Phi }_3$ is $q_3={\displaystyle \frac{\sqrt{2}}{2}}(1+\mathbf{i})(-\mathbf{i}+ϵ)$. From this, we have ${\theta }_3=-{\displaystyle \frac{\pi }{4}}+ϵ$ and the eigenvalues of $A\left({\Phi }_3\right)$ may be computed by (10), i.e.,

$${\sigma }_A\left({\Phi }_3\right)=\{1.9319+0.1725ϵ,-0.5176-0.6440ϵ,-1.4142+0.4714ϵ\}.$$

In the above example, the standard parts of ${\sigma }_A\left({\Phi }_3\right)$ are the same as that of ${\sigma }_A\left({\Phi }_2\right)$ because ${\theta }_{3s}={\theta }_2$. We continue to verify the interlacing Theorem 7. For any cycle in Figure 1, removing any vertex from the cycle shall result in a path with two vertex. It follows from (9) that

$${\sigma }_A({\Phi }_i-v_j)=\{1,-1\},\forall i,j=1,2,3.$$

Thus, we may verify that

$${\lambda }_1\left({\Phi }_i\right)\ge 1\ge {\lambda }_2\left({\Phi }_i\right)\ge -1\ge {\lambda }_3\left({\Phi }_i\right),\forall i=1,2,3.$$

7.2. Large-Scale Examples

In this subsection, we use several large-scale unbalanced dual unit gain cycles to verify the closed solution in (10). Let the number of vertices be $n\in \{10,20,50,100,200,500\}$. We generate random unit dual elements as the gains for each edge and compute the closed-form solutions of all eigenvalues by Theorem 5 and Equation (10). We then verify the eigenvalues of the corresponding adjacency matrices by the supplement matrix method (SMM) in [30]. Define the computational residue by

$$\mathrm{RES}={\displaystyle \frac{1}{n}}{\parallel {\left(\lambda \right)}_{\mathrm{sorted}}-{\left({\sigma }_A\right)}_{\mathrm{sorted}}\parallel }_{2^R},$$

where ${\left(\lambda \right)}_{\mathrm{sorted}}$ and ${\left({\sigma }_A\right)}_{\mathrm{sorted}}$ are the sorted eigenvalues from SMM and (11) in descending order, respectively. Here, ${\parallel \mathbf{x}\parallel }_{2^R}=\sqrt{\parallel {\mathbf{x}}_s{\parallel }^2+{\parallel {\mathbf{x}}_d\parallel }^2}$. We report the RES and CPU time in seconds for both methods in

Table 1. Numerical results for computing all eigenvalues of dual complex and quaternion unit gain cycles.

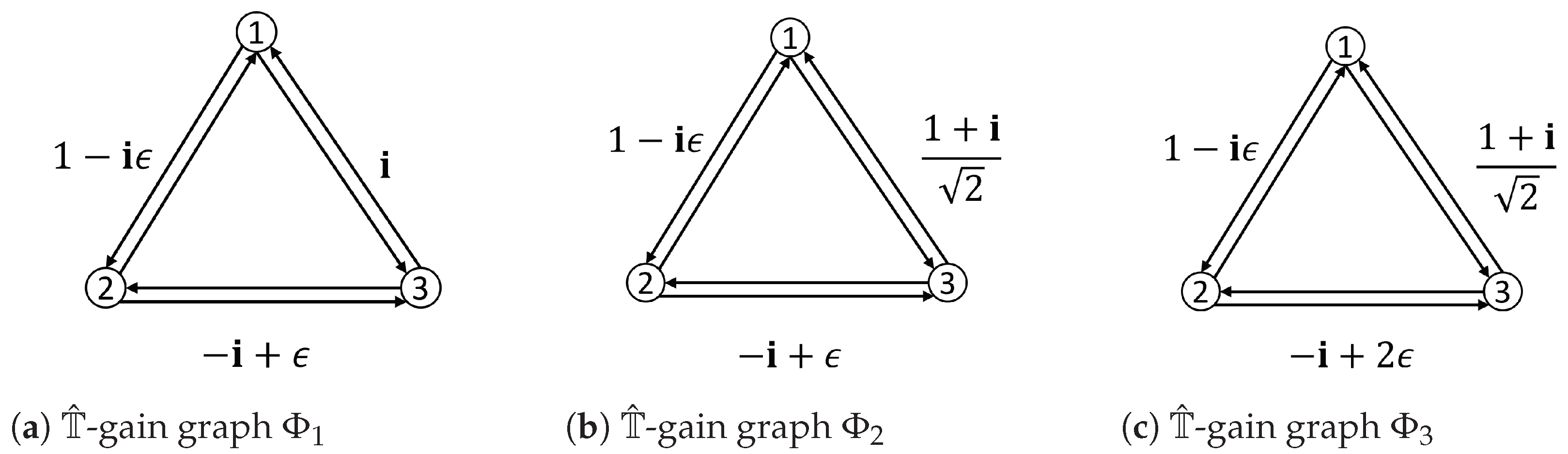
		DCUGG
Method		$n=$ 10	$n=$ 20	$n=$ 50	$n=$ 100	$n=$ 200	$n=$ 500
(10)	CPU (s)	7.06 $\times {10}^{-5}$	2.50 $\times {10}^{-4}$	6.20 $\times {10}^{-4}$	1.38 $\times {10}^{-3}$	1.70 $\times {10}^{-3}$	9.81 $\times {10}^{-4}$
SMM	CPU (s)	5.67 $\times {10}^{-4}$	1.13 $\times {10}^{-3}$	1.20 $\times {10}^{-2}$	9.93 $\times {10}^{-2}$	7.47 $\times {10}^{-1}$	1.49 $\times {10}^1$
	RES	1.77 $\times {10}^{-16}$	2.80 $\times {10}^{-16}$	1.83 $\times {10}^{-16}$	1.62 $\times {10}^{-16}$	1.00 $\times {10}^{-16}$	6.03 $\times {10}^{-17}$
		DQUGG
(10)	CPU (s)	5.44 $\times {10}^{-3}$	3.03 $\times {10}^{-3}$	6.26 $\times {10}^{-3}$	1.13 $\times {10}^{-2}$	2.32 $\times {10}^{-2}$	5.32 $\times {10}^{-2}$
SMM	CPU (s)	9.10 $\times {10}^{-3}$	2.25 $\times {10}^{-2}$	8.93 $\times {10}^{-2}$	3.15 $\times {10}^{-1}$	2.10 $\times {10}^0$	4.86 $\times {10}^1$
	RES	3.71 $\times {10}^{-16}$	2.68 $\times {10}^{-16}$	1.13 $\times {10}^{-16}$	1.59 $\times {10}^{-16}$	6.89 $\times {10}^{-17}$	3.00 $\times {10}^{-16}$

.

From this table, we see that the eigenvalues computed by SMM and (11) are almost the same within a reasonable numerical residue ${10}^{-15}$. Compared with SMM, computing the closed-form solution by (11) is faster.

8. Conclusions

In this paper, we studied dual quaternion, dual complex unit gain graphs, and their spectral properties in a unified frame of dual unit gain graphs. We established the interlacing theorem and coefficient theorem for dual unit gain graphs. The relationship between the spectral radius of a dual unit gain with that of the underlying graph was established. We presented the closed-form solutions of the eigenvalues of the adjacency and Laplacian matrices of dual complex and quaternion unit gain paths and cycles, which may serve as a benchmark for numerical algorithms for computing the eigenvalues of dual Hermitian matrices. Furthermore, we extended the results to spectral properties of the Laplacian matrix of the dual unit gain graph. Finally, we presented several examples and performed numerical experiments to verify the theoretical results.