On the General Divergent Arithmetic Sums over the Primes and the Symmetries of Riemann’s Zeta Function

Abstract

In this paper, we address the problem of the divergent sums of general arithmetic functions over the set of primes. In classical analytic number theory, the sum of the logarithm of the prime numbers plays a crucial role. We consider the sums of powers of the logarithm of primes and its connection with Riemann’s zeta function (z.f.). This connection is achieved through the second Chebyshev function of order n, which can be estimated by exploiting the symmetry properties of Riemann’s zeta function. Finally, a heuristic approach to evaluating more general sums is also given.

1. Introduction

The development of analytic number theory and the classical proof of the prime number theorem is closely related to the definition of the so-called second Chebyshev function [1,2,3,4]:

$${\psi }_0\left(X\right)=\sum _{n⩽X}^{\prime }\Lambda \left(n\right)$$

(1)

where $\Lambda \left(n\right)$ is the von Mangoldt arithmetic function:

$$\Lambda \left(n\right)=\left\{\begin{array}{cc}logp,\hfill & \mathrm{if}n=p^k\mathrm{for}\mathrm{some}\mathrm{prime}p\mathrm{and}\mathrm{integer}k\ge 1,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right..$$

(2)

In (1), the apostrophe denotes that the contribution of the term $n=X$ is $\Lambda \left(n\right)/2$. Closely related with ${\psi }_0\left(X\right)$ is the first Chebyshev function, which involves only a sum over prime numbers, p, instead of the powers of the primes:

$${\vartheta }_0\left(x\right)=\sum _{p\le x}logp.$$

(3)

These two functions are related by

$${\psi }_0\left(X\right)={\vartheta }_0\left(X\right)+{\vartheta }_0\left(X^{1/2}\right)+{\vartheta }_0\left(X^{1/3}\right)+\dots .$$

(4)

By using the Möbius function, this equation can also be inverted, yielding the first Chebyshev function in terms of the second one:

$${\displaystyle {\vartheta }_0\left(X\right)=\sum _{n=1}^{\infty }\mu \left(n\right){\psi }_0\left(X^{1/n}\right).}$$

(5)

As part of the theory of Riemann’s z. f., $\zeta \left(s\right)$, the following estimation of ${\psi }_0\left(X\right)$ has been obtained [5,6]:

$${\psi }_0\left(X\right)=X-{\displaystyle \frac{\zeta \prime \left(0\right)}{\zeta \left(0\right)}}-\sum _{\rho ,\left|\gamma \right|<T}{\displaystyle \frac{X^{\rho }}{\rho }}+\sum _{m=1}^{\infty }{\displaystyle \frac{X^{-2m}}{2m}}+R(X,T),$$

(6)

where $\zeta \prime \left(s\right)$ denotes the derivative of Riemann’s z. f. and X, T are large real parameters. The first sum on the right-hand side of (6) extends over all the non-trivial zeros $\rho =\beta +I\gamma$ of Riemann’s z. f., and T can be chosen freely. Here, $R(X,T)$ is an error term bounded as follows [6]:

$$R(X,T)\ll {\displaystyle \frac{X{(logXT)}^2}{T}}+(logX)min\left\{1,{\displaystyle \frac{X}{T⟨X⟩}}\right\}.$$

(7)

Here, $⟨X⟩$ denotes the integer part of X. As ${\displaystyle \frac{\zeta \prime \left(0\right)}{\zeta \left(0\right)}}=log\left(2\pi \right)$ and the second sum in (6) is $\mathcal{O}\left(X^{-2}\right)$, the dominant contribution to the error of the approximation ${\psi }_0\left(X\right)\simeq X$ for $X\gg 1$ is given by the sum over the non-trivial zeros. To estimate these sums, we will assume throughout this paper that a generally weaker version of Riemann’s hypothesis holds. We will call this condition the restricted Riemann’s hypothesis (RRH):

Definition 1.

Restricted Riemann’s hypothesis (RRH): Let $\alpha \in \mathbb{R}$, $1/2\le \alpha <1$. We say that the RRH is verified for this parameter α if for any non-trivial zero of $\zeta \left(s\right)$ we have $1-\alpha \le \mathrm{Re}\left(s\right)\le \alpha$. If $\alpha =1/2$ then we recover the standard Riemann’s hypothesis.

Although it was not then known by this name, the RRH has already been considered by Ingham in his treatise on the distribution of prime numbers [1]. Assuming RRH, for a given parameter $\alpha$, we can find the bound:

$${\displaystyle \sum _{\rho ,\left|\gamma \right|<T}\frac{X^{\rho }}{\rho }\ll X^{\alpha }\sum _{\rho ,\left|\gamma \right|<T}\frac{1}{\rho }\ll X^{\alpha }\sum _{\rho ,0<\gamma <T}\frac{1}{\gamma }.}$$

(8)

Now, we denote by $N\left(T\right)$ the number of zeros in the critical strip with imaginary part $0<\gamma <T$. This allows us to replace the sum over $1/\gamma$ by an integral:

$$\sum _{\rho ,0<\gamma <T}{\displaystyle \frac{1}{\gamma }}={\int }_0^T{t}^{-1}\mathrm{d}N\left(t\right)={\displaystyle \frac{N\left(T\right)}{T}}+{\int }_0^T{t}^{-2}N\left(t\right)\mathrm{d}t.$$

(9)

Estimates of $N\left(t\right)$ were obtained by von Mangoldt in 1905 and by Backlund in 1918, following a conjecture by Riemann himself [6]. These results imply that $N\left(T\right)=\mathcal{O}(TlogT)$ for $T\gg 1$. Combining this result with (9), we find that

$$\sum _{\rho ,0<\gamma <T}{\displaystyle \frac{1}{\gamma }}=\mathcal{O}\left({(logT)}^2\right).$$

(10)

Finally, we use (6), (7) and (10) with $T=X$ to obtain the estimate of the second Chebyshev function:

$${\psi }_0\left(X\right)=X+\mathcal{O}\left(X^{\alpha }{(logX)}^2\right),$$

(11)

which is equivalent to the prime number theorem proved by Hadamard and de la Vallée Poussin in 1896 [1,2]. This is indeed a stronger result because it assumes the validity of the still unproven RRH for a given $1/2\le \alpha <1$, while in the classical original proof only the previously proven result about the absence of zeros of $\zeta \left(s\right)$ with $\mathrm{Re}\left(s\right)=1$ was taken into account.

Inspired by Equations (1) and (3), we propose the following generalization, to be called the first Chebyshev function of order n:

$${\vartheta }_n\left(x\right)=\sum _{p\le x}{\left(logp\right)}^{n+1},$$

(12)

where $n=1$, 2, … and p denotes the prime numbers. Similarly, we define the second Chebyshev function of order n as a generalization of (1), as follows:

$${\psi }_n\left(X\right)=\sum _{m⩽X}^{\prime }{\Lambda }_n\left(m\right),$$

(13)

where the apostrophe means, as before, that for $m=X$ (if X is an integer) the last term in the sum contributes only ${\Lambda }_n\left(X\right)/2$. Here, ${\Lambda }_n\left(m\right)$ is the von Mangoldt function of order $n=1$, 2, … that we will define as follows:

$${\Lambda }_n\left(m\right)=\left\{\begin{array}{cc}{k}^n{\left(logp\right)}^{n+1},\hfill & \mathrm{if}m=p^k\mathrm{for}\mathrm{some}\mathrm{prime}p\mathrm{and}\mathrm{integer}k\ge 1,\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right..$$

(14)

Note that for $n=0$ we recover the standard von Mangoldt’s function. The relation of the first Chebyshev function of order n and the second Chebyshev function of the same order can be found in terms of a Möbius inversion formula:

$${\displaystyle {\vartheta }_n\left(X\right)=\sum _{m=1}^{\infty }\mu \left(m\right){\psi }_n\left(X^{1/m}\right)m^{n-1},}$$

(15)

which allows us to estimate the sums of the powers of the logarithm of the prime numbers once the second Chebyshev function of order n is also estimated.

The objective of this paper is to extend the classical techniques of analytical number theory, which allow us to estimate the Chebyshev functions, to the case of the generalized Chebyshev functions as defined in Equations (12) and (13). The paper is organized as follows: In Section 2, we discuss the analytical calculation of the Chebyshev functions of order $n=2$ and make some indications for the cases $n=3$, 4, … Some theorems about Riemann’s z. f., which are required in the proof of Section 2, are enumerated in the Appendix A. The results in Section 2 suggest a heuristic approach to calculating general divergent sums of arithmetic functions over the primes, which is presented in Section 3. We also apply this conjecture to evaluating the sum of the logarithm of the logarithm of the prime numbers. The paper ends with some conclusions in Section 4.

2. The Sum of the Squares of the Logarithm of the Prime Numbers

In this section, we evaluate an approximation to the first and second Chebyshev functions of order $n=1$ that, according to (15), are closely related. Our objective, therefore, is to prove the following theorem:

Theorem 1.

Under the assumption of the restricted Riemann hypothesis (RRH), the following result for the sum of the squares of the logarithm of prime numbers, $p\le X$, holds:

$${\vartheta }_1\left(X\right)=X(logX-1)+\mathcal{O}\left(X^{\alpha }{\left(logX\right)}^3\right),$$

(16)

where $1/2\le \alpha <1$ is a real number corresponding to the strip $1-\alpha \le \mathrm{Re}\left(s\right)\le \alpha$, where all non-trivial zeros of $\zeta \left(s\right)$ are located.

We should start by defining the following piecewise function:

$$I\left(Y\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}0<Y<1,\hfill \\ {\displaystyle \frac{1}{2}},\hfill & \mathrm{if}Y=1,\hfill \\ 1,\hfill & \mathrm{if}Y>1.\hfill \end{array}\right.$$

(17)

This function can also be represented as an integral in the complex plane:

$$I\left(Y\right)={\displaystyle \frac{1}{2\pi \mathrm{i}}}{\int }_{c-\mathrm{i}\infty }^{c+\mathrm{i}\infty }{\displaystyle \frac{Y^s}{s}}\mathrm{d}s,$$

(18)

where $c>0$ is a real constant and $Y>0$. This integral can also be defined as the limit, as $T\to \infty$, of the following integral over a segment in the complex plane:

$$I(Y,T)={\displaystyle \frac{1}{2\pi \mathrm{i}}}{\int }_{c-IT}^{c+IT}{\displaystyle \frac{Y^s}{s}}\mathrm{d}s,$$

(19)

i.e., ${lim}_{T\to \infty }I(Y,T)=I\left(Y\right)$. The approach of $I(Y,T)$ to $I\left(Y\right)$ is algebraic in T as T becomes large. In [6], it is proven that

$$|I\left(Y\right)-I(Y,T)|⩽\left\{\begin{array}{cc}{Y}^{c}min\left\{1,{\left(\pi T\right|logY\left|\right)}^{-1}\right\},\hfill & \mathrm{if}Y\ne 1\hfill \\ c{\left(\pi T\right)}^{-1},\hfill & \mathrm{if}Y=1\hfill \end{array}\right.$$

(20)

Now, we have the necessary tool to find a connection among the Chebyshev functions of order $n=1$ and Riemann’s z. f. From the definition in (13) and (17), we have

$${\psi }_1\left(X\right)=\sum _{n=1}^{\infty }{\Lambda }_1\left(n\right)I\left({\displaystyle \frac{X}{n}}\right),$$

(21)

which, obviously, is the limit, as $T\to \infty$, of

$${\psi }_1(X,T)=\sum _{n=1}^{\infty }{\Lambda }_1\left(n\right)I\left({\displaystyle \frac{X}{n}},T\right).$$

(22)

From Equations (19) to (22), we can find an integral representation of ${\psi }_1(X,T)$:

$${\psi }_1(X,T)={\displaystyle \frac{1}{2\pi \mathrm{i}}}\sum _{n=1}^{\infty }{\Lambda }_1\left(n\right){\int }_{c-IT}^{c+IT}{\displaystyle \frac{X^s}{s{n}^s}}\mathrm{d}s.$$

(23)

Absolute convergence for $s>1$ allows us to swap the sum and the integral in (23), yielding

$${\psi }_1(X,T)={\displaystyle \frac{1}{2\pi \mathrm{i}}}{\int }_{c-\mathrm{i}T}^{c+\mathrm{i}T}\left(\sum _{n=1}^{\infty }{\displaystyle \frac{{\Lambda }_1\left(n\right)}{n^s}}\right){\displaystyle \frac{X^s}{s}}\mathrm{d}s.$$

(24)

Here, the sum in parentheses can be evaluated in terms of Riemann’s z. f. To see the connection, we start with Euler’s product:

$$\zeta \left(s\right)=\prod _p{\left({\displaystyle 1-\frac{1}{p^s}}\right)}^{-1},$$

(25)

where, as usual, p denotes all the prime numbers. From (25), we can find the second-order logarithmic derivative of $\zeta \left(s\right)$, as follows:

$${\displaystyle \frac{d^2}{d{s}^2}log\zeta \left(s\right)=\sum _p\sum _{r=1}^{\infty }\frac{r{(logp)}^2}{p^{rs}}=\sum _{n=1}^{\infty }\frac{{\Lambda }_1\left(n\right)}{n^s}.}$$

(26)

This allows us to rewrite (24) in the following form:

$${\displaystyle {\Psi }_1(X,T)=\frac{1}{2\pi \mathrm{i}}{\int }_{c-\mathrm{i}T}^{c+\mathrm{i}T}\frac{\mathrm{d}}{\mathrm{d}s}\left(\frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}\right)\frac{X^s}{s}\mathrm{d}s.}$$

(27)

This equation explicitly states the connection between the second Chebyshev function of order $n=1$ and Riemann’s z. f.

Our next objective is to find an asymptotic expression for ${\Psi }_1\left(X\right)$, estimating the error term. The first step, then, is to calculate the distance between ${\Psi }_1\left(X\right)$ and ${\Psi }_1(X,T)$. From Equations (20)–(22), we obtain

$$\left|{\Psi }_1\left(X\right)-{\Psi }_1(X,T)\right|⩽{\displaystyle \frac{c}{\pi T}}{\Lambda }_1\left(X\right)+\sum _{n=1,n\ne X}^{\infty }{\Lambda }_1\left(n\right){\left({\displaystyle \frac{X}{n}}\right)}^{c}min\left\{1,{\displaystyle \frac{1}{\pi T\mid log\frac{X}{n}\mid }}\right\},$$

(28)

where the first term on the right-hand side of the inequality only appears when X is a prime power. As X is expected to be large, we assume $X>e$ to take c as follows:

$$c=1+{\displaystyle \frac{1}{logX}}\iff X^c=eX.$$

(29)

The second sum on the right-hand side of (28) is better estimated by separating the summation into four regions. To this end, we define

$${\Xi }_{a,b}=\sum _{n=a,n\ne X}^b{\Lambda }_1\left(n\right){\left({\displaystyle \frac{X}{n}}\right)}^{c}min\left\{1,{\displaystyle \frac{1}{\pi T\mid log\frac{X}{n}\mid }}\right\}.$$

(30)

And the sum in (28) can be written as

$${\Xi }_{1,\infty }={\Xi }_{1,3X/4}+{\Xi }_{3X/4,X}+{\Xi }_{X,4X/3}+{\Xi }_{4X/3,\infty }.$$

(31)

To proceed, we need Lemma A1 in the Appendix A. Firstly, we analyze the first and last sums on the right-hand side of (31). If we have $n\ge 4X/3$ or $n\le 3X/4$ then the following inequality holds:

$${\left|log{\displaystyle \frac{X}{n}}\right|}^{-1}⩽{\left(log{\displaystyle \frac{4}{3}}\right)}^{-1}.$$

(32)

Then, from Equations (29) and (30) and Lemma A1, we have

$${\Xi }_{1,3X/4}+{\Xi }_{4X/3,\infty }\ll {\left.X{T}^{-1}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathrm{s}}}{\displaystyle \frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}}\right|}_{s=c}\ll X{T}^{-1}{(logX)}^2.$$

(33)

We now consider the sum ${\Xi }_{3X/4,X}$. We denote by $X_1$ the largest prime power less than X. In the following, we assume that $X_1$ lies in the interval $(3X/4,X)$. If there is no prime power in this interval then ${\Xi }_{3X/4,X}=0$ and the whole sum ${\Xi }_{1,\infty }$ is bounded by the term in (33). But the contribution of the prime powers in this interval may be large, and we need to take that into account. For the term $n=X_1$, we have

$$log{\displaystyle \frac{X}{n}}=-log{\displaystyle \frac{X_1}{X}}=-log\left(1-{\displaystyle \frac{X-X_1}{X}}\right)⩾{\displaystyle \frac{X-X_1}{X}}.$$

(34)

Therefore, the contribution of this term is bounded by

$${\Lambda }_1\left(X_1\right)min\left\{1,{\displaystyle \frac{X}{T\left(X-X_1\right)}}\right\}\ll {(logX)}^{2}min\left\{1,{\displaystyle \frac{X}{T\left(X-X_1\right)}}\right\},$$

(35)

where we have taken into account that for the prime power $X_1=p^r$ and, according to the definition in (14), we have

$${\Lambda }_1\left(X_1\right)=r{(logp)}^2=log{X}_{1}logp\ll {(logX)}^2.$$

(36)

For the rest of the prime powers in the interval $(3X/4,X)$, we can say that $n=X_1-m$, with m being a subset of $0<m<X/4$. In this case, the following inequality holds:

$$log{\displaystyle \frac{X}{n}}⩾log{\displaystyle \frac{X_1}{n}}=-log\left(1-{\displaystyle \frac{m}{X_1}}\right)⩾{\displaystyle \frac{m}{X_1}}.$$

(37)

Consequently, this contribution to ${\Xi }_{3X/4,X}$ would be bounded by

$$\ll \sum _{0<m<X/4}{\Lambda }_1\left(X_1-m\right){\displaystyle \frac{X_1}{T·m}}\ll X·T^{-1}\sum _{0<m<X/4}{\displaystyle \frac{{\Lambda }_1\left(X_1-m\right)}{m}}.$$

(38)

We now consider the sum of the reciprocals of the integers:

$$\sum _{1<m<X}{\displaystyle \frac{1}{m}}=logX+\gamma +\mathcal{O}\left(X^{-1}\right).$$

(39)

Here, $\gamma$ denotes the Euler–Mascheroni constant. From Equations (35), (38) and (39), we then have

$${\Xi }_{3X/4,X}\ll X{T}^{-1}{(logX)}^3+{(logX)}^{2}min\left\{1,{\displaystyle \frac{X}{T⟨X⟩}}\right\}.$$

(40)

A similar argument can be applied to the remaining partial summation, i.e., ${\Xi }_{X,4X/3}$. This would lead to the same result as given in (40). Therefore, from Equations (33) and (40), we obtain

$$\left|{\Psi }_1\left(X\right)-{\Psi }_1(X,T)\right|\ll {\displaystyle \frac{X}{T}}{(logX)}^3+{(logX)}^{2}min\left\{1,{\displaystyle \frac{X}{T⟨X⟩}}\right\}$$

(41)

Our next objective is to evaluate ${\Psi }_1(X,T)$ and, by taking the limit $T\to \infty$, also ${\Psi }_1\left(X\right)$. We begin with an identity for the logarithmic derivative of Riemann’s z. f.:

$$-{\displaystyle \frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}}=1-{\displaystyle \frac{\zeta \prime \left(0\right)}{\zeta \left(0\right)}}+{\displaystyle \frac{1}{s-1}}-\sum _{\rho }{\displaystyle \frac{s}{\rho (s-\rho )}}+\sum _{n=1}^{\infty }{\displaystyle \frac{s}{2n(s+2n)}}.$$

(42)

Here, the sum over $\rho$ extends over all non-trivial zeros of Riemann’s z. f. Absolute convergence allows us to differentiate term-by-term the expression in (42):

$${\displaystyle \frac{d}{ds}}{\displaystyle \frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}}={\displaystyle \frac{1}{{(s-1)}^2}}-\sum _{\rho }{\displaystyle \frac{1}{{(s-\rho )}^2}}+\sum _{n=1}^{\infty }{\displaystyle \frac{1}{{(s+2n)}^2}}.$$

(43)

The sums in (43) are convergent for any value of s. To evaluate the integral in (27), we use Cauchy’s residue theorem on the path plotted in Figure 1.

Figure 1. The path $\mathcal{P}(U,c,T)$ in the complex plane. Note that $N=[U/2]$. c is defined as in (29) and U, T are large real numbers.

The corresponding integral along this path can be written as follows:

$${\mathcal{I}}_{\mathcal{P}}={\displaystyle \frac{1}{2\pi i}}{\int }_{\mathcal{P}(U,c,T)}{\displaystyle \frac{d}{ds}}\left({\displaystyle \frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}}\right){\displaystyle \frac{X^s}{s}}ds.$$

(44)

We note that the poles inside the path $\mathcal{P}(c,U,T)$ are $s=0$, $s=1$ and $s=\rho$ ($\rho$ being a zero of Riemann’s z. f. with imaginary part $\gamma =\left|\mathrm{Im}\rho \right|<T$) and $s=-2n$, with n and integer in the interval $1\le n<U/2$. Both T and U are chosen in such a way that there are no zeros along the path $\mathcal{P}$. By Cauchy’s residue theorem, we have

$$\begin{array}{ccc}\hfill {\mathcal{I}}_{\mathcal{P}}& =& {\displaystyle \frac{\zeta ″\left(0\right)}{\zeta \left(0\right)}-{\left({\displaystyle \frac{\zeta \prime \left(0\right)}{\zeta \left(0\right)}}\right)}^2+XlogX-X}\hfill \\ \hfill & -& {\displaystyle \sum _{\rho ,\left|\gamma \right|<T}\left({\displaystyle \frac{X^{\rho }}{\rho }logX+\frac{X^{\rho }}{{\rho }^2}}\right)}\hfill \\ \hfill & +& {\displaystyle \sum _{m=1}^{⟨U/2⟩}{X}^{-2m}\left({\displaystyle \frac{1}{2m}logX+\frac{1}{{\left(2m\right)}^2}}\right).}\hfill \end{array}$$

(45)

The last summation in (45), as $U\to \infty$, can be written in terms of the polylogarithmic functions:

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{m=1}^{\infty }\frac{X^{-2m}}{2m}}& =& {\displaystyle -\frac{1}{2}log\left({\displaystyle 1-\frac{1}{X^2}}\right)=\frac{1}{2}{\mathrm{Li}}_1\left({\displaystyle \frac{1}{X^2}}\right),}\hfill \\ \hfill {\displaystyle \sum _{m=1}^{\infty }\frac{X^{-2m}}{{\left(2m\right)}^2}}& =& {\displaystyle \frac{1}{4}{\mathrm{Li}}_2\left(\frac{1}{X^2}\right).}\hfill \end{array}$$

(46)

Here, ${\mathrm{Li}}_1\left(z\right)=-log(1-z)$ is the logarithmic function and

$${\mathrm{Li}}_2\left(z\right)={\int }_0^z{\displaystyle \frac{{\mathrm{Li}}_1\left(t\right)}{t}}dt,$$

(47)

is the dilogarithmic function. Although it is not necessary for our calculation, we can also give an explicit expression for the constant term in (45), as follows [5]:

$${\displaystyle \frac{\zeta ″\left(0\right)}{\zeta \left(0\right)}}-{\left({\displaystyle \frac{\zeta \prime \left(0\right)}{\zeta \left(0\right)}}\right)}^2=-{\gamma }^2-2{\gamma }_1+{\displaystyle \frac{{\pi }^2}{12}},$$

(48)

where $\gamma$ is the Euler–Mascheroni constant and ${\gamma }_1$ is the Stieltjes constant of order one.

From Cauchy’s integral theorem, we can now write

$$\begin{array}{ccc}\hfill {\Psi }_1\left(X,T\right)& =& {\displaystyle I_{\mathcal{P}}+\frac{1}{2\pi i}{\int }_{-U+iT}^{c+iT}ds\frac{d}{ds}\left({\displaystyle \frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}}\right)\frac{X^s}{s}}\hfill \\ \hfill & +& {\displaystyle \frac{1}{2\pi i}{\int }_{-U-iT}^{-U+iT}\frac{d}{ds}\left({\displaystyle \frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}}\right)\frac{X^s}{s}ds}\hfill \\ \hfill & -& {\displaystyle \frac{1}{2\pi i}{\int }_{-U-iT}^{c-iT}\frac{d}{ds}\left({\displaystyle \frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}}\right)\frac{X^s}{s}ds.}\hfill \end{array}$$

(49)

To estimate the order of magnitude of these integrals, we should study the integrands in several domains. Firstly, we consider (for $\sigma =\mathrm{Re}\left(s\right)$ and $T=\mathrm{Im}\left(s\right)$) that $-1\le \sigma \le 2$ and $T\gg 1$. T also being different from the imaginary part of a zero of Riemann’s z. f., $T\ne \gamma$. From (42), we can also write

$${\displaystyle \frac{d}{ds}}\left({\displaystyle \frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}}\right)={\displaystyle \frac{1}{{(s-1)}^2}}-\sum _{\rho }{\displaystyle \frac{1}{{(s-\rho )}^2}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{ds}}{\displaystyle \frac{\Gamma \prime (s/2+1)}{\Gamma (s/2+1)}},$$

(50)

where $\rho$ represents the non-trivial zeros of Riemann’s z. f. From Stirling’s formula [5], we have

$$log\Gamma \left({\displaystyle \frac{s}{2}}\right)=\left({\displaystyle \frac{s}{2}}-{\displaystyle \frac{1}{2}}\right)log{\displaystyle \frac{s}{2}}-{\displaystyle \frac{s}{2}}+{\displaystyle \frac{1}{2}}log\left(2\pi \right)+{\mathcal{O}\left(\right|s|}^{-1}),$$

(51)

and, consequently,

$$log\Gamma \left({\displaystyle \frac{s}{2}}+1\right)=\left({\displaystyle \frac{s}{2}}+{\displaystyle \frac{1}{2}}\right)log\left({\displaystyle \frac{s}{2}}+1\right)-{\displaystyle \frac{s}{2}}-1+{\displaystyle \frac{1}{2}}log\left(2\pi \right)+\mathcal{O}\left({\left|s\right|}^{-1}\right),$$

(52)

as $\left|s\right|\to \infty$. And now, taking the logarithmic derivative,

$${\displaystyle \frac{1}{2}\frac{\Gamma \prime (s/2+1)}{\Gamma (s/2+1)}=\frac{1}{2}log(s+2)-\frac{1}{2}\frac{1}{s+2}-\frac{1}{2}+{\mathcal{O}\left(\right|s|}^{-2}),}$$

(53)

and also

$${\displaystyle \frac{1}{2}\frac{d}{ds}\frac{\Gamma \prime (s/2+1)}{\Gamma (s/2+1)}=\frac{1}{2}\frac{1}{s+2}+\frac{1}{2}\frac{1}{{(s+2)}^2}+{\mathcal{O}(|s|}^{-3})}$$

(54)

for $T\gg 1$ and $-1\le \sigma \le 2$, this yields

$${\displaystyle \frac{1}{2}\frac{d}{ds}\frac{\Gamma \prime (s/2+1)}{\Gamma (s/2+1)}=\mathcal{O}\left({\displaystyle \frac{1}{T}}\right).}$$

(55)

From Equations (50) and (55), we have

$${\displaystyle \frac{d}{ds}\frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}=-\sum _{\rho ,|\gamma -T|<1}\frac{1}{{(s-\rho )}^2}-\sum _{\rho ,|\gamma -T|\ge 1}\frac{1}{{(s-\rho )}^2}+\mathcal{O}\left({\displaystyle \frac{1}{T}}\right).}$$

(56)

To proceed, we now need Theorem A1 about the sums of the reciprocal of the squares of the distances of the imaginary part of the non-trivial zeros of Riemann’s z. f. from T for $|\gamma -T|\ge 1$ (see Appendix A). This way, we arrive at

$${\displaystyle \frac{d}{ds}\frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}=-\sum _{\rho ,|\gamma -T|<1}\frac{1}{{(s-\rho )}^2}+\mathcal{O}\left(logT\right).}$$

(57)

We also need the Theorem A2 discussed by Chen [6]: for all sufficiently large positive real numbers T, the number of zeros of the function $\zeta \left(s\right)$ in the critical strip with $|\gamma -T|<1$ is $\mathcal{O}(logT)$. As T is arbitrary, and according also to this theorem, we can choose it in such a way that $|\gamma -T|\gg 1/logT$ for any nontrivial zero of $\zeta \left(s\right)$ with imaginary part $\gamma$. Consequently, in the aforementioned region of the complex plane, we have

$${\displaystyle {\left|{\displaystyle \frac{1}{s-\rho }}\right|}^2\le \frac{1}{{|\gamma -T|}^2}\ll {(logT)}^2,}$$

(58)

and, as the number of zeros of $\zeta \left(s\right)$ such that $|\gamma -T|<1$ is $\mathcal{O}(logT)$, we finally arrive at the following estimate:

$${\displaystyle \frac{d}{ds}\frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}\ll \mathcal{O}\left({(logT)}^3\right),}$$

(59)

valid for $T\gg 1$, $\sigma \in [-1,2]$. We also need another estimate of the second-order logarithmic derivative of $\zeta \left(s\right)$ for $\sigma =\mathrm{Re}\left(s\right)\le -1$ and $|s+2m|\ge 1$ for $m\in \mathbb{N}$. We start with the unsymmetrical form of the functional equation [5,6,7]:

$${\displaystyle \zeta \left(s\right)=2^s{\pi }^{s-1}\Gamma (1-s)\zeta (1-s)cos\frac{\pi }{2}(s-1),}$$

(60)

or, equivalently,

$${\displaystyle \frac{d}{ds}\frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}=-\frac{d}{ds}\frac{\Gamma \prime (1-s)}{\Gamma (1-s)}-\frac{d}{ds}\frac{\zeta \prime (1-s)}{\zeta (1-s)}+{\left({\displaystyle \frac{\pi }{2}}\right)}^2{sec}^2\frac{\pi }{2}(1-s).}$$

(61)

Stirling’s formula for $\left|s\right|\gg 1$ yields

$${\displaystyle \frac{d}{ds}}{\displaystyle \frac{\Gamma \prime (1-s)}{\Gamma (1-s)}}={\displaystyle \frac{1}{s-1}}+\mathcal{O}\left({\displaystyle \frac{1}{{(s-1)}^2}}\right)=\mathcal{O}\left({\displaystyle \frac{1}{\left|s\right|}}\right).$$

(62)

On the other hand, the last two terms in (61) are bounded for $|s+2m|\ge 1$, and we have

$${\displaystyle \frac{d}{ds}\frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}=\mathcal{O}\left(1\right).}$$

(63)

We are now ready to evaluate the integrals on the right-hand side of (49). The first integral is separated for convenience, as follows:

$$\begin{array}{ccc}\hfill {\mathcal{I}}_{-U+iT,c+iT}& =& {\displaystyle \frac{1}{2\pi i}{\int }_{-U+iT}^{-1+iT}ds\frac{d}{ds}\left({\displaystyle \frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}}\right)\frac{X^s}{s}+\frac{1}{2\pi i}{\int }_{-1+iT}^{c+iT}ds\frac{d}{ds}\left({\displaystyle \frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}}\right)\frac{X^s}{s}}\hfill \\ \hfill & =& {\mathcal{I}}_{-U+iT,-1+iT}+{\mathcal{I}}_{-1+iT,c+iT}.\hfill \end{array}$$

(64)

From Equations (29) and (59), we have

$${\displaystyle \left|{\mathcal{I}}_{-1+iT,c+iT}\right|\ll \frac{{(logT)}^3}{T}{\int }_{-\infty }^c{X}^{\sigma }d\sigma =e\frac{X{(logT)}^3}{TlogX}.}$$

(65)

Similarly, by using (63), we can write

$${\displaystyle \left|{\mathcal{I}}_{-U+iT,-1+iT}\right|\ll \frac{1}{T}{\int }_{-U}^1{X}^{\sigma }d\sigma \ll {\int }_{-\infty }^1{X}^{\sigma }d\sigma =\frac{1}{TXlogX}.}$$

(66)

Note that the results in Equations (65) and (66) are also valid if we replace T by $-T$. This means that the third integral on the right-hand side of (49) has the same value as the first one. Finally, we evaluate a bound for the second integral:

$${\displaystyle {\mathcal{I}}_{-U-iT,-U+iT}=\frac{1}{2\pi i}{\int }_{-U-iT}^{-U+iT}ds\frac{d}{ds}\left({\displaystyle \frac{\zeta \prime \left(s\right)}{\zeta \left(s\right)}}\right)\frac{X^s}{s},}$$

(67)

under the conditions $\mathrm{Re}\left(s\right)\le -1$, $|s+2m|\ge 1$ for all $m\in \mathbb{N}$ and also $\left|s\right|\gg 1$ (which is true for $U\gg 1$). Thus, the bound in (63) can be applied again, to obtain

$${\displaystyle \left|{\mathcal{I}}_{-U-iT,-U+iT}\right|\ll \frac{1}{U}{\int }_{-T}^T{X}^{-U}dt=2\frac{T}{U{X}^U}.}$$

(68)

Now, from (49) and the inequalities in Equations (65)–(68), we arrive at

$${\Psi }_1(X,T)=I_{\mathcal{P}}+\mathcal{O}\left({\displaystyle \frac{T}{U{X}^U}}\right)+\mathcal{O}\left({\displaystyle \frac{X{(logT)}^3}{TlogX}}\right)+\mathcal{O}\left({\displaystyle \frac{1}{TXlogX}}\right).$$

(69)

If we take the limit $U\to \infty$ and use Equations (45) and (46) then the following expression for ${\Psi }_1(X,T)$ is deduced:

$$\begin{array}{ccc}\hfill {\Psi }_1(X,T)& =& {\displaystyle XlogX-X+C-\sum _{\rho }\left\{{\displaystyle \frac{X^{\rho }}{\rho }logX+\frac{X^{\rho }}{{\rho }^2}}\right\}+\frac{1}{2}{\mathrm{Li}}_1\left(X^{-2}\right)logX}\hfill \\ \hfill & +& {\displaystyle \frac{1}{4}{\mathrm{Li}}_2\left(X^{-2}\right)+\mathcal{O}\left({\displaystyle \frac{X{(logT)}^3}{TlogX}}\right)+\mathcal{O}\left({\displaystyle \frac{1}{TXlogX}}\right),}\hfill \end{array}$$

(70)

where C is the constant given in (48). The Chebyshev function of order 1 is now calculated from Equations (41) and (70), yielding

$$\begin{array}{ccc}\hfill {\Psi }_1\left(X\right)& =& {\displaystyle XlogX-X+C-\sum _{\rho }\left\{{\displaystyle \frac{X^{\rho }}{\rho }logX+\frac{X^{\rho }}{{\rho }^2}}\right\}+\frac{1}{2}{\mathrm{Li}}_1\left(X^{-2}\right)logX}\hfill \\ \hfill & +& {\displaystyle \frac{1}{4}{\mathrm{Li}}_2\left(X^{-2}\right)+\mathcal{R}(X,T),}\hfill \end{array}$$

(71)

with the following error term:

$$\begin{array}{ccc}\hfill \mathcal{R}(X,T)& =& \mathcal{O}\left({\displaystyle \frac{X{(logX)}^3}{T}}\right)+{(logX)}^{2}min\left\{{\displaystyle 1,\frac{X}{T⟨X⟩}}\right\}\hfill \\ \hfill & +& \mathbb{O}\left({\displaystyle \frac{X{(logT)}^3}{TlogX}}\right)+\mathbb{O}\left({\displaystyle \frac{1}{TXlogX}}\right).\hfill \end{array}$$

(72)

To obtain our estimation of ${\Psi }_1\left(X\right)$, we need first to evaluate a bound on the sums over the nontrivial zeros of Riemann’s z. f. In this calculation, we assume the validity of the restricted Riemann’s hypothesis in Definition 1 for a given real number, $\alpha$.

Under these conditions, we have

$${\displaystyle \left|{\displaystyle \sum _{\rho ,\left|\gamma \right|<T}\frac{X^{\rho }}{\rho }}\right|\ll X^{\alpha }\sum _{\left|\gamma \right|<T}\frac{1}{{\gamma }^2}=X^{\alpha }\mathcal{O}\left(1\right),}$$

(73)

where we have applied the principle that the sum of the reciprocals of all the nontrivial zeros of Riemann’s z. f. is a constant [5]. Similarly,

$${\displaystyle \left|{\displaystyle \sum _{\rho ,\left|\gamma \right|<T}\frac{X^{\rho }}{\rho }logX}\right|\ll X^{\alpha }logX\sum _{\left|\gamma \right|<T}\frac{1}{\gamma }=X^{\alpha }logX\mathcal{O}\left({(logT)}^2\right).}$$

(74)

Here, we have used (10), about the sums of the reciprocals of the imaginary part of the nontrivial zeros of Riemann’s z. f. From Equations (71)–(74), we finally deduce that

$${\Psi }_1\left(X\right)=X(logX-1)+\mathcal{O}\left(\xi (X,T)\right),$$

(75)

with the error term $\Xi (X,T)$ given by

$${\displaystyle \xi (X,T)=X^{\alpha }(logX){(logT)}^2+\frac{X{(logX)}^3}{T}+\frac{X{(logT)}^3}{TlogX}.}$$

(76)

In (76), we have taken into account that the large prime power lesser or equal to X, $⟨X⟩$, is greater than 1, and we have included only the dominant contributions. Note, again, that X and T are large but independent. The error term in (76) can then be optimized for fixed X by finding its minimum as a function of T. Approximately, this is equivalent to taking $T=X^{1-\alpha }\gg 1$ for $1/2\le \alpha <1$. With this choice of T, we finally obtain our estimation of the Chebyshev function of order 1 under the assumption of the validity of the restricted Riemann’s hypothesis:

$${\Psi }_1\left(X\right)=X(logX-1)+\mathcal{O}\left(X^{\alpha }{(logX)}^3\right).$$

(77)

For $\alpha =1/2$, the behavior of ${\Psi }_1\left(X\right)$ given in this equation is equivalent to Riemann’s hypothesis. Now, by using the Möbius inversion formula in (15), we deduce that the first Chebyshev function of order 1 behaves asymptotically in the same way as ${\Psi }_1\left(X\right)$, i.e., the sums of the squares of the logarithm of the primes lesser or equal to X are also given by the asymptotic expression in (77). This proves Theorem 1.

3. The General Divergent Sums

In Equations (11) and (77), we have given the asymptotic behavior of the second Chebyshev functions of order 0 and 1, respectively. According to the Möbius inversion formulas in Equations (5) and (15), we can obtain similar expressions for the asymptotic behavior of the sum over the logarithm of the primes and the square of the logarithm of the primes.

A natural question that arises is whether the analytical techniques discussed in this paper can be extended to yield general formulas for the asymptotics of any divergent sum over a function acting upon the primes. The key point is (27), in which the Chebyshev function is related to an integral in which derivatives of $log\zeta \left(s\right)$ appear. We have shown that this can be done for the squares of the logarithms of the primes, and it can also be obtained for other powers of these logarithms. Nevertheless, finding such a relation for a particular function of the primes can be difficult. Therefore, it would be useful to obtain a heuristic approach to this problem from the two cases of the sums of $logp$ and ${(logp)}^2$. Following this idea, we suggest the following conjecture:

Proposition 1.

Let $f\left(X\right)$ be a real function $X>0\to f\left(X\right)\in \mathbb{R}$, integrable over any finite segment of the real line. We consider the sums over the prime numbers:

$$\sum _{p\le X}f\left(p\right).$$

(78)

Then, under the assumption of the RRH for certain $1/2\le \alpha <1$, we obtain

$${\displaystyle \sum _{p\le X}f\left(p\right)={\int }_2^{X}du\frac{f\left(u\right)}{logu}+\mathcal{O}\left({\displaystyle {\int }_2^{X}du{u}^{\alpha -1}f\left(u\right)}\right).}$$

(79)

This is justified by a well-known version of the prime number theorem, under the assumption of the RRH [2]:

$$\pi \left(X\right)=\mathrm{Li}\left(X\right)+\mathcal{O}\left(X^{\alpha }\right),$$

(80)

where $\pi \left(X\right)$ is the number of primes less than or equal to X, and where $\mathrm{Li}$ is the logarithmic integral function. According to (80), we can deduce that the density of the prime numbers around X is given by

$${\displaystyle \rho \left(X\right)=\frac{1}{logX}+\mathcal{O}\left(X^{\alpha -1}\right).}$$

(81)

And our conjecture in (79) is simply equivalent to

$${\displaystyle \sum _{p\le X}f\left(p\right)={\int }_2^{X}du\rho \left(u\right)f\left(u\right),}$$

(82)

that we expect to be valid in a statistical sense. We will now apply this conjecture to the evaluation of the sum

$${\displaystyle U\left(X\right)=\sum _{p\le X}log(log\left(p\right)).}$$

(83)

From (79), we have

$${\displaystyle U\left(X\right)=\frac{{(loglogX)}^2}{2}+\sum _{n=1}^{\infty }\frac{{(logX)}^n}{n!n^2}\left(nloglogX-1\right)+\mathcal{O}(X^{1/2}loglogX),}$$

(84)

where we have also assumed the validity of the Riemann hypothesis. We now apply the following well-known identities [8]:

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{n=1}^{\infty }\frac{{(logX)}^n}{n!n}}& =& \mathrm{Li}\left(X\right)-\gamma -loglogX,\hfill \end{array}$$

(85)

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{n=1}^{\infty }\frac{{(logX)}^n}{n! n^2}}& =& logX{}_{3}F_3\left(1,1,1;2,2,3;logX\right),\hfill \end{array}$$

(86)

where $\mathrm{Li}\left(X\right)$ is the logarithmic integral and ₃F₃ is the generalized hypergeometric function of order $(3,3)$ [8]. From Equations (84)–(86), we can finally write

$$\begin{array}{ccc}\hfill U\left(X\right)& =& log(logX)\mathrm{Li}\left(X\right)-logX{}_{3}F_3(1,1,1;2,2,2;logX)\hfill \\ \hfill \\ \hfill & -& {\displaystyle \frac{1}{2}{\left(loglogX\right)}^2-\gamma loglogX+\mathcal{O}(X^{1/2}loglogX).}\hfill \end{array}$$

(87)

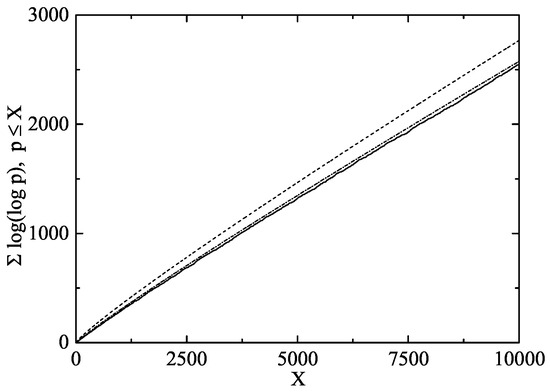
Note that only the first two terms are dominant in comparison with the error term. In Figure 2, we show the results of a numerical calculation of the sum in (83) for $X\le$ 10,000. We compare this with the predictions of the formula in (87) by keeping only the first term and by taking into account this first term and the second one as well.

Figure 2. The solid line is the numerical evaluation of the sum in (83) compared with the prediction of the first term in (87) and the first and second terms of this equation (dashed line and dashed–dotted line, respectively).

4. Conclusions

In this paper, we have studied the asymptotic behavior of a certain class of generalized Chebyshev arithmetic functions of the first and second order under the assumption of a restricted version of the Riemann hypothesis (RRH). In particular, we have obtained an estimation of the sum of the squares of the logarithm of the primes for prime numbers below a certain large quantity. This strongly suggests that the divergent sums over the primes can be estimated from a heuristic approach based upon the prime number density. This also generalizes some previous results by Axler on the sum of the first n prime numbers [9,10]. We conclude that the study of the moments of the distribution of the logarithms of prime numbers, both analytically and numerically, could shed some light on the validity of RH or the restricted version, RRH, for a given real parameter, $\alpha$.