Chebyshev Chaotic Mapping and DWT-SVD-Based Dual Watermarking Scheme for Copyright and Integrity Authentication of Remote Sensing Images

Abstract

Symmetries and symmetry-breaking play significant roles in data security. While remote sensing images, being extremely sensitive geospatial data, require protection against tampering or destruction, as well as assurance of the reliability of the data source during application. In view of the increasing complexity of data security of remote sensing images, a single watermark algorithm is no longer adequate to meet the demand of sophisticated applications. Therefore, this study proposes a dual watermarking algorithm that considers both integrity authentication and copyright protection of remote sensing images. The algorithm utilizes Discrete Wavelet Transform (DWT) to decompose remote sensing images, then constructs integrity watermark information by applying Chebyshev mapping to the mean of horizontal and vertical components. This semi-fragile watermark information is embedded into the high-frequency region of DWT using Quantization Index Modulation (QIM). On the other hand, the robust watermarking uses entropy to determine the embedding position within the DWT domain. It combines the stability of Singular Value Decomposition (SVD) and embeds the watermark according to the relationship between the singular values of horizontal, vertical, and high-frequency components. The experiment showed that the proposed watermarking successfully maintains a high level of invisibility even if embedded with dual watermarks. The semi-fragile watermark can accurately identify tampered regions in remote sensing images under conventional image processing. Moreover, the robust watermark exhibits excellent resistance to various attacks such as noise, filtering, compression, panning, rotating, and scaling.

1. Introduction

Due to the exponential growth of online services, the dissemination and acquisition of digital data have become increasingly convenient. Conversely, the likelihood of illegal copying, distribution, and malicious alteration of data has risen proportionally, and the problem of data abuse has become progressively more severe [1]. Remote sensing images, as typical geospatial data, are frequently employed to detect various geographical features of a region. They have important applications in environmental detection, risk assessment, urban planning, and military security [2,3]. Given the importance and sensitivity of remote sensing images, it is imperative to not only ensure the reliability of the data but also be mindful of their integrity during the use process. Consequently, there is a pressing requirement for a suitable security mechanism to enhance the protection of data copyright and authentication of its authenticity.

As a cutting-edge technology in the field of information security, digital watermarking can embed watermark information into host data through specific algorithms without affecting its usability. In the event of copyright disputes or data tampering issues, the corresponding watermark information can be obtained according to the extraction algorithms to identify the copyright or tampered area, thereby effectively protecting the data [4,5,6]. Digital watermarking technology has been widely used in images, videos, audio, vector graphics, and 3D models due to its unique mechanism of action. As society’s concern regarding the security of remote sensing images has grown in recent years, this technology has been applied progressively to remote sensing images as well [7,8].

Remote sensing image watermarking algorithms can be divided into three distinct categories according to their characteristics: robust watermarking, fragile watermarking, and semi-fragile watermarking [9,10]. In contrast to alternative watermarking, robust watermarking exhibits the strongest ability to resist attacks; notwithstanding the carrier enduring a certain degree of attack, it remains capable of sustaining the watermark extraction and restoration process. Therefore, robust watermarking is often used in various domains such as copyright protection and copy control [11,12]. In most cases, robust watermarking alters the local features of the carrier image. An excessively strong embedding strength may result in carrier image distortion, while an inadequate embedding strength makes it difficult to ensure the robustness of the algorithm. Therefore, achieving a balance between invisibility and robustness in robust watermarking algorithms has been a significant direction of research.

In contrast to robust watermarking, fragile watermarking is designed exclusively for data integrity authentication. The embedded watermark information is exceptionally vulnerable to various attacks and is sensitive to changes in image details. If any content of the image is modified or changed, the corresponding watermark will also be destroyed, thereby revealing the tampering of the content. Therefore, fragile watermarking is used for authenticity or integrity authentication of images [13]. When applied practically, remote sensing images undergo operations such as JPEG compression and decompression, and the transmission process introduces a certain degree of noise. While these operations do not affect the data’s authenticity and integrity, they may cause disruptions to watermark information, thereby impeding the ability of fragile watermarking to meet the practical application requirements of remote sensing images.

Semi-fragile watermarking combines robust and fragile watermarking traits. It can tolerate a certain degree of image processing (compression, noise and filtering, etc.), while effectively detecting maliciously tampered areas in the image [14]. Given the sensitivity of the application of remote sensing images, it is essential to guarantee their integrity and reliability during usage. The current remote sensing image watermarking algorithms generally only address single security issues. For example, Hua et al. [15] embedded a robust watermark in the DWT transform domain by selecting the region with the maximum entropy value. This algorithm only addresses the issue of copyright verification but does not consider the impact of tampering on the image. Zhang et al. [16] used Zernike moments to extract global texture features and employed Accelerated Segment Test feature points for local feature construction. Finally, they combined multiple features to identify tampered areas. However, this algorithm only achieves tamper detection. Heidari et al. [12] embedded the watermark into the host image using a combination of DWT and SVD, similarly focusing solely on copyright issues and neglecting tamper detection. These algorithms can no longer meet practical application requirements. Therefore, this study proposes a novel dual watermarking algorithm that effectively integrates both robustness and semi-fragility. The robust watermark withstands complex image operations and verifies copyright, while the semi-fragile watermark precisely identifies tampering operations for integrity verification.

The main contributions of this study are as follows:

(1)

Traditional block-based watermarking algorithms make it difficult to resist desynchronization attacks (such as translation, rotation, and scaling). This study employed image moments and affine transformations to normalize remote sensing images, thus enhancing the desynchronization attack resistance of the watermarking algorithm;

(2)

The DWT local transformation accurately delineates the tampered and unaffected portions of remote sensing images, ensuring the accurate detection of the semi-fragile watermarking algorithm. To tackle the problem of false alarms often encountered in integrity watermarking, the verification results were optimized through a 3 × 3 window, resulting in a reduction of the false alarm rate caused by Quantization Index Modulation (QIM) extraction errors;

(3)

Entropy was utilized to determine the embedding positions of robust watermarks in the DWT transform domain. The singular value matrix of the horizontal and vertical components of the DWT was used as the embedding template, and the robust watermark embedding algorithm was redesigned, which well solves the false-positive problem that often exists in the SVD and ensures the invisibility and robustness of the robust watermark.

The subsequent sections of this article are structured as follows: Section 2 provides an introduction to the current research status of algorithms linked to remote sensing image watermarking. Section 3 introduces the relevant algorithms used in this study and explains the reasons for their selection. The embedding and extraction process of the proposed dual watermarking algorithm in this article is introduced in Section 4. The corresponding empirical findings will be presented in Section 5, and finally, the conclusion of the study is given in Section 6.

2. Related Works

Due to the ongoing development of information technology, the issues of piracy and tampering with digital material have escalated significantly. This also promotes the continuous improvement and perfection of digital watermarking technology, resulting in the emergence of various types of watermarks. This section provides a concise overview of pertinent studies on robust watermarks, semi-fragile watermarks, and dual watermarks that are related to this article.

The primary application of robust watermarking is to authenticate copyright in images; algorithms for this purpose typically compromise the watermark’s invisibility and robustness. Since the transform domain provides superior data concealment and stability, it is the foundation for numerous robust watermarks. For example, Wang et al. [17] preprocess the watermark information by compressing it to obtain feature watermarks before embedding, then use block Discrete Cosine Transform (DCT) to concentrate the main information of the remote sensing image into the low-frequency coefficients of each block. Finally, they embed watermark information individually through quantization. Based on Redundant Wavelet Transform (RDWT) and SVD, Devl et al. [18] presented a hybrid domain algorithm. This algorithm uses RDWT to decompose remote sensing images into four sub-bands and constructed the embedding domain using SVD, therefore combining the high capacity of RDWT with the stability of SVD matrices. Yuan et al. [19] transformed the RGB channels of remote sensing images into the YCbCr color space based on human visual characteristics, then combined DWT with HSV texture features to perform multilevel decomposition on the luminance space Y. Finally, they embedded watermark information by modifying the low-frequency coefficients of DWT. Heidari et al. [12] addressed the limitations of the DWT algorithm by integrating SVD with a three-level DWT decomposition of images. They employed singular values to embed watermark information, ensuring the algorithm’s resistance to minor rotations. These robust watermarking methods embed watermark information into the transform domain based on fixed templates, exhibiting decent invisibility and demonstrating good robustness against various types of noise, filtering, and compression. However, the susceptibility of these watermark embedding templates to translation, rotation, and scaling poses a significant challenge in safeguarding them against desynchronization attacks.

Semi-fragile watermarks are more used for data integrity and authenticity verification. To distinguish between standard image processing and malicious tampering distinction, Hanen et al. [20] employed perceptual hash values of images as watermarks during JPEG compression. They directly replaced wavelet transform coefficients of the image using QIM, enabling the semi-fragile watermarks to achieve high detection accuracy. However, because the algorithm solely focuses on compression effects, it is not resistant to other forms of image processing. Senol et al. [21] proposed a semi-fragile watermarking scheme based on inner and outer block partitioning. This algorithm divides images into three parts: the central, potentially important, and outer regions based on their significance. Subsequently, the central and outer blocks were subjected to block pairing and processing. During this process, watermark information is embedded into the central blocks, and their binary images are calculated. These binary images were then embedded into the corresponding peripheral blocks, thereby achieving integrity authentication. This algorithm demonstrates excellent resistance against JPEG compression and filtering. However, it does not consider the impact of noise on the verification results. Behrouz et al. [22] proposed a semi-fragile watermarking scheme based on lifting wavelet transform (LWT) and feed-forward neural network (FNN). This algorithm utilizes LWT to decompose images and extract diagonal details for block-wise DCT. Then, it modifies the DC coefficients of each block to embed the watermark. Before watermark extraction, the speeded-up robust features (SURF) algorithm was employed to identify feature points in the images, facilitating the pairing and correction of geometric transformations of the carrier. Finally, FNN was used to extract the watermark and detect tampered regions. This scheme introduces feature point correction and FNN in the wavelet domain to greatly improve the accuracy of integrity verification. However, it is important to note that the algorithm relies on the feature points of the original image before watermark extraction, rending it a semi-blind watermark.

There has been a lot of study on both robust and semi-fragile watermarking recently. However, as the usage scenarios for images become increasingly complex, a single watermarking algorithm is inadequate to fulfill the diverse application requirements. Therefore, many scholars have advocated for dual watermarking. Dual watermarking achieves multiple protections for the carrier data by embedding different types of watermarks into it. However, the integration of multiple watermarks into a single carrier may result in conflicts between the watermarks; hence, it is also challenging to guarantee the invisibility of the watermark algorithm. To avoid any interference between dual watermarks, Liu et al. [23] transformed the host image from the RGB color space to the YCbCr color space and extracted its luminance Y for DWT decomposition. They then embeded robust watermark information in the low-frequency components through block-based quantization. After completing the abovementioned process, they converted YCbCr back to RGB and embedded fragile watermarks separately in RGB using an improved Least Significant Bit (LSB) method. AHMADI et al. [24] utilized the characteristics of DWT multi-scale decomposition to decompose the RGB three bands of the image simultaneously. The low-frequency coefficients of the blue channel for SVD and robust watermarks were embedded based on the relationship between the left and right matrices of singular values. For fragile watermarks, they performed block-wise SVD on the high-frequency coefficients of all channels, and finally embed semi-fragile watermarks by modifying the first and second singular values of the singular value matrix. Although the aforementioned algorithms address the issue of mutual interference between different watermarks, the embedding of multiple watermarks has led to a significant decrease in the quality of the host image, making it difficult to meet the precision requirements of high-quality remote sensing images.

3. Construction of Dual Watermarking

3.1. Remote Sensing Image Normalization

Remote sensing images have geometric distortions throughout the imaging process. Therefore, it is necessary to perform geometric correction and registration before using them. If the remote sensing image contains watermark information, performing this operation may cause the embedded watermark to shift to some degree. If the magnitude of the shift is excessively large, it can seriously impair the efficiency of watermark extraction. Template-based watermarking algorithms rely on the resistance of the transformation domain algorithm itself to various attacks [15,16,17]. However, their resistance to geometric attacks is often unsatisfactory. Therefore, this study fixes the embedding domain of remote sensing images with the idea of normalization, which ensures the robustness of the watermarking algorithm. The basic strategy is to determine the orientation of the remote sensing image based on the image moments and subsequently apply an affine transformation to modify the image’s angular and scale. Image moments have invariance properties to translation, rotation, and scaling, and they also exhibit a certain resistance to image noise [25]. The geometric moment $M_{\alpha \beta }$ of a remote sensing image $R$ can be calculated as follows:

$$M_{\alpha \beta }={\sum }_{x=0}^{m_1-1}{\sum }_{y=0}^{n_1-1}{x}^{\alpha }{y}^{\beta }R\left(x,y\right)$$

(1)

where $\alpha$ and $\beta$ are constant, $m_1$ and $n_1$ are the length and width of the remote sensing image, respectively. $\left(x,y\right)$ denotes the image’s coordinate position. With the geometric moments, the central moment $U_{\alpha \beta }$ of the image can be calculated:

$$U_{\alpha \beta }={\sum }_{x=0}^{m_1-1}{\sum }_{y=0}^{n_1-1}{\left(x-X_c\right)}^{\alpha }{\left(y-Y_c\right)}^{\beta }R\left(x,y\right)$$

(2)

$$X_c={\displaystyle \frac{M_{10}}{M_{00}}}, Y_c={\displaystyle \frac{M_{01}}{M_{00}}}$$

(3)

where $X_c$ and $Y_c$ denote the horizontal and vertical coordinates of the center of mass of the remote sensing image, respectively.

According to (2), the image’s main axis direction $\theta$ can be calculated using the specifical equation:

$$\theta ={\displaystyle \frac{1}{2}}arctan\left({\displaystyle \frac{2U_{11}}{U_{20}-U_{02}}}\right)$$

(4)

This study utilized the main axis direction of the remote sensing image as the reference for angle normalization. The remote sensing image was then normalized using an affine transformation matrix. For the original remote sensing image $R$ and the transformed remote sensing image $R^{\prime }$, there exists the following relationship:

$$R^{\prime }\left(x,y\right)=A·R\left(x,y\right)-B$$

(5)

$$A=\left(\begin{array}{cc}{a}_1& a_2\\ a_3& a_4\end{array}\right),B=\left(\begin{array}{c}{b}_1\\ b_2\end{array}\right)$$

(6)

Normalization of remote sensing images is essentially the cumulative transformation of remote sensing images using affine transformation. The specific steps are as follows:

(1)

Angle normalization: Firstly, the remote sensing image is rotated according to the center of mass. In (5), the transformation matrix $A_1=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$ and $B_1=\left(\begin{array}{c}{X}_c\\ Y_c\end{array}\right)$, resulting in the centrally processed remote sensing image $R_1^{\prime }\left(x,y\right)=A_1·R\left(x,y\right)-B_1$.

Then the angular difference ${\theta }_d$ between the initial angle ${\theta }_1$ of the remote sensing image and the angle ${\theta }_2$ of the processed image is calculated by (4). Set $A_2=\left(\begin{array}{cc}cos{\theta }_d& sin{\theta }_d\\ -sin{\theta }_d& cos{\theta }_d\end{array}\right)$, $B_1=0$ to rotate the centrally processed remote sensing image $R_1^{\prime }\left(x,y\right)$, and then the expression of the image is as follows: $R_2^{\prime }\left(x,y\right)=A_2·R_1^{\prime }\left(x,y\right)+B_1$.

• Scaling normalization: Apart from the rotation, scaling transformation also greatly affects the extraction results, so it is necessary to re-determine the scaling scales $s_1$ and $s_2$ for the horizontal and vertical axes based on the dimensional relationship between the original remote sensing images $R$ and $R_2^{\prime }\left(x,y\right)$:

$$s_1={\displaystyle \frac{m_1}{m_2}},s_2={\displaystyle \frac{n_1}{n_2}}$$

(7)

where $m_2$ and $n_2$ are the length and width of the image, respectively. Set $A_3=\left(\begin{array}{cc}{s}_1& 0\\ 0& s_2\end{array}\right)$, $B=0$. According to (5), perform scaling transformation again on $R_2^{\prime }\left(x,y\right)$: $R_3^{\prime }\left(x,y\right)=A_3·R_2^{\prime }\left(x,y\right)$, thus the remote sensing image has been fully normalized.

3.2. Semi-Fragile Watermarking Based on DWT and Chebyshev Chaotic Mapping

Compared to the RGB color space, the YCbCr color space allows separate processing of luminance Y and chrominance CbCr, without interfering with each other [23]. This study utilizes the Y to conceal a semi-fragile watermark, while the Cr is used as a robust watermark embedding domain. This approach aims to maintain the independence of the two watermarks while preserving the visual quality of the remote sensing image as much as possible. The equation for converting from RGB to YCbCr color space is as follows:

$$\left[\begin{array}{c}Y\\ Cb\\ Cr\end{array}\right]=\left[\begin{array}{ccc}0.2990& 0.5870& 0.1140\\ -0.169& -0.3312& 0.5000\\ 0.50000& -0.4186& -0.0813\end{array}\right]\left[\begin{array}{c}R\\ G\\ B\end{array}\right]+\left[\begin{array}{c}0\\ 128\\ 128\end{array}\right]$$

(8)

3.2.1. DWT Decomposition

The wavelet transform is a common image processing algorithm, and its basic idea is to use the wavelet function as a basis function to decompose the input image into wavelet components with different scale positions and different components [26]. Compared to the continuous wavelet transform, DWT operates in discrete time and space. Taking the remote sensing image $R\left(x,y\right)$ as an example, DWT decomposes the image into multiple levels of resolution by applying various filters along the rows and columns of the image. This process generates four frequency sub-bands: LL, HL, LH, and HH. One of the most significant characteristics of DWT is its ability to independently analyze each frequency sub-band according to their distinct characteristics. Due to the fact that the DWT algorithm is a local transformation in both the spatial and transform domains, it is possible to accurately distinguish between the altered and unaltered regions of a remote sensing image despite cropping and substitution. It meets the requirements of integrity verification applications. Therefore, this study employed the DWT as its watermarking base algorithm so as to meet the different embedding requirements of dual watermarking algorithms. The decomposition of the remote sensing image $R\left(x,y\right)$ using DWT is as follows:

$$\left\{\begin{array}{c}LL\left({\displaystyle \frac{x}{2}},{\displaystyle \frac{y}{2}}\right)={\displaystyle \sum _{k_1=0}^{m_1-1}}{\displaystyle \sum _{k_2=0}^{n_1-1}}g\left(k_1\right)g\left(k_2\right)R\left(x-k_1\right)\left(y-k_2\right)\\ LH\left({\displaystyle \frac{x}{2}},{\displaystyle \frac{y}{2}}\right)={\displaystyle \sum _{k_1=0}^{m_1-1}}{\displaystyle \sum _{k_2=0}^{n_1-1}}g\left(k_1\right)h\left(k_2\right)R\left(x-k_1\right)\left(y-k_2\right)\\ \begin{array}{c}HL\left({\displaystyle \frac{x}{2}},{\displaystyle \frac{y}{2}}\right)={\displaystyle \sum _{k_1=0}^{m_1-1}}{\displaystyle \sum _{k_2=0}^{n_1-1}}h\left(k_1\right)g\left(k_2\right)R\left(x-k_1\right)\left(y-k_2\right)\\ HH\left({\displaystyle \frac{x}{2}},{\displaystyle \frac{y}{2}}\right)={\displaystyle \sum _{k_1=0}^{m_1-1}}{\displaystyle \sum _{k_2=0}^{n_1-1}}g\left(k_1\right)g\left(k_2\right)R\left(x-k_1\right)\left(y-k_2\right)\end{array}\end{array}\right.$$

(9)

where g(k) is the low-pass filter, h(k) is the high-pass filter, $k_1$, $k_2$ are constants, and LL, LH, HL, and HH are the results of the DWT decomposition.

3.2.2. Validation Coefficient Construction Based on Chebyshev Chaos Mapping

Common semi-fragile watermark integrity verification schemes mostly use an external watermark image as a template. During the process of integrity verification, tampered regions are determined by comparing the extracted information with the external watermark and identifying any discrepancies. However, when remote sensing images undergo deformation, the extracted integrity information also experiences alterations, making it difficult for watermarks to correspond to each other and significantly impacting the accuracy of verification. This study is based on the characteristics of DWT local transformation and its multi-scale features. The method uses horizontal and vertical components as templates and employs Chebyshev chaos mapping to construct integrity verification information, which is then embedded into the high-frequency components of DWT, achieving correspondence between the extracted information and the integrity information.

The Chebyshev chaotic mapping is highly sensitive to the initial conditions of the input. No matter how similar the initial values of the inputs are, the iterative output sequences are uncorrelated with each other [27,28]. Therefore, this algorithm is widely used in data encryption. Chebyshev chaotic mapping is given by (10):

$$V_{n+1}^1=\cos \left(t·arccos\left(V_n^1\right)\right),V_n^1ϵ\left[-1, 1\right]$$

(10)

where $V_n^1$ is the input value, $n$ is the number of iterations and $t$ is the order. In this case, $t$ is 4.

This study utilizes the mean coefficient matrix of the horizontal and vertical components obtained by DWT decomposition to generate a watermark sequence for authentication purposes. To filter out the parts of each coefficient that are less affected by noise and to meet the input value requirements of the Chebyshev mapping, the mean coefficient matrix needs to be processed. The specific processing rules are as follows:

$$V_n^1={\displaystyle \frac{floor\left(mod\left(abs\left(Average\right),100\right)/10\right)}{10}}$$

(11)

where $floor(.)$ is a downward rounding function, $mod(.)$ is a modulo operation and $abs(.)$ is the absolute value.

By applying (10) to map $V_n^1$, the resulting sequence $V_{n+1}^1$ is not a binary sequence. The positive values are assigned a value of “1”, while the rest values are assigned a value of “0”, thereby constructing the validation matrix ${Mat}_v$.

3.2.3. Mapping Semi-Fragile Watermark Embedding Method

QIM has been demonstrated that the method is not only robust to a certain degree of image processing but also has little resistance to malicious tampering such as cutting, pasting, and substituting [29]. This satisfies the basic requirements for semi-fragile watermarking of remote sensing images. Therefore, QIM is chosen as the embedding method for semi-fragile watermarking in this study. The main idea of QIM is to quantize the carrier data into different intervals according to different integrity verification information. Then quantize it again when extracting the watermark, so that the interval it belongs to represents the watermarking information [30]. The specific embedding rules are as follows:

$$H{H}^{\prime }=\left\{\begin{array}{c}HH\left(p_1,p_2\right)-{\displaystyle \frac{∆}{2}}; {Mat}_v\left(p_1,p_2\right)=0, mod\left(HH\left(p_1,p_2\right),∆\right)>{\displaystyle \frac{∆}{2}}\\ HH\left(p_1,p_2\right)+{\displaystyle \frac{∆}{2}}; {Mat}_v\left(p_1,p_2\right)=1, mod\left(HH\left(p_1,p_2\right),∆\right)\le {\displaystyle \frac{∆}{2}}\\ HH\left(p_1,p_2\right); others\end{array}\right.$$

(12)

where $∆$ is the quantization step, $H{H}^{\prime }$ is the matrix of modified high-frequency coefficients, and $HH\left(p_1,p_2\right)$ is the high-frequency coefficients at position $\left(p_1,p_2\right)$.

The QIM extracting equation is as follows:

$${Mat}_v^{\prime }=\left\{\begin{array}{c}{Mat}_v^{\prime }\left(p_1,p_2\right)=1; mod\left(HH\prime \left(p_1,p_2\right),∆\right)\ge {\displaystyle \frac{∆}{2}}\\ {Mat}_v^{\prime }\left(p_1,p_2\right)=0; mod\left(HH\prime \left(p_1,p_2\right),∆\right)<{\displaystyle \frac{∆}{2}}\end{array}\right.$$

(13)

where ${Mat}_v^{\prime }$ denotes the extracted integrity verification information.

3.2.4. False Alarm Optimization Method

In this study, the tempered positions in remote sensing images are determined by comparing the differences between the validation watermark ${Mat}_v^{\prime }$ and embedded watermark ${Mat}_v$. That is, when the corresponding position values of ${Mat}_v^{\prime }$ and ${Mat}_v$ are the same, it means that the position of the point is not modified, and the validation result here is set to “0”. Conversely, if the two values are different, the validation result of the point is set to “1”.

In the above-shown process, since the DWT algorithm may cause some errors during the back-and-forth transformation process, the accuracy of the QIM will also be affected. Therefore, the final validation results have some false alarm problems. To address this problem, this study extracts the 3 × 3 neighborhood around a single verification result, and when the total number of “1” in the region is greater than 4, the verification result at the center is set to 1. Otherwise, the verification result is set to 0, thus reducing the false alarm rate of the verification result. The specific optimization process is illustrated in Figure 1.

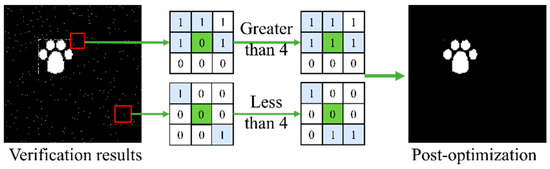
Figure 1. False alarm optimization.

3.3. Robust Watermarking Method Based on Entropy and SVD

The inability to extricate a semi-fragile watermark following substantial image modification may necessitate the use of robust watermarking for copyright prosecution. In the remote sensing image robust watermarking algorithms, ensuring the resistance of the watermark embedding domain to various desynchronization attacks has always been a challenge. The previously proposed remote sensing image normalization process based on image moments still has certain angular errors, which significantly impact the remote sensing image watermarking algorithm that relies on template embedding. Therefore, this study introduces the concept of information entropy applied to a fixed image template. The entropy value is then used to determine the appropriate domain for embedding the watermark. This approach aims to enhance the robustness and transparency of the watermark algorithm.

Information entropy is often used to quantify the degree of uniformity of image pixel distribution. A lower information entropy means that the region of the pixel distribution is relatively centralized, implying a relatively basic structure. Conversely, when the pixel distribution in a region is more uniform, the information entropy is greater. This means that the region carries more information, in which that embedded in the watermark can also obtain better transparency [24].

The information entropy $V_{entropy}$ of the high-frequency region HH after DWT transform is calculated as follows:

$$V_{entropy}=-\sum _{i=1}^{{HH}_{max}}HH\left(i\right){log}_{2}HH\left(i\right)$$

(14)

where ${HH}_{max}$ denotes the maximum value in the high-frequency region of the input computation, and $HH\left(i\right)$ denotes the probability of occurrence of coefficient value $i$.

When embedding robust watermark information directly in the DWT domain, it is difficult to ensure the robustness of the watermark algorithm. However, the SVD algorithm does not exhibit significant sensitivity to small perturbations in input coefficients, thus demonstrating superior data stability [31,32]. In order to further improve the resistance of the watermarking algorithm to various image processing, this study combines SVD on the basis of DWT transform to decompose the region with the largest entropy value and use the singular value matrix as the watermark embedding domain. For an $m_r\times m_r$ DWT coefficient matrix ($Region$), the singular value decomposition formula is as follows:

$$Region=U_r{S}_r{V_r}^T=\left[u_1{,u}_2,\cdots {,u}_{m_r}\right]\left[\begin{array}{cc}{\Sigma }_{S_r}& 0\\ 0& 0\end{array}\right]\left[v_1{,v}_2,\cdots {,v}_{m_r}\right]$$

(15)

where $S_r$ is the singular value matrix, $U_r$ and $V_r$ are orthogonal matrices composed of the left and right singular vectors, respectively. ${V_r}^T$ denotes the transpose matrix of $V_r$. $\left[u_1{,u}_2,\cdots {,u}_{m_r}\right]$ and $\left[v_1{,v}_2,\cdots {,v}_{m_r}\right]$ denote the column vectors in the matrix, and ${\Sigma }_{S_r}=diag\left({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_m\right)$ is a diagonal matrix.

3.4. Watermark Scrambling

Before embedding the watermark, it is generally essential to employ encryption techniques to transform the watermark information into a chaotic state, thus enhancing the security of the watermark. The Arnold transform is a classic image scrambling encryption method based on the characteristics of the watermark digital matrix, it involves nonlinear mapping of pixel points within the watermark matrix to disrupt the watermark information, so as to disturb the information of the watermark, achieving an effect of encryption [33]. This method is widely used in watermarking research due to its simplicity, ease of implementation, and its ability to render the energy distribution of the watermarked image more uniform. For a watermark of $m_w\times m_w$, the Arnold scrambling Equation is as follows:

$$\left[\begin{array}{c}{X}_a^{\prime }\\ Y_b^{\prime }\end{array}\right]=\left[\begin{array}{cc}1& {key}_a\\ {key}_b& 1+{key}_a{key}_b\end{array}\right]\left[\begin{array}{c}{X}_a\\ Y_b\end{array}\right]mod\left(m_w\right)$$

(16)

where ${key}_a$ and ${key}_b$ are positive integers, which are used as recovery keys after scrambling. $(X_a,Y_b)$ and $(X_a^{\prime },Y_b^{\prime })$ represent the original position of the watermark pixel value in the matrix and the position after mapping, respectively. The recovery equation for Arnold scrambling is as follows:

$$\left[\begin{array}{c}{X}_a\\ Y_b\end{array}\right]=\left[\begin{array}{cc}{key}_a{key}_b+1& -{key}_b\\ -{key}_a& 1\end{array}\right]\left[\begin{array}{c}{X}_a^{\prime }\\ Y_b^{\prime }\end{array}\right]mod\left(m_w\right)$$

(17)

4. Embedding and Extraction Processes of the Proposed Dual Watermarking

4.1. Watermark Embedding Process

Prior to the dual watermark embedding, it is necessary to calculate the initial angle ${\theta }_1$ of the main axis of the original remote sensing image according to the image moments outlined in Section 3, Additionally, the length $m_1$ and width $n_1$ of the axis should be recorded. Next, extract the RGB bands and convert them into the YCbCr color space. The dual watermark embedding process is shown in Figure 2, and the pseudo-code is shown in Algorithm 1 and consists of the following steps:

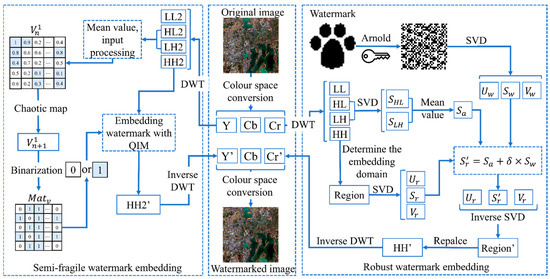
Figure 2. Watermark embedding process.

4.1.1. Robust Watermark Embedding

Step 1. The chromaticity Cr of YCbCr color space is extracted and a 4 × 4 DWT is performed, four frequency components of LL, HL, LH, and HH are obtained.

Step 2. Extract the high-frequency component HH and compute its entropy. Select the part with the maximum entropy value as the watermark information embedding region. Then perform the SVD to obtain the left and right singular values $U_r$ and $V_r$, as well as the singular value matrix $S_r$.

Step 3. Extract the vertical component HL and horizontal component LH. Select the coefficients at the corresponding positions in Step 2 and perform SVD on them separately to obtain the singular value matrices $S_{HL}$ and $S_{LH}$. Then, calculate $S_a$ according to (18).

$$S_a={\displaystyle \frac{S_{HL}+S_{LH}}{2}}$$

(18)

Step 4. Convert the original watermark sequence “0, 1” to the “0, 255” sequence, then perform Arnold scrambling and SVD to obtain $U_w$, $S_w$, and $V_w$.

Step 5. The singular-valued left and right matrices $U_w$ and $V_w$ are served as the key, $S_w$ is used as the embedding information. Apply (19) to embed the watermark information and obtain $S_r^{\prime }$. Substitute $S_r^{\prime }$ with $S_r$ for the inverse SVD transformation to obtain the embedding domain Region’.

$$S_r^{\prime }=S_a+\delta \times S_w$$

(19)

where $\delta$ is the embedding strength.

Step 6. Replace the maximum entropy of the high-frequency component HH with the watermarked embedded domain and get the watermarked high-frequency component HH’. Finally, the chrominance Cr’ with a robust watermark is obtained by inverse DWT.

4.1.2. Semi-Fragile Watermark Embedding

Step 1. The luminance Y of the YCbCr color space is extracted for DWT transformation to obtain the four frequency components LL2, HL2, LH2, and HH2.

Step 2. The components HL2 and LH2 are extracted to find the mean value, and in order to satisfy the input value size requirement of the Chebyshev mapping, the mean value is processed according to (11) to obtain the input coefficient $V_n^1$.

Step 3. $V_n^1$ is chaotically mapped according to (10), resulting in the generation of the mapped matrix coefficients $V_{n+1}^1$. Subsequently, the matrix is binarized, with positive numbers assigned a value of “1” and the other numbers assigned a value of “0”. This step yields the integrity watermark matrix ${Mat}_v$.

Step 4. The high-frequency coefficient HH2 is extracted, and the watermark value in ${Mat}_v$ is indexed sequentially. Then the embedding process is performed according to (12) to obtain the high-frequency coefficient $HH2’$ containing the integrity watermark. Finally, the luminance $Y’$ is obtained by executing the inverse DWT.

Step 5. Finally, the original $Cr$ and $Y$ are replaced with the watermarked chromaticity $Cr’$ and luminance $Y’$. Subsequently, the YCbCr color space is transferred back to the RGB color space to complete the process of embedding dual watermarks in the remote sensing image, resulting in the acquisition of a watermarked remote sensing image.

Algorithm 1 Watermark embedding process

$\mathbf{Input}: \mathrm{Embedding} \mathrm{strength}, \delta$; quantization step, ∆; remote sensing image; Watermark.

Output: Watermarked image;

1: Convert RGB to YCbCr;

2: Extract Cr and perform a 4 × 4 DWT; // Robust watermark embedding

3: Obtain LL, HL, LH and HH;

4: Compute HH’s entropy to determine embedding position;

5: Gain embedding region $(Region$);

6: Convert the watermark, and perform Arnold scrambling and SVD;

7: Obtain $U_w$$, S_w$$, \mathrm{and} V_w$;

8: Perform SVD on $HL, LH, Region$;

9: Gain $S_{HL}$$, S_{LH}$$, S_r$$, U_r$ and $V_r$;

$10: \mathrm{Extract} S_{HL}$$, S_{LH}$$\mathrm{and} \mathrm{calculate} S_a$ according to (18);

11: Embed $S_w$$\mathrm{into} S_a$ according to (19);

$12: \mathrm{Gain} S_r^{\prime }$;

$13: \mathrm{Perform} \mathrm{inverse} \mathrm{SVD} \mathrm{on} S_r^{\prime }$ and then inverse DWT;

14: Gain Cr’;

15: Extract Y and perform DWT; // Semi-fragile watermark embedding

16: Obtain LL2, HL2, LH2 and HH2;

17: Extract HL2 and LH2 to calculate the mean value, then process it according to (11);

18: Obtain the input coefficient $V_n^1$;

19: $V_n^1$ is chaotically mapped according to (10).

20: Gain $V_{n+1}^1$;

21: if $V_{n+1}^1$ > 0 then // Perform binary processing to $V_{n+1}^1$

$22:\hspace{1em}{Mat}_v$ = 1

23: else

$24:\hspace{1em}{Mat}_v$ = 0

25: end if

26: Extract $HH2$ and embed ${Mat}_v$ in it;

27: Obtain HH2’;

28: Perform inverse DWT on HH2’,

29: Obtain $Y\prime$;

30: Convert Y’CbCr’ to RGB;

31: Return: Watermarked image;

4.2. Watermark Extraction Process

The initial angle ${\theta }_2$ of the principal axis of the watermarked image is calculated according to the image moment, and the angle difference ${\theta }_d$ between the watermarked image and the original image is obtained. Correct the watermarked remote sensing image according to the remote sensing image normalization method described in Section 3.1. Then extract the RGB bands and convert them to the YCbCr color space. Since cropping attacks may remove some areas of the remote sensing image, it is known from (1) and (2) that the geometric moments and central moments of the remote sensing image are no longer reliable. Therefore, the proposed correction strategy is not applicable to remote sensing images with obvious missing parts. The watermark extraction process of the dual watermarking algorithm is shown in Figure 3, the pseudo-code is shown in Algorithm 2 and the specific steps are as follows.

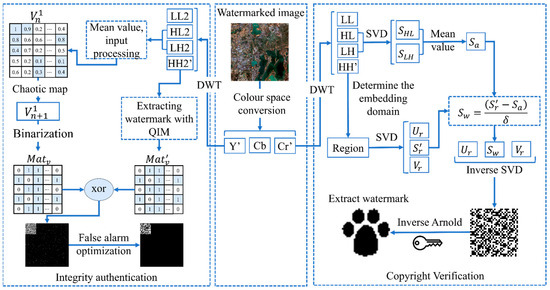
Figure 3. Watermark extraction process.

4.2.1. Extract Robust Watermark

Step 1. Extract the chrominance $Cr\mathrm{’}$ and perform a 4 × 4 block DWT on it to extract four frequency components: LL, HL, LH, and HH’.

Step 2. Select the high-frequency component HH’ and calculate its entropy. Extract the part with the maximum entropy value to obtain the embedding region. Then, perform SVD on it, yielding the left and right singular vectors $U_r$, $V_r$, and the singular value matrix $S_r^{\prime }$.

Step 3. Extract the vertical component HL and the horizontal component LH. Select the coefficients at corresponding positions as determined in step 2 and perform SVD on them to obtain the singular value matrices $S_{HL}$ and $S_{LH}$. Then, calculate $S_a$ according to (18).

Step 4. Calculate the singular value $S_w$ of the watermark by computing the singular value matrix $S_r^{\prime }$ and the mean value matrix $S_a$ according to (20).

$$S_w={\displaystyle \frac{S_r^{\prime }-S_a}{\delta }}$$

(20)

Step 5. Merge the left and right matrices $U_w$ and $V_w$ with $S_w$. Then, perform an inverse SVD and reverse the scrambling process. Finally, convert the “0, 255” back to the “0, 1” sequence to complete the extraction of the robust watermark.

4.2.2. Extract Semi-Fragile Watermark

Step 1. Extract the luminance $Y$ from the YCbCr color space and perform a DWT on it, obtaining four frequency components: LL2, HL2, LH2, and HH2’.

Step 2. The components HL2 and LH2 are extracted to obtain the mean value. In order to meet the requirement of the input value of the Chebyshev map, the average value is processed according to the (10) to obtain the input coefficient $V_n^1$.

Step 3. Perform chaotic mapping on $V_n^1$ according to (10) to obtain the mapped matrix coefficients $V_{n+1}^1$. Then, perform binary processing to the data by assigning a value of “1” to a positive number and “0” to all other values, resulting in the integrity watermark matrix ${Mat}_v$.

Step 4. Extract the high-frequency coefficients HH2’ and use the QIM extraction algorithm defined by (13) to obtain the verification matrix information ${Mat}_v^{\prime }$.

Step 5. Perform the XOR operation between ${Mat}_v$ and ${Mat}_v^{\prime }$. Then, optimize the verification results for false alarms according to Section 3.2.3, thereby completing the integrity verification of the remote sensing image.

Algorithm 2 Watermark extraction process

$\mathbf{Input}: \mathrm{Embedding} \mathrm{strength}, \delta$$; \mathrm{quantization} \mathrm{step}, ∆; \mathrm{watermarked} \mathrm{image}; \mathrm{left} \mathrm{and} \mathrm{right} \mathrm{matrices}, U_w$$\mathrm{and} V_w$;

Output: Extracted watermark, optimized verification results;

1: Convert RGB to YCbCr;

2: Obtain Y’CbCr’;

3: Extract Cr’ and perform a 4 × 4 DWT; // Copyright verification

4: Obtain LL, HL, LH and HH’;

5: Compute HH’s entropy to determine embedding position;

$6: \mathrm{Gain} \mathrm{embedding} \mathrm{region} (Region$);

$7: \mathrm{Perform} \mathrm{SVD} \mathrm{on} HL, LH, \mathrm{and} Region$;

$8: \mathrm{Gain} S_{HL}$$, S_{LH}$, $S_r^{\prime }$$, U_r$$, \mathrm{and} V_r$;

$9: \mathrm{Extract} S_{HL}$$, S_{LH}$$\mathrm{and} \mathrm{calculate} S_a$ according to (18);

$10: \mathrm{Extract} S_r^{\prime }$$\mathrm{and} \mathrm{calculate} S_w$ according to (20);

$11: \mathrm{Gain} S_w$;

$11: \mathrm{Perform} \mathrm{inverse} \mathrm{SVD} \mathrm{on} U_w$$, S_w$$\mathrm{and} V_w$, then reverse the scrambling, and convert back to the “0, 1”;

12: Gain robust watermark;

13: Extract Y’ and perform DWT; // Integrity authentication

14: Obtain LL2, HL2, LH2 and HH2’;

15: Extract HL2 and LH2 to calculate the mean value, then process it according to (11);

16: Obtain the input coefficient $V_n^1$;

17: $V_n^1$ is chaotically mapped according to (10).

18: Gain $V_{n+1}^1$;

19: if $V_{n+1}^1$ > 0 then // Perform binary processing to $V_{n+1}^1$

$20:\hspace{1em}{Mat}_v$ = 1

21: else

$22:\hspace{1em}{Mat}_v$ = 0

23: end if

$24: \mathrm{Extract} HH2’ \mathrm{and} \mathrm{use} \mathrm{QIM} \mathrm{extraction} \mathrm{algorithm} \mathrm{to} \mathrm{extract} {Mat}_v^{\prime }$;

$25: \mathrm{Obtain} {Mat}_v^{\prime }$;

26: $\mathrm{Perform} \mathrm{the} \mathrm{XOR} \mathrm{operation} \mathrm{between} {Mat}_v$$\mathrm{and} {Mat}_v^{\prime }$

27: Obtain verification results;

28: Fale alarm optimization;

29: Obtain optimized verification results

30: Return: Extracted watermark, optimized verification results;

5. Experimental Results and Analysis

5.1. Evaluation Methods

In this study, the peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) were used to assess the invisibility of the watermark and the quality of the watermarked remote sensing image. The normalized correlation coefficient (NC) was used to evaluate the similarity between the extracted watermark image and the original watermark image under different attacks to judge the robustness of the algorithm [5,11,34]. The Equation for calculating the PSNR is as follows:

$$PSNR=10\times {log}_{10}{\displaystyle \frac{{\left({max}_R\right)}^2}{MSE}}$$

(21)

$$MSE={\displaystyle \frac{1}{m_1{n}_1}}\sum _{x=0}^{m_1-1}\sum _{y=0}^{n_1-1}{\left[R\left(x,y\right)-R_w\left(x,y\right)\right]}^2$$

(22)

where $R$ represents the original image, $R_w$ denotes the watermarked image, and ${max}_R$ is the maximum pixel value in the original image. The larger the value of PSNR, the smaller the difference between the watermarked image and the original image.

The primary comparison of SSIM is based on the structural, luminance, and contrast information of the images. The specific calculation Equation is as follows:

$$SSIM=L\left(R,R_w\right)C\left(R,R_w\right)S\left(R,R_w\right)$$

(23)

$$L\left(R,R_w\right)={\displaystyle \frac{2u_R{u}_{R_w}+{\epsilon }_1}{u_R^2+u_{R_w}^2+{\epsilon }_1}}$$

(24)

$$C\left(R,R_w\right)={\displaystyle \frac{2{\sigma }_R^2{\sigma }_{R_w}^2+{\epsilon }_2}{{\sigma }_R^2+{\sigma }_{R_w}^2+{\epsilon }_2}}$$

(25)

$$S\left(R,R_w\right)={\displaystyle \frac{2{\sigma }_{R{R}_w}+{\epsilon }_3}{{\sigma }_R{\sigma }_{R_w}+{\epsilon }_3}}$$

(26)

where $L\left(R,R_w\right)$ is the luminance contrast between images, $C\left(R,R_w\right)$ is the contrast of two images, $S\left(R,R_w\right)$ is the structural contrast, $u_R$ and $u_{R_w}$ are the mean gray values of the original image and the watermarked image, respectively. ${\sigma }_R^2$ and ${\sigma }_{R_w}^2$ are the variances of the two images, ${\sigma }_{R{R}_w}$ is the covariance between the images, and ${\epsilon }_1$, ${\epsilon }_2$, and ${\epsilon }_3$ are constants. The value of SSIM is in the range of 0 to 1, and a larger value indicates a smaller distortion of the image.

The equation for calculating the NC value is as follows:

$$NC={\displaystyle \frac{{\sum }_{m_w}\sum _{n_w}W\left(m_w,n_w\right)W^{\prime }\left(m_w,n_w\right)}{\sqrt{{\sum }_{m_w}\sum _{n_w}{W\left(m_w,n_w\right)}^2}\sqrt{{\sum }_{i_w}\sum _{j_w}{W^{\prime }\left(m_w,n_w\right)}^2}}}$$

(27)

where $W\left(m_w,n_w\right)$ and $W^{\prime }\left(m_w,n_w\right)$ denote the pixel values of the original watermark and the extracted watermark at position $\left(m_w,n_w\right)$, respectively. $m_w$ and $n_w$ are the length and width of the watermarks, respectively. When the value of NC is closer to 1, it means that the similarity between the original and the extracted watermarks is higher, and the algorithm is more robust.

5.2. Experimental Data Sets

To assess the adaptability of the watermarking algorithm to remote sensing image data of varied resolutions and types, this study selected six remote sensing images with varying accuracy, band numbers, data types, and regions as watermark carriers. A 32 × 32 binary image was chosen as the copyright watermark. The information on the remote sensing images is shown in Table 1, and the specific regions are illustrated in Figure 4. Figure 5 displays both the watermark image and the result after scrambling.

Table 1. Details of the datasets.

Data Set	Data Type	Precision	Bit Depth	Bands
Anhui	Landset8	30m	16 Bit	7
Xinjiang	Worldview2	0.5m	16 Bit	8
Suzhou	GF2	0.8m	16 Bit	4
Jilin	Landset5	30m	8 Bit	6
Nanning	Landset3	60m	8 Bit	4
Huaian	Landset7	30m	8 Bit	6

Figure 4. Experimental datasets. (a) Anhui; (b) Xinjiang; (c) Suzhou; (d) Jinlin; (e) Nanning; (f) Huaian.

Figure 5. Original and scrambled watermarks. (a) Original watermark; (b) scrambled watermark.

5.3. Invisibility Analysis

To verify the invisibility of the watermarking algorithm, the PSNR and SSIM values of all watermarked images are respectively calculated. During the watermark embedding phase, this study set the robust watermark embedding strength δ as 0.1. The embedding step ∆ for semi-fragile watermarks is set at 8 for 8-bit images and 80 for 16-bit images. Additionally, the watermarking algorithms from references [15,35,36] are chosen for comparison. The specific statistical results are displayed in Table 2.

Table 2. Results of invisibility calculations.

Index	Datasets	Proposed	Ref. [35]	Ref. [36]	Ref. [15]
PSNR	Anhui	84.094	70.538	77.211	76.594
	Xinjiang	87.724	79.937	77.562	63.187
	Suzhou	84.689	79.677	77.205	61.378
	Jilin	46.427	42.020	45.420	51.043
	Nanning	45.262	40.998	43.211	50.828
	Huaian	47.661	51.361	45.420	47.513
SSIM	Anhui	1.000	0.999	1.000	1.000
	Xinjiang	1.000	1.000	0.999	1.000
	Suzhou	1.000	1.000	0.999	1.000
	Jilin	0.999	0.988	0.998	0.999
	Nanning	0.997	0.991	0.998	0.999
	Huaian	0.996	0.986	0.998	0.997

The results showed that even in the case of embedding dual watermarks, the proposed watermarking algorithm achieved the highest PSNR and SSIM values for datasets such as Anhui, Xinjiang, and Suzhou. For Jilin, Nanning, and Huaian, which have an 8-bit depth, the imperceptibility of the proposed algorithm was slightly lower compared to [15]. This is because the proposed algorithm embeds not only a robust watermark but also a semi-fragile watermark into the images. Nevertheless, both the PSNR and SSIM values exceeded 45 and 0.99, respectively. This suggests that the proposed watermarking algorithm has minimal structural impact on remote sensing images, demonstrating excellent invisibility and applicability to various high-precision remote sensing images.

5.4. Efficiency Analysis

Remote sensing images contain massive surface information, and the data size is much larger than ordinary images. Therefore, the impact of algorithm complexity on efficiency must be considered during the use of watermarking algorithms. This study records the embedding and extracting time of each algorithm, as shown in Figure 6. It can be seen that the algorithm in [35] takes the longest time for both embedding and extraction. This is because the algorithm not only embeds robust watermarks in the R and G bands but also embeds fragile watermarks in the B band. In contrast, the watermarking algorithms in references [15,36] only embed a single robust watermark, making their algorithm efficiency significantly better than that of the proposed algorithm and that in reference [35]. The proposed algorithm embeds a dual watermark, and although its time efficiency is not as good as that of the single watermark algorithms, the invisibility experiment in Section 5.3 shows that the proposed algorithm has excellent invisibility, so the time consumption is worthwhile.

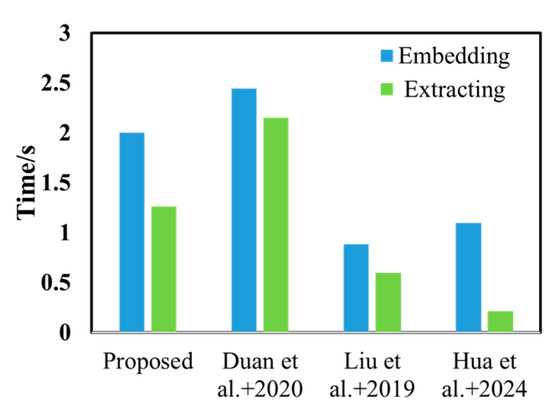
Figure 6. Efficiency analysis. Duan et al.+2022 is reference [35]; Liu et al.+2019 is reference [36]; Hua et al.+2024 is reference [15].

5.5. False Positive Test

The watermarking algorithms based on SVD often encounter the problem of false positive results [37,38]. The test results for false positives are shown in Table 3. We applied the watermark extraction algorithm to the original remote sensing images and did not extract any watermark images, thus eliminating the false positive problem.

Table 3. False positive test.

Datasets	Original Image	Watermarked Image	False Positive Problem
Anhui	NC = 0.000	NC = 0.999	No
Xinjiang	NC = 0.000	NC = 0.999	No
Suzhou	NC = 0.000	NC = 1.000	No
Jilin	NC = 0.000	NC = 0.999	No
Nanning	NC = 0.000	NC = 0.999	No
Haian	NC = 0.000	NC = 0.999	No

In this study, the traditional “0, 1” watermark is transformed into an 8-bit depth “0, 255” watermark sequence to increase the size of the watermark’s singular value $S_w$. Additionally, the watermark embedding method is also redesigned based on the singular value relationship of the horizontal component LH, vertical component HL, and high-frequency component HH. The watermark information is embedded by calculating the mean of the singular values of LH and HL and replacing the singular values of HH. This approach prevents the singular value matrix from appearing to be similar in size, thereby resolving the problem of false positives.

5.6. Robustness Analysis

5.6.1. Noise Attacks

Introducing noise into remote sensing images will seriously degrade their quality and clarity, causing substantial alterations in the pixels within the watermark embedding. Attackers often simulate noise based on this mechanism to deliberately disrupt the watermark. Therefore, robust watermarks must exhibit a certain level of resistance to noise. The common noise in remote sensing images includes salt and pepper noise, gaussian noise, and speckle noise. In order to assess the noise resistance of the proposed watermarking algorithm, the watermark information is extracted from the remote sensing image after adding a certain degree of noise, as shown in Figure 7.

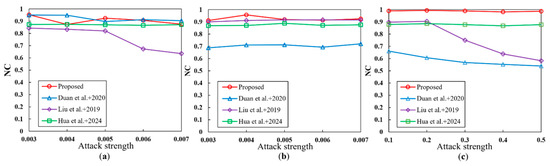
Figure 7. The results of noise attacks. (a) Salt and pepper; (b) Gaussian; (c) speckle. Duan et al.+2022 is reference [35]; Liu et al.+2019 is reference [36]; Hua et al.+2024 is reference [15].

It is evident that the watermarking algorithm in [35] can only resist salt and pepper noise. In [35], the algorithm embeds the watermark in the DWT low-frequency coefficients of the $R$ and $G$ bands of the image. However, since noise can significantly alter these coefficients, the extraction performance is poor. The algorithm in [36] undergoes a significant decrease in NC after the noise intensity exceeds 0.005 in the salt and pepper noise attack experiments, indicating that the watermark embedding domain of the algorithm is highly vulnerable to salt and pepper noise. In contrast, this study selects the high-frequency coefficients of DWT as the watermark embedding domain and utilizes the left and right singular matrices to carry a portion of the image noise information. Therefore, the proposed watermarking algorithm can resist all three types of noise, with NC values all above 0.9.

5.6.2. Geometric Attacks

Typical geometric attacks mainly include translation, rotation, and scaling. These attacks mainly affect the watermark extraction by destroying the synchronization relationship both before and after embedding in the domain. Resisting geometric attacks has always been a challenge in remote sensing image watermarking algorithms. To test the resistance of each algorithm to these attacks, this study carries out a certain degree of translation, rotation, and scaling before extracting the watermark. The specific statistical results are depicted in Figure 8. It can be seen that the proposed watermarking algorithm demonstrates strong resistance to all kinds of attacks, and the NC values of the extracted watermarks are all closest to 1. This is due to the fact that this study uses the image moment and affine transformation to correct the remote sensing images, and adopts the entropy to determine the location of the embedding domain. Consequently, the extraction effectiveness of the watermark can be well maintained. Ref. [35] also adopts entropy to determine the embedding domain, which is validated in the figure to have a certain resistance to geometric attacks. However, both [35] and [36] do not provide any ways to counter desynchronization. Consequently, translation and rotation can disrupt the synchronization between the embedding domain and the extraction domain, hence having a significant impact on the efficiency of watermark extraction.

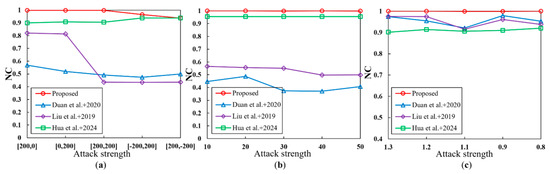
Figure 8. Geometric attack results. (a) Translation; (b) rotation; (c) scaling. Duan et al.+2022 is reference [35]; Liu et al.+2019 is reference [36]; Hua et al.+2024 is reference [15].

5.6.3. Cropping Attacks

Cropping attacks mainly affect the extraction results of watermarks by removing the areas containing watermark information. Region cropping and feature extraction are frequently performed in practical applications of remote sensing images. Therefore, it is essential to consider the impact of cropping on the watermark during the watermarking algorithm design phase. This study examines the resistance of the proposed watermarking to cropping attacks by testing it on different remote sensing images that have been cropped at various scales. The specific cropping modes are depicted in Table 4.

Table 4. Crop attack results.

Attack Mode	Proposed	Ref. [35]	Ref. [36]	Ref. [15]
	NC = 0.999	NC = 0.941	NC = 0.945	NC = 0.916
	NC = 0.999	NC = 0.895	NC = 1.000	NC = 0.942
	NC = 0.999	NC = 0.893	NC = 1.000	NC = 0.936
	NC = 0.999	NC = 0.761	NC = 1.000	NC = 0.955
	NC = 0.999	NC = 0.783	NC = 0.897	NC = 0.940

The results indicate that the proposed algorithm achieved the most stable watermark extraction results. The 4 × 4 blocking strategy used in this study allows for the extraction of complete watermark information, as long as the cropping attack does not destroy all the blocking regions. In contrast, refs. [35,36] transform the entire image and use it as the embedding domain. Therefore, if the cropping ratio is too large or if the cropping includes regions containing the watermark, the extraction effectiveness of the watermark is compromised.

5.6.4. Filtering Attacks

Filtering is a prevalent method used in remote sensing image processing to modify the overall characteristics of an image by applying weightings, averaging, or other operations to the pixels in the image. Filtering plays a crucial role in local enhancement, smoothing, extraction, texture reconstruction, and noise reduction of remote sensing images. Therefore, watermarking algorithms need to be resistant to various filters. In this study, Gaussian, mean, and median filtering were performed on watermarked remote sensing images to test the impact of filtering on the watermarking algorithm. The specific results are shown in Figure 9. The results showed that the proposed algorithm has good resistance to all kinds of filtering. In the mean and median filtering attack experiments, the NC value of the extracted watermark was more than 0.99. In the Gaussian filtering attack experiment, the NC values changed sharply only when the attack strength was more than 2. In contrast, only the algorithm in [36] achieved similar results. For the watermarking algorithm in [35], the watermark extraction was greatly affected because the filtering process smooths the DWT coefficients.

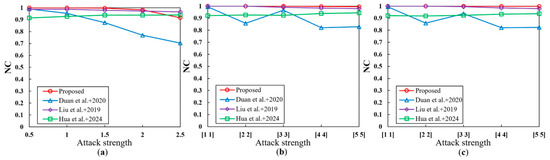
Figure 9. The results of a filtering attack. (a) Gaussian filtering; (b) mean filtering; (c) median filtering. Duan et al.+2022 is reference [35]; Liu et al.+2019 is reference [36]; Hua et al.+2024 is reference [15].

5.6.5. Compression

In many application scenarios, remote sensing images only need to be displayed as images, so data compression is often involved. As a typical lossy compression method, JPEG transfers the remote sensing image into the transform domain and removes the high-frequency information. In this process, the main information is not affected, and the compressed remote sensing image still maintains a sufficient visual quality. Therefore, this compression method is widely used in remote sensing image compression, and its influence must be taken into account in the watermarking algorithm. Figure 10 demonstrates that, among various compression quality factors, only the proposed algorithm and [35] can extract the watermarks in their entirety. This is due to the inherent properties of SVD, which is not prone to data error accumulation and exhibits good data stability. These characteristics ensure that the proposed algorithm can effectively resist various intensities of compression attacks. In contrast, the algorithm in [36] can only extract the complete watermark when the quality factor is less than 60. While [15] achieved the worst watermark extraction results, all of the resulting watermark NC values were above 0.9, indicating good stability.

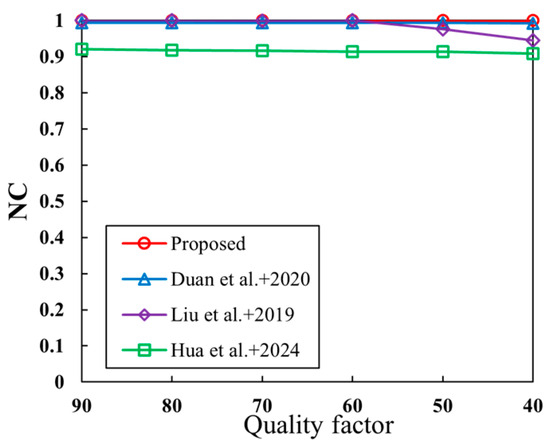
Figure 10. The results of compression attack. Duan et al.+2022 is reference [35]; Liu et al.+2019 is reference [36]; Hua et al.+2024 is reference [15].

5.6.6. Affine Transformation

During the processing of remote sensing images, operations such as image registration, map projection transformation, and geometric correction are often performed, all of which involve affine transformations. Therefore, watermark algorithms also need to exhibit a certain level of resistance to affine transformations. In this study, we set $B$ = 0 in the (5), and the specific transformation matrix $A$ is shown in Table 5. The proposed algorithm achieves watermark NC values all above 0.99, which is second only to the extraction effect of [36]. Ref. [15] uses entropy to determine the watermark embedding domain. Although the extracted watermark NC values exceed 0.9, the algorithm’s robustness is constrained by embedding the watermark directly in the DWT low-frequency coefficients. Unlike the approach given in reference [15], this study combines the stability of SVD with DWT, resulting in overall better extraction effectiveness. Ref. [35] exhibited the worst extraction effectiveness in the affine transformation attack experiments. This is because the affine transformation changes the position of the watermark embedding domain, rendering its extraction template ineffective.

Table 5. The results of affine transformation.

Transformation Matrix	Proposed	Ref. [35]	Ref. [36]	Ref. [15]
$\left[\begin{array}{cc}0.9& 0\\ 0& 1.1\end{array}\right]$
	NC = 0.999	NC = 0.961	NC = 0.966	NC = 0.922
$\left[\begin{array}{cc}1& 0.01\\ 0.01& 1\end{array}\right]$
	NC = 0.998	NC = 0.565	NC = 0.997	NC = 0.915
$\left[\begin{array}{cc}0.9& 0.1\\ 0& 1\end{array}\right]$
	NC = 0.995	NC = 0.501	NC = 1.000	NC = 0.904
$\left[\begin{array}{cc}0.9& 0.1\\ 0.1& 1.1\end{array}\right]$
	NC = 0.995	NC = 0.481	NC = 1.000	NC = 0.905

5.7. Integrity Authentication

5.7.1. Local Tampering

Common modifications in remote sensing images mainly include content replacement, cropping, pasting, and adding ground elements, which can seriously affect the authenticity and credibility of the image. Therefore, in this study, various sets of remote sensing images were subjected to local area replacement, cropping, pasting, and adding ground elements. Subsequently, the integrity verification capability of the semi-fragile watermark algorithm was tested. The specific tampering locations and detection results are presented in Table 6. The results showed that the integrity authentication watermarking algorithm proposed in this study can not only meet the needs of images with varying bit depths but also accurately identify obvious tampering such as cutting, pasting, and adding ground elements. Furthermore, it demonstrates good fragility towards subtle tampering like local replacement, which is difficult to perceive by the naked eye. This is mainly due to the fact that during these attacks, the integrity information of the corresponding location is also corrupted, and the verification matrix generated by the algorithm no longer matches the extracted integrity watermarking information, thus enabling accurate identification of the tampered region.

Table 6. Local tampering results.

Watermarked Image	Modified Image	Authentication Results	Watermarked Image	Modified Image	Authentication Results
Local replacement			Add ground elements
Crop			Paste

5.7.2. Combined Attacks

Remote sensing images undergo a certain degree of data loss or introduce minimal noise during compression and decompression. Additionally, filtering is commonly used to denoise and enhance local image features during usage. These unintentional modifications to the image can potentially affect the recognition of semi-fragile watermarks to varying degrees. Semi-fragile watermarks not only need to exhibit good fragility against malicious tampering but also require a certain level of robustness against unintentional modifications. To verify this point, this study combined various attacks, including noise addition, filtering, and compression, to simulate the image modifications encountered in practical usage scenarios of remote sensing images. The specific attack methods and integrity verification results are presented in the Table 7. The proposed semi-fragile watermarking algorithm performs well under various combined attack conditions. It not only identifies conventional cropping and pasting regions but also accurately detects locally replaced areas that are difficult for the human eye to recognize. This is attributed to the DWT’s excellent local transformation characteristics, enabling accurate differentiation between unaltered and altered regions. QIM represents integrity information using quantized intervals during extraction, allowing the algorithm to accurately extract the watermark even in environments with noise, filtering, and compression.

Table 7. Combined attack results.

Watermarked Image	Modified Image	Authentication Results	Watermarked Image	Modified Image	Authentication Results
0.00001 speckle + 0.1 Gaussian filtering + paste			0.0001 salt and pepper + [1 1] mean filtering +add scenery
[1 1] mean filtering + 0.1 Gaussian filtering + crop			90JPEG compression + [1 1] median filtering + paste
90JPEG + 0.2 Gaussian filtering + add scenery			0.0001 salt and pepper noise + [1 1] median filtering + local replacement

6. Conclusions

This study proposes a dual watermarking algorithm for remote sensing images that can facilitate both data integrity authentication and copyright protection. The algorithm transforms the remote sensing images from the RGB color space to the YCbCr color space and embeds semi-fragile watermarks and robust watermarks separately in the luminance Y and chrominance Cr components, preventing mutual interference between the dual watermarks and ensuring the invisibility of the watermark algorithm. The algorithm leverages the properties of DWT multi-scale decomposition and localized variations. For the semi-fragile watermark, the algorithm constructs integrity verification watermarks by using Chebyshev chaotic mapping to obtain the mean values of DWT horizontal and vertical components and embeds integrity information into high-frequency areas using QIM. For the robust watermark, the algorithm redesigns the watermark embedding method based on the singular value matrix relationships of horizontal, vertical, and high-frequency components in DWT. Furthermore, it converts the watermark from a “0, 1” sequence to a “0, 255” sequence, amplifying the watermark singular values to avoid false positives in SVD, ensuring resistance to conventional image processing. The experimental results confirmed that this dual watermarking algorithm accurately identifies tampered regions under typical combination attacks and successfully extracts robust watermarks in various image processing scenarios, effectively meeting the practical requirements of remote sensing image usage. However, this study did not resolve the trade-off between the robustness and invisibility of watermarking algorithms. In future research, we will incorporate deep learning and adaptive algorithms to address this issue.