Abstract
This paper contains several novel definitions including neutrosophic metric space, neutrosophic quasi--metric space, neutrosophic pseudo--metric space, neutrosophic quasi--metric space and neutrosophic pseudo--metric space. Further, we present some generalized fixed point results with non-trivial examples and the decomposition theorem in the setting of the neutrosophic pseudo--metric space. Moreover, by using the main result, we examine the existence and uniqueness of the solution to an integral equation, a system of linear equations, and nonlinear fractional differential equations.
1. Introduction
There are numerous applications for fixed points (FPs) in neutrosophic metric spaces in the fields of mathematics, computer science, economics, and engineering. By adding the idea of indeterminacy or uncertainty, neutrosophic metric space broadens the concept of metric spaces. The literature on mathematical analysis contains many generalizations of a metric space (MS). The well-known 2-MS concept was first proposed by Gahlar [1]; however, in fact, MS is continuous while 2-MS is not. Following that, Dhage [2] presented the notion of D-MS; however, Mustafa and Sims [3] clarified that several of D-MS’s topological characteristics were false, and they provided the concept of G-MS. According to Jleli and Samet [4], most of the FP theorems in the context of the G-MS can be easily verified by using MS and quasi MS. Authors in [5] presented the notion of S-MS, in 2012, and demonstrated several FP theorems in the context of complete S-MS. Bakhtin [6] introduced b-MS, in 1989, by multiplying the right side of triangle inequality by a real value . In b-MS, it becomes MS if we choose Subsequently, Sedghi et al. [7] combined the concepts of b-MS and S-MS to introduce the idea of -MS; however, -MS is not continuous.
Zadeh [8] presented the notion of fuzzy logic. As compared to the notion of traditional logic, fuzzy logic attributes a number to an element inside the interval [0, 1], even though certain numbers are not contained within the set. Uncertainty, a crucial component of actual difficulty, has assisted Zadeh in learning fuzzy set (FS) theories in order to cope with the problem of indefinites. For a variety of processes, including one that incorporates the use of fuzzy logic, the theory is viewed as an FP in the fuzzy metric space (FMS). Eventually, Heilpern [9] and Zadeh’s results developed the fuzzy mapping idea and a theorem based on FPs for fuzzy contraction mapping in linear MS, representing a fuzzy generalized version of Banach’s contraction concept. If the distance between the elements is not an exact integer, imprecision is introduced in the concept of FMSs given by Kaleva and Saikkala [10]. Following that, the notation of an FMS was introduced, first by Kramosil and Michalek [11] and then by George and Veeramani [12]. The definition and various characteristics of fuzzy b-MS were established by Nadaban [13]. Malviya [14] used contraction mappings to demonstrate several FP results and presented the ideas of N-FMS and pseudo N-FMS. The notion of -FMS and its topological features were demonstrated with several FP theorems for contraction mappings by Fernandez et al. [15]. Using the ideas of intuitionistic FSs, continuous t-norm (CtN), and continuous t-conorm (CtCN), Park [16] introduced intuitionistic fuzzy metric spaces (IFMSs), in 2004, as a generalization of FMSs. Many scholars [17,18,19,20,21,22] then turned their attention to IFMS generalizations and developed FP results for contraction mappings. Several FP theorems for contraction mappings under random conditions were proven by Ionescu et al. [23] and Mehmood et al. [24] in their work on IFMSs and extended b-metric spaces. The concept of neutrosophic metric space (NMS) was introduced and various results were proven by Murat and Necip [25]. Ishtiaq et al. [26] provided the notion of intuitionistic fuzzy metric space and proved numerous FP results. See [27,28,29] for more details related to this study.
The generalizations of NMSs increase the area of mathematical analysis by providing tools for understanding complicated structures and systems, as well as insights into abstract algebraic and topological features. They are critical for building the theoretical foundations of many fields of mathematics, as well as applying mathematical principles to a wide range of scientific and real-world situations. Motivated by [25,26], we present numerous notions including neutrosophic metric space (NNbMS), neutrosophic quasi--metric space (NQSbMS), neutrosophic pseudo--metric space (NPSbMS), neutrosophic quasi--metric space (NQNMS) and neutrosophic pseudo--metric space (NPNbMS). We prove several FP theorems and decomposition theorems in the context of NNBMS. At the end, we apply the main result and find the existence and uniqueness of an integral equation (IE), a system of linear equations (SLEs) and nonlinear fractional differential equations (FDE).
2. Preliminaries
We include several definitions from existing literature to support the main study.
Definition 1
([22]). Assume that be a mapping. is said to be a CtN if it fulfills the following axioms:
- (i)
- (ii)
- (iii)
- * is continuous;
- (iv)
- for
is a to be product CtN and is a minimum CtN.
Definition 2
([22]). Assume that be a mapping. is called a CtCN if it satisfies the conditions below:
- (i)
- (ii)
- (iii)
- is continuous;
- (iv)
- for
is an example of a maximum CtCN.
Definition 3
([14]). A triple is an NFMS with an FS on and is a CtN if it fulfills the axioms below for all and
- (a)
- (b)
- if and only if
- (c)
- (d)
- is a continuous function (CF).
Definition 4
([7]). Let be an arbitrary set that is not empty and be a positive real number. Then, a mapping is said to be -metric if it satisfies for all
- (S1)
- if
- (S2)
Then, is an - MS.
Definition 5
([16]). Let be an IFMS if is an arbitrary set, is a CtN, is a CtCN, and are FSs on fulfilling the axioms which are given below for all and
- (i)
- (ii)
- (iii)
- if and only if
- (iv)
- (v)
- is a CF,
- (vi)
- (vii)
- if and only if
- (viii)
- (ix)
- is a CF.
Definition 6
([26]). Let a six tuple be an IFNbMS if is an arbitrary set, is a real number, is a CtN, is a CtCN, and are FSs on fulfills the following conditions for all and
- (i)
- (ii)
- (iii)
- if and only if
- (iv)
- (v)
- is a CF,
- (vi)
- (vii)
- if and only if
- (viii)
- (ix)
- is a CF.
Here, is said to be a membership function and non-membership function of and concerning
Definition 7
([25]). A sextuple is called an NMS if is an arbitrary set, is a CtN, is a CtCN, and are NSs on fulfills the following conditions for all and
- (i)
- (ii)
- (iii)
- if and only if
- (iv)
- (v)
- is a CF,
- (vi)
- (vii)
- if and only if
- (viii)
- (ix)
- is a CF.
- (x)
- (xi)
- if and only if
- (xii)
- (xiii)
- is a CF.
Definition 8
([26]). A sextuple is an IFQSbMS if is an arbitrary set, is a real number, is a CtN, is a CtCN, and are FSs on satisfies the axioms below for all and
- (a)
- (b)
- (c)
- if and only if where is permutation,
- (d)
- (e)
- is a CF,
- (f)
- (g)
- if and only if where is permutation,
- (h)
- (i)
- is a CF.
Here, is said to be a membership function and is non-membership function of and concerning
Definition 9
([26]). A sextuple is an IFQNMS if is an arbitrary set, is a CtN, is a CtCN, and are FSs on and fulfills the below conditions for all and
- (a)
- (b)
- (c)
- if and only if where is permutation,
- (d)
- (e)
- is a CF,
- (f)
- (g)
- where is permutation,
- (h)
- (i)
- is a CF.
Definition 10
([26]). A sextuple is an IFPNbMS if is an arbitrary set, is a real number, is a CtN, is a CtCN and are FSs on and satisfies the below axioms for all and
- (i)
- (ii)
- (iii)
- if and only if
- (iv)
- (v)
- is a CF,
- (vi)
- (vii)
- if and only if
- (viii)
- (ix)
- is a CF.
3. Neutrosophic Metric Space
The concept of NNbMS is introduced and some non-trivial examples are given in this section.
Definition 11.
A septuple
is said to ba a NNbMS if is an arbitrary set, is a real number, is a CtN, is a CtCN, are NSs on satisfying the axioms below for all and
- i.
- ii.
- iii.
- iv.
- v.
- is a CF,
- vi.
- vii.
- if
- viii.
- ix.
- is a CF.
- x.
- xi.
- if and only if
- xii.
- xiii.
- is a CF.
In this, membership, non-membership and neutral functions of and concerning are .
Remark 1.
The definition of NNMS can be obtained by considering the
in Definition 11.
Example 1.
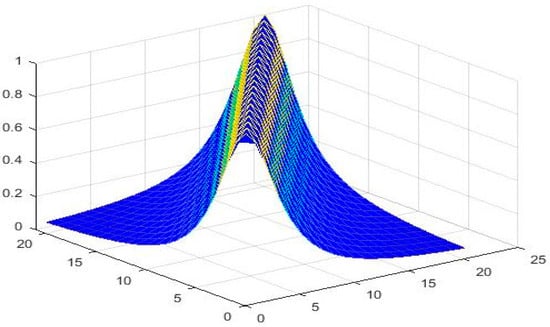
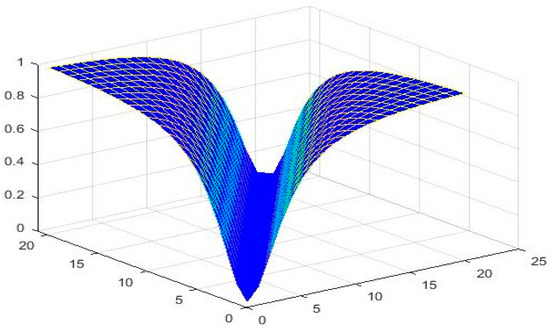
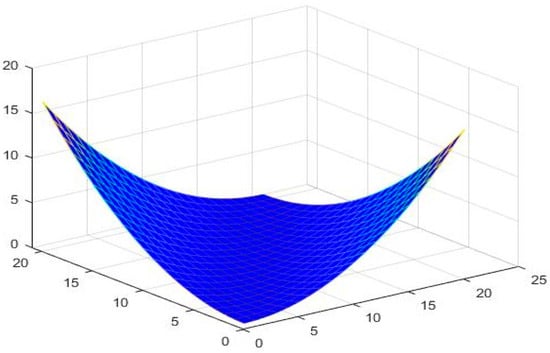
Let
and and are the functions on defined by
for all and Therefore is an NNbMS with CtN CtCN and constant Figure 1, Figure 2 and Figure 3 show the graphical behavior of respectively.

Figure 1.
Demonstrating the performance of for .

Figure 2.
Demonstrating the performance of for .

Figure 3.
Demonstrating the performance of for .
Proof.
We verify (iv) and (viii), others are easy to prove. We can write
Now, let
and
Therefore, (iv) and (viii) are fulfilled. □
Definition 12.
Let
be a NNbMS. Then is called symmetric if
and
for all and
Example 2.
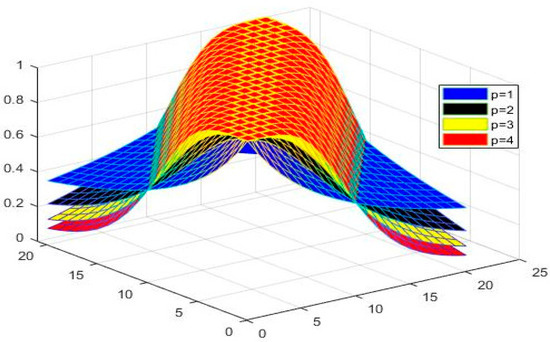
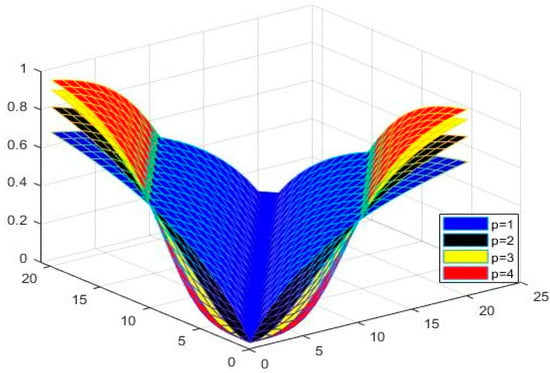
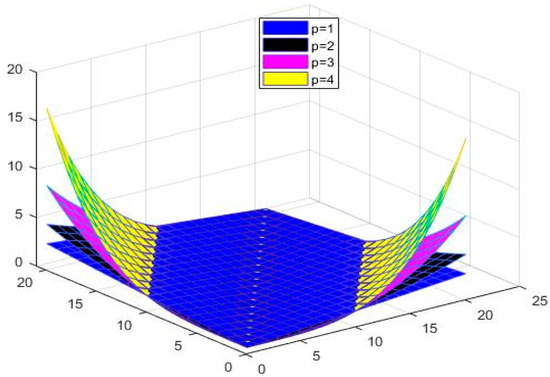
Let and are the functions on defined by
and
for all and Then is a symmetric NNbMS with CtN CtCN and constant Figure 4, Figure 5 and Figure 6 show the graphical behavior of , respectively.

Figure 4.
Shows the performance of for

Figure 5.
Shows the performance of for

Figure 6.
Shows the performance of for
4. Generalized Definitions
In this section, we present some generalized notions and different non-trivial examples.
Definition 13.
A septuple
is an NQSbMS if is an arbitrary set, is a CtN, is a CtCN, is a positive real number, are NSs on and satisfies the conditions below for all and
- i.
- ii.
- iii.
- if and only if where is permutation,
- iv.
- v.
- is a CF,
- vi.
- vii.
- if and only if where is permutation,
- viii.
- ix.
- is a CF.
- x.
- xi.
- if and only if where is permutation,
- xii.
- xiii.
- is a CF.
In this, membership, non-membership and neutral functions of and concerning are .
Remark 2.
The NQSbMS definition is obtained by taking μ = 1 in Definition 13.
Example 3.
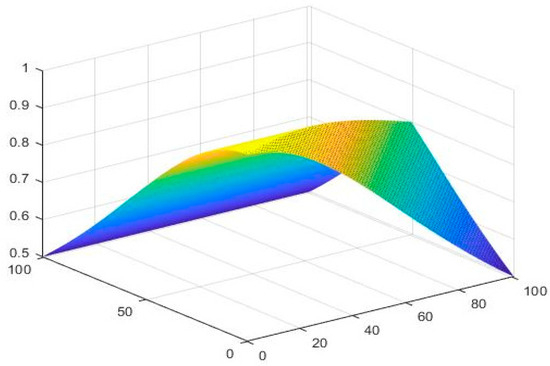
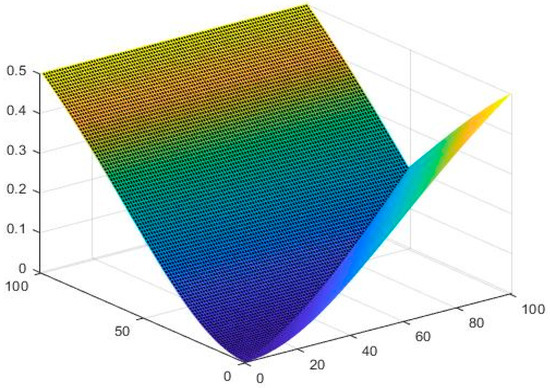
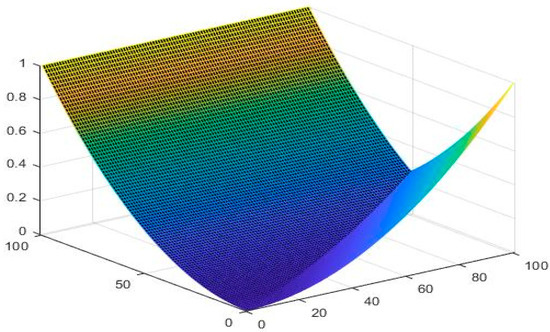
Let
Define and by
and
Then is said to be an NQSbMS with Figure 7, Figure 8 and Figure 9 show the graphical behavior of , respectively.

Figure 7.
Shows the performance of for

Figure 8.
Shows the performance of for

Figure 9.
Shows the performance of for
Remark 3.
If
, then by definition of
and in Example 3
and
Furthermore, In general, NQSbMS is not symmetric.
Definition 14.
A septuple
is an NPSbMS if is an arbitrary set, is a real number, is a CtN, is a CtCN, and are NSs on , and fulfills the conditions below for all and
- (I)
- (II)
- (III)
- if and only if
- (IV)
- (V)
- is a CF,
- (VI)
- (VII)
- if and only if
- (VIII)
- (IX)
- is a CF.
- (X)
- (XI)
- if and only if
- (XII)
- (XIII)
- is a CF.
Remark 4.
The definition of NPSbMS is obtained if we can obtain
in the above definition.
Example 4.
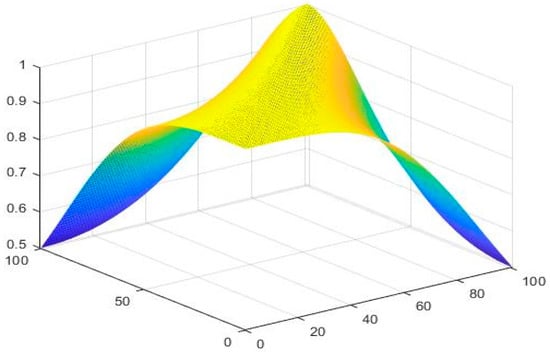
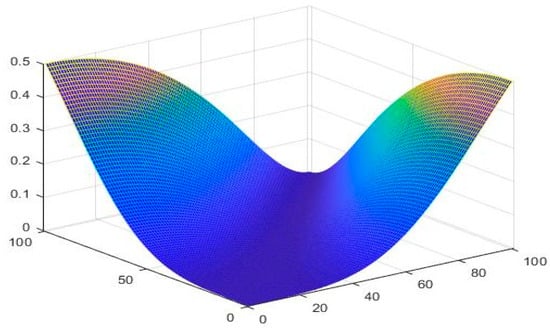
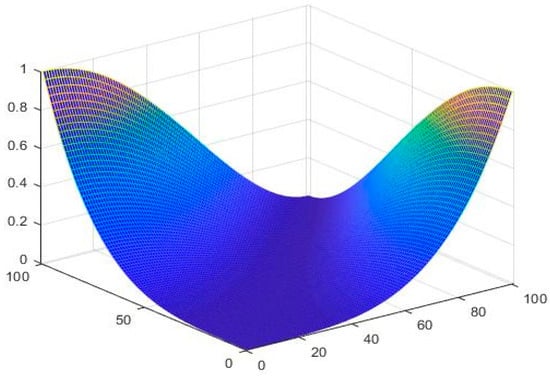
Suppose Define and by
and
Then is said to be an NPSbMS. Figure 10, Figure 11 and Figure 12 show the graphical behavior of , respectively.

Figure 10.
Shows the performance of for

Figure 11.
Shows the performance of for

Figure 12.
Shows the performance of for
Definition 15.
A sextuple
is an NQNMS if is an arbitrary set, is a CtN, is a CtCN, and are NSs on , and satisfies the below conditions for all and
- (j)
- (k)
- (l)
- if and only if where is permutation,
- (m)
- (n)
- is a CF,
- (o)
- (p)
- if and only if where is permutation,
- (q)
- (r)
- is a CF.
- (s)
- (t)
- if and only if where is permutation,
- (u)
- (v)
- is a CF.
Remark 5.
An NNMS satisfies the symmetric property, i.e., and but in NQNMS, the symmetric property is not fulfilled, i.e., and
Definition 16.
A sextuple
is an NPNbMS if arbitrary set, is a CtN, is a CtCN, is a positive real number, and are NSs on and fulfills the following conditions for all and
- (x)
- (xi)
- (xii)
- if and only if
- (xiii)
- (xiv)
- is a CF,
- (xv)
- (xvi)
- if and only if
- (xvii)
- (xviii)
- is a CF.
- (xix)
- (xx)
- if and only if
- (xxi)
- (xxii)
- is a CF.
Example 5.
Suppose that
equipped with a usual metric and
is convergent in Define CtN by
and CtCN by
for all
and
and
Observe that is an NPNbMS but it is not an NNbMS. For this, take and Then, for and in but
Remark 6.
Every NNbMS is an NPNbMS but the converse need not be true.
Definition 17.
Suppose
is a symmetric NNbMS. A sequence in is called convergent, if and or and as for every That is, for and , there exists such that for all and or and
Lemma 1.
Suppose is a symmetric NNbMS with CtN and CtCN Suppose has a convergent sequence which is If sequence converges to and then That is, the limit of is unique if it exists.
Proof.
Let be a convergent sequence in and converges to and Then, and as for every and and as for every
and
as □
Definition 18.
Let
be a symmetric NNbMS. A sequence
is a Cauchy sequence (CS), if for all and there exists such that
or
for each
Definition 19.
Let
be a symmetric NNbMS. is said to be a complete symmetric NNbMS if every Cauchy in is convergent in
Definition 20.
Let
be a symmetric NNbMS. A subset of is called
-bounded if there exist
and
such that
for each
Definition 21.
Let
be an NNbMS. A mapping
is said to be a neutrosophic
-contraction if for each
and for some
we obtain
Lemma 2.
Let be an NNbMS with CtN and CtCN Assume that a sequence converges to in . Then, sequence is called a CS in .
Proof.
There is for every we have
as and
as for all
and
Hence, is a CS. □
Definition 22.
Assume that the symmetric NNbMSs are
and . Then a function is said to be continuous at a point if it is sequentially continuous at that is, whenever is convergent to , we have converging to
Proposition 1.
Let be symmetric NNbMSs and be a fuzzy q-contraction. If any FP of satisfies
then
Proof.
Given that is a fuzzy q-contraction, suppose a point is an FP of then we obtain
as and so
and
as and so
Similarly,
as and so
□
Lemma 3.
Let be symmetric NNbMSs. Let and be two sequences in and suppose as , and as Then and as
Proof.
Since and there is such that for and, so we have
and
and we have
Similarly,
and
By Definition of 17 and combining the arbitrary nature of and the continuity for and concerning for large enough by using Definition 12, we obtain
and consequently, by using Definition 12, we have
We obtain
and
Consequently,
□
Lemma 4.
Let be symmetric NNbMSs. If there exists such that and for all and
Then
Proof.
Assume that there exists such that and for all and Then,
and so
for positive integer Taking the limit as
and so
For positive integer Taking the limit as ,
and so
For positive integer Taking the limit as and hence □
5. Application in FP Theory
In this, we describe the application of a Banach contraction principle via neutrosophic contraction in symmetric NNbMSs
Theorem 1.
Suppose is a symmetric complete NNbMSs with
and
be a neutrosophic
contraction. Then, has a unique FP.
Proof.
Let and by using the iterative process, we create a sequence which satisfies Since , we obtain
and
Hence,
by using (iv) of Definition 11, we obtain
By (4) neutrosophic contraction (since, ) so
as and
by using (viii) of Definition 11, we obtain
By (4), neutrosophic contraction (i.e., ) and taking we obtain
Similarly,
by using (xii) of Definition 11, we obtain
By (4), neutrosophic contraction (i.e., ) and taking we obtain
Hence, is CS. Therefore, is a symmetric complete NNbMSs, there exists we have
The point is an FP of as we will demonstrate below:
subsequently is neutrosophic contraction and as
and
Since is neutrosophic contraction and as
similarly, we have
Since is neutrosophic contraction and as
That is hence, is an FP of Now, we evaluate the uniqueness; let for some then
as
as and
as That is . □
Example 6.
Suppose and is a symmetric complete NNbMSs where are defined by
Let Then, for
where and
where Similarly,
where Therefore, all the conditions of Theorem 1 are satisfied and 0 is a unique FP of in
Let as
be a non-decreasing and CF. Moreover, for every This implies
Theorem 2.
Suppose is a complete symmetric NNbMSs and is a mapping satisfying
for all and Then there exists a unique FP of
Proof.
It is immediate and by using Theorem 1 letting □
6. Application to Integral Equations
Solving equations in any form is one of the most important and interesting aspects of mathematics. There are several approaches to solving various types of equations. Identifying the solution of a problem whether it is singular or multiple. One of the main methods that has made significant progress in the study of IEs is FP theory, which is an iterative procedure with a variety of applications. To determine if a differential or integral problem has a solution, FP theory is essential.
In this section, we prove that Theorem 1 is valid for a specific nonlinear integral problem. The following theorem provides an answer to the question whether “The solution for a specific nonlinear IE exists or not”. Assume the set of real-valued CFs on a bounded interval is denoted by .
Then are complete symmetric NNbMSs defined by by
for and for all and let
where and and are CFs.
Theorem 3.
Let be a symmetric complete NNbMSs provided in (5), (6) and (7). Define the integral operator by
for all and Assume that the following axioms are fulfilled;
- (a)
- For all and
- (b)
- For all
Then
is a unique solution for (8).
Proof.
For each we obtain
and,
Similarly,
Since all conditions of Theorem 1 are fulfilled, then the IE (8) has a unique solution. □
7. Application to Linear Equations
Assume and define a complete symmetric NNbMS on by
for all and , if
The following linear equations have only one solution.
Proof.
Assume be described by where and
For we obtain
Using (15), we have
and
Using (15)
and
Using (15)
Therefore, all the conditions of Theorem 1 are satisfied, and is a neutrosophic contraction. There is a unique solution of the SLEs (16) in □
8. Application to Nonlinear Fractional Differential Equation
In this part, we apply Theorem 1 to determine the existence and uniqueness of a solution to nonlinear FDE given by
with boundary conditions
where means caputo fractional derivative of order, defined by
and is a CF. We suppose that from into with supremum
The Riemann–Liouville fractional integral of order is given by
We first provide a nonlinear FDE in an appropriate form and then investigate the existence of a solution. Now, we suppose the following FDE
with the boundary conditions
where
- i.
- is a CF,
- ii.
- is continuous,
and fulfill the axioms below:
for all and is a constant with where
Then there exists a unique solution to Equation (17).
Proof.
Assume that
defined by Let , for all Then is a complete NNbMS. We describe a mapping by
for all . An Equation (17) has a solution if for all. Now
That is,
Utilizing the fact and (19), we have
and
All axioms of Theorem 1 are satisfied. This shows that has unique solution. □
9. Conclusions
In this study, we presented several new concepts including NNbMS, NQSbMS, NPSbMS, NQNMS and NPNbMS. Further, we established several FP results in the framework of NNbMS and proved a well-known decomposition theorem. Furthermore, we presented several non-trivial examples with their graphs for better understanding by the readers and to show the superiority of the introduced definitions and results. At the end, we presented the existence and uniqueness of a solution of an integral equation, SLEs and nonlinear FDE by applying the main results. This work is extendable in the context of neutrosophic controlled metric spaces, neutrosophic quasi controlled metric spaces, neutrosophic pseudo partial metric spaces and many other structures.
Author Contributions
Conceptualization, M.A., U.I., K.A., T.A.L., V.L.L. and L.G.; methodology, M.A., U.I., K.A., T.A.L., V.L.L. and L.G.; software, M.A., U.I., K.A., T.A.L., V.L.L. and L.G.; validation, M.A., U.I., K.A., T.A.L., V.L.L. and L.G.; formal analysis, M.A., U.I., K.A., T.A.L., V.L.L. and L.G.; investigation, M.A., U.I., K.A., T.A.L., V.L.L. and L.G.; resources, M.A., U.I., K.A., T.A.L., V.L.L. and L.G.; data curation, M.A., U.I., K.A., T.A.L., V.L.L. and L.G.; writing—original draft preparation, M.A., U.I., K.A., T.A.L., V.L.L. and L.G.; writing—review and editing, M.A., U.I., K.A., T.A.L., V.L.L. and L.G.; visualization, M.A., U.I., K.A., T.A.L., V.L.L. and L.G.; supervision, M.A., U.I., K.A., T.A.L., V.L.L. and L.G.; project administration, M.A., U.I., K.A., T.A.L., V.L.L. and L.G.; funding acquisition, M.A., U.I., K.A., T.A.L., V.L.L. and L.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be available on demand from the corresponding authors.
Acknowledgments
The authors are thankful to the Deanship of Scientific Research, Islamic University of Madinah for providing the support under the Post Publication Program III.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gähler, S. 2-metrische Räume und ihre topologische Struktur. Math. Nachrichten 1963, 26, 115–148. [Google Scholar] [CrossRef]
- Dhage, B.C. Generalized metric space and mapping with fixed point. Bull. Cal. Math. Soc. 1992, 84, 329–336. [Google Scholar]
- Mustafa, Z.; Sims, B. A new approach to generalized metric spaces. J. Nonlinear Convex Anal. 2006, 7, 289. [Google Scholar]
- Jleli, M.; Samet, B. Remarks on G-metric spaces and fixed point theorems. Fixed Point Theory Appl. 2012, 2012, 210. [Google Scholar] [CrossRef]
- Sedghi, S.; Shobe, N.; Aliouche, A. A generalization of fixed point theorems in S-metric spaces. Mat. Vesn. 2012, 64, 258–266. [Google Scholar]
- Bakhtin, I.A. The contraction principle in quasi metric spaces, Funct. Anal. Unianowsk Gos. Ped. Inst. 1989, 30, 26–37. [Google Scholar]
- Sedghi, S.; Shobkolaei, N.; Shahraki, M.; Došenović, T. Common fixed point of four maps in S-metric spaces. Math. Sci. 2018, 12, 137–143. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Heilpern, S. Fuzzy mappings and fixed point theorem. J. Math. Anal. Appl. 1981, 83, 566–569. [Google Scholar] [CrossRef]
- Kaleva, O.; Seikkala, S. On fuzzy metric spaces. Fuzzy Sets Syst. 1984, 12, 215–229. [Google Scholar] [CrossRef]
- Kramosil, I.; Michálek, J. Fuzzy metrics and statistical metric spaces. Kybernetika 1975, 11, 336–344. [Google Scholar]
- George, A.; Veeramani, P. On some results in fuzzy metric spaces. Fuzzy Sets Syst. 1994, 64, 395–399. [Google Scholar] [CrossRef]
- Nădăban, S. Fuzzy b-metric spaces. Int. J. Comput. Commun. Control 2016, 11, 273–281. [Google Scholar] [CrossRef]
- Malviya, N. The N-fuzzy metric spaces and mappings with application. Fasc. Math 2015, 55, 133–151. [Google Scholar] [CrossRef]
- Fernandez, J.; Isık, H.; Malviya, N.; Jarad, F. Nb-fuzzy metric spaces with topological properties and applications. AIMS Math. 2023, 8, 5879–5898. [Google Scholar] [CrossRef]
- Park, J.H. Intuitionistic fuzzy metric spaces. Chaos Solitons Fractals 2004, 22, 1039–1046. [Google Scholar] [CrossRef]
- Turkoglu, D.; Alaca, C.; Cho, Y.J.; Yildiz, C. Common fixed point theorems in intuitionistic fuzzy metric spaces. J. Appl. Math. Comput. 2006, 22, 411–424. [Google Scholar] [CrossRef]
- Kanwal, S.; Azam, A.; Shami, F.A. On coincidence theorem in intuitionistic fuzzy b-metric spaces with application. J. Funct. Spaces 2022, 2022, 5616824. [Google Scholar] [CrossRef]
- Hussain, A.; Al Sulami, H.; Ishtiaq, U. Some new aspects in the intuitionistic fuzzy and neutrosophic fixed point theory. J. Funct. Spaces 2022, 2022, 3138740. [Google Scholar] [CrossRef]
- Ishtiaq, U.; Saleem, N.; Uddin, F.; Sessa, S.; Ahmad, K.; di Martino, F. Graphical Views of Intuitionistic Fuzzy Double-Controlled Metric-Like Spaces and Certain Fixed-Point Results with Application. Symmetry 2022, 14, 2364. [Google Scholar] [CrossRef]
- Ishtiaq, U.; Javed, K.; Uddin, F.; Sen, M.D.L.; Ahmed, K.; Ali, M.U. Fixed point results in orthogonal neutrosophic metric spaces. Complexity 2021, 2021, 2809657. [Google Scholar] [CrossRef]
- Schweizer, B.; Sklar, A. Statistical metric spaces. Pacific J. Math. 1960, 10, 313–334. [Google Scholar] [CrossRef]
- Ionescu, C.; Rezapour, S.; Samei, M.E. Fixed points of some new contractions on intuitionistic fuzzy metric spaces. Fixed Point Theory Appl. 2013, 2013, 168. [Google Scholar] [CrossRef]
- Mehmood, F.; Ali, R.; Ionescu, C.; Kamran, T. Extended fuzzy b-metric spaces. J. Math. Anal. 2017, 8, 124–131. [Google Scholar]
- Murat, K.; Necip, Ş. Neutrosophic metric spaces. Math. Sci. 2020, 14, 241–248. [Google Scholar]
- Ishtiaq, U.; Kattan, D.A.; Ahmad, K.; Lazăr, T.A.; Lazăr, V.L.; Guran, L. On intuitionistic fuzzy Nb metric space and related fixed point results with application to nonlinear fractional differential equations. Fractal Fract. 2023, 7, 529. [Google Scholar] [CrossRef]
- Shatanawi, W.; Abodayeh, K.; Mukheimer, A. Some fixed point theorems in extended b-metric spaces. UPB Sci. Bull. Ser. A 2018, 80, 71–78. [Google Scholar]
- Shatanawi, W.; Shatnawi, T.A. Some fixed point results based on contractions of new types for extended b-metric spaces. AIMS Math. 2023, 8, 10929–10946. [Google Scholar] [CrossRef]
- Alamgir, N.; Kiran, Q.; Aydi, H.; Mukheimer, A. A Mizoguchi–Takahashi type fixed point theorem in complete extended b-metric spaces. Mathematics 2019, 7, 478. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).