Accurate Computations with Generalized Green Matrices

Abstract

We consider generalized Green matrices that, in contrast to Green matrices, are not necessarily symmetric. In spite of the loss of symmetry, we show that they can preserve some nice properties of Green matrices. In particular, they admit a bidiagonal decomposition. Moreover, for convenient parameters, the bidiagonal decomposition can be obtained efficiently and with high relative accuracy and it can also be used to compute all eigenvalues, all singular values, the inverse, and the solution of some linear system of equations with high relative accuracy. Numerical examples illustrate the high accuracy of the performed computations using the bidiagonal decompositions. Finally, nonsingular and totally positive generalized Green matrices are characterized.

1. Introduction

A desirable goal in linear algebra is the computation, with high relative accuracy, of linear algebra problems for a matrix, such as the eigenvalues, singular values, inverses, or solutions of associated linear systems (cf. [1]). Although this goal has only been achieved for a few classes of structured matrices, one of these classes is the class of Green matrices (see [2]). Green matrices are symmetric matrices that can be considered as discrete versions of Green functions and arise in important applications (see [3,4,5] and references therein). Here, we focus on generalized Green matrices that were considered in [6]. These generalized Green matrices are not necessarily symmetric. However, here, we see that some relevant nice properties satisfied by (symmetric) Green matrices are preserved by generalized Green matrices. In particular, the fact that we can perform many algebraic computations with high relative accuracy.

It is known that an algorithm can be computed to high relative accuracy (HRA) when it only uses products, quotients, additions of numbers of the same sign, or subtractions of initial data (cf. [7,8,9]). So, the only forbidden arithmetic operation is the subtraction of numbers (which are not initial data) with the same sign. Among the classes of matrices for which algorithms to HRA have been constructed, we can mention some subclasses of nonsingular totally positive matrices (see, for instance, [10,11,12,13]). Let us recall that a matrix is called totally positive (TP) if all its minors are non-negative and it is strictly totally positive (STP) if they are positive (see [14,15]). These matrices are also called totally non-negative and totally positive, respectively (cf. [16]). TP and STP matrices arise in many applications (see [15,17,18,19]). In [20,21], it was proved for a nonsingular TP matrix A that if we know its bidiagonal factorization $\mathcal{BD}(A)$, then we can perform many algebraic computations with HRA. For example, calculations of its eigenvalues, its singular values, its inverse and the solution of linear systems $Ax=b$, where b has alternating signs. In this paper, we characterize generalized Green matrices that are nonsingular TP and present a method of $\mathcal{O}(n)$ elementary operations to obtain bidiagonal factorizations of $n\times n$ generalized Green matrices with HRA.

The paper is organized as follows. Section 2 contains auxiliary results on bidiagonal factorizations and TP matrices. Section 3 introduces generalized Green matrices and obtains their bidiagonal decompositions. Section 4 characterizes nonsingular TP generalized Green matrices. It also presents the algorithm for the bidiagonal decomposition of generalized Green matrices and finds parameters for which many linear algebra computations can be performed with HRA. Finally, Section 5 includes numerical experiments confirming the advantages of using the HRA methods presented in the previous sections, and the last section summarizes the main conclusions of this work.

2. Auxiliary Results

Neville elimination (NE) is an elimination procedure that makes zeros in a column of a matrix by adding to each row an appropriate multiple of the previous one (cf. [22]). Given a nonsingular matrix $A={(a_{ij})}_{1\le i,j\le n}$, NE has $n-1$ steps and produces the next sequence of matrices:

$$A=:A^{(1)}\to A^{(2)}\to \cdots \to A^{(n)}=U,$$

(1)

where U is an upper triangular matrix and $A^{(k)}$ has zeros below the main diagonal in the first $k-1$ columns ($2\le k\le n$). For $1\le k\le n-1$, the matrix $A^{(k+1)}={(a_{ij}^{(k+1)})}_{1\le i,j\le n}$ is derived from the matrix $A^{(k)}={(a_{ij}^{(k)})}_{1\le i,j\le n}$ by using the formula

$$a_{ij}^{(k+1)}=\left\{\begin{array}{cc}{a}_{ij}^{(k)}-{\displaystyle \frac{a_{ik}^{(k)}}{a_{i-1,k}^{(k)}}}{a}_{i-1,j}^{(k)},\hfill & \mathrm{if}k\le j\le n,k+1\le i\le n\mathrm{and}{a}_{i-1,k}^{(k)}\ne 0,\hfill \\ a_{ij}^{(k)},\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(2)

for $k=1,\dots ,n-1$. The $(i,j)$ pivot of the NE of A is given by

$$p_{ij}=a_{ij}^{(j)},1\le j\le i\le n.$$

If $i=j$, we call $p_{ii}$ a diagonal pivot. The $(i,j)$ multiplier of the NE of A, with $1\le j<i\le n$, is given by

$$m_{ij}=\left\{\begin{array}{cc}{\displaystyle \frac{a_{ij}^{(j)}}{a_{i-1,j}^{(j)}}}={\displaystyle \frac{p_{ij}}{p_{i-1,j}}},\hfill & \mathrm{if}{a}_{i-1,j}^{(j)}\ne 0,\hfill \\ 0,\hfill & \mathrm{if}{a}_{i-1,j}^{(j)}=0.\hfill \end{array}\right.$$

(3)

The following condition is satisfied:

$$m_{ij}=0\Rightarrow m_{hj}=0\forall h>i.$$

The $(i,j)$ multiplier of the NE of $A^T$ is denoted by ${\tilde{m}}_{ij}$.

The following theorem is a consequence of Theorems 4.2 and 4.3 of [23] and the arguments of pp. 116 and 120 of [23] and characterizes nonsingular TP matrices by their bidiagonal decomposition.

Theorem 1.

A nonsingular matrix $A={(a_{ij})}_{1\le i,j\le n}$ is TP if and only if it admits the following decomposition:

$$A=F_{n-1}{F}_{n-2}···F_{1}D{G}_1···G_{n-2}{G}_{n-1},$$

(4)

where D is the diagonal matrix diag$(p_{11},\dots ,p_{nn})$ with positive diagonal entries and $F_i$, $G_i$ are the non-negative bidiagonal matrices given by

$$F_i=\left(\begin{array}{ccccccc}1& & & & & & \\ 0& 1& & & & & \\ & \ddots & \ddots & & & & \\ & & 0& 1& & & \\ & & & m_{i+1,1}& 1& & \\ & & & & \ddots & \ddots & \\ & & & & & m_{n,n-i}& 1\end{array}\right),G_i=\left(\begin{array}{ccccccc}1& 0& & & & & \\ & 1& \ddots & & & & \\ & & \ddots & 0& & & \\ & & & 1& {\tilde{m}}_{i+1,1}& & \\ & & & & 1& \ddots & \\ & & & & & \ddots & {\tilde{m}}_{n,n-i}\\ & & & & & & 1\end{array}\right),$$

(5)

for all $i\in \{1,\dots ,n-1\}$. If, in addition, the entries $m_{ij}$ and ${\tilde{m}}_{ij}$ satisfy

$$\begin{array}{c}{m}_{ij}=0\Rightarrow m_{hj}=0\forall h>i,\\ {\tilde{m}}_{ij}=0\Rightarrow {\tilde{m}}_{hj}=0\forall h>i,\end{array}$$

(6)

then the decomposition is unique. Furthermore, A is STP if and only if it admits the decomposition (4) with all entries $p_{ii}$, $m_{ij}$, and ${\tilde{m}}_{ij}$ positive.

Observe that in the bidiagonal decomposition given by (4) and (5) the entries $m_{ij}$ and $p_{ii}$ are the multipliers and diagonal pivots, respectively, corresponding to the NE of A (see Theorem 4.2 of [23] and the comment below it), and the entries ${\tilde{m}}_{ij}$ are the multipliers of the NE of $A^T$ (see p. 116 of [23]). In [21], the matrix notation $\mathcal{BD}(A)$ was used to represent the bidiagonal decomposition of a nonsingular TP matrix:

$${(\mathcal{BD}(A))}_{ij}=\left\{\begin{array}{cc}{m}_{ij},\hfill & \mathrm{if}i>j,\hfill \\ {\tilde{m}}_{ji},\hfill & \mathrm{if}i<j,\hfill \\ p_{ii},\hfill & \mathrm{if}i=j.\hfill \end{array}\right.$$

(7)

From now on, $\mathcal{BD}(A)$ will also be used to denote the bidiagonal decomposition of matrices that are not necessarily TP.

We can derive from Theorem 1 the following corollary characterizing nonsingular TP matrices and STP matrices by the entries of their bidiagonal decomposition.

Corollary 1.

Let A be a square matrix with a given $\mathcal{BD}(A)$ corresponding to (4). Then:

i.

A is nonsingular TP if and only if all diagonal entries of $\mathcal{BD}(A)$ are positive and all off-diagonal entries of $\mathcal{BD}(A)$ are non-negative.

ii.

A is STP if and only if all entries of $\mathcal{BD}(A)$ are positive.

3. Bidiagonal Factorization

We first recall the definition of Green matrices.

Definition 1.

Given two sequences of nonzero real numbers ${(u_i)}_{1\le i\le n}$, ${(v_i)}_{1\le i\le n}$, a Green matrix $A={(a_{ij})}_{1\le i,j\le n}$ is the symmetric matrix given by $a_{ij}=u_i{v}_j$ if $i\le j$ (or, equivalently, $a_{ij}=u_{min\{i,j\}}{v}_{max\{i,j\}}$ for all $i,j$).

The following definition generalizes Green matrices to the nonsymmetric case.

Definition 2.

Given four sequences of nonzero real numbers ${(u_i)}_{1\le i\le n}$, ${(v_i)}_{1\le i\le n}$, ${(w_i)}_{1\le i\le n}$, and ${(z_i)}_{1\le i\le n}$ satisfying that $u_i·v_i=w_i·z_i$ for $i=1,\dots ,n$, a generalized Green matrix $A={(a_{ij})}_{1\le i,j\le n}$ is the matrix defined by

$$a_{ij}:=\left\{\begin{array}{cc}{u}_j·v_i,\hfill & ifi\ge j,\hfill \\ w_i·z_j,\hfill & ifi<j.\hfill \end{array}\right.$$

Observe that, if in the previous definition $w_i=u_i$ and $z_i=v_i$ for all $i=1,\dots ,n$, then we have a usual Green matrix, which is symmetric, so that our definition of the generalized Green matrix includes some symmetric matrices.

In the next result, we present the bidiagonal factorization of any generalized Green matrix.

Theorem 2.

If A is a generalized Green matrix with parameters ${(u_i)}_{1\le i\le n}$, ${(v_i)}_{1\le i\le n}$, ${(w_i)}_{1\le i\le n}$, and ${(z_i)}_{1\le i\le n}$, its bidiagonal decomposition $\mathcal{BD}(A)$ is given by

$${(\mathcal{BD}(A))}_{ij}=\left\{\begin{array}{cc}{w}_1{z}_1=u_1{v}_1,\hfill & fori=j=1,\hfill \\ {\displaystyle \frac{z_j}{z_{j-1}}},\hfill & fori=1andj=2,\dots ,n,\hfill \\ u_i{v}_i\left(1-{\displaystyle \frac{v_i}{v_{i-1}}}·{\displaystyle \frac{w_{i-1}}{w_i}}\right)=w_i{z}_i\left(1-{\displaystyle \frac{v_i}{v_{i-1}}}·{\displaystyle \frac{w_{i-1}}{w_i}}\right),\hfill & fori=j=2,\dots ,n,\hfill \\ {\displaystyle \frac{v_i}{v_{i-1}}},\hfill & forj=1andi=2,\dots ,n,\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

Proof. 

Let us obtain the bidiagonal decomposition of A by applying the Neville elimination procedure to A and $A^T$. So, first with multiplier $v_n/v_{n-1}$, a zero at entry $(n,1)$ of A is produced (the last but one row multiplied by $v_n/v_{n-1}$ is subtracted from the last one). This elementary operation also produces zeros in the remaining off-diagonal entries of the last row. Taking into account that $u_n·v_n=w_n·z_n$, the $(n,n)$ entry of the last row transforms into

$$d_n:=w_n{z}_n-{\displaystyle \frac{v_n}{v_{n-1}}}{w}_{n-1}{z}_n=w_n{z}_n\left(1-{\displaystyle \frac{v_n}{v_{n-1}}}·{\displaystyle \frac{w_{n-1}}{w_n}}\right).$$

Analogously (by symmetry), if we now multiply the columns by $z_n/z_{n-1}$ to make the entry $(1,n)$ a zero, we obtain a matrix B with zeros in the last column up to place $(n,n)$, where $d_n$ remains.

Let us denote by $E_i(\alpha )$ ($2\le i\le n$) the $n\times n$ elementary matrix that has unit diagonal, $\alpha$ in place $(i,i-1)$, and 0 elsewhere. Then, the matrix form of the previous step can be written as $E_n\left({\displaystyle \frac{-v_n}{v_{n-1}}}\right)A{E}_n{\left({\displaystyle \frac{-z_n}{z_{n-1}}}\right)}^T$.

Continuing this procedure to make zeros in entries $(n-1,1),(1,n-1),\dots ,(2,1),(1,2)$, we obtain the factorization

$$E_2\left({\displaystyle \frac{-v_2}{v_1}}\right)\cdots E_n\left({\displaystyle \frac{-v_n}{v_{n-1}}}\right)A{E}_n{\left({\displaystyle \frac{-z_n}{z_{n-1}}}\right)}^T\cdots E_2{\left({\displaystyle \frac{-z_2}{z_1}}\right)}^T=D,$$

(8)

where D is the diagonal matrix with bidiagonal entries

$$\begin{array}{cc}\hfill d_1& =w_1{z}_1=u_1{v}_1,\hfill \\ \hfill d_i& =u_i{v}_i\left(1-{\displaystyle \frac{v_i}{v_{i-1}}}·{\displaystyle \frac{w_{i-1}}{w_i}}\right)=w_i{z}_i\left(1-{\displaystyle \frac{v_i}{v_{i-1}}}·{\displaystyle \frac{w_{i-1}}{w_i}}\right),i>1.\hfill \end{array}$$

(9)

Taking into account that $E_i{(\alpha )}^{-1}=E_i(-\alpha )$, we obtain the following bidiagonal factorization $\mathcal{BD}(A)$ of A:

$$A=E_n\left({\displaystyle \frac{v_n}{v_{n-1}}}\right)\cdots E_2\left({\displaystyle \frac{v_2}{v_1}}\right)D{E}_2{\left({\displaystyle \frac{z_2}{z_1}}\right)}^T\cdots E_n{\left({\displaystyle \frac{z_n}{z_{n-1}}}\right)}^T.$$

(10)

   □

4. Total Positivity and High Relative Accuracy

The following result characterizes the generalized Green matrices with parameters of the same sign that are nonsingular TP.

Theorem 3.

Let A be a generalized Green matrix with parameters ${(u_i)}_{1\le i\le n}$, ${(v_i)}_{1\le i\le n}$, ${(w_i)}_{1\le i\le n}$, and ${(z_i)}_{1\le i\le n}$ with the same sign. Then, A is nonsingular TP if and only if

$${\displaystyle \frac{w_1}{v_1}}<{\displaystyle \frac{w_2}{v_2}}<\cdots <{\displaystyle \frac{w_n}{v_n}}.$$

(11)

Proof. 

Since A is a generalized Green matrix, all parameters are nonzero and, by hypothesis, $(z_k/z_{k-1})>0$ and $(v_k/v_{k-1})>0$ for all $k=2,\dots ,n$, and

$$w_i{z}_i>0,i=1,\dots ,n.$$

(12)

So, by Theorem 2, all off-diagonal entries of $\mathcal{BD}(A)$ are non-negative and the first diagonal entry of $\mathcal{BD}(A)$ is positive.

By Corollary 1 i, it remains to prove that the remaining diagonal entries of $\mathcal{BD}(A)$ are positive if and only if (11) holds. By (12) and Theorem 2, it is sufficient to check if

$$0<1-{\displaystyle \frac{v_i}{v_{i-1}}}{\displaystyle \frac{w_{i-1}}{w_i}}={\displaystyle \frac{v_{i-1}{w}_i-v_i{w}_{i-1}}{v_{i-1}{w}_i}},i=2,\dots ,n,$$

(13)

if and only if (11) holds.

Since $v_{i-1}{w}_i>0$ for $i=2,\dots ,n$, and the equivalence of (13) and (11), it only remains to prove that (11) holds if and only if

$$0<v_{i-1}{w}_i-v_i{w}_{i-1},i=2,\dots ,n.$$

(14)

Taking again into account that all parameters are nonzero, we can divide the right-hand side of (14) by $v_{i-1}{v}_i$, and so, (14) is equivalent to

$$0<{\displaystyle \frac{w_i}{v_i}}-{\displaystyle \frac{w_{i-1}}{v_{i-1}}},$$

or equivalently, to

$${\displaystyle \frac{w_{i-1}}{v_{i-1}}}<{\displaystyle \frac{w_i}{v_i}},$$

and the result follows.    □

In contrast to the previous characterization of nonsingular TP generalized Green matrices, there are no STP generalized Green matrices, as the following remark shows.

Remark 1.

By Theorem 2, a generalized Green $n\times n$ matrix with $n>2$ has some null off-diagonal entries. Then, by Corollary 1 ii, it cannot be STP.

For some subclasses of nonsingular TP matrices it has been possible to obtain algorithms for linear algebra problems with high relative accuracy (HRA). The starting point was the construction with HRA of the bidiagonal decomposition of the matrix, which was used in the algorithms presented in [21,24,25] for linear algebra problems. Here, we focus on sufficient conditions for the bidiagonal decomposition with HRA for generalized Green matrices. An algorithm is said to be performed to HRA if the relative error in the computations is of the order of the unit round-off (or machine precision). A sufficient condition so that an algorithm can be carried out to HRA is the non-inaccurate cancellation condition, also called NIC condition, which holds if the algorithm only uses products, quotients, and sums of numbers with the same sign (see page 52 in [7]). Moreover, if the floating-point arithmetic is well implemented, the subtraction of initial data can also be allowed without losing HRA (see page 53 in [7]).

The following result provides sufficient conditions to ensure HRA calculations for algebra problems related to generalized Green matrices.

Proposition 1.

Let us consider a generalized Green matrix A with parameters of the sequences ${(u_i)}_{1\le i\le n}$, ${(v_i)}_{1\le i\le n}$, ${(w_i)}_{1\le i\le n}$, and ${(z_i)}_{1\le i\le n}$ formed by numbers of the same sign.

i.

If ${\displaystyle \frac{v_i}{v_{i-1}}},{\displaystyle \frac{w_{i-1}}{w_i}}\le 1$ or ${\displaystyle \frac{v_i}{v_{i-1}}},{\displaystyle \frac{w_{i-1}}{w_i}}\ge 1$ for all $i=2,\dots ,n$, then the bidiagonal decomposition of A, $\mathcal{BD}(A)$ can be computed to HRA.

ii.

If ${\displaystyle \frac{v_i}{v_{i-1}}},{\displaystyle \frac{w_{i-1}}{w_i}}<1$ for all $i=2,\dots ,n$, then A is a nonsingular TP matrix, and its eigenvalues, its singular values, its inverse $A^{-1}$, and the solution of linear systems $Ax=b$, where b has a pattern of alternating signs, can also be computed to HRA.

Proof. 

i.

Since ${\displaystyle \frac{v_i}{v_{i-1}}}·{\displaystyle \frac{w_{i-1}}{w_i}}>0$, it is necessary to carry out the subtraction $1-{\displaystyle \frac{v_i}{v_{i-1}}}·{\displaystyle \frac{w_{i-1}}{w_i}}$ to HRA. So, in order to obtain this, using the formula

$$1+a·b={\displaystyle \frac{1}{2}}\left[(1+a)(1+b)+(1-a)(1-b)\right]$$

(15)

with $a=-{\displaystyle \frac{w_{i-1}}{w_i}}$ and $b={\displaystyle \frac{v_i}{v_{i-1}}}$, we obtain

$$\begin{array}{cc}\hfill 1-{\displaystyle \frac{v_i}{v_{i-1}}}·{\displaystyle \frac{w_{i-1}}{w_i}}& ={\displaystyle \frac{1}{2}}\left[\left(1-{\displaystyle \frac{w_{i-1}}{w_i}}\right)\left(1+{\displaystyle \frac{v_i}{v_{i-1}}}\right)+\left(1+{\displaystyle \frac{w_{i-1}}{w_i}}\right)\left(1-{\displaystyle \frac{v_i}{v_{i-1}}}\right)\right]\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{w_i-w_{i-1}}{w_i}}\left(1+{\displaystyle \frac{v_i}{v_{i-1}}}\right)+\left(1+{\displaystyle \frac{w_{i-1}}{w_i}}\right){\displaystyle \frac{v_{i-1}-v_i}{v_{i-1}}}\right],\hfill \end{array}$$

which, for $0<{\displaystyle \frac{v_i}{v_{i-1}}},{\displaystyle \frac{w_{i-1}}{w_i}}\le 1$, is a sum of non-negative numbers if the sequences defining the matrices are positive or a sum of non-negative numbers if the sequences are negative, and, for ${\displaystyle \frac{v_i}{v_{i-1}}},{\displaystyle \frac{w_{i-1}}{w_i}}\ge 1$, is a sum of nonpositive numbers if the sequences are positive or a sum of non-negative numbers if the sequences are negative.

ii.

By i of the proposition, $\mathcal{BD}(A)$ can be computed to HRA. If ${\displaystyle \frac{v_i}{v_{i-1}}},{\displaystyle \frac{w_{i-1}}{w_i}}<1$ for all $i=2,\dots ,n$, then ${\displaystyle \frac{v_i}{v_{i-1}}}·{\displaystyle \frac{w_{i-1}}{w_i}}<1$ for all $i=2,\dots ,n$ because they are positive quotients due to the fact that all parameters have the same sign. The last inequalities are equivalent to (11) and so A is a nonsingular TP matrix by Theorem 3. Then, the methods of [21,25] can be used to solve the four algebraic computations mentioned with HRA.

   □

The bidiagonal decomposition of a generalized Green matrix deduced in the proof of Theorem 1 was implemented in the function TNBDGeneralizedGreen to be used in Matlab and Octave. In Algorithm 1, we can see the pseudocode of this function.

Algorithm 1 Computation of $\mathcal{BD}(A)$ for a generalized Green matrix A

Require: ${(u(i))}_{i=1}^n$, ${(v(i))}_{i=1}^n$, ${(w(i))}_{i=1}^n$ and ${(z(i))}_{i=1}^n$ such that $u(i)·v(i)=w(i)·z(i)$

Ensure: B bidiagonal decomposition of A

$B=zeros(n)$

for i = 2:n do

$M(i,1)=v(i)/v(i-1)$

end for

for $j=2:n$ do

$M(1,j)=z(j)/z(j-1)$

end for

$M(1,1)=u(1)\ast v(1)$

for $i=2:n$ do

$M(i,i)=((u(i)\ast v(i))/2)\ast (((w(i)-w(i-1))/w(i))\ast (1+v(i)/v(i-1))$

$+(1+w(i-1)/w(i))\ast ((v(i-1)-v(i))/v(i-1)))$

end for

Remark 2.

Algorithm 1 has a computational cost of $\mathcal{O}(n)$ elementary operations in order to compute the bidiagonal decomposition of a generalized Green matrix of order n.

5. Numerical Experiments

Assuming the bidiagonal decomposition $\mathcal{BD}(A)$ of a nonsingular TP matrix A is known to HRA, in [20,21,25] algorithms to solve some algebra problems related to A also to HRA were presented:

• Computation of the eigenvalues of A.
• Computation of the singular values of A.
• Computation of the inverse of A, $A^{-1}$.
• Solution of a system of linear equations $Ax=b$ where b has an alternating sign pattern.

These algorithms have been implemented to be used in Matlab and Octave and they are included in the software library TNTool (see [24]). The names of the functions corresponding to the algorithms for the four algebra problems mentioned above are TNEigenValues, TNSingularValues, TNInverseExpand, and TNSolve, respectively. These functions need as input $\mathcal{BD}(A)$ to HRA and, in addition, the latter also needs the vector b of the linear system of equations.

Remark 3.

Taking into account the computational costs of the algorithms given in [21,25] for the four algebra problems mentioned and the computational cost for the computation of the bidiagonal decomposition of a generalized Green matrix given in Remark 2, it can be deduced that, using the bidiagonal factorization of a nonsingular generalized Green matrix, the computational costs to solve each of the four algebra problems mentioned before are the following:

• $\mathcal{O}(n^3)$ elementary operations for the computation of the eigenvalues and singular values using TNEigenValues and TNSingularValues, respectively,
• $\mathcal{O}(n^2)$ elementary operations for the computation of the inverse and the solution of the system of linear equations using TNInverseExpand and TNSolve, respectively.

Now, we illustrate the high relative accuracy of the bidiagonal decomposition of a generalized Green matrix computed to HRA with the function TNBDGeneralizedGreen used together with the four functions of TNTool mentioned before for solving the four algebra problems mentioned.

First, we consider a generalized Green matrix $A_{20}$ of order $n=20$, with parameters of the sequences ${(u_i)}_{1\le i\le n}$, ${(v_i)}_{1\le i\le n}$, ${(w_i)}_{1\le i\le n}$, and ${(z_i)}_{1\le i\le n}$ given by

$$u_i={\displaystyle \frac{1}{2^{60-i}}},v_i=n+1-i,z_i={\displaystyle \frac{1}{2^{9+i}}}\mathrm{and}{w}_i={\displaystyle \frac{u_i·v_i}{z_i}}$$

(16)

for $i=1,\dots ,n$. By Proposition 1, the matrix $A_{20}$ is nonsingular TP, $\mathcal{BD}(A)$ can be obtained to HRA, and the four algebra problems can also be solved to HRA.

First, the eigenvalues and singular values of $A_{20}$ were computed with Mathematica by using 200-digit precision. Then, the eigenvalues were computed with Matlab in two different ways. First, using the usual Matlab command eig. Second, using the function TNEigenValues with TNBDGeneralizedGreen to HRA. Then, the relative errors of the approximations obtained with Matlab were calculated considering the results provided by Mathematica to be exact. Table 1 shows these relative errors.

Table 1. Relative errors when computing the eigenvalues ${\lambda }_1>{\lambda }_2>\cdots >{\lambda }_{20}$ of $A_{20}$.

i	${\mathit{\lambda }}_{\mathit{i}}$	TNEigenValues	eig
		$\left|{\displaystyle \frac{{\mathit{\lambda }}_{\mathit{i}}-\widehat{{\mathit{\lambda }}_{\mathit{i}}}}{{\mathit{\lambda }}_{\mathit{i}}}}\right|$	$\left|{\displaystyle \frac{{\mathit{\lambda }}_{\mathit{i}}-\widehat{{\mathit{\lambda }}_{\mathit{i}}}}{{\mathit{\lambda }}_{\mathit{i}}}}\right|$
1	1.654$\times {10}^{-12}$	2.442$\times {10}^{-16}$	1.343$\times {10}^{-15}$
2	7.337$\times {10}^{-13}$	1.376$\times {10}^{-16}$	2.752$\times {10}^{-16}$
3	4.419$\times {10}^{-13}$	2.285$\times {10}^{-16}$	1.942$\times {10}^{-15}$
4	3.111$\times {10}^{-13}$	4.869$\times {10}^{-16}$	2.11$\times {10}^{-15}$
5	2.042$\times {10}^{-13}$	2.472$\times {10}^{-16}$	6.181$\times {10}^{-16}$
6	1.247$\times {10}^{-13}$	4.048$\times {10}^{-16}$	1.012$\times {10}^{-15}$
7	7.336$\times {10}^{-14}$	1.204$\times {10}^{-15}$	2.237$\times {10}^{-15}$
8	4.212$\times {10}^{-14}$	4.495$\times {10}^{-16}$	2.997$\times {10}^{-16}$
9	2.376$\times {10}^{-14}$	5.311$\times {10}^{-16}$	2.921$\times {10}^{-15}$
10	1.323$\times {10}^{-14}$	3.578$\times {10}^{-16}$	3.817$\times {10}^{-15}$
11	7.286$\times {10}^{-15}$	2.165$\times {10}^{-16}$	4.114$\times {10}^{-15}$
12	3.978$\times {10}^{-15}$	1.983$\times {10}^{-16}$	0
13	2.156$\times {10}^{-15}$	0	1.463$\times {10}^{-15}$
14	1.162$\times {10}^{-15}$	5.092$\times {10}^{-16}$	1.001$\times {10}^{-14}$
15	6.227$\times {10}^{-16}$	9.501$\times {10}^{-16}$	2.09$\times {10}^{-14}$
16	3.321$\times {10}^{-16}$	4.453$\times {10}^{-16}$	2.346$\times {10}^{-14}$
17	1.762$\times {10}^{-16}$	6.997$\times {10}^{-16}$	6.032$\times {10}^{-14}$
18	9.231$\times {10}^{-17}$	1.335$\times {10}^{-16}$	5.088$\times {10}^{-14}$
19	4.658$\times {10}^{-17}$	5.293$\times {10}^{-16}$	1.448$\times {10}^{-13}$
20	2.095$\times {10}^{-17}$	2.942$\times {10}^{-16}$	6.939$\times {10}^{-13}$

Then, the singular values were also computed with Matlab in two different ways. First, using the usual Matlab command svd. Second, using the function TNSingularValues with TNBDGeneralizedGreen to HRA. Then, the relative errors of the approximations obtained with Matlab were calculated, considering the results provided by Mathematica to be exact. Table 2 shows these relative errors.

Table 2. Relative errors when computing the singular values ${\sigma }_1>{\sigma }_2>\cdots >{\sigma }_{20}$ of $A_{20}$.

i	${\mathit{\sigma }}_{\mathit{i}}$	TNSingularValues	svd
		$\left|{\displaystyle \frac{{\mathit{\sigma }}_{\mathit{i}}-\widehat{{\mathit{\sigma }}_{\mathit{i}}}}{{\mathit{\sigma }}_{\mathit{i}}}}\right|$	$\left|{\displaystyle \frac{{\mathit{\sigma }}_{\mathit{i}}-\widehat{{\mathit{\sigma }}_{\mathit{i}}}}{{\mathit{\sigma }}_{\mathit{i}}}}\right|$
1	1.677$\times {10}^{-12}$	6.02$\times {10}^{-16}$	1.204$\times {10}^{-16}$
2	7.452$\times {10}^{-13}$	2.71$\times {10}^{-16}$	1.355$\times {10}^{-16}$
3	4.449$\times {10}^{-13}$	1.135$\times {10}^{-16}$	4.539$\times {10}^{-16}$
4	3.121$\times {10}^{-13}$	0	1.618$\times {10}^{-16}$
5	2.047$\times {10}^{-13}$	1.233$\times {10}^{-16}$	4.933$\times {10}^{-16}$
6	1.249$\times {10}^{-13}$	4.042$\times {10}^{-16}$	4.042$\times {10}^{-16}$
7	7.345$\times {10}^{-14}$	3.437$\times {10}^{-16}$	8.592$\times {10}^{-16}$
8	4.216$\times {10}^{-14}$	7.484$\times {10}^{-16}$	0
9	2.378$\times {10}^{-14}$	5.307$\times {10}^{-16}$	1.327$\times {10}^{-16}$
10	1.324$\times {10}^{-14}$	3.576$\times {10}^{-16}$	4.768$\times {10}^{-16}$
11	7.29$\times {10}^{-15}$	4.329$\times {10}^{-16}$	4.329$\times {10}^{-16}$
12	3.98$\times {10}^{-15}$	1.982$\times {10}^{-16}$	5.946$\times {10}^{-16}$
13	2.157$\times {10}^{-15}$	3.657$\times {10}^{-16}$	1.28$\times {10}^{-15}$
14	1.162$\times {10}^{-15}$	1.697$\times {10}^{-16}$	5.091$\times {10}^{-16}$
15	6.227$\times {10}^{-16}$	4.751$\times {10}^{-16}$	2.692$\times {10}^{-15}$
16	3.318$\times {10}^{-16}$	1.486$\times {10}^{-16}$	2.288$\times {10}^{-14}$
17	1.756$\times {10}^{-16}$	5.615$\times {10}^{-16}$	1.289$\times {10}^{-13}$
18	9.155$\times {10}^{-17}$	6.732$\times {10}^{-16}$	3.835$\times {10}^{-13}$
19	4.585$\times {10}^{-17}$	1.344$\times {10}^{-16}$	1.336$\times {10}^{-13}$
20	2.051$\times {10}^{-17}$	4.507$\times {10}^{-16}$	6.891$\times {10}^{-13}$

As we can observe in Table 1 and Table 2, the lower the eigenvalue or singular value is, the greater the corresponding relative error is for the usual Matlab methods eig and svd. Taking this into account, the generalized nonsymmetric matrices $A_n$ of order $n=5,10,\dots ,50$, with parameters given by (16) for $i=1,\dots ,n$, are considered. By Proposition 1, the matrices $A_n$ are nonsingular and TP, $\mathcal{BD}(A)$ can be obtained to HRA and, with this bidiagonal decomposition, the four algebra problems can also be solved to HRA by using TNTool (see [24]). The condition numbers of these matrices can be seen in Figure 1. As we can observe the generalized matrices of higher degree are ill-conditioned.

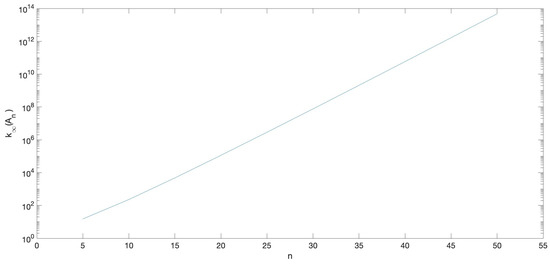
Figure 1. Condition numbers $k_{\infty }(A_n)$ for $n=5,10,\dots ,50$.

In order to show the accuracy of the HRA methods, the lowest eigenvalues and singular values of the matrices $A_n$, $n=5,10,\dots ,50$, were computed with Mathematica by using 200-digit precision. Then, these eigenvalues were computed with Matlab in two different ways. First, by using the usual Matlab command eig. Second, using the function TNEigenValues with $\mathcal{BD}(A_n)$ to HRA. Then, the relative errors of the approximations obtained with Matlab were calculated considering the results provided by Mathematica to be exact. Figure 2 shows the relative error for the lowest eigenvalue of each matrix $A_n$.

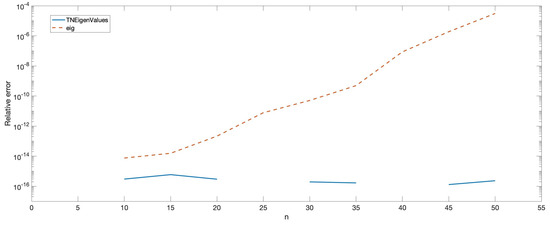
Figure 2. Relative errors when computing the lowest eigenvalue of $A_n$ for $n=5,10,\dots ,50$.

In an analogous way to the eigenvalues, approximations to the lowest singular values of the matrices $A_n$, $n=5,10,\dots ,50$ were obtained with Matlab in two ways. First, using the usual Matlab command svd. Second, using the usual function TNSingularValues with $\mathcal{BD}(A_n)$ to HRA. Then, the relative errors of the approximations obtained with Matlab were calculated considering the results provided by Mathematica to be exact. Figure 3 shows the relative error for the lowest singular value of each matrix $A_n$.

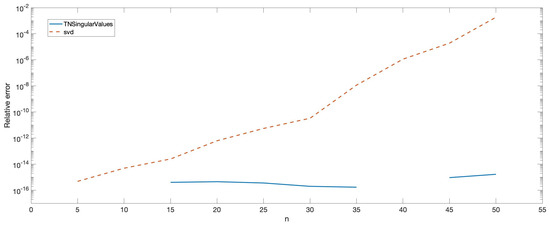
Figure 3. Relative errors when computing the lowest singular value of $A_n$ for $n=5,10,\dots ,50$.

As can be observed in the previous numerical tests, the HRA methods are much better than the usual methods for generalized Green matrices. Finally, let us show that the HRA methods also provide very accurate results for generalized Green matrices of orders greater than 50. In this regard, let us consider a generalized Green matrix A of order 100 with parameters of the sequences ${(u_i)}_{1\le i\le 100}$, ${(v_i)}_{1\le i\le 100}$, ${(w_i)}_{1\le i\le 100}$, and ${(z_i)}_{1\le i\le 100}$ given by

$$u_i={\displaystyle \frac{1}{2^{110-i}}},v_i=101-i,z_i={\displaystyle \frac{1}{2^{9+i}}}\mathrm{and}{w}_i={\displaystyle \frac{u_i·v_i}{z_i}},i=1,\dots ,100.$$

By Proposition 1, the matrix A is nonsingular and TP, $\mathcal{BD}(A)$ can be obtained to HRA, and the four algebra problems can also be solved to HRA. The condition number of matrix A is given by $k_{\infty }(A)=2.66\times {10}^{28}$, so it is an ill-conditioned matrix.

As in the previous examples, the eigenvalues of A were calculated with Mathematica using 200-digit precision, and with Matlab both using TNEigenvalues and using the usual method eig. Then, the relative errors were computed for both approximations obtained with Matlab considering the eigenvalues provided by Mathematica to be exact. Figure 4 shows these relative errors.

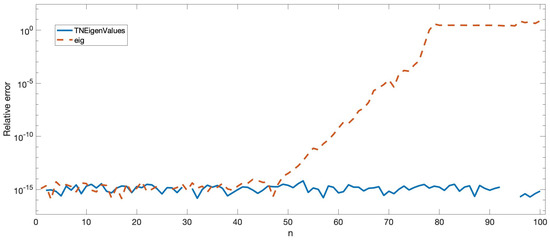
Figure 4. Relative errors when computing all the eigenvalues ${\lambda }_1>{\lambda }_2>\cdots >{\lambda }_{100}$ of A.

The analogous process was carried out for the singular values of A using TNSingularValues and svd in Matlab. In Figure 5, the relative errors for the singular values are shown.

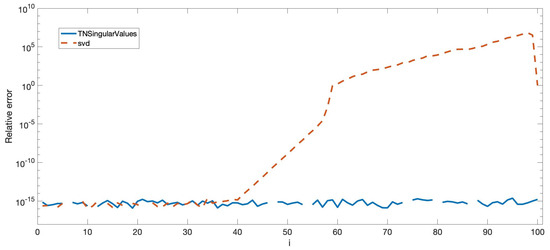
Figure 5. Relative errors when computing all the singular values ${\sigma }_1>{\sigma }_2>\cdots >{\sigma }_{100}$ of A.

The Matlab code used to carry out the numerical tests is available upon request.

6. Conclusions

In this paper, we have seen that some nice properties of Green matrices can be extended to the generalized Green matrices, which are not necessarily symmetric. We find parameter values for which the bidiagonal decomposition of generalized Green matrices can be obtained efficiently and with high relative accuracy. We characterize the parameter values of generalized Green matrices that are nonsingular and totally positive. We prove that many linear algebra computations for generalized Green matrices can be performed efficiently and with high relative accuracy. Numerical experiments confirm this fact.