Hopf-like Bifurcation Analysis of a Fractional-Order Tumor-Lymphatic Model Involving Two Time Delays

Abstract

This paper investigates the Hopf-like bifurcation of a fractional tumor-lymphatic model with two time delays. The two time delays are considered as branching parameters, and we analyze their influences on the dynamic properties of the model. Through an examination of the root distribution of the characteristic equation, we derive the properties of the positive steady state and the conditions for the occurrence of Hopf-like bifurcation near the positive equilibrium point. Numerical simulations are demonstrated to support our theoretical results.

1. Introduction

In recent years, tumor-immune models have garnered extensive attention due to their theoretical and practical significance. These models have attracted a diverse group of researchers, including applied mathematicians, biologists, and medical professionals, resulting in numerous interesting and meaningful findings, see, e.g., [1,2,3,4,5,6,7,8,9,10,11,12,13]. Recently, Wang et al. [14] developed a tumor-lymphatic model with two time delays and examined the effects of these time delays on the dynamics of the new model. During the clinical practice, a symmetrical tumor-lymphatic model is a common model, in which the lymphatic vessels are arranged in a regular pattern around the tumor. This allows for the efficient drainage of lymphatic fluid and ensures that immune cells can access the tumor and attack it. Moreover, the symmetrical structure of the tumor-lymphatic model is also important for the distribution of chemotherapy drugs. If the lymphatic vessels are not arranged in a regular pattern, the drugs may not be evenly distributed throughout the tumor, which could reduce the effectiveness of treatment. Overall, the symmetrical structure of the tumor-lymphatic model is critical for the functioning of the lymphatic system and plays a key role in the immune response to cancer.

It is well-known that biological systems can be effectively described using both fractional calculus and traditional calculus. Nevertheless, as noted by Petras [15], fractional calculus offers more degrees of freedom for modeling dynamical systems when compared to conventional approaches. Furthermore, the utilization of fractional calculus in modeling biological systems can significantly enhance our ability for the discrimination, design, and control of dynamic systems due to its limitless memory [16,17]. Thereupon, fractional order biological systems have gained prominence as a research hotspot, resulting in numerous significant achievements [16,17,18,19,20,21,22,23]. Recently, the study of fractional-order dynamic systems has mainly involved the properties of the fractional-order dynamics system [24,25], such as stability analysis, bifurcations, and chaos.

It is worth noting that the study of nonlinear systems can benefit from robust bifurcation analysis, which enables the acquisition of delicate stability results. Especially, Hopf bifurcation analysis for a nonlinear system is a highly effective approach. We know that Hopf bifurcations are associated with the emergence of oscillatory behavior in a system. By studying these bifurcations in fractional order systems with time delays, researchers can better predict when and how oscillations will occur, which can be crucial for preventing undesirable outcomes in applications like control systems and signal processing. Therefore, Hopf bifurcation analysis has drawn the attention of researchers from various disciplines.

Given the above discussion, we first extend the delayed tumor-lymphatic model to the fractional-order case using the Caputo fractional derivative. Then, we investigate the stability and bifurcation characteristics of the proposed system. The contributions of this paper are shown as below. (1) The initial extension of the tumor-lymphatic model with two time delays to fractional order case by Caputo fractional derivative. (2) A detailed elucidation of the precise conditions for the occurrence of Hopf-like bifurcation near the positive equilibrium point of the delayed fractional tumor-lymphatic model under various combinations of two time delays. (3) The analysis method employed in our paper can be adapted for general fractional-order systems with multiple time delays.

The rest of this paper is organized as below. In Section 2, we quote some definitions of fractional calculus and propose a novel fractional-order tumor-lymphatic model with time delays. In Section 3, we analyze the characteristic equation to examine the linear stability of the equilibrium and derive the conditions for the occurrence of Hopf-like bifurcation at the positive equilibrium for various combinations of two time delays. In Section 4, the simulation example is given to validate our theoretical results. In Section 5, we give a brief discussion to conclude this work.

2. Preliminaries

This section addresses some of the results of the fractional-order derivatives and the fractional-order tumor-lymphatic model. It is widely recognized that several definitions of fractional-order derivatives exist due to varying interpretations. Typically, the Riemann–Liouville definition and the Caputo definition are the more commonly used ones. They are preferred because they can effectively represent well-understood aspects of physical situations, making them more applicable to real-world problems. In this paper, the Caputo derivative is taken into account when discussing the fractional-order tumor-lymphatic model.

Definition 1

([15]). The Caputo derivative of order α for one function $g(t)$ is defined by

$$\begin{array}{c}\hfill {}_{C}D_{t_0,t}^{\alpha }g(t)=\frac{1}{\Gamma (n-\alpha )}{\int }_{t_0}^t{(t-s)}^{n-\alpha -1}g\left(s\right)ds,\end{array}$$

where $n-1<\alpha \le n\in Z^{+}$, $\Gamma (·)$ is the Gamma function and $\Gamma \left(s\right)={\int }_0^{\infty }{t}^{s-1}{e}^{-t}dt$.

As a special case, when $0<\alpha \le 1$ we have ${}_{C}D_{0,t}^{\alpha }g\left(t\right)=\frac{1}{\Gamma (1-\alpha )}{\int }_0^t{(t-\tau )}^{-\alpha }{g}^{\prime }\left(\tau \right)d\tau$.

It is well known that the Laplace transform of the fractional Caputo derivative is shown as below:

$$L\left\{{}_{C}D_{0,t}^{\alpha }g\left(t\right);s\right\}=s^{\alpha }F\left(s\right)-\sum _{k=0}^{n-1}{s}^{\alpha -k-1}{g}^{\left(k\right)}\left(0\right),$$

where $n-1<\alpha \le n\in Z^{+}$.

Then, we can easily derived $L\left\{{}_{C}D_{0,t}^{\alpha }g\left(t\right);s\right\}=s^{\alpha }F\left(s\right)$ when $g^{\left(k\right)}\left(0\right)=0$ where $k=1,2,\dots ,n$.

For simplicity, the notation $D^{\alpha }g\left(t\right)$ is represented the Caputo derivative operator ${}_{C}D_{0,t}^{\alpha }g\left(t\right)$ in this paper.

Next, we will introduce the fractional-order tumor-lymphatic model with two time delays, which can be expressed as

$$\left\{\begin{array}{c}{D}^{p_1}{L}_1\left(t\right)=-a\left(L_1\left(t\right)-\frac{b}{a}{L}_0\right)+{\alpha }_1\frac{T\left(t\right)L_2\left(t\right)}{\eta +T\left(t\right)},\hfill \\ D^{p_2}{L}_2\left(t\right)=a{L}_1\left(t-\widetilde{{\tau }_1}\right)-{\alpha }_3{L}_2\left(t\right),\hfill \\ D^{p_3}T\left(t\right)=cT\left(t-\widetilde{{\tau }_2}\right)-{\alpha }_{2}T\left(t\right)L_2\left(t\right),\hfill \end{array}\right.$$

(1)

where $p_i\in (0,1]$ for $i=1$, 2, and 3; $\widetilde{{\tau }_i}\ge 0$ represents the time delay for $i=1$ and 2, and the other variables and parameters of system (1) are well expounded in Table 1.

Table 1. The meaning of variables and parameters for system (1).

Symbols	Descriptions
$L_1\left(t\right)$	The immature T lymphocytes at time t
$L_2\left(t\right)$	The mature T lymphocytes at time t
$T\left(t\right)$	Tumor cells at time t
a	The transformation rate from the immature T lymphocytes to the mature T lymphocytes
${\alpha }_1$	The maximum recruitment rate
${\alpha }_2$	The rate of tumor cells killed by mature T lymphocytes
${\alpha }_3$	The inactivation rate of the mature T lymphocytes
c	The growth rate of tumor cells
$b{L}_0$	Young lymphocytes can be produced at a fixed rate from the hemopoietic system
${\alpha }_{1}T\left(t\right)L_2\left(t\right)/(\eta +T\left(t\right)$)	The recruitment term

For convenience’s sake, we employ the notation in Wang et al. [14] as follows to system (1),

$$L_1-\frac{b}{a}{L}_0=\frac{{\alpha }_1}{{\alpha }_2}x, L_2=\frac{a}{{\alpha }_2}y, T=\eta z,$$

(2)

$$t=\frac{1}{a}s,\widetilde{{\tau }_1}=\frac{1}{a}{\tau }_1,\widetilde{{\tau }_2}=\frac{1}{a}{\tau }_2.$$

(3)

Hence, we derive the following simplified fractional-order tumor-lymphatic model:

$$\left\{\begin{array}{c}{D}^{p_1}x\left(t\right)=-x\left(t\right)+\frac{y\left(t\right)z\left(t\right)}{1+z\left(t\right)},\hfill \\ D^{p_2}y\left(t\right)=\alpha x\left(t-{\tau }_1\right)-\beta y\left(t\right)+\gamma ,\hfill \\ D^{p_3}z\left(t\right)=\delta z\left(t-{\tau }_2\right)-y\left(t\right)z\left(t\right),\hfill \end{array}\right.$$

(4)

with $\alpha =\frac{{\alpha }_1}{a}$, $\beta =\frac{{\alpha }_3}{a}$, $\gamma =\frac{{\alpha }_{2}b{L}_0}{a^2}$, and $\delta =\frac{c}{a}$.

Here, we presume that the following condition is true:

$\left(\mathbf{H}\mathbf{1}\right)$$max\{0, (\beta -\alpha \left)\delta \right\}<\gamma <\beta \delta$.

According to the hypothesis $\left(\mathbf{H}\mathbf{1}\right)$, we know that system (4) has a unique positive equilibrium point $E*(x*,y*,z*)$ with

$$\left\{\begin{array}{c}x*=\frac{\beta \delta -\gamma }{\alpha },\hfill \\ y*=\delta ,\hfill \\ z*=\frac{\beta \delta -\gamma }{\gamma +\alpha \delta -\beta \delta }.\hfill \end{array}\right.$$

(5)

If $p_1=p_2=p_3=1$, system (4) changes into the following integer-order system:

$$\left\{\begin{array}{c}\dot{x}\left(t\right)=-x\left(t\right)+\frac{y\left(t\right)z\left(t\right)}{1+z\left(t\right)},\hfill \\ \dot{y}\left(t\right)=\alpha x\left(t-{\tau }_1\right)-\beta y\left(t\right)+\gamma ,\hfill \\ \dot{z}\left(t\right)=\delta z\left(t-{\tau }_2\right)-y\left(t\right)z\left(t\right).\hfill \end{array}\right.$$

(6)

The primary objective of this paper is to determine the conditions of Hopf-like bifurcation for system (4) with two time delays serving as bifurcation parameters using the stability analysis method [4]. Additionally, we aim to elucidate the influence of these parameters on the bifurcation.

3. Main Results

In this section, we conduct an analysis of the local stability of system (4). We derive the conditions for Hopf-like bifurcation in system (4) while considering time delays ${\tau }_1$ and ${\tau }_2$ as the bifurcation parameters. Initially, we linearize system (4) and calculate the Jacobian matrix of the system at the equilibrium $E*(x*,y*,z*)$. Therefore, we have the associated characteristic equation as below:

$$\begin{array}{c}\left|\begin{array}{ccc}{\lambda }^{p_1}+1& -\frac{z*}{1+z*}& -\frac{y*}{{\left(1+z*\right)}^2}\\ -\alpha e^{-\lambda {\tau }_1}& {\lambda }^{p_2}+\beta & 0\\ 0& z*& {\lambda }^{p_3}+y*-\delta e^{-\lambda {\tau }_2}\end{array}\right|=0.\end{array}$$

(7)

According to Equation (7), we have

$${\mathfrak{P}}_{\mathfrak{0}}\left(\lambda \right)+{\mathfrak{P}}_{\mathfrak{1}}\left(\lambda \right)e^{-\lambda {\tau }_1}+{\mathfrak{P}}_{\mathfrak{2}}\left(\lambda \right)e^{-\lambda {\tau }_2}+{\mathfrak{P}}_{\mathfrak{3}}\left(\lambda \right)e^{-\lambda \left({\tau }_1+{\tau }_2\right)}=0,$$

(8)

where

$$\begin{array}{cc}\hfill {\mathfrak{P}}_{\mathfrak{0}}\left(\lambda \right)& ={\lambda }^{q_1+q_2+q_3}+\delta {\lambda }^{q_1+q_2}+\beta {\lambda }^{q_1+q_3}+{\lambda }^{q_2+q_3}+\beta \delta {\lambda }^{q_1}+\delta {\lambda }^{q_2}+\beta {\lambda }^{q_3}+\beta \delta ,\hfill \\ \hfill {\mathfrak{P}}_{\mathfrak{1}}\left(\lambda \right)& =\left(-\beta +\frac{\gamma }{\delta }\right){\lambda }^{q_3}-\frac{{\left(\gamma -\beta \delta \right)}^2}{\alpha \beta },\hfill \\ \hfill {\mathfrak{P}}_{\mathfrak{2}}\left(\lambda \right)& =-\delta {\lambda }^{q_1+q_2}-\beta \delta {\lambda }^{q_1}-\delta {\lambda }^{q_2}-\beta \delta ,\hfill \\ \hfill {\mathfrak{P}}_{\mathfrak{3}}\left(\lambda \right)& =\beta \delta -\gamma .\hfill \end{array}$$

To deeply study the dynamic behavior of system (4) at $E^{*}$, we mainly consider three cases as follows.

Case 1:

${\tau }_1>0$ and ${\tau }_2=0$.

When ${\tau }_2=0$, we convert Equation (8) into

$$\begin{array}{c}\hfill {\mathfrak{P}}_{\mathfrak{0}}\left(\lambda \right)+{\mathfrak{P}}_{\mathfrak{2}}\left(\lambda \right)+\left({\mathfrak{P}}_{\mathfrak{1}}\left(\lambda \right)+{\mathfrak{P}}_{\mathfrak{3}}\left(\lambda \right)\right)e^{-\lambda {\tau }_1}=0.\end{array}$$

(9)

At $E^{*}$ it follows from Equation (9) that

$$\begin{array}{c}\hfill Q_1\left(\lambda \right)+Q_2\left(\lambda \right)e^{-\lambda {\tau }_1}=0,\end{array}$$

(10)

where $Q_1\left(\lambda \right)={\lambda }^{q_1+q_2+q_3}+\beta {\lambda }^{q_1+q_3}+{\lambda }^{q_2+q_3}+\beta {\lambda }^{q_3}$, and $Q_2\left(\lambda \right)={\displaystyle \frac{\left(-\beta \delta +\gamma \right)}{\delta }}{\lambda }^{q_3}+\beta \delta -\gamma -{\displaystyle \frac{{\left(\gamma -\beta \delta \right)}^2}{\alpha \beta }}$.

Let $\lambda =\iota \omega$ be one root of Equation (10) with $\omega >0$, where $\iota$ is the imaginary unit of a complex number. Plugging $\lambda =\iota \omega$ into Equation (10) and thus performing elementary calculations leads to

$$\left\{\begin{array}{c}{\mathcal{A}}_2\cos \omega {\tau }_1+{\mathcal{B}}_2\sin \omega {\tau }_1=-{\mathcal{A}}_1,\hfill \\ {\mathcal{B}}_2\cos \omega {\tau }_1-{\mathcal{A}}_2\sin \omega {\tau }_1=-{\mathcal{B}}_1,\hfill \end{array}\right.$$

(11)

where ${\mathcal{A}}_i$ and ${\mathcal{B}}_i$ stand for the real part and the imaginary part of $Q_i\left(\lambda \right)(i=1,2)$, respectively, which are shown as below:

$$\begin{array}{cc}\hfill {\mathcal{A}}_1& ={\omega }^{p_1+p_2+p_3}\cos \left(\frac{\left(p_1+p_2+p_3\right)\pi }{2}\right)+\beta {\omega }^{p_1+p_3}\cos \left(\frac{\left(p_1+p_3\right)\pi }{2}\right)+{\omega }^{p_2+p_3}\cos \left(\frac{\left(p_2+p_3\right)\pi }{2}\right)\hfill \\ \hfill & +\beta {\omega }^{p_3}\cos \frac{p_3\pi }{2},\hfill \\ \hfill {\mathcal{B}}_1& ={\omega }^{p_1+p_2+p_3}\sin \left(\frac{\left(p_1+p_2+p_3\right)\pi }{2}\right)+\beta {\omega }^{p_1+p_3}\sin \left(\frac{\left(p_1+p_3\right)\pi }{2}\right)+{\omega }^{p_2+p_3}\sin \left(\frac{\left(p_2+p_3\right)\pi }{2}\right)\hfill \\ \hfill & +\beta {\omega }^{p_3}\sin \frac{p_3\pi }{2},\hfill \\ \hfill {\mathcal{A}}_2& =\frac{\left(-\beta \delta +\gamma \right)}{\delta }{\omega }^{q_3}\cos \left(\frac{p_3\pi }{2}\right)+\beta \delta -\gamma -\frac{{\left(\gamma -\beta \delta \right)}^2}{\alpha \delta },\hfill \\ \hfill {\mathcal{B}}_2& =\frac{\left(-\beta \delta +\gamma \right)}{\delta }{\omega }^{q_3}\sin \left(\frac{p_3\pi }{2}\right).\hfill \end{array}$$

Based on Equation (11), we easily have

$$\left\{\begin{array}{c}\cos \omega {\tau }_1=-\frac{{\mathcal{A}}_1{\mathcal{A}}_2+{\mathcal{B}}_1{\mathcal{B}}_2}{{\mathcal{A}}_2^2+{\mathcal{B}}_2^2}={\mathcal{G}}_1\left(\omega \right),\hfill \\ \sin \omega {\tau }_1=\frac{{\mathcal{A}}_2{\mathcal{B}}_1-{\mathcal{A}}_1{\mathcal{B}}_2}{{\mathcal{A}}_2^2+{\mathcal{B}}_2^2}={\mathcal{G}}_2\left(\omega \right).\hfill \end{array}\right.$$

(12)

Hence,

$$\begin{array}{c}{\mathcal{G}}_1^2\left(\omega \right)+{\mathcal{G}}_2^2\left(\omega \right)=1.\end{array}$$

(13)

In the sequel of this paper, we make the following hypothesis.

$\left(\mathbf{H}\mathbf{2}\right)$ Positive roots exist for Equation (13).

By the first equation of (12), we have

$$\begin{array}{c}{\tau }^{\left(k\right)}=\frac{1}{\omega }[\arccos {\mathcal{G}}_1\left(\omega \right)+2k\pi ],k=0,1,2,\dots \end{array}$$

(14)

We define the following bifurcation point:

$$\begin{array}{c}\hfill {\tau }_0^1=\min \{{\tau }^{\left(k\right)}\},k=0,1,2,\dots \end{array}$$

(15)

To obtain the bifurcation conditions, we give the following useful hypothesis in detail:

$(\mathbf{H}\mathbf{3}){\displaystyle \frac{{\mathcal{M}}_1{\mathcal{N}}_1+{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{N}}_1^2+{\mathcal{N}}_2^2}}\ne 0$,

where ${\mathcal{M}}_i$ and ${\mathcal{N}}_i$ are described by Appendix A where $i=1$ and 2.

Lemma 1.

Assume that $\lambda \left({\tau }_1\right)=\nu \left({\tau }_1\right)+\iota \omega \left({\tau }_1\right)$ is the root of Equation (10) near ${\tau }_1={\tau }_0^1$ satisfying $\nu \left({\tau }_0^1\right)=0$ and $\omega \left({\tau }_0^1\right)={\omega }_0$. Then, the transversality condition $\mathrm{Re}\left[\frac{d\lambda }{d{\tau }_1}\right]{|}_{({\tau }_1={\tau }_0^1,\omega ={\omega }_0)}\ne 0$ holds.

Proof. 

Differentiating both sides of Equation (10) with respect to ${\tau }_1$, we have

$$\begin{array}{c}{Q_1}^{\prime }\left(\lambda \right)\frac{d\lambda }{d{\tau }_1}+{Q_2}^{\prime }\left(\lambda \right)e^{-\lambda {\tau }_1}\frac{d\lambda }{d{\tau }_1}+Q_2\left(\lambda \right)e^{-\lambda {\tau }_1}\left(-{\tau }_1\frac{d\lambda }{d{\tau }_1}-\lambda \right)=0,\end{array}$$

where $Q_i^{\prime }\left(\lambda \right)$ are the derivatives of $Q_i\left(\lambda \right)$ with $i=1$ and 2.

Thus,

$$\begin{array}{c}\hfill \frac{d\lambda }{d{\tau }_1}=\frac{\mathcal{M}\left(\lambda \right)}{\mathcal{N}\left(\lambda \right)},\end{array}$$

(16)

where

$$\begin{array}{c}\mathcal{M}\left(\lambda \right)=\left[\frac{\left(-\beta \delta +\gamma \right)}{\delta }{\lambda }^{q_3}+\beta \delta -\gamma -\frac{{\left(\gamma -\beta \delta \right)}^2}{\alpha \beta }\right]\lambda e^{-\lambda {\tau }_1},\hfill \\ \mathcal{N}\left(\lambda \right)=\left(q_1+q_2+q_3\right){\lambda }^{q_1+q_2+q_3-1}+\beta \left(q_1+q_3\right){\lambda }^{q_1+q_3-1}+\left(q_2+q_3\right){\lambda }^{q_2+q_3-1}+\beta q_3{\lambda }^{q_3-1}\hfill \\ \left[\frac{\left(-\beta \delta +\gamma \right)}{\delta }{q}_3{\lambda }^{q_3-1}\right]e^{-\lambda {\tau }_1}-\left[\frac{\left(-\beta \delta +\gamma \right)}{\delta }{\lambda }^{q_3}+\beta \delta -\gamma -\frac{{\left(\gamma -\beta \delta \right)}^2}{\alpha \beta }\right]{\tau }_1{e}^{-\lambda {\tau }_1}.\hfill \end{array}$$

It follows from Equation (16) that

$$\begin{array}{c}\hfill \mathrm{Re}\left[\frac{d\lambda }{d{\tau }_1}\right]{|}_{({\tau }_1={\tau }_0^1,\omega ={\omega }_0)}=\frac{{\mathcal{M}}_1{\mathcal{N}}_1+{\mathcal{M}}_2{\mathcal{N}}_2}{{\mathcal{N}}_1^2+{\mathcal{N}}_2^2},\end{array}$$

(17)

where ${\mathcal{M}}_1$, ${\mathcal{M}}_2$, ${\mathcal{N}}_1$, and ${\mathcal{N}}_2$ are the real and imaginary parts of $\mathcal{M}\left(\lambda \right)$, and the real and imaginary parts of $\mathcal{N}\left(\lambda \right)$, respectively.

Clearly, hypothesis $\left(\mathbf{H}\mathbf{3}\right)$ shows that the transversality condition holds. This completes the proof. □

From the above results and notations, we directly obtain the following result.

Theorem 1.

If $\left(\mathit{H}\mathit{1}\right)$–$\left(\mathit{H}\mathit{3}\right)$ hold, then the following results are available for system (4).

(1) 

The tumor-present equilibrium point $E^{*}$ of system (4) is asymptotically stable for ${\tau }_1\in [0,{\tau }_0^1)$.

(2) 

For ${\tau }_1={\tau }_0^1$, system (4) undergoes a Hopf-like bifurcation at tumor-present equilibrium $E^{*}$. That is, system (4) has a branch of periodic solutions bifurcating from the tumor-present equilibrium point $E^{*}$ near ${\tau }_1={\tau }_0^1$.

Case 2:

${\tau }_1=0$ and ${\tau }_2>0$.

When ${\tau }_1=0$, for Equation (8) we directly have

$$\begin{array}{c}{\mathfrak{P}}_0\left(\lambda \right)+{\mathfrak{P}}_1\left(\lambda \right)+\left({\mathfrak{P}}_2\left(\lambda \right)+{\mathfrak{P}}_3\left(\lambda \right)\right)e^{-\lambda {\tau }_2}=0.\end{array}$$

(18)

At $E^{*}$, the characteristic Equation (18) takes the form

$$\begin{array}{c}\hfill R_1\left(\lambda \right)+R_2\left(\lambda \right)e^{-\lambda {\tau }_2}=0,\end{array}$$

(19)

where $R_1\left(\lambda \right)={\lambda }^{q_1+q_2+q_3}+\delta {\lambda }^{q_1+q_2}+\beta {\lambda }^{q_1+q_3}+{\lambda }^{q_2+q_3}+\beta \delta {\lambda }^{q_1}+\delta {\lambda }^{q_2}+{\displaystyle \frac{\gamma }{\delta }}{\lambda }^{q_3}+\beta \delta -{\displaystyle \frac{{\left(\gamma -\beta \delta \right)}^2}{\alpha \delta }}$, and $R_2\left(\lambda \right)=-\delta {\lambda }^{q_1+q_2}-\beta \delta {\lambda }^{q_1}-\delta {\lambda }^{q_2}-\gamma$.

Assume that $\lambda =\iota \omega$ is one root of Equation (19) where $\omega >0$. We perform elementary calculations by substituting $\lambda$ into Equation (19), yielding

$$\left\{\begin{array}{c}{\mathcal{E}}_2\cos \omega {\tau }_2+{\mathcal{F}}_2\sin \omega {\tau }_2=-{\mathcal{E}}_1,\hfill \\ {\mathcal{F}}_2\cos \omega {\tau }_2-{\mathcal{E}}_2\sin \omega {\tau }_2=-{\mathcal{F}}_1,\hfill \end{array}\right.$$

(20)

where ${\mathcal{E}}_i$, ${\mathcal{F}}_i$ are the real part and the imaginary part of $R_i\left(\lambda \right)$ with $i=1$ and 2, respectively, which are as follows:

$$\begin{array}{cc}\hfill {\mathcal{E}}_1& ={\omega }^{p_1+p_2+p_3}\cos \frac{\left(p_1+p_2+p_3\right)\pi }{2}+\delta {\omega }^{p_1+p_2}\cos \frac{\left(p_1+p_2\right)\pi }{2}+\beta {\omega }^{p_1+p_3}\cos \frac{\left(p_1+p_3\right)\pi }{2}\hfill \\ \hfill & +{\omega }^{p_2+p_3}\cos \frac{\left(p_2+p_3\right)\pi }{2}+\beta \delta {\omega }^{p_1}\cos \frac{p_1\pi }{2}+\delta {\omega }^{p_2}\cos \frac{p_2\pi }{2}+\frac{\gamma }{\delta }{\omega }^{p_3}\cos \frac{p_3\pi }{2}+\beta \delta -\frac{{\left(\gamma -\beta \delta \right)}^2}{\alpha \delta },\hfill \\ \hfill {\mathcal{F}}_1& ={\omega }^{p_1+p_2+p_3}sin\frac{\left(p_1+p_2+p_3\right)\pi }{2}+\delta {\omega }^{p_1+p_2}sin\frac{\left(p_1+p_2\right)\pi }{2}+\beta {\omega }^{p_1+p_3}sin\frac{\left(p_1+p_3\right)\pi }{2}\hfill \\ \hfill & +{\omega }^{p_2+p_3}sin\frac{\left(p_2+p_3\right)\pi }{2}+\beta \delta {\omega }^{p_1}\sin \frac{p_1\pi }{2}+\delta {\omega }^{p_2}\sin \frac{p_2\pi }{2}+\frac{\gamma }{\delta }{\omega }^{p_3}sin\frac{p_3\pi }{2},\hfill \\ \hfill {\mathcal{E}}_2& =-\delta {\omega }^{p_1+p_2}\cos \frac{\left(p_1+p_2\right)\pi }{2}-\beta \delta {\omega }^{p_1}\cos \frac{p_1\pi }{2}-\delta {\omega }^{p_2}\cos \frac{p_2\pi }{2}-\gamma ,\hfill \\ \hfill {\mathcal{F}}_2& =-\delta {\omega }^{p_1+p_2}sin\frac{\left(p_1+p_2\right)\pi }{2}-\beta \delta {\omega }^{p_1}\sin \frac{p_1\pi }{2}-\delta {\omega }^{p_2}\sin \frac{p_2\pi }{2}.\hfill \end{array}$$

By Equation (20), it is easy to obtain

$$\left\{\begin{array}{c}\cos \omega {\tau }_2=-\frac{{\mathcal{E}}_1{\mathcal{E}}_2+{\mathcal{F}}_1{\mathcal{F}}_2}{{\mathcal{E}}_2^2+{\mathcal{F}}_2^2}={\mathcal{J}}_1\left(\omega \right),\hfill \\ \sin \omega {\tau }_2=\frac{{\mathcal{E}}_2{\mathcal{F}}_1-{\mathcal{E}}_1{\mathcal{F}}_2}{{\mathcal{E}}_2^2+{\mathcal{F}}_2^2}={\mathcal{J}}_2\left(\omega \right).\hfill \end{array}\right.$$

(21)

It follows from the Equation (21) that we have

$$\begin{array}{c}{\mathcal{J}}_1^2\left(\omega \right)+{\mathcal{J}}_2^2\left(\omega \right)=1.\end{array}$$

(22)

We further assume that

$\left(\mathbf{H}\mathbf{4}\right)$ Positive roots exist for Equation (22).

Therefore, Equation (21) implies that

$$\begin{array}{c}\hfill {\tau }^{\left(k\right)}=\frac{1}{\omega }[\arccos {\mathcal{J}}_1\left(\omega \right)+2k\pi ],k=0,1,2,\dots \end{array}$$

(23)

Then, we can define the critical value as follows:

$$\begin{array}{c}{\tau }_0^2=\min \{{\tau }^{\left(k\right)}\},k=0,1,2,\dots \end{array}$$

(24)

To obtain the bifurcation conditions, we need the following hypothesis:

$(\mathbf{H}\mathbf{5}){\displaystyle \frac{{\mathcal{H}}_1{\mathcal{I}}_1+{\mathcal{H}}_2{\mathcal{I}}_2}{{\mathcal{I}}_1^2+{\mathcal{I}}_2^2}}\ne 0$,

where ${\mathcal{H}}_i$ and ${\mathcal{I}}_i$ are described by Appendix B, where $i=1$ and 2.

Lemma 2.

Assume that $\lambda \left({\tau }_2\right)=\nu \left({\tau }_2\right)+\iota \omega \left({\tau }_2\right)$ is the root of Equation (19) near ${\tau }_2={\tau }_0^2$ satisfying $\nu \left({\tau }_0^2\right)=0$ and $\omega \left({\tau }_0^2\right)={\omega }_0$. Then, the transversality condition $\mathrm{Re}\left[\frac{d\lambda }{d{\tau }_2}\right]{|}_{({\tau }_2={\tau }_0^2,\omega ={\omega }_0)}\ne 0$ holds.

Proof. 

Differentiating both sides of Equation (19) with respect to ${\tau }_2$, we have

$$\begin{array}{c}{R_1}^{\prime }\left(\lambda \right)\frac{d\lambda }{d{\tau }_2}+{R_2}^{\prime }\left(\lambda \right)e^{-\lambda {\tau }_2}\frac{d\lambda }{d{\tau }_2}+R_2\left(\lambda \right)e^{-\lambda {\tau }_2}\left(-{\tau }_2\frac{d\lambda }{d{\tau }_2}-\lambda \right)=0,\end{array}$$

where $R_i^{\prime }\left(\lambda \right)$ are the derivatives of $R_i\left(\lambda \right)$ with $i=1$ and 2.

Therefore,

$$\begin{array}{c}\hfill \frac{d\lambda }{d{\tau }_2}=\frac{\mathcal{H}\left(\lambda \right)}{\mathcal{I}\left(\lambda \right)},\end{array}$$

(25)

where

$$\begin{array}{l}\mathcal{H}\left(\lambda \right)=\left(-\delta {\lambda }^{p_1+p_2}-\beta \delta {\lambda }^{p_1}-\delta {\lambda }^{p_2}-\gamma \right)\lambda e^{-\lambda {\tau }_2},\\ \mathcal{I}\left(\lambda \right)=\left(p_1+p_2+p_3\right){\lambda }^{p_1+p_2+p_3-1}+\delta \left(p_1+p_2\right){\lambda }^{p_1+p_2-1}+\beta \left(p_1+p_3\right){\lambda }^{p_1+p_3-1}+\left(p_2+p_3\right){\lambda }^{p_2+p_3-1}\\ +\beta \delta p_1{\lambda }^{p_1-1}-\delta p_2{\lambda }^{p_2-1}+\left(-\delta \left(p_1+p_2\right){\lambda }^{p_1+p_2-1}-\beta \delta p_1{\lambda }^{p_1-1}-\delta p_2{\lambda }^{p_2-1}\right)e^{-\lambda {\tau }_2}\\ +\left(\delta {\lambda }^{p_1+p_2}+\beta \delta {\lambda }^{p_1}+\delta {\lambda }^{p_2}+\gamma \right){\tau }_2{e}^{-\lambda {\tau }_2}.\end{array}$$

It follows from Equation (25) that

$$\begin{array}{c}\mathrm{Re}\left[\frac{d\lambda }{d{\tau }_2}\right]{|}_{({\tau }_2={\tau }_0^2,\omega ={\omega }_0)}=\frac{{\mathcal{H}}_1{\mathcal{I}}_1+{\mathcal{H}}_2{\mathcal{I}}_2}{{\mathcal{I}}_1^2+{\mathcal{I}}_2^2},\end{array}$$

(26)

where ${\mathcal{H}}_1$, ${\mathcal{H}}_2$, ${\mathcal{I}}_1$, and ${\mathcal{I}}_2$ are the real and imaginary parts of $\mathcal{H}\left(\lambda \right)$, and the real and imaginary parts of $\mathcal{I}\left(\lambda \right)$, respectively.

Clearly, the hypothesis $\left(\mathbf{H}\mathbf{5}\right)$ shows that the transversality condition holds. Thus, we have proved Lemma 2. □

We procure the following main theorem under the above results and notations.

Theorem 2.

If $\left(\mathit{H}\mathit{1}\right)$, $\left(\mathit{H}\mathit{4}\right)$, and $\left(\mathit{H}\mathit{5}\right)$ hold, the following results are available for system (4):

(1)

For ${\tau }_2\in [0,{\tau }_0^2)$, the tumor-present equilibrium point $E^{*}$ of system (4) is asymptotically stable.

(2)

For ${\tau }_2={\tau }_0^2$, system (4) undergoes a Hopf-like bifurcation at the tumor-present equilibrium $E^{*}$. Namely, system (4) has a branch of periodic solutions bifurcating from the tumor-present equilibrium point $E^{*}$ near ${\tau }_2={\tau }_0^2$.

Case 3:

${\tau }_1>0$ and ${\tau }_2>0$.

To investigate the effect of the two delays on the local stability of equilibrium point $E^{*}$, we regard one time delay ${\tau }_1$ (or ${\tau }_2$) as the varying parameter for the fixed delay ${\tau }_2$ (or ${\tau }_1$). In the following, we select ${\tau }_1>0$ as a bifurcation parameter to study the bifurcation of the fractional-order tumor-lymphatic model (4). Based on the Laplace transform, we have the following characteristic equation:

$$\begin{array}{c}{\mathrm{U}}_1\left(\lambda \right)+{\mathrm{U}}_2\left(\lambda \right)e^{-\lambda {\tau }_1}=0,\end{array}$$

(27)

where

$$\begin{array}{cc}\hfill {\mathrm{U}}_1\left(\lambda \right)& =P_0\left(\lambda \right)+P_2\left(\lambda \right)e^{-\lambda {\tau }_2}\hfill \\ \hfill & ={\lambda }^{{\mathrm{p}}_1+p_2+p_3}+\delta {\lambda }^{{\mathrm{p}}_1+p_2}+\beta {\lambda }^{{\mathrm{p}}_1+p_3}+{\lambda }^{p_2+p_3}+\beta \delta {\lambda }^{{\mathrm{p}}_1}+\delta {\lambda }^{p_2}+\beta {\lambda }^{p_3}+\beta \delta \hfill \\ \hfill & +\left(-\delta {\lambda }^{{\mathrm{p}}_1+p_2}-\beta \delta {\lambda }^{{\mathrm{p}}_1}-\delta {\lambda }^{p_2}-\beta \delta \right)e^{-{\tau }_2},\hfill \\ \hfill {\mathrm{U}}_2\left(\lambda \right)& =P_1\left(\lambda \right)+P_3\left(\lambda \right)e^{-\lambda {\tau }_2}\hfill \\ \hfill & =\left(-\beta +\frac{\gamma }{\delta }\right){\lambda }^{p_3}-\frac{{\left(\gamma -\beta \delta \right)}^2}{\alpha \beta }+\left(\beta \delta -\gamma \right)e^{-{\tau }_2}.\hfill \end{array}$$

Here, we define the real and imaginary parts of $U_k\left(\lambda \right)$ as $U_k^r\left(\lambda \right)$ and $U_k^i\left(\lambda \right)$ with $k=1$ and 2, respectively.

Assume that $\lambda =\iota \omega (\omega >0)$ is a purely imaginary root of Equation (27). Then, we deduce from Equation (27) that

$${{\mathrm{U}}_1}^i\cos \omega {\tau }_1+{{\mathrm{U}}_2}^i\sin \omega {\tau }_1=-{{\mathrm{U}}_1}^r,$$

(28)

$${{\mathrm{U}}_2}^i\cos \omega {\tau }_1-{{\mathrm{U}}_1}^i\sin \omega {\tau }_2=-{{\mathrm{U}}_2}^r.$$

(29)

Define

$$\begin{array}{c}{\varphi }_1\left(\omega \right)={{\mathrm{U}}_1}^r{{\mathrm{U}}_1}^i+{{\mathrm{U}}_2}^r{{\mathrm{U}}_2}^i,\\ {\varphi }_2\left(\omega \right)={{\mathrm{U}}_1}^i{{\mathrm{U}}_2}^r-{{\mathrm{U}}_1}^r{{\mathrm{U}}_2}^i,\\ {\varphi }_3\left(\omega \right)={\left({{\mathrm{U}}_1}^i\right)}^2+{\left({{\mathrm{U}}_2}^i\right)}^2.\end{array}$$

It derives from Equations (28) and (29) that

$$\left\{\begin{array}{c}\cos \omega {\tau }_1=-\frac{{\varphi }_1\left(\omega \right)}{{\varphi }_3\left(\omega \right)}={\mathcal{K}}_1\left(\omega \right),\hfill \\ \sin \omega {\tau }_1=\frac{{\varphi }_2\left(\omega \right)}{{\varphi }_3\left(\omega \right)}={\mathcal{K}}_2\left(\omega \right).\hfill \end{array}\right.$$

(30)

Through Equation (30), we have

$$\begin{array}{c}{\mathcal{K}}_1^2\left(\omega \right)+{\mathcal{K}}_2^2\left(\omega \right)=1.\end{array}$$

(31)

We further need the following hypothesis for ensuring the existence of the roots of Equation (31).

$\left(\mathbf{H}\mathbf{6}\right)$ Positive roots exist for Equation (31).

It follows from the fact $\cos \omega {\tau }_1={\mathcal{K}}_1\left(\omega \right)$ that we have

$$\begin{array}{c}{\tau }^{\left(k\right)}=\frac{1}{\omega }[\arccos {\mathcal{K}}_1\left(\omega \right)+2k\pi ],k=0,1,2,\dots \end{array}$$

(32)

Then, we define the critical value as follows:

$$\begin{array}{c}{\tau }_{10}=\min \left\{{\tau }^{\left(k\right)}\right\},k=0,1,2,\dots \end{array}$$

(33)

Next, we eliminate ${\tau }_1$ from Equation (27), and Equation (27) becomes equivalent to

$${\Phi }_1\left(\lambda \right)+{\Phi }_2\left(\lambda \right)e^{-\lambda {\tau }_2}=0,$$

where

$${\Phi }_1\left(\lambda \right)={\lambda }^{p_1+p_2+p_3}+\delta {\lambda }^{p_1+p_2}+\beta {\lambda }^{p_1+p_3}+{\lambda }^{p_2+p_3}+\beta \delta {\lambda }^{p_1}+\delta {\lambda }^{p_2}+\beta {\lambda }^{p_3}+\beta \delta -\frac{{\beta }^2\delta }{\alpha }+\frac{\gamma }{\delta }{\lambda }^{p_3}+\frac{2\gamma \beta }{\alpha }-\frac{{\gamma }^2}{\alpha \delta },$$

$${\Phi }_2\left(\lambda \right)=-\delta {\lambda }^{p_1+p_2}-\beta \delta {\lambda }^{p_1}-\delta {\lambda }^{p_2}-\lambda .$$

If ${\tau }_2=0$, we have

$${\lambda }^{p_1+p_2+p_3}+X_1{\lambda }^{p_1+p_3}+{\lambda }^{p_2+p_3}+X_2{\lambda }^{p_3}+X_3=0,$$

where $X_1=\delta$, $X_2=\beta +{\displaystyle \frac{\gamma }{\delta }}$, and $X_3=\beta \delta -\lambda -{\displaystyle \frac{{(\gamma -\beta \delta )}^2}{\alpha \delta }}$.

Let ${\Phi }_k^R\left(\lambda \right)$ and ${\Phi }_k^I\left(\lambda \right)$ be the real and imaginary parts of ${\Phi }_k\left(\lambda \right)$ ($k=1$ and 2), respectively. Set $\lambda =\overline{\omega }(cos\frac{\pi }{2}+\iota sin\frac{\pi }{2})$; then,

$$\left\{\begin{array}{c}{\Phi }_2^R\cos \overline{\omega }{\tau }_2+{\Phi }_2^I\sin \overline{\omega }{\tau }_2=-{\Phi }_1^R,\\ {\Phi }_2^I\cos \overline{\omega }{\tau }_2-{\Phi }_2^R\sin \overline{\omega }{\tau }_2=-{\Phi }_1^I.\end{array}\right.$$

Therefore, we have

$$\begin{array}{c}\left\{\begin{array}{c}\cos \overline{\omega }{\tau }_2=-{\displaystyle \frac{{\Phi }_1^R{\Phi }_2^R+{\Phi }_1^I{\Phi }_2^I}{{\left({\Phi }_2^R\right)}^2+{\left({\Phi }_2^I\right)}^2}}=O_1\left(\overline{\omega }\right),\\ \sin \overline{\omega }{\tau }_2={\displaystyle \frac{{\Phi }_1^I{\Phi }_2^R-{\Phi }_1^R{\Phi }_2^I}{{\left({\Phi }_2^R\right)}^2+{\left({\Phi }_2^I\right)}^2}}=O_2\left(\overline{\omega }\right).\end{array}\right.\end{array}$$

(34)

Then, it is obvious that

$$\begin{array}{c}\hfill O_1^2\left(\overline{\omega }\right)+O_2^2\left(\overline{\omega }\right)=1.\end{array}$$

(35)

In fact, we can use Maple to derive one positive solution, but it is somewhat imprecise to directly describe its solution as a positive solution. Therefore, in order to maintain the integrity of the theoretical framework, we assume that Equation (34) has a positive real root. Similarly, Equations (34) and (35) can deduce the value of ${\overline{\omega }}_0$, and then bringing it into the first formula in Equation (34) can logically solve for the value of ${\overline{\tau }}_2^{\left(k\right)}$ where $k=0,1,2,\dots$

In the last resort, defining ${\tau }_{20}$ as follows:

$${\overline{\tau }}_{20}=\min \left\{{\overline{\tau }}_2^{\left(k\right)}\right\},$$

where $k=0,1,2,\dots$

To derive the bifurcation conditions, we need the following hypothesis:

$\left(\mathbf{H}\mathbf{7}\right)$${\displaystyle \frac{{\mathcal{S}}_1{\mathcal{T}}_1+{\mathcal{S}}_2{\mathcal{T}}_2}{{\mathcal{T}}_1^2+{\mathcal{T}}_2^2}}\ne 0$,

where ${\mathcal{S}}_i$ and ${\mathcal{T}}_i$ are shown in Appendix C where $i=1$ and 2.

Lemma 3.

Assume that $\lambda \left({\tau }_1\right)=\nu \left({\tau }_1\right)+\iota \omega \left({\tau }_1\right)$ is one root of Equation (27) near ${\tau }_1={\tau }_{10}$ satisfying $\nu \left({\tau }_{10}\right)=0$ and $\omega \left({\tau }_{10}\right)={\omega }_0$. Then, the transversality condition $\mathrm{Re}\left[\frac{d\lambda }{d{\tau }_1}\right]{|}_{({\tau }_1={\tau }_{10},\omega ={\omega }_0)}\ne 0$ holds.

Proof. 

Differentiating both sides of Equation (27) with respect to ${\tau }_1$, we have

$$\begin{array}{c}{U_1}^{\prime }\left(\lambda \right)\frac{d\lambda }{d{\tau }_1}+{U_2}^{\prime }\left(\lambda \right)e^{-\lambda {\tau }_1}+U_2\left(\lambda \right)e^{-\lambda {\tau }_1}\left(-{\tau }_1\frac{d\lambda }{d{\tau }_1}-\lambda \right)=0,\end{array}$$

where $U_i^{\prime }\left(\lambda \right)$ are the derivatives of $U_i\left(\lambda \right)$ with $i=1$ and 2.

Therefore,

$$\begin{array}{c}\frac{d\lambda }{d{\tau }_1}=\frac{\mathcal{S}\left(\lambda \right)}{\mathcal{T}\left(\lambda \right)},\end{array}$$

(36)

where

$$\begin{array}{c}\mathcal{S}\left(\lambda \right)=\lambda U_2\left(\lambda \right)e^{-\lambda {\tau }_1},\hfill \\ \mathcal{T}\left(\lambda \right)={U_1}^{\prime }\left(\lambda \right)+{U_2}^{\prime }\left(\lambda \right)e^{-\lambda {\tau }_1}-{\tau }_1{U}_2\left(\lambda \right)e^{-\lambda {\tau }_1}.\hfill \end{array}$$

According to Equation (36), we have

$$\begin{array}{c}\mathrm{Re}\left[\frac{d\lambda }{d{\tau }_1}\right]{|}_{({\tau }_1={\tau }_{10},\omega ={\omega }_0)}=\frac{{\mathcal{S}}_1{\mathcal{T}}_1+{\mathcal{S}}_2{\mathcal{T}}_2}{{\mathcal{T}}_1^2+{\mathcal{T}}_2^2},\end{array}$$

(37)

where ${\mathcal{S}}_1$, ${\mathcal{S}}_2$, ${\mathcal{T}}_1$, and ${\mathcal{T}}_2$ are the real and imaginary parts of $\mathcal{S}\left(\lambda \right)$, and the real and imaginary parts of $\mathcal{T}\left(\lambda \right)$, respectively.

From the hypothesis $\left(\mathbf{H}\mathbf{7}\right)$, we have that the transversality condition holds. Then, we have proved Lemma 3. □

To sum up, we can obtain the following results.

Theorem 3.

If $\left(\mathit{H}\mathit{1}\right)$, $\left(\mathit{H}\mathit{6}\right)$, and $\left(\mathit{H}\mathit{7}\right)$ hold, the following results are available for system (4):

(1)

For ${\tau }_2\in [0,{\overline{\tau }}_{20})$, the tumor-present equilibrium point $E^{*}$ of system (4) is asymptotically stable when ${\tau }_1\in [0,{\overline{\tau }}_{10})$.

(2)

For ${\tau }_2\in [0,{\overline{\tau }}_{20})$, system (4) undergoes a Hopf-like bifurcation at the tumor-present equilibrium $E^{*}$ near ${\tau }_1={\overline{\tau }}_{10}$.

Similarly, we can alternate the selection of bifurcation parameters and choose ${\tau }_2$ as the bifurcation parameter to discuss the bifurcation of system (4). No more detailed information will be provided here.

4. Numerical Results

This section provides a typical numerical example to illustrate the validity of our theoretical results. In this example, we use time delays as the bifurcation parameter to examine the dynamical behavior of system (4). The simulation results all are based on the Adama–Bashforth–Moulton predictor-corrector scheme [26] and step-length $h=0.01$. To facilitate comparison, we consider system (4) with $\alpha =0.3$, $\beta =0.6$, $\delta =10$, and $\gamma =3.5$, which are taken from the literature [14]. As a result, system (4) takes the following form:

$$\left\{\begin{array}{l}{D}^{p_1}x\left(t\right)=-x\left(t\right)+\frac{y\left(t\right)z\left(t\right)}{1+z\left(t\right)},\\ D^{p_2}y\left(t\right)=0.3x\left(t-{\tau }_1\right)-0.6y\left(t\right)+3.5,\\ D^{p_3}z\left(t\right)=10z\left(t-{\tau }_2\right)-y\left(t\right)z\left(t\right).\end{array}\right.$$

(38)

The positive tumor-present equilibrium point of system (38) is $E^{*}=(8.3333,10,5)$. To investigate the influence of time delays on the dynamic characteristics of system (38), we need to establish the bifurcation point. In general, we set $p_1=0.97$, $p_2=0.98$, and $p_3=0.99$ in system (38).

Case 1:

In this case, we can derive that the critical frequency ${\omega }_0$ and the bifurcation point ${\tau }_0^1$ are 0.4811 and 0.3825, respectively. Hence, it follows from Theorem 1 that the positive tumor-present equilibrium point $E^{*}$ is asymptotically stable provided ${\tau }_1=0.1<{\tau }_0^1$, as is shown in Figure 1. On the other hand, when ${\tau }_1$ is increased to pass ${\tau }_0^1$, $E^{*}$ loses its stability and a Hopf-like bifurcation occurs. For example, when ${\tau }_1=1>{\tau }_0^1$ the positive tumor-present equilibrium point $E^{*}$ is unstable, as is illustrated in Figure 2.

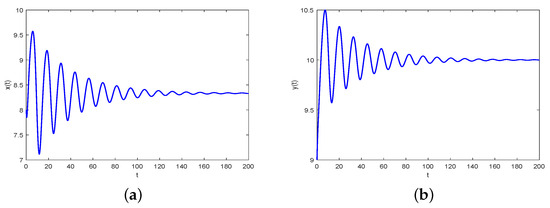
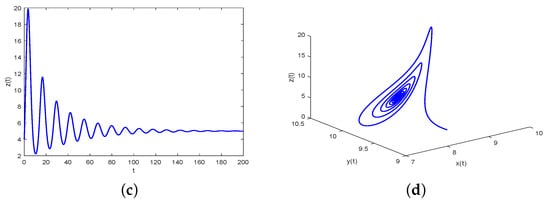Figure 1. Waveform plots and phase portrait of system (38) with ${\tau }_1=0.1$ and fixed ${\tau }_2=0$. (a) represents waveform plot of $x\left(t\right)$ for system (38). (b) represents waveform plot of $y\left(t\right)$ for system (38). (c) represents waveform plot of $z\left(t\right)$ for system (38). (d) represents phase portrait of $x\left(t\right)$, $y\left(t\right)$ and $z\left(t\right)$ for system (38).

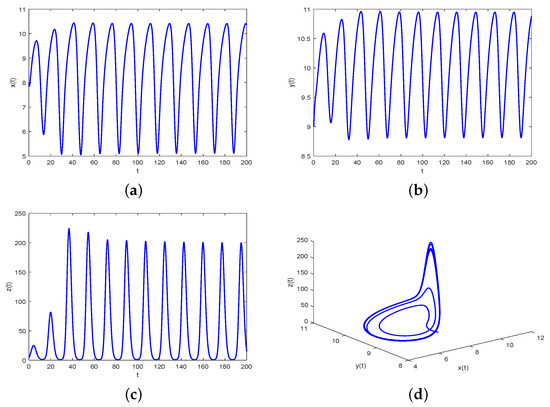Figure 2. Waveform plots and phase portrait of system (38) with ${\tau }_1=1$ and fixed ${\tau }_2=0$. (a) represents waveform plot of $x\left(t\right)$ for system (38). (b) represents waveform plot of $y\left(t\right)$ for system (38). (c) represents waveform plot of $z\left(t\right)$ for system (38). (d) represents phase portrait of $x\left(t\right)$, $y\left(t\right)$ and $z\left(t\right)$ for system (38).

Case 2:

We have that in Case 2 the critical frequency ${\omega }_0$ and the bifurcation point ${\tau }_0^2$ are 0.6478 and 0.0409, respectively. According to Theorem 2, when ${\tau }_2=0.02<{\tau }_0^2$ the positive tumor-present equilibrium point $E^{*}$ is asymptotically stable, as represented in Figure 3. On the flip side, as ${\tau }_2$ is increased to pass ${\tau }_0^2$, $E^{*}$ loses its stability and a Hopf bifurcation occurs. That is, when ${\tau }_2=10>{\tau }_0^2$ the positive tumor-present equilibrium point $E^{*}$ is unstable, which is displayed in Figure 4.

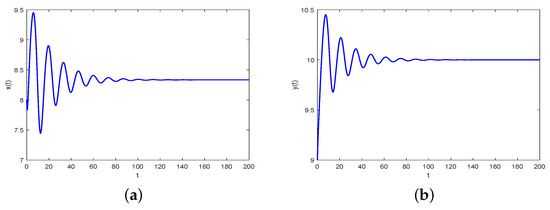
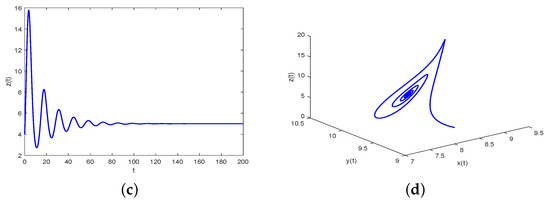Figure 3. Waveform plots and phase portrait of system (38) with ${\tau }_2=0.02$ and fixed ${\tau }_1=0$. (a) represents waveform plot of $x\left(t\right)$ for system (38). (b) represents waveform plot of $y\left(t\right)$ for system (38). (c) represents waveform plot of $z\left(t\right)$ for system (38). (d) represents phase portrait of $x\left(t\right)$, $y\left(t\right)$ and $z\left(t\right)$ for system (38).

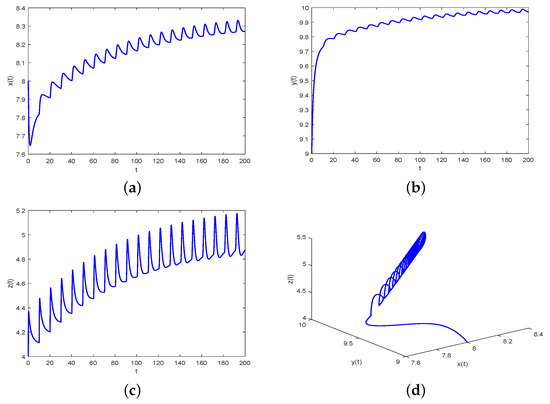Figure 4. Waveform plots and phase portrait of system (38) with ${\tau }_2=10$ and fixed ${\tau }_1=0$. (a) represents waveform plot of $x\left(t\right)$ for system (38). (b) represents waveform plot of $y\left(t\right)$ for system (38). (c) represents waveform plot of $z\left(t\right)$ for system (38). (d) represents phase portrait of $x\left(t\right)$, $y\left(t\right)$ and $z\left(t\right)$ for system (38).

Case 3:

Based on Equations (34) and (35), it is easy to obtain ${\overline{w}}_0=0.6479$ and ${\overline{\tau }}_{20}=0.0410$. Then, we choose ${\tau }_2=0.02\in [0,0.0410)$. Then, it is easy to find that the critical frequency ${\omega }_0$ and the bifurcation point ${\tau }_{10}$ are 0.4296 and 0.5956, respectively. Based on Theorem 3, the positive tumor-present equilibrium point $E^{*}$ is asymptotically stable when ${\tau }_1=0.1<{\tau }_{10}$, as revealed in Figure 5. Moreover, as ${\tau }_1$ is increased to pass ${\tau }_{10}$, $E^{*}$ loses its stability and a Hopf-like bifurcation occurs. For instance, the positive tumor-present equilibrium point $E^{*}$ is unstable when ${\tau }_1=1>{\tau }_{10}$, which is shown in Figure 6.

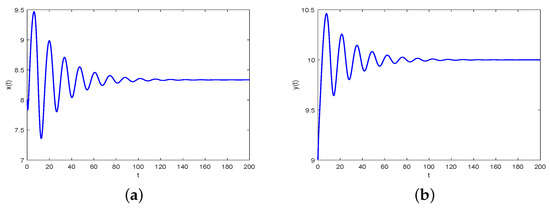
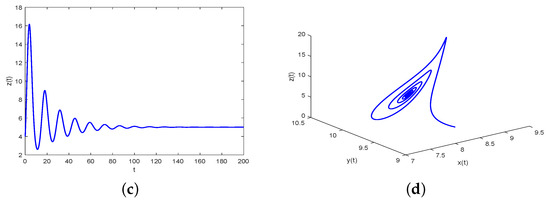Figure 5. Waveform plots and phase portrait of system (38) with ${\tau }_1=0.1<{\tau }_{10}=0.5956$. (a) represents waveform plot of $x\left(t\right)$ for system (38). (b) represents waveform plot of $y\left(t\right)$ for system (38). (c) represents waveform plot of $z\left(t\right)$ for system (38). (d) represents phase portrait of $x\left(t\right)$, $y\left(t\right)$ and $z\left(t\right)$ for system (38).

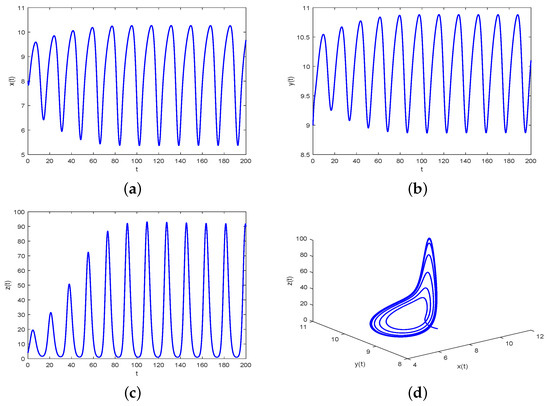Figure 6. Waveform plots and phase portrait of system (38) with ${\tau }_1=1>{\tau }_{10}=0.5956$. (a) represents waveform plot of $x\left(t\right)$ for system (38). (b) represents waveform plot of $y\left(t\right)$ for system (38). (c) represents waveform plot of $z\left(t\right)$ for system (38). (d) represents phase portrait of $x\left(t\right)$, $y\left(t\right)$ and $z\left(t\right)$ for system (38).

Further, considering $p_1=p_2=p_3=1$ in system (38), then system (38) clearly develops into the integer-order tumor-lymphatic model, and the critical frequency and bifurcation point can be obtained as ${\tilde{\omega }}_0=0.5841$ and ${\tilde{\tau }}_{10}=0.0239$, respectively. It is obvious that ${\tilde{\tau }}_{10}<{\tau }_{10}$, which implies that the onset of bifurcation can lag in system (38). Figure 7 indicates that the equilibrium point of system (38) is unstable and Hopf-like bifurcation occurs when choosing $p_1=p_2=p_3=1$. Figure 7 shows that system (38) has better stability performance than that of the corresponding integer-order ones for the same system parameters. It is not difficult to observe that fractional orders play an important role in postponing the onset of bifurcation for the developed system (38).

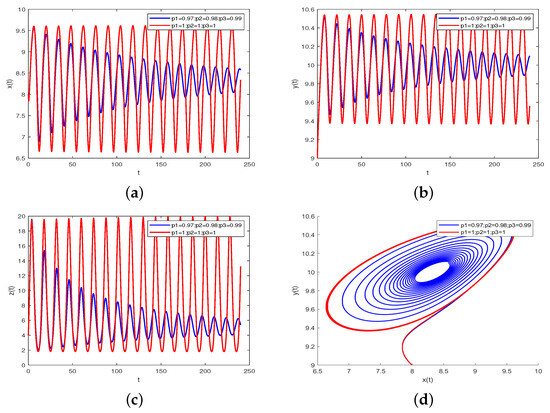
Figure 7. Comparison of convergence for system (38) with $p_1=0.97$, $p_2=0.98$, $p_3=0.99$, and ${\tau }_1=0.4<{\tau }_{10}=0.5956$ versus integer-order tumor-lymphatic model. (a) represents waveform plot of $x\left(t\right)$ for system (38). (b) represents waveform plot of $y\left(t\right)$ for system (38). (c) represents waveform plot of $z\left(t\right)$ for system (38). (d) represents phase portrait of $x\left(t\right)$, $y\left(t\right)$ and $z\left(t\right)$ for system (38).

5. Conclusions

Based on the tumor-lymphatic model proposed by Wang et al. [14], we have proposed the delayed fractional-order tumor-lymphatic model and conducted a thorough analysis of its dynamics. We explored the stability of the positive tumor-present equilibrium point in three different cases by considering two time delays as bifurcation parameters. Furthermore, we derived sufficient conditions for the occurrence of Hopf-like bifurcations within the model. Some numerical simulations have been carried out to confirm the validity and effectiveness of the developed results. The above research results can provide mathematical support for practical clinical research. However, there is a lack of extensive experimental data fitting, and its application to specific actual tumor models is still lacking. Therefore, in-depth research will be conducted on the above content in future work.