A Fast Method for the Off-Boundary Evaluation of Laplace Layer Potentials by Convolution Sums

Abstract

In off-boundary computations of layer potentials, the near-singularities in integrals near the boundary presents challenges for conventional quadrature methods in achieving high precision. Additionally, the significant complexity of $\mathcal{O}\left(n^2\right)$ interactions between n targets and n sources reduces the efficiency of these methods. A fast and accurate numerical algorithm is presented for computing the Laplace layer potentials on a circle with a boundary described by a polar curve. This method can maintain high precision even when evaluating targets located at a close distance from the boundary. The radial symmetry of the integral kernels simplifies their description. By exploiting the polar form of the boundary and applying a one-dimensional exponential sum approximation along the radial direction, an approximation of layer potentials by the convolution sum is obtained. The algorithm uses FFT convolution to accelerate computation and employs a local quadrature to maintain accuracy for nearly singular terms. Consequently, it achieves spectral accuracy in regions outside of a sufficiently small neighborhood of the boundary and requires $\mathcal{O}(nlogn)$ arithmetic operations. With the help of this algorithm, layer potentials can be efficiently evaluated on a computational domain.

1. Introduction

The boundary integral equation (BIE) method is attractive for addressing boundary value problems of partial differential equations (PDEs) like the Laplace equation [1,2], Helmholtz equation [3], biharmonic equation [4], and other classical elliptic equations in mathematical physics. It offers a number of numerically attractive properties, including reducing the dimension of the computational problem by one, enabling boundary-only discretizations for homogeneous problems, and being well-suited for problems involving infinite or semi-infinite domains. Moreover, the BIE method is widely applied in physics and engineering, including inverse acoustic and electromagnetic scattering problems [3], multi-media elasticity problems [5], wetting problems [6], Navier–Stokes equations [7,8], etc.

The BIE method seems to have less advantage in accuracy and computational complexity when it recovers the solutions of boundary value problems from the BIE solutions, requiring the evaluation of layer potentials both near and away from the source layer. This off-boundary evaluation, particularly with complex boundaries, presents two numerical challenges: 1. The accuracy of conventional quadrature methods diminishes rapidly as the target point approaches the boundary due to the near-singularity of boundary integrals. 2. There is significant computing complexity for the $\mathcal{O}\left(n^2\right)$ interactions between n targets and n sources. To address the computational challenges posed by nearly singular integrals, many innovative computational methods have been proposed. These methods include quadrature by expansion [9,10,11,12], asymptotic approximation methods [13,14,15], barycentric-type formulas leveraging Cauchy’s integral formula [16,17], singularity swapping methods [18,19], kernel regularization methods [20,21], a method using the Stokes theorem [22], nonlinear transformation methods [23,24], etc. However, due to the reliance of computations on target points, most of these methods are rarely developed into fast methods that are capable of facilitating the evaluation of $\mathcal{O}\left(n^2\right)$ interactions in linear or quasi-linear (linear up to a logarithmic factor) time. The scheme based on coupling quadrature by expansion and a fast multipole method [25,26] is one such fast algorithm that is capable of accurately computing layer potentials near boundaries. Nevertheless, in order to overcome extra geometry refinement, this scheme needs to be carefully designed in cases for which some parts of the source geometry come so close to other parts that they almost touch each other [25].

In this paper, we propose a fast and accurate numerical algorithm for computing the layer potentials for Laplace equations. This method requires only quasi-linear computational costs and still achieves high precision in regions that exclude a sufficiently small neighborhood of the boundary. Moreover, it permits discontinuities of layer potentials in the field across the boundary and is capable of handling cases for which some parts of the source geometry are close to other parts without too much additional work. Consider the surface integral operator $\mathcal{A}:L^2\left({\mathsf{\Gamma }}_1\right)\to L^2\left({\mathsf{\Gamma }}_2\right)$ defined by

$$\mathcal{A}f\left(\mathbf{x}\right):={\int }_{{\mathsf{\Gamma }}_1}K(\mathbf{x},\mathbf{y})f\left(\mathbf{y}\right)\mathrm{d}{s}_{\mathbf{y}},\mathbf{x}\in {\mathsf{\Gamma }}_2,$$

(1)

where ${\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2\subset {\mathbb{R}}^2$ are simple closed curves and are of class ${\mathcal{C}}^2$, $f\in L^2\left({\mathsf{\Gamma }}_1\right)$ is a density function, and K is defined and continuous for all $\mathbf{x}\in {\mathsf{\Gamma }}_2,\mathbf{y}\in {\mathsf{\Gamma }}_1,\mathbf{x}\ne \mathbf{y}$. Many numerical applications of boundary integral equation methods require the computation of $\mathcal{A}f$. For instance, solutions to boundary integral equations are frequently used to evaluate single- and double-layer potentials for applications in a broad range of simulations in physics and engineering. In addition, the application of Tikhonov regularization to solve boundary value problems using potentials with densities on curves different from the actual boundary of the underlying domain also necessitates the evaluation of $\mathcal{A}f$ [1]. For cases wherein ${\mathsf{\Gamma }}_1$ is a closed polar curve and ${\mathsf{\Gamma }}_2$ is an origin-centered circle, two algorithm are presented in this paper. Notice that the integral kernel K for Laplace equations in (1) can be expressed as a product of a singular part and a finite sum of separable functions. In order to construct a fast method, we concentrate on approximating the singular part using convolution sums. Due to the radial symmetry of the singular part, this only requires approximation along the radial direction. By utilizing the polar form of ${\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2$ and applying exponential sum approximations to the singular part along the radial direction [27], we derive an efficient approximation using convolution sums. An error estimate for this approximation is provided in this paper. Leveraging this efficient approximation, we propose algorithms for computing the layer potentials for Laplace equations with a computational complexity of $\mathcal{O}(nlogn)$ for the evaluation of $\mathcal{O}\left(n^2\right)$ interactions. Currently, there are few fast layer methods capable of accurately computing potentials near boundaries, among which an important one is the fast QBX method [25,26]. Our proposed method also efficiently handles such cases. Unlike the fast QBX, our method does not require handling of the boundary partition. As noted in the summary of [25], some situations, such as when some parts of the source geometry come close to other parts, often require extra geometry refinement. Our method effectively addresses such cases. Moreover, this method accommodates discontinuities in the field across the boundary, which is a feature that is not commonly addressed by existing methods.

The structure of this paper is as follows. Section 2 introduces the approximation of $\mathcal{A}f$ by convolution sums and provides an analysis of the approximation error. We then propose two algorithms based on the approximation. Subsequently, in Section 3, we present some numerical experiments to examine the performance of the algorithms. Finally, we provide conclusions about the proposed methods and discuss their drawbacks in Section 4.

2. Fast Methods for the Evaluation of Layer Potentials

The kernel K of the integral (1) can be expressed as

$$K(\mathbf{x},\mathbf{y})=\psi (\mathbf{x},\mathbf{y})\varphi \left({\left|\mathbf{x}-\mathbf{y}\right|}^2\right).$$

(2)

In the context of certain layer potentials, such as those for the Laplace, biharmonic, and Stokes equations [1,4,28], the function $\psi :{\mathsf{\Gamma }}_2\times {\mathsf{\Gamma }}_1\to \mathbb{C}$ can be represented as a finite sum of separable functions. Specifically, $\psi (\mathbf{x},\mathbf{y})={\sum }_{k=1}^{N_{\psi }}{\psi }_k\left(\mathbf{x}\right){\tilde{\psi }}_k\left(\mathbf{y}\right)$. Additionally, the function $\varphi :(0,\infty )\to \mathbb{R}$ is a logarithmic function satisfying

$$\varphi \left(\alpha x\right)=\varphi \left(x\right)+\varphi \left(\alpha \right),$$

or $\varphi$ is homogeneous of $\gamma \in \mathbb{R}$; meaning that for all $\alpha >0$,

$$\varphi \left(\alpha x\right)={\alpha }^{\gamma }\varphi \left(x\right),$$

or $\varphi$ is a linear combination of a logarithmic function, a homogeneous function, and their products, as is the case for the biharmonic equation [4]. In the case of the Laplace equation, the kernel for the single-layer potential can be expressed as (2), with $\psi (\mathbf{x},\mathbf{y})\equiv 1$ and $\varphi \left(x\right)=-\frac{1}{4\pi }logx$. Similarly, the kernel for the double-layer potential can also be represented as (2), with $\psi (\mathbf{x},\mathbf{y})=(\mathbf{y}-\mathbf{x})·\mathbf{v}\left(\mathbf{y}\right)$, and $\varphi \left(x\right)=-\frac{1}{2\pi x}$, where $\mathbf{v}\left(\mathbf{y}\right)$ is the unit outer normal vector perpendicular to the curve ${\mathsf{\Gamma }}_1$ at $\mathbf{y}$. To handle other kernels for equations like the Helmholtz equation [3,9], the singularity subtraction method is often used. This involves splitting the kernel into two parts: $K_1$, which has the same leading-order singularity as K, and a smoother function $K-K_1$, which is easier to integrate numerically. The singular kernel $K_1$ often has the form (2). In this paper, we focus on the evaluation of the single- and double-layer potentials for the Laplace equation.

In the subsequent sections of this paper, we suppose that ${\mathsf{\Gamma }}_1$ in (1) is a boundary of a star domain and is described by the parametrization

$$\mathbf{r}\left(t\right):=(r\left(t\right)cos\left(t\right),r\left(t\right)sin\left(t\right)),t\in I_{2\pi }:=[0,2\pi ),$$

(3)

where r is a twice-differentiable, $2\pi$-periodic, positive function defined on $\mathbb{R}$. We suppose that ${\mathsf{\Gamma }}_2$ in (1) is a circle with a radius $R>0$ defined by

$${\mathbf{c}}_R\left(t\right):=(Rcos\left(t\right),Rsin\left(t\right)),t\in I_{2\pi }.$$

(4)

The assumption of polar parameterization is made here to enable the squared distance function to take a form that closely resembles a convolution, as expressed in (5). This form of the squared distance function is used to construct the layer potential in the form of convolution sums, with $\varphi$ approximated by exponential sums. With the parametrizations (3) and (4), let us define

$$\mathcal{A}f\left(\eta \right):=\mathcal{A}f\left({\mathbf{c}}_R\left(\eta \right)\right)={\int }_{I_{2\pi }}K({\mathbf{c}}_R\left(\eta \right),\mathbf{r}\left(\theta \right))\tilde{f}\left(\theta \right)\mathrm{d}\theta ,\eta \in I_{2\pi },$$

where $\tilde{f}\left(\theta \right):=f\circ \mathbf{r}\left(\theta \right)\left|{\mathbf{r}}^{\prime }\left(\theta \right)\right|,\theta \in I_{2\pi }$. To ensure clarity, we adopt this definition of $\mathcal{A}:L^2\left({\mathsf{\Gamma }}_1\right)\to L^2\left(I_{2\pi }\right)$ throughout the subsequent discussions. It is important to note that when ${\mathsf{\Gamma }}_1\cap {\mathsf{\Gamma }}_2=\varnothing$, meaning that the targets are distant from the sources, the layer potential $\mathcal{A}f$ is smooth. However, due to the jump relations of the layer potential across the boundary, when ${\mathsf{\Gamma }}_1\cap {\mathsf{\Gamma }}_2\ne \varnothing$, $\mathcal{A}f$ is not smooth. Specifically, in the case of the Laplace single-layer potential, the derivative of $\mathcal{A}f$ is discontinuous at the intersection of ${\mathsf{\Gamma }}_1$ and ${\mathsf{\Gamma }}_2$, and in the case of the Laplace double-layer potential, $\mathcal{A}f$ itself is discontinuous at the intersection [1].

2.1. An Approximation of $\mathcal{A}f$ by Convolution Sums

In this subsection, we propose an approximation of $\mathcal{A}f$ by convolution sums, which regularizes $\mathcal{A}f$ and is utilized in the development of a fast algorithm in the next subsection. With the parametrizations (3) and (4), we write the square of the distance function between the points at ${\mathsf{\Gamma }}_1$ and ${\mathsf{\Gamma }}_2$ as

$$d(\eta ,\theta ):={\left|{\mathbf{c}}_R\left(\eta \right)-\mathbf{r}\left(\theta \right)\right|}^2={(R-r\left(\theta \right))}^2+4Rr\left(\theta \right){sin}^2\left(\frac{\eta -\theta }{2}\right).$$

(5)

In order to utilize the exponential sum approximation described in the following content, we rewrite $d(\eta ,\theta )$ as

$$d(\eta ,\theta )=d_{1,\beta }(\eta ,\theta )d_{2,\beta }\left(\theta \right),$$

where

$$d_{1,\beta }(\eta ,\theta )=\frac{{\left|{\mathbf{c}}_R\left(\eta \right)-\mathbf{r}\left(\theta \right)\right|}^2}{d_{2,\beta }\left(\theta \right)}=\frac{{(R-r\left(\theta \right))}^2}{\beta Rr\left(\theta \right)}+\frac{4}{\beta }{sin}^2\left(\frac{\eta -\theta }{2}\right),\mathrm{and}{d}_{2,\beta }\left(\theta \right)=\beta Rr\left(\theta \right),$$

with $\beta >0$ denoting a scale parameter.

For the case of the Laplace single-layer potential, from $\psi =1$ and $\varphi \left(x\right)=-\frac{1}{4\pi }logx$ in (2), it follows that

$$\mathcal{A}f\left(\eta \right)={\int }_{I_{2\pi }}\varphi \circ d_{1,\beta }(\eta ,\theta )\tilde{f}\left(\theta \right)\mathrm{d}\theta +{\int }_{I_{2\pi }}\varphi \circ d_{2,\beta }\left(\theta \right)\tilde{f}\left(\theta \right)\mathrm{d}\theta .$$

(6)

According to Appendix A.1, the function $\varphi$ can be approximated by M-term exponential sums on $[1,\infty )$. This approximation is based on the techniques described in [27] and is given by

$${\varphi }_M\left(x\right)=\sum _{k=0}^M{c}_k{e}^{-a_{k}x}-b_M,$$

(7)

where $a_k,b_k,c_k\in \mathbb{R}$, $a_0=log2$, and $a_k>0$ decreases with respect to k. Selecting an appropriate $\beta$ and replacing $\varphi$ in the first term on the right-hand side of (6) with ${\varphi }_M$ yields the approximation for the Laplace single-layer potential:

$${\mathcal{S}}_{M,\beta }f\left(\eta \right):={\int }_{I_{2\pi }}{\varphi }_M\circ d_{1,\beta }(\eta ,\theta )\tilde{f}\left(\theta \right)\mathrm{d}\theta +{\int }_{I_{2\pi }}\varphi \circ d_{2,\beta }\left(\theta \right)\tilde{f}\left(\theta \right)\mathrm{d}\theta .$$

(8)

The first term on the right-hand side of (8) can be represented as a sum of periodic convolutions, and this approximation is expressed as follows:

$${\mathcal{S}}_{M,\beta }f=\sum _{k=0}^M{c}_k{\mu }_{k,\beta }\ast \left({\omega }_{k,\beta }\tilde{f}\right)+{\mathcal{I}}_{M,\beta }\tilde{f},$$

where

$${\mu }_{k,\beta }\left(\theta \right):=e^{-\frac{a_k}{\beta }4{sin}^2\left(\frac{\theta }{2}\right)},{\omega }_{k,\beta }\left(\theta \right):=e^{-\frac{a_k}{\beta }\frac{{(R-r\left(\theta \right))}^2}{Rr\left(\theta \right)}},$$

(9)

and

$${\mathcal{I}}_{M,\beta }\tilde{f}:={\int }_{I_{2\pi }}\left(\varphi \circ d_{2,\beta }\left(\theta \right)-b_M\right)\tilde{f}\left(\theta \right)\mathrm{d}\theta .$$

For the case of the Laplace double-layer potential, from $\psi (\mathbf{x},\mathbf{y})=(\mathbf{y}-\mathbf{x})·\mathbf{v}\left(\mathbf{y}\right)$ and $\varphi \left(x\right)=-\frac{1}{2\pi x}$, it follows that   

$$\mathcal{A}f\left(\eta \right)={\int }_{I_{2\pi }}\varphi \circ d_{1,\beta }(\eta ,\theta )\mathbf{n}\left(\theta \right)·\mathbf{r}\left(\theta \right)\tilde{f}\left(\theta \right)/d_{2,\beta }\left(\theta \right)\mathrm{d}\theta$$

(10)

$$-{\mathbf{c}}_R\left(\eta \right)·{\int }_{I_{2\pi }}\varphi \circ d_{1,\beta }(\eta ,\theta )\mathbf{n}\left(\theta \right)\tilde{f}\left(\theta \right)/d_{2,\beta }\left(\theta \right)\mathrm{d}\theta ,$$

where $\mathbf{n}\left(\theta \right):=\mathbf{v}\left(\mathbf{r}\right(\theta \left)\right)$. Here, the function $\varphi$ can be approximated by M-term exponential sums:

$${\varphi }_M\left(x\right)=\sum _{k=0}^M{\tilde{c}}_k{e}^{-a_{k}x},$$

(11)

on $[1,\infty )$, where $a_k,{\tilde{c}}_k$ are defined in Appendix A.2. Similar to the evaluation method employed for the Laplace single-layer potential, replacing $\varphi$ in (10) with ${\varphi }_M$ gives

$${\mathcal{D}}_{M,\beta }f\left(\eta \right):={\int }_{I_{2\pi }}{\varphi }_M\circ d_{1,\beta }(\eta ,\theta )\mathbf{n}\left(\theta \right)·\mathbf{r}\left(\theta \right)\tilde{f}\left(\theta \right)/d_{2,\beta }\left(\theta \right)\mathrm{d}\theta$$

$$+{\mathbf{c}}_R\left(\eta \right)·{\int }_{I_{2\pi }}{\varphi }_M\circ d_{1,\beta }(\eta ,\theta )\mathbf{n}\left(\theta \right)\tilde{f}\left(\theta \right)/d_{2,\beta }\left(\theta \right)\mathrm{d}\theta .$$

The function ${\mathcal{D}}_{M,\beta }f$ can be rewritten as

$${\mathcal{D}}_{M,\beta }f=\sum _{k=0}^M{\tilde{c}}_k{\mu }_{k,\beta }\ast \left({\omega }_{k,\beta }{\tilde{f}}_1\right)-{\mathbf{c}}_R·\sum _{k=0}^M{\tilde{c}}_k{\mu }_{k,\beta }\ast \left({\omega }_{k,\beta }{\tilde{\mathbf{f}}}_2\right),$$

where ${\tilde{f}}_1:=\mathbf{n}·\mathbf{r}\tilde{f}/d_{2,\beta },{\tilde{\mathbf{f}}}_2:=\mathbf{n}\tilde{f}/d_{2,\beta }$, and ${\mu }_{k,\beta },{\omega }_{k,\beta }$ are defined in (9). Notice that in higher dimensions, the principal singularity of the Laplace layer potential remains radially symmetric. Therefore, it suffices to work with exponential approximations of $\varphi$ to develop higher-dimensional convolution approximations.

For convenience, we denote the operator ${\mathcal{A}}_{M,\beta }={\mathcal{S}}_{M,\beta }$ for the Laplace single-layer potential and ${\mathcal{A}}_{M,\beta }={\mathcal{D}}_{M,\beta }$ for the Laplace double-layer potential. It is noteworthy that ${\mathcal{A}}_{M,\beta }f$ exhibits smoothness and approximates $\mathcal{A}f$ notably well at points distant from ${\mathsf{\Gamma }}_1$. The parameter M controls the accuracy of approximation, while $\beta$ determines the distance from ${\mathsf{\Gamma }}_1$ for approximating $\mathcal{A}f$. Hence, ${\mathcal{A}}_{M,\beta }f$ serves as regularization for $\mathcal{A}f$ and is governed by the parameters M and $\beta$. In Section 2.3 and Section 2.4, we propose methods for computing ${\mathcal{A}}_{M,\beta }f$. Preceding that, in the upcoming section, we estimate the error between ${\mathcal{A}}_{M,\beta }f$ and $\mathcal{A}f$, which is referred to as the smoothing error in this paper.

2.2. The Smoothing Error

In this section, we estimate the smoothing error $\parallel \mathcal{A}f-{\mathcal{A}}_{M,\beta }{f\parallel }_{\infty ,\lambda },$ where ${\parallel g\parallel }_{\infty ,\lambda }:={sup}_{\mathbf{x}\in {\mathsf{\Gamma }}_2\setminus {\mathsf{\Gamma }}_{1,\lambda }}\left|g\left(\mathbf{x}\right)\right|$ for a piecewise continuous function g defined on ${\mathsf{\Gamma }}_2$, ${\mathsf{\Gamma }}_{1,\lambda }:=\{\mathbf{x}:|\mathbf{x}-\mathbf{y}|<\lambda ,\mathbf{y}\in {\mathsf{\Gamma }}_1\}$, $\beta \in \left(0,\frac{{\lambda }^2}{R{r}_{max}}\right]$ with some $\lambda >0$ in (8), and $r_{max}:={max}_{\theta \in I_{2\pi }}r\left(\theta \right)$. In order to present the smoothing error estimate, we define $r_{min}:={min}_{\theta \in I_{2\pi }}r\left(\theta \right)$ and introduce the notation ${∥g∥}_{\infty ,H}:={sup}_{x\in H}\left|g\left(x\right)\right|,H\subset [1,\infty ),$ for a continuous function g defined on $[1,\infty )$. The next two theorems present the smoothing error estimate for the Laplace single- and double-layer potentials. The proofs of these theorems are in Appendix B.

Theorem 1.

In the case of the Laplace single-layer potential, there exist positive constants $C_1,C_2$ such that for all $\lambda ,R>0$, $M\in {\mathbb{Z}}^{+}$ and $f\in L^2\left({\mathsf{\Gamma }}_1\right)$, by choosing $h=log\left(4\pi M\right)/M$ and $\beta \in \left(0,\frac{{\lambda }^2}{R{r}_{max}}\right]$,

$$\parallel \mathcal{A}f-{\mathcal{S}}_{M,\beta }{f\parallel }_{\infty ,\lambda }\le \left(C_1\iota exp\left(-\frac{{\pi }^{2}M}{log\left(3\iota \right)log\left({\pi }^{2}M\right)}\right)+\right.$$

$$\left.\left(2^{-s}-{\left(1+e^{sinh(log(4\pi M\left)\right)}\right)}^{-s}\right)/(4\pi slog2)+C_{2}s{2}^{-s}log{\left(4\pi M\right)}^2/M\right){∥f∥}_1,$$

(12)

where $s={\lambda }^2/\left(\beta R{r}_{max}\right),\iota ={(R+r_{max})}^2/\left(\beta R{r}_{min}\right)$.

Theorem 2.

In the case of the Laplace double-layer potential, there exist positive constants $C_1,C_2$ such that for all $\lambda ,R>0$, $M\in {\mathbb{Z}}^{+}$ and $f\in L^2\left({\mathsf{\Gamma }}_1\right)$, by choosing $h=log\left(4\pi M\right)/M$ and $\beta \in \left(0,\frac{{\lambda }^2}{R{r}_{max}}\right]$,

$$\parallel \mathcal{A}f-{\mathcal{D}}_{M,\beta }{f\parallel }_{\infty ,\lambda }\le \left(C_{1}exp\left(-\frac{{\pi }^{2}M}{log\left(3\iota \right)log\left({\pi }^{2}M\right)}\right)+\right.$$

$$\left.\left(2^{-s}-{\left(1+e^{sinh(log(4\pi M\left)\right)}\right)}^{-s}\right)/\left(2\pi s\right)+C_{2}s{2}^{-s}log{\left(4\pi M\right)}^2/M\right)\tau {∥f∥}_1,$$

(13)

where $s={\lambda }^2/\left(\beta R{r}_{max}\right),\iota ={(R+r_{max})}^2/\left(\beta R{r}_{min}\right),\tau ={max}_{x\in I_{2\pi }}\left|{\mathbf{r}}^{\prime }\left(x\right)\right|\left(1/R+1/r_{min}\right)/\beta$.

Theorems 1 and 2 indicate that the smoothing error of ${\mathcal{A}}_{M,\beta }f$ decreases exponentially on ${\mathsf{\Gamma }}_2\setminus {\mathsf{\Gamma }}_{1,\lambda }$ as the parameters M and $\beta$ increase. In these theorems, the selection strategy of h is based on the Sinc quadrature error estimates from Proposition 2.1 in [27], ensuring the exponential decay of the smoothing error with M. Notice that the second term on the right-hand side of (12) and (13) depends on s, and $s={\lambda }^2/\left(\beta R{r}_{max}\right)$. Selecting a sufficiently small $\beta$ ensures this second term becomes negligible. We choose $\beta ={\lambda }^2/\left(50R{r}_{max}\right)$ to ensure $2^{-s}=2^{-50}\approx 8.9\times {10}^{-16}$, nearly reaching double precision relative to the machine epsilon. Thus, the second term on the right-hand side of (12) and (13) can be ignored relative to the first term within machine precision. The choice of $\beta$ also determines $\iota =50{(R+r_{max})}^2{r}_{max}/\left({\lambda }^2{r}_{min}\right)$, which increases as $\lambda$ decreases. Thus, in order to ensure that the first term on the right-hand side of (12) and (13) is sufficiently small, an appropriate value of M needs to be found based on $\iota$. Theorem 1 suggests that selecting $M=C(log\iota )+{(log\iota )}^2$ with a positive constant C ensures the smoothing error in cases for which the single-layer potential remains bounded regardless of $\iota$ and $\lambda$. In addition, Theorem 2 suggests $M=C(log\iota )$ for the double-layer potential. In summary, in this paper, we select $\beta ={\lambda }^2/\left(50R{r}_{max}\right),M=-C_s(log\beta )+{(log\beta )}^2$ for the single-layer potential and $M=-C_d(log\beta )$ for the double-layer potential, where $C_s,C_d>0$.

2.3. A Method for Computing ${\mathcal{A}}_{M,\beta }f$ Using FFT Convolution

The function ${\mathcal{A}}_{M,\beta }f$, introduced in Section 2.1 for both the single- and double-layer potential cases, takes the form

$${\mathcal{A}}_{M,\beta }f=\mathbf{C}·\left(\sum _{k=0}^M{w}_k{\mu }_{k,\beta }\ast \left({\omega }_{k,\beta }\mathbf{g}\right)\right)+B_{M,\beta },$$

(14)

with $\mathbf{C}=\left[1\right],w_k=c_k,\mathbf{g}=\left[\tilde{f}\right],B_{M,\beta }={\mathcal{I}}_{M,\beta }\tilde{f}$ for the Laplace single potential, and $\mathbf{C}=[1,-{\mathbf{c}}_R],w_k={\tilde{c}}_k,\mathbf{g}=[{\tilde{f}}_1,{\tilde{\mathbf{f}}}_2],B_{M,\beta }=0$ for the Laplace double potential. Notice that ${\mathcal{A}}_{M,\beta }f$ consists of a periodic convolution sum. It is well known that applying the FFT convolution method leads to a fast evaluation of ${\mathcal{A}}_{M,\beta }f$.

Denote ${\mathbb{Z}}_k:=\{0,1\dots ,k-1\},k\in {\mathbb{Z}}^{+}$. Given $n\in {\mathbb{Z}}^{+}$, the values of $\mathbf{r}$ and $|{\mathbf{r}}^{\prime }|$ on $I_{2\pi ,n}:=\{2k\pi /n:k\in {\mathbb{Z}}_n\},$ and the values of the density function on ${\mathbf{S}}_n:=\{\mathbf{r}\left({\theta }_k\right):{\theta }_k\in I_{2\pi ,n}\}.$ We now present a fast algorithm for computing the values of ${\mathcal{A}}_{M,\beta }f$ on ${\mathbf{T}}_{R,n}:=\{{\mathbf{c}}_R\left({\theta }_k\right):{\theta }_k\in I_{2\pi ,n}\},$ with a radius $R>0$.

We next present an estimate of the computational costs of Algorithm 1. Let ${\mathcal{M}}_{M,n}$ denote the number of multiplications used in Algorithm 1.

Algorithm 1 1An algorithm for computing ${\mathcal{A}}_{M,\beta }f$ using n-point FFT convolution.

Input: $M,n\in {\mathbb{Z}}^{+},\beta ,R>0$, a function f on ${\mathbf{S}}_n$, and $\mathbf{r}$, $|{\mathbf{r}}^{\prime }|$ defined on $I_{2\pi ,n}$. Output: Approximate values of ${\mathcal{A}}_{M,\beta }f$ on ${\mathbf{T}}_{R,n}$. Step 1: Compute the periodic convolution of ${\mu }_{k,\beta }\ast \left({\omega }_{k,\beta }\mathbf{g}\right)\left({\mathbf{T}}_{R,n}\right)$ using the n-point FFT method, denoted as ${\mathbf{I}}_{k,\beta }\left({\mathbf{T}}_{R,n}\right)$ for $k=0,\dots ,M$. Step 2: Compute the integral $B_{M,\beta }$ using the n-point periodic trapezoidal rule. Step 3: Compute the approximate values of ${\mathcal{A}}_{M,\beta }f$ on ${\mathbf{T}}_{R,n}$ by $\mathbf{C}·{\sum }_{k=0}^M{w}_k{\mathbf{I}}_{k,\beta }\left({\mathbf{T}}_{R,n}\right)+B_{M,\beta }$.

Theorem 3.

There exists $C>0$ such that for all $M,n\in {\mathbb{Z}}^{+}$,

$${\mathcal{M}}_{M,n}\le CMn{log}_{2}n.$$

Proof. 

The number of multiplications used in Step 1 is bounded by $\mathcal{O}\left(Mn{log}_{2}n\right)$. The number of multiplications used in Step 2 is not greater than the amount of $\mathcal{O}\left(n\right)$. The number of multiplications used in Step 3 is bounded by $\mathcal{O}\left(Mn\right)$. Therefore, we obtain the $\mathcal{O}\left(Mn{log}_{2}n\right)$ upper bound on the total number of multiplications used in Algorithm 1.    □

Denote the output of Algorithm 1 as ${\mathcal{A}}_{M,\beta ,FFT}f\left({\mathbf{T}}_{R,n}\right)$. The computational error $\mathcal{A}f\left({\mathbf{T}}_{R,n}\right)-{\mathcal{A}}_{M,\beta ,FFT}f\left({\mathbf{T}}_{R,n}\right)$ comprises both the smoothing error and the error in convolution computation. We estimated the smoothing error in ${\mathsf{\Gamma }}_2\setminus {\mathsf{\Gamma }}_{1,\lambda }$ in Section 2.2. We turn to discuss the convolution error. The aliasing error of the discrete Fourier transform and the truncation error of the Fourier series contribute to the convolution error when using FFT. The decay rates of the coefficients of the Fourier series of ${\mu }_{k,\beta }$ and ${\omega }_{k,\beta }\mathbf{g}$ determine this convolution computation error. It is important to note that as $\beta$ decreases, the decay rates of ${\mu }_{k,\beta }$ and ${\omega }_{k,\beta }\mathbf{g}$ also decrease, as illustrated in Figure 1, indicating the near-singularity of the layer potential. This leads to a decrease in the accuracy of computing the convolution using the n-point FFT. Indeed, when $a_k/\beta$ is large, ${\mu }_{k,\beta }\left(x\right)\approx {\sum }_{j\in \mathbb{Z}}{G}_{a_k/\beta }(x+2j\pi )$ for $x\in \mathbb{R}$, where $G_{a_k/\beta }:=exp\left(-a_k{x}^2/\beta \right)$. According to the Fourier transform of $G_{a_k/\beta }$, the jth Fourier coefficient of ${\sum }_{j\in \mathbb{Z}}{G}_{a_k/\beta }(x+2j\pi )$ is $\sqrt{\beta /\left(2a_k\right)}exp\left(-\beta j^2/\left(4a_k\right)\right)$. Therefore, the Fourier coefficients of ${\mu }_{k,\beta }$ decay nearly as $\mathcal{O}\left(exp\left(-\beta j^2/\left(4a_k\right)\right)\right)$.

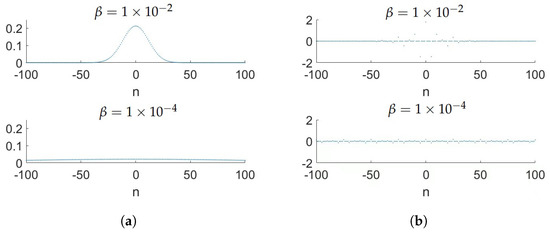
Figure 1. The Fourier coefficients of ${\mu }_{0,\beta }$ and ${\omega }_{0,\beta }$. The radius function of the boundary ${\mathsf{\Gamma }}_1$ is $r\left(t\right)=1+0.3cos\left(5t\right)$, and the target point is located at $(0.66,0.37)$, which is a distance of $6\times {10}^{-3}$ from the boundary. Top row: $\beta =1\times {10}^{-2}$. Bottom row: $\beta =1\times {10}^{-4}$. (a) The Fourier coefficients of ${\mu }_{0,\beta }$. (b) The Fourier coefficients of ${\omega }_{0,\beta }$.

2.4. An Improved Method for Computing ${\mathcal{A}}_{M,\beta }f$

In order to avoid inaccuracies in the computation of ${\mu }_{\sigma }\ast \left({\omega }_{\sigma }\mathbf{g}\right)$ in (14) using the FFT convolution method with very small $\beta$ values, we directly evaluate it using local quadrature methods. Let $g\in L^1\left(I_{2\pi }\right)$ and $\sigma \ge 0$. We define the periodic convolution as follows:

$${\mathcal{C}}_{\sigma }g:={\mu }_{\sigma }\ast \left({\omega }_{\sigma }g\right),$$

where

$${\mu }_{\sigma }\left(\theta \right):=e^{-4\sigma {sin}^2\left(\frac{\theta }{2}\right)},{\omega }_{k,\beta }\left(\theta \right):=e^{-\sigma \frac{{(R-r\left(\theta \right))}^2}{Rr\left(\theta \right)}},\theta \in \mathbb{R}.$$

The form (14) can be rewritten as

$${\mathcal{A}}_{M,\beta }f=\mathbf{C}·\left(\sum _{k=0}^M{w}_k{\mathcal{C}}_{\frac{a_k}{\beta }}\mathbf{g}\right)+B_{M,\beta }.$$

We now address the computation of ${\mathcal{C}}_{\sigma }g$ with large values of $\sigma$. Suppose ${\mathcal{C}}_{\sigma }g$ can be accurately computed using the FFT convolution method with $\sigma \le {\sigma }_0$ for a sufficiently large ${\sigma }_0$. Note that the function ${\mu }_{\sigma }$ exhibits a sharp peak at $\theta =0$ with a large $\sigma$. Thus, instead of the convolution method, we apply the Gauss quadrature to ${\mathcal{C}}_{\sigma }g$. For the machine epsilon $ϵ>0$, we define $C_{ϵ}:=2\sqrt{\sigma }arcsin\frac{\sqrt{-logϵ}}{2\sqrt{\sigma }}\approx \sqrt{-logϵ}$. This ensures ${\mu }_{\sigma }\left(\theta \right)<ϵ$ for $\theta \in [-\pi ,\pi ]\setminus [-C_{ϵ}/\sqrt{\sigma },C_{ϵ}/\sqrt{\sigma }]$. Here, we set $C_{ϵ}=6$ to make ${\mu }_{\sigma }$ on $[-\pi ,\pi ]\setminus [-C_{ϵ}/\sqrt{\sigma },C_{ϵ}/\sqrt{\sigma }]$ reach double precision. Neglecting the integral part of $[\eta -\pi ,\eta +\pi ]\setminus [\eta -C_{ϵ}/\sqrt{\sigma },\eta +C_{ϵ}/\sqrt{\sigma }]$ yields

$${\mathcal{C}}_{\sigma }g\left(\eta \right)\approx {\int }_{\eta -C_{ϵ}/\sqrt{\sigma }}^{\eta +C_{ϵ}/\sqrt{\sigma }}{\mu }_{\sigma }(\eta -\theta ){\omega }_{\sigma }\left(\theta \right)g\left(\theta \right)\mathrm{d}\theta .$$

Applying the m-point Gauss quadrature to the above integral, denoted by ${\mathcal{C}}_{\sigma }^{m}g\left(\eta \right)$, provides an evaluation of ${\mathcal{C}}_{\sigma }g\left(\eta \right)$. Here, the values of g at the quadrature points can be obtained by the Fourier interpolation from $g\left({\mathbf{S}}_n\right)$. This process can be accelerated by converting the Fourier interpolation to B-spline interpolation, allowing for the computation of the m quadrature points in linear time. We also write ${\mathcal{C}}_{\sigma }^{m}g\left(\mathbf{x}\right),\mathbf{x}={\mathbf{c}}_R\left(\eta \right)$ in place of ${\mathcal{C}}_{\sigma }^{m}g\left(\eta \right)$ for simplicity. Given a continuous function g and a point $\mathbf{x}$, ${\mathcal{C}}_{\sigma }g\left(\mathbf{x}\right)$ decays with respect to $\sigma$, as illustrated in Figure 2a. Figure 2b–d illustrate the relative error of the Gauss–Chebyshev quadrature against $\sigma$ with $25,40$, and 55 integral points, respectively. As the number of integral points increases, the relative error decreases. In addition, the relative error remains bounded within a certain range of $\sigma$, indicating that the absolute error decays with respect to $\sigma$. This demonstrates that ${\mathcal{C}}_{\sigma }g\left(\mathbf{x}\right)$ with a large $\sigma$ can be efficiently computed using the Gauss quadrature. Furthermore, due to the rapid decay of the integrand with a large $\sigma$, we neglect computing ${\mathcal{C}}_{\sigma }^{m}g$ at the points $\mathbf{x}$ in ${\mathsf{\Gamma }}_2$ such that $\mathrm{dist}(\mathbf{x},{\mathsf{\Gamma }}_1)>C_{ϵ}\sqrt{R{r}_{max}/\sigma }$ for the machine epsilon.

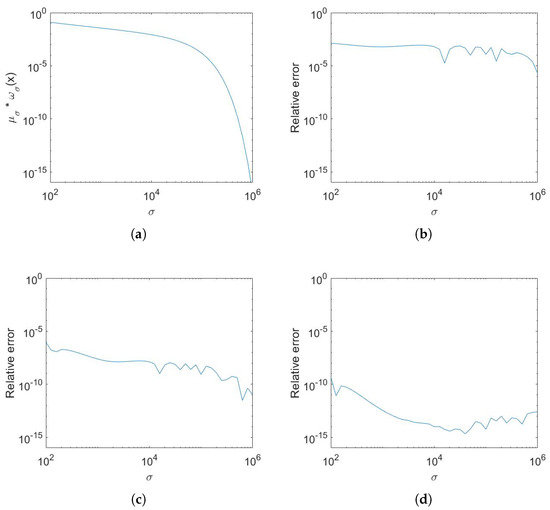
Figure 2. The values of ${\mu }_{\sigma }\ast {\omega }_{\sigma }(0.66,0.37)$ and the relative error of the Gauss–Chebyshev quadrature against $\sigma$. The radius function of the boundary ${\mathsf{\Gamma }}_1$ is $r\left(t\right)=1+0.3cos\left(5t\right)$, and the target point is at a distance of $6\times {10}^{-3}$ from the boundary. (a) The values of ${\mu }_{\sigma }\ast {\omega }_{\sigma }\left(\mathbf{x}\right),\mathbf{x}=(0.66,0.37)$. (b) The relative error of the 25-point Gauss quadrature. (c) The relative error of the 40-point Gauss quadrature. (d) The relative error of the 55-point Gauss quadrature.

Let $M_x\in \mathbb{Z}$ satisfy $a_{M_x}\le x<a_{M_x-1}$ if $x\in [a_M,a_0)$, and $M_x=0$ if $x\ge a_0$. The Algorithm 2 derived from the above discussion is as follows:

Algorithm 2 An algorithm using the n-point FFT convolution and the m-point Gauss quadrature.

Input: $M,m,n\in {\mathbb{Z}}^{+},\beta ,{\sigma }_0,R>0$, a function f on ${\mathbf{S}}_n$, and $\mathbf{r},|{\mathbf{r}}^{\prime }|$ defined on $I_{2\pi ,n}$. Output: Approximate values of ${\mathcal{A}}_{M,\beta }f$ on ${\mathbf{T}}_{R,n}$. Step 1: Compute the periodic convolution of ${\mathcal{C}}_{\frac{a_k}{\beta }}\mathbf{g}\left({\mathbf{T}}_{R,n}\right)$ using the n-point FFT method, denoted as ${\mathbf{I}}_{k,\beta }\left({\mathbf{T}}_{R,n}\right)$, for $k=M_{\beta {\sigma }_0},\dots ,M$. Step 2: Compute $Q_k^m\mathbf{g}\left({\mathbf{T}}_{R,n}\right)$ by the Gauss quadrature for $k=0,\dots ,M_{\beta {\sigma }_0}-1$, with $Q_k^m\mathbf{g}\left(\mathbf{x}\right)={\mathcal{C}}_{\frac{a_k}{\beta }}^m\mathbf{g}\left(\mathbf{x}\right)$ for $\mathbf{x}\in {\mathbf{T}}_{R,n}^{k,\beta }:=\left\{\mathbf{x}\in {\mathbf{T}}_{R,n}:\mathrm{dist}(\mathbf{x},{\mathsf{\Gamma }}_1)\le 6\sqrt{R{r}_{max}\beta /a_k}\right\}$ and $Q_k^m\mathbf{g}\left(\mathbf{x}\right)=0$ for $\mathbf{x}\in {\mathbf{T}}_{R,n}\setminus {\mathbf{T}}_{R,n}^{k,\beta }$. Step 3: Compute the integral $B_{M,\beta }$ using the n-point periodic trapezoidal rule. Step 4: Compute the approximate values of ${\mathcal{A}}_{M,\beta }f$ on ${\mathbf{T}}_{R,n}$ by $\mathbf{C}·\left({\sum }_{k=M_{\beta {\sigma }_0}}^M{w}_k{\mathbf{I}}_{k,\beta }\left({\mathbf{T}}_{R,n}\right)+{\sum }_{k=0}^{M_{\beta {\sigma }_0}-1}{w}_k{Q}_k^m\mathbf{g}\left({\mathbf{T}}_{R,n}\right)\right)+B_{M,\beta }$.

To close this section, we present an estimate of the computational costs of Algorithm 2. Let ${\mathcal{M}}_{M,m,n,\beta {\sigma }_0}^Q$ denote the number of multiplications used in Algorithm 2.

Theorem 4.

There exists $C>0$ such that for all $R,\beta ,{\sigma }_0>0$ and $M,m,n\in {\mathbb{Z}}^{+}$,

$${\mathcal{M}}_{M,m,n,\beta {\sigma }_0}^Q\le Cn\left((M-M_{\beta {\sigma }_0}){log}_{2}n+M_{\beta {\sigma }_0}\xi m\right),$$

where $\xi \in [0,1]$ satisfies $\left|{\mathbf{T}}_{R,\ell }^{k,\beta }\right|\le \xi \ell$ for all $k=0,\dots ,M_{\beta {\sigma }_0}-1$, $\ell \in {\mathbb{Z}}^{+}$.

Proof. 

The number of multiplications used in Step 1 is bounded by $\mathcal{O}\left((M-M_{\beta {\sigma }_0}+1)n{log}_{2}n\right)$. The number of multiplications used in Step 2 is not greater than $\mathcal{O}(M_{\beta {\sigma }_0}\xi mn+n{log}_{2}n)$. The number of multiplications used in Step 3 is bounded by $\mathcal{O}\left(n\right)$. The number of multiplications used in Step 4 is bounded by $\mathcal{O}((M-M_{\beta {\sigma }_0}+1)n+M_{\beta {\sigma }_0}\xi n)$. Therefore, we obtain the result. □

In the next section, the performances of the periodic trapezoidal rule and Algorithms 1 and 2 are presented. The periodic trapezoidal rule is a straightforward quadrature method to implement. This quadrature is exponentially accurate for computing real analytic functions [29]. Thus, it has high accuracy in computing layer potentials that are far from boundaries. However, when computing layer potentials near boundaries, the method converges very slowly due to the near-singularity of the integral. Additionally, its complexity is $\mathcal{O}\left(n^2\right)$ for computing interactions between n targets and n sources. Theorem 3 indicates that Algorithm 1 has a complexity of $\mathcal{O}(nlogn)$. However, as discussed in Section 2.3, the convolution error for the nearly singular terms leads to inaccuracy near the boundary, similar to the periodic trapezoidal rule. Algorithm 2 improves the accuracy near the boundary by using the local Gauss quadrature for the nearly singular terms instead of the FFT convolution method . Moreover, Theorem 4 indicates that Algorithm 2 still maintains a complexity of $\mathcal{O}(nlogn)$.

3. Numerical Experiments

In this section, we present illustrative examples demonstrating the performance of the methods by evaluating layer potentials using the proposed methods. We begin by presenting the results for double-layer potentials when ${\mathsf{\Gamma }}_1$ and ${\mathsf{\Gamma }}_2$ intersect, showing errors near the intersection points with the periodic trapezoidal rule (PTR) and Algorithms 1 and 2. We then investigate the performance of these algorithms when ${\mathsf{\Gamma }}_2$ is closed to ${\mathsf{\Gamma }}_1$. Finally, we employ these methods as components of an integral equation solver for Laplace Neumann boundary value problems. MATLAB (R2020a) is used for these implementations. All test computations are conducted on a PC equipped with a 3.6 GHz AMD Ryzen 5 3600 CPU and 32 GB memory.

The starfish curve of Figure 3a that we use for our numerical experiments is given by

$$\mathbf{r}\left(t\right)=(1+0.3cos\left(5t\right))\left(\begin{array}{c}cos\left(t\right)\\ sin\left(t\right)\end{array}\right),$$

(15)

and the limaçon of Figure 3b is given by

$$\mathbf{r}\left(t\right)=(10-(9+{10}^{-3})cos\left(t\right))\left(\begin{array}{c}cos\left(t\right)\\ sin\left(t\right)\end{array}\right).$$

(16)

In each case, $t\in I_{2\pi }$.

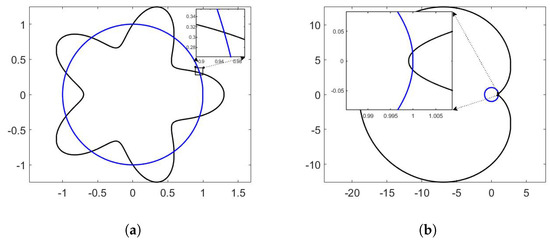
Figure 3. Test curves ${\mathsf{\Gamma }}_1$ (black) and ${\mathsf{\Gamma }}_2$ (blue). (a) A starfish curve (black) and a unit circle (blue). (b) A limaçon (black) and a unit circle (blue).

3.1. Double-Layer Potential Evaluation

The experiments with intersecting curves in Figure 3 and curves in close proximity in Figure 6a examine the performance of the proposed algorithm near the boundary ${\mathsf{\Gamma }}_1$. To this end, we employ these methods to compute the double-layer potential $\mathcal{D}{f}_d$ with a source function $f_d$. In order to derive an analytical expression of $\mathcal{D}{f}_d$ in the interior and exterior domains for result verification, we chose $f_d=1$ on ${\mathsf{\Gamma }}_1$, and the corresponding double-layer potential satisfies

$$\mathcal{D}{f}_d\left(\mathbf{x}\right)=\left\{\begin{array}{ccc}\hfill & -1,\hfill & \hfill \mathbf{x}\in \Omega ,\\ \hfill & -1/2,\hfill & \hfill \mathbf{x}\in {\mathsf{\Gamma }}_1,\\ \hfill & 0,\hfill & \hfill \mathbf{x}\in {\mathbb{R}}^2\setminus \overline{\Omega },\end{array}\right.$$

where $\Omega$ is the domain enclosed by ${\mathsf{\Gamma }}_1$.

The geometries of the first two examples with the boundaries described by (15) and (16) are shown in Figure 3. We compute ${10}^4$ equispaced points on the unit circle by employing n-point PTR and Algorithms 1 and 2, with $n={10}^4$. In Algorithms 1 and 2, we set $\beta ={\lambda }^2/\left(50R{r}_{max}\right),\lambda ={10}^{-3}$, and $M=⌈-40{log}_{10}\beta ⌉$ according to the analysis in Section 2.2. Here, the selection of $\lambda$ ensures the accuracy of the layer potentials at distances greater than ${10}^{-3}$ from the boundary. In addition, we select $m=55$ and ${\sigma }_0={10}^5$ in Algorithm 2. The parameter m determines the number of integral points for the local Gauss quadrature used to handle the nearly singular terms. The relative errors shown in Figure 2 indicate that $m=55$ is an appropriate choice, as the local quadrature error reaches double-precision. The ${\sigma }_0$ sets the range of $\sigma$ values at which the fast convolution method is employed to compute ${\mathcal{C}}_{\sigma }g$, as discussed in Section 2.4. A larger ${\sigma }_0$ means more terms are evaluated using the FFT convolution method, which can result in a loss of accuracy due to the near singularity of some convolution terms.

The first example presents the error of computing $\mathcal{D}{f}_d$ on a unit circle ${\mathsf{\Gamma }}_2$ with a starfish ${\mathsf{\Gamma }}_1$ in Figure 3a. For simplicity, we write $\tilde{\mathcal{D}}{f}_d\left(\eta \right),\eta \in \mathbb{R}$ instead of $\mathcal{D}{f}_d\left({\mathbf{c}}_1\left(\eta \right)\right)$. Figure 4a shows $\tilde{\mathcal{D}}{f}_d\left(\eta \right)$ for $\eta \in (0.09\pi ,0.11\pi )$. Note that the double-layer potential has a jump at $\eta =\pi /10$ since ${\mathsf{\Gamma }}_1$ and ${\mathsf{\Gamma }}_2$ intersect. Figure 4b–d illustrate the error of PTR and Algorithms 1 and 2, respectively, with $n={10}^4$. Algorithms 1 and 2 use the parameter setting discussed above. Compared to PTR and Algorithm 1, Algorithm 2 shows higher accuracy near the intersection point at $\eta =\pi /10$.

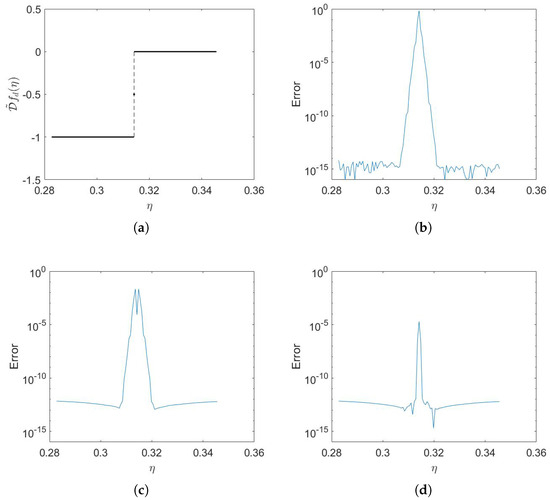
Figure 4. Double-layer potential evaluation at ${10}^4$ equispaced points on a unit circle with the starfish boundary described by (15). (a) The graph of $\tilde{\mathcal{D}}{f}_d$ on $(0.09\pi ,0.11\pi )$. (b) The ${10}^4$-point PTR. (c) Algorithm 1 with $n={10}^4,\beta =1.54\times {10}^{-8},M=312$. (d) Algorithm 2 with $m=55,n={10}^4,\beta =1.54\times {10}^{-8},M=312,{\sigma }_0={10}^5$.

The second example presents the results with a limaçon ${\mathsf{\Gamma }}_1$ in Figure 3b. The unit circle is inside the domain $\Omega$ except for a small segment near $(1,0)$. Note that the parts of limaç near $(1,0)$ are very close to each other, and some of the targets are inside the “slit”. Algorithms 1 and 2 use the same parameter settings as the first example. The graph of $\tilde{\mathcal{D}}{f}_d$ on $(-\pi /10,\pi /10)$ is shown in Figure 5a. This function is piecewise, with only a small region centered at 0 with a width of $2arccos(9/(10-0.999\left)\right)\approx 0.03$ being 0, while the remainder is $-1$ almost everywhere. Figure 5b,c show that the errors of PTR and Algorithm 1 are significant at the discontinuity points and are also not negligible in the central region. In comparison, Algorithm 2 computes accurately in the central region, though the error is still significant at the discontinuity points, as shown in Figure 5d. The computational results of this method can clearly distinguish the central region, with a width of only $0.03$.

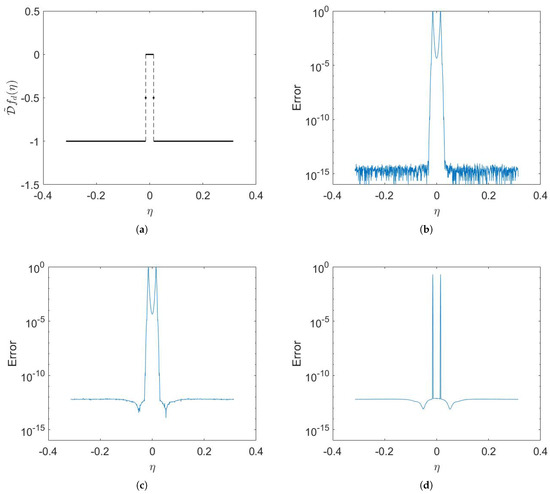
Figure 5. Double-layer potentials evaluation at ${10}^4$ equispaced points on a unit circle with the limaçon boundary described by (16). (a) The graph of $\tilde{\mathcal{D}}{f}_d$ on $(-\pi /10,\pi /10)$. (b) A ${10}^4$-point PTR. (c) Algorithm 1 with $n={10}^4,\beta =1.54\times {10}^{-8},M=312$. (d) Algorithm 2 with $m=55,n={10}^4,\beta =1.54\times {10}^{-8},M=312,{\sigma }_0={10}^5$.

We next show the evaluation errors of the proposed methods on a circle of radius R close to the starfish boundary described by (15). Here, we chose $\beta ={(R-r_{max})}^2/\left(50R{r}_{max}\right)$ in Algorithms 1 and 2, with the selection of other parameters following the same rules as in the first example. Figure 6a shows two curves ${\mathsf{\Gamma }}_1$ and ${\mathsf{\Gamma }}_2$ in this example, which are at a distance of ${10}^{-4}$ from each other. Figure 6b,c illustrate that the results of PTR and Algorithm 1 are inaccurate at points near ${\mathsf{\Gamma }}_1$, whereas Algorithm 2 achieves a precision of 13 decimal places, as shown in Figure 6d. We denote the distance between ${\mathsf{\Gamma }}_1$ and ${\mathsf{\Gamma }}_2$ as $\mathrm{dist}({\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2)$. Table 1 presents the ${\ell }^{\infty }$ errors on ${\mathbf{T}}_{1.3001,n}$ and the computation time for computing $\tilde{\mathcal{D}}{f}_d$ on a circle with a radius of $1.3001$ with different values of n. The errors of PTR and Algorithm 1 decay slowly, while the error of Algorithm 2 maintains a precision of 13 decimal places. The computing time for Algorithms 1 and 2 grows quasi-linearly as n increases, whereas the time of PTR grows quadratically.

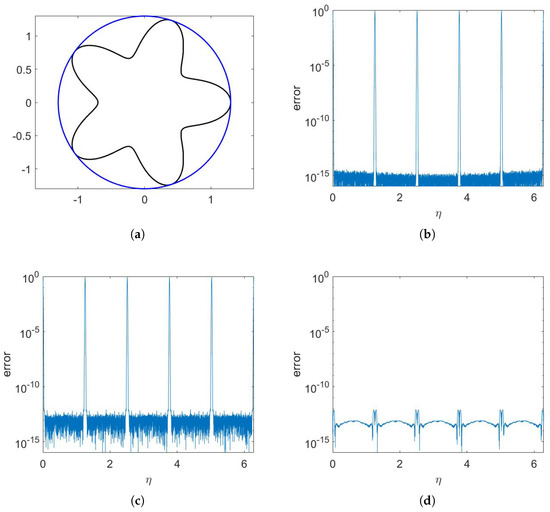
Figure 6. Double-layer potential evaluations at ${10}^4$ equispaced points on a circle located at a distance of ${10}^{-4}$ from the starfish boundary described by (15). (a) A starfish curve (black) and a circle of radius $1.3001$ (blue). (b) A ${10}^4$-point PTR. (c) Algorithm 1 with $n={10}^4,\beta =1.18\times {10}^{-10},M=397$. (d) Algorithm 2 with $m=55,n={10}^4,\beta =1.18\times {10}^{-10},M=397,{\sigma }_0={10}^5$.

Table 1. The ${\mathit{\ell }}^{\infty }$ errors of the Laplace double-layer potential evaluated on ${\mathbf{T}}_{1.3001,n}$ and the computation time, where n varies from ${10}^4$ to $8\times {10}^4$, and $\mathrm{dist}({\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2)={10}^{-4}$.

	${\mathit{\ell }}^{\mathit{\infty }}$ Error			Time (s)
$\mathbf{n}$	PTR	Algorithm 1	Algorithm 2	PTR	Algorithm 1	Algorithm 2
$1\times {10}^4$	$8.6\times {10}^{-1}$	$8.6\times {10}^{-1}$	$8.2\times {10}^{-13}$	$7.5$	$0.6$	$1.5$
$2\times {10}^4$	$2.7\times {10}^{-1}$	$2.7\times {10}^{-1}$	$8.4\times {10}^{-13}$	$22.3$	$1.5$	$2.9$
$4\times {10}^4$	$4.8\times {10}^{-2}$	$4.8\times {10}^{-2}$	$9.5\times {10}^{-13}$	$75.2$	$2.8$	$5.7$
$8\times {10}^4$	$2.1\times {10}^{-3}$	$2.1\times {10}^{-3}$	$9.3\times {10}^{-13}$	$259.5$	$7.0$	$12.1$

Table 2 shows the ${\ell }^{\infty }$ errors on ${\mathbf{T}}_{R,{10}^4}$ with $\mathrm{dist}({\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2)$ varying from ${10}^{-1}$ to ${10}^{-4}$, confirming that the proposed parameter selection for Algorithm 2 ensures the errors remain bounded regardless of $\mathrm{dist}({\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2)$, as discussed in Section 2.2.

Table 2. The ${\ell }^{\infty }$ errors in computing the Laplace double-layer potentials on ${\mathbf{T}}_{R,{10}^4}$, where R varies from $1.4$ to $1.3001$, and $\mathrm{dist}({\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2)$ varies from ${10}^{-1}$ to ${10}^{-4}$.

	${\mathit{\ell }}^{\mathit{\infty }}$ Error
dist$({\mathsf{\Gamma }}_{\mathbf{1}},{\mathsf{\Gamma }}_{\mathbf{2}})$	PTR	Algorithm 1	Algorithm 2
${10}^{-1}$	$3.0\times {10}^{-15}$	$6.7\times {10}^{-14}$	$6.7\times {10}^{-14}$
${10}^{-2}$	$6.5\times {10}^{-15}$	$1.1\times {10}^{-12}$	$1.1\times {10}^{-12}$
${10}^{-3}$	$4.7\times {10}^{-4}$	$4.7\times {10}^{-4}$	$6.6\times {10}^{-13}$
${10}^{-4}$	$8.6\times {10}^{-1}$	$8.6\times {10}^{-1}$	$8.2\times {10}^{-13}$

3.2. Integral Equation Solvers

In this section, we examine the proposed methods in the context of solving integral equations of the second kind. A numerical experiment of the exterior Neumann boundary value problems for the Laplace equation is conducted. Let $\Omega \subset {\mathbb{R}}^2$ be the bounded open domain, with boundary ${\mathsf{\Gamma }}_1$ described by (15), and let $u_{ex}\left(\mathbf{x}\right):=(x_1-0.1)/{|\mathbf{x}-(0.1,0.4)|}^2$ be the solution, where $\mathbf{x}\in {\mathbb{R}}^2\setminus \Omega$. We use the single-layer potential representation $u_{ex}=\mathcal{S}\phi$ [1]. Here, $\phi \in C\left({\mathsf{\Gamma }}_1\right)$ satisfies

$$\left(-\frac{1}{2}+{\mathcal{D}}^{\prime }\right)\phi =\frac{\partial u_{ex}}{\partial \mathbf{v}},$$

where

$$\left({\mathcal{D}}^{\prime }\phi \right)\left(\mathbf{x}\right):={\int }_{{\mathsf{\Gamma }}_1}\frac{\partial K(\mathbf{x},\mathbf{y})}{\partial \mathbf{v}\left(\mathbf{x}\right)}\phi \left(\mathbf{y}\right)\mathrm{d}{s}_{\mathbf{y}},\mathbf{x}\in {\mathsf{\Gamma }}_1.$$

In order to obtain the potential density function f, we solve the BIEs using the Fourier Galerkin method described in [2]. The tested methods are employed to compute $\mathcal{S}\phi$ on $\mathbb{T}\setminus \Omega$, where

$$\mathbb{T}:=\left\{\mathbf{x}:\mathbf{x}\in {\mathbf{T}}_{R_k,256},R_k=0.7+0.01k,k=0,\dots ,90\right\},$$

The first column of Figure 7 shows the absolute error of the PTR with 256 points. The last two columns of Figure 7 illustrated the absolute error of Algorithms 1 and 2. Here, $E_{\infty }$ in Figure 7 denotes the ${\ell }_{\infty }$ error of the evaluations on $\mathbb{T}\setminus \Omega$. Algorithms 1 and 2 are employed with $n=256,\beta ={\lambda }^2/\left(50R{r}_{max}\right),\lambda =max\{R-r_{max},{10}^{-6}\}$, and $M=⌈-28{log}_{10}\beta +{log}_{10}^2\beta ⌉$. In addition, we select $m=55$ and ${\sigma }_0=100$ for Algorithm 2. Figure 7 illustrates that Algorithm 2 achieves a precision of nine digits in evaluating the single-layer potential, even for target points near the boundary with a distance of $1.4\times {10}^{-5}$. Conversely, both the PTR and Algorithm 1 exhibit inaccuracies close to the boundary.

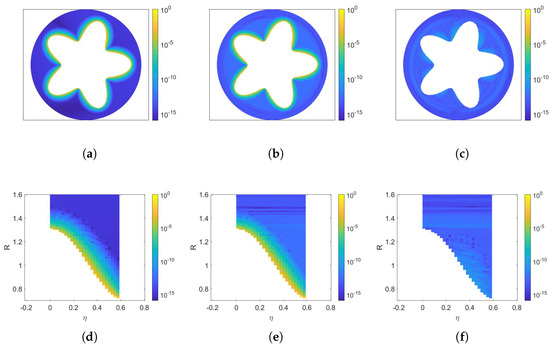
Figure 7. Absolute errors of computing single-layer potentials at targets on $\mathbb{T}\setminus \Omega$ with a minimum distance of $1.4\times {10}^{-5}$ from the exterior Laplace Neumann BVPs. The first column shows the errors of the 256-point PTR. The last two columns present the errors of Algorithms 1 and 2 using the proposed parameter selection scheme with $n=256$, $\lambda =max\{R-r_{max},{10}^{-6}\}$, $m=55$, and ${\sigma }_0=100$. The bottom row shows the errors relative to the points parameterized by angle $\eta$ and radius R. (a) PTR: $E_{\infty }=6.4\times {10}^{-2}$. (b) Algorithm 1: $E_{\infty }=6.4\times {10}^{-2}$. (c) Algorithm 2: $E_{\infty }=1.4\times {10}^{-9}$. (d) PTR. (e) Algorithm 1. (f) Algorithm 2.

4. Conclusions

In this paper, we introduce a convolution sum approximation of layer potentials and provide an approximation error analysis. A parameter selection scheme for the approximation is proposed in Section 2.2 to ensure high approximating accuracy outside a sufficiently small neighborhood of the boundary. Then two fast methods using convolution sums are presented for the evaluation of layer potentials in this paper. Due to the nearly singular convolution terms, Algorithm 1 exhibits inaccuracies near the boundary similar to PTR, as shown in the experiments in Section 3. Algorithm 2, which still maintains a complexity of $\mathcal{O}(nlogn)$, improves the accuracy of the evaluation near the boundary via computing the nearly singular convolution terms by the Gauss quadrature.

The improved method offers several advantages: Firstly, this approach leverages periodic convolution sums to approximate layer potentials on a circle, enabling fast computation compared to traditional methods. This technique significantly reduces computational time. In the meantime, a local quadrature is applied to the nearly singular convolution terms in order to maintain the algorithm’s accuracy near the boundary. Secondly, the algorithm allows for handling discontinuities in the field across the boundary, which is a feature that is not commonly addressed by existing methods. Lastly, our method is capable of handling scenarios where parts of the source geometry almost touch each other. This robustness is achieved without requiring much additional work, making the algorithm practical and efficient in real-world applications.

On the one hand, the algorithms proposed in this paper allow for fast off-boundary computation of layer potentials while accommodating discontinuities in the potential across the boundary. On the other hand, applications to practical problems when restricted to either the exterior or interior may result in redundant computations. Additionally, the assumption of a polar boundary limits the algorithm’s applicability to practical scenarios. Nevertheless, this method still presents an opportunity to accelerate the evaluation of integral operators with logarithmic or power-law singularities and to develop algorithms for higher dimensions.

Appendix A.1. Logarithmic Function

In this subsection, we consider using the exponential sum to approximate the logarithmic function $\varphi \left(x\right)=-\frac{1}{4\pi }log\left(x\right)$. This approach is based on the techniques described in [27]. The logarithmic function has the exponential integral form

$$\varphi \left(x\right)=-\frac{1}{4\pi }{\int }_1^x\frac{1}{t}\mathrm{d}t=-\frac{1}{4\pi }{\int }_1^x{\int }_0^{\infty }{e}^{-\rho t}\mathrm{d}\rho \mathrm{d}t=-\frac{1}{4\pi }{\int }_0^{\infty }{\int }_1^x{e}^{-\rho t}\mathrm{d}t\mathrm{d}\rho ,$$

(A1)

for $x\ge 1$. Since

$${\int }_1^x{e}^{-\rho t}\mathrm{d}t=\frac{1}{\rho }(e^{-\rho }-e^{-\rho x}),$$

(A2)

substituting (A2) into the right-hand side of (A1) implies that

$$\varphi \left(x\right)=\frac{1}{4\pi }{\int }_0^{\infty }\frac{1}{\rho }(e^{-\rho x}-e^{-\rho })\mathrm{d}\rho .$$

Applying a substitution of $\rho =log(1+e^{\xi })$ yields

$$\varphi \left(x\right)={\int }_{-\infty }^{+\infty }{f}_1(\xi ,x)\mathrm{d}\xi ,x\ge 1,$$

(A3)

where

$$f_1(\xi ,x):=\frac{1}{4\pi }\frac{e^{-xlog(1+e^{\xi })}-e^{-log(1+e^{\xi })}}{(1+e^{-\xi })log(1+e^{\xi })}.$$

By substituting $\xi =sinh\left(t\right)$ into (A3), the integrand changes into

$$f_2(t,x):=cosh\left(t\right)f_1(sinh\left(t\right),x).$$

We then use the truncated Sinc quadrature rules [29,30] for computing the integral as follow

$$T_{h,M}\left(f_2\right)\left(x\right):=h\sum _{\ell =-M}^M{f}_2(\ell h,x).$$

(A4)

In the numerical examples of this paper, we truncate the sum (A4) and approximate the integral (A3) by

$${\tilde{T}}_{h,M}\left(f_2\right)\left(x\right):=h\sum _{\ell =-M}^0{\tilde{f}}_2(\ell h,x)-h\sum _{\ell =-M}^M{\tilde{f}}_2(\ell h,1)$$

$$=h\sum _{k=0}^M{\tilde{f}}_2(-kh,x)-b_M=\sum _{k=0}^M{c}_k{e}^{-a_{k}x}-b_M,$$

(A5)

where

$${\tilde{f}}_2(t,x):=\frac{1}{4\pi }\frac{e^{-xlog(1+e^{sinh\left(t\right)})}cosh\left(t\right)}{(1+e^{-sinh\left(t\right)})log(1+e^{sinh\left(t\right)})},a_k:=log\left(1+e^{-sinh\left(kh\right)}\right),$$

and

$$b_M:=\sum _{k=-M}^M{c}_k{e}^{-a_k},c_k:=\frac{hcosh\left(kh\right)}{4\pi (1+e^{sinh\left(kh\right)})log(1+e^{-sinh\left(kh\right)})}.$$

Remark A1.

There is precision loss in the evaluation of $log(1+exp(-sinh\left(kh\right)\left)\right)$ in $a_k,c_k$ when $kh$ is large. In such cases, using its Taylor series for computation can provide better accuracy.

Appendix A.2. Function 1/x

When $\varphi \left(x\right)=-\frac{1}{2\pi x}$, we introduce the corresponding exponential sums in [2]. Consider the Laplace integral transform

$$\varphi \left(x\right)=-\frac{1}{2\pi x}=-\frac{1}{2\pi }{\int }_0^{\infty }{e}^{-xt}\mathrm{d}t.$$

By applying substitutions of $t=log(1+e^{\rho }),\rho =sinh\left(\xi \right)$, we have

$$\varphi \left(x\right)={\int }_{-\infty }^{+\infty }{f}_3(\xi ,x)\mathrm{d}\xi ,x\ge 1,$$

(A6)

where

$$f_3(\xi ,x):=cosh\left(\xi \right)f_4(sinh\left(\xi \right),x),f_4(\rho ,x):=-\frac{1}{2\pi }\frac{e^{-xlog(1+e^{\rho })}}{1+e^{-\rho }}.$$

Use the truncated Sinc quadrature, we have

$$T_{h,M}\left(f_3\right)\left(x\right):=h\sum _{k=-M}^M{f}_3(kh,x),$$

(A7)

and in this paper, we compute (A6) as

$${\tilde{T}}_{h,M}\left(f_3\right)\left(x\right):=h\sum _{\ell =-M}^0{f}_3(\ell h,x)=h\sum _{k=0}^M{f}_3(-kh,x)=\sum _{k=0}^M{\tilde{c}}_k{e}^{-a_{k}x},$$

(A8)

where

$$a_k=log\left(1+e^{-sinh\left(kh\right)}\right),{\tilde{c}}_k=\frac{hcosh\left(kh\right)}{1+e^{sinh\left(kh\right)}}.$$

Remark A2.

The function $\varphi \left(x\right)=c{x}^{-\alpha }$ for $c,\alpha >0$ can also be approximated by exponential sums (see [27]).

Appendix A.3. Error Estimates

In this subsection, we provide an error estimate for the M-term approximation of the exponential sums discussed in the preceding two subsections. To this end, we first estimate the truncated error between $T_{h,M}\left(f_k\right)$ and ${\tilde{T}}_{h,M}\left(f_k\right)$ for $k=2,3$, which represent the cases for $\varphi \left(x\right)=log\left(x\right)$ and $\varphi \left(x\right)=x^{-1}$, respectively. We provide a lemma for estimating the error for the case of $\varphi \left(x\right)={(-2\pi x)}^{-1}$ for $x\ge s\ge 1$.

Lemma A1

(Function ${(-2\pi x)}^{-1}$). There exists a positive constant C such that for all $M\in {\mathbb{Z}}^{+}$, $s\ge 1$ and $h>0$,

$${∥T_{h,M}\left(f_3\right)-{\tilde{T}}_{h,M}\left(f_3\right)∥}_{\infty ,[s,\infty )}\le \left(2^{-s}-{\left(1+e^{sinh\left(Mh\right)}\right)}^{-s}\right)/\left(2\pi s\right)+Cs{2}^{-s}M{h}^2.$$

Proof. 

Since

$${∥T_{h,M}\left(f_3\right)-{\tilde{T}}_{h,M}\left(f_3\right)∥}_{\infty ,[s,\infty )}={∥h\sum _{\ell =1}^M{f}_3(\ell h,·)∥}_{\infty ,[s,\infty )},$$

(A9)

it suffices to estimate the upper bound of ${∥h{\sum }_{\ell =1}^M{f}_3(\ell h,·)∥}_{\infty ,[s,\infty )}$. According to the triangle inequality, we have

$${∥h\sum _{\ell =1}^M{f}_3(\ell h,·)∥}_{\infty ,[s,\infty )}\le {∥h\sum _{\ell =1}^M{f}_3(\ell h,·)-{\int }_0^{Mh}{f}_3(\xi ,·)\mathrm{d}\xi ∥}_{\infty ,[s,\infty )}+{∥{\int }_0^{Mh}{f}_3(\xi ,·)\mathrm{d}\xi ∥}_{\infty ,[s,\infty )}.$$

(A10)

The error estimate of the right rectangle rule implies that for all $x\in [s,\infty )$,

$$\left|h\sum _{\ell =1}^M{f}_3(\ell h,x)-{\int }_0^{Mh}{f}_3(\xi ,x)\mathrm{d}\xi \right|\le \frac{M{h}^2}{2}\underset{\xi \in [0,Mh]}{max}\left|\frac{\partial f_3}{\partial \xi }(\xi ,x)\right|.$$

(A11)

Since it can be derived that there exists a positive constant C such that for all $s\ge 1$

$$\underset{(\xi ,x)\in [0,Mh]\times [s,\infty )}{max}\left|\frac{\partial f_3}{\partial \xi }(\xi ,x)\right|\le Cs{2}^{-(s-1)},$$

(A12)

it follows from (A11) and (A12) that

$${∥h\sum _{\ell =1}^M{f}_3(\ell h,·)-{\int }_0^{Mh}{f}_3(\xi ,·)\mathrm{d}\xi ∥}_{\infty ,[s,\infty )}\le Cs{2}^{-s}M{h}^2.$$

(A13)

Note that

$${∥{\int }_0^{Mh}{f}_3(\xi ,·)\mathrm{d}\xi ∥}_{\infty ,[s,\infty )}\le \frac{1}{2\pi }{\int }_{log2}^{Mh}{e}^{-st}\mathrm{d}t=\left(2^{-s}-{\left(1+e^{sinh\left(Mh\right)}\right)}^{-s}\right)/\left(2\pi s\right).$$

(A14)

Combining (A9), (A10), (A13) and (A14) leads to the result. □

Similarly, we can derive the error estimate for the case when $\varphi \left(x\right)=\frac{1}{4\pi }log\left(x\right)$ for $x\ge s$.

Lemma A2

(Logarithmic Function). There exists a positive constant C such that for all $M\in {\mathbb{Z}}^{+}$, $s\ge 1$ and $h>0$,

$${∥T_{h,M}\left(f_2\right)-{\tilde{T}}_{h,M}\left(f_2\right)∥}_{\infty ,[s,\infty )}\le \left(2^{-s}-{\left(1+e^{sinh\left(Mh\right)}\right)}^{-s}\right)/(4\pi slog2)+Cs{2}^{-s}M{h}^2.$$

Proof. 

Note that

$${∥T_{h,M}\left(f_2\right)-{\tilde{T}}_{h,M}\left(f_2\right)∥}_{\infty ,[s,\infty )}={∥h\sum _{\ell =1}^M{\tilde{f}}_2(\ell h,·)∥}_{\infty ,[s,\infty )}.$$

(A15)

It suffices to bound the right-hand side of (A15). According to the triangle inequality, we have

$${∥h\sum _{\ell =1}^M{\tilde{f}}_2(\ell h,·)∥}_{\infty ,[s,\infty )}\le {∥h\sum _{\ell =1}^M{\tilde{f}}_2(\ell h,·)-{\int }_0^{Mh}{\tilde{f}}_2(\xi ,·)\mathrm{d}\xi ∥}_{\infty ,[s,\infty )}+{∥{\int }_0^{Mh}{\tilde{f}}_2(\xi ,·)\mathrm{d}\xi ∥}_{\infty ,[s,\infty )}.$$

(A16)

Similar to the proof of Lemma A1, it can be demonstrated that there exists a positive constant C such that for all $M\in {\mathbb{Z}}^{+}$, $s\ge 1$ and $h>0$,

$${∥h\sum _{\ell =1}^M{\tilde{f}}_2(\ell h,·)-{\int }_0^{Mh}{\tilde{f}}_2(\xi ,·)\mathrm{d}\xi ∥}_{\infty ,[s,\infty )}\le Cs{2}^{-s}M{h}^2.$$

(A17)

From

$${∥{\int }_0^{Mh}{\tilde{f}}_2(\xi ,·)\mathrm{d}\xi ∥}_{\infty ,[s,\infty )}\le \frac{1}{4\pi }{\int }_{log2}^{Mh}{e}^{-st}/t\mathrm{d}t\le \frac{1}{4\pi }{\int }_{log2}^{Mh}{e}^{-st}\mathrm{d}t/log2$$

and (A14), it follows that

$${∥{\int }_0^{Mh}{\tilde{f}}_2(\xi ,·)\mathrm{d}\xi ∥}_{\infty ,[s,\infty )}\le \left(2^{-s}-{\left(1+e^{sinh\left(Mh\right)}\right)}^{-s}\right)/(4\pi slog2).$$

(A18)

Combining (A16)–(A18) leads to the result. □

We restate an estimate for ${∥T_{h,M}\left(f_3\right)-\varphi ∥}_{\infty ,[1,\iota ]}$ with $\varphi \left(x\right)=x^{-1}$ and $\iota >1$, as presented in Lemma 4.3 in [27].

Lemma A3

(Hackbusch, Khoromskij). Let $\varphi \left(x\right)={(-2\pi x)}^{-1}$. There exists a positive constant C such that for all $\iota >1$ and $M\in {\mathbb{Z}}^{+}$, by choosing $h=log\left(4\pi M\right)/M$,

$${∥T_{h,M}\left(f_3\right)-\varphi ∥}_{\infty ,[1,\iota ]}\le Cexp\left(-\frac{{\pi }^{2}M}{log\left(3\iota \right)log\left({\pi }^{2}M\right)}\right).$$

For convenience, denote

$$\nu \left(z\right):=\frac{e^z-1-z}{z},$$

on $\mathbb{C}$ and introduce $a\lesssim b$ to mean $a\le Cb$ for some positive constant C and $a,b\in \mathbb{R}$. We next present an estimate of ${∥T_{h,M}\left(f_2\right)-\varphi ∥}_{\infty ,[1,\iota ]}$ for $\varphi \left(x\right)=-\frac{1}{2\pi }logx$ and $\iota >1$.

Lemma A4.

Let $\varphi \left(x\right)=-\frac{1}{2\pi }logx$. There exists a positive constant C such that for all $\iota >1$ and $M\in {\mathbb{Z}}^{+}$, by choosing $h=log\left(4\pi M\right)/M$,

$${∥T_{h,M}\left(f_2\right)-\varphi ∥}_{\infty ,[1,\iota ]}\le C\iota exp\left(-\frac{{\pi }^{2}M}{log\left(3\iota \right)log\left({\pi }^{2}M\right)}\right).$$

(A19)

Proof. 

Let $D_{\delta }:=\{z\in \mathbb{C}:|\Im mz|\le \delta \}$ with $\delta \le 0.93<\frac{\pi }{2}$. Since

$$f_2(z,x)=\frac{coshz(-x+1-x\nu (-xlog(1+exp(sinh\left(z\right)\left)\right))+\nu (-log(1+exp(sinh\left(z\right)\left)\right)\left)\right)}{4\pi (1+exp(sinh\left(z\right))},$$

$\nu$ is analytic on $\mathbb{C}$, and the zeros of $1+exp(sinh(z\left)\right)$ are outside of $D_{\delta }$, the function $f_2(·,x)$ is analytic in $D_{\delta }$, with $x\ge 1$.

To utilize Lemma 4.3 from [27] for the proof of this lemma, it is necessary to establish the following inequalities:

$$|f_2(z,x)|\le \frac{1}{2\pi log2}\left(\left|\frac{cosh\left(z\right)e^{-xlog(1+exp(sinh\left(z\right)\left)\right)}}{1+exp(-sinh(z\left)\right)}\right|+\left|\frac{cosh\left(z\right)e^{-log(1+exp(sinh\left(z\right)\left)\right)}}{1+exp(-sinh(z\left)\right)}\right|\right),$$

(A20)

for all $z\in D_{\delta },\Re ez\ge 0,x\ge 1,$ and

$$|f_2(z,x)|\le \frac{3.33(x+1)}{4\pi }\left|\frac{cosh\left(z\right)}{1+exp(-sinh(z\left)\right)}\right|,$$

(A21)

for all $z\in D_{\delta },\Re ez<0,x\ge 1$.

Firstly, we prove

$${|log(1+exp(sinh\left(z\right)))|}^{-1}\le {\left(log\sqrt{2}\right)}^{-1}$$

(A22)

for all $z\in D_{\delta },\Re ez\ge 0$. In the case of $z\in D_{\delta },\Re ez>x_1\left(\delta \right):=arsinh(1/cos\delta )$, we have $\Re e(sinh(z\left)\right)=sinh(\Re ez)cos(\Im mz)>cos(\Im mz)/cos\delta \ge 1$. It follows that

$$|log(1+exp(sinh(z\left)\right)\left)\right|\ge \Re e(log(1+exp(sinh(z\left)\right)\left)\right)$$

$$\ge log\left(1+2exp(\Re esinhz)cos(\Im msinhz)+exp(2\Re esinhz)\right)/2$$

$$\ge log(exp(\Re esinhz)-1)\ge log(e-1)\ge log\sqrt{2}.$$

Thus, the inequality (A22) holds. In the case of $z\in D_{\delta },0\le \Re ez\le x_1\left(\delta \right)$, we have $sinh(\Re ez)\le 1/cos\delta$, which leads to

$$\Im msinhz=cosh(\Re ez)sin(\Im mz)\le \sqrt{1+{cos}^2\delta }tan\delta .$$

The restriction $0<\delta \le 0.93$ guarantees $|\Im msinhz|<\pi /2$. Additionally, the inequalities $\Re ez\ge 0$ and $|\Im mz|<\delta <\pi /2$ imply

$$\Re e(sinh(z\left)\right)=sinh(\Re ez)cos(\Im mz)>0.$$

Thus, it follows that

$$|log(1+exp(sinh\left(z\right)))|\ge log\left(1+2exp(\Re esinhz)cos(\Im msinhz)+exp(2\Re esinhz)\right)/2$$

$$>log\left(1+exp(2\Re esinhz)\right)/2>log\sqrt{2}.$$

The above inequality implies (A22). We finish the proof of (A22) for all $z\in D_{\delta },\Re ez\ge 0$. From (A22) and the triangle inequality, we obtain (A20). Applying Lemma 4.3 in [27] to (A20) leads to

$$|f_2(z,x)|\lesssim exp\left(\Re ez-\frac{cos0.93}{2}exp(\Re ez)\right)$$

(A23)

for $z\in D_{\delta },\Re ez\ge 0$, and $x\in [1,\iota ]$. This bound of $f_2(z,x)$ is independent of x and decays double-exponentially.

Secondly, we prove

$$\left|\frac{e^{-xlog(1+exp(sinh\left(z\right)\left)\right)}-e^{-log(1+exp(sinh\left(z\right)\left)\right)}}{log(1+exp(sinh\left(z\right)\left)\right)}\right|\le 3.33(x+1)$$

(A24)

for all $z\in D_{\delta },\Re ez<0,x\ge 1$. In the case of $z\in D_{\delta },x_0\left(x\right)<\Re ez<0,x\ge 1,$ where $x_0$ is defined by (4.5) in [27], we have

$$\Re e\left(-xlog(1+exp(sinh\left(z\right)\left)\right)\right)<0$$

(A25)

according to proof (d) of Lemma 4.3 in [27]. In the case of $z\in D_{\delta },\Re ez\le x_0\left(x\right),x\ge 1,$ according to proof (e) of Lemma 4.3 in [27], we have

$$\Re e\left(-xlog(1+exp(sinh\left(z\right)\left)\right)\right)\le \frac{log3}{2}.$$

(A26)

We conclude that for all $z\in D_{\delta },\Re ez<0,x\ge 1,$ the inequality (A26) holds. Consider the upper bound of $\left|\nu \right|$ for $\Re ez\le \frac{log3}{2}$. We have $\left|\nu \left(z\right)\right|\le \nu \left(R_0\right)$ for $\left|z\right|\le R_0$. In the case of $\left|z\right|\ge R_0$ and $\Re ez\le \frac{log3}{2}$, it follows that $\left|\nu \left(z\right)\right|\le \left(e^{\Re ez}+1\right)/R_0+1\le \left(e^{\frac{log3}{2}}+1\right)/R_0+1$. We choose $R_0$ as the zero of $\left(e^{\frac{log3}{2}}+1\right)/R_0+1=\nu \left(R_0\right)$ and $\left|\nu \left(z\right)\right|\le \nu \left(R_0\right)\le 2.33$ for all $\Re e\left(z\right)\le \frac{log3}{2}$. Thus, the inequality (A26) implies that

$$\left|\nu \left(-xlog(1+exp(sinh\left(z\right)\left)\right)\right)\right|\le 2.33,$$

(A27)

for $z\in D_{\delta },\Re ez<0,x\ge 1$. Combining (A27) and

$$\left|\frac{e^{-xlog(1+exp(sinh\left(z\right)\left)\right)}-e^{-log(1+exp(sinh\left(z\right)\left)\right)}}{log(1+exp(sinh\left(z\right)\left)\right)}\right|$$

$$\le 1+x+x\left|\nu (-xlog(1+exp(sinh(z\left)\right))\right|+\left|\nu (-log(1+exp(sinh(z\left)\right))\right|$$

leads to (A24) for $z\in D_{\delta },\Re ez<0,x\ge 1$. Inequality (A24) implies (A21). According to (A21) and the bound of $\left|\frac{cosh\left(z\right)}{1+exp(-sinh(z\left)\right)}\right|$ in proof (d)(e) of Lemma 4.3 in [27], it can be obtained that

$$|f_2(z,x)|\lesssim \iota exp\left(|\Re ez|-\frac{cos0.93}{2}exp\left(\right|\Re ez\left|\right)\right)$$

(A28)

for $z\in D_{\delta },\Re ez<0$, and $x\in [1,\iota ]$. By (A23) and (A28), we conclude that (A28) holds for $z\in D_{\delta }$ and $x\in [1,\iota ]$. Therefore, according to Proposition 2.1 in [27], the choice $a=1,b=1/2,\delta =\delta \left(x\right)$ defined by (4.5) in [27] leads to (A19). □