Invariant Subspaces of Short Pulse-Type Equations and Reductions

Abstract

In this paper, we extend the invariant subspace method to a class of short pulse-type equations. Complete classification results with invariant subspaces from 2 to 5 dimensions are provided. The key step is to take subspaces of solutions of linear ordinary differential equations as invariant subspaces that nonlinear operators admit. Some concrete examples and corresponding reduced systems are presented to illustrate this method.

1. Introduction

The short pulse (SP) equation

$$u_{xt}=u+\frac{1}{6}{\left(u^3\right)}_{xx}$$

(1)

can be used to display the propagation of ultra-short optical pulses in silicon fiber, where $u=u(x,t)$ represents the magnitude of the optical field. SP and two-component SP equations are obtained as special integrable cases in the negative WKI hierarchy for the first time in Refs. [1,2,3].

In Ref. [4], the authors present a classification of the following SP-type equations

$$\begin{array}{c}\hfill u_{xt}=u+{\beta }_0{u}^2+{\beta }_{1}u{u}_x+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2+{\gamma }_0{u}^3+{\gamma }_1{u}^2{u}_x+{\gamma }_2{u}^2{u}_{xx}+{\gamma }_{3}u{u}_x^2.\end{array}$$

(2)

Because of these constants $\{{\beta }_j,{\gamma }_j,j=0,1,2,3\}$, the dispersion relationship will have variable speeds, and solitons can change the speed, for example, through accelerating. Equation (2) may be a good candidate for accelerating ultra-short optical pulse applications. The purpose of this article is to classify Equation (2) by using the invariant subspace method. In addition, in Ref. [5], the authors considered Lie symmetry analysis for some special SP-type equations.

The invariant subspace method is powerful for studying nonlinear partial differential equations (PDEs). Various invariant subspaces to a number of nonlinear PDEs have been obtained (see [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22], as well as the references therein). Accordingly, exact solutions stemming from this method play important roles in the study of their asymptotical behavior, blow up and geometric properties, etc. It turns out that the invariant subspace method is closely related to the Lie-Bäcklund symmetry and the conditional Lie-Bäcklund symmetry.

Let us introduce the invariant subspace method briefly [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. Consider the following nonlinear PDEs

$$\begin{array}{c}\hfill u_t=F(x,u,u_x,u_{xx},\dots ,u_{kx}),\end{array}$$

(3)

where $F\left[u\right]\equiv F\left(x,u,u_x,\cdots ,u_{kx}\right)$ is a sufficiently smooth function of its arguments and $u_{jx}=\frac{{\partial }^{j}u}{\partial x^j}$ ($j=1,2,\cdots ,k$). Let $\{f_j\left(x\right),(j=1,2,\cdots ,n)\}$ be a finite set of linearly independent functions and $W_n$ denote their linear span $W_n=\mathcal{L}\{f_1\left(x\right),f_2\left(x\right),\cdots ,f_n\left(x\right)\}$. The subspace $W_n$ is said to be invariant under the given nonlinear operator F, namely, F is said to preserve $W_n$ if $F\left(W_n\right)\subseteq W_n$; this means

$$\begin{array}{c}\hfill F\left[\sum _{j=1}^n{c}_j{f}_j\left(x\right)\right]=\sum _{j=1}^n{\Psi }_j(c_1,c_2,\dots ,c_n)f_j\left(x\right)\end{array}$$

(4)

for any $(c_1,c_2,\cdots ,c_n)\in {\mathbb{R}}^n$. It follows that if the linear subspace $W_n$ is invariant with respect to F, then Equation (3) has exact solutions of the form

$$\begin{array}{c}\hfill u(x,t)=\sum _{j=1}^n{C}_j\left(t\right)f_j\left(x\right),\end{array}$$

(5)

where the coefficients $\{C_1\left(t\right),C_2\left(t\right),\cdots ,C_n\left(t\right)\}$ satisfy the following dynamical system

$$\begin{array}{c}\hfill C_j^{\prime }\left(t\right)={\Psi }_j\left(C_1\left(t\right),C_2\left(t\right),\cdots ,C_n\left(t\right)\right),j=1,2,\cdots ,n.\end{array}$$

(6)

Let $W_n$ be defined as the space of solutions to a linear nth-order ordinary differential equation (ODE),

$$\begin{array}{c}\hfill L\left[y\right]\equiv y^{\left(n\right)}+a_{n-1}{y}^{(n-1)}+\cdots +a_1{y}^{\prime }+a_{0}y=0,\end{array}$$

(7)

then, the invariant condition with respect to nonlinear operator F takes the form

$$\begin{array}{c}\hfill L\left[F\left[u\right]\right]{|}_{\left[H\right]}=0,\end{array}$$

(8)

where $\left[H\right]$ denotes equation $L\left[u\right]=0$ and its differential consequences with respect to x. Of course, Equation (7) can also be an equation with variable coefficients.

For nonlinear PDEs $u_{xt}=F(x,u,u_x,u_{xx},\dots ,u_{kx})$, there will be a different set of constraint equations. That is, substituting Equation (5) with (7) and (8) into these equations, we can obtain

$$\begin{array}{c}\hfill \sum _{j=1}^n{C}_j^{\prime }\left(t\right)f_j^{\prime }\left(x\right)-\sum _{j=1}^n{\Psi }_j(C_1\left(t\right),C_2\left(t\right),\dots ,C_n\left(t\right))f_j\left(x\right)=0.\end{array}$$

(9)

It is not difficult to notice that $f_j^{\prime }\left(x\right)={\alpha }_{jk}{f}_k\left(x\right)+{\alpha }_{jl}{f}_l\left(x\right)$. So, the coefficients $\{C_1\left(t\right),C_2\left(t\right),\cdots ,C_n\left(t\right)\}$ satisfy the following system

$$\begin{array}{c}{\Phi }_l(C_1\left(t\right),C_2\left(t\right),\dots ,C_n\left(t\right))=0,\hfill \\ C_j^{\prime }\left(t\right)={\Phi }_j(C_1\left(t\right),C_2\left(t\right),\dots ,C_n\left(t\right)),j\in \{1,\cdots ,l-1,l+1,\cdots ,n\}.\hfill \end{array}$$

(10)

Comparing Equations (6) and (10), we can find that by means of the invariant subspace method, (1 + 1)-dimensional nonlinear equation $u_t=F\left[u\right]$ is reduced to a dynamical system, while the other equation $u_{xt}=F\left[u\right]$ is reduced to a one-dimensional system of equations, which includes constraint equations and a dynamical system. In other words, we extend the application range of solving nonlinear equations by using the invariant subspace method.

There is an important proposition, that is, the maximum dimension estimation of invariant subspaces. Namely, if a linear subspace $W_n$ derived from Equation (7) is invariant under a nonlinear operator F of order k, then

$$\begin{array}{c}\hfill n\le 2k+1.\end{array}$$

In Refs. [7,8,10], the authors have extended the estimation of the maximal dimension of invariant subspaces to nonlinear vector operators.

2. Invariant Subspaces of the SP-Type Equations

For SP-type Equation (2), we only need to consider cases $W_2$, $W_3$, $W_4$, and $W_5$, which are obtained by linear ODE (7).

We first analyze the case of $W_2$. Let

$$\begin{array}{c}\hfill L\left[y\right]\equiv y^{″}+a_1{y}^{\prime }+a_{0}y=0,\end{array}$$

(11)

and

$$\begin{array}{c}\hfill F=u+{\beta }_0{u}^2+{\beta }_{1}u{u}_x+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2+{\gamma }_0{u}^3+{\gamma }_1{u}^2{u}_x+{\gamma }_2{u}^2{u}_{xx}+{\gamma }_{3}u{u}_x^2,\end{array}$$

(12)

a direct computation by using symbolic computation softwares such as Maple. From the invariant condition (8), we have

$$\begin{array}{cc}\hfill L\left[F\left[u\right]\right]{|}_{\left[H\right]}& =(2a_0^2{\gamma }_2+2a_0^2{\gamma }_3-2a_0{\gamma }_0)u^3\hfill \\ \hfill & +(6a_0{a}_1{\gamma }_2+4a_0{a}_1{\gamma }_3-6a_0{\gamma }_1)u_x{u}^2\hfill \\ \hfill & +(4a_1^2{\gamma }_2+2a_1^2{\gamma }_3-6a_0{\gamma }_2-6a_0{\gamma }_3-4a_1{\gamma }_1+6{\gamma }_0)u_x^{2}u\hfill \\ \hfill & +(a_0^2{\beta }_2+2a_0^2{\beta }_3-a_0{\beta }_0)u^2+(3a_0{a}_1{\beta }_2+4a_0{a}_1{\beta }_3-3a_0{\beta }_1)u{u}_x\hfill \\ \hfill & +(-2a_1{\gamma }_2-4a_1{\gamma }_3+2{\gamma }_1)u_x^3\hfill \\ \hfill & +(2a_1^2{\beta }_2+2a_1^2{\beta }_3-2a_0{\beta }_2-a_0{\beta }_3-2a_1{\beta }_1+2{\beta }_0)u_x^2\hfill \\ \hfill & =0.\hfill \end{array}$$

(13)

To remove all the coefficients of Equation (13), we obtain the following over-determined system,

$$\begin{array}{cc}\hfill & 2a_0^2{\gamma }_2+2a_0^2{\gamma }_3-2a_0{\gamma }_0=0,\hfill \\ \hfill & 6a_0{a}_1{\gamma }_2+4a_0{a}_1{\gamma }_3-6a_0{\gamma }_1=0,\hfill \\ \hfill & 4a_1^2{\gamma }_2+2a_1^2{\gamma }_3-6a_0{\gamma }_2-6a_0{\gamma }_3-4a_1{\gamma }_1+6{\gamma }_0=0,\hfill \\ \hfill & a_0^2{\beta }_2+2a_0^2{\beta }_3-a_0{\beta }_0=0,\hfill \\ \hfill & 3a_0{a}_1{\beta }_2+4a_0{a}_1{\beta }_3-3a_0{\beta }_1=0,\hfill \\ \hfill & -2a_1{\gamma }_2-4a_1{\gamma }_3+2{\gamma }_1=0,\hfill \\ \hfill & 2a_1^2{\beta }_2+2a_1^2{\beta }_3-2a_0{\beta }_2-a_0{\beta }_3-2a_1{\beta }_1+2{\beta }_0=0.\hfill \end{array}$$

(14)

By solving the above system (14), we have four cases,

$$\begin{array}{c}\mathrm{Case}1:a_0=0,{\beta }_0=-a_1^2{\beta }_2-a_1^2{\beta }_3+a_1{\beta }_1,{\gamma }_0=a_1^2{\gamma }_3,{\gamma }_1=a_1{\gamma }_2+2a_1{\gamma }_3.\hfill \\ \mathrm{Case}2:a_1=0,{\beta }_0=a_0{\beta }_2,{\beta }_1=0,{\beta }_3=0,{\gamma }_0=a_0{\gamma }_2+a_0{\gamma }_3,{\gamma }_1=0.\hfill \\ \mathrm{Case}3:{\beta }_0=a_0{\beta }_2,{\beta }_1=a_1{\beta }_2,{\beta }_3=0,{\gamma }_0=a_0{\gamma }_2,{\gamma }_1=a_1{\gamma }_2,{\gamma }_3=0.\hfill \\ \mathrm{Case}4:a_0=\frac{2a_1^2}{9},{\beta }_0=\frac{2}{9}{a}_1^2{\beta }_2+\frac{4}{9}{a}_1^2{\beta }_3,{\beta }_1=a_1{\beta }_2+\frac{4}{3}{a}_1{\beta }_3,{\gamma }_0=\frac{2a_1^2{\gamma }_2}{9},\hfill \\ {\gamma }_1=a_1{\gamma }_2,{\gamma }_3=0.\hfill \end{array}$$

Let us consider each of these cases in turn.

Subcase 1.1: $a_1=0$. Substituting $a_1=0$ into Case 1, the corresponding solution can be easily obtained and listed as the first entry in Table 1.

Table 1. Classifications of $W_2$ generated by linear ODE (7) for Equation (2).

No.	Operator F	ODE (7)
1	$F=u+{\beta }_{1}u{u}_x+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2+{\gamma }_2{u}^2{u}_{xx}+{\gamma }_{3}u{u}_x^2$	$y^{″}=0$
2	$\begin{array}{cc}\hfill F=u& +(-\frac{{\gamma }_1^2}{{\gamma }_2^2}{\beta }_2-\frac{{\gamma }_1^2}{{\gamma }_2^2}{\beta }_3+\frac{{\gamma }_1}{{\gamma }_2}{\beta }_1)u^2+{\beta }_{1}u{u}_x+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2\hfill \\ & +{\gamma }_1{u}^2{u}_x+{\gamma }_2{u}^2{u}_{xx}\hfill \end{array}$       ${\gamma }_2\ne 0$	$y^{″}+\frac{{\gamma }_1}{{\gamma }_2}$$y^{\prime }=0$
3	$\begin{array}{cc}\hfill F=u& +(-\frac{{\gamma }_0}{{\gamma }_3}{\beta }_2-\frac{{\gamma }_0}{{\gamma }_3}{\beta }_3\pm \sqrt{\frac{{\gamma }_0}{{\gamma }_3}}{\beta }_1)u^2+{\beta }_{1}u{u}_x+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2\hfill \\ & +{\gamma }_0{u}^3\pm \sqrt{\frac{{\gamma }_0}{{\gamma }_3}}({\gamma }_2+2{\gamma }_3)u^2{u}_x+{\gamma }_2{u}^2{u}_{xx}+{\gamma }_{3}u{u}_x^2\hfill \end{array}$       ${\gamma }_3\ne 0$,$\frac{{\gamma }_0}{{\gamma }_3}>0$	$y^{″}\pm \sqrt{\frac{{\gamma }_0}{{\gamma }_3}}$$y^{\prime }=0$
4	$F=u-{\beta }_{3}u{u}_{xx}+{\beta }_3{u}_x^2$       ${\beta }_3\ne 0$	$y^{″}$ + $a_1{y}^{\prime }$ $=0$
5	$F=u+{\beta }_0{u}^2+{\beta }_{1}u{u}_x-{\beta }_{3}u{u}_{xx}+{\beta }_3{u}_x^2{\beta }_1\ne 0$	$y^{″}$ + $\frac{{\beta }_0}{{\beta }_1}{y}^{\prime }$ $=0$
6	$F=u+{\beta }_0{u}^2+{\beta }_{1}u{u}_x+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2{\beta }_2\ne -{\beta }_3$	$y^{″}$ + $\frac{{\beta }_1\pm \sqrt{{\beta }_1^2-4{\beta }_0({\beta }_2+{\beta }_3)}}{2({\beta }_2+{\beta }_3)}{y}^{\prime }$ $=0$
7	$F=u-{\gamma }_3{u}^2{u}_{xx}+{\gamma }_{3}u{u}_x^2{\gamma }_3\ne 0$	$y^{″}$ + $a_{0}y=0$
8	$F=u+{\gamma }_0{u}^3+{\gamma }_2{u}^2{u}_{xx}+{\gamma }_{3}u{u}_x^2$       ${\gamma }_2\ne -{\gamma }_3$	$y^{″}$ + $\frac{{\gamma }_0}{{\gamma }_2+{\gamma }_3}y=0$
9	$F=u+{\beta }_0{u}^2+{\beta }_{2}u{u}_{xx}+\frac{{\beta }_0}{{\beta }_2}({\gamma }_2+{\gamma }_3)u^3+{\gamma }_2{u}^2{u}_{xx}+{\gamma }_{3}u{u}_x^2$       ${\beta }_2\ne 0$	$y^{\prime \prime }$$+\frac{{\beta }_0}{{\beta }_2}y=0$
10	$F=u+{\beta }_0{u}^2+{\beta }_{1}u{u}_x+{\beta }_{2}u{u}_{xx}+\frac{{\beta }_0}{{\beta }_2}{\gamma }_2{u}^3+\frac{{\beta }_1}{{\beta }_2}{\gamma }_2{u}^2{u}_x+{\gamma }_2{u}^2{u}_{xx}{\beta }_2\ne 0$	$y^{\prime \prime }$$+\frac{{\beta }_1}{{\beta }_2}{y}^{\prime }$$+\frac{{\beta }_0}{{\beta }_2}y=0$
11	$F=u+{\gamma }_0{u}^3+{\gamma }_1{u}^2{u}_x+{\gamma }_2{u}^2{u}_{xx}{\gamma }_2\ne 0$	$y^{″}+\frac{{\gamma }_1}{{\gamma }_2}{y}^{\prime }+\frac{{\gamma }_0}{{\gamma }_2}y=0$
12	$F=u+{\beta }_0{u}^2-\frac{4}{3}{\beta }_{3}u{u}_{xx}+{\beta }_3{u}_x^2{\beta }_3\ne 0$, $\frac{{\beta }_0}{{\beta }_3}>0$	$y^{″}\pm \frac{3\sqrt{3}}{2}\sqrt{\frac{{\beta }_0}{{\beta }_3}}{y}^{\prime }+\frac{3{\beta }_0}{2{\beta }_3}y=0$
13	$F=u+\frac{2{\beta }_1^2}{9{({\beta }_2+\frac{4}{3}{\beta }_3)}^2}({\beta }_2+2{\beta }_3)u^2+{\beta }_{1}u{u}_x+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2{\beta }_2\ne -\frac{4}{3}{\beta }_3$	$y^{″}+\frac{{\beta }_1}{{\beta }_2+\frac{4}{3}{\beta }_3}{y}^{\prime }+\frac{2{\beta }_1^2}{9{({\beta }_2+\frac{4}{3}{\beta }_3)}^2}y=0$
14	$\begin{array}{cc}\hfill F=u& +(\frac{2{\gamma }_1^2}{9{\gamma }_2^2}{\beta }_2+\frac{4{\gamma }_1^2}{9{\gamma }_2^2}{\beta }_3)u^2+(\frac{{\gamma }_1}{{\gamma }_2}{\beta }_2+\frac{4{\gamma }_1}{3{\gamma }_2}{\beta }_3)u{u}_x+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2\hfill \\ & +\frac{2{\gamma }_1^2}{9{\gamma }_2}{u}^3+{\gamma }_1{u}^2{u}_x+{\gamma }_2{u}^2{u}_{xx}\hfill \end{array}$       ${\gamma }_2\ne 0$	$y^{″}+\frac{{\gamma }_1}{{\gamma }_2}{y}^{\prime }+\frac{2{\gamma }_1^2}{9{\gamma }_2^2}y=0$

Subcase 1.2: $a_1\ne 0$.

Subcase 1.2.1: ${\gamma }_3=0$, then ${\gamma }_0=0$. If ${\gamma }_2\ne 0$, it is easy to obtain $a_1=\frac{{\gamma }_1}{{\gamma }_2}$ and ${\beta }_0=-\frac{{\gamma }_1^2}{{\gamma }_2^2}{\beta }_2-\frac{{\gamma }_1^2}{{\gamma }_2^2}{\beta }_3+\frac{{\gamma }_1}{{\gamma }_2}{\beta }_1$, which is represented as the second entry in Table 1. If ${\gamma }_2=0$, it is easy to see that ${\gamma }_0={\gamma }_1={\gamma }_2={\gamma }_3=0$. Then, from $({\beta }_2+{\beta }_3)a_1^2-{\beta }_1{a}_1+{\beta }_0=0$, we have three choices,

$$\begin{array}{ccc}& & {\beta }_2=-{\beta }_3,{\beta }_1=0,{\beta }_0=0.\hfill \\ & & {\beta }_2=-{\beta }_3,{\beta }_1\ne 0,a_1=\frac{{\beta }_0}{{\beta }_1}.\hfill \\ & & {\beta }_2\ne -{\beta }_3,a_1=\frac{{\beta }_1\pm \sqrt{{\beta }_1^2-4{\beta }_0({\beta }_2+{\beta }_3)}}{2({\beta }_2+{\beta }_3)}.\hfill \end{array}$$

The results are listed as the fourth to sixth entries of Table 1.

Subcase 1.2.2: ${\gamma }_3\ne 0$. The corresponding classification result is listed as the third entry in Table 1.

In Cases 2 to 4, we obtained equations using similar calculations, which are listed in Table 1, Equations with invariant subspaces $W_3,W_4,W_5$ are listed in Table 2. It is obvious that when ${\beta }_3=0$, Case 4 becomes Case 3.

Table 2. Classifications of $W_n(n=3,4,5)$ generated by linear ODE (7) for Equation (2).

No.	Operator F	ODE (7)
1	$F=u+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2-2{\gamma }_3{u}^2{u}_{xx}+{\gamma }_{3}u{u}_x^2$	$y^{‴}=0$
2	$F=u-\frac{{\gamma }_0}{{\gamma }_3}({\beta }_2+{\beta }_3)u^2+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2+{\gamma }_0{u}^3-2{\gamma }_3{u}^2{u}_{xx}+{\gamma }_{3}u{u}_x^2{\gamma }_3\ne 0$	$y^{‴}-\frac{{\gamma }_0}{{\gamma }_3}{y}^{\prime }=0$
3	$F=u+{\beta }_0{u}^2+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2{\beta }_2\ne -{\beta }_3$	$y^{‴}+\frac{{\beta }_0}{{\beta }_2+{\beta }_3}{y}^{\prime }=0$
4	$F=u-{\beta }_{3}u{u}_{xx}+{\beta }_3{u}_x^2$	$y^{‴}+a_1{y}^{\prime }=0$
5	$F=u+{\beta }_0{u}^2-\frac{4}{3}{\beta }_{3}u{u}_{xx}+{\beta }_3{u}_x^2{\beta }_3\ne 0$,$\frac{{\beta }_0}{{\beta }_3}>0$	$y^{‴}\pm \frac{3\sqrt{3}}{2}\sqrt{\frac{{\beta }_0}{{\beta }_3}}{y}^{″}+\frac{3{\beta }_0}{2{\beta }_3}{y}^{\prime }=0$
6	$F=u+(\frac{4}{9}{\beta }_3+\frac{2}{9}{\beta }_2)\frac{{\beta }_1^2}{{({\beta }_2+\frac{4}{3}{\beta }_3)}^2}{u}^2+{\beta }_{1}u{u}_x+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2{\beta }_2\ne -\frac{4}{3}{\beta }_3$	$y^{‴}+\frac{{\beta }_1}{{\beta }_2+\frac{4}{3}{\beta }_3}{y}^{″}+\frac{2{\beta }_1^2}{9{({\beta }_2+\frac{4}{3}{\beta }_3)}^2}{y}^{\prime }=0$
7	$F=u+{\beta }_0{u}^2+{\beta }_{1}u{u}_x+{\beta }_{2}u{u}_{xx}$       ${\beta }_2\ne 0$	$y^{‴}+\frac{{\beta }_1}{{\beta }_2}{y}^{″}+\frac{{\beta }_0}{{\beta }_2}{y}^{\prime }=0$
8	$F=u+\frac{4{\beta }_1^2}{{\beta }_3}{u}^2+{\beta }_{1}u{u}_x-\frac{3}{2}{\beta }_{3}u{u}_{xx}+{\beta }_3{u}_x^2{\beta }_3\ne 0$	$y^{\left(4\right)}-\frac{4{\beta }_1}{{\beta }_3}{y}^{‴}-\frac{4{\beta }_1^2}{{\beta }_3^2}{y}^{″}+\frac{16{\beta }_1^3}{{\beta }_3^3}{y}^{\prime }=0$
9	$F=u+{\beta }_0{u}^2-\frac{4}{3}{\beta }_{3}u{u}_{xx}+{\beta }_3{u}_x^2{\beta }_3\ne 0$	$y^{\left(5\right)}-\frac{15{\beta }_0}{4{\beta }_3}{y}^{‴}+\frac{9{\beta }_0^2}{4{\beta }_3^2}{y}^{\prime }=0$

3. Some Concrete Examples

In this section, we provide several specific examples to demonstrate the classification results derived from the invariant subspace method.

Example 1. 

We consider the following SP-type equation

$$u_{xt}=u+{\beta }_0{u}^2+{\beta }_{1}u{u}_x-{\beta }_{3}u{u}_{xx}+{\beta }_3{u}_x^2,{\beta }_0\ne 0,{\beta }_1\ne 0,$$

(15)

which is located in the fifth row of Table 1. The operator $F=u+{\beta }_0{u}^2+{\beta }_{1}u{u}_x-{\beta }_{3}u{u}_{xx}+{\beta }_3{u}_x^2$ admits $W_2=\mathcal{L}\{1,e^{-\frac{{\beta }_{0}x}{{\beta }_1}}\}$, which is generated by the linear ODE

$$y^{″}+\frac{{\beta }_0}{{\beta }_1}{y}^{\prime }=0.$$

Thus, an exact solution is provided by

$$u(x,t)=C_1\left(t\right)+C_2\left(t\right)e^{-\frac{{\beta }_{0}x}{{\beta }_1}},$$

where $C_1\left(t\right)$ and $C_2\left(t\right)$ satisfy the following reduced system

$$\begin{array}{cc}\hfill & C_1{\beta }_1^2(C_1{\beta }_0+1)=0,\hfill \\ \hfill & C_2^{\prime }=\frac{1}{{\beta }_0{\beta }_1}{C}_2(({\beta }_0^2{\beta }_3-{\beta }_0{\beta }_1^2)C_1-{\beta }_1^2).\hfill \end{array}$$

(16)

For ease of understanding, these special parameters ${\beta }_0=2,{\beta }_1={\beta }_3=1$, have an exact solution of $u=-\frac{1}{2}+c{e}^{-2x-t}$, which is drawn in Figure 1.

Figure 1. An exact solution of Equation (15) with $c=1$.

Example 2. 

Here, we consider the following SP-type equation

$$\begin{array}{c}\hfill u_{xt}=u+{\gamma }_0{u}^3+{\gamma }_2{u}^2{u}_{xx}+{\gamma }_{3}u{u}_x^2,{\gamma }_2\ne -{\gamma }_3.\end{array}$$

(17)

The operator $F=u+{\gamma }_0{u}^3+{\gamma }_2{u}^2{u}_{xx}+{\gamma }_{3}u{u}_x^2$ admits the invariant subspace $W_2$ generated by the linear ODE

$$y^{″}+\frac{{\gamma }_0}{{\gamma }_2+{\gamma }_3}y=0.$$

Case 1: Renaming $s=\frac{{\gamma }_0}{{\gamma }_2+{\gamma }_3}$, when $s<0$, from $y^{″}+sy=0$, we have the invariant subspace

$$\mathcal{L}\{e^{-\sqrt{-s}x},e^{\sqrt{-s}x}\}.$$

Thus, an exact solution is provided by

$$u(x,t)=C_1\left(t\right)e^{-\sqrt{-s}x}+C_2\left(t\right)e^{\sqrt{-s}x},$$

where $C_1\left(t\right)$ and $C_2\left(t\right)$ satisfy the dynamical system

$$\begin{array}{cc}\hfill & C_1^{\prime }=\frac{-4}{({\gamma }_2+{\gamma }_3)\sqrt{-s}}({\gamma }_0{\gamma }_3{C}_1{C}_2+\frac{1}{4}{\gamma }_2+\frac{1}{4}{\gamma }_3)C_1,\hfill \\ \hfill & C_2^{\prime }=\frac{4}{({\gamma }_2+{\gamma }_3)\sqrt{-s}}({\gamma }_0{\gamma }_3{C}_1{C}_2+\frac{1}{4}{\gamma }_2+\frac{1}{4}{\gamma }_3)C_2.\hfill \end{array}$$

(18)

Case 2: When $s>0$, from $y^{″}+sy=0$, we have the invariant subspace

$$\mathcal{L}\{sin\left(\sqrt{s}x\right),cos\left(\sqrt{s}x\right)\}.$$

Thus, an exact solution is provided by

$$u(x,t)=C_1\left(t\right)sin\left(\sqrt{s}x\right)+C_2\left(t\right)cos\left(\sqrt{s}x\right),$$

where $C_1\left(t\right)$ and $C_2\left(t\right)$ satisfy the dynamical system

$$\begin{array}{cc}\hfill & C_1^{\prime }=\frac{1}{({\gamma }_2+{\gamma }_3)\sqrt{s}}{C}_2({\gamma }_0{\gamma }_3{C}_1^2+{\gamma }_0{\gamma }_3{C}_2^2+{\gamma }_2+{\gamma }_3),\hfill \\ \hfill & C_2^{\prime }=-\frac{1}{({\gamma }_2+{\gamma }_3)\sqrt{s}}{C}_1({\gamma }_0{\gamma }_3{C}_1^2+{\gamma }_0{\gamma }_3{C}_2^2+{\gamma }_2+{\gamma }_3).\hfill \end{array}$$

(19)

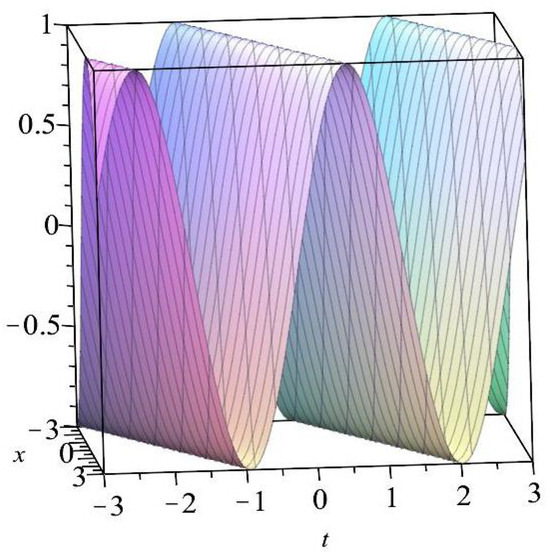
Let these special parameters ${\gamma }_0=2,{\gamma }_2={\gamma }_3=1$, have an exact solution

$$\begin{array}{ccc}& & u=\cos (\frac{3\sqrt{2}}{2}t+c)\cos (\frac{\sqrt{2}}{2}x)+\sin (\frac{3\sqrt{2}}{2}t+c)\sin (\frac{\sqrt{2}}{2}x)\hfill \\ & & =\cos (\frac{3\sqrt{2}}{2}t-\frac{\sqrt{2}}{2}x+c),\hfill \end{array}$$

which is drawn in Figure 2.

Figure 2. An exact solution of Equation (17) with $c=1$.

Example 3. 

Let us consider the following SP-type equation

$$\begin{array}{c}\hfill u_{xt}=u+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2-2{\gamma }_3{u}^2{u}_{xx}+{\gamma }_{3}u{u}_x^2,\end{array}$$

(20)

where the operator $F=u+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2-2{\gamma }_3{u}^2{u}_{xx}+{\gamma }_{3}u{u}_x^2$ admits $W_3=\mathcal{L}\{1,x,x^2\}$ determined by the linear ODE

$$y^{‴}=0.$$

Thus, an exact solution is provided by

$$u(x,t)=C_1\left(t\right)+C_2\left(t\right)x+C_3\left(t\right)x^2,$$

where $C_1\left(t\right)$ and $C_2\left(t\right)$ satisfy the following reduced system

$$\begin{array}{cc}\hfill & C_1=\frac{{\gamma }_3{C}_2^2+2{\beta }_2{C}_3+4{\beta }_3{C}_3+1}{4{\gamma }_3{C}_3},\hfill \\ \hfill & C_2^{\prime }=(-4{\gamma }_3{C}_1^2+2{\beta }_2{C}_1)C_3+({\gamma }_3{C}_1+{\beta }_3)C_2^2+C_1,\hfill \\ \hfill & C_3^{\prime }=(-2{\gamma }_3{C}_1+{\beta }_2+2{\beta }_3)C_2{C}_3+\frac{1}{2}({\gamma }_3{C}_2^3+C_2).\hfill \end{array}$$

(21)

Example 4. 

We consider the following SP-type equation

$$u_{xt}=u+{\beta }_0{u}^2+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2,{\beta }_2\ne -{\beta }_3.$$

(22)

The operator $F=u+{\beta }_0{u}^2+{\beta }_{2}u{u}_{xx}+{\beta }_3{u}_x^2$ admits the invariant subspace $W_3$ determined by the linear ODE

$$y^{‴}+\frac{{\beta }_0}{{\beta }_2+{\beta }_3}{y}^{\prime }=0.$$

Case 1: Renaming $p=\frac{{\beta }_0}{{\beta }_2+{\beta }_3}$, when $p<0$, from $y^{‴}+p{y}^{\prime }=0$, we have an invariant subspace

$$\mathcal{L}\{1,e^{-\sqrt{-p}x},e^{\sqrt{-p}x}\}.$$

Then, an exact solution is provided by

$$u(x,t)=C_1\left(t\right)+C_2\left(t\right)e^{-\sqrt{-p}x}+C_3\left(t\right)e^{\sqrt{-p}x},$$

where $C_1\left(t\right)$, $C_2\left(t\right)$, and $C_3\left(t\right)$ satisfy the following reduced system

$$\begin{array}{cc}\hfill & C_1=-{\beta }_0{C}_1^2-\frac{4{\beta }_0{\beta }_3{C}_2{C}_3}{{\beta }_2+{\beta }_3},\hfill \\ \hfill & C_2^{\prime }=-\sqrt{-\frac{{\beta }_2+{\beta }_3}{{\beta }_0}}\frac{({\beta }_0({\beta }_2+2{\beta }_3)C_1+{\beta }_2+{\beta }_3)C_2}{{\beta }_2+{\beta }_3},\hfill \\ \hfill & C_3^{\prime }=\sqrt{-\frac{{\beta }_2+{\beta }_3}{{\beta }_0}}\frac{({\beta }_0({\beta }_2+2{\beta }_3)C_1+{\beta }_2+{\beta }_3)C_3}{{\beta }_2+{\beta }_3}.\hfill \end{array}$$

(23)

Case 2: When $p>0$, from $y^{‴}+p{y}^{\prime }=0$, we have an invariant subspace

$$\mathcal{L}\{1,sin\left(\sqrt{p}x\right),cos\left(\sqrt{p}x\right)\}.$$

Then, an exact solution is provided by

$$u(x,t)=C_1\left(t\right)+C_2\left(t\right)sin\left(\sqrt{p}x\right)+C_3\left(t\right)cos\left(\sqrt{p}x\right),$$

where $C_1\left(t\right)$, $C_2\left(t\right)$, and $C_3\left(t\right)$ satisfy the following reduced system

$$\begin{array}{cc}\hfill & C_1=-{\beta }_0{C}_1^2-\frac{{\beta }_0{\beta }_3}{{\beta }_2+{\beta }_3}(C_2^2+C_3^2),\hfill \\ \hfill & C_2^{\prime }=\sqrt{\frac{{\beta }_2+{\beta }_3}{{\beta }_0}}\frac{({\beta }_0({\beta }_2+2{\beta }_3)C_1+{\beta }_2+{\beta }_3)C_3}{{\beta }_2+{\beta }_3},\hfill \\ \hfill & C_3^{\prime }=-\sqrt{\frac{{\beta }_2+{\beta }_3}{{\beta }_0}}\frac{({\beta }_0({\beta }_2+2{\beta }_3)C_1+{\beta }_2+{\beta }_3)C_2}{{\beta }_2+{\beta }_3}.\hfill \end{array}$$

(24)

Example 5. 

We consider the following SP-type equation

$$u_{xt}=u+4u^2+u{u}_x-\frac{3}{2}u{u}_{xx}+u_x^2.$$

(25)

The operator $F=u+4u^2+u{u}_x-\frac{3}{2}u{u}_{xx}+u_x^2$ admits $W_4=\mathcal{L}\{1,e^{2x},e^{4x},e^{-2x}\}$ determined by the linear ODE

$$y^{\left(4\right)}-4y^{‴}-4y^{″}+16y^{\prime }=0.$$

The corresponding exact solution is provided by

$$u(x,t)=C_1\left(t\right)+C_2\left(t\right)e^{2x}+C_3\left(t\right)e^{4x}+C_4\left(t\right)e^{-2x},$$

where $C_1\left(t\right)$, $C_2\left(t\right)$, $C_3\left(t\right)$, and $C_4\left(t\right)$ satisfy the following reduced system

$$\begin{array}{cc}\hfill & C_1=12C_{2}C4-4C_1^2,\hfill \\ \hfill & C_2^{\prime }=2C_1{C}_2-18C_3{C}_4+\frac{C_2}{2},\hfill \\ \hfill & C_3^{\prime }=C_2^2-3C_1{C}_3+\frac{C_3}{4},\hfill \\ \hfill & C_4^{\prime }=-\frac{C_4}{2}.\hfill \end{array}$$

(26)

So, an exact solution of the SP-type equation can be obtained as

$$u(x,t)=-\frac{1}{8}-\frac{e^{2x+\frac{t}{2}}}{192c_1}+\frac{e^{t+4x}}{13824c_1^2}+c_1{e}^{-2x-\frac{t}{2}},$$

where $c_1$ is an arbitrary constant.

Example 6. 

We consider the following SP-type equation

$$u_{xt}=u-u^2-\frac{4}{3}u{u}_{xx}+u_x^2.$$

(27)

Here, the operator $F=u-u^2-\frac{4}{3}u{u}_{xx}+u_x^2$ admits $W_5=\mathcal{L}\{1,sin(\sqrt{3}x),cos(\sqrt{3}x),sin(\frac{\sqrt{3}x}{2}),$$cos(\frac{\sqrt{3}x}{2})\}$, which is determined by the linear ODE

$$y^{\left(5\right)}+\frac{15}{4}{y}^{‴}+\frac{9}{4}{y}^{\prime }=0.$$

Thus, an exact solution is provided by

$$u(x,t)=C_1\left(t\right)+C_2\left(t\right)sin(\sqrt{3}x)+C_3\left(t\right)cos(\sqrt{3}x)+C_4\left(t\right)sin(\frac{\sqrt{3}x}{2})+C_5\left(t\right)cos(\frac{\sqrt{3}x}{2})$$

where $\{C_1\left(t\right),C_2\left(t\right),\cdots ,C_5\left(t\right)\}$ satisfy the following reduced system

$$\begin{array}{cc}\hfill & C_1=C_1^2-3C_2^2-3C_3^2-\frac{3C_4^2}{8}-\frac{3C_5^2}{8},\hfill \\ \hfill & C_2^{\prime }=\frac{\sqrt{3}}{24}(16C_1{C}_3+3C_4^2-3C_5^2+8C_3),\hfill \\ \hfill & C_3^{\prime }=\frac{\sqrt{3}}{12}(-8C_1{C}_2+3C_4{C}_5-4C_2),\hfill \\ \hfill & C_4^{\prime }=\frac{2\sqrt{3}}{3}(3C_2{C}_4-C_5(C_1-3C_3-1)),\hfill \\ \hfill & C_5^{\prime }=\frac{2\sqrt{3}}{3}((C_1+3C_3-1)C_4-3C_2{C}_5).\hfill \end{array}$$

(28)

4. Conclusions and Discussions

In this paper, we study SP-type equations by using the invariant subspace method. A class of Equation (2) admitting invariant subspaces generated by Equation (7) are obtained and listed in Table 1 and Table 2. Some concrete examples and corresponding reduced systems are presented to illustrate this method.

In the future, we will consider the classification of two-component SP-type equations. Of course, the extension to the case of nonlocal equations and the case of fractional differential equations should be further investigated.