Based on Symmetric Jump Risk Market: Study on the Ruin Problem of a Risk Model with Liquid Reserves and Proportional Investment

Abstract

In order to deal with complex risk scenarios involving claims, uncertainty, and investments, we consider the ruin problems in a compound Poisson risk model with liquid reserves and proportional investments and study the expected discounted penalty function under threshold dividend strategies. Firstly, the integral differential equation of the expected discounted penalty function is derived. Secondly, since the closed-form solution of the equation cannot be obtained, a sinc method is used to obtain the numerical approximation solution of the equation. Finally, the feasibility and superiority of the sinc method are illustrated by error analysis. In addition, based on a symmetric jump risk market, we discuss the influence of some parameters on the ruin probability with some examples. This study can help actuaries develop more robust risk management strategies and ensure the long-term stability and profitability of insurance companies. It provides a theoretical basis for actuaries to carry out risk management.

1. Introduction

With the development of the economy, the risks faced by insurance companies have also increased. Therefore, it is necessary to effectively prevent and control operational risks. The key lies in how insurance companies use reasonable means, such as dividends, capital injection, investment, and reinsurance strategies, to control the surplus process of funds in order to minimize corporate risks or maximize shareholder returns [1].

Risk theory is the core content of actuarial mathematics research, which has been paid much attention in the field of finance and insurance. Since the Cram$\acute{\mathrm{e}}$r–Lundberg classic risk model was proposed, it has been paid attention to and promoted by many researchers as an important method to study corporate ruin risk. Zhang et al. [2] assumed that the jump terms in the classical model are two-sided jumps; that is, upward and downward jumps. Based on the classic model, Zhang and Han [3] consider the mixed dividend strategy. Then, Liu et al. [4] proposed a dual risk model subject to diffusion perturbation under a threshold strategy.

Ruin theory is one of the important subjects of risk theory, and ruin probability is the most important quantitative index in ruin theory. In the actual operation, the insurer not only pays attention to the ruin probability but also focuses on the quantity related to ruin. In 1998, Gerber and Shiu proposed a powerful tool for unifying these variables—the expected discount penalty function (Gerber–Shiu function) [5]. Lin and Pavlova [6] adapted this function to the classical model. In the past ten years, the Gerber–Shiu function played an important role in the risk management of insurance companies, which has attracted wide attention from scholars [7]. Yu et al. [8] and Wang et al. [9] discussed the ruin problem under different models with the help of this function.

In reality, insurance companies do not invest all of their assets, but keep a portion of their funds to cover contingencies. Considering this situation, Cai et al. [10] put forward the liquid reserve strategy; that is, assuming that the surplus is higher than the level of liquid reserve, make a risk-free investment. Subsequently, Peng et al. [11] and Zhang et al. [12] studied the issue of liquid reserves successively. Both of these papers assumed that the insurer would invest their surplus at fixed interest rates, but in reality, the investment method of insurers may not be so simple. Inspired by Chen et al. [13], we assume that surplus is invested in a financial market consisting of riskless assets and risky assets in a fixed proportion, consider a classical model with a liquid reserve and threshold strategy, and study the Gerber–Shiu function of this model; the dividend problem of this model can be seen in reference [14]. In order to show the innovation of this paper intuitively, we compare the models in this study with those in the literature in Table 1.

Table 1. Compared with previous literature.

Existing Literature	Model			Penalty Function	Sinc	Error Analysis
	Liquid Reserve	Investment	Threshold Strategy
Wang et al. [9]		✓	✓	✓	✓	✓
Wan [15]			✓	✓
Zhi and Pu [16]			✓
Peng et al. [11]	✓	✓	✓	✓
Cai et al. [10]	✓	✓	✓	✓
Yang and He [17]	✓	✓		✓
Lu and Li [18]		✓	✓
Chen and Ou [13]		✓	✓	✓	✓
Zhang et al. [12]	✓	✓	✓	✓
Gao and Liu [19]		✓	✓	✓
This paper	✓	✓	✓	✓	✓	✓

Contribution of this paper: Both proportional investment and liquid reserves are important measures taken by insurance companies in the face of various risk events to ensure that companies can effectively manage risks, maintain financial soundness, and meet their insurance liabilities on time. For now, there are few studies that consider proportional investment and liquid reserve factors in risk models, and there are no studies that consider both factors in one model. Therefore, the research in this paper enriches the ruin theory and provides a theoretical basis for insurance companies to better prevent risks.

2. The Model

We introduce the classical risk model, and the expression of the surplus process ${\left\{U_t\right\}}_{t\ge 0}$ is

$$U_t=u+ct-Z_t,t\ge 0,$$

(1)

where $c>0$ is the premium rate. The cumulative claim amount $Z_t={\displaystyle \sum _{i=1}^{N_1\left(t\right)}}{Y}_i$ is a compound Poisson process, and the intensity of the homogeneous Poisson process $N_1\left(t\right)=sup\{k:D_1+D_2+\cdots +D_k\le t\}$ is $\gamma \ge 0$. The independent identically distributed (i.i.d) claim size ${\left\{Y_i\right\}}_{i=1}^{\infty }$ is a general non-negative continuous random variable with cumulative distribution function (c.d.f.) $F_Y$ and probability density function (p.d.f.) $f_Y$, and the i.i.d claim interval ${\left\{D_i\right\}}_{i=1}^{\infty }$ has a common exponential distribution with the parameter $\mu$.

There is a financial market made up of riskless assets and risk assets. The riskless asset ${\left\{Q_t\right\}}_{t\ge 0}$ satisfies

$$\mathrm{d}{Q}_t=r_1{Q}_t\mathrm{d}t.$$

(2)

where $r_1>0$ is the riskless interest rate. Risk assets ${\left\{R_t\right\}}_{t\ge 0}$ follow a geometric Lévy process, which satisfies

$$\begin{array}{cc}\hfill R_t& =e^{r_{2}t+{\sigma }_r{W}_t+{\displaystyle \sum _{i=1}^{N_2\left(t\right)}}{X}_i},\hfill \end{array}$$

(3)

where $r_2(r_2>0)$ represents the expected instantaneous rate of return of the risk assets and ${\sigma }_r$ represents the price volatility of the risk assets. ${\left\{W_t\right\}}_{t\ge 0}$ denotes a standard Brownian motion. ${\left\{X_i\right\}}_{i=1}^{\infty }$ is a i.i.d random variable that takes value from real numbers $\mathbb{R}$, with c.d.f.$F_X$ and p.d.f.$f_X$. The intensity of the homogeneous Poisson process $N_2\left(t\right)=sup\{k:H_1+H_2+\cdots +H_k\le t\}$ is $\eta \ge 0$, and the i.i.d jump interval ${\left\{H_i\right\}}_{i=1}^{\infty }$ has a common exponential distribution with parameter $\eta \ge 0$. In addition, ${\left\{Y_i\right\}}_{i=1}^{\infty }$, ${\left\{X_i\right\}}_{i=1}^{\infty }$, ${\left\{N_1\left(t\right)\right\}}_{t\ge 0}$, and ${\left\{N_2\left(t\right)\right\}}_{t\ge 0}$ are independent of each other. So, we obtain

$$\frac{\mathrm{d}{R}_t}{R_t}=(r_2+\frac{1}{2}{{\sigma }_r}^2)\mathrm{d}t+{\sigma }_r\mathrm{d}{W}_t+\mathrm{d}\sum _{i=1}^{N_2\left(t\right)}(e^{X_i}-1).$$

(4)

In order to reduce risk and obtain high returns, we assume that insurer invests its surplus in the risk market with the ratio of q $(0<q<1)$, and invests its surplus in the riskless market with the ratio of $1-q$. So, ${\left\{U_t\right\}}_{t\ge 0}$ satisfies

$$\mathrm{d}{U}_t=q{U}_{t-}\frac{\mathrm{d}{R}_t}{R_t}+(1-q)U_{t-}\frac{\mathrm{d}{Q}_t}{Q_t}+c\mathrm{d}t-\mathrm{d}{Z}_t.$$

(5)

Then, we consider a model with a liquid reserve and a threshold strategy. We let $\Delta$ represent the liquid reserve level and b represent the threshold level. Based on model (5), we further assume that if $0\le U_t<\Delta$, the insurer neither invests nor pays dividends; if $\Delta \le U_t<b$, the portion above $\Delta$ will be invested proportionally; if $U_t\ge b$, the portion above b will be a dividendat a constant rate $\theta (0<\theta <c)$. So, ${\left\{U_t\right\}}_{t\ge 0}$ satisfies

$$\begin{array}{c}\hfill \mathrm{d}{U}_t=\left\{\begin{array}{cc}c\mathrm{d}t-\mathrm{d}{Z}_t,\hfill & 0\le U_{t-}<\Delta ,\\ \\ q{\widehat{U}}_t\frac{\mathrm{d}{R}_t}{R_t}+(1-q){\widehat{U}}_t\frac{\mathrm{d}{Q}_t}{Q_t}+c\mathrm{d}t-\mathrm{d}{Z}_t,\hfill & \Delta \le U_{t-}<b,\\ \\ q{\widehat{U}}_t\frac{\mathrm{d}{R}_t}{R_t}+(1-q){\widehat{U}}_t\frac{\mathrm{d}{Q}_t}{Q_t}+(c-\theta )\mathrm{d}t-\mathrm{d}{Z}_t,\hfill & b\le U_{t-}<\infty ,\end{array}\right.\end{array}$$

(6)

where ${\widehat{U}}_t=U_{t-}-\Delta$. Expanding model (6), we have

$$\begin{array}{c}\hfill \mathrm{d}{U}_t=\left\{\begin{array}{cc}c\mathrm{d}t-\mathrm{d}{Z}_t,\hfill & 0\le U_{t-}<\Delta ,\\ \\ q{\sigma }_r{\widehat{U}}_t\mathrm{d}{W}_t-\mathrm{d}{\displaystyle \sum _{i=1}^{N_1\left(t\right)}}{Y}_i+(\check{r}{\widehat{U}}_t+c)\mathrm{d}t+q{\widehat{U}}_t\mathrm{d}{\displaystyle \sum _{i=1}^{N_2\left(t\right)}}(e^{X_i}-1),\hfill & \Delta \le U_{t-}<b,\\ \\ q{\sigma }_r{\widehat{U}}_t\mathrm{d}{W}_t-\mathrm{d}{\displaystyle \sum _{i=1}^{N_1\left(t\right)}}{Y}_i+(\check{r}{\widehat{U}}_t+c-\theta )\mathrm{d}t+q{\widehat{U}}_t\mathrm{d}{\displaystyle \sum _{i=1}^{N_2\left(t\right)}}(e^{X_i}-1),\hfill & b\le U_{t-}<\infty ,\end{array}\right.\end{array}$$

(7)

where $\check{r}=(1-q)r_1+q(r_2+\frac{1}{2}{{\sigma }_r}^2)$, and the security loading condition is $c-\theta >\gamma E\left[Y_1\right]$.

The expected discount penalty function is

$$\begin{array}{c}\hfill \varphi \left(u\right)=\varphi (u;b)=E\left[e^{-\tau T_u}\omega (U\left(T_{u-}\right),|U(T_u)\right|)I(T_u<\infty )|U\left(0\right)=u],\end{array}$$

(8)

where $\omega (·,·)$ is a non-negative penalty function, $T_u=inf\{t:U_t<0\}$ denotes the moment of ruin, $U\left(T_{u-}\right)$ denotes the instantaneous surplus before ruin, and $\left|U\right(T_u\left)\right|$ denotes the deficit at ruin time, $\tau >0$ is the discounted factor, and $I\left(A\right)$ is the indicator function of a set A. We let $\omega (0,0)=1$, and assume that $\varphi \left(u\right)$ is completely smooth in this paper.

Remark 1. 

When $\tau =0$, $\omega (·,·)=1$, $\varphi \left(u\right)$ will become the ruin probability $\psi \left(u\right)=\psi (u;b)=P(T_u<\infty |U\left(0\right)=u)$.

In this paper, the remainder content is as follows. In Section 3, we derive a system of integral differential equations (IDEs) for $\varphi \left(u\right)$, satisfying certain boundary conditions. In Section 4, we obtain an approximate solution of $\varphi \left(u\right)$ by the sinc method and find the upper bound of the error of sinc approximation. In Section 5, the relative errors of exact and approximate solutions under certain conditions are given, and the superiority of the sinc method is demonstrated. Finally, based on a symmetric jump risk market, the impact of some parameters on $\phi \left(u\right)$ is illustrated by numerical examples.

3. Integral Differential Equations for $\mathit{\varphi }\left(\mathit{u}\right)$

When the initial surplus is different, $\varphi \left(u\right)$ satisfying different expressions, let

$$\begin{array}{c}\hfill \varphi \left(u\right)=\left\{\begin{array}{cc}{\varphi }_1\left(u\right),\hfill & 0\le u<\Delta ;\\ \\ {\varphi }_2\left(u\right),\hfill & \Delta \le u<b;\\ \\ {\varphi }_3\left(u\right),\hfill & b\le u<+\infty .\end{array}\right.\end{array}$$

So, we obtain the following theorem.

Theorem 1. 

$\varphi \left(u\right)$ satisfies the following systerm of IDEs. When $0\le u<\Delta$,

$$\begin{array}{cc}\hfill & c{{\varphi }_1}^{\prime }\left(u\right)-(\tau +\gamma +\eta ){\varphi }_1\left(u\right)+\gamma \left[{\int }_0^u{\varphi }_1(u-y)\mathrm{d}{F}_Y\left(y\right)+{\int }_u^{\infty }\omega (u,y-u)d{F}_Y\left(y\right)\right]=0,\hfill \end{array}$$

(9)

when $\Delta \le u<b$,

$$\begin{array}{cc}\hfill & \frac{1}{2}{q}^2{{\sigma }_r}^2{(u-\Delta )}^2{\varphi }_2^{″}\left(u\right)+[\check{r}(u-\Delta )+c]{\varphi }_2^{\prime }\left(u\right)-(\tau +\gamma +\eta ){\varphi }_2\left(u\right)\hfill \\ \hfill & +\gamma \left[{\int }_0^{u-\Delta }{\varphi }_2(u-y)\mathrm{d}{F}_Y\left(y\right)+{\int }_{u-\Delta }^u{\varphi }_1(u-y)\mathrm{d}{F}_Y\left(y\right)+{\int }_u^{\infty }\omega (u,y-u)d{F}_Y\left(y\right)\right]\hfill \\ \hfill & +\eta \left[{\int }_{-\infty }^{L_q}{\varphi }_2\left(C_q\right)\mathrm{d}{F}_X\left(x\right)+{\int }_{L_q}^{+\infty }{\varphi }_3\left(C_q\right)\mathrm{d}{F}_X\left(x\right)\right]=0,\hfill \end{array}$$

(10)

when $b\le u<+\infty$,

$$\begin{array}{cc}\hfill & \frac{1}{2}{q}^2{{\sigma }_r}^2{(u-\Delta )}^2{\varphi }_3^{″}\left(u\right)+[\check{r}(u-\Delta )+c-\theta ]{\varphi }_3^{\prime }\left(u\right)-(\tau +\gamma +\eta ){\varphi }_3\left(u\right)\hfill \\ \hfill & +\gamma \left[{\int }_0^{u-b}{\varphi }_3(u-y)\mathrm{d}{F}_Y\left(y\right)+{\int }_{u-b}^{u-\Delta }{\varphi }_2(u-y)\mathrm{d}{F}_Y\left(y\right)+{\int }_{u-\Delta }^u{\varphi }_1(u-y)\mathrm{d}{F}_Y\left(y\right)\right]\hfill \\ \hfill & +\eta I\left(u<B_q\right)\left[{\int }_{-\infty }^{L_q}{\varphi }_2\left(C_q\right)\mathrm{d}{F}_X\left(x\right)+{\int }_{L_q}^{+\infty }{\varphi }_3\left(C_q\right)\mathrm{d}{F}_X\left(x\right)\right]\hfill \\ \hfill & +\eta I\left(u\ge B_q\right){\int }_{-\infty }^{+\infty }{\varphi }_3\left(C_q\right)\mathrm{d}{F}_X\left(x\right)+\gamma {\int }_u^{\infty }\omega (u,y-u)d{F}_Y\left(y\right)=0,\hfill \end{array}$$

with boundary conditions

$$\begin{array}{cc}\hfill & \varphi \left(0\right)=\omega (0,0)=1,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & \underset{u\to \infty }{lim}\varphi \left(u\right)=0,\hfill \end{array}$$

(12)

where

$$\begin{array}{cc}\hfill B_q& ={\displaystyle \frac{b-q\Delta }{1-q}},\hfill \\ \hfill C_q& =u+q(u-\Delta )(e^x-1),\hfill \\ \hfill L_q& =ln\frac{q(u-\Delta )+b-u}{q(u-\Delta )}.\hfill \end{array}$$

Proof. 

According to the processing procedure in reference [15], within a small interval $[0,dt]$, considering whether the claims and the jumps of the risk investment process occur, there are four scenarios.

(1) Neither the claims nor the jumps of the risk investment process occur, and the probability of this event occurring is $P(H_1>\mathrm{d}t,D_1>\mathrm{d}t)$;

(2) The claims occur, but the jumps of the risk investment process do not occur, and the probability of this event occurring is $P(H_1>\mathrm{d}t,D_1\le \mathrm{d}t)$;

(3) The jumps of the risk investment process occur, but no claims occur, and the probability of this event occurring is $P(H_1\le \mathrm{d}t,D_1>\mathrm{d}t)$;

(4) Both the claims and the jumps of the risk investment process occur, and the probability of this event occurring is $P(H_1\le \mathrm{d}t,D_1\le \mathrm{d}t)$.

We expand the probabilities of these four events using Taylor’s formula; we can obtain

$$\begin{array}{cc}\hfill & A_1=P(H_1>\mathrm{d}t,D_1>\mathrm{d}t)=1-(\eta +\gamma )\mathrm{d}t+o\left(\mathrm{d}t\right),\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & A_2=P(H_1>\mathrm{d}t,D_1\le \mathrm{d}t)=\gamma \mathrm{d}t+o\left(\mathrm{d}t\right),\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & A_3=P(H_1\le \mathrm{d}t,D_1>\mathrm{d}t)=\eta \mathrm{d}t+o\left(\mathrm{d}t\right),\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & A_4=P(H_1\le \mathrm{d}t,D_1>\mathrm{d}t)=\eta \gamma {\left(dt\right)}^2+o\left(\mathrm{d}t\right),\hfill \end{array}$$

(16)

where the fourth scenario is a low probability event and will not be considered. Therefore, using the total probability formula, when $0\le u<\Delta$,

$$\begin{array}{c}\hfill {\varphi }_1=e^{-\tau \mathrm{d}t}\left\{A_{1}E\left[{\varphi }_1(u+c\mathrm{d}t)\right]+A_{2}E\left[{\varphi }_1(u+c\mathrm{d}t-Y_1)\right]\right\}.\end{array}$$

(17)

According to Taylor’s formula, we have

$$\begin{array}{cc}E\left[{\varphi }_1(u+c\mathrm{d}t)\right]\hfill & ={\varphi }_1+c{\varphi }_1^{\prime }\mathrm{d}t+o\left(\mathrm{d}t\right).\hfill \end{array}$$

(18)

Next, substituting (13), (14) and (18) into (17), letting $\mathrm{d}t\to 0$, and then sorting it out, you obtain Equation (9).

Similarly, when $\Delta \le u<b$,

$$\begin{array}{cc}{\varphi }_2=\hfill & e^{-\tau \mathrm{d}t}\{A_{1}E\left[{\varphi }_2\left(B_1\right)\right]+A_{2}E[E\left[{\varphi }_2(B_1-Y_1)\right|Y_1\in (0,B_1-\Delta )]\hfill \\ \hfill & +E\left[{\varphi }_1(B_1-Y_1)\right|Y_1\in (B_1-\Delta ,+\infty )\left]\right]\hfill \\ \hfill & +A_{3}E[E\left[{\varphi }_2(B_1+q(u-\Delta )(e^{X_1}-1))\right|X_1\in (-\infty ,E_1)]\hfill \\ \hfill & +E\left[{\varphi }_3(B_1+q(u-\Delta )(e^{X_1}-1))\right|X_1\in (E_1,+\infty )\left]\right].\hfill \end{array}$$

(19)

When $b\le u<+\infty$,

$$\begin{array}{cc}{\varphi }_3=\hfill & e^{-\tau \mathrm{d}t}\{A_{1}E\left[{\varphi }_3\left(B_2\right)\right]+A_2[E\left[{\varphi }_3(B_2-Y_1)\right|Y_1\in (0,B_2-b)]\hfill \\ \hfill & +E\left[{\varphi }_2(B_2-Y_1)\right|Y_1\in (B_2-b,B_2-\Delta )]+E\left[{\varphi }_1(B_2-Y_1)\right|Y_1\in (B_2-\Delta ,+\infty )]]\hfill \\ \hfill & +A_3[E\left[{\varphi }_2(B_2+q(u-\Delta )(e^{X_1}-1))\right|X_1\in (-\infty ,E_2)]\hfill \\ \hfill & +E\left[{\varphi }_3(B_2+q(u-\Delta )(e^{X_1}-1))\right|X_1\in (E_2,+\infty )\left]\right],\hfill \end{array}$$

(20)

where

$$\begin{array}{cc}{B}_1\hfill & =u+q{\sigma }_r(u-\Delta )\mathrm{d}{W}_t+(\check{r}(u-\Delta )+c)\mathrm{d}t,\hfill \\ B_2\hfill & =u+q{\sigma }_r(u-\Delta )\mathrm{d}{W}_t+(\check{r}(u-\Delta )+c-\theta )\mathrm{d}t,\hfill \\ E_1\hfill & =ln\frac{q(u-\Delta )+b-B_1}{q(u-\Delta )},E_2=ln\frac{q(u-\Delta )+b-B_2}{q(u-\Delta )}.\hfill \end{array}$$

By the $\mathrm{It}\widehat{\mathrm{o}}$ formula, we can obtain

$$\begin{array}{cc}E\left[{\varphi }_2\left(B_1\right)\right]\hfill & =E\left[{\varphi }_2(u+q{\sigma }_r(u-\Delta )\mathrm{d}{W}_t+(\check{r}(u-\Delta )+c)\mathrm{d}t)\right]\hfill \\ \hfill & ={\varphi }_2+[\check{r}(u-\Delta )+c]{\varphi }_2^{\prime }\mathrm{d}t+\frac{1}{2}{q}^2{{\sigma }_r}^2{(u-\Delta )}^2{\varphi }_2^{″}\mathrm{d}t,\hfill \\ E\left[{\varphi }_3\left(B_2\right)\right]\hfill & =E\left[{\varphi }_3(u+q{\sigma }_r(u-\Delta )\mathrm{d}{W}_t+(\check{r}(u-\Delta )+c-\theta )\mathrm{d}t)\right]\hfill \\ \hfill & ={\varphi }_3+(\check{r}(u-\Delta )+c-\theta ){\varphi }_3^{\prime }\mathrm{d}t+\frac{1}{2}{q}^2{{\sigma }_r}^2{(u-\Delta )}^2{\varphi }_3^{″}\mathrm{d}t.\hfill \end{array}$$

(21)

By substituting (13)–(15) and (21) into (19) and (20), letting $\mathrm{d}t\to 0$, and then sorting it out, you obtain Equations (10) and (11).

Finally, when $u=0$, ruin will happen immediately, so (11) can be obtained; when $u\to \infty$, ruin will never happen, so (12) can be obtained. □

Remark 2. 

When $u>\Delta$, there is $q(u-\Delta )+\Delta -u<0$, which shows that $ln\frac{q(u-\Delta )+\Delta -u}{q(u-\Delta )}$ does not exist and $\underset{u\to \infty }{lim}ln\frac{q(u-\Delta )+\Delta -B_i}{q(u-\Delta )}=0,i=1,2$ does not exist either. So, asset jumps do not produce items smaller than Δ in (19) and (20).

Remark 3. 

According to the similar discussion in reference [15], we assume that $\varphi \left(u\right)$, ${\varphi }^{\prime }\left(u\right)$, and ${\varphi }^{″}\left(u\right)$ exist and are continuous.

4. Sinc Asymptotic Analysis

4.1. Approximate Solution of $\varphi \left(u\right)$

In this section, a sinc method to find the approximate solution of Equations (9)–(11) is provided. Since the sinc method [20] was proposed, it has been widely consideredand applied by scholars. It is often used in numerical calculus and numerical integration, especially in interpolation and approximation problems. In conclusion, the sinc method is a very useful tool and is widely used in numerical computation [21].

We define a one-to-one mapping

$$\begin{array}{c}\zeta \left(z\right)=logz.\hfill \end{array}$$

Then, the sinc grid point is

$$\begin{array}{c}{z}_k={\zeta }^{-1}\left(kh\right)=e^{kh},\hfill \end{array}$$

(22)

where $z\in \mathbb{R}$, k is an integer, and $h>0$ indicates the step size of grid points. Just as Definition 1.5.2 in reference [22] defines space, we have

$$\begin{array}{c}\Gamma =\{z\in \mathbb{R};z={\zeta }^{-1}\left(u\right),u\in \mathbb{R}\}.\hfill \end{array}$$

(23)

Merging the IDEs (9)–(11), we obtain

$$\begin{array}{cc}\hfill & {\rho }_1\left(u\right){\varphi }^{\prime \prime }\left(u\right)+{\rho }_2\left(u\right){\varphi }^{\prime }\left(u\right)+{\rho }_3\left(u\right)\varphi \left(u\right)+\gamma {\int }_0^u\varphi (u-y)f_Y\left(y\right)\mathrm{d}y\hfill \\ \hfill & +{\rho }_4{\int }_{-\infty }^{+\infty }\varphi (u+q(u-\Delta )(e^x-1))f_X\left(x\right)\mathrm{d}x+\gamma {\int }_u^{\infty }\omega (u,y-u)f_Y\left(y\right)\mathrm{d}y=0,\hfill \end{array}$$

(24)

where

$$\begin{array}{cc}{\rho }_1\left(u\right)\hfill & =\frac{1}{2}{q}^2{{\sigma }_r}^2{(u-\Delta )}^2{I}_{u>\Delta },{\rho }_2\left(u\right)=\check{r}(u-\Delta )I_{u>\Delta }+c-\theta I_{u>b},\hfill \\ {\rho }_3\left(u\right)\hfill & =-(\tau +\gamma +\eta ),{\rho }_4\left(u\right)=\eta I_{u>\Delta }.\hfill \end{array}$$

Then, transforming Equation (24), we have

$$\begin{array}{cc}\hfill & {\rho }_1\left(u\right){\varphi }^{″}\left(u\right)+{\rho }_2\left(u\right){\varphi }^{\prime }\left(u\right)+{\rho }_3\left(u\right)\varphi \left(u\right)+\gamma {\int }_0^u\varphi \left(y\right)J_1(u-y)\mathrm{d}y\hfill \\ \hfill & +{\rho }_4\left(u\right){\int }_{(1-q)u+q\Delta }^{+\infty }\varphi \left(z\right)J_2(u,z)\mathrm{d}z+\gamma {\int }_u^{\infty }\omega (u,y-u)f_Y\left(y\right)\mathrm{d}y=0,\hfill \end{array}$$

(25)

with boundary conditions

$$\begin{array}{c}\varphi \left(0\right)=1,\hfill \\ \underset{u\to \infty }{lim}\varphi \left(u\right)=0,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & J_1(u-y)=f_y(u-y),\hfill \\ \hfill & J_2(u,z)=\frac{f_X(ln\frac{z-u+q(u-\Delta )}{q(u-\Delta )})}{z-u+q(u-\Delta )}.\hfill \end{array}$$

By reference [22] (p. 73), we can let $M\left(u\right)=\varphi \left(u\right)-\frac{1}{1+u}$. So, we have

$$\begin{array}{cc}\hfill & {\rho }_1\left(u\right)M^{″}\left(u\right)+{\rho }_2\left(u\right)M^{\prime }\left(u\right)+{\rho }_3\left(u\right)M\left(u\right)+\gamma {\int }_0^{u}M\left(y\right)J_1(u-y)\mathrm{d}y\hfill \\ \hfill & +{\rho }_4\left(u\right){\int }_{(1-q)u+q\Delta }^{\infty }M\left(z\right)J_2(u,z)\mathrm{d}z+K\left(u\right)=0,\hfill \end{array}$$

(26)

with boundary conditions

$$\begin{array}{c}M\left(0\right)=0,\hfill \\ \underset{u\to \infty }{lim}M\left(u\right)=0,\hfill \end{array}$$

where

$$\begin{array}{cc}K\left(u\right)=\hfill & 2{(1+u)}^{-3}{\rho }_1\left(u\right)-{(1+u)}^{-2}{\rho }_2\left(u\right)+{(1+u)}^{-1}{\rho }_3\left(u\right)+\gamma {\int }_0^u\frac{J_1(u-y)}{1+y}\mathrm{d}y\hfill \\ \hfill & +\gamma {\int }_u^{\infty }\omega (u,y-u)f_y\left(y\right)\mathrm{d}y+{\rho }_4\left(u\right){\int }_{(1-q)u+q\Delta }^{\infty }\frac{J_2(u,z)}{1+z}\mathrm{d}z.\hfill \end{array}$$

Then, according to Theorems 1.5.13, 1.5.14, and 1.5.20 of reference [22], we define

$$\begin{array}{c}M=\left[\frac{\widehat{\kappa }N}{\widehat{\alpha }}\right],h={\left(\frac{\pi d}{\widehat{\kappa }N}\right)}^{\frac{1}{2}},\hfill \end{array}$$

where $0<\widehat{\alpha },\widehat{\kappa }\le 1$, $0<d<\pi$ and N is a positive integer. Then, we have

$$\begin{array}{cc}\hfill & {\int }_0^{u}M\left(y\right)J_1(u-y)\mathrm{d}y\approx {\displaystyle \sum _{j=-M}^N}{\displaystyle \sum _{i=-M}^N}{\vartheta }_i{A}_{ij}{M}_j,\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & {\int }_{(1-q)u+q\Delta }^{\infty }{J}_2(u,z)M\left(z\right)\mathrm{d}z\approx h{\displaystyle \sum _{j=-M}^N}{\displaystyle \sum _{i=-M}^N}{\vartheta }_i{\varsigma }_{ji}^{(-1)}\frac{J_2(u,u_j)}{{\varphi }^{\prime }\left(u_j\right)}{M}_j,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & M\left(u\right)\approx \widehat{M}\left(u\right)={\displaystyle \sum _{j=-M}^N}{M}_{j}S(j,h)\circ \zeta \left(u\right),\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & {\vartheta }_i=S(i,h)\circ \zeta \left(u\right)=sinc\left(\frac{\zeta \left(u\right)-ih}{h}\right),i=-M,...,N,\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & A=h{I}^{(-1)}{D}_m\left(\frac{1}{{\zeta }^{\prime }}\right),\hfill \end{array}$$

(31)

where

$$\begin{array}{c}{I}^{(-1)}=\left[{\varsigma }_{kj}^{(-1)}\right],{\varsigma }_{kj}^{(-1)}=\frac{1}{2}+{\int }_0^{k-j}\frac{sin\left(\pi x\right)}{\pi x}dx,sinc\left(x\right)=\left\{\begin{array}{cc}\frac{sinc\left(\pi x\right)}{\pi x},\hfill & x\ne 0,\\ \\ 1,\hfill & x=0,\end{array}\right.\hfill \end{array}$$

$M_j$ is an approximate estimate of $M\left(u_j\right)$ and $A_{ij}$ is the element of matrix A. Let $u_k=e^{kh}$, then we have

$$\begin{array}{cc}\widehat{M}\left(u_k\right)\hfill & ={\displaystyle \sum _{j=-M}^N}{M}_j[S(j,h)\circ \zeta \left(u_k\right)]={\displaystyle \sum _{j=-M}^N}{M}_j{\varsigma }_{jk}^{\left(0\right)},\hfill \end{array}$$

(32)

$$\begin{array}{cc}{\widehat{M}}^{\prime }\left(u_k\right)\hfill & ={\displaystyle \sum _{j=-M}^N}{M}_j{[S(j,h)\circ \zeta \left(u_k\right)]}^{\prime }={\displaystyle \sum _{j=-M}^N}{M}_j{\zeta }^{\prime }\left(u_k\right)h^{-1}{\varsigma }_{jk}^{\left(1\right)},\hfill \end{array}$$

(33)

$$\begin{array}{cc}{\widehat{M}}^{″}\left(u_k\right)\hfill & ={\displaystyle \sum _{j=-M}^N}{M}_j{[S(j,h)\circ \zeta \left(u_k\right)]}^{″}={\displaystyle \sum _{j=-M}^N}{M}_j[{\zeta }^{″}\left(u_k\right)h^{-1}{\varsigma }_{jk}^{\left(1\right)}+{\left({\zeta }^{\prime }\left(u_k\right)\right)}^2{h}^{-2}{\varsigma }_{jk}^{\left(2\right)}],\hfill \end{array}$$

(34)

where

$$\begin{array}{c}{\varsigma }_{jk}^{\left(0\right)}=\left\{\begin{array}{cc}0,\hfill & j\ne k,\\ \\ 1,\hfill & else,\end{array}\right.{\varsigma }_{jk}^{\left(1\right)}=\left\{\begin{array}{cc}\frac{{(-1)}^{(k-j)}}{k-j},\hfill & j\ne k;\\ \\ 0,\hfill & else,\end{array}\right.{\varsigma }_{jk}^{\left(2\right)}=\left\{\begin{array}{cc}\frac{-2{(-1)}^{(k-j)}}{{(k-j)}^2},\hfill & j\ne k,\\ \\ -\frac{{\pi }^2}{3},\hfill & else.\end{array}\right.\hfill \end{array}$$

Substituting Equations (27)–(29) and Equations (32)–(34) into Equation (26), we obtain

$${\displaystyle \sum _{j=-M}^N}\{{\rho }_1\left(u_k\right){\zeta }^{″}\left(u_k\right)\frac{{\varsigma }_{jk}^{\left(1\right)}}{h}+{\rho }_1\left(u_k\right){\left({\zeta }^{\prime }\left(u_k\right)\right)}^2\frac{{\varsigma }_{jk}^{\left(2\right)}}{h^2}+{\rho }_2\left(u_k\right){\zeta }^{\prime }\left(u_k\right)\frac{{\varsigma }_{jk}^{\left(1\right)}}{h}+{\rho }_3\left(u_k\right){\varsigma }_{jk}^{\left(0\right)}$$

$$+\gamma {\displaystyle \sum _{i=-M}^N}{\vartheta }_i\left(u_k\right)A_{ij}+h{\rho }_4\left(u_k\right){\displaystyle \sum _{i=-M}^N}{\vartheta }_i\left(u_k\right){\varsigma }_{ji}^{(-1)}\frac{J_2(u_k,u_j)}{{\zeta }^{\prime }\left(u_j\right)}\}{M}_j=-K\left(u_k\right).$$

(35)

Let us multiply both sides of Equation (35) by $\frac{h^2}{{\left({\zeta }^{\prime }\left(u_k\right)\right)}^2}$, then

$${\displaystyle \sum _{j=-M}^N}\{{\rho }_1\left(u_k\right){\varsigma }_{jk}^{\left(2\right)}+h\left[{\rho }_1\left(u_k\right)\frac{{\zeta }^{″}\left(u_k\right)}{{\left({\zeta }^{\prime }\left(u_k\right)\right)}^2}+\frac{{\rho }_2\left(u_k\right)}{{\zeta }^{\prime }\left(u_k\right)}\right]{\varsigma }_{jk}^{\left(1\right)}+h^2\frac{{\rho }_3\left(u_k\right)}{{\left({\zeta }^{\prime }\left(u_k\right)\right)}^2}{\varsigma }_{jk}^{\left(0\right)}$$

$$+\gamma \frac{h^2}{{\left({\zeta }^{\prime }\left(u_k\right)\right)}^2}{\displaystyle \sum _{i=-M}^N}{\vartheta }_i\left(u_k\right)A_{ij}+\frac{{\rho }_4\left(u_k\right)h^3}{{\left({\zeta }^{\prime }\left(u_k\right)\right)}^2{\zeta }^{\prime }\left(u_j\right)}{\displaystyle \sum _{i=-M}^N}{\vartheta }_i\left(u_k\right){\varsigma }_{ji}^{(-1)}{J}_2(u_k,u_j)\}{M}_j$$

$$=-\frac{h^{2}K\left(u_k\right)}{{\left({\zeta }^{\prime }\left(u_k\right)\right)}^2}.$$

(36)

Since

$${\varsigma }_{jk}^{\left(0\right)}={\varsigma }_{kj}^{\left(0\right)},{\varsigma }_{jk}^{\left(1\right)}=-{\varsigma }_{kj}^{\left(1\right)},{\varsigma }_{jk}^{\left(2\right)}={\varsigma }_{kj}^{\left(2\right)},\frac{{\zeta }^{″}\left(u_k\right)}{{\left({\zeta }^{\prime }\left(u_k\right)\right)}^2}=-{\left(\frac{1}{{\zeta }^{\prime }\left(u_k\right)}\right)}^{\prime },$$

Equation (36) can be rewritten as

$${\displaystyle \sum _{j=-M}^N}\{{\rho }_1\left(u_k\right){\varsigma }_{kj}^{\left(2\right)}+h\left[{\rho }_1\left(u_k\right){\left(\frac{1}{{\zeta }^{\prime }\left(u_k\right)}\right)}^{\prime }-\frac{{\rho }_2\left(u_k\right)}{{\zeta }^{\prime }\left(u_k\right)}\right]{\varsigma }_{kj}^{\left(1\right)}+h^2\frac{{\rho }_3\left(u_k\right)}{{\left({\zeta }^{\prime }\left(u_k\right)\right)}^2}{\varsigma }_{kj}^{\left(0\right)}$$

$$+\gamma \frac{h^2}{{\left({\zeta }^{\prime }\left(u_k\right)\right)}^2}{\displaystyle \sum _{i=-M}^N}{\vartheta }_i\left(u_k\right)A_{ij}+\frac{{\rho }_4\left(u_k\right)h^3}{{\left({\zeta }^{\prime }\left(u_k\right)\right)}^2{\zeta }^{\prime }\left(u_j\right)}{\displaystyle \sum _{i=-M}^N}{\vartheta }_i\left(u_k\right){\varsigma }_{ji}^{(-1)}{J}_2(u_k,u_j)\}{M}_j$$

$$=-\frac{h^{2}K\left(u_k\right)}{{\left({\zeta }^{\prime }\left(u_k\right)\right)}^2},k=-M,\dots ,N.$$

(37)

Next, we let $I^{\left(m\right)}=\left[{\varsigma }_{kj}^{\left(m\right)}\right],m=-1,0,1,2$,

$$\begin{array}{cc}\hfill & M={\left[M_j\right]}^T,j=-M,\cdots ,N,\hfill \\ \hfill & K=\left[-h^2\frac{K\left(u_{-M}\right)}{{\left({\zeta }^{\prime }\left(u_{-M}\right)\right)}^2},\dots ,-h^2\frac{K\left(u_N\right)}{{\left({\zeta }^{\prime }\left(u_N\right)\right)}^2}\right],\hfill \\ \hfill & C={\rho }_1{I}^{\left(2\right)}+h{D}_m\left({\rho }_1{\left(\frac{1}{{\zeta }^{\prime }}\right)}^{\prime }-\frac{{\rho }_2}{{\zeta }^{\prime }}\right)I^{\left(1\right)}+h^2{D}_m\left(\frac{{\rho }_3}{{\left({\zeta }^{\prime }\right)}^2}\right)I^{\left(0\right)}+h^2\gamma D_m\left(\frac{1}{{\left({\zeta }^{\prime }\right)}^2}\right){\vartheta }_{M}A\hfill \\ \hfill & +h^3{D}_m\left(\frac{{\rho }_4}{{\left({\zeta }^{\prime }\right)}^2}\right){\vartheta }_M{\left[I^{(-1)}\right]}^T{J}_2,\hfill \end{array}$$

where $J_2=\left[\frac{J_2(u_k,u_j)}{{\zeta }^{\prime }\left(u_k\right)}\right]$, ${\vartheta }_M=({\vartheta }_{-M},...,{\vartheta }_N)$, $D_m(.)$ represents a diagonal matrix, $I^{\left(m\right)}$ is a square matrix of order $M+N+1$, and ${\varsigma }_{kj}^{\left(m\right)}$ is the element of $I^{\left(m\right)}$. Then, we can rewrite Equation (37) as

$$\begin{array}{c}CM=K.\hfill \end{array}$$

(38)

By solving Equation (38), we can obtain $\widehat{M}\left(u\right)$, then obtain

$$\begin{array}{c}\varphi \left(u\right)\approx \tilde{\varphi }\left(u\right)={\displaystyle \sum _{j=-M}^N}{M}_{j}S(j,h)\circ \zeta \left(u\right)+\frac{1}{1+u}.\hfill \end{array}$$

(39)

4.2. Error Analysis

In this section, we will look for an upper bound on the error resulting from the sinc method approximation. When $\Delta \le u<b$, we divide both sides of Equation (10) by $\frac{q^2{{\sigma }_r}^2{(u-\Delta )}^2}{2}$, and we obtain

$$\begin{array}{c}{\varphi }^{″}\left(x\right)+{\tilde{\rho }}_1\left(x\right){\varphi }^{\prime }\left(x\right)+{\tilde{\rho }}_2\left(x\right)\varphi \left(x\right)+\tilde{G}\left(x\right)=0,\hfill \end{array}$$

(40)

where ${\tilde{\rho }}_1\left(x\right)=\frac{2[\breve{r}(u-\Delta )+c]}{q^2{{\sigma }_r}^2{(u-\Delta )}^2}$, ${\tilde{\rho }}_2\left(x\right)=-\frac{2(\tau +\gamma +\eta )}{q^2{{\sigma }_r}^2{(u-\Delta )}^2}$,

$$\begin{array}{cc}\tilde{G}\left(x\right)=\hfill & \frac{2\gamma }{q^2{{\sigma }_r}^2{(u-\Delta )}^2}\left[{\int }_0^u\varphi (u-y)d{F}_Y\left(y\right)+{\int }_u^{\infty }\omega (u,y-u)d{F}_Y\left(y\right)\right]\hfill \\ \hfill & +\frac{2\eta }{q^2{{\sigma }_r}^2{(u-\Delta )}^2}{\int }_{-\infty }^{+\infty }\varphi (u+q(u-\Delta )(e^x-1))d{F}_X\left(x\right).\hfill \end{array}$$

Then, Equation (40) satisfies the form of Equation (4.12) in reference [20], and according to the method in Section 4.2 of reference [20], we can obtain the following theorem.

Theorem 2. 

If $\varphi \left(u\right)$ is an exact solution to Equation (10) and $\tilde{\varphi }\left(u\right)$ is the approximate solution expressed by Equation (39), then there exists a constant $\tilde{c}$ independent of N, such that

$$\underset{u\in \Gamma }{sup}|\varphi \left(u\right)-\tilde{\varphi }\left(u\right)|\le \tilde{c}{N}^{5/2}{e}^{-\sqrt{\left(\pi d\widehat{\alpha }N\right)}}.$$

(41)

Proof. 

Let

$${\vartheta }_N\left(u\right)={\displaystyle \sum _{j=-M}^N}\varphi \left(u_j\right)S(j,h)\circ \zeta \left(u\right),$$

(42)

using the triangle inequality, it is easy to obtain

$$|\varphi \left(u\right)-\tilde{\varphi }\left(u\right)|\le |\varphi \left(u\right)-{\vartheta }_N\left(u\right)|+|{\vartheta }_N\left(u\right)-\tilde{\varphi }\left(u\right)|.$$

(43)

Based on Theorem 4.2.5 of [23], there exists a constant $c_1$, which is independent of N. We have

$$\underset{u\in \Gamma }{sup}|\varphi \left(u\right)-{\vartheta }_N\left(u\right)|\le c_1{N}^{1/2}{e}^{-\sqrt{\left(\pi d\widehat{\alpha }N\right)}}.$$

(44)

In inequality (43), $|{\vartheta }_N\left(u\right)-\tilde{\varphi }\left(u\right)|$ satisfies the following relation

$$|{\vartheta }_N\left(u\right)-\tilde{\varphi }\left(u\right)|=|{\displaystyle \sum _{j=-M}^N}[\varphi \left(u_j\right)-M_j]S(j,h)\circ \zeta \left(u\right)-\frac{1}{1+u}|$$

$$\le {\displaystyle \sum _{j=-M}^N}|\varphi \left(u_j\right)-M_j\left|\right|S(j,h)\circ \zeta \left(u\right)|$$

$$\le \sqrt{\left({\displaystyle \sum _{j=-M}^N}{|\varphi \left(u_j\right)-M_j|}^2\right)\left({\displaystyle \sum _{j=-M}^N}{\left|S\right(j,h)\circ \zeta (u\left)\right|}^2\right)}$$

$$\le \sqrt{\left({\displaystyle \sum _{j=-M}^N}{|\varphi \left(u_j\right)-M_j|}^2\right)}=\parallel \mathbf{H}-\mathbf{M}\parallel .$$

(45)

where $\mathbf{H}={\left[\varphi \left(u_j\right)\right]}^T,j=-M,\dots ,N.$ Similar to Theorem 7.2.6 of [23], if $u\in \Gamma$, then ${\sum }_{j\in \mathbb{Z}}{\left|S\right(j,h)\circ \zeta (u\left)\right|}^2=1$. We have

$$\parallel \mathbf{H}-\mathbf{M}\parallel =\parallel C^{-1}C(\mathbf{H}-\mathbf{M})\parallel$$

$$=\parallel C^{-1}[C\mathbf{H}-K]\parallel$$

$$\le \parallel C^{-1}\parallel \parallel C\mathbf{H}-K\parallel$$

$$\le c_2{N}^{5/2}{e}^{-\sqrt{\left(\pi d\widehat{\alpha }N\right)}},$$

(46)

where $c_2$ is independent of N. Let $\tilde{c}=max\{c_1,c_2\}$; then, the inequality (41) is finally obtained by combining Formulas (42)–(46). □

In the same way, we can obtain an upper bound on the error when $0\le u\le \Delta$ and $b<u<\infty$.

5. Numerical Analysis

5.1. Error Analysis of a Special Case

In this subsection, we assume that the claim follows an exponential distribution, and its p.d.f. is $f_Y\left(y\right)=\mu e^{-\mu y},0<y<\infty$. In addition, we also assume that $q=0$ and $r_1=0$. Therefore, we can obtain the real solution of the equation under certain conditions. By comparing it with the approximate solution obtained by the sinc method and calculating the relative error between them, the accuracy of the sinc method can be verified.

Firstly, let us rearrange Equations (9)–(11). For $b\le u<+\infty$, we have

$$(c-\theta ){\varphi }_3^{\prime }\left(u\right)-(\tau +\gamma ){\varphi }_3\left(u\right)+\gamma \left[{\int }_b^u{\varphi }_3\left(y\right)f_Y(u-y)dy+{\int }_{\Delta }^b{\varphi }_2\left(y\right)f_Y(u-y)dy\right]$$

$$+\gamma \left[{\int }_0^{\Delta }{\varphi }_1\left(y\right)f_Y(u-y)dy+{\int }_0^{\infty }\omega (u,y)f_Y(u+y)dy\right]=0.$$

(47)

Next, using operation $\frac{d^2}{d{u}^2}-{\mu }^2$, we can obtain

$$\begin{array}{c}(c-\theta ){\varphi }_3^{‴}\left(u\right)-(\tau +\gamma ){\varphi }_3^{″}\left(u\right)+(\gamma \mu -c{\mu }^2-\theta {\mu }^2){\varphi }_3^{\prime }\left(u\right)+\tau {\mu }^2{\varphi }_3\left(u\right)=0.\hfill \end{array}$$

So, the characteristic equation of the above equation is

$$\begin{array}{c}(c-\theta )s^3-(\tau +\gamma )s^2+(\gamma \mu -c{\mu }^2-\theta {\mu }^2)s+\tau {\mu }^2=0.\hfill \end{array}$$

According to the properties of the characteristic equation, we can obtain three roots $s_1$, $s_2$, and $s_3$, which has $s_1<0<s_2<s_3$.

Similarly, we can obtain that the characteristic equations in the other two cases are consistent, both of which are

$$\begin{array}{c}c{t}^3-(\tau +\gamma )t^2-\mu (c\mu -\theta )t+\tau {\mu }^2=0,\hfill \end{array}$$

which has three roots $t_1$, $t_2$, and $t_3$ ($t_1<0<t_2<t_3$). So, we can obtain

$$\begin{array}{c}\varphi \left(u\right)=\left\{\begin{array}{cc}{W}_1{e}^{t_{1}u}+W_2{e}^{t_{2}u}+W_3{e}^{t_{3}u},\hfill & 0\le u<b;\\ \\ R_1{e}^{s_{1}u}+R_2{e}^{s_{2}u}+R_3{e}^{s_{3}u},\hfill & b\le u<+\infty ,\end{array}\right.\hfill \end{array}$$

where $R_1$, $R_2$, $R_3$, $W_1$, $W_2$, and $W_3$ are the coefficient of uncertainty. According to boundary conditions (12), we obtain $R_1=R_2=0$. In addition, according to the analysis method in reference a, we can obtain

$$W_1+W_2+W_3=1,$$

$$W_1{e}^{t_{1}b}+W_2{e}^{t_{2}b}+W_3{e}^{t_{3}b}=R_1{e}^{s_{1}b},$$

$$W_1{t}_1{e}^{t_{1}b}+W_2{t}_2{e}^{t_{2}b}+W_3{t}_3{e}^{t_{3}b}=R_1{s}_1{e}^{s_{1}b},$$

$$(c{t}_1-\tau -\gamma )W_1{e}^{t_{1}b}+(c{t}_2-\tau -\gamma )W_2{e}^{t_{2}b}+(c{t}_3-\tau -\gamma )W_3{e}^{t_{3}b}=\check{c}{R}_1{e}^{s_{1}b},$$

(48)

where $\check{c}=(c-\theta -\tau -\gamma )$.

Finally, we set $c=0.6$, $\mu =2$, $\gamma =1$, $\tau =0.06$, $\theta =0.1$, and $b=10$, and by solving for (48), we can obtain an exact expression for $\varphi \left(u\right)$, and thus an exact solution. By comparing with the approximate solution, the relative error can be obtained, and the results are listed in the following table.

From Table 2, we can see that the relative error between the exact solution and the approximate solution is small, so the superiority of the sinc method can be explained.

Table 2. The relative error of $\varphi \left(u\right)$.

u	2.00	2.05	2.10	2.15	2.20	2.25	2.30	2.35	2.40
ES	0.4199	0.4109	0.4021	0.3935	0.3850	0.3767	0.3686	0.3607	0.3530
SA	0.4055	0.3999	0.3945	0.3891	0.3838	0.3785	0.3734	0.3684	0.3634
RE(%)	−3.44	−2.67	−1.90	−1.12	−0.32	0.48	1.29	2.12	2.96

5.2. Examples

In this subsection, two examples will be used to discuss the influence of different parameters on $\psi \left(u\right)$ when the claim follows different distributions. In the following, we assume that under a symmetric jump risk market, X obeys

$$\begin{array}{c}{f}_X\left(x\right)=p_1{\lambda }_1{e}^{-{\lambda }_{1}x}{I}_{x\ge 0}+q_1{\lambda }_2{e}^{{\lambda }_{2}x}{I}_{x<0},\hfill \end{array}$$

(49)

where $p_1+q_1=1,0<p_1,q_1<1,{\lambda }_1\ge 1,{\lambda }_2>0$. The details are given in the following discussion.

5.2.1. The Exponential Distribution Case

In this part, we assume that the claim follows

$$\begin{array}{c}{f}_Y\left(y\right)=\mu e^{-\mu y},0<y<\infty \hfill \end{array}$$

In the following example, we set the parameter as $\gamma =1$, $\theta =0.1$, $\delta =0$, $b=1$, $r_1=0.06$, $r_2=0.5$, $c=0.4$, $\mu =5$, $N=10,\widehat{\alpha }=\frac{\pi }{4},\widehat{\kappa }=\frac{1}{8},d=\frac{\pi }{12}$.

Example 1. 

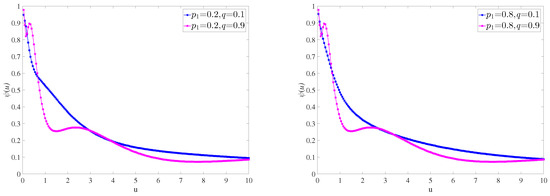
Firstly, we study the influence of q and $p_1$ on $\psi \left(u\right)$, respectively, taking two extreme cases. As shown in Figure 1, the larger the q, the greater the fluctuation of the $\psi \left(u\right)$ curve. When $u\in (0,1]$ and q is large, $\psi \left(u\right)$ is larger. When $u\in (1,10]$ and q is large, $\psi \left(u\right)$ will be relatively small. In real life, if we want to make more risky investments and minimize the ruin probability, we need to ensure that the initial surplus is large enough. Comparing the two pictures, we can find that $p_1$ has little effect on $\psi \left(u\right)$.

Figure 1. $\psi \left(u\right)$ for parameters ${\sigma }_r=0.2$, $\eta =5$, and $\Delta =0.01$.

Example 2. 

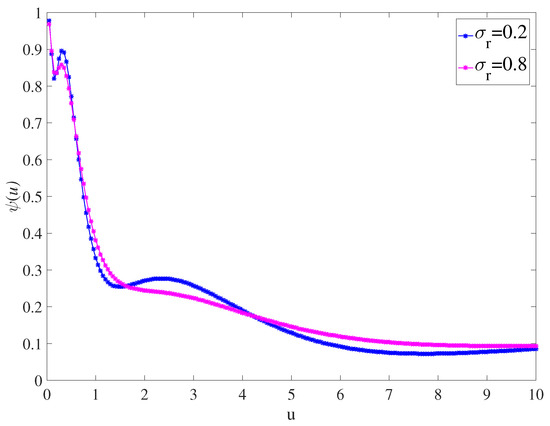
Secondly, we discuss the influence of ${\sigma }_r$ on $\psi \left(u\right)$, and still take two extreme cases for comparison, as shown in Figure 2. We can find that, on the whole, when $u\in (0,10]$, $\psi \left(u\right)$ shows a decreasing trend with the increase of initial surplus. In addition, when $u\in (0,1]$, ${\sigma }_r$ has little influence on $\psi \left(u\right)$, but when $u\in (1,10]$, ${\sigma }_r$ has a greater influence on $\psi \left(u\right)$. Therefore, in the actual situation, if we want to reduce the ruin probability by changing ${\sigma }_r$, we also need to consider the value of the initial surplus.

Figure 2. $\psi \left(u\right)$ for parameters $q=0.9$, $p_1=0.8$, $\eta =5$, and $\Delta =0.01$.

Example 3. 

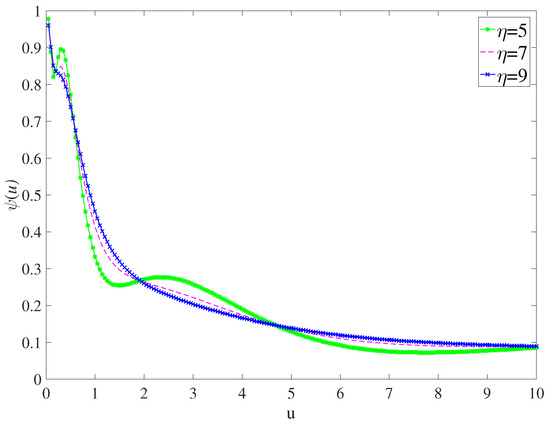
Next, we discuss the effect of η on $\psi \left(u\right)$, as shown in Figure 3. On the whole, when $u\in (0,10]$, $\psi \left(u\right)$ shows a decreasing trend with the increase of initial surplus. By comparing the three curves, it is found that the smaller the η, the greater the fluctuation of the curve. When $u\in (0,0.5]$, the smaller η is, the greater $\psi \left(u\right)$ is. When $u\in (0.5,2]$, the smaller η is, the smaller $\psi \left(u\right)$ is. When $u\in (2,5]$, the smaller η is, the greater $\psi \left(u\right)$ is. When $u\in (5,10]$, the smaller η is, the smaller $\psi \left(u\right)$ is. This experiment shows that the effect of η on $\psi \left(u\right)$ is not simply “the greater η, the smaller $\psi \left(u\right)$".

Figure 3. $\psi \left(u\right)$ for parameters $q=0.9$, $p_1=0.8$, ${\sigma }_r=0.2$, and $\Delta =0.01$.

Example 4. 

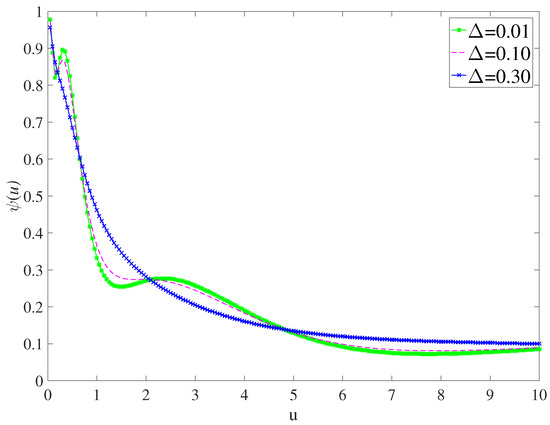
Finally, we discuss the effect of Δ on $\psi \left(u\right)$, as shown in Figure 4. On the whole, when $u\in (0,10]$, $\psi \left(u\right)$ shows a decreasing trend with the increase of initial surplus. By comparing the three curves, it is found that the larger the Δ, the smoother the trend of the $\psi \left(u\right)$ curve, and when the Δ is large enough, the Δ has almost no influence on $\psi \left(u\right)$. When u is in different interval segments, the effect of Δ on $\psi \left(u\right)$ is not invariable.

Figure 4. $\psi \left(u\right)$ for parameters $q=0.9$, $p_1=0.8$, $\eta =5$, and ${\sigma }_r=0.2$.

5.2.2. The Lognormal Distribution Case

In this part, we assume that the claim follows

$$\begin{array}{c}{f}_Y\left(y\right)=\left\{\begin{array}{cc}\frac{1}{2\pi \upsilon y}{e}^{-}\frac{{(lny-\chi )}^2}{4{\upsilon }^2},\hfill & 0<y<+\infty ;\\ \\ 0,\hfill & -\infty <y\le 0,\end{array}\right.\hfill \end{array}$$

where the mean and variance are $\chi$ and $2{\upsilon }^2$, respectively.

In the following example, the basic parameter settings are consistent with the exponential distribution example. In addition, we assume $\chi =0.1$, $\upsilon =0.1$.

Example 5. 

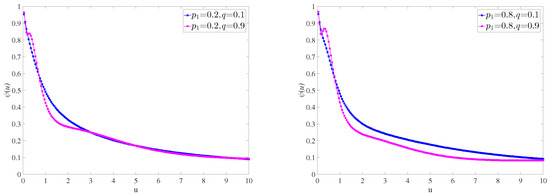
Firstly, we study the influence of q and $p_1$ on $\psi \left(u\right)$, again taking two extreme cases, as shown in Figure 5. Comparing the two pictures, we can find that when $p_1$ is a small value and $u\in (0,3]$, q has a greater impact on $\psi \left(u\right)$; when $u\in (3,10]$, q has little effect on $\psi \left(u\right)$. However, when $p_1$ is taken to a large value, q has a large effect on $\psi \left(u\right)$, and these effects become small only when u is sufficiently large.

Figure 5. $\psi \left(u\right)$ for parameters $b=1$, ${\sigma }_r=0.2$, $\eta =5$, and $\Delta =0.01$.

Example 6. 

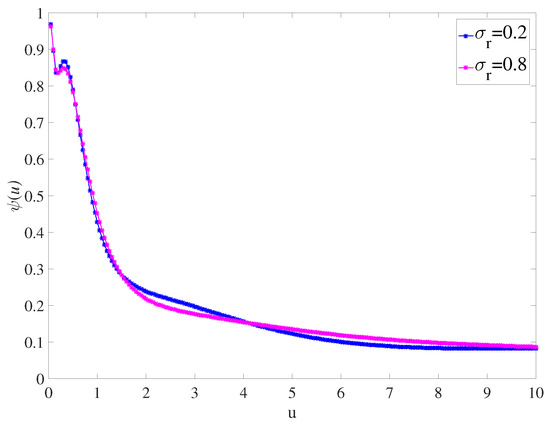
Secondly, we discuss the effect of ${\sigma }_r$ on $\psi \left(u\right)$, as shown in Figure 6. On the whole, $\psi \left(u\right)$ decreases with the increase of initial surplus; when $u\in (0,1]$, ${\sigma }_r$ has little influence on $\psi \left(u\right)$, but when $u\in (1,10]$, ${\sigma }_r$ has a great influence on $\psi \left(u\right)$. In addition, according to the trend of the curve, we can see that when u is large enough, the effect of the parameter ${\sigma }_r$ on $\psi \left(u\right)$ becomes small.

Figure 6. $\psi \left(u\right)$ for parameters $q=0.9$, $p_1=0.8$, $\eta =5$, and $\Delta =0.01$.

Example 7. 

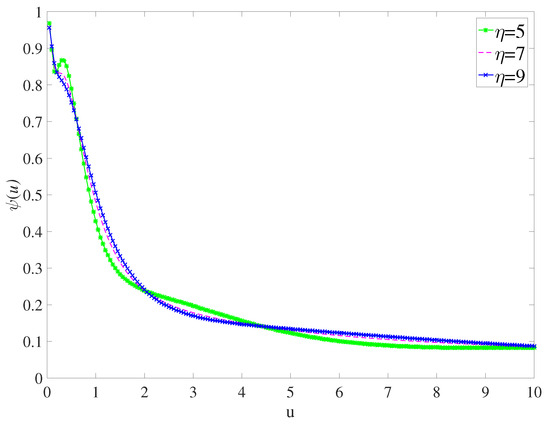
Next, we discuss the effect of η on $\psi \left(u\right)$, as shown in Figure 7. On the whole, with the increase of initial surplus, $\psi \left(u\right)$ shows a decreasing trend. By comparing the three curves, it is also found that the smaller the η, the greater the fluctuation of the curve. In addition, η has little effect on $\psi \left(u\right)$ when u is large enough.

Figure 7. $\psi \left(u\right)$ for parameters $q=0.9$, $p_1=0.8$, ${\sigma }_r=0.2$, and $\Delta =0.01$.

Example 8. 

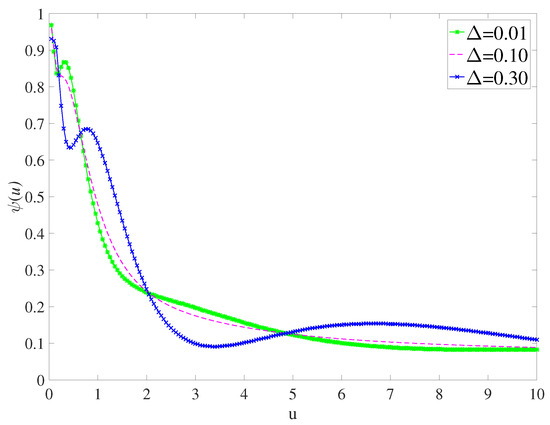
Finally, we discuss the effect of Δ on $\psi \left(u\right)$, as shown in Figure 8. We can intuitively see that the parameter Δ has a greater impact on $\psi \left(u\right)$, and it is shown that the larger the Δ, the greater the curve fluctuation of $\psi \left(u\right)$. However, we can still see that when u is large enough, the effect of Δ on $\psi \left(u\right)$ will become smaller.

Figure 8. $\psi \left(u\right)$ for parameters $q=0.9$, $p_1=0.8$, $\eta =5$, and ${\sigma }_r=0.2$.

6. Conclusions

In this paper, a new model that is more practical is proposed, and the approximate solution of the expected discounted penalty function is obtained by the sinc numerical approximation method. Then, we calculate the real solution of $\psi \left(u\right)$ under certain conditions and compare the error with the approximate solution obtained by the sinc method to show the feasibility and superiority of the sinc method. Finally, the numerical analysis is carried out under the assumption that the claims obey different distributions. The analysis shows that the parameters have significant effects on the ruin probability, and presents that the influence is not a simple linear relationship. As for the investment ratio, when the initial surplus is in different ranges, the impact of the investment ratio on the ruin probability is also different. However, on the whole, with the increase of initial surplus, the ruin probability shows a decreasing trend, which is consistent with the law of the actual situation.

This study provides a new model that is more practical and provides a theoretical basis for actuaries to carry out risk management. When insurance companies are faced with trade-offs between investment assets and liquid reserves, this study can be used to analyze the potential impact of different investment strategies to ensure they have enough liquid assets to pay claims while maintaining earnings. In addition, actuaries can use the model to predict the ruin probability of insurance companies under different claims and investment scenarios. This can help companies develop capital reserves and premium strategies to reduce the risk of ruin. In conclusion, this study is useful for dealing with complex risk scenarios involving claims, uncertainty, and investments, and can help actuaries develop more robust risk management strategies and ensure the long-term stability and profitability of insurance companies.

There are still two aspects of this study that need to be further improved. On the one hand, we need to find an approximate method with a better approximation effect to solve it. On the other hand, we hope to cooperate with insurance companies in the future and use real data for analysis in the future.