Differential Transform Method (DTM) and Physics-Informed Neural Networks (PINNs) in Solving Integral–Algebraic Equation Systems

Abstract

Integral–algebraic equations and their systems are a common description of many technical and engineering problems. Often, such models also describe certain dependencies occurring in nature (e.g., ecosystem behaviors). The integral equations occurring in this problem may have two types of domains—symmetric or asymmetric. Depending on whether such symmetry exists in the system describing a given problem, we must choose the appropriate method to solve this system. In this task, the absence of symmetry is more advantageous, but the presented examples demonstrate how one can approach cases where symmetry is present. In this paper, we present the application of two methods for solving such tasks: the analytical Differential Transform Method (DTM) and Physics-informed Neural Networks (PINNs). We consider a wide class of these types of equation systems, including Volterra and Fredholm integrals (which are also in a single model). We demonstrate that despite the complex nature of the problem, both methods are capable of handling such tasks, and thus, they can be successfully applied to the issues discussed in this article.

1. Introduction

Integral–algebraic equations and their systems (IAEs) are an important problem. Such tasks often appear in the description of mathematical models in various fields, including biology, heat conduction, viscoelasticity, electrical engineering, and chemical reactor processes [1,2,3,4,5,6]. At the same time, IAEs pose a challenging problem as there are no general analytical methods for solving such equations. Of course, in certain specific cases, with the appropriate form of the equation, this is possible. However, more often than not, the form of the task precludes such approaches. Various approximate techniques for solving these types of tasks also exist. In the literature, we encounter methods such as the use of Legendre polynomials, regularization methods, various types of multistep methods, and block pulse functions [7,8,9,10,11,12]. In most scientific papers, the IAEs describing a given problem are not too complex, and in many cases, there is no system of such equations, only a single equation. In some instances, systems of IAEs are considered; for example, in articles [7,9,13], systems of two equations are examined, while in [12,14], systems of three equations are analyzed. In this paper, we consider systems of IAEs in a very general form, not limiting ourselves to either the number of equations or their structure. The studied systems may include equations containing both the integral part and the algebraic part. The integrals present in the IAEs can be either Volterra-type or Fredholm-type. These integrals may also appear multiple times in the equations, and the relationships describing dependencies can be nonlinear. Of course, the number of equations that contain or do not contain the above-mentioned components can vary, and there may also be cases where certain components do not occur in the system of IAEs.

In general, we, therefore, consider systems of the following form:

$$\mathrm{\Phi }(x,\mathit{y},\mathit{F},\mathit{V})=\mathbf{0},$$

(1)

where

$$\mathrm{\Phi }={\left[{\phi }_1,{\phi }_2,\dots ,{\phi }_n\right]}^T,\mathit{y}={\left[y_1,y_2,\dots ,y_n\right]}^T,\mathit{F}={\left[f_1,f_2,\dots ,f_m\right]}^T,\mathit{V}={\left[v_1,v_2,\dots ,v_k\right]}^T,$$

(2)

and

$$f_i={\int }_a^b{\mathcal{F}}_i(x,\mathit{y}\left(x\right))dx,i=1,2,\dots ,m,$$

$$v_i={\int }_a^x{\mathcal{G}}_i(t,\mathit{y}\left(t\right))dt,i=1,2,\dots ,k,$$

and where the functions ${\phi }_i:{\mathbb{R}}^{s_i}\to \mathbb{R}$, $s_i\le 1+n+m+k$, $i=1,2,\dots ,n$, $y_i:\mathbb{R}\to \mathbb{R}$, $i=1,2,\dots ,n$, ${\mathcal{F}}_i:{\mathbb{R}}^{s_i}\to \mathbb{R}$, $s_i\le 1+n$, $i=1,2,\dots ,m$, ${\mathcal{G}}_i:{\mathbb{R}}^{s_i}\to \mathbb{R}$, $s_i\le 1+n$, $i=1,2,\dots ,k$, $x\in [a,b]\subset \mathbb{R}$ describe the relationships connecting the equations in the considered IAEs or in the integrals that appear in these equations.

To solve the system (1), we use the DTM method (see Section 2) and PINNs (see Section 3). DTM is a method applied to many different problems. The authors have successfully applied this method, among others, to solve ODE problems and integral–differential equations with delayed arguments [15,16,17]. There are also other applications of this method, mainly for solving differential equations, including partial differential equations, integral equations, equations with shifted arguments, or fractional-order differential equations [18,19,20,21,22]. The PINN method also has a wide range of applications, which allows it to be used for solving various types of problems. Recently, a number of publications on PINNs have appeared in the scientific literature. For example, paper [23] concerns PINNs and metalearning and transfer learning concepts. The authors evaluate their approach to several canonical forward-parameterized PDEs presented in the scientific literature on PINNs. In [24], an algorithm for PINNs applied to the acoustic wave equation and full waveform inversions is presented. The authors of the following paper have successfully tested this method, for example, for solving variational calculus problems [25]. PINNs are also applicable for solving integro-differential equations [26]. The article [27] presents the application of stochastic procedures of the Levenberg–Marquardt backpropagation neural networks (LMBNNs) in modeling kidney dysfunction caused by hard water consumption. The accuracy of the model was validated by comparing the results, with a negligible absolute error observed.

2. Different Transform Method

Zhou can be considered the creator of DTM, as he described and applied it to certain electronic problems in 1986 [28].

Definition 1.

The original is a function that can be expanded into a Taylor series around a certain point $x_0$ [28,29].

According to the above definition, and assuming that the function f is the original, we can write (for the specific case of the Taylor series where $x_0=0$, i.e., in the case of the Maclaurin series):

$$f\left(x\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{f^{\left(k\right)}\left(0\right)}{k!}}{x}^k.$$

Thus, based on the theorem of the uniqueness of this expansion, a function (transformation) can be assigned to each original f. Let $F:\mathbb{N}\cup \left\{0\right\}\to \mathbb{R}$:

$$F\left(k\right)={\displaystyle \frac{f^{\left(k\right)}\left(0\right)}{k!}},k=0,1,\dots$$

Considering the transformation F of the original f, we can represent this original in the form of

$$f\left(x\right)=\sum _{k=0}^{\infty }F\left(k\right)x^k.$$

Thanks to the properties of the Taylor transformation and the known forms of transforms of basic functions, we can relatively easily determine the transforms of more complex functions, their derivatives, and integrals. By applying these properties and using a computational platform, we can efficiently solve IAEs tasks.

Properties of the Taylor Transform

In this subsection, the basic properties of the DTM transformation are presented. We limit these properties to only those that are used in presented examples. Many other properties and their proofs can be found in the cited literature.

In the following properties, we assume that x is an element of domain of the considered function f, and $\mathbb{Z}\ni k\ge 0$.

• If $f\left(x\right)=x^m$, $\mathbb{Z}\ni m\ge 0$, then

  $$F\left(k\right)=\delta (k-m)=\left\{\begin{array}{cc}1,\hfill & k=m,\hfill \\ 0,\hfill & k\ne m.\hfill \end{array}\right.$$

  (3)
• If $f\left(x\right)=e^{ax}$, $a\in \mathbb{R}$, then

  $$F\left(k\right)={\displaystyle \frac{a^k}{k!}}.$$

  (4)
• If $f\left(x\right)=sin\left(ax\right)$, $a\in \mathbb{R}$, then

  $$F\left(k\right)={\displaystyle \frac{a^k}{k!}}sin{\displaystyle \frac{k\pi }{2}}.$$

  (5)
• If $f\left(x\right)=cos\left(ax\right)$, $a\in \mathbb{R}$, then

  $$F\left(k\right)={\displaystyle \frac{a^k}{k!}}cos{\displaystyle \frac{k\pi }{2}}.$$

  (6)
• If $f\left(x\right)=u\left(x\right)\pm v\left(x\right)$, then

  $$F\left(k\right)=U\left(x\right)\pm V\left(x\right).$$

  (7)
• If $f\left(x\right)=a·u\left(x\right)$, $a\in \mathbb{R}$, then

  $$F\left(k\right)=a·U\left(x\right).$$

  (8)
• If $f\left(x\right)=x^m·u\left(x\right)$, then

  $$F\left(k\right)=\left\{\begin{array}{cc}0,\hfill & k<m,\hfill \\ U(k-m),\hfill & k\ge m.\hfill \end{array}\right.$$

  (9)
• If $f\left(x\right)=u\left(x\right)·v\left(x\right)$, then

  $$F\left(k\right)=\sum _{i=0}^{k}U\left(i\right)V(k-i)=\sum _{i=0}^{k}V\left(i\right)U(k-i).$$

  (10)
• If $f\left(x\right)=u\left(x\right)·v\left(x\right)·w\left(x\right)$, then

  $$F\left(k\right)=\sum _{i=0}^k\sum _{j=0}^{k-i}U\left(i\right)V\left(j\right)W(k-i-j)=\sum _{i=0}^k\sum _{j=0}^{i}U\left(j\right)V(i-j)W(k-i).$$

  (11)
• If ${\displaystyle f\left(x\right)=\underset{0}{\overset{x}{\int }}u\left(t\right)dt}$, then

  $$F\left(k\right)=\left\{\begin{array}{cc}0,\hfill & k=0,\hfill \\ {\displaystyle \frac{U(k-1)}{k},}\hfill & k\ge 1.\hfill \end{array}\right.$$

  (12)
• If ${\displaystyle f\left(x\right)=\underset{0}{\overset{x}{\int }}u\left(t\right)v\left(t\right)dt}$, then $F\left(0\right)=0$ and, for $k\ge 1$:

  $$F\left(k\right)=\sum _{i=0}^{k-1}{\displaystyle \frac{U\left(i\right)V(k-i-1)}{k}}=\sum _{i=0}^{k-1}{\displaystyle \frac{V\left(i\right)U(k-i-1)}{k}}.$$

  (13)
• If ${\displaystyle f\left(x\right)=u\left(x\right)\underset{0}{\overset{x}{\int }}v\left(t\right)dt}$, then $F\left(0\right)=0$ and, for $k\ge 1$:

  $${\displaystyle F\left(k\right)=\sum _{i=0}^{k-1}U\left(i\right)\frac{V(k-i-1)}{k-i}.}$$

  (14)
• If ${\displaystyle f\left(x\right)=u\left(x\right)\underset{0}{\overset{x}{\int }}v\left(t\right)w\left(t\right)dt}$, then $F\left(0\right)=0$ and, for $k\ge 1$:

  $$F\left(k\right)=\sum _{i=0}^{k-1}\sum _{j=0}^{k-i-1}{\displaystyle \frac{U\left(i\right)V\left(j\right)W(k-i-j-1)}{k-i}}.$$

  (15)

The proofs of these properties are not difficult (some of them directly follow from the Taylor series expansions of known functions) and can be found in the cited literature.

3. Physics-Informed Neural Networks—Description

Physics-informed neural networks (PINNs) are an innovative method for solving both ordinary and partial differential equations, as well as integro-differential equations, by leveraging deep learning. Early contributions to this approach include the articles of Raisi et al. [30] and Karniadakis et al. [31]. PINNs combine neural network architectures with the governing principles of physics by embedding differential or integro-differential equations and initial or boundary conditions directly into the network’s loss function. This ensures that the model’s predictions remain consistent with the underlying physical laws.

One of the key advantages of PINNs lies in their flexibility and efficiency, offering an alternative to classical numerical methods, which can be hindered by computational expenses and scalability issues, particularly in high-dimensional problems. Once trained, PINNs can generate solutions across any grid, offering a notable benefit over classical techniques such as finite difference methods or other and other mesh-based methods. Furthermore, they are adept at managing complex boundary and initial conditions and can seamlessly integrate experimental data into the model. This capability not only enhances solution accuracy but also enables PINNs to learn and adjust to real-world situations where data might be limited or noisy. As a result, PINNs have demonstrated considerable success in diverse fields, including fluid dynamics, materials science, and biological systems [32,33,34].

The architecture of PINN is built upon traditional elements of neural networks, such as feedforward processing, backpropagation, hidden layers, the number of nodes in each hidden layer, and activation functions. The training of the neural network is typically performed using optimization methods like the Adam optimizer. The PINN framework described in the article comprises two key components (see Figure 1): a fully connected neural network and a loss function module, which calculates the loss as the weighted $L2$ norm of the residuals from both the governing system of IAEs and the boundary conditions. In Figure 1, X represents the input to the fully connected neural network, and Y is the output of this network. The output Y represents the approximate solutions of the desired functions in the considered problem. The loss function is defined as the sum of domain errors (arising from the system of integro-algebraic equations defining the problem) and boundary errors (resulting from the initial and boundary conditions). The neural network is trained to minimize this loss function. This process leads to finding the network parameters ${\mathrm{\Theta }}^{*}$ that allow for approximating the solution to the problem defined by the system of equations. Once the model is trained, a grid of points (arguments) can be provided as input to the network. At the network’s output, we obtain approximate values of the unknown functions at these points, which enables the solution of the problem in a discrete form.

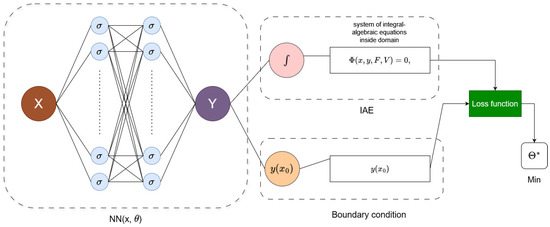
Figure 1. Schema of physics-informed neural network for solving system of IAEs with boundary conditions.

For the considered system of integral–algebraic equations

$$\mathrm{\Phi }(x,\mathit{y},\mathit{F},\mathit{V})=\mathbf{0},$$

and boundary conditions

$$\mathit{y}\left(x_0\right)={\mathit{y}}_0,$$

a loss function is constructed:

$$\mathcal{L}=\sum _{i=1}^N\mathrm{\Phi }(x,\mathit{y},\mathit{F},\mathit{V})+(\mathit{y}\left(x_0\right)-{\mathit{y}}_0),$$

(16)

where N is the number of training points inside the domain used in the training process. The process of building and training a neural network aims to learn a model to find the best weights and biases (parameters of the model) ${\mathrm{\Theta }}^{*}$ by finding (optimizing) the loss function $\mathcal{L}$.

4. Examples

In this section, we present four examples to demonstrate the universality and effectiveness of the discussed methods. The examples differ in terms of the number and type of equations. They also include typical problems that may arise when solving IDE tasks (along with a discussion on how to address these problems).

4.1. Example 1

Consider a system of integro-algebraic equations consisting of one integral equation and one algebraic equation:

$$\left\{\begin{array}{c}{\displaystyle y_2\left(x\right)=e^x\left(2cosx-1\right)+e^x{\int }_0^x{e}^{-t}{y}_2\left(t\right)dt,}\hfill \\ {\displaystyle y_1\left(x\right)y_2\left(x\right)=2e^x{y}_1\left(x\right)cosx-sin2x+1,}\hfill \end{array}\right.$$

(17)

where $x\in [0,\pi ]$ and $y_1$, $y_2$ are the searched functions.

4.1.1. DTM Approach

Assume that $Y_1\left(k\right)$ and $Y_2\left(k\right)$ are transforms of the functions $y_1\left(x\right)$ and $y_2\left(x\right)$. To simplify the form of the following formulas, let us assume $x=0$ in the system (17) (we would obtain a similar result by taking $k=0$). From the first equation of this system, we will obtain $y_2\left(0\right)=1$, while from the second one (also using the calculated value of $y_2\left(0\right)$), we will obtain $y_1\left(0\right)=-1$. This means $Y_1\left(0\right)=-1$ and $Y_2\left(0\right)=1$. Now for $k\ge 1$, the system (17), based on the properties (3)–(8), (10) and (15) will transform into the following:

$$\begin{array}{cc}\hfill Y_2\left(k\right)& =2\sum _{i=0}^k{\displaystyle \frac{cos\frac{i\pi }{2}}{i!(k-i)!}}-{\displaystyle \frac{1}{k!}}+\sum _{i=0}^{k-1}\sum _{j=0}^{k-i-1}{\displaystyle \frac{{(-1)}^j{Y}_2(k-i-j-1)}{i!j!(k-i)}},\hfill \\ \hfill \sum _{i=0}^k{Y}_1\left(i\right)Y_2(k-i)& =-{\displaystyle \frac{2^{k}sin\frac{k\pi }{2}}{k!}}+2\sum _{i=0}^k\sum _{j=0}^{k-i}{\displaystyle \frac{cos\frac{(k-i-j)\pi }{2}{Y}_1\left(j\right)}{i!(k-i-j)!}}.\hfill \end{array}$$

By limiting ourselves to nine terms ($0\le k\le 8$), we obtain approximate solutions:

$$\begin{array}{cc}\hfill y_{1,8}\left(x\right)& =\sum _{i=0}^8{Y}_1\left(i\right)x^i=-1+2x-x^2+{\displaystyle \frac{1}{6}}{x}^4-{\displaystyle \frac{1}{15}}{x}^5+{\displaystyle \frac{1}{90}}{x}^6-{\displaystyle \frac{1}{2520}}{x}^8,\hfill \\ \hfill y_{2,8}\left(x\right)& =\sum _{i=0}^8{Y}_2\left(i\right)x^i=1+2x+x^2-{\displaystyle \frac{1}{6}}{x}^4-{\displaystyle \frac{1}{15}}{x}^5-{\displaystyle \frac{1}{90}}{x}^6+{\displaystyle \frac{1}{2520}}{x}^8.\hfill \end{array}$$

Figure 2 presents a comparison of this solution with the exact solutions, while Figure 3 shows a comparison of the approximate solutions $y_{i,15}$, $i=1,2$ with the exact solutions, which are functions:

$$y_1\left(x\right)=e^{-x}\left(sinx-cosx\right),y_2\left(x\right)=e^x\left(sinx+cosx\right).$$

The $\Delta \left(x\right)$ error is calculated as follows:

$$\Delta \left(x\right)=\left|y_{i,n}-y_i\right|i=1,2,\dots ,k,$$

where k is the number of unknowns in the system (1).

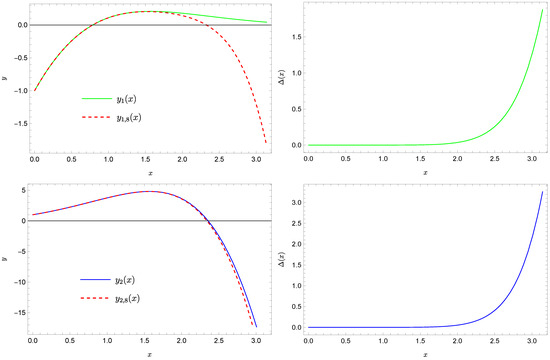
Figure 2. The exact solution $y_1$ (solid green line), the approximate $y_{1,8}$ (dashed red line), and the absolute errors $\Delta$ of this approximation, as well as the exact solution $y_2$ (solid blue line), the approximate $y_{2,8}$ (dashed red line), and absolute errors $\Delta$ of this approximation.

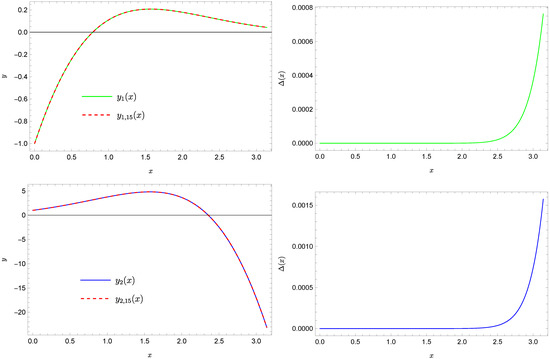
Figure 3. The exact solution $y_1$ (solid green line), the approximate $y_{1,15}$ (dashed red line), and the absolute errors $\Delta$ of this approximation, as well as the exact solution $y_2$ (solid blue line), the approximate $y_{2,15}$ (dashed red line), and the absolute errors $\Delta$ of this approximation.

By expanding the functions $y_1$ and $y_2$ into their respective Taylor series, it turns out that the obtained solutions exactly correspond to the successive terms of these series.

4.1.2. PINN Approach

The system of Equations (17) was also solved using neural networks (PINNs). In the considered example, the following architecture and parameters are set:

• The network consists of three hidden layers, each containing 20 neurons;
• The network takes one input and two outputs (there are two unknown functions in the system);
• A fully connected neural network (FNN) is defined, which is used to model the solution;
• The activation function in each layer is the hyperbolic tangent, which helps in nonlinear modeling of relationships;
• The weights are initialized using the “Glorot uniform” method, a common technique that ensures proper scaling of the weights to improve training stability;
• 32 training points are considered.

In Figure 4, the obtained results, along with the errors, are presented. On the left side, the plots of the approximate solution (red dashed line) and the exact solution (solid lines) are shown. As can be observed, the approximate solutions for the functions $y_1$ and $y_2$ almost overlap with the exact solutions. The corresponding errors are presented on the right side. Errors for the function $y_1$ (maximum error $\approx 0.02$) are significantly smaller than those for the function $y_2$ (maximum error $\approx 1.5$). For the function $y_2$, the largest errors are observed at the right boundary of the domain.

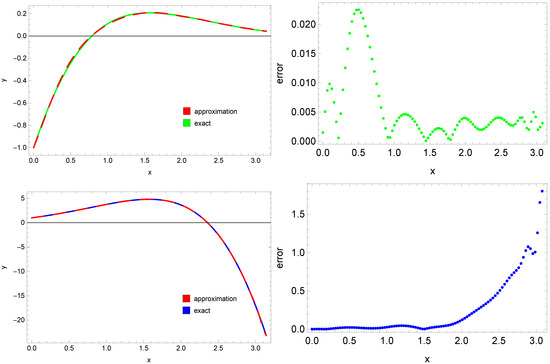
Figure 4. The exact solution $y_1$ (solid green line), the approximation (dashed red line), the absolute errors of approximation of $y_1$ (green dotted line—right side), the exact solution $y_2$ (solid blue line), the approximation (dashed red line), and the absolute errors of approximation of $y_2$ (blue dotted line—right side).

4.2. Example 2

We consider a system of integro-algebraic equations, which consists of two integral equations and one algebraic equation:

$$\left\{\begin{array}{c}{\displaystyle y_1\left(x\right)=y_2\left(x\right)y_3\left(x\right)+x\frac{1-\sqrt{2}}{e^{\pi /4}}+x{\int }_0^{\frac{\pi }{4}}\left(2sint-1\right)\left(2y_1\left(t\right)-e^t\right)dt,}\hfill \\ {\displaystyle y_2\left(x\right)=x+e^{-x}+y_1\left(x\right)+{\int }_0^x\left(\left(e^{2t}+1\right)y_3\left(t\right)-e^{2t}\right)dt,}\hfill \\ {\displaystyle y_1\left(x\right)+y_2\left(x\right)+\left(e^{2x}+1\right)y_3\left(x\right)=e^x+e^{2x}-1,}\hfill \end{array}\right.$$

(18)

where $x\in [0,{\displaystyle \frac{\pi }{4}}]$ and $y_1$, $y_2$, $y_3$ are the searched functions.

4.2.1. DTM Approach

Let $Y_1\left(k\right)$, $Y_2\left(k\right)$, and $Y_3\left(k\right)$ be the transforms of the functions $y_1\left(x\right)$, $y_2\left(x\right)$, and $y_3\left(x\right)$. If we substitute $x=0$ (or equivalently $k=0$) into system (18), we obtain the following system of equations:

$$\left\{\begin{array}{c}{y}_1\left(0\right)=y_2\left(0\right)y_3\left(0\right),\hfill \\ y_2\left(0\right)=1+y_1\left(0\right),\hfill \\ y_1\left(0\right)+y_2\left(0\right)+2y_3\left(0\right)=1,\hfill \end{array}\right.$$

which is equivalent to the system

$$\left\{\begin{array}{c}{Y}_1\left(0\right)=Y_2\left(0\right)Y_3\left(0\right),\hfill \\ Y_2\left(0\right)=1+Y_1\left(0\right),\hfill \\ Y_1\left(0\right)+Y_2\left(0\right)+2Y_3\left(0\right)=1.\hfill \end{array}\right.$$

It turned out that the solution $Y_1\left(0\right)=-2$, $Y_2\left(0\right)=-1$, $Y_3\left(0\right)=2$ generates three groups of approximate solutions, each of which results in large errors $|{\phi }_i|$. We therefore assume $Y_1\left(0\right)=0$, $Y_2\left(0\right)=1$, $Y_3\left(0\right)=0$ (in this case, the errors $|{\phi }_i|$ are significantly smaller). Applying the DTM transform to system (18), for $k\ge 1$, we obtain the following:

$$\begin{array}{cc}\hfill Y_1\left(k\right)& =\sum _{i=0}^k{Y}_2\left(i\right)Y_3(k-i)+\alpha \delta (k-1)+{\displaystyle \frac{1-\sqrt{2}}{e^{\pi /4}}}\delta (k-1),\hfill \\ \hfill Y_2\left(k\right)& =\delta (k-1)+Y_1\left(k\right)+{\displaystyle \frac{{(-1)}^k-2^{k-1}}{k!}}+{\displaystyle \frac{Y_3(k-1)}{k}}+\sum _{i=0}^{k-1}{\displaystyle \frac{2^i{Y}_3(k-i-1)}{k·i!}},\hfill \\ \hfill Y_1\left(k\right)& +Y_2\left(k\right)+Y_3\left(k\right)+\sum _{i=0}^k{\displaystyle \frac{2^i{Y}_3(k-i)}{i!}}={\displaystyle \frac{1+2^k}{k!}}-\delta (k-1).\hfill \end{array}$$

We obtained these formulas by using, among others, the properties (3)–(8), (10), (12) and (13) and by transforming the second equation of the system (18):

$${\int }_0^x\left(\left(e^{2t}+1\right)y_3\left(t\right)-e^{2t}\right)dt={\int }_0^x{e}^{2t}{y}_3\left(t\right)dt+{\int }_0^x{y}_3\left(t\right)dt-{\displaystyle \frac{1}{2}}\left(e^{2x}-1\right).$$

All the coefficients $Y_1\left(k\right)$ and $Y_2\left(k\right)$ for $k\ge 1$ depend on an unknown parameter $\alpha$ (the k-th coefficient is a polynomial of degree k), which from the first equation of system (18) takes the following form:

$$\alpha ={\int }_0^{{\displaystyle \frac{\pi }{4}}}\left(2sint-1\right)\left(2y_1\left(t\right)-e^t\right)dt.$$

Taking nine consecutive coefficients determined in this way ($0\le k\le 8$), we obtain the approximate solutions $y_{1,8}$, $y_{2,8}$, and $y_{3,8}$, which still depend on the parameter $\alpha$. We determine this parameter by solving the equation:

$$\alpha ={\int }_0^{{\displaystyle \frac{\pi }{4}}}\left(2sint-1\right)\left(2y_{1,8}\left(t\right)-e^t\right)dt.$$

The equation has two solutions: $-3.23382$ and $-1.54\times {10}^{-8}$ (so we have two groups of solutions, similar to the previous example where we generated three groups). After conducting the tests mentioned in the initial part of this example, it turns out that the second value, $\alpha =-1.54\times {10}^{-8}$, yields satisfactory results. For this value of the parameter $\alpha$, the approximate solutions take the form:

$$\begin{array}{cc}\hfill y_{1,8}\left(x\right)& =\sum _{i=0}^8{Y}_1\left(i\right)x^i=x-9.63\times {10}^{-9}{x}^2+0.166667x^3+1.97\times {10}^{-9}{x}^4\hfill \\ \hfill & +0.00833334x^5+1.1\times {10}^{-9}{x}^6+0.000198412x^7-6.26\times {10}^{-10}{x}^8,\hfill \\ \hfill y_{2,8}\left(x\right)& =\sum _{i=0}^8{Y}_2\left(i\right)x^i=1-7.7\times {10}^{-9}x+0.5x^2+9.63\times {10}^{-10}{x}^3+0.0416667x^4\hfill \\ \hfill & +1.9\times {10}^{-9}{x}^5+0.00138889x^6-5.7\times {10}^{-10}{x}^7+0.0000248011x^8,\hfill \\ \hfill y_{3,8}\left(x\right)& =\sum _{i=0}^8{Y}_3\left(i\right)x^i=x-1.9\times {10}^{-9}{x}^2-0.333333x^3-6.02\times {10}^{-10}{x}^4\hfill \\ \hfill & +0.133333x^5+9.28\times {10}^{-10}{x}^6-0.0539683x^7-3.98\times {10}^{-10}{x}^8.\hfill \end{array}$$

Figure 5 compares the approximate solutions $y_{i,8}$, $i=1,2,3$ with the exact solutions (where we know that $\alpha =0$), which are the functions:

$$y_1\left(x\right)=sinhx,y_2\left(x\right)=coshx,y_3\left(x\right)=tanhx.$$

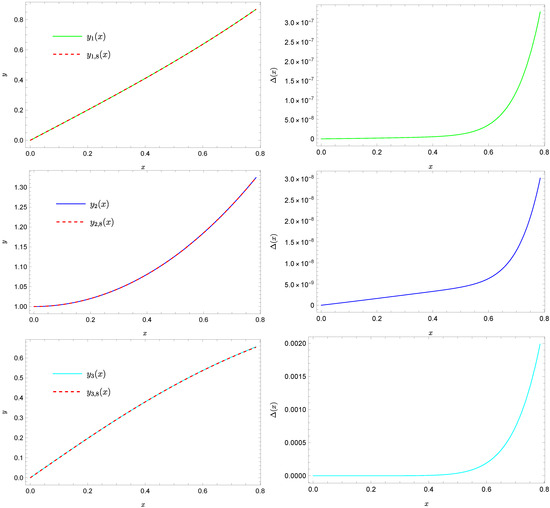
Figure 5. Exact solution $y_1$ (solid green line), approximate $y_{1,8}$ (dashed red line), exact solution $y_2$ (solid blue line), approximate $y_{2,8}$ (dashed red line), exact solution $y_3$ (solid cyan line), approximate solution $y_{3,8}$ (dashed red line), and absolute errors $\Delta$ of these approximations.

This time, we cannot find the exact values of the terms in the expansion of the Taylor series, but we can (by applying the appropriate methods) find a good numerical approximation of these solutions.

4.2.2. PINN Approach

To solve the system of Equation (18), a fully connected neural network was used with the following settings: three hidden layers, each containing 20 neurons; hyperbolic tangent as an activation function; “Glorot uniform” as a method to initialize weights; 32 training points are taken to learning model.

The obtained results, in the form of exact solution plots and error plots, are presented in Figure 6. As can be seen, all three approximated solutions fit relatively well to the exact solutions. The smallest errors were obtained for the function $y_3$ (these errors do not exceed $5\times {10}^{-3}$). In the case of the functions $y_1$ and $y_2$, the errors of the approximated solutions are larger (with a maximum error at the level of $2\times {10}^{-2}$). Comparing the error plots obtained by the PINNs and DTM methods, one can observe differences in both their nature and magnitude. In the case of DTM, the largest errors occur at the end of the interval. Only in the case of the approximated solution for the function $y_3$ is the order of magnitude of the errors comparable in both methods. For the remaining functions, the errors obtained using PINNs are significantly larger than those from DTM.

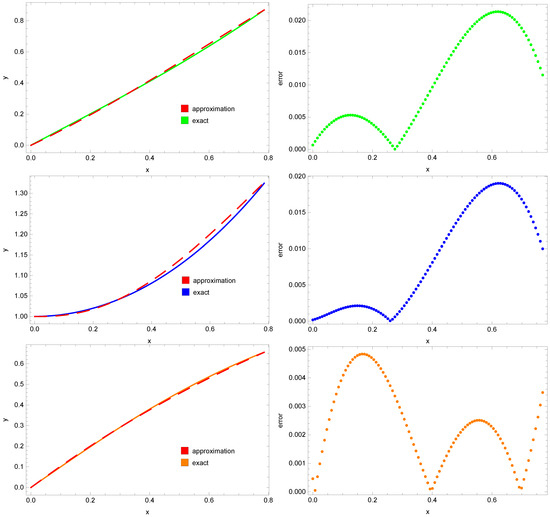
Figure 6. Exact solution $y_i$, $i=1,2,3$ (green, blue, and orange solid lines—left side), approximation $y_i$, $i=1,2,3$ (red dashed line—left side), and absolute errors of these approximations (green, blue, and orange dotted lines—right side) for example 2.

4.3. Example 3

We focus on the following system of integral–algebraic equations:

$$\left\{\begin{array}{c}{\displaystyle y_3\left(x\right)=(x-1)sinx+1-x^2+\frac{4x}{\pi (\pi -1)}{\int }_0^{\pi }(y_1\left(t\right)+sint)y_2\left(t\right)dt}\hfill \\ {\displaystyle -{\int }_0^x\left((x-t)y_1\left(t\right)+2y_2\left(t\right)\right)dt,}\hfill \\ {\displaystyle y_1\left(x\right)sinx+y_2\left(x\right)cosx+y_3\left(x\right)=x-x^2,}\hfill \\ {\displaystyle (x+1)y_1\left(x\right)+y_3\left(x\right)sinx=0.}\hfill \end{array}\right.$$

(19)

where $x\in [0,\pi ]$ and $y_1$, $y_2$ i $y_3$ are the searched functions.

4.3.1. DTM Approach

If we assume that $Y_1\left(k\right)$, $Y_2\left(k\right)$, and $Y_3\left(k\right)$ are the transforms of the functions $y_1\left(x\right)$, $y_2\left(x\right)$, and $y_3\left(x\right)$, then by taking $x=0$ (or equivalently $k=0$) in the system (19), we obtain $y_1\left(0\right)=0$, $y_2\left(0\right)=-1$, and $y_3\left(0\right)=1$, which means that $Y_1\left(0\right)=0$, $Y_2\left(0\right)=-1$, and $Y_3\left(0\right)=1$.

If for $k\ge 1$ we apply to the equations of the system (19) properties such as (3), (5)–(10) and (12)–(14), then we obtain the following:

$$\begin{array}{cc}\hfill Y_3\left(k\right)& ={\displaystyle \frac{sin\frac{(k-1)\pi }{2}}{(k-1)!}}-{\displaystyle \frac{sin\frac{k\pi }{2}}{k!}}-\delta (k-2)+\sum _{i=0}^{k-1}{\displaystyle \frac{\delta (i-1)Y_1(k-i-1)}{k}}+\alpha \delta (k-1)\hfill \\ \hfill & -\sum _{i=0}^{k-1}{\displaystyle \frac{\delta (i-1)Y_1(k-i-1)}{k-i}}-2{\displaystyle \frac{Y_2(k-1)}{k}},\hfill \\ \hfill Y_3\left(k\right)& =\delta (k-1)-\delta (k-2)-\sum _{i=0}^k{\displaystyle \frac{Y_1(k-i)sin\frac{i\pi }{2}}{i!}}-\sum _{i=0}^k{\displaystyle \frac{Y_2(k-i)cos\frac{i\pi }{2}}{i!}},\hfill \\ \hfill \sum _{i=0}^k& \left(\delta (i-0)+\delta (i-1)\right)Y_1(k-i)+\sum _{i=0}^k{\displaystyle \frac{Y_3(k-i)sin\frac{i\pi }{2}}{i!}}=0,\hfill \end{array}$$

where

$$\alpha ={\displaystyle \frac{4}{\pi (\pi -1)}}{\int }_0^{\pi }(y_1\left(t\right)+sint)y_2\left(t\right)dt.$$

(20)

By determining the successive coefficients from this system, we obtain the following:

$$\begin{array}{cccccccc}\hfill Y_1\left(1\right)& =-1,\hfill & \hfill Y_1\left(2\right)& =-\alpha ,\hfill & \hfill Y_1\left(3\right)& ={\displaystyle \frac{1}{6}},\hfill & \hfill Y_1\left(4\right)& =-{\displaystyle \frac{3\alpha +4}{6}},\hfill \\ \hfill Y_2\left(1\right)& =-\alpha ,\hfill & \hfill Y_2\left(2\right)& =-{\displaystyle \frac{2\alpha +1}{2}},\hfill & \hfill Y_2\left(3\right)& =-{\displaystyle \frac{\alpha +4}{6}},\hfill & \hfill Y_2\left(4\right)& =-{\displaystyle \frac{16\alpha +17}{4}},\hfill \\ \hfill Y_3\left(1\right)& =1+\alpha ,\hfill & \hfill Y_3\left(2\right)& =\alpha ,\hfill & \hfill Y_3\left(3\right)& ={\displaystyle \frac{2(\alpha +1)}{3}},\hfill & \hfill Y_3\left(4\right)& ={\displaystyle \frac{1+\alpha }{6}}.\hfill \end{array}$$

By calculating 13 terms in this way, i.e., taking $0\le k\le 12$, we obtain approximate solutions $y_{i,12}$, for $i=1,2,3$, which depend on the parameter $\alpha$. The value of this parameter is determined by solving Equation (20) that defines this parameter. After solving this system, we obtain two almost identical solutions: $-0.999999998695$ and $-1.0000023$. The first solution turned out to be better. This was not a coincidence, as the exact solutions, which are the functions:

$$y_1\left(x\right)=(x-1)sinx,y_2\left(x\right)=(x-1)cosx,y_3=1-x^2,$$

it follows that $\alpha =-1$. For this value of $\alpha$, we obtain approximate solutions, the interpretation of which is presented in Figure 7.

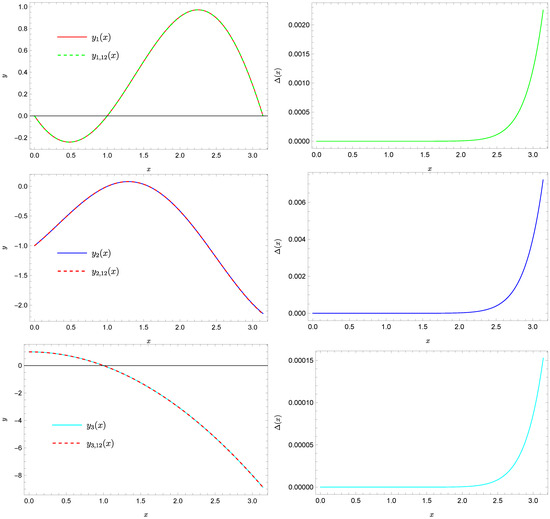
Figure 7. Exact solution $y_1$ (solid green line), approximate $y_{1,12}$ (dashed red line), exact solution $y_2$ (solid blue line), approximate $y_{2,12}$ (dashed red line), exact solution $y_3$ (solid cyan line), approximate solution $y_{3,12}$ (dashed red line), and absolute errors $\Delta$ of these approximations.

4.3.2. PINN Approach

As in the previous examples, the results obtained from both methods were compared. In this example, we used the same neural network architecture and its parameters as in the two previous examples (see Section 4.1.2 and Section 4.2.1). The solutions obtained using PINNs are close to the exact solutions. However, in this case as well, the approximation errors are larger than in the case of DTM. The largest errors were obtained for the function $y_3$ (maximum error $\approx 0.2$), while for the functions $y_1$ and $y_2$, the errors were approximately ≈0.07 and $0.05$, respectively (see right column of Figure 8).

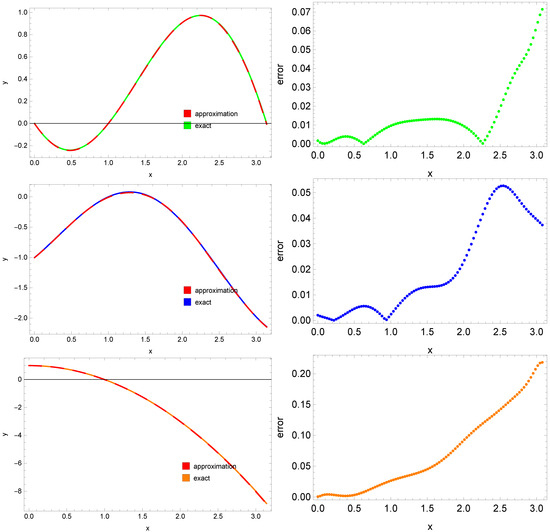
Figure 8. Exact solution $y_i$, $i=1,2,3$ (green, blue, and orange solid lines—left side), approximation $y_i$, $i=1,2,3$ (red dashed line—left side), and absolute errors of these approximations (green, blue, and orange dotted lines—right side) for example 3.

4.4. Example 4

Consider the following system of equations:

$$\left\{\begin{array}{c}{\displaystyle y_1\left(x\right)-3x^2{\int }_0^{1}t{y}_2\left(t\right)dt-e^x{\int }_0^x{y}_3\left(t\right)dt-5{\int }_0^x{t}^2{y}_4\left(t\right)dt=2e^x-e^{2x}-x^5-x^2,}\hfill \\ {\displaystyle y_2\left(x\right)-x^2{\int }_0^1{y}_3\left(t\right)dt-{\int }_0^{x}t{y}_1\left(t\right)dt-3x{\int }_0^x{y}_4\left(t\right)dt=e^x-x{e}^x-e{x}^2}\hfill \\ -1+x+x^2-x^4,\hfill \\ x{y}_1\left(x\right)-e^x{y}_2\left(x\right)-y_3\left(x\right)+y_4\left(x\right)=x^2-e^x,\hfill \\ e^{-x}{y}_1\left(x\right)+x{y}_2\left(x\right)-y_3\left(x\right)-y_4\left(x\right)=1-e^x,\hfill \end{array}\right.$$

(21)

where $x\in [0,1]$, the exact solution of which is the following:

$$y_1\left(x\right)=e^x,y_2\left(x\right)=x,y_3\left(x\right)=e^x,y_4\left(x\right)=x^2.$$

4.4.1. DTM Approach

Substituting $x=0$ into the first two equations of the system (21), we obtain $y_1\left(0\right)=1$ and $y_2\left(0\right)=0$. The remaining two values, $y_i\left(0\right)$ for $i=3,4$, can be obtained from the other two equations of the system (21), from which it follows that

$$\left\{\begin{array}{c}-y_2\left(0\right)-y_3\left(0\right)+y_4\left(0\right)=-1,\hfill \\ y_1\left(0\right)-y_3\left(0\right)-y_4\left(0\right)=0.\hfill \end{array}\right.$$

Solving the above system of equations, we obtain the following:

$$y_3\left(0\right)={\displaystyle \frac{1}{2}}(y_1\left(0\right)-y_2\left(0\right)+1)=1,y_4\left(0\right)={\displaystyle \frac{1}{2}}(y_1\left(0\right)+y_2\left(0\right)-1)=0,$$

so consequently, we have the following:

$$Y_1\left(0\right)=1,Y_2\left(0\right)=0,Y_3\left(0\right)=1,Y_4\left(0\right)=0.$$

Using, among others, the properties (3), (4), (7)–(10), and (13)–(15) from the equations of the system (21) for $k\ge 1$, we obtain the following:

$$\begin{array}{cc}\hfill & Y_1\left(k\right)-\sum _{i=0}^{k-1}{\displaystyle \frac{Y_3(k-i-1)}{i!(k-i)}}-3\delta (k-2)\alpha -5\sum _{i=0}^{k-1}{\displaystyle \frac{\delta (i-2)Y_4(k-i-1)}{k}}={\displaystyle \frac{2-2^k}{k!}}\hfill \\ \hfill & -\delta (k-5)-\delta (k-2),\hfill \\ \hfill & Y_2\left(k\right)-\sum _{i=0}^{k-1}{\displaystyle \frac{\delta (i-1)Y_1(k-i-1)}{k}}-3\sum _{i=0}^{k-1}{\displaystyle \frac{\delta (i-1)Y_4(k-i-1)}{k-i}}-\delta (k-2)\beta \hfill \\ \hfill & ={\displaystyle \frac{1}{k!}}-{\displaystyle \frac{1}{(k-1)!}}-\delta (k-4)+\delta (k-1)+(1-e)·\delta (k-2),\hfill \\ \hfill & Y_1(k-1)-\sum _{i=0}^k{\displaystyle \frac{Y_2(k-i)}{i!}}-Y_3\left(k\right)+Y_4\left(k\right)-\delta (k-2)+{\displaystyle \frac{1}{k!}}=0,\hfill \\ \hfill & Y_2(k-1)+\sum _{i=0}^k{\displaystyle \frac{{(-1)}^i{Y}_1(k-i)}{i!}}-Y_3\left(k\right)-Y_4\left(k\right)+{\displaystyle \frac{1}{k!}}=0,\hfill \end{array}$$

(22)

where

$$\alpha ={\int }_0^{1}t{y}_2\left(t\right)dt,\beta ={\int }_0^1{y}_3\left(t\right)dt.$$

(23)

By determining the values of $Y_i\left(k\right)$ for $k=1,2$ from Equation (23), we obtain approximate solutions

$$\begin{array}{cccc}\hfill y_{1,2}\left(x\right)& =1+x+{\displaystyle \frac{1}{2}}(6\alpha -1)x^2,\hfill & \hfill y_{2,2}\left(x\right)& =x+(\beta -e+1)x^2,\hfill \\ \hfill y_{3,2}\left(x\right)& =1+x+{\displaystyle \frac{1}{2}}(3\alpha -\beta +e-1)x^2,\hfill & \hfill y_{4,2}\left(x\right)& ={\displaystyle \frac{1}{2}}(3\alpha +\beta -e+2)x^2,\hfill \end{array}$$

dependent on the parameters $\alpha$ and $\beta$, which can be found by solving the system (23), where the functions $y_2\left(t\right)$ and $y_3\left(t\right)$ are replaced by the functions $y_{2,2}\left(t\right)$ and $y_{3,2}\left(t\right)$. The solution to this system is a pair of numbers:

$$\alpha ={\displaystyle \frac{73-18e}{75}}\approx 0.320946,\beta ={\displaystyle \frac{39+e}{25}}\approx 1.66873.$$

Since the functions $y_1\left(x\right)=y_3\left(x\right)=e^x$, $y_2\left(x\right)=x$, and $y_4\left(x\right)=x^2$ are exact solutions, the parameters $\alpha$ and $\beta$ take the exact values $\alpha ={\displaystyle \frac{1}{3}}$ and $\beta =e-1$.

By determining five terms, we obtain $\alpha =0.333223$ and $\beta =1.71805$, along with the corresponding approximate solutions $y_{i,5}$ for $i=1,2,3,4$:

$$\begin{array}{cc}\hfill y_{1,5}& =1+x+0.499668x^2+0.16665x^3+0.0416484x^4+0.00806994x^5,\hfill \\ \hfill y_{2,5}& =x-0.000234614x^2-0.000366151x^4+0.0000635703x^5,\hfill \\ \hfill y_{3,5}& =1+x+0.499951x^2+0.166659x^3+0.0418163x^4+0.008213x^5,\hfill \\ \hfill y_{4,5}& =0.999717x^2+0.0000890795+x^3-0.000317591x^4-0.000443792x^5.\hfill \end{array}$$

Figure 9 presents a comparison of the exact solutions with the corresponding approximate solutions obtained for the five determined terms.

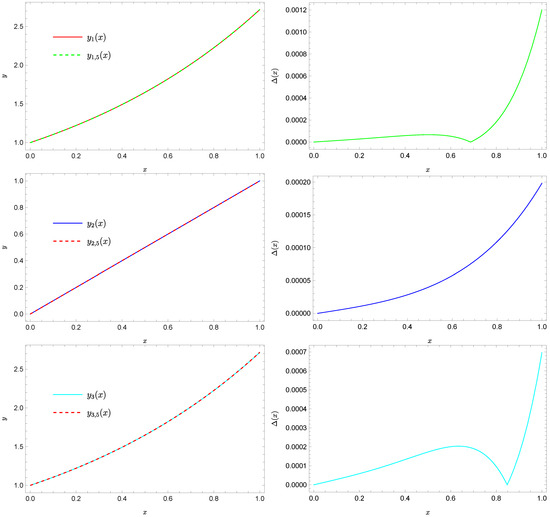
Figure 9. Exact solution $y_1$ (solid green line), approximate $y_{1,5}$ (dashed red line), exact solution $y_2$ (solid blue line), approximate $y_{2,5}$ (dashed red line), exact solution $y_3$ (solid cyan line), approximate solution $y_{3,5}$ (dashed red line), exact solution $y_4$ (solid purple line), approximate solution $y_{4,5}$ (dashed red line), and absolute errors $\Delta$ of these approximations.

4.4.2. PINN Approach

We solve the system of Equation (21) using a neural network. The parameters and network architecture were set the same as in the previous examples, with the only change being an increase in the number of training points to 64. In this example as well, DTM provided more accurate solutions. Figure 10 shows the approximate solutions (left column) and their errors (right column), which were obtained using PINNs.

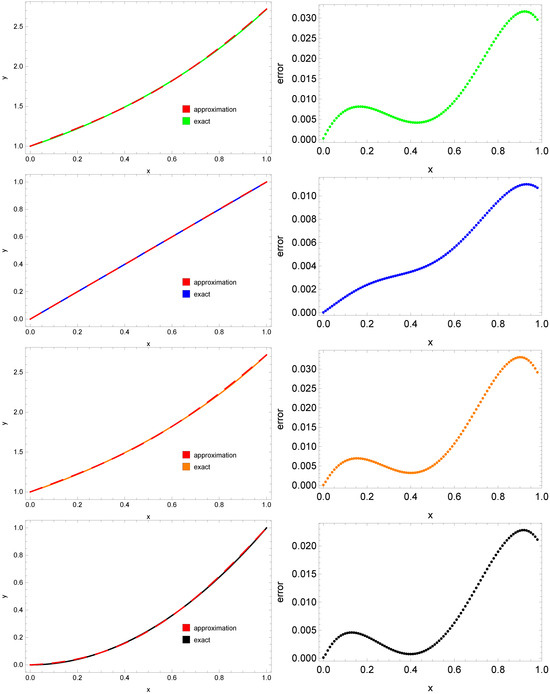
Figure 10. Exact solution $y_i$, $i=1,2,3,4$ (green, blue, orange, and black solid lines—left side), approximation $y_i$, $i=1,2,3$ (red dashed line—left side), and absolute errors of these approximations (green, blue, orange, and black dotted lines—right side).

5. Conclusions

The DTM is a universal technique that allows for solving various types of equations and their systems. This article presents the application of this method to systems of integral–algebraic equations. Such systems are complex enough that classical methods struggle to handle these types of tasks. This work demonstrates that despite the complexity of these systems and their significant level of complication, the DTM successfully addresses these tasks, providing very good approximate solutions (and sometimes, as in the first example, an exact solution). The examples presented varied in terms of complexity, the number of equations, and the number of integrals (and their types) in these equations. This further argument supports the usefulness of the discussed method.

In this article, the DTM was compared with the application of Physics-Informed Neural Networks (PINNs) in solving a system of integral–algebraic equations. PINNs also proved to be an effective tool for addressing such problems. In each of the four examples presented in the paper, the neural networks successfully dealt with the considered system of equations. However, it should be emphasized that the error of the approximate solution obtained from PINNs was greater than that of DTM in each case. The advantage of PINNs lies in their relatively simple implementation and versatility. In the Section 4, four numerical examples with varying degrees of complexity were presented. As can be observed in the numerous figures provided (Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10), both methods yielded fairly accurate results with small errors. However, it should be emphasized once again that the results obtained using DTM exhibited smaller errors, compared to those obtained with PINNs.

Of course, in the case of more complex problems, the application of the DTM cannot proceed without the assistance of a computational platform. It is often desirable for such a platform to also be capable of performing symbolic computations. In this article, the authors utilized Mathematica (version 13.3) [35,36]. For the implementation of PINNs, the authors employed Python and the TensorFlow library.