A Novel Family of q-Mittag-Leffler-Based Bessel and Tricomi Functions via Umbral Approach

Abstract

Many properties of special polynomials, such as recurrence relations, sum formulas, integral transforms and symmetric identities, have been studied in the literature with the help of generating functions and their functional equations. In this paper, we introduce hybrid forms of q-Mittag-Leffler functions. The q-Mittag-Leffler–Bessel and q-Mittag-Leffler–Tricomi functions are constructed using a q-symbolic operator. The generating functions, series definitions, q-derivative formulas and q-recurrence formulas for q-Mittag-Leffler–Bessel and q-Mittag-Leffler–Tricomi functions are obtained. The $N_q$-transforms and ${}_{q}N$-transforms of q-Mittag-Leffler–Bessel and q-Mittag-Leffler–Tricomi functions are obtained. These hybrid q-special functions are also studied by plotting their graphs for specific values of the indices and parameters.

1. Introduction

Symmetric identities for special functions often describe relationships between functions that exhibit symmetry in their arguments, which can simplify expressions or provide insights into their properties. These identities are powerful tools for simplifying integrals and series expansions and for solving differential equations involving special functions. For specific classes of q-special functions, the behavior under a change of the parameter q might reveal certain symmetry properties. Bessel functions of the first kind satisfy the symmetry identity, which reflects their even and odd properties under the transformation. The q-Bessel functions, which are deformations of the classical Bessel functions based on the quantum group parameter q, satisfy various symmetry relations. These functions arise in the study of q-special functions and are often used in contexts like quantum algebra, integrable systems, and statistical mechanics. These identities are powerful tools in understanding the structure of q-special functions and play a key role in many areas of mathematical research, from combinatorics to mathematical physics.

The q-calculus, or quantum calculus, is currently an essential topic that is very much relevant to the theory of special functions. There is growing interest in quantum calculus, primarily due to its applications in mathematical sciences, physics, and engineering. In recent years, hybrid forms of q-special functions and polynomials have been investigated by many researchers (see [1,2]).

We recall certain notations and preliminaries of the quantum theory to understand the work properly. For $n\in \mathbb{N}$ and $q\in \mathbb{C}-\left\{1\right\}$, the q-analogue of the factorial function is defined by [3,4]:

$${\left[n\right]}_q!=\prod _{m=1}^n{\left[m\right]}_q={\left[1\right]}_q{\left[2\right]}_q\cdots {\left[n\right]}_q,{\left[0\right]}_q!=1;0<q<1.$$

The corresponding q-exponential functions are defined as [3,4]:

$$e_q\left(u\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{u^n}{{\left[n\right]}_q!}},$$

$$E_q\left(u\right)=\sum _{n=0}^{\infty }{q}^{n(n-1)/2}{\displaystyle \frac{u^n}{{\left[n\right]}_q!}}$$

and

$${\widehat{D}}_{q,u}{e}_q\left(\alpha u\right)=\alpha e_q\left(\alpha u\right),\alpha \in \mathbb{C},$$

where ${\widehat{D}}_{q,u}$ is the q-derivative with respect to u. Also, the q-derivative of the product of two functions, $g\left(u\right)$ and $h\left(u\right)$, is given by

$${\widehat{D}}_{q,u}\left(g\left(u\right)h\left(u\right)\right)=g\left(u\right){\widehat{D}}_{q,u}h\left(u\right)+h\left(qu\right){\widehat{D}}_{q,u}g\left(u\right).$$

The q-Jackson integrals are specified as [5]:

$${\int }_0^{u}f\left(t\right)d_{q}t=u(1-q)\sum _{k=0}^{\infty }{q}^{k}f\left(u{q}^k\right)$$

$${\int }_0^{\infty /A}f\left(t\right)d_{q}t=(1-q)\sum _{k\in \mathbb{Z}}{\displaystyle \frac{q^k}{A}}f\left({\displaystyle \frac{q^k}{A}}\right).$$

The respective integral representations of q-gamma functions are given as [4]:

$${\mathrm{\Gamma }}_q\left(\alpha \right)={\int }_0^{1/(1-q)}{u}^{(\alpha -1)}{E}_q(-qu)d_{q}u,\alpha >0,$$

$${}_q\mathrm{\Gamma }\left(\alpha \right)=K(A;\alpha ){\int }_0^{\infty /A(1-q)}{u}^{(\alpha -1)}{e}_q(-u)d_{q}u,\alpha >0,$$

where $K(A;\alpha )$ is given as [4]:

$$K(A;\alpha )=A^{\alpha -1}{\displaystyle \frac{{(-q/\alpha ;q)}_{\infty }}{{(-q^t/\alpha ;q)}_{\infty }}}{\displaystyle \frac{{(-\alpha ;q)}_{\infty }}{{(-\alpha q^{1-t};q)}_{\infty }}},\alpha \in \mathbb{R}.$$

The q-gamma functions ${\mathrm{\Gamma }}_q\left(\alpha \right)$ and ${}_q\mathrm{\Gamma }\left(\alpha \right)$ satisfy the following as [4]:

$${\mathrm{\Gamma }}_q\left(\alpha \right)={\displaystyle \frac{{(q;q)}_{\infty }}{{(1-q)}^{\alpha -1}}}\sum _{k=0}^{\infty }{\displaystyle \frac{q^{k\alpha }}{{(q;q)}_k}}={\displaystyle \frac{{(q;q)}_{\infty }}{{(q^{\alpha };q)}_{\infty }}}{(1-q)}^{1-\alpha },$$

(1)

$${}_q\mathrm{\Gamma }\left(\alpha \right)={\displaystyle \frac{K(A;\alpha )}{{(1-q)}^{\alpha -1}{(-(1/A);q)}_{\infty }}}\sum _{k\in \mathbb{Z}}{\left({\displaystyle \frac{q^k}{A}}\right)}^{\alpha }{\left(-{\displaystyle \frac{1}{A}};q\right)}_k.$$

(2)

The q-Bessel functions of the first kind $J_{n,q}\left(u\right)$ are defined by following generating function [6,7]:

$$e_q\left({\displaystyle \frac{ut}{2}}\right)e_q\left(-{\displaystyle \frac{u}{2t}}\right)=\sum _{n=-\infty }^{\infty }{J}_{n,q}\left(u\right)t^n,t\ne 0,\left|u\right|<\infty$$

(3)

Additionally, they have the following series representations:

$$J_{n,q}\left(u\right)={\displaystyle \frac{1}{{(q;q)}_n}}\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k{\left(\frac{u}{2}\right)}^{n+2k}}{{(q;q)}_k{(q^{n+1};q)}_k}},$$

or, equivalently,

$$J_{n,q}\left(u\right)={\displaystyle \frac{{(q^{n+1};q)}_{\infty }}{{(q;q)}_{\infty }}}\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k{\left(\frac{u}{2}\right)}^{n+2k}}{{(q;q)}_k{(q^{n+1};q)}_k}},$$

which converges absolutely for $\left|u\right|<2$.

The q-Tricomi functions $C_{n,q}\left(u\right)$ are defined as [2]:

$$e_q\left(t\right)e_q(-u{t}^{-1})=\sum _{n=0}^{\infty }{C}_{n,q}\left(u\right)t^n,t\ne 0;\left|u\right|<\infty$$

(4)

and

$$C_{n,q}\left(u\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k{u}^k}{{\left[k\right]}_q!{[n+k]}_q!}}.$$

(5)

The series given in Equation (5) converges absolutely for all values of u.

The q-Mittag-Leffler functions $E_q^{(\alpha ,\beta )}\left(u\right)$ are defined as follows [8]:

$$E_q^{(\alpha ,\beta )}\left(u\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{u^n}{{\mathrm{\Gamma }}_q(\alpha n+\beta )}},\left|u\right|<{(1-q)}^{-n},\alpha ,\beta \in {\mathbb{R}}^{+}.$$

In [1], authors established the q-Mittag-Leffler function in terms of symbolic definition as follows:

$$E_q^{(\alpha ,\beta )}\left(u\right)=e_q\left(u{\widehat{d}}_{{(\alpha ,\beta )}_q}\right){\psi }_{0,q},$$

(6)

where ${\widehat{d}}_{{(\alpha ,\beta )}_q}$ is the q-symbolic operator, acting on function ${\psi }_{z,q}={\mathrm{\Gamma }}_q(z+1)/{\mathrm{\Gamma }}_q(\alpha z+\beta )$ as

$${\widehat{d}}_{{(\alpha ,\beta )}_q}^k{\psi }_{z,q}={\displaystyle \frac{{\mathrm{\Gamma }}_q(k+z+1)}{{\mathrm{\Gamma }}_q(\alpha (k+z)+\beta )}},k\in \mathbb{R},k+z>-1$$

and

$${\widehat{d}}_{{(\alpha ,\beta )}_q}^k{\psi }_{0,q}={\widehat{d}}_{{(\alpha ,\beta )}_q}^k{\psi }_{z,q}{|}_{z=0}={\displaystyle \frac{{\mathrm{\Gamma }}_q(k+1)}{{\mathrm{\Gamma }}_q(\alpha k+\beta )}},k\in \mathbb{R},k>-1.$$

(7)

Here, the umbral images of the q-Bessel function $J_{n,q}\left(u\right)$ and 0^th-order q-Tricomi-Bessel function $C_{0,q}\left(u\right)$ are defined as follows:

$$J_{n,q}\left(u\right)={\left(\widehat{c}{\displaystyle \frac{u}{2}}\right)}^n{e}_q\left(-\widehat{c}{\left({\displaystyle \frac{u}{2}}\right)}^2\right){\varphi }_{0,q}$$

(8)

and

$$C_{0,q}\left(u\right)=e_q\left(-\widehat{c}u\right){\varphi }_{0,q},\mathrm{for}\mathrm{all}\mathrm{u}\in \mathbb{R},$$

(9)

respectively.

The q-Tricomi functions $C_{n,q}\left(u\right)$ are defined as

$$C_{n,q}\left(u\right)={\widehat{c}}^n{e}_q\left(-\widehat{c}u\right){\varphi }_{0,q},\mathrm{for}\mathrm{all}\mathrm{u}\in \mathbb{R},$$

where $\widehat{c}$ is the shift operator acting on vacuum function ${\varphi }_{z,q}={\displaystyle \frac{1}{{\mathrm{\Gamma }}_q(z+1)}}$ as

$${\widehat{c}}^{\alpha }{\varphi }_{z,q}={\displaystyle \frac{1}{{\mathrm{\Gamma }}_q(z+\alpha +1)}},\alpha \in \mathbb{C}.$$

(10)

The symmetry of q-Tricomi functions, like many special functions, typically manifests in their behavior under transformations of variables or parameters. q-Tricomi functions may also exhibit symmetry in relation to other q-special functions. For instance, there might be symmetries with q-hypergeometric functions, q-Bessel functions, or other q-analogues of classical functions, and these symmetries can often be explored through their interrelations and recurrence properties. Symmetry may also manifest in the asymptotic behavior of the q-Tricomi function as certain parameters (such as q) or variables approach their limits.

Motivated by the significance of hybrid q-special functions in diverse fields, in this paper, q-Mittag-Leffler–Bessel and q-Mittag-Leffler–Tricomi functions are constructed in view of symbolic definitions. In Section 2, generating functions, series definitions, and other important properties of these hybrid q-special functions are established. Certain q-natural transforms of q-Mittag-Leffler–Bessel and q-Mittag-Leffler–Tricomi functions are explored in Section 3. In Section 4, q-derivative formulas and q-recurrence formulas are obtained. Using “Wolfram Mathematica”, q-Mittag-Leffler–Bessel and q-Mittag-Leffler–Tricomi functions are studied graphically in Section 5.

2. q-Mittag-Leffler–Bessel Functions and q-Mittag-Leffler–Tricomi Functions

In this section, q-Mittag-Leffler–Bessel functions (qMLBF), denoted by ${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)$, and q-Mittag-Leffler–Tricomi functions (qMLTF), denoted by ${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)$, are obtained through convolutions of q-Mittag-Leffler functions $E_q^{(\alpha ,\beta )}\left(u\right)$ with q-Bessel functions $J_{n,q}\left(u\right)$ and q-Tricomi functions $C_{n,q}\left(u\right)$, respectively, using a q-symbolic operator ${\widehat{d}}_{{(\alpha ,\beta )}_q}$. With the help of relation (6), we receive umbral images of qMLBF ${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)$ and qMLTF ${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)$ as:

$${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)=J_{n,q}\left(u{\widehat{d}}_{{(\alpha ,\beta )}_q}\right){\psi }_{0,q}.$$

(11)

Alternatively, in view of relation (8), it follows that

$${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)={\left({\displaystyle \frac{\widehat{c}u{\widehat{d}}_{{(\alpha ,\beta )}_q}}{2}}\right)}^n{e}_q\left(-\widehat{c}{\left({\displaystyle \frac{u{\widehat{d}}_{{(\alpha ,\beta )}_q}}{2}}\right)}^2\right){\varphi }_{0,q}{\psi }_{0,q}$$

(12)

and

$${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)=C_{n,q}\left(u{\widehat{d}}_{{(\alpha ,\beta )}_q}\right){\psi }_{0,q},$$

(13)

or, in view of relation (9), we receive

$${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)={\widehat{c}}^n{e}_q\left(-\widehat{c}u{\widehat{d}}_{{(\alpha ,\beta )}_q}\right){\varphi }_{0,q}{\psi }_{0,q}.$$

(14)

Theorem 1.

For $t\ne 0,\left|u\right|<\infty$, the generating functions for qMLBF ${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)$ and qMLTF ${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)$ are given as

$$\sum _{n=-\infty }^{\infty }{}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)t^n=E_q^{(\alpha ,\beta )}\left({\displaystyle \frac{u}{2}}\left(t-{\displaystyle \frac{1}{t}}\right)\right),\mathrm{if}{u}^2{\widehat{d}}_{{(\alpha ,\beta )}_q}=q{u}^2{\widehat{d}}_{{(\alpha ,\beta )}_q}$$

(15)

and

$$\sum _{n=-\infty }^{\infty }{}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)t^n=e_q\left(t\right)E_q^{(\alpha ,\beta )}\left(-{\displaystyle \frac{u}{t}}\right),\mathrm{if}u{\widehat{d}}_{{(\alpha ,\beta )}_q}=qu{\widehat{d}}_{{(\alpha ,\beta )}_q},$$

(16)

respectively.

Proof. 

Multiply both sides of Equation (11) by $t^n$ and, through taking the summation of both sides, we receive

$$\sum _{n=-\infty }^{\infty }{}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)t^n=\sum _{n=-\infty }^{\infty }{J}_{n,q}\left(u{\widehat{d}}_{{(\alpha ,\beta )}_q}\right){\psi }_{0,q}{t}^n,$$

(17)

which in view of relations (3) and (6), yields assertion (15).

Similarly, multiply both sides of Equation (13) by $t^n$ and, through taking the summation of both sides of the resultant equation and then using relations (4) and (6), assertion (16) is obtained.

□

Remark 1.

For $t=1$ in Equation (15), we get

$$\sum _{n=-\infty }^{\infty }{}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)=1.$$

(18)

Remark 2.

Taking $n=0$ in Equations (12) and (14), it follows that

$${}_{E}J_{0,q}^{(\alpha ,\beta )}\left(u\right)=e_q\left(-\widehat{c}{\left({\displaystyle \frac{u{\widehat{d}}_{{(\alpha ,\beta )}_q}}{2}}\right)}^2\right){\varphi }_{0,q}{\psi }_{0,q},$$

(19)

$${}_{E}C_{0,q}^{(\alpha ,\beta )}\left(u\right)=e_q\left(-\widehat{c}u{\widehat{d}}_{{(\alpha ,\beta )}_q}\right){\varphi }_{0,q}{\psi }_{0,q}.$$

(20)

Theorem 2.

For $\alpha ,\beta \in \mathbb{R}$, the following series definitions for qMLBF ${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)$ and qMLTF ${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)$ are given as

$${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)=\sum _{k=0}^{\infty }{\left({\displaystyle \genfrac{}{}{0pt}{}{n+2k}{k}}\right)}_q{\displaystyle \frac{{(-1)}^k{(u/2)}^{n+2k}}{{\mathrm{\Gamma }}_q(\alpha (n+2k)+\beta )}}$$

(21)

and

$${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k{u}^k}{{\mathrm{\Gamma }}_q(\alpha k+\beta ){[n+k]}_q!}},$$

(22)

respectively.

Proof. 

In Equation (12), we have

$${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)={\displaystyle \frac{{\widehat{c}}^n{u}^n{\widehat{d}}_{{(\alpha ,\beta )}_q}^n}{2^n}}\sum _{k=0}^{\infty }{\displaystyle \frac{{(-\widehat{c})}^k{u}^{2k}{\widehat{d}}_{{(\alpha ,\beta )}_q}^{2k}}{{\left[k\right]}_q!2^{2k}}}{\psi }_{0,q}{\varphi }_{0,q},$$

(23)

which can be rewritten as

$${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k{\left(\frac{u}{2}\right)}^{n+2k}}{{\left[k\right]}_q!}}{\widehat{c}}^{n+k}{\varphi }_{0,q}{\widehat{d}}_{{(\alpha ,\beta )}_q}^{n+2k}{\psi }_{0,q}.$$

(24)

In view of relations (7) and (10), assertion (21) is obtained. Similarly, through expanding the q-exponential function in Equation (14), we receive

$${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)={\widehat{c}}^n\sum _{k=0}^{\infty }{\displaystyle \frac{{(-\widehat{c})}^k{u}^k{\widehat{d}}_{{(\alpha ,\beta )}_q}^k}{{\left[k\right]}_q!}}{\psi }_{0,q}{\varphi }_{0,q}.$$

(25)

Using Equations (7) and (10) in Equation (25), we are led to assertion (22). □

3. Some q-Integral Transforms

The theory of q-integral transforms serves as a core part of q-calculus. The q-analogues of numerous classical integrals have been explored by many researchers (see, for example, [9,10,11,12]. The q-Laplace transforms of a product q-Bessel function are obtained in [12]. Furthermore, Omari [11] established q-analogues of the Natural transform of the first type on some set $A_1$, which is defined as:

$$N_q\left(f\left(t\right)\right)(u;v)={\displaystyle \frac{1}{(1-q)u}}{\int }_0^{{\displaystyle \frac{u}{v}}}f\left(t\right)E_q\left(q{\displaystyle \frac{v}{u}}t\right)d_{q}t,$$

(26)

where $A_1$ is given by

$$A_1=\left\{f\left(t\right)|\exists M,{\tau }_1,{\tau }_2>0,\left|f\left(t\right)\right|<M{E}_q\left({\displaystyle \frac{\left|t\right|}{{\tau }_j}}\right),t\in {(-1)}^j\times [0,\infty )\right\}.$$

(27)

The q-analogues of the Natural transform of the second type are defined as [11]:

$${}_{q}N\left(f\left(t\right)\right)(u;v)={\displaystyle \frac{1}{(1-q)}}{\int }_0^{\infty }f\left(t\right)e_q\left(-{\displaystyle \frac{v}{u}}t\right)d_{q}t,$$

(28)

where $A_2$ is given by

$$A_2=\left\{f\left(t\right)|\exists M,{\tau }_1,{\tau }_2>0,\left|f\left(t\right)\right|<M{e}_q\left({\displaystyle \frac{\left|t\right|}{{\tau }_j}}\right),t\in {(-1)}^j\times [0,\infty )\right\}.$$

(29)

The series expansions for the $N_q$-transform and ${}_{q}N$-transform are given as [11]:

$$N_q\left(f\left(t\right)\right)(u;v)={\displaystyle \frac{{(q;q)}_{\infty }}{v}}\sum _{k=0}^{\infty }{\displaystyle \frac{q^k}{{(q;q)}_k}}f\left(q^k{\displaystyle \frac{u}{v}}\right),$$

(30)

$${}_{q}N\left(f\left(t\right)\right)(u;v)={\displaystyle \frac{1}{{\left(-\frac{v}{u};q\right)}_{\infty }}}\sum _{k\in \mathbb{Z}}{\left(-{\displaystyle \frac{v}{u}};q\right)}_k{q}^{k}f\left(q^k\right).$$

(31)

Remark 3.

Taking $u=1$ in Equations (26) and (28), the q-Laplace transforms of the function $f\left(t\right)$ are obtained [13].

Theorem 3.

Let $0<q<1$; $u,v\in {\mathbb{R}}^{+}$, $\nu \in \mathbb{C}$ with $\mathfrak{R}\left(\nu \right)>1$. Consider a $t^{\nu -1}$-weighted product of n different qMLBF ${}_{E}J_{2{\mu }_j,q}^{(\alpha ,\beta )}\left(2\sqrt{a_{j}t}\right),j=1,2,\cdots ,n$, then their $N_q$-transform is given by

$$\begin{array}{cc}\hfill N_q\left\{t^{\nu -1}\prod _{j=1}^n{}_{E}J_{2{\mu }_j,q}^{(\alpha ,\beta )}\left(2\sqrt{a_{j}t}\right)\right\}(u;v)& =A_{\nu ,q}\prod _{j=1}^n\sum _{m_j=0}^{\infty }{\left({\displaystyle \genfrac{}{}{0pt}{}{2{\mu }_j+2m_j}{m_j}}\right)}_q{\left({\displaystyle \frac{(1-q)u{a}_j}{v}}\right)}^{{\mu }_j+m_j}\hfill \\ \hfill & \times {\displaystyle \frac{{(-1)}^{m_j}{\mathrm{\Gamma }}_q(\nu +{\mu }_j+m_j)}{{\mathrm{\Gamma }}_q(\alpha (2{\mu }_j+2m_j)+\beta )}},\hfill \end{array}$$

(32)

where $A_{\nu ,q}={\displaystyle \frac{u^{\nu -1}}{v^{\nu }}}{(1-q)}^{\nu -1}$ and $Re(\nu +{\mu }_j+m_j)>0$.

Proof. 

Let $f\left(t\right)=t^{\nu -1}{\displaystyle \prod _{j=1}^n}{}_{E}J_{2{\mu }_j,q}^{(\alpha ,\beta )}(2\sqrt{a_{j}t})$ in definition (30); we obtain

$$\begin{array}{cc}\hfill & N_q\left\{t^{\nu -1}\prod _{j=1}^n{}_{E}J_{2{\mu }_j,q}^{(\alpha ,\beta )}(2\sqrt{a_{j}t})\right\}(u;v)={\displaystyle \frac{{(q;q)}_{\infty }}{v}}\sum _{k=0}^{\infty }{\displaystyle \frac{q^k}{{(q;q)}_k}}{\left({\displaystyle \frac{q^{k}u}{v}}\right)}^{\nu -1}\prod _{j=1}^n{}_{E}J_{2{\mu }_j,q}^{(\alpha ,\beta )}\left(2\sqrt{a_j{q}^k{\displaystyle \frac{u}{v}}}\right),\hfill \end{array}$$

(33)

which, through using relation (21), gives

$$\begin{array}{cc}\hfill N_q\left\{t^{\nu -1}\prod _{j=1}^n{}_{E}J_{2{\mu }_j,q}^{(\alpha ,\beta )}\left(2\sqrt{a_{j}t}\right)\right\}(u;v)& ={\displaystyle \frac{{(q;q)}_{\infty }}{v}}\sum _{k=0}^{\infty }\prod _{j=1}^n\sum _{m_j=0}^{\infty }{\displaystyle \frac{q^k}{{(q;q)}_k}}{\left({\displaystyle \frac{q^{k}u}{v}}\right)}^{\nu -1}\hfill \\ \hfill & \times {\left({\displaystyle \genfrac{}{}{0pt}{}{2{\mu }_j+2m_j}{m_j}}\right)}_q{\displaystyle \frac{{(-1)}^{m_j}{\left(\frac{a_j{q}^{k}u}{v}\right)}^{{\mu }_j+m_j}}{{\mathrm{\Gamma }}_q(\alpha (2{\mu }_j+2m_j)+\beta )}}\hfill \end{array}$$

(34)

Using relation (1) in Equation (34), and letting $A_{\nu ,q}={\displaystyle \frac{u^{\nu -1}}{v^{\nu }}}{(1-q)}^{\nu -1}$, we are led to assertion (32). □

Theorem 4.

Let $0<q<1$; $u,v\in {\mathbb{R}}^{+}$, $\nu \in \mathbb{C}$ with $\mathfrak{R}\left(\nu \right)>1$. Consider a $t^{\nu -1}$-weighted product of n different qMLBF ${}_{E}J_{2{\mu }_j,q}^{(\alpha ,\beta )}\left(2\sqrt{a_{j}t}\right),j=1,2,\cdots ,n$; then their ${}_{q}N$-transform is given by

$$\begin{array}{cc}\hfill {}_{q}N\left\{t^{\nu -1}\prod _{j=1}^n{}_{E}J_{2{\mu }_j,q}^{(\alpha ,\beta )}\left(2\sqrt{a_{j}t}\right)\right\}(u;v)& =B_{\nu ,q}\prod _{j=1}^n\sum _{m_j=0}^{\infty }{\left({\displaystyle \genfrac{}{}{0pt}{}{2{\mu }_j+2m_j}{m_j}}\right)}_q{\left({\displaystyle \frac{(1-q)u{a}_j}{v}}\right)}^{{\mu }_j+m_j}\hfill \\ \hfill & \times {\displaystyle \frac{{(-1)}^{m_j}{}_q\mathrm{\Gamma }(\nu +{\mu }_j+m_j)}{{\mathrm{\Gamma }}_q(\alpha (2{\mu }_j+2m_j)+\beta )K\left(\frac{u}{v};\nu +{\mu }_j+m_j\right)}},\hfill \end{array}$$

(35)

where $B_{\nu ,q}={\left({\displaystyle \frac{u}{v}}\right)}^{\nu }{(1-q)}^{\nu -1}$.

Proof. 

Let $f\left(t\right)=t^{\nu -1}{\displaystyle \prod _{j=1}^n}{}_{E}J_{2{\mu }_j,q}^{(\alpha ,\beta )}\left(2\sqrt{a_{j}t}\right)$; in definition (31), it follows that

$$\begin{array}{c}\hfill {}_{q}N\left\{t^{\nu -1}\prod _{j=1}^n{}_{E}J_{2{\mu }_j,q}^{(\alpha ,\beta )}\left(2\sqrt{a_{j}t}\right)\right\}(u;v)={\displaystyle \frac{1}{{\left(-\frac{v}{u};q\right)}_{\infty }}}\sum _{k\in \mathbb{Z}}{q}^k{\left(-{\displaystyle \frac{v}{u}};q\right)}_k{q}^{k(\nu -1)}\prod _{j=1}^n{}_{E}J_{2{\mu }_j,q}^{(\alpha ,\beta )}\left(2\sqrt{a_j{q}^k}\right)\end{array}$$

(36)

and (21) becomes

$$\begin{array}{cc}\hfill {}_{q}N\left\{t^{\nu -1}\prod _{j=1}^n{}_{E}J_{2{\mu }_j,q}^{(\alpha ,\beta )}\left(2\sqrt{a_{j}t}\right)\right\}(u;v)& ={\displaystyle \frac{1}{{\left(-\frac{v}{u};q\right)}_{\infty }}}\sum _{k\in \mathbb{Z}}\prod _{j=1}^n\sum _{m_j=0}^{\infty }{q}^{k\nu }{\left(-{\displaystyle \frac{v}{u}};q\right)}_k\hfill \\ \hfill & \times {\left({\displaystyle \genfrac{}{}{0pt}{}{2{\mu }_j+2m_j}{m_j}}\right)}_q{\displaystyle \frac{{(-1)}^{m_j}{\left(a_j{q}^k\right)}^{{\mu }_j+m_j}}{{\mathrm{\Gamma }}_q(\alpha (2{\mu }_j+2m_j)+\beta )}}.\hfill \end{array}$$

(37)

Using Equation (2) for $A={\displaystyle \frac{u}{v}}$ in Equation (37), by performing some simplifications, assertion (35) is proven. □

Now, we give the $N_q$-transforms and ${}_{q}N$-transform for the qMLTF ${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)$.

Theorem 5.

Let $0<q<1$; $u,v\in {\mathbb{R}}^{+}$, $\nu \in \mathbb{C}$ with $\mathfrak{R}\left(\nu \right)>1$. Consider a $t^{\nu -1}$-weighted product of n different qMLTF ${}_{E}C_{{\mu }_j,q}^{(\alpha ,\beta )}\left(a_{j}t\right),j=1,2,\cdots ,n$, then their $N_q$-transform is given by

$$\begin{array}{c}\hfill N_q\left\{t^{\nu -1}\prod _{j=1}^n{}_{E}C_{{\mu }_j,q}^{(\alpha ,\beta )}\left(a_{j}t\right)\right\}(u;v)=A_{\nu ,q}\prod _{j=1}^n\sum _{m_j=0}^{\infty }{\left({\displaystyle \frac{(1-q)u{a}_j}{v}}\right)}^{m_j}{\displaystyle \frac{{(-1)}^{m_j}{\mathrm{\Gamma }}_q(\nu +m_j)}{{\mathrm{\Gamma }}_q(\alpha m_j+\beta ){[{\mu }_j+m_j]}_q!}},\end{array}$$

(38)

where $Re(\nu +m_j)>0$ and $A_{\nu ,q}$ is same as given in Theorem 3.

Proof. 

Letting $f\left(t\right)=t^{\nu -1}{\displaystyle \prod _{j=1}^n}{}_{E}C_{{\mu }_j,q}^{(\alpha ,\beta )}\left(a_{j}t\right)$ in definition (30), we find

$$\begin{array}{cc}\hfill & N_q\left\{t^{\nu -1}\prod _{j=1}^n{}_{E}C_{{\mu }_j,q}^{(\alpha ,\beta )}\left(a_{j}t\right)\right\}(u;v)={\displaystyle \frac{{(q;q)}_{\infty }}{v}}\sum _{k=0}^{\infty }{\displaystyle \frac{q^k}{{(q;q)}_k}}{\left({\displaystyle \frac{q^{k}u}{v}}\right)}^{\nu -1}\prod _{j=1}^n{}_{E}C_{{\mu }_j,q}^{(\alpha ,\beta )}\left(a_j{q}^k{\displaystyle \frac{u}{v}}\right).\hfill \end{array}$$

(39)

Using (22) becomes

$$\begin{array}{cc}\hfill N_q\left\{t^{\nu -1}\prod _{j=1}^n{}_{E}C_{{\mu }_j,q}^{(\alpha ,\beta )}\left(a_{j}t\right)\right\}(u;v)& ={\displaystyle \frac{{(q;q)}_{\infty }}{v}}\sum _{k=0}^{\infty }\prod _{j=1}^n\sum _{m_j=0}^{\infty }{\displaystyle \frac{q^k}{{(q;q)}_k}}{\left({\displaystyle \frac{q^{k}u}{v}}\right)}^{\nu -1}\hfill \\ \hfill & \times {\displaystyle \frac{{(-1)}^{m_j}{\left(\frac{a_j{q}^{k}u}{v}\right)}^{m_j}}{{\mathrm{\Gamma }}_q(\alpha m_j+\beta ){[{\mu }_j+m_j]}_q!}}.\hfill \end{array}$$

(40)

Using relation (1) in Equation (40) and letting $A_{\nu ,q}={\displaystyle \frac{u^{\nu -1}}{v^{\nu }}}{(1-q)}^{\nu -1}$, we are led to assertion (38). □

Theorem 6.

Let $0<q<1$; $u,v\in {\mathbb{R}}^{+}$, $\nu \in \mathbb{C}$ with $\mathfrak{R}\left(\nu \right)>1$. Consider a $t^{\nu -1}$-weighted product of n different qMLTF ${}_{E}C_{{\mu }_j,q}^{(\alpha ,\beta )}\left(a_{j}t\right),j=1,2,\cdots ,n$, then their ${}_{q}N$-transform is given by

$$\begin{array}{c}\hfill {}_{q}N\left\{t^{\nu -1}\prod _{j=1}^n{}_{E}C_{{\mu }_j,q}^{(\alpha ,\beta )}\left(a_{j}t\right)\right\}(u;v)=B_{\nu ,q}\prod _{j=1}^n\sum _{m_j=0}^{\infty }{\displaystyle \frac{{(-1)}^{m_j}{\left(\frac{(1-q)u{a}_j}{v}\right)}^{m_j}{}_q\mathrm{\Gamma }(\nu +m_j)}{{[{\mu }_j+m_j]}_q!{\mathrm{\Gamma }}_q(\alpha m_j+\beta )K\left(\frac{u}{v};\nu +m_j\right)}},\end{array}$$

(41)

where $B_{\nu ,q}$ is same as given in Theorem 4.

Proof. 

Let $f\left(t\right)=t^{\nu -1}{\displaystyle \prod _{j=1}^n}{}_{E}C_{{\mu }_j,q}^{(\alpha ,\beta )}\left(a_{j}t\right)$ in definition (31), it follows that

$$\begin{array}{c}\hfill {}_{q}N\left\{t^{\nu -1}\prod _{j=1}^n{}_{E}C_{{\mu }_j,q}^{(\alpha ,\beta )}\left(a_{j}t\right)\right\}(u;v)={\displaystyle \frac{1}{{\left(-\frac{v}{u};q\right)}_{\infty }}}\sum _{k\in \mathbb{Z}}{q}^k{\left(-{\displaystyle \frac{v}{u}};q\right)}_k{q}^{k(\nu -1)}\prod _{j=1}^n{}_{E}C_{{\mu }_j,q}^{(\alpha ,\beta )}\left(a_j{q}^k\right).\end{array}$$

(42)

Using Equation (22) becomes

$$\begin{array}{c}\hfill {}_{q}N\left\{t^{\nu -1}\prod _{j=1}^n{}_{E}C_{{\mu }_j,q}^{(\alpha ,\beta )}\left(a_{j}t\right)\right\}(u;v)={\displaystyle \frac{1}{{\left(-\frac{v}{u};q\right)}_{\infty }}}\sum _{k\in \mathbb{Z}}\prod _{j=1}^n\sum _{m_j=0}^{\infty }{q}^{k\nu }{\left(-{\displaystyle \frac{v}{u}};q\right)}_k{\displaystyle \frac{{(-1)}^{m_j}{\left(a_j{q}^k\right)}^{m_j}}{{[{\mu }_j+m_j]}_q!{\mathrm{\Gamma }}_q(\alpha m_j+\beta )}}.\end{array}$$

(43)

Using Equation (2) for $A={\displaystyle \frac{u}{v}}$ in Equation (43), and by performing some simplifications, assertion (41) is proven. □

Special Cases

Corollary 1.

In consideration of $n=1,a_1=a,m_1=m$ and ${\mu }_1={\displaystyle \frac{1}{2}}$ in Theorem 3 and 4, the $N_q$-transform and ${}_{q}N$-transform for the qMLBF ${}_{E}J_{1,q}^{(\alpha ,\beta )}\left(2\sqrt{at}\right)$ are given as:

$$\begin{array}{cc}\hfill N_q\left\{t^{\nu -1}{}_{E}J_{1,q}^{(\alpha ,\beta )}\left(2\sqrt{at}\right)\right\}(u;v)& ={\displaystyle \frac{\sqrt{a}}{v}}{\left({\displaystyle \frac{(1-q)u}{v}}\right)}^{\nu -{\displaystyle \frac{1}{2}}}\sum _{m=0}^{\infty }{\left({\displaystyle \genfrac{}{}{0pt}{}{2m+1}{m}}\right)}_q{\left({\displaystyle \frac{(1-q)ua}{v}}\right)}^m\hfill \\ \hfill & \times {\displaystyle \frac{{(-1)}^m{\mathrm{\Gamma }}_q(\nu +m+1/2)}{{\mathrm{\Gamma }}_q(\alpha (2m+1)+\beta )}}\hfill \end{array}$$

(44)

and

$$\begin{array}{cc}\hfill {}_{q}N\left\{t^{\nu -1}{}_{E}J_{1,q}^{(\alpha ,\beta )}\left(2\sqrt{at}\right)\right\}(u;v)& ={\left({\displaystyle \frac{u}{v}}\right)}^{\nu +{\displaystyle \frac{1}{2}}}{(1-q)}^{\nu -{\displaystyle \frac{1}{2}}}\sum _{m=0}^{\infty }{\left({\displaystyle \genfrac{}{}{0pt}{}{2m+1}{m}}\right)}_q{\left({\displaystyle \frac{(1-q)ua}{v}}\right)}^m\hfill \\ \hfill & \times {\displaystyle \frac{{(-1)}^m{}_q\mathrm{\Gamma }(\nu +m+1/2)}{{\mathrm{\Gamma }}_q(\alpha (2m+1)+\beta )K\left(\frac{u}{v};\nu +m+1/2\right)}},\hfill \end{array}$$

(45)

respectively.

Corollary 2.

In consideration of $n=1,a_1=a,m_1=m$ and ${\mu }_1=1$ in Theorem 5 and 6, the $N_q$-transform and ${}_{q}N$-transform for the qMLTF ${}_{E}C_{1,q}^{(\alpha ,\beta )}\left(at\right)$ are given as:

$$\begin{array}{c}\hfill N_q\left\{t^{\nu -1}{}_{E}C_{1,q}^{(\alpha ,\beta )}\left(at\right)\right\}(u;v)={\displaystyle \frac{1}{v}}{\left({\displaystyle \frac{(1-q)u}{v}}\right)}^{\nu -1}\sum _{m=0}^{\infty }{\left({\displaystyle \frac{(1-q)ua}{v}}\right)}^m{\displaystyle \frac{{(-1)}^m{\mathrm{\Gamma }}_q(\nu +m)}{{\mathrm{\Gamma }}_q(\alpha m+\beta ){[1+m]}_q!}}\end{array}$$

(46)

and

$$\begin{array}{c}\hfill {}_{q}N\left\{t^{\nu -1}{}_{E}C_{1,q}^{(\alpha ,\beta )}\left(at\right)\right\}(u;v)={\left({\displaystyle \frac{u}{v}}\right)}^{\nu }{(1-q)}^{\nu -1}\sum _{m=0}^{\infty }{\displaystyle \frac{{(-1)}^m{\left(\frac{(1-q)ua}{v}\right)}^m{}_q\mathrm{\Gamma }(\nu +m)}{{[m+1]}_q!{\mathrm{\Gamma }}_q(\alpha m+\beta )K\left(\frac{u}{v};\nu +m\right)}},\end{array}$$

(47)

respectively.

4. Miscellaneous Properties

Theorem 7.

The qMLBF ${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)$ satisfies the following identity

$${}_{E}J_{n,q}^{(\alpha ,\beta )}(-u)={(-1)}^n{}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right).$$

(48)

Proof. 

Replacing u by $-u$ in Equation (12), we obtain

$${}_{E}J_{n,q}^{(\alpha ,\beta )}(-u)={\left({\displaystyle \frac{-\widehat{c}u{\widehat{d}}_{{(\alpha ,\beta )}_q}}{2}}\right)}^n{e}_q\left(-\widehat{c}{\left({\displaystyle \frac{-u{\widehat{d}}_{{(\alpha ,\beta )}_q}}{2}}\right)}^2\right){\varphi }_{0,q}{\psi }_{0,q},$$

(49)

which, by conducting some simplifications and using Equation (12), yields assertion (48). □

Theorem 8.

For qMLBF ${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)$, the following q-recurrence formula holds true:

$$2{\widehat{D}}_{q,u}{}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)={\widehat{d}}_{{(\alpha ,\beta )}_q}\left({}_{E}J_{n-1,q}^{(\alpha ,\beta )}\left(u\right)-{}_{E}J_{n+1,q}^{(\alpha ,\beta )}\left(u\right)\right).$$

(50)

Proof. 

Using Equation (6) in relation (15), it follows that

$$\sum _{n=-\infty }^{\infty }{}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)t^n=e_q\left({\displaystyle \frac{u}{2}}{\widehat{d}}_{{(\alpha ,\beta )}_q}\left(t-{\displaystyle \frac{1}{t}}\right)\right){\psi }_{0,q},t\ne 0,$$

(51)

which, upon taking the q-derivative on both sides with respect to u, becomes

$${\widehat{D}}_{q,u}\left(\sum _{n=-\infty }^{\infty }{}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)t^n\right)={\displaystyle \frac{{\widehat{d}}_{{(\alpha ,\beta )}_q}}{2}}\left(t-{\displaystyle \frac{1}{t}}\right)e_q\left({\displaystyle \frac{u}{2}}{\widehat{d}}_{{(\alpha ,\beta )}_q}\left(t-{\displaystyle \frac{1}{t}}\right)\right){\psi }_{0,q}.$$

(52)

Using Equation (51) on the right-hand-side of Equation (52), and through equating the coefficient identical powers of t on both sides of the resultant equation, assertion (50) is proven. □

Theorem 9.

For qMLTF ${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)$, the following q-recursive formula holds:

$${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)=-{\widehat{c}}^{-m}{}_{E}C_{n+m,q}^{(\alpha ,\beta )}\left(u\right).$$

(53)

Proof. 

Replacing n by $n+m$ in Equation (14), we receive

$${}_{E}C_{n+m,q}^{(\alpha ,\beta )}\left(u\right)={\widehat{c}}^{n+m}{e}_q\left(-\widehat{c}u{\widehat{d}}_{{(\alpha ,\beta )}_q}\right){\varphi }_{0,q}{\psi }_{0,q},$$

(54)

which, through replacing $\widehat{c}$ by $-\widehat{c}$ and by performing some simplifications, leads to assertion (53). □

Theorem 10.

For $u{\widehat{d}}_{{(\alpha ,\beta )}_q}=qu{\widehat{d}}_{{(\alpha ,\beta )}_q}$, the qMLTF ${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)$ satisfy the following q-derivative formulas:

$${\widehat{D}}_{q,u}{}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)=-{\widehat{d}}_{{(\alpha ,\beta )}_q}{}_{E}C_{n+1,q}^{(\alpha ,\beta )}\left(u\right),$$

(55)

$${\widehat{D}}_{q,u}{}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)=-\widehat{c}{\widehat{d}}_{{(\alpha ,\beta )}_q}{}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right).$$

(56)

Proof. 

In view of identity (6), Equation (16) can be written as

$$\sum _{n=-\infty }^{\infty }{}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)t^n=e_q\left(t\right)e_q\left(-{\displaystyle \frac{u{\widehat{d}}_{{(\alpha ,\beta )}_q}}{t}}\right){\psi }_{0,q}.$$

(57)

Differentiating Equation (57) with respect to u gives

$${\widehat{D}}_{q,u}\left(\sum _{n=-\infty }^{\infty }{}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)t^n\right)=\left(-{\displaystyle \frac{{\widehat{d}}_{{(\alpha ,\beta )}_q}}{t}}\right)e_q\left(t\right)e_q\left(-{\displaystyle \frac{u{\widehat{d}}_{{(\alpha ,\beta )}_q}}{t}}\right){\psi }_{0,q},$$

(58)

which, through using relation (57) on the right-hand-side, yields

$${\widehat{D}}_{q,u}\left(\sum _{n=-\infty }^{\infty }{}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)t^n\right)=\left(-{\displaystyle \frac{{\widehat{d}}_{{(\alpha ,\beta )}_q}}{t}}\right)\sum _{n=-\infty }^{\infty }{}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)t^n.$$

(59)

Adjusting the powers of t in Equation (59), assertion (55) is obtained.

• Similarly, through taking the q-derivative of relation (14) and by performing some simplifications, assertion (56) is proven. □

The addition of relations (55) and (56) gives the following result:

Corollary 3.

For the qMLTF ${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)$, the following q-derivative formula holds:

$${\widehat{D}}_{q,u}{}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)=-{\displaystyle \frac{{\widehat{d}}_{{(\alpha ,\beta )}_q}}{2}}\left({}_{E}C_{n+1,q}^{(\alpha ,\beta )}\left(u\right)+\widehat{c}{}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)\right).$$

(60)

5. Graphical Representation

To explore the properties of ${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)$ and ${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)$ in q-MLBF and q-MLTF, understanding their shapes is crucial. Using software like “Wolfram Mathematica”, we analyze these functions across various index values. Recent advancements in computer software have empowered researchers to swiftly visualize and address numerous mathematical challenges, facilitating pattern recognition and data analysis. This capability significantly enhances mathematicians ability to comprehend fundamental concepts more effectively than ever before.

The graphs of qMLBF ${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)$ are drawn by taking $q=0.75$, $\alpha =1.15$, $\beta =0.25$, $n=10$ and $n=11$, respectively, in relation (21) (see Figure 1 and Figure 2):

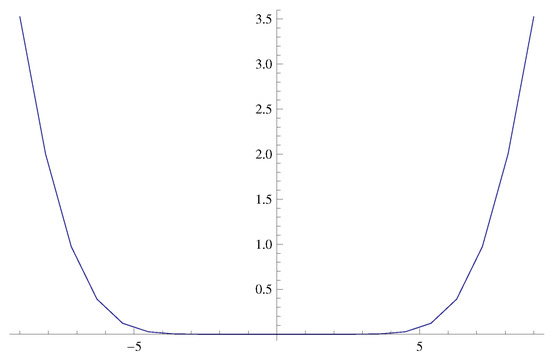
Figure 1. Shape of ${}_{E}J_{10,0.75}^{(1.15,0.25)}\left(u\right)$.

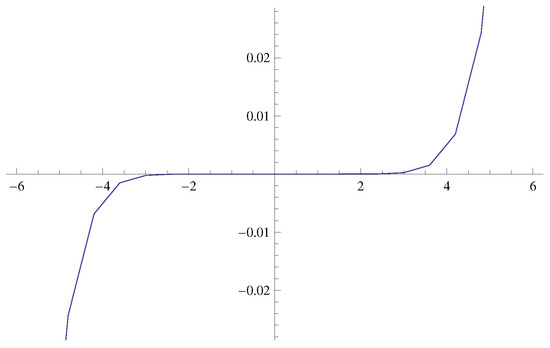
Figure 2. Shape of ${}_{E}J_{11,0.75}^{(1.15,0.25)}\left(u\right)$.

Again, by choosing $q=0.95$, $\alpha =1$, $\beta =1$, $n=10$ and $n=11$, respectively, in Equation (21), the shapes of qMLBF ${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)$ are plotted in Figure 3 and Figure 4.

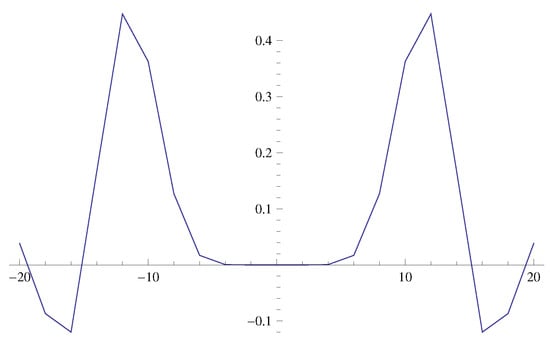
Figure 3. Shape of ${}_{E}J_{10,0.95}^{(1,1)}\left(u\right)$.

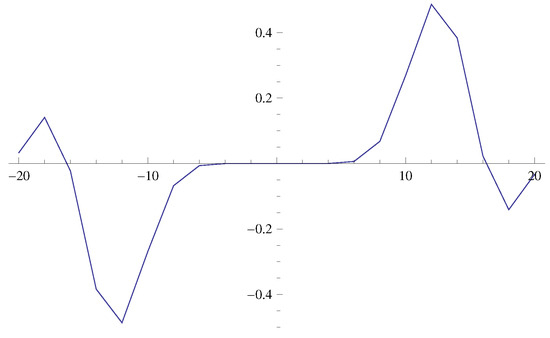
Figure 4. Shape of ${}_{E}J_{11,0.95}^{(1,1)}\left(u\right)$.

Now, the graphs of the qMLTF ${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)$ are obtained by taking $n=10$, $q=0.09$, $\alpha =3.4$, $\beta =1.5$ (Figure 5) and $n=10$, $q=0.9$, $\alpha =0.4$, $\beta =0.5$ (Figure 6) in Equation (22).

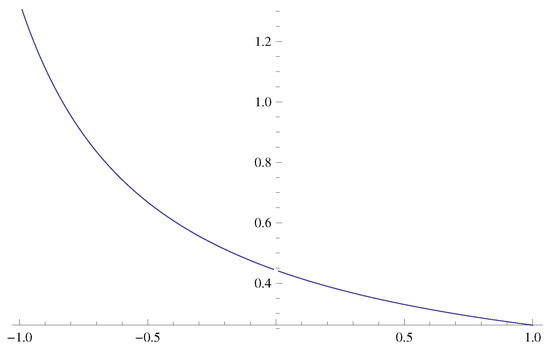
Figure 5. Shape of ${}_{E}C_{10,0.09}^{(3.4,1.5)}\left(u\right)$.

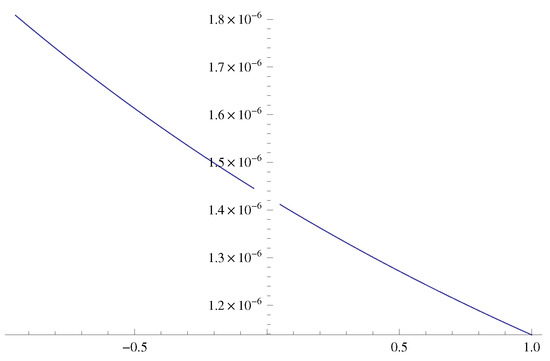
Figure 6. Shape of ${}_{E}C_{10,0.9}^{(0.4,0.5)}\left(u\right)$.

The graphs show the behaviour of the qMLBF ${}_{E}J_{n,q}^{(\alpha ,\beta )}\left(u\right)$ and qMLTF ${}_{E}C_{n,q}^{(\alpha ,\beta )}\left(u\right)$. The investigation regarding the shapes of the hybrid q-special functions will be very helpful for researchers in regard to understanding the properties of these hybrid q-special functions.