Gröbner–Shirshov Bases for Temperley–Lieb Algebras of Type F

Abstract

For the Temperley–Lieb algebras of type $F_n$ with $n\ge 4$, we construct their Gröbner–Shirshov bases. Explicitly, the corresponding finite sets consisting of the standard monomials of type $F_n$, which are exactly the fully commutative elements of $F_n$, are enumerated when n = 4, 5, and 6.

1. Introduction

The Temperley–Lieb algebra stems from the context of statistical mechanics in the 1970s [1]. Later, its structure was studied in connection with knot theory, where it is known to be a quotient of the Hecke algebra of type A in [2].

Our main tool for understanding the structure of the Temperley–Lieb algebra is from the Gröbner–Shirshov basis theory, that is, the noncommutative Gröbner basis theory, which provides a powerful method for finding the structure of (non-)associative algebras and their representations, especially in computational aspects. The central interest in the notion of Gröbner–Shirshov bases originates from Buchberger’s algorithm for computing Gröbner bases for commutative algebras [3] and independently from Shirshov’s Composition Lemma and his algorithm for Lie algebras [4,5]. After a decade, Bokut applied Shirshov’s method to associative algebras [6], and Bergman mentioned the diamond lemma for ring theory [7]. The main strategy of the composition–diamond lemma is to establish an algorithm for constructing standard monomials of a quotient algebra by a two-sided ideal generated by a set of relations called a Gröbner–Shirshov basis.

One of the applications of Gröbner–Shirshov bases in group theory is the word problem [8]. We see that it is solvable in a finite Coxeter group since any element has a unique normal form with respect to a Gröbner–Shirshov basis. It is worthwhile to mention that a Coxeter group is the group of symmetries of a regular or semiregular polytope in the Euclidean space. Some computational results on Coxeter groups appeared in a series of papers [9,10,11,12,13,14,15]. In addition, Gröbner–Shirshov bases for various structures were investigated by the Bokut school in Guangzhou [16]. It is notable to mention that there are algebras with finite Gröbner–Shirshov bases and unsolvable zero divisors problems [17], and there are also some examples from different algebraic structures [18].

For any Temperley–Lieb algebra, its basis consisting of standard monomials coming from a Gröbner–Shirshov basis is indexed by a subset of fully commutative elements [19,20]. The fully commutative element of a Coxeter group is an element with no braid relation in its reduced expression. Motivated by the bijective correspondence of the homogeneous representations of KLR algebras (or quiver Hecke algebras) with fully commutative elements of the corresponding Coxeter group (for simply laced cases only) [21], Feinberg and Lee studied the packet decomposition of fully commutative elements for the Coxeter groups of types A and D [22]. It is known that the finite sets of fully commutative elements for the Coxeter groups are classified into seven families: $A_n,B_n,D_n,E_n,F_n,H_n, \mathrm{and} I_2\left(m\right)$ [19,23].

For Temperley–Lieb algebras of types A, B, and D (moreover, of imprimitive complex reflection groups), their explicit basis elements are enumerated in the papers [9,24,25]. In this article, we focus on the algebras of type F.

2. Gröbner–Shirshov Bases

Let X be a set and let $⟨X⟩$ be the free monoid of associative words on X. We denote the empty word by 1 and the length (or degree) of a word u by $l\left(u\right)$. We also define a monomial order < on $⟨X⟩$ to be a well ordered such that $x<y$ implies $axb<ayb$ for all $a,b\in ⟨X⟩$.

We fix a monomial order < on $⟨X⟩$ and let $\mathbb{F}⟨X⟩$ be the free associative algebra generated by X over a field $\mathbb{F}$. Given a nonzero element $p\in \mathbb{F}⟨X⟩$, we denote by $\overline{p}$ the maximal monomial (called the leading monomial) appearing in p under the ordering <. Thus

$$p=\alpha \overline{p}+\sum {\beta }_i{w}_i$$

with $\alpha ,{\beta }_i\in \mathbb{F}$, $w_i\in ⟨X⟩$, $\alpha \ne 0$, and $w_i<\overline{p}$. If $\alpha =1$, p is said to be monic.

Let S be a subset of monic elements in $\mathbb{F}⟨X⟩$, and let I be the two-sided ideal of $\mathbb{F}⟨X⟩$ generated by S. Then, we say that the algebra $A=\mathbb{F}⟨X⟩/I$ is defined by S.

Definition 1. 

Given a subset S of monic elements in $\mathbb{F}⟨X⟩$, a monomial $u\in ⟨X⟩$ is said to be S-standard (or S-reduced) if $u\ne a\overline{s}b$ for any $s\in S$ and $a,b\in ⟨X⟩$. Otherwise, the monomial u is said to be S-reducible.

Lemma 1 

([6,7]). Every $p\in \mathbb{F}⟨X⟩$ can be expressed as

$$p=\sum {\alpha }_i{a}_i{s}_i{b}_i+\sum {\beta }_j{u}_j,$$

(1)

where ${\alpha }_i,{\beta }_j\in \mathbb{F}$, $a_i,b_i,u_j\in ⟨X⟩$, $s_i\in S$, $a_i\overline{s_i}{b}_i\le \overline{p}$, $u_j\le \overline{p}$, and $u_j$ are S-standard.

Remark 1. 

The term $\sum {\beta }_j{u}_j$ in the expression (1) is called a normal form (or a remainder) of p with respect to the subset S (and with respect to the monomial order <). We note that a normal form is not unique in general.

As a corollary of Lemma 1, we obtain the following:

Proposition 1. 

The set of S-standard monomials spans the algebra $A=\mathbb{F}⟨X⟩/I$ defined by the subset S as a vector space over $\mathbb{F}$.

Let p and q be monic polynomials in $\mathbb{F}⟨X⟩$ with leading monomials $\overline{p}$ and $\overline{q}$. We define the composition of p and q as follows:

Definition 2. 

(a) If there are a and b in $⟨X⟩$ such that $\overline{p}a=b\overline{q}=w$ with $l\left(\overline{p}\right)>l\left(b\right)$, then the composition of intersection is defined as ${(p,q)}_w=pa-bq$.

(b) If there are a and b in $⟨X⟩$ such that $a\ne 1$, $a\overline{p}b=\overline{q}=w$, then the composition of inclusion is defined to be ${(p,q)}_{a,b}=apb-q$.

Let $p,q\in \mathbb{F}⟨X⟩$ and $w\in ⟨X⟩$. We define the congruence relation on $\mathbb{F}⟨X⟩$ as follows: $p\equiv qmod(S;w)$ if and only if $p-q=\sum {\alpha }_i{a}_i{s}_i{b}_i$, where ${\alpha }_i\in \mathbb{F}$, $a_i,b_i\in ⟨X⟩$, $s_i\in S$, $a_i\overline{s_i}{b}_i<w$.

Definition 3. 

A subset S of monic elements in $\mathbb{F}⟨X⟩$ is said to be closed under composition if ${(p,q)}_w\equiv 0mod(S;w)$ and ${(p,q)}_{a,b}\equiv 0mod(S;w)$ for all $p,q\in S$, $a,b\in ⟨X⟩$ whenever the compositions ${(p,q)}_w$ and ${(p,q)}_{a,b}$ are defined.

The following theorem is the main tool for our results in the next two sections:

Theorem 1 ([6,7]). 

Let S be a subset of monic elements in $\mathbb{F}⟨X⟩$. Then, the following conditions are equivalent:

(a) 

S is closed under composition;

(b) 

For each $p\in \mathbb{F}⟨X⟩$, a normal form of p with respect to S is unique;

(c) 

The set of S-standard monomials forms the $\mathbb{F}$-linear basis of the algebra $A=\mathbb{F}⟨X⟩/I$ defined by S.

Definition 4. 

A subset S of monic elements in $\mathbb{F}⟨X⟩$ is a Gröbner–Shirshov basis if S satisfies one of the equivalent conditions in Theorem 1. In this case, we say that S is a Gröbner–Shirshov basis for the algebra A defined by S.

Remark 2. 

The first condition (a) in Theorem 1 gives an analogue of Buchberger’s algorithm or Shirshov’s algorithm. Let $S^{\left(0\right)}:=S$ be any subset of monic elements in $\mathbb{F}⟨X⟩$. For $i\ge 0$, set

$$\begin{array}{cc}\hfill S_{\left(i\right)}& :=\{{(p,q)}_w\not\equiv 0mod(S^{\left(i\right)};w)|p,q\in S^{\left(i\right)}\}\cup \{{(p,q)}_{a,b}\not\equiv 0mod(S^{\left(i\right)};w)|p,q\in S^{\left(i\right)}\},\hfill \\ \hfill S^{(i+1)}& :=S^{\left(i\right)}\cup S_{\left(i\right)}.\hfill \end{array}$$

Then, clearly, set $\widehat{S}:={\bigcup }_{i\ge 0}{S}^{\left(i\right)}$ is closed under composition.

3. Temperley–Lieb Algebras of Types ${\mathit{A}}_{\mathit{n}}$ and $B_n$

3.1. Type $A_n$

First, we review the results ofn the Temperley–Lieb algebra $\mathcal{TL}\left(A_n\right)$. We define $\mathcal{TL}\left(A_n\right)$ as the associative algebra over the complex field $\mathbb{C}$, generated by $X=\{E_1,E_2,\dots ,E_n\}$ with the following defining relations:

$$\begin{array}{ccc}\hfill & E_i^2=\delta E_i& \mathrm{for} 1\le i\le n,(\mathrm{idempotent} \mathrm{relations})\hfill \\ \hfill R_{\mathcal{TL}\left(A_n\right)}:& E_i{E}_j=E_j{E}_i& \mathrm{for} i>j+1,(\mathrm{commutative} \mathrm{relations})\hfill \\ & E_i{E}_j{E}_i=E_i& \mathrm{for} j=i\pm 1,(\mathrm{untwisting} \mathrm{relations})\hfill \end{array}$$

where $\delta \in \mathbb{C}$ is a parameter. Our monomial order < is taken to be the degree-lexicographic order with

$$E_1<E_2<\cdots <E_n.$$

We write $E_{i,j}=E_i{E}_{i-1}\cdots E_j$ for $i\ge j$ (hence, $E_{i,i}=E_i$). By convention, $E_{i,i+1}=1$ for $i\ge 1$.

Proposition 2 

([9], p. 287). The Temperley–Lieb algebra $\mathcal{TL}\left(A_n\right)$ has a Gröbner–Shirshov basis as follows:

$$\begin{array}{ccc}\hfill & E_i^2-\delta E_i& \mathrm{for} 1\le i\le n,\hfill \\ \hfill {\widehat{R}}_{\mathcal{TL}\left(A_n\right)}:& E_i{E}_j-E_j{E}_i& \mathrm{for} i>j+1,\hfill \\ & E_{i,j}{E}_i-E_{i-2,j}{E}_i& \mathrm{for} i>j,\hfill \\ & E_j{E}_{i,j}-E_j{E}_{i,j+2}& \mathrm{for} i>j.\hfill \end{array}$$

(2)

The corresponding ${\widehat{R}}_{\mathcal{TL}\left(A_n\right)}$-standard monomials are of the form

$$E_{i_1,j_1}{E}_{i_2,j_2}\cdots E_{i_p,j_p}(0\le p\le n)$$

(3)

where

$$\begin{array}{cc}& 1\le i_1<i_2<\cdots <i_p\le n,1\le j_1<j_2<\cdots <j_p\le n,\hfill \\ & i_1\ge j_1,i_2\ge j_2,\dots ,i_p\ge j_p\hfill \end{array}$$

(the case of $p=0$ is the monomial 1). We denote the set of ${\widehat{R}}_{\mathcal{TL}\left(A_n\right)}$-standard monomials by $M_{\mathcal{TL}\left(A_n\right)}$. Note that the number $|M_{\mathcal{TL}\left(A_n\right)}|$ of ${\widehat{R}}_{\mathcal{TL}\left(A_n\right)}$-standard monomials is

$${\displaystyle \frac{1}{n+2}}\left({\displaystyle \genfrac{}{}{0pt}{}{2n+2}{n+1}}\right):=C_{n+1},$$

representing the ${(n+1)}^{th}$ Catalan number.

Example 1 

($A_3$). Note that $|M_{\mathcal{TL}\left(A_2\right)}|=C_3=5$ and $|M_{\mathcal{TL}\left(A_3\right)}|=C_4=14$. Explicitly, the ${\widehat{R}}_{\mathcal{TL}\left(A_3\right)}$-standard monomials are as follows:

$$\begin{array}{cc}& 1,E_1,E_2,E_1{E}_2,E_{2,1},\\ & E_3,E_1{E}_3,E_2{E}_3,E_1{E}_2{E}_3,E_{2,1}{E}_3,E_{3,2},E_1{E}_{3,2},E_{2,1}{E}_{3,2},E_{3,1}.\end{array}$$

Remark 3. 

(1) Considering the standard monomials in the Temperley–Lieb algebra, we see that the product of two standard monomials becomes a standard monomial up to a scalar multiple. For example, if we multiply $E_1{E}_2$ by $E_{2,1}{E}_{3,2}$ in the previous example, then we obtain

$$\left(E_1{E}_2\right)\left(E_{2,1}{E}_{3,2}\right)=\delta E_1{E}_2{E}_1{E}_{3,2}=\delta E_1{E}_{3,2},$$

which is a multiple of another standard monomial $E_1{E}_{3,2}$. For another one, the multiplication of $E_{2,1}$ by $E_{3,1}$ leads us to have

$$E_{2,1}{E}_{3,1}=E_2\left(E_1{E}_{3,1}\right)=E_2\left(E_1{E}_3\right)=E_{2,1}{E}_3$$

based on the Gröbner–Shirshov basis (2).

(2) Note that the collection of sets of pairs $(i_1,j_1),(i_2,j_2),\dots ,(i_p,j_p)$ in (3) is in 1-1 correspondence to the family of paths going to the east and north from $(0,0)$ to $(n+1,n+1)$ in the lattice of integer points, not going above the line of the diagonal points. The cardinality is known as the Catalan number, arising in many counting problems in combinatorics (See [26] for details).

(3) Also, we note that the number of standard monomials is equal to the number of fully commutative elements [19,20].

3.2. Type $B_3$

Instead of defining the Temperley–Lieb algebra $\mathcal{TL}\left(B_n\right)$$(n\ge 2)$ with

$$dim\mathcal{TL}\left(B_n\right)=(n+2)C_n-1,$$

we just define the algebra of type $B_3$ in this paper.

Consider the Coxeter diagram for type $B_3$ as follows:

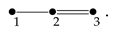
The algebra $\mathcal{TL}\left(B_3\right)$ is the associative algebra over $\mathbb{C}$, generated by $X=\{E_1,E_2,E_3\}$ with the following defining relations:

$$\begin{array}{ccc}\hfill & E_i^2=\delta E_i& \mathrm{for} 1\le i\le 3,\hfill \\ \hfill R_{\mathcal{TL}\left(B_3\right)}:& E_3{E}_1=E_1{E}_3,& \hfill \\ & E_i{E}_j{E}_i=E_i& \mathrm{for} \{i,j\}=\{1,2\},\hfill \\ & E_i{E}_j{E}_i{E}_j=2E_i{E}_j& \mathrm{for} \{i,j\}=\{2,3\},\hfill \end{array}$$

where $\delta \in \mathbb{C}$ is a parameter. We then take our monomial order < to be the degree-lexicographic order with

$$E_1<E_2<E_3.$$

Proposition 3 

([24]). The algebra $\mathcal{TL}\left(B_3\right)$ has a Gröbner–Shirshov basis ${\widehat{R}}_{\mathcal{TL}\left(B_3\right)}$ with respect to our monomial order < as follows:

$$\begin{array}{ccc}\hfill & E_i^2-\delta E_i& \mathrm{for} 1\le i\le 3,\hfill \\ & E_3{E}_1-E_1{E}_3,\\ \hfill {\widehat{R}}_{\mathcal{TL}\left(B_3\right)}:& E_i{E}_j{E}_i-E_i& \mathrm{for} \{i,j\}=\{1,2\},\hfill \\ & E_1{E}_{3,1}-E_1{E}_3,\\ & E_i{E}_j{E}_i{E}_j-2E_i{E}_j& \mathrm{for} \{i,j\}=\{2,3\}.\hfill \end{array}$$

The cardinality of the set $M_{\mathcal{TL}\left(B_3\right)}$, i.e., the set of ${\widehat{R}}_{\mathcal{TL}\left(B_3\right)}$-standard monomials, is $dim\mathcal{TL}\left(B_3\right)=(3+2)C_3-1=24.$

Explicitly, the ${\widehat{R}}_{\mathcal{TL}\left(B_3\right)}$-standard monomials that are not ${\widehat{R}}_{\mathcal{TL}\left(A_3\right)}$-standard are as follows:

$$\begin{array}{cc}& E_2{E}_{3,2},E_1{E}_2{E}_{3,2},E_2{E}_{3,1},E_1{E}_2{E}_{3,1},E_{3,2}{E}_3,\\ & E_1{E}_{3,2}{E}_3,E_{2,1}{E}_{3,2}{E}_3,E_{3,1}{E}_3,E_{3,1}{E}_{3,2},E_{3,1}{E}_{3,2}{E}_3.\end{array}$$

4. Temperley–Lieb Algebras of Type ${\mathit{F}}_{\mathit{n}}$

Now, we consider the Coxeter diagram for type $F_n$:

Let $\mathcal{TL}\left(F_n\right)$$(n\ge 4)$ be the Temperley–Lieb algebra of type $F_n$, that is, the associative algebra over $\mathbb{C}$, generated by $X=\{E_1,E_2,\dots ,E_n\}$ with defining relations as follows:

$$\begin{array}{ccc}\hfill & E_i^2=\delta E_i& \mathrm{for} 1\le i\le n,\hfill \\ \hfill R_{\mathcal{TL}\left(F_n\right)}:& E_i{E}_j=E_j{E}_i& \mathrm{for} i>j+1,\hfill \\ & E_i{E}_j{E}_i=E_i& \mathrm{for} \{i,j\}=\{1,2\},\{3,4\},\{4,5\},\dots ,\{n-1,n\},\hfill \\ & E_i{E}_j{E}_i{E}_j=2E_i{E}_j& \mathrm{for} \{i,j\}=\{2,3\},\hfill \end{array}$$

where $\delta \in \mathbb{C}$ is a parameter. We then ix our monomial order < to be the degree-lexicographic order with

$$E_1<E_2<\cdots <E_n.$$

4.1. Type $F_4$

From the relations given in $R_{\mathcal{TL}\left(F_4\right)}$, we calculate the Gröbner–Shirshov basis for the algebra $\mathcal{TL}\left(F_4\right)$.

Theorem 2. 

The algebra $\mathcal{TL}\left(F_4\right)$ has a Gröbner–Shirshov basis ${\widehat{R}}_{\mathcal{TL}\left(F_4\right)}$ with respect to our monomial order < as follows:

$$\begin{array}{ccc}\hfill & E_i^2-\delta E_i& \mathrm{for} 1\le i\le 4,\hfill \\ & E_i{E}_j-E_j{E}_i& \mathrm{for} i>j+1,\hfill \\ & E_i{E}_j{E}_i-E_i& \mathrm{for} \{i,j\}=\{1,2\},\{3,4\},\hfill \\ \hfill {\widehat{R}}_{\mathcal{TL}\left(F_4\right)}:& E_1{E}_{i,1}-E_1{E}_{i,3}& \mathrm{for} i>1,\hfill \\ & E_{4,j}{E}_4-E_{2,j}{E}_4& \mathrm{for} j<3,\hfill \\ & E_i{E}_j{E}_i{E}_j-2E_i{E}_j& \mathrm{for} \{i,j\}=\{2,3\},\hfill \\ & E_2{E}_{4,j}{E}_3-2E_{2,j}{E}_{4,3}& \mathrm{for} j<3.\hfill \end{array}$$

The set of ${\widehat{R}}_{\mathcal{TL}\left(F_4\right)}$-standard monomials is denoted by $M_{\mathcal{TL}\left(F_4\right)}$. Note that the number $|M_{\mathcal{TL}\left(F_4\right)}|$ is $dim\mathcal{TL}\left(F_4\right)=106$ (See [27], p. 319).

Explicitly, the ${\widehat{R}}_{\mathcal{TL}\left(F_4\right)}$-standard monomials that are not ${\widehat{R}}_{\mathcal{TL}\left(B_3\right)}$-standard are as follows:

$$\begin{array}{cc}& m{E}_4(m\in M_{\mathcal{TL}\left(B_3\right)}),\\ & E_{4,3},m{E}_{4,3}(m\in M_{\mathcal{TL}\left(B_3\right)},which ends with E_1 or E_2),\\ & E_{4,2},m{E}_{4,2}(m\in M_{\mathcal{TL}\left(B_3\right)},which ends with E_1 or E_2),\\ & E_{4,1},m{E}_{4,1}(m\in M_{\mathcal{TL}\left(B_3\right)},which ends with E_2),\\ & E_{4,2}{E}_3,m{E}_{4,2}{E}_3(m\in M_{\mathcal{TL}\left(B_3\right)},which ends with E_1),\\ & E_{4,2}{E}_3{E}_4,m{E}_{4,2}{E}_3{E}_4(m\in M_{\mathcal{TL}\left(B_3\right)},which ends with E_1),\\ & E_{4,1}{E}_3,E_{4,1}{E}_3{E}_4,E_{4,1}{E}_{3,2},E_{4,1}{E}_{3,2}{E}_4,E_{4,1}{E}_{3,2}{E}_{4,3},\\ & E_{4,1}{E}_{3,2}{E}_{4,2},E_{4,1}{E}_{3,2}{E}_{4,1},E_{4,1}{E}_{3,2}{E}_3,E_{4,1}{E}_{3,2}{E}_3{E}_4.\end{array}$$

Proof. 

First, it can be easily proved that the relations in ${\widehat{R}}_{\mathcal{TL}\left(F_4\right)}$ hold. Counting the number of ${\widehat{R}}_{\mathcal{TL}\left(F_4\right)}$-standard monomials, we see that the number $|M_{\mathcal{TL}\left(F_4\right)}|=106$ is exactly the dimension of the Temperley–Lieb algebra $\mathcal{TL}\left(F_4\right)$, which is the same as the number of fully commutative elements of type $F_4$, as given in [27]. Hence, by Theorem 1 (c), the set ${\widehat{R}}_{\mathcal{TL}\left(F_4\right)}$ is the Gröbner–Shirshov basis for the algebra $\mathcal{TL}\left(F_4\right)$ defined by $R_{\mathcal{TL}\left(F_4\right)}$. □

Example 2. 

We have the multiplication table between the standard monomials. For example, we multiply the monomial $E_{4,1}{E}_{3,2}{E}_3{E}_4$ by $E_1$ from the right to obtain

$$E_{4,1}{E}_{3,2}{E}_3{E}_4{E}_1=E_{4,1}{E}_{3,1}{E}_3{E}_4=E_{4,2}{E}_1{E}_3{E}_3{E}_4=\delta E_{4,1}{E}_3{E}_4$$

from the relations in ${\widehat{R}}_{\mathcal{TL}\left(F_4\right)}$.

4.2. Type $F_5$

Adding one more generator, we compute the Gröbner–Shirshov and the corresponding finite set of standard monomials.

Theorem 3. 

The algebra $\mathcal{TL}\left(F_5\right)$ has a Gröbner–Shirshov basis ${\widehat{R}}_{\mathcal{TL}\left(F_5\right)}$ with respect to our monomial order < as follows:

$$\begin{array}{ccc}\hfill & E_i^2-\delta E_i& \mathrm{for} 1\le i\le 5,\hfill \\ & E_i{E}_j-E_j{E}_i& \mathrm{for} i>j+1,\hfill \\ & E_i{E}_j{E}_i-E_i& \mathrm{for} \{i,j\}=\{1,2\},\{3,4\},\{4,5\}\hfill \\ & E_1{E}_{i,1}-E_1{E}_{i,3}& \mathrm{for} i>1,\hfill \\ \hfill {\widehat{R}}_{\mathcal{TL}\left(F_5\right)}:& E_3{E}_{5,3}-E_3{E}_5,\\ & E_{i,j}{E}_i-E_{i-2,j}{E}_i& \mathrm{for} i>3\ge j,\hfill \\ & E_{5,2}{E}_3{E}_5-E_{3,2}{E}_3{E}_5,\\ & E_i{E}_j{E}_i{E}_j-2E_i{E}_j& \mathrm{for} \{i,j\}=\{2,3\},\hfill \\ & E_2{E}_{i,j}{E}_3-2E_{2,j}{E}_{i,3}& \mathrm{for} i>3>j.\hfill \end{array}$$

We denote the set of ${\widehat{R}}_{\mathcal{TL}\left(F_5\right)}$-standard monomials based on $M_{\mathcal{TL}\left(F_5\right)}$. Note that the number $|M_{\mathcal{TL}\left(F_5\right)}|$ is $dim\mathcal{TL}\left(F_5\right)=464$ (See [27], p. 319).

Explicitly, the ${\widehat{R}}_{\mathcal{TL}\left(F_5\right)}$-standard monomials that are not ${\widehat{R}}_{\mathcal{TL}\left(F_4\right)}$-standard are as follows:

$$\begin{array}{cc}& m{E}_5(m\in M_{\mathcal{TL}\left(F_4\right)}),\\ & E_{5,4},m{E}_{5,4}(m\in M_{\mathcal{TL}\left(F_4\right)},which ends with E_1 or E_2 or E_3),\\ & E_{5,3},m{E}_{5,3}(m\in M_{\mathcal{TL}\left(F_4\right)},which ends with E_1 or E_2),\\ & E_{5,2},m{E}_{5,2}(m\in M_{\mathcal{TL}\left(F_4\right)},which ends with E_1 or E_2),\\ & E_{5,1},m{E}_{5,1}(m\in M_{\mathcal{TL}\left(F_4\right)},which ends with E_2),\\ & E_{5,2}{E}_3,m{E}_{5,2}{E}_3(m\in M_{\mathcal{TL}\left(F_4\right)},which ends with E_1),\\ & E_{5,2}{E}_3{E}_4,m{E}_{5,2}{E}_3{E}_4(m\in M_{\mathcal{TL}\left(F_4\right)},which ends with E_1),\\ & E_{5,2}{E}_3{E}_4{E}_5,m{E}_{5,2}{E}_3{E}_4{E}_5(m\in M_{\mathcal{TL}\left(F_4\right)},which ends with E_1),\\ & E_{5,1}{E}_3,E_{5,1}{E}_3{E}_4,E_{5,1}{E}_{3,2},E_{5,1}{E}_{3,2}{E}_4,E_{5,1}{E}_{3,2}{E}_{4,3},\\ & E_{5,1}{E}_{3,2}{E}_{4,2},E_{5,1}{E}_{3,2}{E}_{4,1},E_{5,1}{E}_{3,2}{E}_3,E_{5,1}{E}_{3,2}{E}_3{E}_4,\\ & E_{5,1}{E}_3{E}_4{E}_5,E_{5,1}{E}_{3,2}{E}_4{E}_5,E_{5,1}{E}_{3,2}{E}_{4,3}{E}_5,E_{5,1}{E}_{3,2}{E}_{4,3}{E}_{5,4},\\ & E_{5,1}{E}_{3,2}{E}_{4,2}{E}_5,E_{5,1}{E}_{3,2}{E}_{4,2}{E}_{5,4},E_{5,1}{E}_{3,2}{E}_{4,2}{E}_{5,3},E_{5,1}{E}_{3,2}{E}_{4,2}{E}_{5,2},E_{5,1}{E}_{3,2}{E}_{4,2}{E}_{5,1},\\ & E_{5,1}{E}_{3,2}{E}_{4,1}{E}_5,E_{5,1}{E}_{3,2}{E}_{4,1}{E}_{5,4},E_{5,1}{E}_{3,2}{E}_{4,1}{E}_{5,3},E_{5,1}{E}_{3,2}{E}_{4,1}{E}_{5,2},\\ & E_{5,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_3,E_{5,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_3{E}_4,E_{5,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_3{E}_4{E}_5,E_{5,1}{E}_{3,2}{E}_3{E}_4{E}_5.\end{array}$$

4.3. Type $F_6$

Theorem 4. 

The algebra $\mathcal{TL}\left(F_6\right)$ has a Gröbner–Shirshov basis ${\widehat{R}}_{\mathcal{TL}\left(F_6\right)}$ with respect to our monomial order < as follows:

$$\begin{array}{ccc}\hfill & E_i^2-\delta E_i& \mathrm{for} 1\le i\le 6,\hfill \\ & E_i{E}_j-E_j{E}_i& \mathrm{for} i>j+1,\hfill \\ & E_i{E}_j{E}_i-E_i& \mathrm{for} \{i,j\}=\{1,2\},\{3,4\},\{4,5\},\{5,6\}\hfill \\ & E_1{E}_{i,1}-E_1{E}_{i,3}& \mathrm{for} i>1,\hfill \\ \hfill {\widehat{R}}_{\mathcal{TL}\left(F_5\right)}:& E_j{E}_{i,j}-E_j{E}_{i,j+2}& \mathrm{for} i>j+1>3,\hfill \\ & E_{i,j}{E}_i-E_{i-2,j}{E}_i& \mathrm{for} i>3\ge j,i>j>3\hfill \\ & E_{i,2}{E}_3{E}_i-E_{i-2,2}{E}_3{E}_i& \mathrm{for} i>4,\hfill \\ & E_i{E}_j{E}_i{E}_j-2E_i{E}_j& \mathrm{for} \{i,j\}=\{2,3\},\hfill \\ & E_2{E}_{i,j}{E}_3-2E_{2,j}{E}_{i,3}& \mathrm{for} i>3>j.\hfill \end{array}$$

We denote the set of ${\widehat{R}}_{\mathcal{TL}\left(F_6\right)}$-standard monomials by $M_{\mathcal{TL}\left(F_6\right)}$. Note that the number $|M_{\mathcal{TL}\left(F_6\right)}|$ is $dim\mathcal{TL}\left(F_5\right)=2003$ (See [27], p. 319).

Explicitly, the ${\widehat{R}}_{\mathcal{TL}\left(F_6\right)}$-standard monomials that are not ${\widehat{R}}_{\mathcal{TL}\left(F_5\right)}$-standard are as follows:

$$\begin{array}{cc}& m{E}_6(m\in M_{\mathcal{TL}\left(F_5\right)}),\\ & E_{6,5},m{E}_{6,5}(m\in M_{\mathcal{TL}\left(F_5\right)},which ends with E_i (i<5),\\ & E_{6,4},m{E}_{6,4}(m\in M_{\mathcal{TL}\left(F_5\right)},which ends with E_i (i<4),\\ & E_{6,3},m{E}_{6,3}(m\in M_{\mathcal{TL}\left(F_5\right)},which ends with E_i (i<3),\\ & E_{6,2},m{E}_{6,2}(m\in M_{\mathcal{TL}\left(F_5\right)},which ends with E_i (i<3),\\ & E_{6,1},m{E}_{6,1}(m\in M_{\mathcal{TL}\left(F_5\right)},which ends with E_2),\\ & E_{6,2}{E}_3,m{E}_{6,2}{E}_3(m\in M_{\mathcal{TL}\left(F_5\right)},which ends with E_1),\\ & E_{6,2}{E}_3{E}_4,m{E}_{6,2}{E}_3{E}_4(m\in M_{\mathcal{TL}\left(F_5\right)},which ends with E_1),\\ & E_{6,2}{E}_3{E}_4{E}_5,m{E}_{6,2}{E}_3{E}_4{E}_5(m\in M_{\mathcal{TL}\left(F_5\right)},which ends with E_1),\\ & E_{6,2}{E}_3{E}_4{E}_5{E}_6,m{E}_{6,2}{E}_3{E}_4{E}_5{E}_6(m\in M_{\mathcal{TL}\left(F_5\right)},which ends with E_1),\end{array}$$

$$\begin{array}{cc}& E_{6,1}{E}_3,E_{6,1}{E}_3{E}_4,E_{6,1}{E}_{3,2},E_{6,1}{E}_{3,2}{E}_4,E_{6,1}{E}_{3,2}{E}_{4,3},\\ & E_{6,1}{E}_{3,2}{E}_{4,2},E_{6,1}{E}_{3,2}{E}_{4,1},E_{6,1}{E}_{3,2}{E}_3,E_{6,1}{E}_{3,2}{E}_3{E}_4,\\ & E_{6,1}{E}_3{E}_4{E}_5,E_{6,1}{E}_{3,2}{E}_4{E}_5,E_{6,1}{E}_{3,2}{E}_{4,3}{E}_5,E_{6,1}{E}_{3,2}{E}_{4,3}{E}_{5,4},\\ & E_{6,1}{E}_{3,2}{E}_{4,2}{E}_5,E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,4},E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,3},E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,2},E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,1},\\ & E_{6,1}{E}_{3,2}{E}_{4,1}{E}_5,E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,4},E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,3},E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2},\\ & E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_3,E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_3{E}_4,E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_3{E}_4{E}_5,E_{6,1}{E}_{3,2}{E}_3{E}_4{E}_5,\\ & E_{6,1}{E}_3{E}_4{E}_5{E}_6,E_{6,1}{E}_{3,2}{E}_4{E}_5{E}_6,E_{6,1}{E}_{3,2}{E}_{4,3}{E}_5{E}_6,E_{6,1}{E}_{3,2}{E}_{4,3}{E}_{5,4}{E}_6,E_{6,1}{E}_{3,2}{E}_{4,3}{E}_{5,4}{E}_{6,5},\\ & E_{6,1}{E}_{3,2}{E}_{4,2}{E}_5{E}_6,E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,4}{E}_6,E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,4}{E}_{6,5},E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,3}{E}_6,\\ & E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,3}{E}_{6,5},E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,3}{E}_{6,4},E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,2}{E}_6,E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,2}{E}_{6,5},\\ & E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,2}{E}_{6,4},E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,2}{E}_{6,3},E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,2}{E}_{6,2},E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,2}{E}_{6,1},\\ & E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,1}{E}_6,E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,1}{E}_{6,5},E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,1}{E}_{6,4},E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,1}{E}_{6,3},\\ & E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,1}{E}_{6,2},E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,1}{E}_{6,2}{E}_3,E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,1}{E}_{6,2}{E}_3{E}_4,E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,1}{E}_{6,2}{E}_3{E}_4{E}_5,\\ & E_{6,1}{E}_{3,2}{E}_{4,2}{E}_{5,1}{E}_{6,2}{E}_3{E}_4{E}_5{E}_6,E_{6,1}{E}_{3,2}{E}_{4,1}{E}_5{E}_6,E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,4}{E}_6,E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,4}{E}_{6,5},\\ & E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,3}{E}_6,E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,3}{E}_{6,5},E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,3}{E}_{6,4},E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_6,\\ & E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_{6,5},E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_{6,4},E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_{6,3},E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_{6,2},\\ & E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_{6,1},E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_3{E}_6,E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_3{E}_{6,5},E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_3{E}_{6,4},\\ & E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_3{E}_4{E}_6,E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_3{E}_4{E}_{6,5},E_{6,1}{E}_{3,2}{E}_{4,1}{E}_{5,2}{E}_3{E}_4{E}_5{E}_6,E_{6,1}{E}_{3,2}{E}_3{E}_4{E}_5{E}_6.\end{array}$$

4.4. Type $F_n(n\ge 7)$

In general, we obtain a Gröbner–Shirshov for the Temperley–Lieb algebra of type $F_n(n\ge 7)$ as follows:

Theorem 5. 

The algebra $\mathcal{TL}\left(F_n\right)$ has a Gröbner–Shirshov basis ${\widehat{R}}_{\mathcal{TL}\left(F_n\right)}$ with respect to our monomial order < as follows:

$$\begin{array}{ccc}\hfill & E_i^2-\delta E_i& \mathrm{for} 1\le i\le n,\hfill \\ & E_i{E}_j-E_j{E}_i& \mathrm{for} i>j+1,\hfill \\ & E_i{E}_j{E}_i-E_i& \mathrm{for} \{i,j\}=\{1,2\},\{3,4\},\{4,5\},\{5,6\},\dots ,\{n-1,n\}\hfill \\ & E_1{E}_{i,1}-E_1{E}_{i,3}& \mathrm{for} i>1,\hfill \\ \hfill {\widehat{R}}_{\mathcal{TL}\left(F_n\right)}:& E_j{E}_{i,j}-E_j{E}_{i,j+2}& \mathrm{for} i>j+1>3,\hfill \\ & E_{i,j}{E}_i-E_{i-2,j}{E}_i& \mathrm{for} i>3\ge j,i>j>3\hfill \\ & E_{i,2}{E}_3{E}_i-E_{i-2,2}{E}_3{E}_i& \mathrm{for} i>4,\hfill \\ & E_i{E}_j{E}_i{E}_j-2E_i{E}_j& \mathrm{for} \{i,j\}=\{2,3\},\hfill \\ & E_2{E}_{i,j}{E}_3-2E_{2,j}{E}_{i,3}& \mathrm{for} i>3>j.\hfill \end{array}$$

We denote the set of ${\widehat{R}}_{\mathcal{TL}\left(F_n\right)}$-standard monomials with $M_{\mathcal{TL}\left(F_n\right)}$. Note that the number $|M_{\mathcal{TL}\left(F_n\right)}|$ is

$$dim\mathcal{TL}\left(F_n\right)=5f_{3n-4}-5\sum _{k=2}^{n-1}{\displaystyle \frac{f_{3k-5}}{n-k+1}}\left({\displaystyle \genfrac{}{}{0pt}{}{2n-2k}{n-k}}\right)+{\displaystyle \frac{1}{n}}\left({\displaystyle \genfrac{}{}{0pt}{}{2n-2}{n-1}}\right)-2n{f}_{2n-2}-2f_{2n-4}+f_{n-1}-1$$

where $\left\{f_n\right\}$ is the Fibonacci sequence (See [27], p. 306).

Proof. 

We use the algorithm following part (a) of Theorem 1. Taking all possible compositions from the relations in the previous step, we obtain new relations that cannot be reducible with respect to the prior relations. It is clearly shown that all the relations in ${\widehat{R}}_{\mathcal{TL}\left(F_n\right)}$ hold and that any composition between the polynomials in ${\widehat{R}}_{\mathcal{TL}\left(F_n\right)}$ reduces to 0 with respect to ${\widehat{R}}_{\mathcal{TL}\left(F_n\right)}$, which means that ${\widehat{R}}_{\mathcal{TL}\left(F_n\right)}$ is closed under composition. □

Remark 4. 

For the Temperley–Lieb algebras of types $E_n$$(n\ge 6)$ and $H_n$$(n\ge 2)$, we are working on their Gröbner–Shirshov bases and the corresponding standard monomials, which will be a new interpretation for the fully commutative elements of the associated types.