Abstract
In the present paper, we mainly studied the Riemann problem and wave interaction of a simplified magnetohydrodynamic equation system. Due to the complex Riemann problem and wave interactions in the magnetohydrodynamic equations, most previous studies either did not investigate the interaction of elementary waves or, if they did, lacked supporting numerical experiments. This paper simplifies the magnetohydrodynamic equations using variable substitution. Using the characteristic line method to solve the Riemann problem and elementary wave interaction of the simplified magnetohydrodynamic equations, the form of the solution is more symmetrical and the interaction between waves has also become more regular. The correctness of the results was verified by numerical experiments.
1. Introduction
Magnetogasdynamics plays a significant role in plasma physics and astrophysics [1], and it can be applied to industrial production [2]. According to the laws of conservation of mass, momentum, and energy, the one-dimensional ideal magnetohydrodynamic equations can be expressed in Lagrangian coordinates as follows:
where , u, , , and represent specific volume, velocity, pressure, magnetic flux density, magnetic permeability, and total energy, respectively, and specific internal energy for polytropic gas satisfies the relation . For most gases, (where ) is the adiabatic gas constant. When considering the initial value problem of Equation (1), no matter how smooth the initial data, discontinuity may still take place in the solution. In view of the essential feature of quasilinear hyperbolic equations, it is natural to take account of initial data with discontinuities at certain points. The simplest case, called the Riemann problem, is the Cauchy problem for (1) with initial condition
By using the characteristic line method to solve this problem, the conditions for the generation of evacuation waves, shock waves, contact discontinuities, vacuum, and mass concentration phenomena can be obtained.
Y. Hu studied the Riemann problem [3] and found that the projection of the contact discontinuity on the plane is a straight line parallel to the p-axis. Due to the magnetic field, the result becomes more complex and difficult to analyze. This situation was also observed in the research of other scholars [4,5,6,7,8,9,10,11], indicating that the method of dividing the phase plane by the elementary wave curve is not suitable.
Since the full governing system for magnetohydrodynamics is highly nonlinear and complicated, it is necessary to study the various simplified models. In plasma physics, the sum of pressure and magnetic pressure is referred to as the total pressure, which is also known as the surface force. To simplify the Riemann problem of (1), denoting the as an independent variable, and , the system (1) can be rewritten in the form
with the initial data
It has been rigorously proven that the projection of the contact discontinuity on the plane is a point, which implies that the elementary wave curve can be used to divide the phase plane. This paper focus on the elementary wave interactions with the following initial data:
for arbitrary . There are many conclusions regarding the elementary wave interactions of the hyperbolic system, and readers can view the references for more details.
The rest of this paper is organized as follows. In Section 2, we provide the methods used in this article. In Section 3, we obtain the expressions of the elementary wave curves including the rarefaction wave curves, shock wave curves, and contact discontinuity curves, and then we construct the Riemann solutions for arbitrary initial data. In Section 4, we analyze all possible results of the elementary wave interactions. In Section 5, we use numerical experiments to verify all possible results of elementary wave interactions.
2. Preliminaries
2.1. Characteristic Line Method
The systems of quasilinear hyperbolic equations that often arise in mathematical models formulated to describe nonlinear wave phenomena in various continuum media that result from the balance laws of continuum physics. The simplest model is the equation
where is a smooth nonlinear given function defined on an interval .
We rewrite the equation as and consider the characteristics defined by the following characteristic equations:
It is obvious that there exists a family of parallel lines on the plane that make u invariant. These parallel straight lines are called characteristic lines.
2.2. Lax–Friedrichs Method
The Lax–Friedrichs method is a numerical solution for solving systems of quasilinear hyperbolic equations. The numerical format is
The data used in this article will be detailed in Section 5.
3. The Riemann Problem of Simplifying Models
In this section, to reduce the difficulty of analyzing elementary wave interactions, the Riemann problem for Equation (2) has some differences compared to the previous article.
Equation (2) can be rewritten as
It is easy to obtain that . These eigenvalues are real and distinct because , indicating that Equation (3) is a strictly hyperbolic system. The right eigenvectors are and . It is obvious that the characteristic field is linearly degenerate, which means that the elementary wave associated with it is a contact discontinuity and the characteristic fields are genuinely nonlinear, meaning that the elementary waves associated with and characteristic fields will be either rarefaction waves or shock waves.
There are piecewise smooth solutions of Equation (3), which are of the form such that
where , assuming , system (3) becomes
The expression of the rarefaction wave passing through can be written as follows:
and
Theorem 1.
Across (), , , (, , ) if and only if the wave speed increases from the left state to the right state.
Proof.
Without the loss of generality, we assume that is the left state. For , it is found that
where . It is obvious that since . According to the first equation of Formula (6), it is found that
so and . Conversely, , and for . □
Additionally, contact discontinuity J satisfies , and .
Theorem 2.
The projection of contact discontinuity on the plane is a point.
For a bounded discontinuity , the Rankine–Hugoniot jump conditions are
where . From Equation (7), the shock curves satisfy
and
Theorem 3.
Across (), , , (, , ).
Proof.
According to the second equation of Formula (9), , and cannot be positive or negative at the same time. Thus, we have to apply the Lax entropy conditions, so and . Similarly, across , , , and . □
Theorem 4.
The curve is monotonic decreasing and convex in the plane. The curve is monotonic increasing and concave in the plane. has an intersection with the u-axis, and has no asymptote. is the projection of on the plane.
Proof.
Moreover, it is easy to verify that intersects the u-axis at a point. A similar proof applies to the curve . The proof is completed. □
Theorem 5.
The curve is monotonic decreasing and convex in the plane. The curve is monotonic increasing and concave in the plane. has an intersection with the u-axis, and has no asymptote.
Proof.
The proof for follows similarly, so we must focus on for convenience. From the first equation of Formula (9) and , it is found that
owing to
Then, according to the second equation of Formula (9) and Theorem 3, it is found that
Moreover, it is easy to verify that has no asymptote. The proof is completed. □
Summarizing the work above, the plane can be divided into four regions, as follows (see Figure 1):
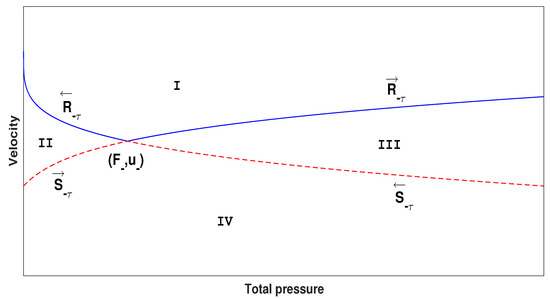
Figure 1.
phase divided by four fundamental wave curves starting from the left state.
Theorem 6.
There are four cases for the Riemann problem.
where and are the intermediate states. Contact discontinuity J will not exist when , and are connected by rarefaction waves and shock waves.
4. The Elementary Wave Interactions
In order for two fundamental waves to interact, they must meet in finite time and space. Due to the fact that the interaction problem of waves can be regarded as a solution of partial differential equations with three initial values, one-dimensional space can be divided into left, middle, and right parts. Once the intermediate state is determined, based on the calculated dispersion wave velocity, shock wave velocity, and contact discontinuity wave velocity in the previous section, as long as the fundamental wave velocity generated in the left and middle parts exceeds that generated in the middle and right parts, wave interaction will occur. The initial data of the elementary wave interactions are as follows:
The middle can be considered right relative to the left, and left relative to the right. Considering the particularity of the middle position relative to the left and right, the elementary wave interactions from the projection of intermediate state are as follows:
See Figure 2. The projection of left state is on the curve or passing through , and the projection of right state is on the curve or passing through . Therefore,
and
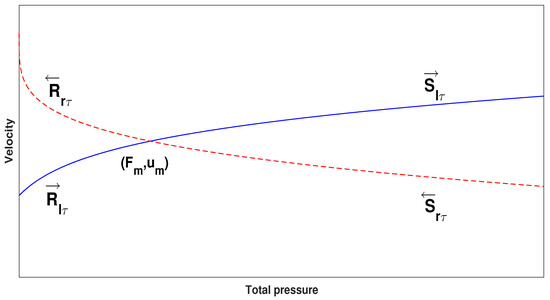
Figure 2.
phase divided by four fundamental wave curves starting from the intermediate state.
The elementary wave will meet another elementary wave and interact if it propagates for a period of time. When the left state is selected, a backward wave curve through and a forward wave curve through can be confirmed by (13) and (14).
Case 1. The projection of left state is on the curve (Figure 3).
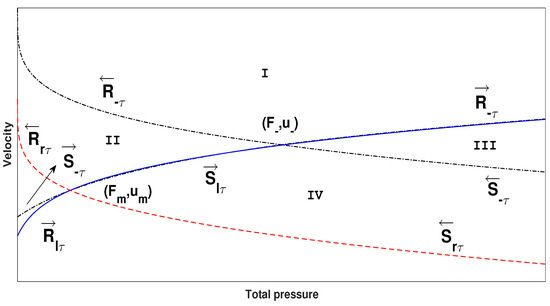
Figure 3.
phasewhen is generated in the left and middle states.
Via (14), it is found that is a point on the curve , and when the projection of the right state is on the curve , are on the region ; the result of this interaction is ⋃.
When the projection of the right state is on the curve , are on the region ; thus, the result of this interaction is ⋃.
Case 2. The projection of the left state is on the curve (Figure 4).
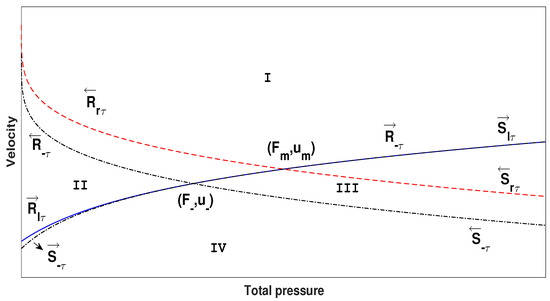
Figure 4.
phasewhen is generated in the left and middle states.
Via (13), it is found that is a point on the curve , when the projection of the right state is on the curve , are on the region ; thus, the results of this interaction is ⋃.
When the projection of the right state is on the curve , are on the region I; the results of this interaction is ⋃.
Next, consider the interactions involving contact discontinuity.
Case 1. Changes in the phase plane when increases (Figure 5).
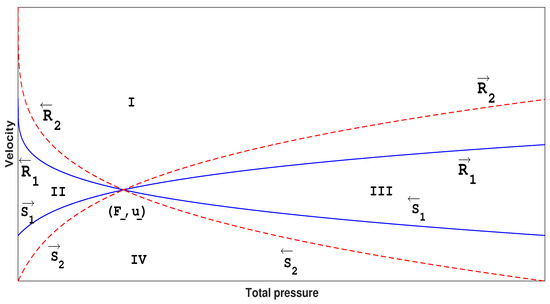
Figure 5.
phase when increases.
Considering the variation in the rarefaction curve and shock curve in the plane when increases, using monotony to solve the problems from the first equation of (6), it is found that
This means that F increases when is not changing. According to Theorem 1, this implies that will increase when F is not changing. Then, by the second equation of (6), will increase when F is not changing, so u will increase when F is not changing for . The same applies for . For shock curves, by the first equation of (9), it is found that
and
This means that F will increase when is not changing. According to Theorem 5, this implies that will increase when F is not changing. Thus, will increase when F is not changing. Then, by the second equation of (9), according to Theorem 3, u will decrease when F is not changing. The same applies for . Therefore, the interactions with contact discontinuity are evident.
Case 2. Changes in the phase plane when decreases (Figure 6).
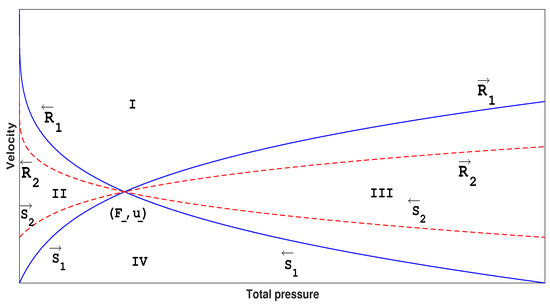
Figure 6.
phase when decreases.
This situation is similar to the first situation.
Therefore, there are eight cases for elementary wave interactions, as follows:
Theorem 7.
- (i)
- +.+→⋃.
- (ii)
- +.+→⋃.
- (iii)
- +J.+J→⋃(),+J→⋃().
- (iv)
- +.+→⋃.
- (v)
- +.+→⋃.
- (vi)
- +J.+J→⋃(),+J→⋃().
- (vii)
- J+.J+→⋃(),J+→⋃().
- (viii)
- J+.J+→⋃(),J+→⋃().
5. Results and Discussion
In the previous section, the Riemann problem and elementary wave interactions were discussed. Now, we use a numerical experiment to verify them. To facilitate the calculation of initial values, assuming that in the numerical experiment, we use the Lax–Friedrichs method, where space step and time step , see Table 1.

Table 1.
Initial data when the intermediate state is .
The initial values given in the table are calculated based on expressions (13)–(16) corresponding to , , , and .
The initial data are
From Figure 7a, it can be seen that surface force and velocity increase, while specific volume decreases. According to Theorem 1, appears. From Figure 7b, it can be seen that surface force and velocity decrease, while specific volume increases. According to Theorem 3, appears. From Figure 7c, it can be seen that specific volume and velocity increase, while surface force decreases. According to Theorem 1, appears. From Figure 7d, it can be seen that specific volume and velocity decrease, while surface force increases. According to Theorem 3, appears. The results in Figure 7 validate the correctness of Section 3.
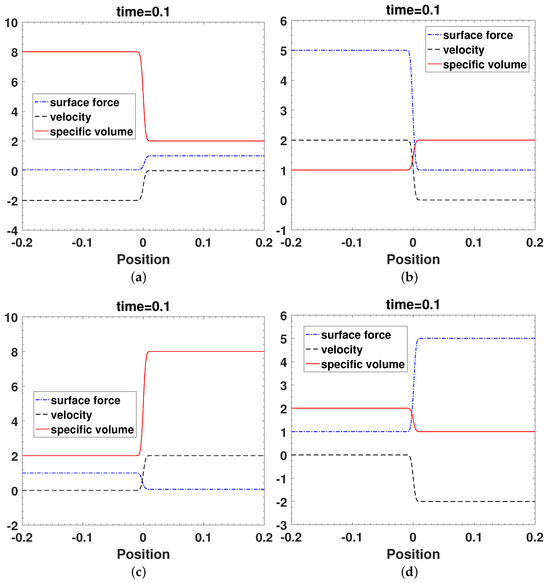
Figure 7.
The Riemann problem with different initial values. (a) , . (b) , . (c) , . (d) , .
The initial data of the elementary wave interactions are as follows:
By using the results of Figure 7 and Theorem 2, the initial values can be set to the twelve cases in Theorem 7. As long as time is long enough, the two elementary waves can interact with each other, allowing us to obtain the results of the interaction. The results can be determined based on Theorems 1–3.
From Figure 8a, it can be seen that specific volume first decreases and then increases, velocity continues to decrease, and surface force first increases and then decreases, indicating the generation of and . The interaction result is →. Similarly, from Figure 8b, it can be seen that specific volume continues to increase, velocity first increases and then decreases, and surface force continues to decrease. Moreover, there is a point in Figure 8b where velocity and surface force are constants, but specific volume has changed. This means that the interaction result is →J. From Figure 8c, it can be seen that specific volume continues to increase, velocity first increases and then decreases, and surface force continues to decrease. Moreover, there is a point in Figure 8c where velocity and surface force are constants, but specific volume has changed. This means that the interaction result is J→J. From Figure 8d, it can be seen that specific volume first decreases and then increases, velocity continues to decrease, and surface force first increases and then decreases. Unlike Figure 8a, there is a point in Figure 8d where velocity and surface force are constants, but specific volume has changed. This means that the interaction result is J→J. From Figure 8e, it can be seen that specific volume continues to decrease, velocity first decreases and then increases, and surface force continues to increase. This means that the interaction result is →J. From Figure 8f, since the value of specific volume changes too much, it is replaced by its reciprocal density. It can be seen that density first decreases and then increases, velocity continues to increase, and surface force first decreases and then increases. This means that the interaction result is →. From Figure 8g, it can be seen that specific volume decreases first, then increases and then decreases again, velocity first decreases and then increases, and surface force continues to increase. This means that the interaction result is J→J. From Figure 8h, it can be seen that specific volume decreases first, then increases and then decreases again, velocity continues to increase, and surface force continues to increase. This means that the interaction result is J→J. From Figure 8i, it can be seen that specific volume continues to decrease, velocity first decreases and then increases, and surface force continues to increase. Moreover, there is a point in Figure 8i where velocity and surface force are constants, but specific volume has changed. This means that the interaction result is J→J. From Figure 8j, it can be seen that specific volume first decreases and then increases, velocity continues to decrease, and surface force first decreases and then increases. Moreover, there is a point in Figure 8j where velocity and surface force are constants, but specific volume has changed. This means that the interaction result is J→J. From Figure 8k, it can be seen that specific volume increases first, then decreases and then increases again, velocity first decreases and then increases, and surface force continues to decrease. This means that the interaction result is J→J. From Figure 8l, it can be seen that specific volume increases first, then decreases and then increases again, velocity continues to increase, and surface force continues to decrease. This means that the interaction result is J→J.
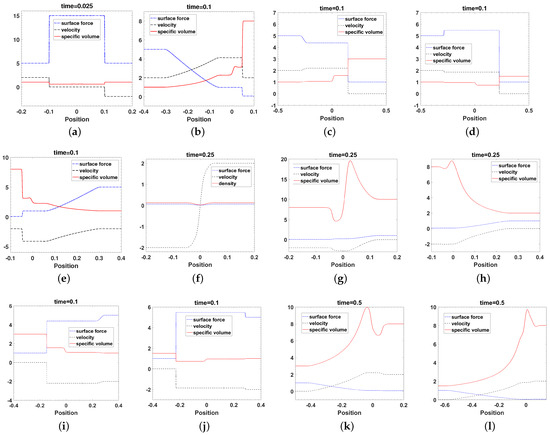
Figure 8.
Elementary wave interactions with different initial values. (a) , , . (b) , , . (c) , , . (d) , , . (e) , , . (f) , , . (g) , , . (h) , , . (i) , , . (j) , , . (k) , , . (l) , , .
Many previous theoretical studies on the equations of magnetohydrodynamics have yielded complex results, and no numerical experiments were conducted to validate the conclusions presented in this article. This article simplifies the form of the equation system by replacing variables, making the expression of the fundamental wave solution simpler. Therefore, the expression can be used to determine the initial values used in numerical experiments. The significance of this approach is as follows: Firstly, the results of numerical experiments can verify the conclusions of this paper (Theorems 6 and 7). Secondly, the model in this article is obtained through the variable transformation method, with the aim of simplifying previous models. The results of numerical experiments can prove the rationality of variable transformation. Finally, the solution of the simplified model in this article is a special case and a supplement to previous research.
6. Conclusions
Most previous studies either did not investigate the interaction of elementary waves or, if they did, lacked supporting numerical experiments. This article makes up for the shortcomings of previous research. By changing variables, the equations of magnetohydrodynamics can be simplified, and the basic wave solution expression of Riemann problems can also be simplified, thereby simplifying the study of wave interactions.
For our future research, we plan to use variable transformation methods to simplify the form of solutions in other complex equations of fluid mechanics.
Author Contributions
Conceptualization, K.Y. and G.L.; methodology, K.Y. and G.L.; software, K.Y. and G.L.; validation, K.Y., S.L. and G.L.; formal analysis, K.Y. and S.L.; investigation, K.Y., S.L. and G.L.; resources, K.Y. and G.L.; data curation, K.Y.; writing—original draft preparation, K.Y. and S.L.; writing—review and editing, G.L.; visualization, G.L.; supervision, G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hartmann, J. Theory of the laminar flow of an electrically conductive liquid in a homogeneous magnetic field. J. Math.-Fys. Meddelelser 1937, 6, 1–28. [Google Scholar]
- Radler, K.H. Mean-field approach to spherical dynamo models. J. Astronom. Nachr. 1980, 301, 101–129. [Google Scholar] [CrossRef]
- Hu, Y.; Sheng, W. The Riemann problem of conservation laws in magnetogasdynamics. J. Commun. Pure Appl. Anal. 2013, 12, 755–769. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, W. Riemann problem and wave interactions in magnetogasdynamics. J. Math. Anal. Appl. 2013, 397, 454–466. [Google Scholar] [CrossRef]
- Kuila, S.; Sekhar, T.R. Riemann solution for ideal isentropic magnetogasdynamics. J. Mecc. 2014, 49, 2453–2465. [Google Scholar] [CrossRef]
- Kuila, S.; Sekhar, T.R. Riemann solution for one dimensional non-ideal isentropic magnetogasdynamics. J. Comput. Appl. Math. 2016, 35, 119–133. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, W. Elementary wave interactions in magnetogasdynamics. J. Indian J. Pure Appl. Math. 2016, 47, 33–57. [Google Scholar] [CrossRef]
- Yang, H.; Wang, J. Delta-shocks and vacuum states in the vanishing pressure limit of solutions to the isentropic Euler equations for modified Chaplygin gas. J. Math. Anal. Appl. 2014, 413, 800–820. [Google Scholar] [CrossRef]
- Zhiqiang, S. Vanishing Magnetic Field Limits of Solutions to the Isentropic Chaplygin Gas Magnetogasdynamics Equations. Bull. Malays. Math. Sci. Soc. 2022, 45, 3101–3129. [Google Scholar]
- Trushlyakov, V.I.; Pavlenko, A.N.; Zhukov, V.E.; Urbansky, V.A.; Mezentseva, N.N. Dynamics of Condensation and Evaporation of Liquid Nitrogen in a Closed Vessel Pressurized with Helium, Nitrogen, and Their Mixture. J. Eng. Thermophys. 2024, 33, 231–249. [Google Scholar] [CrossRef]
- Boscheri, W.; Dumbser, M.; Maire, H.P. A New Thermodynamically Compatible Finite Volume Scheme for Lagrangian Gas Dynamics. SIAM J. Sci. Comput. 2024, 46, A2224–A2247. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).