A New Fractional Curvature of Curves and Surfaces in Euclidean Space Using the Caputo’s Fractional Derivative

Abstract

In this paper, the authors generalize the fractional curvature of plane curves introduced by Rubio et al. in 2023, to regular curves in the Euclidean space ${\mathbb{R}}^3$, and study the geometric properties of the curve using Caputo’s fractional derivative. Furthermore, we introduce a new definition of fractional curvature and fractional mean curvature of a regular surface, using fractional principal curvatures; and prove that such concepts are invariant under isometries; i.e., they belong to the intrinsic geometry of the regular surface. Also, a geometric interpretation is given to Caputo’s fractional derivative of algebraic polynomials.

1. Introduction

The fractional calculus is a branch of mathematics that studies the properties of derivatives and integrals of non-integer order; actually, it has different applications such as in the theory of viscoelasticity [1,2,3,4], dynamical systems [5,6,7], medicine [8], mechanics [9], economics [10], Newtonian dynamics [11], etc.

In 1967, Caputo [12], working on problems of differential equations related to the theory of viscoelasticity, formulated a new definition of fractional derivative, which had the advantage that the fractional initial conditions of fractional differential equations behaved like the initial conditions in the integer case of differential equations; another advantage of this fractional derivative, called Caputo’s fractional derivative, is that when applied to constants it cancels; which allows its use in other areas of knowledge, such as differential geometry.

In geometry, the fractional derivative is used in the study of geometric properties of curves [13,14,15,16,17], surfaces [18] and Riemannian manifolds [19,20].

In [16], Yajima et al., were forced to make a simplification of the fractional derivative of the composite function; since the formula for the fractional derivative of the composite function involves a series, which made it difficult to apply fractional calculus to the study of geometry.

In 2023, Rubio et al. [15] gave a new definition of fractional curvature of plane curves, different from that given by Yajima et al. [16], who makes use of integration in their approximations, which in practice is complicated.

In this paper, we generalize the definition of Rubio et al. [15], to curves in the 3-dimensional Euclidian space; and a new definition of fractional torsion of a regular curves is given; furthermore, a new definition of fractional curvature and fractional mean curvature of regular surfaces is given, using fractional principal curvatures, which differs from the approach given by Yajima et al. [18]; and it is shown that these curvatures are invariant under local isometries; i.e., they belong to the intrinsic geometry of regular curves and surfaces. 1,2-dimensional Euclidian space is characterized as that space whose fractional curvature is zero at all points.

This paper is organized as follow: Section 2 we provide some results on differential geometry of curves and surfaces [21,22] and the Caputo fractional derivative [12]. In Section 3 we define the curvature and fractional torsion and develops theory. Section 4 defines curvature and fractional mean curvature of surfaces and develops theory. In Section 5, we provide some examples of the fractional curvature of curves and surfaces and of the fractional torsion of a curve. In Example 1, we obtain a result that allows us to give a geometric interpretation of the Caputo fractional derivative in the case of polynomial functions.

2. Preliminaries

Definition 1 

([15,21]). A parametrized curve differentiable in ${\mathbb{R}}^n$ is a mapping $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^n$ differentiable of class $C^{\infty }$, on an open interval $I\subset \mathbb{R}$. The variable t is called a parameter, and the subset of ${\mathbb{R}}^n$ formed by the points $\alpha \left(t\right)$, is called the trace of the curve.

Definition 2 

([15,21]). Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^n$ a differentiable parametrized curve. The vector

$${\alpha }^{\prime }\left(t\right)=\left(x_1^{\prime }\left(t\right),x_2^{\prime }\left(t\right),\dots ,x_n^{\prime }\left(t\right)\right)$$

is called the Tangent vector of α at t.

The curve $\alpha \left(t\right)$ is called regular [15,21,22] if ${\alpha }^{\prime }\left(t\right)\ne 0,\forall t\in I$. Furthermore, if $\alpha$ is a regular curve, it can be reparametrized by the arc length parameter s, where

$$s=s\left(t\right)={\int }_{t_0}^t\parallel {\alpha }^{\prime }\left(\tau \right)\parallel d\tau .$$

(1)

If $\alpha$ is parametrized by are length, then $\parallel {\alpha }^{\prime }\left(s\right)\parallel =1,\forall s\in I$, [15,21,22].

2.1. Space Curves

Definition 3 

([15,21]). Let be $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ a regular curve parametrized by arc length, then the curvature of α at $s\in I$ is the real number

$$k\left(s\right)=\parallel {\alpha }^{″}\left(s\right)\parallel .$$

(2)

Definition 4 

([15,21,22]). Let be $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ a regular curve parametrized by arc length, such that $k\left(s\right)>0$. The vector

$$n\left(s\right)={\displaystyle \frac{{\alpha }^{″}\left(s\right)}{k\left(s\right)}},$$

(3)

is called the normal vector to α in $s.$

Definition 5 

([15,21,22]). Let be $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ a regular curve parametrized by arc length, such that $k\left(s\right)>0$. The Binormal vector de α in s is:

$$b\left(s\right)=t\left(s\right)\times n\left(s\right).$$

(4)

The Frenet-Serret frame [15,21,22] of the curve $\alpha \left(s\right)=\left(x\left(s\right),y\left(s\right),z\left(s\right)\right)$ is given by the orthonormal basis $\left\{t\left(s\right),n\left(s\right),b\left(s\right)\right\},\forall s\in I$, and the Frenet-Serret formulas are given by

$$\begin{array}{ccc}\hfill t^{\prime }\left(s\right)& =& k\left(s\right)n\left(s\right),\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill n^{\prime }\left(s\right)& =& -k\left(s\right)t\left(s\right)-\tau \left(s\right)b\left(s\right),\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill b^{\prime }\left(s\right)& =& \tau \left(s\right)n\left(s\right),\hfill \end{array}$$

(7)

where $\tau \left(s\right)$ is the torsion function of the curve α in s.

2.2. Regular Surface

Definition 6 

([22]). A subset $S\subset {\mathbb{R}}^3$ is a regular surface if, for each $p\in S$, there exists a neighborhood V in ${\mathbb{R}}^3$ and a map $X:U\to V\cap S$ of an open set $U\subset {\mathbb{R}}^2$ onto $V\cap S\subset {\mathbb{R}}^3$ such that

1. 

X is differentiable.

2. 

X is homeomorphism.

3. 

(The regularity condition). For each $q\in U$, the differential $d{X}_q:{\mathbb{R}}^2\to {\mathbb{R}}^3$ is one-to-one.

Let S be a regular orientable surface, $N:S\to S^2$ the normal map of Gauss, $d{N}_p:T_{p}S\to T_{p}S$ the differential of normal map of Gauss.

Definition 7 

([22]). The quadratic form ${⨿}_p$, defined in $T_{p}S$ by ${⨿}_p\left(v\right)=-⟨d{N}_p\left(v\right),v⟩$ is called the second fundamental form of S at p.

Definition 8 

([22]). Let C be a regular curve in S passing through $p\in S$, k the curvature of C at p, and $cos\theta =⟨n,N⟩$, where n is the normal vector to C and N is the normal vector to S at p. The number $k_n=kcos\theta$ is then called the normal curvature of $C\subset S$ at p.

Let $v\in T_{p}S$, $\parallel v\parallel =1$, then:

$${⨿}_p\left(v\right)=-⟨dNp\left(v\right),v⟩=K_n\left(p\right)=K_n\left(v\right).$$

(8)

Definition 9 

([22]). Let $p\in S$ and let $d{N}_p:T_{p}S\to T_{p}S$ be the differential of the Gauss map. The determinant of $d{N}_p$ is the Gaussian curvature K of S at p. The negative of half of the trace of $d{N}_p$ is called the mean curvature H of S at p.

In terms of the principal curvatures we can write

$$K=k_1.k_{2}andH={\displaystyle \frac{k_1+k_2}{2}},$$

(9)

where the functions $k_1$ and $k_2$ are the principal curvatures of S at p.

2.3. Caputo Fractional Derivative

In this work we will use the Caputo fractional derivative, since this fractional derivative has certain properties that allow the study of Differential Geometry [7,23] on regular curves and surfaces. Properties such as the derivative of a constant is zero, and in the field of the theory of fractional differential equations, fractional initial conditions behave like integer initial conditions [7,24,25], make this fractional derivative a fundamental tool.

Let $f:[a,b]\to \mathbb{R}$ be a function of class $C^1\left([a,b]\right)$. The Caputo fractional derivative of order $\lambda$ is defined by [12,15,23].

$${}^{c}D^{\lambda }f\left(t\right)={\displaystyle \frac{1}{\mathrm{\Gamma }(1-\lambda )}}{\int }_a^t{\displaystyle \frac{1}{{(t-u)}^{\lambda }}}{f}^{\prime }\left(u\right)du,$$

(10)

where $\lambda \in \mathbb{R}$, $0<\lambda <1$, and $\mathrm{\Gamma }$ is Euler’s gamma function. Furthermore, as in [15], our analysis is based on this property

$$\underset{\lambda \to 1}{lim}{}^{c}D^{\lambda }f\left(t\right)=f^{\prime }\left(t\right),\forall t\in [a,b].$$

(11)

Therefore [15], for $\lambda$ close to 1, the properties of the integer derivative can be approximated by the Caputo’s fractional derivative.

3. Fractional Curvature of Curves in Space

In this section we generalize the fractional curvature of plane curves given by Rubio et al. [15], to curves in space; and we give a new definition of fractional torsion.

Definition 10. 

Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ be a regular curve parametrized by arc length. The fractional derivative vector of order λ, $0<\lambda <1$, of α in $s\in I$, is given by

$${}^{c}D^{\lambda }\alpha \left(s\right)=\left({}^{c}D^{\lambda }x\left(s\right),{}^{c}D^{\lambda }y\left(s\right),{}^{c}D^{\lambda }z\left(s\right)\right).$$

(12)

Let $\left\{t\right(s),n(s,b\left(s\right)\left)\right\}$, $\forall s\in I$, the Frenet-Serret trihedron, then [15]:

$${}^{c}D^{\lambda }\alpha \left(s\right)=a^{\lambda }\left(s\right)t\left(s\right)+b^{\lambda }\left(s\right)n\left(s\right)+c^{\lambda }\left(s\right)b\left(s\right).$$

(13)

Figure 1a shows the vector ${\alpha }^{\prime }\left(s\right)$ tangent to the curve $\alpha$ at s, as well as the fractional derivative vector ${}^{c}D^{\lambda }\alpha \left(s\right)$, which is not necessarily tangent to $\alpha$ at s. Figure 1b expresses the vector ${}^{c}D^{\lambda }\alpha \left(s\right)$ as a linear combination of the basis given by the Frenet–Serret trihedron.

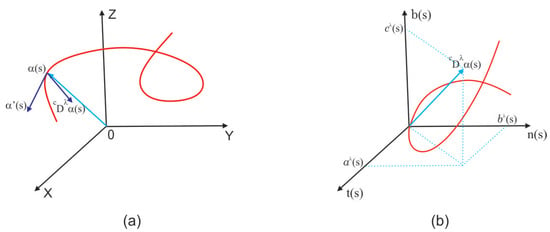
Figure 1. Figure (a), shows the vectors ${\alpha }^{\prime }\left(s\right)$ and ${}^{c}D^{\lambda }\alpha \left(s\right)$. Figure (b), shows the vector ${}^{c}D^{\lambda }\alpha \left(s\right)$ as a linear conbination of the basis $\left\{t\right(s),n(s),b(s\left)\right\}$.

Theorem 1. 

Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ be a regular curve parametrized by arc length. Then:

$$\underset{\lambda \to 1}{lim}{}^{c}D^{\lambda }\alpha \left(s\right)={\alpha }^{\prime }\left(s\right),\forall s\in I.$$

(14)

$$\underset{\lambda \to 1}{lim}{a}^{\lambda }\left(s\right)=1,\underset{\lambda \to 1}{lim}{b}^{\lambda }\left(s\right)=0,\underset{\lambda \to 1}{lim}{c}^{\lambda }\left(s\right)=0,\forall s\in I.$$

(15)

Proof. 

By Definition 10 we have

$${}^{c}D^{\lambda }\alpha \left(s\right)=\left({}^{c}D^{\lambda }x\left(s\right),{}^{c}D^{\lambda }y\left(s\right),{}^{c}D^{\lambda }z\left(s\right)\right),\forall s\in I,$$

and using the base given by the Frenet-Serret frame, we have:

$${}^{c}D^{\lambda }\alpha \left(s\right)=a^{\lambda }\left(s\right)t\left(s\right)+b^{\lambda }\left(s\right)n\left(s\right)+c^{\lambda }\left(s\right)b\left(s\right),\forall s\in I,\forall \lambda \in <0,1>.$$

Then

$$\begin{array}{ccc}\hfill \underset{\lambda \to 1}{lim}{}^{c}D^{\lambda }\alpha \left(s\right)& =& \left(\underset{\lambda \to 1}{lim}{a}^{\lambda }\left(s\right)\right)t\left(s\right)+\left(\underset{\lambda \to 1}{lim}{b}^{\lambda }\left(s\right)\right)n\left(s\right)+\left(\underset{\lambda \to 1}{lim}{c}^{\lambda }\left(s\right)\right)b\left(s\right)\hfill \\ & =& \left(\underset{\lambda \to 1}{lim}{}^{c}D^{\lambda }x\left(s\right),\underset{\lambda \to 1}{lim}{}^{c}D^{\lambda }y\left(s\right),\underset{\lambda \to 1}{lim}{}^{c}D^{\lambda }z\left(s\right)\right)\hfill \\ & =& \left(x^{\prime }\left(s\right),y^{\prime }\left(s\right),z^{\prime }\left(s\right)\right)={\alpha }^{\prime }\left(s\right)=t\left(s\right),\forall s\in I,\mathrm{por} \left(11\right)\hfill \\ & =& \left(1\right)t\left(s\right)+\left(0\right)n\left(s\right)+\left(0\right)b\left(s\right),\forall s\in I.\hfill \end{array}$$

Since the decomposition in the base is unique, we have

${\displaystyle \underset{\lambda \to 1}{lim}{a}^{\lambda }\left(s\right)=1,\underset{\lambda \to 1}{lim}{b}^{\lambda }\left(s\right)=0,\underset{\lambda \to 1}{lim}{c}^{\lambda }\left(s\right)=0,\forall s\in I.}$□

Theorem 2. 

Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ be a regular curve parametrized by arc length, $k\left(s\right)>0$, $\forall s\in I$ and derivative vector ${}^{c}D^{\lambda }\alpha \left(s\right)=a^{\lambda }\left(s\right)t\left(s\right)+b^{\lambda }\left(s\right)n\left(s\right)+c^{\lambda }\left(s\right)b\left(s\right).$

Then:

$$\begin{array}{ccc}\hfill a^{\lambda }\left(s\right)& =& x^{\prime }\left(s\right){}^{c}D^{\lambda }x\left(s\right)+y^{\prime }\left(s\right){}^{c}D^{\lambda }y\left(s\right)+z^{\prime }\left(s\right){}^{c}D^{\lambda }z\left(s\right),\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill b^{\lambda }\left(s\right)& =& {\displaystyle \frac{1}{k\left(s\right)}}\left[x^{″}\left(s\right){}^{c}D^{\lambda }x\left(s\right)+y^{″}\left(s\right){}^{c}D^{\lambda }y\left(s\right)+z^{″}\left(s\right){}^{c}D^{\lambda }z\left(s\right)\right],\hfill \end{array}$$

(17)

$$c^{\lambda }\left(s\right)={\displaystyle \frac{1}{k\left(s\right)}}\left[{}^{c}D^{\lambda }x\left(s\right)(y^{\prime }{z}^{″}-y^{″}{z}^{\prime })+{}^{c}D^{\lambda }y\left(s\right)(x^{″}{z}^{\prime }-x^{\prime }{z}^{″})+{}^{c}D^{\lambda }z\left(s\right)(x^{\prime }{y}^{″}-x^{″}{y}^{\prime })\right].$$

(18)

Proof. 

Since $\left\{t\right(s),n(s),b(s\left)\right\}$ is an orthonormal basis, we have:

$$a^{\lambda }\left(s\right)=⟨{}^{c}D^{\lambda }\alpha \left(s\right),t\left(s\right)⟩,b^{\lambda }\left(s\right)=⟨{}^{c}D^{\lambda }\alpha \left(s\right),n\left(s\right)⟩,c^{\lambda }\left(s\right)=⟨{}^{c}D^{\lambda }\alpha \left(s\right),b\left(s\right)⟩,$$

from which we have the result. □

By (13) we have ${}^{c}D^{\lambda }\alpha \left(s\right)=a^{\lambda }\left(s\right)t\left(s\right)+b^{\lambda }\left(s\right)n\left(s\right)+c^{\lambda }\left(s\right)b\left(s\right),$ then:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }\alpha \left(s\right)\right)& =& {\displaystyle \frac{d}{ds}}\left(a^{\lambda }\left(s\right)\right)t\left(s\right)+a^{\lambda }\left(s\right)t^{\prime }\left(s\right)+{\displaystyle \frac{d}{ds}}\left(b^{\lambda }\left(s\right)\right)n\left(s\right)+b^{\lambda }\left(s\right)n^{\prime }\left(s\right)+\hfill \\ & & +{\displaystyle \frac{d}{ds}}\left(c^{\lambda }\left(s\right)\right)b\left(s\right)+c^{\lambda }\left(s\right)b^{\prime }\left(s\right).\hfill \end{array}$$

(19)

Using the Frenet-Serret Equations (5)–(7), we have:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }\alpha \left(s\right)\right)& =& \left[{\displaystyle \frac{d}{ds}}\left(a^{\lambda }\left(s\right)\right)-b^{\lambda }\left(s\right)k\left(s\right)\right]t\left(s\right)+\left[a^{\lambda }\left(s\right)k\left(s\right)+{\displaystyle \frac{d}{ds}}\left(b^{\lambda }\left(s\right)\right)+\right.\hfill \\ & +& \left.c^{\lambda }\left(s\right)\tau \left(s\right)\right]n\left(s\right)+\left[-b^{\lambda }\left(s\right)\tau \left(s\right)+{\displaystyle \frac{d}{ds}}\left(c^{\lambda }\left(s\right)\right)\right]b\left(s\right).\hfill \end{array}$$

(20)

By (20), we have the next definition.

Definition 11. 

Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ be a regular curve parametrized by arc length, ${}^{c}D^{\lambda }\alpha \left(s\right)=a^{\lambda }\left(s\right)t\left(s\right)+b^{\lambda }\left(s\right)n\left(s\right)+c^{\lambda }\left(s\right)b\left(s\right),$ the fractional derivative vector of order λ of α in s, $0<\lambda <1.$ The fractional curvature of order λ, $0<\lambda <1,$ of α in s, is defined by:

$$k^{\lambda }\left(s\right)=a^{\lambda }\left(s\right)k\left(s\right)+{\displaystyle \frac{d}{ds}}\left(b^{\lambda }\left(s\right)\right)+c^{\lambda }\left(s\right)\tau \left(s\right),$$

(21)

where $k\left(s\right)$ and $\tau \left(s\right)$ are the integer curvature and torsion of α in s, respectively.

Theorem 3. 

Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ be a regular curve parametrized by arc length,

• If α is a plane curve, then

  $$k^{\lambda }\left(s\right)=a^{\lambda }\left(s\right)k\left(s\right)+{\displaystyle \frac{d}{ds}}{b}^{\lambda }\left(s\right),$$

  (22)
• $$k^{\lambda }\left(s\right)=⟨{\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }\alpha \left(s\right)\right),n\left(s\right)⟩.$$

  (23)

Proof. 

1. If $\alpha$ is a plane curve, then

$$\tau \left(s\right)=0,\forall s\in I,\mathrm{and}{k}^{\lambda }\left(s\right)=a^{\lambda }\left(s\right)k\left(s\right)+{\displaystyle \frac{d}{ds}}{b}^{\lambda }\left(s\right).$$

2. It is inmediately. □

Definition 12. 

Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ be a regular curve parametrized by arc length, the fractional torsion of order λ, $0<\lambda <1,$ of α in s is given by

$${\tau }^{\lambda }\left(s\right)=a^{\lambda }\left(s\right)\tau \left(s\right)-c^{\lambda }\left(s\right)k\left(s\right),$$

(24)

where $k\left(s\right)$ and $\tau \left(s\right)$ are the integer curvature and torsion of α in s, respectively.

Theorem 4. 

Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ be a regular curve parametrized by arc length, then:

$$\begin{array}{ccc}\hfill \underset{\lambda \to 1}{lim}{k}^{\lambda }\left(s\right)& =& k\left(s\right),\forall s\in I=[a,b].\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill \underset{\lambda \to 1}{lim}{\tau }^{\lambda }\left(s\right)& =& \tau \left(s\right),\forall s\in I=[a,b].\hfill \end{array}$$

(26)

Proof. 

By (15) and (21), we have:

${\displaystyle \underset{\lambda \to 1}{lim}k\left(s\right)=\left(\underset{\lambda \to 1}{lim}{a}^{\lambda }\left(s\right)\right)k\left(s\right)+\frac{d}{ds}\left(\underset{\lambda \to 1}{lim}{b}^{\lambda }\left(s\right)\right)+\left(\underset{\lambda \to 1}{lim}{c}^{\lambda }\left(s\right)\right)\tau \left(s\right)=k\left(s\right),\forall s\in I.}$

By (15) and (24), we have:

${\displaystyle \underset{\lambda \to 1}{lim}{\tau }^{\lambda }\left(s\right)=\left(\underset{\lambda \to 1}{lim}{a}^{\lambda }\left(s\right)\right)\tau \left(s\right)-\left(\underset{\lambda \to 1}{lim}{c}^{\lambda }\left(s\right)\right)k\left(s\right)=\tau \left(s\right),\forall s\in I=\left[a,b\right]}$□

Theorem 5. 

Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ be a regular curve parametrized by arc length, $k\left(s\right)>0$, $\forall s\in [a,b]$. Then

$$k^{\lambda }\left(s\right)={\displaystyle \frac{1}{k\left(s\right)}}\left[x^{″}\left(s\right){\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }x\left(s\right)\right)+y^{″}\left(s\right){\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }y\left(s\right)\right)+z^{″}\left(s\right){\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }z\left(s\right)\right)\right]$$

(27)

Proof. 

By (12) we have ${}^{c}D^{\lambda }\alpha \left(s\right)=\left({}^{c}D^{\lambda }x\left(s\right),{}^{c}D^{\lambda }y\left(s\right),{}^{c}D^{\lambda }z\left(s\right)\right)$, then

$${\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }\alpha \left(s\right)\right)=\left({\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }x\left(s\right)\right),{\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }y\left(s\right)\right),{\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }z\left(s\right)\right)\right).$$

Using (20):

$$\begin{array}{ccc}\hfill ⟨{\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }\alpha \left(s\right)\right),n\left(s\right)⟩& =& ⟨\left[{\displaystyle \frac{d}{ds}}\left(a^{\lambda }\left(s\right)\right)-b^{\lambda }\left(s\right)k\left(s\right)\right]t\left(s\right)+\left[a^{\lambda }\left(s\right)k\left(s\right)+{\displaystyle \frac{d}{ds}}\left(b^{\lambda }\left(s\right)\right)\right.\hfill \\ & & \left.+c^{\lambda }\left(s\right)\tau \left(s\right)\right]n\left(s\right)+\left[-b^{\lambda }\left(s\right)\tau \left(s\right)+{\displaystyle \frac{d}{ds}}\left(c^{\lambda }\left(s\right)\right)\right]b\left(s\right),n\left(s\right)⟩\hfill \\ & =& ⟨\left[a^{\lambda }\left(s\right)k\left(s\right)+{\displaystyle \frac{d}{ds}}\left(b^{\lambda }\left(s\right)\right)+c^{\lambda }\left(s\right)\tau \left(s\right)\right]n\left(s\right),n\left(s\right)⟩\hfill \\ & =& ⟨k^{\lambda }\left(s\right)n\left(s\right),n\left(s\right)⟩\hfill \\ & =& k^{\lambda }\left(s\right).\hfill \end{array}$$

Then

$$\begin{array}{ccc}\hfill k^{\lambda }\left(s\right)& =& ⟨{\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }\alpha \left(s\right)\right),n\left(s\right)⟩\hfill \\ & =& ⟨\left({\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }x\left(s\right)\right),{\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }y\left(s\right)\right),{\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }z\left(s\right)\right)\right),n\left(s\right)⟩\hfill \\ & =& ⟨\left({\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }x\left(s\right)\right),{\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }y\left(s\right)\right),{\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }z\left(s\right)\right)\right),{\displaystyle \frac{{\alpha }^{″}\left(s\right)}{k\left(s\right)}}⟩\hfill \\ & =& ⟨\left({\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }x\left(s\right)\right),{\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }y\left(s\right)\right),{\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }z\left(s\right)\right)\right),{\displaystyle \frac{\left(x^{″}\left(s\right),y^{″}\left(s\right),z^{″}\left(s\right)\right)}{k\left(s\right)}}⟩.\hfill \end{array}$$

Therefore

$$\begin{array}{ccc}\hfill k^{\lambda }\left(s\right)& =& {\displaystyle \frac{1}{k\left(s\right)}}\left[x^{″}\left(s\right){\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }x\left(s\right)\right)+y^{″}\left(s\right){\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }y\left(s\right)\right)+z^{″}\left(s\right){\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }z\left(s\right)\right)\right]\hfill \end{array}$$

□

Using (20), we define the following functions:

$$\begin{array}{ccc}\hfill h_1^{\lambda }\left(s\right)& =& {\displaystyle \frac{d}{ds}}\left(a^{\lambda }\left(s\right)\right)-b^{\lambda }\left(s\right)k\left(s\right),\forall s\in [a,b].\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill h_2^{\lambda }\left(s\right)& =& {\displaystyle \frac{d}{ds}}\left(c^{\lambda }\left(s\right)\right)-b^{\lambda }\left(s\right)\tau \left(s\right),\forall s\in [a,b].\hfill \end{array}$$

(29)

Then:

$$\parallel {\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }\alpha \left(s\right)\right){\parallel }^2={\left(h_1^{\lambda }\left(s\right)\right)}^2+{\left(k^{\lambda }\left(s\right)\right)}^2+{\left(h_2^{\lambda }\left(s\right)\right)}^2,\forall s\in [a,b].$$

Theorem 6. 

Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ be a regular curve parametrized by arc length. Then

$$2\left[a^{\lambda }\left(s\right)h_1^{\lambda }\left(s\right)+b^{\lambda }\left(s\right)k^{\lambda }\left(s\right)+c^{\lambda }\left(s\right)h_2^{\lambda }\left(s\right)\right]={\displaystyle \frac{d}{ds}}{\left(\parallel {}^{c}D^{\lambda }\alpha \left(s\right)\parallel \right)}^2.$$

(30)

Proof. 

From (28) and (29) following the result. □

Theorem 7. 

Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ be a regular plane curve parametrized by arc length. Then

$${\tau }^{\lambda }\left(s\right)=0,\forall s\in [a,b],\forall 0<\lambda <1.$$

(31)

Proof. 

Since $\alpha$ is plane curve, then there exists a plane $\mathrm{\Pi }$ that contains it with parametric equation:

$$X(u,v)=p_0+u{w}_1+v{w}_2,$$

(32)

where $w_1$ and $w_2$ are orthonormals vectors. Therefore, the curve $\alpha$ is written as

$$\alpha \left(s\right)=X(u\left(s\right),v\left(s\right))=p_0+u\left(s\right)w_1+v\left(s\right)w_2.$$

Then

$$\begin{array}{ccc}\hfill {}^{c}D^{\lambda }\alpha \left(s\right)& =& {}^{c}D^{\lambda }\left(p_0\right)+{}^{c}D^{\lambda }u\left(s\right)w_1+{}^{c}D^{\lambda }v\left(s\right)w_2,\forall s\in [a,b]\hfill \\ & =& {}^{c}D^{\lambda }u\left(s\right)w_1+{}^{c}D^{\lambda }v\left(s\right)w_2.\hfill \end{array}$$

In addition, the binormal vector $b\left(s\right)$ is paralell to $w_1\times w_2$, $\forall s\in [a,b]$.

Therefore: $c^{\lambda }\left(s\right)=0,\forall s\in [a,b]$; and since $\tau \left(s\right)=0,\forall s\in [a,b]$, we have ${\tau }^{\lambda }\left(s\right)=a^{\lambda }\left(s\right)\tau \left(s\right)-c^{\lambda }\left(s\right)k\left(s\right)=0,\forall s\in [a,b].$ □

Theorem 8. 

Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ be a regular curve parametrized by arc length, $k\left(s\right)>0$, $\forall s\in I$.

$$If{\tau }^{\lambda }\left(s\right)=0,\forall s\in I,\forall \lambda \in <0,1>,entonces\tau \left(s\right)=0,\forall s\in I.$$

(33)

Proof. 

We have

$$\begin{array}{ccc}\hfill {\tau }^{\lambda }\left(s\right)& =& a^{\lambda }\left(s\right)\tau \left(s\right)-c^{\lambda }\left(s\right)k\left(s\right)\hfill \\ & =& ⟨{}^{c}D^{\lambda }\alpha \left(s\right),t\left(s\right)⟩\tau \left(s\right)-⟨{}^{c}D^{\lambda }\alpha \left(s\right),b\left(s\right)⟩k\left(s\right)\hfill \\ & =& ⟨{}^{c}D^{\lambda }\alpha \left(s\right),\tau \left(s\right)t\left(s\right)-k\left(s\right)b\left(s\right)⟩.\hfill \end{array}$$

Now, if ${\tau }^{\lambda }\left(s\right)=0,\forall s\in I,\forall \lambda \in <0,1>$, we have

$${}^{c}D^{\lambda }\alpha \left(s\right)\perp v=\tau \left(s\right)t\left(s\right)-k\left(s\right)b\left(s\right).$$

(34)

We assume that it exists $s_0\in I$, such that $\tau \left(s_0\right)\ne 0$. Without loss of generality assume that $\tau \left(s_0\right)>0$, and let $V_0=\tau \left(s_0\right)t\left(s_0\right)-k\left(s_0\right)b\left(s_0\right)$, and $V_0^{\perp }$ the orthogonal plane to $V_0$.

From (34):

$${}^{c}D^{\lambda }\alpha \left(s_0\right)\in V_0^{\perp },\forall \lambda \in <0,1>.$$

In addition, from (14) we have ${lim}_{\lambda \to 1}{}^{c}D^{\lambda }\alpha \left(s_0\right)={\alpha }^{\prime }\left(s_0\right)\notin V_0^{\perp }$, which is absurd.

Therefore: $\tau \left(s\right)=0$, $\forall s\in I.$ □

Theorem 9. 

Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ be a regular curve parametrized by arc length. Then, exists functions $f,g:[a,b]\to \mathbb{R}$, suhc that

$$\begin{array}{ccc}\hfill f\left(s\right)k^{\lambda }\left(s\right)& =& k\left(s\right),\forall s\in [a,b].\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill g\left(s\right)k^{\lambda }\left(s\right)& =& \tau \left(s\right),\forall s\in [a,b].\hfill \end{array}$$

(36)

Proof. 

We have: ${\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }\alpha \left(s\right)\right)=h_1^{\lambda }\left(s\right)t\left(s\right)+k^{\lambda }\left(s\right)n\left(s\right)+h_2^{\lambda }\left(s\right)b\left(s\right),$ then $Pro{y}_{n\left(s\right)}{\displaystyle \frac{d}{ds}}\left({}^{c}D^{\lambda }\alpha \left(s\right)\right)$ is paralell to $t^{\prime }\left(s\right)=k\left(s\right)n\left(s\right)$, and $k^{\lambda }\left(s\right)n\left(s\right)$ is paralell to $k\left(s\right)n\left(s\right)$, $\forall s\in [a,b].$

Then, there is a function $f:[a,b]\to \mathbb{R}$, such that:

$$f\left(s\right)k^{\lambda }\left(s\right)=k\left(s\right),\forall s\in [a,b].$$

Similarly, there is a function $g:[a,b]\to \mathbb{R}$, such that: $g\left(s\right){\tau }^{\lambda }\left(s\right)=\tau \left(s\right),\forall s\in [a,b].$ □

Corollary 1. 

Let $\alpha :[a,b]\to {\mathbb{R}}^3$, be a regular curve parametrized by arc length. Then, there is functios $f,g:[a,b]\to \mathbb{R}$ such that:

$$g\left(s\right)k\left(s\right)-f\left(s\right)\tau \left(s\right)=0,$$

(37)

$$2f\left(s\right)g\left(s\right)k^{\lambda }\left(s\right)=g\left(s\right)k\left(s\right)+f\left(s\right)\tau \left(s\right).$$

(38)

Proof. 

From (35) and (36) the result is obtained. □

Theorem 10. 

Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ be a regular curve parametrized by arc length. Then

$$k^{\lambda }\left(s\right)=0\mathit{if} \mathit{and} \mathit{only} \mathit{if}k\left(s\right)=0,\forall s\in [a,b],\forall \lambda \in <0,1>.$$

Proof. 

We assume that $k^{\lambda }\left(s\right)=0,\forall s\in [a,b],\forall \lambda \in <0,1>$, then from (35):

$$f\left(s\right)k^{\lambda }\left(s\right)=k\left(s\right)=0,s\in [a,b],\forall \lambda \in <0,1>.$$

Reciprocally, we assume that $k\left(s\right)=0,\forall s\in [a,b]$. Then, by the Frenet-Serret Equations (5)–(7), we have: $\alpha \left(s\right)=(x_0+s{v}_1,y_0+s{v}_2,z_0+s{v}_3)$, where $v=(v_1,v_2,v_3)\in {\mathbb{R}}^3$, $\parallel v\parallel =1$.

Then:

$$x\left(s\right)=x_0+s{v}_1,y\left(s\right)=y_0+s{v}_2,z\left(s\right)=z_0+s{v}_3,$$

$$x^{\prime }\left(s\right)=v_1,y^{\prime }\left(s\right)=v_2,z^{\prime }\left(s\right)=v_3.$$

$${}^{c}D^{\lambda }x\left(s\right)={\displaystyle \frac{s^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}}{v}_1,{}^{c}D^{\lambda }y\left(s\right)={\displaystyle \frac{s^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}}{v}_2,{}^{c}D^{\lambda }z\left(s\right)={\displaystyle \frac{s^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}}{v}_3.$$

Then:

$$a^{\lambda }\left(s\right)={\displaystyle \frac{s^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}},\forall s\in [a,b].$$

Therefore

$${}^{c}D^{\lambda }\alpha \left(s\right)={\displaystyle \frac{s^{(}1-\lambda )}{\mathrm{\Gamma }(2-\lambda )}}t\left(s\right),\forall s\in [a,b].$$

Consequently

$$\left\{\begin{array}{ccc}\hfill b^{\lambda }\left(s\right)& =& 0,\hfill \\ \hfill c^{\lambda }\left(s\right)& =& 0,\hfill \\ \hfill k^{\lambda }\left(s\right)& =& 0,\hfill \end{array}\right.\forall s\in [a,b],\forall \lambda \in <0,1>.$$

□

Note that straight lines or line segments are the only curves whose classical curvature or integer curvature $k\left(s\right)=0$ at all points, which characterizes Euclidean spaces. In this sense, if there exists an $s_0\in I$ such that $k\left(s_0\right)>0$, then $k^{\lambda }\left(s_0\right)\ne 0$; therefore, the curve moves away from its tangent line at s; that is, the fractional curvature indicates how the curve moves away from being a Euclidean space. Figure 2.

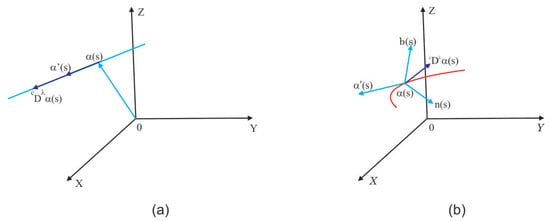
Figure 2. In figure (a), a straight line segment with $k\left(s\right)=0,\forall s\in I$ is shown, and ${\alpha }^{\prime }\left(s\right)$ is parallel to ${}^{c}D^{\lambda }\alpha \left(s\right)$. In figure (b) we have a curve with $k^{\lambda }\left(s_0\right)\ne 0$.

Theorem 11. 

Let $\alpha :I\subset \mathbb{R}\to {\mathbb{R}}^3$ be a regular curve parametrized by arc length, $F:{\mathbb{R}}^3\to {\mathbb{R}}^3$ a isometric, $\beta =F\circ \alpha :[a,b]\to {\mathbb{R}}^3$. Then

$$\begin{array}{ccc}\hfill {}^{c}D^{\lambda }\beta \left(s\right)& =& d{F}_{\alpha \left(s\right)}\left({}^{c}D^{\lambda }\alpha \left(s\right)\right),\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill k_{\beta }^{\lambda }\left(s\right)& =& k_{\alpha }^{\lambda }\left(s\right),\hfill \end{array}$$

(40)

$$\begin{array}{ccc}\hfill {\tau }_{\beta }^{\lambda }\left(s\right)& =& \pm {\tau }_{\alpha }^{\lambda }\left(s\right),\hfill \end{array}$$

(41)

where $k_{\alpha }^{\lambda }\left(s\right)$, $k_{\beta }^{\lambda }\left(s\right)$ are the fractional curvatures of the curves α and β respectively, ${\tau }_{\alpha }^{\lambda }\left(s\right)$, ${\tau }_{\beta }^{\lambda }\left(s\right)$ are the fractional torsions of the curves α and β respectively.

Proof. 

Let $\{t_{\alpha }\left(s\right),n_{\alpha }\left(s\right),b_{\alpha }\left(s\right)\}$, $\{t_{\beta }\left(s\right),n_{\beta }\left(s\right),b_{\beta }\left(s\right)\}$ be Frenet-Serret frames of the curves $\alpha$ and $\beta$ respectively. Since F is an isometry, we have:

$$\begin{array}{ccc}\hfill t_{\beta }\left(s\right)& =& d{F}_{\alpha \left(s\right)}\left(t_{\alpha }\left(s\right)\right),\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\hfill n_{\beta }\left(s\right)& =& d{F}_{\alpha \left(s\right)}\left(n_{\alpha }\left(s\right)\right),\hfill \end{array}$$

(43)

$$\begin{array}{ccc}\hfill b_{\beta }\left(s\right)& =& \pm d{F}_{\alpha \left(s\right)}\left(b_{\alpha }\left(s\right)\right),\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\hfill k_{\beta }\left(s\right)& =& k_{\alpha }\left(s\right),\hfill \end{array}$$

(45)

$$\begin{array}{ccc}\hfill {\tau }_{\beta }\left(s\right)& =& \pm {\tau }_{\alpha }\left(s\right).\hfill \end{array}$$

(46)

Moreover, let:

$$\begin{array}{ccc}\hfill {}^{c}D^{\lambda }\alpha \left(s\right)& =& a^{\lambda }\left(s\right)t_{\alpha }\left(s\right)+b^{\lambda }\left(s\right)n_{\alpha }\left(s\right)+c^{\lambda }\left(s\right)b_{\alpha }\left(s\right),\hfill \\ \hfill {}^{c}D^{\lambda }\beta \left(s\right)& =& A^{\lambda }\left(s\right)t_{\beta }\left(s\right)+B^{\lambda }\left(s\right)n_{\beta }\left(s\right)+C^{\lambda }\left(s\right)b_{\beta }\left(s\right).\hfill \end{array}$$

Since F is an isometry, then:

$$F=T_p\circ C,$$

(47)

where $T_p$ is a traslation and C is orthogonal transformation.

Now $\beta \left(s\right)=\left(T_p\circ C\right)\left(\alpha \left(s\right)\right)=p+C\left(\alpha \left(s\right)\right)=p+x\left(s\right)C\left(e_1\right)+y\left(s\right)C\left(e_2\right)+z\left(s\right)C\left(e_3\right)$, following

$$\begin{array}{ccc}\hfill {}^{c}D^{\lambda }\beta \left(s\right)& =& C\left({}^{c}D^{\lambda }x\left(s\right)e_1\right)+C\left({}^{c}D^{\lambda }y\left(s\right)e_2\right)+C\left({}^{c}D^{\lambda }z\left(s\right)e_3\right)\hfill \\ & =& C\left({}^{c}D^{\lambda }\alpha \left(s\right)\right)=d{F}_{\alpha \left(s\right)}\left({}^{c}D^{\lambda }\alpha \left(s\right)\right).\hfill \end{array}$$

We assume that F preserves orientation. Furthermore, from (42)–(46)

$\begin{array}{cc}\hfill A^{\lambda }\left(s\right)t_{\beta }\left(s\right)+B^{\lambda }\left(s\right)n_{\beta }\left(s\right)& +C^{\lambda }\left(s\right)b_{\beta }\left(s\right)={}^{c}D^{\lambda }\beta \left(s\right)=d{F}_{\alpha \left(s\right)}\left({}^{c}D^{\lambda }\alpha \left(s\right)\right)\hfill \\ & =a^{\lambda }\left(s\right)d{F}_{\alpha \left(s\right)}\left(t_{\alpha }\left(s\right)\right)+b^{\lambda }\left(s\right)d{F}_{\alpha \left(s\right)}\left(n_{\alpha }\left(s\right)\right)+c^{\lambda }\left(s\right)d{F}_{\alpha \left(s\right)}\left(b_{\alpha }\left(s\right)\right)\hfill \\ & =a^{\lambda }\left(s\right)t_{\beta }\left(s\right)+b^{\lambda }\left(s\right)n_{\beta }\left(s\right)+c^{\lambda }\left(s\right)b_{\beta }\left(s\right),\forall s\in [a,b].\hfill \end{array}$

Then

$$\begin{array}{ccc}\hfill A^{\lambda }\left(s\right)& =& a^{\lambda }\left(s\right),\hfill \\ \hfill B^{\lambda }\left(s\right)& =& b^{\lambda }\left(s\right),\hfill \\ \hfill C^{\lambda }\left(s\right)& =& c^{\lambda }\left(s\right),\hfill \end{array}\forall s\in [a,b].$$

Therefore

$$\begin{array}{ccc}\hfill k_{\beta }^{\lambda }\left(s\right)& =& A^{\lambda }\left(s\right)k_{\beta }\left(s\right)+{\displaystyle \frac{d}{ds}}\left(B^{\lambda }\left(s\right)\right)+C^{\lambda }\left(s\right){\tau }_{\beta }\left(s\right)\hfill \\ & =& a^{\lambda }\left(s\right)k_{\alpha }\left(s\right)+{\displaystyle \frac{d}{ds}}\left(b_{\alpha }^{\lambda }\left(s\right)\right)+c^{\lambda }\left(s\right){\tau }_{\alpha }\left(s\right)=k_{\alpha }^{\lambda }\left(s\right),\forall s\in [a,b].\hfill \end{array}$$

In addition

$$\begin{array}{ccc}\hfill {\tau }_{\beta }^{\lambda }\left(s\right)& =& A^{\lambda }\left(s\right){\tau }_{\beta }\left(s\right)-C^{\lambda }\left(s\right)k_{\beta }\left(s\right)\hfill \\ & =& a^{\lambda }\left(s\right){\tau }_{\alpha }\left(s\right)-c^{\lambda }\left(s\right)k_{\alpha }\left(s\right)={\tau }_{\alpha }^{\lambda }\left(s\right),\forall s\in [a,b],\forall \lambda \in <0,1>.\hfill \end{array}$$

We assume that F reverses orientation, then:

$$b_{\beta }\left(s\right)=-d{F}_{\alpha \left(s\right)}\left(b_{\alpha }\left(s\right)\right),{\tau }_{\beta }\left(s\right)=-{\tau }_{\alpha }\left(s\right),$$

then

$$A^{\lambda }\left(s\right)=a^{\lambda }\left(s\right),B^{\lambda }\left(s\right)=b^{\lambda }\left(s\right),C^{\lambda }\left(s\right)=c^{\lambda }\left(s\right),$$

therefore $k_{\beta }^{\lambda }\left(s\right)=k_{\alpha }^{\lambda }\left(s\right),\forall s\in [a,b],\forall \lambda \in <0,1>,$ ${\tau }_{\beta }^{\lambda }\left(s\right)=-{\tau }_{\alpha }^{\lambda }\left(s\right),\forall s\in [a,b],\forall \lambda \in <0,1>.$ □

4. Fractional Curvature of Regular Surfaces

4.1. Fractional Normal Curvature

Let $S\subset {\mathbb{R}}^3$ be a regular orientable surface, $\mathcal{C}\subset S$ a regular curve, $\alpha :I\subset \mathbb{R}\to S$ a parameterization of $\mathcal{C}$ by arc length, $\alpha \left(0\right)=p\in \mathcal{C},v\in T_{p}S,v={\alpha }^{\prime }\left(0\right)$.

Then, the normal curvature of S at p, with respect to v, is given by:

$${⨿}_p\left(v\right)=k\left(0\right)cos\theta =⟨N\left(p\right),k\left(0\right)n\left(0\right)⟩=k_n\left(v\right),$$

(48)

where

• ${⨿}_p$ is the second fundamental form of S at p,
• $k\left(0\right)$ is the curvature of the curve $\alpha$ at $s=0$,
• $n\left(0\right)$ is the vector normal to $\alpha$ at $s=0$,
• $N\left(p\right)$ is the vector normal to S at p,
• $\theta =\measuredangle \left(n\right(0),N(p\left)\right)$.

Definition 13. 

Let S be a regular orientable surface, $p\in S$, $v\in T_{p}S$, $\parallel v\parallel =1$. The fractional normal curvature of order λ, $0<\lambda <1$, of S in p with respect to v, is given by:

$$k_n^{\lambda }\left(v\right)=⟨N\left(p\right),k^{\lambda }\left(0\right)n\left(0\right)⟩,$$

(49)

where $k^{\lambda }\left(0\right)$ is the fractional curvature of the curve $\alpha :I\to S$, $\alpha \left(0\right)=p,{\alpha }^{\prime }\left(0\right)=v$.

Theorem 12. 

Let S be a regular orientable surface, $p\in S$, $v\in T_{p}S$, $\parallel v\parallel =1,$$0<\lambda <1$. Then

$$\underset{\lambda \to 1}{lim}{k}_n^{\lambda }\left(v\right)=k_n\left(v\right).$$

(50)

Proof. 

By (49), $k_n^{\lambda }\left(v\right)=⟨N\left(p\right),k^{\lambda }\left(0\right)n\left(0\right)⟩,$ then

$$\begin{array}{ccc}\hfill \underset{\lambda \to 1}{lim}{k}_n^{\lambda }\left(v\right)& =& ⟨N\left(p\right),\underset{\lambda \to 1}{lim}{k}^{\lambda }\left(0\right)n\left(0\right)⟩\hfill \\ & =& ⟨N\left(p\right),k\left(0\right)n\left(0\right)⟩=k_n\left(v\right).\hfill \end{array}$$

□

Theorem 13. 

Let S be a regular orientable surface, $p\in S$, $v\in T_{p}S$, $\parallel v\parallel =1,$$0<\lambda <1$. Then

$$k_n\left(v\right)=r^{\lambda }\left(0\right)k_n^{\lambda }\left(v\right).$$

(51)

Proof. 

By (35), we have

$$\begin{array}{ccc}\hfill k_n\left(v\right)& =& ⟨N\left(p\right),k\left(0\right)n\left(0\right)⟩=⟨N\left(p\right),r^{\lambda }\left(0\right)k^{\lambda }\left(0\right)n\left(0\right)⟩\hfill \\ & =& r^{\lambda }\left(0\right)⟨N\left(p\right),k^{\lambda }\left(0\right)n\left(0\right)⟩=r^{\lambda }\left(0\right)k_n^{\lambda }\left(v\right).\hfill \end{array}$$

Therefore $k_n\left(v\right)=r^{\lambda }\left(0\right)k_n^{\lambda }\left(v\right).$ □

Remark 1. 

Throughout the paper we use the notation

$$r^{\lambda }\left(v\right)=r^{\lambda }\left(0\right),v\in T_{p}S,\parallel v\parallel =1.$$

Now, let $p\in S$, $k_1\left(p\right)$ and $k_2\left(p\right)$ the principal curvatures of S in p. Then

$$k_2\left(p\right)\le k_n\left(p\right)\le k_1\left(p\right).$$

(52)

By (51):

$$k_2\left(p\right)\le r^{\lambda }\left(v\right)k_n^{\lambda }\left(v\right)\le k_1\left(p\right),$$

then

$${\displaystyle \frac{k_2\left(p\right)}{r^{\lambda }\left(v\right)}}\le k_n^{\lambda }\left(v\right)\le {\displaystyle \frac{k_1\left(p\right)}{r^{\lambda }\left(v\right)}}.$$

(53)

Let $\mathcal{C}\subset S$ be given by

$$\mathcal{C}=\left\{v\in T_{p}S/\parallel v\parallel =1\right\}.$$

(54)

Then $k_n^{\lambda }:\mathcal{C}\subset T_{p}S\to \mathbb{R}$ is a coninuous function defined by $k_n^{\lambda }\left(v\right)=⟨N\left(p\right),k^{\lambda }\left(0\right)n\left(0\right)⟩.$

Since $\mathcal{C}$ is a compact set, then $k_n^{\lambda }$ attains its maximum and minimum over $\mathcal{C}$, that is, there exist $e_1^{\lambda },e_2^{\lambda }\in \mathcal{C}$ such that

$$\begin{array}{ccc}\hfill k_1^{\lambda }\left(p\right)& =& \underset{v\in \mathcal{C}}{max}{k}_n^{\lambda }\left(v\right)=k_n^{\lambda }\left(e_1^{\lambda }\right).\hfill \end{array}$$

(55)

$$\begin{array}{ccc}\hfill k_2^{\lambda }\left(p\right)& =& \underset{v\in \mathcal{C}}{min}{k}_n^{\lambda }\left(v\right)=k_n^{\lambda }\left(e_2^{\lambda }\right).\hfill \end{array}$$

(56)

$k_1^{\lambda }$ and $k_2^{\lambda }$ are called the fractional principal curvatures of order $\lambda$, $0<\lambda <1$, of S at p; and the following is true:

$$k_2^{\lambda }\left(p\right)\le k_n^{\lambda }\left(v\right)\le k_1^{\lambda }\left(p\right),\forall v\in \mathcal{C}.$$

(57)

By (49), we have

$$k_n\left(v\right)=r^{\lambda }\left(v\right)k_n^{\lambda }\left(v\right),\forall v\in T_{p}S,\parallel v\parallel =1.$$

Moreover:

$$\begin{array}{ccc}\hfill k_1\left(p\right)& =& \underset{v\in \mathcal{C}}{max}{k}_n\left(v\right)=\underset{v\in \mathcal{C}}{max}\left(r^{\lambda }\left(v\right)k_n^{\lambda }\left(v\right)\right)=\left(\underset{v\in \mathcal{C}}{max}{r}^{\lambda }\left(v\right)\right)\left(\underset{v\in \mathcal{C}}{max}{k}_n^{\lambda }\left(v\right)\right),\hfill \\ & =& k_n\left(e_1\right)=r^{\lambda }\left(e_1\right)k_n^{\lambda }\left(e_1\right).\hfill \end{array}$$

Therefore

$$r^{\lambda }\left(e_1\right)=\underset{v\in \mathcal{C}}{max}{r}^{\lambda }\left(v\right),$$

then:

$$k_1\left(p\right)=r^{\lambda }\left(e_1\right)k_1^{\lambda }\left(p\right),e_1^{\lambda }=e_1.$$

(58)

Similarly

$$k_2\left(p\right)=r^{\lambda }\left(e_2\right)k_2^{\lambda }\left(p\right),e_2^{\lambda }=e_2.$$

(59)

Theorem 14. 

Let S be a regular orientable surface, $p\in S$. Then

$$\begin{array}{ccc}\hfill k_1\left(p\right)& =& r^{\lambda }\left(e_1\right)k_1^{\lambda }\left(p\right),\hfill \end{array}$$

(60)

$$\begin{array}{ccc}\hfill k_2\left(p\right)& =& r^{\lambda }\left(e_2\right)k_2^{\lambda }\left(p\right)\hfill \end{array}$$

(61)

Proof. 

The proof is in the lines above. □

4.2. Fractional Curvature of a Regular Surface

In this section we introduce a new definition of fractional curvature and fractional mean curvature of regular surfaces, different from the one introduced by Yajima et al. [18], and show that they are invariant under isometries.

Definition 14. 

Let S be a regular orientable surface. The fractional curvature of order λ, $0<\lambda <1$, of S at p is given by:

$$K^{\lambda }\left(p\right)=k_1^{\lambda }\left(p\right).k_2^{\lambda }\left(p\right),$$

(62)

where $k_1^{\lambda }\left(p\right)$ and $k_2^{\lambda }\left(p\right)$ are the fractional principal curvatures of order λ, $0<\lambda <1$, of S at p.

Consider the plane $S=\left\{(x,y,z)\in {\mathbb{R}}^3/ax+by+cz+d=0\right\}$. See Figure 3.

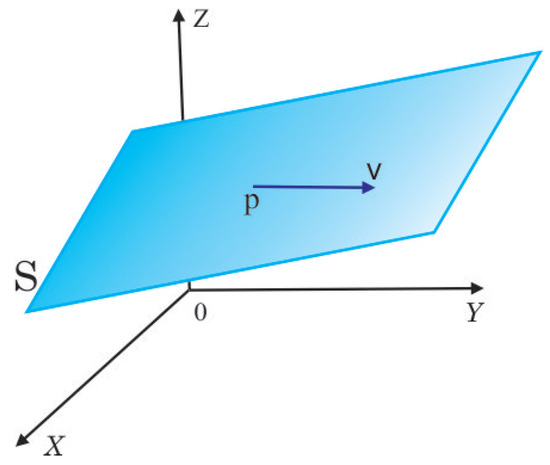
Figure 3. Plot of a plane with null Gaussian curvature.

In the plane S the Gaussian curvature $K\left(p\right)=0,\forall p\in S$, and at any point $p\in S$, all directions $v\in T_{p}S$, are principal directions, and it is verified

$$0=k_2\left(p\right)\le k_n\left(p\right)\le k_1\left(p\right)=0,$$

where $k_1\left(p\right)$ and $k_2\left(p\right)$ are the principal curvatures of S at p and $k_n\left(p\right)$ is the normal curvature of S at p.

Then, by (60) and (61), we have:

$$k_1^{\lambda }\left(p\right)=k_2^{\lambda }\left(p\right),\forall p\in S,\forall \lambda \in <0,1>.$$

Therefore, by (62), the fractional curvature of the plane S is given by:

$$K^{\lambda }\left(p\right)=0,\forall p\in S,\forall \lambda \in <0,1>,$$

and conversely, if $K^{\lambda }\left(p\right)=0$, then $K\left(p\right)=0,\forall p\in S,\forall \lambda \in <0,1>.$

Therefore, if there exists a point $p\in S$, and a ${\lambda }_0\in <0,1>$, such that $K^{{\lambda }_0}\left(p\right)\ne 0$, then the surface would not be a plane; i.e., it curved.

Definition 15. 

Let S be a regular orientable surface. The fractional mean curvature of order λ, $0<\lambda <1$, of S at p is given by:

$$H^{\lambda }\left(p\right)={\displaystyle \frac{k_1^{\lambda }\left(p\right)+k_2^{\lambda }\left(p\right)}{2}},$$

(63)

where $k_1^{\lambda }\left(p\right)$ and $k_2^{\lambda }\left(p\right)$ are the fractional principal curvatures of order λ, $0<\lambda <1$, of S at p.

Theorem 15. 

Let S be a regular orientable surface, $p\in S$. Then:

$$\begin{array}{ccc}\hfill K\left(p\right)& =& r_1^{\lambda }{r}_2^{\lambda }{K}^{\lambda }\left(p\right),\hfill \end{array}$$

(64)

$$\begin{array}{ccc}\hfill H\left(p\right)& =& {\displaystyle \frac{r_1^{\lambda }{k}_1^{\lambda }\left(p\right)+r_2^{\lambda }{k}_2^{\lambda }\left(p\right)}{2}},\hfill \end{array}$$

(65)

$$\begin{array}{ccc}\hfill {\displaystyle \underset{\lambda \to 1}{lim}{K}^{\lambda }\left(p\right)}& =& K\left(p\right),\hfill \end{array}$$

(66)

$$\begin{array}{ccc}\hfill {\displaystyle \underset{\lambda \to 1}{lim}{H}^{\lambda }\left(p\right)}& =& H\left(p\right).\hfill \end{array}$$

(67)

Proof. 

$K\left(p\right)=k_1\left(p\right).k_2\left(p\right)=r_1^{\lambda }{k}_1^{\lambda }\left(p\right).r_2^{\lambda }{k}_2^{\lambda }\left(p\right)=r_1^{\lambda }{r}_2^{\lambda }{k}_1^{\lambda }\left(p\right).k_2^{\lambda }\left(p\right)=r_1^{\lambda }{r}_2^{\lambda }{K}^{\lambda }\left(p\right)$.

(65) is inmediately.

(66), ${\displaystyle K\left(p\right)=\underset{\lambda \to 1}{lim}K\left(p\right)=\underset{\lambda \to 1}{lim}\left(r_1^{\lambda }{r}_2^{\lambda }{k}^{\lambda }\left(p\right)\right)}$

$=\left(\underset{\lambda \to 1}{lim}{r}_1^{\lambda }\right)\left(\underset{\lambda \to 1}{lim}{r}_2^{\lambda }\right)\underset{\lambda \to 1}{lim}{k}^{\lambda }\left(p\right)=\underset{\lambda \to 1}{lim}{K}^{\lambda }\left(p\right).$

Finally the Equation (67),

$${\displaystyle \underset{\lambda \to 1}{lim}{H}^{\lambda }\left(p\right)=\frac{1}{2}\left[\underset{\lambda \to 1}{lim}{k}_1^{\lambda }\left(p\right)+\underset{\lambda \to 1}{lim}{k}_2^{\lambda }\left(p\right)\right]=\frac{1}{2}\left[k_1\left(p\right)+k_2\left(p\right)\right]=H\left(p\right).}$$

□

Theorem 16. 

Let S and $\overline{S}$ be regular orientable surfaces, $\varphi :s\to \overline{s}$ a local isometry. Then

$$\begin{array}{c}\hfill K^{\lambda }\left(p\right)={\overline{K}}^{\lambda }\left(\varphi \left(p\right)\right),\forall p\in S.\end{array}$$

(68)

$$\begin{array}{c}\hfill H^{\lambda }\left(p\right)=\pm {\overline{H}}^{\lambda }\left(\varphi \left(p\right)\right),\forall p\in S.\end{array}$$

(69)

where $K^{\lambda }$ and ${\overline{K}}^{\lambda }$ are the fractional curvatures of S and $\overline{S}$ respectively, and $H^{\lambda }$ and ${\overline{H}}^{\lambda }$ are the mean curvatures of S and $\overline{S}$ respectively.

Proof. 

Let $k_1$, $k_2$ and ${\overline{k}}_1$, ${\overline{k}}_2$ be the principal curvatures of S and $\overline{S}$ respectively. Since $\varphi$ is a local isometry, then

$$K\left(p\right)=\overline{K}\left(\varphi \left(p\right)\right),H\left(p\right)=\overline{H}\left(\varphi \left(p\right)\right),\forall p\in S.$$

Furthermore, the principal curvatures of S and $\overline{S}$, are roots of the equation

$$x^2-Hx+K=x^2-\overline{H}x+\overline{K}=0,$$

and it is fulfilled that

$$k_i\left(p\right)={\overline{k}}_i\left(\varphi \left(p\right)\right),\forall p\in S,\forall i=1,2.$$

Let $e_1$, $e_2$ and ${\overline{e}}_1$, ${\overline{e}}_2$ be the principal directions of S and $\overline{S}$ at p and $\varphi \left(p\right)$, respectively.

Then ${\overline{e}}_i=d{\varphi }_p\left(e_i\right),\forall i=1,2.$

Let $\alpha :<-ϵ,ϵ>\to S$, $\overline{\alpha }:<-ϵ,ϵ>\to \overline{S}$ be the normal sections determined by $\{e_i,N\left(p\right)\}$ and $\{{\overline{e}}_i,\overline{N}\left(\varphi \left(p\right)\right)\}$ respectively. Then, using theorem 11 of curves in ${\mathbb{R}}^3$, we have:

$$k_i^{\lambda }\left(p\right)={\overline{k}}_i^{\lambda }\left(\varphi \left(p\right)\right),\forall i=1,2,\forall p\in \overline{S}.$$

Therefore

$$K^{\lambda }\left(p\right)=k_1^{\lambda }\left(p\right).k_2^{\lambda }\left(p\right)={\overline{K}}^{\lambda }\left(\varphi \left(p\right)\right),\forall p\in S.$$

In Addition, if $\varphi$ preserves orientation, we have

$$H^{\lambda }\left(p\right)={\overline{H}}^{\lambda }\left(\varphi \left(p\right)\right),\forall p\in S,$$

in case $\varphi$ reverses orientation, we have

$$H^{\lambda }\left(p\right)=-{\overline{H}}^{\lambda }\left(\varphi \left(p\right)\right),\forall p\in S.$$

□

Theorem 17. 

Let S be a regular orientable surface. If S is a minimal surface, then

$$H^{\lambda }\left(p\right)=0,\forall p\in S,\forall \lambda \in <0,1>.$$

Proof. 

Let $p_0\in S$, then we have $H\left(p_0\right)={\displaystyle \frac{k_1\left(p_0\right)+k_2\left(p_0\right)}{2}}$.

$$k_2\left(p_0\right)=-k_1\left(p_0\right).$$

(70)

Let $\{e_1,e_2\}$ be the orthonormal basis of $T_{p_0}S$ formed by the principal directions of S at $p_0$; $\alpha :<-ϵ,ϵ>\to S$ the normal section determined by $\{e_1,N\left(p_0\right)\}$, $\beta :<-ϵ,ϵ>\to S$, $\beta \left(0\right)=p_0$, the normal section determined by $\{e_2,N\left(p_0\right)\}$.

Then

$$\begin{array}{ccc}\hfill \alpha \left(0\right)=p_0,& {\alpha }^{\prime }\left(0\right)=e_1,& {\alpha }^{″}\left(0\right)=k_1\left(p_0\right)N\left(p_0\right),\hfill \\ \hfill \beta \left(0\right)=p_0,& {\beta }^{\prime }\left(0\right)=e_2,& {\beta }^{″}\left(0\right)=-k_1\left(p_0\right)N\left(p_0\right).\hfill \end{array}$$

Since the rotation is an isometry, we perform 2 rotations:

First rotation: We rotate the curve $\beta \left(s\right)$ by an angle of ${\displaystyle \frac{\pi }{2}}$ around the N axis, so that the curve $\beta \left(s\right)$ is located in the rectifying plane.

Second rotation: We rotate the curve $\beta \left(s\right)$ by an angle of $\pi$, around the $e_1$ axis, so that its normal vector coincides with $N\left(p\right)$.

Now using the fundamental theorem of curves in ${\mathbb{R}}^3$, we have that $\alpha \left(s\right)=\beta \left(s\right)$, and by Theorem 11, we have that

$$k_{\alpha }^{\lambda }\left(p_0\right)=k_{\beta }^{\lambda }\left(p_0\right)=k_1^{\lambda }\left(p_0\right),$$

then

$$k_2^{\lambda }\left(p_0\right)=-k_1^{\lambda }\left(p_0\right).$$

Therefore

$$r_1^{\lambda }=r_2^{\lambda }.$$

Consequently

$$H^{\lambda }\left(p_0\right)={\displaystyle \frac{k_1^{\lambda }\left(p_0\right)+k_2^{\lambda }\left(p_0\right)}{2}}=0.$$

Since, $p_0\in S$ is arbitrary, we have $H^{\lambda }\left(p\right)=0$, $\forall p\in S$, $\forall \lambda \in <0,1>$. □

5. Numerical Examples

Now, we give some examples of fractional curvature, fractional torsion of a regular curves and fractional curvature of regular surfaces. The examples were coded and run in MATLAB R2015a, with Windows operating system, using a Core 4C+8G 2.70 GHz computer and 12 GB RAM.

Example 1. 

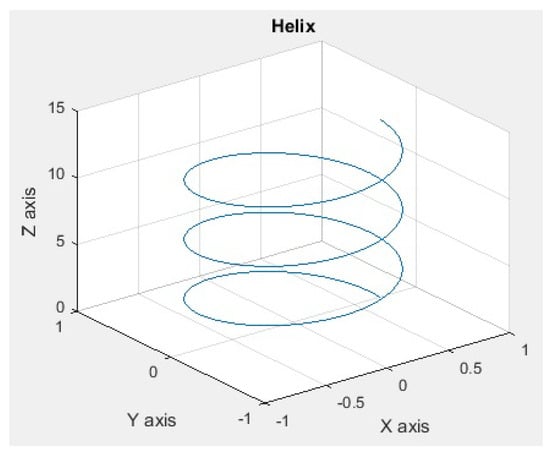
Consider the Helix $\alpha :\mathbb{R}\to {\mathbb{R}}^3$ defined by $\alpha \left(s\right)={\displaystyle \frac{1}{\sqrt{2}}}(cos\left(s\right),sin\left(s\right),s)$. See Figure 4.

Figure 4. Plot of the Helix curve.

The Frenet-Serret trihedron is given by

$$\begin{array}{ccc}\hfill t\left(s\right)& =& {\displaystyle \frac{1}{\sqrt{2}}}(-sin\left(s\right),cos\left(s\right),1),\hfill \end{array}$$

(71)

$$\begin{array}{ccc}\hfill n\left(s\right)& =& (-cos(s),-sin(s),0),\hfill \end{array}$$

(72)

$$\begin{array}{ccc}\hfill b\left(s\right)& =& {\displaystyle \frac{1}{\sqrt{2}}}(sin\left(s\right),-cos\left(s\right),1).\hfill \end{array}$$

(73)

The classical curvature and torsion of α are given by

$$k\left(s\right)={\displaystyle \frac{\sqrt{2}}{2}},\tau \left(s\right)={\displaystyle \frac{-\sqrt{2}}{2}},$$

(74)

and the derivative vector of $\alpha \left(s\right)$ of fractional order is:

$${}^{c}D^{\lambda }\alpha \left(s\right)={\displaystyle \frac{1}{\sqrt{2}}}\left({}^{c}D^{\lambda }(cos\left(s\right)),{}^{c}D^{\lambda }(sin\left(s\right)),{}^{c}D^{\lambda }\left(s\right)\right),\forall s\in <0,+\infty >.$$

(75)

Further, we have

$$\begin{array}{ccc}\hfill {}^{c}D^{\lambda }(sin\left(s\right))& =& \sum _{j=0}^{+\infty }{\displaystyle \frac{{(-1)}^j}{\mathrm{\Gamma }(2j+2-\lambda )}}{s}^{2j+1-\lambda }=S_1\left(s\right),\hfill \end{array}$$

(76)

$$\begin{array}{ccc}\hfill {}^{c}D^{\lambda }(cos\left(s\right))& =& \sum _{j=0}^{+\infty }{\displaystyle \frac{{(-1)}^{j+1}}{\mathrm{\Gamma }(2j+3-\lambda )}}{s}^{2j+2-\lambda }=S_2\left(s\right).\hfill \end{array}$$

(77)

Then

$${}^{c}D^{\lambda }\left(\alpha \left(s\right)\right)={\displaystyle \frac{1}{\sqrt{2}}}\left(S_2\left(s\right),S_1\left(s\right),{}^{c}D^{\lambda }\left(s\right)\right),\forall s\in <0,+\infty >.$$

Therefore

$$\begin{array}{ccc}\hfill a^{\lambda }\left(s\right)& =& {\displaystyle \frac{1}{2}}\left(-sin\left(s\right)S_2\left(s\right)+cos\left(s\right)S_1\left(s\right)+{}^{c}D^{\lambda }\left(s\right)\right),\hfill \end{array}$$

(78)

$$\begin{array}{ccc}\hfill b^{\lambda }\left(s\right)& =& {\displaystyle \frac{1}{\sqrt{2}}}\left(-cos\left(s\right)S_2\left(s\right)-sin\left(s\right)S_1\left(s\right)\right),\hfill \end{array}$$

(79)

$$\begin{array}{ccc}\hfill c^{\lambda }\left(s\right)& =& {\displaystyle \frac{1}{2}}\left(sin\left(s\right)S_2\left(s\right)-cos\left(s\right)S_1\left(s\right)+{}^{c}D^{\lambda }\left(s\right)\right).\hfill \end{array}$$

(80)

$${\displaystyle \frac{d}{ds}}\left(b^{\lambda }\left(s\right)\right)={\displaystyle \frac{1}{\sqrt{2}}}\left(sin\left(s\right)S_2\left(s\right)-cos\left(s\right)S_2^{\prime }\left(s\right)-cos\left(s\right)S_1\left(s\right)-sin\left(s\right)S_1^{\prime }\left(s\right)\right).$$

(81)

From Equations (74), (78), (80) and (81), we obtain that fractional curvature $k^{\lambda }$ is given by

$$k^{\lambda }\left(s\right)={\displaystyle \frac{-\sqrt{2}}{2}}\left(cos\left(s\right)S_2^{\prime }\left(s\right)+sin\left(s\right)S_1^{\prime }\left(s\right)\right).$$

(82)

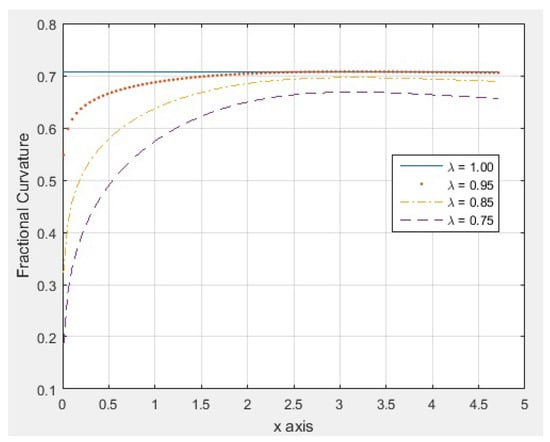
Table 1 shows the first 20 results of evaluation of the $k^{\lambda }\left(s\right)$ and $k\left(s\right)$ curvatures, for differents values of $\lambda :0.75,0.85,0.95$ and $1.0$, over the interval $[0.01,1.5\pi ]$, with $N=100$ for the Interval partition. As can be observed, as λ approaches 1, the values of the fractional curvature approach the classic curvature $k\left(s\right)=0.5\sqrt{2}.$

Table 1. Values of $k^{\lambda }\left(s\right)$ and $k\left(s\right)$, for different values of $\lambda :0.75,0.85,0.95$ and $1.0$.

s	${\mathit{k}}^{0.75}\left(\mathit{s}\right)$	${\mathit{k}}^{0.85}\left(\mathit{s}\right)$	${\mathit{k}}^{0.95}\left(\mathit{s}\right)$	${\mathit{k}}^{1.0}\left(\mathit{s}\right)$
0.0100	0.1850	0.3229	0.5481	0.7071
0.0575	0.2865	0.4197	0.5982	0.7071
0.1050	0.3330	0.4593	0.6165	0.7071
0.1525	0.3655	0.4857	0.6280	0.7071
0.2000	0.3910	0.5058	0.6366	0.7071
0.2475	0.4122	0.5221	0.6433	0.7071
0.2950	0.4305	0.5358	0.6489	0.7071
0.3425	0.4466	0.5478	0.6537	0.7071
0.3900	0.4611	0.5583	0.6579	0.7071
0.4375	0.4742	0.5678	0.6616	0.7071
0.4850	0.4862	0.5763	0.6649	0.7071
0.5325	0.4972	0.5842	0.6679	0.7071
0.5800	0.5074	0.5913	0.6706	0.7071
0.6275	0.5170	0.5980	0.6731	0.7071
0.6750	0.5259	0.6041	0.6754	0.7071
0.7225	0.5343	0.6098	0.6775	0.7071
0.7700	0.5422	0.6152	0.6795	0.7071
0.8175	0.5496	0.6202	0.6813	0.7071
0.8650	0.5566	0.6249	0.6830	0.7071
0.9125	0.5632	0.6294	0.6846	0.7071

Figure 5 indicates the behavior of plot of the function $k^{\lambda }\left(s\right)$ for different values of $\lambda :0.75,0.85,0.95$ and $1.0.$ From Figure 5 we can observed that if λ approaches to 1, the plot of the function $k^{\lambda }\left(s\right)$ approaches the plot of the classic curvature $k\left(s\right)$.

Figure 5. Plot of $k^{\lambda }\left(s\right)$ for different values of $\lambda$.

The fractional torsion of $\alpha \left(s\right)$ is given by

$${\tau }^{\lambda }\left(s\right)=-{\displaystyle \frac{\sqrt{2}}{2}}{\displaystyle \frac{s^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}}.$$

(83)

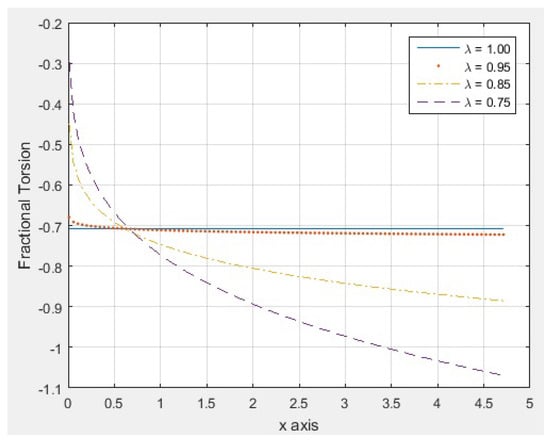
Table 2 shows the first 20 results of evaluation of the ${\tau }^{\lambda }\left(s\right)$ and $\tau \left(s\right)$ torsion, for various values of $\lambda :0.79,0.89,0.99$ and $1.0$, over the interval $[0.01,1.5\pi ]$, with $N=100$ for the Interval partition. As can observed, as λ approaches 1, the values of the fractional torsion approach the classic torsion $\tau \left(s\right)=-0.5\sqrt{2}$.

Table 2. Values of ${\tau }^{\lambda }\left(s\right)$ and $\tau \left(s\right)$, for different values of $\lambda :0.79,0.89,0.99$ and $1.0$.

s	${\mathit{\tau }}^{0.79}\left(\mathit{s}\right)$	${\mathit{\tau }}^{0.89}\left(\mathit{s}\right)$	${\mathit{\tau }}^{0.99}\left(\mathit{s}\right)$	${\mathit{\tau }}^{1.0}\left(\mathit{s}\right)$
0.0100	−0.2936	−0.4497	−0.6791	−0.7071
0.0575	−0.4240	−0.5452	−0.6911	−0.7071
0.1050	−0.4811	−0.5825	−0.6953	−0.7071
0.1525	−0.5203	−0.6069	−0.6979	−0.7071
0.2000	−0.5508	−0.6253	−0.6998	−0.7071
0.2475	−0.5760	−0.6401	−0.7013	−0.7071
0.2950	−0.5977	−0.6526	−0.7025	−0.7071
0.3425	−0.6167	−0.6634	−0.7036	−0.7071
0.3900	−0.6337	−0.6729	−0.7045	−0.7071
0.4375	−0.6492	−0.6815	−0.7053	−0.7071
0.4850	−0.6634	−0.6893	−0.7060	−0.7071
0.5325	−0.6766	−0.6964	−0.7067	−0.7071
0.5800	−0.6888	−0.7030	−0.7073	−0.7071
0.6275	−0.7003	−0.7091	−0.7078	−0.7071
0.6750	−0.7111	−0.7148	−0.7084	−0.7071
0.7225	−0.7213	−0.7202	−0.7088	−0.7071
0.7700	−0.7311	−0.7252	−0.7093	−0.7071
0.8175	−0.7403	−0.7300	−0.7097	−0.7071
0.8650	−0.7491	−0.7346	−0.7101	−0.7071
0.9125	−0.7576	−0.7389	−0.7105	−0.7071

Figure 6 indicates the behavior of plot of the function ${\tau }^{\lambda }\left(s\right)$ for different values of $\lambda :0.79,0.89,0.99$ and $1.0$. From Figure 6, we can observed that if λ approaches to 1, the plot of the function ${\tau }^{\lambda }\left(s\right)$ approaches the graph of the classic torsion $\tau \left(s\right)=-0.5\sqrt{2}$.

Figure 6. Plot of the torsion ${\tau }^{\lambda }\left(s\right)$ for different values of $\lambda$.

Next, we obtain a geometric interpretation of the Caputo fractional derivative of algebraic polynomials.

From Equation (83), the fractional torsion of $\alpha \left(s\right)$ is given by

$${\tau }^{\lambda }\left(s\right)=-{\displaystyle \frac{\sqrt{2}}{2}}{\displaystyle \frac{s^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}}=-{\displaystyle \frac{\sqrt{2}}{2}}{}^{c}D^{\lambda }\left(s\right).$$

Therefore, we have

$${}^{c}D^{\lambda }\left(s\right)=-\sqrt{2}{\tau }^{\lambda }\left(s\right)=-2k\left(s\right){\tau }^{\lambda }\left(s\right).$$

(84)

From (84), we observe that the Caputo fractional derivative of the identity function is a multiple of the fractional torsion of the Helix. Therefore, for values of λ close to 1, the Caputo fractional derivative of the identity function is a measure of how rapidly the curve pulls away from the tangent line and osculating plane at s, in a neighborhood of s.

Now, we get other relations

1. 

${}^{c}D^{\lambda }\left(s^2\right)={\displaystyle \frac{2s^{2-\lambda }}{\mathrm{\Gamma }(3-\lambda )}}={\displaystyle \frac{-2\sqrt{2}s}{2-\lambda }}{\tau }^{\lambda }\left(s\right).$

2. 

${}^{c}D^{\lambda }\left(s^3\right)={\displaystyle \frac{6s^{3-\lambda }}{\mathrm{\Gamma }(4-\lambda )}}={\displaystyle \frac{-6\sqrt{2}{s}^2}{(3-\lambda )(2-\lambda )}}{\tau }^{\lambda }\left(s\right).$

3. 

${}^{c}D^{\lambda }\left(s^4\right)={\displaystyle \frac{24s^{4-\lambda }}{\mathrm{\Gamma }(5-\lambda )}}={\displaystyle \frac{-24\sqrt{2}{s}^3}{(4-\lambda )(3-\lambda )(2-\lambda )}}{\tau }^{\lambda }\left(s\right).$

4. 

In general

$$\begin{array}{ccc}\hfill {}^{c}D^{\lambda }\left(s^n\right)& =& {\displaystyle \frac{-n!\sqrt{2}{s}^{n-1}}{(n-\lambda )(n-1-\lambda )\dots (3-\lambda )(2-\lambda )}}{\tau }^{\lambda }\left(s\right)\hfill \\ & =& {\displaystyle \frac{-2n!s^{n-1}}{(n-\lambda )(n-1-\lambda )\dots (3-\lambda )(2-\lambda )}}k\left(s\right){\tau }^{\lambda }\left(s\right),n=2,3,\dots .\hfill \end{array}$$

(85)

Consider the algebraic polynomial of degree n

$$p_n\left(s\right)=\sum _{j=0}^n{a}_j{s}^j.$$

Then

$${}^{c}D^{\lambda }\left(p_n\left(s\right)\right)=\sum _{j=2}^n{a}_j{}^{c}D^{\lambda }\left(s^j\right)-a_1\sqrt{2}{\tau }^{\lambda }\left(s\right).$$

By (85)

$${}^{c}D^{\lambda }\left(p_n\left(s\right)\right)={\varphi }^{\lambda }\left(s\right){\tau }^{\lambda }\left(s\right)={\psi }^{\lambda }\left(s\right)k\left(s\right){\tau }^{\lambda }\left(s\right),$$

(86)

where the fractional factor is

$${\varphi }^{\lambda }\left(s\right)=-\sqrt{2}\left(\sum _{j=2}^n{\displaystyle \frac{j!a_j{s}^{j-1}}{(j-\lambda )(j-1-\lambda )\dots (3-\lambda )(2-\lambda )}}+a_1\right)or$$

$${\psi }^{\lambda }\left(s\right)=-2\left(\sum _{j=1}^n{\displaystyle \frac{j!a_j{s}^{j-1}}{(j-\lambda )(j-1-\lambda )\dots (3-\lambda )(2-\lambda )}}+a_1\right).$$

Therefore, the Caputo fractional derivative of the polynomial $p_n\left(s\right)$, is a multiple of the fractional torsion of the helix ${\tau }^{\lambda }\left(s\right)$.

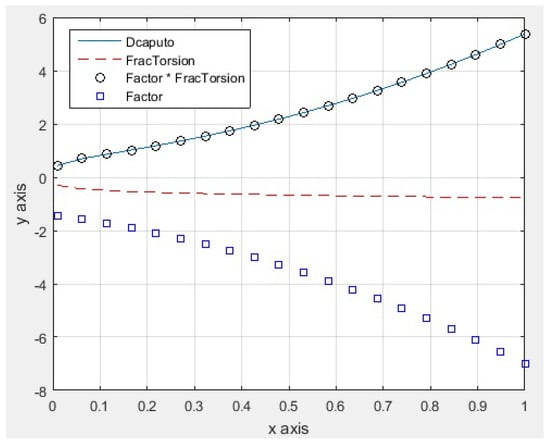
Now, consider the polynomial $p_3\left(s\right)=s^3+s^2+s$. In the Figure 7, we show the plots of ${}^{c}D^{\lambda }\left(p_3\left(s\right)\right)$ with blue color (Dcaputo), the fractional torsion ${\tau }^{\lambda }\left(s\right)$ with red color (FracTorsion), the fractional factor ${\varphi }^{\lambda }\left(s\right)$ with blue colored squares (Factor), and the product ${\varphi }^{\lambda }\left(s\right){\tau }^{\lambda }\left(s\right)\left(s\right)$ with black colored circles (Factor*FracTorsion). It is observed that Caputo’s fractional derivative of the third degree polynomial, is a multiple of the fractional torsion of the Helix.

Figure 7. Plots of the functions ${}^{0.8}D^c\left(s\right)$, ${\tau }^{0.8}\left(s\right),{\varphi }^{0.8}\left(s\right)$ and ${\varphi }^{0.8}\left(s\right).{\tau }^{0.8}\left(s\right)$.

Example 2. 

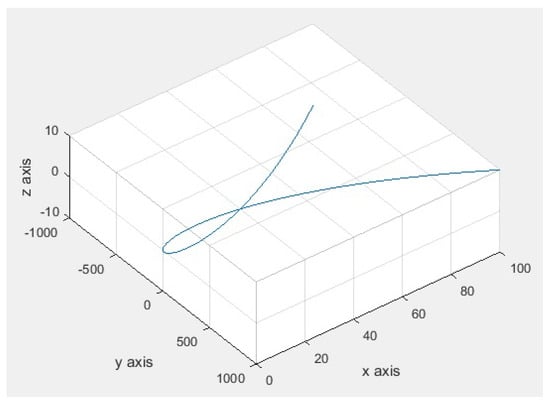
Consider the regular curve $\alpha :\mathbb{R}\to {\mathbb{R}}^3$ defined by $\alpha \left(r\right)=(r^2,r^3,r)$. See Figure 8.

Figure 8. Curve with arbitrary parameter.

Observe that the curve α is not parameterized by arc length, so following Rubio et al. [15], we express our results in arbitrary parameter.

The Frenet-Serret trihedron is given by $\left\{t\right(r),n(r),b(r\left)\right\}$, where

$$\begin{array}{ccc}\hfill t\left(r\right)& =& {\displaystyle \frac{1}{{\mathsf{\Delta }}_1}}(2r,3r^2,1),\hfill \end{array}$$

(87)

$$\begin{array}{ccc}\hfill n\left(r\right)& =& {\displaystyle \frac{1}{{\mathsf{\Delta }}_1{\mathsf{\Delta }}_2}}\left(1-9r^4,3r+6r^3,-9r^3-2r\right),\hfill \end{array}$$

(88)

$$\begin{array}{ccc}\hfill b\left(r\right)& =& {\displaystyle \frac{1}{{\mathsf{\Delta }}_2}}\left(-3r,1,3r^2\right),\hfill \end{array}$$

(89)

where ${\mathsf{\Delta }}_1=\parallel {\alpha }^{\prime }\left(r\right)\parallel =\sqrt{9r^4+4r^2+1}$, ${\mathsf{\Delta }}_2=\sqrt{9r^4+9r^2+1}$. Furthermore, the integer curvature and torsion of α are given by:

$$\begin{array}{ccc}\hfill k\left(r\right)& =& {\displaystyle \frac{2{\mathsf{\Delta }}_2}{{\left({\mathsf{\Delta }}_1\right)}^3}},\hfill \end{array}$$

(90)

$$\begin{array}{ccc}\hfill \tau \left(r\right)& =& {\displaystyle \frac{3}{9r^4+9r^2+1}}.\hfill \end{array}$$

(91)

The fractional derivative vector of $\alpha \left(r\right)$ is:

$${}^{c}D^{\lambda }\alpha \left(r\right)=\left({\displaystyle \frac{2r^{2-\lambda }}{\mathrm{\Gamma }(3-\lambda )}},{\displaystyle \frac{6r^{3-\lambda }}{\mathrm{\Gamma }(4-\lambda )}},{\displaystyle \frac{r^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}}\right).$$

(92)

By (87)–(89), and (92), we obtain:

$$\begin{array}{ccc}\hfill a^{\lambda }\left(r\right)& =& {\displaystyle \frac{1}{{\mathsf{\Delta }}_1}}\left({\displaystyle \frac{4r^{3-\lambda }}{\mathrm{\Gamma }(3-\lambda )}}+{\displaystyle \frac{18r^{5-\lambda }}{\mathrm{\Gamma }(4-\lambda )}}+{\displaystyle \frac{r^{1-\lambda })}{\mathrm{\Gamma }(2-\lambda )}}\right),\hfill \\ \hfill b^{\lambda }\left(r\right)& =& D_1\left(D_2{r}^{6-\lambda }+D_3{r}^{4-\lambda }+D_4{r}^{2-\lambda }\right),\hfill \\ \hfill c^{\lambda }\left(r\right)& =& {\displaystyle \frac{1}{{\mathsf{\Delta }}_2}}{D}_5{r}^{3-\lambda }={\displaystyle \frac{3(1-\lambda )}{{\mathsf{\Delta }}_2(3-\lambda )\mathrm{\Gamma }(2-\lambda )}}{r}^{3-\lambda },\hfill \end{array}$$

where $D1={\left({\mathsf{\Delta }}_1{\mathsf{\Delta }}_2\right)}^{-1}$, $D_2={\displaystyle \frac{36}{\mathrm{\Gamma }(4-\lambda )}}-{\displaystyle \frac{18}{\mathrm{\Gamma }(3-\lambda )}}$, $D_3={\displaystyle \frac{18}{\mathrm{\Gamma }(4-\lambda )}}-{\displaystyle \frac{9}{\mathrm{\Gamma }(2-\lambda )}},D_4={\displaystyle \frac{2}{\mathrm{\Gamma }(3-\lambda )}}-{\displaystyle \frac{2}{\mathrm{\Gamma }(2-\lambda )}}$,

$D_5={\displaystyle \frac{-6}{\mathrm{\Gamma }(3-\lambda )}}+{\displaystyle \frac{6}{\mathrm{\Gamma }(4-\lambda )}}+{\displaystyle \frac{3}{\mathrm{\Gamma }(2-\lambda )}}={\displaystyle \frac{3(1-\lambda )}{{\mathsf{\Delta }}_2(3-\lambda )\mathrm{\Gamma }(2-\lambda )}}.$

Furthermore, we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{dr}}{b}^{\lambda }\left(r\right)& =& {\displaystyle \frac{d}{dr}}{D}_1\left[D_2{r}^{6-\lambda }+D_3{r}^{4-\lambda }+D_4{r}^{2-\lambda }\right]+\hfill \\ & +& D_1\left[D_2(6-\lambda )r^{5-\lambda }+D_3(4-\lambda )r^{3-\lambda }+D_4(2-\lambda )r^{1-\lambda }\right],\hfill \end{array}$$

where

$${\displaystyle \frac{d{D}_1}{dr}}=-{\displaystyle \frac{324r^7+351r^5+108r^3+13r}{{\left({\mathsf{\Delta }}_1{\mathsf{\Delta }}_2\right)}^3}}.$$

In arbitrary parameter, the fractional curvature is given by

$$k^{\lambda }\left(r\right)={\displaystyle \frac{k_1^{\lambda }\left(r\right)}{\parallel {\alpha }^{\prime }{\left(r\right)\parallel }^2}},$$

where

$$k_1^{\lambda }\left(r\right)=a^{\lambda }\left(r\right)\parallel {\alpha }^{\prime }\left(r\right)\parallel k\left(r\right)+{\displaystyle \frac{d}{dr}}{b}^{\lambda }\left(r\right)+c^{\lambda }\left(r\right)\parallel {\alpha }^{\prime }\left(r\right)\parallel \tau \left(r\right).$$

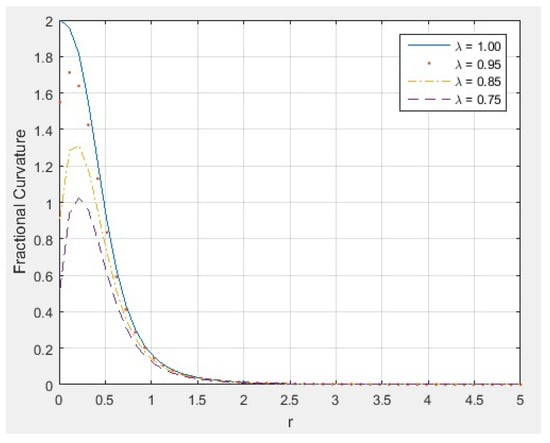
Table 3 shows the first 20 results of evaluation of the $k^{\lambda }\left(r\right)$ and $k\left(r\right)$ curvatures, for differents values of $\lambda :0.75,0.85,0.95$ and $1.0$, over the interval $[0.01,5]$, with $N=50$ for the interval partition. As can be observed, as λ approaches 1 , the values of the fractional curvature approach the values of the classic curvature $k\left(r\right)$.

Table 3. Values of $k^{\lambda }\left(r\right)$ and $k\left(r\right)$, for different values of $\lambda :0.75,0.85,0.95$ and $1.0$.

r	${\mathit{k}}^{0.75}\left(\mathit{r}\right)$	${\mathit{k}}^{0.85}\left(\mathit{r}\right)$	${\mathit{k}}^{0.95}\left(\mathit{r}\right)$	${\mathit{k}}^{1.0}\left(\mathit{r}\right)$
0.0100	0.5233	0.9130	1.5501	1.9997
0.1118	0.9404	1.2855	1.7124	1.9579
0.2137	1.0262	1.3117	1.6385	1.8160
0.3155	0.9595	1.1813	1.4249	1.5534
0.4173	0.7966	0.9577	1.1300	1.2193
0.5192	0.6079	0.7187	0.8350	0.8945
0.6210	0.4415	0.5153	0.5917	0.6304
0.7229	0.3137	0.3625	0.4123	0.4373
0.8247	0.2221	0.2545	0.2873	0.3035
0.9265	0.1585	0.1804	0.2022	0.2129
1.0284	0.1146	0.1296	0.1445	0.1517
1.1302	0.0842	0.0947	0.1050	0.1100
1.2320	0.0629	0.0704	0.0777	0.0811
1.3339	0.0477	0.0532	0.0584	0.0609
1.4357	0.0368	0.0409	0.0447	0.0465
1.5376	0.0288	0.0318	0.0347	0.0360
1.6394	0.0228	0.0251	0.0273	0.0282
1.7412	0.0183	0.0201	0.0217	0.0225
1.8431	0.0149	0.0163	0.0175	0.0181
1.9449	0.0122	0.0133	0.0142	0.0147

Figure 9 indicates the behavior of plot of the function $k^{\lambda }\left(r\right)$ for different values of $\lambda :0.75,0.85,0.95$ and $1.0$. From Figure 9, we can observed that if λ approaches 1, the plot of the function $k^{\lambda }\left(r\right)$ approaches the plot of the classic curvature $k\left(r\right)$.

Figure 9. Plot of $k^{\lambda }\left(r\right)$ for different values of $\lambda$.

The fractional torsion in arbitrary parameter, is given by

$${\tau }^{\lambda }\left(r\right)={\displaystyle \frac{{\tau }_1^{\lambda }\left(r\right)}{\parallel {\alpha }^{\prime }{\left(r\right)\parallel }^2}},$$

where

$${\tau }_1^{\lambda }\left(r\right)=a^{\lambda }\left(r\right)\parallel {\alpha }^{\prime }\left(r\right)\parallel \tau \left(r\right)-c^{\lambda }\left(r\right)\parallel {\alpha }^{\prime }\left(r\right)\parallel k\left(r\right).$$

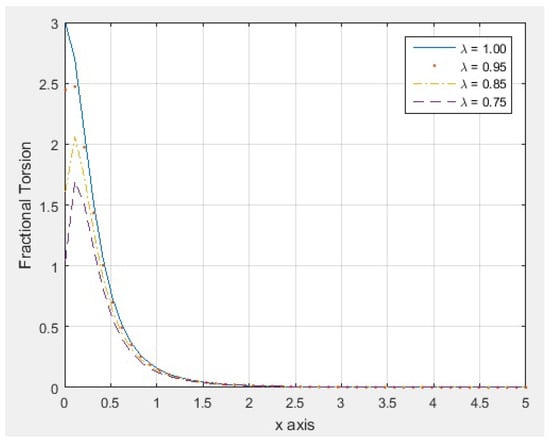
Table 4 shows the first 20 results of evaluation of the ${\tau }^{\lambda }\left(r\right)$ and $\tau \left(r\right)$ torsions, for different values of $\lambda :0.75,0.85,0.95$ and $1.0$, over the interval $[0.01,5]$, with $N=50$ for the interval partition. As can be observed, as λ approaches 1, the values of the fractional torsion approach the values of the classical torsion $\tau \left(r\right)$.

Table 4. Values of ${\tau }^{\lambda }\left(r\right)$ and $\tau \left(r\right)$, for different vaulues of $\lambda :0.75,0.85,0.95$ and $1.0$.

r	${\mathit{\tau }}^{0.75}\left(\mathit{r}\right)$	${\mathit{\tau }}^{0.85}\left(\mathit{r}\right)$	${\mathit{\tau }}^{0.95}\left(\mathit{r}\right)$	${\mathit{\tau }}^{1.0}\left(\mathit{r}\right)$
0.0100	1.0456	1.6099	2.4456	2.9973
0.1118	1.6964	2.0609	2.4720	2.6931
0.2137	1.5032	1.7323	1.9744	2.0984
0.3155	1.1362	1.2822	1.4341	1.5113
0.4173	0.8062	0.9031	1.0043	1.0561
0.5192	0.5641	0.6302	0.6996	0.7353
0.6210	0.3984	0.4439	0.4917	0.5164
0.7229	0.2864	0.3178	0.3507	0.3676
0.8247	0.2099	0.2317	0.2543	0.2659
0.9265	0.1566	0.1718	0.1874	0.1953
1.0284	0.1188	0.1294	0.1403	0.1457
1.1302	0.0915	0.0990	0.1066	0.1104
1.2320	0.0715	0.0768	0.0821	0.0848
1.3339	0.0565	0.0603	0.0641	0.0659
1.4357	0.0452	0.0479	0.0506	0.0519
1.5376	0.0365	0.0385	0.0404	0.0413
1.6394	0.0298	0.0313	0.0326	0.0333
1.7412	0.0246	0.0256	0.0266	0.0270
1.8431	0.0204	0.0212	0.0218	0.0222
1.9449	0.0171	0.0176	0.0181	0.0183

Figure 10 indicates the behavior of plot of the function ${\tau }^{\lambda }\left(r\right)$ for different values of $\lambda :0.75,0.85,0.95$ and $1.0$. From Figure 10, we can observed that if λ approaches 1, the plot of the function ${\tau }^{\lambda }\left(r\right)$ approaches the plot of the classic torsion $\tau \left(r\right)$.

Figure 10. Plot of ${\tau }^{\lambda }\left(r\right)$ for different values of $\lambda$.

Now, considering the fractional curvature $k^{\lambda }\left(r\right)$, we obtain the fractional curvature surface $X(r,\lambda )=k^{\lambda }\left(r\right)$. Figure 11 shows the plot of the fractional curvature surface over the region $[0,5]\times [0,1]$; and Figure 12 shows the evolution of the fractional curvature of the curve $\alpha$, for values of the parameter $\lambda$ from 0 to 1. If $\lambda =1$, we obtain the classical curvature or integer curvature $k^1\left(r\right)=k\left(r\right)$ of the curve $\alpha$. If $\alpha$ is close to 1, we obtain curves close to the integer curvature $k\left(r\right)$.

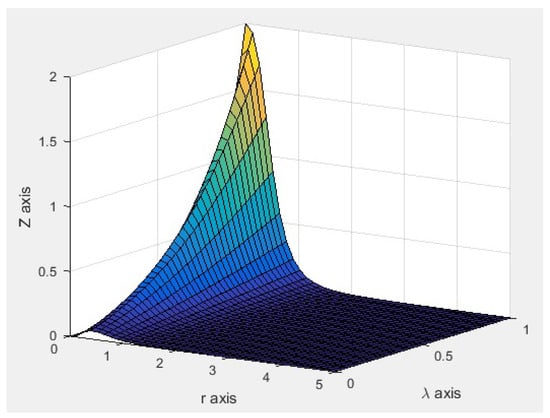
Figure 11. Plot of the fractional curvature surface $X(r,\lambda )=k^{\lambda }\left(r\right)$.

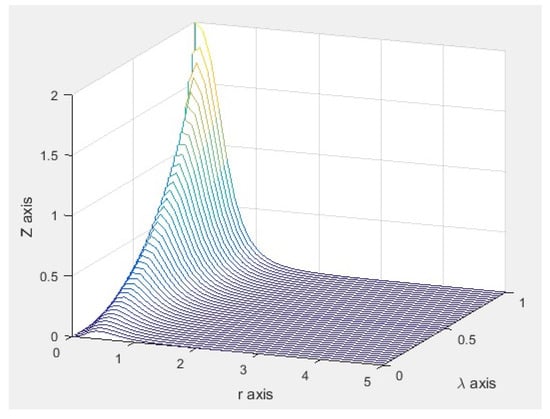
Figure 12. Evolution of the fractional curvature of the $\alpha$ curve, for values of the parameter $\lambda$ from 0 to 1.

Example 3. 

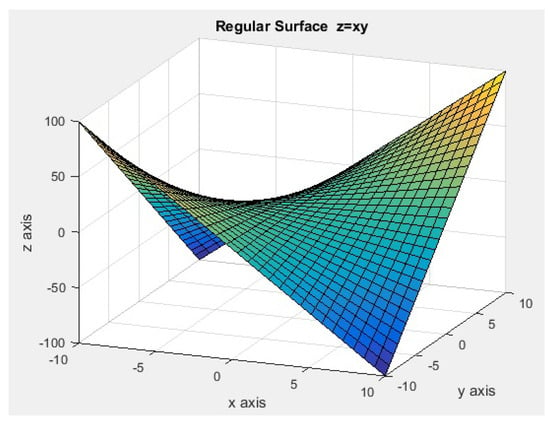
Let us consider the regular surface

$$S=\left\{(x,y,z)\in {\mathbb{R}}^3/z=xy\right\}.$$

See Figure 13

Figure 13. The plot of the hyperbolic paraboloid.

A parametrization of S is given by the map $X:{\mathbb{R}}^2\to S$ defined by

$$X(u,v)=(u,v,uv).$$

The Gaussian curvature is given by

$$K(u,v)={\displaystyle \frac{-1}{{(1+u^2+v^2)}^2}},$$

(93)

and the mean curvature is given by

$$H(u,v)={\displaystyle \frac{-uv}{{(1+u^2+v^2)}^{3/2}}}.$$

(94)

The principal directions $w_1,w_2\in T_{p}S$ of the surface S at point $p\in S$, are given by

$$w_1=\left(1,\sqrt{{\displaystyle \frac{1+v^2}{1+u^2}}}\right),w_2=\left(-\sqrt{{\displaystyle \frac{1+v^2}{1+u^2}}},1\right).$$

Now, let $R=\sqrt{{\displaystyle \frac{1+v^2}{1+u^2}}}$, then the tangent curves to $w_1$ and $w_2$ respectively, are the plane curves given by:

$$\begin{array}{ccc}\hfill {\alpha }_1\left(t\right)& =& \left(u+t,v+tR,uv+(v+uR)t+t^{2}R\right),\hfill \\ \hfill {\alpha }_2\left(t\right)& =& \left(u-tR,v+t,uv+(u-vR)t-t^{2}R\right).\hfill \end{array}$$

The Frenet-Serret trihedron of the curve ${\alpha }_1$ is given by

$$\begin{array}{ccc}\hfill T_1\left(t\right)& =& \left({\displaystyle \frac{1}{M_1}},{\displaystyle \frac{R}{M_1}},{\displaystyle \frac{v+uR+2tR}{M_1}}\right),\hfill \end{array}$$

(95)

$$\begin{array}{ccc}\hfill N_1\left(t\right)& =& \left(-{\displaystyle \frac{v+uR+2tR}{M_1\sqrt{R^2+1}}},-{\displaystyle \frac{Rv+u{R}^2+2t{R}^2}{M_1\sqrt{R^2+1}}},{\displaystyle \frac{R^2+1}{M_1\sqrt{R^2+1}}}\right),\hfill \end{array}$$

(96)

$$\begin{array}{ccc}\hfill B_1\left(t\right)& =& \left({\displaystyle \frac{R}{\sqrt{R^2+1}}},-{\displaystyle \frac{1}{\sqrt{R^2+1}}},0\right),\hfill \end{array}$$

(97)

where $M_1=\sqrt{1+R^2+{(v+uR+2tR)}^2}=\parallel {\alpha }_1^{\prime }\left(t\right)\parallel .$

In addition

$$N_1^{\prime }\left(t\right)=\left(-{\displaystyle \frac{2R{M}_1-(v+uR+2tR)M_1^{\prime }}{M_1^2\sqrt{R^2+1}}},-{\displaystyle \frac{2R^2{M}_1-(Rv+u{R}^2+2t{R}^2)M_1^{\prime }}{M_1^2\sqrt{R^2+1}}},-{\displaystyle \frac{\sqrt{R^2+1}{M}_1^{\prime }}{M_1^2}}\right).$$

(98)

Further, ${}^{c}D^{\lambda }{\alpha }_1\left(t\right)=\left({}^{c}D^{\lambda }x\left(t\right),{}^{c}D^{\lambda }y\left(t\right),{}^{c}D^{\lambda }z\left(t\right)\right)$,

$${}^{c}D^{\lambda }{\alpha }_1\left(t\right)=\left({\displaystyle \frac{{(t-a)}^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}},R{\displaystyle \frac{{(t-a)}^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}},(v+uR){\displaystyle \frac{{(t-a)}^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}}+R\left({\displaystyle \frac{2a{(t-a)}^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}}+{\displaystyle \frac{2{(t-a)}^{2-\lambda }}{\mathrm{\Gamma }(3-\lambda )}}\right)\right),$$

(99)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{dt}}\left({}^{c}D^{\lambda }{\alpha }_1\left(t\right)\right)& =& \left({\displaystyle \frac{(1-\lambda ){(t-a)}^{-\lambda }}{\mathrm{\Gamma }(2-\lambda )}},{\displaystyle \frac{R(1-\lambda ){(t-a)}^{-\lambda }}{\mathrm{\Gamma }(2-\lambda )}},(v+uR)\left[{\displaystyle \frac{(1-\lambda ){(t-a)}^{-\lambda })}{\mathrm{\Gamma }(2-\lambda )}}\right]\right.\hfill \\ & +& \left.R\left[{\displaystyle \frac{2a(1-\lambda ){(t-a)}^{-\lambda }}{\mathrm{\Gamma }(2-\lambda )}}+{\displaystyle \frac{2(2-\lambda ){(t-a)}^{1-\lambda }}{\mathrm{\Gamma }(3-\lambda )}}\right]\right).\hfill \end{array}$$

(100)

where $M_1^{\prime }={\displaystyle \frac{2Rv+2u{R}^2+4t{R}^2}{M_1}}$.

Then, the integer or classic curvature in arbitrary parameter of the curve ${\alpha }_1$ is given by

$$k_1\left(t\right)={\displaystyle \frac{\parallel {\alpha }_1^{\prime }\left(t\right)\times {\alpha }_1^{″}\left(t\right)\parallel }{\parallel {\alpha }_1^{\prime }{\left(t\right)\parallel }^3}}={\displaystyle \frac{2R\sqrt{R^2+1}}{1+R^2+{(v+uR+2tR)}^2{)}^{3/2}}}.$$

(101)

Using (95), (96), (98)–(100), we have

$$\begin{array}{ccc}\hfill a_1^{\lambda }\left(t\right)& =& ⟨{}^{c}D^{\lambda }{\alpha }_1\left(t\right),T_1\left(t\right)⟩,\hfill \end{array}$$

(102)

$$\begin{array}{ccc}\hfill b_1^{\lambda }\left(t\right)& =& ⟨{}^{c}D^{\lambda }{\alpha }_1\left(t\right),N_1\left(t\right)⟩,\hfill \end{array}$$

(103)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{dt}}\left(b_1^{\lambda }\left(t\right)\right)& =& ⟨{\displaystyle \frac{d}{dt}}\left({}^{c}D^{\lambda }{\alpha }_1\left(t\right)\right),N_1\left(t\right)⟩+⟨{}^{c}D^{\lambda }{\alpha }_1\left(t\right),N_1^{\prime }\left(t\right)⟩.\hfill \end{array}$$

(104)

Using (101), (102) and (104), we obtain

$$r_1^{\lambda }\left(t\right)={\displaystyle \frac{k_1\left(t\right)}{k_1^{\lambda }}}.$$

(105)

Analogously, with respect to the curve ${\alpha }_2$, we have

$${\alpha }_2\left(t\right)=\left(u-tR,v+t,uv+(u-vR)t-t^{2}R\right).$$

The Frenet-Serret trihedron of the curve ${\alpha }_2$ is given by

$$\begin{array}{ccc}\hfill T_2\left(t\right)& =& \left({\displaystyle \frac{-R}{M_2}},{\displaystyle \frac{1}{M_2}},{\displaystyle \frac{u-vR-2tR}{M_2}}\right),\hfill \end{array}$$

(106)

$$\begin{array}{ccc}\hfill N_2\left(t\right)& =& \left(-{\displaystyle \frac{Ru-v{R}^2-2t{R}^2}{M_2\sqrt{R^2+1}}},{\displaystyle \frac{u-vR-2tR}{M_2\sqrt{R^2+1}}},-{\displaystyle \frac{R^2+1}{M_2\sqrt{R^2+1}}}\right)\hfill \end{array}$$

(107)

$$\begin{array}{ccc}\hfill B_2\left(t\right)& =& \left({\displaystyle \frac{-1}{\sqrt{R^2+1}}},{\displaystyle \frac{-R}{\sqrt{R^2+1}}},0\right)\hfill \end{array}$$

(108)

where $M_2=\sqrt{1+R^2+{(u-vR-2tR)}^2}=\parallel {\alpha }_2^{\prime }\left(t\right)\parallel$.

In Addition

$$N_2^{\prime }\left(t\right)=\left({\displaystyle \frac{2R^2{M}_2+(uR-v{R}^2-2t{R}^2)M_2^{\prime }}{M_2^2\sqrt{R^2+1}}},{\displaystyle \frac{-2R{M}_2-(u-vR-2tR)M_2^{\prime }}{M_2^2\sqrt{R^2+1}}},{\displaystyle \frac{M_2^{\prime }\sqrt{R^2+1}}{M_2^2}}\right).$$

(109)

$${}^{c}D^{\lambda }{\alpha }_2\left(t\right)=\left({\displaystyle \frac{-R{(t-a)}^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}},{\displaystyle \frac{{(t-a)}^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}},(u-vR){\displaystyle \frac{{(t-a)}^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}}-R\left({\displaystyle \frac{2a{(t-a)}^{1-\lambda }}{\mathrm{\Gamma }(2-\lambda )}}+{\displaystyle \frac{2{(t-a)}^{2-\lambda }}{\mathrm{\Gamma }(3-\lambda )}}\right)\right)$$

(110)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{dt}}\left({}^{c}D^{\lambda }{\alpha }_2\left(t\right)\right)& =& \left({\displaystyle \frac{-R(1-\lambda ){(t-a)}^{-\lambda }}{\mathrm{\Gamma }(2-\lambda )}},{\displaystyle \frac{(1-\lambda ){(t-a)}^{-\lambda }}{\mathrm{\Gamma }(2-\lambda )}},(u-vR)\left[{\displaystyle \frac{(1-\lambda ){(t-a)}^{-\lambda }}{\mathrm{\Gamma }(2-\lambda )}}\right]\right.-\hfill \\ & & \left.-R\left[{\displaystyle \frac{2a(1-\lambda ){(t-a)}^{-\lambda }}{\mathrm{\Gamma }(2-\lambda )}}+{\displaystyle \frac{2(2-\lambda ){(t-a)}^{1-\lambda }}{\mathrm{\Gamma }(3-\lambda )}}\right]\right),\hfill \end{array}$$

(111)

where $M_2^{\prime }={\displaystyle \frac{-2uR+2v{R}^2+4t{R}^2}{M_2}}.$

Then, the integer or classic curvature in arbitrary parameter of the curve ${\alpha }_2$ is given by

$$k_2\left(t\right)={\displaystyle \frac{\parallel {\alpha }_2^{\prime }\left(t\right)\times {\alpha }_2^{″}\left(t\right)\parallel }{\parallel {\alpha }_2^{\prime }{\left(t\right)\parallel }^3}}={\displaystyle \frac{2R\sqrt{R^2+1}}{{(1+R^2+{(u-vR-2tR)}^2)}^{3/2}}}.$$

(112)

Using (106), (107), (109)–(111), we obtain

$$\begin{array}{ccc}\hfill a_2^{\lambda }\left(t\right)& =& ⟨{}^{c}D^{\lambda }{\alpha }_2\left(t\right),T_2\left(t\right)⟩,\hfill \end{array}$$

(113)

$$\begin{array}{ccc}\hfill b_2^{\lambda }\left(t\right)& =& ⟨{}^{c}D^{\lambda }{\alpha }_2\left(t\right),N_2\left(t\right)⟩,\hfill \end{array}$$

(114)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{dt}}\left(b_2^{\lambda }\left(t\right)\right)& =& ⟨{\displaystyle \frac{d}{dt}}\left({}^{c}D^{\lambda }{\alpha }_2\left(t\right)\right),N_2\left(t\right)⟩+⟨{}^{c}D^{\lambda }{\alpha }_2\left(t\right),N_2^{\prime }\left(t\right)⟩.\hfill \end{array}$$

(115)

Using (112), (113) and (115), we obtain

$$r_2^{\lambda }\left(t\right)={\displaystyle \frac{k_2\left(t\right)}{k_2^{\lambda }\left(t\right)}}.$$

(116)

Therefore, by (93), (105) and (116), the fractional curvature of S at the point $p\in S$, is given by

$$K^{\lambda }\left(p\right)={\displaystyle \frac{-1}{r_1^{\lambda }\left(t\right)r_2^{\lambda }\left(t\right){(1+u^2+v^2)}^2}}.$$

In the computational implementation, we show approximations to the fractional curvature surface, for different values of the parameter λ. We worked on the square region $D=[-2,2]\times [-2,2]$, and considered a partition with $N=41$, for the interval $[-2,2]$ on the x and y axis respectively; and we chose the vertical section corresponding to $x=0$. In addition, we used $a=-1$ in Caputo’s fractional derivative.

The numerical results show symmetry with respect to the z axis; in this sense, Table 5 shows a part of the results corresponding to the vertical sections, for different values of the parameter $\lambda :0.7,0.8,0.9,0.95$ and $1.0$.

Table 5. Vertical section data for different values of $\lambda$.

	${\mathit{\lambda }}^{0.7}$ Values in a Vertical Section	${\mathit{\lambda }}^{0.8}$ Values in a Vertical Section	${\mathit{\tau }}^{0.9}\left(\mathit{s}\right)$ Values in a Vertical Section	${\mathit{\tau }}^{0.95}\left(\mathit{s}\right)$ Values in a Vertical Section	${\mathit{\tau }}^{1.0}\left(\mathit{s}\right)$ Values in a Vertical Section
1	−0.1857	−0.2317	−0.2732	−0.2907	−0.3052
2	−0.2262	−0.2823	−0.3327	−0.3541	−0.3718
3	−0.2740	−0.3419	−0.4031	−0.4289	−0.4504
4	−0.3289	−0.4104	−0.4839	−0.5149	−0.5407
5	−0.3893	−0.4859	−0.5728	−0.6095	−0.6400
6	−0.4521	−0.5642	−0.6651	−0.7077	−0.7432
7	−0.5120	−0.6390	−0.7533	−0.8015	−0.8417
8	−0.5625	−0.7019	−0.8274	−0.8805	−0.9246
9	−0.5964	−0.7442	−0.8773	−0.9335	−0.9803
10	−0.6084	−0.7592	−0.8950	−0.9523	−1.0000
11	−0.5964	−0.7442	−0.8773	−0.9335	−0.9803
12	−0.5625	−0.7019	−0.8274	−0.8805	−0.9246
13	−0.5120	−0.6390	−0.7533	−0.8015	−0.8417
14	−0.4521	−0.5642	−0.6651	−0.7077	−0.7432
15	−0.3893	−0.4859	−0.5728	−0.6095	−0.6400
16	−0.3289	−0.4104	−0.4839	−0.5149	−0.5407
17	−0.2740	−0.3419	−0.4031	−0.4289	−0.4504
18	−0.2262	−0.2823	−0.3327	−0.3541	−0.3718
19	−0.1857	−0.2317	−0.2732	−0.2907	−0.3052

In Table 5, the symmetry of the data by column is observed, with respect to the data in row 10; moreover, if the parameter λ tends to 1, the values of the vertical sections tend to the integer case corresponding to column $\lambda =1.0$.

In Figure 14, Figure 16, Figure 18, Figure 20 and Figure 22, the vertical sections are shown for different values of $\lambda :0.7,0.8,0.9,0.95$ and $1.0$, and it is observed that as λ approaches 1, the vertical sections approach the vertical section determinate by $\lambda =1.0$.

Figure 15, Figure 17, Figure 19, Figure 21 and Figure 23, show the plots of the fractional curvature functions for different values of $\lambda :0.7,0.8,0.9,0.95$ and $1.0$, and it is observed that as λ approaches 1, the graph of the functions $K^{\lambda }(u,v)$, approximate the graph of the Gaussian curvature function $K(u,v)$ of the surface S.

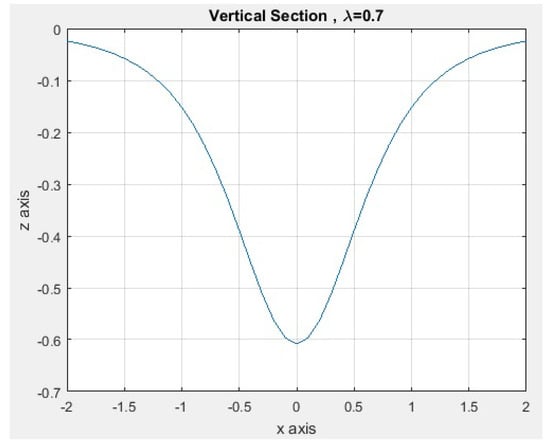
Figure 14. Vertical section for $\lambda =0.7$.

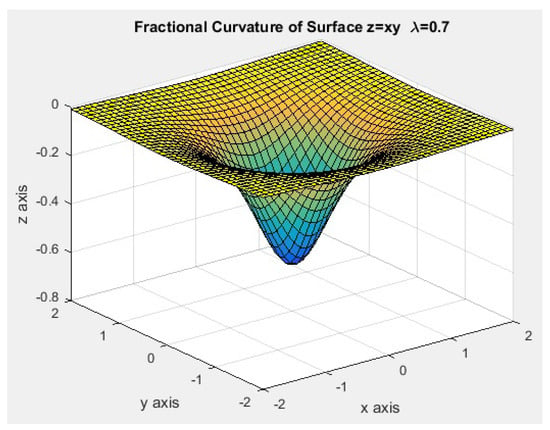
Figure 15. Fractional curvature surface for $\lambda =0.7$.

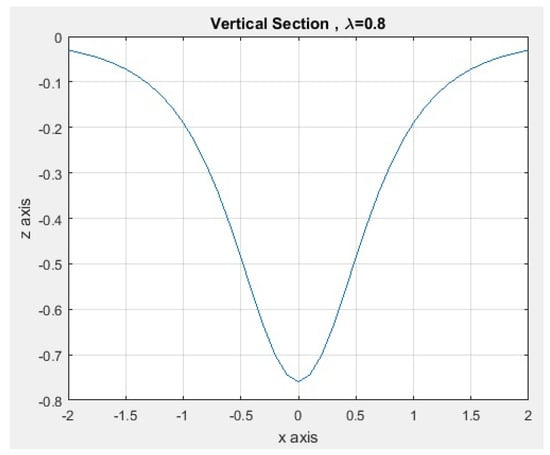
Figure 16. Vertical section for $\lambda =0.8$.

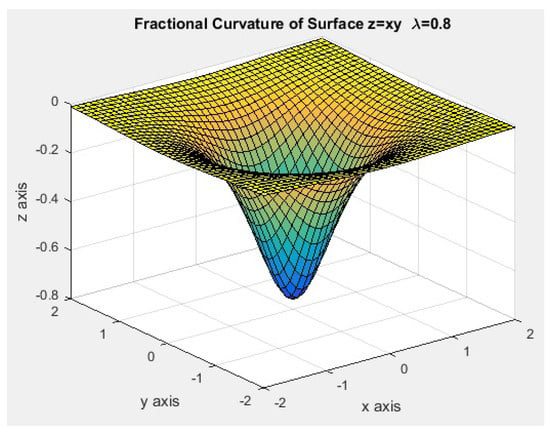
Figure 17. Fractional curvature surface for $\lambda =0.8$.

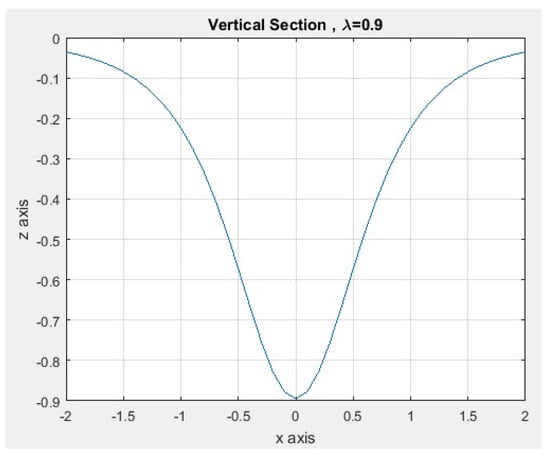
Figure 18. Vertical section for $\lambda =0.9$.

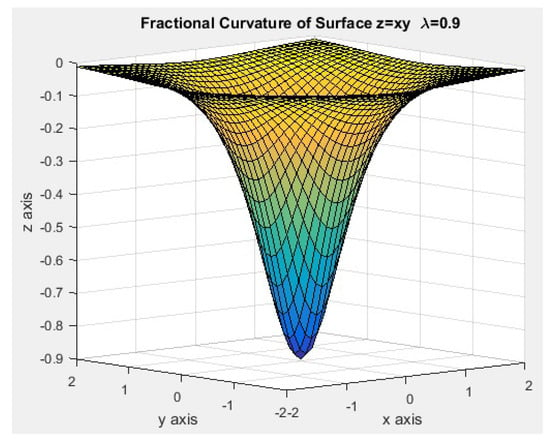
Figure 19. Fractional curvature surface for $\lambda =0.9$.

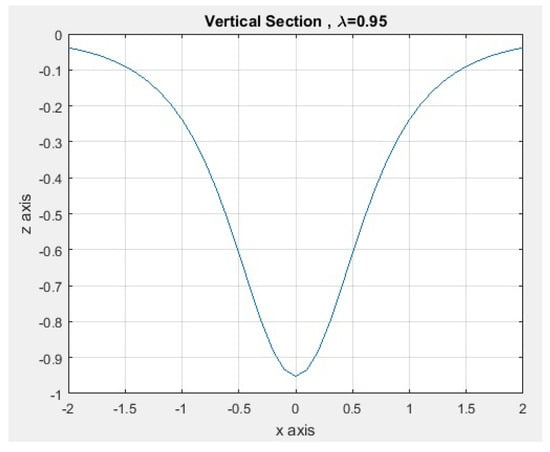
Figure 20. Vertical section for $\lambda =0.95$.

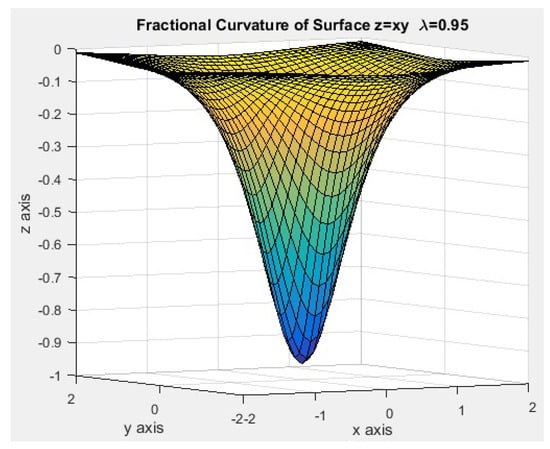
Figure 21. Fractional curvature surface for $\lambda =0.95$.

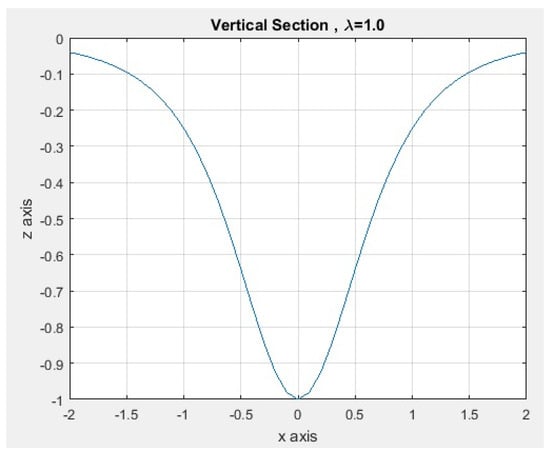
Figure 22. Vertical section for $\lambda =1.0$.

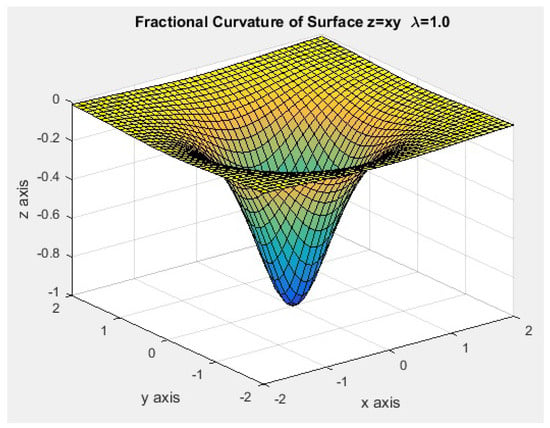
Figure 23. Fractional curvature surface for $\lambda =1.0$.

6. Conclusions

In this paper, we generalize the fractional curvature of plane curves introduced by Rubio et al. [15] to regular curves in 3-dimensional Euclidean space, and give a new definition of fractional torsion of curves; furthermore, we prove that these concepts belong to intrinsic geometry.

From our study, we obtain a geometric interpretation of the Caputo fractional de-rivative of algebraic polynomials.

A new definition of fractional curvature and fractional mean curvature of regular surfaces is given using fractional principal directions, and it is proved that these cur-vatures are invariant under local isometries; that is, they belong to intrinsic geometry. The importance of our study lies in the analysis of the geometric properties of curves and surfaces from the point of view of fractional calculus. One-dimensional Euclidean spaces are characterized as those curves whose fractional curvature of order $\lambda$ is zero at all points for all $\lambda$.