Synchronization of Chaotic Satellite Systems with Fractional Derivatives Analysis Using Feedback Active Control Techniques

Abstract

This research article introduces a novel chaotic satellite system based on fractional derivatives. The study explores the characteristics of various fractional derivative satellite systems through detailed phase portrait analysis and computational simulations, employing fractional calculus. We provide illustrations and tabulate the phase portraits of these satellite systems, highlighting the influence of different fractional derivative orders and parameter values. Notably, our findings reveal that chaos can occur even in systems with fewer than three dimensions. To validate our results, we utilize a range of analytical tools, including equilibrium point analysis, dissipative measures, Lyapunov exponents, and bifurcation diagrams. These methods confirm the presence of chaos and offer insights into the system’s dynamic behavior. Additionally, we demonstrate effective control of chaotic dynamics using feedback active control techniques, providing practical solutions for managing chaos in satellite systems.

1. Introduction

Fractional calculus has long been recognized as one of the most effective techniques for modeling dynamical systems. It is applied across various scientific, engineering, and multidisciplinary fields. Numerous physical systems have been thoroughly described using fractional-order differential equations, which often exhibit chaotic or hyper-chaotic behavior. Notable examples include the fractional-order Chen system, the fractional-order hyper-chaotic Chen system, the fractional-order Lorenz system, the fractional-order Rössler system, the fractional derivative Duffing system, and the fractional derivative financial system. These systems demonstrate the rich dynamics and complexity that fractional-order calculus can capture [1,2,3]. Fractional derivatives are employed to model the behavior of real-world systems across diverse research and engineering fields, including medicine, biological tissues, bioengineering, ECG testing, cardiac tissue, photoelasticity, fluid mechanics, and material science. By utilizing fractional derivatives, researchers can more accurately capture the complex dynamics of these systems [4,5,6]. Fractional-order systems and their equivalent ordinary differential equations differ in several ways [7]. Kumar et al., for instance, used sliding mode techniques to study fractional derivative Rabinovich–Fabrikant systems and fractional derivative hyper-chaotic financial systems [8].

Chaos control and synchronization in fractional-order systems have garnered significant research attention. Over the past few decades, chaotic synchronization has become a captivating topic in nonlinear sciences due to its wide-ranging practical applications in fields such as chemical reactions, weather forecasting, power converters, aerospace, signal processing, radar technology, laser physics, secure communication, global positioning systems (GPS), and biological systems [9]. The synchronization of fractional-order chaotic systems was first developed by Deng and Li, who also synchronized fractional-order Lü systems. Since then, several academics and researchers have explored the synchronization of various chaotic systems with fractional orders. Gao et al. examined master-response synchronization in chaotic and hyper-chaotic systems with fractional orders [10,11]. Fundamental synchronization techniques have been applied to synchronize fractional-derivative chaotic Arneodo systems using a scalar drive signal [12]. Additionally, Hegazi et al. extended projective synchronization to two chaotic or hyper-chaotic non-integer systems [13].

Satellite systems play a crucial role in advancing space technology, scientific research, telecommunications, and civil and military applications. Key techniques for the synchronization and control of satellite systems include predictive control, adaptive synchronization and control, and sliding mode synchronization and control. Modern space mission designs, which often involve multiple satellites flying in formation, have increasingly utilized fractional-order synchronization through control methods that manage and minimize relative inaccuracies between satellite systems [14,15]. The study of chaotic satellite systems has attracted significant attention, with researchers such as Kuang and Tan, Tsui and Jones, Kong and Zhou, and Kuang, Tan, Arichandran, and Leung making notable contributions [16,17]. Farid and Moghaddam studied the generalized projective control and synchronization of chaotic satellites using linear matrix inequality (LMI) techniques [18]. Goeree and Fasse [19] explored sliding mode attitude control and synchronization of small satellites for ground tracking operations. Kumar and Khan have extensively researched chaos in satellite systems, using various tools to measure chaos and establish chaotic satellite systems with synchronization techniques across multiple methodologies [20]. Despite these advancements, further research is needed to investigate and enhance the synchronization and control of satellite systems.

This research paper explores the chaotic behavior of satellite systems modeled with fractional orders, expanding on previous discussions in the field. We analyze the equilibrium points, dissipativity, bifurcation diagrams, and Lyapunov exponents to examine the characteristics of fractional-order satellite systems. Our findings confirm the occurrence of chaos in systems with fractional orders less than 3, emphasizing their behavior in lower dimensions. Additionally, we employ feedback and active control strategies to achieve chaos control and synchronization in these systems. These efforts significantly enhance the understanding of satellite systems with fractional-order derivatives. The applications of this research, such as in telecommunications, weather forecasting, GPS systems, and earth observation, stand to benefit from these advancements. Our study highlights its uniqueness by demonstrating how these findings contribute to both the understanding and practical use of fractional-order satellite systems.

This paper is structured as follows: Section 1 provides the introduction. Section 2 outlines the basic definitions of fractional-order chaotic systems. In Section 3, we discuss the system description and the assumptions related to satellite systems. Section 4 focuses on controlling chaos in satellite systems with fractional-order derivatives. In Section 5, we present the synchronization of two identical satellite systems with fractional orders using the active control technique. Section 6 includes numerical simulations. The conclusion is presented in Section 7.

2. Basic Concepts of Fractional Derivatives

The non-integer-order integro-differential operator ${}_{a}D_{\mathrm{t}}^{{\alpha }_1}$ in fractional calculus is a generalization of integration and differentiation notions. It is written in the following manner:

$${}_{a}D_{\mathrm{t}}^{{\alpha }_1}=\left\{\begin{array}{cc}{\displaystyle \frac{d^{{\alpha }_1}}{d{t}^{{\alpha }_1}}},\hfill & \mathrm{if}\mathcal{R}\left({\alpha }_1\right)>0\hfill \\ 1,\hfill & \mathrm{if}\mathcal{R}\left({\alpha }_1\right)=0\hfill \\ {\int }_a^t{\left(d\tau \right)}^{-{\alpha }_1},\hfill & \mathrm{if}\mathcal{R}\left({\alpha }_1\right)<0.\hfill \end{array}\right.$$

(1)

The definition of the generalized Riemann–Liouville definition [21] is as follows:

$$D^{{\alpha }_1}f\left(t\right)={\displaystyle \frac{d^{{\alpha }_1}}{d{t}^{{\alpha }_1}}}{J}^{n-{\alpha }_1}f\left(t\right),{\alpha }_1>0,$$

(2)

where $n=\left[{\alpha }_1\right]$ and n is the first integer greater than or equal to ${\alpha }_1$; $J^{\beta 1}$ is the Riemann–Liouville integral operator of ${\beta }_1$ order, which is defined as follows:

$$J^{{\beta }_1}f\left(t\right)={\displaystyle \frac{1}{\Gamma \left({\beta }_1\right)}}{\int }_0^t{\displaystyle \frac{f\left(\tau \right)}{{(t-\tau )}^{1-{\beta }_1}}}d\tau$$

(3)

for $0<{\beta }_1\le 1,$ where $\Gamma (.)$ is the gamma function.

The definitions below are utilized as:

$$D^{{\alpha }_1}f\left(t\right)=J^{n-{\alpha }_1}{f}^n\left(t\right),{\alpha }_1>0,$$

(4)

where $n=\left[{\alpha }_1\right].$ The operator $D^{{\alpha }_1}$ is commonly referred to as the Caputo differential operator of order ${\alpha }_1$ because it was initially employed for the solution of practical problems by Caputo [21,22].

Fractional Derivatives and Integrals: Basic Definitions and Properties

Definition 1

([21,22,23]). A real function $f\left(t\right),t>0$ is indeed in Caputo space $\mathcal{C}{\alpha }_1,{\alpha }_1\in \mathcal{R}$ if there is a real integer $p(>{\alpha }_1),$ such that $f\left(t\right)=t^{p}f1\left(t\right)$ with $f1\left(t\right)\in \mathcal{C}[0,\infty ).$

Definition 2

([21,22,23]). A real function $f\left(t\right),t>0$ is indeed in Caputo space ${\mathcal{C}}_{{\alpha }_1}^m,m\in IN\cup 0$ if $f^{\left(m\right)}\in {\mathcal{C}}_{{\alpha }_1}.$

Definition 3

([21,22,23]). If $f\in {\mathcal{C}}_{{\alpha }_1}\mathrm{and}{\alpha }_1\ge -1,$ then the Riemann–Liouville integral of order ${\alpha }_1,({\alpha }_1>0)$ can be obtained by:

$$\begin{array}{c}\hfill I^{{\alpha }_1}f\left(t\right)={\displaystyle \frac{1}{\Gamma \left({\alpha }_1\right)}}{\int }_0^t{(t-{\alpha }_1)}^{{\alpha }_1-1}f\left(\tau \right)d\tau ,t>0.\end{array}$$

(5)

Definition 4

([21,22,23]). The fractional derivative of $f,f\in {\mathcal{C}}_{-1}^m,m\in IN\cup 0,$ described by Caputo is

$$\begin{array}{c}\hfill D^{{\alpha }_1}f\left(t\right)={\displaystyle \frac{d^m}{d{t}^m}}f\left(t\right),{\alpha }_1=m=I^{m-{\alpha }_1}{\displaystyle \frac{d^{m}f\left(t\right)}{d{t}^m}},m-1<{\alpha }_1<m,m\in IN.\end{array}$$

(6)

Note that for $m-1<{\alpha }_1\le m,m\in IN,$

$$\begin{array}{c}\hfill I^{{\alpha }_1}{D}^{{\alpha }_1}f\left(t\right)=f\left(t\right)-\sum _{k=0}^{m-1}{\displaystyle \frac{d^{k}f}{d{t}^k}}\left(0\right){\displaystyle \frac{t^k}{k!}},I^{{\alpha }_1}{t}^{{\alpha }_1}={\displaystyle \frac{\Gamma (v+1)}{\Gamma ({\alpha }_1+v+1)}}{t}^{{\alpha }_1+v}.\end{array}$$

(7)

3. System Description and Assumption of Satellite System

The satellite systems with attitude dynamics are described in the inertial reference frame as [24,25]

$$\dot{\mathrm{T}}={\mathrm{T}}_a+{\mathrm{T}}_b+{\mathrm{T}}_c,$$

(8)

The overall momentum affecting the satellite is $\mathrm{T}$. The torques from the flywheel, gravitational forces, and disturbances are represented by ${\mathrm{T}}_a$,${\mathrm{T}}_b$, and ${\mathrm{T}}_c$, respectively. The overall momentum $\mathrm{T}$ is calculated as follows:

$$\mathrm{T}=\mathit{I}\omega ,$$

(9)

where $\omega$ denotes the angular velocity and $\mathit{I}$ is the inertia matrix. The total momentum derivatives $\mathrm{T}$ are represented as

$$\dot{\mathrm{T}}=\mathit{I}\dot{\omega }+\omega \times \mathit{I}\omega .$$

(10)

The cross-product of vectors is denoted by the symbol ×. When we combine these equations, we have

$$\mathit{I}\dot{\omega }+\omega \times \mathit{I}\omega ={\mathrm{T}}_a+{\mathrm{T}}_b+{\mathrm{T}}_c.$$

(11)

We have made our decision $\mathit{I}=diag({\mathit{I}}_x,{\mathit{I}}_y,{\mathit{I}}_z)$.

$${\mathrm{T}}_a=\left[\begin{array}{c}{\mathrm{T}}_{ax}\\ {\mathrm{T}}_{ay}\\ {\mathrm{T}}_{az}\end{array}\right];{\mathrm{T}}_b=\left[\begin{array}{c}{\mathrm{T}}_{bx}\\ {\mathrm{T}}_{by}\\ {\mathrm{T}}_{bz}\end{array}\right];{\mathrm{T}}_c=\left[\begin{array}{c}{\mathrm{T}}_{cx}\\ {\mathrm{T}}_{cy}\\ {\mathrm{T}}_{cz}\end{array}\right].$$

The satellite system [14,24,25] is written as

$$\begin{array}{c}{\mathit{I}}_x\dot{{\omega }_x}={\omega }_y{\omega }_z({\mathit{I}}_y-{\mathbf{I}}_z)+h_x+u_x,\\ {\mathit{I}}_y\dot{{\omega }_y}={\omega }_x{\omega }_z({\mathit{I}}_z-{\mathbf{I}}_x)+h_y+u_y,\\ {\mathit{I}}_z\dot{{\omega }_z}={\omega }_x{\omega }_y({\mathit{I}}_x-{\mathbf{I}}_y)+h_z+u_z,\end{array}$$

(12)

where

$$h_x=\left[\begin{array}{c}{\mathrm{T}}_{ax}+{\mathrm{T}}_{bx}+{\mathrm{T}}_{cx}\end{array}\right];h_y=\left[\begin{array}{c}{\mathrm{T}}_{ay}+{\mathrm{T}}_{by}+{\mathrm{T}}_{cy}\end{array}\right];$$

$$h_z=\left[\begin{array}{c}{\mathrm{T}}_{az}+{\mathrm{T}}_{bz}+{\mathrm{T}}_{cz}\end{array}\right].$$

Here, $u_x$, $u_y$, and $u_z$ are three control torques, whereas $h_x$, $h_y$, and $h_z$ are perturbing disturbance torques. We suppose that ${\mathit{I}}_x>{\mathit{I}}_y>{\mathit{I}}_z=1$ and ${\mathit{I}}_x=3$, ${\mathit{I}}_y=2$, and ${\mathit{I}}_z=1$. The perturbing torques [20] are defined in the form as

$$\left(\begin{array}{c}{h}_x\\ h_y\\ h_z\end{array}\right)=\left(\begin{array}{ccc}(-1.2& 0& {\displaystyle \frac{\sqrt{6}}{2}}\\ 0& 0.35& 0\\ -\sqrt{6}& 0& -0.4)\end{array}\right)\left(\begin{array}{c}{\omega }_x\\ {\omega }_y\\ {\omega }_z\end{array}\right).$$

(13)

The following is the formula for a three-dimensional (3D) chaotic satellite system:

$$\begin{array}{c}\hfill \begin{array}{c}\dot{x}={\displaystyle \frac{d}{dt}}\left(x\left(t\right)\right)={\sigma }_{x}yz-{\displaystyle \frac{1.2}{{\mathit{I}}_x}}x+{\displaystyle \frac{\sqrt{6}}{2{\mathit{I}}_x}}z,\hfill \\ \dot{y}={\displaystyle \frac{d}{dt}}\left(y\left(t\right)\right)={\sigma }_{y}xz+{\displaystyle \frac{0.35}{{\mathit{I}}_y}}y,\hfill \\ \dot{z}={\displaystyle \frac{d}{dt}}\left(z\left(t\right)\right)={\sigma }_{z}xy-{\displaystyle \frac{\sqrt{6}}{{\mathit{I}}_z}}x-{\displaystyle \frac{0.4}{{\mathit{I}}_z}}z,\hfill \end{array}\end{array}$$

(14)

where ${\sigma }_x={\displaystyle \frac{{\mathit{I}}_y-{\mathit{I}}_z}{{\mathit{I}}_x}}$, ${\sigma }_y={\displaystyle \frac{{\mathit{I}}_z-{\mathit{I}}_x}{{\mathit{I}}_y}}$, and ${\sigma }_z={\displaystyle \frac{{\mathit{I}}_x-{\mathit{I}}_y}{{\mathit{I}}_z}}$; and ${\sigma }_x={\displaystyle \frac{1}{3}}$, ${\sigma }_y=-1$, and ${\sigma }_z=1$. The 3D chaotic satellite system becomes

$$\begin{array}{c}\hfill \begin{array}{c}\dot{x}={\displaystyle \frac{d}{dt}}\left(x\left(t\right)\right)={\displaystyle \frac{1}{3}}yz-ax+{\displaystyle \frac{1}{\sqrt{6}}}z,\hfill \\ \dot{y}={\displaystyle \frac{d}{dt}}\left(y\left(t\right)\right)=-xz+by,\hfill \\ \dot{z}={\displaystyle \frac{d}{dt}}\left(z\left(t\right)\right)=xy-\sqrt{6}x-cz,\hfill \end{array}\end{array}$$

(15)

where a, b, and c are known parameter values; $a=0.4$, $b=0.175$, and $c=0.4$ are the values we have. The order ${\alpha }_1=0.95$ of the 3D fractional derivative satellite system is represented as

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \frac{d^{{\alpha }_1}x\left(t\right)}{d{t}^{{\alpha }_1}}}={\displaystyle \frac{1}{3}}yz-ax+{\displaystyle \frac{1}{\sqrt{6}}}z,\hfill \\ {\displaystyle \frac{d^{{\alpha }_1}y\left(t\right)}{d{t}^{{\alpha }_1}}}=-xz+by,\hfill \\ {\displaystyle \frac{d^{{\alpha }_1}z\left(t\right)}{d{t}^{{\alpha }_1}}}=xy-\sqrt{6}x-cz.\hfill \end{array}\end{array}$$

(16)

Equilibrium Points: The equilibrium point of the dynamical system with fractional order derivative is the same as that of an integer-order dynamical system [23]. By solving the system of equations below, the satellite system’s equilibrium points (16) can be determined; $\dot{X}\left(t\right)=0.$

$$\begin{array}{c}\hfill F\left(X\right)=\left[\begin{array}{cc}& {\displaystyle \frac{1}{3}}yz-ax+{\displaystyle \frac{1}{\sqrt{6}}}z=0\\ & -xz+by=0\\ & xy-\sqrt{6}x-cz=0\end{array}\right].\end{array}$$

Equilibrium points are

$$\begin{array}{c}\hfill {\aleph }_0=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right],{\aleph }_1=\left[\begin{array}{c}1.1910\\ 2.5766\\ 0.3785\end{array}\right],{\aleph }_2=\left[\begin{array}{c}0.1582\\ -1.3641\\ -1.5086\end{array}\right],{\aleph }_3=\left[\begin{array}{c}-0.1582\\ -1.3641\\ 1.5086\end{array}\right],{\aleph }_4=\left[\begin{array}{c}-1.1910\\ 2.5766\\ -0.3785\end{array}\right].\end{array}$$

(17)

The satellite system’s (16) Jacobian matrix is calculated as follows:

$$\begin{array}{c}\hfill J\left(X\right)=\left[\begin{array}{ccc}-a& 0.33\ast z& (0.33\ast y+{\displaystyle \frac{1}{\sqrt{6}}})\\ -z& b& -x\\ (y-\sqrt{6})& x& -c.\end{array}\right].\end{array}$$

(18)

At each equilibrium point, one of the eigenvalues of the Jacobian matrix (18) has a positive real portion. This demonstrates that the equilibrium points ${\aleph }_0$, ${\aleph }_1$, ${\aleph }_2$, ${\aleph }_3$, and ${\aleph }_4$ are saddle-focus, which is inherently unstable. As a result, all five equilibrium points of the satellite system (16) are unstable [20].

Invariant: Around y-axis

We set $z\left(0\right)=0$ and $x\left(0\right)=0$ in Equation (16) for all t; $\dot{x}$ and $\dot{z}$ retain zero. As a result, the y-axis is an orbit.

$$\begin{array}{c}\hfill {\displaystyle \frac{d^{{\alpha }_1}y\left(t\right)}{d{t}^{{\alpha }_1}}}=by\left(t\right),\mathrm{hence}y\left(t\right)=y\left(0\right)e^{bt};\mathrm{for}x,z=0.\end{array}$$

(19)

As a result, for the equilibrium, the y-axis illustrated the section of the unstable manifold at the origin.

Dissipative system: The system (16) in vector notation is

$$\begin{array}{c}\hfill {\displaystyle \frac{d^{{\alpha }_1}X\left(t\right)}{d{t}^{{\alpha }_1}}}=\mathit{F}\left(X\right)=\left[\begin{array}{c}{\mathit{F}}_1(x,y,z)\\ {\mathit{F}}_2(x,y,z)\\ {\mathit{F}}_3(x,y,z)\end{array}\right],\end{array}$$

(20)

where $X\left(t\right)=(x,y,z)$ and

$$\begin{array}{c}\hfill \mathit{F}\left(X\right)=\left[\begin{array}{cc}& {\mathit{F}}_1(x,y,z)={\displaystyle \frac{1}{3}}yz-ax+{\displaystyle \frac{1}{\sqrt{6}}}z,\\ & {\mathit{F}}_2(x,y,z)=-xz+by\\ & {\mathit{F}}_3(x,y,z)=xy-\sqrt{6}x-cz\end{array}\right];\end{array}$$

where $c=0.4$, $a=0.4$, and $b=0.175$. We assume any smooth boundary area $\Lambda \left(t\right)\in {\mathcal{R}}^3$ with $\Lambda \left(t\right)={\Theta }_t(\Lambda ),$ where ${\Theta }_t$ displayed the flow of f.

The volume of $\Lambda \left(t\right)$ is $\mathbf{V}\left(t\right)$.

We get, through Liouville’s theorem,

$$\begin{array}{c}\hfill \dot{\mathbf{V}}\left(t\right)={\int }_{\Lambda \left(t\right)}(\nabla .\mathit{F})dxdydz.\end{array}$$

(21)

The divergence of the satellite system (21) is calculated as

$$\begin{array}{c}\hfill \nabla .f=\left[\begin{array}{c}{\displaystyle \frac{\partial {\mathit{F}}_1}{\partial x}}+{\displaystyle \frac{\partial {\mathit{F}}_2}{\partial y}}+{\displaystyle \frac{\partial {\mathit{F}}_3}{\partial z}}\end{array}\right]=-a+b-c=-0.625.\end{array}$$

(22)

From (21) and (22), the first derivatives ordinary differential equation can be written as follows:

$$\dot{\mathbf{V}}\left(t\right)=-0.625\mathbf{V}\left(t\right).$$

(23)

We derive the following solution by integrating Equation (23):

$$\mathbf{V}\left(t\right)=e^{-0.625t}\mathbf{V}\left(0\right).$$

(24)

That is, the volumes with initial points decline by a factor of e as time t passes. Equation (24) is $\mathbf{V}\left(t\right)\to 0$ when $t\to \infty$. The system’s limit settings are constrained to a single limit set with zero volume. Strange attractors are identified by the asymptotic motion of the fractional derivative satellite system (16), illustrating the dissipative nature of the satellite system (24). The phase portraits of the fractional-order chaotic satellite system form strange attractors, which are part of fractal geometry (fractal dynamics). Fractal dynamics exhibit self-similarity, meaning that, in some sense, the phase portraits of the chaotic system display symmetrical behavior. These phase portraits of the chaotic system are shown in Figure 1, Figure 2, Figure 3, Figure 4.

4. The Fractional Derivative Unpredicted Satellite System: Chaos Control

The fractional derivative highly nonlinear system in the form is written as

$${\displaystyle \frac{d^{{\alpha }_1}x}{d{t}^{{\alpha }_1}}}=f\left(x\right)+\mathbf{B}u,$$

(25)

where $x\in {\mathbf{R}}^n$ is a system’s state vector, $u\in {\mathbf{R}}^m$ is a system’s input vector, $f:{\mathbf{R}}^n\to {\mathbf{R}}^n$ is a nonlinear map from ${\mathbf{R}}^n$ to ${\mathbf{R}}^n$, and $\mathbf{B}\in {\mathbf{R}}^{n\times m}$ is a constant matrix. Assume $x^{*}\in {\mathbf{R}}^n$ is the controlled chaotic system’s equilibrium point. That means $f\left(x^{*}\right)=0$.

Remark 1.

The goal of this study is to determine and analyze the stability of $x^{*}$. For the sake of simplicity, we state all formulations and conclusions for the scenario where the equilibrium point of the controlled dynamic system (25) is at the origin of ${\mathbf{R}}^n$. That is, $x^{*}=0.$ By adjusting variables, it is possible to move every equilibrium point to the origin; hence, there is no loss of generality.

Remark 2.

Consider the change of variables $y=x-x^{*}$ and assume $x^{*}=0$ is an equilibrium point of the controlled chaotic system (25). Then, the y derivative is equal to

$${\displaystyle \frac{d^{{\alpha }_1}y}{d{t}^{{\alpha }_1}}}={\displaystyle \frac{d^{{\alpha }_1}{x}^{*}}{d{t}^{{\alpha }_1}}}=f\left(x\right)+\mathbf{B}u=f(y+x^{*})=s\left(y\right),$$

(26)

where $s\left(0\right)=0$. The system is in equilibrium at the origin with the new variable y. As a result, we will always assume that $f\left(x\right)$ fulfills $f\left(0\right)=0$ and analyze the stability of the origin $x=0$ without losing generality. Using Taylor series for the nonlinear function $f\left(x\right)$ of the system (25)

$$f\left(x\right)=f\left(0\right)+{\displaystyle \frac{\partial f\left(x\right)}{\partial x}}+h\left(x\right),$$

(27)

where $h\left(x\right)$ fulfills ${lim}_{\parallel x\parallel \to 0}{\displaystyle \frac{\parallel h\left(x\right)\parallel }{\parallel x\parallel }}=0.$

We notice that when $f\left(0\right)=0$ is substituted into the controlled chaotic system (25) and combined with (27), we get

$${\displaystyle \frac{d^{{\alpha }_1}x}{d{t}^{{\alpha }_1}}}=Ax+h\left(x\right)+Bu,$$

(28)

where $A={\displaystyle \frac{\partial f\left(x\right)}{\partial x}}$ at $x=0.$

4.1. Controllers with Linear State Feedback Technique

Theorem 1

([8]). "For the linearization of the dynamical system (28) of the controlled chaotic system (25), (A;B) is completely state controllable. Because P is a unique positive definite symmetry matrix, the control law of the linear state feedback is $u=-B^{T}P$. As a result, the controlled chaotic system (25) is asymptotically stable in origin: $PA+A^{T}P-PB{B}^{T}P+Q=0$ is the equation for Riccati algebra matrices, in which Q is an arbitrary positive definite matrix".

4.2. Controlling Chaotic Satellite Systems with Fractional Derivatives and Their Simulation

At the equilibrium point ${\aleph }_0=(0,0,0)$, the eigenvalues of the system (18) are

${\lambda }_{01}=-0.4+0.99\iota ,$${\lambda }_{02}=-0.4+0.99\iota ,\mathrm{and}$${\lambda }_{03}=0.175$, where $\iota as\sqrt{-1}$. Because one of the eigenvalues is positive, the original forms of the satellite system with the fractional order are unstable.

The mathematics of the after controllers provides the linear state feedback law of the unpredictable system:

$$\begin{array}{c}\hfill u=-{\mathbf{B}}^{T}P\left[\begin{array}{c}x\\ y\\ z\end{array}\right].\end{array}$$

(29)

At equilibrium points ${\aleph }_0$, ${\aleph }_1$, ${\aleph }_2$, ${\aleph }_3$, and ${\aleph }_4$, the corresponding positive definite symmetric matrices are denoted as

$$\begin{array}{c}\hfill p_0=\left[\begin{array}{ccc}0.0977& 0& 0.0160\\ 0& 0& 0\\ 0.0160& 0& 0.0350\end{array}\right];\end{array}\begin{array}{c}\hfill p_1=\left[\begin{array}{ccc}0.2803& 0.2246& 0.2132\\ 0.2246& 0.1799& -0.1708\\ -0.2132& -0.1708& 0.1622\end{array}\right];\end{array}$$

$$\begin{array}{c}\hfill p_2=\left[\begin{array}{ccc}0.0278& 0.0129& 0.0080\\ 0.0129& 0.0060& 0.0037\\ 0.0080& 0.0037& 0.0023\end{array}\right];\end{array}$$

$$\begin{array}{c}\hfill p_3=\left[\begin{array}{ccc}0.3607& -0.1673& 0.1040\\ -0.1673& 0.0776& -0.0482\\ 0.1040& -0.0482& 0.0300\end{array}\right];\end{array}\begin{array}{c}\hfill p_4=\left[\begin{array}{ccc}0.0068& -0.0070& -0.0214\\ -0.0070& 0.0349& 0.0220\\ -0.0214& 0.0220& 0.0673\end{array}\right].\end{array}$$

5. Synchronization of Identical Fractional Derivative Satellite Systems Using Active Control Methodologies

For the satellite system in Equation (16), two identical master (drive) and slave (response) systems are rebuilt in the form of x and y subscripts, respectively:

• Drive (master) system:

$$\begin{array}{c}{\displaystyle \frac{d^{{\alpha }_1}{x}_1\left(t\right)}{d{t}^{{\alpha }_1}}}={\displaystyle \frac{1}{3}}{x}_2\left(t\right)x_3\left(t\right)-a{x}_1\left(t\right)+{\displaystyle \frac{1}{\sqrt{6}}}{x}_3\left(t\right),\hfill \\ {\displaystyle \frac{d^{{\alpha }_1}{x}_1\left(t\right)}{d{t}^{{\alpha }_1}}}=-x_1\left(t\right)x_3\left(t\right)+b{x}_2\left(t\right),\hfill \\ {\displaystyle \frac{d^{{\alpha }_1}{x}_1\left(t\right)}{d{t}^{{\alpha }_1}}}=x_1\left(t\right)x_2\left(t\right)-\sqrt{6}{x}_1\left(t\right)-c{x}_3\left(t\right).\hfill \end{array}$$

(30)

Response (slave) system:

$$\begin{array}{c}{\displaystyle \frac{d^{{\alpha }_1}{y}_1\left(t\right)}{d{t}^{{\alpha }_1}}}={\displaystyle \frac{1}{3}}{y}_2\left(t\right)y_3\left(t\right)-a{y}_1\left(t\right)+{\displaystyle \frac{1}{\sqrt{6}}}{y}_3\left(t\right)+u_1\left(t\right),\hfill \\ {\displaystyle \frac{d^{{\alpha }_1}{y}_2\left(t\right)}{d{t}^{{\alpha }_1}}}=-y_1\left(t\right)y_3\left(t\right)+b{y}_2\left(t\right)+u_2\left(t\right),\hfill \\ {\displaystyle \frac{d^{{\alpha }_1}{y}_3\left(t\right)}{d{t}^{{\alpha }_1}}}=y_1\left(t\right)y_2\left(t\right)-\sqrt{6}{y}_1\left(t\right)-c{y}_3\left(t\right)+u_3\left(t\right),\hfill \end{array}$$

(31)

where the three controller torques are $u_1\left(t\right)$, $u_2\left(t\right)$, and $u_3\left(t\right)$. The synchronization of the error signal is defined as

$$\begin{array}{c}\hfill e_1\left(t\right)=y_1\left(t\right)-x_1\left(t\right),\\ \hfill e_2\left(t\right)=y_2\left(t\right)-x_2\left(t\right),\\ \hfill e_3\left(t\right)=y_3\left(t\right)-x_3\left(t\right).\end{array}$$

(32)

The error dynamics are written as

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d^{{\alpha }_1}{e}_1\left(t\right)}{d{t}^{{\alpha }_1}}}={\displaystyle \frac{d^{{\alpha }_1}{y}_1\left(t\right)}{d{t}^{{\alpha }_1}}}-{\displaystyle \frac{d^{{\alpha }_1}{x}_1\left(t\right)}{d{t}^{{\alpha }_1}}}\hfill \\ \hfill & ={\displaystyle \frac{1}{3}}(y_2\left(t\right)y_3\left(t\right)-x_2\left(t\right)x_3\left(t\right))-a(y_1\left(t\right)-x_1\left(t\right))+1/\sqrt{6}(y_3\left(t\right)-x_3\left(t\right))+u_1\left(t\right),\hfill \\ \hfill & {\displaystyle \frac{d^{{\alpha }_1}{e}_2\left(t\right)}{d{t}^{{\alpha }_1}}}={\displaystyle \frac{d^{{\alpha }_1}{y}_2\left(t\right)}{d{t}^{{\alpha }_1}}}-{\displaystyle \frac{d^{{\alpha }_1}{x}_2\left(t\right)}{d{t}^{{\alpha }_1}}}\hfill \\ & =(x_3\left(t\right)x_1\left(t\right)-y_3\left(t\right)y_1\left(t\right))+b(y_2\left(t\right)-x_2\left(t\right))+u_2\left(t\right),\hfill \\ \hfill & {\displaystyle \frac{d^{{\alpha }_1}{e}_3\left(t\right)}{d{t}^{{\alpha }_1}}}={\displaystyle \frac{d^{{\alpha }_1}{y}_3\left(t\right)}{d{t}^{{\alpha }_1}}}-{\displaystyle \frac{d^{{\alpha }_1}{x}_3\left(t\right)}{d{t}^{{\alpha }_1}}}\hfill \\ \hfill & =(y_1\left(t\right)y_2\left(t\right)-x_1\left(t\right)x_2\left(t\right))-\sqrt{6}(y_3\left(t\right)-x_3\left(t\right)-c(y_3\left(t\right)-x_3\left(t\right))+u_3\left(t\right).\hfill \end{array}$$

(33)

We define the active control function as

$$\begin{array}{c}\hfill u_1\left(t\right)=-{\displaystyle \frac{1}{3}}(y_2\left(t\right)y_3\left(t\right)-x_2\left(t\right)x_3\left(t\right))+{\displaystyle \frac{1}{\sqrt{6}}}{e}_3\left(t\right)+v_1\left(t\right),\\ \hfill u_2\left(t\right)=-(x_3\left(t\right)x_1\left(t\right)-y_2\left(t\right)y_3\left(t\right))+b{e}_2-e_2\left(t\right)+v_2\left(t\right),\\ \hfill u_1\left(t\right)=-(y_1\left(t\right)y_2\left(t\right)-x_1\left(t\right)x_2\left(t\right))+\sqrt{6}{e}_1\left(t\right)+v_3\left(t\right).\end{array}$$

(34)

The terms $v_i\left(t\right)$ are the linear function of the error terms $e_i\left(t\right),$$i=1,2,3.$ With the choice of $u_i\left(t\right)$ given by the previous equations, the error dynamics are written as

$$\begin{array}{c}\hfill {\displaystyle \frac{d^{{\alpha }_1}{e}_1\left(t\right)}{d{t}^{{\alpha }_1}}}=-a{e}_1\left(t\right)+v_1\left(t\right),\\ \hfill {\displaystyle \frac{d^{{\alpha }_1}{e}_2\left(t\right)}{d{t}^{{\alpha }_1}}}=-e_2\left(t\right)+v_2\left(t\right),\\ \hfill {\displaystyle \frac{d^{{\alpha }_1}{e}_3\left(t\right)}{d{t}^{{\alpha }_1}}}=-c{e}_3\left(t\right)+v_3\left(t\right).\end{array}$$

(35)

The control terms $v_i\left(t\right)$ are selected to stabilize the error system. For such functions, there is not a single option. We take

$$\begin{array}{c}\hfill \left[\begin{array}{c}{v}_1\left(t\right)\\ v_2\left(t\right)\\ v_3\left(t\right)\end{array}\right]=A\left[\begin{array}{c}{e}_1\left(t\right)\\ e_2\left(t\right)\\ e_3\left(t\right)\end{array}\right];A={\left[a_{ij}\right]}_{3x3}.\end{array}$$

(36)

The value of A is chosen so that the criterion $|arg\left({\lambda }_i\left(J\right)\right)|>{\alpha }_1{\displaystyle \frac{\pi }{2}}$ is satisfied for all eigenvalues ${\lambda }_i$ of the error system. At the equilibrium point of the error system, the Jacobi matrix of the above system is J. We take

$$\begin{array}{c}\hfill A=\left[\begin{array}{ccc}a-1& 0& 0\\ 0& 0& 0\\ 0& 0& c-1\end{array}\right].\end{array}$$

(37)

The eigenvalues of the linear error system are $-1,0,-1.$ According to the fractional derivative stability theory, the error $e_i\left(t\right),i=1,2,3$ will converge to zero when $t\to \infty .$ That is,

$$\underset{t\to \infty }{lim}e\left(t\right)=0.$$

This indicates that the slave and master systems are synchronized. The stability theory of fractional-order systems is thus used to create synchronization between fractional-order master and slave systems.

6. Numerical Simulation

Take $x\left(0\right)={(3.5,0.5,0.8)}^T$ and $y\left(0\right)={(2.5,1.5,0.3)}^T$ as the initial conditions for the fractional derivative master and slave satellite systems. The phase portraits and time series graphs of the satellite systems with different orders are illustrated in Figure 1, Figure 2, Figure 3. Table 1 provides the characteristics of satellite systems with fractional derivatives by analyzing the phase portrait diagrams and time series of the systems with different orders and parameter values. The two- and three-dimensional phase portraits of the fractional-order satellite system with order ${\alpha }_1=0.95$ are displayed in Figure 4.

Table 1. Fractional-order satellite systems phase portrait analysis versus parameters (${\alpha }_1;a;b;c$).

		Nature of the System
Figure 1a	${\alpha }_1\le 0.90;a=0.4;b=0.175;c=0.4$	Stable
Figure 1b	${\alpha }_1=0.91;a=0.4;b=0.175;c=0.4$	Stable
Figure 1c	${\alpha }_1=0.92;a=0.4;b=0.175;c=0.4$	Stable
Figure 1d	${\alpha }_1=0.93;a=0.4;b=0.175;c=0.4$	Stable
Figure 2a	${\alpha }_1=0.94;a=0.4;b=0.175;c=0.4$	Chaotic
Figure 2b	${\alpha }_1=0.95;a=0.4;b=0.175;c=0.4$	Quasi-Periodic
Figure 2c	${\alpha }_1=0.95;a=0.30;b=0.175;c=0.4$	Stable
Figure 2d	${\alpha }_1=0.95;a=0.35;b=0.175;c=0.4$	Periodic
Figure 3a	${\alpha }_1=0.95;a=0.4;b=0.100;c=0.4$	Chaotic
Figure 3b	${\alpha }_1=0.95;a=0.4;b=0.150;c=0.4$	Chaotic
Figure 3c	${\alpha }_1=0.95;a=0.4;b=0.175;c=0.10$	Quasi-Periodic
Figure 3d	${\alpha }_1=0.95;a=0.4;b=0.175;c=0.30$	Chaotic

Table 1. Fractional-order satellite systems phase portrait analysis versus parameters (${\alpha }_1;a;b;c$).

		Nature of the System
Figure 1a	${\alpha }_1\le 0.90;a=0.4;b=0.175;c=0.4$	Stable
Figure 1b	${\alpha }_1=0.91;a=0.4;b=0.175;c=0.4$	Stable
Figure 1c	${\alpha }_1=0.92;a=0.4;b=0.175;c=0.4$	Stable
Figure 1d	${\alpha }_1=0.93;a=0.4;b=0.175;c=0.4$	Stable
Figure 2a	${\alpha }_1=0.94;a=0.4;b=0.175;c=0.4$	Chaotic
Figure 2b	${\alpha }_1=0.95;a=0.4;b=0.175;c=0.4$	Quasi-Periodic
Figure 2c	${\alpha }_1=0.95;a=0.30;b=0.175;c=0.4$	Stable
Figure 2d	${\alpha }_1=0.95;a=0.35;b=0.175;c=0.4$	Periodic
Figure 3a	${\alpha }_1=0.95;a=0.4;b=0.100;c=0.4$	Chaotic
Figure 3b	${\alpha }_1=0.95;a=0.4;b=0.150;c=0.4$	Chaotic
Figure 3c	${\alpha }_1=0.95;a=0.4;b=0.175;c=0.10$	Quasi-Periodic
Figure 3d	${\alpha }_1=0.95;a=0.4;b=0.175;c=0.30$	Chaotic

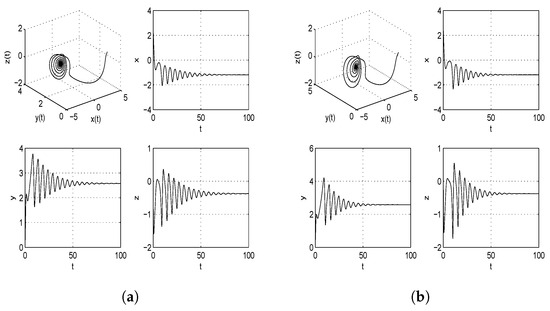
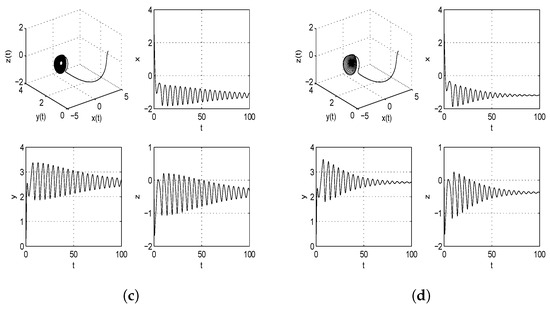
Figure 1. Three-dimensional phase portrait and time series graphs of chaotic satellite systems with different fractional orders (${\alpha }_1=0.90$, ${\alpha }_1=0.91$, ${\alpha }_1=0.92$, and ${\alpha }_1=0.93$) (without controller). Nature of systems are explained in Table 1.

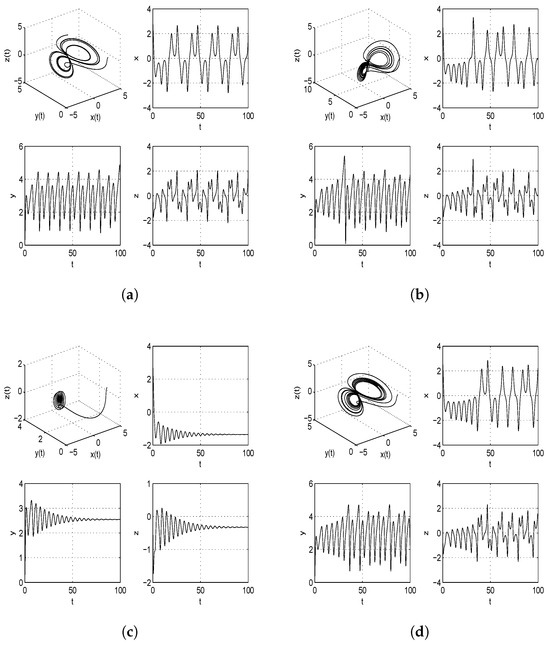
Figure 2. Three-dimensional phase portrait and time series graphs of chaotic satellite systems with different fractional orders (${\alpha }_1=0.94$ and ${\alpha }_1=0.95$) (without controller). Nature of systems are explained in Table 1.

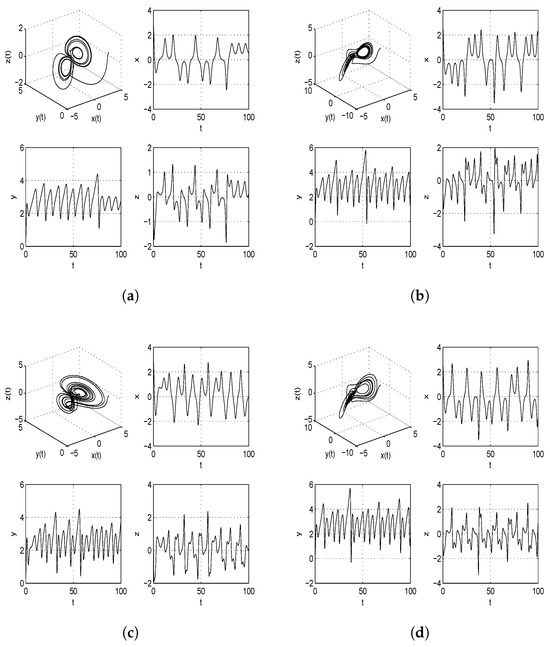
Figure 3. Three-dimensional phase portrait and time series graphs of chaotic satellite systems with different fractional order (${\alpha }_1=0.95$) (without controller). Nature of systems are explained in Table 1.

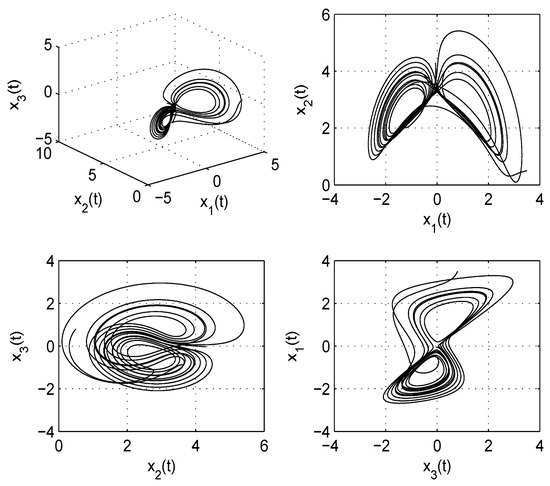
Figure 4. Three-dimensional and two-dimensional phase portraits of fractional order satellite system with ${\alpha }_1=0.95$. Nature of systems are explained in Table 1.

The bifurcation diagrams are plotted by varying the parameters. Let $a=[0.20-0.50],b=[0-0.20],\mathrm{and}c=[0.20-0.50]$. These bifurcation diagrams of the chaotic system, depending on changes in parameters a, b, and c, are displayed in Figure 5a–c. Figure 5a–c are plotted with parameters versus $F(x,y,z)$. At $t=200$, the Lyapunov exponents of the satellite system are computed, and the results are shown in Figure 6. Figure 7 also displays the feedback control of the fractional derivative chaotic satellite system when control is initiated at $t=20$. The tracking trajectories of the slave to master fractional derivative satellite system with order ${\alpha }_1=0.95$ are shown in Figure 8a–c for $x_1{y}_1$, $x_2{y}_2$, and $x_3{y}_3$, respectively.

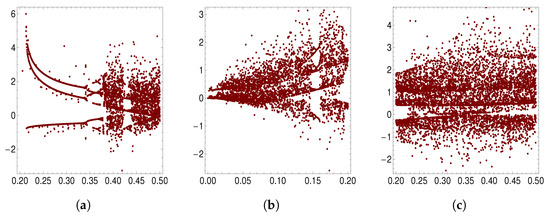
Figure 5. Bifurcation plotting with varying parameters a, b, and c, respectively.

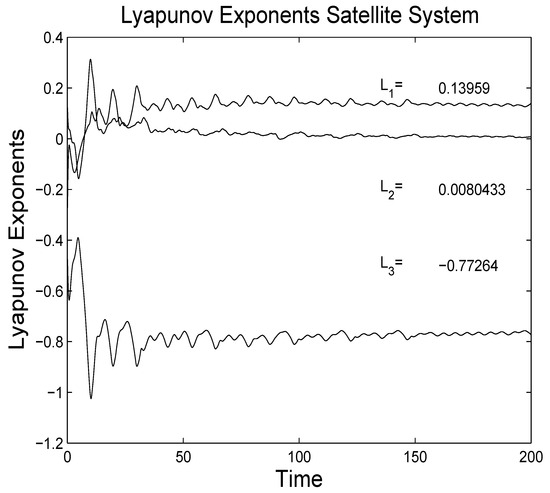
Figure 6. Lyapunov exponent values of the fractional-order chaotic satellite system.

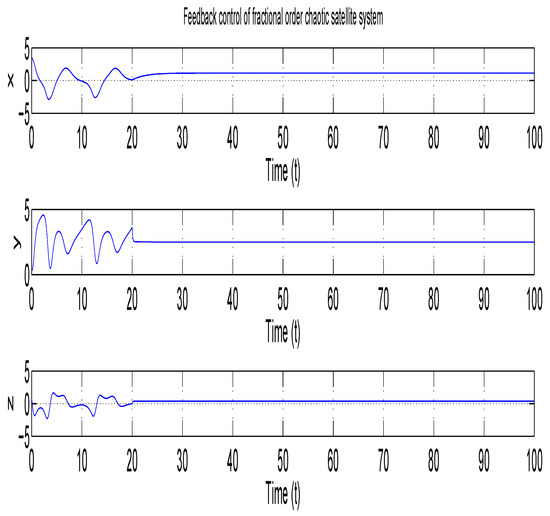
Figure 7. Feedback controllers of the fractional−order chaotic satellite system started at $t=20$ s.

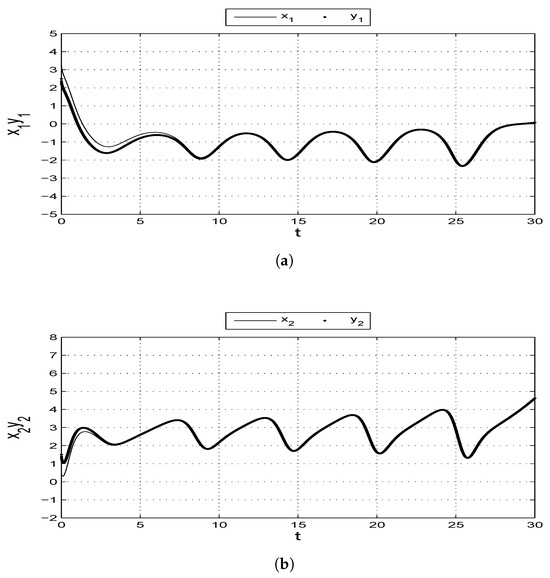
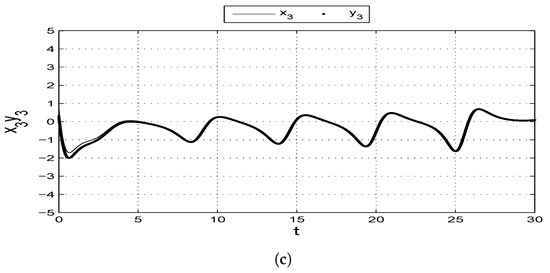
Figure 8. Tracking trajectories for the fractional-order master to salve satellite systems with order ${\alpha }_1=0.95$ (with controllers).

At the initial condition of the error system $e\left(0\right)=(-1.0,1.0,-0.5)$, Figure 9 illustrates the synchronization of the fractional derivative error dynamics, represented by the evolution of $e_1$, $e_2$, and $e_3$ with respect to time t. As time progresses, the figure reveals how the error terms between the master and slave satellite systems gradually diminish and approach zero, signaling that the synchronization process is effectively taking place. The distinct trajectories of $e_1$, $e_2$, and $e_3$ highlight the convergence behavior and the stabilization of the system’s chaotic dynamics through the applied control methodology.

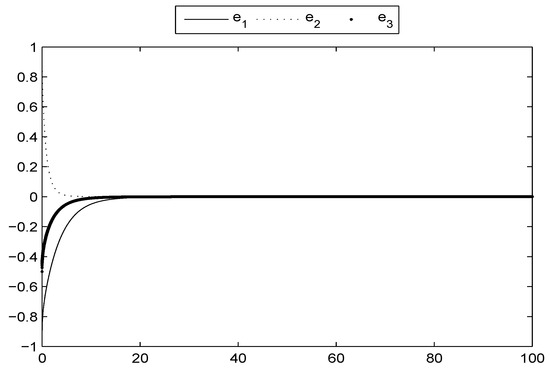
Figure 9. Stabilization of fractional error dynamics (with controllers).

This synchronization is not only an indication of the success of the control strategy but also demonstrates the robustness of the system in achieving alignment between the master and slave states. The initial discrepancies in the error terms, starting from $e\left(0\right)=(-1.0,1.0,-0.5)$, progressively reduce, reflecting the efficiency of the feedback control mechanism in handling the chaotic fractional-order system. This reduction in error across all three dimensions $e_1$, $e_2$, and $e_3$, as depicted in the figure, ensures that the chaotic oscillations are stabilized, and the dynamics are synchronized over time. The figure underscores the importance of synchronization in controlling chaos within fractional-order satellite systems. Achieving such synchronization is essential in practical applications like satellite navigation, where precise coordination between systems is required. That is, ${lim}_{t\to \infty }e\left(t\right)=0.$

7. Conclusions

In our research paper, we focused on solving fractional-order dynamical systems and established the fundamentals of the concept of fractional dynamics. We analyzed the chaotic behavior of specific fractional-order satellite systems by examining their equilibrium points. Techniques such as dissipativity, bifurcation diagrams, Lyapunov exponents, and phase portrait analysis were used to study this behavior across various parameters. To confirm the chaotic nature, we determined the equilibrium points and calculated the eigenvalues of the Jacobian matrix at these points. Additionally, we implemented a feedback control approach for a novel fractional-order satellite system and successfully synchronized two identical fractional-order satellite systems using an active control methodology. These results were validated through the synchronization of the fractional-order systems. Our findings contribute to advancements in secure telecommunications, data security, radar detection, weather forecasting, GPS systems, and Earth observation. Future research will aim to enhance the efficiency of synchronization algorithms for real-time applications, examine the influence of varying fractional orders on system dynamics, and explore broader applications in areas such as secure communication systems, GPS technology, and space exploration. These efforts will further extend the practical use of feedback active control techniques in complex, real-world chaotic systems.