Cycle Embedding in Enhanced Hypercubes with Faulty Vertices

Abstract

The enhanced hypercube is a well-known variant of the hypercube and can be constructed from a hypercube by adding an edge to every pair of vertices with complementary addresses. Let $F_v$ denote the set of faulty vertices in an n-dimensional enhanced hypercube $Q_{n,k}(1\le k\le n-1)$. In this paper, we conclude that if $n\ge 2$, then every fault-free edge of $Q_{n,k}-F_v$ lies on a fault-free cycle of every even length from 4 to $2^n-2\left|F_v\right|$, and if $n(\ge 2)$ and k have the different parity, then every fault-free edge of $Q_{n,k}-F_v$ lies on a fault-free cycle of every possible odd length from $n-k+4$ to $2^n-2\left|F_v\right|-1$, where $|F_v|\le n-2$.

1. Introduction

The well-known hypercue has several excellent properties, such as recursive structure, regularity, symmetry, small diameter, low degree, and logarithmic diameter [1]. One variant of the hypercube that has been the focus of a great deal of research is the enhanced hypercube $Q_{n,k}$ [2,3], which can be obtained from the well-known n-dimensional hypercube $Q_n$ by adding each edge from the vertex $x_1{x}_2\cdots x_{k-1}{x}_k\cdots x_n$ to the vertex $x_1{x}_2\cdots x_{k-1}{\overline{x}}_k\cdots {\overline{x}}_n$. The n-dimensional enhanced hypercube $Q_{n,k}(1\le k\le n-1)$ is proposed to improve the efficiency of the hypercube structure $Q_n$, as it possesses many attractive properties that are superior to that of the hypercube [4,5,6,7,8,9,10,11]. Moreover, the folded hypercube $F{Q}_n$ is the special case of the enhanced hypercube $Q_{n,k}$ when $k=1$ [12,13,14,15,16,17,18,19,20,21].

In computer network topology design, one of the central issues in evaluating a network is to study the network embedding problem. The embedding of one guest graph $G_1$ into another host graph $G_2$ is a one-to-one mapping m from the vertex set of $G_1$ to the vertex set $G_2$ [1]. Recently, the multiprocessor system is becoming prevalent and significant. Using the fault-tolerant embedding properties to evaluate the reliability of a parallel computing system is a significant issue. Therefore, many research fields and topics focus on the reliability analysis problems regarding the fault-tolerant embedding of distributed networks [19].

The concept of ISTs was first introduced by Itai and Rodeh [22]. At a later time, a large number of researchers were attracted by the problems regarding the reliability of parallel and distributed networks. The construction of ISTs is obtained to receive high levels of fault-tolerant properties and security. To pursue the above goals, one is to design an efficient construction or investigate the fault-tolerant embedding properties. Note that the class of enhanced hypercube is a general case of the folded hypercube. The enhanced hypercubes have attracted much attention, e.g., the diagnosability, embedding, and others. Fault-tolerant cycle embedding with respect to vertex is related to investigating the property of a more cost-effective constructure.

Problems regarding the fault-tolerant embedding for hypercubes and folded hypercubes have been studied in [14,15,23,24]. Let $F_v$ and $F_e$ be the sets of faulty vertices and faulty edges, respectively. Tsai [25] proved that every fault-free edge of $Q_n-F_v$ lies on a fault-free cycle of every even length from 4 to $2^n-2\left|F_v\right|$ inclusive, where $|F_v|\le n-2$. Furthermore, Hsieh and Shen [26] extended the above result to show that every fault-free edge of $Q_n-F_e-F_v$ lies on a fault-free cycle of every even length from 4 to $2^n-2\left|F_v\right|$, where $|F_v|+|F_e|\le n-2$ and $n\ge 3$. Xu et al. [21] showed that every fault-free edge of $F{Q}_n-F_e$ lies on a fault-free cycle of every even length from 4 to $2^n$ and also lies on a fault-free cycle of every odd length from $n+1$ to $2^n-1$ if n is even, where $|F_e|\le n-1$. Cheng et al. [13] proved that every fault-free edge of $F{Q}_n-F_v$ lies on a fault-free cycle of every even length from 4 to $2^n-2\left|F_v\right|$ if $n\ge 3$, and also lies on a fault-free cycle of every odd length from $n+1$ to $2^n-2\left|F_v\right|-1$ if n is even and $n\ge 2$, where $|F_v|\le n-2$. After that, Kuo and Stewart [16] further proved that every fault-free edge of $F{Q}_n-F_v-F_e$ lies on a fault-free cycle of every even length from 4 to $2^n-2\left|F_v\right|$ if $n\ge 3$, and also lies on a fault-free cycle of every odd length from $n+1$ to $2^n-2\left|F_v\right|-1$ if $n\ge 2$ is even, where $|F_v|+|F_e|\le n-2$. Due to the above motivations, in this paper, we consider the faulty enhanced hypercube $Q_{n,k}(1\le k\le n-1)$ with $|F_v|\le n-2$, where $F_v$ denotes the set of faulty vertices of $Q_{n,k}(1\le k\le n-1)$, proving that every fault-free edge of $Q_{n,k}-F_v$ lies on a fault-free cycle of every even length from 4 to $2^n-2\left|F_v\right|$ if $n\ge 2$, and every fault-free edge of $Q_{n,k}-F_v$ lies on a fault-free cycle of every possible odd length from $n-k+2$ to $2^n-2\left|F_v\right|-1$ if $n(\ge 2)$ and k have different parity.

The remainder of this paper is organized as follows. In Section 2, we introduce some basic definitions and lemmas used in our discussion. We give the main results related to even cycles and odd cycles embedding in the faulty enhanced hypercube in Section 3 and Section 4 respectively. Finally, we conclude this paper in Section 5.

2. Preliminaries

For the graph theoretical terminology and notations not mentioned here, see [27]. A graph $G=(V,E)$ is an ordered pair in which V is a finite set and E is a subset of $\left\{\right(u,v\left)\right|(u,v)$ is an unordered pair of $V\}$. We call V as the vertex set and E as the edge set. For a set of edges or vertices S in G, the graph $G-S$ is a subgraph of G by deleting all elements in S from G. Two vertices u and v are adjacent if $(u,v)\in E$. A path, represented as $P[v_0,v_m]=⟨v_0,v_1,v_2,\cdots ,v_m⟩$, is a sequence of distinct vertices in which any two consecutive vertices are adjacent. We call $v_0$ and $v_m$ the end-vertices of the path $P[v_0,v_m]$. A path $P[v_0,v_m]$ forms a cycle if $v_0=v_m$ and $m\ge 3$. The length of a path P (respectively, a cycle C) is denoted by $l\left(P\right)$ (respectively, $l\left(C\right)$). Let $F_v$ and $F_e$ be the sets of faulty vertices and faulty edges in G, where $F_v\subseteq V\left(G\right)$, $F_e\subseteq E\left(G\right)$. A vertex v is fault-free if $v\in F_v$. An edge $e\in E\left(G\right)$ is fault-free if the two end-vertices and the edge between them are not faulty, i.e., $e\in F_e$. A path (respectively, a cycle) is fault-free if it contains no faulty edges.

The n-dimensional hypercube, denoted by $Q_n$, is a graph with $2^n$ vertices which are labeled as binary strings of length n from $\underset{n}{\underbrace{00\cdots 0}}$ to $\underset{n}{\underbrace{11\cdots 1}}$. Two vertices u and v in $Q_n$ are linked by an edge if and only if u and v differ exactly on one bit position. For convenience, we define the vertex $u=x_1{x}_2\cdots x_{i-1}{x}_i{x}_{i+1}\cdots x_n$ and the vertex $u^i=x_1{x}_2\cdots x_{i-1}\overline{x_i}{x}_{i+1}\cdots x_n$, where $\overline{x_i}$ is the complement of $x_i$, i.e., $\overline{x_i}=1-x_i$ for some $1\le i\le n$ and $x_i\in \{0,1\}$. In other words, u and $u^i$ have the different binary strings exactly on the ith position. We call the edge $(u,u^i)$ as an ith dimension edge which is along dimension i. Let $E_i$ be the set of ith dimensional edges. Clearly, $|E\left(Q_n\right)|=n·2^{n-1}$. For a given integer i$(1\le i\le n)$, partition $Q_n$ along dimension i into two $(n-1)$-dimensional cubes, then $Q_{n-1}^{i0}$ (respectively, $Q_{n-1}^{i1}$) denotes the subgraph of $Q_n$ induced by $x_1{x}_2\cdots x_{i-1}0x_{i+1}\cdots x_n$ (respectively, $x_1{x}_2\cdots x_{i-1}1x_{i+1}\cdots x_n$), where $x_j\in \{0,1\}$, $1\le j\le n$ $j\ne i$. Obviously, we have $Q_{n-1}^{i0}$ and $Q_{n-1}^{i0}$ being isomorphic to $Q_n$.

A graph G is bipartite if the vertex set V can be divided into two disjoint partite subsets $V_0$ and $V_1$ such that each edge in G connects one end-vertex in $V_0$ and another in $V_1$. A bipartite graph $G=(V_0\cup V_1,E)$ is hyper-Hamiltonian laceable if for any vertex $v\in V_i$, $i=0,1$, there exists a Hamiltonian path of $G-\left\{v\right\}$ between any two vertices in $V_{1-i}$.

The distance between u and v denoted by $d_G(u,v)$ is the length of the shortest path between u and v in G. The Hamming distance between two vertices $u=x_1{x}_2\cdots x_n$ and $v=y_1{y}_2\cdots y_n$ in $Q_n$ is denoted by $d_H(u,v)={\sum }_{i=1}^n|x_i-y_i|$, where $x_i\in \{0,1\}$ and $y_i\in \{0,1\}$. The Hamming weight of the vertex $u=x_1{x}_2\cdots x_n$, denoted by $hw\left(u\right)$, is the number of i’s such that $x_i=1$. We can use $hw\left(u\right)$ to check the parity of the vertex u, i.e., u is an even vertex (respectively, an odd vertex) if $hw\left(u\right)$ is even (respectively, $hw\left(u\right)$ is odd). Note that $Q_n$ is a bipartite graph with two disjoint partite subsets $\left\{u\right|hw\left(u\right)$ is odd} and $\left\{u\right|hw\left(u\right)$ is even}. Clearly, $d_{Q_n}(u,v)=d_H(u,v)$, $E_i=\left\{(u,u^i)\right|d_H(u,u^i)=1,i\in \{1,2,\cdots ,n\}\}$.

Definition 1.

Ref. [2] Enhanced hypercube $Q_{n,k}(1\le k\le n-1)$ is an undirected simple graph. Its vertex set is $V\left(Q_{n,k}\right)=\{x_1{x}_2\cdots x_n:x_i=0\mathrm{or}1,$ $1\le i\le n\}$. Its edge set is $E\left(Q_{n,k}\right)=\left\{(x,y)\right\}$; for clarity, $x=x_1{x}_2\cdots x_n$, $x_i\in \{0,1\}$, and y satisfies one of the following two conditions: $\left(1\right)$ $y=x_1{x}_2\cdots x_{i-1}{\overline{x}}_i{x}_{i+1}\cdots x_n$, $1\le i\le n$ or $\left(2\right)$ $y=x_1{x}_2\cdots x_{k-1}{\overline{x}}_k{\overline{x}}_{k+1}\cdots {\overline{x}}_n$.

One can observe that the enhanced hypercube $Q_{n,k}(1\le k\le n-1)$ is obtained from the well known hypercube by adding the edges in the set $\left\{\right(x_1{x}_2\cdots x_n,x_1{x}_2\cdots x_{k-1}$ ${\overline{x}}_k{\overline{x}}_{k+1}\cdots$ ${\overline{x}}_n),\forall k,1\le k\le n-1\}$, which is called the set of complementary edges, denoted by $E_c=\{(u,\overline{u})\in E\left(Q_{n,k}\right)|d_H(u,\overline{u})=n-k+1,u=x_1{x}_2\cdots x_n,\overline{u}=x_1{x}_2\cdots x_{k-1}{\overline{x}}_k$ ${\overline{x}}_{k+1}\cdots {\overline{x}}_n\}$. As mentioned above, $|V\left(Q_{n,k}\right)|=2^n$ and $|E\left(Q_{n,k}\right)|=(n+1)2^{n-1}$. We can define the edge set of $Q_{n,k}$ as $E\left(Q_{n,k}\right)=E\left(Q_n\right)\cup E_c=\left\{(u,v)\right|d_H(u,v)=1,(u,v)\in E\left(Q_n\right)\}\cup \left\{(u,v)\right|d_H(u,v)=n-k+1,(u,v)\in E_c\}$. Note that $Q_{n,k}(1\le k\le n-1)$ is $(n+1)$-regular, vertex-transitive, but not edge-transitive [3]. For three-dimensional enhanced hypercubes $Q_{3,1}$ and $Q_{3,2}$, see Figure 1.

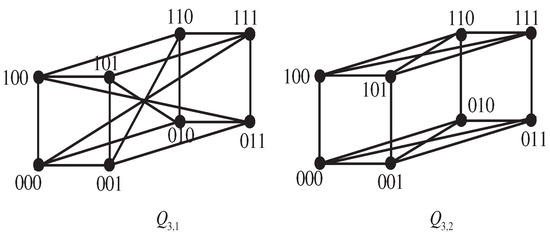
Figure 1. Illustrations of $Q_{3,1}$ and $Q_{3,2}$.

Definition 2.

Ref. [6] An i-partition on $Q_{n,k}(1\le k\le n-1)$, where $1\le i\le n$, is a partition of $Q_{n,k}(1\le k\le n-1)$ along dimension i into two $(n-1)$-dimensional cubes.

For $k\le i\le n$, $1\le k\le n-1$, $Q_{n,k}(1\le k\le n-1)$ can be partitioned into two $(n-1)$-dimensional hypercubes, we call $Q_{n-1}^{i0}$(respectively, $Q_{n-1}^{i1}$) as the subgraph of $Q_{n,k}$ induced by $x_1{x}_2\cdots x_k\cdots x_{i-1}0x_{i+1}\cdots x_n$(respectively, $x_1{x}_2\cdots x_k\cdots x_{i-1}1x_{i+1}\cdots x_n$). And all the edges in $E_c$ are between $Q_{n-1}^{i0}$ and $Q_{n-1}^{i1}$, i.e., $E\left(Q_{n,k}\right)=E\left(Q_{n-1}^{i0}\right)\cup E\left(Q_{n-1}^{i1}\right)\cup E_c\cup E_i$.

For $1\le i\le k-1$, $2\le k\le n-1$, $Q_{n,k}(1\le k\le n-1)$ can be partitioned into two $(n-1)$-dimensional enhanced hypercubes, we call $Q_{n-1,k-1}^{i0}$(respectively, $Q_{n-1,k-1}^{i1}$) as the subgraph of $Q_{n,k}$ induced by $x_1{x}_2\cdots x_{i-1}0x_{i+1}\cdots x_k\cdots x_n$(respectively, $x_1{x}_2\cdots x_{i-1}1x_{i+1}\cdots x_k\cdots x_n$). And we have $E\left(Q_{n,k}\right)=E\left(Q_{n-1,k-1}^{i0}\right)\cup E\left(Q_{n-1,k-1}^{i1}\right)\cup E_i$.

Lemma 1.

Ref. [8] For any positive integers $i,$ $j\in \{1,2,\dots ,n,c\}$, an automorphism σ of $Q_{n,k}(1\le k\le n-1)$ is denoted as $\sigma \left(E_i\right)=E_j$. Moreover, if $i\in \{k,$ $k+1,$ $k+2,$ $\cdots ,n\}$, it follows that $Q_{n,k}-E_i=Q_{n-1}^{i0}\cup Q_{n-1}^{i1}\cup E_c$ is isomorphic to $Q_n$(represented as $Q_{n,k}-E_i\cong Q_n$, $k\le i\le n$). Particularly, if $i=c$, $Q_{n,k}-E_c\cong Q_n$. However, if $i\in \{1,2,\cdots k-1\}$, it implies that $Q_{n,k}-E_i=Q_{n-1,k-1}^{i0}\cup Q_{n-1,k-1}^{i1}$ is a disconnected graph.

Let $F_v$ and $F_e$ denote the sets of faulty vertices and faulty edges, respectively.

Lemma 2.

Ref. [25] Let $Q_n(n\ge 3)$ be with $|F_v|\le n-2$, every fault-free edge of $Q_n-F_v$ lies on a fault-free cycle, whose length is of every even length from 4 to $2^n-2\left|F_v\right|$ inclusive.

Lemma 3.

Ref. [28] Assume that u and v are any two distinct vertices in $Q_n(n\ge 2)$. Thus, there exists a path of length l joining u and v with $d_H(u,v)\le l\le 2^n-1$ and $2\left|\right(l-d_H(u,v))$.

Lemma 4.

Ref. [29] Let $Q_n$ be with $n\ge 2$ and $|F_v|\le n-2$. Assume that u and v are any two distinct fault-free vertices in $Q_n$. Thus, $Q_n-F_v$ contains a fault-free path joining u and v, whose length l satisfies that $d_H(u,v)+2\le l\le 2^n-2\left|F_v\right|-1$ and $2\left|\right(l-d_H(u,v))$.

Lemma 5.

Ref. [30] Let X and Y be any two partite subsets of $Q_n(n\ge 2)$. Assume x and u are two distinct vertices of X, and y and v are two distinct vertices of Y. Then there exist two vertex-disjoint paths $P_1$ and $P_2$ such that $P_1$ connects x and y, $P_2$ connects u and v. Moreover, $P_1[x,y]$ and $P_2[u,v]$ spanning $V\left(Q_n\right)$, i.e., $V\left(P_1[x,y]\right)\cup V\left(P_2[u,v]\right)=V\left(Q_n\right)$.

Lemma 6.

Ref. [31] Let $Q_n(n\ge 3)$ be with $|F_e|\le n-3$. Then $Q_n-F_e$ is hyper-Hamiltonian-laceable.

3. Even Cycles Embedding in ${\mathit{Q}}_{\mathit{n},\mathit{k}}$ with $|{\mathit{F}}_{\mathit{v}}|\le \mathit{n}-\mathit{2}$

Theorem 1.

Let $Q_{n,k}(1\le k\le n-1)$ be with $|F_v|\le n-2$, $n\ge 2$. Then every fault-free edge of $Q_{n,k}-F_v$ lies on a fault-free cycle of every even length from 4 to $2^n-2\left|F_v\right|$.

Proof. 

Applying Definition 1, it follows that $E\left(Q_{n,k}\right)=E\left(Q_n\right)\cup E_c$, and $V\left(Q_{n,k}\right)=V\left(Q_n\right)$. Let $e\in E\left(Q_{n,k}\right)$ be an arbitrary fault-free edge. In $Q_{2,1}$, since $|F_v|=0$, two 4-cycles, $(00,01,11,10,00)$ and $(00,11,10,01,00)$, contain all the edges of $Q_{n,k}$; i.e., every edge of $Q_{2,1}$ lies on a fault-free cycle of length 4. Now we consider the case $n\ge 3$. We have the following two subcases according to the distributions of the fault-free edge e.

Case 1: $e\in E\left(Q_n\right)$.

Lemma 2 ensures that the theorem holds.

Case 2: $e\in E_c$.

For any arbitrary edge $e^{\prime }\in E\left(Q_n\right)$, applying Lemma 1, we know that there exists an automorphism $\sigma \in Aut\left(Q_{n,k}\right)$ such that $\sigma \left(e^{\prime }\right)=e$. Since $e=\sigma \left(e^{\prime }\right)\in E\left(\sigma \left(Q_n\right)\right)$, and $\sigma \left(Q_n\right)$ is isomorphic to $Q_n$, it implies that $V\left(\sigma \left(Q_n\right)\right)=V\left(Q_n\right)=V\left(Q_{n,k}\right)$. Note that e is a fault-free edge, so it implies that $e\in E(\sigma \left(Q_n\right)-F_v)$. Lemma 2 indicates that $e\in E(\sigma \left(Q_n\right)-F_v)$ lies on a fault-free cycle of every even length from 4 to $2^n-2\left|F_v\right|$.

In summary, all cases have been concerned, so the proof is completed. □

4. Odd Cycles Embedding in ${\mathit{Q}}_{\mathit{n},\mathit{k}}$ with $|{\mathit{F}}_{\mathit{v}}|\le \mathit{n}-\mathbf{2}$

In this section, let $F_v$ denote the set of faulty vertices in $Q_{n,k}(1\le k\le n-1)$. We will prove that every fault-free edge of $Q_{n,k}-F_v$ lies on a fault-free cycle of every possible odd length from $n-k+4$ to $2^n-2\left|F_v\right|-1$ if $|F_v|\le n-2$ and $n(\ge 2),k$ have different parity. We first give three useful lemmas as follows.

Lemma 7.

Partition $Q_{n,k}(1\le k\le n-1,n\ge 3)$ along dimension n into two $(n-1)$-dimensional hypercubes $Q_{n-1}^{n0}$ and $Q_{n-1}^{n1}$ by Definition 2. Let $(u,v)$ be a jth dimensional edge in $Q_{n,k}$ such that $(u,v)\in E\left(Q_{n-1}^{n0}\right)$ and $\{\overline{u},u^n,\overline{v},v^n\}\subseteq V\left(Q_{n-1}^{n1}\right)$, where $1\le j\le n-1$. Then, for $1\le j\le k-1$, $2\le k\le n-1$, we have $d_H(\overline{u},v^n)=n-k+1$ and $d_H(u^n,\overline{v})=n-k+1$; for $k\le j\le n-1$, $1\le k\le n-1$, we have $d_H(\overline{u},v^n)=n-k-1$ and $d_H(u^n,\overline{v})=n-k-1$.

Proof. 

Assume $(u,v)$ is an arbitrary jth dimensional edge in $E\left(Q_{n-1}^{n0}\right)$. Note that $Q_{n,k}$ is partitioned along dimension n. Obviously, $\{\overline{u},u^n,\overline{v},v^n\}\subseteq V\left(Q_{n-1}^{n1}\right)$. We check two possible situations regarding dimensions of the selected edge $(u,v)$.

(i)

For $1\le j\le k-1$, $2\le k\le n-1$. We can denote the two vertices in $V\left(Q_{n-1}^{n0}\right)$ by the binary strings as $u=x_1{x}_2\cdots x_{j-1}{x}_j{x}_{j+1}\cdots x_{k-1}{x}_k{x}_{k+1}\cdots x_{n-1}0$ and $v=x_1{x}_2\cdots x_{j-1}{\overline{x}}_j{x}_{j+1}\cdots x_{k-1}{x}_k$ $x_{k+1}\cdots x_{n-1}0$. By the definition and connection of the binary strings of two vertices, we have $\overline{u}=x_1{x}_2\cdots x_{j-1}{x}_j{x}_{j+1}$ ...$x_{k-1}{\overline{x}}_k{\overline{x}}_{k+1}\cdots {\overline{x}}_{n-1}1$ and $v^n=x_1{x}_2\cdots x_{j-1}{\overline{x}}_j{x}_{j+1}\cdots x_{k-1}{x}_k{x}_{k+1}\cdots$ $x_{n-1}1$. Accordingly, by the calculating of the numbers of the different bits in the binary bits of the two selected vertices, we can conclude that $d_H(\overline{u},v^n)=(n-k+1)-1+1=n-k+1$. As an immediate result, we have $d_H(u^n,\overline{v})=(n-k+1)-1+1=n-k+1$.

(ii)

For $k\le j\le n-1$, $1\le k\le n-1$. We can denote the two vertices in $V\left(Q_{n-1}^{n0}\right)$ by the binary strings as $u=x_1{x}_2\cdots x_{k-1}{x}_k{x}_{k+1}\cdots x_{j-1}{x}_j{x}_{j+1}\cdots x_{n-1}0$ and $v=x_1{x}_2\cdots x_{k-1}{x}_k{x}_{k+1}\cdots x_{j-1}{\overline{x}}_j$ $x_{j+1}\cdots x_{n-1}0$. By the definition and connection of the binary strings of two vertices, we have $\overline{u}=x_1{x}_2\cdots$ $x_{k-1}{\overline{x}}_k{\overline{x}}_{k+1}$ $\cdots {\overline{x}}_{j-1}{\overline{x}}_j{\overline{x}}_{j+1}\cdots {\overline{x}}_{n-1}1$ and $v^n=x_1{x}_2\cdots x_{k-1}{x}_k{x}_{k+1}\cdots x_{j-1}{\overline{x}}_j{x}_{j+1}\cdots$ $x_{n-1}1$. Similarly as above, it follows that $d_H(\overline{u},v^n)=(n-k+1)-2=n-k-1$ and $d_H(u^n,\overline{v})=(n-k+1)-2=n-k-1$.

In summary, for any $u\in V\left(Q_{n-1}^{n0}\right)$, there exist $n-1$ distinct vertices v’s in $V\left(Q_{n-1}^{n0}\right)$, such that $d_H(u^n,\overline{v})=n-k-1$ or $d_H(u^n,\overline{v})=n-k+1$ (respectively, $d_H(\overline{u},v^n)=n-k-1$ or $d_H(\overline{u},v^n)=n-k+1$). □

Lemma 8.

Partition $Q_{n,k}(1\le k\le n-1,n\ge 4)$ along dimension n into two $(n-1)$-dimensional hypercubes $Q_{n-1}^{n0}$ and $Q_{n-1}^{n1}$ by Definition 2. Assume $(u,v)$ is an ith dimensional edge in $Q_{n-1}^{n0}$, where $1\le i\le n-1$. Then we can select $n-2$ distinct w’s in $Q_{n-1}^{n0}$ such that $w\ne v$, and the edges $(\overline{u},w^n)$ and $(u^n,\overline{w})$ are both the jth dimension edges in $Q_{n,k}$ and $\{(\overline{u},w^n),(u^n,\overline{w})\}\subseteq E\left(Q_{n-1}^{n1}\right)$; i.e., $d_H(\overline{u},w^n)=1$ and $d_H(u^n,\overline{w})=1$, where $1\le i\le n-1$, $1\le j\le n-1$ and $j\ne i$.

Proof. 

Let $(u,v)$ be an arbitrary ith dimensional edge in $E\left(Q_{n-1}^{n0}\right)$. We distinguish two possible situations regarding dimensions of the selected edge $(u,v)$ as follows:

When $1\le i\le k-1$, $2\le k\le n-1$, we can select $(n-2)$w’s in $V\left(Q_{n-1}^{n0}\right)$ such that $\{(u^n,\overline{w}),(\overline{u},w^n)\}\subseteq E\left(Q_{n-1}^{n1}\right)$ are both the jth dimensional edges, $1\le j\le n-1$, $j\ne i$. We distinguish the following two subcases:

• For $1\le i\le k-1$, we can select $(k-2)$ distinct w’s in $Q_{n-1}^{n0}$ such that $(u^n,\overline{w})$ and $(\overline{u},w^n)$ are both the jth dimensional edges in $Q_{n-1}^{n1}$, i.e., $1\le j\le k-1$, and $j\ne i$. For clarity, let $u=x_1{x}_2\cdots x_i\cdots x_j\cdots x_k\cdots x_{n-1}0$ and $v=x_1{x}_2\cdots {\overline{x}}_i\cdots x_j\cdots x_k\cdots x_{n-1}0$ be two vertices in $Q_{n-1}^{n0}$. Thus $(u,v)\in E\left(Q_{n-1}^{n0}\right)$ is an ith dimensional edge. We can select a vertex $w=x_1{x}_2\cdots x_i\cdots x_{j-1}{\overline{x}}_j{x}_{j+1}\cdots x_{k-1}{\overline{x}}_k\cdots {\overline{x}}_{n-1}0$, $1\le j\le k-1$ and $j\ne i$. It implies that $d_H(u,w)=n-k+1$ and $d_H(v,w)=n-k+2$. It follows that the vertices $\{u^n,\overline{w},w^n,\overline{w}\}\subseteq V\left(Q_{n-1}^{n1}\right)$ can be denoted as $u^n=x_1\cdots x_i\cdots x_j\cdots x_k\cdots x_{n-1}1$, $\overline{w}=x_1{x}_2\cdots x_i\cdots x_{j-1}{\overline{x}}_j{x}_{j+1}\cdots x_k\cdots x_{n-1}1$, $\overline{u}=x_1\cdots x_i\cdots x_j\cdots x_{k-1}{\overline{x}}_k\cdots {\overline{x}}_{n-1}1$, and $w^n=x_1\cdots x_i\cdots x_{j-1}{\overline{x}}_j{x}_{j+1}$ $\cdots x_{k-1}{\overline{x}}_k$ $\cdots {\overline{x}}_{n-1}1$. As an immediate result, we have $d_H(u^n,\overline{w})=1$ and $d_H(\overline{u},w^n)=1$.
• For $1\le i\le k-1$, we can select $(n-k)$ distinct w’s in $Q_{n-1}^{n0}$ such that $(u^n,\overline{w})$ and $(\overline{u},w^n)$ are both the jth dimensional edges in $Q_{n-1}^{n1}$, i.e., $k\le j\le n-1$. For clarity, let $u=x_1{x}_2\cdots x_i\cdots x_k\cdots x_j\cdots$ $x_{n-1}0$ and $v=x_1{x}_2\cdots x_{i-1}{\overline{x}}_i{x}_{i+1}\cdots x_k\cdots x_j\cdots x_{n-1}0$ be two vertices in $Q_{n-1}^{n0}$. Thus, $(u,v)\in E\left(Q_{n-1}^{n0}\right)$ is an ith dimensional edge. We can select a vertex $w=x_1{x}_2\cdots x_i\cdots x_{k-1}{\overline{x}}_k\cdots {\overline{x}}_{j-1}{x}_j{\overline{x}}_{j+1}$ $\cdots {\overline{x}}_{n-1}0$, $k\le j\le n-1$. It implies that $d_H(u,w)=n-k-1$ and $d_H(v,w)=n-k$. Subsequently, we have $d_H(u^n,\overline{w})=1$ and $d_H(\overline{u},w^n)=1$.

When $k\le i\le n-1$, $1\le k\le n-1$, we can select $(n-2)$w’s in $V\left(Q_{n-1}^{n0}\right)$ such that $\{(u^n,\overline{w}),(\overline{u},w^n)\}\subseteq E\left(Q_{n-1}^{n1}\right)$ are both the jth dimensional edges, $1\le j\le n-1$, $j\ne i$. We distinguish the following two subcases:

• For $k\le i\le n-1$, we can select $(k-1)$ distinct w’s in $Q_{n-1}^{n0}$ such that $(u^n,\overline{w})$ and $(\overline{u},w^n)$ are both the jth dimensional edges in $Q_{n-1}^{n1}$, i.e., $1\le j\le k-1$. For clarity, let $u=x_1{x}_2\cdots x_j\cdots x_k\cdots x_i\cdots$ $x_{n-1}0$ and $v=x_1{x}_2\cdots x_j\cdots x_k\cdots x_{i-1}{\overline{x}}_i{x}_{i+1}\cdots x_{n-1}0$ be two vertices in $Q_{n-1}^{n0}$. Thus $(u,v)\in E\left(Q_{n-1}^{n0}\right)$ is an ith dimensional edge. We can select a vertex $w=x_1{x}_2\cdots x_{j-1}{\overline{x}}_j{x}_{j+1}\cdots x_{k-1}{\overline{x}}_k\cdots$ ${\overline{x}}_i\cdots {\overline{x}}_{n-1}0$, $1\le j\le k-1$. It implies that $d_H(u,w)=n-k+1$ and $d_H(v,w)=n-k$. It is easy to see that $d_H(u^n,\overline{w})=1$ and $d_H(\overline{u},w^n)=1$.
• For $k\le i\le n-1$, we can select $(n-k-1)$ distinct w’s in $Q_{n-1}^{n0}$ such that $(u^n,\overline{w})$ and $(\overline{u},w^n)$ are both the jth dimensional edges in $Q_{n-1}^{n1}$, i.e., $k\le j\le n-1$, and $j\ne i$. For clarity, let $u=x_1{x}_2\cdots x_k\cdots x_i\cdots$ $x_j\cdots x_{n-1}0$ and $v=x_1{x}_2\cdots x_k\cdots x_{i-1}{\overline{x}}_i{x}_{i+1}\cdots x_j\cdots x_{n-1}0$ be two vertices in $Q_{n-1}^{n0}$. Thus, $(u,v)\in E\left(Q_{n-1}^{n0}\right)$ is an ith dimensional edge. We can select a vertex $w=x_1{x}_2\cdots x_{k-1}{\overline{x}}_k\cdots {\overline{x}}_{i-1}{\overline{x}}_i{\overline{x}}_{i+1}\cdots {\overline{x}}_{j-1}{x}_j$ ${\overline{x}}_{j+1}\cdots {\overline{x}}_{n-1}0$ in $Q_{n-1}^{n0}$, $k\le j\le n-1$. Accordingly, we have $d_H(u,w)=n-k-1$ and $d_H(v,w)=n-k-2$. As a consequence, we have $d_H(u^n,\overline{w})=1$ and $d_H(\overline{u},w^n)=1$.

In summary, for any ith dimension edge $(u,v)$ in $Q_{n-1}^{n0}$, there exist $n-2$ distinct w’s in $Q_{n-1}^{n0}$ such that $w\ne v$, and $d_H(\overline{u},w^n)=1$, $d_H(u^n,\overline{w})=1$ simultaneously. □

Lemma 9.

Let $Q_{n,k}(1\le k\le n-1)$ be with $|F_v|=1$, where $n(\ge 3)$ and k have the different parity. Let $(u,v)$ be an ith dimensional fault-free edge in $E\left(Q_{n,k}\right)$. If $i\in \{k,k+1,\cdots ,n,c\}$ (respectively, $i\in \{1,2,\cdots ,k-1\}$), then the edge $(u,v)$ lies on a fault-free cycle of every possible odd length l with $n-k+2\le l\le 2^n-1$ (respectively, $n-k+4\le l\le 2^n-1$).

Proof. 

The proof of this lemma is in Appendix A. □

Theorem 2.

Let $Q_{n,k}(1\le k\le n-1)$ be with $|F_v|=f_v\le n-2$, where $n(\ge 2)$ and k have the different parity. For an ith dimensional edge $(u,v)$, if $i\in \{k,k+1,\cdots ,n,c\}$, then the edge lies on a fault-free cycle of every possible odd length l with $n-k+2\le l\le 2^n-2f_v-1$ in $Q_{n,k}-F_v$; if $i\in \{1,2,\cdots ,k-1\}$, then the edge lies on a fault-free cycle of every possible odd length l with $n-k+4\le l\le 2^n-2f_v-1$ in $Q_{n,k}-F_v$.

Proof. 

The proof of this theorem is by induction on n. It is trivial to check the theorem holds for $Q_{2,1}$ and $Q_{3,2}$. Assume the theorem holds for $3\le m<n$, where m and k have the different parity. We now would like to show the theorem holds for every $m=n\ge 4$, where m and k have the different parity. Recall that Lemma 9 proved the theorem holds for $|F_v|\le 1$. In the following, we consider $2\le |F_v|\le n-2$. Let $f=x_1{x}_2\cdots x_n$, $x_i\in \{0,1\}$ and $f^{\prime }=y_1{y}_2\cdots y_n$, $y_i\in \{0,1\}$ be two arbitrary distinct faulty vertices in $Q_{n,k}$. Thus, there exists an integer i, $1\le i\le n$, such that $x_i+y_i=1$. Applying Definition 2, if we partition $Q_{n,k}$ along dimension i, where $1\le i\le n$, then we can obtain two $(n-1)$-dimensional cubes, and each of the cubes contains at least one faulty vertex. Let $e=(u,v)$ be an arbitrary fault-free edge in $Q_{n,k}$. We distinguish the following subcases according to the partition of $Q_{n,k}$ (see Table 1).

Table 1. Cases in Theorem 2 for the desired cycle containing the edge e.

Case	The Distribution of e	The Desired Cycle of Length l
Case 1.1	$e\in E\left(Q_{n-1,k-1}^{10}\right)\cup E\left(Q_{n-1,k-1}^{11}\right)$	$n-k+2\le l\le 2^n-2f_v-1$
Case 1.2	$e\in E_1$	$n-k+4\le l\le 2^n-2f_v-1$
Case 2.1	$e\in E\left(Q_{n-1}^{n0}\right)\cup E\left(Q_{n-1}^{n1}\right)$	$n-k+2\le l\le 2^n-2f_v-1$
Case 2.2	$e\in E_n$	$n-k+4\le l\le 2^n-2f_v-1$
Case 2.3	$e\in E_c$	$n-k+4\le l\le 2^n-2f_v-1$

Case 1: $1\le i\le k-1$, $2\le k\le n-1$. Without loss of generality, we can assume $i=1$. Definition 2 ensures that $Q_{n,k}$ is partitioned into two $(n-1)$-dimensional enhanced hypercubes, denoted as $Q_{n-1,k-1}^{10}$ and $Q_{n-1,k-1}^{11}$. Denote $F_v^0=F_v\cap V\left(Q_{n-1,k-1}^{10}\right)$, $F_v^1=F_v\cap V\left(Q_{n-1,k-1}^{11}\right)$, $f_v^0=\left|F_v^0\right|$, and $f_v^1=\left|F_v^1\right|$. By the partition of $Q_{n,k}$, it follows that $1\le f_v^0\le n-3$ and $1\le f_v^1\le n-3$. We have two subcases according to the distributions of the fault-free edge e.

• First, $e\in E\left(Q_{n-1,k-1}^{10}\right)\cup E\left(Q_{n-1,k-1}^{11}\right)$. By the symmetric structure of $Q_{n-1,k-1}^{10}$ and $Q_{n-1,k-1}^{11}$, and the distribution of faulty vertices, without loss of generality, we can assume that $e\in E\left(Q_{n-1,k-1}^{10}\right)$. On one hand, in $Q_{n-1,k-1}^{10}$, $f_v^0\le n-3$, by induction hypothesis, the edge e lies on a fault-free cycle of every possible odd length from $n-k+2$ to $2^{n-1}-2f_v^0-1$ in $Q_{n-1,k-1}^{10}-F_v^0$. Let $C_0$ be a cycle of length $2^{n-1}-2f_v^0-1$ in $Q_{n-1,k-1}^{10}-F_v^0$ containing the edge e. Let $(s,t)\ne (u,v)$ denote that $\left(\right\{s\}\cap \{u,v\left\}\right)\cup \left(\right\{t\}\cap \{u,v\left\}\right)=\varnothing$. Note that we can select an edge $(s,t)\ne (u,v)$ such that $(s,t)\in E\left(C_0\right)$, $(s^1,t^1)\in E\left(Q_{n-1,k-1}^{11}\right)$ and $\{s^1,t^1\}\cap F_v^1=\varnothing$. (If not, it implies that $f_v^1\ge \frac{(2^{n-1}-2f_v^0-1)-3}{2}$. Thus, we have $f_v=f_v^0+f_v^1\ge 2^{n-2}-2>n-2$ for $n\ge 5$, a contradiction. Specially, for $Q_{4,3}$, Lemma 9 implies that $Q_{3,2}^{10}$ contains a cycle of length 7 when $f_v^0=1$ and $f_v^1=1$. Thus, it is easy to select the desired edge $(s,t)$ on the cycle.) For clarity, we set $C_1=⟨s^1,P_1[s^1,t^1],t^1,s^1⟩$, and $1\le l_1=l\left(P_1[s^1,t^1]\right)\le 2^{n-1}-2f_v^1-1$. On the other hand, we can construct the desired cycle as $⟨s,P_0[s,t],t,t^1,P_1[t^1,s^1],s^1,s⟩$, whose length is $l=l_0+l_1+2$, i.e., $2^{n-1}-2f_v^0+1\le l\le 2^n-2f_v-1$.
• Now, $e\in E_1$. $C_0=⟨s,P_0[s,t],t,s⟩$, and $l_0=l\left(P_0[s,t]\right)=2^{n-1}-2f_v^0-2$. Recall that $f_v^1\le n-3$, Theorem 1 implies that the fault-free edge $(s^1,t^1)$ lies on a fault-free cycle $C_1$ of every even length from 4 to $2^{n-1}-2f_v^1$ in $Q_{n-1,k-1}^{11}$. Assume that $u\in V\left(Q_{n-1,k-1}^{10}\right)$ and $v\in V\left(Q_{n-1,k-1}^{11}\right)$. Thus, $v=u^1$. Note that u have n neighbors in $Q_{n-1,k-1}^{10}$, i.e., $w_j$, $j\in \{2,3,4,\cdots ,n,c\}$, where $w_c=\overline{u}$, and $w_j=u^j$, $j\in \{2,3,\cdots ,n\}$. We can observe that there exist n cycles of length four containing the edge $e=(u,u^1)$ in common, i.e., $⟨u,w_j,w_j^1,u^1,u⟩$, $j\in \{2,3,\cdots ,n,c\}$. Recall that $f_v\le n-2$. Thus, there exists at least one fault-free pair $(w_j,w_j^1)$, $j\in \{2,3,\cdots ,n,c\}$ such that the cycle of length 4 is fault-free. Assume $⟨u,w,w^1,u^1,u⟩$ forms such a fault-free cycle of length 4 containing the edge $e=(u,u^1)$. Obviously, $d_H(u^1,w^1)=1$. On one hand, by induction hypothesis, $(u,w)$ lies on a fault-free cycle $C_0$ of every odd length from $n-k+2$ to $2^{n-1}-2f_v^0-1$. For clarity, $C_0=⟨u,P_0[u,w],w,u⟩$. Therefore the desired cycle of every odd length from $n-k+4$ to $2^{n-1}-2f_v^0+1$ can be constructed as $⟨u,P_0[u,w],w,w^1,u^1,u⟩$. On the other hand, we can construct the desired cycle of every odd length from $2^{n-1}-2f_v^0+3$ to $2^n-2f_v-1$. Let $C_0$ be a fault-free cycle of length $2^{n-1}-2f_v^0-1$ in $Q_{n-1,k-1}^{10}$, which contains the edge $(u,w)$. Denote $l_0=l\left(P_0[u,w]\right)=2^{n-1}-2f_v^0-2$. Applying Theorem 1, $(u^1,w^1)$ lies on a cycle $C_1$ of every even length from 4 to $2^{n-1}-2f_v^1$. For clarity, $C_1=⟨u^1,P_1[u^1,w^1],w^1,u^1⟩$, and $3\le l_1=l\left(P_1[u^1,w^1]\right)\le 2^{n-1}-2f_v^1-1$. Subsequently, merging the two paths $P_0[u,w]$ and $P_1[w^1,u^1]$ as well as the two fault-free edges $(u,u^1)$ and $(w,w^1)$, the desired cycle can be constructed as $⟨u,P_0[u,w],w,w^1,P_1[w^1,u^1],u^1,u⟩$, and the cycle is of every odd length from $2^{n-1}-2f_v^0+3$ to $2^n-2f_v-1$.

Case 2: $k\le i\le n$, $1\le k\le n-1$. Without loss of generality, we can select $i=n$. Definition 2 ensures that $Q_{n,k}$ can be partitioned into two $(n-1)$-dimensional hypercubes, denoted as $Q_{n-1}^{n0}$ and $Q_{n-1}^{n1}$. Denote $F_v^0=F_v\cap V\left(Q_{n-1}^{n0}\right)$, $F_v^1=F_v\cap V\left(Q_{n-1}^{n1}\right)$, $|F_v^0|=f_v^0$ and $|F_v^1|=f_v^1$. It follows that $1\le f_v^0\le n-3$ and $1\le f_v^1\le n-3$. We have three subcases according to the distributions of the fault-free edge e.

• First, $e\in E\left(Q_{n-1}^{n0}\right)\cup E\left(Q_{n-1}^{n1}\right)$. Without loss of generality, we can assume that $e=(u,v)\in E\left(Q_{n-1}^{n0}\right)$.

  (i)

  $1\le f_v^0\le n-4$ and $2\le f_v^1\le n-3$. Lemma 8 ensures that there exist $(n-2)$ distinct vertices $w_j$’s such that $w_j\ne v$, and $d_H(u^n,{\overline{w}}_j)=1$ or $d_H(\overline{u},w_j^n)=1$. Assuming the vertex u as a faulty vertex temporarily, since $1\le f_v^0\le n-4$, we obtain $|F_v\cap Q_{n-1}^{n0})\cup \left\{u\right\}|\le n-3$ for $n\ge 4$. Lemma 4 implies that $Q_{n-1}^{n0}-F_v^0-\left\{u\right\}$ contains a fault-free path $P_0[v,w_j]$ joining v and $w_j$. Merging the path $P_0[v,w_j]$ and the edges $(u,u^n)$, $(w_j,{\overline{w}}_j)$ and $(u^n,{\overline{w}}_j)$ (respectively, $(u,\overline{u})$, $(w_j,w_j^n)$ and $(\overline{u},w_j^n)$), there exist $2(n-2)$ cycles $C_j$’s containing the edge $(u,v)$, i.e., $C_j=⟨u,v,P_0[v,w_j],w_j,{\overline{w}}_j,u^n,u⟩$, or $C_j=⟨u,v,P_0[v,w_j],w_j,w_j^n,\overline{u},u⟩$. Obviously, the cycles $C_j$’s have the common vertices in the path $P_0[v,w_j]$. We can observe that there are at most $2f_v^0$ cycles $C_j$’s with faulty vertices in $P_0[v,w_j]$. Since $f_v=f_v^0+f_v^1\le n-2$, we have $2(n-2)\ge 2(f_v^0+f_v^1)$. It implies there are at least $2f_v^1$ cycles $C_j$’s with fault-free vertices in $Q_{n-1}^{n0}$. Since $f_v^0\le f_v^1$, there exist at least $f_v^1$ fault-free cycles $C_j$’s in $Q_{n,k}$. Without loss of generality, we can assume that $⟨u,v,P_0[v,w],w,\overline{w},u^n,u⟩$ is such a fault-free cycle and $d_H(u^n,\overline{w})=1$. Lemma 8 indicates that $d_H(v,w)=n-k-2,n-k,\mathrm{or}n-k+2$. Obviously, $n-k\le l_0=l\left(P_0[v,w]\right)\le 2^{n-1}-2(f_v^0+1)-1$. In $Q_{n-1}^{n1}$, $f_v^1\le n-3$ and $d_H(u^n,\overline{w})=1$, applying Lemma 4, there exists a fault-free path $P_1[u^n,\overline{w}]$ of every odd length $l_1$ joining $u^n$ and $\overline{w}$, where $1\le l_1\le 2^{n-1}-2f_v^1-1$. As an immediate result, $⟨u,v,P_0[v,w],w,\overline{w},P_1[\overline{w},u^n],u^n,u⟩$ forms the desired cycle of every possible odd length $l=l_0+l_1+3$ in $Q_{n,k}-F_v$. Since $n-k\le l_0\le 2^{n-1}-2f_v^0-3$ and $1\le l_1\le 2^{n-1}-2f_v^1-1$, we can obtain $n-k+4\le l\le 2^n-2f_v-1$ (see Figure 2a). (In Figure 2, Figure 3, Figure 4 and Figure 5, we use white vertices and black vertices to distinguish the different parity of the vertices, and we use gray vertices to denote the vertices with unknown parity.)

  

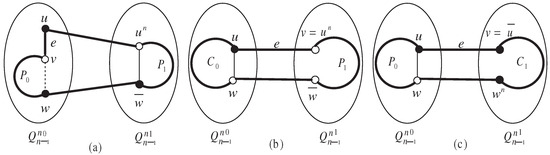  Figure 2. Illustrations of (a) Case 2, (b) Case 2, and (c) Case 2 in the proof of Theorem 2.

  

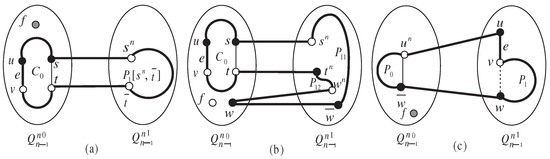  Figure 3. Illustrations of (a) Subcase 1.1, (b) Subcase 1.2, and (c) Subcase 2.1 in the proof of Lemma 9.

  

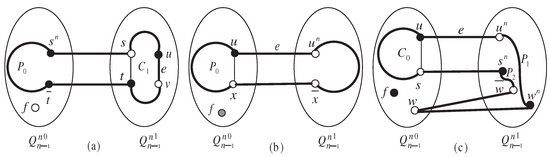  Figure 4. Illustrations of (a) Subcase 2.2, (b) Subcase 3.1, and (c) Subcase 3.2.1 in the proof of Lemma 9.

  

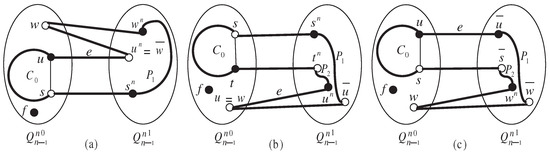  Figure 5. Illustrations of (a) Subcase 3.2.1, (b) Subcase 3.2.2, and (c) Subcase 4.2.1 in the proof of Lemma 9.

  (ii)

  $f_v^0=n-3$ and $f_v^1=1$. Specially, Lemmas 3 and 7 imply that we can construct the cycles $⟨u,v,v^n,P_1[v^n,\overline{u}],\overline{u},u⟩$ and $⟨u,v,\overline{v},P_1[\overline{v},u^n],u^n,u⟩$, whose length is $n-k+2$ or $n-k+4$. Since $f_v^1=1$, it follows that there exists at least one of the above fault-free cycle of odd length $n-k+2$ or $n-k+4$ containing the edge $(u,v)$. Generally, we construct the desired cycle of every odd length from $n-k+6$ to $2^n-2f_v-1$. Since $f_v^0=n-3$, applying Lemma 2, $(u,v)$ lies on a fault-free cycle $C_0$ of length $l_0^{\prime }$ in $Q_{n-1}^{n0}$, where $4\le l_0^{\prime }\le 2^{n-1}-2f_v^0$. Assume that $(s,t)$ is an edge on $C_0$, $(s,t)\ne (u,v)$. For clarity, $C_0=⟨s,P_0[s,t],t,s⟩$, $3\le l_0=l\left(P_0[s,t]\right)\le 2^{n-1}-2f_v^0-1$. Since $f_v^1=1$, we have $\{s^n,\overline{t}\}\cap F_v^1=\varnothing$ or $\{\overline{s},t^n\}\cap F_v^1=\varnothing$. It implies that we can assume $s^n$ and $\overline{t}$ are both fault-free vertices in $V\left(Q_{n-1}^{n1}\right)$. Note that $d_H(s^n,\overline{t})=n-k-1$ or $d_H(s^n,\overline{t})=n-k+1$. Lemma 4 ensures that $Q_{n-1}^{n1}-F_v^1$ contains a fault-free path $P_1[s^n,\overline{t}]$ of every even length $l_1$, where $n-k+1\le l_1\le 2^{n-1}-2f_v^1-2$. Accordingly, merging the two paths $P_0[s,t]$ and $P_1[s^n,\overline{t}]$ as well as the two edges $(s,s^n)$ and $(t,\overline{t})$, we can construct the desired cycle as $⟨s,P_0[s,t],t,\overline{t},P_1[\overline{t},s^n],s^n,s⟩$, whose length is $n-k+6\le l=l_0+l_1+2\le 2^n-2f_v-1$.

• Next, $e\in E_n$. Obviously, $v=u^n$. Applying Lemma 7, we can select $n-1$ distinct vertices $w_j$ adjacent to u in $Q_{n-1}^{n0}$ such that $d_H(u^n,{\overline{w}}_j)=n-k-1$ or $d_H(u^n,{\overline{w}}_j)=n-k+1$, and $w_j=u^j$ for $j\in \{1,2,\cdots ,n-1\}$. Since $f_v^1\le n-3$, Lemma 4 implies that $Q_{n-1}^{n1}$ contains a path $P_1[u^n,{\overline{w}}_j]$ joining $u^n$ and ${\overline{w}}_j$. Subsequently, there exist $n-1$ cycles $C_j$’s denoted as $C_j=⟨u,w_j,{\overline{w}}_j,P_1[{\overline{w}}_j,u^n],u^n,u⟩$, where $j\in \{1,2,\cdots ,n-1\}$. Note that $f_v\le n-2$. It implies that there exists at least one fault-free cycle $C_j$. Assume $⟨u,w,\overline{w},P_1[\overline{w},u^n],u^n,u⟩$ is such a fault-free cycle. For clarity, $l_1=l\left(P_1[u^n,\overline{w}]\right)$, it follows that $n-k+1\le l_1\le 2^{n-1}-2f_v^0-2$. Recall that $f_v^0\le n-3$, Lemma 4 ensures that $Q_{n-1}^{n0}$ contains a fault-free path $P_0[u,w]$ of every odd length $l_0$ joining u and v, where $1\le l_0\le 2^{n-1}-2f_v^1-1$. Accordingly, the desired cycle containing the edge e can be constructed as $⟨u,P_0[u,w],w,\overline{w},P_1[\overline{w},u^n],u^n,u⟩$, whose length is $l=l_0+l_1+2$. As a result, $n-k+4\le l\le 2^n-2f_v-1$ (see Figure 2b).
• Finally, $e\in E_c$. Note that $E_c$ is the set of complementary edges between $Q_{n-1}^{n0}$ and $Q_{n-1}^{n1}$. It follows that $v=\overline{u}$. Lemma 7 implies that $Q_{n-1}^{n0}$ contains $n-1$ distinct vertices $w_j$’s, which are adjacent to u and satisfy $d_H(\overline{u},w_j^n)=n-k-1$ or $d_H(\overline{u},w_j^n)=n-k+1$, and $w_j=u^j$ for $j\in \{1,2,\cdots ,n-1\}$. As mentioned above, there exist $n-1$ cycles $C_j$’s denoted as $C_j=⟨u,w_j,w_j^n,P_1[w_j^n,\overline{u}],\overline{u},u⟩$, where $j\in \{1,2,\cdots ,n-1\}$. Since $f_v\le n-2$, there exists at least one fault-free cycle $C_j$. Assume $⟨u,w,w^n,P_1[w^n,\overline{u}],\overline{u},u⟩$ is such a fault-free cycle in $Q_{n,k}$. Lemma 4 indicates that there exists a fault-free path $P_1[\overline{u},w^n]$ of every even length $l_1$ in $Q_{n-1}^{n1}$, and there also exists a fault-free path $P_0[u,w]$ of every odd length $l_0$ in $Q_{n-1}^{n0}$, where $n-k+1\le l_1\le 2^{n-1}-2f_v^1-2$ and $1\le l_0\le 2^{n-1}-2f_v^0-1$. It is easy to see that $⟨u,P_0[u,w],w,w^n,P_1[w^n,\overline{u}],\overline{u},u⟩$ forms the desired odd cycle, whose length is $l=l_0+l_1+2$. It follows that $n-k+4\le l\le 2^n-2f_v-1$ (see Figure 2c).

In summary, all cases have been concerned, so the proof is completed. □

5. Concluding Remarks

Let $F_v$ be the set of faulty vertices in $Q_{n,k}(1\le k\le n-1)$. In this paper, we consider the faulty enhanced hypercube $Q_{n,k}(1\le k\le n-1)$ with $|F_v|\le n-2$ faulty vertices. For a fault-free edge $(u,v)$ of $Q_{n,k}-F_v$, we show that it lies on a fault-free cycle of every even length from 4 to $2^n-2\left|F_v\right|$, where $n\ge 2$; moreover, it lies on a fault-free cycle of every possible odd length from $n-k+4$ to $2^n-2\left|F_v\right|-1$ in $Q_{n,k}-F_v$, where $n(\ge 2)$ and k have different parity.