Symmetric Difference Operators Derived from Overlap and Grouping Functions

Abstract

This paper introduces the concept of symmetric difference operators in terms of overlap and grouping functions, for which the associativity property is not strongly required. These symmetric difference operators are weaker than symmetric difference operators in terms of positive and continuous t-norms and t-conorms. Therefore, in the sense of the characters of mathematics, these operators do not necessarily satisfy certain properties, such as associativity and the neutrality principle. We analyze several related important properties based on two models of symmetric differences.

1. Introduction

Symmetric difference is a basic operation on classical set theory. The symmetric difference of two crisp sets E and F, denoted by $E\setminus F$, could be represented as

$$\begin{array}{cc}\hfill E\Delta F& =(E\cap F^c)\cup (E^c\cap F),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill E\Delta F& =(E\cup F)\cap {(E\cap F)}^c,\hfill \end{array}$$

(2)

where $F^c$ is the complement of F. Since the introduction of fuzzy sets beginning with Zadeh [1], it was generalized to fuzzy settings. Agell and Rovira [2] obtained several symmetric difference operators in the lattice $\left(P\right(X),min,max,1-j)$. Alsina and Trillas [3] studied some models for the symmetric difference of fuzzy sets. Dombi [4] studied two models of fuzzy symmetric differences in the Pliant operator case. Shen and Zhang [5] defined the symmetric difference operator of fuzzy sets as a continuous and associative binary operator and investigated their structures and properties. Dombi [6] studied two formulas of symmetric difference operators based on thresholds. Renedo et al. [7] studied symmetric differences in types of lattices. Dai and Cheng [8] introduced the noncommutative symmetric difference derived from fuzzy difference operators. The symmetric difference is also the representation of the connective “exclusive or” (Xor, for short). The fuzzy Xor connective was well-studied in [9,10,11].

In fuzzy set theory, the analogue of Formulas (1) and (2) are, respectively [2,3,4,5,6], $\forall a,b\in [0,1]$

$$\begin{array}{cc}\hfill a\Delta b& =S\left(T(a,N(b\left)\right),T\left(N\right(a),b)\right),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill a\Delta b& =T\left(S(a,b),N\left(T\right(a,b\left)\right)\right),\hfill \end{array}$$

(4)

where T is a t-norm, S is a t-conorm, and N is a fuzzy negation on $[0,1]$.

However, as pointed out by Fodor and Keresztfalvi [12] and Bustince et al. [13,14], the associative properties of the t-norm and t-conorm are not demanded in some applications. Therefore, Bustince et al. [13,14] introduced the concepts of overlap functions and grouping functions, which are two kinds of non-necessarily associative bivariate aggregation operators. By considering overlap functions and grouping functions instead of t-norms and t-conorms, respectively, many important notions are investigated, such as $R_O$ implications derived from overlap functions [15,16], (G,N) implications derived from grouping functions [17], binary relations induced from overlap and grouping functions [18], and (IO, O)-fuzzy rough sets derived from overlap functions [19].

In this paper, we take a step forward to define symmetric difference operators by considering overlap functions and grouping functions instead of t-norms and t-conorms, respectively, in the above Formulas (3) and (4). In particular, they are weaker than the symmetric differences in Formulas (3) and (4) for positive and continuous t-norms and t-conorms, in the sense that they do not necessarily satisfy certain properties, such as the neutrality principle.

The remainder of this article is structured as follows. Section 2 provides a brief overview of key concepts related to overlap functions and grouping functions. Section 3 is concerned with the model $G(O_1(a,N_1\left(b\right)),O_2(N_2\left(a\right),b))$ of symmetric difference operators. Section 4 is concerned with the model $O\left(G\right(a,b),N(O(a,b)\left)\right)$ of symmetric difference operators. Section 5 gives a comparative study. Conclusions are presented in Section 6.

2. Preliminaries

Definition 1

([13]). An overlap function is a two-place function O: ${[0,1]}^2\to [0,1]$ satisfying the following properties: $\forall a,b\in [0,1]$—

• (O1) $O(a,b)=O(b,a)$;
• (O2) $O(a,b)=0⟺ab=0$;
• (O3) $O(a,b)=1⟺ab=1$;
• (O4) O is increasing;
• (O5) O is continuous.

Definition 2

([14]). A grouping function is a two-place function G: ${[0,1]}^2\to [0,1]$ satisfying the following properties: $\forall a,b\in [0,1]$

• (G1) $G(a,b)=G(b,a)$;
• (G2) $G(a,b)=0⟺a=b=0$;
• (G3) $G(a,b)=1⟺a=1\mathrm{or}b=1$;
• (G4) G is increasing;
• (G5) G is continuous.

Definition 3

([20]). A fuzzy negation is a non-increasing function N: $[0,1]\to [0,1]$ with $N\left(0\right)=1$ and $N\left(1\right)=0$.

Moreover, N is called strong if $N\left(N\right(a\left)\right)=a,\forall a\in [0,1]$. $N\left(a\right)=1-a$ is called the standard negation.

The overlap function, given by

$$\begin{array}{c}\hfill O(a,b)=N\left(G\left(N\left(a\right),N\left(b\right)\right)\right),\forall a,b\in [0,1],\end{array}$$

(5)

is called the dual overlap function of G for N and, analogously, the grouping function G, given by

$$\begin{array}{c}\hfill G(x,y)=N\left(O\left(N\left(x\right),N\left(y\right)\right)\right),\end{array}$$

(6)

is said to be the dual grouping function of the overlap function O for N.

Example 1.

The following are typical examples of overlap and grouping functions in [14,21].

• $O_{nm}(a,b)=min(a,b)max(a^2,b^2)$, and its dual grouping function for the standard negation: $G_{nm}(a,b)=1-min(1-a,1-b)max({(1-a)}^2,{(1-b)}^2)$;
• $O_p(a,b)=a^p{b}^p$, and its dual grouping function for the standard negation: $G_p(a,b)=1-{(1-a)}^p{(1-b)}^p$, where $p>0$;
• $O_{mp}(a,b)=min(a^p,b^p)$, and its dual grouping function for the standard negation: $G_{mp}(a,b)$$=1-min({(1-a)}^p,{(1-b)}^p)$, where $p>0$;
• $O_{Mp}(a,b)=1-max({(1-a)}^p,{(1-b)}^p)$, and its dual grouping function for the standard negation: $G_{Mp}(a,b)=max(a^p,b^p)$, where $p>0$.

3. The Model $\mathbf{G}({\mathbf{O}}_{\mathbf{1}}(\mathbf{a},{\mathbf{N}}_{\mathbf{1}}\left(\mathbf{b}\right)),{\mathbf{O}}_{\mathbf{2}}({\mathbf{N}}_{\mathbf{2}}\left(\mathbf{a}\right),\mathbf{b}))$

Suppose O is an overlap function, G is a grouping function, and N is a fuzzy negation. Based on Formula (1), we consider the function ${▴: [0,1]}^2\to [0,1]$, given by

$$\begin{array}{cc}\hfill a▴b& =G\left(O(a,N(b\left)\right),O\left(N\right(a),b)\right).\hfill \end{array}$$

(7)

Similar to [3], we can let the two overlap functions and negations in Formula (7) be different and then generalize a special kind of symmetric difference operator that is not necessarily commutative.

Theorem 1.

Suppose $O_1$ and $O_2$ are two overlap functions, G is a grouping function, and $N_1$ and $N_2$ are two fuzzy negations. Then, the function ${▴: [0,1]}^2\to [0,1]$ given by

$$\begin{array}{cc}\hfill a▴b& =G\left(O_1(a,N_1\left(b\right)),O_2(N_2\left(a\right),b)\right)\hfill \end{array}$$

(8)

satisfies $\forall a,b\in [0,1]$

(i)

If $O_1=O_2$ and $N_1=N_2$, then $a▴b=b▴a$;

(ii)

$1▴0=0▴1=1$;

(iii)

$1▴1=0▴0=0$;

(iv)

If both $N_1$ and $N_2$ are continuous, then $▴$ is continuous;

(v)

If $O_1$ has 1 as a neutral element, i.e., $O_1(1,a)=a$, $\forall a\in [0,1]$, and G has 0 as a neutral element, i.e., $G(0,a)=a$, $\forall a\in [0,1]$, then $0▴a=a▴0=a$;

(vi)

If $O_2$ has 1 as a neutral element, i.e., $O_2(1,a)=a$, $\forall a\in [0,1]$, and G has 0 as a neutral element, i.e., $G(0,a)=a$, $\forall a\in [0,1]$, then $1▴a=a▴1=N_2\left(a\right)$;

(vii)

If both $N_1$ and $N_2$ are defined as

$$\begin{array}{c}\hfill N_{\mathbf{0}}\left(a\right)=\left\{\begin{array}{cc}0,\hfill & ifa>0,\hfill \\ 1,\hfill & ifa=0,\hfill \end{array}\right.\end{array}$$

(9)

then $a▴a=0$.

Proof. 

(i)  If $O_1=O_2$ and $N_1=N_2$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & a▴b\hfill \\ \hfill & =G\left(O_1(a,N_1\left(b\right)),O_2(N_2\left(a\right),b)\right)ByEquation\left(7\right)\hfill \\ \hfill & =G\left(O_2(N_2\left(a\right),b),O_1(a,N_1\left(b\right))\right)By\left(G1\right)\hfill \\ \hfill & =G\left(O_2(b,N_2\left(a\right)),O_1(N_1\left(b\right),a)\right)By\left(O1\right)\hfill \\ \hfill & =G\left(O_1(b,N_1\left(a\right)),O_2(N_2\left(b\right),a)\right)\hfill \\ \hfill & =b▴a.ByEquation\left(7\right).\hfill \end{array}\end{array}$$

(ii)

Taking $a=1$ and $b=0$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & 1▴0\hfill \\ \hfill & =G\left(O_1(1,N_1\left(0\right)),O_2(N_2\left(1\right),0)\right)ByEquation\left(7\right)\hfill \\ \hfill & =G\left(O_1(1,1),O_2(0,0)\right)\hfill \\ \hfill & =G\left(1,0\right)By\left(O2\right)and\left(O3\right)\hfill \\ \hfill & =1.By\left(G3\right).\hfill \end{array}\end{array}$$

by (i), $0▴1=1▴0=1$.

(iii)

Taking $a=0$ and $b=0$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & 0▴0\hfill \\ \hfill & =G\left(O_1(0,N_1\left(0\right)),O_2(N_2\left(0\right),0)\right)ByEquation\left(7\right)\hfill \\ \hfill & =G\left(O_1(0,1),O_2(1,0)\right)\hfill \\ \hfill & =G\left(0,0\right)By\left(O2\right)\hfill \\ \hfill & =0.By\left(G2\right).\hfill \end{array}\end{array}$$

Taking $a=b=1$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & 1▴1\hfill \\ \hfill & =G\left(O_1(1,N_1\left(1\right)),O_2(N_2\left(1\right),1)\right)ByEquation\left(7\right)\hfill \\ \hfill & =G\left(O_1(1,0),O_2(0,1)\right)\hfill \\ \hfill & =G\left(0,0\right)By\left(O2\right)\hfill \\ \hfill & =0.By\left(G2\right).\hfill \end{array}\end{array}$$

(iv)

It is a direct consequence of the continuity of G, $O_1$, $O_2$, $N_1$, and $N_2$.

(v)

Since $O_1$ has 1 as a neutral element and G has 0 as a neutral element, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & a▴0\hfill \\ \hfill & =G\left(O_1(a,N_1\left(0\right)),O_2(N_2\left(a\right),0)\right)ByEquation\left(7\right)\hfill \\ \hfill & =G\left(O_1(a,1),O_2(N_2\left(a\right),0)\right)\hfill \\ \hfill & =G\left(a,0\right)\hfill \\ \hfill & =a.\hfill \end{array}\end{array}$$

by (i), $0▴a=a▴0=a$.

(vi)

Since $O_2$ has 1 as a neutral element and G has 0 as a neutral element, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & a▴1\hfill \\ \hfill & =G\left(O_1(a,N_1\left(1\right)),O_2(N_2\left(a\right),1)\right)ByEquation\left(7\right)\hfill \\ \hfill & =G\left(O_1(a,0),O_2(N_2\left(a\right),1)\right)\hfill \\ \hfill & =G\left(0,N_2\left(a\right)\right)\hfill \\ \hfill & =N_2\left(a\right).\hfill \end{array}\end{array}$$

by (i), $1▴a=a▴1=N_2\left(a\right)$.

(vii)

If $N_1=N_2=N_{\mathbf{0}}$, case 1, if $a=0$ or $a=1$, then $a▴a=0$. Case 2, if $a\in (0,1)$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & a▴a\hfill \\ \hfill & =G\left(O_1(a,N_1\left(a\right)),O_2(N_2\left(a\right),a)\right)ByEquation\left(7\right)\hfill \\ \hfill & =G\left(O_1(a,0),O_2(0,a)\right)By\left(O2\right)\hfill \\ \hfill & =G\left(0,0\right)\hfill \\ \hfill & =0.\hfill \end{array}\end{array}$$

□

Example 2.

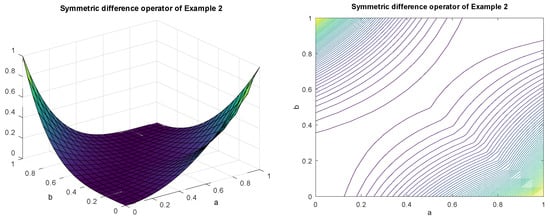
Consider the $O_1=O_{nm}$, $O_2=O_{p=2}$, $N_1$ and $N_2$ are the standard negation, and $G=G_{M2}$. Then,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & a▴b\hfill \\ \hfill & =G\left(O_1(a,N_1\left(b\right)),O_2(N_2\left(a\right),b)\right)\hfill \\ \hfill & =max\left({\left(min(a,1-b)max(a^2,{(1-b)}^2)\right)}^2,{\left({(1-a)}^2{b}^2\right)}^2\right).\hfill \end{array}\end{array}$$

(10)

See Figure 1, which reflects the characteristics of this symmetric difference operator.

Figure 1. Characteristics of symmetric difference of Example 2 and its contour line.

Example 3.

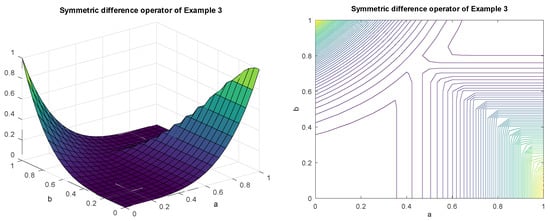
Consider the $O_1=O_{m2}$, $O_2=O_{p=2}$, $N_1=N_2=N\left(a\right)=1-a^2$, and $G=G_{M2}$. Then,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & a▴b\hfill \\ \hfill & =G\left(O_1(a,N\left(b\right)),O_2(N\left(a\right),b)\right)\hfill \\ \hfill & =max\left({\left(min(a^2,{(1-b^2)}^2)\right)}^2,{\left({(1-a^2)}^2{b}^2\right)}^2\right).\hfill \end{array}\end{array}$$

(11)

See Figure 2, which reflects the characteristics of this symmetric difference operator.

Figure 2. Characteristics of symmetric difference of Example 3 and its contour line.

4. The Model $\mathbf{O}\left(\mathbf{G}\right(\mathbf{a},\mathbf{b}),\mathbf{N}(\mathbf{O}(\mathbf{a},\mathbf{b})\left)\right)$

Suppose O is an overlap function, G is a grouping function, and N is a fuzzy negation. Based on Formula (2), we consider the function $▾:{[0,1]}^2\to [0,1]$ given by

$$\begin{array}{cc}\hfill a▾b& =O\left(G(a,b),N\left(O\right(a,b\left)\right)\right)\hfill \end{array}$$

(12)

Theorem 2.

The function $▾$ given by Formula (12) satisfies: $\forall a,b\in [0,1]$

(i)

$a▾b=b▾a$;

(ii)

$1▾0=0▾1=1$;

(iii)

$1▾1=0▾0=0$;

(iv)

If N is continuous, then $▾$ is continuous;

(v)

If O has 1 as a neutral element, i.e., $O(1,a)=a$, $\forall a\in [0,1]$, and G has 0 as a neutral element, i.e., $G(0,a)=a$, $\forall a\in [0,1]$, then $0▾a=a▾0=a$ and $1▾a=a▾1=N\left(a\right)$;

(vi)

If $N=N_{\mathbf{0}}$, then $a▾a=0$.

Proof. 

(i)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & a▾b\hfill \\ \hfill & =O\left(G(a,b),N\left(O\right(a,b\left)\right)\right)ByEquation\left(12\right)\hfill \\ \hfill & =O\left(G(b,a),N\left(O\right(b,a\left)\right)\right)By\left(G1\right)and\left(O1\right)\hfill \\ \hfill & =b▾a.ByEquation\left(12\right).\hfill \end{array}\end{array}$$

(ii)

Taking $a=1$ and $b=0$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & 1▾0\hfill \\ \hfill & =O\left(G(1,0),N\left(O\right(1,0\left)\right)\right)ByEquation\left(12\right)\hfill \\ \hfill & =G\left(1,N\left(0\right)\right)By\left(G3\right)and\left(O2\right)\hfill \\ \hfill & =G\left(1,1\right)\hfill \\ \hfill & =1.By\left(G3\right).\hfill \end{array}\end{array}$$

by (i), $0▾1=1▾0=1$.

(iii)

Taking $a=0$ and $b=0$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & 0▾0\hfill \\ \hfill & =O\left(G(0,0),N\left(O\right(0,0\left)\right)\right)ByEquation\left(12\right)\hfill \\ \hfill & =G\left(0,N\left(0\right)\right)By\left(G2\right)and\left(O2\right)\hfill \\ \hfill & =G\left(0,1\right)\hfill \\ \hfill & =1.By\left(G3\right).\hfill \end{array}\end{array}$$

Taking $a=1$ and $b=1$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & 1▾1\hfill \\ \hfill & =O\left(G(1,1),N\left(O\right(1,1\left)\right)\right)ByEquation\left(12\right)\hfill \\ \hfill & =G\left(1,N\left(1\right)\right)By\left(G3\right)and\left(O3\right)\hfill \\ \hfill & =G\left(1,0\right)\hfill \\ \hfill & =1.By\left(G3\right).\hfill \end{array}\end{array}$$

(iv)

It is a direct consequence of the continuity of G, O, and N.

(v)

Taking $b=0$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & a▾0\hfill \\ \hfill & =O\left(G(a,0),N\left(O\right(a,0\left)\right)\right)ByEquation\left(12\right)\hfill \\ \hfill & =G\left(a,N\left(0\right)\right)\hfill \\ \hfill & =G\left(a,1\right)\hfill \\ \hfill & =a.\hfill \end{array}\end{array}$$

by (i), $0▾a=a▾0=a$.

Taking $b=1$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & a▾1\hfill \\ \hfill & =O\left(G(a,1),N\left(O\right(a,1\left)\right)\right)ByEquation\left(12\right)\hfill \\ \hfill & =G\left(1,N\left(a\right)\right)\hfill \\ \hfill & =N\left(a\right).\hfill \end{array}\end{array}$$

by (i), $1▾a=a▾1=N\left(a\right)$.

(vi)

If $N=N_{\mathbf{0}}$, case 1, if $a=0$ or $a=1$, then $a▾a=0$, case 2, consider $a\in (0,1)$, clearly $O(a,a)\in (0,1)$ by (O2) and (O3), then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & a▾a\hfill \\ \hfill & =O\left(G(a,a),N\left(O\right(a,a\left)\right)\right)ByEquation\left(12\right)\hfill \\ \hfill & =O\left(G(a,a),0\right)\hfill \\ \hfill & =0.\hfill \end{array}\end{array}$$

□

Example 4.

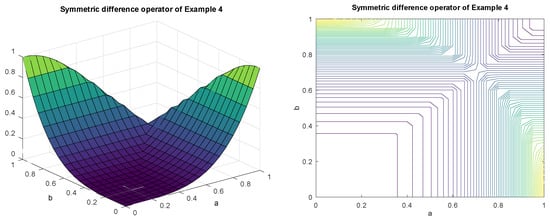
Consider the $O=O_{p=2}$, N is the standard negation, and $G=G_{M2}$. Then,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & a▾b\hfill \\ \hfill & =O\left(G(a,b),N\left(O\right(a,b\left)\right)\right)\hfill \\ \hfill & ={\left(a^2{b}^2\right)}^2{\left(1-min(a^2,b^2)\right)}^2.\hfill \end{array}\end{array}$$

(13)

See Figure 3, which reflects the characteristics of this symmetric difference operator.

Figure 3. Characteristics of symmetric difference of Example 4 and its contour line.

Example 5.

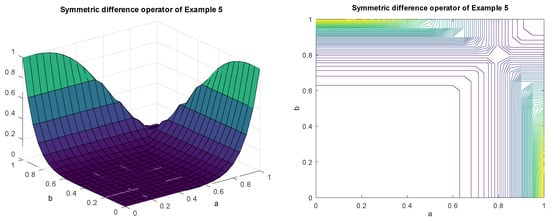
Consider the $O=O_{p=3}$, N is the standard negation, and $G=G_{M3}$. Then,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & a▾b\hfill \\ \hfill & =O\left(G(a,b),N\left(O\right(a,b\left)\right)\right)\hfill \\ \hfill & ={\left(a^3{b}^3\right)}^3{\left(1-min(a^3,b^3)\right)}^3.\hfill \end{array}\end{array}$$

(14)

See Figure 4, which reflects the characteristics of this symmetric difference operator.

Figure 4. Characteristics of symmetric difference of Example 5 and its contour line.

5. Comparative Study

In this section, we establish a comparison of the proposed fuzzy symmetric differences.

In [3], Alsina and Trillas defined the symmetric difference operator to be a two-place function $\Delta :{[0,1]}^2\to [0,1]$ that satisfies the conditions $a,b\in [0,1]$

• ($\Delta 1$) $0\Delta a=a\Delta 0=a$  (neutrality property);
• ($\Delta 2$) $1\Delta a=a\Delta 1=N\left(a\right)$;
• ($\Delta 3$) $a\Delta a=0$.

They proposed the following model for symmetric difference

$$\begin{array}{cc}\hfill a{\Delta }_{1}b& =S\left(T_1(a,N_1\left(b\right)),T_2(N_2\left(a\right),)\right),\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill a{\Delta }_{2}b& =T\left(S(a,b),N\left(T\right(a,b\left)\right)\right).\hfill \end{array}$$

(16)

In [5], Shen and Zhang defined the symmetric difference operator to be a two-place function ${\Delta }^{\prime }:{[0,1]}^2\to [0,1]$ that satisfies the conditions $a,b,c\in [0,1]$

• ($\Delta 1^{\prime }$) $0{\Delta }^{\prime }a=a{\Delta }^{\prime }0=a$;
• ($\Delta 2^{\prime }$) $1{\Delta }^{\prime }1=0$;
• ($\Delta 3^{\prime }$) ${\Delta }^{\prime }$ is associative, i.e., $\left(a{\Delta }^{\prime }b\right){\Delta }^{\prime }c=a{\Delta }^{\prime }\left(b{\Delta }^{\prime }c\right)$;
• ($\Delta 4^{\prime }$) ${\Delta }^{\prime }$ is continuous.

In [11], Bedregal, Reiser, and Dimuro defined the symmetric difference operator to be a two-place function ${\Delta }^{″}:{[0,1]}^2\to [0,1]$ that satisfies the conditions $a,b,c\in [0,1]$

• ($\Delta 1^{″}$) $0{\Delta }^{″}a=a{\Delta }^{″}0=a$;
• ($\Delta 2^{″}$) $1{\Delta }^{″}1=0$;
• ($\Delta 3^{″}$) ${\Delta }^{″}$ is associative;
• ($\Delta 4^{″}$) $a{\Delta }^{″}b=b{\Delta }^{″}a$  (symmetry).

The comparison is demonstrated in the following Remarks.

Remark 1.

Since $▴$ and $▾$ satisfy (ii) $1▴0=0▴1=1$ and (iii) $1▴1=0▴0=0$, so they are generalizations of classical symmetric difference operators. These two properties (ii) and (iii) are weaker than ($\Delta 1$) and ($\Delta 2$) in [3], ($\Delta 1^{\prime }$) and ($\Delta 2^{\prime }$) in [5,11].

Remark 2.

Similar to the symmetric difference in [3], both $▴$ and $▾$ drop the requirement of associativity. Moreover, both $▴$ and ${\Delta }_1$ also drop the requirement of symmetry.

Remark 3.

In particular, $▴$ and $▾$ are, respectively, weaker than ${\Delta }_1$ and ${\Delta }_2$ for positive and continuous t-norms and t-conorms, in the sense that $▴$ and $▾$ do not necessarily satisfy certain properties, such as the neutrality principles, as discussed above.

6. Conclusions

The main contribution of this paper was the introduction of fuzzy symmetric differences based on the notions of overlap functions, grouping functions, and fuzzy negations, together with an extensive analysis of the related properties. These new symmetric differences are weaker than symmetric difference operators in terms of positive and continuous t-norms and t-conorms. The symmetric differences $\Delta$ and ${\Delta }^{\prime }$ in [3,5] have 0 as a neutral element. The symmetric differences ${\Delta }^{\prime }$ and ${\Delta }^{″}$ in [5,11] are associative. The symmetric differences proposed in this paper are more flexible, since they do not necessarily satisfy associativity and the neutrality principle.

Future theoretical work will consider the investigation of the interval-valued symmetric differences based on interval-valued overlap or grouping functions. Moreover, the investigation of additive and multiplicative generators of the symmetric differences is necessary. We give some possible topics for future consideration.

(1)

We focus on the symmetric difference operator based on overlap and grouping functions. There are various operators in fuzzy logics. As future work, we can consider other fuzzy operators, such as equivalence operators, based on overlap and grouping functions.

(2)

Overlap and grouping functions have been extended to interval-valued overlap and grouping functions. As future work, we can consider interval-valued fuzzy operators based on interval-valued overlap and grouping functions.

(3)

As we know, additive and multiplicative generators of overlap and grouping functions were well-studied in [22,23]. Thus, it is interesting to study different generators of the symmetric differences.