Symmetry Analysis for the 2D Aw-Rascle Traffic-Flow Model of Multi-Lane Motorways in the Euler and Lagrange Variables

Abstract

A detailed symmetry analysis is performed for a microscopic model used to describe traffic flow in two-lane motorways. The traffic flow theory employed in this model is a two-dimensional extension of the Aw-Rascle theory. The flow parameters, including vehicle density, and vertical and horizontal velocities, are described by a system of first-order partial differential equations belonging to the family of hydrodynamic systems. This fluid-dynamics model is expressed in terms of the Euler and Lagrange variables. The admitted Lie point symmetries and the one-dimensional optimal system are determined for both sets of variables. It is found that the admitted symmetries for the two sets of variables form different Lie algebras, leading to distinct one-dimensional optimal systems. Finally, the Lie symmetries are utilized to derive new similarity closed-form solutions.

1. Introduction

The theory of invariant transformations, known as symmetry analysis and established by Sophus Lie, offers a systematic approach to studying nonlinear differential equations [1,2,3]. In the context of a given differential equation, the existence of invariant transformations implies the presence of similarity variables. These variables allow the given differential equation to be expressed in a simpler equivalent form by either reducing the order of derivatives or the number of independent variables. The reduction in degrees of freedom is a fundamental step in the Lie symmetry analysis for partial differential equations, while in the case of ordinary differential equations, it involves reducing the order of the equation [4,5].

Once the equation is reduced, it may either become a differential equation with a known solution or be further investigated using the symmetry approach to potentially transform it into an algebraic form, if feasible.

The Lie symmetry analysis has been applied with success in the study of dynamical systems in physics and in all areas of applied mathematics. In [6], it was performed a complete classification of the admitted Lie symmetries for two-dimensional Newtonian; see also the recent studies [7,8], where the conservation laws are determined. An extension of the Lie symmetry analysis in higher-dimensional Newtonian systems is given in [9]. The Ermakov-Pinney system it is a Newtonian dynamical system that has the property to be invariant under the $SL\left(2,R\right)$ Lie algebra [10,11]. Hence, with the requirement of a higher-order dynamical system to admit as Lie symmetries the elements of the $SL\left(2,R\right)$ Lie algebra, the Ermakov-Pinney system has been generalized to higher-dimensions [12,13] and to non-flat geometries [14]. The Hénon-Heiles system is a dynamical system that has been proposed to describe the galactic dynamics. The system possesses only one Lie symmetry vector; however, in [15,16,17], extensions of the Hénon-Heiles system have been derived with additional Lie symmetries and non-trivial conservation laws. The third law of Kepler of Newtonian gravity is related to the existence of the scaling symmetry for the gravitational potential [18]. There are various studies in the literature where the Lie symmetries are used for the study of gravitational systems in general relativity and cosmology; see, for instance, [19,20,21,22] and the references therein.

The Lie symmetries for the one-dimensional shallow-water system were determined in [23]. The complete symmetry classification of shallow-water equations for a two-dimensional flow was performed in [24], while the same problem in a rotating frame with non-zero Coriolis component was investigated in [25], while a varying bottom topography was considered in [26]; see also [27,28,29]. The group properties for the hyperbolic equations of two-phase flow models of fluid dynamics were investigated in [30,31,32]. As far as MHD systems are concerned, the Lie symmetries were investigated in a series of studies [33,34,35]. Applications of the Lie symmetries in biology, financial mathematics, and others can be found in [36,37,38,39,40] and the references therein.

Recently in [41], the Lie symmetry method was applied for the study of the Aw-Rascle-Zhang model for traffic estimation. Specifically, the Aw-Rascle-Zhang model is a macroscopic models for the traffic description, which is consisted by two first-order hyperbolic partial differential equations, which describe the evolution of vehicles density and of the velocity components. With the use of the Lie symmetries, new similarity solutions for the Aw-Rascle-Zhang model were determined while invariant functions were constructed. In this study, we consider a two-dimensional (2D) Aw-Rascle model that describes the traffic in multi-lanes in a highway [42]. This specific 2D Aw-Rascle model is the simplest generalization of the macroscopic Aw-Rascle-Zhang model in higher dimensions. It consists of three first-order hyperbolic partial differential equations which describe the evolution of the vehicle density and of the two velocities in the plane. Other extensions of this model have been considered in [43,44,45].

For the 2D Aw-Rascle model, we performed a detailed symmetry classification and we determine the one-dimensional optimal system. The Lie symmetries are applied to determine similarity transformations and find closed-form exact solutions. We investigate the Lie symmetries for the 2D Aw-Rascle model expressed in the Euler and in the Lagrange variables. The systems are equivalent; however, they are related based on a nonlocal transformation, which means that the point symmetries are not survived. Thus, with this study, we would also to investigate if there exists a preference frame for the symmetry analysis of the such hydrodynamics models. For the system expressed in the Euler variables, we found that the admitted Lie symmetries in the generic case form a seven-dimensional Lie algebra, while for special values of the free parameters, additional symmetries exist. On the other hand, for the equivalent system in the Lagrange variables, the dynamical system admits infinity Lie symmetries with a five dimensional finite subalgebra. Consequently, there are differences in the admitted Lie symmetries in the two frames.

For the one-dimensional Aw-Rascle, there are various known exact solutions which describe shock waves [46], solitary waves [47], and others [48,49]. As far as our knowledge extends, no nontrivial exact and analytic solutions for the 2D Aw-Rascle system have been discovered in the existing literature. Instead, researchers have relied on numerical techniques to solve the 2D Aw-Rascle equations. This characteristic of the research renders our study notably relevant and valuable for solving the traffic estimation problem. The paper’s structure is outlined as follows.

In Section 2, we present the 2D Aw-Rascle model. The basic properties and definitions of the Lie symmetry analysis are presented in Section 3. The main results of this work are presented in Section 4, where we give the complete symmetry analysis for the 2D Aw-Rascle in the Euler and in the Lagrange variables, respectively. New similarity closed-form solutions are presented. Finally, in Section 5, we draw our conclusions.

2. The 2D Aw-Rascle Model

Macroscopic traffic flow models have been proved to be in consistency with short-term forecast for traffic management since they can provide shock wave and collisions behaviours. The simplest macroscopic model for traffic estimation is the Lighthill-Whitham-Richards (LWR) model related to the density $\rho$ of the one-dimensional traffic with a flux function $Q$ with the first-order partial differential equation [50,51,52]

$${\rho }_{,t}+Q_{,x}=0.$$

(1)

The main assumption of the LWR model is that all vehicles have the same velocity, which however, is not true in real situations.

The 1D Aw-Rascle model [53] is a second-order model for the traffic estimation where the flux $Q=\rho u$ and

$${\rho }_{,t}+{\left(\rho u\right)}_{,x}=0,$$

(2)

$$u_{,t}+\left(u-\rho p_{,\rho }\left(\rho \right)\right)u_{,x}=\frac{V\left(\rho \right)-u}{\tau },$$

(3)

in which $p\left(\rho \right)$ is a the pressure component for the traffic flow, considered to be $p\left(\rho \right)=p_0{\rho }^{\gamma }$, $\gamma >0$, and constant $\tau$ is the relaxation time which describes drivers’ driving behaviour adapting to equilibrium density-velocity relation over time. $V\left(\rho \right)$ defines the equilibrium velocity-density relation, and it is a decreasing function.

A similar second-order traffic estimation model was proposed independently by Zhang [54]

$${\rho }_{,t}+{\left(\rho u\right)}_{,x}=0,$$

(4)

$$u_{,t}+\left(u+\rho V_{,\rho }\left(\rho \right)\right)u_{,x}=0.$$

(5)

The combination of the latter two second-order models leads to the so-called 1D Aw-Rascle-Zhang model.

A simple generalization of the 1D Aw-Rascle-Zhang model for traffic estimation in multi-lane highways was proposed in [42]. Multi-lane models introduce the coupling of the vehicles with lane-changing [55].

In the Euler variables, the 2D Aw-Rascle model for traffic flow is [42]

$${\rho }_{,t}+{\left(\rho u\right)}_{,x}+{\left(\rho v\right)}_{,y}=0,$$

(6)

$${\left(\rho w\right)}_{,t}+{\left(\rho wu\right)}_{,x}+{\left(\rho wv\right)}_{,y}=0,$$

(7)

$${\left(\rho \sigma \right)}_{,t}+{\left(\rho \sigma u\right)}_{,x}+{\left(\rho \sigma v\right)}_{,y}=0,$$

(8)

where $u\left(t,x,y\right)$, $v\left(t,x,y\right)$ are the velocity components of the two different lanes and functions $w\left(t,x,y\right)$ and $\sigma \left(t,x,y\right)$ are defined as

$$w\left(t,x,y\right)=u\left(t,x,y\right)+P_1\left(\rho \left(t,x,y\right)\right)\mathrm{and}\sigma \left(t,x,y\right)=v\left(t,x,y\right)+P_2\left(\rho \left(t,x,y\right)\right),$$

(9)

in which $P_1\left(\rho \right)$ and $P_2\left(\rho \right)$ are the traffic pressures. In the following, we consider $P_1\left(\rho \right)=\alpha {\rho }^{{\gamma }_1}$ and $P_2\left(\rho \right)=\beta {\rho }^{{\gamma }_2}$.

In the Lagrange variables, the 2D Aw-Rascle model reads [42]

$${\tau }_{,t}-u_{,\chi }^L-v_{,\psi }^L=0$$

(10)

$$w_{,t}^L=0,{\sigma }_{,t}^L=0$$

(11)

where now

$$w^L\left(t,\chi ,\psi \right)=u^L\left(t,\chi ,\psi \right)+{\overline{P}}_1\left(\tau \left(t,\chi ,\psi \right)\right),{\sigma }^L\left(t,\chi ,\psi \right)=v^L\left(t,\chi ,\psi \right)+{\overline{P}}_2\left(\tau \left(t,\chi ,\psi \right)\right),$$

(12)

where now $\tau =\frac{1}{\rho }$, and $dx={\tau }^L\left(t,\chi ,\psi \right)d\chi ,dy={\tau }^L\left(t,x,\psi \right)d\psi$. Therefore, ${\overline{P}}_1\left(\tau \right)=\alpha {\rho }^{{\delta }_1}$ and ${\overline{P}}_2\left(\tau \right)=\beta {\rho }^{{\delta }_2},$ in which ${\delta }_1=-{\gamma }_1$, ${\delta }_2=-{\gamma }_2.$

In the following, we study the group properties for the dynamical systems (6)–(8) and (10)–(12) respectively.

3. The Theory of Lie Symmetries

In this section, we briefly discuss the basic properties and definitions of Sophus Lie theory on the symmetries of differential equations.

Consider a map of a one-parameter point transformation which transforms points $P\to P^{\prime }$ defined by the function $\mathbf{\Phi }$, that is, $\mathbf{\Phi }\left(P\left(t,x,y\right)\right)=P^{\prime }\left(t^{\prime },x^{\prime },y^{\prime }\right)$ and corresponding infinitesimal transformation with generator the vector field [56]

$$\mathbf{X}={\xi }^t\left(t,x,y,\mathbf{u}\right){\partial }_t+{\xi }^x\left(t,x,y,\mathbf{u}\right){\partial }_x+{\xi }^y\left(t,x,y,\mathbf{u}\right){\partial }_y+\mathsf{ȷ}\left(t,x,y,\mathbf{u}\right){\partial }_{\mathbf{u}}.$$

(13)

Variables $\left\{t,x,y\right\}$ are the independent variables of the dynamical system $\mathbf{u}\left(t,x,y\right)$ are the dependent variables where for the two-dimensional Aw-Rascle model $dim\mathbf{u}\left(t,x\right)=3$, and $\mathbf{u}\left(t,x\right)={\left(\rho \left(t,x,y\right),u\left(t,x,y\right),v\left(t,x,y\right)\right)}^T$.

We can define the generator of the infinitesimal transformation as follows:

$$\mathbf{X}=\frac{\partial t^{\prime }}{\partial \epsilon }{\partial }_t+\frac{\partial x^{\prime }}{\partial \epsilon }{\partial }_x+\frac{\partial y^{\prime }}{\partial \epsilon }{\partial }_y+\frac{\partial \mathbf{u}}{\partial \epsilon }{\partial }_{\mathbf{u}},$$

(14)

or equivalently

$$\mathbf{X}={\xi }^t\left(t,x,y,\mathbf{u}\right){\partial }_t+{\xi }^x\left(t,x,y,\mathbf{u}\right){\partial }_x+{\xi }^y\left(t,x,y,\mathbf{u}\right){\partial }_y+\mathsf{ȷ}\left(t,x,y,\mathbf{u}\right){\partial }_{\mathbf{u}}.$$

(15)

The vector field $\mathbf{X}$ is a Lie point symmetry for the system of differential equations:

$$\mathcal{H}\left(t,x,y,\mathbf{u},{\mathbf{u}}_{,t},{\mathbf{u}}_{,x},\dots \right)=0,$$

(16)

if and only if

$$\underset{\epsilon \to 0}{lim}\frac{\mathbf{\Phi }\left(\mathcal{H}\left(t,x,y,\mathbf{u},{\mathbf{u}}_{,t},{\mathbf{u}}_{,x},\dots \right)\right)-\mathcal{H}\left(t,x,y,\mathbf{u},{\mathbf{u}}_{,t},{\mathbf{u}}_{,x},\dots \right)}{\epsilon }=0.$$

(17)

Equation (17) defines the Lie derivative of a function $\mathcal{H}$ along the vector field X, that is, expression (17) is written in the equivalent form [5]:

$${\mathcal{L}}_{{\mathbf{X}}^{\left[n\right]}}\left(\mathcal{H}\left(t,x,y,\mathbf{u},{\mathbf{u}}_{,t},{\mathbf{u}}_{,x},\dots \right)\right)=0,$$

(18)

where ${\mathbf{X}}^{\left[n\right]}$ is now the nth-extension of $\mathbf{X}$ in the jet-space $\left\{t,x,y,\mathbf{u},{\mathbf{u}}_t,{\mathbf{u}}_x,\dots ,{\mathbf{u}}_{i_1,\dots ,i_n}\right\},$ defined as

$${\mathbf{X}}^{\left[n\right]}=\mathbf{X}+{\eta }^{\left[t\right]}{\partial }_{{\mathbf{u}}_t}+{\eta }^{\left[x\right]}{\partial }_{{\mathbf{u}}_x}+{\eta }^{\left[y\right]}{\partial }_{{\mathbf{u}}_y}+\dots {\eta }^{\left[i_1{i}_2\dots i_n\right]}{\partial }_{u_{i_1{i}_2\dots i_n},}$$

(19)

with

$${\eta }^{\left[i\right]}=D_i\eta -{\xi }^i{\mathbf{u}}_i,$$

(20)

$${\eta }^{\left[i_1{i}_2\dots i_n\right]}=D_{i_n}{\eta }^{\left[i_1{i}_2\dots i_{n-1}\right]}-{\xi }^{i_n}{\mathbf{u}}_{i_1{i}_2\dots i_n},$$

(21)

in which $i=t,x,y$.

The admitted point transformations, which leave a given differential equation invariant, form a closed Lie group, while the corresponding generators $\mathbf{X}$ form a Lie algebra under the operation of taking the Lie Bracket. Hence, if ${\mathbf{u}}_{sol}\left(t,x,y\right)$ is a solution of the differential equation $\mathcal{H}\left(t,x,\mathbf{u},{\mathbf{u}}_{,t},{\mathbf{u}}_{,x},\dots \right)=0,$ and $\mathbf{X}$ is a Lie symmetry, then under the one-parameter point transformation with map $\mathsf{\Phi }$, ${\mathbf{u}}_{sol}^{\prime }\left(t^{\prime },x^{\prime },y^{\prime }\right)=\mathbf{\Phi }\left({\mathbf{u}}_{sol}\left(t,x,y\right)\right)$, function ${\mathbf{u}}_{sol}^{\prime }$ is also a solution of the differential equation $\mathcal{H}\left(t,x,y,\mathbf{u},{\mathbf{u}}_{,t},{\mathbf{u}}_{,x},\dots \right)=0$. We shall say that Lie symmetries drag solution trajectories to solution trajectories.

The existence of a Lie symmetry for a given system of differential equations means that there exists a point transformation where the differential equation can be simplified. Let $\mathbf{X}$ be a Lie symmetry; then, we can define a set of new variables

$$\left(Y^J,\mathbf{U}\right)=\left(Y^J\left(t,x,y,\mathbf{u}\right),\mathbf{U}\left(t,x,y,\mathbf{u}\right)\right),$$

(22)

such that $\mathbf{X}$ is written in the canonical form $\mathbf{X}={\partial }_I$, where it holds

$$\mathbf{X}\left(Y^J\right)={\delta }_I^J,\mathbf{X}\left(\mathbf{U}\right)=0.$$

(23)

Consequently, in the canonical variables, the number of independent variables is reduced by one in the case of partial differential equations. The transformation which gives the canonical variables is called similarity transformation, and the resulting solutions are known as similarity solutions or invariant solutions.

One-Dimensional Optimal System

Not all the similarity transformations related to the Lie symmetries of a differential equation lead to independent similarity solutions, that is, because there exist a map, known as the Adjoint representation of the Lie algebra, which connects the similarity solutions. The classification of all the independent similarity transformation is essential for the complete Lie symmetry analysis of differential equations. The one-dimensional Lie algebras with independent similarity transformations form the one-dimensional optimal system [57].

Now, assume the $\kappa$th-dimensional Lie algebra $G_{\kappa }$ with elements $\left\{X_1,X_2,\dots X_n\right\}$ and structure constants $C_{BC}^A$, $A,B,C=1,2,3\dots \kappa$, i.e., $\left[X_A,X_B\right]=C_{BC}^A{X}_A.$

The two generic Lie symmetry vectors

$$\mathbf{Z}=\sum _{A=1}^{\kappa }{a}_A{X}_A,\mathbf{W}=\sum _{A=1}^{\kappa }{b}_A{X}_A,$$

(24)

are equivalent if and only if

$$\mathbf{W}=\prod _{i=1}^{n}Ad\left(exp\left({ϵ}_A{X}_A\right)\right)\mathbf{Z}$$

(25)

or

$$\mathbf{W}=c\mathbf{Z},c=const\mathrm{that}\mathrm{is}{b}_A=c{a}_A,$$

(26)

where $a_A,$$b_A$ are constant coefficients and $Ad\left(exp\left({ϵ}_A{X}_A\right)\right)$ is the Adjoint operator expressed as

$$Ad\left(exp\left(ϵX_A\right)\right)X_B=X_B-ϵ\left[X_A,X_B\right]+\frac{1}{2}{ϵ}^2\left[X_A,\left[X_A,X_B\right]\right]+\dots .$$

(27)

The one-dimensional subalgebras of $G_{\kappa }$, which are not related through the Adjoint representation, form the one-dimensional optimal system. The determination of the one-dimensional system is essential in order to perform a complete classification of all the possible similarity transformations and solutions.

The independent constants coefficients $a_A$ are invariant functions of the Adjoint operator $Ad$. Specifically, if $\varphi \left(a_A\right)$ is a function of $a_A$, the invariants are given by the linear system of partial differential equations:

$${\Delta }_A\left(\varphi \right)=C_{BC}^A{a}^B\frac{\partial \varphi }{\partial a^C}\equiv 0.$$

(28)

The latter system is essential for the derivation of the one-dimensional system.

4. Lie Symmetries in the Euler Variables

In this section, we proceed with the application of the Lie symmetry condition (18) for the derivation of the one-parameter point transformations where the 2D Aw-Rascle model expressed in the Euler variables is invariant.

4.1. Lie Symmetries for Arbitrary Parameters ${\gamma }_1$ and ${\gamma }_2$

For arbitrary values of the free parameters ${\gamma }_1$ and ${\gamma }_2$, the admitted Lie symmetries for the 2D Aw-Rascle system (6)–(8) are

$$X_1={\partial }_t,X_2={\partial }_x,X_3={\partial }_y,$$

$$X_4=t{\partial }_t+x{\partial }_x+y{\partial }_y,X_5=t{\partial }_x+{\partial }_u,X_6=t{\partial }_y+{\partial }_v,$$

$$X_7={\gamma }_{2}t{\partial }_t+\left({\gamma }_2-{\gamma }_1\right)x{\partial }_x-\rho {\partial }_{\rho }-{\gamma }_{1}u{\partial }_u+{\gamma }_{2}v{\partial }_v.$$

The admitted Lie symmetries form a seven-dimensional Lie algebra, namely $G_7$ with nonzero commutators:

$$\left[X_1,X_4\right]=X_1,\left[X_1,X_5\right]=X_2,\left[X_1,X_6\right]=X_3,$$

$$\left[X_1,X_7\right]={\gamma }_2{X}_1,\left[X_2,X_4\right]=X_2,\left[X_2,X_7\right]=\left({\gamma }_2-{\gamma }_1\right)X_1,$$

$$\left[X_3,X_4\right]=X_3,\left[X_5,X_7\right]={\gamma }_1{X}_5,\left[X_6,X_7\right]={\gamma }_2{X}_6.$$

In Table 1, we summarize the commutators for the seven-dimensional Lie algebra $G_7$. In the Morozov-Mubarakzyanov Classification Scheme [58,59,60,61], the Lie algebra $G_7$ is expressed as $\left\{3A_1{\otimes }_s{A}_1\right\}{\otimes }_s{A}_{3,3}.$ Furthermore, in Table 2, we present the Adjoint representation for the Lie algebra $G_7$.

Table 1. Commutator table for the admitted Lie point symmetries for the 2D Aw-Rascle system in Euler variables.

$\left[{\mathit{X}}_{\mathit{I}},{\mathit{X}}_{\mathit{J}}\right]$	${\mathit{X}}_1$	${\mathit{X}}_2$	${\mathit{X}}_3$	${\mathit{X}}_4$	${\mathit{X}}_5$	${\mathit{X}}_6$	${\mathit{X}}_7$
${\mathbf{X}}_1$	0	0	0	$X_1$	$X_2$	$X_3$	${\gamma }_2{X}_1$
${\mathbf{X}}_2$	0	0	0	$X_2$	0	0	$\left({\gamma }_2-{\gamma }_1\right)X_1$
${\mathbf{X}}_3$	0	0	0	$X_3$	0	0	0
${\mathbf{X}}_4$	$-X_1$	$-X_2$	$-X_3$	0	0	0	0
${\mathbf{X}}_5$	$-X_2$	0	0	0	0	0	${\gamma }_1{X}_5$
${\mathbf{X}}_6$	$-X_3$	0	0	0	0	0	${\gamma }_2{X}_6$
${\mathbf{X}}_7$	$-{\gamma }_2{X}_1$	$-\left({\gamma }_2-{\gamma }_1\right)X_1$	0	0	$-{\gamma }_1{X}_5$	$-{\gamma }_2{X}_6$	0

Table 2. Adjoint representation for the admitted Lie point symmetries of for the 2D Aw-Rascle system in Euler variables.

$\mathit{Ad}\left({\mathit{e}}^{\mathit{\epsilon }{\mathit{X}}_{\mathit{\mu }}}\right){\mathit{X}}_{\mathit{\nu }}$	${\mathit{X}}_1$	${\mathit{X}}_2$	${\mathit{X}}_3$	${\mathit{X}}_4$	${\mathit{X}}_5$	${\mathit{X}}_6$	${\mathit{X}}_7$
${\mathbf{X}}_1$	$X_1$	$X_2$	$X_3$	$X_4-\epsilon X_1$	$X_5-\epsilon X_2$	$X_6-\epsilon X_3$	$X_7-{\gamma }_2{X}_1$
${\mathbf{X}}_2$	$X_1$	$X_2$	$X_3$	$X_4-\epsilon X_2$	$X_5$	$X_6$	$X_7-\epsilon \left({\gamma }_2-{\gamma }_1\right)X_2$
${\mathbf{X}}_3$	$X_1$	$X_2$	$X_3$	$X_4-\epsilon X_3$	$X_5$	$X_6$	$X_7$
${\mathbf{X}}_4$	$e^{\epsilon }{X}_1$	$e^{\epsilon }{X}_2$	$e^{\epsilon }{X}_3$	$X_4$	$X_5$	$X_6$	$X_7$
${\mathbf{X}}_5$	$X_1+\epsilon X_2$	$X_2$	$X_3$	$X_4$	$X_5$	$X_6$	$X_7+\epsilon {\gamma }_1{X}_5$
${\mathbf{X}}_6$	$X_1+\epsilon X_3$	$X_2$	$X_3$	$X_4$	$X_5$	$X_6$	$X_7+\epsilon {\gamma }_2{X}_6$
${\mathbf{X}}_7$	$e^{{\gamma }_2\epsilon }{X}_1$	$e^{\left({\gamma }_2-{\gamma }_1\right)\epsilon }{X}_2$	$X_3$	$X_4$	$e^{-\epsilon {\gamma }_1}{X}_5$	$e^{-\epsilon {\gamma }_2}{X}_6$	$X_7$

Lie Symmetries for ${\gamma }_1={\gamma }_2$

In the special case where ${\gamma }_1={\gamma }_2=\gamma$, there exist additional Lie symmetries admitted by the 2D Aw-Rascle system (6)–(8). In particular, the admitted Lie symmetries form a ten-dimensional Lie algebra, namely $G_{10}$, with subalgebra $G_7$ studied before and the additional Lie symmetries

$$X_8=\left(\beta x-\alpha x\right){\partial }_y+\left(\beta u-\alpha v\right){\partial }_v,$$

$$X_9=\alpha \beta t{\partial }_t+{\alpha }^{2}y{\partial }_x-{\beta }^{2}x{\partial }_y+\left({\alpha }^2-\alpha \beta u\right){\partial }_u-\left(\alpha \beta v-u{\beta }^2\right){\partial }_v,$$

$$X_{10}=\gamma \left(\alpha y-\beta x\right){\partial }_t+\left(\beta u-\alpha v\right)\rho {\partial }_{\rho }+\gamma \left(\beta u^2-\alpha uv\right){\partial }_u-\gamma \left(\alpha v^2-\beta uv\right){\partial }_v.$$

For the Lie algebra $G_{10}$, the additional nonzero commutators are

$$\left[X_5,X_8\right]=\beta X_6,\left[X_5,X_9\right]=-\alpha \beta X_5+{\beta }^2{X}_6,$$

$$\left[X_5,X_{10}\right]=\beta X_7-\frac{\gamma }{\alpha }{X}_9-\gamma \frac{\beta }{\alpha }{X}_8-\gamma \beta X_4,$$

$$\left[X_6,X_8\right]=-\alpha X_6,\left[X_6,X_8\right]={\alpha }^2{X}_5-\alpha \beta X_6,$$

$$\left[X_6,X_{10}\right]=-\alpha X_7+\gamma X_8,\left[X_7,X_{10}\right]=\gamma X_{10}.$$

4.2. One-Dimensional Optimal System

The first step for the derivation of the one-dimensional optimal system which corresponds to the Lie algebra $G_7$ is the calculation of the invariants for the Adjoint representation.

Therefore, from expression (28) and Table 1, we end with the following linear system of partial differential equations:

$$\left(a_4+a_7{\gamma }_2\right)\frac{\partial \varphi }{\partial a_1}+a_5\frac{\partial \varphi }{\partial a_2}+a_6\frac{\partial \varphi }{\partial a_3}=0,$$

(29)

$$a_4\frac{\partial \varphi }{\partial a_2}+a_7\left({\gamma }_2-{\gamma }_1\right)\frac{\partial \varphi }{\partial a_1}=0,$$

(30)

$$a_4\frac{\partial \varphi }{\partial a_3}=0,$$

(31)

$$a_1\frac{\partial \varphi }{\partial a_1}+a_2\frac{\partial \varphi }{\partial a_2}+a_3\frac{\partial \varphi }{a_3}=0,$$

(32)

$$a_1\frac{\partial \varphi }{\partial a_2}-a_7{\gamma }_1\frac{\partial \varphi }{\partial a_5}=0,$$

(33)

$$a_1\frac{\partial \varphi }{\partial a_3}-a_7{\gamma }_2\frac{\partial \varphi }{\partial a_6}=0,$$

(34)

$$\left(a_1{\gamma }_2+a_2\left({\gamma }_2-{\gamma }_1\right)\right)\frac{\partial \varphi }{\partial a_1}+a_5{\gamma }_1\frac{\partial \varphi }{\partial a_5}+a_6{\gamma }_2\frac{\partial \varphi }{\partial a_6}=0.$$

(35)

The solution to the latter system is $\varphi =\varphi \left(a_4,a_7\right)$ from where it follows that the invariants of the Adjoint representation are $a_4$ and $a_7$.

Assume now case $a_4{a}_7$ and the generic symmetry vector are

$$X=a_1{X}_1+a_2{X}_2+a_3{X}_3+a_4{X}_4+a_5{X}_5+a_6{X}_6+a_7{X}_7;$$

(36)

then, the vector field

$$\widehat{X}=Ad\left(e^{{\epsilon }_1{X}_1}\right)\left(Ad\left(e^{{\epsilon }_2{X}_2}\right)\left(Ad\left(e^{{\epsilon }_3{X}_3}\right)\left(Ad\left(e^{{\epsilon }_{5}X{5}_5}\right)\left(Ad\left(e^{{\epsilon }_6{X}_6}\right)X\right)\right)\right)\right),$$

for specific values of the parameters ${\epsilon }_1,{\epsilon }_2$, ${\epsilon }_3$, ${\epsilon }_5$, and ${\epsilon }_6$ read

$$\widehat{X}={\widehat{a}}_4{X}_4+{\widehat{a}}_7{X}_7.$$

(37)

which is the equivalent symmetry vector to the generic vector field X.

When $a_7=0$ and the Lie algebra $G_6=\left\{X_1,X_2,X_3,X_4,X_5,X_6\right\}$, the invariants of the Adjoint representation for the $G_6$ are given by the following system:

$$a_4\frac{\partial \varphi }{\partial a_1}+a_5\frac{\partial \varphi }{\partial a_2}+a_6\frac{\partial \varphi }{\partial a_3}=0,$$

(38)

$$a_1\frac{\partial \varphi }{\partial a_1}+a_2\frac{\partial \varphi }{\partial a_2}+a_3\frac{\partial \varphi }{a_3}=0,$$

(39)

$$a_4\frac{\partial \varphi }{\partial a_2}=0,a_4\frac{\partial \varphi }{\partial a_3}=0,$$

(40)

$$a_1\frac{\partial \varphi }{\partial a_2}=0,a_1\frac{\partial \varphi }{\partial a_3}=0.$$

(41)

We calculate $\varphi =\varphi \left(a_4,a_5,a_6\right)$ from where we infer that $a_4,a_5$ and $a_6$ are the invariants.

Therefore, the generic symmetry vector field X can be written in the equivalent form:

$$\check{X}={\check{a}}_4{X}_4+{\check{a}}_5{X}_5+{\check{a}}_6{X}_6.$$

(42)

Similarly, for $a_4=0$, the unique invariant of the Adjoint representation is $a_7$, which means that the generic vector field X can be written as the symmetry vector:

$$\overline{X}={\overline{a}}_7{X}_7.$$

(43)

Finally, for $a_4=0$ and $a_7=0$, the invariants of the Adjoint representation are $a_1,a_5$ and $a_6$, from where it follows that the generic symmetry vector can be written in the equivalent form:

$$\mathring{X}={\mathring{a}}_1{X}_1+{\mathring{a}}_5{X}_5+{\mathring{a}}_6{X}_6.$$

(44)

In a similar way, we conclude that if $a_4=0$, $a_7=0$ and $a_6=0$, the generic symmetry vector field is

$${\mathring{X}}^{\prime }={\mathring{a}}_1^{\prime }{X}_1+{\mathring{a}}_5^{\prime }{X}_5+{\mathring{a}}_3^{\prime }{X}_3,$$

while for $a_4=0$, $a_7=0$ and $a_5=0$, it follows

$${\mathring{X}}^{″}={\mathring{a}}_1^{″}{X}_1+{\mathring{a}}_2^{″}{X}_2+{\mathring{a}}_6^{″}{X}_6.$$

(45)

Finally for $a_4=0$, $a_5=0$, $a_6=0$ and $a_7=0,$ we have the invariants $a_1,a_2$ and $a_3$ with generic vector field:

$$\tilde{X}={\tilde{a}}_1{X}_1+{\tilde{a}}_2{X}_2+{\tilde{a}}_3{X}_3.$$

We conclude that the one-dimensional optimal system for the 2D Aw-Rascle system (6)–(8) and arbitrary nonzero parameters ${\gamma }_1$, ${\gamma }_2$, consists of one-dimensional Lie algebras:

$$\left\{X_1\right\},\left\{X_2\right\},\left\{X_3\right\},\left\{X_1+a{X}_2\right\},$$

$$\left\{X_1+a{X}_3\right\},\left\{X_2+a{X}_3\right\},\left\{X_1+a{X}_2+b{X}_3\right\},$$

$$\left\{X_5\right\},\left\{X_1+a{X}_5\right\},\left\{X_5+a{X}_3\right\},\left\{X_1+a{X}_5+b{X}_3\right\}$$

$$\left\{X_6\right\},\left\{X_1+a{X}_6\right\},\left\{X_6+a{X}_2\right\},\left\{X_1+a{X}_6+b{X}_2\right\}$$

$$\left\{X_5+a{X}_6\right\},\left\{X_1+a{X}_5+a{X}_6\right\},$$

$$\left\{X_4\right\},\left\{X_4+a{X}_5\right\},\left\{X_4+a{X}_6\right\},$$

$$\left\{X_4+a{X}_5+b{X}_6\right\},\left\{X_7\right\},\left\{X_4+a{X}_7\right\}.$$

4.3. Similarity Solutions

In order to demonstrate the novelty of the Lie symmetries, we continue with the application of the Lie invariants in order to reduce the system of partial differential equations and to determine closed-form similarity solutions. Since the dynamical system has three independent variables, we have to make use of two Lie symmetries so that the reduced equations are ordinary differential equations.

Consider the two symmetry vectors $\left\{X_5,X_6\right\};$ then, the resulting similarity transformation is

$$\rho =\rho \left(t\right),u=\frac{x}{t}+U\left(t\right),v=\frac{y}{t}+V\left(t\right),$$

(46)

where the 2D Aw-Rascle system (6)–(8) now becomes

$$\begin{array}{ccc}\hfill t{\rho }_{,t}+2\rho & =& 0,\hfill \end{array}$$

(47)

$$\begin{array}{ccc}\hfill t{U}_{,t}+\left(U-2\alpha {\gamma }_1{\rho }^{{\gamma }_1}\right)& =& 0,\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill t{V}_{,t}+\left(V-2\beta {\gamma }_2{\rho }^{{\gamma }_2}\right)& =& 0,\hfill \end{array}$$

(49)

where the closed-form solution reads

$$\begin{array}{ccc}\hfill \rho \left(t\right)& =& \frac{{\rho }_0}{t^2},\hfill \end{array}$$

(50)

$$\begin{array}{ccc}\hfill U\left(t\right)& =& -\frac{2{\gamma }_1{\rho }_0^{1+{\gamma }_1}{t}^{1-2{\gamma }_1}-U_1}{\left(2{\gamma }_1-1\right){\rho }_{0}t},\hfill \end{array}$$

(51)

$$\begin{array}{ccc}\hfill V\left(t\right)& =& -\frac{2{\gamma }_2{\rho }_0^{1+{\gamma }_2}{t}^{1-2{\gamma }_2}-V_1}{\left(2{\gamma }_2-1\right){\rho }_{0}t}.\hfill \end{array}$$

(52)

Therefore, at $t\to \infty$, $\left(\rho ,U,V\right)\to \left(0,0,0\right)$ for ${\gamma }_1>0$, ${\gamma }_2>0$.

Similarly, the application of the vector fields $\left\{X_5,X_1+X_2\right\}$ provides the similarity transformation

$$\rho =\rho \left(t\right),u=\frac{x-y}{t}+U\left(t\right),v=V\left(t\right),$$

and reduced system

$$\begin{array}{ccc}\hfill t{\rho }_{,t}+\rho & =& 0,\hfill \end{array}$$

(53)

$$\begin{array}{ccc}\hfill t{U}_{,t}-\left(V-U+\alpha {\gamma }_1{\rho }^{{\gamma }_1}\right)& =& 0,\hfill \end{array}$$

(54)

$$\begin{array}{ccc}\hfill t{V}_{,t}-{\gamma }_2\beta {\rho }^{{\gamma }_2}& =& 0.\hfill \end{array}$$

(55)

Hence, the closed-form solution is

$$\begin{array}{ccc}\hfill \rho & =& \frac{{\rho }_0}{t},\hfill \end{array}$$

(56)

$$\begin{array}{ccc}\hfill U\left(t\right)& =& -\frac{\alpha {\gamma }_1}{{\gamma }_1-1}{\left(\frac{{\rho }_0}{t}\right)}^{{\gamma }_1}+\frac{\beta }{{\gamma }_2-1}{\left(\frac{{\rho }_0}{t}\right)}^{{\gamma }_2}+\frac{V_1}{{\rho }_0}+\frac{U_1}{t},\hfill \end{array}$$

(57)

$$\begin{array}{ccc}\hfill V\left(t\right)& =& {\left(\frac{{\rho }_0}{t}\right)}^{{\gamma }_2}\beta +\frac{V_1}{{\rho }_0}.\hfill \end{array}$$

(58)

Consequently, at $t\to \infty$, $\left(\rho ,U,V\right)\to \left(0,\frac{V_1}{{\rho }_0},\frac{V_1}{{\rho }_0}\right)$ for ${\gamma }_1>0$, ${\gamma }_2>0$.

Furthermore, if we consider the vector fields $\left\{X_5,X_7+X_4\right\}$ for ${\gamma }_1=1$, ${\gamma }_2=2$, we determine the close-form solution

$$\rho =\frac{\varrho \left(\xi \right)}{t},u=\frac{x}{t}+U\left(\xi \right),v=V\left(\xi \right),\xi =yt,$$

(59)

in which

$$\varrho \left(\xi \right)=-\frac{\xi }{3},U\left(\xi \right)=2\alpha \sqrt{\frac{\xi }{3\beta }},V\left(\xi \right)=\sqrt{\frac{\xi }{3\beta }}.$$

(60)

On the other hand, application of the Lie symmetry vectors $\left\{X_6,X_7+X_4\right\}$ for ${\gamma }_1=1$, ${\gamma }_2=2$, gives the closed-form solution:

$$\rho =\frac{{\rho }_0}{t},u=-\frac{{\rho }_0\alpha }{t},v=\frac{y}{t}+v_1{e}^{-\frac{t}{{\rho }_0\alpha }}-2{\rho }_0^2\beta .$$

(61)

with a limit at $t\to \infty$, $\left(\rho ,u,v\right)=\left(0,0,-2{\rho }_0^2\beta \right)$.

5. Lie Symmetries in the Lagrange Variables

We proceed with the derivation of the Lie symmetries for the 2D Aw-Rascle model in the Lagrange variables, that is, for the system (10) and (11). In the Lagrange variables, the independent variables are $\left\{t,\chi ,\psi \right\}$ and the dependent variables are $\left\{\tau ,u^L,v^L\right\}$.

The Lie symmetry condition (18) gives that the admitted Lie symmetries of the system (10) and (11) form an infinity Lie algebra, $G_{\infty }$, consisting of the vector fields:

$$Y_1={\partial }_t,Y_2={\partial }_{\chi },Y_3={\partial }_{\psi },Y_4=t{\partial }_t+\chi {\partial }_{\chi }+\psi {\partial }_{\psi },$$

$$Y_5=\left({\delta }_2+2\right)t{\partial }_t+{\delta }_2\chi {\partial }_{\chi }+{\delta }_1\psi {\partial }_{\psi }-\tau {\partial }_{\tau }-{\delta }_1{u}^L{\partial }_{u^L}-{\delta }_2{v}^L{\partial }_{v^L},$$

$$Y_{\infty }=F_1\left(\chi ,\psi \right){\partial }_{u^L}+F_2\left(\chi ,\psi \right){\partial }_{v^L};{\left(F_1\right)}_{,\chi }+{\left(F_2\right)}_{,\psi }=0.$$

In the following, we focus on the five-dimensional Lie algebra: $G_5=\left\{Y_1,Y_2,Y_3,Y_4,Y_5\right\}$.

The nonzero commutators for the Lie algebra $G_5$ are

$$\left[Y_1,Y_4\right]=Y_1,\left[Y_1,Y_5\right]=\left({\delta }_2+2\right)Y_1,$$

$$\left[Y_2,Y_4\right]=Y_2,\left[Y_2,Y_5\right]={\delta }_2{Y}_2,$$

$$\left[Y_3,Y_4\right]=Y_3,\left[Y_3,Y_5\right]={\delta }_1{Y}_3.$$

Therefore, we conclude that $G_5$ is expressed as the $3A_1{\otimes }_{s}2A_1$ Lie algebra with commutators given in Table 3, while the corresponding Adjoint representation is given in Table 4.

Table 3. Commutator table for the admitted Lie point symmetries for the 2D Aw-Rascle system in Lagrange variables.

$\left[{\mathit{Y}}_{\mathit{I}},{\mathit{Y}}_{\mathit{J}}\right]$	${\mathit{Y}}_1$	${\mathit{Y}}_2$	${\mathit{Y}}_3$	${\mathit{Y}}_4$	${\mathit{Y}}_5$
${\mathbf{Y}}_1$	0	0	0	$Y_1$	$\left({\delta }_2+2\right)Y_1$
${\mathbf{Y}}_2$	0	0	0	$Y_2$	${\delta }_2{Y}_2$
${\mathbf{Y}}_3$	0	0	0	$Y_3$	${\delta }_1{Y}_3$
${\mathbf{Y}}_4$	$-Y_1$	$-Y_2$	$-Y_3$	0	0
${\mathbf{Y}}_5$	$-\left({\delta }_2+2\right)Y_1$	$-{\delta }_2{Y}_2$	$-{\delta }_1{Y}_3$	0	0

Table 4. Adjoint representation for the admitted Lie point symmetries of for the 2D Aw-Rascle system in Lagrange variables.

$\mathit{Ad}\left({\mathit{e}}^{\mathit{\epsilon }{\mathit{X}}_{\mathit{\mu }}}\right){\mathit{X}}_{\mathit{\nu }}$	${\mathit{Y}}_1$	${\mathit{Y}}_2$	${\mathit{Y}}_3$	${\mathit{Y}}_4$	${\mathit{Y}}_5$
${\mathbf{Y}}_1$	$Y_1$	$Y_2$	$Y_3$	$Y_4-\epsilon Y_1$	$Y_5-\left({\delta }_2+2\right)Y_1$
${\mathbf{Y}}_2$	$Y_1$	$Y_2$	$Y_3$	$Y_4-\epsilon Y_2$	$Y_5-{\delta }_2{Y}_2$
${\mathbf{Y}}_3$	$Y_1$	$Y_2$	$Y_3$	$Y_4-\epsilon Y_3$	$Y_5-{\delta }_1{Y}_3$
${\mathbf{Y}}_4$	$e^{\epsilon }{Y}_1$	$e^{\epsilon }{Y}_2$	$e^{\epsilon }{Y}_3$	$Y_4$	$Y_5$
${\mathbf{Y}}_5$	$e^{-\left({\delta }_2+2\right)\epsilon }{Y}_1$	$e^{-{\delta }_2\epsilon }{Y}_2$	$e^{-{\delta }_1\epsilon }{Y}_3$	$Y_4$	$Y_5$

In the special case where ${\delta }_1={\delta }_2$ and when ${\delta }_1=1$ or ${\delta }_2=1$, additional vector fields which describe infinity symmetries for the system (10) and (11) exist. Since in this study, we are interested in the finite symmetries, we focus on the generic case.

We observe that the 2D Aw-Rascle model in the Lagrange variables admits five finite Lie symmetries while the equivalent system in the Euler variables admits seven Lie symmetries. Hence, someone will ask what happened with the symmetries which have been lost. We remark that the transformation between the Euler and the Lagrange variables is a nonlocal transformation; as a result, some of the Lie symmetries for the one system reduce to nonlocal symmetries for the other system. Note that we have focused in the determination of the point symmetries and not in any other kind of symmetry vectors.

5.1. One-Dimensional Optimal System

In order to determine the one-dimensional optimal system, we apply the same procedure as before. Thus, we determine the invariants of the Adjoint representations by solving the following system of linear partial differential equations:

$$\begin{array}{ccc}\hfill \left(a_4+a_5\left({\delta }_2+2\right)\right)\frac{\partial \varphi }{\partial a_1}& =& 0,\hfill \\ \hfill \left(a_4+{\delta }_2{a}_5\right)\frac{\partial \varphi }{\partial a_2}& =& 0,\hfill \\ \hfill \left(a_4+{\delta }_1{a}_5\right)\frac{\partial \varphi }{\partial a_3}& =& 0,\hfill \\ \hfill a_1\frac{\partial \varphi }{\partial a_1}+a_2\frac{\partial \varphi }{\partial a_2}+a_3\frac{\partial \varphi }{\partial a_3}& =& 0,\hfill \\ \hfill a_1\left({\delta }_2+2\right)\frac{\partial \varphi }{\partial a_1}+a_2{\delta }_2\frac{\partial \varphi }{\partial a_2}+a_3{\delta }_1\frac{\partial \varphi }{\partial a_3}& =& 0.\hfill \end{array}$$

That is, $\varphi =\varphi \left(a_4,a_5\right)$, which means that the invariants of the Adjoint representations are the coefficients $a_4$ and $a_5$.

We consider the generic vector field

$$Y=a_1{Y}_1+a_2{Y}_2+a_3{Y}_3+a_4{Y}_4+a_5{Y}_5,$$

(62)

which means that after the application of the Adjoint representation

$$\check{Y}=Ad\left(e^{{\epsilon }_1{Y}_1}\right)\left(Ad\left(e^{{\epsilon }_2{Y}_2}\right)\left(Ad\left(e^{{\epsilon }_3{Y}_3}\right)\left(Y\right)\right)\right),$$

(63)

for specific values of the free parameters ${\epsilon }_1,{\epsilon }_2$, ${\epsilon }_3$, the equivalent form of the generic symmetry vector Y is

$$\check{Y}={\check{a}}_4{Y}_4+{\check{a}}_5{Y}_5.$$

(64)

We conclude that the one-dimensional optimal system for the five-dimensional Lie algebra consists of the Lie algebras

$$\left\{Y_1\right\},\left\{Y_2\right\},\left\{Y_3\right\},\left\{Y_1+a{Y}_2\right\},$$

$$\left\{Y_1+a{Y}_3\right\},\left\{Y_2+a{Y}_3\right\},\left\{Y_1+a{Y}_2+b{Y}_3\right\},$$

$$\left\{Y_4\right\},\left\{Y_4+a{Y}_5\right\}.$$

5.2. Similarity Transformations

From the two symmetry vectors $\left\{Y_1+Y_2+{\partial }_{u^L}+{\partial }_{v^L},Y_1+Y_3\right\}$, we find the similarity transformation:

$$\tau =\tau \left(\zeta \right),u^L=x+U^L\left(\zeta \right),v^L=y+V^L\left(\zeta \right),\zeta =x+y-t$$

(65)

with solution

$$\tau +U^L+V^L=\zeta +{\tau }_0,$$

(66)

$$\begin{array}{ccc}\hfill U^L+\alpha {\tau }^{{\delta }_1}& =& U_0,\hfill \end{array}$$

(67)

$$\begin{array}{ccc}\hfill V^L+\beta {\tau }^{{\delta }_2}& =& V_0.\hfill \end{array}$$

(68)

Similarly, the application of the vector fields $\left\{Y_2+Y_3,Y_4+{\partial }_{u^L}\right\}$ gives the similarity transformation

$$\tau =\tau \left(\lambda \right),u^L=lnt+U\left(\lambda \right),v^L=U\left(\lambda \right),\lambda =\frac{y-x}{t},$$

with solution

$${\left(ln\tau \right)}_{,\lambda }={\left(\lambda \left(\lambda \tau +\alpha {\delta }_1{\tau }^{{\delta }_1}-\beta {\delta }_2{\tau }^{{\delta }_2}\right)\right)}^{-1},$$

(69)

$$U_{,\lambda }=\frac{\beta {\delta }_2{\tau }^{{\delta }_2}-\lambda \tau }{\lambda \left(\lambda \tau +\alpha {\delta }_1{\tau }^{{\delta }_1}-\beta {\delta }_2{\tau }^{{\delta }_2}\right)},$$

(70)

$$V_{,\lambda }=-\frac{\beta {\delta }_2{\tau }^{{\delta }_2}}{\lambda \left(\lambda \tau +\alpha {\delta }_1{\tau }^{{\delta }_1}-\beta {\delta }_2{\tau }^{{\delta }_2}\right)}.$$

(71)

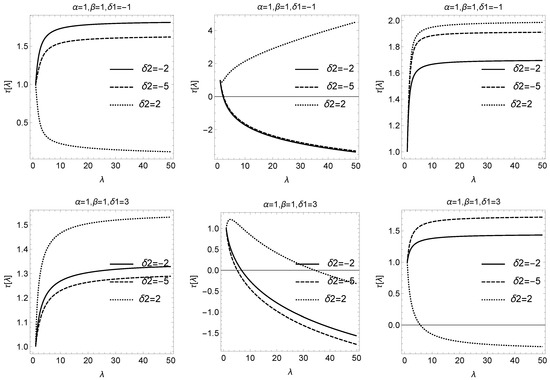
In Figure 1, we present the numerical simulation of the latter three-dimensional system for different values of the free parameters. We observe that there exist an attractor where the variables $\tau$, U, and $\lambda$ become constant.

Figure 1. Numerical simulation of $\tau \left(\lambda \right),U\left(\lambda \right)$, and $V\left(\lambda \right)$ as given by the system (69)–(71) for different values of the free parameters.

Equations (70) and (71) can be written as

$$\begin{array}{ccc}\hfill \frac{dU}{d\tau }& =& \beta {\delta }_2{\tau }^{{\delta }_2-1}-\lambda ,\hfill \end{array}$$

(72)

$$\begin{array}{ccc}\hfill \frac{dV}{d\tau }& =& -\beta {\delta }_2{\tau }^{{\delta }_2-1},\hfill \end{array}$$

(73)

from where it follows the closed-form solution

$$\begin{array}{ccc}\hfill U\left(\tau \right)& =& \beta {\tau }^{{\delta }_2}-\lambda \tau +U_0,\hfill \end{array}$$

(74)

$$\begin{array}{ccc}\hfill V\left(\tau \right)& =& -\beta {\tau }^{{\delta }_2}+V_0.\hfill \end{array}$$

(75)

Last but not least, reduction with respect to the vector fields $\left\{Y_4,Y_5\right\}$ for ${\delta }_1=2,{\delta }_2=3$ gives the similarity transformation:

$$\tau ={\left(\frac{t}{x}\right)}^{\frac{1}{3}}T\left(\mu \right),u^L={\left(\frac{x}{t}\right)}^{\frac{2}{3}}{U}^L\left(\mu \right),v^L=\frac{x}{t}{V}^L\left(\mu \right),\mu ={\left(yt{x}^{-4}\right)}^3,$$

(76)

with reduced equations

$$\begin{array}{ccc}\hfill T_{,\mu }+\frac{T\left(8\mu \alpha T-9\left(\beta +V^L{T}^3\right)+\mu T^4+6\mu T^3{U}^L\right)}{\mu \left(\mu {\left(V^L\right)}^4+8\alpha \mu V^L-9\beta \right)}& =& 0,\hfill \end{array}$$

(77)

$$\begin{array}{ccc}\hfill U_{,\mu }^L-\frac{2\left(\mu T^3{U}^L-9\beta U^L+2U^{L}T\mu \alpha +9\alpha V^L{U}^L\right)}{\mu \left(\mu {\left(V^L\right)}^4+8\alpha \mu V^L-9\beta \right)}& =& 0,\hfill \end{array}$$

(78)

$$\begin{array}{ccc}\hfill V_{,\mu }^L-\frac{3\left(V^L{T}^4-6\beta U^L+8\alpha V^{L}T\right)}{\left(\mu {\left(V^L\right)}^4+8\alpha \mu V^L-9\beta \right)}& =& 0.\hfill \end{array}$$

(79)

The latter dynamical system can be investigated further numerically, but such an analysis is not within the scope of this work.

6. Conclusions

In this piece, we extended our investigation of the application of the Lie symmetries in traffic estimation models. Specifically, we performed a detailed investigation of the group invariant properties for a macroscopic traffic estimation model with multi-lane vehicle transition. The model of our consideration, which is a simple extension of the Aw-Rascle theory in the two-dimensional case, consists of three hyperbolic first-order partial differential equations, similar to that of the shallow-water equations.

We expressed the 2D Aw-Rascle system in two different frames, by using the Euler variables and the Lagrange variables. For each frame, we determined the Lie symmetries and we investigated the group properties of the admitted Lie symmetries. Furthermore, we constructed a one-dimensional optimal system and we made use of the Lie symmetries in order to construct closed-form similarity solutions.

For the Euler variables, we found that the resulting system admits seven Lie symmetries which form the $\left\{3A_1{\otimes }_s{A}_1\right\}{\otimes }_s{A}_{3,3}$ Lie algebra. The one-dimensional optima system consists of twenty three one-dimensional Lie algebras. On the other hand, in the Lagrange variables, the dynamical system admits an infinite number of symmetries with a five-dimensional finite subalgebra. The finite elements form the $3A_1{\otimes }_{s}2A_1$ Lie algebra where the one-dimensional optimal system is constructed via nine one-dimensional Lie algebras.

We remark that while the two systems are equivalent, the Lie symmetry analysis provides different results. Thus, it is of special interest to investigate the symmetries of hydrodynamic systems in the two different frames.

From the results of this study, it is clear that the Lie symmetry analysis can be used to construct important invariants for the traffic estimation. In future work, we plan to extend our analysis by introducing multiple types of vehicles and also apply other methods for the derivation of new solutions; see, for instance, the approach applied in [62,63,64] and the references therein.