Symmetry Analysis for the 2D Aw-Rascle Traffic-Flow Model of Multi-Lane Motorways in the Euler and Lagrange Variables
Abstract
1. Introduction
2. The 2D Aw-Rascle Model
3. The Theory of Lie Symmetries
One-Dimensional Optimal System
4. Lie Symmetries in the Euler Variables
4.1. Lie Symmetries for Arbitrary Parameters and
Lie Symmetries for
4.2. One-Dimensional Optimal System
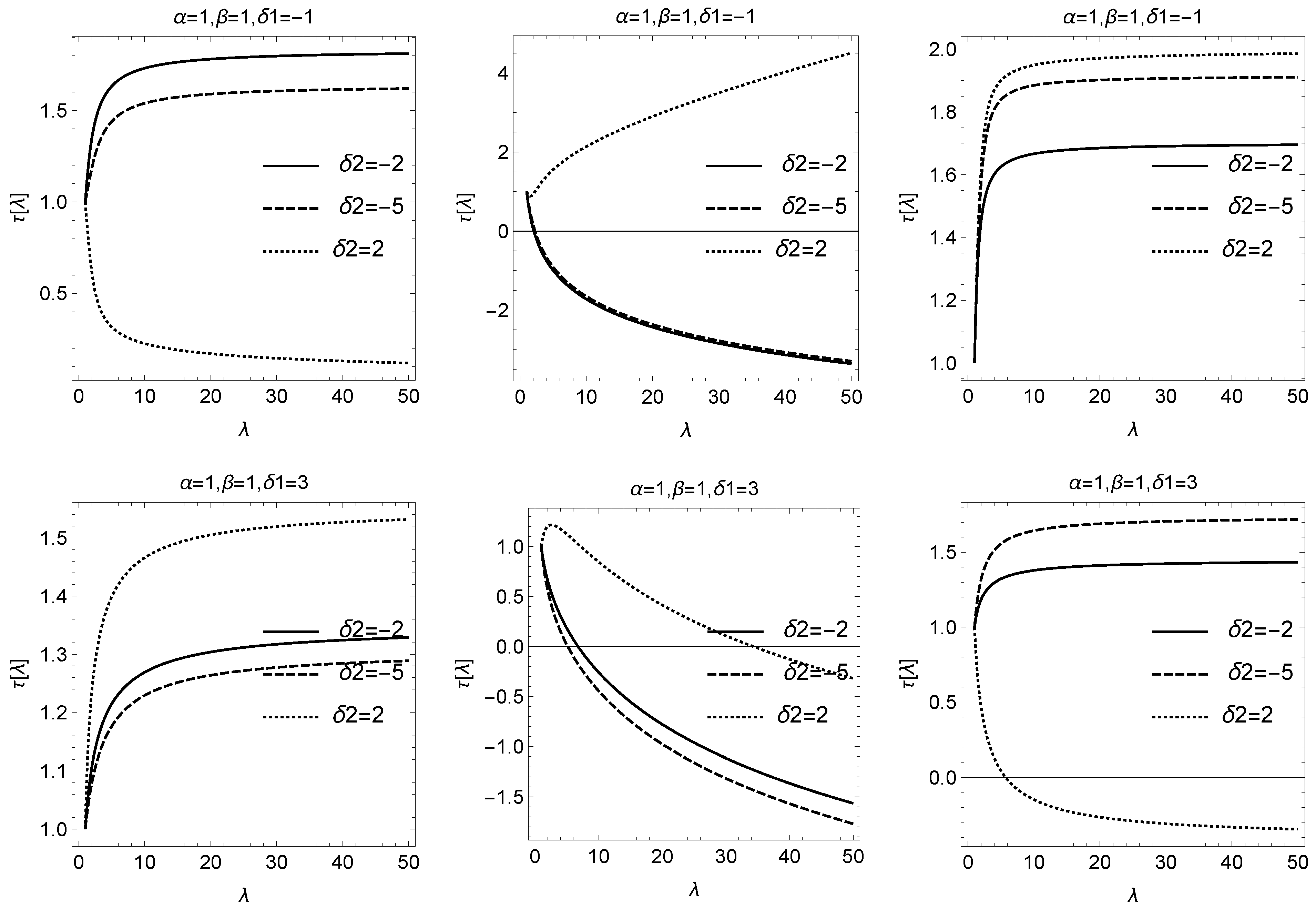
4.3. Similarity Solutions
5. Lie Symmetries in the Lagrange Variables
5.1. One-Dimensional Optimal System
5.2. Similarity Transformations
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lie, S. Theorie der Transformationsgrupprn: Volume I; Chelsea: New York, NY, USA, 1970. [Google Scholar]
- Lie, S. Theorie der Transformationsgrupprn: Volume II; Chelsea: New York, NY, USA, 1970. [Google Scholar]
- Lie, S. Theorie der Transformationsgrupprn: Volume III; Chelsea: New York, NY, USA, 1970. [Google Scholar]
- Ibragimov, N.H. CRC Handbook of Lie Group Analysis of Differential Equations, Volume I: Symmetries, Exact Solutions, and Conservation Laws; CRS Press LLC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic Press: Boston, MA, USA, 1982. [Google Scholar]
- Sen, T. Lie symmetries and integrability. Phys. Lett. A 1987, 122, 327. [Google Scholar] [CrossRef]
- Tsamparlis, M.; Paliathanasis, A. Two-dimensional dynamical systems which admit Lie and Noether symmetries. J. Phys. A Math. Theor. 2011, 44, 175202. [Google Scholar] [CrossRef]
- Mitsopoulos, A.; Tsamparlis, M.; Paliathanasis, A. Integrable and Superintegrable Potentials of 2d Autonomous Conservative Dynamical Systems. Symmetry 2020, 12, 1655. [Google Scholar] [CrossRef]
- Tsamparlis, M.; Paliathanasis, A.; Karpathopoulos, L. Autonomous three-dimensional Newtonian systems which admit Lie and Noether point symmetries. J. Phys. A Math. Theor. 2012, 45, 275201. [Google Scholar] [CrossRef][Green Version]
- Haas, F.; Goedert, J. Dynamical symmetries and the Ermakov invariant. Phys. Lett. A 2001, 279, 181. [Google Scholar] [CrossRef][Green Version]
- Leach, P.G.L.; Andriopoulos, K. The Ermakov equation: A commentary. Appl. Anal. Discrete Math. 2008, 2, 146. [Google Scholar] [CrossRef]
- Moyo, S.; Leach, P.G.L. A note on the construction of the Ermakov–Lewis invariant. J. Phys. A Math. Gen. 2002, 35, 5333. [Google Scholar] [CrossRef]
- Mitsopoulos, A.; Tsamparlis, M. The generalized Ermakov conservative system. Eur. Phys. J. Plus 2021, 136, 1. [Google Scholar] [CrossRef]
- Tsamparlis, M.; Paliathanasis, A. Generalizing the autonomous Kepler–Ermakov system in a Riemannian space. J. Phys. A Math. Theor. 2012, 45, 275202. [Google Scholar] [CrossRef]
- Abraham-Shrauner, B. Lie group symmetries and invariants of the Hénon–Heiles equations. J. Math. Phys. 1990, 31, 1627. [Google Scholar] [CrossRef]
- Leach, P.G.L. A direct approach to finding exact invariants for one-dimensional time-dependent classical Hamiltonians. J. Math. Phys. 1981, 22, 679. [Google Scholar] [CrossRef]
- Fordy, A.P. Stochastic resonance in a bistable system. Phys. Lett. A 1983, 97, 21. [Google Scholar] [CrossRef]
- Prince, G.; Eliezer, C.J. Symmetries of the time-dependent N-dimensional oscillator. J. Phys. A Math. Gen. 1981, 14, 587. [Google Scholar] [CrossRef]
- Khalique, C.M.; Ntsime, P. Exact solutions of the Lane–Emden-type equation. New Astron. 2008, 13, 476. [Google Scholar] [CrossRef]
- Kweyama, M.C.; Govinder, K.S.; Maharaj, S.D. Noether and Lie symmetries for charged perfect fluids. Class. Quantum Grav. 2011, 28, 105005. [Google Scholar] [CrossRef]
- Christodoulakis, T.; Dimakis, N.; Terzis, P.A. Lie point and variational symmetries in minisuperspace Einstein gravity. J. Phys. A Math. Gen. 2014, 47, 095202. [Google Scholar] [CrossRef]
- Tsamparlis, M.; Paliathanasis, A. Symmetries of Differential Equations in Cosmology. Symmetry 2018, 10, 233. [Google Scholar] [CrossRef]
- Velan, M.S.; Lakshmanan, M. Lie symmetries and invariant solutions of the shallow-water equation. Int. J. Non-Linear Mech. 1996, 31, 339. [Google Scholar] [CrossRef]
- Chesnokov, A.A. Symmetries and exact solutions of the shallow water equations for a two-dimensional shear flow. J. Appl. Mech. Technol. Phys. 2008, 49, 737. [Google Scholar] [CrossRef]
- Paliathanasis, A. Shallow-water equations with complete Coriolis force: Group properties and similarity solutions. Math. Meth. Appl. Sci. 2021, 44, 6037. [Google Scholar] [CrossRef]
- Bihlo, A.; Poltavets, N.; Popovych, R.O. Lie symmetries of two-dimensional shallow water equations with variable bottom topography. Chaos 2020, 30, 073132. [Google Scholar] [CrossRef]
- Pandey, M. Lie Symmetries and Exact Solutions of Shallow Water Equations with Variable Bottom. Int. J. Nonlinear Sci. Numer. Simul. 2015, 16, 93. [Google Scholar] [CrossRef]
- Stapathy, P.; Sekhar, T.R. Optimal system, invariant solutions and evolution of weak discontinuity for isentropic drift flux model. Eur. Phys. J. Plus 2022, 137, 1183. [Google Scholar] [CrossRef]
- Huo, C.; Li, L. Lie Symmetry Analysis, Particular Solutions and Conservation Laws of a New Extended (3+1)-Dimensional Shallow Water Wave Equation. Symmetry 2022, 14, 1855. [Google Scholar] [CrossRef]
- Bira, B.; Sekhar, T.R. Exact solutions to drift-flux multiphase flow models through Lie group symmetry analysis. Appl. Math. Mech.-Engl. Ed. 2015, 36, 1105. [Google Scholar] [CrossRef]
- Bira, B.; Sekhar, T.R.; Zeidan, D. Application of Lie groups to compressible model of two-phase flows. Comput. Math. Appl. 2016, 71, 46. [Google Scholar]
- Banda, M.K.; Herty, M.; Ngnotghouye, J.-M.T. Toward a mathematical analysis for drift-flux multiphase flow models in networks. SIAM J. Sci. Comput. 2010, 31, 4633. [Google Scholar] [CrossRef]
- Moawad, S.M. Variational principles for ideal MHD of steady incompressible flows via Lie-point symmetries with application to the magnetic structures of bipolar sunspots. Eur. Phys. J. Plus 2020, 135, 585. [Google Scholar] [CrossRef]
- Webb, G.M.; Zank, G.P.; Kaghashvili, E.K.; Ratkiewicz, R.E. Magnetohydrodynamic waves in non-uniform flows II: Stress-energy tensors, conservation laws and Lie symmetries. J. Plasma Phys. 2005, 71, 811. [Google Scholar] [CrossRef]
- Webb, G.M.; Zank, G.P. Fluid relabelling symmetries, Lie point symmetries and the Lagrangian map in magnetohydrodynamics and gas dynamics. J. Phys. A Math. Theor. 2006, 40, 545. [Google Scholar] [CrossRef]
- Torrisi, M.; Tracina, R. Lie symmetries and solutions of reaction diffusion systems arising in biomathematics. Symmetry 2021, 13, 1530. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Li, G.-F. Lie symmetry analysis and exact solutions of the time-fractional biological population model. Phys. A Stat. Mech. Appl. 2020, 540, 123134. [Google Scholar] [CrossRef]
- Gazizov, R.K.; Ibragimov, N.H. Lie symmetry analysis of differential equations in finance. Nonlinear Dyn. 1998, 17, 387. [Google Scholar] [CrossRef]
- del Pilar Marquez, A.; Garrido, T.M.; Recio, E.; de la Rosa, R. Lie symmetries and exact solutions for a fourth-order nonlinear diffusion equation. Math. Math. Appl. Sci. 2022, 45, 10614. [Google Scholar] [CrossRef]
- Rehman, K.U.; Malik, M.Y. On Lie symmetry mechanics for Navier–Stokes equations unified with non-Newtonian fluid model: A classical directory. Phys. A Stat. Mech. Appl. 2019, 535, 122469. [Google Scholar] [CrossRef]
- Paliathanasis, A.; Leach, P.G.L. Lie Symmetry Analysis of the Aw–Rascle–Zhang Model for Traffic State Estimation. Mathematics 2023, 11, 81. [Google Scholar] [CrossRef]
- Herty, M.; Moutari, S.; Visconti, G. Macroscopic Modeling of Multilane Motorways Using a Two-Dimensional Second-Order Model of Traffic Flow. SIAM J. Appl. Math. 2018, 78, 2252. [Google Scholar] [CrossRef]
- Xin, X.; Guo, L. Characteristic Decomposition of the Two-Dimensional ARZ Traffic Flow System. Bull. Malays. Math. Soc. 2023, 46, 69. [Google Scholar] [CrossRef]
- Piu, M.; Puppo, G. Stability analysis of microscopic models for traffic flow with lane changing. NHM 2022, 17, 495. [Google Scholar] [CrossRef]
- Yu, H.; Kvstic, M. Two-Lane Traffic Control. In Traffic Congestion Control by PDE Backstepping; Systems & Control: Foundations & Applications; Birkhäuser: Cham, Switzerland, 2022. [Google Scholar]
- Goatin, P. The Aw–Rascle vehicular traffic flow model with phase transitions. Math. Comp. Mod. 2006, 44, 287. [Google Scholar] [CrossRef]
- Wu, C.-X.; Zhang, P.; Wong, S.C.; Qao, D.-L.; Dai, S.-Q. Solitary wave solution to Aw- Rascle viscous model of traffic flow. Appl. Math. Mech. 2013, 34, 523. [Google Scholar] [CrossRef][Green Version]
- Yin, G.; Chen, J. Existence and Stability of Riemann Solution to the Aw-Rascle Model with Friction. Indian J. Pure Appl. Math. 2018, 49, 671. [Google Scholar] [CrossRef]
- Greenberg, J.M. Extensions and Amplifications of a Traffic Model of Aw and Rascle. SIAM J. Appl. Math. 2001, 62, 729. [Google Scholar] [CrossRef]
- Lighthill, M.J.; Whitham, G.B. On kinematic waves II. A theory of traffic flow on long crowded roads. Proc. R. Soc. A 1955, 229, 317. [Google Scholar]
- Richards, P.I. Shock waves on the highway. Oper. Res. 1956, 4, 42. [Google Scholar] [CrossRef]
- Daganzo, C.F. The cell transmission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory. Transp. Res. B 1994, 28, 269. [Google Scholar] [CrossRef]
- Aw, A.; Rascle, M. Derivation of continuum traffic flow models from microscopic follow-the-leader models. SIAM J. Appl. Math. 2000, 60, 916. [Google Scholar] [CrossRef]
- Zhang, H.M. A non-equilibrium traffic model devoid of gas-like behavior. Transp. Res. B 2002, 36, 275. [Google Scholar] [CrossRef]
- Xing, J.; Wu, W.; Cheng, Q.; Liu, R. Traffic state estimation of urban road networks by multi-source data fusion: Review and new insights. Phys. A Stat. Mech. Appl. 2022, 595, 127079. [Google Scholar] [CrossRef]
- Stephani, H. Differential Equations: Their Solutions Using Symmetry; Cambridge University Press: New York, NY, USA, 1989. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Morozov, V.V. Classification of nilpotent Lie algebras of sixth order. Izvestia Vysshikh Uchebn Zavendeniĭ Matematika 1958, 5, 161. [Google Scholar]
- Mubarakzyanov, G.M. On solvable Lie algebras. Izvestia Vysshikh Uchebn Zavendeniĭ Matematika 1963, 32, 114. [Google Scholar]
- Mubarakzyanov, G.M. Classification of real structures of Lie algebras of fifth order. Izvestia Vysshikh Uchebn Zavendeniĭ Matematika 1963, 34, 99. [Google Scholar]
- Mubarakzyanov, G.M. Classification of solvable Lie algebras of sixth order with a non-nilpotent basis element. Izvestia Vysshikh Uchebn Zavendeniĭ Matematika 1963, 35, 104. [Google Scholar]
- Zhang, X.; Li, X.P. New explicit solutions for the (1+ 1)-dimensional mikhailov-novikov-wang equation via two analytical methods. Optik 2021, 236, 166968. [Google Scholar]
- Khater, M.M.A. Advancements in Computational Techniques for Precise Solitary Wave Solutions in the (1+ 1)-Dimensional Mikhailov-Novikov-Wang Equation. Int. J. Theor. Phys. 2023, 62, 152. [Google Scholar] [CrossRef]
- Hoseini, K.; Hincal, E.; Mirekhtiary, F.; Sadri, K.; Obi, O.A.; Denker, A.; Mirzazadeh, M. A fourth-order nonlinear Schrödinger equation involving power law and weak nonlocality: Its solitary waves and modulational instability analysis. Optik 2023, 284, 170927. [Google Scholar] [CrossRef]
| 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 |
| 0 | 0 | 0 | |||
| 0 | 0 | 0 | |||
| 0 | 0 | 0 | |||
| 0 | 0 | ||||
| 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paliathanasis, A. Symmetry Analysis for the 2D Aw-Rascle Traffic-Flow Model of Multi-Lane Motorways in the Euler and Lagrange Variables. Symmetry 2023, 15, 1525. https://doi.org/10.3390/sym15081525
Paliathanasis A. Symmetry Analysis for the 2D Aw-Rascle Traffic-Flow Model of Multi-Lane Motorways in the Euler and Lagrange Variables. Symmetry. 2023; 15(8):1525. https://doi.org/10.3390/sym15081525
Chicago/Turabian StylePaliathanasis, Andronikos. 2023. "Symmetry Analysis for the 2D Aw-Rascle Traffic-Flow Model of Multi-Lane Motorways in the Euler and Lagrange Variables" Symmetry 15, no. 8: 1525. https://doi.org/10.3390/sym15081525
APA StylePaliathanasis, A. (2023). Symmetry Analysis for the 2D Aw-Rascle Traffic-Flow Model of Multi-Lane Motorways in the Euler and Lagrange Variables. Symmetry, 15(8), 1525. https://doi.org/10.3390/sym15081525







