Quantile-Based Multivariate Log-Normal Distribution

Abstract

We introduce a quantile-based multivariate log-normal distribution, providing a new multivariate skewed distribution with positive support. The parameters of this distribution are interpretable in terms of quantiles of marginal distributions and associations between pairs of variables, a desirable feature for statistical modeling purposes. We derive statistical properties of the quantile-based multivariate log-normal distribution involving the transformations, closed-form expressions for the mixed moments, expected value, covariance matrix, mode, Shannon entropy, and Kullback–Leibler divergence. We also present results on marginalization, conditioning, and independence. Additionally, we discuss parameter estimation and verify its performance through simulation studies. We evaluate the model fitting based on Mahalanobis-type distances. An application to children data is presented.

1. Introduction

Quantile regression modeling has been widely applied in different fields such as economics, environmental science, ecology, and medicine, among many others (Cade and Noon [1], Yu et al. [2]). A number of studies on nonparametric quantile regression and its applications have been developed since the seminal work of Koenker and Bassett [3]. Recently, several parametric quantile models have been studied in the regression literature, which have motivated the study of probability distributions that are useful for this purpose.

In the univariate setting, some distributions suitable for parametric quantile modeling appear in Ferrari and Fumes [4], Gijbels et al. [5], Mazucheli et al. [6], and Smithson and Shou [7]. Multivariate quantile modeling is less frequent in the statistical literature and often uses nonparametric methods. Several studies are based on extensions of the quantile concept to a multivariate setting. Some examples can be found in Breckling and Chambers [8], Kong and Mizera [9], McKeague et al. [10], and Wei [11]. Other multivariate models are based on the univariate quantile notion. For instance, Petrella and Raponi [12], Morán-Vásquez and Ferrari [13], and Morán-Vásquez et al. [14] propose methods for jointly modeling univariate marginal quantiles, taking into account the potential correlation between marginals.

In the present article, we define a quantile-based multivariate log-normal distribution. This distribution has positive support, and is simplified to the quantile-based log-normal distribution (Saulo et al. [15]) in the univariate setting. On the other hand, the usual multivariate log-normal distribution (Morán-Vásquez and Ferrari [13] and Morán-Vásquez et al. [14]) can be expressed as a quantile-based multivariate log-normal distribution. The parameters of the proposed distribution are interpretable in terms of marginal quantiles and associations between pairs of variables, making this model attractive to quantile modeling for correlated multivariate positive skewed data.

In this article, we study some statistical properties of the quantile-based multivariate log-normal family, describe the estimation of its parameters, and show its usefulness through an application to real data. We derive distributional properties obtained through transformations, as well as results related to the mixed moments, expected value, covariance matrix, mode, Shannon entropy, Kullback–Leibler divergence, marginal and conditional distributions, and independence. Applications of some of our results derived in this article establish new properties of the multivariate log-normal distribution. We compute the maximum likelihood estimates of the parameters of the quantile-based multivariate log-normal distribution from the maximum likelihood estimates of the multivariate log-normal distribution. We evaluate the performance of the proposed estimation procedure through Monte Carlo simulations. The usefulness of the proposed distribution for modeling multivariate positive skewed data is illustrated through an analysis of real data on children’s weights and heights.

The paper is organized as follows. Section 2 presents the quantile-based multivariate log-normal distribution. Section 3 deals with the derivation of various statistical properties of the proposed distribution. Section 4 focuses on maximum likelihood estimation and simulation studies. Also, a graphical method to assess the goodness of fit is described. Section 5 presents an application to real data. Finally, Section 6 closes the paper with concluding remarks.

2. Quantile-Based Multivariate Log-Normal Distribution

We denote vectors with lowercase Greek letters in bold and matrices with capital Greek letters in bold. For vectors and matrices, the components are denoted by the respective Greek letter in normal font. For example, if $\mathit{\theta }\in {\mathbb{R}}^p$ and $\mathbf{\Omega }(p\times q)$ are a real matrix, then $\mathit{\theta }={({\theta }_1,\dots ,{\theta }_p)}^{\prime }$ and $\mathbf{\Omega }={\left({\omega }_{jk}\right)}_{p\times q}$. We denote by $\mathbf{0}={(0,\dots ,0)}^{\prime }$ and $\mathbf{1}={(1,\dots ,1)}^{\prime }$ the p-dimensional vectors whose components are all zero and one, respectively. We denote by ${\mathit{I}}_p$ the $p\times p$ identity matrix. Let $\mathbf{\Omega }(p\times p)$ be a square matrix. We denote by $\det \left(\mathbf{\Omega }\right)$ and $\mathrm{tr}\left(\mathbf{\Omega }\right)$ the determinant and trace of $\mathbf{\Omega }$, respectively. If $\mathbf{\Omega }$ is a symmetric matrix, then $\mathbf{\Omega }>0$ means that $\mathbf{\Omega }$ is the positive definite. Additionally, ${\mathbf{\Omega }}^{1/2}$ is the unique symmetric positive definite square root of $\mathbf{\Omega }>0$. If ${\mathbf{\Omega }}_1$ and ${\mathbf{\Omega }}_2$ are matrices of the same dimension, then ${\mathbf{\Omega }}_1\odot {\mathbf{\Omega }}_2$ denotes the Hadamard product of ${\mathbf{\Omega }}_1$ and ${\mathbf{\Omega }}_2$. If $\mathit{\theta }\in {\mathbb{R}}^p$ is a vector, then ${\mathit{D}}_{\mathit{\theta }}$ denotes the diagonal matrix with diagonal elements of $\mathit{\theta }$, that is, ${\mathit{D}}_{\mathit{\theta }}=\mathrm{diag}({\theta }_1,\dots ,{\theta }_p)$. We define the set ${\mathbb{R}}_{+}^p$ as

$${\mathbb{R}}_{+}^p=\left\{\mathit{\theta }\in {\mathbb{R}}^p:{\theta }_k>0,k=1,\dots ,p\right\}.$$

If $\mathit{\theta }\in {\mathbb{R}}^p$ and f are a real function, we denote $f\left(\mathit{\theta }\right)={(f\left({\theta }_1\right),\dots ,f\left({\theta }_p\right))}^{\prime }$, provided that the components of $\mathit{\theta }$ are in the domain of f. If $\mathit{\theta }\in {\mathbb{R}}_{+}^p$ and $\mathit{\beta }\in {\mathbb{R}}^p$, we write ${\mathit{\theta }}^{\mathit{\beta }}={({\theta }_1^{{\beta }_1},\dots ,{\theta }_p^{{\beta }_p})}^{\prime }$. We denote random vectors and their components with capital Roman letters in bold and normal fonts, respectively.

It is well known that the PDF of a multivariate normal vector $\mathit{X}\sim {\mathrm{N}}_p(\mathit{\mu },\mathbf{\Sigma })$ is given by

$${\varphi }_p(\mathit{x};\mathit{\mu },\mathbf{\Sigma })={\left(2\pi \right)}^{-p/2}\det {\left(\mathbf{\Sigma }\right)}^{-1/2}\exp \left(-\frac{1}{2}{\delta }_{\mathbf{\Sigma }}(\mathit{x},\mathit{\mu })\right),$$

where ${\delta }_{\mathbf{\Sigma }}(\mathit{x},\mathit{\mu })={(\mathit{x}-\mathit{\mu })}^{\prime }{\mathbf{\Sigma }}^{-1}(\mathit{x}-\mathit{\mu })$ is the square of the Mahalanobis distance between $\mathit{x}$ and $\mathit{\mu }$ with respect to $\mathbf{\Sigma }$. On the other hand, the random vector $\mathit{Y}\in {\mathbb{R}}_{+}^p$ has a multivariate log-normal distribution with median vector $\mathit{\mu }\in {\mathbb{R}}_{+}^p$ and dispersion matrix $\mathbf{\Sigma }(p\times p)>0$, denoted by $\mathit{Y}\sim \mathrm{L}{\mathrm{N}}_p(\mathit{\mu },\mathbf{\Sigma })$, if $\log \left(\mathit{Y}\right)\sim {\mathrm{N}}_p(\log \left(\mathit{\mu }\right),\mathbf{\Sigma })$, where the log denotes the natural logarithm function. The PDF of $\mathit{Y}\sim \mathrm{L}{\mathrm{N}}_p(\mathit{\mu },\mathbf{\Sigma })$ is (Morán-Vásquez et al. [14])

$$\mathrm{L}{\mathrm{N}}_p(\mathit{y};\mathit{\mu },\mathbf{\Sigma })={\varphi }_p(\log \left(\mathit{y}\right);\log \left(\mathit{\mu }\right),\mathbf{\Sigma })\prod _{k=1}^p\frac{1}{y_k},\mathit{y}\in {\mathbb{R}}_{+}^p.$$

(1)

The multivariate log-normal distribution given in (1) has a slightly different parameterization than the one used by Fang et al. ([16], Section 2.8).

Let ${\alpha }_1,\dots ,{\alpha }_p$ be fixed values in $(0,1)$. Theorem 5 and Corollary 2 of Morán–Vásquez and Ferrari [13] permits us to establish that the ${\alpha }_k$-quantile $Q_k$ of $Y_k$ satisfies $Q_k={\mu }_k\exp \left(\sqrt{{\sigma }_{kk}}{q}_k\right)$, where $q_k$ is the ${\alpha }_k$-quantile of a standard normal distribution, $k=1,\dots ,p$. Note that the quantile vector $\mathit{Q}={(Q_1,\dots ,Q_p)}^{\prime }$ can be expressed as

$$\mathit{Q}={\mathit{D}}_{\mathit{\mu }}\exp \left(\mathbf{\Omega }\mathit{q}\right),$$

(2)

where $\mathbf{\Omega }={(\mathbf{\Sigma }\odot {\mathit{I}}_p)}^{1/2}$ and $\mathit{q}={(q_1,\dots ,q_p)}^{\prime }$. A reparameterization of the multivariate log-normal distribution in terms of $\mathit{Q}$ is obtained by replacing $\mathit{\mu }={\mathit{D}}_{\mathit{Q}}\exp (-\mathbf{\Omega }\mathit{q})$ in (1). Based on this, we present the quantile-based multivariate log-normal distribution in Definition 1.

Definition 1.

Let $\mathit{\alpha }={({\alpha }_1,\dots ,{\alpha }_p)}^{\prime }\in {(0,1)}^p$ and $\mathit{q}={(q_1,\dots ,q_p)}^{\prime }\in {\mathbb{R}}^p$ be fixed vectors such that $q_k$ is the ${\alpha }_k$-quantile of a standard normal distribution, $k=1,\dots ,p$. The random vector $\mathit{Y}\in {\mathbb{R}}_{+}^p$ is said to have a quantile-based multivariate log-normal distribution with quantile vector $\mathit{Q}={(Q_1,\dots ,Q_p)}^{\prime }$ and dispersion matrix $\mathbf{\Sigma }(p\times p)>0$, denoted by $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$, if its PDF is

$$\mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{y};\mathit{Q},\mathbf{\Sigma },\mathit{q})={\varphi }_p(\log \left(\mathit{y}\right);\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })\prod _{k=1}^p\frac{1}{y_k},\mathit{y}\in {\mathbb{R}}_{+}^p,$$

(3)

where $\mathbf{\Omega }={(\mathbf{\Sigma }\odot {\mathit{I}}_p)}^{1/2}$.

If we choose $\mathit{\alpha }={(1/2,\dots ,1/2)}^{\prime }$, then Definition 1 coincides with the definition of a multivariate log-normal distribution (Morán-Vásquez et al. [14]). In this case, $\mathit{Q}=\mathit{\mu }$ is the median vector. Note that $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$ if $\log \left(\mathit{Y}\right)\sim {\mathrm{N}}_p(\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })$, which establishes the way in which the quantile-based multivariate log-normal and normal distributions are related through the logarithmic transformation.

Figure 1 displays contour plots (at levels 0.15, 0.1, 0.05, 0.02, 0.01) of the quantile-based bivariate log-normal distribution. The legend indicates the values of ${\alpha }_1$, ${\alpha }_2$, and all the parameters considered in the first plot and the values that are changed from a plot to the subsequent one (in alphabetical order). The parameters $Q_1$ and $Q_2$ of the distribution in Figure 1a are the marginal medians of $Y_1$ and $Y_2$, respectively. For Figure 1b–f, these parameters are the first quartile of $Y_1$ and the median of $Y_2$, respectively. The parameter $Q_2$ impacts the scale of the marginal distribution of $Y_2$ (Figure 1b,c). The parameter ${\sigma }_{11}$ controls the dispersion of the marginal distribution of $Y_1$ (Figure 1c,d). The parameter ${\sigma }_{12}$ controls the association between the marginal distributions of $Y_1$ and $Y_2$, ranging from a negative to positive association (Figure 1d–f).

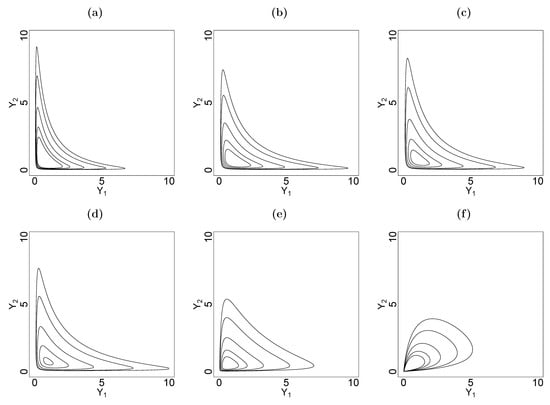
Figure 1. Contour plots at levels 0.15, 0.1, 0.05, 0.02, 0.01 of the joint PDF of $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_2(\mathit{Q},\mathbf{\Sigma },\mathit{q})$ given in Definition 1, where (a) ${\alpha }_1={\alpha }_2=0.5$, $Q_1=0.8$, $Q_2=1$, ${\sigma }_{11}=0.8, {\sigma }_{22}=1$, ${\sigma }_{12}=-0.5$, (b) ${\alpha }_1=0.25$, (c) $Q_2=1.2$, (d) ${\sigma }_{11}=1$, (e) ${\sigma }_{12}=0$, (f) ${\sigma }_{12}=0.7$.

The quantile-based multivariate log-normal distribution is suitable in situations where it is necessary to model quantiles of the marginals, taking into account the correlation between them. Additionally, our model can be useful for regression modeling purposes. For instance, assume that, for fixed k, $\log \left(Q_k\right)={\sum }_{j=1}^r{\beta }_j{x}_j$, where ${\beta }_1,\dots ,{\beta }_r$ are unknown regression parameters and $x_1,\dots ,x_r$ are fixed covariates. So, $\exp \left({\beta }_j\right)$ is the multiplicative effect of a one unit increase in $x_j$ on the ${\alpha }_k$-quantile of $Y_k$. This is a parametric methodology that allows us to jointly analyze marginal quantiles, taking into account the association among the response variables through the dispersion matrix $\mathbf{\Sigma }(p\times p)>0$. These types of models can provide more accurate estimates than those that consider univariate models for each marginal assuming independence among them (Morán-Vásquez et al. [14]).

3. Main Properties

Theorems 1–3 state distributional results involving the transformation of quantile-based multivariate log-normal random vectors.

Theorem 1.

Let $\mathit{\theta }\in {\mathbb{R}}_{+}^p$. If $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$, then ${\mathit{D}}_{\mathit{\theta }}\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p({\mathit{D}}_{\mathit{\theta }}\mathit{Q},\mathbf{\Sigma },\mathit{q})$.

Proof. 

From the transformation $\mathit{U}={\mathit{D}}_{\mathit{\theta }}\mathit{Y}$, with the Jacobian $J(\mathit{y}\to \mathit{u})={\prod }_{k=1}^p{\theta }_k^{-1}$, in (3), we arrive at

$$\begin{array}{cc}\hfill f_{\mathit{U}}\left(\mathit{u}\right)& ={\varphi }_p(\log \left({\mathit{D}}_{\mathit{\theta }}^{-1}\mathit{u}\right);\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })\prod _{k=1}^p\frac{1}{u_k}\hfill \\ \hfill & ={\varphi }_p(\log \left(\mathit{u}\right)-\log \left(\mathit{\theta }\right);\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })\prod _{k=1}^p\frac{1}{u_k}.\hfill \end{array}$$

(4)

Since ${\varphi }_p(\log \left(\mathit{u}\right)-\log \left(\mathit{\theta }\right);\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })={\varphi }_p(\log \left(\mathit{u}\right);\log \left(\mathit{Q}\right)+\log \left(\mathit{\theta }\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })$, (4) can be expressed as

$$f_{\mathit{U}}\left(\mathit{u}\right)={\varphi }_p(\log \left(\mathit{u}\right);\log \left({\mathit{D}}_{\mathit{\theta }}\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })\prod _{k=1}^p\frac{1}{u_k},$$

where the last line is obtained by using the identity $\log \left(\mathit{Q}\right)+\log \left(\mathit{\theta }\right)=\log \left({\mathit{D}}_{\mathit{\theta }}\mathit{Q}\right)$. □

Corollary 1.

Let $\mathit{\theta }\in {\mathbb{R}}_{+}^p$. If $\mathit{Y}\sim \mathrm{L}{\mathrm{N}}_p(\mathit{\mu },\mathbf{\Sigma })$, then ${\mathit{D}}_{\mathit{\theta }}\mathit{Y}\sim \mathrm{L}{\mathrm{N}}_p({\mathit{D}}_{\mathit{\theta }}\mathit{\mu },\mathbf{\Sigma })$.

Proof. 

The result follows by applying Theorem 1 to the quantile-based multivariate log-normal distribution generated by $\mathit{\alpha }={(1/2,\dots ,1/2)}^{\prime }$. □

The result stated in the above corollary can also be obtained as a particular case of Theorem 3(1) of Morán–Vásquez and Ferrari [13].

Theorem 2.

Let $\mathit{\beta }\in {\mathbb{R}}^p$ have nonzero components. If $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$, then ${\mathit{Y}}^{\mathit{\beta }}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p({\mathit{Q}}^{\mathit{\beta }},{\mathit{D}}_{\mathit{\beta }}\mathbf{\Sigma }{\mathit{D}}_{\mathit{\beta }},{\mathit{q}}^{*})$, where ${\mathit{q}}^{*}={\mathit{D}}_{\mathrm{sgn}\left(\mathit{\beta }\right)}\mathit{q}$.

Proof. 

Transforming $\mathit{T}={\mathit{Y}}^{\mathit{\beta }}$, with the Jacobian $J(\mathit{y}\to \mathit{t})={\prod }_{k=1}^p{\beta }_k^{-1}{t}_k^{1/{\beta }_k-1}$, in (3), we have

$$\begin{array}{cc}\hfill f_{\mathit{T}}\left(\mathit{t}\right)& ={\varphi }_p(\log \left({\mathit{t}}^{1/\beta }\right);\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })\prod _{k=1}^p\frac{1}{|{\beta }_k|t_k}\hfill \\ \hfill & ={\varphi }_p({\mathit{D}}_{\beta }^{-1}\log \left(\mathit{t}\right);\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })\prod _{k=1}^p\frac{1}{|{\beta }_k|t_k}.\hfill \end{array}$$

(5)

By using the identity

$${\varphi }_p({\mathit{D}}_{\mathit{\beta }}^{-1}\log \left(\mathit{t}\right);\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })\prod _{k=1}^p\frac{1}{|{\beta }_k|}={\varphi }_p(\log \left(\mathit{t}\right);{\mathit{D}}_{\mathit{\beta }}\log \left(\mathit{Q}\right)-{\mathbf{\Omega }}^{*}{\mathit{q}}^{*},{\mathit{D}}_{\mathit{\beta }}\mathbf{\Sigma }{\mathit{D}}_{\beta }),$$

with ${\mathbf{\Omega }}^{*}={({\mathit{D}}_{\mathit{\beta }}\mathbf{\Sigma }{\mathit{D}}_{\mathit{\beta }}\odot {\mathit{I}}_p)}^{1/2}$ and ${\mathit{q}}^{*}={\mathit{D}}_{\mathrm{sgn}\left(\mathit{\beta }\right)}\mathit{q}$, in (5), we have

$$f_{\mathit{T}}\left(\mathit{t}\right)={\varphi }_p(\log \left(\mathit{t}\right);\log \left({\mathit{Q}}^{\mathit{\beta }}\right)-{\mathbf{\Omega }}^{*}{\mathit{q}}^{*},{\mathit{D}}_{\mathit{\beta }}\mathbf{\Sigma }{\mathit{D}}_{\mathit{\beta }})\prod _{k=1}^p\frac{1}{t_k},$$

where the last line is derived by noting that ${\mathit{D}}_{\beta }\log \left(\mathit{Q}\right)=\log \left({\mathit{Q}}^{\mathit{\beta }}\right)$. □

Corollary 2.

Let $\mathit{\beta }\in {\mathbb{R}}^p$ with nonzero components. If $\mathit{Y}\sim \mathrm{L}{\mathrm{N}}_p(\mathit{\mu },\mathbf{\Sigma })$, then ${\mathit{Y}}^{\mathit{\beta }}\sim \mathrm{L}{\mathrm{N}}_p({\mathit{\mu }}^{\mathit{\beta }},{\mathit{D}}_{\mathit{\beta }}\mathbf{\Sigma }{\mathit{D}}_{\mathit{\beta }})$.

Proof. 

The result follows by applying Theorem 2 to the quantile-based multivariate log-normal distribution generated by $\mathit{\alpha }={(1/2,\dots ,1/2)}^{\prime }$. □

The above corollary can also be obtained as a particular case of Theorem 3(2) of Morán–Vásquez and Ferrari [13].

Theorem 3.

Let $\mathit{\lambda }\in {\mathbb{R}}^p\setminus \mathbf{0}$. If $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$, then

$$\prod _{k=1}^p{Y}_k^{{\lambda }_k}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_1\left(\prod _{k=1}^p{Q}_k^{{\lambda }_k},{\lambda }^{\prime }\mathbf{\Sigma }\lambda ,\tilde{q}\right),$$

where $\tilde{q}={\left({\mathit{\lambda }}^{\prime }\mathbf{\Sigma }\mathit{\lambda }\right)}^{-1/2}{\lambda }^{\prime }\mathbf{\Omega }\mathit{q}$.

Proof. 

Since $\log \left(\mathit{Y}\right)\sim {\mathrm{N}}_p(\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })$, we have

$${\mathit{\lambda }}^{\prime }\log \left(\mathit{Y}\right)=\log \left(\prod _{k=1}^p{Y}_k^{{\lambda }_k}\right)\sim {\mathrm{N}}_1\left(\log \left(\prod _{k=1}^p{Q}_k^{{\lambda }_k}\right)-\tilde{\omega }\tilde{q},{\mathit{\lambda }}^{\prime }\mathbf{\Sigma }\lambda \right),$$

where $\tilde{\omega }={\left({\mathit{\lambda }}^{\prime }\mathbf{\Sigma }\mathit{\lambda }\right)}^{1/2}$ and $\tilde{q}={\left({\mathit{\lambda }}^{\prime }\mathbf{\Sigma }\mathit{\lambda }\right)}^{-1/2}{\mathit{\lambda }}^{\prime }\mathbf{\Omega }\mathit{q}$. This completes the proof. □

Corollary 3.

Let $\mathit{\lambda }\in {\mathbb{R}}^p\setminus \mathbf{0}$. If $\mathit{Y}\sim \mathrm{L}{\mathrm{N}}_p(\mathit{\mu },\mathbf{\Sigma })$, then

$$\prod _{k=1}^p{Y}_k^{{\lambda }_k}\sim \mathrm{L}{\mathrm{N}}_1\left(\prod _{k=1}^p{\mathit{\mu }}_k^{{\lambda }_k},{\mathit{\lambda }}^{\prime }\mathbf{\Sigma }\lambda \right).$$

Proof. 

Simply apply Theorem 3 to the quantile-based multivariate log-normal distribution generated by $\mathit{\alpha }={(1/2,\dots ,1/2)}^{\prime }$. □

In Theorem 4, we give a closed-form expression for the mixed moments of quantile-based multivariate log-normal random vectors.

Theorem 4.

Let $\mathit{\lambda }\in {\mathbb{R}}^p\setminus \mathbf{0}$. If $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$, then

$$\mathrm{E}\left(\prod _{k=1}^p{Y}_k^{{\lambda }_k}\right)=\exp \left(-{\mathit{\lambda }}^{\prime }\mathbf{\Omega }\mathit{q}+\frac{1}{2}{\mathit{\lambda }}^{\prime }\mathbf{\Sigma }\lambda \right)\prod _{k=1}^p{Q}_k^{{\lambda }_k}.$$

(6)

Proof. 

From (3), we have

$$\mathrm{E}\left(\prod _{k=1}^p{Y}_k^{{\lambda }_k}\right)={\int }_{{\mathbb{R}}_{+}^p}{\varphi }_p(\log \left(\mathit{y}\right);\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })\prod _{k=1}^p{y}_k^{{\lambda }_k-1}\mathrm{d}\mathit{y}.$$

(7)

By making the change of variables $\mathit{y}=\exp \left(\mathit{x}\right)$, with the Jacobian $J(\mathit{y}\to \mathit{x})=\exp \left({\sum }_{k=1}^p{x}_k\right)$, in (7), we arrive at $\mathrm{E}\left({\prod }_{k=1}^p{Y}_k^{{\lambda }_k}\right)=M_{\mathit{X}}\left(\mathit{\lambda }\right)$, where $M_{\mathit{X}}$ is the moment-generating function of $\mathit{X}\sim {\mathrm{N}}_p(\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })$. This completes the proof. □

In the following corollary, we derive the expected value and the covariance matrix of a quantile-based multivariate log-normal random vector.

Corollary 4.

Let $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$. Then,

• $\mathrm{E}\left(\mathit{Y}\right)={\mathit{D}}_{\mathit{Q}}\exp (-\mathbf{\Omega }\mathit{q}+\sigma /2)$, where $\sigma ={({\sigma }_{11},\dots ,{\sigma }_{pp})}^{\prime }$ is the vector with elements being the main diagonal elements of Σ.
• $\mathrm{Cov}\left(\mathit{Y}\right)={\left(\mathrm{Cov}(Y_j,Y_k)\right)}_{p\times p}$, where

  $$\mathrm{Cov}(Y_j,Y_k)=Q_j{Q}_k\exp \left(-\sqrt{{\sigma }_{jj}}{q}_j-\sqrt{{\sigma }_{kk}}{q}_k+\frac{1}{2}({\sigma }_{jj}+{\sigma }_{kk})\right)(\exp \left({\sigma }_{jk}\right)-1).$$

  (8)

Proof. 

For each $k=1,\dots ,p$, by choosing $\mathit{\lambda }$ with all its components being 0, except the kth which is 1, in (6), we obtain

$$\mathrm{E}\left(Y_k\right)=Q_k\exp \left(-\sqrt{{\sigma }_{kk}}{q}_k+\frac{{\sigma }_{kk}}{2}\right).$$

From the above expression, we get the first assertion. Similarly, for each $j,k=1,\dots ,p$, by choosing $\mathit{\lambda }$ with all components equal to 0, except the jth and kth, which are 1, in (6), we have

$$\mathrm{E}\left(Y_j{Y}_k\right)=Q_j{Q}_k\exp \left(-\sqrt{{\sigma }_{jj}}{q}_j-\sqrt{{\sigma }_{kk}}{q}_k+\frac{1}{2}({\sigma }_{jj}+{\sigma }_{kk})+{\sigma }_{jk}\right).$$

The second assertion is obtained from the identity $\mathrm{Cov}(Y_j,Y_k)=\mathrm{E}\left(Y_j{Y}_k\right)-\mathrm{E}\left(Y_j\right)\mathrm{E}\left(Y_k\right)$. □

In Section 2, we described the behavior of the quantile-based multivariate log-normal distribution in terms of the parameters involved in the matrix $\mathbf{\Sigma }$. The following corollary establishes an exact interpretation of these parameters in terms of covariance between pairs of variables according to their signs.

Corollary 5.

Let $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$. Then,

• $\mathrm{Cov}(Y_j,Y_k)>0$ if and only if ${\sigma }_{jk}>0$, $j\ne k$.
• $\mathrm{Cov}(Y_j,Y_k)=0$ if and only if ${\sigma }_{jk}=0$, $j\ne k$.

Proof. 

The result follows from (8). □

Corollary 6.

Let $\mathit{\lambda }\in {\mathbb{R}}^p\setminus \mathbf{0}$. If $\mathit{Y}\sim \mathrm{L}{\mathrm{N}}_p(\mathit{\mu },\mathbf{\Sigma })$, then

$$\mathrm{E}\left(\prod _{k=1}^p{Y}_k^{{\lambda }_k}\right)=\exp \left(\frac{1}{2}{\mathit{\lambda }}^{\prime }\mathbf{\Sigma }\mathit{\lambda }\right)\prod _{k=1}^p{\mathit{\mu }}_k^{{\lambda }_k}.$$

Moreover, $\mathrm{E}\left(\mathit{Y}\right)={\mathit{D}}_{\mathit{\mu }}\exp (\mathit{\sigma }/2)$, where $\mathit{\sigma }={({\sigma }_{11},\dots ,{\sigma }_{pp})}^{\prime }$ is the vector with elements being the main diagonal elements of Σ, and $\mathrm{Cov}\left(\mathit{Y}\right)={\left(\mathrm{Cov}(Y_j,Y_k)\right)}_{p\times p}$, with

$$\mathrm{Cov}(Y_j,Y_k)={\mathit{\mu }}_j{\mathit{\mu }}_k\exp \left(\frac{1}{2}({\sigma }_{jj}+{\sigma }_{kk})\right)(\exp \left({\sigma }_{jk}\right)-1).$$

Proof. 

Apply Theorem 4 and Corollary 4 to the quantile-based multivariate log-normal distribution generated by $\mathit{\alpha }={(1/2,\dots ,1/2)}^{\prime }$. □

Theorem 5 gives a closed-form expression for the mode of the quantile-based multivariate log-normal distribution.

Theorem 5.

The mode of $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$ is given by $\mathrm{Mode}\left(\mathit{Y}\right)={\mathit{D}}_{\mathit{Q}}\exp (-\mathbf{\Omega }\mathit{q}-\mathbf{\Sigma }\mathbf{1})$. The value of the PDF of $\mathit{Y}$ at the mode is

$$\mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathrm{Mode}\left(\mathit{Y}\right);\mathit{Q},\mathbf{\Sigma },\mathit{q})={\left(2\pi \right)}^{-p/2}\det \left(\mathbf{\Sigma }\right)\exp \left(\frac{1}{2}{\mathbf{1}}^{\prime }\mathbf{\Sigma }\mathbf{1}-{\mathbf{1}}^{\prime }(\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q})\right).$$

Proof. 

The mode of $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$ is obtained by maximizing (3) with respect to $\mathit{y}$, which is the one that maximizes the function

$$f\left(\mathit{y}\right)=-\frac{1}{2}{\delta }_{\mathbf{\Sigma }}(\log \left(\mathit{y}\right),\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q})-\sum _{k=1}^p\log \left(y_k\right)$$

with respect to $\mathit{y}$. By using results on vector differentiation (Seber ([17], Chapter 17)), we find that the equation $\partial f/\partial \mathit{y}=\mathbf{0}$ is equivalent to

$${\mathbf{\Sigma }}^{-1}(\log \left(\mathit{y}\right)-\log \left(\mathit{Q}\right)+\mathbf{\Omega }\mathit{q})+\mathbf{1}=\mathbf{0}.$$

The solution for $\mathit{y}$ of the above equation is ${\mathit{D}}_{\mathit{Q}}\exp (-\mathbf{\Omega }\mathit{q}-\mathbf{\Sigma }\mathbf{1})$.

Now, for $\mathit{y}\in {\mathbb{R}}_{+}^p$, we have

$${(\log \left(\mathit{y}\right)-\log \left(\mathit{Q}\right)+\mathbf{\Omega }\mathit{q}+\mathbf{\Sigma }\mathbf{1})}^{\prime }{\mathbf{\Sigma }}^{-1}(\log \left(\mathit{y}\right)-\log \left(\mathit{Q}\right)+\mathbf{\Omega }\mathit{q}+\mathbf{\Sigma }\mathbf{1})\ge 0,$$

which implies that

$$\begin{array}{cc}\hfill \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{y};\mathit{Q},\mathbf{\Sigma },\mathit{q})& \le \mathrm{Q}\mathrm{L}{\mathrm{N}}_p({\mathit{D}}_{\mathit{Q}}\exp (-\mathbf{\Omega }\mathit{q}-\mathbf{\Sigma }\mathbf{1});\mathit{Q},\mathbf{\Sigma },\mathit{q})\hfill \\ \hfill & ={\left(2\pi \right)}^{-p/2}\det \left(\mathbf{\Sigma }\right)\exp \left(\frac{1}{2}{\mathbf{1}}^{\prime }\mathbf{\Sigma }\mathbf{1}-{\mathbf{1}}^{\prime }(\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q})\right),\hfill \end{array}$$

for all $\mathit{y}\in {\mathbb{R}}_{+}^p$. Hence, $\mathrm{Mode}\left(\mathit{Y}\right)={\mathit{D}}_{\mathit{Q}}\exp (-\mathbf{\Omega }\mathit{q}-\mathbf{\Sigma }\mathbf{1})$. □

Corollary 7.

The mode of $\mathit{Y}\sim \mathrm{L}{\mathrm{N}}_p(\mathit{\mu },\mathbf{\Sigma })$ is given by $\mathrm{Mode}\left(\mathit{Y}\right)={\mathit{D}}_{\mathit{\mu }}\exp (-\mathbf{\Sigma }\mathbf{1})$. The value of the PDF of $\mathit{Y}$ at the mode is

$$\mathrm{L}{\mathrm{N}}_p(\mathrm{Mode}\left(\mathit{Y}\right);\mathit{\mu },\mathbf{\Sigma })={\left(2\pi \right)}^{-p/2}\det \left(\mathbf{\Sigma }\right)\exp \left(\frac{1}{2}{\mathbf{1}}^{\prime }\mathbf{\Sigma }\mathbf{1}-{\mathbf{1}}^{\prime }\log \left(\mathit{\mu }\right)\right).$$

Proof. 

Apply Theorem 5 to the quantile-based multivariate log-normal distribution generated by $\mathit{\alpha }={(1/2,\dots ,1/2)}^{\prime }$. □

Theorem 6 provides the distribution of a Mahalanobis-type distance involving a quantile-based multivariate log-normal random vector.

Theorem 6.

If $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$, then ${\delta }_{\mathbf{\Sigma }}(\log \left(\mathit{Y}\right),\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q})\sim {\chi }_p^2$.

Proof. 

The result follows by noting that $\log \left(\mathit{Y}\right)\sim {\mathrm{N}}_p(\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })$. □

The above result allows us to evaluate the goodness of fit of the quantile-based multivariate log-normal distribution by using quantile–quantile plots to compare empirical Mahalanobis distances with theoretical quantiles obtained from a chi-squared distribution with p degrees of freedom.

The Shannon entropy (also called differential entropy) of a continuous random vector $\mathit{X}\in {\mathbb{R}}^p$ with PDF $f_{\mathit{X}}$ is defined as

$$H\left(\mathit{X}\right)=-\mathrm{E}\left[\log \left(f_{\mathit{X}}\left(\mathit{X}\right)\right)\right].$$

On the other hand, the Kullback–Leibler (KL) divergence between the distributions of two p-dimensional random vectors $\mathit{T}$ and $\mathit{U}$ is given by

$$D_{K\mathrm{L}}(\mathit{T},\mathit{U})=\mathrm{E}\left[\log \left(\frac{f_{\mathit{T}}\left(\mathit{T}\right)}{f_{\mathit{U}}\left(\mathit{T}\right)}\right)\right],$$

where $f_{\mathit{T}}$ and $f_{\mathit{U}}$ denote the PDFs of $\mathit{T}$ and $\mathit{U}$, respectively. The above expected value is defined with respect to the PDF $f_{\mathit{T}}$. A detailed study about Shannon entropy and KL divergence can be found in Pardo [18].

Lemmas 1 and 2 provide the Shannon entropy and the KL divergence for the multivariate normal distribution, respectively.

Lemma 1.

The Shannon entropy of $\mathit{X}\sim {\mathrm{N}}_p(\mathit{\mu },\mathbf{\Sigma })$ is given by

$$H\left(\mathit{X}\right)=\frac{1}{2}\log \left[\det \left(\mathbf{\Sigma }\right){\left(2\pi e\right)}^p\right].$$

Proof. 

See Pardo ([18], p. 32). □

Note that $H\left(\mathit{X}\right)$ in the above lemma can be expressed as

$$H\left(\mathit{X}\right)=\frac{p}{2}(1+\log \left(2\pi \right))+\frac{1}{2}\log \left(\det \left(\mathbf{\Sigma }\right)\right).$$

Lemma 2.

The KL divergence between $\mathit{X}\sim {\mathrm{N}}_p({\mathit{\mu }}_a,{\mathbf{\Sigma }}_a)$ and $\mathbf{W}\sim {\mathrm{N}}_p({\mathit{\mu }}_b,{\mathbf{\Sigma }}_b)$ is given by

$$D_{K\mathrm{L}}(\mathit{X},\mathbf{W})=\frac{1}{2}\left[\log \left(\frac{\det \left({\mathbf{\Sigma }}_b\right)}{\det \left({\mathbf{\Sigma }}_a\right)}\right)+tr({\mathbf{\Sigma }}_b^{-1}{\mathbf{\Sigma }}_a-{\mathit{I}}_p)+{({\mathit{\mu }}_a-{\mathit{\mu }}_b)}^{\prime }{\mathbf{\Sigma }}_b^{-1}({\mathit{\mu }}_a-{\mathit{\mu }}_b)\right].$$

Proof. 

See Pardo ([18], p. 33). □

In the following Theorem, we derive the Shannon entropy of the quantile-based multivariate log-normal distribution.

Theorem 7.

The Shannon entropy of $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$ is given by

$$H\left(\mathit{Y}\right)=\frac{p}{2}(1+\log \left(2\pi \right))+\frac{1}{2}\log \left(\det \left(\mathbf{\Sigma }\right)\right)+{\mathbf{1}}^{\prime }(\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q}).$$

Proof. 

By definition,

$$\begin{array}{cc}\hfill H\left(\mathit{Y}\right)& =-\mathrm{E}\left[\log \left(\mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Y};\mathit{Q},\mathbf{\Sigma },\mathit{q})\right)\right]\hfill \\ \hfill & =-{\int }_{{\mathbb{R}}_{+}^p}\log \left(\mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{y};\mathit{Q},\mathbf{\Sigma },\mathit{q})\right)\mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{y};\mathit{Q},\mathbf{\Sigma },\mathit{q})\mathrm{d}\mathit{y}.\hfill \end{array}$$

By making the change of variables $\mathit{y}=\exp \left(\mathit{x}\right)$, with Jacobian $J(\mathit{y}\to \mathit{x})=\exp \left({\sum }_{k=1}^p{x}_k\right)$, in the above integral, we have

$$\begin{array}{cc}\hfill H\left(\mathit{Y}\right)& =-{\int }_{{\mathbb{R}}^p}[\log \left({\varphi }_p(\mathit{x};\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })\right)-{\mathbf{1}}^{\prime }\mathit{x}]{\varphi }_p(\mathit{x};\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })\mathrm{d}\mathit{x}\hfill \\ \hfill & =H\left(\mathit{X}\right)+{\mathbf{1}}^{\prime }\mathrm{E}\left(\mathit{X}\right),\hfill \end{array}$$

where $\mathit{X}\sim {\mathrm{N}}_p(\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })$. The result follows by calculating $H\left(\mathit{X}\right)$ by using Lemma 1 and replacing $\mathrm{E}\left(\mathit{X}\right)=\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q}$ in the above expression. □

Corollary 8.

The Shannon entropy of $\mathit{Y}\sim \mathrm{L}{\mathrm{N}}_p(\mathit{\mu },\mathbf{\Sigma })$ is given by

$$H\left(\mathit{Y}\right)=\frac{p}{2}(1+\log \left(2\pi \right))+\frac{1}{2}\log \left(\det \left(\mathbf{\Sigma }\right)\right)+{\mathbf{1}}^{\prime }\log \left(\mathit{\mu }\right).$$

Proof. 

The result follows by applying Theorem 7 to the quantile-based multivariate log-normal distribution generated by $\mathit{\alpha }={(1/2,\dots ,1/2)}^{\prime }$. □

In Theorem 8, we derive the KL divergence between two quantile-based multivariate log-normal distributions.

Theorem 8.

The KL divergence between $\mathit{T}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p({\mathit{Q}}_a,{\mathbf{\Sigma }}_a,{\mathit{q}}_a)$ and $\mathit{U}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p({\mathit{Q}}_b,{\mathbf{\Sigma }}_b,{\mathit{q}}_b)$ is given by

$$\begin{array}{cc}\hfill D_{K\mathrm{L}}& (\mathit{T},\mathit{U})=\frac{1}{2}[\log \left(\frac{\det \left({\mathbf{\Sigma }}_b\right)}{\det \left({\mathbf{\Sigma }}_a\right)}\right)+\mathrm{tr}({\mathbf{\Sigma }}_b^{-1}{\mathbf{\Sigma }}_a-{\mathit{I}}_p)\hfill \\ & +{(\log \left({\mathit{Q}}_a\right)-{\mathbf{\Omega }}_a{\mathit{q}}_a-\log \left({\mathit{Q}}_b\right)+{\mathbf{\Omega }}_b{\mathit{q}}_b)}^{\prime }{\mathbf{\Sigma }}_b^{-1}(\log \left({\mathit{Q}}_a\right)-{\mathbf{\Omega }}_a{\mathit{q}}_a-\log \left({\mathit{Q}}_b\right)+{\mathbf{\Omega }}_b{\mathit{q}}_b)].\hfill \end{array}$$

Proof. 

By definition,

$$\begin{array}{cc}\hfill D_{K\mathrm{L}}(\mathit{T},\mathit{U})& =\mathrm{E}\left[\log \left(\frac{\mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{T};{\mathit{Q}}_a,{\mathbf{\Sigma }}_a,{\mathit{q}}_a)}{\mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{T};{\mathit{Q}}_b,{\mathbf{\Sigma }}_b,{\mathit{q}}_b)}\right)\right]\hfill \\ \hfill & ={\int }_{{\mathbb{R}}_{+}^p}\log \left(\frac{\mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{t};{\mathit{Q}}_a,{\mathbf{\Sigma }}_a,{\mathit{q}}_a)}{\mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{t};{\mathit{Q}}_b,{\mathbf{\Sigma }}_b,{\mathit{q}}_b)}\right)\mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{t};{\mathit{Q}}_a,{\mathbf{\Sigma }}_a,{\mathit{q}}_a)\mathrm{d}\mathit{t}.\hfill \end{array}$$

We substitute $\mathit{t}=\exp \left(\mathrm{w}\right)$, with Jacobian $J(\mathit{t}\to \mathrm{w})=\exp \left({\sum }_{k=1}^p{w}_k\right)$, above to arrive at

$$\begin{array}{cc}\hfill D_{K\mathrm{L}}(\mathit{T},\mathit{U})& ={\int }_{{\mathbb{R}}^p}\log \left(\frac{{\varphi }_p(\mathrm{w};\log \left({\mathit{Q}}_a\right)-{\mathbf{\Omega }}_a{\mathit{q}}_a,{\mathbf{\Sigma }}_a)}{{\varphi }_p(\mathrm{w};\log \left({\mathit{Q}}_b\right)-{\mathbf{\Omega }}_b{\mathit{q}}_b,{\mathbf{\Sigma }}_b)}\right){\varphi }_p(\mathrm{w};\log \left({\mathit{Q}}_a\right)-{\mathbf{\Omega }}_a{\mathit{q}}_a,{\mathbf{\Sigma }}_a)\mathrm{d}\mathrm{w}\hfill \\ \hfill & =D_{K\mathrm{L}}({\mathit{T}}^{*},{\mathit{U}}^{*}),\hfill \end{array}$$

where ${\mathit{T}}^{*}\sim {\mathrm{N}}_p(\log \left({\mathit{Q}}_a\right)-{\mathbf{\Omega }}_a{\mathit{q}}_a,{\mathbf{\Sigma }}_a)$ and ${\mathit{U}}^{*}\sim {\mathrm{N}}_p(\log \left({\mathit{Q}}_b\right)-{\mathbf{\Omega }}_b{\mathit{q}}_b,{\mathbf{\Sigma }}_b)$. By using Lemma 2 to calculate $D_{K\mathrm{L}}({\mathit{T}}^{*},{\mathit{U}}^{*})$ we arrive at the desired result. □

Corollary 9.

The KL divergence between $\mathit{T}\sim Q\mathrm{L}{\mathrm{N}}_p({\mathit{Q}}_a,{\mathbf{\Sigma }}_a,{\mathit{q}}_a)$ and $\mathit{U}\sim \mathrm{L}{\mathrm{N}}_p({\mathit{\mu }}_b,{\mathbf{\Sigma }}_b)$ is given by

$$\begin{array}{cc}\hfill D_{K\mathrm{L}}(\mathit{T},\mathit{U})=\frac{1}{2}[& \log \left(\frac{\det \left({\mathbf{\Sigma }}_b\right)}{\det \left({\mathbf{\Sigma }}_a\right)}\right)+\mathrm{tr}({\mathbf{\Sigma }}_b^{-1}{\mathbf{\Sigma }}_a-{\mathit{I}}_p)\hfill \\ \hfill & +{(\log \left({\mathit{Q}}_a\right)-{\mathbf{\Omega }}_a{\mathit{q}}_a-\log \left({\mathit{\mu }}_b\right))}^{\prime }{\mathbf{\Sigma }}_b^{-1}(\log \left({\mathit{Q}}_a\right)-{\mathbf{\Omega }}_a{\mathit{q}}_a-\log \left({\mathit{\mu }}_b\right))].\hfill \end{array}$$

Proof. 

Take the quantile-based multivariate log-normal random vector $\mathit{U}$ in Theorem 8 generated by $\alpha ={(1/2,\dots ,1/2)}^{\prime }$. □

Corollary 10.

The KL divergence between $\mathit{T}\sim \mathrm{L}{\mathrm{N}}_p({\mathit{\mu }}_a,{\mathbf{\Sigma }}_a)$ and $\mathit{U}\sim \mathrm{L}{\mathrm{N}}_p({\mathit{\mu }}_b,{\mathbf{\Sigma }}_b)$ is given by

$$\begin{array}{cc}\hfill D_{K\mathrm{L}}(\mathit{T},\mathit{U})=\frac{1}{2}[& \log \left(\frac{\det \left({\mathbf{\Sigma }}_b\right)}{\det \left({\mathbf{\Sigma }}_a\right)}\right)+tr({\mathbf{\Sigma }}_b^{-1}{\mathbf{\Sigma }}_a-{\mathit{I}}_p)+\hfill \\ & {(\log \left({\mathit{\mu }}_a\right)-\log \left({\mathit{\mu }}_b\right))}^{\prime }{\mathbf{\Sigma }}_b^{-1}(\log \left({\mathit{\mu }}_a\right)-\log \left({\mathit{\mu }}_b\right))].\hfill \end{array}$$

Proof. 

Generate the quantile-based multivariate log-normal random vector $\mathit{T}$ in Corollary 9 with $\mathit{\alpha }={(1/2,\dots ,1/2)}^{\prime }$. □

With the aim to derive results on marginal and conditional distributions and independence, relating sub-vectors of the random vector having a quantile-based multivariate log-normal distribution, we introduce notations for partitions of $\mathit{Y}\in {\mathbb{R}}_{+}^p$, $\mathit{Q}\in {\mathbb{R}}_{+}^p$, $\mathit{q}\in {\mathbb{R}}^p$, and $\mathbf{\Sigma }(p\times p)>0$ as follows:

$$\mathit{Y}={({\mathit{Y}}_1^{\prime },{\mathit{Y}}_2^{\prime })}^{\prime },\mathit{Q}={({\mathit{Q}}_1^{\prime },{\mathit{Q}}_2^{\prime })}^{\prime },\mathit{q}={({\mathit{q}}_1^{\prime },{\mathit{q}}_2^{\prime })}^{\prime },\mathbf{\Sigma }=\left[\begin{array}{cc}{\mathbf{\Sigma }}_{11}& {\mathbf{\Sigma }}_{12}\\ {\mathbf{\Sigma }}_{21}& {\mathbf{\Sigma }}_{22}\end{array}\right],$$

(9)

where ${\mathit{Y}}_1\in {\mathbb{R}}_{+}^{p_1}$, ${\mathit{Y}}_2\in {\mathbb{R}}_{+}^{p_2}$, ${\mathit{Q}}_1\in {\mathbb{R}}_{+}^{p_1}$, ${\mathit{Q}}_2\in {\mathbb{R}}_{+}^{p_2}$, ${\mathit{q}}_1\in {\mathbb{R}}^{p_1}$, ${\mathit{q}}_2\in {\mathbb{R}}^{p_2}$, ${\mathbf{\Sigma }}_{11}(p_1\times p_1)>0$, ${\mathbf{\Sigma }}_{22}(p_2\times p_2)>0$, and ${\mathbf{\Sigma }}_{12}(p_1\times p_2)$ and ${\mathbf{\Sigma }}_{21}(p_2\times p_1)$ are such that ${\mathbf{\Sigma }}_{12}^{\prime }={\mathbf{\Sigma }}_{21}$. The Schur complement of the block ${\mathbf{\Sigma }}_{11}$ of $\mathbf{\Sigma }$ is given by ${\mathbf{\Sigma }}_{22·1}={\mathbf{\Sigma }}_{22}-{\mathbf{\Sigma }}_{21}{\mathbf{\Sigma }}_{11}^{-1}{\mathbf{\Sigma }}_{12}$. Also, we define ${\mathbf{\Omega }}_1={({\mathbf{\Sigma }}_{11}\odot {\mathit{I}}_{p_1})}^{1/2}$, ${\mathbf{\Omega }}_2={({\mathbf{\Sigma }}_{22}\odot {\mathit{I}}_{p_2})}^{1/2}$, and ${\mathit{Q}}_{2·1}={\mathit{D}}_{{\mathit{Q}}_2}\exp \left({\mathbf{\Sigma }}_{21}{\mathbf{\Sigma }}_{11}^{-1}(\log \left({\mathit{y}}_1\right)-\log \left({\mathit{Q}}_1\right)+{\mathbf{\Omega }}_1{\mathit{q}}_1)\right)$. The dimension p is such that $p=p_1+p_2$.

In Lemma 3, we give a factorization of the PDF of the quantile-based multivariate log-normal distribution.

Lemma 3.

Consider the partitions given in (9). The PDF of $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$ can be expressed as

$$\mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{y};\mathit{Q},\mathbf{\Sigma },\mathit{q})=\mathrm{Q}\mathrm{L}{\mathrm{N}}_{p_1}({\mathit{y}}_1;{\mathit{Q}}_1,{\mathbf{\Sigma }}_{11},{\mathit{q}}_1)\mathrm{Q}\mathrm{L}{\mathrm{N}}_{p_2}({\mathit{y}}_2;{\mathit{Q}}_{2·1},{\mathbf{\Sigma }}_{22·1},{\mathit{q}}_{2·1}),$$

(10)

where ${\mathit{q}}_{2·1}={\mathbf{\Omega }}_{2·1}^{-1}{\mathbf{\Omega }}_2{\mathit{q}}_2$, with ${\mathbf{\Omega }}_{2·1}={({\mathbf{\Sigma }}_{22·1}\odot {\mathit{I}}_{p_2})}^{1/2}$.

Proof. 

It suffices to show that

$$\begin{array}{cc}\hfill {\delta }_{\mathbf{\Sigma }}(\log \left(\mathit{y}\right),\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q})=& {\delta }_{{\mathbf{\Sigma }}_{11}}(\log \left({\mathit{y}}_1\right),\log \left({\mathit{Q}}_1\right)-{\mathbf{\Omega }}_1{\mathit{q}}_1)\hfill \\ \hfill & +{\delta }_{{\mathbf{\Sigma }}_{22·1}}(\log \left({\mathit{y}}_2\right),\log \left({\mathit{Q}}_{2·1}\right)-{\mathbf{\Omega }}_{2·1}{\mathit{q}}_{2·1}).\hfill \end{array}$$

The straightforward calculation shows that

$$\begin{array}{cc}\hfill {\delta }_{\mathbf{\Sigma }}(\log \left(\mathit{y}\right),& \log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q})-{\delta }_{{\mathbf{\Sigma }}_{11}}(\log \left({\mathit{y}}_1\right),\log \left({\mathit{Q}}_1\right)-{\mathbf{\Omega }}_1{\mathit{q}}_1)\hfill \\ \hfill & ={(\log \left({\mathit{y}}_1\right)-\log \left({\mathit{Q}}_1\right)+{\mathbf{\Omega }}_1{\mathit{q}}_1)}^{\prime }{\mathbf{\Sigma }}_{11}^{-1}{\mathbf{\Sigma }}_{12}{\mathbf{\Sigma }}_{22·1}^{-1}{\mathbf{\Sigma }}_{21}{\mathbf{\Sigma }}_{11}^{-1}(\log \left({\mathit{y}}_1\right)-\log \left({\mathit{Q}}_1\right)+{\mathbf{\Omega }}_1{\mathit{q}}_1)\hfill \\ \hfill & -2{(\log \left({\mathit{y}}_1\right)-\log \left({\mathit{Q}}_1\right)+{\mathbf{\Omega }}_1{\mathit{q}}_1)}^{\prime }{\mathbf{\Sigma }}_{11}^{-1}{\mathbf{\Sigma }}_{12}{\mathbf{\Sigma }}_{22·1}^{-1}(\log \left({\mathit{y}}_2\right)-\log \left({\mathit{Q}}_2\right)+{\mathbf{\Omega }}_2{\mathit{q}}_2)\hfill \\ \hfill & +{(\log \left({\mathit{y}}_2\right)-\log \left({\mathit{Q}}_2\right)+{\mathbf{\Omega }}_2{\mathit{q}}_2)}^{\prime }{\mathbf{\Sigma }}_{22·1}^{-1}(\log \left({\mathit{y}}_2\right)-\log \left({\mathit{Q}}_2\right)+{\mathbf{\Omega }}_2{\mathit{q}}_2).\hfill \end{array}$$

Now, using the result

$$(\log \left({\mathit{Q}}_{2·1}\right)-{\mathbf{\Omega }}_{2·1}{\mathit{q}}_{2·1})-(\log \left({\mathit{Q}}_2\right)-{\mathbf{\Omega }}_2{\mathit{q}}_2)={\mathbf{\Sigma }}_{21}{\mathbf{\Sigma }}_{11}^{-1}(\log \left({\mathit{y}}_1\right)-\log \left({\mathit{Q}}_1\right)+{\mathbf{\Omega }}_1{\mathit{q}}_1),$$

we have

$$\begin{array}{cc}\hfill {\delta }_{\mathbf{\Sigma }}(\log \left(\mathit{y}\right),& \log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q})-{\delta }_{{\mathbf{\Sigma }}_{11}}(\log \left({\mathit{y}}_1\right),\log \left({\mathit{Q}}_1\right)-{\mathbf{\Omega }}_1{\mathit{q}}_1)\hfill \\ \hfill & ={(\log \left({\mathit{y}}_2\right)-\log \left({\mathit{Q}}_{2·1}\right)+{\mathbf{\Omega }}_{2·1}{\mathit{q}}_{2·1})}^{\prime }{\mathbf{\Sigma }}_{22·1}^{-1}(\log \left({\mathit{y}}_2\right)-\log \left({\mathit{Q}}_{2·1}\right)+{\mathbf{\Omega }}_{2·1}{\mathit{q}}_{2·1})\hfill \\ \hfill & ={\delta }_{{\mathbf{\Sigma }}_{22·1}}(\log \left({\mathit{y}}_2\right),\log \left({\mathit{Q}}_{2·1}\right)-{\mathbf{\Omega }}_{2·1}{\mathit{q}}_{2·1}),\hfill \end{array}$$

which is the desired result. □

In Theorem 9, we show that the quantile-based multivariate log-normal family is preserved under marginalization and conditioning. In this theorem, we also present a characterization of the independence between subvectors of this family.

Theorem 9.

Let $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$. Consider the partitions given in (9). Then,

• ${\mathit{Y}}_1\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_{p_1}({\mathit{Q}}_1,{\mathbf{\Sigma }}_{11},{\mathit{q}}_1)$.
• ${\mathit{Y}}_2|{\mathit{Y}}_1={\mathit{y}}_1\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_{p_2}({\mathit{Q}}_{2·1},{\mathbf{\Sigma }}_{22·1},{\mathit{q}}_{2·1})$.
• ${\mathit{Y}}_1$ and ${\mathit{Y}}_2$ are independent if and only if ${\mathbf{\Sigma }}_{12}=\mathbf{0}$.

Proof. 

Statements 1 and 2 follow from the factorization given in (10). To prove the statement 3, note that ${\mathit{Y}}_1$ and ${\mathit{Y}}_2$ are independent if and only if

$$\mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{y};\mathit{Q},\mathbf{\Sigma },\mathit{q})=\mathrm{Q}\mathrm{L}{\mathrm{N}}_{p_1}({\mathit{y}}_1;{\mathit{Q}}_1,{\mathbf{\Sigma }}_{11},{\mathit{q}}_1)\mathrm{Q}\mathrm{L}{\mathrm{N}}_{p_2}({\mathit{y}}_2;{\mathit{Q}}_2,{\mathbf{\Sigma }}_{22},{\mathit{q}}_2),$$

which, from (10), is satisfied if and only if ${\mathbf{\Sigma }}_{12}=\mathbf{0}$. □

4. Parameter Estimation

The reparameterization used in Definition 1 permits us to compute the maximum likelihood estimates of the parameters of the quantile-based multivariate log-normal distribution through the maximum likelihood estimates of the parameters of the multivariate log-normal distribution. Let ${\mathit{y}}_1,\dots ,{\mathit{y}}_n$ be the observed values of a random sample ${\mathit{Y}}_1,\dots ,{\mathit{Y}}_n$ of $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$. We denote the maximum likelihood estimators of $\mathit{Q}$ and $\mathbf{\Sigma }$ by $\widehat{\mathit{Q}}$ and $\widehat{\mathbf{\Sigma }}$, respectively. From (2), we have

$$\widehat{\mathit{Q}}={\mathit{D}}_{\widehat{\mathit{\mu }}}\exp \left(\widehat{\mathbf{\Omega }}\mathit{q}\right),$$

(11)

where $\widehat{\mathbf{\Omega }}={(\widehat{\mathbf{\Sigma }}\odot {\mathit{I}}_p)}^{1/2}$, and $\widehat{\mathit{\mu }}$ and $\widehat{\mathbf{\Sigma }}$ are the maximum likelihood estimators of the multivariate log-normal distribution given by (Morán-Vásquez et al. [14])

$$\begin{array}{cc}\hfill \widehat{\mathit{\mu }}& =\exp \left(\frac{1}{n}\sum _{i=1}^n\log \left({\mathit{y}}_i\right)\right),\hfill \\ \hfill \widehat{\mathbf{\Sigma }}& =\frac{1}{n}\sum _{i=1}^n(\log \left({\mathit{y}}_i\right)-\log \left(\widehat{\mathit{\mu }}\right)){(\log \left({\mathit{y}}_i\right)-\log \left(\widehat{\mathit{\mu }}\right))}^{\prime }.\hfill \end{array}$$

Note that the maximum likelihood estimator of $\mathbf{\Sigma }$ in the quantile-based multivariate log-normal distribution is the same as in the multivariate log-normal distribution. Furthermore, this estimator is the same for any choice of $\mathit{q}$.

We assess the goodness of fit of the quantile-based multivariate log-normal distributions by using quantile–quantile plots, comparing the empirical Mahalanobis distances ${\delta }_{\widehat{\mathbf{\Sigma }}}(\log \left({\mathit{y}}_i\right),\log \left(\widehat{\mathit{Q}}\right)-\widehat{\mathbf{\Omega }}\mathit{q})$, $i=1,\dots ,n$, with the theoretical quantiles ${\delta }_{{\alpha }_i}^2$, where ${\alpha }_i=i/(n+1)$, $i=1,\dots ,n$, obtained from a chi-squared distribution with p degrees of freedom. Additionally, we plot simulated envelopes (Atkinson [19]) for the quantile–quantile plots in order to help the comparison between quantiles and judge the adequacy of the models.

To evaluate the estimation procedure, we conducted simulations with the quantile-based bivariate log-normal distribution. We consider the sample sizes of $n=50,100,500,1000$, and $10,000$ Monte Carlo replicates. The random samples of $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$ were generated through the following steps:

• Generate a random sample ${\mathit{x}}_1,\dots ,{\mathit{x}}_n$ of of $\mathit{X}\sim {\mathrm{N}}_p(\log \left(\mathit{Q}\right)-\mathbf{\Omega }\mathit{q},\mathbf{\Sigma })$.
• Compute ${\mathit{y}}_1=\exp \left({\mathit{x}}_1\right),\dots ,{\mathit{y}}_n=\exp \left({\mathit{x}}_n\right)$. Then, ${\mathit{y}}_1,\dots ,{\mathit{y}}_n$ is a random sample of $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_p(\mathit{Q},\mathbf{\Sigma },\mathit{q})$.

The true parameters were yielded by fitting the quantile-based bivariate log-normal distribution to the children data set considered in Section 5. Table 1 reports the median and the interquartile range for the estimated values of the parameters of the investigated models. The medians get close to the true parameters and the interquartile range gets smaller as the sample size grows, indicating a satisfactory performance of the estimators. All the computations were conducted in the R software [20].

Table 1. Median (M) and interquartile range (IQR) of the parameter estimates of the quantile-based bivariate log-normal distributions.

			$\mathit{n}=\mathbf{50}$		$\mathit{n}=\mathbf{100}$		$\mathit{n}=\mathbf{500}$		$\mathit{n}=\mathbf{1000}$
Probability	True Parameter		M	IQR	M	IQR	M	IQR	M	IQR
${\alpha }_1=0.75$	$Q_1$	101.62	101.59	1.6480	101.59	1.1849	101.60	0.5391	101.61	0.3747
${\alpha }_2=0.25$	$Q_2$	13.101	13.115	0.4923	13.108	0.3378	13.102	0.1557	13.103	0.1115
${\alpha }_1=0.50$	$Q_1$	96.368	96.373	1.4397	96.365	1.0000	96.365	0.4582	96.367	0.3229
${\alpha }_2=0.50$	$Q_2$	14.764	14.768	0.4965	14.766	0.3417	14.763	0.1625	14.764	0.1123
${\alpha }_1=0.25$	$Q_1$	91.392	91.429	1.5166	91.406	1.0509	91.397	0.4784	91.396	0.3437
${\alpha }_2=0.75$	$Q_2$	16.640	16.632	0.6190	16.634	0.4332	16.635	0.2016	16.636	0.1412
	${\sigma }_{11}$	0.0062	0.0062	0.0016	0.0062	0.0012	0.0062	0.0005	0.0062	0.0004
	${\sigma }_{22}$	0.0314	0.0313	0.0085	0.0313	0.0059	0.0313	0.0027	0.0313	0.0019
	${\sigma }_{12}$	0.0121	0.0121	0.0035	0.0121	0.0025	0.0121	0.0011	0.0121	0.0008

5. Application

Anthropometric measures are useful for monitoring the growth and identification of childhood developmental problems. The World Health Organization [21,22] provides quantile estimations of several children’s anthropometric characteristics as height, weight, and head and arm circumferences, among others. These estimations are obtained by fitting univariate models for each anthropometric measurement separately, ignoring the association between them. We use the quantile-based bivariate log-normal distribution to estimate quantiles of children’s weights (in kilograms) and heights (in centimeters), considering the natural correlation between them. We consider a sample of 587 children between 2 and 5 years of age collected at the year 2018 in the El Poblado neighborhood, located in Medellín, Colombia [23].

The bagplot in Figure 2 shows that children’s weights and heights are positively associated with slight joint skewedness and highlights two outliers. In order to estimate the third quartile of weight and the first quartile of height, we fitted the quantile-based bivariate log-normal distribution $\mathit{Y}\sim \mathrm{Q}\mathrm{L}{\mathrm{N}}_2(\mathit{Q},\mathbf{\Sigma },\mathit{q})$, with ${\alpha }_1=0.75(q_1=0.67)$ and ${\alpha }_2=0.25(q_2=-0.67)$. The maximum likelihood estimates of the parameters are ${\widehat{Q}}_1=101.62$, ${\widehat{Q}}_2=13.101$, ${\widehat{\sigma }}_{11}=0.0062$, ${\widehat{\sigma }}_{22}=0.0314$, and ${\widehat{\sigma }}_{12}=0.0121$. Therefore, the third quartile of the children’s height is estimated to be $101.62$ cm, and the first quartile of the children’s weight is estimated to be $13.101$ kg. Since ${\widehat{\sigma }}_{12}=0.0121$, thereby the children’s weights and heights are estimated to be positively correlated, which is consistent with the descriptive analysis presented in Figure 2.

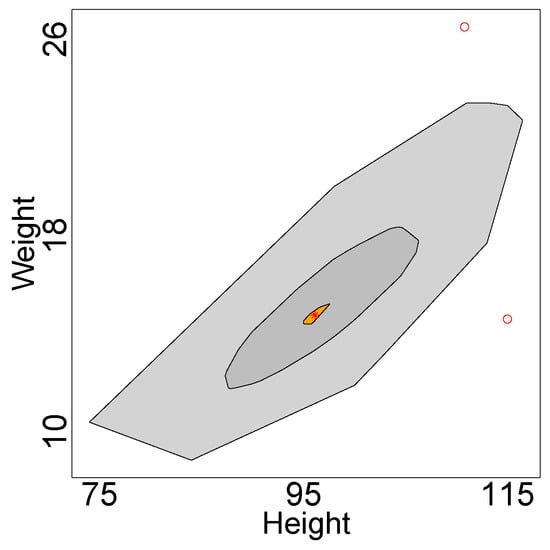
Figure 2. Bagplot of weight vs. height; children’s data.

Figure 3 shows the quantile–quantile plot with simulated envelopes for the Mahalanobis distances for the fitted quantile-based bivariate log-normal distribution. This plot suggests a suitable fit.

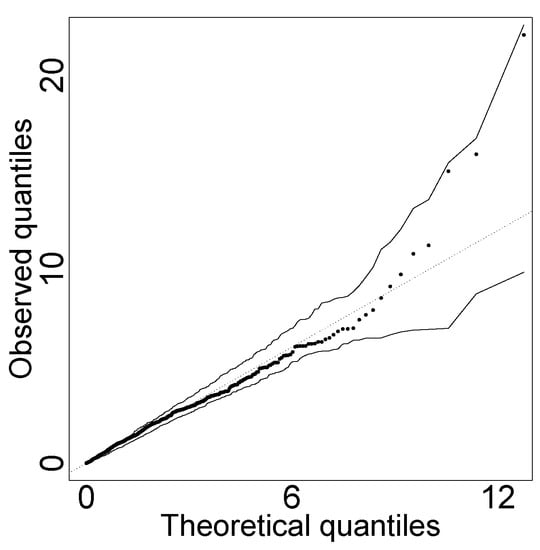
Figure 3. Quantile–quantile plot with simulated envelopes for the Mahalanobis distances for the fitted distribution.

6. Final Remarks

In this article, we have proposed a multivariate distribution with positive support derived by applying a parameterization of the multivariate log-normal distribution by using their marginal quantiles. This distribution will attract researchers in the area of quantile modeling for correlated multivariate positive skewed data. We derived a number of important statistical properties of this distribution involving the transformations, mixed moments, expected value, covariance matrix, mode, Shannon entropy, Kullback–Leibler divergence, marginalization, conditioning, and independence. Needless to say, the quantile-based multivariate log-normal distribution defined in this article is rich in theoretical properties and can easily be manipulated from a mathematical viewpoint. The parameter estimation was approached by using the maximum likelihood estimation method. The satisfactory behavior of the estimation procedure was verified through simulation studies. Also, a graphical diagnostic tool was employed in order to assess the quality of the fitted distributions. On the other hand, an application to real data is presented and discussed as an alternative for the quantile estimation of the children’s weights and heights, considering the natural association between these variables.

There are several aspects that will be addressed in future articles. Bayesian approaches for the estimation of the parameters of the quantile-based multivariate log-normal distribution will be developed. The study of regression models based on the quantile-based multivariate log-normal distributions together with inferential developments and applications to real data will also be undertaken. These models will allow us to analyze the relationship between marginal quantiles of response vectors and a set of explanatory variables, taking into account the potential association among the marginal response variables. Additionally, a comparative analysis of this methodology with the model proposed by Petrella and Raponi [12] will be included in a forthcoming article.