Abstract
We consider symmetric fuzzy stochastic differential equations where diffusion and drift terms arise in a symmetric way at both sides of the equations and diffusion parts are driven by fractional Brownian motions. Such equations can be used in real-life hybrid systems, which include properties of being both random and fuzzy and reflecting long-range dependence. By imposing on the mappings occurring in the equation the conditions of Lipschitzian continuity and additional constraints by an integrable stochastic process, we construct an approximation sequence of fuzzy stochastic processes and apply this to prove the existence of a unique solution to the studied equation. Finally, a model from population dynamics is considered to illustrate the potential application of our equations.
1. Introduction
There are different types of uncertainties that arise when modeling physical phenomena. The most common is stochasticity, which is related to random forces. On the other hand, the inability to accurately determine the value of a phenomenon in the form of a single number leads to the use of fuzzy sets. Since reality goes even further, systems are constructed whose nature requires the implementation of these two different types of uncertainty, see, e.g., [1,2,3,4,5,6,7,8,9,10,11]. Among them, fuzzy stochastic differential equations (FSDEs) [3,4,5,6,7,8,9] have been proposed for modeling the dynamics of such systems, which aim to model real hybrid dynamical systems that are characterized by stochastic behaviors and fuzzy values. Therefore, association of stochasticity and fuzziness in our research is reflected by the use of stochastic processes whose values are fuzzy sets. Let us mention that fuzzy stochastic differential equations are already well established in the literature by the author M.T. Malinowski and colleagues, but are still a new area of research.
In the fuzzy stochastic differential equations studied in [3,4,5,6,7,8,9], the diffusion part of the equations is described by standard Brownian motion (Wiener process). However, for analyzing phenomena that reveal long-range dependence, fractional Brownian motion (fBm) may be a better choice than standard Brownian motion. By using fBm, a wider range of possible applications can be obtained. Therefore, in [12], we focused on FSDEs where the diffusion part was driven by fBm.
The form of the equation considered in [12] is one-sided and can be called asymmetric. Thus, in this paper, we now propose to consider symmetric (bipartite, two-sided) equations driven by fBm. Let us explain why we would like to study such symmetric equations. The starting point is connected with an interesting feature of FSDEs driven by standard Brownian motion that was indicated in [5]. Namely, the fuzziness of the values in the sample paths of solutions of the asymmetric equations studied there increases more and more with respect to the time variable. Thus, such asymmetric equations could not provide the tools to model all possible cases that could practically occur, including one where the fuzziness of solution paths decreases as the time variable increases. Therefore, a different second type of asymmetric FSDEs, driven by standard Brownian motion, was proposed, whose solutions had decreasing fuzziness in sample path values [7]. The two types of asymmetric FSDEs (driven by standard Brownian motions) mentioned above were joined in one equation, which has been called Symmetric (Bipartite, Two-sided) and is FSDE driven by standard Brownian motion [8]. The fuzziness of the values represented by the solution to such symmetric equations can change the nature of monotonicity with the change in time. Therefore, in this article, progressing in the direction just described, we consider symmetric FSDEs driven by fBm. These equations are a new type of fuzzy stochastic differential equation and have not been studied elsewhere yet. They generalize the types of equations introduced in previous articles [5,6,7] on asymmetric FSDEs driven by standard Brownian motion, for example, [8,9] on symmetric FSDEs driven by standard Brownian motion and [12] about asymmetric FSDEs driven by fBm [12]. For a clear distinction, we refer to them as the Symmetric Fractional FSDEs (SFFSDEs, for short). With these equations, it is possible to model stochastic systems subjected to data imprecision expressed by fuzzy sets, in which long-range dependence of achieved states is assumed. In this first article, we focus on extremely important theoretical issues, such as the existence of a solution to such an equation, because only then will it be possible to apply such equations in practice. Thus, subject to the boundedness and Lipschitz assumptions on the diffusion and drift coefficients, we follow an approximation method (which was applied in [12] and goes beyond the standards, because we use a semimartingale approximation sequence of fractional Brownian motion) to prove the existence of a unique solution.
The paper is organized as follows. In Section 2, we recall some preliminary information on fBm and some concepts of fuzzy stochastic analysis. In the main Section 3, we introduce a class of symmetric FSDEs with diffusion and drift terms at both sides of the equation, in which the diffusion parts are driven by fBm. We use an approximation technique to study the existence of the unique solutions. In Section 4, as an illustration of our theoretical results, we provide an example of SFFSDE in population models and obtain the explicit form of a unique solution. The paper ends with some conclusions, contained in Section 5.
2. Preliminaries
This section is devoted to some preliminaries on the properties of the fBm and a representation of this process. Also some notions from fuzzy analysis are presented for convenience of the reader.
2.1. Fractional Brownian Motion
By , for , we denote the fractional Brownian motion (fBm), i.e., a Gaussian process with covariance function .
In the literature, there are two ways of defining the integral relative to fBm. Namely, for , a first approach is based on the Riemann–Stieltjes stochastic integral [13], and the other way is to use Malliavin calculus to create stochastic integrals driven by fBm (see [14,15,16,17]). According to [18], we can write
where W is the Wiener process and , with , and is the Liouville form of fBm. It was shown (see [14]), using the Malliavin calculus method, that has approximations in form of semimartingales:
Moreover,
where
Due to [19], is convergent to in as approaches zero.
2.2. Fuzzy Analysis Framework
Let denote the family of all nonempty, convex, and compact subsets of . Consider the Hausdorff metric , where denotes a norm in .
A function is called a fuzzy set of the space . Let us denote, by , the set of fuzzy sets that satisfy the condition for every , where , and is continuous with respect to the Hausdorff metric .
We consider the following metric:
It is easy to notice that every is a fuzzy set. This is by considering its characteristic function, denoted in this paper by .
We use the following properties (see e.g., [7,20]):
for , , and ;
- (W1)
- (W2)
- exists iff exists.
Moreover, ;
- (W3)
- ;
- (W4)
- ;
- (W5)
- ;
- (W6)
- , where ⊖ denotes Hukuhara difference of fuzzy sets.
Let us recall that a mapping is a fuzzy random variable iff it is -measurable, with the Skorohod metric in , and is the -algebra generated by the topology induced by (see [21]).
By , we denote the set of all fuzzy random variables that are -integrably bounded.
Let , where , and let us consider a filtered, complete probability space , with the filtration satisfying usual conditions.
The mapping is a fuzzy stochastic process if, for every , is a fuzzy random variable.
A fuzzy stochastic process X is said to be h-continuous if almost all (with respect to P) mappings are h-continuous.
Denote, by (see [3]), the set of all equivalence classes (with respect to equality -a.e., where is the Lebesgue measure) of non-anticipating and -integrally bounded fuzzy stochastic processes.
For , by the Fubini Theorem, the fuzzy stochastic Lebesgue integral is given by , where and (see [3,4]).
Proposition 1
(see [5]). Let , where . Then, we have the following properties:
- (1)
- ;
- (2)
- is h-continuous;
- (3)
- With probability one for every , the following holds:
- (4)
- For every :
For the stochastic Itô integral, with respect to the Wiener process, we have the following proposition (see [3,4]).
Proposition 2.
Let . Then:
- (1)
- The fuzzy stochastic process belongs to ;
- (2)
- The process is h-continuous;
- (3)
- for every :
At the end of this section, we include the inequality which is well-known as the Hölder inequality or Buniakowski–Schwarz inequality.
Lemma 1
(Hölder inequality, Buniakowski–Schwarz inequality). If A is a measurable subset of with the Lebesgue measure, and f and g are measurable real-valued functions on A, then:
3. Main Results
This section of the article presents the results on the symmetric fractional fuzzy stochastic differential equations (SFFSDEs). These results are preceded by markings and assumptions within the framework of which the achievements have been obtained.
Let denote an m-dimensional () -adapted fBm on the filtered probability space . We have
where are independent -adapted fractional Brownian motions. By , we denote an n-dimensional fBm independent of .
In the paper we study SFFSDEs in the following form:
with initial condition , where is a fuzzy random variable, and with mappings . Taking into account the fact that , , where for and , and that the differential form of the stochastic equation has an equivalent integral form, by replacing the differential form with an integral form, we can see that the subject of our research will be equations:
In a particular case, this equation could reduce to the following one-sided equation:
this is, of course, if we take and , in Equation (5). Such equations have been introduced and studied in [12]. Furthermore, if and, for , , then (5) is transformed to one-sided equation:
and such equations have not yet been examined.
In the paper, we study existence and uniqueness of the solution to (5), which generalizes both the particular equations mentioned above and captures propagation of the fuzziness of both one-sided equations.
We want to simplify the form of the equation under consideration a bit. Therefore, invoking properties (W1) and (W2) and applying them in (5), we obtain
which leads us to a formulation of SFFSDEs in a bit more convenient form:
where is a fuzzy random variable, , , and are adapted independent fractional Brownian motions.
We now write clearly what we mean by the solution of the equation under consideration and what the uniqueness of the solution means. Let ] and .
Definition 1.
Our main goal is to justify that SFFSDEs have a solution under certain conditions with the coefficients of the equations. Therefore, let us consider the following assumptions:
- (A0)
- ;
- (A1)
- are -measurable and , are -measurable;
- (A2)
- There exists a constant such that, for every , for -a.a. , and :
- (A3)
- For some real-valued stochastic processes it holds that, for -a.a. and :
- (A4)
- There exists ] such that consisting of : , where ,is well defined, and the Hukuhara differences exist.
To begin our deduction, let us first note that, following the method applied in [12] and using notation appearing in representation (1) with , we can write an approximation of Equation (6) as follows:
Addtionally, an approximation formula of (7) is given as shown:
A preliminary result indicates that the sequence is uniformly bounded. Hence, we are able to infer that the solution to Equation (8) is bounded as well.
Proposition 3.
Suppose that satisfy assumptions (A0)–(A4). Then, for every and for every , we have
Proof.
For and , denote . Applying (2), we obtain
where one-dimensional processes are the independent Wiener processes. By properties (W3)–(W5), we have
Then, we can write
Due to Propositions 1 and 2 and Doob’s inequality, we can write
On the other hand,
Using (3) in (11) and applying the Hölder inequality, we obtain
From (11) and (12), we have
Similarly, we can show
Using (13) and (14) in (11), we obtain
Hence, using assumptions (A2) and (A3), we obtain
Then, for and , we can write as shown:
By the Gronwall inequality, we obtain
Therefore
The proof is completed. □
Now we formulate the result on existence of the unique solution to SFFSDE (8), which is the foundation for the next main result on such equations. In proving this fact, we will use some steps used also for asymmetric equations, e.g., [3,5,7,8].
Theorem 1.
Let the assumptions (A0)–(A4) be satisfied. Then SFFSDE (8) has a unique solution.
Proof.
Let us denote
Applying (W3), (W6), (W4) and (2), we have
By Proposition 1, Proposition 2 and Doob’s inequality, and similar arguments as in Proposition 3, we obtain
By assumptions (A2) and (A3), we get
where . Similarly, for we get
Hence, for
By Chebyshev’s inequality, we get
The series is convergent. Then, from the Borel-Cantelli lemma, we have
Thanks to this, we can deduce that there exists an h-continuous fuzzy stochastic process such that a.s., as . It can also be verified that
By assumption (A2), Proposition 1, Proposition 2 and the Lebesgue Dominated Convergence Theorem, we obtain that the expression
tends to zero as n goes to infinity. This leads us to the observation
for every . In a further step, we get that with probability one it holds
The processes are h-continuous, hence with probability one
This shows that is a solution (possibly a local solution) to Equation (8).
Now we shall show the uniqueness of this solution. Assume that are two solutions to Equation (8). Let us consider
Then we have
By similar reasoning as in (13), we obtain
Invoking Gronwall inequality, we have that for . Hence with probability one
which completes the proof. □
Now we proceed to obtain a unique solution to the main, original SFFSDE (6). This kind of result is important because for any potential future research it justifies the existence of solution in the case of the impossibility of obtaining a solution in an explicit form. In our derivation, we will use the fact that for every and ,
Theorem 2.
Proof.
For , we have
Furthermore
Hence
Using representation (2), we obtain
Then
By Hölder inequality and Doob’s inequality, we get
Using (15) and assumptions (A2)–(A3), we obtain
Hence
By the usage of Gronwall’s inequality
where . If we get
This implies that for every the sequence is a Cauchy sequence in the space . Hence, invoking [22], we get that there exists such that
as . Let us define a fuzzy stochastic process as follows . We shall show that X is the unique solution to Equation (6). By (16) and Chebyshev’s inequality, we obtain for every
as . Hence there exists subsequence of the sequence such that
Thus, X is h-continuous and -measurable. Together with the property that for every fuzzy random variable is -measurable, we obtain that X is nonanticipating. Moreover, since for every , one can write
This means that .
Because , it remains to show that the second term on right hand side of the above inequality converges to zero. Let us observe that
Furthermore
Hence
Applying (2), we get
Then
According to Hölder inequality and Doob’s inequality, we obtain
Using inequality (15) and assumptions (A2)–(A3), we obtain
Therefore,
By Gronwall’s lemma, as . Hence, X satisfies Equation (6).
Now, we prove that the solution X is unique. Assume that are the two solutions to Equation (6). For every , we have
From Theorem 1 and discussions above, we obtain
From this, we conclude that, for every with probability one, we have . Since processes are h-continuous, we obtain
from which the uniqueness of the solution follows. The proof is completed. □
By proving the above theorem, we have achieved the goal of this paper. We have shown that the Symmetric Fuzzy Stochastic Differential Equation Driven by Fractional Brownian Motion (6) has a unique solution.
4. Application to Population Growth Model
The following crisp stochastic differential equation can be used in population growth models:
where underlying stochastic process B is the standard Brownian motion. Taking into account fuzzy processes that appear in real world and long-range dependence of states, the corresponding fractional fuzzy stochastic differential equation would be more suitable for modeling and it can be proposed, for instance, as follows:
where , is the fractional Brownian motion, , such that , , and . However, the solutions to such an equation will be burdened with the property of the non-decreasing fuzziness of the value of the solution. To avoid this situation and to allow all possible cases of propagation of fuzziness, we consider a new type of equation proposed in this paper, namely, the symmetric equation, which is an extension of Equation (17) and is given by
In most cases of crisp (classic) stochastic differential equations, they are solved numerically, provided that the existence of a solution to such an equation is justified. In the case of our fuzzy Equation (18), we have justified the existence of a solution in theoretical considerations in the previous section, and we now do even more by showing what the solution of this equation looks like clearly. This is possible because the equation is of a linear type.
According to a remark mentioned in (6) and properties (P1) and (P2), Equation (18) can be written in a slightly easier form, and it is, in this case, as follows:
and taking , we have, furthermore,
In order to find an explicit solution to (19), we write the following equations:
Hence,
The explicit solution of the crisp linear stochastic differential Equation (21) reads
Hence, using (2) again, we obtain
Now, for every , we proceed similarly and obtain, for -cuts ,
Firstly, we solve the first equation of the system written above. Using (22), we obtain
Thus, the solution is
Applying (2) once again, we arrive at
Similar calculations can be performed to determine the value of that solves the second equation in (23). This way we obtain
Hence,
Letting proceed to zero, we obtain that the desired fuzzy stochastic solution for our equation is
Finding explicit solutions to other more complicated equations than Equation (19) can be difficult or even impossible. However, if only the considered equation meets the assumptions implying the existence of a unique solution, one can try to find exemplary trajectories of the solution using numerical methods. For the Equation (19) studied in this section, we present two numerical illustrations. As such, let us return to Equation (19), i.e.,
Let us consider as a triangular fuzzy number such that and . Due to the linearity of the above equation and the shape-preserving integral property, we can conclude that, for the solution X, the fuzzy set is a triangular fuzzy number such that , where .
Hence, with the previous data, we can write
To obtain some illustrations of the -cuts of the solution to Equation (19), we took and performed a simulation using fBm with the Hurst index of 0.8. For , , , the exemplary sample path is as in Figure 1.
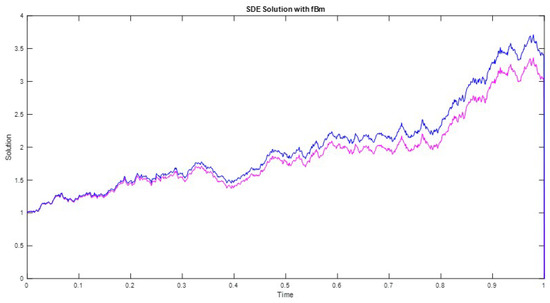
Figure 1.
A trajectory of the boundaries of the -cut of solution to (19). The blue line represents and the purple line represents .
For , the sample path is as drawn in Figure 2.
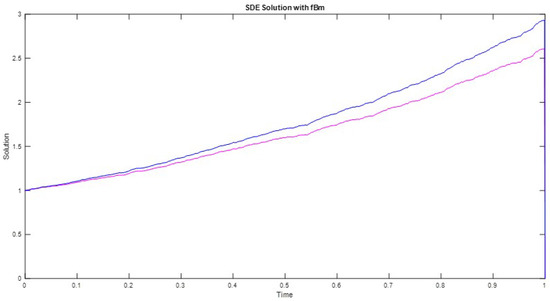
Figure 2.
A trajectory of the boundaries of the -cut of solution to (19). The blue line represents and the purple line represents .
5. Concluding Remarks
In this paper, we examined a new class of stochastic differential equations in an extension to the fuzzy case, namely, symmetric fuzzy stochastic differential equations driven by fractional Brownian motion, which are a new type of equations preserving the non-monotonic fuzziness property of the solution value of such an equation. Such equations generalize asymmetric [5,6,7] and symmetric [8,9] fuzzy stochastic differential equations driven by standard Brownian motion. They also generalize asymmetric the fuzzy stochastic differential equations driven by fractional Brownian motion studied in [12]. We mainly focused on theoretical issues such as the existence of a solution, because only then is it possible to apply such equations in practice. Thus, subject to the boundedness and Lipschitz assumptions on the diffusion and drift coefficients of equation, we applied an approximation method to the approximate fuzzy fractional stochastic equations to obtain existence of their unique solutions. This method surpasses the standards, because we used a semimartingale approximation sequence of fractional Brownian motion. Then, we proved that the obtained approximate solutions converge uniformly to the exact solution of the main equation. Finally, we presented an example of how our equations can be applied to model population dynamics. We showed how the equation of the type considered in this paper can be solved explicitly. The current article may initiate a broader study of the newly proposed equations. Future research can cover both purely theoretical and practical areas. In particular, the stability of solutions, the existence of solutions under weaker assumptions, and the periodicity of the solution can be studied. Such equations may have applications in real-life hybrid systems which include properties of being both random and fuzzy, as well as reflecting long-range dependence. In terms of applications, these equations can be used for modeling in biology, finance, mechanics, or physics, and many other fields that use stochastic differential equations in the mathematical description of the studied phenomena.
Author Contributions
Conceptualization, H.J. and M.T.M.; methodology, H.J. and M.T.M.; formal analysis, H.J. and M.T.M.; first draft preparation, H.J.; review, editing, final draft, M.T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, C.; Liu, Z.; Xie, K.; Zhang, Y.; Chen, C.L.P. Asymptotic fuzzy neural network control for pure-feedback stochastic systems based on a semi-nussbaum function technique. IEEE Trans. Cyber. 2017, 47, 2448–2459. [Google Scholar]
- Jiang, B.; Karimi, H.R.; Yang, S.; Kao, Y.; Gao, C. Takagi–Sugeno model-based reliable sliding mode control of descriptor systems with semi-Markov parameters: Average Dwell time approach. IEEE Trans. Syst. Man Cyber. Syst. 2021, 51, 1549–1558. [Google Scholar] [CrossRef]
- Malinowski, M.T. Strong solutions to stochastic fuzzy differential equations of Itô type. Math. Comput. Model. 2012, 55, 918–928. [Google Scholar]
- Malinowski, M.T. Itô type stochastic fuzzy differential equations with delay. Syst. Control Lett. 2012, 61, 692–701. [Google Scholar] [CrossRef]
- Malinowski, M.T. Some properties of strong solutions to stochastic fuzzy differential equations. Inf. Sci. 2013, 252, 62–80. [Google Scholar] [CrossRef]
- Malinowski, M.T. Fuzzy and set-valued stochastic differential equations with local Lipschitz condition. IEEE Trans. Fuzzy Syst. 2015, 23, 1891–1898. [Google Scholar] [CrossRef]
- Malinowski, M.T. Stochastic fuzzy differential equations of a nonincreasing type. Commun. Nonlinear Sci. Numer. Simul. 2016, 33, 99–117. [Google Scholar] [CrossRef]
- Malinowski, M.T. Bipartite fuzzy stochastic differential equations with global Lipschitz condition. Math. Probl. Eng. 2016, 2016, 3830529. [Google Scholar] [CrossRef]
- Malinowski, M.T. Symmetric fuzzy stochastic differential equations with generalized global Lipschitz condition. Symmetry 2020, 12, 819. [Google Scholar] [CrossRef]
- Qi, W.; Park, J.H.; Zong, G.; Cao, J.; Cheng, J. A fuzzy Lyapunov function approach to positive L observer design for positive fuzzy semi-Markovian switching systems with its application. IEEE Trans. Syst. Man Cyber. Syst. 2021, 51, 775–785. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, H.; Liu, C.; Liu, Y. Dissipativity-based intermittent fault detection and tolerant control for multiple delayed uncertain switched fuzzy stochastic systems with unmeasurable premise variables. IEEE Trans. Cybern. 2021, 52, 8766–8780. [Google Scholar] [CrossRef] [PubMed]
- Jafari, H.; Malinowski, M.T.; Ebadi, M.J. Fuzzy stochastic differential equations driven by fractional Brownian motion. Adv. Differ. Equ. 2021, 2021, 16. [Google Scholar] [CrossRef]
- Young, L.C. An inequality of the Hölder type connected with Stieltjes integration. Acta Math. 1936, 67, 251–282. [Google Scholar] [CrossRef]
- Alòs, E.; Mazet, O.; Nualart, D. Stochastic calculus with respect to fractional Brownian motion with Hurst parameter lesser than 1/2. Stoch. Process. Their Appl. 2000, 86, 121–139. [Google Scholar] [CrossRef]
- Alòs, E.; Nualart, D. Stochastic integration with respect to the fractional Brownian motion. Stoch. Stoch. Rep. 2002, 75, 129–152. [Google Scholar]
- Carmona, P.; Coutin, L.; Montseny, G. Stochastic integration with respect to fractional Brownian motion. Ann. Inst. Henri Poincaré 2003, 39, 27–68. [Google Scholar] [CrossRef]
- Decreusefond, L.; Üstünel, A.S. Stochastic analysis of the fractional Brownian motion. Potential Anal. 1998, 10, 177–214. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Thao, T.H. An approximate approach to fractional analysis for finance. Nonlinear Anal. Real World Appl. 2006, 7, 124–132. [Google Scholar] [CrossRef]
- Puri, M.L.; Ralescu, D.A. Fuzzy random variables. J. Math. Anal. Appl. 1986, 114, 409–422. [Google Scholar] [CrossRef]
- Kim, Y.K. Measurability for fuzzy valued functions. Fuzzy Sets Syst. 2002, 129, 105–109. [Google Scholar] [CrossRef]
- Feng, Y. Mean-square integral and differential of fuzzy stochastic processes. Fuzzy Sets Syst. 1999, 102, 271–280. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).