Some Fixed-Point Results for the KF-Iteration Process in Hyperbolic Metric Spaces

Abstract

In this paper, we modify the $KF$-iteration process into hyperbolic metric spaces where the symmetry condition is satisfied and establish the weak $w^2$-stability and data dependence results for contraction mappings. We also prove some $\Delta$-convergence and strong convergence theorems for generalized $(\alpha ,\beta )$-nonexpansive type 1 mappings. Finally, we offer a numerical example of generalized $(\alpha ,\beta )$-nonexpansive type 1 mappings and show that the $KF$-iteration process is more effective than some other iterations. Our results generalize and improve several relevant results in the literature.

1. Introduction

Some physical problems in engineering, physics, economics, etc., are generally emulated into a fixed-point problem, more precisely, to a problem aiming at finding $a\in X$ such that $Sa=a,$ where S is a nonlinear mapping (self or non-self) of an arbitrary space X. Many researchers have paid very good attention to finding an analytical solution, but this has been almost practically impossible. In view of this, iterative processes have been adopted to find approximate solutions.

The Picard iterative process is one of the very first iterative processes used to approximate a fixed point of a contraction mapping S on a metric space $(X,m)$. Note that a mapping $S:X\to X$ is called a contraction if there exists a constant $k\in [0,1)$ such that

$$m(Sa,Sb)\le km(a,b),\forall a,b\in X.$$

If $k=1$ in inequality above, then S is said to be a nonexpansive mapping. Even though the existence of the fixed point is guaranteed in the case of nonexpansive mapping, the Picard iterative process fails to approximate the fixed point of S. To overcome this problem, researchers of this field developed different iterative processes to approximate fixed points of nonexpansive mappings and other mappings, which are more general than nonexpansive. For example, look at Mann [1], Ishikawa [2], Noor [3], Agarwal et al. [4], Abbas et al. [5], Thakur et al. [6,7], M-iteration [8], etc.

In 2017, Pant and Shukla [9] introduced the class of generalized α-nonexpansive mappings, which is a larger class of mappings than the classes of nonexpansive, Suzuki-generalized nonexpansive, and α-nonexpansive mappings. A vast of researchers studied the approximation of fixed points of these mappings in different spaces, such as Banach, CAT(0), and hyperbolic metric spaces; see [10,11,12,13,14].

Recently, in 2021, Akutsah and Narain [15] introduced a new mapping, namely generalized $(\alpha ,\beta )$-nonexpansive type 1, which generalizes a lot of mappings as well as generalized $\alpha$-nonexpansive mappings in the literature.

Very recently, in 2022, Ullah et al. [16] and Temir and Korkut [17] introduced a new iteration process involving generalized $\alpha$-nonexpansive mappings. If S is a self-mapping on a convex subset Y of a Banach space X, then the iteration process is stated as follows:

$$\left\{\begin{array}{c}{a}_1\in Y,\\ c_n=S((1-{\eta }_n)a_n+{\eta }_{n}S{a}_n),\\ b_n=S{c}_n,\\ a_{n+1}=S((1-{\sigma }_n)S{a}_n+{\sigma }_{n}S{b}_n),\forall n\ge 1,\end{array}\right.$$

(1)

where ${\left\{{\sigma }_n\right\}}_{n=1}^{\infty }$ and ${\left\{{\eta }_n\right\}}_{n=1}^{\infty }$ are real sequences in $[0,1].$ This iteration is called the $KF$-iteration process by Ullah et al. [16]. Throughout this paper, we will use this name for the iteration process (1).

Motivated by the above results, in this paper, we study the weak $w^2$-stability, data dependence, and convergence of the iteration process (1) in hyperbolic metric spaces. This paper is organized as follows: In Section 2, we collect some basic definitions and needed results. Section 3 proves the weak $w^2$-stability and data dependence results using the $KF$-iteration process for contraction mappings in hyperbolic metric spaces. In Section 4, we establish some results related to the strong and $\mathrm{\Delta }$-convergence of the $KF$-iteration process for generalized $(\alpha ,\beta )$-nonexpansive type 1 mappings in hyperbolic metric spaces. Finally, in Section 5, we give a numerical example of this class of mappings and show that the $KF$-iteration process converges faster than some iteration processes. Our results extend the corresponding results of [16,17].

2. Preliminaries

Let $(X,m)$ be a metric space and Y be a nonempty subset of $X.$ A mapping $S:Y\to Y$ is said to be the following:

(i)

(Ref. [18]) Quasi-nonexpansive if $m(Sa,e)\le m(a,e)$ for all $a\in Y$ and $e\in F_{ix}\left(S\right),$ where $F_{ix}\left(S\right)$ is the set of all fixed points of S;

(ii)

(Ref. [19]) Mean nonexpansive mapping if, for all $a,b\in Y,$ there exist $\alpha ,\beta \in [0,1),$ with $\alpha +\beta \le 1$ such that $m(Sa,Sb)\le \alpha m(a,b)+\beta m(a,Sb);$

(iii)

(Ref. [20], p. 1089) Suzuki-generalized nonexpansive (or satisfy condition $\left(C\right)$) if $\frac{1}{2}m(Sa,a)\le m(a,b)\Rightarrow m(Sa,Sb)\le m(a,b)$ for all $a,b\in Y;$

(iv)

(Ref. [21], Definition 2) Satisfy condition $\left(C_{\lambda }\right)$ if $\lambda m(Sa,b)\le m(a,b)\Rightarrow m(Sa,Sb)\le m(a,b)$ for all $a,b\in Y;$

(v)

(Ref. [9], Definition 3.1) Generalized $\alpha$-nonexpansive mapping if, for all $a,b\in Y,$ there exists $\alpha \in [0,1)$ such that $\frac{1}{2}m(Sa,a)\le m(a,b)\Rightarrow m(Sa,Sb)\le \alpha m(Sa,b)+\alpha m(a,Sb)+(1-2\alpha )m(a,b).$

Akutsah and Narain [15] introduced the class of generalized $(\alpha ,\beta )$-nonexpansive type 1 mappings, which generalizes the mappings above, and they gave some basic properties for this class of mappings.

Definition 1

([15], Definition 3.1). Let Y be a nonempty subset of a metric space $(X,m).$ A mapping $S:Y\to Y$ is said to be generalized $(\alpha ,\beta )$-nonexpansive type 1 if there exist $\alpha ,\beta ,\lambda \in [0,1),$ with $\alpha \le \beta$ and $\alpha +\beta <1$ such that

$$\lambda m(Sa,a)\le m(a,b)\Rightarrow m(Sa,Sb)\le \alpha m(Sa,b)+\beta m(a,Sb)+(1-(\alpha +\beta \left)\right)m(a,b)$$

for all $a,b\in Y.$

Proposition 1.

(i) ([15], Proposition 3.6) If S is a generalized $(\alpha ,\beta )$-nonexpansive type 1 mapping and has a fixed point, then S is quasi-nonexpansive.

(ii) 

([15], Lemma 3.14) If S is a generalized $(\alpha ,\beta )$-nonexpansive type 1 mapping, then for all $a,b\in Y,$

$$m(a,Sb)\le \frac{2+\alpha +\beta }{1-\beta }m(a,Sa)+m(a,b).$$

(iii) 

([15], Theorem 3.7) If S is a generalized $(\alpha ,\beta )$-nonexpansive type 1 mapping, then $F_{ix}\left(S\right)$ is closed.

Definition 2

([22]). Let $(X,m)$ be a metric space and ${\left\{a_n\right\}}_{n=1}^{\infty }$ and ${\left\{b_n\right\}}_{n=1}^{\infty }$ be two sequences in X. We say that these sequences are equivalent if ${lim}_{n\to \infty }m(a_n,b_n)=0.$

Timiş [23] gave the following definition of weak $w^2$-stability using equivalent sequences.

Definition 3

([23], Definition 2.4). Let $(X,m)$ be a metric space, S be a self-mapping on X, and ${\left\{a_n\right\}}_{n=1}^{\infty }\subset X$ be an iterative sequence defined by

$$\left\{\begin{array}{c}{a}_1\in X,\\ a_{n+1}=f(S,a_n),\forall n\ge 1,\end{array}\right.$$

where f is a function. Suppose that ${\left\{a_n\right\}}_{n=1}^{\infty }$ converges strongly to $e\in F_{ix}\left(S\right).$ If for any equivalent sequence ${\left\{b_n\right\}}_{n=1}^{\infty }\subset X$ of ${\left\{a_n\right\}}_{n=1}^{\infty },$

$$\underset{n\to \infty }{lim}m(b_{n+1},f(S,b_n))=0\Rightarrow \underset{n\to \infty }{lim}{b}_n=e,$$

then the iterative sequence ${\left\{a_n\right\}}_{n=1}^{\infty }$ is said to be weak $w^2$-stable with respect to $S.$

In 1990, Reich and Shafrir [24] introduced hyperbolic metric spaces and studied an iteration process for nonexpansive mappings in these spaces. In 2004, Kohlenbach [25] introduced a more general hyperbolic metric space as follows.

Definition 4.

Let $(X,m)$ be a metric space, and then $(X,m,W)$ will be the hyperbolic metric space if the function $W:X\times X\times [0,1]\to X$ is satisfying

(i) $m(c,W(a,b,\alpha \left)\right)\le (1-\alpha )m(c,a)+\alpha m(c,b),$

(ii) $m\left(W\right(a,b,\alpha ),W(a,b,\beta \left)\right)=|\alpha -\beta |m(a,b),$

(iii) $W(a,b,\alpha )=W(b,a,1-\alpha ),$

(iv) $m\left(W\right(a,c,\alpha ),W(b,w,\alpha \left)\right)\le (1-\alpha )m(a,b)+\alpha m(c,w),$for all $a,b,c,w\in X$ and $\alpha ,\beta \in [0,1].$

A linear example of a hyperbolic metric space is a Banach space, and nonlinear examples are Hadamard manifolds, the Hilbert open unit ball equipped with the hyperbolic metric (see [26]), and CAT(0) spaces in the sense of Gromov (see [27]).

Definition 5.

We consider a hyperbolic metric space $(X,m,W).$ If $a,b\in X$ and α$\in [0,1],$ then we will use $(1-\alpha )a\oplus \alpha b$ for $W(a,b,\alpha ).$

(i) A subset Y of this hyperbolic metric space is called convex if $a,b\in Y$ implies that $W(a,b,\alpha )\in Y$. The following equalities hold even for the more general setting of a convex metric space (see [28], Proposition 1.2):

$$m(b,W(a,b,\alpha \left)\right)=(1-\alpha )m(a,b)\mathrm{and}m(a,W(a,b,\alpha \left)\right)=\alpha m(a,b)$$

for all $a,b\in X$ and α$\in [0,1].$ As a consequence, we obtain

$$W(a,b,0)=a\mathrm{and}W(a,b,1)=b.$$

(2)

(ii) This hyperbolic metric space is called uniformlyconvex (see [29]) if for any $r>0$ and $\epsilon \in (0,2],$ there exists a constant $\delta \in (0,1]$ such that

$$m(W(a,b,\frac{1}{2}),u)\le (1-\delta )r$$

for all $u,a,b\in X$ with $m(a,u)\le r,$$m(b,u)\le r$ and $m(a,b)\ge r\epsilon$.

(iii) A mapping $\eta :(0,\infty )\times (0,2]\to (0,1]$ is said to be a modulus of uniform convexity if $\delta =\eta (r,\epsilon )$ for a given $r>0$ and $\epsilon \in (0,2]$. Furthermore, the mapping η is called monotone if it decreases with respect to r for a fixed ε.

Definition 6.

Let ${\left\{a_n\right\}}_{n=1}^{\infty }$ be a bounded sequence in a nonempty subset Y of a metric space $(X,m)$. Then, the mapping $r($·$,\left\{a_n\right\}):X\to [0,\infty )$ is defined by

$$r(a,\left\{a_n\right\})=\underset{n\to \infty }{lim\; sup}m(a,a_n),a\in X.$$

The infimum of $r(.,\left\{a_n\right\})$ over Y is called the asymptotic radius of ${\left\{a_n\right\}}_{n=1}^{\infty }$ relative to Y and is denoted by $r(Y,\left\{a_n\right\}).$ A point $c\in Y$ is said to be an asymptotic center of the sequence ${\left\{a_n\right\}}_{n=1}^{\infty }$ relative to Y if

$$r(c,\left\{a_n\right\})=inf\{r(a,\left\{a_n\right\}):a\in Y\},$$

and the set of all asymptotic centers of ${\left\{a_n\right\}}_{n=1}^{\infty }$ relative to Y is denoted by $A(Y,\left\{a_n\right\})$.

In 1976, Lim [30] introduced the concept of $\mathrm{\Delta }$-convergence, which is an analog of weak convergence, in metric spaces using the asymptotic center.

Definition 7

([30]). A sequence ${\left\{a_n\right\}}_{n=1}^{\infty }$ in a metric space $(X,m)$ is said to Δ-converge to a point $a\in X$ if a is the unique asymptotic center of ${\left\{u_n\right\}}_{n=1}^{\infty }$ for every subsequence ${\left\{u_n\right\}}_{n=1}^{\infty }$ of ${\left\{a_n\right\}}_{n=1}^{\infty }.$ In this case, we write $\mathrm{\Delta }-{lim}_{n\to \infty }{a}_n=a$ and call a as Δ-limit of ${\left\{a_n\right\}}_{n=1}^{\infty }.$

We end this section with the upcoming three lemmas that will be helpful in proving our main results.

Lemma 1

([31], Proposition 3.3). Let $(X,m,W)$ be a complete uniformly convex hyperbolic metric space with the monotone modulus of uniform convexity η and Y be a nonempty closed and convex subset of $X.$ Then, every bounded sequence ${\left\{a_n\right\}}_{n=1}^{\infty }$ in X has a unique asymptotic center relative to $Y.$

Lemma 2

([32], Lemma 2.5). Let $(X,m,W)$ be a uniformly convex hyperbolic metric space with the monotone modulus of uniform convexity $\eta .$ Let $a\in X$ and $\left\{{\sigma }_n\right\}$ be a sequence in $[p,q]$ for some $p,q\in (0,1).$ If ${\left\{a_n\right\}}_{n=1}^{\infty }$ and ${\left\{b_n\right\}}_{n=1}^{\infty }$ are sequences in X such that

$$\underset{n\to \infty }{lim\; sup}m(a_n,a)\le r,\underset{n\to \infty }{lim\; sup}m(b_n,a)\le r,\underset{n\to \infty }{lim}m(W(a_n,b_n,{\sigma }_n),a)=r$$

for some $r\ge 0,$ then

$$\underset{n\to \infty }{lim}m(a_n,b_n)=0.$$

Lemma 3

([33]). Let ${\left\{g_n\right\}}_{n=1}^{\infty },{\left\{r_n\right\}}_{n=1}^{\infty }$ and ${\left\{t_n\right\}}_{n=1}^{\infty }$ be non-negative real sequences with $r_n\in (0,1)$, $\forall n\ge 1$, and ${\sum }_{n=1}^{\infty }{r}_n=\infty .$ Suppose that there exists $n_0\in \mathbb{N}$ such that, for all $n\ge n_0,$ one has the inequality

$$g_{n+1}\le (1-r_n)g_n+r_n{t}_n.$$

Then, the following inequality holds:

$$0\le \underset{n\to \infty }{lim\; sup}{g}_n\le \underset{n\to \infty }{lim\; sup}{t}_n.$$

3. Weak ${\mathit{w}}^{\mathbf{2}}$-Stability and Data Dependence Results

First, we extend the iteration process (1) into the hyperbolic metric spaces as follows:

$$\left\{\begin{array}{c}{a}_1\in Y,\\ c_n=S\left(W(a_n,S{a}_n,{\eta }_n)\right),\\ b_n=S{c}_n,\\ a_{n+1}=S\left(W(S{a}_n,S{b}_n,{\sigma }_n)\right),\forall n\ge 1,\end{array}\right.$$

(3)

where Y is a nonempty convex subset of a hyperbolic metric space $X$, S is a self-mapping on $Y,$ and ${\left\{{\sigma }_n\right\}}_{n=1}^{\infty }$,${\left\{{\eta }_n\right\}}_{n=1}^{\infty }$ are two real sequences in [0, 1].

We have the following strong convergence theorem.

Theorem 1.

Let Y be a nonempty closed convex subset of a hyperbolic metric space $X$, $S:Y\to Y$ be a contraction mapping with the constant $k\in [0,1)$ such that $F_{ix}\left(S\right)\ne \varnothing$, and ${\left\{a_n\right\}}_{n=1}^{\infty }$ be the iterative sequence (3) with real sequences ${\left\{{\sigma }_n\right\}}_{n=1}^{\infty }$ and ${\left\{{\eta }_n\right\}}_{n=1}^{\infty }$ in $[0,1]$, satisfying ${\sum }_{n=1}^{\infty }{\sigma }_n{\eta }_n=\infty .$ Then, the sequence ${\left\{a_n\right\}}_{n=1}^{\infty }$ converges strongly to a fixed point of $S.$

Proof. 

Because the contraction mapping S has a fixed point, then it is easily seen that the fixed point of S is unique. Let the unique fixed point be $e.$ Hence, from (3), we have

$$\begin{array}{ccc}\hfill m(c_n,e)& =& m(S\left(W(a_n,S{a}_n,{\eta }_n)\right),Se)\hfill \\ & \le & km(W(a_n,S{a}_n,{\eta }_n),e)\hfill \\ & \le & k[(1-{\eta }_n)m(a_n,e)+{\eta }_{n}m(S{a}_n,e)]\hfill \\ & \le & k[(1-{\eta }_n)m(a_n,e)+{\eta }_{n}km(a_n,e)]\hfill \\ & =& k(1-{\eta }_n(1-k))m(a_n,e).\hfill \end{array}$$

Because $k\in [0,1)$, then we obtain

$$\begin{array}{ccc}\hfill m(b_n,e)& =& m(S{c}_n,Se)\le km(c_n,e)\hfill \\ & \le & k\left[k(1-{\eta }_n(1-k))m(a_n,e)\right]\hfill \\ & =& k^2(1-{\eta }_n(1-k))m(a_n,e)\hfill \\ & \le & (1-{\eta }_n(1-k))m(a_n,e).\hfill \end{array}$$

Similarly, we obtain

$$\begin{array}{ccc}\hfill m(a_{n+1},e)& =& m(S\left(W(S{a}_n,S{b}_n,{\sigma }_n)\right),Se)\hfill \\ & \le & km(W(S{a}_n,S{b}_n,{\sigma }_n),e)\hfill \\ & \le & k[(1-{\sigma }_n)m(S{a}_n,e)+{\sigma }_{n}m(S{b}_n,e)]\hfill \\ & \le & k[(1-{\sigma }_n)km(a_n,e)+{\sigma }_{n}km(b_n,e)]\hfill \\ & =& k^2[(1-{\sigma }_n)m(a_n,e)+{\sigma }_{n}m(b_n,e)]\hfill \\ & \le & k^2[(1-{\sigma }_n)m(a_n,e)+{\sigma }_n(1-{\eta }_n(1-k))m(a_n,e)]\hfill \\ & =& k^2(1-{\sigma }_n{\eta }_n(1-k))m(a_n,e).\hfill \end{array}$$

Repetition of the above processes gives the following inequalities:

$$\begin{array}{ccc}\hfill m(a_{n+1},e)& \le & k^2(1-{\sigma }_n{\eta }_n(1-k))m(a_n,e),\hfill \\ \hfill m(a_n,e)& \le & k^2(1-{\sigma }_{n-1}{\eta }_{n-1}(1-k))m(a_{n-1},e),\hfill \\ \hfill m(a_{n-1},e)& \le & k^2(1-{\sigma }_{n-2}{\eta }_{n-2}(1-k))m(a_{n-2},e),\hfill \\ & & ⋮\hfill \\ \hfill m(a_2,e)& \le & k^2(1-{\sigma }_1{\eta }_1(1-k))m(a_1,e).\hfill \end{array}$$

(4)

From (4), we can easily derive

$$m(a_{n+1},e)\le m(a_1,e){\left(k^2\right)}^n{\prod }_{m=1}^n(1-{\sigma }_m{\eta }_m(1-k)),$$

(5)

where $1-{\sigma }_m{\eta }_m(1-k)\le 1,$ because $k\in [0,1),$ and ${\left\{{\sigma }_n\right\}}_{n=1}^{\infty }$ and ${\left\{{\eta }_n\right\}}_{n=1}^{\infty }$ in $[0,1]$ for all $n\in \mathbb{N}.$ It is well-known from the classical analysis that $1-a\le e^{-a}$ for all $a\in [0,1].$ Taking into account this fact together with (5), we obtain

$$m(a_{n+1},e)\le m(a_1,e)k^{2n}{e}^{-(1-k){\sum }_{m=1}^n{\sigma }_m{\eta }_m}.$$

(6)

Taking the limit of both sides of (6) and then using the hypotheses $k\in [0,1)$ and ${\sum }_{n=1}^{\infty }{\sigma }_n{\eta }_n=\infty$, we obtain ${lim}_{n\to \infty }m(a_n,e)=0$, i.e., $a_n\to e$ as $n\to \infty ,$ as desired. □

Now, we prove that the modified iteration process defined by (3) is weak $w^2$-stable with respect to $S.$

Theorem 2.

Suppose that all conditions of Theorem 1 hold. Then, the iteration process (3) is weak $w^2$-stable with respect to $S.$

Proof. 

Let ${\left\{a_n\right\}}_{n=1}^{\infty }$ be the iterative sequence given by (3) and ${\left\{p_n\right\}}_{n=1}^{\infty }\subset Y$ be an equivalent sequence of ${\left\{a_n\right\}}_{n=1}^{\infty }.$ Set

$${\epsilon }_n=m(p_{n+1},S\left(W(S{p}_n,S{q}_n,{\sigma }_n)\right)),$$

where $q_n=S{r}_n$ with $r_n=S\left(W(p_n,S{p}_n,{\eta }_n)\right).$ Suppose that ${lim}_{n\to \infty }{\epsilon }_n=0.$ It follows that

$$\begin{array}{ccc}\hfill m(c_n,r_n)& =& m(S\left(W(a_n,S{b}_n,{\eta }_n)\right),S\left(W(p_n,S{p}_n,{\eta }_n)\right))\hfill \\ & \le & km(W(a_n,S{a}_n,{\eta }_n),W(p_n,S{p}_n,{\eta }_n))\hfill \\ & \le & k[(1-{\eta }_n)m(a_n,p_n)+{\eta }_{n}m(S{a}_n,S{p}_n)]\hfill \\ & \le & k[(1-{\eta }_n)m(a_n,p_n)+{\eta }_{n}km(a_n,p_n)]\hfill \\ & =& k(1-{\eta }_n(1-k))m(a_n,p_n).\hfill \end{array}$$

(7)

Using (7) together with the hypothesis $k\in [0,1)$, we have

$$\begin{array}{ccc}\hfill m(b_n,q_n)& =& m(S{c}_n,S{r}_n)\hfill \\ & \le & km(c_n,r_n)\hfill \\ & \le & k^2(1-{\eta }_n(1-k))m(a_n,p_n)\hfill \\ & \le & (1-{\eta }_n(1-k))m(a_n,p_n).\hfill \end{array}$$

(8)

Similarly, by (8), we obtain

$$\begin{array}{cc}\hfill & m(p_{n+1},e)\hfill \\ \hfill & \le m(p_{n+1},a_{n+1})+m(a_{n+1},e)\hfill \\ \hfill & \le m(p_{n+1},S\left(W(S{p}_n,S{q}_n,{\sigma }_n)\right))+m(S\left(W(S{p}_n,S{q}_n,{\sigma }_n)\right),S\left(W(S{a}_n,S{b}_n,{\sigma }_n)\right))\hfill \\ \hfill & +m(a_{n+1},e)\hfill \\ \hfill & \le {\epsilon }_n+km(W(S{p}_n,S{q}_n,{\sigma }_n),W(S{a}_n,S{b}_n,{\sigma }_n))+m(a_{n+1},e)\hfill \\ \hfill & \le {\epsilon }_n+k[(1-{\sigma }_n)m(S{p}_n,S{a}_n)+{\sigma }_{n}m(S{q}_n,S{b}_n)]+m(a_{n+1},e)\hfill \\ \hfill & \le {\epsilon }_n+k[(1-{\sigma }_n)km(p_n,a_n)+{\sigma }_{n}km(q_n,b_n)]+m(a_{n+1},e)\hfill \\ \hfill & \le {\epsilon }_n+k^2[(1-{\sigma }_n)m(p_n,a_n)+{\sigma }_n\left[(1-{\eta }_n(1-k))m(a_n,p_n)\right]+m(a_{n+1},e)\hfill \\ \hfill & ={\epsilon }_n+k^2(1-{\sigma }_n{\eta }_n(1-k))m(a_n,p_n)+m(a_{n+1},e).\hfill \end{array}$$

(9)

From Theorem 1, it follows that ${lim}_{n\to \infty }m(a_{n+1},e)=0.$ Because ${\left\{a_n\right\}}_{n=1}^{\infty }$ and ${\left\{p_n\right\}}_{n=1}^{\infty }$ are equivalent sequences, we have ${lim}_{n\to \infty }m(a_n,p_n)=0.$ Now, taking the limit of both sides of (9) and then using the assumption ${lim}_{n\to \infty }{\epsilon }_n=0,$ yield to ${lim}_{n\to \infty }m(p_{n+1},e)=0.$ Thus, ${\left\{a_n\right\}}_{n=1}^{\infty }$ is weak $w^2$-stable with respect to $S.$ □

Definition 8

([34], p. 166). Let $(X,m)$ be a metric space and $S,\tilde{S}:X\to X$ be two operators. $\tilde{S}$ is called an approximate operator of S, if $m(Sa,\tilde{S}a)\le \epsilon$ for all $a\in X$ and for a fixed $\epsilon >0.$

Next, we prove the data dependence result for the modified iteration process (3) using the definition above.

Theorem 3.

Let $X,Y$, and S be the same as in Theorem 1 and $\tilde{S}:Y\to Y$ be an approximate operator of S for given ε. Let ${\left\{a_n\right\}}_{n=1}^{\infty }$ be an iterative sequence generated by (3) and define an iterative sequence ${\left\{{\tilde{a}}_n\right\}}_{n=1}^{\infty }$ as follows:

$$\left\{\begin{array}{c}{\tilde{a}}_1\in Y,\\ {\tilde{c}}_n=\tilde{S}\left(W({\tilde{a}}_n,\tilde{S}{\tilde{a}}_n,{\eta }_n)\right),\\ {\tilde{b}}_n=\tilde{S}{\tilde{c}}_n,\\ {\tilde{a}}_{n+1}=\tilde{S}\left(W(\tilde{S}{\tilde{a}}_n,\tilde{S}{\tilde{b}}_n,{\sigma }_n)\right),\forall n\ge 1,\end{array}\right.$$

(10)

with real sequences ${\left\{{\sigma }_n\right\}}_{n=1}^{\infty }$ and ${\left\{{\eta }_n\right\}}_{n=1}^{\infty }$ in $[0,1]$ satisfying ${\sigma }_n{\eta }_n\ge \frac{1}{2},$$\forall n\ge 1$, and ${\sum }_{n=1}^{\infty }{\sigma }_n{\eta }_n=\infty$. If $e=Se$ and $\tilde{e}=\tilde{S}\tilde{e}$ such that ${lim}_{n\to \infty }{\tilde{a}}_n=\tilde{e},$ then one has

$$m(e,\tilde{e})\le \frac{9\epsilon }{1-k},$$

where $k\in [0,1).$

Proof. 

It follows from (3) and (10) that

$$\begin{array}{ccc}\hfill m(c_n,{\tilde{c}}_n)& =& m(S\left(W(a_n,S{a}_n,{\eta }_n)\right),\tilde{S}\left(W({\tilde{a}}_n,\tilde{S}{\tilde{a}}_n,{\eta }_n)\right))\hfill \\ & \le & m(S\left(W(a_n,S{a}_n,{\eta }_n)\right),S\left(W({\tilde{a}}_n,\tilde{S}{\tilde{a}}_n,{\eta }_n)\right))\hfill \\ & & +m(S\left(W({\tilde{a}}_n,\tilde{S}{\tilde{a}}_n,{\eta }_n)\right),\tilde{S}\left(W({\tilde{a}}_n,\tilde{S}{\tilde{a}}_n,{\eta }_n)\right))\hfill \\ & \le & km(W(a_n,S{a}_n,{\eta }_n),W({\tilde{a}}_n,\tilde{S}{\tilde{a}}_n,{\eta }_n))+\epsilon \hfill \\ & \le & k[(1-{\eta }_n)m(a_n,{\tilde{a}}_n)+{\eta }_{n}m(S{a}_n,\tilde{S}{\tilde{a}}_n)]+\epsilon \hfill \\ & \le & k(1-{\eta }_n)m(a_n,{\tilde{a}}_n)+k{\eta }_n[m(S{a}_n,S{\tilde{a}}_n)+m(S{\tilde{a}}_n,\tilde{S}{\tilde{a}}_n)]+\epsilon \hfill \\ & \le & k(1-{\eta }_n)m(a_n,{\tilde{a}}_n)+k{\eta }_n[km(a_n,{\tilde{a}}_n)+\epsilon ]+\epsilon \hfill \\ & =& k(1-{\eta }_n(1-k))m(a_n,{\tilde{a}}_n)+k{\eta }_n\epsilon +\epsilon .\hfill \end{array}$$

(11)

By (11), we have

$$\begin{array}{ccc}\hfill m(b_n,{\tilde{b}}_n)& =& m(S{c}_n,\tilde{S}{\tilde{c}}_n)\hfill \\ & \le & m(S{c}_n,S{\tilde{c}}_n)+m(S{\tilde{c}}_n,\tilde{S}{\tilde{c}}_n)\hfill \\ & \le & km(c_n,{\tilde{c}}_n)+\epsilon \hfill \\ & \le & k[k(1-{\eta }_n(1-k))m(a_n,{\tilde{a}}_n)+k{\eta }_n\epsilon +\epsilon ]+\epsilon \hfill \\ & =& k^2(1-{\eta }_n(1-k))m(a_n,{\tilde{a}}_n)+k^2{\eta }_n\epsilon +k\epsilon +\epsilon .\hfill \end{array}$$

(12)

Similarly, using (12) and the hypothesis $k\in [0,1)$, we obtain

$$\begin{array}{ccc}\hfill m(a_{n+1},{\tilde{a}}_{n+1})& =& m(S(W(S{a}_n,S{b}_n,{\sigma }_n)),\tilde{S}(W(\tilde{S}{\tilde{a}}_n,\tilde{S}{\tilde{b}}_n,{\sigma }_n)))\hfill \\ & \le & m(S(W(S{a}_n,S{b}_n,{\sigma }_n)),S(W(\tilde{S}{\tilde{a}}_n,\tilde{S}{\tilde{b}}_n,{\sigma }_n)))\hfill \\ & & +m(S(W(\tilde{S}{\tilde{a}}_n,\tilde{S}{\tilde{b}}_n,{\sigma }_n)),\tilde{S}(W(\tilde{S}{\tilde{a}}_n,\tilde{S}{\tilde{b}}_n,{\sigma }_n)))\hfill \\ & \le & km(W(S{a}_n,S{b}_n,{\sigma }_n),W(\tilde{S}{\tilde{a}}_n,\tilde{S}{\tilde{b}}_n,{\sigma }_n))+\epsilon \hfill \\ & \le & k[(1-{\sigma }_n)m(S{a}_n,\tilde{S}{\tilde{a}}_n)+{\sigma }_{n}m(S{b}_n,\tilde{S}{\tilde{b}}_n)]+\epsilon \hfill \\ & \le & k(1-{\sigma }_n)[m(S{a}_n,S{\tilde{a}}_n)+m(S{\tilde{a}}_n,\tilde{S}{\tilde{a}}_n)]\hfill \\ & & +k{\sigma }_n[m(S{b}_n,S{\tilde{b}}_n)+m(S{\tilde{b}}_n,\tilde{S}{\tilde{b}}_n)]+\epsilon \hfill \\ & \le & k(1-{\sigma }_n)[km(a_n,{\tilde{a}}_n)+\epsilon ]+k{\sigma }_n[km(b_n,{\tilde{b}}_n)+\epsilon ]+\epsilon \hfill \\ & =& k^2(1-{\sigma }_n)m(a_n,{\tilde{a}}_n)+k(1-{\sigma }_n)\epsilon +k^2{\sigma }_{n}m(b_n,{\tilde{b}}_n)+k{\sigma }_n\epsilon +\epsilon \hfill \\ & \le & k^2(1-{\sigma }_n)m(a_n,{\tilde{a}}_n)+k(1-{\sigma }_n)\epsilon \hfill \\ & & +k^2{\sigma }_n[k^2(1-{\eta }_n(1-k))m(a_n,{\tilde{a}}_n)+k^2{\eta }_n\epsilon +k\epsilon +\epsilon ]+k{\sigma }_n\epsilon +\epsilon \hfill \\ & =& k^2(1-{\sigma }_n)m(a_n,{\tilde{a}}_n)+k(1-{\sigma }_n)\epsilon +k^4{\sigma }_n(1-{\eta }_n(1-k))m(a_n,{\tilde{a}}_n)\hfill \\ & & +k^4{\sigma }_n{\eta }_n\epsilon +k^3{\sigma }_n\epsilon +k^2{\sigma }_n\epsilon +k{\sigma }_n\epsilon +\epsilon \hfill \\ & \le & [{\sigma }_n(1-{\eta }_n(1-k))+(1-{\sigma }_n)]m(a_n,{\tilde{a}}_n)\hfill \\ & & +(1-{\sigma }_n)\epsilon +{\sigma }_n{\eta }_n\epsilon +{\sigma }_n\epsilon +{\sigma }_n\epsilon +{\sigma }_n\epsilon +\epsilon \hfill \\ & =& (1-{\sigma }_n{\eta }_n(1-k))m(a_n,{\tilde{a}}_n)+{\sigma }_n{\eta }_n\epsilon +2{\sigma }_n\epsilon +2\epsilon .\hfill \end{array}$$

Because ${\sigma }_n\le 1$ for all $n\ge 1,$ then we obtain

$$\begin{array}{cc}\hfill & m(a_{n+1},{\tilde{a}}_{n+1})\hfill \\ \hfill & \le (1-{\sigma }_n{\eta }_n(1-k))m(a_n,{\tilde{a}}_n)+{\sigma }_n{\eta }_n\epsilon +4\epsilon \hfill \\ \hfill & =(1-{\sigma }_n{\eta }_n(1-k))m(a_n,{\tilde{a}}_n)+{\sigma }_n{\eta }_n\epsilon +4(1-{\sigma }_n{\eta }_n+{\sigma }_n{\eta }_n)\epsilon .\hfill \end{array}$$

(13)

By the assumption ${\sigma }_n{\eta }_n\ge \frac{1}{2}$, we have $1-{\sigma }_n{\eta }_n\le$${\sigma }_n{\eta }_n$. Using this together with (13), we obtain

$$\begin{array}{ccc}\hfill m(a_{n+1},{\tilde{a}}_{n+1})& \le & (1-{\sigma }_n{\eta }_n(1-k))m(a_n,{\tilde{a}}_n)+9{\sigma }_n{\eta }_n\epsilon \hfill \\ & =& (1-{\sigma }_n{\eta }_n(1-k))m(a_n,{\tilde{a}}_n)+{\sigma }_n{\eta }_n(1-k)\frac{9\epsilon }{1-k}.\hfill \end{array}$$

(14)

Let $g_n=m(a_n,{\tilde{a}}_n),$$r_n={\sigma }_n{\eta }_n(1-k)$, and $t_n=\frac{9\epsilon }{1-k},$ and then from Lemma 3 together with (14), we have

$$0\le \underset{n\to \infty }{lim\; sup}{g}_n\le \underset{n\to \infty }{lim\; sup}\frac{9\epsilon }{1-k}.$$

(15)

By Theorem 1, we have ${lim}_{n\to \infty }{a}_n=e$, and by the assumption in the hypotheses, we have ${lim}_{n\to \infty }{\tilde{a}}_n=\tilde{e}.$ Using these together with (15), we obtain

$$m(e,\tilde{e})\le \frac{9\epsilon }{1-k}$$

as required. □

4. Convergence Results

We first prove several preparatory results, which are needed for developing our convergence theorems.

Lemma 4.

Let S be a generalized $(\alpha ,\beta )$-nonexpansive type 1 mapping defined on a nonempty convex subset Y of a hyperbolic metric space X with $F_{ix}\left(S\right)\ne \varnothing .$ If $e\in F_{ix}\left(S\right)$ and ${\left\{a_n\right\}}_{n=1}^{\infty }$ is the iterative sequence defined by (3), then ${lim}_{n\to \infty }m(a_n,e)$ exists.

Proof. 

By Proposition 1 (i), we have

$$\begin{array}{ccc}\hfill m(c_n,e)& =& m(S\left(W(a_n,S{a}_n,{\eta }_n)\right),e)\hfill \\ & \le & m(W(a_n,S{a}_n,{\eta }_n),e)\hfill \\ & \le & (1-{\eta }_n)m(a_n,e)+{\eta }_{n}m(S{a}_n,e)\hfill \\ & \le & (1-{\eta }_n)m(a_n,e)+{\eta }_{n}m(a_n,e)\hfill \\ & =& m(a_n,e),\hfill \end{array}$$

(16)

which implies that

$$m(b_n,e)=m(S{c}_n,e)\le m(c_n,e)\le m(a_n,e).$$

(17)

Similarly, using Proposition 1 (i) and the inequality (17), we obtain

$$\begin{array}{ccc}\hfill m(a_{n+1},e)& =& m(S\left(W(S{a}_n,S{b}_n,{\sigma }_n)\right),e)\hfill \\ & \le & m(W(S{a}_n,S{b}_n,{\sigma }_n),e)\hfill \\ & \le & (1-{\sigma }_n)m(S{a}_n,e)+{\sigma }_{n}m(S{b}_n,e)\hfill \\ & \le & (1-{\sigma }_n)m(a_n,e)+{\sigma }_{n}m(b_n,e)\hfill \\ & \le & (1-{\sigma }_n)m(a_n,e)+{\sigma }_{n}m(a_n,e)\hfill \\ & =& m(a_n,e).\hfill \end{array}$$

(18)

Hence, we obtain

$$m(a_{n+1},e)\le m(a_n,e).$$

This shows that ${\left\{m(a_n,e)\right\}}_{n=1}^{\infty }$ is a non-increasing sequence and it is bounded from the below for each $e\in F_{ix}\left(S\right)$. So, we obtain that ${lim}_{n\to \infty }m(a_n,e)$ exists for any $e\in F_{ix}\left(S\right)$. □

Theorem 4.

Let Y be a nonempty closed convex subset of a complete uniformly convex hyperbolic metric space X with the monotone modulus of uniform convexity η and $S:Y\to Y$ be a generalized $(\alpha ,\beta )$-nonexpansive type 1 mapping. Let ${\left\{a_n\right\}}_{n=1}^{\infty }$ be the iterative sequence (3) with real sequences ${\left\{{\sigma }_n\right\}}_{n=1}^{\infty }$ and ${\left\{{\eta }_n\right\}}_{n=1}^{\infty }$ in $[p,q]$ for some $p,q\in (0,1).$ Then, $F_{ix}\left(S\right)\ne \varnothing$ if and only if ${\left\{a_n\right\}}_{n=1}^{\infty }$ is bounded and ${lim}_{n\to \infty }m(a_n,S{a}_n)=0.$

Proof. 

Suppose $F_{ix}\left(S\right)\ne \varnothing$ and choose $e\in F_{ix}\left(S\right).$ Then, by Lemma 4, ${lim}_{n\to \infty }m(a_n,e)$ exists and ${\left\{a_n\right\}}_{n=1}^{\infty }$ is bounded. Therefore, we can consider that

$$\underset{n\to \infty }{lim}m(a_n,e)=r\mathrm{for}\mathrm{some}r\ge 0.$$

(19)

By Proposition 1 (i), we obtain

$$m(S{a}_n,e)\le m(a_n,e),$$

and taking lim sup of both sides of the inequality above, we obtain that

$$\underset{n\to \infty }{lim\; sup}m(S{a}_n,e)\le r.$$

(20)

However, from the inequality (17), we know that

$$m(b_n,e)\le m(a_n,e),$$

and using a procedure similar to the one mentioned above, we obtain

$$\underset{n\to \infty }{lim\; sup}m(b_n,e)\le r.$$

(21)

From the relation (18), it follows that

$$\begin{array}{ccc}\hfill m(a_{n+1},e)& \le & (1-{\sigma }_n)m(a_n,e)+{\sigma }_{n}m(b_n,e)\hfill \\ & =& m(a_n,e)+{\sigma }_n(m(b_n,e)-m(a_n,e)),\hfill \end{array}$$

which implies

$$\frac{m(a_{n+1},e)-m(a_n,e)}{{\sigma }_n}\le m(b_n,e)-m(a_n,e).$$

Because ${\left\{{\sigma }_n\right\}}_{n=1}^{\infty }$ is a sequence in $[p,q]$, we obtain

$$\frac{1}{q}(m(a_{n+1},e)-m(a_n,e))\le \frac{m(a_{n+1},e)-m(a_n,e)}{{\sigma }_n}\le m(b_n,e)-m(a_n,e).$$

Using this last inequality and (19), we obtain that

$$r\le \underset{n\to \infty }{lim\; inf}m(b_n,e).$$

(22)

Obviously, from (21) and (22), we have

$$\underset{n\to \infty }{lim}m(b_n,e)=r.$$

(23)

By (17), (19) and (23), we obtain

$$\underset{n\to \infty }{lim}m(c_n,e)=r.$$

(24)

From (16), we know that

$$m(c_n,e)\le m(W(a_n,S{a}_n,{\eta }_n),e)\le m(a_n,e),$$

and from this inequality, (19) and (24), it follows that

$$\underset{n\to \infty }{lim}m(W(a_n,S{a}_n,{\eta }_n),e))=r.$$

(25)

Finally, from (19), (20), (25) and Lemma 2, we deduce that ${lim}_{n\to \infty }m(a_n,S{a}_n)=0.$ Conversely, we assume that ${\left\{a_n\right\}}_{n=1}^{\infty }$ is bounded and ${lim}_{n\to \infty }m(a_n,S{a}_n)=0.$ Let $e\in A(Y,\left\{a_n\right\}).$ By Proposition 1 (ii), we have

$$\begin{array}{ccc}\hfill r(Se,\left\{a_n\right\})& =& \underset{n\to \infty }{lim\; sup}m(a_n,Se)\hfill \\ & \le & \frac{2+\alpha +\beta }{1-\beta }\underset{n\to \infty }{lim\; sup}m(a_n,S{a}_n)+\underset{n\to \infty }{lim\; sup}m(a_n,e)\hfill \\ & =& \underset{n\to \infty }{lim\; sup}m(a_n,e)\hfill \\ & =& r(e,\left\{a_n\right\}).\hfill \end{array}$$

This implies that $Se\in A(Y,\left\{a_n\right\}).$ Because the sequence ${\left\{a_n\right\}}_{n=1}^{\infty }$ is bounded, by Lemma 1, $A(Y,\left\{a_n\right\})$ consists of exactly one point. Hence, we have $Se=e.$ Thus, $F_{ix}\left(S\right)\ne \varnothing .$ □

Considering the previous two results, we are now ready to prove the $\mathrm{\Delta }$-convergence theorem of the modified iterative sequence ${\left\{a_n\right\}}_{n=1}^{\infty }$ defined by (3) for a generalized $(\alpha ,\beta )$-nonexpansive type 1 mapping.

Theorem 5.

Let Y be a nonempty closed convex subset of a complete uniformly convex hyperbolic metric space X with the monotone modulus of uniform convexity η and $S:Y\to Y$ be a generalized $(\alpha ,\beta )$-nonexpansive type 1 mapping with $F_{ix}\left(S\right)\ne \varnothing .$ Let ${\left\{a_n\right\}}_{n=1}^{\infty }$ be the iterative sequence (3) with real sequences ${\left\{{\sigma }_n\right\}}_{n=1}^{\infty }$ and ${\left\{{\eta }_n\right\}}_{n=1}^{\infty }$ in $[p,q]$ for some $p,q\in (0,1).$ Then, the sequence ${\left\{a_n\right\}}_{n=1}^{\infty }$ Δ-converges to a fixed point of $S.$

Proof. 

By Lemma 1, the sequence ${\left\{a_n\right\}}_{n=1}^{\infty }$ has a unique asymptotic center $A(Y,\left\{a_n\right\})=\left\{a\right\}.$ Let ${\left\{u_n\right\}}_{n=1}^{\infty }$ be any subsequence of ${\left\{a_n\right\}}_{n=1}^{\infty }$ such that $A(Y,\left\{u_n\right\})=\left\{u\right\}.$ Then, by Theorem 4, we have

$$\underset{n\to \infty }{lim}m(u_n,S{u}_n)=0.$$

(26)

It follows similarly from the proof of Theorem 4 that u is a fixed point of $S.$ Next, we claim that the fixed point u is the unique asymptotic center for each subsequence ${\left\{u_n\right\}}_{n=1}^{\infty }$ of ${\left\{a_n\right\}}_{n=1}^{\infty }.$ On the contrary, we assume that $a\ne u.$ From Lemma 4, we deduce that ${lim}_{n\to \infty }m(a_n,u)$ exists. Therefore, by the uniqueness of the asymptotic center, we can see that

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim\; sup}m(u_n,u)& <& \underset{n\to \infty }{lim\; sup}m(u_n,a)\hfill \\ & \le & \underset{n\to \infty }{lim\; sup}m(a_n,a)\hfill \\ & <& \underset{n\to \infty }{lim\; sup}m(a_n,u)\hfill \\ & =& \underset{n\to \infty }{lim\; sup}m(u_n,u),\hfill \end{array}$$

which is obviously a contradiction. So, $u\in F_{ix}\left(S\right)$ is the unique asymptotic center for each subsequence ${\left\{u_n\right\}}_{n=1}^{\infty }$ of ${\left\{a_n\right\}}_{n=1}^{\infty }.$ This proves that the sequence ${\left\{a_n\right\}}_{n=1}^{\infty }$$\mathrm{\Delta }$-converges to a fixed point of $S.$ □

Next, we prove two strong convergence results for a generalized $(\alpha ,\beta )$-nonexpansive type 1 mapping.

Theorem 6.

Under the assumptions of Theorem 5, if Y is a compact subset of $X,$ then the sequence ${\left\{a_n\right\}}_{n=1}^{\infty }$ converges strongly to a fixed point of $S.$

Proof. 

We consider an element $e\in Y.$ Because Y is a compact set, we can say that there exists a subsequence ${\left\{a_{n_k}\right\}}_{k=1}^{\infty }$ of ${\left\{a_n\right\}}_{n=1}^{\infty }$ such that ${lim}_{k\to \infty }m(a_{n_k},e)=0.$ By Proposition 1 (ii), we have

$$\underset{k\to \infty }{lim}m(a_{n_k},Se)\le \frac{2+\alpha +\beta }{1-\beta }\underset{k\to \infty }{lim}m(a_{n_k},S{a}_{n_k})+\underset{k\to \infty }{lim}m(a_{n_k},e).$$

From Theorem 4, we obtain ${lim}_{k\to \infty }m(a_{n_k},S{a}_{n_k})=0.$ Then, we obtain $Se=e,$ that is, $e\in F_{ix}\left(S\right).$ Using Lemma 4, ${lim}_{n\to \infty }m(a_n,e)$ exists and hence $\left\{a_n\right\}$ converges strongly to $e.$ □

Theorem 7.

Let $X,Y,S$ and ${\left\{a_n\right\}}_{n=1}^{\infty }$ be the same as in Theorem 5. Then, the sequence ${\left\{a_n\right\}}_{n=1}^{\infty }$ converges strongly to a fixed point of S if and only if

$$\underset{n\to \infty }{lim\; inf}m(a_n,F_{ix}\left(S\right))=0\mathrm{or}\underset{n\to \infty }{lim\; sup}m(a_n,F_{ix}\left(S\right))=0,$$

where $m(a,F_{ix}\left(S\right))=inf\{m(a,e):e\in F_{ix}\left(S\right)\}.$

Proof. 

If the sequence ${\left\{a_n\right\}}_{n=1}^{\infty }$ converges strongly to a point $e\in F_{ix}\left(S\right),$ then ${lim}_{n\to \infty }m(a_n,e)=0.$ Because $0\le m(a_n,F_{ix}\left(S\right))\le m(a_n,e),$ we have ${lim}_{n\to \infty }m(a_n,F_{ix}\left(S\right))=0$.

For the converse part, assume that $lim{inf}_{n\to \infty }m(a_n,F_{ix}\left(S\right))=0.$ It follows from Lemma 4 that ${lim}_{n\to \infty }m(a_n,F_{ix}\left(S\right))$ exists and hence ${lim}_{n\to \infty }m(a_n,F_{ix}\left(S\right))=0.$ Therefore, there exist a subsequence ${\left\{a_{n_k}\right\}}_{k=1}^{\infty }$ of ${\left\{a_n\right\}}_{n=1}^{\infty }$ and a sequence ${\left\{e_k\right\}}_{k=1}^{\infty }$ in $F_{ix}\left(S\right)$ such that

$$m(a_{n_k},e_k)<\frac{1}{2^k}\mathrm{for}\mathrm{all}k\ge 1.$$

By the proof of Lemma 4, we have

$$m(a_{n_{k+1}},e_{k+1})\le m(a_{n_k},e_k)<\frac{1}{2^k},$$

which implies that

$$\begin{array}{ccc}\hfill m(e_{k+1},e_k)& \le & m(e_{k+1},a_{n_{k+1}})+m(a_{n_{k+1}},e_k)\hfill \\ & <& \frac{1}{2^{k+1}}+\frac{1}{2^k}<\frac{1}{2^{k-1}}\hfill \\ & \to & 0\mathrm{as}k\to \infty .\hfill \end{array}$$

Hence, ${\left\{e_k\right\}}_{k=1}^{\infty }$ is a Cauchy sequence in $F_{ix}\left(S\right).$ By Proposition 1 (iii), $F_{ix}\left(S\right)$ is closed and so ${\left\{e_k\right\}}_{k=1}^{\infty }$ converges strongly to $e\in F_{ix}\left(S\right).$ On the other hand, we have

$$m(a_{n_k},e)\le m(a_{n_k},e_k)+m(e_k,e).$$

Taking the limit of both sides of this inequality, we obtain that ${\left\{a_{n_k}\right\}}_{k=1}^{\infty }$ converges strongly to $e\in F_{ix}\left(S\right)$. Because ${lim}_{n\to \infty }m(a_n,e)$ exists by Lemma 4, e is the strong limit of ${\left\{a_n\right\}}_{n=1}^{\infty }$. □

In 1974, Senter and Dotson [35] introduced a mapping satisfying Condition (I), which is stated as follows:

A mapping $S:Y\to Y$ is said to satisfy Condition (I) if there exists a non-decreasing function $f:[0,\infty )\to [0,\infty )$ with $f\left(0\right)=0$ and $f\left(r\right)>0$ for all $r\in (0,\infty )$ such that $m(a,Sa)\ge f\left(m(a,F_{ix}\left(S\right))\right)$ for all $a\in Y$.

Now, we present the final strong convergence result using Condition (I).

Theorem 8.

Let Y be a nonempty closed convex subset of a complete uniformly convex hyperbolic metric space X with the monotone modulus of uniform convexity η and $S:Y\to Y$ be a generalized $(\alpha ,\beta )$-nonexpansive type 1 mapping with $F_{ix}\left(S\right)\ne \varnothing$. If S satisfies Condition (I) and ${\left\{a_n\right\}}_{n=1}^{\infty }$ is the iterative sequence defined by (3) with real sequences ${\left\{{\sigma }_n\right\}}_{n=1}^{\infty }$ and ${\left\{{\eta }_n\right\}}_{n=1}^{\infty }$ in $[p,q]$ for some $p,q\in (0,1)$, then ${\left\{a_n\right\}}_{n=1}^{\infty }$ converges strongly to a point of $F_{ix}\left(S\right)$.

Proof. 

By Theorem 4, we have ${lim}_{n\to \infty }m(a_n,S{a}_n)=0$. Then, by Condition (I), we obtain ${lim}_{n\to \infty }f\left(m(a_n,F_{ix}\left(S\right))\right)\le {lim}_{n\to \infty }m(a_n,S\left(a_n\right))=0,$ that is, ${lim}_{n\to \infty }f\left(m(a_n,F_{ix}\left(S\right))\right)=0$. Because $f:[0,\infty )\to [0,\infty )$ is a function with $f\left(0\right)=0$ and $f\left(r\right)>0$ for all $r\in (0,\infty )$, we have ${lim}_{n\to \infty }m(a_n,F_{ix}\left(S\right))=0$. All the conditions of Theorem 7 are now satisfied; therefore, ${\left\{a_n\right\}}_{n=1}^{\infty }$ converges strongly to a point of $F_{ix}\left(S\right)$. □

Remark 1.

In this section, we used the generalized $(\alpha ,\beta )$-nonexpansive type 1 mapping which contains the class of generalized α-nonexpansive mapping on the hyperbolic metric space. Thus, Theorems 5–8 generalize the results of [16,17] in two ways: (1) the class of underlying space, and (2) the class of mappings.

5. Numerical Example

In this section, we construct the following example of a generalized $(\alpha ,\beta )$-nonexpansive type 1 mapping.

Example 1.

Let $X=\mathbb{R}$ with the usual metric and $Y=[0,\infty ).$ Define a mapping $S:Y\to Y$ by

$$Sa=\left\{\begin{array}{c}0\mathit{if}a\in [0,\frac{6}{5}),\\ \frac{5a}{12}\mathit{if}a\in [\frac{6}{5},\infty ).\end{array}\right.$$

Clearly, $a=0$ is the fixed point of $S.$ Then, the following:

(i) 

Because S is not continuous at the point $a=\frac{6}{5},$ S is not a nonexpansive mapping.

(ii) 

Let $a=\frac{4}{5}$ and $b=\frac{6}{5}.$ Then,

$$\frac{1}{2}|a-Sa|=\frac{2}{5}\le \frac{2}{5}=|a-b|.$$

On the other hand,

$$|Sa-Sb|=\frac{1}{2}>\frac{2}{5}=|a-b|.$$

Thus, S is not a Suzuki-generalized nonexpansive mapping.

(iii) 

Let $a=\frac{4}{5}$ and $b=\frac{6}{5}$. Then,

$$\begin{array}{ccc}\hfill |Sa-Sb|& \le & \alpha |a-b|+\beta |a-Sb|\hfill \\ \hfill \frac{1}{2}& \le & \frac{2\alpha }{5}+\frac{3\beta }{10}\hfill \\ \hfill 5& \le & 4\alpha +3\beta .\hfill \end{array}$$

Therefore, the implications fail to be satisfied, which leads to the conclusion that S is not a mean nonexpansive mapping.

(iv) 

Now, we prove that S is a generalized $(\alpha ,\beta )$-nonexpansive type 1 mapping. For this purpose, let $\lambda =\frac{1}{3},\alpha =\frac{5}{12},\beta =\frac{6}{12},$ and consider the following cases:

• Case A: $a\in [0,\frac{6}{5}).$ Then, $\lambda |a-Sa|=\frac{1}{3}a\le |a-b|,$ which gives two possibilities:

  (1) 

  Let $a<b$. Then, $\frac{1}{3}a\le b-a⟹a\le \frac{3b}{4}⟹$$b\in [0,\frac{8}{5}).$

  (a) 

  If $b\in [0,\frac{6}{5}),$ then we have

  $$|Sa-Sb|=0\le \frac{5}{12}\left|b\right|+\frac{6}{12}\left|a\right|+\frac{1}{12}|a-b|.$$

  (b) 

  If $b\in [\frac{6}{5},\frac{8}{5}),$ then we have

  $$|Sa-Sb|=\frac{5}{12}\left|b\right|\le \frac{5}{12}\left|b\right|+\frac{6}{12}\left|a-\frac{5b}{12}\right|+\frac{1}{12}|a-b|.$$

  (2) 

  Let $a>b$. Then, $\frac{1}{3}a\le a-b⟹b\le \frac{2a}{3}⟹$$b\in [0,\frac{4}{5})\subset [0,\frac{6}{5})$, which is already included in case (1)(a).

• Case B: $a\in [\frac{6}{5},\infty ).$ Then, $\lambda |a-Sa|=\frac{1}{3}|a-\frac{5}{12}a|=\frac{7}{36}a\le |a-b|,$ which gives two possibilities:

  (1) 

  Let $a<b$. Then, $\frac{7}{36}a\le b-a⟹b\ge \frac{43a}{36}⟹$$b\in [\frac{43}{30},\infty )\subset [\frac{6}{5},\infty ).$ So,

  $$\begin{array}{ccc}\hfill |Sa-Sb|& =& \frac{5}{12}|a-b|\hfill \\ & <& \frac{5}{12}\left(\left|\frac{17a}{12}-\frac{17b}{12}\right|\right)+\frac{1}{12}\left|a-b\right|\hfill \\ & \le & \frac{5}{12}\left|\frac{5a}{12}-b\right|+\frac{5}{12}\left|a-\frac{5b}{12}\right|+\frac{1}{12}|a-b|\hfill \\ & \le & \frac{5}{12}\left|\frac{5a}{12}-b\right|+\frac{6}{12}\left|a-\frac{5b}{12}\right|+\frac{1}{12}|a-b|.\hfill \end{array}$$

  (2) 

  Let $a>b$. Then, $\frac{7}{36}a\le a-b⟹a\ge \frac{36b}{29}⟹$$b\in [\frac{29}{30},\infty ).$

  (a) 

  If $b\in [\frac{29}{30},\frac{6}{5}),$ then we have

  $$|Sa-Sb|=\frac{5}{12}\left|a\right|\le \frac{5}{12}\left|\frac{5a}{12}-b\right|+\frac{6}{12}\left|a\right|+\frac{1}{12}|a-b|.$$

  (b) 

  $b\in [\frac{6}{5},\infty )$ is already included in case (1).

Hence, S is a generalized $(\frac{5}{12},\frac{6}{12})$-nonexpansive type 1 mapping with $F_{ix}\left(S\right)\ne \varnothing$.

We now present the convergence analysis involving the above mapping via different iterations by choosing $a_1$ = 50,000 $\in Y$ and ${\sigma }_n={\eta }_n={\gamma }_n=\frac{n}{n+10}$ for all $n\ge 1$. We obtain the following, Table 1 and Figure 1.

Table 1. The comparison of convergence of different iterations for mapping S of Example 1.

Iteration Number	Agarwal	Abbas	Thakur	Thakur New	M	KF
1	50,000	50,000	50,000	50,000	50,000	50,000
2	20,732.8971	9646.8733	8638.7071	19,633.4253	8220.2230	8021.1525
3	8498.7280	1977.8457	1475.4736	7265.5898	1288.3740	1196.8442
4	3431.1309	420.5066	248.2010	2538.4195	193.5658	167.0390
5	1361.5599	91.3799	41.0385	839.4244	28.0043	21.9129
6	530.5461	20.1147	6.6629	263.4896	3.9164	2.7135
7	202.9269	4.4589	1.0618	78.7354	0.5312	0
8	76.1902	0.9915	0	22.4611	0	0
9	28.0879	0	0	6.1336	0	0
10	10.1715	0	0	1.6074	0	0
11	3.6200	0	0	0	0	0
12	1.2669	0	0	0	0	0
13	0.2399	0	0	0	0	0

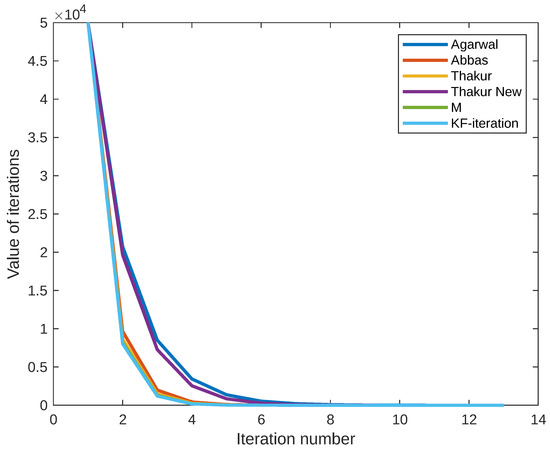
Figure 1. Graph corresponding to Table 1.

Clearly, the $KF$-iteration process is moving fast to the fixed point of S as compared to other iteration processes.

Remark 2.

We used MATLAB online software to obtain the numerical results and the graph in the proposed example.

6. Conclusions

In the above sections, we have modified the $KF$-iterative scheme into the hyperbolic metric space and established the weak $w^2$-stability and data dependence results for contraction mappings and derived some convergence results for generalized $(\alpha ,\beta )$-nonexpansive type 1 mappings using this modified iterative scheme. Using similar approaches of this article, the generalized $(\alpha ,\beta )$-nonexpansive type 2 mapping, which is introduced by Akutsah and Narain [15], can be studied in hyperbolic metric spaces as a future work. Moreover, some numerical examples for this class of mappings in hyperbolic metric spaces can be constructed.