Event-Triggered Distributed Sliding Mode Control of Fractional-Order Nonlinear Multi-Agent Systems

Abstract

In this study, the state consensus problem is investigated for a class of nonlinear fractional-order multi-agent systems (FOMASs) by using a dynamics event-triggered sliding mode control approach. The main objective is to steer all agents to some bounded position based on their own information and the information of neighbor agent. Different from the existing results, both asymptotic consensus problem and Zeno-free behavior are ensured simultaneously. To reach this objective, a novel event-triggered sliding mode control approach is proposed, composed of distributed dynamic event-triggered schemes, event-triggered sliding mode controllers, and auxiliary switching functions. Moreover, to implement the distributed control scheme, the fractional-order adaptive law is also developed to tuning the coupling weight, which is addressed in distributed protocol. With the improved distributed control scheme, all signals in the fractional-order closed-loop systems are guaranteed to be consensus and bounded, and a novel approach is developed to avoid the Zeno behavior. Finally, the availability and the effectiveness of the above-mentioned approach are demonstrated by means of a numerical example.

1. Introduction

There is an extensive and promising range of applications for the problem of cooperative control in multi-agent systems (MASs), from coordinating a group of mobile robots to forming a group of unmanned aircraft. In particular, there are a large number of cooperative control results for MASs with various tasks, such as cooperative detection, cooperative assistance seeking, formation, and swarming, that have been extensively researched in recent years [1,2,3,4,5]. In [6], second-order nonlinear MASs have been studied, and the fault-tolerant agreement robust control algorithm has been used to address the leader-following agreement issue with uncertain dynamics and actuator failures, while the findings have been generalized to the special case of the above problem [7,8,9]. In [10,11], local and global performances for MASs based on a class of nonlinear dynamics have been addressed, respectively. Note that from the system point of view, the above results aim to be applicable in an integer-order multi-agent system. Therefore, the direct generalization of these results to fractional-order nonlinear systems is difficult due to the inherent challenges in the noninteger character of the derivative powers. In addition, unnecessary communication between agents causes a waste of resources.

In the field of research on uncertain nonlinear systems, everyone is aware of how frequently the adaptive control scheme is addressed for the system and proposed for the control algorithms [12]. A priori awareness of the input gain signs of agents as control directions of agents has been the primary presumption of adaptive/robust consensus procedures in the literature [13,14,15]. Distributed consensus techniques have been devised to address the MASs issue under the assumption that the uncertainty can be linearly quantified using an artificial neural network. Numerous positive outcomes have been produced thus far for the state or output consensus issues with various agent dynamics, including single integration, double integration, T-S fuzzy, discrete-time, fractional-order, descriptor, general linear, and nonlinear systems [16,17,18,19,20].

Fractional-order systems are better suited to simulate various real-world application systems than integer-order systems, including electromagnetic waves, dielectric polarization, and viscoelastic systems [21,22,23]. In agreement with the vast majority of mathematicians, integer-order systems are a special case of fractional-order systems, which is an obvious conclusion. In [24,25,26,27], the authors have been informed that the stability issue of fractional-order systems is exceedingly challenging and complex because the traditional stability theory cannot be transplanted and applied. Recent studies have concentrated on the coordination issue for fractional-order MASs (FOMASs) due to the broad application potential of such systems. The case of networked FOMASs has been generalized for the first-order consensus problem in [20]. For FOMASs with communication delays, [28] has explored the trouble caused by time delays by designing a novel consensus algorithm. In [29], the uncertainty dynamics have been investigated in the fractional-order consensus problem by designing novel co-controllers with output feedback. Reference [30] has addressed the synchronization challenge for an universal fractional-order dynamical network model. When leader-following fractional-order consensus problems with nonlinear dynamics were first proposed, most results were obtained by converting them to states or output consistency problems by establishing an error system between followers and the leader. Subsequently, in [31], a relative state error feedback-based control approach has been presented to overcome the constraints of such situations. To handle the leader-following agreement problem of nonlinear FOMASs, a novel adaptive control method was developed in [32]. Ref. [33] has explored the consensus problem for uncertain linear FOMASs, whereas [34] has addressed the associated confinement challenge.

To decrease disturbance and uncertainty, a robust control mechanism called sliding mode control (SMC) can be applied [35,36]. Over the last couple of decades, many outstanding results of SMC theory and even-triggered control have been reported [37,38,39]. Therein, by considering limited computation resources for the digital platform, distributed event-triggered sliding mode control problem for various systems has received widespread attention [40,41]. The event-triggered scheme is designed in [42], which does not require continuous communication among followers. In [43], the sufficient conditions are proposed for guaranteed cost consensus and a Lyapunov–Krasovskii functional is constructed for a Markov jumping multi-agent system. The integral-type sliding surface and distributed event-triggered sliding mode control approach are proposed such that the practical tracking consensus is reached. It should be noted that the integral-type sliding surface of each agent proposed in [40] depends on the continuous states of the leader. However, when the agent cannot receive the states of the leader, this type of controller may make the integral-type sliding surface unavailable. The event-triggered consensus tracking control issue in second-order MASs with nonlinear terms was examined in [44].

Since fractional-order systems can describe more complex practical application scenarios, and inspired by the mentioned results, the cooperative control issue of the FOMASs with Lipschitz nonlinear is studied by designing the event-triggered sliding mode control law. Furthermore, it is worth pointing out that most existing relevant results (see, e.g., the references mentioned above) are rarely concerned with the FOMASs, which is an important case in reality. The main challenge in this study is how to collaboratively control each agent described by fractional-order system to achieve consensus and to ensure a certain level of robustness. Based on the fractional-order adaptive law, the novel distributed event-triggered sliding mode control protocol is re-designed in this study.

In comparison with the existing works, a summary of the main contributions of this study is concluded as follows.

(1)

In contrast with earlier studies in [45], the system considered in this paper can be adapted to more complex scenarios. In addition, a fractional-order distributed coordinator framework with adaptive capacity are designed based on the event-triggered sliding mode control.

(2)

To overcome difficulties in distributed sliding control, different from [44], an auxiliary sliding mode function is constructed without sustaining communication among agents, which makes distributed event-triggered sliding mode control laws only receive signals at triggering instants, such that the use of communication resources is saved.

(3)

Compared with the previously reported approach in [31], the novel fractional-order adaptive law is proposed to ensure that the convergence speed of the agent and robustness. Moreover, the nonlinear fractional-order stability theory is applied to guarantee the achievement of the distributed consensus objective.

The remaining portion of this study is organized as follows. Section 2 covers the nomenclature, some preliminary details, and the structure of proposal. Section 3 develops the key findings. A simulation scenario is offered in Section 4 as an illustration and verification of our theoretical results. Section 5 is the conclusion.

Notations: In this study, symbols ${\mathbb{R}}_{+}$, $\mathbb{C}$, and ${\mathbb{Z}}^{+}$ are used to represent the positive real number, complex number, and positive integer, respectively. We use $|·|$ to represent the Euclidean norm for real vectors. For real matrices M and N, $M\otimes N$ denotes the Kronecker product. We use ${\mathbf{1}}_N$ to represent the N-dimensional ${\left[\begin{array}{cccc}1& 1& \cdots & 1\end{array}\right]}^T$. For vectors $z_i\in {\mathbb{R}}^n,i=1,2,\cdots ,N$, define ${\mathbf{1}}_N^{n}z={\sum }_{i=1}^N{z}_i$ with $z={\left[\begin{array}{cccc}{z}_1^T& z_2^T& \cdots & z_N^T\end{array}\right]}^T$. For the matrix $L\in {\mathbb{R}}^{n\times n}$, ${\lambda }_{min}\left(L\right)$ denotes the minimum characteristic value of matrix L. For a function $\varphi :{\mathbb{R}}^n\to \mathbb{R}$, $D^{\alpha }\varphi$ represents the $\alpha$-th order differintegration operator of function $\varphi$. Lastly, $\mathrm{sign}(·)$ denotes the sign function.

2. Preliminaries

This section introduces basic essential graph theory and Caputo fractional derivative concepts. Following that, the problem statement and necessary lemmas are supplied.

2.1. Graph Theory

Throughout this paper, relevant concepts of graph theory will be introduced, which are defined in [8,46,47,48], including convexity, $\omega$-strongly convexity, connected graph, and weight-balanced digraph. Specifically, $\mathcal{G}$ (i.e., a triple $(\mathcal{N},\mathcal{E},\mathcal{A})$) is used to denote the weight-balanced digraph, where $\mathcal{A}={\left[a_{mn}\right]}_{N\times N}$, $\mathcal{N}=\{1,\dots ,N\}$, and L is the Laplacian of this digraph, which is defined as $L={\left[r_{mn}\right]}_{N\times N}$ with $r_{mm}={\sum }_{n\ne m}{a}_{mn}$ and $r_{mn}=-a_{mn}$ for $n\ne m$. When $\mathcal{G}$ is an undirected graph, L is a positive symmetric constant matrix. Whether L is an undirected graph or a weighted digraph, the Laplacian matrix has at least one eigenvalue of zero and a matching eigenvector of ${\mathbf{1}}_N$.

2.2. Gaputo Fractional Derivative

It should be noted that fractional-order derivatives come in many different varieties, and the specific varieties of derivatives have no effect on the stability results, such as the Grunward–Letnikov derivative, Riemann–Liouville derivative, and Caputo derivative. In this paper, the Caputo fractional operator will be used to describe the model of MASs and establish the consensus stability properties. The Caputo derivative definition of a continuous function $h\left(t\right)$ is given as follows [49]:

$$\begin{array}{c}\hfill D^{\alpha }h\left(t\right)=\frac{1}{G(n-\alpha )}{\int }_0^t{(t-\omega )}^{n-\alpha -1}{h}^{\left(n\right)}\left(\omega \right)d\omega \end{array}$$

(1)

with

$$\begin{array}{c}\hfill G\left(\alpha \right)={\int }_0^{\infty }{e}^{-\omega }{\omega }^{\alpha -1}d\omega \end{array}$$

(2)

being the Gamma function generalizing fractional for noninteger argument, where $n\in {\mathbb{Z}}^{+}$ and $n-1<\alpha <n$.

Then, the Mittag–Leffler function is introduced to describe the solutions of the fractional-order system, which is defined as follows:

$$\begin{array}{c}\hfill M_{\alpha ,\beta }\left(t\right)=\sum _{k=0}^{\infty }\frac{t^k}{G(k\alpha +\beta )}\end{array}$$

(3)

for any $\alpha ,\beta \in \mathbb{C}$. In particular, when $\beta =0$, (3) can be rewritten as

$$\begin{array}{c}\hfill M_{\alpha }\left(t\right)=\sum _{k=0}^{\infty }\frac{t^k}{G(k\alpha +1)}.\end{array}$$

(4)

Lemma 1 

([50]). If a continuous function $F\left(t\right):[0,+\infty )\to [0,+\infty )$ satisfies:

$$\begin{array}{c}\hfill D^{\alpha }F\left(t\right)\le \rho F\left(t\right)\end{array}$$

(5)

with $\alpha \in (0,1)$ and ρ denoting a constant, then for any $t\ge 0$, one has:

$$\begin{array}{c}\hfill F\left(t\right)\le F\left(0\right)M_{\alpha }\left(\rho t^{\alpha }\right).\end{array}$$

(6)

Lemma 2 

([51]). Consider the following system:

$$\begin{array}{c}\hfill D^{\alpha }z=Az,\end{array}$$

(7)

where $z\in {\mathbb{R}}^n$ denotes the system state vector, $\alpha \in (0,1]$ denotes the fractional order, and $A\in {\mathbb{R}}^{n\times n}$ is a constant matrix. If there exists a positive definite matrix $P\in {\mathbb{R}}^{n\times n}$ such that

$$\begin{array}{c}\hfill V\left(z\right)=z^{T}P{D}^{\alpha }z<0\end{array}$$

(8)

holds, the system is asymptotically stable.

2.3. Problem Formulation

Consider a FOMAS containing N agents with each agent i modeled by:

$$\begin{array}{cc}\hfill D^{\alpha }{x}_i& =f\left(x_i\right)+u_i,\hfill \end{array}$$

(9)

for $i\in \mathcal{N}:=\{1,2,\cdots ,N\}$, where $x_i\in {\mathbb{R}}^n$ represents the state vector of agent i, and $u_i\in {\mathbb{R}}^n$ represents the control input signal of agent i, respectively; note that $\alpha \in (0,1)$. $f:{\mathbb{R}}^n\to {\mathbb{R}}^n$ denotes the nonlinear system dynamic function, and f is a continuous function.

In this study, the objective aims at designing distributed controller for the agents to solve the coordinate state consensus problem. In particular, under specific initial conditions, the state $x_i$ of the agent i keep bounded, and the state satisfies:

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}|x_i\left(t\right)-x_j\left(t\right)|=0,i\in \mathcal{N}.\end{array}$$

(10)

In our system setup, the controller for agents has access to the outputs $y_i$ of the agent and the output $y_j$ of the neighbor agents.

This paper is also interested in the distributed implementation of the controllers. In this study, a weighted digraph $\mathcal{G}=(\mathcal{N},\mathcal{E},\mathcal{A})$ is considered to denote the information exchange topology among the agents.

The following assumptions are made for the nonlinear dynamic function of the system and the communication topology.

Assumption 1. 

The nonlinear function f is Lipschitz, that is:

$$\begin{array}{c}\hfill |f\left(z_1\right)-f\left(z_2\right)|\le k|z_1-z_2|,\end{array}$$

(11)

where $z_1,z_2\in {\mathbb{R}}^n$ and $k>0$ denotes a constant.

Assumption 2. 

The digraph $\mathcal{G}$ is quasi-strongly connected and weight-balanced.

3. Main Results

To achieve the objectives of this study, the controller design of this paper is divided into three parts. Firstly, a novel distributed dynamic event-triggered schemes framework for each agent is proposed. Secondly, a new auxiliary switching function for each agent is constructed to prevent sliding mode controllers from receiving communication information at each triggering instant. Finally, the consensus problem and Zeno-free behavior are ensured simultaneously.

3.1. Dynamic Event-Triggered Communication Scheme

In this subsection, a dynamic event-triggered communication scheme is designed to reduce the use of the communication among the agent. Consider the following triggered instant $t_{k+1}^i$ for agent i:

$$\begin{array}{c}\hfill t_{k+1}^i=inf\{t>t_k^i:\vartheta |{\tilde{e}}_i{|}^2\ge {\Pi }_i+c_1{\theta }_i\left(t\right)\},\end{array}$$

(12)

where $\vartheta$ is a positive constant, ${\tilde{e}}_i=x_i\left(t_k^i\right)-x_i\left(t\right)$;

$$\begin{array}{c}\hfill {\Pi }_i={\left|\sum _{j=1}^N{a}_{ij}\left(x_j\left(t_k^j\right)\right)-\left(x_i\left(t_k^i\right)\right)\right|}^2,\end{array}$$

(13)

and the dynamic variable ${\theta }_i\left(t\right)$ being generated by:

$$\begin{array}{c}\hfill {\dot{\theta }}_i\left(t\right)=-c_2{\theta }_i\left(t\right)+{\Pi }_i-\vartheta {\left|{\tilde{e}}_i\right|}^2\end{array}$$

(14)

with $c_1$ and $c_2$ being two positive constants. Note that the sequence $\left\{t_k^i\right\},k=0,1,\cdots$ is the triggering instant of the ith agent and $t_0^i=0$ for $i\in \mathcal{N}$.

By (12), we have:

$$\begin{array}{c}\hfill {\dot{\theta }}_i\left(t\right)\ge -c_1{\theta }_i\left(t\right)-c_2{\theta }_i\left(t\right).\end{array}$$

(15)

Therefore, by the comparison principle, we obtain:

$$\begin{array}{c}\hfill {\theta }_i\left(t\right)\ge e^{-(c_1+c_2)(t-t_0)}{\theta }_i\left(0\right),\end{array}$$

(16)

where $t_0$ is the initial time. Therefore, ${\theta }_i\left(t_0\right)\ge 0$, and it is derived that ${\theta }_i\left(t\right)\ge 0$.

3.2. Sliding Surface Design

For any agent i, the sliding surface is design by:

$$\begin{array}{cc}\hfill s_i\left(t\right)=& \sum _{j=1}^N{a}_{ij}(x_i\left(t\right)-x_j\left(t\right))\hfill \\ \hfill & -{\int }_0^t\sum _{j=1}^N{a}_{ij}(u_{it}\left(\omega \right)-u_{jt}\left(\omega \right)+{\rho }_i{u}_{it}\left(\omega \right))d\omega \hfill \end{array}$$

(17)

for $i\in \mathcal{N}$, where ${\rho }_i>0$ denotes constant and $u_{it}\left(t\right)$ is designed by:

$$\begin{array}{c}\hfill u_{it}\left(t\right)=\tilde{\lambda }\sum _{j=1}^N{a}_{ij}(x_j\left(t_k^j\right)-x_i\left(t_k^i\right))\end{array}$$

(18)

with $\tilde{\lambda }>0$ being a positive constant and $t\in \left[t_k^i,t_{k+1}^i\right)$.

Moreover, for each agent i, only the state $x_i\left(t_k^j\right)$ is sent to the dynamic event-triggered schemes law at the time $t_k$. Based on this situation, an auxiliary switching function is constructed for each agent i only containing the signal at each triggering instant as follows:

$$\begin{array}{cc}\hfill s_{ik}\left(t\right)=& \sum _{j=1}^N{a}_{ij}(x_i\left(t_k^i\right)-x_j\left(t_k^j\right))\hfill \\ \hfill & -{\int }_0^t\sum _{j=1}^N{a}_{ij}(u_{it}\left(\omega \right)-u_{jt}\left(\omega \right)+{\rho }_i{u}_{it}\left(\omega \right))d\omega .\hfill \end{array}$$

(19)

Define $x={\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_N\end{array}\right]}^T$ and $u_t={\left[\begin{array}{cccc}{u}_{1t}& u_{2t}& \cdots & u_{Nt}\end{array}\right]}^T$. The compact form of the sliding surface is written as:

$$\begin{array}{c}\hfill S\left(t\right)=L\otimes I_{n}x\left(t\right)-{\int }_0^{t}L\otimes I_n{u}_t\left(\omega \right)d\omega .\end{array}$$

(20)

The event-triggered sliding mode control law is design by:

$$\begin{array}{c}\hfill u_i\left(t\right)=u_{it}\left(t\right)+u_{ie}\left(t\right)\end{array}$$

(21)

for $t\in \left[t_k^i,t_{k+1}^i\right)$, where

$$\begin{array}{c}\hfill u_{ie}\left(t\right)=-\left(k\right|{\tilde{e}}_i\left(t\right)|+ϵ)\mathrm{sign}\left(s_{ik}\left(t\right)\right)\end{array}$$

(22)

with $ϵ>0$ being a constant to be determined.

Remark 1. 

In this subsection, an auxiliary function (19) for each agent is constructed. The function (19) causes that the controller only acquire the state $x_j\left(t_k^j\right)$. Thus, the function (19) that only contains the state $x_j\left(t_k^j\right)$ is developed to design the distributed event-triggered sliding mode controller, which can save more communication resources.

Lemma 3. 

Consider the event-based sliding surface (17) and the auxiliary sliding function (19). The sliding region is obtained under the (12) for each agent i as follows:

$$\begin{array}{c}\hfill |s_i\left(t\right)-s_{ik}\left(t\right)|\le {\mathcal{K}}_i\left(t\right)\end{array}$$

(23)

for $t\in \left[t_k^i,t_{k+1}^i\right)$, where ${\mathcal{K}}_i\left(t\right)=|L\otimes I_n\tilde{e}\left(t\right)|$ with $\tilde{e}={[{\tilde{e}}_1^T,{\tilde{e}}_2^T,\cdots ,{\tilde{e}}_N^T]}^T$.

Proof. 

By (17) and (12), we have:

$$\begin{array}{cc}\hfill |s_i\left(t\right)-s_{ik}\left(t\right)|=& |\sum _{j=1}^N{a}_{ij}(x_i\left(t\right)-x_j\left(t\right))\hfill \\ \hfill & -\sum _{j=1}^N{a}_{ij}(x_i\left(t_k^i\right)-x_j\left(t_k^j\right))|\hfill \\ \hfill \le & |\sum _{j=1}^N{a}_{ij}({\tilde{e}}_j\left(t\right)-{\tilde{e}}_j\left(t\right))|\hfill \\ \hfill \le & |L\otimes I_n\tilde{e}\left(t\right)|\hfill \end{array}$$

(24)

for $t\in \left[t_k^i,t_{k+1}^i\right)$ and $i\in \mathcal{N}$. Thus, (23) holds. □

Theorem 1. 

Under the Assumptions 1 and 2, consider the FOMASs (9) distributed dynamic event-triggered schemes (12) and event-triggered sliding mode control law (21). Then, the state trajectories of all agent will be remained to the sliding region $\Omega =\left\{x\left(t\right)\right|\left|S\left(t\right)\right|\le \sqrt{{\sum }_{i=1}^N{\mathcal{K}}_i^2\left(t\right)}$ from the initial time.

Proof Theorem 1. 

Case 1: Firstly, when $\mathrm{sign}\left(s_i\left(t\right)\right)\ne \mathrm{sign}\left(s_{ik}\left(t\right)\right)$ holds, then the state trajectories of all agents remain inside the set $\widehat{\Omega }=\left\{x\left(t\right)\right||s_i\left(t\right)|\le {\mathcal{K}}_i\left(t\right)\}$. Based on Lemma 4, it follows that $|s_i\left(t\right)-s_{ik}\left(t\right)|\le {\mathcal{K}}_i\left(t\right)$. Therefore:

$$\begin{array}{c}\hfill s_i\left(t\right)-{\mathcal{K}}_i\left(t\right)\le s_{ik}\left(t\right)\le s_i\left(t\right)+{\mathcal{K}}_i\left(t\right)\end{array}$$

(25)

for $t\in \left[t_k^i,t_{k+1}^i\right)$ and $i\in \mathcal{N}$.

Since $\mathrm{sign}\left(s_i\left(t\right)\right)\ne \mathrm{sign}\left(s_{ik}\left(t\right)\right)$, if $s_i\left(t\right)>0$, $\mathrm{sign}\left(s_{ik}\left(t\right)\right)\le 0$, then $s_i\left(t\right)\le {\mathcal{K}}_i\left(t\right)$; if $s_i\left(t\right)<0$, $s_{ik}\left(t\right)\ge 0$, then $s_i\left(t\right)\ge -{\mathcal{K}}_i\left(t\right)$. In summary, the state of agent will inside the set $\widehat{\Omega }$.

Case 2: In this case, the set $\widehat{\Omega }$ will be proved to be a positively invariant set.

Consider the Lyapunov function candidate:

$$\begin{array}{c}\hfill V_s\left(t\right)=\frac{1}{2}{S}^T\left(t\right)S\left(t\right).\end{array}$$

(26)

Then, the derivative of $V_s\left(t\right)$ along the trajectories of the system (9) satisfies for $t\in \left[t_k^i,t_{k+1}^i\right)$:

$$\begin{array}{cc}\hfill D^{\alpha }{V}_s\left(t\right)=& S^T\left(t\right)D^{\alpha }S\left(t\right)\hfill \\ \hfill =& S^T\left(t\right)(L\otimes I_n(D^{\alpha }x\left(t\right)-u_t\left(t\right)))\hfill \\ \hfill =& S^T\left(t\right)L\otimes I_n(f\left(x\right)-u_e\left(t\right))\hfill \\ \hfill \le & \sum _{i=1}^N|s_i\left(t\right)\left|\right(k|{\tilde{e}}_i\left(t\right)|-u_{ie}\left(t\right))\hfill \\ \hfill \le & -ϵ\sum _{i=1}^N{\left|s_i\left(t\right)\right|}^2\hfill \\ \hfill \le & 0,\hfill \end{array}$$

(27)

where $f\left(x\right)={\left[\begin{array}{cccc}{f}^T\left(x_1\right)& f^T\left(x_2\right)& \cdots & f^T\left(x_N\right)\end{array}\right]}^T$ and $u_e={\left[\begin{array}{cccc}{u}_{1e}^T& u_{2e}^T& \cdots & u_{Ne}^T\end{array}\right]}^T$. Thus, by Lemma 2 and [49], it shows that the state trajectories of all agents remain the set form of the initial time, that is, the set is a positively invariant set. □

Remark 2. 

From Theorem 1, it is worth noting that the asymptotic consensus and Zeno-free behavior can be guaranteed simultaneously in the study. That is, the proposed method based on the distributed dynamic event-triggered scheme is proposed to ensure the exclusion of Zeno behavior in Theorem 1. According to definition in [52], the Zeno behavior is mathematically equivalent to ${lim}_{l\to \infty }{\sum }_{l=0}^{k+1}(t_{l+1}-t_l)\le \infty$. Thus, the corresponding conclusion is employed in the paper, and the Zeno behavior can be eliminated.

3.3. Design of Adaptive Distributed Controller

In order to improve the convergence rate, $u_{it}$ of the event-triggered sliding mode control law with adaptive coupling weights law is re-designed as follows:

$$\begin{array}{cc}\hfill u_{it}& =-G\sum _{j\in {\mathcal{N}}_i}{c}_{ij}{a}_{ij}(x_i\left(t\right)-x_j\left(t\right)),\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill D^{\alpha }{c}_{ij}& =-k_{ij}(c_{ij}-\beta )+k_{ij}{a}_{ij}{(x_i\left(t\right)-x_j\left(t\right))}^T\Phi (x_i\left(t\right)-x_j\left(t\right))\hfill \end{array}$$

(29)

for $t\in \left[t_k^i,t_{k+1}^i\right)$ and $i\in \mathcal{N}$, G and $\Phi$ are the feedback protocol gains to be designed, and $k_{ij}=k_{ji}>0$ and $\beta >0$ are constants. $c_{ij}$ denotes the coupling weight between agents i and j. In addition, $c_{ij}\left(0\right)=c_{ji}\left(0\right)$.

Define the following error:

$$\begin{array}{c}\hfill e_i\left(t\right)=x_i\left(t\right)-(1/N)\sum _{j=1}^N{x}_j\left(t\right)\end{array}$$

(30)

for $t\in \left[t_k^i,t_{k+1}^i\right)$ and $i\in \mathcal{N}$.

Therefore, the error dynamic of agent i and the adaptive law are as follows:

$$\begin{array}{cc}\hfill D^{\alpha }{e}_i& =f\left(x_i\right)-(1/N)\sum _{j=1}^{N}f\left(x_j\left(t\right)\right)-G\sum _{j=1}^N{c}_{ij}{a}_{ij}(x_i\left(t\right)-x_j\left(t\right))\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =f\left(x_i\right)-(1/N)\sum _{j=1}^{N}f\left(x_j\left(t\right)\right)-G\sum _{j=1}^N{c}_{ij}{a}_{ij}(e_i\left(t\right)-e_j\left(t\right)),\hfill \\ \hfill D^{\alpha }{c}_{ij}& =-k_{ij}(c_{ij}-\beta )+k_{ij}{a}_{ij}{(x_i\left(t\right)-x_j\left(t\right))}^T\Phi (x_i\left(t\right)-x_j\left(t\right))\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & =-k_{ij}(c_{ij}-\beta )+k_{ij}{a}_{ij}{(e_i\left(t\right)-e_j\left(t\right))}^T\Phi (e_i\left(t\right)-e_j\left(t\right))\hfill \end{array}$$

(32)

for $t\in \left[t_k^i,t_{k+1}^i\right)$ and $i\in \mathcal{N}$.

Define the following:

$$\begin{array}{cc}\hfill e& ={\left[\begin{array}{cccc}{e}_1^T& e_2^T& \cdots & e_N^T\end{array}\right]}^T,\hfill \\ \hfill f_0\left(x\right)& =(1/N)\sum _{j=1}^{N}f\left(x_j\right),\hfill \\ \hfill C& ={\left[c_{ij}\right]}_{i,j\in \mathcal{N}}.\hfill \end{array}$$

Therefore, from (31), we have:

$$\begin{array}{c}\hfill D^{\alpha }e\left(t\right)=f\left(x\left(t\right)\right)-f_0\left(x\left(t\right)\right)-GCLe\left(t\right)\end{array}$$

(33)

for $t\in \left[t_k^i,t_{k+1}^i\right)$, which is a compact form of the FOMASs (31).

Lemma 4. 

Consider the nonlinear dynamic function $f,i\in \mathcal{N}$ under Assumption 1. The following condition holds:

$$\begin{array}{c}\hfill |f\left(z_1\right)-\frac{1}{N}\sum _{j=1}^{N}f\left(z_2\right)|\le k_{max}|z_1-z_2|,\end{array}$$

(34)

where $k_{max}=\frac{1}{N}k$ is a positive constant.

Proof of Lemma 4. 

Under Assumption 1, we have:

$$\begin{array}{cc}\hfill |f\left(z_1\right)-\frac{1}{N}\sum _{j=1}^{N}f\left(z_2\right)|& =\frac{1}{N}\sum _{j=1}^N|f\left(z_1\right)-f\left(z_2\right)|\hfill \\ \hfill & \le \frac{1}{N}\sum _{j=1}^N\left(k\right|z_1-z_2\left|\right)\hfill \\ \hfill & \le k_{max}|z_1-z_2|\hfill \end{array}$$

(35)

for any $z_1,z_2\in {\mathbb{R}}^n$, where $k_{max}=\frac{1}{N}k$. □

3.4. Stability Analysis

In this part, the stability property of closed-loop FOMASs with a Lipschitz nonlinear value is established under the weight-balanced graph. Then, in a special case, the stability conditions of linear FOMASs are presented.

Theorem 2. 

Consider the FOMASs (9) distributed dynamic event-triggered schemes (12) and event-triggered sliding mode control law (21). Under Assumptions 1 and 2, the objective (10) can be achieved for any initial conditions if there exists a positive constant $l_{max}$ such that:

$$\begin{array}{c}\hfill k_{max}-\left|G\right|c_{min}{\lambda }_{min}\left(L\right)+l_{max}=0\end{array}$$

(36)

holds. In addition, an infinite number of triggering will not occur in the closed-loop system over any interval with finite-length time.

Proof of Theorem 2. 

From Assumption 1 and Lemma 4, by (31), we have:

$$\begin{array}{cc}\hfill |D^{\alpha }{e}_i\left(t\right)|& \le k_{max}|e_i\left(t\right)|-|G|c_{min}\left|L\right|\left|e\left(t\right)\right|\hfill \\ \hfill & \le k_{max}|e_i\left(t\right)|-|G|c_{min}{\lambda }_{min}\left(L\right)\left|e\left(t\right)\right|\hfill \end{array}$$

(37)

for $t\in \left[t_k^i,t_{k+1}^i\right)$, where $c_{min}={min}_{i,j\in \mathcal{N}}{c}_{ij}$.

We chose the following candidate Lyapunov function:

$$\begin{array}{c}\hfill V\left(t\right)=\underset{i\in \mathcal{N}}{max}\left|e_i\left(t\right)\right|\end{array}$$

(38)

for $t\in \left[t_k^i,t_{k+1}^i\right)$.

Apparently, there exists a integer $k\in \mathcal{N}$ such that:

$$\begin{array}{c}\hfill V\left(t\right)=|e_k\left(t\right)|\end{array}$$

(39)

for $t\in \left[t_k^i,t_{k+1}^i\right)$.

Based on (36), by fractional-order differential, it follows that:

$$\begin{array}{cc}\hfill D^{\alpha }V\left(t\right)& =\mathrm{sign}\left(e_k\left(t\right)\right)D^{\alpha }{e}_k\left(t\right)\hfill \\ \hfill & \le \mathrm{sign}\left(e_k\left(t\right)\right)k_{max}\left|e_k\left(t\right)\right|\hfill \\ \hfill & -\mathrm{sign}\left(e_k\left(t\right)\right)\left|G\right|c_{min}{\lambda }_{min}\left(L\right)\left|e_k\left(t\right)\right|\hfill \\ \hfill & \le -l_{max}\left|e_k\left(t\right)\right|\hfill \\ \hfill & =-l_{max}V\left(t\right)\hfill \end{array}$$

(40)

for $t\in \left[t_k^i,t_{k+1}^i\right)$.

Note that $e_k=0$ if and only if $e_i=0,i\in \mathcal{N}$, i.e., $x_i=x_j$ for $i,j\in \mathcal{N}$. Then, we claim:

$$\begin{array}{c}\hfill D^{\alpha }V\left(t\right)\le -l_{max}V\left(t\right)\end{array}$$

(41)

for any $t\ge 0$ and $t\in \left[t_k^i,t_{k+1}^i\right)$.

To prove this claim, we assume that there are an time $t_1\in (t_0,t)$ and $j\in \mathcal{N}$, such that:

$$\begin{array}{cc}\hfill V\left(t\right)& = |e_k\left(t\right)|,t\in [t_0,t_1],\hfill \\ \hfill V\left(t\right)& = |e_j\left(t\right)|,t\in [t_1,+\infty ],\hfill \end{array}$$

and $|e_k\left(t_1\right)| = |e_j\left(t_1\right)|$ for $t_0,t_1\in \left[t_k^i,t_{k+1}^i\right)$.

Similarly, we have:

$$\begin{array}{c}\hfill D^{\alpha }\left|e_j\left(t\right)\right|\le l_{max}V\left(t\right),\end{array}$$

(42)

for any $t\ge t_1$. Therefore, it follows that:

$$\begin{array}{cc}\hfill {\int }_0^{t_1}\frac{d\frac{V\left(\omega \right)-|e_j\left(\omega \right)|}{dt}}{{(t-\omega )}^{\alpha }}d\omega =& \frac{V\left(0\right)-|e_j\left(0\right)|}{t^{\alpha }}\hfill \\ \hfill & -\alpha {\int }_0^{t_1}\frac{V\left(\omega \right)-|e_j\left(\omega \right)|}{{(t-\omega )}^{\alpha +1}}d\omega \hfill \\ \hfill \le & 0\hfill \end{array}$$

(43)

for $t\ge t_1$, where $\frac{dh\left(t\right)}{d{t}^{\alpha }}=D^{\alpha }h\left(t\right)$, then:

$$\begin{array}{c}\hfill {\int }_0^{t_1}\frac{\frac{dV\left(\omega \right)}{dt}}{{(t-\alpha )}^{\alpha }}d\omega \le {\int }_0^{t_1}\frac{\frac{d|e_j\left(t\right)|}{dt}}{{(t-\omega )}^{\alpha }}d\omega \end{array}$$

(44)

for $t\ge t_1$.

By using the Caputo fractional derivative and (44), it follows that:

$$\begin{array}{cc}\hfill D^{\alpha }V\left(t\right)& =\frac{1}{G(1-\alpha )}{\int }_0^t\frac{\frac{dV\left(\omega \right)}{dt}}{{(t-\omega )}^{\alpha }}d\omega \hfill \\ \hfill & =\frac{1}{G(1-\alpha )}{\int }_0^{t_1}\frac{\frac{dV\left(\omega \right)}{dt}}{{(t-\omega )}^{\alpha }}d\omega \hfill \\ \hfill & +\frac{1}{G(1-\alpha )}{\int }_{t_1}^t\frac{\frac{d|e_j\left(\omega \right)|}{dt}}{{(t-\omega )}^{\alpha }}d\omega \hfill \\ \hfill & \le \frac{1}{G(1-\alpha )}{\int }_0^t\frac{\frac{d|e_j\left(\omega \right)|}{dt}}{{(t-\omega )}^{\alpha }}d\omega \hfill \\ \hfill & =D^{\alpha }\left|e_j\left(t\right)\right|.\hfill \end{array}$$

(45)

By using (42) and (45), we conclude that (41) holds for any $t\ge 0$. Based on Lemma 2, we have:

$$\begin{array}{c}\hfill V\left(t\right)\le V\left(0\right)M_{\alpha }(-l_{max}{t}^{\alpha }),\end{array}$$

(46)

which implies that:

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\left|e_k\left(t\right)\right|=0.\end{array}$$

(47)

Therefore, it follows that ${lim}_{t\to \infty }\left|e_j\left(t\right)\right|=0$ for $i\in \mathcal{N}$, which shows that the consensus of all state of agent can be achieved.

Next, we will prove that the distributed dynamic event-triggered schemes (12) for each agent does not exhibit Zeno behavior. Since ${\tilde{e}}_i\left(t_0\right)=0$, the following solution can be obtained:

$$\begin{array}{c}\hfill |{\tilde{e}}_i\left(t\right)|\le {\varphi }_i(t-t_k),\end{array}$$

(48)

where $\varphi >0$. By (15), we can obtain that:

$$\begin{array}{c}\hfill {\theta }_i\left(t\right)\ge e^{-(c_1+c_2)(t-t_k)}{\theta }_i\left(t_k\right).\end{array}$$

(49)

Thus, the next event will not be triggered before $\vartheta |{\tilde{e}}_i{|}^2=c_1{\theta }_i\left(t\right)$, that is:

$$\begin{array}{c}\hfill {\vartheta }^2{\varphi }_i^2{(t-t_k)}^2=c_1{\theta }_i\left(t\right)\ge c_1{e}^{-(c_1+c_2)(t-t_k)}{\theta }_i\left(t_k\right).\end{array}$$

(50)

Therefore, for the interexecution interval length $h_l=t_{k+1}-t_k$, ${lim}_{l\to \infty }{\sum }_{l=1}^{l=k+1}{h}_l\to \infty$, and thus, the Zeno-free behavior is obtained. □

Remark 3. 

In Theorem 1, all agents are in consensus and bounded by using distributed controller (28) when the coupling weight is a constant. In order to increase the convergence speed, the following results will be presented for FOMASs by using the adaptive distributed control laws (28) and (29).

Theorem 3. 

Consider the FOMASs (9) distributed dynamic event-triggered schemes (12), event-triggered sliding mode control law (21), and the adaptive distributed protocols (28) and (29). Under Assumptions 1 and 2, the objective (10) can be achieved for any initial conditions if the following hold:

$$\begin{array}{cc}\hfill (k_{max}-\beta )(P\otimes I_N-L\otimes PG)& <0,\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill \Phi -PG& =0\hfill \end{array}$$

(52)

In addition, an infinite number of triggering will not occur in the closed-loop system over any interval with finite-length time.

Proof of Theorem 3. 

Consider a candidate Lyapunov function as follows:

$$\begin{array}{c}\hfill V\left(t\right)=\sum _{i=1}^N{e}_i{\left(t\right)}^{T}P{e}_i\left(t\right)+\sum _{i=1}^N\sum _{j=1,j\ne i}^N\frac{{(c_{ij}-\beta )}^2}{2k_{ij}}\end{array}$$

(53)

for $t_0,t_1\in \left[t_k^i,t_{k+1}^i\right)$, where P is a positive matrix to be designed. The Caputo fractional derivative of V along the trajectory is as follows:

$$\begin{array}{cc}\hfill D^{\alpha }V\left(t\right)=& 2\sum _{i=1}^N{e}_i{\left(t\right)}^{T}P{D}^{\alpha }{e}_i\left(t\right)+\sum _{i=1}^N\sum _{j=1,j\ne i}N\frac{c_{ij}-\beta }{k_{ij}}{D}^{\alpha }{c}_{ij}\hfill \\ \hfill =& 2\sum _{i=1}^N{e}_i{\left(t\right)}^{T}P(f\left(x_i\right)-\frac{1}{N}\sum _{j=1}^{N}f\left(x_j\right))\hfill \\ \hfill & -2\sum _{i=1}^N{e}_i{\left(t\right)}^T\sum _{j=1}^N{c}_{ij}{a}_{ij}PG(e_i\left(t\right)-e_j\left(t\right))\hfill \\ \hfill & +\sum _{i=1}^N\sum _{j=1,j\ne i}^N(c_{ij}-\beta )(-(c_{ij}-\beta )\hfill \\ \hfill & +a_{ij}{(e_i\left(t\right)-e_j\left(t\right))}^T\Phi (e_i\left(t\right)-e_j\left(t\right))).\hfill \end{array}$$

(54)

for $t_0,t_1\in \left[t_k^i,t_{k+1}^i\right)$. It is easy to check that:

$$\begin{array}{cc}\hfill & \sum _{i=1}^N\sum _{j=1,j\ne i}^N(c_{ij}-\beta )a_{ij}{(e_i\left(t\right)-e_j\left(t\right))}^T\Phi (e_i\left(t\right)-e_j\left(t\right))\hfill \\ \hfill =& 2\sum _{i=1}^N\sum _{j=1,j\ne i}^N(c_{ij}-\beta )a_{ij}{e}_i{\left(t\right)}^T\Phi (e_i\left(t\right)-e_j\left(t\right)).\hfill \end{array}$$

(55)

By selecting the appropriate matrix P and $\Phi$ such that $\Phi -PG=0$ (i.e., (52)), then (54) can be written as:

$$\begin{array}{cc}\hfill D^{\alpha }V\left(t\right)=& 2\sum _{i=1}^N{e}_i{\left(t\right)}^{T}P(f\left(x_i\right)-\frac{1}{N}\sum _{j=1}^{N}f\left(x_j\right))\hfill \\ \hfill & -2\beta \sum _{i=1}^N{e}_i{\left(t\right)}^T\sum _{j=1,j\ne i}^N{a}_{ij}PG(e_i\left(t\right)-e_j\left(t\right))\hfill \\ \hfill & -\sum _{i=1}^N\sum _{j=1,j\ne i}^N{(c_{ij}-\beta )}^2\hfill \\ \hfill =& 2\sum _{i=1}^N{e}_i{\left(t\right)}^{T}P(f\left(x_i\right)-\frac{1}{N}\sum _{j=1}^{N}f\left(x_j\right))\hfill \\ \hfill & -2\alpha \sum _{i=1}^N\sum _{j=1,j\ne i}^N{L}_{ij}{e}_i{\left(t\right)}^{T}PG{e}_j\left(t\right)\hfill \\ \hfill & -\sum _{i=1}^N\sum _{j=1,j\ne i}^N{(c_{ij}-\beta )}^2\hfill \\ \hfill & \le 2(k_{max}-\beta )e{\left(t\right)}^T(P\otimes I_N-L\otimes PG)e\left(t\right)\hfill \\ \hfill & -\sum _{i=1}^N\sum _{j=1,j\ne i}^N{(c_{ij}-\beta )}^2.\hfill \end{array}$$

(56)

for $t_0,t_1\in \left[t_k^i,t_{k+1}^i\right)$.

Based on (51), we have:

$$\begin{array}{c}\hfill D^{\alpha }V\left(t\right)<0.\end{array}$$

(57)

for $t_0,t_1\in \left[t_k^i,t_{k+1}^i\right)$.

By Lemma 3, we conclude that the error systems (31) and (32) are asymptotically stable. Therefore, the objective (10) can be achieved for any initial conditions. Similarly, Zeno-free behavior can be obtained. □

Remark 4. 

Theorem 3 is an effective generalization and promotion of Theorem 2. Two results show that if better convergence performance is required, distributed control protocols with adaptive parameters can be applied; however, the parameter restrictions on the controller will become more strict. Later simulations will verify this conclusion.

4. Numerical Example

In this section, in order to verify the validity of the proposed dynamics event-triggered distributed sliding mode control approach, a numerical example is performed and two distributed algorithms are discussed: without adaptive law and with adaptive law.

In [45,53,54], the numerical simulations of fractional-order multi-intelligent body systems considered are mostly for first-order integrators, second-order integrators, linear systems, etc., whereas the results in this paper are able to handle general nonlinear FOMASs. To illustrate the effectiveness of designing distributed event-triggered controllers in this paper, FOMASs with general nonlinear terms, including trigonometric functions, polynomial nonlinear functions, etc., are considered. Thus, the nonlinear four agents of the fractional order will be considered with the fractional order $\alpha =\frac{1}{3}$, described by:

$$\begin{array}{c}\hfill D^{\alpha }{x}_i=\left[\begin{array}{c}-sin\left(x_{i1}\right)-cos\left(x_{i2}\right)\\ -x_{i1}-sin\left(x_{i2}^3\right)\end{array}\right]+u_i,\end{array}$$

(58)

where $i=1,2,3,4$, $x_i={\left[\begin{array}{cc}{x}_{i1}& x_{i2}\end{array}\right]}^T\in {\mathbb{R}}^2$ denotes the system state, and $u_i={\left[\begin{array}{cc}{u}_{i1}& u_{i2}\end{array}\right]}^T\in {\mathbb{R}}^2$ denotes the control input. The graph $\mathcal{G}$ and adjacency matrix $\mathcal{A}$ are shown in Figure 1. Consequently, Assumptions 1 and 2 are satisfied.

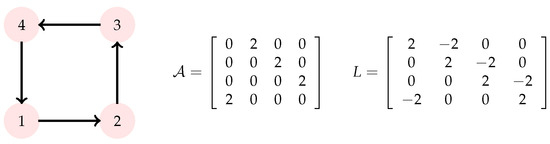
Figure 1. The network interaction topology and the adjacency matrix.

Let $G=\left[\begin{array}{cc}2.6& 1\\ 1& 2.6\end{array}\right]$, $\Phi =\left[\begin{array}{cc}0.53& 0.46\\ 0.46& 0.53\end{array}\right]$, $k_{ij}=0.5,i,j=1,2,3,4$, $\beta =0.1$, and ${\lambda }_{min}\left(L\right)=2$. Based on the system (58) and the network interaction topology, it follows that $k=2$ and $N=4$. Therefore, $k_{max}=0.5$. The parameters ${\rho }_i=0.2$ for $i=1,2,3,4$ and $\epsilon =0.1$.

Case 1: The event-triggered sliding mode control law (21) and (28) without adaptive law (29).

Consider $c_{ij}=0.5,i,j=1,2,3,4$. By the results of this study, there exists a positive constant $l_{max}=3.1$ such that the condition (36) holds. The condition (36) is guaranteed by Theorem 2. Then, states of all agents can be shown to converge to some bounded constant by the proposed the event-triggered sliding mode control law (21) and (28).

Consider the following initial states of the system: for $x_{i1}\left(0\right)={\left[\begin{array}{cccc}1.4& 4& -0.8& -3.6\end{array}\right]}^T$, $x_{i2}\left(0\right)={\left[\begin{array}{cccc}-1.3& -3& 2& 3.1\end{array}\right]}^T$. Using the above initial conditions and parameters of the system controller, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 shows the results of the numerical simulation. Figure 2 and Figure 3 show that all states of the controlled fractional-order agents are bounded and converge to $-0.9$ and 1, respectively, which implies that Theorem 1 holds. Moreover, as shown in Figure 4 and Figure 5, all control input signals of the fractional-order agents are bounded. Sliding mode surfaces $s_i\left(t\right)$ for agent are presented in Figure 6. The event release instants and release intervals are given in Figure 7.

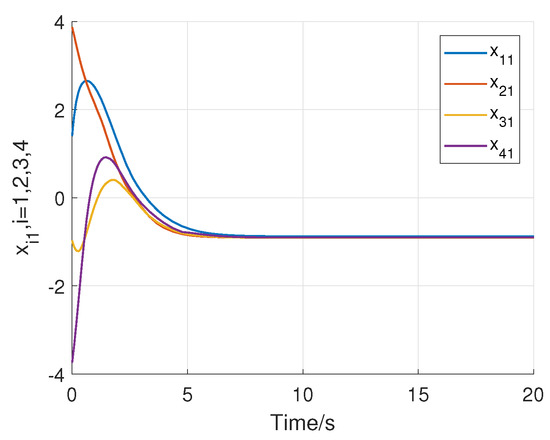
Figure 2. Trajectories of the state $x_{i1}$ of the controlled fractional-order agents.

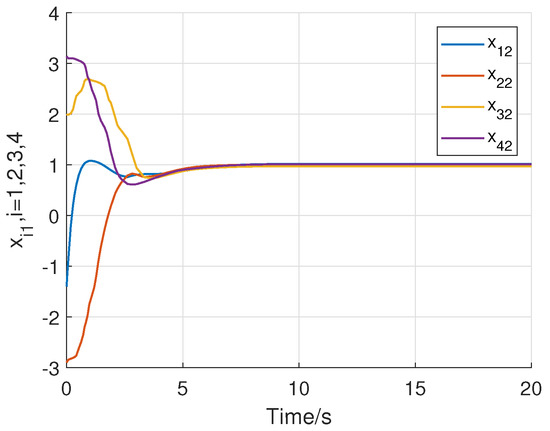
Figure 3. Trajectories of the state $x_{i2}$ of the controlled fractional-order agents.

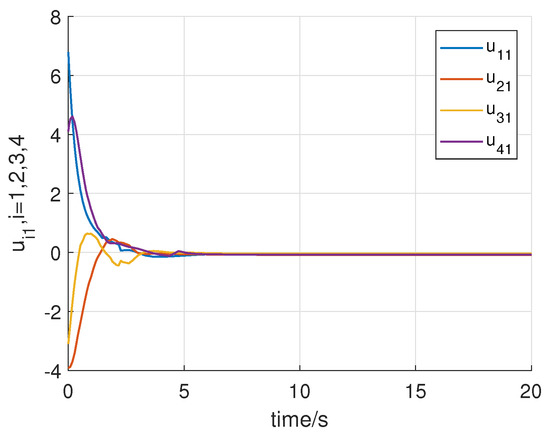
Figure 4. Trajectories of the input signals $u_{i1}$.

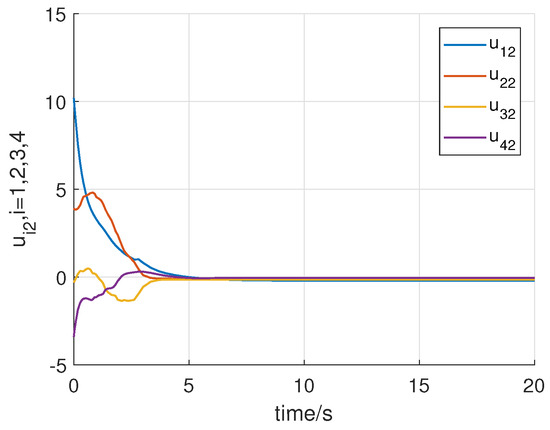
Figure 5. Trajectories of the input signals $u_{i2}$.

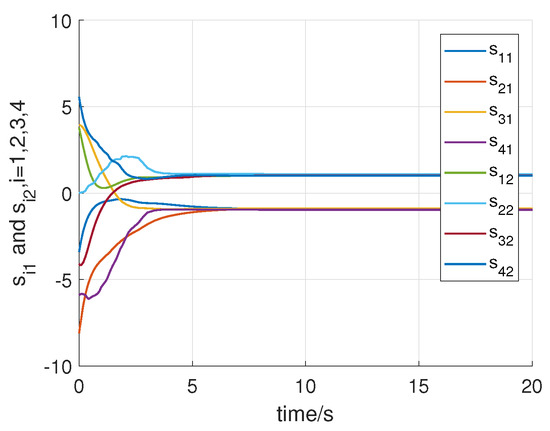
Figure 6. Trajectories of the sliding surface $s_i$.

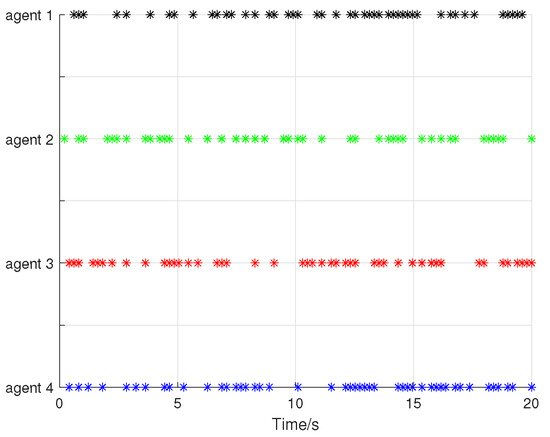
Figure 7. The release instants and release interval.

Case 2: The event-triggered sliding mode control law (21) and (28) with adaptive law (29).

Let $P=\left[\begin{array}{cc}0.2& 0.1\\ 0.1& 0.2\end{array}\right]$. It is easy to verify that conditions (51) and (52) are satisfied, which implies that Theorem 3 holds. Therefore, The event-triggered sliding mode control laws (21) and (28) with the adaptive law (29) are applied to guarantee that states of all agents converge to some bounded constant.

Consider the following initial states of the system: for $x_{i1}\left(0\right)={\left[\begin{array}{cccc}1.1& 3.7& -1.1& -4\end{array}\right]}^T$, $x_{i2}\left(0\right)={\left[\begin{array}{cccc}-1.4& -3& 2& 3.03\end{array}\right]}^T$. Using the above initial conditions and system controller parameters, the numerical simulation results are shown in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14. Figure 8 and Figure 9 show that all states of the controlled fractional-order agents are bounded and converge to $-0.9$ and 1, respectively. Nevertheless, the event-triggered sliding mode control law with the adaptive law (29) converge faster than the without the adaptive law by comparing with the Case 1. Similarly, Figure 10, Figure 11 and Figure 12 show that all control inputs and the adaptive paremeter $c_{ij}$ are bounded. Sliding mode surfaces $s_i\left(t\right)$ for agent are presented in Figure 13. The event release instants and release intervals are given in Figure 14.

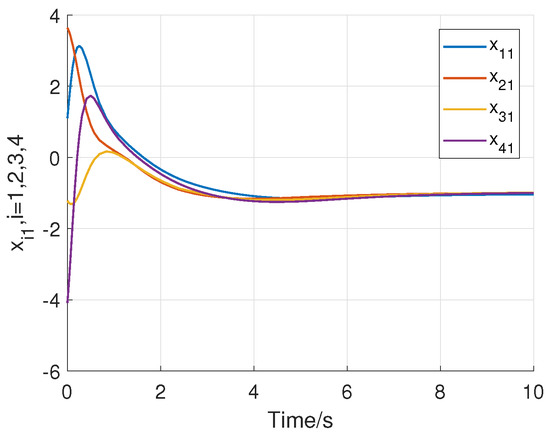
Figure 8. Trajectories of the state $x_{i1}$ of the controlled fractional-order agents with the adaptive law (29).

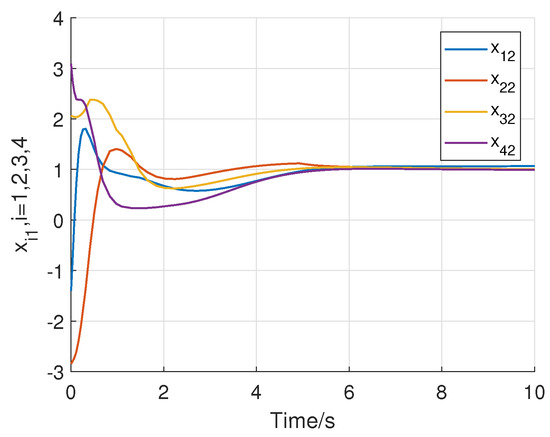
Figure 9. Trajectories of the state $x_{i2}$ of the controlled fractional-order agents with the adaptive law (29).

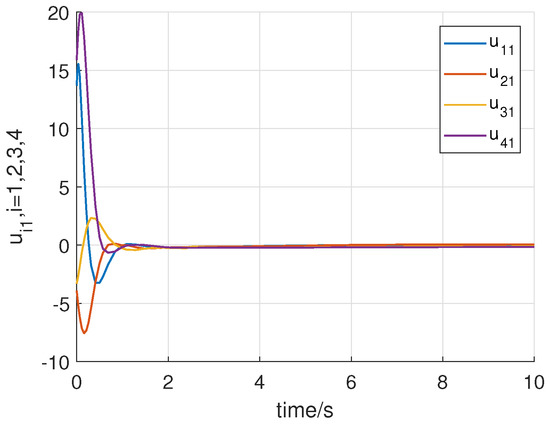
Figure 10. Trajectories of the control input $u_{i2}$ with the adaptive law (29).

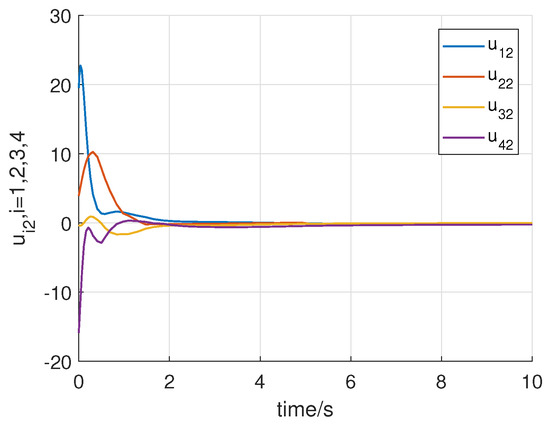
Figure 11. Trajectories of the control input $u_{i2}$ with the adaptive law (29).

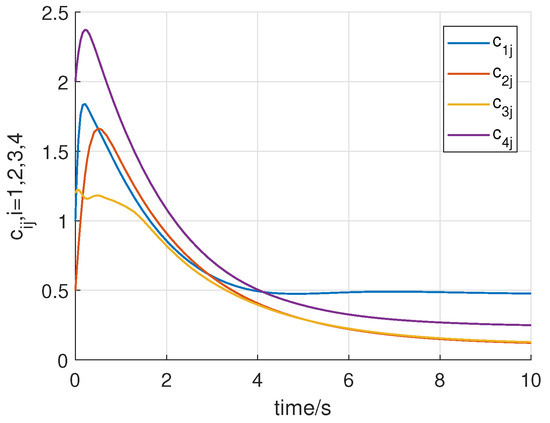
Figure 12. Trajectories of the adaptive law (29).

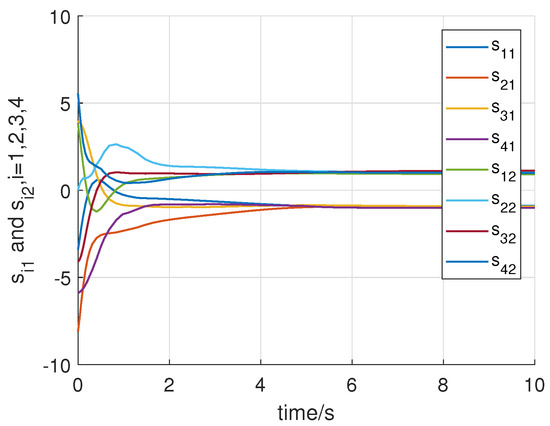
Figure 13. Trajectories of the sliding surface $s_i$.

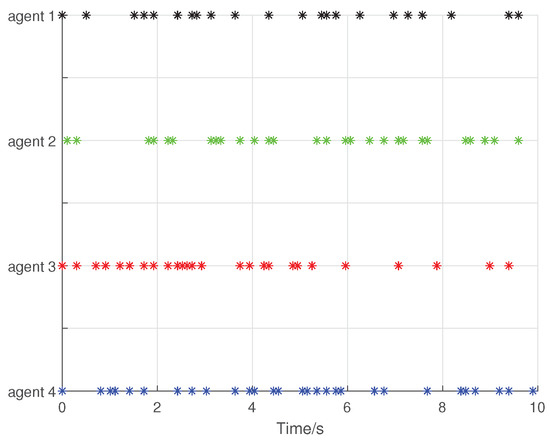
Figure 14. The release instants and release interval.

5. Conclusions

In this study, the state consensus problem of the nonlinear FOMASs has been addressed by using the dynamic event-triggered sliding mode control method. To solve this problem, a novel framework of event-triggered sliding mode control has been proposed, composed of event-triggered sliding mode controllers and auxiliary switching functions. In addition, the asymptotic consensus property and Zeno-free behavior are guaranteed simultaneously. Then, the network occupation has been reduced and distributed event-triggered sliding mode controllers without real-time information of agent have been designed to confine the state trajectories of all agents to the sliding region. Meantime, an auxiliary distributed switching functions have removed the requirements of continuous states among agents, and the stability of closed-loop FOMASs has been established by the Lyapunov theory. Finally, the application of the proposed method to a numerical example has been developed.

In the future, the problem of dynamic self-triggered sliding mode control for more complex nonlinear systems. For example, in the case of dynamic self-triggered sliding mode control under switching structure situations, the asymptotic stability and Zero-free behavior aspects of such issues are difficult to demonstrate, because of the difficulty of the switching structure analysis.