Event-Triggered Distributed Sliding Mode Control of Fractional-Order Nonlinear Multi-Agent Systems
Abstract
1. Introduction
- (1)
- In contrast with earlier studies in [45], the system considered in this paper can be adapted to more complex scenarios. In addition, a fractional-order distributed coordinator framework with adaptive capacity are designed based on the event-triggered sliding mode control.
- (2)
- To overcome difficulties in distributed sliding control, different from [44], an auxiliary sliding mode function is constructed without sustaining communication among agents, which makes distributed event-triggered sliding mode control laws only receive signals at triggering instants, such that the use of communication resources is saved.
- (3)
- Compared with the previously reported approach in [31], the novel fractional-order adaptive law is proposed to ensure that the convergence speed of the agent and robustness. Moreover, the nonlinear fractional-order stability theory is applied to guarantee the achievement of the distributed consensus objective.
2. Preliminaries
2.1. Graph Theory
2.2. Gaputo Fractional Derivative
2.3. Problem Formulation
3. Main Results
3.1. Dynamic Event-Triggered Communication Scheme
3.2. Sliding Surface Design
3.3. Design of Adaptive Distributed Controller
3.4. Stability Analysis
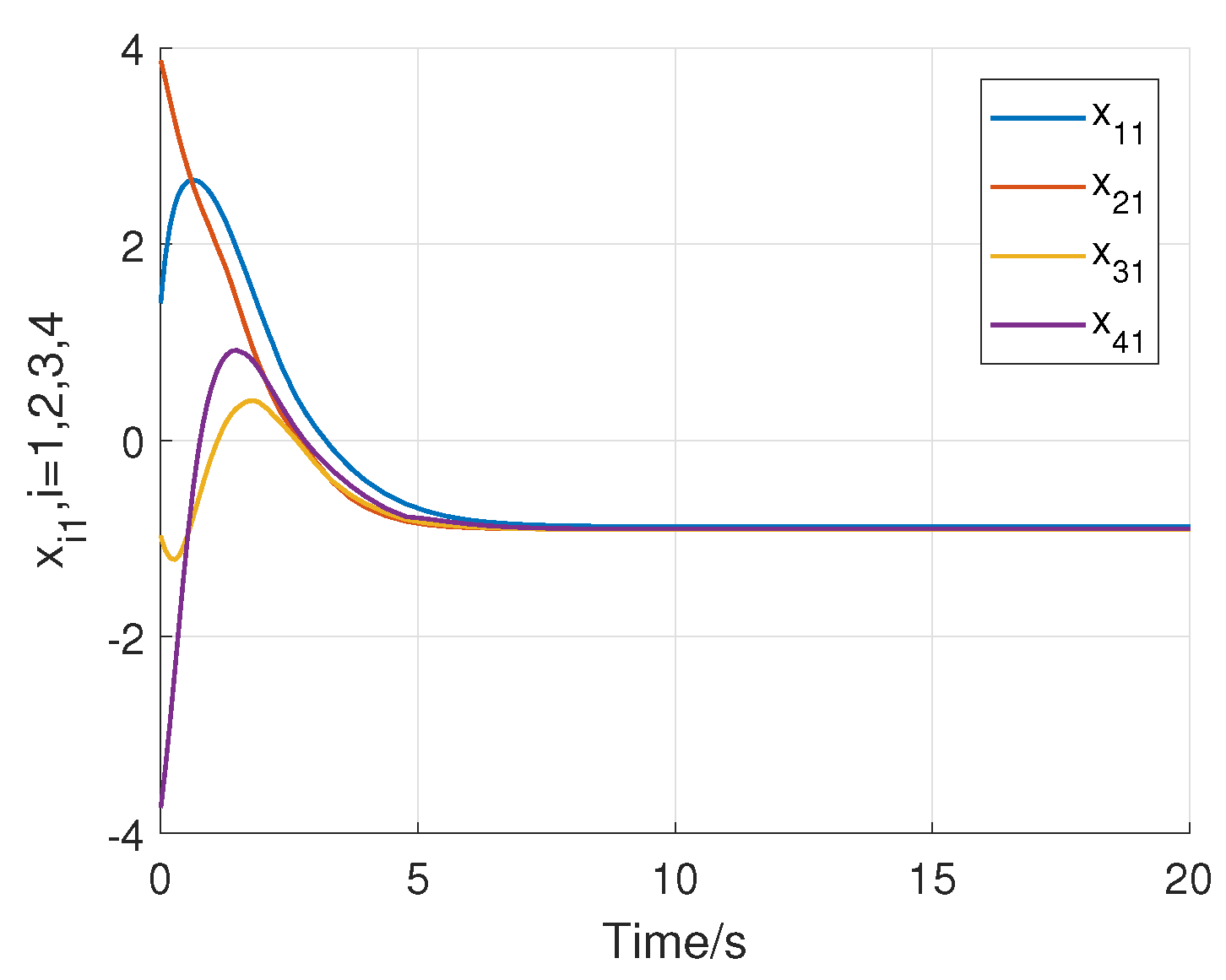
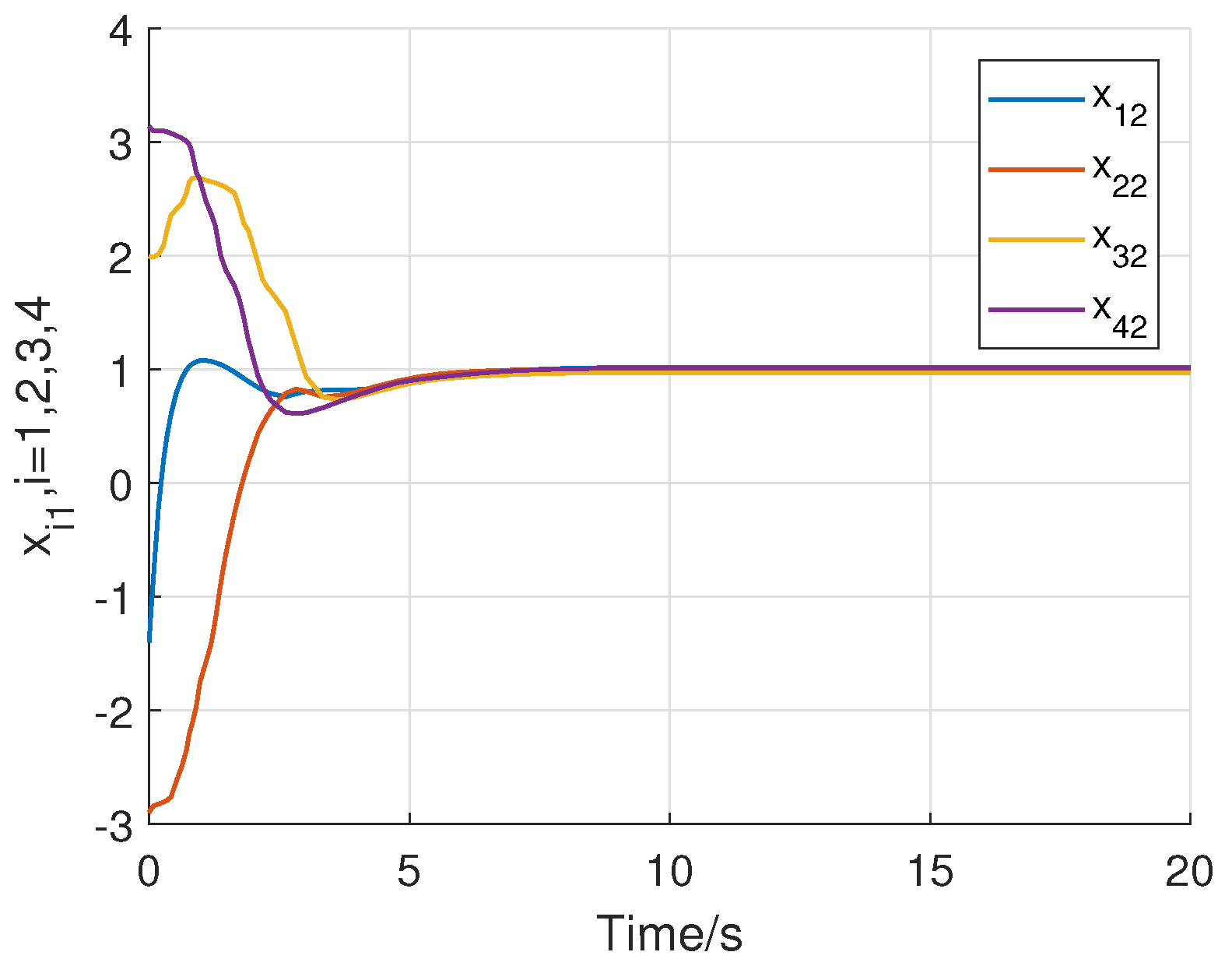
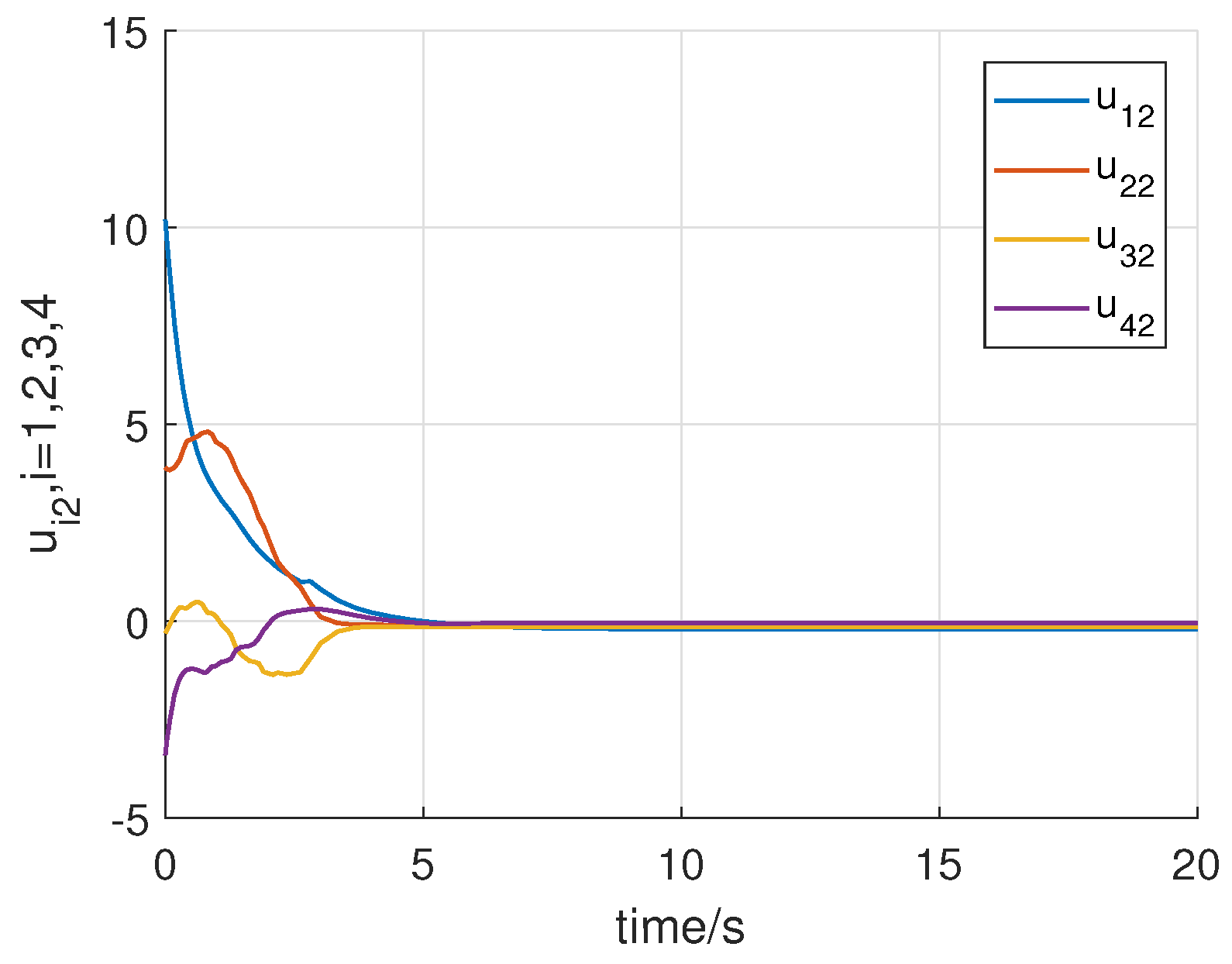
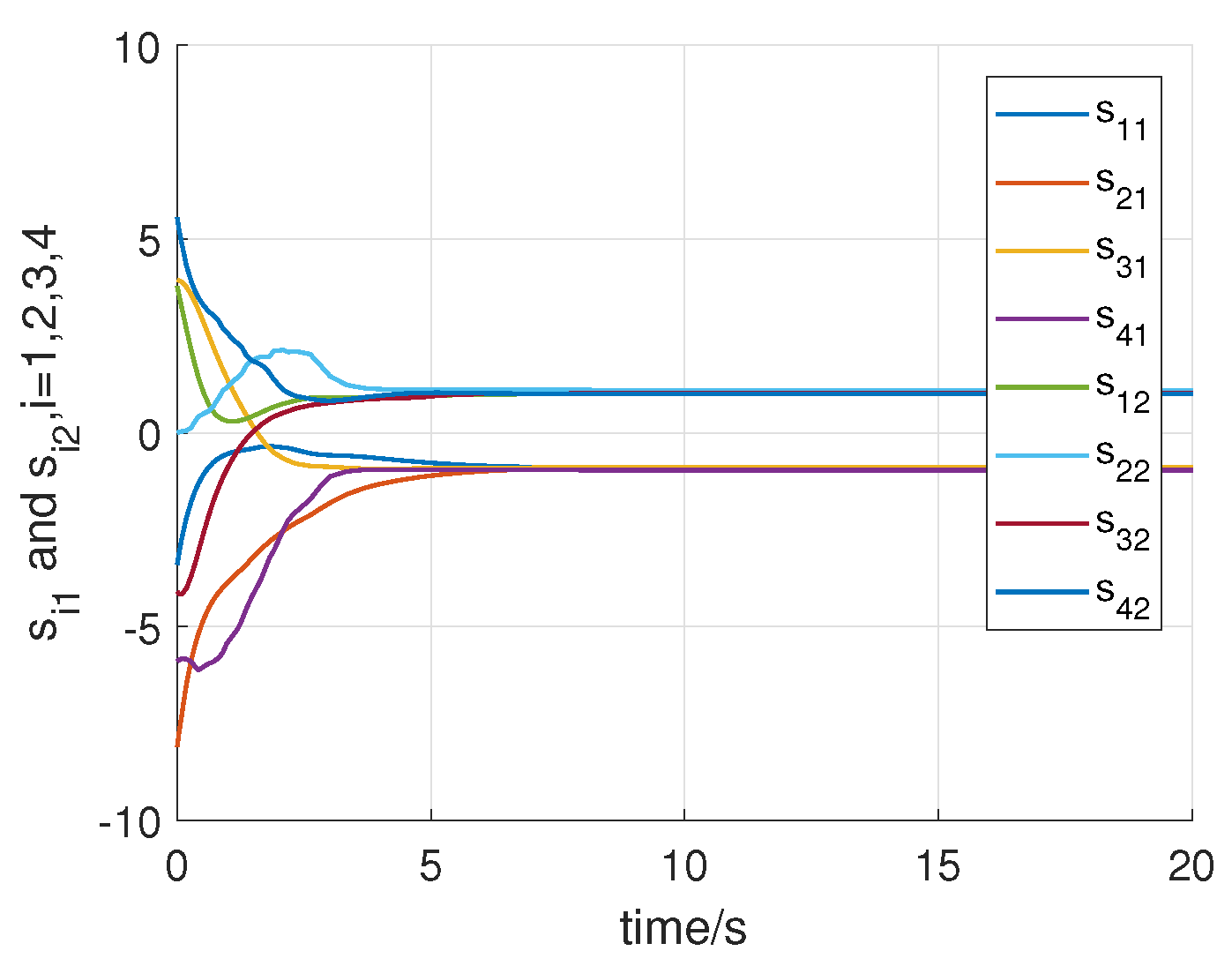
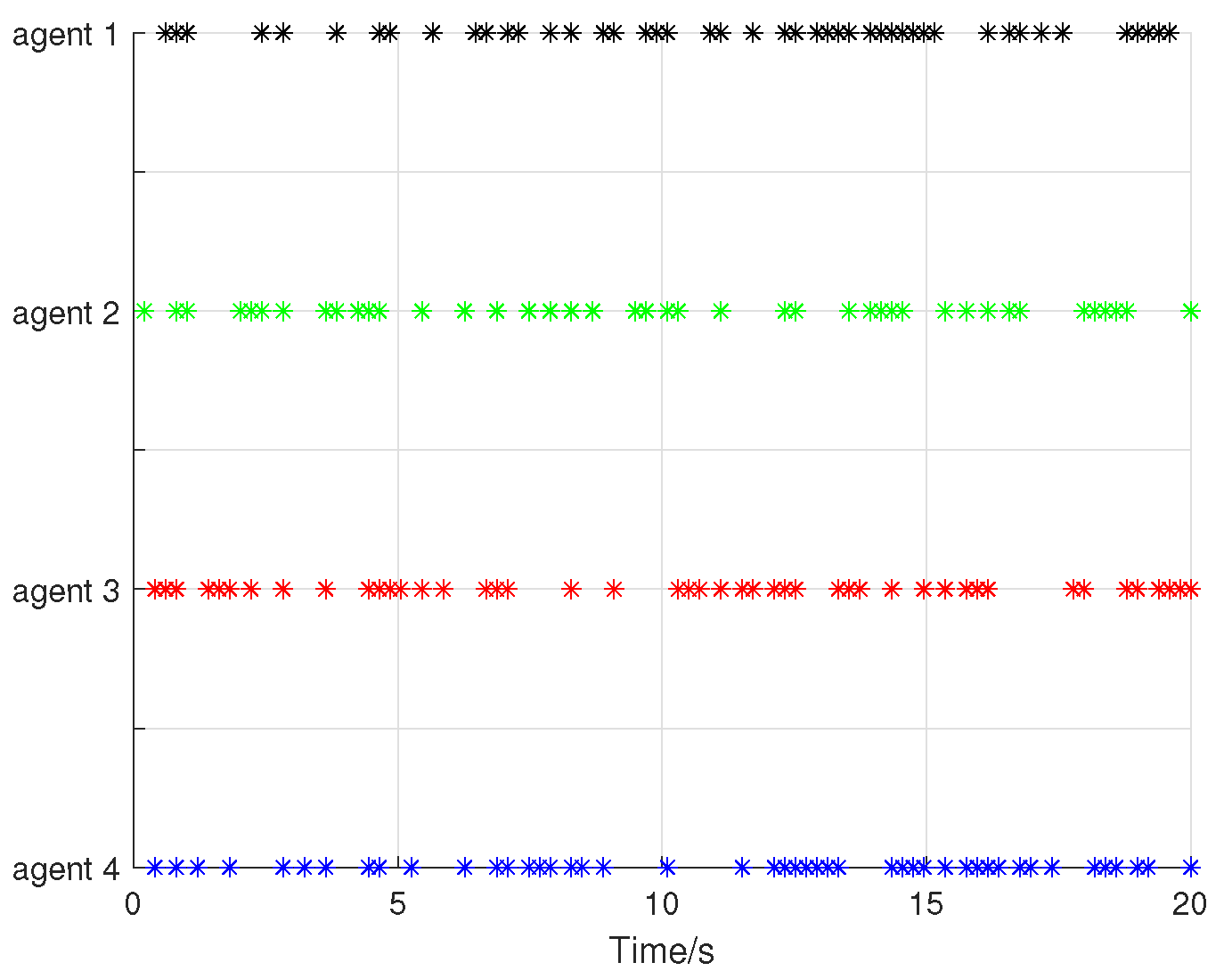
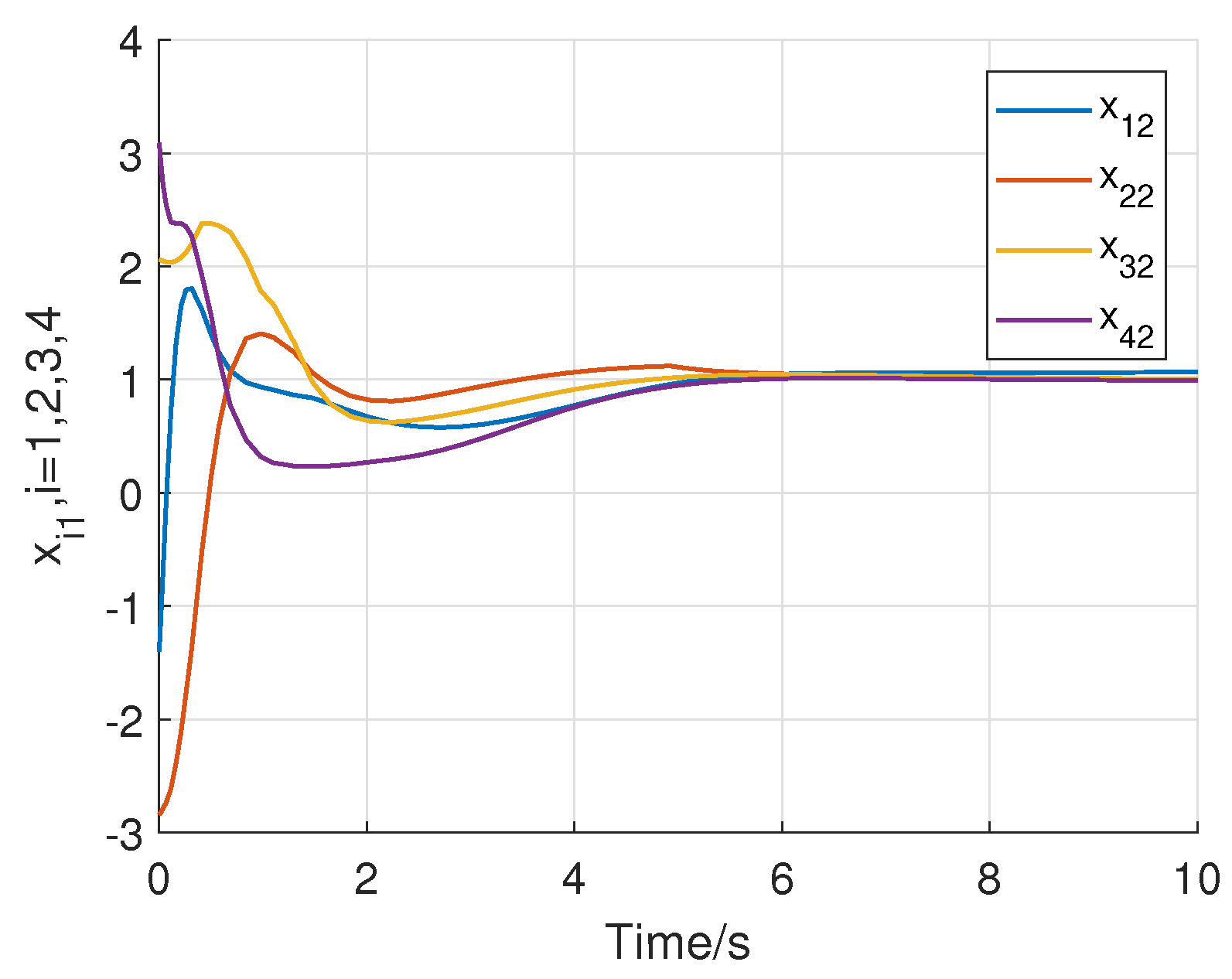
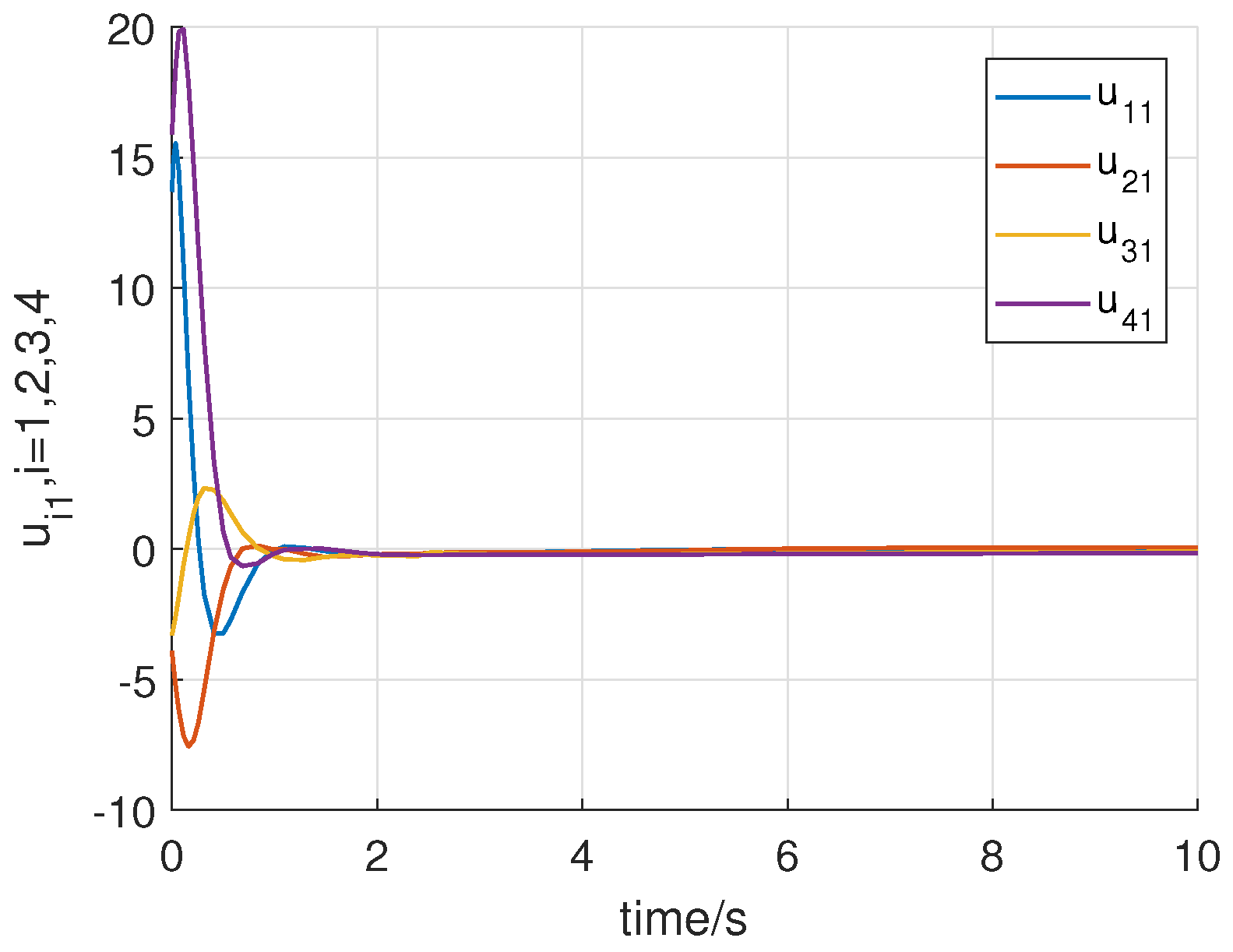
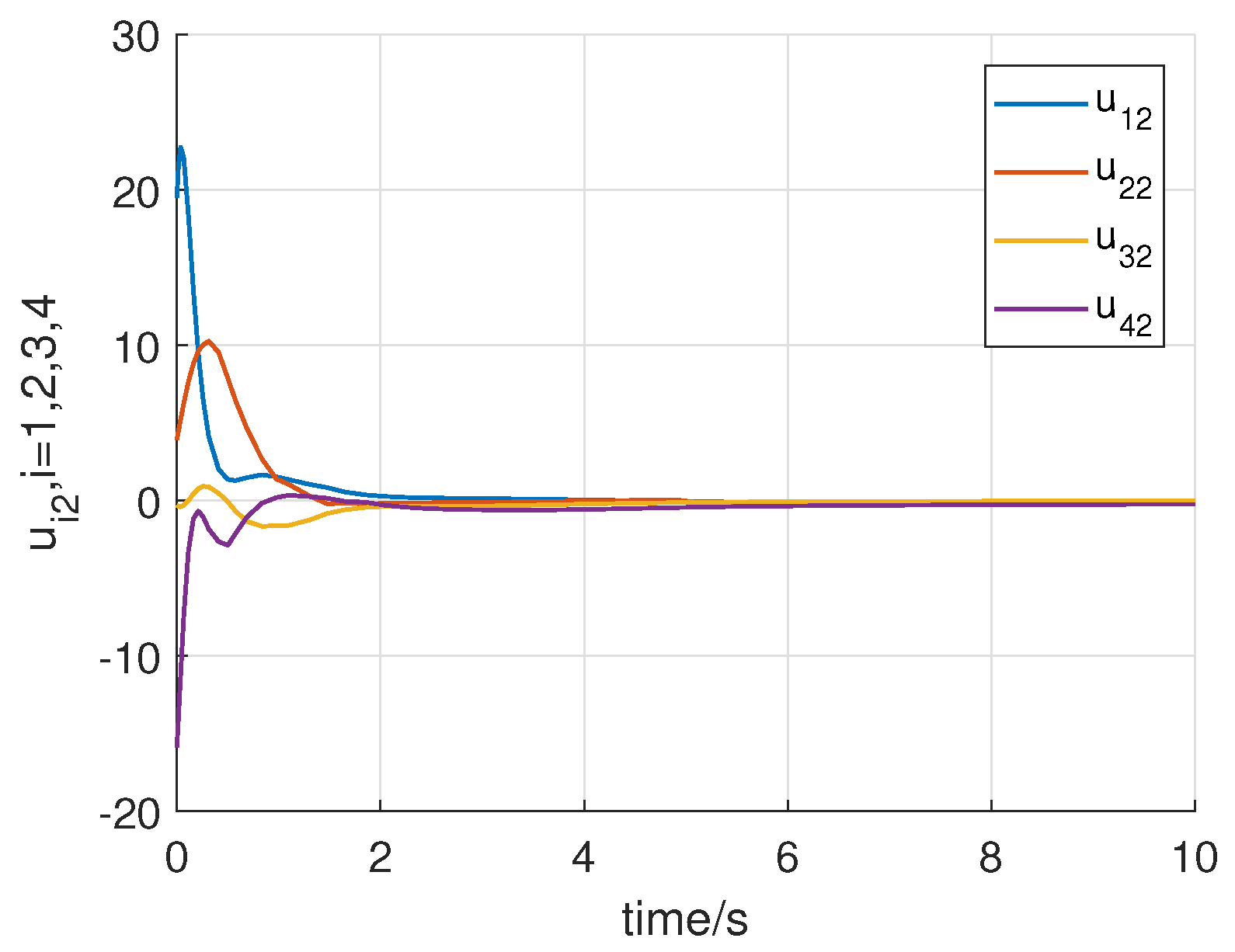
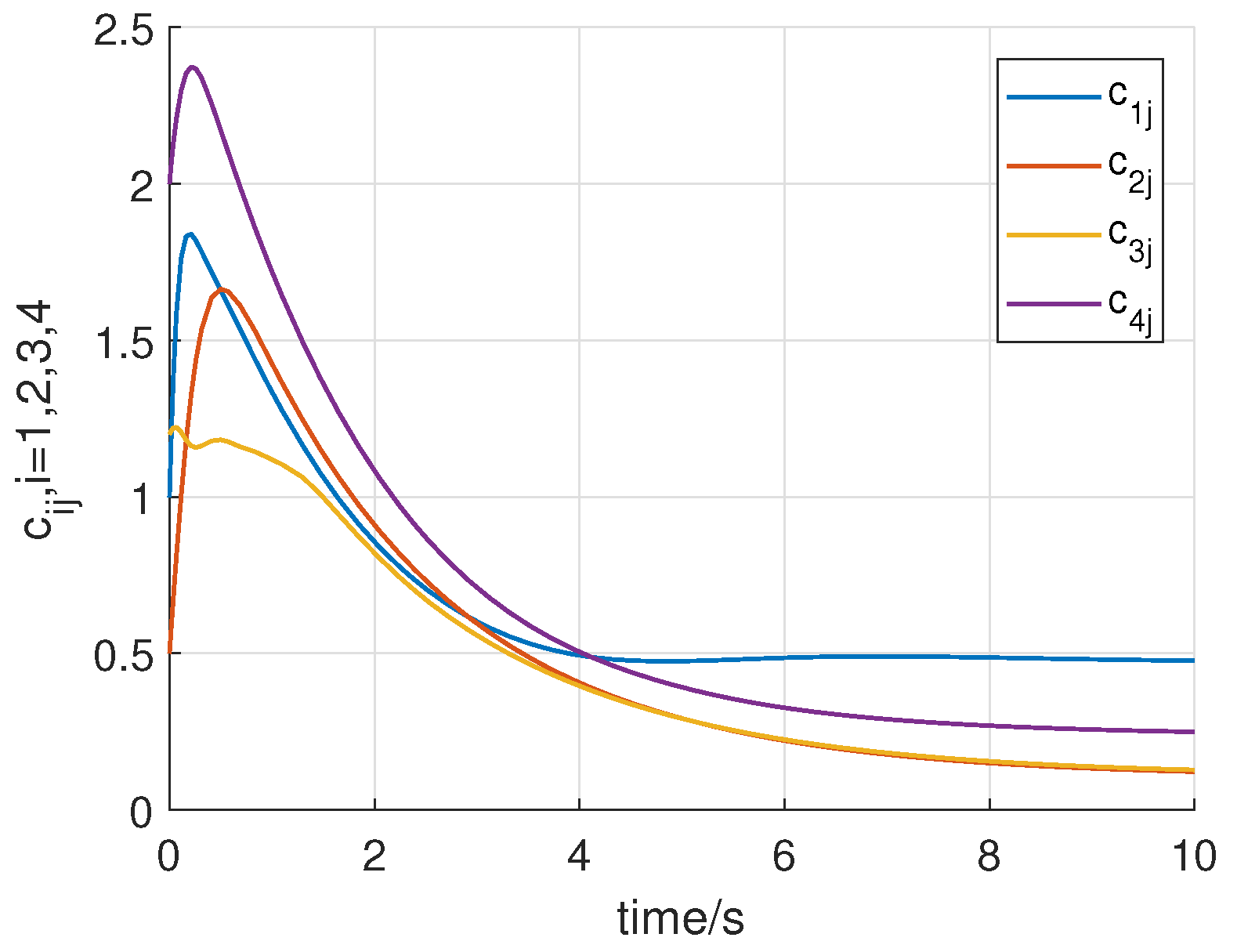
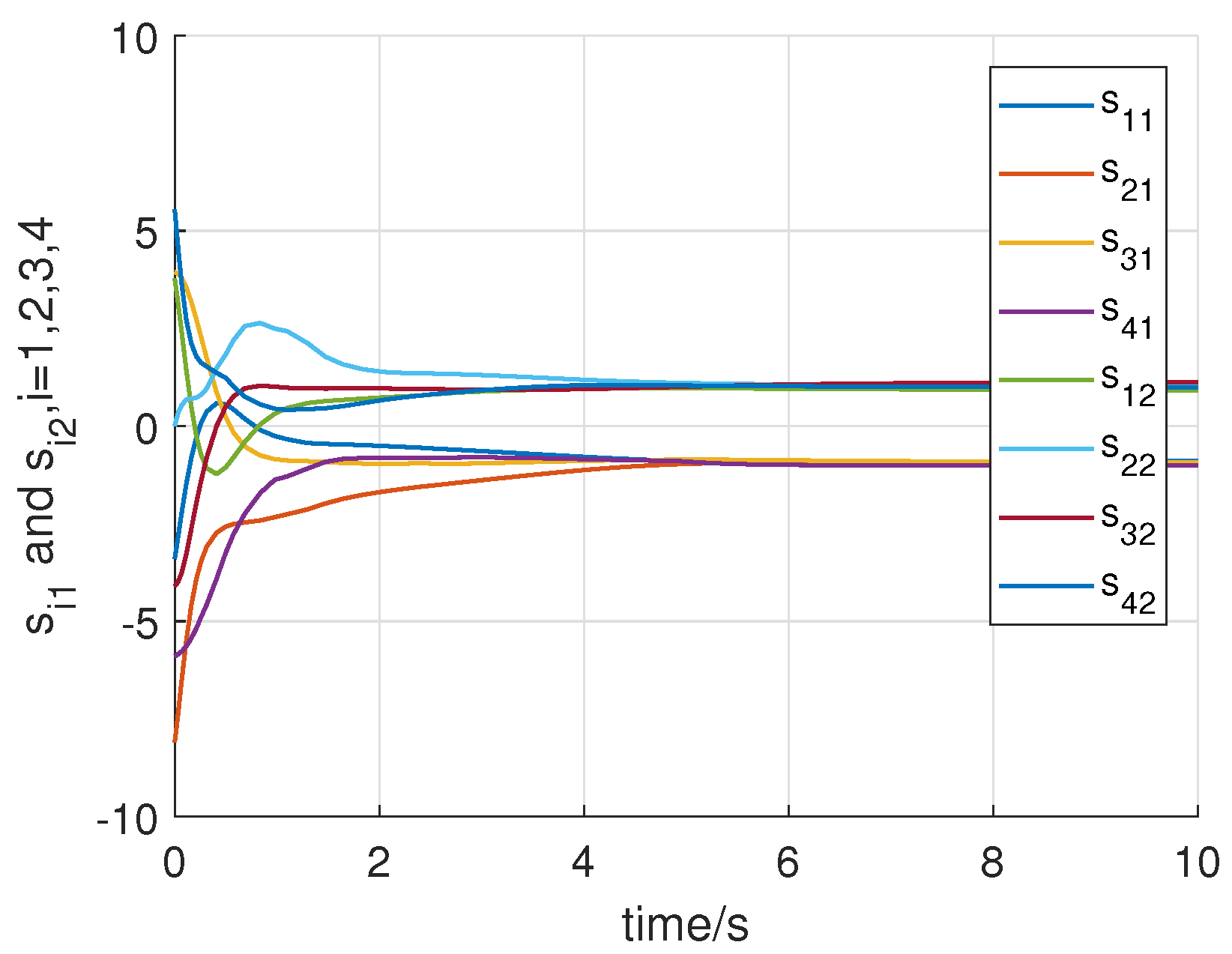
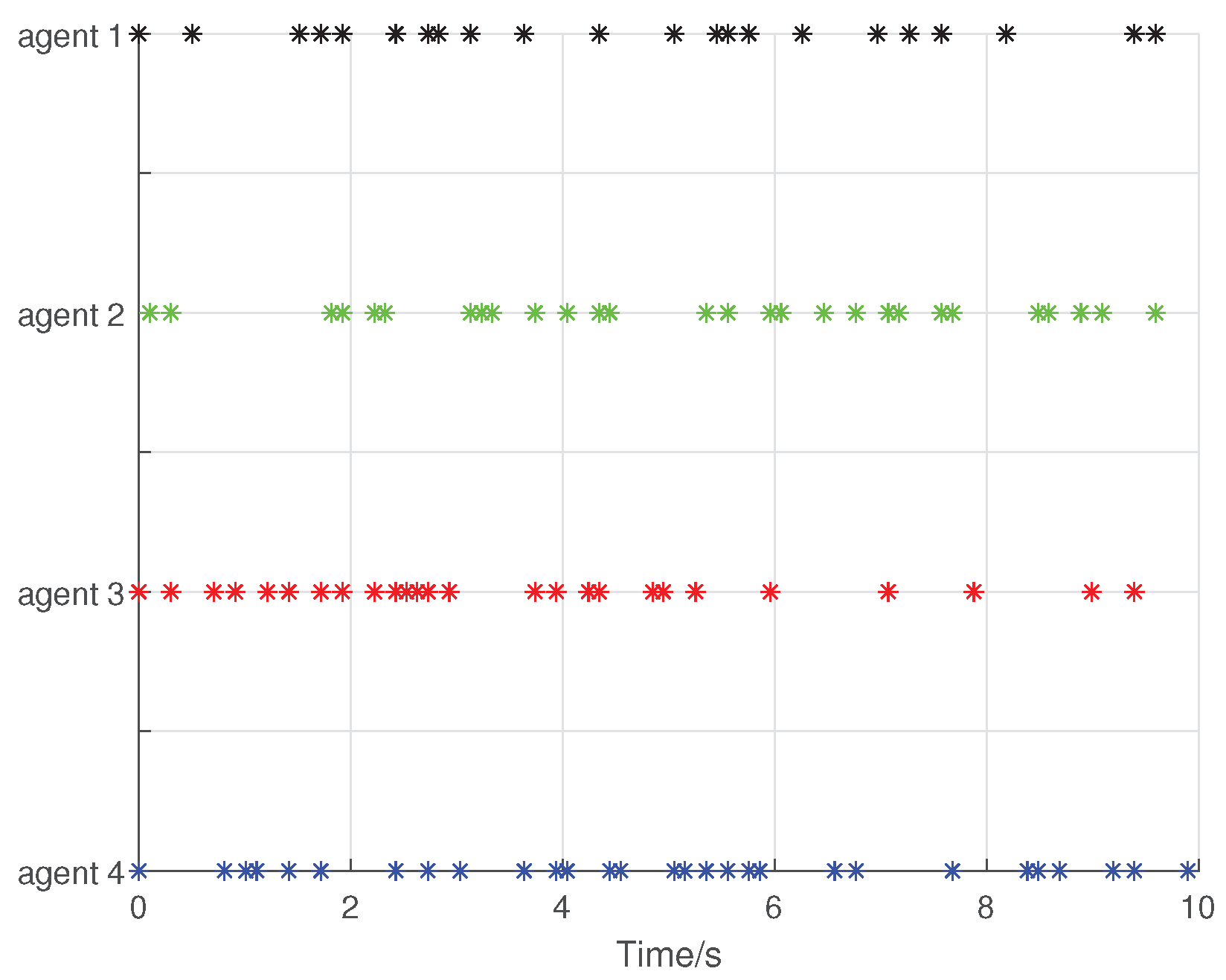
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, T.; Liu, H.; Yao, Y.; Li, T.; Cheng, Z. Distributed adaptive formation tracking control under fixed and switching topologies: Application on general linear multi-agent systems. Symmetry 2020, 16, 941. [Google Scholar] [CrossRef]
- Hong, Y.G.; Hu, J.; Gao, L. Tracking control for multi-agent consensus with an active leader and variable topology. Automatica 2006, 42, 1177–1182. [Google Scholar] [CrossRef]
- Wang, X.L.; Hong, Y.G.; Huang, J.; Jiang, Z.-P. A distributed control approach to robust output regulation of networked linear systems. IEEE Trans. Autom. Control. 2010, 55, 2891–2895. [Google Scholar] [CrossRef]
- Sharf, M.; Zelazo, D. Analysis and synthesis of MIMO multi-agent systems using network optimization. IEEE Trans. Autom. Control. 2019, 64, 4512–4524. [Google Scholar] [CrossRef]
- Jin, Z.H.; Wang, Z.X.; Zhang, X.F. Cooperative control problem of Takagi-Sugeno fuzzy multiagent systems via observer based distributed adaptive sliding mode control. J. Frankl. Inst. 2022, 359, 3405–3426. [Google Scholar] [CrossRef]
- Jin, X.Z.; Wang, S.F.; Qin, J.H.; Zheng, W.X.; Kang, Y. Adaptive fault-tolerant consensus for a class of uncertain nonlinear second-order multi-agent systems with circuit implementation. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 2243–2255. [Google Scholar] [CrossRef]
- Lewis, F.L.; Cui, B.; Ma, T.; Song, Y.D.; Zhao, C.H. Heterogeneous multi-agent systems: Reduced-order synchronization and geometry. IEEE Trans. Autom. Control. 2016, 61, 1391–1396. [Google Scholar] [CrossRef]
- Jin, Z.H.; Qin, Z.Y.; Zhang, X.F.; Guan, C. A Leader-following consensus problem via a distributed observer and fuzzy input-to-output small-gain theorem. IEEE Trans. Control. Netw. Syst. 2022, 9, 62–74. [Google Scholar] [CrossRef]
- Rawad, A.; Sultan, A. A fast non-linear symmetry approach for guaranteed consensus in network of multi-agent systems. Symmetry 2020, 12, 1692. [Google Scholar]
- Mei, J.; Ren, W.; Li, B.; Ma, G.F. Distributed containment control for multiple unknown second-order nonlinear systems with application to networked Lagrangian systems. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1885–1899. [Google Scholar] [CrossRef]
- Lu, M.; Huang, J. Cooperative global robust output regulation for a class of nonlinear multi-agent systems with a nonlinear leader. IEEE Trans. Autom. Control. 2016, 61, 3557–3562. [Google Scholar] [CrossRef]
- Liu, J.; Liu, D.Y.; Boutat, D.; Zhang, X.F.; Wu, Z.H. Innovative non-asymptotic and robust estimation method using auxiliary modulating dynamical systems. Automatica 2023, 152, 110953. [Google Scholar] [CrossRef]
- Zhang, H.; Lewis, F.L. Adaptive cooperative tracking control of higher-order nonlinear systems with unknown dynamics. Automatica 2012, 48, 1432–1439. [Google Scholar] [CrossRef]
- Su, H.S.; Chen, G.R.; Wang, X.F.; Lin, Z.L. Adaptive second-order consensus of networked mobile agents with nonlinear dynamics. Automatica 2011, 47, 368–375. [Google Scholar] [CrossRef]
- Jin, Z.H.; Wang, Z.X. Input-to-state stability of the nonlinear singular systems via small-gain theorem. Appl. Math. Comput. 2021, 402, 126171. [Google Scholar] [CrossRef]
- Jin, Z.H.; Wang, Z.X.; Li, J.W. Input-to-state stability of the nonlinear fuzzy systems via small-gain theorem and decentralized sliding-mode control. IEEE Trans. Fuzzy Syst. 2022, 30, 2993–3008. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z.H.; Zhang, Q.L. Impulse elimination of the Takagi–Sugeno fuzzy singular system via sliding-mode control. IEEE Trans. Fuzzy Syst. 2022, 30, 1164–1174. [Google Scholar] [CrossRef]
- Zhang, J.-X.; Yang, G.-H. Robust adaptive fault-tolerant control for a class of unknown nonlinear systems. IEEE Trans. Ind. Electron. 2017, 64, 585–594. [Google Scholar] [CrossRef]
- Lu, Y.; Liao, F.; Deng, J.; Pattinson, C. Cooperative optimal preview tracking for linear descriptor multi-agent systems. J. Frankl. Inst. 2019, 356, 908–934. [Google Scholar] [CrossRef]
- Cao, Y.; Li, Y.; Ren, W.; Chen, Y. Distributed coordination of networked fractional-order systems. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2009, 40, 362–370. [Google Scholar]
- Akram, T.; Abbas, M.; Ali, A.; Iqbal, A.; Baleanu, D. A numerical approach of a time fractional reaction–diffusion model with a non-singular kernel. Symmetry 2020, 12, 1653. [Google Scholar] [CrossRef]
- Zhang, X.F. Relationship between integer order systems and fractional order systems and its two applications. IEEE-CAA J. Autom. Sin. 2018, 5, 539–643. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, J.X.; Zhang, X.F. Injected infrared and visible image fusion via L1 decomposition model and guided filtering. IEEE Trans. Comput. Imaging 2022, 8, 162–173. [Google Scholar] [CrossRef]
- Trigeassou, J.; Maamri, N.; Sabatier, J.; Oustaloup, A. A Lyapunov approach to the stability of fractional differential equations. Signal Process. 2011, 91, 437–445. [Google Scholar] [CrossRef]
- Li, C.P.; Zhang, F.R. A survey on the stability of fractional differential equations. Eur. Phys. J. Spec. Top. 2011, 193, 27–47. [Google Scholar] [CrossRef]
- Gallegos, J.; Duarte-Mermoud, M. On the Lyapunov theory for fractional order systems. Appl. Math. Comput. 2016, 287, 161–170. [Google Scholar] [CrossRef]
- Zhang, X.F.; Boutat, D.; Liu, D.Y. Applications of fractional operator in image processing and stability of control systems. Fractal Fract 2023, 7, 359. [Google Scholar] [CrossRef]
- Shen, J.W.; Cao, J.D.; Lu, J.Q. Consensus of fractional-order systems with non-uniform input and communication delays. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2012, 226, 271–283. [Google Scholar] [CrossRef]
- Yin, X.X.; Hu, S.L. Consensus of fractional-order uncertain multi-agent systems based on output feedback. Asian J. Control. 2013, 15, 1538–1542. [Google Scholar] [CrossRef]
- Wang, J.W.; Xiong, X.H. A general fractional-order dynamical network: Synchronization behavior and state tuning. Chaos 2012, 22, 362–370. [Google Scholar] [CrossRef]
- Yu, Z.Y.; Jiang, H.J.; Hu, C. Leader-following consensus of fractional-order multi-agent systems under fixed topology. Neurocomputing 2015, 149, 613–620. [Google Scholar] [CrossRef]
- Yu, Z.Y.; Jiang, H.J.; Hu, C.; Yu, J. Leader-following consensus of fractional-order multi-agent systems via adaptive pinning control. Int. J. Control. 2015, 88, 1746–1756. [Google Scholar] [CrossRef]
- Chen, J.; Guan, Z.H.; Li, T.; Zhang, D.X.; Ge, M.F.; Zheng, D.F. Multiconsensus of fractional-order uncertain multi-agent systems. Neurocomputing 2015, 149, 698–705. [Google Scholar] [CrossRef]
- Chen, J.; Guan, Z.H.; Yang, C.; Li, T.; He, D.X.; Ge, M.F.; Zhang, X.H. Distributed containment control of fractional-order uncertain multi-agent systems. J. Frankl. Inst. 2016, 353, 1672–1688. [Google Scholar] [CrossRef]
- Ackermann, J.; Utkin, V. Sliding mode control design based on Ackermann’s formula. IEEE Trans. Autom. Control. 1998, 43, 234–237. [Google Scholar] [CrossRef]
- Niu, Y.; Ho, D.W.C.; Lam, J. Robust integral sliding mode control for uncertain stochastic systems with time-varying delay. Automatica 2005, 41, 873–880. [Google Scholar] [CrossRef]
- Jin, Z.H.; Li, J.W.; Wang, Z.X. Input-to-state stability and sliding mode control of the nonlinear singularly perturbed systems via trajectory-based small-gain theorem. Nonlinear Anal. Hybrid Syst. 2022, 44, 101175. [Google Scholar] [CrossRef]
- Kavikumar, R.; Kwon, O.-M.; Lee, S.-H.; Lee, S.; Sakthivel, R. Event-triggered input–output finite-time stabilization for IT2 fuzzy systems under deception attacks. IEEE Trans. Fuzzy Syst. 2023, 31, 1139–1151. [Google Scholar] [CrossRef]
- Kavikumar, R.; Kwon, O.-M.; Lee, S.-H. Input-output finite-time IT2 fuzzy dynamic sliding mode control for fractional-order nonlinear systems. Nonlinear Dyn. 2022, 108, 3745–3760. [Google Scholar] [CrossRef]
- Nair, R.R.; Behera, L.; Kumar, S. Event-triggered finite-time integral sliding mode controller for consensus-based formation of multirobot systems with disturbances. IEEE Trans. Control. Syst. Technol. 2019, 27, 39–47. [Google Scholar] [CrossRef]
- Wu, X.; Mu, X. New design on distributed event-based sliding mode controller for disturbed second-order multi-agent systems. IEEE Trans. Autom. Control. 2022, 67, 2590–2596. [Google Scholar] [CrossRef]
- Jeong, J.; Lim, Y.; Parivallal, A. An asymmetric Lyapunov-Krasovskii functional approach for event-triggered consensus of multi-agent systems with deception attacks. Appl. Math. Comput. 2023, 439, 127584. [Google Scholar] [CrossRef]
- Parivallal, A.; Sakthivel, R.; Wang, C. Guaranteed cost leaderless consensus for uncertain Markov jumping multi-agent systems. J. Exp. Theor. Artif. Intell. 2023, 35, 257–273. [Google Scholar] [CrossRef]
- Yao, D.; Li, H.; Lu, R.; Shi, Y. Distributed sliding-mode tracking control of second-order nonlinear multiagent systems: An event-triggered approach. IEEE Trans. Cybern. 2020, 50, 3892–3902. [Google Scholar] [CrossRef]
- Li, Z.T.; Gao, L.X.; Chen, W.H.; Xu, Y. Distributed adaptive cooperative tracking of uncertain nonlinear fractional-order multi-agent systems. IEEE/CAA J. Autom. Sin. 2020, 7, 292–300. [Google Scholar] [CrossRef]
- Liu, T.F.; Qin, Z.Y.; Hong, Y.G.; Jiang, Z.-P. Distributed optimization of nonlinear multi-agent systems: A small-gain approach. IEEE Trans. Autom. Control. 2022, 67, 676–691. [Google Scholar] [CrossRef]
- Jin, Z.H.; Sun, X.J.; Qin, Z.Y.; Ahn, C.K. Fuzzy small-gain approach for the distributed optimization of T-S fuzzy cyber–physical systems. IEEE Trans. Cybern. 2022. Early Access. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.H.; Ahn, C.K.; Li, J.W. Momentum-based distributed continuous-time nonconvex optimization of nonlinear multi-agent systems via timescale separation. IEEE Trans. Netw. Sci. Eng. 2022, 10, 980–989. [Google Scholar] [CrossRef]
- Li, R.C.; Zhang, X.F. Adaptive sliding mode observer design for a class of T–S fuzzy descriptor fractional order systems. IEEE Trans. Fuzzy Syst. 2019, 28, 1951–1960. [Google Scholar] [CrossRef]
- Yang, X.J.; Li, C.D.; Song, Q.K.; Chen, J.Y.; Huang, J.J. Input-to-state stability of the nonlinear fuzzy systems via small-gain theorem and decentralized sliding-mode control. IEEE Trans. Cybern. 2018, 105, 88–103. [Google Scholar]
- Song, Q.; Liu, F.; Cao, J.D.; Yu, W.W. Pinning-controllability analysis of complex networks: An M-matrix approach. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 2692–2701. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, J. A Zeno-free event-triggered control strategy for asymptotic stabilization of switched affine systems. IEEE Trans. Autom. Control 2022, 67, 5509–5516. [Google Scholar] [CrossRef]
- Ye, Y.; Su, H.; Chen, J.; Peng, Y. Consensus in Fractional-Order Multi-Agent Systems With Intermittence Sampled Data Over Directed Networks. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 365–369. [Google Scholar] [CrossRef]
- Yang, H.; Wang, F.; Han, F. Containment Control of Fractional Order Multi-Agent Systems With Time Delays. IEEE/CAA J. Autom. Sin. 2018, 5, 727–732. [Google Scholar]
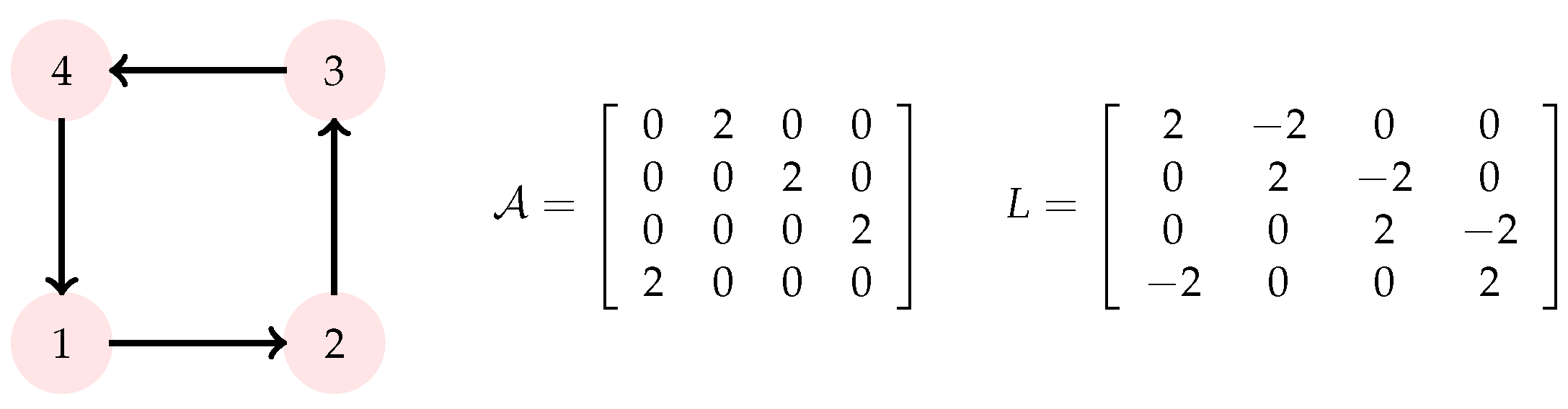


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Y.; Xu, Y.; Liu, G.; Jin, Z.; Li, H. Event-Triggered Distributed Sliding Mode Control of Fractional-Order Nonlinear Multi-Agent Systems. Symmetry 2023, 15, 1247. https://doi.org/10.3390/sym15061247
Jin Y, Xu Y, Liu G, Jin Z, Li H. Event-Triggered Distributed Sliding Mode Control of Fractional-Order Nonlinear Multi-Agent Systems. Symmetry. 2023; 15(6):1247. https://doi.org/10.3390/sym15061247
Chicago/Turabian StyleJin, Yi, Yan Xu, Gang Liu, Zhenghong Jin, and Huanhuan Li. 2023. "Event-Triggered Distributed Sliding Mode Control of Fractional-Order Nonlinear Multi-Agent Systems" Symmetry 15, no. 6: 1247. https://doi.org/10.3390/sym15061247
APA StyleJin, Y., Xu, Y., Liu, G., Jin, Z., & Li, H. (2023). Event-Triggered Distributed Sliding Mode Control of Fractional-Order Nonlinear Multi-Agent Systems. Symmetry, 15(6), 1247. https://doi.org/10.3390/sym15061247






