Some Common Fixed Circle Results on Metric and 𝕊-Metric Spaces with an Application to Activation Functions

Abstract

In this paper, we modify various contractive conditions (C.C.)s such as Ciric type (C.C.), Rhoades type (C.C.), Seghal type (C.C.), Bianchini type (C.C.), and Berinde type (C.C.) for two self-mappings, considering that the contractive property plays a major role in establishing a fixed circle (F.C.) on both metric spaces (M-s) and $\mathbb{S}$-(M-s) where the symmetry condition is satisfied, and we utilize them to establish a common (F.C.). We prove new (F.C.) results on both (M-s) and $\mathbb{S}$-(M-s) with illustrative examples. Finally, we provide an application to activation functions such as rectified linear unit activation functions and parametric rectified linear unit activation functions.

1. Introduction

Fixed point (F.P.) theory has been extensively studied under different aspects. One of the most commonly studied areas of (F.P.) theory is metric (F.P.) theory. This theory began with Banach’s theorem on (F.P.)s. The theorem is often known as the principle of Banach’s contraction (Cn.). This theory has been extended in three mechanisms:

(1) To generalize the (C.C.) being employed.

(2) To extend the utilized (M-s).

(3) To examine the geometric characteristics of an (F.P.) set of a self-mapping.

Under the first approach, many (C.C.)s were defined in the literature. For example, Ciric type (C.C.) [1,2], Rhoades type (C.C.) [3], Seghal type (C.C.) [4], Bianchini type (C.C.) [5], and Berinde type (C.C.) [6,7] were introduced for this purpose.

Under the second approach, many generalizations of an (M-s) were defined [8,9,10,11,12,13]. For instance, the concept of an $\mathbb{S}$-(M-s) was created for this reason in [14] which is a new type of symmetric metric spaces. Now, let us review some fundamental principles of $\mathbb{S}$-(M-s)s.

Definition 1

([14]). Let $Q\notin \varphi$ and consider the function $\mathbb{S}:Q\times Q\times Q\to [0,\infty )$. If $\mathbb{S}$ meets the requirements listed below for all $j,n,p,t\in Q$:

$\left(S1\right)$ $\mathbb{S}(j,n,p)=0⟺j=n=p$,

$\left(S2\right)$ $\mathbb{S}(j,n,p)\le S(j,j,t)+S(n,n,t)+S(p,p,t)$,

then $\mathbb{S}$ is termed an $\mathbb{S}$-metric on Q; hence, the pair $\left(Q,\mathbb{S}\right)$ is said to be $\mathbb{S}$-(M-s).

Lemma 1

([14]). Consider $\left(Q,\mathbb{S}\right)$ to be an $\mathbb{S}$-(M-s) and $j,n\in Q$. Hence, we obtain

$$\mathbb{S}(j,j,n)=\mathbb{S}(n,n,j).$$

Refs. [15,16,17] examined the links among a metric and an $\mathbb{S}$-(M-s). The following is a formula for an $\mathbb{S}$-(M-s) that is created by a metric $\delta .$

Let $\left(Q,\delta \right)$ be an (M-s). Thus, the function ${\mathbb{S}}_{\delta }:Q\times Q\times Q\to [0,\infty )$ specified by

$${\mathbb{S}}_{\delta }(j,n,p)=\delta (j,p)+\delta (n,p),$$

for all $j,n,p\in Q$ is an $\mathbb{S}$-metric on Q. The $\mathbb{S}$-metric ${\mathbb{S}}_{\delta }$ is called the $\mathbb{S}$-metric generated by $\delta ,$ and also a model of an $\mathbb{S}$-metric that is not extended by any metric $\delta$ (for further information, see [15]).

Under the third approach, recently, the geometric features of non-unique (F.P.)s have been intensively explored in a variety of contexts, such as the (F.C.) problem, the fixed-disc problem, and so on. Özgür and Taş [18] introduced the concept of an (F.C.) in an (M-s) as a novel strategy for the generalization of (F.P.) theory. Several writers have elaborately refined the notion of (F.C.)s and its applications for usage in topology and geometry. Significantly, Refs. [19,20,21,22,23] have introduced the concepts of (F.C.)s in different generalized (M-s)s. In addition, some open questions were provided in the literature related to the (F.C.) problem. For instance, in [24], the below problem was provided for common (F.C.)s:

Open Problem: What condition(s) is(are) necessary for any circle $C_{x_0,r}$ to be the common (F.C.) for two or more self-mappings?

Now, we recall the following definition:

Let $\left(Q,\delta \right)$ be an (M-s), let $C_{j_0,r}=\left\{j\in Q:\delta \left(j,j_0\right)=0\right\}$ be any circle on Q, and let f, h be two self-mappings on Q. If $fj=hj=j$ for all $j\in C_{j_0,r}$, then $C_{j_0,r}$ is said to be a common (F.C.) of the pair $\left(f,h\right)$ (as in [25]).

A few solutions have been proposed for this open problem (see [25,26,27]). In order to obtain novel solutions, we specify some (Cn.)s for the pair $(f,h)$ and prove some common (F.C.) results on (M-s)s. In fact, this study can be considered as a continuation of [26].

The present paper attempts to obtain common (F.C.) theorems for self-mappings under various types of (C.C.)s. Inspired by Wardowski [28], in the context of F-(Cn.), we have proven certain common (F.C.) theorems.

Let $\mathcal{E}$ represent the collection of all the mappings $E:[0,\infty )$ $\to (-\infty ,\infty )$ that hold for the axioms listed below:

$\left(E1\right)$

E is firmly increasing, then ∀, $j,n\in (0,\infty )$, such that $j<n,E\left(j\right)<E\left(n\right).$

$\left(E2\right)$

For every sequence $\left\{x_n\right\}$ in $\left(0,\infty \right),$ the subsequent is true.

${lim}_{n\to \infty }{x}_n=0$ if and only if ${lim}_{n\to \infty }E\left(x_n\right)=-\infty .$

$\left(E3\right)$

∃$l\in \left(0,1\right)$ where ${lim}_{x\to 0^{+}}{x}^{l}E\left(x\right)=0.$

Many examples of the functions that belong to $\mathcal{E}$ are $E_1\left(x\right)=lnx,E_2\left(x\right)=x+lnx,E_3\left(x\right)=-\frac{1}{\sqrt{x}},$ and $E_4\left(x\right)=ln\left(x^2+x\right)$.

In this sequel, we examine new solutions to the listed open problems under these three approaches. In order to achieve this, we change several recognized (C.C.)s on (M-s), and the defined conditions are generalized on $\mathbb{S}$-(M-s). For this purpose, we introduce the notions of a Ciric type $E_{fh}$-(Cn.), a Rhoades type $E_{fh}$-(Cn.), a Seghal type $E_{fh}$-(Cn.), a Bianchini type $E_{fh}$-(Cn.), and a Berinde type $E_{fh}$-(Cn.) on (M-s). In addition, these (Cn.)s are generalized on $\mathbb{S}$-(M-s), such as a Ciric type $E_{fh}^{\mathbb{S}}$-(Cn.), a Rhoades type $E_{fh}^{\mathbb{S}}$-(Cn.), a Seghal type $E_{fh}^{\mathbb{S}}$-(Cn.), a Bianchini type $E_{fh}^{\mathbb{S}}$-(Cn.), and a Berinde type $E_{fh}^{\mathbb{S}}$-(Cn.). Utilizing these new (Cn.)s, we prove some common (F.C.) results on both metric and $\mathbb{S}$-(M-s) with some illustrative examples. Finally, we give an application to the activation functions, such as rectified linear unit activation functions ($ReLU$), as well as parametric rectified linear unit activation functions ($PReLU$).

2. Some Common (F.C.) Results on (M-s)s

In this part, we demonstrate brand-new common (F.C.) theorem metric spaces. In order to obtain some typical (F.C.) results on (M-s)s, we begin by introducing the new (Cn.) type for two mappings.

Let $\left(Q,\delta \right)$ be an (M-s), and let f, h be two self-mappings on a set Q. The number $\omega$ is defined by

$$\omega =inf\left\{\delta \left(j,fj\right)+\delta \left(j,hj\right):j\ne fj,j\ne hj,j\in Q\right\}.$$

(1)

Definition 2.

Let $\left(Q,\delta \right)$ be an (M-s) and let $f,h:Q\to Q$ be two self-mappings. It is defined that the pair $\left(f,h\right)$ is a Ciric type $E_{fh}$-(Cn.) on Q if ∃$\mathrm{Y}>0$, $E\in \mathcal{E}$, and $j_0\in Q$, where for any $j\in Q$, the following is true:

$$max\left\{\delta (j,fj),\delta \left(j,hj\right)\right\}>0\Rightarrow \mathrm{Y}+E\left(\delta \left(j,fj\right)+\delta \left(j,hj\right)\right)\le E\left(c\left(j,j_0\right)\right),$$

where

$$c\left(j,n\right)=max\left\{\delta \left(j,n\right),\delta \left(j,fj\right),\delta \left(n,hn\right),\frac{1}{2}\left[\delta \left(j,fn\right)+\delta \left(j,hn\right)\right]\right\}.$$

Proposition 1.

Let $\left(Q,\delta \right)$ be an (M-s) and let $f,h:Q\to Q$ be two self-mappings. If the pair $\left(f,h\right)$ is a Ciric type $E_{fh}$-(Cn.) with $j_0\in Q$, then we have $f{j}_0=j_0=h{j}_0.$

Proof. 

On the contrary, suppose that $j_0$ is not a common (F.P.) of f and h. Hence, we obtain $\delta \left(j_0,f{j}_0\right)>0$ or $\delta \left(j_0,h{j}_0\right)>0$; that is,

$$max\left\{\delta \left(j_0,f{j}_0\right),\delta \left(j_0,h{j}_0\right)\right\}>0.$$

Hence, we obtain

$$\begin{array}{cc}\hfill & \mathrm{Y}+E\left(\delta (j_0,f{j}_0)+\delta \left(j_0,h{j}_0\right)\right)\hfill \\ \hfill & \le E\left(max\left\{\delta \left(j_0,j_0\right),\delta \left(j_0,f{j}_0\right),\delta \left(j_0,h{j}_0\right),\frac{1}{2}\left[\delta \left(j_0,f{j}_0\right)+\delta \left(j_0,h{j}_0\right)\right]\right\}\right)\hfill \\ \hfill & =E\left(max\left\{\delta \left(j_0,f{j}_0\right),\delta \left(j_0,h{j}_0\right),\frac{1}{2}\left[\delta \left(j_0,f{j}_0\right)+\delta \left(j_0,h{j}_0\right)\right]\right\}\right)\hfill \\ \hfill & <E\left(\delta (j_0,f{j}_0)+\delta \left(j_0,h{j}_0\right)\right).\hfill \end{array}$$

However, this leads to a contradiction because $\mathrm{Y}>0$ and E is a strict increase. Consequently, we obtain

$$f{j}_0=j_0=h{j}_0.$$

 □

Theorem 1.

Let $\left(Q,\delta \right)$ be an (M-s), let $f,h:Q\to Q$ be two self-mappings, and let the pair $\left(f,h\right)$ be a Ciric type $E_{fh}$-(Cn.) with $j_0\in Q$ and ω be defined as in (1). Then, $C_{j_0,\omega }$ is a common (F.C.) of the pair $\left(f,h\right).$ In particular, the pair $\left(f,h\right)$ fixes every circle $C_{j_0,\varrho }$ with $\varrho <\omega .$

Two cases are identified.

Case 1: Assume that $\omega =0.$ Obviously, $C_{j_0,\omega }=\left\{j_0\right\}$, and along with Proposition 1, we observe that $C_{j_0,\omega }$ is a common (F.C.) of the pair $\left(f,h\right).$

Case 2: Assume that $\omega >0$ and $j\in C_{j_0,\omega }$ with $max\left\{\delta (j,fj),\delta \left(j,hj\right)\right\}>0$. Using the Ciric type $E_{fh}$-(Cn.) property in addition to the fact that E is strictly rising, we obtain

$$\begin{array}{cc}\hfill E\left(\omega \right)& \le E\left(\delta (j,fj)+\delta \left(j,hj\right)\right)\hfill \\ \hfill & \le E\left(max\left\{\delta \left(j,j_0\right),\delta \left(j,fj\right),\delta \left(j_0,h{j}_0\right),\frac{1}{2}\left[\delta \left(j,f{j}_0\right)+\delta \left(j,h{j}_0\right)\right]\right\}\right)-\mathrm{Y}\hfill \\ \hfill & <E\left(max\left\{\omega ,\delta \left(j,fj\right),0,\omega \right\}\right)\hfill \\ \hfill & =E\left(max\left\{\omega ,\delta \left(j,fj\right)\right\}\right)=E\left(\omega \right).\hfill \end{array}$$

This creates a contradiction. Hence, $max\left\{\delta (j,fj),\delta \left(j,hj\right)\right\}=0$, and so,

$$fj=j=hj.$$

Consequently, $C_{j_0,\omega }$ is a common (F.C.) of the pair $\left(f,h\right)$.

Meanwhile, we prove that the pair $\left(f,h\right)$ fixes any circle $C_{j_0,\varrho }$ with $\varrho <\omega .$ Suppose that $j\in C_{j_0,\varrho }$ with $max\left\{\delta (j,fj),\delta \left(j,hj\right)\right\}>0$. According to the Ciric type $E_{fh}$-(Cn.), it yields to

$$\begin{array}{cc}\hfill E\left(\varrho \right)& \le E\left(\delta (j,fj)+\delta \left(j,hj\right)\right)\hfill \\ \hfill & \le E\left(max\left\{\delta \left(j,j_0\right),\delta \left(j,fj\right),\delta \left(j_0,h{j}_0\right),\frac{1}{2}\left[\delta \left(j,f{j}_0\right)+\delta \left(j,h{j}_0\right)\right]\right\}\right)-\mathrm{Y}\hfill \\ \hfill & <E\left(max\left\{\delta \left(j,j_0\right),\delta \left(j,fj\right),\delta \left(j_0,h{j}_0\right),\frac{1}{2}\left[\delta \left(j,f{j}_0\right)+\delta \left(j,h{j}_0\right)\right]\right\}\right)\hfill \\ \hfill & =E\left(\varrho \right),\hfill \end{array}$$

which is a contradiction. So, we have $max\left\{\delta (j,fj),\delta \left(j,hj\right)\right\}=0$, and so,

$$fj=j=hj.$$

Consequently, $C_{j_0,\varrho }$ is a common (F.C.) of the pair $\left(f,h\right).$

Definition 3.

Let $\left(Q,\delta \right)$ be an (M-s) and let $f,h:Q\to Q$ be two self-mappings. If ∃$\mathrm{Y}>0,E\in \mathcal{E}$ and $j_0\in Q$, where ∀$j\in Q,$ if it fulfills the following:

$$max\left\{\delta (j,fj),\delta \left(j,hj\right)\right\}>0⟹\mathrm{Y}+E\left(\delta (j,fj)+\delta \left(j,hj\right)\right)\le E\left(r\left(j,j_0\right)\right),$$

where

$$r(j,n)=max\left\{\delta \left(j,n\right),\delta \left(j,fj\right),\delta \left(n,hn\right),\delta \left(j,hn\right),\delta \left(n,fj\right)\right\};$$

hence, the pair $\left(f,h\right)$ is called a Rhoades type $E_{fh}$-(Cn.).

Proposition 2.

Consider $\left(Q,\delta \right)$ to be an (M-s) and let $f,h:Q\to Q$ be two self-mappings. We have $f{j}_0=j_0=h{j}_0$ if the pair $\left(f,h\right)$ is a Rhoades type $E_{fh}$-(Cn.) with $j_0\in Q.$

Proof. 

The similar justifications offered in Proposition 1 make it simple to demonstrate. □

Theorem 2.

Let $\left(Q,\delta \right)$ be an (M-s), and $f,h:Q\to Q$ be two self-mappings; let the pair $\left(f,h\right)$ be a Rhoades type $E_{fh}$-(Cn.) with $j_0\in Q$ and ω is defined as follows (1). If $\delta \left(j_0,fj\right)\le \omega$, then $C_{j_0,\omega }$ is a common (F.C.) of the pair $\left(f,h\right).$ Furthermore, the pair $\left(f,h\right)$ fixes every circle $C_{j_0,\varrho }$ with $\varrho <\omega .$

Proof. 

We differentiate two situations.

Case 1: Let $\omega =0.$ It is obvious that $C_{j_0,\omega }=\left\{j_0\right\},$ and Proposition 2 demonstrates that $C_{j_0,\omega }$ is a common (F.C.) of the pair $\left(f,h\right).$

Case 2: Let $\omega >0$ and $j\in C_{j_0,\omega }$ with $max\left\{\delta (j,fj),\delta \left(j,hj\right)\right\}>0$. According to the Rhoades type $E_{fh}$-(Cn.) property, as well as the fact that E is strictly rising, it yields to

$$\begin{array}{cc}\hfill E\left(\omega \right)& \le E\left(\delta (j,fj)+\delta \left(j,hj\right)\right)\hfill \\ \hfill & \le E\left(r\left(j,j_0\right)\right)-\mathrm{Y}\hfill \\ \hfill & \le E\left(max\left\{\delta \left(j,j_0\right),\delta \left(j,fj\right),\delta \left(j_0,h{j}_0\right),\delta \left(j,h{j}_0\right),\delta \left(j_0,fj\right)\right\}\right)-\mathrm{Y}\hfill \\ \hfill & <E\left(max\left\{\omega ,\delta \left(j,fj\right),0,\omega ,\omega \right\}\right)\hfill \\ \hfill & \le E\left(max\left\{\omega ,\delta \left(fj,j\right)\right\}\right)\hfill \\ \hfill & =E\left(\omega \right).\hfill \end{array}$$

It is contradictory in this way, due to the fact that $max\left\{\delta (j,fj),\delta \left(j,hj\right)\right\}=0$, that is,

$$fj=j=hj.$$

As a result, $C_{j_0,\omega }$ is a common (F.C.) of the pair $\left(f,h\right).$ The pair $\left(f,h\right)$ also fixes any circle $C_{j_0,\varrho }$ with $\varrho <\omega ,$ using the same justifications as in the proof of Theorem 1. □

Definition 4.

Let $\left(Q,\delta \right)$ be an (M-s) and let $f,h:Q\to Q$ be two self-mappings. It is defined that the pair $\left(f,h\right)$ is a Seghal type $E_{fh}$-(Cn.) on Q, if ∃ exists, $\mathrm{Y}>0$, $E\in \mathcal{E},$ as well as $j_0\in Q$, such that for any $j\in Q$, the following holds:

$$max\left\{\delta \left(j,fj\right),\delta \left(j,hj\right)\right\}>0⟹\mathrm{Y}+E\left(\delta \left(j,fj\right)+\delta \left(j,hj\right)\right)\le E\left(s\left(j,j_0\right)\right),$$

where

$$s(j,n)=max\left\{\delta \left(j,n\right),\delta \left(j,fj\right),\delta \left(n,hn\right)\right\}.$$

Remark 1.

If the pair $\left(f,h\right)$ is a Seghal type $E_{fh}$-(Cn.) with $j_0\in Q$, then the pair $\left(f,h\right)$ is a Rhoades type $E_{fh}$-(Cn.) with $j_0\in Q$. Indeed, we have

$$\begin{array}{cc}\hfill & \mathrm{Y}+E\left(\delta \left(j,fj\right)+\delta \left(j,hj\right)\right)\hfill \\ \hfill & \le E\left(s\left(j,j_0\right)\right)\hfill \\ \hfill & =E\left(max\left\{\delta \left(j,j_0\right),\delta \left(j,fj\right),\delta \left(j_0,h{j}_0\right)\right\}\right)\hfill \\ \hfill & \le E\left(max\left\{\delta \left(j,j_0\right),\delta \left(j,fj\right),\delta \left(j_0,h{j}_0\right),\delta \left(j,h{j}_0\right),\delta \left(j,f{j}_0\right)\right\}\right)\hfill \\ \hfill & =E\left(r\left(j,j_0\right)\right),\hfill \end{array}$$

when $max\left\{\delta \left(j,fj\right),\delta \left(j,hj\right)\right\}>0$.

The converse statement is not always true.

Example 1.

Suppose that $Q=\mathbb{R}$ is a usual (M-s) and that the self-mappings $f,h:\mathbb{R}\to \mathbb{R}$ are characterized as

$$fj=\left\{\begin{array}{cc}1,& \mathrm{if}j=2\\ j,& \mathrm{otherwise}\end{array}\right.$$

and

$$hj=\left\{\begin{array}{cc}-2,& \mathrm{if}j=0\\ 1,& \mathrm{if}j=2\\ j,& \mathrm{otherwise}\end{array}\right.,$$

for all $j\in \mathbb{R}$. For $j=2$, the pair $\left(f,h\right)$ satisfies the condition of Rhoades type $E_{fh}$-(Cn.) with $j_0=0$, $E\left(j\right)=lnj$, and $\mathrm{Y}=ln2$. Indeed, we have

$$max\left\{\delta \left(j,fj\right),\delta \left(j,hj\right)\right\}=max\{1,1\}=1>0$$

, and

$$\begin{array}{cc}\hfill & \mathrm{Y}+E\left(\delta \left(j,fj\right)+\delta \left(j,hj\right)\right)\hfill \\ \hfill & =\mathrm{Y}+E\left(2\right)=ln2+ln2=ln4\hfill \\ \hfill & =E\left(max\left\{\delta \left(j,j_0\right),\delta \left(j,fj\right),\delta \left(j_0,h{j}_0\right),\delta \left(j,h{j}_0\right),\delta \left(j,f{j}_0\right)\right\}\right)\hfill \\ \hfill & =E\left(r\left(j,j_0\right)\right).\hfill \end{array}$$

However, the pair $\left(f,h\right)$ does not satisfy the condition of the Seghal type $E_{fh}$-(Cn.) with $j_0=0$, $E\in \mathcal{E}$, and $\mathrm{Y}>0$.

Definition 5.

Let $\left(Q,\delta \right)$ be an (M-s) and let $f,h:Q\to Q$ be two self-mappings. If ∃$\mathrm{Y}>0,E\in \mathcal{E}$, as well as $j_0\in Q$, where ∀$j\in Q,$ it fulfills the following:

$$max\left\{\delta \left(j,fj\right),\delta \left(j,hj\right)\right\}>0⟹\mathrm{Y}+E\left(\delta \left(j,fj\right)+\delta \left(j,hj\right)\right)\le E\left(b_1(j,j_0)\right),$$

where

$$b_1(j,n)=hmax\left\{\delta \left(j,fj\right),\delta \left(n,hn\right)\right\}$$

with $h\in \left(0,1\right);$ hence, the pair $\left(f,h\right)$ is called a Bianchini type $E_{fh}$-(Cn.).

Proposition 3.

Suppose that $\left(Q,\delta \right)$ is an (M-s) along with $f;leth:Q\to Q$ be two self-mappings. We have $f{j}_0=j_0=h{j}_0$, if the pair $\left(f,h\right)$ is a Bianchini type $E_{fh}$-(Cn.) with $j_0\in Q.$

Proof. 

If $j_0$ is not a common (F.P.) of f and h, it yields to $\delta \left(j_0,f{j}_0\right)>0$ or $\delta \left(j_0,h{j}_0\right)>0$, that is,

$$max\left\{\delta (j_0,f{j}_0),\delta \left(j_0,h{j}_0\right)\right\}>0.$$

Hence, we obtain

$$\begin{array}{cc}\hfill \mathrm{Y}+E\left(\delta (j_0,f{j}_0)+\delta \left(j_0,h{j}_0\right)\right)& \le E\left(b_1(j,j_0)\right)\hfill \\ \hfill & \le E\left(hmax\left\{\delta \left(j_0,f{j}_0\right),\delta \left(j_0,h{j}_0\right)\right\}\right)\hfill \\ \hfill & <E\left(\delta (j_0,f{j}_0)+\delta \left(j_0,h{j}_0\right)\right).\hfill \end{array}$$

where $h\in \left(0,1\right)$. However, this creates a contradiction since E is strictly increased. Consequently, we obtain

$$f{j}_0=j_0=h{j}_0.$$

 □

Theorem 3.

Let $\left(Q,\delta \right)$ be an (M-s), and let $f,h:Q\to Q$ be two self-mappings; the pair $\left(f,h\right)$ is a Bianchini type $E_{fh}$-(Cn.) with $j_0\in Q$ and ω is defined as in (1). Then, $C_{j_0,\omega }$ is a common (F.C.) of the pair $\left(f,h\right).$ Especially, the pair $\left(f,h\right)$ fixes every circle $C_{j_0,\varrho }$ with $\varrho <\omega .$

Proof. 

We differentiate two situations:

Case 1. Assume that $\omega =0$. It is obvious that $C_{j_0,\omega }=\left\{j_0\right\}$, and Proposition 3 demonstrates that $C_{j_0,\omega }$ is a common (F.C.) of the pair $\left(f,h\right).$

Case 2: Assume that $\omega >0$ and $j\in C_{j_0,\omega }$ with $max\left\{\delta (j,fj),\delta \left(j,hj\right)\right\}>0$. Using the Bianchini type $E_{fh}$-(Cn.) and Proposition 3, along with the fact that E is increasing, we have

$$\begin{array}{cc}\hfill E\left(\omega \right)& \le E\left(\delta \left(j,fj\right)+\delta \left(j,hj\right)\right)\hfill \\ \hfill & \le E\left(hmax\left\{\delta \left(j,fj\right),\delta \left(j_0,h{j}_0\right)\right\}\right)-\mathrm{Y}\hfill \\ \hfill & <E\left(h\delta \left(j,fj\right)\right)\hfill \\ \hfill & <E\left(\omega \right).\hfill \end{array}$$

This creates a contradiction. Thus, $max\left\{\delta (j,fj),\delta \left(j,hj\right)\right\}=0,$ that is,

$$fj=j=hj.$$

Consequently, $C_{j_0,\omega }$ is a common (F.C.) of the pair $\left(f,h\right).$ By using similar considerations in the proof of Theorem 1, f and h also fix any circle $C_{j_0,\varrho }$ with $\varrho <\omega .$ □

Definition 6.

Let $\left(Q,\delta \right)$ be an (M-s) and let $f,h:Q\to Q$ be two self-mappings. If ∃$\mathrm{Y}>0,E\in \mathcal{E}$ and $j_0\in Q$, such that where ∀$j\in Q,$ it yields to the following:

$$max\left\{\delta \left(j,fj\right),\delta \left(j,hj\right)\right\}>0⟹\mathrm{Y}+E\left(\delta \left(j,fj\right)+\delta \left(j,hj\right)\right)\le E\left(b_2(j,j_0)\right),$$

where

$$b_2(j,n)=\varphi \delta \left(j,n\right)+Lmin\left\{\delta \left(j,fj\right),\delta \left(n,hn\right),\delta \left(j,fn\right),\delta \left(j,hn\right)\right\},$$

with $\varphi \in \left(0,1\right]$ and $L\ge 0$, then the pair $\left(f,h\right)$ is called a Berinde type $E_{fh}$-(Cn.).

Proposition 4.

Let $\left(Q,\delta \right)$ be an (M-s) and let $f,h:Q\to Q$ be two self-mappings. If the pair $\left(f,h\right)$ is a Berinde type $E_{fh}$-(Cn.) with $j_0\in Q,$ then we have $f{j}_0=j_0=h{j}_0.$

Proof. 

The proof is simple because of the similar justifications offered in Proposition 1. □

Theorem 4.

Let $\left(Q,\delta \right)$ be an (M-s) and let $f,h:Q\to Q$ be two self-mappings; the pair $\left(f,h\right)$ is a Berinde type $E_{fh}$-(Cn.) with $j_0\in Q$ and ω is defined as in (1). Then, $C_{j_0,\omega }$ is a common (F.C.) of the pair $\left(f,h\right).$ Particularly, the pair $\left(f,h\right)$ fixes every circle $C_{j_0,\varrho }$ with $\varrho <\omega .$

Proof. 

We differentiate two cases:

Case 1. Let $\omega =0.$ It is obvious that $C_{j_0,\omega }=\left\{j_0\right\},$ and Proposition 4 demonstrates that $C_{j_0,\omega }$ is a common (F.C.) of the pair $\left(f,h\right).$

Case 2: Let $\omega >0$ and $j\in C_{j_0,\omega }$ with $max\left\{\delta (j,fj),\delta \left(j,hj\right)\right\}>0$. Using the Berinde type $E_{fh}$-(Cn.), Proposition 4, and the fact that E is strictly increasing, we obtain

$$\begin{array}{cc}\hfill E\left(\omega \right)& \le E\left(\delta \left(j,fj\right)+\delta \left(j,hj\right)\right)\hfill \\ \hfill & \le E\left(b_2(j,j_0)\right)\hfill \\ \hfill & \le E\left(\varphi \delta \left(j,j_0\right)+Lmin\left\{\delta \left(j,fj\right),\delta \left(j_0,h{j}_0\right),\delta \left(j,f{j}_0\right),\delta \left(j,h{j}_0\right)\right\}\right)-\mathrm{Y}\hfill \\ \hfill & <E\left(\varphi \delta \left(j,j_0\right)+Lmin\left\{\delta \left(j,fj\right),0,\omega ,\omega \right\}\right)\hfill \\ \hfill & =E\left(\varphi \omega +0\right)\hfill \\ \hfill & <E\left(\omega \right).\hfill \end{array}$$

This creates a contradiction since E is a strictly increasing. So, $max\left\{\delta (j,fj),\delta \left(j,hj\right)\right\}=0$, that is,

$$fj=j=hj.$$

Consequently, $C_{j_0,\omega }$ is a common (F.C.) of the pair $\left(f,h\right).$ By using similar considerations in the proof of Theorem 1, the pair $\left(f,h\right)$ also fixes any circle $C_{j_0,\varrho }$ with $\varrho <\omega .$ □

This is an example to illustrate our argument.

Example 2.

Let $Q=\left\{1,2,e^3,e^3-2,e^3+2\right\}$ be the (M-s) with the usual metric. We define the self-mapping $f,h:Q\to Q$ as

$$fj=\left\{\begin{array}{cc}2,& \mathrm{if}j=1\\ j,& \mathrm{otherwise}\end{array}\right.$$

and

$$hj=\left\{\begin{array}{cc}2,& \mathrm{if}j=1\\ j,& \mathrm{otherwise}\end{array}\right.$$

for all $j\in Q.$

The pair $\left(f,h\right)$ is a Ciric type $E_{fh}$-(Cn.) (resp. Rhoades type $E_{fh}$-(Cn.) and Seghal type $E_{fh}$-(Cn.)) with $E\left(j\right)=j+lnj$, $\mathrm{Y}=e^3-3$, and $j_0=e^3.$ Indeed, we get

$$max\left\{\delta \left(j,fj\right),\delta \left(j,hj\right)\right\}=max\left\{\delta \left(1,2\right),\delta \left(1,2\right)\right\}=1>0$$

for $j=1$, and we obtain

$$\begin{array}{cc}\hfill c\left(j,j_0\right)& =max\left\{\delta \left(j,j_0\right),\delta \left(j,fj\right),\delta \left(j_0,h{j}_0\right),\frac{1}{2}\left[\delta \left(j,f{j}_0\right)+\delta \left(j,h{j}_0\right)\right]\right\}\hfill \\ \hfill & =max\left\{\delta \left(1,e^3\right),\delta \left(1,2\right),\delta \left(e^3,e^3\right),\frac{1}{2}\left[\delta \left(1,e^3\right)+\delta \left(1,e^3\right)\right]\right\}\hfill \\ \hfill & =max\left\{e^3-1,1,0,e^3-1\right\}\hfill \\ \hfill & =e^3-1.\hfill \end{array}$$

Then, we have

$$\begin{array}{cc}\hfill \mathrm{Y}+E\left(\delta \left(j,fj\right)+\delta \left(j,hj\right)\right)& =e^3-3+2+ln2\hfill \\ \hfill & \le E\left(e^3-1\right)\hfill \\ \hfill & =e^3-1+ln\left(e^3-1\right).\hfill \end{array}$$

Similarly, we can easily see that the pair $\left(f,h\right)$ is a Rhoades type $E_{fh}$-(Cn.) and a Seghal type $E_{fh}$-(Cn.). In addition, the pair $\left(f,h\right)$ is a Berinde type $E_{fh}$-(Cn.) with $E\left(j\right)=j+lnj,$$\mathrm{Y}=1$, $\varphi =\frac{1}{2}$, and $j_0=e^3.$ Indeed, we obtain

$$max\left\{\delta \left(j,fj\right),\delta \left(j,hj\right)\right\}=max\left\{\delta \left(1,2\right),\delta \left(1,2\right)\right\}=1>0$$

for $j=1$, and we have

$$\begin{array}{cc}\hfill b_2(j,j_0)& =\varphi \delta \left(j,j_0\right)+Lmin\left\{\delta \left(j,fj\right),\delta \left(j_0,h{j}_0\right),\delta \left(j,f{j}_0\right),\delta \left(j,h{j}_0\right)\right\}\hfill \\ \hfill & =\frac{1}{2}\delta \left(1,e^3\right)+Lmin\left\{\delta \left(1,2\right),\delta \left(e^3,e^3\right),\delta \left(1,e^3\right),\delta \left(1,e^3\right)\right\}\hfill \\ \hfill & =\frac{e^3-1}{2}+Lmin\left\{1,0,e^3-1,e^3-1\right\}\hfill \\ \hfill & =\frac{e^3-1}{2}.\hfill \end{array}$$

Then, we have

$$\begin{array}{cc}\hfill \mathrm{Y}+E\left(\delta \left(j,fj\right)+\delta \left(j,hj\right)\right)& =1+2+ln2\hfill \\ \hfill & \le E\left(\frac{e^3-1}{2}\right)\hfill \\ \hfill & =\frac{e^3-1}{2}+ln\left(\frac{e^3-1}{2}\right).\hfill \end{array}$$

Consequently, the pair $\left(f,h\right)$ fixes the circle $C_{e^3,2}.$

3. Some Common (F.C.) Results on $\mathbb{S}$-(M-s)s

In this section, we explore some common (F.C.) theorems on $\mathbb{S}$-(M-s)s. To achieve this, we generalize the proven results in the previous section. Some basic notions were presented that were related to the (F.C.) problem on $\mathbb{S}$-(M-s)s in [14,29,30].

Let $\left(Q,\mathbb{S}\right)$ be an $\mathbb{S}$-(M-s), and let $C_{j_0,r}^{\mathbb{S}}=\left\{j\in Q:\mathbb{S}\left(j,j,j_0\right)=r\right\}$ be any circle on Q and f; let h be two self-mappings on a set Q. If $fj=hj=j$ for all $j\in C_{j_0,r}^{\mathbb{S}}$, then $C_{j_0,r}^{\mathbb{S}}$ is called a common (F.C.) of the pair $\left(f,h\right)$.

Definition 7.

Let $\left(Q,\mathbb{S}\right)$ be an $\mathbb{S}$-(M-s) and let $f,h:Q\to Q$ be two self-mappings. It is defined that the pair $\left(f,h\right)$ is a Ciric type $E_{fh}^{\mathbb{S}}$-(Cn.) on Q if ∃$\mathrm{Y}>0$, $E\in \mathcal{E}$, along with $j_0\in Q$, such that for any $j\in Q$, the following affirms:

$$max\left\{\mathbb{S}(j,j,fj),\mathbb{S}\left(j,j,hj\right)\right\}>0\Rightarrow \mathrm{Y}+E\left(\mathbb{S}(j,j,fj)+\mathbb{S}\left(j,j,hj\right)\right)\le E\left(c_{\mathbb{S}}\left(j,j_0\right)\right),$$

where

$$c_{\mathbb{S}}\left(j,n\right)=max\left\{\mathbb{S}\left(j,j,n\right),\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(n,n,hn\right),\frac{1}{2}\left[\mathbb{S}\left(j,j,fn\right)+\mathbb{S}\left(j,j,hn\right)\right]\right\}.$$

Proposition 5.

Let $\left(Q,\mathbb{S}\right)$ be an $\mathbb{S}$-(M-s) and let $f,h:Q\to Q$ be two self-mappings. If the pair $\left(f,h\right)$ is a Ciric type $E_{fh}^{\mathbb{S}}$-(Cn.) with $j_0\in Q$, then we have $f{j}_0=j_0=h{j}_0.$

Proof. 

On the contrary, suppose that $j_0$ is not a common (F.P.) of f and h. Hence, we obtain $\mathbb{S}\left(j_0,j_0,f{j}_0\right)>0$ or $\mathbb{S}\left(j_0,j_0,h{j}_0\right)>0$, that is,

$$max\left\{\mathbb{S}\left(j_0,j_0,f{j}_0\right),\mathbb{S}\left(j_0,j_0,h{j}_0\right)\right\}>0.$$

Hence, we obtain

$$\begin{array}{cc}\hfill & \mathrm{Y}+E\left(\mathbb{S}(j_0,j_0,f{j}_0)+\mathbb{S}\left(j_0,j_0,h{j}_0\right)\right)\hfill \\ \hfill & \le E\left(max\left\{\begin{array}{c}\mathbb{S}\left(j_0,j_0,j_0\right),\mathbb{S}\left(j_0,j_0,f{j}_0\right),\mathbb{S}\left(j_0,j_0,h{j}_0\right),\\ \frac{1}{2}\left[\mathbb{S}\left(j_0,j_0,f{j}_0\right)+\mathbb{S}\left(j_0,j_0,h{j}_0\right)\right]\end{array}\right\}\right)\hfill \\ \hfill & =E\left(max\left\{\begin{array}{c}\mathbb{S}\left(j_0,j_0,f{j}_0\right),\mathbb{S}\left(j_0,j_0,h{j}_0\right),\\ \frac{1}{2}\left[\mathbb{S}\left(j_0,j_0,f{j}_0\right)+\mathbb{S}\left(j_0,j_0,h{j}_0\right)\right]\end{array}\right\}\right)\hfill \\ \hfill & <E\left(\mathbb{S}(j_0,j_0,f{j}_0)+\mathbb{S}\left(j_0,j_0,h{j}_0\right)\right).\hfill \end{array}$$

However, this creates a contradiction because of $\mathrm{Y}>0$, and E is a strict increase. Consequently, we obtain

$$f{j}_0=j_0=h{j}_0.$$

□

Theorem 5.

Let $\left(Q,\mathbb{S}\right)$ be an $\mathbb{S}$-(M-s); let $f,h:Q\to Q$ be two self-mappings and the pair $\left(f,h\right)$ be a Ciric type $E_{fh}^{\mathbb{S}}$-(Cn.) with $j_0\in Q$, and let μ be defined as

$$\mu =inf\left\{\mathbb{S}\left(j,j,fj\right)+\mathbb{S}\left(j,j,hj\right):j\ne fj,j\ne hj,j\in Q\right\}.$$

(2)

Then, $C_{j_0,\mu }^{\mathbb{S}}$ is a common (F.C.) of the pair $\left(f,h\right).$ Particularly, the pair $\left(f,h\right)$ fixes every circle $C_{j_0,\varrho }^{\mathbb{S}}$ with $\varrho <\mu .$

Proof. 

Let us examine the following cases:

Case 1: Take $\mu =0.$ Clearly, $C_{j_0,\mu }^{\mathbb{S}}=\left\{j_0\right\}$. Moreover, according to Proposition 5, we observe that $C_{j_0,\mu }^{\mathbb{S}}$ is a common (F.C.) of the pair $\left(f,h\right).$

Case 2: Let $\mu >0$ and $j\in C_{j_0,\mu }^{\mathbb{S}}$, with $max\left\{\mathbb{S}(j,j,fj),\mathbb{S}\left(j,j,hj\right)\right\}>0$. Using the Ciric type $E_{fh}^{\mathbb{S}}$-(Cn.) property, along with the fact that E is strictly rising, it yields to

$$\begin{array}{cc}\hfill E\left(\mu \right)& \le E\left(\mathbb{S}(j,j,fj)+\mathbb{S}\left(j,j,hj\right)\right)\hfill \\ \hfill & \le E\left(max\left\{\begin{array}{c}\mathbb{S}\left(j,j,j_0\right),\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(j_0,j_0,h{j}_0\right),\\ \frac{1}{2}\left[\mathbb{S}\left(j,j,f{j}_0\right)+\mathbb{S}\left(j,j,h{j}_0\right)\right]\end{array}\right\}\right)-\mathrm{Y}\hfill \\ \hfill & <E\left(max\left\{\mu ,\mathbb{S}\left(j,j,fj\right),0,\mu \right\}\right)\hfill \\ \hfill & =E\left(max\left\{\mu ,\mathbb{S}\left(j,j,fj\right)\right\}\right)=E\left(\mu \right).\hfill \end{array}$$

This creates a contradiction. Hence, $max\left\{\mathbb{S}(j,j,fj),\mathbb{S}\left(j,j,hj\right)\right\}=0$, and so,

$$fj=j=hj.$$

Consequently, $C_{j_0,\mu }^{\mathbb{S}}$ is a common (F.C.) of the pair $\left(f,h\right)$.

Now, we prove that the pair $\left(f,h\right)$ fixes any circle $C_{j_0,\varrho }$ with $\varrho <\mu .$ Let $j\in C_{j_0,\varrho }^{\mathbb{S}}$ with $max\left\{\mathbb{S}(j,j,fj),\mathbb{S}\left(j,j,hj\right)\right\}>0$. According to the Ciric type $E_{fh}^{\mathbb{S}}$-(Cn.), we obtain

$$\begin{array}{cc}\hfill E\left(\varrho \right)& \le E\left(\mathbb{S}(j,j,fj)+\mathbb{S}\left(j,j,hj\right)\right)\hfill \\ \hfill & \le E\left(max\left\{\begin{array}{c}\mathbb{S}\left(j,j,j_0\right),\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(j_0,j_0,h{j}_0\right),\\ \frac{1}{2}\left[\mathbb{S}\left(j,j,f{j}_0\right)+\mathbb{S}\left(j,j,h{j}_0\right)\right]\end{array}\right\}\right)-\mathrm{Y}\hfill \\ \hfill & <E\left(max\left\{\begin{array}{c}\mathbb{S}\left(j,j,j_0\right),\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(j_0,j_0,h{j}_0\right),\\ \frac{1}{2}\left[\mathbb{S}\left(j,j,f{j}_0\right)+\mathbb{S}\left(j,j,h{j}_0\right)\right]\end{array}\right\}\right)\hfill \\ \hfill & =E\left(\varrho \right),\hfill \end{array}$$

which is a contradiction. So, we have $max\left\{\mathbb{S}(j,j,fj),\mathbb{S}\left(j,j,hj\right)\right\}=0$ and so,

$$fj=j=hj.$$

Consequently, $C_{j_0,\varrho }^{\mathbb{S}}$ is a common (F.C.) of the pair $\left(f,h\right).$ □

Definition 8.

Let $\left(Q,\mathbb{S}\right)$ be an $\mathbb{S}$-(M-s) and $f,h:Q\to Q$ be two self-mappings. If ∃ $\mathrm{Y}>0$, $E\in \mathcal{E}$, as well as $j_0\in Q$, where ∀$j\in Q,$ and it fulfills the following:

$$max\left\{\mathbb{S}(j,j,fj),\mathbb{S}\left(j,j,hj\right)\right\}>0⟹\mathrm{Y}+E\left(\mathbb{S}(j,j,fj)+\mathbb{S}\left(j,j,hj\right)\right)\le E\left(r_{\mathbb{S}}\left(j,j_0\right)\right),$$

where

$$r_{\mathbb{S}}(j,n)=max\left\{\mathbb{S}\left(j,j,n\right),\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(n,n,hn\right),\mathbb{S}\left(j,j,hn\right),\mathbb{S}\left(n,n,fj\right)\right\};$$

hence, the pair $\left(f,h\right)$ is called a Rhoades type $E_{fh}^{\mathbb{S}}$-(Cn.).

Proposition 6.

Consider $\left(Q,\mathbb{S}\right)$ to be an $\mathbb{S}$-(M-s) and let $f,h:Q\to Q$ be two self-mappings. We have $f{j}_0=j_0=h{j}_0$, if the pair $\left(f,h\right)$ is a Rhoades type $E_{fh}^{\mathbb{S}}$-(Cn.) with $j_0\in Q.$

Proof. 

We apply similar reasons to those presented in Proposition 5, which is plainly visible. □

Theorem 6.

Consider $\left(Q,\mathbb{S}\right)$ to be an $\mathbb{S}$-(M-s), and let $f,h:Q\to Q$ be two self-mappings; let the pair $\left(f,h\right)$ be a Rhoades type $E_{fh}^{\mathbb{S}}$-(Cn.) with $j_0\in Q$, and let μ be defined as follows (2). If $\mathbb{S}\left(j_0,j_0,fj\right)\le \mu$, then $C_{j_0,\mu }^{\mathbb{S}}$ is a common (F.C.) of the pair $\left(f,h\right).$ Furthermore, the pair $\left(f,h\right)$ fixes every circle $C_{j_0,\varrho }^{\mathbb{S}}$ with $\varrho <\mu .$

Proof. 

This is straightforward to prove by using the same methods as in Theorem 5. □

Definition 9.

Let $\left(Q,\mathbb{S}\right)$ be an $\mathbb{S}$-(M-s) and let $f,h:Q\to Q$ be two self-mappings. It is defined that the pair $\left(f,h\right)$ is a Seghal type $E_{fh}^{\mathbb{S}}$-(Cn.) on Q if ∃$\mathrm{Y}>0$, $E\in \mathcal{E},$ as well as $j_0\in Q$, such that for any $j\in Q$, the following holds:

$$max\left\{\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(j,j,hj\right)\right\}>0⟹\mathrm{Y}+E\left(\mathbb{S}\left(j,j,fj\right)+\mathbb{S}\left(j,j,hj\right)\right)\le E\left(s_{\mathbb{S}}\left(j,j_0\right)\right),$$

where

$$s_{\mathbb{S}}(j,n)=max\left\{\mathbb{S}\left(j,j,n\right),\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(n,n,hn\right)\right\}.$$

Remark 2.

If the pair $\left(f,h\right)$ is a Seghal type $E_{fh}^{\mathbb{S}}$-(Cn.) with $j_0\in Q$, then the pair $\left(f,h\right)$ is a Rhoades type $E_{fh}^{\mathbb{S}}$-(Cn.) with $j_0\in Q$. Nevertheless, the converse might not be constantly correct.

Definition 10.

Consider $\left(Q,\mathbb{S}\right)$ to be an $\mathbb{S}$-(M-s) and $f,h:Q\to Q$ to be two self-mappings. If ∃ $\mathrm{Y}>0,E\in \mathcal{E}$ as well as $j_0\in Q$ where ∀$j\in Q,$ it fulfills the following:

$$max\left\{\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(j,j,hj\right)\right\}>0⟹\mathrm{Y}+E\left(\mathbb{S}\left(j,j,fj\right)+\mathbb{S}\left(j,j,hj\right)\right)\le E\left(b_1^{\mathbb{S}}(j,j_0)\right),$$

where

$$b_1^{\mathbb{S}}(j,n)=hmax\left\{\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(n,n,hn\right)\right\}$$

with $h\in \left(0,1\right);$ thus, the pair $\left(f,h\right)$ is called a Bianchini type $E_{fh}^{\mathbb{S}}$-(Cn.).

Proposition 7.

Let $\left(Q,\mathbb{S}\right)$ be an $\mathbb{S}$-(M-s) and let $f,h:Q\to Q$ be two self-mappings. We have $f{j}_0=j_0=h{j}_0$, if the pair $\left(f,h\right)$ is a Bianchini type $E_{fh}^{\mathbb{S}}$-(Cn.) with $j_0\in Q.$

Proof. 

This can be easily checked. □

Theorem 7.

Let $\left(Q,\mathbb{S}\right)$ be an $\mathbb{S}$-(M-s) and let $f,h:Q\to Q$ be two self-mappings; the pair $\left(f,h\right)$ is a Bianchini type $E_{fh}^{\mathbb{S}}$-(Cn.) with $j_0\in Q$, and let μ be defined as in (2). Then, $C_{j_0,\mu }^{\mathbb{S}}$ is a common (F.C.) of the pair $\left(f,h\right).$ Particularly, the pair $\left(f,h\right)$ fixes every circle $C_{j_0,\varrho }^{\mathbb{S}}$ with $\varrho <\mu .$

Proof. 

This is straightforward to prove by using the same methods as in Theorem 5. □

Definition 11.

Consider $\left(Q,\mathbb{S}\right)$ to be an $\mathbb{S}$-(M-s) and $f,h:Q\to Q$ to be two self-mappings. If ∃$\mathrm{Y}>0$, $E\in \mathcal{E}$, as well as $j_0\in Q$, where ∀$j\in Q,$ it fulfills the following:

$$max\left\{\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(j,j,hj\right)\right\}>0⟹\mathrm{Y}+E\left(\mathbb{S}\left(j,j,fj\right)+\mathbb{S}\left(j,j,hj\right)\right)\le E\left(b_2^{\mathbb{S}}(j,j_0)\right),$$

where

$$b_2^{\mathbb{S}}(j,n)=\delta \mathbb{S}\left(j,j,n\right)+Lmin\left\{\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(n,n,hn\right),\mathbb{S}\left(j,j,fn\right),\mathbb{S}\left(j,j,hn\right)\right\},$$

with $\delta \in \left(0,1\right]$, and $L\ge 0$, then the pair $\left(f,h\right)$ is called a Berinde type $E_{fh}^{\mathbb{S}}$-(Cn.).

Proposition 8.

Consider $\left(Q,\mathbb{S}\right)$ to be an $\mathbb{S}$-(M-s) and $f,h:Q\to Q$ to be two self-mappings. If the pair $\left(f,h\right)$ is a Berinde type $E_{fh}^{\mathbb{S}}$-(Cn.) with $j_0\in Q,$ then we have $f{j}_0=j_0=h{j}_0.$

Proof. 

On the contrary, suppose that $j_0$ is not a common (F.P.) of f and h. Thus, we obtain $\mathbb{S}\left(j_0,j_0,f{j}_0\right)>0$ or $\mathbb{S}\left(j_0,j_0,h{j}_0\right)>0$, that is,

$$max\left\{\mathbb{S}\left(j_0,j_0,f{j}_0\right),\mathbb{S}\left(j_0,j_0,h{j}_0\right)\right\}>0.$$

Hence, we obtain

$$\begin{array}{cc}\hfill & \mathrm{Y}+E\left(\mathbb{S}(j_0,j_0,f{j}_0)+\mathbb{S}\left(j_0,j_0,h{j}_0\right)\right)\hfill \\ \hfill & \le E\left(\delta \mathbb{S}\left(j_0,j_0,j_0\right)+Lmin\left\{\begin{array}{c}\mathbb{S}\left(j_0,j_0,f{j}_0\right),\mathbb{S}\left(j_0,j_0,h{j}_0\right),\\ \mathbb{S}\left(j_0,j_0,f{j}_0\right),\mathbb{S}\left(j_0,j_0,h{j}_0\right)\end{array}\right\}\right)\hfill \\ \hfill & =E\left(Lmin\left\{\mathbb{S}\left(j_0,j_0,f{j}_0\right),\mathbb{S}\left(j_0,j_0,h{j}_0\right)\right\}\right)\hfill \\ \hfill & <E\left(\mathbb{S}(j_0,j_0,f{j}_0)+\mathbb{S}\left(j_0,j_0,h{j}_0\right)\right).\hfill \end{array}$$

However, this creates a contradiction because of $\mathrm{Y}>0$ and because E is strictly increasing. Consequently, we obtain

$$f{j}_0=j_0=h{j}_0.$$

□

Theorem 8.

Let $\left(Q,\mathbb{S}\right)$ be an $\mathbb{S}$-(M-s), and let $f,h:Q\to Q$ be two self-mappings; the pair $\left(f,h\right)$ is a Berinde type $E_{fh}^{\mathbb{S}}$-(Cn.) with $j_0\in Q$, and let μ be defined as in (2). Then, $C_{j_0,\mu }^{\mathbb{S}}$ is a common (F.C.) of the pair $\left(f,h\right).$ Especially, the pair $\left(f,h\right)$ fixes every circle $C_{j_0,\varrho }^{\mathbb{S}}$ with $\varrho <\mu .$

Proof. 

Under the above cases, we prove:

Case 1. Let $\mu =0.$ It is obvious that $C_{j_0,\mu }^{\mathbb{S}}=\left\{j_0\right\},$ and Proposition 8 demonstrates that $C_{j_0,\mu }^{\mathbb{S}}$ is a common (F.C.) of the pair $\left(f,h\right).$

Case 2: Take $\mu >0$ and $j\in C_{j_0,\mu }^{\mathbb{S}}$ with $max\left\{\mathbb{S}(j,j,fj),\mathbb{S}\left(j,j,hj\right)\right\}>0$. Using the Berinde type $E_{fh}^{\mathbb{S}}$-(Cn.), Proposition 8, and the fact that E is strictly increasing, we have

$$\begin{array}{cc}\hfill E\left(\mu \right)& \le E\left(\mathbb{S}\left(j,j,fj\right)+\mathbb{S}\left(j,j,hj\right)\right)\hfill \\ \hfill & \le E\left(\delta \mathbb{S}\left(j,j,j_0\right)+Lmin\left\{\begin{array}{c}\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(j_0,j_0,h{j}_0\right),\\ \mathbb{S}\left(j,j,f{j}_0\right),\mathbb{S}\left(j,j,h{j}_0\right)\end{array}\right\}\right)-\mathrm{Y}\hfill \\ \hfill & <E\left(\delta \mathbb{S}\left(j,j,j_0\right)+Lmin\left\{\mathbb{S}\left(j,j,fj\right),0,\mu ,\mu \right\}\right)\hfill \\ \hfill & =E\left(\delta \mu +0\right)\hfill \\ \hfill & <E\left(\mu \right).\hfill \end{array}$$

This creates a contradiction since E is strictly increasing. So, $max\left\{\mathbb{S}(j,j,fj),\mathbb{S}\left(j,j,hj\right)\right\}=0$, that is,

$$fj=j=hj.$$

Consequently, $C_{j_0,\mu }^{\mathbb{S}}$ is a common (F.C.) of the pair $\left(f,h\right).$ By using the same reasoning in the proof of Theorem 5, the pair $\left(f,h\right)$ also fixes any circle $C_{j_0,\varrho }^{\mathbb{S}}$ with $\varrho <\mu .$ □

We present a model which demonstrates the effectiveness of the proven common fixed-circle theorems on $\mathbb{S}$-(M-s)s.

Example 3.

Let $Q=\left\{1,2,e^3,e^3-2,e^3+2\right\}$ be the $\mathbb{S}$-(M-s), with the $\mathbb{S}$-metric defined as

$$\mathbb{S}(j,n,p)=\left|j-p\right|+\left|j+p-2v\right|,$$

for all $j,n,p\in Q$ [15]. This $\mathbb{S}$-metric is not generated by any metric. Therefore, this example is important for showing the validity of our obtained results. To achieve this, take the self-mapping $f,h:Q\to Q$, defined as in Example 2.

The pair $\left(f,h\right)$ is a Ciric type $E_{fh}^{\mathbb{S}}$-(Cn.), with $E\left(j\right)=j+lnj$, $\mathrm{Y}=2\left(e^3-3\right)$ and $j_0=e^3.$ Indeed, we obtain

$$max\left\{\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(j,j,hj\right)\right\}=max\left\{\mathbb{S}\left(1,1,2\right),\mathbb{S}\left(1,1,2\right)\right\}=2>0$$

for $j=1$, and we obtain

$$\begin{array}{cc}\hfill c_{\mathbb{S}}\left(j,j_0\right)& =max\left\{\begin{array}{c}\mathbb{S}\left(j,j,j_0\right),\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(j_0,j_0,h{j}_0\right),\\ \frac{1}{2}\left[\mathbb{S}\left(j,j,f{j}_0\right)+\mathbb{S}\left(j,j,h{j}_0\right)\right]\end{array}\right\}\hfill \\ \hfill & =max\left\{\begin{array}{c}\mathbb{S}\left(1,1,e^3\right),\mathbb{S}\left(1,1,2\right),\mathbb{S}\left(e^3,e^3,e^3\right),\\ \frac{1}{2}\left[\mathbb{S}\left(1,1,e^3\right)+\mathbb{S}\left(1,1,e^3\right)\right]\end{array}\right\}\hfill \\ \hfill & =max\left\{2\left(e^3-1\right),2,0,2\left(e^3-1\right)\right\}\hfill \\ \hfill & =2\left(e^3-1\right).\hfill \end{array}$$

Then, we have

$$\begin{array}{cc}\hfill \mathrm{Y}+E\left(\mathbb{S}\left(j,j,fj\right)+\mathbb{S}\left(j,j,hj\right)\right)& =2\left(e^3-3\right)+4+ln4\hfill \\ \hfill & \le E\left(2\left(e^3-1\right)\right)\hfill \\ \hfill & =2\left(e^3-1\right)+ln\left(2\left(e^3-1\right)\right).\hfill \end{array}$$

Similarly, we can easily see that the pair $\left(f,h\right)$ is a Rhoades type $E_{fh}^{\mathbb{S}}$-(Cn.) and Seghal type $E_{fh}^{\mathbb{S}}$-(Cn.). In addition, the pair $\left(f,h\right)$ is a Berinde type $E_{fh}^{\mathbb{S}}$-(Cn.) with $E\left(j\right)=j+lnj,$$\mathrm{Y}=2$, $\delta =\frac{1}{2}$, and $j_0=e^3.$ Indeed, we obtain

$$max\left\{\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(j,j,hj\right)\right\}=max\left\{\mathbb{S}\left(1,1,2\right),\mathbb{S}\left(1,1,2\right)\right\}=2>0$$

for $j=1$, and we have

$$\begin{array}{cc}\hfill b_2^{\mathbb{S}}(j,j_0)& =\delta \mathbb{S}\left(j,j,j_0\right)+Lmin\left\{\begin{array}{c}\mathbb{S}\left(j,j,fj\right),\mathbb{S}\left(j_0,j_0,h{j}_0\right),\\ \mathbb{S}\left(j,j,f{j}_0\right),\mathbb{S}\left(j,j,h{j}_0\right)\end{array}\right\}\hfill \\ \hfill & =\frac{1}{2}\mathbb{S}\left(1,1,e^3\right)+Lmin\left\{\begin{array}{c}\mathbb{S}\left(1,1,2\right),\mathbb{S}\left(e^3,e^3,e^3\right),\\ \mathbb{S}\left(1,1,e^3\right),\mathbb{S}\left(1,1,e^3\right)\end{array}\right\}\hfill \\ \hfill & =e^3-1+Lmin\left\{2,0,2\left(e^3-1\right),2\left(e^3-1\right)\right\}\hfill \\ \hfill & =e^3-1.\hfill \end{array}$$

Then, we have

$$\begin{array}{cc}\hfill \mathrm{Y}+E\left(\mathbb{S}\left(j,j,fj\right)+\mathbb{S}\left(j,j,hj\right)\right)& =2+4+ln4\hfill \\ \hfill & \le E\left(e^3-1\right)\hfill \\ \hfill & =e^3-1+ln\left(e^3-1\right).\hfill \end{array}$$

Consequently, the pair $\left(f,h\right)$ fixes the circle $C_{e^3,4}^{\mathbb{S}}=\left\{e^3-2,e^3+2\right\}.$

4. An Application to Activation Functions

In neural networks, activation functions have already been broadly applied. There are many examples of activation functions in the literature. In this section, we focus on both rectified linear unit activation functions and parametric rectified linear unit activation functions (for more details, see [31,32] and the citations within these).

The rectified linear unit activation function (ReLU) see Figure 1, was defined as

$$ReLU\left(j\right)=\left\{\begin{array}{ccc}0& ,& j<0\\ j& ,& j\ge 0\end{array}\right.$$

and the parametric rectified linear unit activation function (PReLU) see Figure 2, was defined as

$$PReLU\left(j\right)=\left\{\begin{array}{ccc}\alpha j& ,& j<0\\ j& ,& j\ge 0\end{array}\right.,$$

where $\alpha$ is the coefficient.

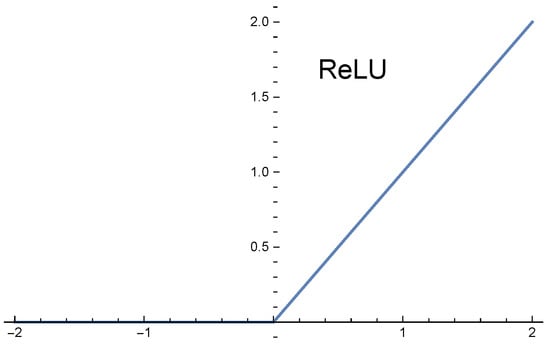
Figure 1. The graph of the function ReLU.

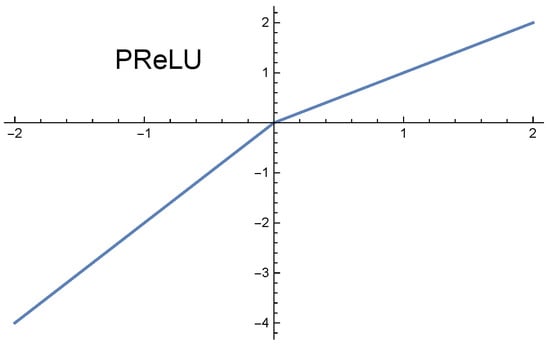
Figure 2. The graph of the function PReLU.

Let us consider these activation functions on $Q={\mathbb{R}}^{+}\cup \left\{-1,0\right\}$ with the usual metric. If we take $\alpha =2$, then we have

$$PReLU\left(j\right)=\left\{\begin{array}{ccc}2j& ,& j<0\\ j& ,& j\ge 0\end{array}\right..$$

The pair $\left(PReLU,ReLU\right)$ is a Ciric type $E_{fh}$-(Cn.) with $E\left(j\right)=lnj$, $\mathrm{Y}=ln2$, and $j_0=\pi .$ Indeed, for $j=-1$, we obtain

$$max\left\{\delta \left(j,PReLU\left(j\right)\right),\delta \left(j,ReLU\left(j\right)\right)\right\}=max\left\{\delta \left(-1,-2\right),\delta \left(-1,0\right)\right\}=1>0$$

, and we obtain

$$\begin{array}{cc}\hfill c\left(j,j_0\right)& =max\left\{\begin{array}{c}\delta \left(j,j_0\right),\delta \left(j,PReLU\left(j\right)\right),\delta \left(j_0,ReLU\left(j_0\right)\right),\\ \frac{1}{2}\left[\delta \left(j,PReLU\left(j_0\right)\right)+\delta \left(j,ReLU\left(j_0\right)\right)\right]\end{array}\right\}\hfill \\ \hfill & =max\left\{\delta \left(-1,\pi \right),\delta \left(-1,-2\right),\delta \left(\pi ,\pi \right),\frac{1}{2}\left[\delta \left(-1,\pi \right)+\delta \left(-1,\pi \right)\right]\right\}\hfill \\ \hfill & =max\left\{\pi +1,1,0,\pi +1\right\}\hfill \\ \hfill & =\pi +1.\hfill \end{array}$$

Then, we have

$$\begin{array}{cc}\hfill \mathrm{Y}+E\left(\delta \left(j,fj\right)+\delta \left(j,hj\right)\right)& =ln2+ln2=ln4\hfill \\ \hfill & \le ln\left(\pi +1\right)\hfill \\ \hfill & =E\left(\pi +1\right).\hfill \end{array}$$

In addition, we obtain

$$\sigma =inf\left\{\begin{array}{c}\delta \left(j,PReLU\left(j\right)\right)+\delta \left(j,ReLU\left(j\right)\right)\\ :j\ne PReLU\left(j\right),j\ne ReLU\left(j\right),j\in Q\end{array}\right\}=2$$

, and so $C_{\pi ,2}$ is a common (F.C.) of the pair $\left(PReLU,ReLU\right)$.