Abstract
In this paper, we modify various contractive conditions (C.C.)s such as Ciric type (C.C.), Rhoades type (C.C.), Seghal type (C.C.), Bianchini type (C.C.), and Berinde type (C.C.) for two self-mappings, considering that the contractive property plays a major role in establishing a fixed circle (F.C.) on both metric spaces (M-s) and -(M-s) where the symmetry condition is satisfied, and we utilize them to establish a common (F.C.). We prove new (F.C.) results on both (M-s) and -(M-s) with illustrative examples. Finally, we provide an application to activation functions such as rectified linear unit activation functions and parametric rectified linear unit activation functions.
1. Introduction
Fixed point (F.P.) theory has been extensively studied under different aspects. One of the most commonly studied areas of (F.P.) theory is metric (F.P.) theory. This theory began with Banach’s theorem on (F.P.)s. The theorem is often known as the principle of Banach’s contraction (Cn.). This theory has been extended in three mechanisms:
(1) To generalize the (C.C.) being employed.
(2) To extend the utilized (M-s).
(3) To examine the geometric characteristics of an (F.P.) set of a self-mapping.
Under the first approach, many (C.C.)s were defined in the literature. For example, Ciric type (C.C.) [1,2], Rhoades type (C.C.) [3], Seghal type (C.C.) [4], Bianchini type (C.C.) [5], and Berinde type (C.C.) [6,7] were introduced for this purpose.
Under the second approach, many generalizations of an (M-s) were defined [8,9,10,11,12,13]. For instance, the concept of an -(M-s) was created for this reason in [14] which is a new type of symmetric metric spaces. Now, let us review some fundamental principles of -(M-s)s.
Definition 1
([14]). Let and consider the function . If meets the requirements listed below for all :
,
,
then is termed an -metric on Q; hence, the pair is said to be -(M-s).
Lemma 1
([14]). Consider to be an -(M-s) and . Hence, we obtain
Refs. [15,16,17] examined the links among a metric and an -(M-s). The following is a formula for an -(M-s) that is created by a metric
Let be an (M-s). Thus, the function specified by
for all is an -metric on Q. The -metric is called the -metric generated by and also a model of an -metric that is not extended by any metric (for further information, see [15]).
Under the third approach, recently, the geometric features of non-unique (F.P.)s have been intensively explored in a variety of contexts, such as the (F.C.) problem, the fixed-disc problem, and so on. Özgür and Taş [18] introduced the concept of an (F.C.) in an (M-s) as a novel strategy for the generalization of (F.P.) theory. Several writers have elaborately refined the notion of (F.C.)s and its applications for usage in topology and geometry. Significantly, Refs. [19,20,21,22,23] have introduced the concepts of (F.C.)s in different generalized (M-s)s. In addition, some open questions were provided in the literature related to the (F.C.) problem. For instance, in [24], the below problem was provided for common (F.C.)s:
Open Problem: What condition(s) is(are) necessary for any circle to be the common (F.C.) for two or more self-mappings?
Now, we recall the following definition:
Let be an (M-s), let be any circle on Q, and let f, h be two self-mappings on Q. If for all , then is said to be a common (F.C.) of the pair (as in [25]).
A few solutions have been proposed for this open problem (see [25,26,27]). In order to obtain novel solutions, we specify some (Cn.)s for the pair and prove some common (F.C.) results on (M-s)s. In fact, this study can be considered as a continuation of [26].
The present paper attempts to obtain common (F.C.) theorems for self-mappings under various types of (C.C.)s. Inspired by Wardowski [28], in the context of F-(Cn.), we have proven certain common (F.C.) theorems.
Let represent the collection of all the mappings that hold for the axioms listed below:
- E is firmly increasing, then ∀, , such that
- For every sequence in the subsequent is true.
if and only if
- ∃ where
Many examples of the functions that belong to are and .
In this sequel, we examine new solutions to the listed open problems under these three approaches. In order to achieve this, we change several recognized (C.C.)s on (M-s), and the defined conditions are generalized on -(M-s). For this purpose, we introduce the notions of a Ciric type -(Cn.), a Rhoades type -(Cn.), a Seghal type -(Cn.), a Bianchini type -(Cn.), and a Berinde type -(Cn.) on (M-s). In addition, these (Cn.)s are generalized on -(M-s), such as a Ciric type -(Cn.), a Rhoades type -(Cn.), a Seghal type -(Cn.), a Bianchini type -(Cn.), and a Berinde type -(Cn.). Utilizing these new (Cn.)s, we prove some common (F.C.) results on both metric and -(M-s) with some illustrative examples. Finally, we give an application to the activation functions, such as rectified linear unit activation functions (), as well as parametric rectified linear unit activation functions ().
2. Some Common (F.C.) Results on (M-s)s
In this part, we demonstrate brand-new common (F.C.) theorem metric spaces. In order to obtain some typical (F.C.) results on (M-s)s, we begin by introducing the new (Cn.) type for two mappings.
Let be an (M-s), and let f, h be two self-mappings on a set Q. The number is defined by
Definition 2.
Let be an (M-s) and let be two self-mappings. It is defined that the pair is a Ciric type -(Cn.) on Q if ∃, , and , where for any , the following is true:
where
Proposition 1.
Let be an (M-s) and let be two self-mappings. If the pair is a Ciric type -(Cn.) with , then we have
Proof.
On the contrary, suppose that is not a common (F.P.) of f and h. Hence, we obtain or ; that is,
Hence, we obtain
However, this leads to a contradiction because and E is a strict increase. Consequently, we obtain
□
Theorem 1.
Let be an (M-s), let be two self-mappings, and let the pair be a Ciric type -(Cn.) with and ω be defined as in (1). Then, is a common (F.C.) of the pair In particular, the pair fixes every circle with
Two cases are identified.
Case 1: Assume that Obviously, , and along with Proposition 1, we observe that is a common (F.C.) of the pair
Case 2: Assume that and with . Using the Ciric type -(Cn.) property in addition to the fact that E is strictly rising, we obtain
This creates a contradiction. Hence, , and so,
Consequently, is a common (F.C.) of the pair .
Meanwhile, we prove that the pair fixes any circle with Suppose that with . According to the Ciric type -(Cn.), it yields to
which is a contradiction. So, we have , and so,
Consequently, is a common (F.C.) of the pair
Definition 3.
Let be an (M-s) and let be two self-mappings. If ∃ and , where ∀ if it fulfills the following:
where
hence, the pair is called a Rhoades type -(Cn.).
Proposition 2.
Consider to be an (M-s) and let be two self-mappings. We have if the pair is a Rhoades type -(Cn.) with
Proof.
The similar justifications offered in Proposition 1 make it simple to demonstrate. □
Theorem 2.
Let be an (M-s), and be two self-mappings; let the pair be a Rhoades type -(Cn.) with and ω is defined as follows (1). If , then is a common (F.C.) of the pair Furthermore, the pair fixes every circle with
Proof.
We differentiate two situations.
Case 1: Let It is obvious that and Proposition 2 demonstrates that is a common (F.C.) of the pair
Case 2: Let and with . According to the Rhoades type -(Cn.) property, as well as the fact that E is strictly rising, it yields to
It is contradictory in this way, due to the fact that , that is,
As a result, is a common (F.C.) of the pair The pair also fixes any circle with using the same justifications as in the proof of Theorem 1. □
Definition 4.
Let be an (M-s) and let be two self-mappings. It is defined that the pair is a Seghal type -(Cn.) on Q, if ∃ exists, , as well as , such that for any , the following holds:
where
Remark 1.
If the pair is a Seghal type -(Cn.) with , then the pair is a Rhoades type -(Cn.) with . Indeed, we have
when .
The converse statement is not always true.
Example 1.
Suppose that is a usual (M-s) and that the self-mappings are characterized as
and
for all . For , the pair satisfies the condition of Rhoades type -(Cn.) with , , and . Indeed, we have
, and
However, the pair does not satisfy the condition of the Seghal type -(Cn.) with , , and .
Definition 5.
Let be an (M-s) and let be two self-mappings. If ∃, as well as , where ∀ it fulfills the following:
where
with hence, the pair is called a Bianchini type -(Cn.).
Proposition 3.
Suppose that is an (M-s) along with be two self-mappings. We have , if the pair is a Bianchini type -(Cn.) with
Proof.
If is not a common (F.P.) of f and h, it yields to or , that is,
Hence, we obtain
where . However, this creates a contradiction since E is strictly increased. Consequently, we obtain
□
Theorem 3.
Let be an (M-s), and let be two self-mappings; the pair is a Bianchini type -(Cn.) with and ω is defined as in (1). Then, is a common (F.C.) of the pair Especially, the pair fixes every circle with
Proof.
We differentiate two situations:
Case 1. Assume that . It is obvious that , and Proposition 3 demonstrates that is a common (F.C.) of the pair
Case 2: Assume that and with . Using the Bianchini type -(Cn.) and Proposition 3, along with the fact that E is increasing, we have
This creates a contradiction. Thus, that is,
Consequently, is a common (F.C.) of the pair By using similar considerations in the proof of Theorem 1, f and h also fix any circle with □
Definition 6.
Let be an (M-s) and let be two self-mappings. If ∃ and , such that where ∀ it yields to the following:
where
with and , then the pair is called a Berinde type -(Cn.).
Proposition 4.
Let be an (M-s) and let be two self-mappings. If the pair is a Berinde type -(Cn.) with then we have
Proof.
The proof is simple because of the similar justifications offered in Proposition 1. □
Theorem 4.
Let be an (M-s) and let be two self-mappings; the pair is a Berinde type -(Cn.) with and ω is defined as in (1). Then, is a common (F.C.) of the pair Particularly, the pair fixes every circle with
Proof.
We differentiate two cases:
Case 1. Let It is obvious that and Proposition 4 demonstrates that is a common (F.C.) of the pair
Case 2: Let and with . Using the Berinde type -(Cn.), Proposition 4, and the fact that E is strictly increasing, we obtain
This creates a contradiction since E is a strictly increasing. So, , that is,
Consequently, is a common (F.C.) of the pair By using similar considerations in the proof of Theorem 1, the pair also fixes any circle with □
This is an example to illustrate our argument.
Example 2.
Let be the (M-s) with the usual metric. We define the self-mapping as
and
for all
The pair is a Ciric type -(Cn.) (resp. Rhoades type -(Cn.) and Seghal type -(Cn.)) with , , and Indeed, we get
for , and we obtain
Then, we have
Similarly, we can easily see that the pair is a Rhoades type -(Cn.) and a Seghal type -(Cn.). In addition, the pair is a Berinde type -(Cn.) with , , and Indeed, we obtain
for , and we have
Then, we have
Consequently, the pair fixes the circle
3. Some Common (F.C.) Results on -(M-s)s
In this section, we explore some common (F.C.) theorems on -(M-s)s. To achieve this, we generalize the proven results in the previous section. Some basic notions were presented that were related to the (F.C.) problem on -(M-s)s in [14,29,30].
Let be an -(M-s), and let be any circle on Q and f; let h be two self-mappings on a set Q. If for all , then is called a common (F.C.) of the pair .
Definition 7.
Let be an -(M-s) and let be two self-mappings. It is defined that the pair is a Ciric type -(Cn.) on Q if ∃, , along with , such that for any , the following affirms:
where
Proposition 5.
Let be an -(M-s) and let be two self-mappings. If the pair is a Ciric type -(Cn.) with , then we have
Proof.
On the contrary, suppose that is not a common (F.P.) of f and h. Hence, we obtain or , that is,
Hence, we obtain
However, this creates a contradiction because of , and E is a strict increase. Consequently, we obtain
□
Theorem 5.
Let be an -(M-s); let be two self-mappings and the pair be a Ciric type -(Cn.) with , and let μ be defined as
Then, is a common (F.C.) of the pair Particularly, the pair fixes every circle with
Proof.
Let us examine the following cases:
Case 1: Take Clearly, . Moreover, according to Proposition 5, we observe that is a common (F.C.) of the pair
Case 2: Let and , with . Using the Ciric type -(Cn.) property, along with the fact that E is strictly rising, it yields to
This creates a contradiction. Hence, , and so,
Consequently, is a common (F.C.) of the pair .
Now, we prove that the pair fixes any circle with Let with . According to the Ciric type -(Cn.), we obtain
which is a contradiction. So, we have and so,
Consequently, is a common (F.C.) of the pair □
Definition 8.
Let be an -(M-s) and be two self-mappings. If ∃ , , as well as , where ∀ and it fulfills the following:
where
hence, the pair is called a Rhoades type -(Cn.).
Proposition 6.
Consider to be an -(M-s) and let be two self-mappings. We have , if the pair is a Rhoades type -(Cn.) with
Proof.
We apply similar reasons to those presented in Proposition 5, which is plainly visible. □
Theorem 6.
Consider to be an -(M-s), and let be two self-mappings; let the pair be a Rhoades type -(Cn.) with , and let μ be defined as follows (2). If , then is a common (F.C.) of the pair Furthermore, the pair fixes every circle with
Proof.
This is straightforward to prove by using the same methods as in Theorem 5. □
Definition 9.
Let be an -(M-s) and let be two self-mappings. It is defined that the pair is a Seghal type -(Cn.) on Q if ∃, as well as , such that for any , the following holds:
where
Remark 2.
If the pair is a Seghal type -(Cn.) with , then the pair is a Rhoades type -(Cn.) with . Nevertheless, the converse might not be constantly correct.
Definition 10.
Consider to be an -(M-s) and to be two self-mappings. If ∃ as well as where ∀ it fulfills the following:
where
with thus, the pair is called a Bianchini type -(Cn.).
Proposition 7.
Let be an -(M-s) and let be two self-mappings. We have , if the pair is a Bianchini type -(Cn.) with
Proof.
This can be easily checked. □
Theorem 7.
Let be an -(M-s) and let be two self-mappings; the pair is a Bianchini type -(Cn.) with , and let μ be defined as in (2). Then, is a common (F.C.) of the pair Particularly, the pair fixes every circle with
Proof.
This is straightforward to prove by using the same methods as in Theorem 5. □
Definition 11.
Consider to be an -(M-s) and to be two self-mappings. If ∃, , as well as , where ∀ it fulfills the following:
where
with , and , then the pair is called a Berinde type -(Cn.).
Proposition 8.
Consider to be an -(M-s) and to be two self-mappings. If the pair is a Berinde type -(Cn.) with then we have
Proof.
On the contrary, suppose that is not a common (F.P.) of f and h. Thus, we obtain or , that is,
Hence, we obtain
However, this creates a contradiction because of and because E is strictly increasing. Consequently, we obtain
□
Theorem 8.
Let be an -(M-s), and let be two self-mappings; the pair is a Berinde type -(Cn.) with , and let μ be defined as in (2). Then, is a common (F.C.) of the pair Especially, the pair fixes every circle with
Proof.
Under the above cases, we prove:
Case 1. Let It is obvious that and Proposition 8 demonstrates that is a common (F.C.) of the pair
Case 2: Take and with . Using the Berinde type -(Cn.), Proposition 8, and the fact that E is strictly increasing, we have
This creates a contradiction since E is strictly increasing. So, , that is,
Consequently, is a common (F.C.) of the pair By using the same reasoning in the proof of Theorem 5, the pair also fixes any circle with □
We present a model which demonstrates the effectiveness of the proven common fixed-circle theorems on -(M-s)s.
Example 3.
Let be the -(M-s), with the -metric defined as
for all [15]. This -metric is not generated by any metric. Therefore, this example is important for showing the validity of our obtained results. To achieve this, take the self-mapping , defined as in Example 2.
The pair is a Ciric type -(Cn.), with , and Indeed, we obtain
for , and we obtain
Then, we have
Similarly, we can easily see that the pair is a Rhoades type -(Cn.) and Seghal type -(Cn.). In addition, the pair is a Berinde type -(Cn.) with , , and Indeed, we obtain
for , and we have
Then, we have
Consequently, the pair fixes the circle
4. An Application to Activation Functions
In neural networks, activation functions have already been broadly applied. There are many examples of activation functions in the literature. In this section, we focus on both rectified linear unit activation functions and parametric rectified linear unit activation functions (for more details, see [31,32] and the citations within these).
The rectified linear unit activation function (ReLU) see Figure 1, was defined as
and the parametric rectified linear unit activation function (PReLU) see Figure 2, was defined as
where is the coefficient.
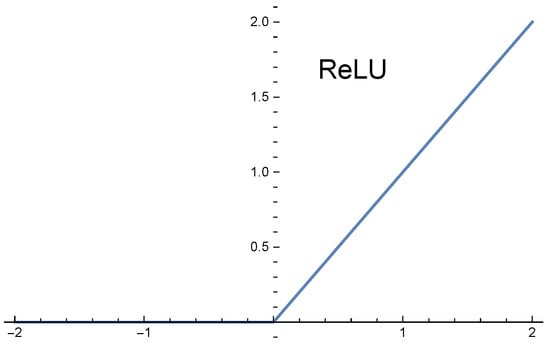
Figure 1.
The graph of the function ReLU.
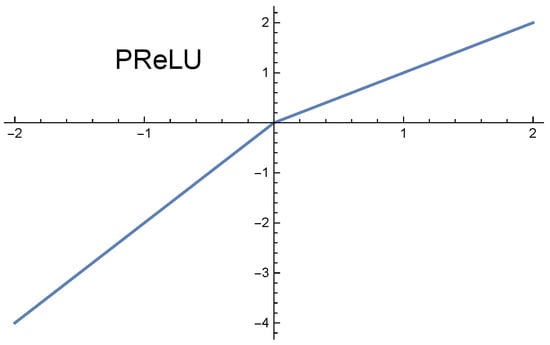
Figure 2.
The graph of the function PReLU.
Let us consider these activation functions on with the usual metric. If we take , then we have
The pair is a Ciric type -(Cn.) with , , and Indeed, for , we obtain
, and we obtain
Then, we have
In addition, we obtain
, and so is a common (F.C.) of the pair .
Author Contributions
N.T.: conceptualization, writing—original draft; E.K.: conceptualization, supervision, writing—original draft; D.S.: investigation, writing—review and editing; N.M.: writing—original draft, supervision, methodology; W.S.: investigation, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The authors D. Santina, N. Mlaiki, and W. Shatanawi would like to thank Prince Sultan University for covering the article processing charge for this work via TAS LAB. The authors thank the referees for their valuable comments and remarks, which improved the original manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ciric, L.B. A generalization of Banach’s contraction principle. Proc. Am. Math. Soc. 1974, 45, 267–273. [Google Scholar] [CrossRef]
- Ciric, L.B. Generalized contractions and fixed-point theorems. Publ. L’Institut Matheematique 1971, 12, 19–26. [Google Scholar]
- Rhoades, B.E. A comparison of various definitions of contractive mappings. Trans. Am. Math. Soc. 1977, 226, 257–290. [Google Scholar] [CrossRef]
- Sehgal, V.M. On fixed and periodic points for a class of mappings. J. Lond. Math. Soc. 1972, 2, 571–576. [Google Scholar] [CrossRef]
- Bianchini, R.M.T. Su un problema di S. Reich aguardante la teoría dei punti fissi. Boll. dell’Unione Mat. Ital. 1972, 5, 103–110. [Google Scholar]
- Berinde, V. Approximating fixed points of weak contractions using the Picard iteration. Nonlinear Anal. Forum. 2004, 9, 43–53. [Google Scholar]
- Berinde, V. General constructive fixed point theorem for Ciric-type almost contractions in metric spaces. Carpath. J. Math. 2008, 24, 10–19. [Google Scholar]
- Aslam, M.S.; Chowdhury, M.S.R.; Guran, L.; Alqudah, M.A.; Abdeljawad, T. Fixed point theory in complex valued controlled metric spaces with an application. AIMS Math. 2022, 7, 11879–11904. [Google Scholar] [CrossRef]
- Bouftouh, O.; Kabbaj, S.; Abdeljawad, T.; Mukheimer, A. On fixed point theorems in C-algebra valued b-asymmetric metric spaces. AIMS Math. 2022, 7, 11851–11861. [Google Scholar] [CrossRef]
- Shoaib, M.; Sarwar, M.; Abdeljawad, T. Common fixed point results for couples (f,g) and (S,T) satisfy strong common limit range property. AIMS Math. 2020, 5, 3480–3494. [Google Scholar] [CrossRef]
- Asif, A.; Khan, S.U.; Abdeljawad, T.; Arshad, M.; Savas, E. 3D analysis of modified F-contractions in convex b-metric spaces with application to Fredholm integral equations. AIMS Math. 2020, 5, 6929–6948. [Google Scholar] [CrossRef]
- Shatanawi, W.; Shatnawi, T.A. Some fixed point results based on contractions of new types for extended b-metric spaces. AIMS Math. 2023, 8, 10929–10946. [Google Scholar] [CrossRef]
- Gharib, G.M.; Malkawi, A.A.-R.M.; Rabaiah, A.M.; Shatanawi, W.A.; Alsauodi, M.S. A Common Fixed Point Theorem in an M*-Metric Space and an Application. Nonlinear Funct. Anal. Appl. 2022, 27, 289–308. [Google Scholar]
- Sedghi, S.; Shobe, N.; Aliouche, A. A generalization of fixed point theorems in 𝕊-metric spaces. Mat. Vesnik. 2012, 64, 258–266. [Google Scholar]
- Özgür, N.Y.; Taş, N. Some new contractive mappings on 𝕊-metric spaces and their relationships with the mapping (S25). Math. Sci. 2017, 11, 7–16. [Google Scholar] [CrossRef]
- Gupta, A. Cyclic contraction on 𝕊-metric space. Int. J. Anal. Appl. 2013, 3, 119–130. [Google Scholar]
- Hieu, N.T.; Ly, N.T.; Dung, N.V. A generalization of Ciric quasi-contractions for maps on 𝕊-metric spaces. Thai. J. Math. 2015, 13, 369–380. [Google Scholar]
- Özgür, N.Y.; Taş, N. Some fixed-circle theorems on metric spaces. Bull. Malays. Math. Sci. Soc. 2019, 42, 1433–1449. [Google Scholar] [CrossRef]
- Özgür, N.Y.; Taş, N.; Çelik, U. New fixed-circle results on 𝕊-metric spaces. Bull. Math. Anal. Appl. 2017, 9, 10–23. [Google Scholar]
- Aydi, H.; Taş, N.; Özgür, N.Y.; Mlaiki, N. Fixed-discs in rectangular metric spaces. Symmetry 2019, 11, 294. [Google Scholar] [CrossRef]
- Kaplan, E.; Mlaiki, N.; Taş, N.; Haque, S.; Souayah, A.K. Some Fixed-Circle Results with Different Auxiliary Functions. J. Funct. Spaces 2022, 2022, 2775733. [Google Scholar] [CrossRef]
- Mlaiki, N.; Özgür, N.Y.; Mukheimer, A.; Taş, N. A new extension of the Mb-metric spaces. J. Math. Anal. 2018, 9, 118–133. [Google Scholar]
- Tas, N. Various types of fixed-point theorems on 𝕊-metric spaces. Balıkesir Üniversitesi Fen Bilimleri Enstitüsü Dergisi 2018, 20, 211–223. [Google Scholar]
- Mlaiki, N.; Ozgur, N.; Tas, N. New fixed-circle results related to Fc-contractive and Fc-expanding mappings on metric spaces. arXiv 2021, arXiv:2101.10770. [Google Scholar]
- Mlaiki, N.; Tas, N.; Özgür, N.Y. On the fixed-circle problem and Khan type contractions. Axioms 2018, 7, 80. [Google Scholar] [CrossRef]
- Mlaiki, N.; Tas, N.; Kaplan, E.; Subhi Aiadi, S.; Karoui Souayah, A. Some Common Fixed-Circle Results on Metric Spaces. Axioms 2022, 11, 454. [Google Scholar] [CrossRef]
- Tas, N. Bilateral-type solutions to the fixed-circle problem with rectified linear units application. Turk. J. Math. 2020, 44, 1330–1344. [Google Scholar] [CrossRef]
- Wardowski, D. Fixed points of new type of contractive mappings in complete metric spaces. Fixed Point Theory Appl. 2012, 94, 1–6. [Google Scholar] [CrossRef]
- Özgür, N.Y.; Taş, N. Fixed-circle problem on 𝕊-metric spaces with a geometric viewpoint, Facta Universitatis. Ser. Math. Inform. 2019, 34, 459–472. [Google Scholar] [CrossRef]
- Mlaiki, N.; Çelik, U.; Taş, N.; Özgür, N.Y.; Mukheimer, A. Wardowski type contractions and the fixed-circle problem on 𝕊-metric spaces. J. Math. 2018, 2018, 127486. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet classification with deep convolutional neural networks. Commun. ACM 60, 84–90. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).