Abstract
The violation of charge-parity symmetry and the baryon asymmetry of the universe are two of the most significant unresolved problems in physics. This article presents further research on the CP violation problem in the Standard Model with 32 candidate sets of the 10 “natural” parameters that exhibit the same Cabibbo–Kobayashi–Maskawa performance. These parameters are considered “natural” because they consist solely of the Yukawa couplings and the vacuum expectation value of the unique Higgs doublet in the Standard Model. Then, the problems of CP violation and the baryon asymmetry of the universe are investigated by using the Jarlskog measure of CP violation, , given that CP symmetry is violated following the breakdown of symmetries. Subsequently, numerical tests are performed in a simplified scenario where eight of the ten parameters are assumed to be fixed by two assumptions, and the remaining two parameters are allowed to vary from the -symmetric point to their current values in all 32 parameter sets. To estimate the enhancement of CP violation in such processes, a ratio is proposed between the running and its current value, denoted by , which is approximately . In all 32 cases, the three-dimensional plots of exhibit many regions that stick out of the plane, especially in regions very close to . These results demonstrate that the -breaking Standard Model is already sufficient to violate CP symmetry explicitly and generate a significant amount of baryon asymmetry of the universe. Furthermore, it solves existing problems without creating new ones, at least in the scenario presented in this article.
1. Introduction
The problem of how charge-parity (CP) symmetry was violated in electroweak interactions has not been solved since it was discovered in 1964 [1]. In the Standard Model (SM) of electroweak interactions, CP violation (CPV) comes solely from a complex phase in the Cabibbo–Kobayashi–Maskawa (CKM) matrix [2,3]. However, the CKM matrix is a product of two unitary transformation matrices that diagonalize the mass matrices of up- and down-type quarks, respectively. Naturally, the key to igniting CPV is concealed in the quark mass matrices.
In our previous research, we found that in SM and in its extension with one extra Higgs doublet, the two-Higgs doublet model (2HDM), symmetries among three fermion generations always make the CP symmetry conserved [4,5,6,7,8]. However, if the symmetries are broken down into various residual symmetries, a complex phase appears explicitly in the CKM matrix, which means that CP symmetry was violated following the breakdown of symmetries [9,10]. The Jarlskog invariant thus derived is about 5700 times that of its current value given by current experiments [11].
In two subsequent research studies [10,12], the symmetries can be further broken down to be completely asymmetric, and the derived CKM matrix contains only four parameters: two from up-type quarks and two from down-type quarks. These four parameters are natural since they are solely composed of the Yukawa couplings and v, the vacuum expectation value (VEV) of the only Higgs doublet in SM. The CKM elements thus derived fit experiments to an accuracy of or better at tree level.
How and when the baryon asymmetry of the universe (BAU) [13,14,15] was produced and remains to this day is another long-unsolved problem in physics. In cosmology, BAU is estimated by the excess of baryons over anti-baryons, denoted by or , where , , , and s are number densities of baryon, anti-baryon, photon, and entropy density observed in the current universe, respectively. By combining the results from both the mission [13,14] and the Wilkinson Microwave Anisotropy Probe () [15], a value of is obtained.
However, such a quantity is measured in the Standard Model of particle physics by the Jarlskog measure of CPV [16,17],
Here, J is the Jarlskog invariant, 100 GeV is the temperature of the electroweak phase transition, and are squares of quark masses. In many other studies, the factor has been replaced by , where 246 GeV is the VEV of the SM Higgs doublet. However, in this article, choosing between or is not a problem at all, since this factor will be canceled out automatically, as will be shown in Section 3.
Substituting all parameters in with their current empirical values, is given by [11,18,19,20,21], which is much smaller than the cosmologically observed . The discrepancy between these two quantities is called the BAU problem [13,14,15].
The Jarlskog measure of CPV incorporates a term related to and a CKM-related Jarlskog invariant given by
where and are Levi-Civita symbols, are the ith column and jth row elements of CKM matrix, and = 1 to 3. Due to the unitarity of , J must always be smaller than 1. Obviously, increasing J alone is never enough to account for the discrepancy. In addition to J, squared quark masses also contribute to , and our previous research showed that the mass eigenvalues rely on five parameters for each quark type. This suggests that varying the quark masses could be another approach to enhance the strength of . This topic will be explored in this article.
In Section 2, a summary of our previous research on the CPV problem is provided, which is essential background information for subsequent investigations. Following the principle of simplicity and elegance in nature, we prefer to study the CPV problem in the SM, if possible, to avoid introducing new physics that can lead to additional problems. We have previously studied the -symmetric 2HDM in [4,5] and found that the CP symmetry is conserved. In [9], we have studied three less symmetric and more complicated patterns for the mass matrices when symmetries were broken down to residual symmetries and observed that the breakdown of symmetries leads to the violation of CP symmetry. However, the breakdown of symmetries and the violation of CP symmetry are likely two effects of the same cause rather than being causally related.
Moreover, it was found that, for every mass matrix pattern obtained in the 2HDM, there is always a corresponding pattern in the SM if each of the elements is re-parameterized by a complex Yukawa coupling and the VEV of the unique Higgs doublet in the SM. Therefore, it is sensible to study the problems in the SM since it will not introduce additional problems. The model was further improved in [9] by replacing the assumed Hermitian M matrices with naturally Hermitian matrices, which increases the generality of the study. In such a case, only a very trivial assumption was required that the real part and the imaginary part of can be simultaneously and respectively diagonalized by the same unitary matrix to solve the CPV problem. This concept solves problems instead of introducing extra problems, such as the FCNC problem in the 2HDM or the masses and Yukawa couplings of new quarks in the fourth-generation extension, and so on.
In Section 3, these materials are applied to , and we perform some simple tests on it, resulting in 64 candidate parameter sets with the same CKM performance, of which half are excluded by their predictions of imaginary quark masses. Then, the ratio is proposed to compare the running with its current value . Since there are 10 parameters in , it is always possible to tune the parameters to obtain , but this is arbitrary and lacks physical meaning.
Therefore, the subsequent study will focus on a simplified case where six of the parameters are fixed to their current values and two parameters to the symmetry of down-type quarks. Then, the remaining parameters and are allowed to vary from their -symmetric values to their current values, searching for regions where . The findings reveal that all 32 cases exhibit numerous such regions, with the most intriguing observation being that there is always a high region around the -symmetric point in their three-dimensional (3D) plots, where is precisely zero. This implies that these cases can offer a highly productive environment for baryon asymmetry generation when the symmetry of up-type quarks starts to break down. Therefore, an -breaking Standard Model may already be sufficient to resolve both the CPV and BAU issues.
In Section 4, brief concluding remarks on this study are provided.
2. CP Violation in the Standard Model
To solve the problems of CPV and BAU, various physical models such as multi-Higgs doublets, fourth fermion generation, super-symmetry, and others have been proposed to extend the Standard Model. However, many of these models have the side effect of introducing new problems, and some even create more problems than they solve. For example, the 2HDM introduces an FCNC problem but does not solve the CPV problem, although this issue was recently addressed in [12]. Therefore, we prefer to explore solutions to these problems using the simplest possible means. If feasible, we hope to solve these issues using the Standard Model alone without any extensions. This article demonstrates that the Standard Model alone is capable of violating CP symmetry and generating a significant amount of BAU, without introducing any new problems.
In the Standard Model, which has three fermion generations, the matrices have a general pattern of a matrix containing nine elements and eighteen independent parameters, where nine come from real coefficients and nine from imaginary coefficients, assuming that all elements are complex. The ideal solution to the CPV problem is to analytically diagonalize the matrices and use the resulting matrices to generate a complex phase in the CKM matrix, which is defined as a product of two matrices, i.e.,
The diagonalization of the full matrix is a complicated task, which has led physicists to use simplifying assumptions to make progress in their research. These assumptions include symmetries (such as , , etc.), hermiticity, ad hoc zero elements, and others. However, such constraints always reduce the generality of the models, leading to differences between the obtained solutions and reality. The degree of difference between the predicted and observed values depends on the strength of the employed constraints. In other words, models with fewer assumptions are expected to be closer to reality, and the ideal solution is obtained by directly diagonalizing the full matrix.
In some previous research, an symmetry was introduced among three fermion generations in the Standard Model [7,8,22], resulting in an oversimplified pattern with only two parameters per quark type. This simplification was achieved through the invariance of the Lagrangian. However, this model had two degenerate mass eigenvalues and a CP-conserving CKM matrix since both matrices were real. This conflicted with the first necessary condition for obtaining a complex , which requires at least one of the matrices to be complex [9].
To address the mass-degeneracy problem, researchers extended the -symmetric Standard Model with an extra Higgs doublet [4,5], which introduced a third parameter into and resulted in non-degenerate mass eigenvalues. However, this -symmetric 2HDM did not solve the CPV problem, since the and matrices were the same (i.e., ), despite having some complex elements. Although they satisfied the first condition for a complex , as stated in [9], they conflicted with the second condition, which requires . These research studies demonstrated that oversimplified patterns are inadequate for obtaining a satisfactory . Therefore, to achieve a satisfactory solution to the CPV problem, researchers must search for a model with fewer and/or weaker constraints.
The -symmetric Standard Model, as mentioned earlier, oversimplifies the pattern and leads to a CP-conserving , indicating the need for a more complicated pattern with fewer and/or weaker constraints to address the CPV problem. In [9], researchers explored three residual symmetries between two of the three fermion generations, resulting in three additional and patterns, The combination of these extra patterns with the -symmetric one creates an opportunity to satisfy both necessary conditions stated in [9]. Notably, under certain conditions, CP symmetry was explicitly violated, with a Jarlskog invariant of , approximately 5700 times larger than that predicted by the SM.
Originally, the goal of [9] was to find matrix pairs that can be diagonalized simultaneously by the same matrix to address the FCNC problem in the 2HDM. During the derivation, the NFC condition proposed by G. C. Branco [23], , was frequently used. However, researchers found that such matrix pairs could be rearranged as a product of a complex Yukawa-coupling matrix and the VEV of the unique Higgs doublet in the SM, resulting in a Standard Model that violates CP symmetry explicitly. As such, if the SM is sufficient to solve these problems, researchers prefer to study them in the SM rather than in the 2HDM or other new physics.
In subsequent research, the symmetries were further removed, and only two assumptions were kept: the hermiticity of and a common matrix that diagonalizes the real and imaginary parts of simultaneously [12]. In [10], the assumption of the hermiticity of was further removed. The researchers studied a naturally hermitian matrix , where the subindex L denotes left-handed quarks, which has the same matrix as . The only assumption that remained was that the real and imaginary parts of can be diagonalized by the same simultaneously. This solution to the CPV problem is not the ultimate one, but it predicts CKM elements that fit their corresponding empirical values with an accuracy of or better at tree level.
In [10], a very general pattern for the squared mass matrix of quarks, , was given in terms of five parameters: , , , , and , which are composed solely of the Yukawa couplings and the VEV of the SM Higgs doublet, as shown in Equations (6)–(14) of [10]. The pattern is given by:
where is the real part of , and is the imaginary part.
The eigenvalues of this matrix were given analytically by:
The unitary matrix that simultaneously diagonalizes and for up-type quarks is given by:
Both the up-type quark mass matrix and the down-type quark mass matrix exhibit a similar pattern, depending only on two of the five parameters. In the case of , the parameters are denoted by primed symbols: , , , , and . By considering both matrices, a CKM matrix that depends on four parameters—two from up-type quarks and two from down-type quarks—can be obtained. When all the materials mentioned above are collected, it becomes feasible to study how BAU was generated in the Standard Model.
3. Variation of in the Natural Parameters
As mentioned in Section 1, Jarlskog proposed a measure of CPV as given in Equation (1). However, the current value of this quantity is about ten orders of magnitude smaller than what is needed to account for the cosmologically observed BAU. Examining the components of , one can see that it comprises a CKM-related Jarlskog invariant J and two mass-related factors, defined as follows:
If one substitutes the eigenvalues in Equation (5) into Equations (7) and (8), with the assignment and , then Equations (7) and (8) can be expressed in terms of five natural parameters as follows:
However, this is just one of the 36 possible assignments, as there is no inherent reason to associate a particular eigenvalue with a particular quark flavor q, where denotes the eigenvalues and denotes the up-type quark flavors.
By utilizing the mass differences, one can express Equation (1) in terms of these differences as follows:
However, the current value of is at most , which is much smaller than the value required to explain the observed BAU, as discussed in Section 1 and reported in [18].
In the study by [9], it was observed that, in several cases with -symmetry, the value of J was about 5700 times larger than what the Standard Model predicts. Despite such significant enhancements, the resulting value is still insufficient to account for the observed discrepancy in the BAU. It should be noted that the masses of quarks also contribute to , and there are a total of ten free parameters in the equation. However, due to the complexity of the equation, it is too difficult to study it analytically. Therefore, to determine if this model can generate a significant amount of BAU, a simplified example of the parameter sets will be considered.
In [10], the author highlighted the difficulty in assigning which eigenvalue corresponds to which up-type quark flavor . It was noted that there are 36 possible ways to make such assignments, but only eight of them were classified as being of . Furthermore, the author found that only four out of the eight ways were able to fit the empirical CKM elements to an accuracy of or better at the tree level, as shown in Equations (29) and (34)–(37) of that paper.
The four candidate CKM matrices given in Equations (32) and (33) of [10] can be denoted here by:
The numbers in square brackets denote their positions in Table 1 of the same reference, and the matrix elements p, , q, r, and s are also provided in Equations (20)–(24) of the paper. Notably, the value of J for and is the same, and so is the value for and . Additionally, the absolute value of J for and is identical, but with opposite signs, given by:
when , , , and are taken into account.

Table 1.
According to Equations (34)–(37) in [10], there are 32 candidate sets of 10 parameters that yield the same predictions for the CKM elements. These sets satisfy the following values: , , , and .
If one divides each of p, r, and s into its real and imaginary parts as follows: , , and , it is straightforward to show that:
when taking , , , and into account.
By substituting Equations (9), (10), and (15) into Equation (11), one can obtain a comprehensive expression for in terms of 10 natural parameters. The next step involves varying these parameters from their current values to -symmetric values and then comparing the resulting with its current value at every stage of the process.
Afterwards, the derived CKM elements were subjected to several tests by fitting them with empirical data given by [11]:
where is one of the Wolfenstein’s parameters.
Taking the case as an example, it predicts that , , , , , and . Then one may let , , , and run respectively from to to see if there are parameter spaces in which
Among these four equations, Equations (19) and (20) are the most critical. The absolute value of r is expected to lie between the maximum 0.00854 and the minimum 0.00361 of the elements and , while the absolute value of s is expected to lie between the maximum 0.22650 and the minimum 0.03987 of the elements , , , and . Additionally, it would be desirable for them to lie closer to their geometric or arithmetic means, as such degeneracies may split in opposite directions when loop corrections are taken into account. For example, the geometric mean of is , and its arithmetic mean is , while the geometric mean of is , and its arithmetic mean is . Therefore, , , , and will be tested from to to see where the predicted CKM elements fit the empirical values best.
Consequently, 64 sets of , , , and that yield the same values for , , , and are found. Substituting these , , , and values along with the current quark masses into Equation (11) results in 64 sets of , , , , , and values. The quark masses used here are given by:
where are current quark masses for , and b. Using the current values of the CKM matrix elements and quark masses, one obtains a value of approximately for the mass-squared part of Equation (11), denoted as . Such a value will be compared with the corresponding value obtained when the quark masses vary in the natural parameters.
In this way, one obtains 64 sets of , , , , , and values. However, half of them are excluded because some of the masses of down-type quarks are predicted to be imaginary at the -symmetric point = (−1, 1), which is obviously irrational. As a result, only 32 of them are presented in Table 1.
If all 10 parameters vary arbitrarily, it is theoretically always possible to find parameter spaces in which is on the tens order stronger than . However, it is really too arbitrary to have any physical meanings. Thus, assumptions for some of the parameters will be made, and the discussion will concentrate on one very simplified case.
Firstly, it is assumed that , , , , , and are fixed or very slowly varying quantities during the -breaking process to be studied below, so one may use their current values listed in Table 1 in the following calculations. Secondly, it is assumed that the residual symmetries for up- and down-type quarks are not broken down simultaneously, and that it happened among up-type quarks first while the down-type ones still possessed symmetry. As mentioned in [9], there are three -symmetric patterns: , , and . Here, the , or () = (−1, 1), case is selected for an example in the following calculations.
The proposed method for examining parameter spaces for an extremely large is to numerically test the values of and from their -symmetric values () = (−1, 1) to their current values. To quantify the magnitude of in different parameter spaces, the ratio of the running to its current value is defined as:
in which a common factor is canceled out naturally. In this way, putting or into Equation (1) given in Section 1 will not affect the final result at all.
If one examines by letting and run from () = (−1, 1) to their current values given in Table 1, the 3D plots of all 32 candidate sets demonstrate many parameter spaces in which . This means that under such circumstances, CPV could be extremely strong, leading to the generation of a large amount of BAU.
As shown in Figure 1, all 32 3D plots exhibit many areas in which . In some of them, a peak emerging from the green plane near the point () = (−1, 1) is observed. In fact, such a peak always exists in all 32 plots. The reason why one cannot see them in cases 01, 04, 14, and 15 is that they are hidden by the plot ranges of and in the software Wolfram Mathematica. However, if one zooms in on the area around () = (−1,1) as depicted in Figure 2, the peak becomes more noticeable.
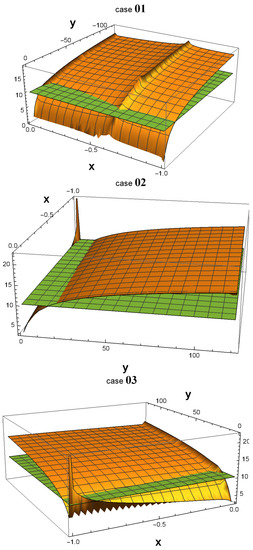
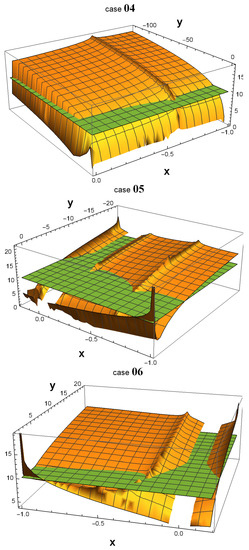
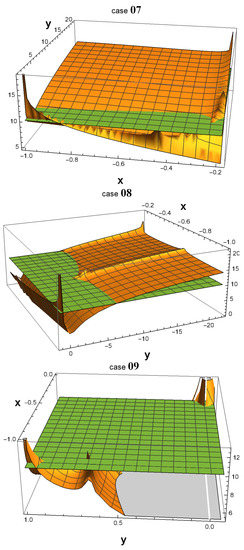
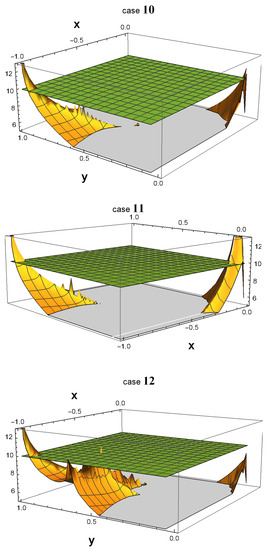
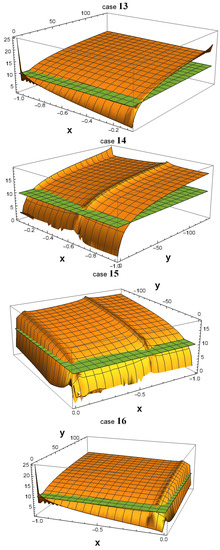
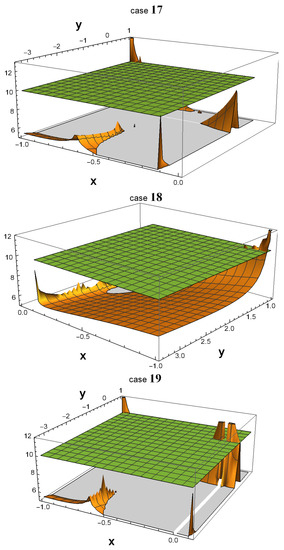
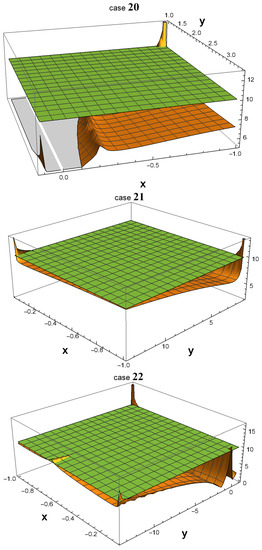
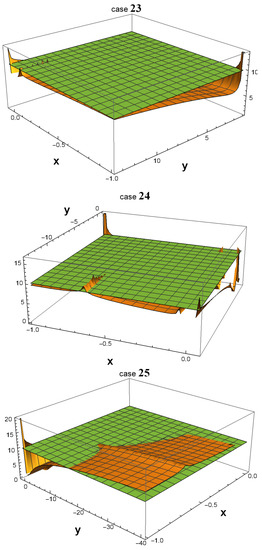
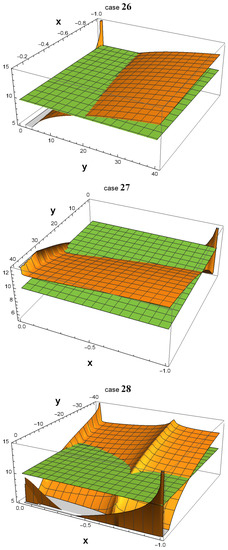
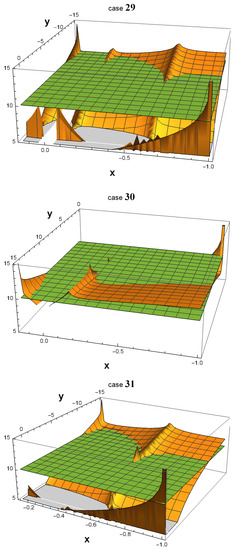
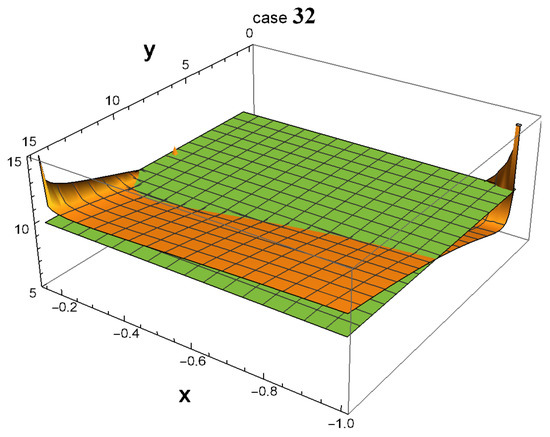
Figure 1.
Using Wolfram Mathematica, 3D plots were generated to depict the values of in the x and y parameter spaces, with the logarithm (base 10) of represented along the z-axis. The parameter ranges from −1 to its current value, as given in Table 1, while ranges from 1 to its current value. Notably, the plots reveal multiple parameter spaces where is significantly greater than , particularly in the vicinity of the point () = (−1, 1). This observation implies that, regardless of the specific scenario that occurred in our universe, there must have been a highly productive era during which the symmetry of down-type quarks was broken.
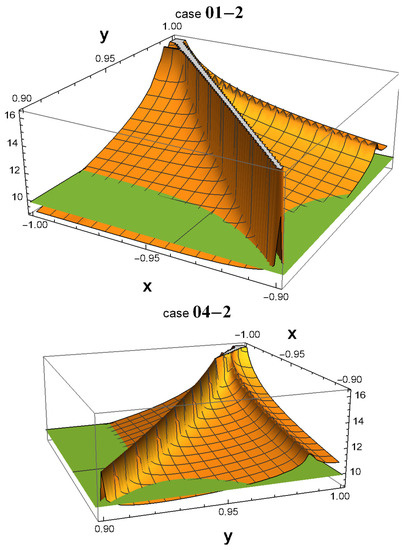
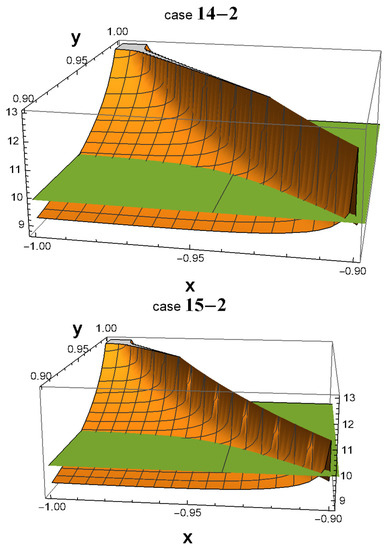
Figure 2.
In cases 01, 04, 14, and 15, the peaks that extend beyond the plane around the point () = (−1, 1) are not particularly conspicuous. To obtain a clearer view, we zoom in on this area in the four corresponding figures.
It is worth noting that in all 32 cases, becomes extremely large, on the order of , as the values of and approach the -symmetric point () = (−1, 1). However, at that exact point, is equal to 0 since , and therefore if one substitutes () = (−1, 1) into Equation (22). This discontinuity at the -symmetric point indicates that is highly sensitive to small variations in the values of and near that point.
To summarize, all 32 cases studied in this article have regions where , indicating the possibility of extremely strong CPV that could generate the observed baryon asymmetry in the universe. These regions are often concentrated around the -symmetric point () = (−1, 1). It is suggested that the evolution of the universe, from a state where both up- and down-type quarks were -symmetric to a state where only the down-type quarks remained -symmetric, may have caused a variation in the strength of CPV. This variation in CPV strength could have been exceptionally strong in certain parameter spaces, resulting in the generation of the observed baryon asymmetry in the universe. It also suggests that CP symmetry can be violated in conjunction with the breakdown of symmetries, at least in the scenario presented in this article. This provides a potential solution to both the CPV problem and the BAU problem without introducing additional complications.
4. Conclusions and Discussions
This article explored the production of the BAU in the SM by studying the Jarlskog measure of CP violation, . Previous research has shown that the SM alone is already enough to ignite CPV explicitly, that the results fit experiments to an accuracy of or better, and that six quark masses were composed of ten natural parameters, while the nine CKM elements were composed of only four of these parameters. These parameters were considered “natural” since they are solely composed of the Yukawa couplings and the vacuum expectation value v. Such a parameterization of the CKM matrix in four parameters is as natural as the Kobayashi–Maskawa parameterization [3] or the standard parameterization [24], which are similar to different coordinate systems in geometry. This provided us with a new perspective to investigate the relationships between the CKM matrix and the Yukawa coupling matrices that was not present in other parameterizations.
By examining 32 sets of , , , and that have the same CKM performances, one can obtain 32 sets of the parameters , , , , , and . In order to investigate their potential for producing BAU, we simplified the problem by assuming that six of the parameters are constants and that two are fixed by assuming an symmetry in the down-quark sector. To measure the performance of in the remaining free parameters and , a ratio was introduced.
Then, and were allowed to vary from the -symmetric point to their current values, and we found regions in all 32 cases where was much larger than , providing evidence that SM alone can produce a significant amount of BAU, at least in the scenario presented in this article. Interestingly, we also observed that in all 32 plots, diverges as the parameters approach the point , where and . This suggests a discontinuity at that point.
It is important to note that, while the investigation presented here is simplified, it still provides valuable insights into the CPV and BAU problems within the SM. Furthermore, the natural parametrization derived here is a significant contribution to the field and can potentially lead to further advancements in this area of research. It is also important to continue exploring other candidate states and further refining the model in order to better understand the complexities of these problems. Ultimately, continued research in this area will help us gain a deeper understanding of the universe and the fundamental processes that govern it.
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
The author would like to thank Hai-Yang Cheng for helpful discussions and suggestions during the revision of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Christenson, J.H.; Cronin, J.; Fitch, V.L.; Turlay, R. Evidence for the 2π Decay of the K02 Meson. Phys. Rev. Lett. 1964, 13, 138. [Google Scholar] [CrossRef]
- Cabibbo, N. Unitary Symmetry and Leptonic Decays. Phys. Rev. Lett. 1963, 10, 531. [Google Scholar] [CrossRef]
- Kobayashi, M.; Maskawa, T. CP-Violation in the Renormalizable Theory of Weak Interaction. Prog. Theor. Phys. 1973, 49, 652–657. [Google Scholar] [CrossRef]
- Lin, C.L.; Lee, C.E.; Yang, Y.W. The Two Higgss-Doublet Extension of the Standard Model and S3 Symmetry. Chin. J. Phys. 1988, 26, 180. [Google Scholar]
- Lee, C.E.; Lin, C.L.; Yang, Y.W. Weak mixing matrix under permutation symmetry breaking. Phys. Rev. D 1990, 42, 2355. [Google Scholar] [CrossRef]
- Lin, C.L.; Lee, C.E.; Yang, Y.W. Feyman rules in the Type III natural flavour-conserving Two-Higgs Doublet Model. Phys. Rev. D 1994, 50, 558–564. [Google Scholar] [CrossRef]
- Lee, C.E.; Yang, Y.W.; Chang, Y.L.; Lai, S.N. Quark Mass Matrix Under SN Symmetry. Chin. J. Phys. 1986, 24, 188. [Google Scholar]
- Lee, C.E.; Yang, Y.W.; Lai, S.N.; Chang, Y.L. Quark Mass Matrix with Non-Hermitian Basis Under SN Symmetry. Chin. J. Phys. 1986, 24, 254. [Google Scholar]
- Lin, C.L. An Improved Standard Model Comes with Explicit CPV and Productive of BAU. J. Mod. Phys. 2020, 11, 1157–1169. [Google Scholar] [CrossRef]
- Lin, C.L. Exploring the Origin of CP Violation in the Standard Model. Lett. High Energy Phys. 2021, 221, 1. [Google Scholar]
- Particle Data Group; Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 8, 083C01. [Google Scholar]
- Lin, C.L. A Two-Higgs-Doublet Model without Flavor-Changing Neutral Currents at Tree-Level. J. Mod. Phys. 2019, 10, 35–42. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astro-Phys. 2014, 571, A16. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astro-Phys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; Limon, M.; Meyer, S.S.; Page, L.; Spergel, D.N.; Tucke, G.S.; et al. First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results. Astrophys. J. Suppl. 2003, 148, 1. [Google Scholar] [CrossRef]
- Jarlskog, C. Commutator of the Quark Mass Matrices in the Standard Electroweak Model and a Measure of Maximal CP Nonconservation. Phys. Rev. Lett. 1985, 55, 1039. [Google Scholar] [CrossRef]
- Tranberg, A. Standard model CP violation and cold electroweak baryogenesis. Phys. Rev. D 2011, 84, 083516. [Google Scholar] [CrossRef]
- Shaposhnikov, M. Possible Appearance of the Baryon Asymmetry of the Universe in an Electroweak Theory. JETP Lett. 1986, 44, 465. [Google Scholar]
- Gavela, M.; Hernansez, P.; Prloff, J.; Pene, O. Standard Model CP-violation and Baryon asymmetry. Mod. Phys. Lett. 1994, A9, 795–810. [Google Scholar]
- Farrar, G.; Shaposhnikov, M. Baryon asymmetry of the Universe in the minimal standard model. Phys. Rev. Lett. 1993, 70, 2833–2836. [Google Scholar] [CrossRef]
- Huet, P.; Sather, E. Electroweak baryogenesis and standard model CP violation. Phys. Rev. D 1995, 51, 379–394. [Google Scholar] [CrossRef] [PubMed]
- Derman, E.; Tsao, H.S. [SU2 × U1] × Sn flavor dynamics and a bound on the number of flavors. Phys. Rev. D 1979, 20, 1207. [Google Scholar] [CrossRef]
- Branco, G.C.; Buras, A.J.; Gerard, J.M. CP violation in models with two- and three-scalar doublets. Nucl. Phys. B 1985, 259, 306. [Google Scholar]
- Chau, L.L.; Keung, W.-Y. Comments on the Parametrization of the Kobayashi-Maskawa Matrix. Phys. Rev. Lett. 1984, 53, 1802. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).