Abstract
The codimension is an important invariant, which measures the complexity of map germs and play an important role in classification and recognition problems. The restricted -equivalence was introduced to obtain a classification of reducible curves. The aim was to classify simple parameterized curves with two components, one of them being smooth with respect to the -equivalence in characteristic p. In characteristic 0, the corresponding classification was given by Kolgushkin and Sadykov. The aim of this article is to present an algorithm to compute the codimension of germs of singularities under a restricted left–right equivalence (-symmetry). We also give the implementation of this algorithm in the computer algebra system singular.
MSC:
58Q05; 14H20
1. Introduction
Let be a field of characteristic 0 and be a map germ. A symmetry of f is a pair , where is a diffeomorphism germ of and is a diffeomorphism germ of , such that the following diagram commutes:
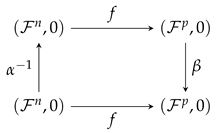
Let , where denotes the local ring of formal power series in m-indeterminates. Consider a local ordering > on and we denote by ≫ the extension of ordering > on , where , and defined as: , if or and .
Let and , where . Define the left–right group . The action of the group on is given as follows:
such that
Any two map germs are said to be -equivalent () if they lie in the same orbit under the group action of . For , the orbit map can be defined as: such that Particularly, The orbit of h under the group action of is the image of ; we set Img. We denote by a tangent space which is the image of the tangent map
to the orbit at h. Note that the orbit map is separable, since char. It is easy to see that
and
Definition 1.
is -finitely determined if there exists a such that for all with , g is in the orbit of f under the action of .
Definition 2.
Let be a subspace of -vector space and a local monomial ordering. A subset is called a standard basis of if . Here, is the vector space generated by the leading monomials of with respect to the ordering >.
In the history of the theory of singularities of map germs, -equivalence has been the most natural equivalence among map germs from the view point of differential topology. Group , the tangent space to the orbit under the action of this group and its codimension play an important role in the classification of map germs (see [1,2,3,4,5,6,7,8,9,10,11,12]). In [13], the authors gave an algorithm to compute the codimension of map germs under an -equivalence. Our aim is to present a similar algorithm, which computes the codimension of map germs under an -equivalence (restricted -equivalence).
2. Computation of Codimension under Restricted Left–Right Action
Let define a germ of a parameterized curve singularity, . Let , and . Let G act on the set by
Definition 3.
Let . They are called -equivalent if they are in the same orbit under the action of G. We write in this case .
Let us consider a special case. Let , , and . Then, if and only if, for suitable ,
Let ; then, we must have and . This implies that the classification of parameterized curves with two components, one of them smooth, is equivalent to the classification of simple irreducible curves with respect to the action of the following group (the action is as above for ) with
In [10,14], the authors introduced a direct and natural generalization of -equivalence denoted by -equivalence, where was a subgroup of . Define the group . The action of the group on is defined as follows:
such that
Any two map germs are said to be -equivalent () if they lie in the same orbit under the group action of .
Example 1.
(1) , therefore and .
(2) since .
(3) since
Proposition 1.
Let and be a subgroup of Aut. The tangent space with respect to the -equivalence is
where Lie denote the Lie algebra associated with group , i.e., Lie.
Proof.
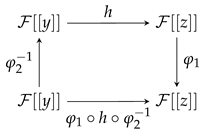
Let
and We have Lie Lie Lie and
Given , we obtain the following commutative diagram:
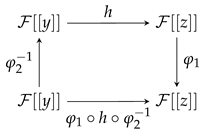
This way, acts on
For , we have the orbit map
defined by
The orbit map induces a map
where Lie Lie and . This gives
Since the characteristic of is zero, the image of is the tangent space to the orbit at f:
□
The following theorem is a generalization of a theorem of Du Plessis [9] (Corollary 3.10) and can be proved similarly to [13].
Theorem 1.
Let and assume that
Then, h is ()-determined and .
The theorem is the basis to pass to ℓ-jets. We assume that h is ℓ-determined and let jet and jet. Then, we have an induced action of on . Moreover, we have
and
Remark 1.
1. If , then , i.e., the right equivalence. In this case, the computation of the codimension of map germs is trivial.
2. If , then , i.e., the left–right equivalence. For this case an algorithm to compute the codimension of map germs can be found in [13].
We consider the following case:
Let then , i.e., the restricted left–right equivalence. This equivalence relation is considered in [15], where it reduces the -classification of simple multigerms into the -classification of irreducible simple germs. In this article, our aim was to give an implementation of an algorithm in the computer algebra system Singular [16] to compute the -codimension of map germs.
Proposition 2.
If , then Lie.
Proof.
If is a subgroup of , then, by definition, Lie, the tangent space of the group at the identity (). If we take any curve in such that , then gives a tangent vector. Thus, for the case , such a curve is of type
with and , if . This gives
Therefore, we obtain the required result. □
Theorem 1 is the basis for the following algorithm (Algorithm 1):
| Algorithm 1 (codim) |
| Input:
and N a -basis of Lie. Output: -codimension of h.
|
Remark 2.
An estimated value for the determinacy of h can be computed by using the code . We compute a standard basis of and check the condition case by case for computing the value of p satisfying . As an initial bound, it uses and the value of the bound q increases as long as the condition has been satisfied. Then, Theorem 1 gives h as -determined.
3. Singular Examples
We give some examples.
ring R=0,t,ds;
> ideal I=t3,t5,t6+t7;
> coDimMap(I);
[1]:
13
[2]:
11
ring R=0,t,ds;
> ideal I=t4,t7+t9,t17;
> coDimMap(I);
[1]:
44
[2]:
37
ring R=0,(x,y),ds;
> ideal I=x,xy+y4;
> coDimMap(I);
[1]:
13
[2]:
3
By using Algorithm 1, we computed the codimension of different map germs. Moreover, Table 1 gives a comparison between the -codimension and -codimension of map germs from the plane to the plane.

Table 1.
A comparison between the -codimension and -codimension of map germs from the plane to the plane.
4. Conclusions
In [13], the authors computed the codimension of map germs with respect to the left–right equivalence and contact equivalence. In this work, we gave an algorithm to compute the codimension of map germs with respect to the restricted left–right equivalence. Moreover, this algorithm was implemented in the computer algebra system singular. In the future, one can find the codimension of map germs with respect to several other equivalence relations, such as the -equivalence.
Author Contributions
Conceptualization, P.X., M.A.B. and A.A.; methodology, M.A.B. and A.A.; validation, P.X., M.A.B. and A.A.; investigation, P.X., M.A.B. and A.A.; writing—original draft preparation, P.X., M.A.B. and A.A.; writing—review and editing, P.X., M.A.B. and A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded in part by the National Natural Science Foundation of China (grant No. 62002079). The research of the second authors is supported by the Higher Education Commission of Pakistan by the project No. 7495/Punjab/NRPU/R&D/HEC/2017.
Data Availability Statement
The code used in this paper can be downloaded from the following link: https://www.mathcity.org/files/ahsan/classifyMapGerms2.txt (accessed on 1 April 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kolgushkin, P.A.; Sadykov, R.R. Simple Singularities of Multigerms of Curves. Rev. Mat. Complut. 2001, 14, 311–344. [Google Scholar] [CrossRef]
- Aslam, S.; Binyamin, M.A.; Pfister, G. Recognition of unimodal map germs from the plane to the plane by invariants. Int. J. Algebra Comput. 2018, 28, 1199–1208. [Google Scholar] [CrossRef]
- Binyamin, M.A.; Mahmood, H.; Kanwal, S. On the classification of simple maps from the plane to the plane. J. Algebra Appl. 2017, 16, 1750199. [Google Scholar] [CrossRef]
- Gaffney, T. The structure of T𝒜f classification and an application to differential geometry, In singularities, Part I, Proceedings of Symposia in Pure Mathematics. Am. Math. Soc. 1983, 40, 409–427. [Google Scholar]
- Kabata, Y. Recognition of plane-to-plane map-germs. Top. Appl. 2016, 202, 216–238. [Google Scholar] [CrossRef]
- Rieger, J.H. Families of maps from the plane to the plane. J. Lond. Math. Soc. 1987, 26, 351–369. [Google Scholar] [CrossRef]
- Rieger, J.H. A-unimodal map-germs into the plane. Hokkaido Math. J. 2004, 33, 47–64. [Google Scholar] [CrossRef]
- Saji, K. Criteria for singularities of smooth maps from the plane into the plane and their applications. Hiroshima Math. J. 2010, 40, 229–239. [Google Scholar] [CrossRef]
- Du Plessis, A. On the Determinancy of Smooth Map Germs. Invent. Math. 1980, 58, 107–160. [Google Scholar] [CrossRef]
- Bruce, J.W.; Krik, N.P.; Du Plessis, A.A. Complete Transversals and the Classification of Singularities. Nonlinearity 1997, 10, 253–275. [Google Scholar] [CrossRef]
- Binyamin, M.A.; Greuel, G.-M.; Mehmood, K.; Pfister, G. Classification of Unimodal Parametric Plane Curve Singularities in Positive Characteristic. arXiv 2023, arXiv:2301.09409. [Google Scholar]
- Binyamin, M.A.; Mehmood, K.; Pfister, G. On the Mond’s Classification of Simple Map Germs from C2 to C3, C.R. Acid. Bulg. Sci. 2021, 74, 1109–1119. [Google Scholar]
- Afzal, D.; Kanwal, S.; Pfister, G. Tangent space of the orbit of an algebraic group action. Bull. Math. Soc. Sci. Roum. 2018, 61, 135–146. [Google Scholar]
- Izymiya, S.; Takahasi, M.; Teramoto, H. Geometric equivalence among smooth map germs. arXiv 2019, arXiv:1908.08232v1. [Google Scholar] [CrossRef]
- Binyamin, M.A.; Mehmood, K.; Pfister, G. Simple Singularities of Reducible Curves in Characteristic p > 0. Commun. Algebra 2022, 50, 1010–1037. [Google Scholar] [CrossRef]
- Decker, W.; Greuel, G.-M.; Pfister, G.; Schönemann, H. SINGULAR 4-1-0—A Computer Algebra System for Polynomial Computations. 2017. Available online: http://www.singular.uni-kl.de (accessed on 30 December 2017).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).