Abstract
This work is dedicated to the investigation of the superradiant stability of a rotating black hole derived from the nonlinear Maxwell theory of gravity, . The evaluation of stability and instability in this study will be based on the absence and presence of the magnetic field, respectively, when the magnetic field constant is and . For the black hole under discussion, analyses of the greybody factors (GFs) and quasi-normal modes (QNMs) are also carried out. To this end, we first consider the Klein–Gordon equation for the scalar waves propagating in the black hole’s geometry. The resulting radial equation is then reduced to a one-dimensional Schrödinger-like wave equation with effective potential energy. The effects of the nonlinear Maxwell gravity theory parameters (q, c, and ) on the effective potential, GFs, and QNMs are examined. The results demonstrate that, although the parameters q, c, and all influence the effective potential, they do not affect the GFs and QNMs. All results are presented and summarized using appropriate graphics and tables.
1. Introduction
Superradiance is a term used to describe a radiation amplification system that involves a scattering mechanism. Superradiance plays a noteworthy role in the study of relativity, astrophysics, quantum mechanics, and optics []. This phenomenon can be considered a quantum aspect of black hole (BH) physics. In the context of quantum gravity phenomenology, superradiance can play a crucial role in the study of BHs. For example, the emission of Hawking radiation (HR) (or thermal/blackbody radiation) [,] from a BH can be enhanced by the presence of surrounding matter, leading to a process known as BH superradiance. This phenomenon has been proposed as a possible explanation for observed properties of BH systems, such as the large amounts of energy emitted from the centers of galaxies. Superradiance is influenced by the BH’s area theorem, tidal forces, the Penrose process, and HR []. The concept of superradiance was first introduced by Dicke in 1954 []. Subsequently, in 1971, Zel’dovich further developed this phenomenon during his investigation of reflected wave amplification from a rotating BH (Kerr metric) [,]. Zel’dovich proved that if the frequency of the ingoing wave with a plane wave structure of (where represents the angular velocity, is the cyclic coordinate and m denotes the magnetic quantum number) satisfies , the scattered waves amplify in such a way that the waves coming out of the BH become stronger than the ones entering it, i.e., the dispersed wave is amplified.
The combination of superradiance with a confining procedure forces waves to consistently interact with a black hole, resulting in an exponential increase known as the “BH bomb” phenomenon []. This active area of study dates back to the 1970s []. One method of inducing instability in the system is by placing a mirror around the rotating body []. In Ref. [], it was suggested that this mirror can be detected by breeding a charged massive scalar field in the Kerr–Newman spacetime. Additionally, spinning black holes can be transformed into efficient particle detectors by imposing strong constraints on ultralight bosons via superradiant instabilities. However, the formation of instability and whether its nonlinear time evolution follows linear intuition remain poorly understood [].
A Kerr black hole (BH) might be thought of as a strong candidate for superradiant phenomena [,,]. However, BHs in the Kerr form do not exhibit superradiant instabilities with significant growth rates [,,,]. In fact, there are various methods for using superradiance to extract energy from BHs, including: (1) BH fission [], (2) BH bombs (as mentioned above) [,], (3) accretion disks and tori [], (4) BH bombs in anti-de Sitter (AdS) spacetime [,], (5) massive fields, soft bombs, and particle physics [,,], (6) floating orbits [], (7) generalized scalar-tensor theories [], and superradiance [,], and (8) ergoregion instability [,]. On the other hand, today there are various theories for modified gravity, such as brane world gravity [], Dvali–Gabadadze–Porrati gravity [], Einstein–Aether theory [,], tensor-vector-scalar theory [], and gravity [,,,], which have all attracted much attention in the literature. theories of gravity are straightforwardly generated by replacing the Ricci scalar R in the Einstein–Hilbert action. Namely, we have a generic action for as follows:
where represents the gravitational constant and g denotes the determinant of metric. Throughout the paper, unless otherwise noted, we shall work in natural units with . Since general relativity (GR) has had many unresolved problems, including the existence of dark energy and dark matter, deflection from Einstein’s theory allows us to estimate the fundamental matters and extension of GR (modified gravity). There are three types of gravity models based on different formalisms: metric, Palatini, and metric-affine [,,]. The use of gravity in many contexts is significant; for example, see its astrophysical perspective in [,,,], the cosmological models with in [,], and the derivations of novel BH solutions in [,,,]. Moreover, we refer the reader to the studies [] for some good reviews about . In particular, spherically symmetric BH solutions in gravity have been receiving special attention (see for instance [], in which the exact static spherically symmetric solutions in gravity coupled with nonlinear electrodynamics derived by Hollestein and Lobo []). Searching for alternative gravitational theories to conventional Einstein’s general relativity (GR) is supported by difficult challenges ranging from quantum gravity to dark energy and dark matter. Indeed, there are a lot of unresolved problems with GR, such as singularities, the nature of dark energy and dark matter. Furthermore, the possibility that gravity can be used to explain cosmic tensions was recently discussed in Ref. []. These challenges motivate researchers to modify GR to address the issues at the UV and IR scales []. However, the obtained feasible modified/extended theories should be consistent with the present observational/experimental restrictions. In light of these challenges, researchers have conducted an ambitious study on the nonlinear Maxwell gravity []. By using dynamical Ricci scalars that asymptotically converge to flat or (A)dS spacetimes, Nashed and Saridakis [] have derived a new charged rotating BH solutions, which will be our main reference metrics in this study.
Due to the quantum effects, a BH can act as a blackbody object, which emits thermal waves [,]. The mass of a BH decreases during its HR, which can lead to complete BH evaporation. As a matter of course, the emitted particles are affected by an effective potential originating from the curvature of the spacetime. As a result, although some waves penetrate the potential barrier and extend to infinity, the remainder are reflected back to the BH. Due to the structure of the effective potential, the radiation spectra are altered and different from those near the event horizon. As a result, the term GF [] refers to a quantity that measures the deviation of the radiation spectrum from the blackbody radiation. At the event horizon, the BH emission rate [] is defined as follows
by which represents the wave frequency, and k denote the Hawking temperature and surface gravity, respectively. The relation between emission rate and GF is given by []
where represents the GF. There are various methods of computing the GF, such as the matching technique [,,], WKB approximation [,,], finding Bogoliubov coefficients method [,,,], the Miller–Good transformation method [,], and rigorous bounds [].
The Teukolsky equation [] describes an oscillation system that naturally dissipates. Such a system generates quasinormal modes (QNMs) instead of the classical normal mode solution. Vishveshwara was the first to identify the QNMs of a black hole (BH) []. The QNMs are described by complex frequencies that carry characteristic information about the BH spacetime, which is in the ringdown phase. The QNMs have a broad literature in BH physics. Specifically, explicit superpositions of QNMs may be utilized to estimate the gravitational wave frequencies in the gravitational wave phenomenon [,,,]. There are many rich and excellent investigations on the QNMs of various solutions of black holes [,,,,], which are considered seminal works of the subject [,,]. In this work, our main motivation is based on the following idea: studying the superradiant instability/stability of a rotating BH in non-linear Maxwell gravity can provide insights into the behavior of black holes in modified gravity theories and deepen our understanding of the interplay between the electromagnetic and gravitational fields in curved spacetimes. Moreover, since the GFs and QNMs are important quantities in the study of BH physics, their analyses can also provide valuable insights into the properties of black holes and their surroundings. Namely, calculating these values in the context of a rotating BH in non-linear Maxwell gravity can assist us in identifying the impacts of curvature modifications on the electromagnetic and gravitational fields, as well as the black hole’s thermal and quantum properties.
The paper is organized as follows: In Section 2, we introduce the metric of the rotating BH in nonlinear Maxwell gravity and demonstrate some of its physical features. Section 3 is devoted to the Klein–Gordon equation (KGE) for charged massive scalar fields in that rotating BH geometry. In this section, we show that the radial wave equation reduces a one-dimensional Schrödinger-like wave equation with a corresponding effective potential. We also study the behaviors of the obtained effective potential under the influence of charge q and magnetic field constant . In Section 4, we examine the superradiant instability for zero and non-zero values. Section 5 and Section 6 are reserved for the analysis of the greybody radiation and QNMs, respectively. Our results are summarized and discussed in Section 7. We follow the metric convention .
2. Rotating BHs in Nonlinear Maxwell Gravity
In this section, we briefly review new static and rotating black hole solutions obtained in nonlinear Maxwell gravity []. The total action for these solutions is given by
where k is a gravitational constant, which can be considered as without loss of generality in this study. Moreover, indicates a general gauge-invariant electromagnetic Lagrangian where the usual antisymmetric Faraday tensor is . represents the determinant of the metric The corresponding gravitational field equations of action (4) can be derived as follows
by which denotes the energy-momentum tensor and . Using the following ansatz for a spherically symmetric line element:
in Equation (5), after making some tedious calculations, the following metric function was finally obtained by Nashed and Saridakis []
where c is a positive constant that takes limited values: . q and M represent the charge and mass, respectively (referr to Ref. [] for details). In Figure 1, we show the behavior of the metric function under the influence of varying parameters q and c. It is evident that the spacetime exhibits flatness at asymptotic distances, irrespective of the values of q and c. In this scenario, the horizon radius can be calculated as follows
Hence, it will be a Schwarzschild black hole if we set and . Furthermore, the extremal limit is given by the following condition,
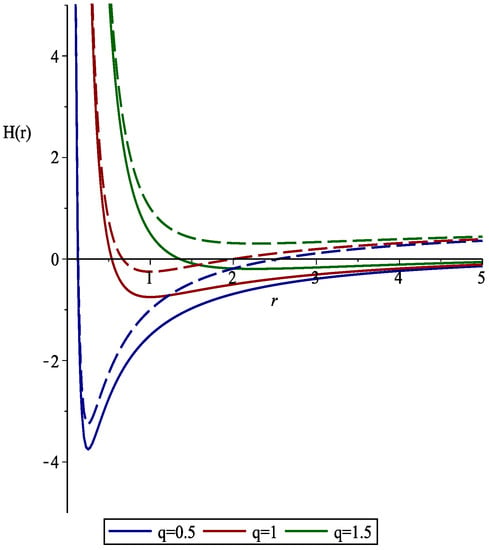
Figure 1.
Schematic plots of versus r. Solid lines represent and dash lines are for The physical parameters are chosen as and .
The rotating version of the BH solution can be derived by applying the following transformations [,]
to the static and spherically symmetric metric (6). In Equation (10), a is the rotating parameter and . Thus, we have
in which is provided by the static solution (7) previously derived. On the other hand, the general gauge potential is defined by []
where , , and are three free functions generating the electric and magnetic charges in the vector potential as follows
in which represents the magnetic field constant. In the following sections, our investigation will consider cases in which the magnetic field constant does not exist () and exists ().
3. Scalar Perturbation
In recent decades, perturbations of black holes and stars have emerged as one of the main topics in relativistic astrophysics. Furthermore, perturbations are currently a hot topic due to their role in gravitational waves. In this section, we use the charged Klein–Gordon equation to derive the one-dimensional Schrödinger wave equation. The effective potential obtained in this section is crucial for studying superradiance, greybody radiation, and QNMs.
Let us consider the charged and massive KGE:
where Q and m are the charge and mass of the scalar field (spin-0), respectively. Moreover, represents the determinant of the metric. Here, for metric (11), we consider the following ansatz for the spinor field
where represents the frequency of the wave and k is azimuthal quantum number. During the derivation of the scalar wave equation, we will consider the dyonic case. Furthermore, we set in Equation (12). Thus, the components of the vector potential read
Throughout the paper, for the sake of convenience in our calculations, and without loss of generality, we will consider . After substituting Equation (16) and the ansatz (15) into the massive charged KGE (14), one can obtain
where is the eigenvalue whose value can be found with the help of the angular part:
In the meantime, throughout the paper, a prime (dash) symbol is used to denote the derivative of a function with respect to its argument. By considering the definition of the tortoise coordinate:
and in the sequel applying the transformation to Equation (18), one can acquire one-dimensional Schrödinger-like wave equation as follows:
in which and the effective potential is given by
The behaviors of the effective potential (21) when the charge parameter q is changed for various values of c are depicted in Figure 2. As can be seen from the figure, potentials have stable minima. It means that the system has reached a state of the lowest possible energy, also known as its ground state. In this state, the system cannot release any further energy as it has already reached its lowest possible energy level. Therefore, in this case, there will not be any accumulation of energy in the system.
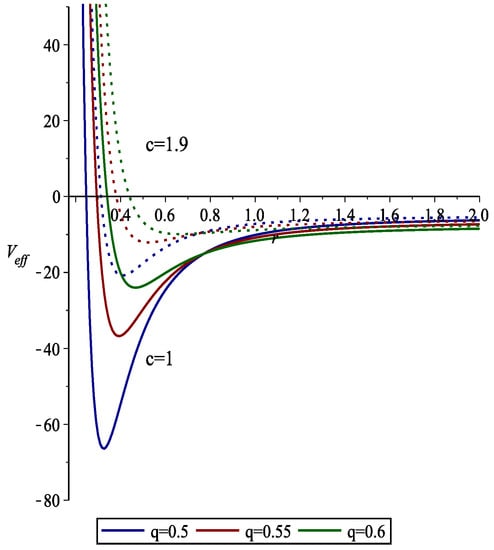
Figure 2.
Plots of versus r for the spin-0 particles in the case of zero magnetic constant. The physical parameters are chosen as; and .
4. Superradiance Phenomenon
4.1. Case of Magnetic Field Absence:
We investigate the stability of a rotating black hole obtained from non-linear Maxwell gravity. To do this, we follow the method described in Refs. [,]. After applying the transformation to the Schrödinger Equation (20), we obtain the following result:
By replacing the tortoise coordinate (19) with the naive radial coordinate r, we obtain
Imposing and , and multiplying Equation (23) by , one can derive the final differential equation by performing the well-known integration by parts method. Thus, we obtain
where the second term of the integrand can be expanded to
Therefore, Equation (24) recasts in
It is also possible to write Equation (26) as
In Equation (27), stands for the potential terms without q parameter in . In addition, it is discovered that the final term of Equation (27) has almost no impact on superradiance calculations and the sign of expression is critical for evaluating the stability of the black hole. Meanwhile, the potential (21) is positive outside the horizon, which means must be negative. Thus, in light of the Dirichlet boundary conditions, one can conclude that the scalar field propagation will be stable. In order to assess the superradiant instability of the rotating black hole in non-linear Maxwell gravity in a more authentic form, we shall define the reflection/transmission coefficients to determine the superradiant condition. To this end, we shall perform our computations in three different regions. The first region (Region I) is the region that is close to the event horizon where the potential is approximated to
and correspondingly
Thus, in Region I, the solution of the radial Equation (20) is obtained as
which is slightly away from the event horizon approximates to []
where the near horizon tortoise coordinate is defined as .
Between the event horizon and the distant regions, Region II acts as an intermediate zone and is defined as:
Therefore, the radial Equation (20) reads
By comparing the solutions in the first and second regions, we define the constants as as and .
To find the solution in Region II, we take into consideration an asymptotic series for tortoise coordinate, i.e., . Hence, we obtain
where
The third region (Region III) is the asymptotic zone (), where the conducting terms of the effective potential become
Thus, one can obtain the Region III solution as
Then, after matching the solution of Region II with the solution of Region III, we obtain
where
The above Dirichlet boundary conditions were applied using information from Chandrasekhar’s famous monograph “Mathematical Theory of Black Holes” [] and references therein. To obtain the reflection coefficient and the GFs, and to complete our assessment of superradiant stability/instability, we employ the following flux expression:
where the * symbol over a quantity denotes the complex conjugation. Therefore, one can obtain the near-horizon flux as
Similarly, the asymptotic flux at spatial infinity becomes
where By considering and , the asymptotic incoming and outgoing fluxes (42) can be written as follows
and
By employing the definition of the reflection coefficient and GF, we obtain
and
Now, based on Equations (45) and (46), we are able to determine the superradiant condition. To this end, either the reflection coefficient should be greater than 1 or the GF should be negative:
By taking into account superradiant instability conditions, in the relevant sub-cases, we now review the behavior of the effective potential in Figure 2. It is obvious from Figure 2 that the potential does not contain wells and hence there are no bound states, which can prevent the accumulation of energy that might cause the instability. This indicates that the rotating BH in non-linear Maxwell gravity can readily absorb the charged scalar wave and whence the associated background becomes stable under the charged scalar perturbations.
4.2. Case of Magnetic Field Presence
In this sub-section, our aim is to evaluate the superradiant stability/instability of the stationary BH found in the non-linear Maxwell gravity with a case of . However, we shall choose the magnetic field constant to be infinitesimally small to facilitate calculations. Moreover, we shall determine the effective potential with the aid of Equation (22), not from the Schrödinger equation as in the previous sub-section. So, following the same steps as earlier, we obtain
where and the effective potential is determined as a complex expression. In Region 3, its real part can be expressed as
and its imaginary part reads
In Equations (49) and (50), the terms including and are ignored. In addition, our analysis has shown us that it is reasonable to consider only the real component of the effective potential.
The wave solutions of Regions 1 and 2 for the existing magnetic fields of the BH are the same as the absent magnetic field cases, Equations (30) and (34), but the wave solution of Region 3 with is different than the one:
where
and is nothing but Equation (29). Comparing Equation (51) with the solution obtained for Region 2 (Equation (34)), one can determine the unknown constants as and
in which
To determine the flux expressions at the horizon and spatial infinity, we apply the same method followed in the previous sub-section. Thus, we have
and
where
By substituting and in Equation (56), one can obtain
Therefore, the reflection coefficient of the rotating BH with small reads
and the corresponding GF becomes
Since the result is almost the same as in Equation (46) and there is no explicit well in the effective potential behavior shown in Figure 3, the interpretation for the stability in the presence of a magnetic field will be similar to that for a nonexistent one.
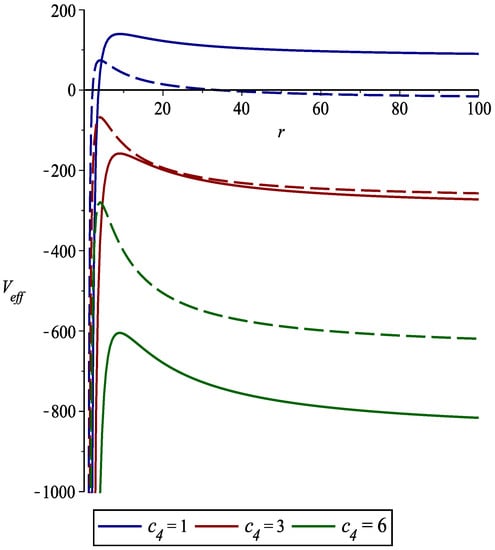
Figure 3.
Plots of versus r for the spin-0 particles and non-zero . The solid lines represent the effective potential for and the dashed ones stand for . The physical parameters are chosen as; and .
5. Semi-Analytical Greybody Radiation
In this section, we shall follow the method which was reviewed in [] (and the references therein) to analyze the greybody radiation for both cases of and .
The general semi-analytic bounds for GFs are given by []
where represents the GF and ℘ is formulated as follows
where h is a positive function that satisfies the following condition: Normally, one follows the method of replacing the V parameter with the potential obtained in Equation (36) and then employs the tortoise coordinate to evaluate the GF (62). On the other hand, that method is not always the best course of action to take. In fact, this method also fails in our situation. So, to overcome this discrepancy, we set in Equation (63). This allows us to rewrite the expression for GF (62) as
which corresponds to
One can immediately observe that Equation (65) is valid for , the peak value of the potential []. Besides, Equation (65) can be rewritten as
To find the maximum or peak of the potential, first, we derive the from the effective potential equations by taking the derivative with respect to r. As is well-known, one should find where the graph shifts from increasing to decreasing. To find out the rate at which the graph shifts from increasing to decreasing, we look at the second derivative and see when the value changes from positive to negative. Depending on the values of , the GFs are obtained. For instance, by setting and , in relation to the variables q and c, the expression is given by
By substituting Equation (67) into Equation (66), we first compute the GFs of the rotating black hole in non-linear Maxwell- gravity with for various values of c and q. The behavior of the obtained GFs for is illustrated in Figure 4. It is worth noting that although c values are constrained to according to Ref. [], we have used values of c above this limit to better reveal differences in GF behavior. This exaggeration is intentional, as the differences in GF behavior are nearly indistinguishable within the theoretical limit of . Figure 4 shows that, with , the GF increases as the c factor increases, but this trend is reversed with increasing charge q.
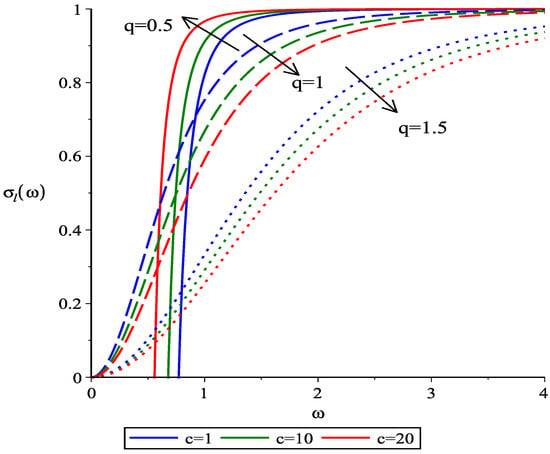
Figure 4.
Plots of versus for scalar particles.The physical parameters are chosen as; and .
In a same circumstance, for an infinitesimal case, the is found to be
where . After substituting Equation (68) in Equation (66), the obtained greybody radiation is depicted in Figure 5, which shows that the greybody radiation explicitly increases with the magnetic field parameter .
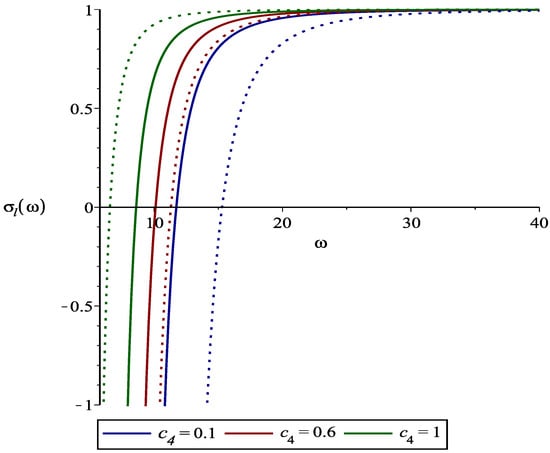
Figure 5.
Plots of versus for scalar particles. The dotted lines are represented for and solid lines for . The physical parameters are chosen as; , and .
6. QNMs
QNMs are important in the study of BH perturbations because they provide a method of understanding the behavior of a BH in the presence of external perturbations, such as scalar, electromagnetic, and gravitational fields. When a BH is perturbed, it responds by emitting gravitational waves with a characteristic frequency known as the QNM. The QNM is determined by the properties of the BH, such as its mass, charge, and spin, and is characterized by complex numbers. The complex frequency of a QNM has a real part that represents the oscillatory frequency of the mode, and an imaginary part that represents the rate of decay or growth of the mode. By observing the QNMs in gravitational waves, we can learn about the physical characteristics of the object that produced the waves.
In this section, for the scalar perturbations, we consider a semi-analytical approach to derive the frequencies of the QNMs of the charged rotating BHs in nonlinear Maxwell gravity. To this end, we employ the WKB (Wentzel–Kramers–Brillouin) approximation, which is a mathematical method used to solve differential Equations (DEs) with a large-scale parameter. This approximation allows for a simplified solution to the differential equation and provides an estimate of the energy levels (frequency) within a certain accuracy. Conventionally, the WKB approach is based on the assumption that the solutions can be expressed as an exponential power series, where the coefficients of the series are determined by solving a set of recursive equations:
The DE has a general form as
where , which contains two turning points. The boundary condition of waves is chosen to be for outgoing waves such as and for incoming waves while First, Mashhoon [] invented this approach and applied it to the BHs in 1983. Then it was developed by [,]. The WKB approximation can be extended from the third to sixth order. The sixth-order WKB approximation, also known as the Konoplya approximation, is a method used to approximate the solutions of differential equations with complex potentials. The sixth-order WKB approximation by Konoplya can be found in his seminal papers [,]. The Konoplya approximation uses a series expansion of the solution to the DE in powers of the small parameter , which is the wavelength of the solution. The Konoplya approximation for obtaining the complex frequencies of the QNMs is given by the following expression []:
where
and
In Equations (71)–(73), the primes and superscripts ( for the higher order derivatives) denote the differentiation with respect to and , where n denotes the tone number. By considering the effective potentials of both solutions, the results are tabulated in Table 1 and Table 2 for the zero and non-zero magnetic field constants, respectively.

Table 1.
Bosonic QNMs of rotating BH in non-linear Maxwell gravity for the zero magnetic field parameter .

Table 2.
Bosonic QNMs of rotating BH in non-linear Maxwell gravity for an infinitesimal magnetic field parameter .
The behaviors of the QNMs for are illustrated in Figure 6. One can observe that both parts (real and imaginary) of the QNMs decrease by increasing the charge parameter, q. Moreover, for , QNMs increase by growing the c parameter and then start to decrease. In addition, when and q increases, the oscillation frequency increases and the damping mode decreases.
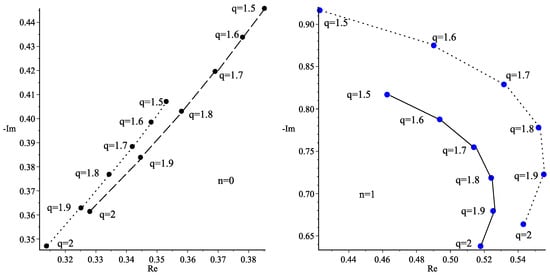
Figure 6.
Plots of QNMs of the rotating BH with under varying charge parameter q. The dotted line represents and the dashed line stands for , both for (left). The solid line is for and the dotted line stands for , both for (right).
On the other hand, for the case of , both parts of the QNMs decrease by increasing the magnetic field constant. The corresponding behaviors are depicted in Figure 7 and Figure 8.
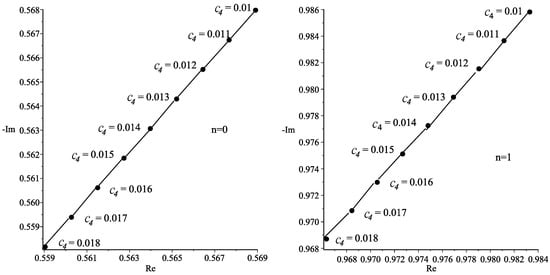
Figure 7.
Plots of QNMs of the rotating BH under varying values and fix charge ; for the tones of (left) and (right).
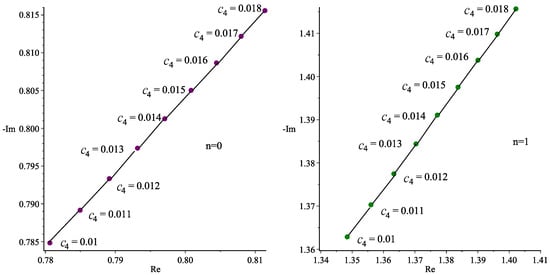
Figure 8.
Plots of QNMs of the rotating BH under varying values and fix charge ; for the tones of (left) and (right).
7. Conclusions
In this paper, we have studied the superradiant instability/stability of a rotating BH in non-linear Maxwell gravity under the influences of q, c, and . To examine the (in)stability in this spacetime under the Dirichlet boundary condition, we have expanded the solutions into three different regions—near the event horizon (Region 1), intermediate (Region 2), and asymptotic (Region 3) regions. We next used the semi-analytic method outlined in Section 5 to determine the GFs of the BH. To this end, we have followed a less problematic method and replaced the expression with Equation (63) to reach Equation (65) or Equation (66). Then by defining the , the GFs of the rotating BH in non-linear Maxwell gravity with/without a magnetic field constant have been computed. The results obtained have been depicted in Figure 4 and Figure 5 to reveal the effects of the q and c parameters on the GFs. The supreme point in the GFs’ behavior belongs to the and thereafter by increasing the values of both c and q the GFs decrease.
To analyze the QNMs originating from the scalar perturbations of the rotating BH in non-linear Maxwell gravity with/without magnetic field constant, we have considered the 6th order WKB approximation or the so-called Konoplya approximation. The results obtained have been both tabulated and illustrated in Figure 7 and Figure 8. Thus, we have shown the influence of q and c parameters on the QNMs. According to the relevant results, the QNMs with the case have more stability than the state. Similar to the real part of the QNMs, which decrease when the charge parameter is increased, the damping rate component (imaginary part) of the QNMs exhibits almost the same behavior, as illustrated in Figure 7 and Figure 8. In addition, the obtained QNMs have been presented in Table 1 and Table 2 under different physical parameter changes which show that the results support Figure 7 and Figure 8.
In our findings, we have discovered that all unstable modes exhibit superradiance and all stable modes do not, consistent with the superradiant condition (47). This means that scalar waves can experience superradiant amplification by extracting charge from the BH, indicating that the BH geometry is unstable. Additionally, superradiance can also be used to probe the fundamental principles of quantum gravity, such as the behavior of quantum particles in the presence of strong gravitational fields, because the strong gravitational field can cause the particles to synchronize their behavior and emit a burst of radiation, which is more intense than the radiation that individual particles would emit. Thus, through the study of superradiance, researchers can gain a better understanding of the interplay between quantum mechanics and general relativity, leading to new insights into the nature of space, time, and gravity. It may be better understood if one considers black hole thermal fluctuations []. Finally, we would like to state that we plan to extend this study to the fermionic perturbations of the rotating BH of the non-linear Maxwell gravity in the near future.
Author Contributions
Conceptualization, İ.S. and S.K.; Methodology, S.K. and İ.S.; Software, S.K. and B.P.; Formal analysis, İ.S., S.K. and B.P.; Investigation, S.K. and İ.S.; Writing—original draft, İ.S. and S.K.; Writing—review and editing, İ.S., S.K. and B.P.; Visualization, B.P.; Supervision, İ.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
We are thankful to the Editor and anonymous Referees for their constructive suggestions and comments. İ.S. would also like to acknowledge COST Action CA18108, TÜBİTAK, and SCOAP3.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Braidotti, M.C.; Faccio, D.; Wright, E.M. Penrose Superradiance in nonlinear optics. Phys. Rev. Lett. 2020, 125, 193902. [Google Scholar] [CrossRef] [PubMed]
- Hawking, S.W. Black hole explosions. Nature 1974, 248, 30. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199, Erratum in Commun. Math. Phys. 1976, 46, 206. [Google Scholar] [CrossRef]
- Mc Caughey, E. Hawking radiation screening and Penrose process shielding in the Kerr black hole. Eur. Phys. J. C 2016, 76, 179. [Google Scholar] [CrossRef]
- Dicke, R. Coherence in spontaneous radiation processes. Phys. Rev. 1954, 93, 99110. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. Generation of waves by a rotating body. Sov. J. Exp. Theor. Phys. Lett. 1971, 14, 180. [Google Scholar]
- Zel’dovich, Y.B. Amplification of cylindrical electromagnetic waves reflected from a rotating body. Sov. J. Exp. Theor. Phys. Lett. 1972, 35, 1085. [Google Scholar]
- Press, W.H.; Teukolsky, S.A. Floating orbits, superradiant scattering and the black-hole bomb. Nature 1972, 238, 211. [Google Scholar] [CrossRef]
- Brito, R.; Cardoso, V.; Pani, P. Superradiance. Lect. Notes Phys. 2015, 906, 1. [Google Scholar]
- Cardoso, V.; Dias, O.J.C.; Lemos, J.P.S.; Yoshida, S. The black hole bomb and superradiant instabilities. Phys. Rev. D 2004, 70, 044039, Erratum in Phys. Rev. D 2004, 70, 049903. [Google Scholar] [CrossRef]
- Damour, T.; Deruelle, N.; Ruffini, R. On quantum resonances in stationary geometries. Lett. Nuovo Cim. 1976, 15, 257. [Google Scholar] [CrossRef]
- Brito, R.; Cardoso, V.; Pani, P. Black holes as particle detectors: Evolution of superradiant instabilities. Class. Quantum Gravity 2015, 32, 134001. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating black holes: Locally nonrotating frames, energy extraction, and scalar synchrotron radiation. Astrophys. J. 1972, 178, 347. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Amplification of waves reflected from a rotating “black hole”. Sov. Phys. JETP 1973, 37, 28. [Google Scholar]
- Teukolsky, S.A.; Press, W.H. Perturbations of a rotating black hole. III. Interaction of the hole with gravitational and electromagnetic radiation. Astrophys. J. 1974, 193, 443. [Google Scholar] [CrossRef]
- Dolan, S.R. Scattering by a draining bathtub vortex. Phys. Rev. D 2013, 87, 124026. [Google Scholar] [CrossRef]
- Xu, J.H.; Zheng, Z.H.; Luo, M.J.; Huang, J.H. Analytic study of superradiant stability of Kerr–Newman black holes under charged massive scalar perturbation. Eur. Phys. J. C 2021, 81, 402. [Google Scholar] [CrossRef]
- Biswas, S. Massive scalar perturbation of extremal rotating braneworld black hole: Superradiant stability analysis. Phys. Lett. B 2021, 820, 136597. [Google Scholar] [CrossRef]
- Brito, R.; Cardoso, V.; Pani, P. Superradiance: New frontiers in black hole physics. Lect. Notes Phys. 2020, 971, 1. [Google Scholar]
- Bekenstein, J.D.; Schiffer, M. The many faces of superradiance. Phys. Rev. D 1998, 58, 064014. [Google Scholar] [CrossRef]
- Cardoso, V.; Dias, O.J.C. Small Kerr-anti-de Sitter black holes are unstable. Phys. Rev. D 2004, 70, 084011. [Google Scholar] [CrossRef]
- Hawking, S.W.; Reall, H.S. Charged and rotating AdS black holes and their CFT duals. Phys. Rev. D 2000, 61, 024014. [Google Scholar] [CrossRef]
- Cardoso, V. Black hole bombs and explosions: From astrophysics to particle physics. Gen. Relativ. Gravit. 2013, 45, 2079. [Google Scholar] [CrossRef]
- Pani, P.; Cardoso, V.; Gualtieri, L.; Berti, E.; Ishibashi, A. Black hole bombs and photon mass bounds. Phys. Rev. Lett. 2012, 109, 131102. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Dubovsky, S. Exploring the string axiverse with precision black hole physics. Phys. Rev. D 2011, 83, 044026. [Google Scholar] [CrossRef]
- Kapadia, S.J.; Kennefick, D.; Glampedakis, K. Do floating orbits in extreme mass ratio binary black holes exist? Phys. Rev. D 2013, 87, 044050. [Google Scholar] [CrossRef]
- Yunes, N.; Pani, P.; Cardoso, V. Gravitational waves from quasicircular extreme mass-ratio inspirals as probes of scalar-tensor theories. Phys. Rev. D 2012, 85, 102003. [Google Scholar] [CrossRef]
- Cardoso, V.; Carucci, I.P.; Pani, P.; Sotiriou, T.P. Matter around Kerr black holes in scalar-tensor theories: Scalarization and superradiant instability. Phys. Rev. D 2013, 88, 044056. [Google Scholar] [CrossRef]
- Friedman, J.L. Ergosphere instability. Commun. Math. Phys. 1978, 63, 243. [Google Scholar] [CrossRef]
- Moschidis, G. A proof of Friedman’s ergosphere instability for scalar waves. Commun. Math. Phys. 2018, 358, 437–520. [Google Scholar] [CrossRef]
- Maartens, R. Brane-world gravity. Living Rev. Relativ. 2004, 7, 7. [Google Scholar] [CrossRef] [PubMed]
- Dvali, G.R.; Gabadadze, G.; Porrati, M. 4D gravity on a brane in 5D Minkowski space. Phys. Lett. B 2000, 485, 208. [Google Scholar] [CrossRef]
- Jacobson, T.; Mattingly, D. Gravity with a dynamical preferred frame. Phys. Rev. D 2001, 64, 024028. [Google Scholar] [CrossRef]
- Pasqua, A.; Gashti, S.N. Einstein-aether scalar-tensor anisotropic constant-roll inflationary scenario in noncommutative phase space. J. Hologr. Appl. Phys. 2022, 2, 63–81. [Google Scholar]
- Bekenstein, J.D. Are there hyperentropic objects? Phys. Rev. D 2004, 70, 083509. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Methods Mod. Phys. 2007, 4, 115. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) theories of gravity. Rev. Mod. Phys. 2010, 82, 451. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) Theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D. Unified cosmic history in modified gravity: From f(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Non-linear Lagrangians and cosmological theory. Mon. Not. R. Astron. Soc. 1970, 150, 1. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Liberati, S. The metric-affine formalism of f(R) gravity. J. Phys. Conf. Ser. 2007, 68, 012022. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Liberati, S. Metric-affine f(R) theories of gravity. Ann. Phys. 2007, 322, 935. [Google Scholar] [CrossRef]
- Frolov, A.V. Singularity Problem with f(R) Models for Dark Energy. Phys. Rev. Lett. 2008, 101, 061103. [Google Scholar] [CrossRef] [PubMed]
- Upadhye, A.; Hu, W. Existence of relativistic stars in f(R) gravity. Phys. Rev. D 2009, 80, 064002. [Google Scholar] [CrossRef]
- Cooney, A.; DeDeo, S.; Psaltis, D. Neutron stars in f(R) gravity with perturbative constraints. Phys. Rev. D 2010, 82, 064033. [Google Scholar] [CrossRef]
- Bamba, K.; Nojiri, S.; Odintsov, S.D. The future of the universe in modified gravitational theories: Approaching a finite-time future singularity. J. Cosmol. Astropart. Phys. 2008, 2008, 045. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Disappearing cosmological constant in f(R) gravity. JETP Lett. 2007, 86, 157. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Transition from a matter-dominated era to a dark energy universe. Phys. Rev. D 2006, 74, 086005. [Google Scholar] [CrossRef]
- Capozziello, S.; Vignolo, S. A comment on “The Cauchy problem of f(R) gravity”. Class. Quantum Gravity 2009, 26, 168001. [Google Scholar] [CrossRef]
- Faraoni, V. Reply to ‘A comment on ‘The Cauchy problem of f(R) gravity’’. Class. Quantum Gravity 2009, 26, 168002. [Google Scholar] [CrossRef]
- Olmo, G.J.; Singh, P. Covariant effective action for loop quantum cosmology à la Palatini. J. Cosmol. Astropart. Phys. 2009, 2009, 030. [Google Scholar] [CrossRef]
- Faraoni, V.; Lanahan-Tremblay, N. Breakdown of the initial value formulation of scalar-tensor gravity and its physical meaning. Phys. Rev. D 2008, 78, 064017. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rep. 2017, 692, 1. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Capozziello, S. Effective field description of the Anton-Schmidt cosmic fluid. Phys. Rev. D 2019, 99, 104018. [Google Scholar] [CrossRef]
- Hollenstein, L.; Lobo, F.S.N. Exact solutions of f(R) gravity coupled to nonlinear electrodynamics. Phys. Rev. D 2008, 78, 124007. [Google Scholar] [CrossRef]
- Bajardi, F.; D’Agostino, R.; Benetti, M.; Falco, V.D.; Capozziello, S. Early and late time cosmology: The f(R) gravity perspective. Eur. Phys. J. Plus 2022, 137, 1239. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended theories of gravity. Phys. Rep. 2011, 509, 167. [Google Scholar] [CrossRef]
- Nashed, G.G.; Saridakis, E.N. Barrow holographic dark energy. Phys. Rev. D 2020, 102, 124072. [Google Scholar] [CrossRef]
- Sakallı, İ.; Kanzi, S. Topical review: Greybody factors and quasinormal modes for black holes in various theories—Fingerprints of invisibles. Turk. J. Phys. 2022, 46, 51. [Google Scholar] [CrossRef]
- Rocha, J.V. Evaporation of large black holes in AdS: Greybody factor and decay rate. J. High Energy Phys. 2009, 2009, 027. [Google Scholar] [CrossRef]
- Harmark, T.; Natario, J.; Schiappa, R. Greybody factors for d-dimensional black holes. Adv. Theor. Math. Phys. 2010, 14, 727. [Google Scholar] [CrossRef]
- Ford, L. Quantization of a scalar field in the Kerr spacetime. Phys. Rev. D 1975, 12, 2963. [Google Scholar] [CrossRef]
- Creek, S.; Efthimiou, O.; Kanti, P.; Tamvakis, K. Greybody factors in a rotating black-hole background: Fermions and gauge bosons. Phys. Rev. D 2007, 76, 104013. [Google Scholar] [CrossRef]
- Iyer, S. Black-hole normal modes: A WKB approach. II. Schwarzschild black holes. Phys. Rev. D 1987, 35, 12. [Google Scholar] [CrossRef] [PubMed]
- Iyer, S.; Will, C.M. Black-hole normal modes: A WKB approach. I. Foundations and application of a higher-order WKB analysis of potential-barrier scattering. Phys. Rev. D 1987, 35, 3621. [Google Scholar] [CrossRef] [PubMed]
- Kanzi, S.; Sakallı, İ. GUP-modified Hawking radiation and transmission/reflection coefficients of rotating polytropic black hole. Eur. Phys. J. Plus 2022, 137, 14. [Google Scholar] [CrossRef]
- Shankaranarayanan, S. Temperature and entropy of Schwarzschild–de Sitter space-time. Phys. Rev. D 2003, 67, 084026. [Google Scholar] [CrossRef]
- Boonserm, P.; Visser, M. Analytic bounds on transmission probabilities. Ann. Phys. 2010, 325, 1328–1339. [Google Scholar] [CrossRef]
- Kanzi, S.; Sakallı, İ. GUP modified Hawking radiation in bumblebee gravity. Nucl. Phys. B 2019, 946, 114703. [Google Scholar] [CrossRef]
- Al-Badawi, A.; Sakallı, İ.; Kanzi, S. Solution of Dirac equation and greybody radiation around a regular Bardeen black hole surrounded by quintessence. Ann. Phys. 2020, 412, 168026. [Google Scholar] [CrossRef]
- Al-Badawi, A.; Kanzi, S.; Sakallı, İ. Effect of quintessence on geodesics and Hawking radiation of Schwarzschild black hole. Eur. Phys. J. Plus 2020, 135, 219. [Google Scholar] [CrossRef]
- Kanzi, S.; Mazharimousavi, S.H.; Sakallı, İ. Greybody factors of black holes in dRGT massive gravity coupled with nonlinear electrodynamics. Ann. Phys. 2020, 422, 168301. [Google Scholar] [CrossRef]
- Teukolsky, S.A. Perturbations of a rotating black hole. I. Fundamental equations for gravitational, electromagnetic, and neutrino-field perturbations. Astrophys. J. 1973, 185, 635–647. [Google Scholar] [CrossRef]
- Vishveshwara, C.V. Scattering of gravitational radiation by a Schwarzschild black-hole. Nature 1970, 227, 936–938. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, V.; Mashhoon, B. New approach to the quasinormal modes of a black hole. Phys. Rev. D 1984, 30, 295–304. [Google Scholar] [CrossRef]
- Horowitz, G.T.; Hubeny, V.E. Quasinormal modes of AdS black holes and the approach to thermal equilibrium. Phys. Rev. D 2000, 62, 024027. [Google Scholar] [CrossRef]
- Berti, E.; Kokkotas, K.D. Quasinormal modes of Reissner–Nordström–anti-de Sitter black holes: Scalar, electromagnetic, and gravitational perturbations. Phys. Rev. D 2003, 67, 064020. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Panotopoulos, G. Electromagnetic quasinormal modes of the nearly-extremal higher-dimensional Schwarzschild–de Sitter black hole. Mod. Phys. Lett. A 2018, 33, 1850130. [Google Scholar] [CrossRef]
- Destounis, K.; Fontana, R.D.B.; Mena, F.C. Accelerating black holes: Quasinormal modes and late-time tails. Phys. Rev. D 2020, 102, 044005. [Google Scholar] [CrossRef]
- Kanzi, S.; Sakallı, İ. Greybody radiation and quasinormal modes of Kerr-like black hole in Bumblebee gravity model. Eur. Phys. J. C 2021, 81, 501. [Google Scholar] [CrossRef]
- Kanzi, S.; Sakallı, İ. Reply to “Comment on ‘Greybody radiation and quasinormal modes of Kerr-like black hole in Bumblebee gravity model’”. Eur. Phys. J. C 2022, 82, 93. [Google Scholar] [CrossRef]
- Kanzi, S.; Alipour, M.R. Quasinormal modes of Dirac particle near Reissner-Nordstrom black hole. J. Hologr. Appl. Phys. 2022, 2, 101–110. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a compact binary coalescence with total mass 3.4M⊙. Astrophys. J. Lett. 2020, 892, L3. [Google Scholar] [CrossRef]
- Berti, E.; Cardoso, V.; Starinets, A.O. Quasinormal modes of black holes and black branes. Class. Quant. Grav. 2009, 26, 163001. [Google Scholar] [CrossRef]
- Konoplya, R.A. Quasinormal modes of a small Schwarzschild–anti-de Sitter black hole. Phys. Rev. D 2002, 66, 044009. [Google Scholar] [CrossRef]
- Lemos, J.P.S. Cylindrical black hole in general relativity. Phys. Lett. B 1995, 353, 46. [Google Scholar] [CrossRef]
- Awad, A.M.; Nashed, G.G.L.; Hanafy, W.E. Rotating charged AdS solutions in quadratic f(T) gravity. Eur. Phys. J. C 2019, 79, 668. [Google Scholar] [CrossRef]
- Gonzales, P.A.; Rincon, A.; Saavedra, J.; Vasquez, Y. Superradiant instability and charged scalar quasinormal modes for (2+1)-dimensional Coulomb-like AdS black holes from nonlinear electrodynamics. Phys. Rev. D 2021, 104, 084047. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: New York, NY, USA, 1983. [Google Scholar]
- Miao, Y.G.; Xu, Z.M. Hawking radiation of five-dimensional charged black holes with scalar fields. Phys. Lett. B 2017, 772, 542. [Google Scholar] [CrossRef]
- Mashhoon, B.B. Proceedings of the Third Marcel Grossmann Meeting on General Relativity; Science Press: North-Holland, The Netherlands, 1983; pp. 599–608. [Google Scholar]
- Konoplya, R.A.; Zhidenko, A.; Zinhailo, A.F. Higher order WKB formula for quasinormal modes and grey-body factors: Recipes for quick and accurate calculations. Class. Quantum Gravity 2019, 36, 155002. [Google Scholar] [CrossRef]
- Upadhyay, S.; ul Islam, N.; Ganai, P.A. A modified thermodynamics of rotating and charged BTZ black hole. J. Hologr. Appl. Phys. 2022, 1, 25–48. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).